Introduction

Ever since the first chaotic attractor was discovered (1963) and the significant work of synchronization was established by Pecora and Carroll [23] (1990), chaos theory and synchronization has invoked huge interest among researchers. The careful modeling of chaotic systems and designing of various control techniques [18] have been done [33] such as active control, sliding mode control, feedback control, adaptive control, tracking control, etc., developing various synchronization schemes such as complete synchronization, anti-synchronization [6, 17], projective synchronization, function projective synchronization, compound synchronization [12], dislocated synchronization [15], and so on [9,10,11, 13, 32, 34].

By synchronization [16], we mean that the trajectories of two different chaotic systems take a common path. Where, on one hand, synchronizing two chaotic systems [7] is in itself a big challenge, to synchronize the different co-ordinates of the systems by different synchronization techniques adds to the complexity of the goal to be attained. Undoubtedly, achieving this modified synchronization [20] would bring nightmares to the hackers as it would be very difficult to predict the order in which different co-ordinates have been synchronized. In other words, anti-attack resistance of systems would increase which would be fruitful in fields of secure communication, data encryption, cryptography, etc. [8, 10, 14, 27,28,29]. Also, with the introduction of fractional-ordered systems [1, 5, 24], more accurate modeling of chaotic systems is possible. One of the reasons of the gaining popularity of fractional-ordered systems is their ability to model memory properties in life models. It is worth noting that most of the published literary work includes the projective matrix as a scalar matrix or a diagonal matrix with constant elements [4]. However, in our work, we have considered the projective matrix as non-diagonal matrix with non-constant, time-variant entries too. Certainly, not much work has been done using difference synchronization [3] which happens to be an alternative to combination synchronization.

The rest of manuscript is laid out as follows: Sect. 2 consists of some preliminaries and stability criterion. Section 3 includes problem formulation of modified fractional and inverse matrices hybrid function projective difference synchronization scheme. In Sect. 4, we have described the systems on which numerical simulations have been performed. Section 5 consists of the discussions on numerical simulations and displays the results performed in MATLAB. Section 6 compares the attained results with some previous published results. Section 7 illustrates the synchronization results in secure communication and Sect. 8 concludes the article.

Preliminaries

Definition

Caputo Definition: [26]

$$\begin{aligned} {}_{a}D_x^{\alpha }g(x)=\frac{1}{\Gamma (n-\alpha )}\int _a^x \frac{g^{(n)} (\tau )\mathrm{{d}}\tau }{(x-\tau )^{\alpha -n+1}}, \end{aligned}$$

where n is integer, \(\alpha\) is real number, \((n-1)\le \alpha < n\), and \(\Gamma (.)\) is the Gamma function.

Throughout our studies, Caputo’s version of fractional derivative has been used.

Stability Criterion

  1. (i)

    Consider the system:

    $$\begin{aligned} _{a}D_t^{q}z_i=h_i(z_1,z_2, \ldots , z_n), 0<q<1,i=1,2, \ldots , \end{aligned}$$

    where \(z_i\) are the variables describing the system, then the system is asymptotically stable at its equilibrium point if all the eigenvalues of the Jacobi matrix \(J=\frac{\partial h_i}{\partial z_i}\) fulfill the criterion \(|\mathrm{{arg}}(\mathrm{{eigen values}})|>\frac{q \pi }{2}\).

  2. (ii)

    Lyapunov Boundedness Theorem: Let V be a function satisfying the following properties:

  3. (a)

    all sublevel sets of V are bounded.

  4. (b)

    \(\dot{V(z)} \le 0 \forall z\). Then, all the trajectories are bounded, i.e., for each trajectory x there is an R, such that:

    $$\begin{aligned} ||x(t)||\le R \forall t \ge 0. \end{aligned}$$

    Here, the function V is the Lyapunov function proving that the trajectories are bounded.

Problem Formulation

We consider two master systems.

Master system I:

$$\begin{aligned} \frac{\mathrm{{D}}^q X}{\mathrm{{D}}t^q}=A_1 X+F_1(X), \end{aligned}$$
(1)

where X is the state vector, \(A_1\) is the coefficient matrix corresponding to the linear part of the first master system, and \(F_1(X)\) is the remaining nonlinear part of the first master system.

Master system II:

$$\begin{aligned} \frac{\mathrm{{D}}^q Y}{\mathrm{{D}}t^q}=A_2 Y+F_2(Y), \end{aligned}$$
(2)

where Y is the state vector, \(A_2\) is the coefficient matrix corresponding to the linear part of the second master system, and \(F_2(Y)\) is the remaining nonlinear part of the second master system. Next, we consider two slave systems.

Slave system I:

$$\begin{aligned} \frac{\mathrm{{D}}^q Z}{\mathrm{{D}}t^q}=B_1 Z+G_1(Z)+U, \end{aligned}$$
(3)

where Z is the state vector, \(B_1\) is the coefficient matrix corresponding to the linear part of the first slave system, \(G_1(Z)\) is the remaining nonlinear part of the first slave system, and U is the controller which is to be constructed.

Slave System II:

$$\begin{aligned} \frac{\mathrm{{D}}^q W}{\mathrm{{D}}t^q}=B_2 W+G_2(W)+V, \end{aligned}$$
(4)

where W is the state vector, \(B_2\) is the coefficient matrix corresponding to the linear part of the second-slave system, \(G_2(W)\) is the remaining nonlinear part of the second-slave system, and V is the controller which is to be constructed.

Modified Fractional Matrix Hybrid Function Projective Difference Synchronization Scheme

We define the modified fractional matrix hybrid function projective difference synchronization error as:

$$\begin{aligned} e=(Z-W)-P(X-Y), \end{aligned}$$
(5)

where P is a non-constant, non-diagonal matrix.

Here, we choose the matrix P, such that the first co-ordinates get completely synchronized, the second co-ordinates get anti-synchronized, the third co-ordinates gets projectively synchronized, the fourth co-ordinates gets function projective anti-synchronized, the fifth and sixth co-ordinates are dislocated (disorderly)synchronized:

$$\begin{aligned} D^{q}e=\,\, & {} (D^{q}Z-D^{q}W)-D^{q}[P(X-Y)]\nonumber \\=\,\, & {} (D^{q}Z-D^{q}(PX))-(D^{q}W-D^{q}(PY)). \end{aligned}$$
(6)

Using (1)–(4) in (5), we get:

$$\begin{aligned}=\,\, & {} [B_1Z+G_1(Z)+U-P.D^{q}X-D^{q}P.X]\nonumber \\&-[B_2W+G_2(W)+V-P.D^{q}Y-D^{q}P.Y]\nonumber \\=\,\, & {} [(B_1Z+G_1(Z)+U)-P(A_1X+F_1(X)-D^{q}P.X)]\nonumber \\&-[(B_2W+G_2(W)+V)-P(A_2Y +F_2(Y)-D^{q}P.Y)]. \end{aligned}$$
(7)

We design the controllers U and V as follows:

$$\begin{aligned} U=\,\, & {} K_1Z-(B_1+K_1)PX+P[A_1X+F_1(X)]\nonumber \\&-G_1(Z)+\mathrm{{D}}^qP.X\nonumber \\ V=\,\, & {} K_2W-(B_2+K_2)PY\nonumber \\&+P[A_2Y+F_2(Y)]-G_2(W)+\mathrm{{D}}^qP.Y \end{aligned}$$
(8)

Substituting (8) into (7),the error dynamics simplifies to:

$$\begin{aligned} (B_1+K_1)(Z-PX)-(B_2+K_2)(W-PY) \end{aligned}$$

Modified Inverse Matrix Hybrid Function Projective Difference Synchronization Scheme

We define the modified inverse matrix hybrid function projective difference synchronization error as:

$$\begin{aligned} e=(X-Y)-P(Z-W), \end{aligned}$$
(9)

where P is a non-constant, non-diagonal matrix.

Here, we choose the matrix P, such that the first co-ordinates get completely synchronized, the second co-ordinates get anti-synchronized, the third co-ordinates get projectively synchronized, the fourth co-ordinates get function projective anti-synchronized [21, 22, 31], and the fifth and sixth co-ordinates are dislocated synchronized:

$$\begin{aligned} D^{q}e=\,\, & {} (D^{q}X-D^{q}Y)-D^{q}[P(Z-W)]\nonumber \\=\,\, & {} (D^{q}X-D^{q}(PZ))-(D^{q}Y-D^{q}(PW)). \end{aligned}$$
(10)

Using (1)–(4) in (5), we get:

$$\begin{aligned}=\,\, & {} [A_1X+F_1(X)-P.D^{q}Z-D^{q}P.Z]\nonumber \\&-[A_2Y+F_2(Y)-P.D^{q}W-D^{q}P.W]\nonumber \\=\,\, & {} [(A_1X+F_1(X))-P(B_1Z+G_1(Z)+U-D^{q}P.Z)]\nonumber \\&-[(A_2Y+F_2(Y))-P(B_2W+G_2(W)-D^{q}P.W)]. \end{aligned}$$
(11)

We design the controllers U and V as follows:

$$\begin{aligned} U=\,\, & {} P^{-1}[(A_1+K_1)PZ-K_1X+F_1(X)-(D^{q}P)Z]-B_1Z-G_1(Z)\nonumber \\ V=\,\, & {} P^{-1}[(A_2+K_2)PW-K_2Y+F_2(Y)-(D^{q}P)W]-B_2W-G_2(W). \end{aligned}$$
(12)

Substituting (12) into (11), the error dynamics simplifies to:

$$\begin{aligned} (A_1+K_1)(X-PZ)-(A_2+K_2)(Y-PW). \end{aligned}$$

System Description

Complex Fractional Rikitake System

The first master system is taken as the complex Rikitake system of fractional order [19] given by:

$$\begin{aligned} \frac{\mathrm{{d}}^q x'_1}{\mathrm{{d}}t^q}=\,\, & {} -ax'_1+x'_2 x'_3\\ \frac{\mathrm{{d}}^q x'_2}{\mathrm{{d}}t^q}=\,\, & {} -ax'_2+x'_1 (x'_3-b)\\ \frac{\mathrm{{d}}^q x'_3}{\mathrm{{d}}t^q}=\,\, & {} 1-x'_1x'_2. \end{aligned}$$

Substituting:

$$\begin{aligned} x'_1=x_1+i x_2, x'_2=x_3+i x_4 ,x'_3=x_5+i x_6. \end{aligned}$$

Segregating the real and imaginary parts, we get:

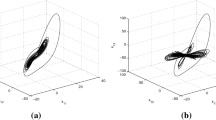
$$\begin{aligned} \frac{\mathrm{{d}}^q x_1}{\mathrm{{d}}t^q}=\,\, & {} -ax_1+x_3 x_5-x_4x_6\nonumber \\ \frac{\mathrm{{d}}^q x_2}{\mathrm{{d}}t^q}=\,\, & {} -ax_2+x_4 x_5+x_3x_6\nonumber \\ \frac{\mathrm{{d}}^q x_3}{\mathrm{{d}}t^q}=\,\, & {} -ax_3+x_1( x_5-b)-x_2x_6\nonumber \\ \frac{\mathrm{{d}}^q x_4}{\mathrm{{d}}t^q}=\,\, & {} -ax_4+x_1 x_6+x_2(x_5-b)\nonumber \\ \frac{\mathrm{{d}}^q x_5}{\mathrm{{d}}t^q}=\,\, & {} 1-x_1x_3+x_2 x_4\nonumber \\ \frac{\mathrm{{d}}^q x_6}{\mathrm{{d}}t^q}=\,\, & {} -x_2 x_3-x_1 x_4. \end{aligned}$$
(13)

The system (13) exhibits chaotic attractor for parameter values a = 5, b = 2, initial conditions (\(-4,-0.7,2.5,0.7,2,0.77\)), and fractional order q = 0.987 (Fig. 1).

Complex Fractional El-Nino System

The second master system is chosen as the complex fractional-order El-Nino system [2] given by:

$$\begin{aligned} \frac{\mathrm{{d}}^q y'_1}{\mathrm{{d}}t^q}=\,\, & {} \mu '(y'_2-y'_3)-b' y'_1\\ \frac{\mathrm{{d}}^q y'_2}{\mathrm{{d}}t^q}=\,\, & {} y'_1y'_3-y'_2+c'y'_1\\ \frac{\mathrm{{d}}^q y'_3}{\mathrm{{d}}t^q}=\,\, & {} -y'_3-c'y'_1\\&-\frac{1}{2}(y'_1 \bar{y'_2}+\bar{y'_1} y'_2). \end{aligned}$$

Substituting:

$$\begin{aligned} y'_1=y_1+i y_2, y'_2=y_3+i y_4 ,y'_3=y_5+i y_6. \end{aligned}$$

Segregating the real and imaginary parts, we get:

$$\begin{aligned} \frac{\mathrm{{d}}^q y_1}{\mathrm{{d}}t^q}=\,\, & {} \mu y_3-\mu y_5-b'y_1\nonumber \\ \frac{\mathrm{{d}}^q y_2}{\mathrm{{d}}t^q}=\,\, & {} \mu y_4-\mu y_6-b'y_2\nonumber \\ \frac{\mathrm{{d}}^q y_3}{\mathrm{{d}}t^q}=\,\, & {} y_1y_5-y_2y_6-y_3+c' y_1\nonumber \\ \frac{\mathrm{{d}}^q y_4}{\mathrm{{d}}t^q}=\,\, & {} y_2y_5+y_1y_6-y_4+c' y_2\nonumber \\ \frac{\mathrm{{d}}^q y_5}{\mathrm{{d}}t^q}=\,\, & {} -y_5-c'y_1-y_1y_3+y_2y_4\nonumber \\ \frac{\mathrm{{d}}^q y_6}{\mathrm{{d}}t^q}=\,\, & {} -y_6-c'y_2-y_2y_3-y_1y_4. \end{aligned}$$
(14)

The system (14) displays chaotic attractor for parameter values \(\mu '=83.6, b'=10, c'=12\), initial conditions (5, 1, 3, 0.4, 4, 0.1), and fractional order q = 0.987.

Complex Fractional Generalized Lotka Volterra System-I

The first slave system is chosen as the complex fractional-order Generalized Lotka Volterra system [25, 30] given by:

$$\begin{aligned} \frac{\mathrm{{d}}^q z'_1}{\mathrm{{d}}t^q}=\,\, & {} z'_1-z'_1z'_2\\&+\bar{c}{z'_1}^2-\bar{a}{z'_1}^2z'_3\\ \frac{\mathrm{{d}}^q z'_2}{\mathrm{{d}}t^q}=\,\, & {} -z'_2\\&+\frac{1}{2}(z'_1 \bar{z'_2}+\bar{z'_1}z'_2)\\ \frac{\mathrm{{d}}^q z'_3}{\mathrm{{d}}t^q}=\,\, & {} -\bar{b}z'_3+\bar{a}{z'_1}^2 z'_3. \end{aligned}$$

Substituting:

$$\begin{aligned} z'_1=z_1+i z_2, z'_2=z_3+i z_4 ,z'_3=z_5+i z_6. \end{aligned}$$

Segregating the real and imaginary parts, we get:

Fig. 1
figure 1

Phase portraits of the complex fractional-order a Rikitake chaotic system, b El-Nino chaotic system, c G.L.V. system-I, and d G.L.V. system-II

Full size image
$$\begin{aligned} \frac{\mathrm{{d}}^q z_1}{\mathrm{{d}}t^q}=\,\, & {} z_1-z_1z_3+z_2z_4\nonumber \\&+\bar{c}{z_1}^2-\bar{c}{z_2}^2\nonumber \\&-\bar{a}{z_1}^2z_5+\bar{a}{z_2}^2 z_5\nonumber \\&+2\bar{a}z_1z_2z_6\nonumber \\ \frac{\mathrm{{d}}^q z_2}{\mathrm{{d}}t^q}=\,\, & {} z_2-z_1z_4-z_2z_3+2\bar{c}{z_1}{z_2}\nonumber \\&-2\bar{a}{z_1z_2z_5}-\bar{a}{z_1}^2z_6\nonumber \\&+\bar{a}{z_2}^2 z_6\nonumber \\ \frac{\mathrm{{d}}^q z_3}{\mathrm{{d}}t^q}=\,\, & {} -z_3+z_1z_3-z_2z_4\nonumber \\ \frac{\mathrm{{d}}^q z_4}{\mathrm{{d}}t^q}=\,\, & {} -z_4+z_2z_3+z_1z_4\nonumber \\ \frac{\mathrm{{d}}^q z_5}{\mathrm{{d}}t^q}=\,\, & {} -\bar{b}z_5+\bar{a}{z_1}^2z_5\nonumber \\&-\bar{a }{z_2}^2z_5-2\bar{a}z_1z_2z_6\nonumber \\ \frac{\mathrm{{d}}^q z_6}{\mathrm{{d}}t^q}=\,\, & {} -\bar{b}z_6+2\bar{a}z_1z_2z_5\nonumber \\&+\bar{a}{z_1}^2z_6-\bar{a }{z_2}^2z_6. \end{aligned}$$
(15)

The system (15) illustrates chaotic attractor for parameter values \(\bar{a}=5.1, \bar{b}=7.4, \bar{c}=20.8\), initial conditions (1.2, 0.112, 1.2, 0, 1.2, 0), and fractional order q = 0.987.

Complex Fractional Generalized Lotka Volterra System-II

The second-slave system is chosen as the complex fractional-order Generalized Lotka Volterra system given by:

$$\begin{aligned} \frac{\mathrm{{d}}^q w'_1}{\mathrm{{d}}t^q}=\,\, & {} w'_1-w'_1w'_2\\&+C{w'_1}^2-A{w'_1}^2w'_3\\ \frac{\mathrm{{d}}^q w'_2}{\mathrm{{d}}t^q}=\,\, & {} -w'_2\\&+\frac{1}{2}(w'_1 \bar{w'_2}+\bar{w'_1}w'_2)\\ \frac{\mathrm{{d}}^q w'_3}{\mathrm{{d}}t^q}=\,\, & {} -Bw'_3+A{w'_1}^2 w'_3. \end{aligned}$$

Substituting:

$$\begin{aligned} w'_1=w_1+i w_2, w'_2=w_3+i w_4 ,w'_3=w_5+i w_6. \end{aligned}$$

Separating into real and imaginary parts, we obtain the system as:

$$\begin{aligned} \frac{\mathrm{{d}}^q w_1}{\mathrm{{d}}t^q}=\,\, & {} w_1-w_1w_3+w_2w_4+C{w_1}^2\nonumber \\&-C{w_2}^2-A{w_1}^2w_5+A{w_2}^2 w_5+2Aw_1w_2w_6\nonumber \\ \frac{\mathrm{{d}}^q w_2}{\mathrm{{d}}t^q}=\,\, & {} w_2-w_1w_4-w_2w_3+2C{w_1}{w_2}-2A{w_1w_2w_5}\nonumber \\&-A{w_1}^2w_6+A{w_2}^2 w_6\nonumber \\ \frac{\mathrm{{d}}^q w_3}{\mathrm{{d}}t^q}=\,\, & {} -w_3+w_1w_3-w_2w_4\nonumber \\ \frac{\mathrm{{d}}^q w_4}{\mathrm{{d}}t^q}=\,\, & {} -w_4+w_2w_3+w_1w_4\nonumber \\ \frac{\mathrm{{d}}^q w_5}{\mathrm{{d}}t^q}=\,\, & {} -Bw_5+A{w_1}^2w_5-A{w_2}^2w_5\nonumber \\&\quad -2Aw_1w_2w_6\nonumber \\ \frac{\mathrm{{d}}^q w_6}{\mathrm{{d}}t^q}=\,\, & {} -Bw_6\nonumber \\&\quad +2Aw_1w_2w_5+A{w_1}^2w_6-A{w_2}^2w_6. \end{aligned}$$
(16)

The plots (16) show chaotic attractor for parameter vales \(A=2.9851, B=3, C=2\), initial conditions (1.2, 0, 1.2, 0, 1.2, 0.112), and fractional order q = 0.987.

Numerical Simulations and Discussion

We consider here the complex fractional Rikitake (13) (the Earth’s magnetic field system) and El-Nino system (14) (the weather system) as the drive system and the complex fractional Generalize Lotka Volterra systems (15) and (16) (the predator–prey system) as the slave systems. The numerical simulations are performed on the above models.

Modified Fractional Matrix Hybrid Function Projective Difference Synchronization Scheme

Taking the projective matrix:

$$\begin{aligned} P=\begin{bmatrix} 1 &{}0&{}0&{}0&{}0&{}0\\ 0 &{} -1 &{} 0 &{}0 &{}0 &{}0\\ 0 &{}0&{}2&{}0&{}0&{}0\\ 0&{}0&{}0&{} -t&{} 0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}1&{}0\\ \end{bmatrix}. \end{aligned}$$

The error from (5) can be described as:

$$\begin{aligned} e_1=\,\, & {} (z_1-w_1)-(x_1-y_1)\\ e_2=\,\, & {} (z_2-w_2)+(x_2-y_2)\\ e_3=\,\, & {} (z_3-w_3)-2(x_3-y_3)\\ e_4=\,\, & {} (z_4-w_4)+t(x_4-y_4)\\ e_5=\,\, & {} (z_5-w_5)-(x_6-y_6)\\ e_6=\,\, & {} (z_6-w_6)-(x_5-y_5). \end{aligned}$$
Fig. 2
figure 2

Modified fractional matrix hybrid function projective difference synchronized trajectories and error plot

Full size image

Then, the error dynamics is:

$$\begin{aligned} D^{q}e_1=\,\, & {} D^{q}z_1-D^{q}w_1-D^{q}x_1+D^{q}y_1\\ D^{q}e_2=\,\, & {} D^{q}z_2-D^{q}w_2+D^{q}x_2-D^{q}y_2\\ D^{q}e_3=\,\, & {} D^{q}z_3-D^{q}w_3-2D^{q}x_3+2D^{q}y_3\\ D^{q}e_4=\,\, & {} D^{q}z_4-D^{q}w_4+D^{q}[t(x_4-y_4)]\\ D^{q}e_5=\,\, & {} D^{q}z_5-D^{q}w_5-D^{q}x_6+D^{q}y_6\\ D^{q}e_6=\,\, & {} D^{q}z_6-D^{q}w_6-D^{q}x_5+D^{q}y_5. \end{aligned}$$

Note:

$$\begin{aligned} D^{q}[t(x_4-y_4)]=D^{q}t.(x_4-y_4)+t(D^{q}x_4-D^{q}y_4) =1.00739t^{.013}x_4-1.00739t^{.013}y_4+tD^{q}x_4-tD^{q}y_4, \end{aligned}$$

Now, choosing suitable controller gain matrix elements:

$$\begin{aligned} k_11=\,\, & {} -5,k_12=-5,k_13=-1,\\ k_14=\,\, & {} -1,k_15=2.4,k_16=2.4\\ k_21=\,\, & {} -5,k_22=-5,k_23=-1,\\ k_24=\,\, & {} -1,k_25=-2,k_26=-2 \end{aligned}$$

and designing controllers as in (8), we have the following:

$$\begin{aligned} u_1=\,\, & {} -5z_1-x_1+x_3x_5-x_4x_6+z_1z_3-z_2z_4-20.8{z_1}^2+20.8{z_2}^2+5.1{z_1}^2z_5-5.1{z_2}^2z_5-10.2z_1z_2z_6\\ u_2=\,\, & {} -5z_2-x_2-x_4x_5-x_3x_6+z_1z_4+z_2z_3-41.6z_1z_2+10.2z_1z_2z_5+5.1{z_1}^2z_6-5.1{z_2}^2z_6\\ u_3=\,\, & {} -z_3+4x_3-4x_1-10x_3-2x_2x_6+2x_1x_5-z_1z_3+z_2z_4\\ u_4=\,\, & {} -z_4+3tx_4-tx_1x_6-tx_2x_5+2tx_2-z_2z_3-z_1z_4-1.00739t^{.013}x_4\\ u_5=\,\, & {} 2.4z_5+5x_6-x_2x_3-x_1x_4-5.1{z_1}^2z_5+5.1{z_2}^2z_5+10.2z_1z_2z_6\\ u_6=\,\, & {} 2.4z_6+5x_5+1-x_1x_3+x_2x_4-10.2z_1z_2z_5-5.1{z_1}^2z_6+5.1{z_2}^2z_6\\ v_1=\,\, & {} -5w_1-6y_1+83.6y_3-83.6y_5+w_1w_3-w_2w_4-2{w_1}^2+2{w_2}^2+2.9851{w_1}^2w_5-2.9851{w_2}^2w_5-5.9702w_1w_2w_6\\ v_2=\,\, & {} -5w_2+6y_2-83.6y_4+83.6y_6+w_1w_4+w_2w_3-4w_1w_2+5.9702w_1w_2w_5\\&+2.9851{w_1}^2w_6-2.9851{w_2}^2w-6\\ v_3=\,\, & {} -w_3+4y_3+24y_1-2y_3+2y_1y_5-2y_2y_6-w_1w_3+w_2w_4\\ v_4=\,\, & {} -w_4-ty_4-ty_2y_5-ty_1y_6-12ty_2-w_2w_3-w_1w_4-1.00739t^{.013}y_4\\ v_5=\,\, & {} -2w_5+4y_6-12y_2-y_2y_3-y_1y_4-2.9851{w_1}^2w_5+2.9851{w_2}^2w_5+5.9702w_1w_2w_6\\ v_6=\,\, & {} -2w_6+4y_5-12y_1-y_1y_3+y_2y_4-5.9702w_1w_2w_5-2.9851{w_1}^2w_6+2.9851{w_2}^2w_6.\\ \end{aligned}$$

Thus, the error dynamics simplifies to:

$$\begin{aligned} D^{q}e_1=\,\, & {} -4e_1\nonumber \\ D^{q}e_2=\,\, & {} -4e_2\nonumber \\ D^{q}e_3=\,\, & {} -2e_3\nonumber \\ D^{q}e_4=\,\, & {} -2e_4\nonumber \\ D^{q}e_5=\,\, & {} -5e_5\nonumber \\ D^{q}e_6=\,\, & {} -5e_6. \end{aligned}$$
(17)

The eigenvalues of the error system (17) are \(-4,-4,-2,-2,-5,-5\) which satisfy the above stability condition (i), i.e., the argument of the obtained eigenvalues satisfies the condition \(|\mathrm{{arg}}(\mathrm{{eigen values}})|>\frac{q \pi }{2}\). Hence, the system is asymptotically stable about its equilibrium point. Also, the error converges to zero, implying that the modified fractional matrix hybrid function projective difference synchronization is achieved.

Simulation Results

The initial conditions of the complex fractional Rikitake system and complex fractional El-Nino system have been taken as (\(-4,-0.7,2.5,0.7,2,0.77\)) and (5, 1, 3, 0.4, 4, 0.1), respectively. Also, the initial conditions for the complex fractional G.L.V.-I and G.L.V.-II have been taken as (1.2, 0.112, 1.2, 0, 1, 2, 0) and (1.2, 0, 1.2, 0, 1.2, 0.112). Thereby, the initial conditions of the Modified Fractional Matrix Hybrid Function Projective Difference Synchronization Error are (\(9,-1.588,1,0,-0.67,1.888\)) for fractional order 0.987. Numerical simulations have been performed in MATLAB. The synchronized trajectories and the simultaneous error plot are displayed in Fig. 2.

Modified Inverse Matrix Hybrid Function Projective Difference Synchronization Scheme

Taking the projective matrix:

$$\begin{aligned} P=\begin{bmatrix} 1 &{}0&{}0&{}0&{}0&{}0\\ 0 &{} -1 &{} 0 &{}0 &{}0 &{}0\\ 0 &{}0&{}2&{}0&{}0&{}0\\ 0&{}0&{}0&{} -e^{t}&{} 0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}1&{}0\\ \end{bmatrix}. \end{aligned}$$

Here, P is an invertible matrix with its inverse as:

$$\begin{aligned} P^{-1}=\begin{bmatrix} 1 &{}0&{}0&{}0&{}0&{}0\\ 0 &{} -1 &{} 0 &{}0 &{}0 &{}0\\ 0 &{}0&{}\frac{1}{2}&{}0&{}0&{}0\\ 0&{}0&{}0&{} -e^{-t}&{} 0&{}0\\ 0&{}0&{}0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0&{}1&{}0\\ \end{bmatrix}. \end{aligned}$$

The error from (9) can be described as:

$$\begin{aligned} e_1=\,\, & {} (x_1-y_1)-(z_1-w_1)\\ e_2=\,\, & {} (x_2-y_2)+(z_2-w_2)\\ e_3=\,\, & {} (x_3-y_3)-2(z_3-w_3)\\ e_4=\,\, & {} (x_4-y_4)+e^{t}(z_4-w_4)\\ e_5=\,\, & {} (x_5-y_5)-(z_6-w_6)\\ e_6=\,\, & {} (x_6-y_6)-(z_5-w_5). \end{aligned}$$
Fig. 3
figure 3

Modified inverse matrix hybrid function projective difference synchronized trajectories and error plot

Full size image

Therefore, the error dynamics so obtained is:

$$\begin{aligned} D^{q}e_1=\,\, & {} D^{q}x_1-D^{q}y_1-D^{q}z_1+D^{q}w_1\\ D^{q}e_2=\,\, & {} D^{q}x_2-D^{q}y_2+D^{q}z_2-D^{q}w_2\\ D^{q}e_3=\,\, & {} D^{q}x_3-D^{q}y_3-2D^{q}z_3+2D^{q}w_3\\ D^{q}e_4=\,\, & {} D^{q}x_4-D^{q}y_4+D^{q}[e^{t}(z_4-w_4)]\\ D^{q}e_5=\,\, & {} D^{q}x_5-D^{q}y_5-D^{q}z_6+D^{q}w_6\\ D^{q}e_6=\,\, & {} D^{q}x_6-D^{q}y_6-D^{q}z_5+D^{q}w_5 \end{aligned}$$

Note:

$$\begin{aligned} D^{q}[e^{t}(x_4-y_4)]=\,\, & {} D^{q}e^{t}.(x_4-y_4)\\&+e^{t}(D^{q}x_4-D^{q}y_4)\\=\,\, & {} e^{t}.(x_4-y_4)+e^{t}(D^{q}x_4-D^{q}y_4). \end{aligned}$$

Now, choosing suitable controller gain matrix elements:

$$\begin{aligned} k_11=\,\, & {} -45,k_12=-45,k_13=-45,\\ k_14=\,\, & {} -46,k_15=-50,k_16=-50\\ k_21=\,\, & {} -40,k_22=-40,k_23=-49,\\ k_24=\,\, & {} -50,k_25=-49,k_26=-49, \end{aligned}$$

and designing controllers as in (12), we have the following:

$$\begin{aligned} u_1=\,\, & {} -51z_1+45x_1+x_3x_5-x_4x_6+z_1z_3-z_2z_4-20.8{z_1}^2\\&+20.8{z_2}^2+5.1{z_1}^2z_5-5.1{z_2}^2z_5-10.2z_1z_2z_6\\ u_2=\,\, & {} -50z_2-45x_2-x_4x_5-x_3x_6-z_2+z_1z_4\\&+z_2z_3-41.6z_1z_2+10.2z_1z_2z_5\\&+5.1{z_1}^2z_6-5.1{z_2}^2z_6\\ u_3=\,\, & {} -z_1-50z_3+\frac{45}{2}x_3+\frac{1}{2}x_1x_5\\&-\frac{1}{2}x_2x_6+z_3-z_1z_3+z_2z_4\\ u_4=\,\, & {} -2e^{-t}z_2-51z_4-45e^{-t}x_4-e^{-t}x_1x_6\\&-e^{-t}x_2x_5+z_4-z_2z_3-z_1z_4\\ u_5=\,\, & {} -42.6z_5+50x_6-x_2x_3-x_1x_4-5.1{z_1}^2z_5\\&+5.1{z_2}^2z_5+10.2z_1z_2z_6\\ u_6=\,\, & {} -42.6z_6+50x_5+1-x_1x_3+x_2x_4-10.2z_1z_2z_5\\&-5.1{z_1}^2z_6+5.1{z_2}^2z_6\\ v_1=\,\, & {} -51w_1+167.2w_3-83.6w_6+40y_1\\&+w_1w_3-w_2w_4-2{w_1}^2+2{w_2}^2\\&+2.9851{w_1}^2w_5-2.9851{w_2}^2w_5-5.9702w_1w_2w_6\\ v_2=\,\, & {} -51w_2+83.6e^{t}w_4+83.6w_5-40y_2+w_1w_4+w_2w_3-4w_1w_2\\&+5.9702w_1w_2w_5+2.9851{w_1}^2w_5-2.9851{w_2}^2w_6\\ v_3=\,\, & {} 6w_1-49w_3+\frac{49}{2}y_3+\frac{1}{2}y_1y_5\\&-\frac{1}{2}y_2y_6-w_1w_3+w_2w_4\\ v_4=\,\, & {} 12e^{-t}w_2-50w_4-49e^{-t}y_4-e^{-t}y_2y_5\\&-e^{-t}y_1y_6-w_2w_3-w_1w_4\\ v_5=\,\, & {} 12w_2-47w_5+49y_6-y_2y_3-y_1y_4-2.9851{w_1}^2w_5\\&+2.9851{w_2}^2w_5+5.9702w_1w_2w_6\\ v_6=\,\, & {} -12w_1-47w_6+49y_5-y_1y_3\\&+y_2y_4-5.9702w_1w_2w_5\\&-2.9851{w_1}^2w_6+2.9851{w_2}^2w_6. \end{aligned}$$

Thus, the error dynamics simplifies to:

$$\begin{aligned} D^{q}e_1=\,\, & {} -50e_1-83.6(y_3-2w_3)+83.6(y_5-w_6))\nonumber \\ D^{q}e_2=\,\, & {} -50e_2-83.6(y_4+e^{t}w_4)+83.6(y_6-w_5)\nonumber \\ D^{q}e_3=\,\, & {} -50e_3-2(x_1-z_1)-12(y_1-w_1)\nonumber \\ D^{q}e_4=\,\, & {} -50e_4-2(x_2+z_2)\nonumber \\&\quad -12(y_2+w_2)-100(y_4+e^{t}w_4)))\nonumber \\ D^{q}e_5=\,\, & {} -50e_5+12(y_1-w_1)\nonumber \\ D^{q}e_6=\,\, & {} -50e_6+12(y_2+w_2). \end{aligned}$$
(18)

We now consider the Lyapunov function:

$$\begin{aligned} V(e(t))=\,\, & {} \frac{1}{2}({e_1}^2+{e_2}^2\\&+{e_3}^2+{e_4}^2+{e_5}^2+{e_6}^2)\\ \Longrightarrow \dot{V(e(t)}=\,\, & {} e_1 \dot{e_1}+e_2 \dot{e_2}+e_3 \dot{e_3}\\&+e_4 \dot{e_4}+e_5 \dot{e_5}+e_6 \dot{e_6}. \end{aligned}$$

Using the error dynamics as in (18), we obtain:

$$\begin{aligned}\le & {} -50 {e_1}^2-50 {e_2}^2-50 {e_3}^2-50 {e_4}^2\\&-50 {e_5}^2-50 {e_6}^2+50|e_1e_3|\\&+50|e_1e_5|+50|e_2e_4|+50|e_2e_6|\\\le & {} -25[{e_1}^2+{e_3}^2-2|e_1e_3|]\\&-25[{e_2}^2+{e_4}^2-2|e_2e_4|]\\&-25[{e_1}^2+{e_5}^2-2|e_1e_5|]\\&-25[{e_2}^2+{e_6}^2-2|e_2e_6|]\\&-25{e_3}^2]-25{e_4}^2]-25{e_5}^2]-25{e_6}^2 \le 0.\\ \end{aligned}$$

Therefore, by Lyapunov Boundedness Theorem, the error becomes bounded.

Simulation Results

The initial conditions for the complex fractional G.L.V.-I and G.L.V.-II have been taken as (1.2, 0.112, 1.2, 0, 1, 2, 0) and (1.2, 0, 1.2, 0, 1.2, 0.112). Also, the initial conditions of the complex fractional Rikitake system and complex fractional El-Nino system have been taken as (\(-4,-0.7,2.5,0.7,2,0.77\)) and (5, 1, 3, 0.4, 4, 0.1), respectively. Therefore, the initial conditions of the modified inverse matrix hybrid function projective difference synchronization error are (\(-9,-1.588,-0.5,0,-1.888,0.67\)) for fractional order 0.987. Numerical simulations have been performed in MATLAB. The synchronized trajectories and the simultaneous error plot are displayed in Fig. 3.

The main disadvantage of the obtained results is the complex nature of the controllers designed. Also in case of Inverse Matrix Hybrid Function Projective Difference Synchronization, the error could only be bounded. Therefore, in future, better controllers can be designed to make the error converge to zero.

Comparison with Previously Published Literature

In [4], Jinman He et al. have studied fractional matrix and inverse matrix projective synchronization between two systems of dimension four. For the case of fractional matrix projective synchronization, they have achieved the errors tending to zero, one at 1 unit and other at 5 units. In our study, while performing the modified fractional matrix hybrid function projective difference synchronization among four chaotic systems of dimension six, we have 4 errors tending to zero at 1 unit and two errors tending to zero at 2 units, respectively. This clearly indicates the efficacy of our designed controllers as on increasing the number of systems, and hence, the complexity the synchronization time is reduced.

The modified fractional inverse matrix hybrid function projective synchronization in our paper has been achieved using Lyapunov Boundedness Theorem, where the constant bounded behavior is achieved after 2 units, whereas in [4], the errors reach zero at 0.1, 1, 1.5, and 5 units, respectively.

Application in Secure Communication

Fig. 4
figure 4

a Original signal. b Transmitted signal. c Recovered signal. d Comparison of the signals

Full size image

Chaos synchronization finds application in various science and engineering fields such as secure communication, control systems, etc. Many synchronization techniques have been developed to increase the diverseness in the possible synchronization schemes applicable. With the increasing cashless economy trend in the countries, the number of online purchases/transactions is increasing without bounds. Therefore, it is the demand of the hour to keep the communicated information safe, i.e., security of transmission of information is must to grow in this direction. The introduced techniques in this paper would strengthen secure communication manifolds as now all the components of the system are differently synchronized, and it is difficult for the hackers to predict the order and type of synchronization applicable to each component of the system.

It is based on the idea of hiding the information signal among the chaotic signals. Then, the original signals are recovered only after performed synchronization.

Illustration Let the information signal be \(r(t)=sin(4t)\). We mix it with the chaotic signals \(x_1(t)-y_1(t)\) and transmit. The recovered signal \(r_1(t)\) is obtained after performing the required synchronization. A comparison of the information signal and recovered signal is also displayed in Fig. 4.

Conclusions

In this paper, modified fractional and inverse matrices hybrid function projective difference synchronization theory has been developed and implemented on a study of bio-diversity. Here, synchronization has been achieved between complex fractional Rikitake system (model for earth’s magnetic field), El-Nino system (weather model), and Generalized Lotka Volterra system (biological predator-prey models). Particularly, the co-ordinates have undergone complete synchronization, anti-synchronization, projective synchronization, function projective anti-synchronization, and dislocated synchronization. These synchronizations methods increases the anti-attack capability in case of secure communications because of random existence of synchronization methods between the components of the system.

This study can also be extended to on systems interrupted by model uncertainties and external disturbances.