1 Introduction

The chaotic behaviour of the dynamic systems can be observed in several real applications in the world, such as circuits, mathematics, power systems, medicine, electrochemical biology, etc. [1,2]. Thus, chaos is one of the most interesting subjects to attract the experts from various fields of science. The fractional calculus was established about 300 years ago. But, its applications in physics and engineering have been studied only in recent decades. Most of the practical and industrial systems could be modelled with fractional-order derivations [3]. Currently, the control and synchronization of chaotic systems is one of the most appealing subject, to many scientists [4]. For instance, in [5], the stabilization of an integrated fractional-order chaos system was studied. In [6], the stabilization of the fractional-order system using the active control method was investigated. In [7], a method for the stabilization of a fractional-order system based on the active sliding mode was presented. In [8], the Routh–Hurwitz method in fractional-order systems was used to synchronize the Duffing–vander Pol fractional-order chaos system. In [9], a smart resistant fractional-order sliding level was determined and the sliding control was studied for a non-linear system. In [10], a new hyperchaotic fractional-order system was presented and the synchronization of a class of non-linear fractional-order systems was considered. In [11], the adaptive sliding mode control for a new class of chaotic fractional-order systems, which are non-deterministic, was proposed. For this aim, the fractional-order derivation was used to produce sliding level. In [12], the scientists analysed the behaviour of fractional-order chaotic systems, investigating the stabilization conditions by using the projective method. In [13], a simple but efficient way to control the fractional-order chaos system, using the TS fuzzy model and adaptive regulation mechanism was presented. In [14], the second-order sliding mode control to stabilize one class of non-deterministic fractional-order system with external disturbances was studied. In [15], an adaptive fractional-order feedback controller to stabilize the chaos systems was presented. Then, a simple but practical method to synchronize the fractional-order chaos system was investigated. In [16], synchronization of chaotic systems based on adaptive fuzzy control was expressed. In [17] adaptive schemes were proposed for the synchronization of the fractional-order chaotic system based on the stability theory of fractional-order systems. In [18], an adaptive synchronization approach for fractional-order chaotic systems with fractional order based on the Mittag–Leffler function and the generalized Gronwall inequality was presented. In [19] an adaptive control law was designed to realize the complex modified projective synchronization (CMPS) for two different types of fractional-order chaotic systems.

In this paper, a fractional-order chaotic system with unknown parameters is considered, for which the adaptive controller is designed. Using the Lyapunov theory and the appropriate adaptive rule, the control rule is proved. The organization of this paper is as follows: In §2, the basic concepts of fractional calculus is presented. In §3, the problem is introduced. Section 4 includes the process of obtaining the adaptive control and the parameter estimation rule to synchronize the fractional-order chaotic system with unknown parameters. In §5, the simulation results of the proposed method are presented. Section 6 contains the conclusion of appropriate performance of this method to synchronize the fractional-order chaotic systems.

2 Mathematical preliminaries

The derivative-integrator operator is represented by \({~}_{a}{D_{t}^{q}} \), which is used to show the fractional derivation and integral operator. For positive values of q, it is a derivation symbol and for negative values of q it turns into an integral symbol. The definitions usually used for the fractional derivation are Grunwald–Letnikov, Riemann–Liouville and Caputo.

$$ {~}_{a}{D_{t}^{q}} =D^{q}=\left\{{\begin{array}{l} {\mathrm{d}^{q}}/{\mathrm{d}t^{q}},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\begin{array}{*{20}c} \hfill & {\,\,\,\,\,\,\,\,\,\,\,q>0} \hfill \end{array}} \\ 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\begin{array}{*{20}c} \hfill & {\,\,\,\,\,\,\,\,\,\,\,\,} \hfill &{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,q=0} \hfill \end{array}} \, \\ {\int\limits_{a}^{t}} {(\mathrm{d}\tau )^{q} \triangleq I^{-q},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\begin{array}{*{20}c} {\,\,\,\,\,\,} \hfill & {q<0} \hfill \end{array}} } \end{array}} \right.. $$
(1)

The second definition of Riemann–Liouville [14] is the definition of RL, which is known as the simplest one as follows:

$$ {~}_{a}{D_{t}^{q}} f(t)=\frac{1}{\Gamma (n-q)}\frac{\mathrm{d}}{\mathrm{d}t}{{\int}_{a}^{t}} {\frac{f(\tau )}{(t-\tau )^{q-n+1}}} \mathrm{d}\tau , $$
(2)

where n − 1< q < n and Γ(⋅) is the gamma function.

According to eqs (1) and (2), the Riemann–Liouville fractional derivative and integral operators of order 0 < q < 1 are defined as

$$D^{q}={~}_{0}{D_{t}^{q}} f(t)=\frac{1}{\Gamma (1-q)}\frac{\mathrm{d}}{\mathrm{d}t}{{\int}_{0}^{t}} {(t-\tau )^{-q}f(\tau){\mathrm{d}}\tau} $$

and

$${~}_{0}{I_{t}^{q}} f(t)=\frac{1}{{\Gamma}(q)}{{\int}_{0}^{t}} {(t-\tau )}{~}^{q-1}f(\tau){{\mathrm{d}}}\tau $$

respectively. From the above definition, note that [3]

$${~}_{0} {D_{t}^{q}} =\frac{\mathrm{d}}{\mathrm{d}t}({~}_{0}I_{t}^{1-q} ). $$

3 Description of the problem

3.1 Designing an adaptive controller for the synchronization of a chaos system

In order to synchronize the behaviour of chaotic system, the Liu system with three degrees of freedom is defined by the following equations [21]:

$$ \left\{ {\begin{array}{l} \dot{x}=a(z-x)\\ \dot{y}=bx-dxz\\ \dot{z}=kxy-cy-gz \end{array}} \right., $$
(3)

where x, y, z are the state variables and a, b, c, d, g, k∈R are the system parameters.

To synchronize two systems, the master system is defined as follows:

$$\begin{array}{@{}rcl@{}} {D_{t}^{q}} x_{1} &=&a({z_{1} -x_{1}}), \\ {D_{t}^{q}} y_{1} &=&bx_{1} -dx_{1} z_{1} , \\ {D_{t}^{q}} z_{1} &=&kx_{1} y_{1} -cy_{1} -gz_{1} , \end{array} $$
(4)

where z 1, y 1, x 1 are the master system variables and q is the order of fractional derivation. The slave system is as follows:

$$\begin{array}{@{}rcl@{}} {D_{t}^{q}} x_{2} &=&a_{1}({z_{2} -x_{2}})+u_{1}(t ), \\ {D_{t}^{q}} y_{2} &=&b_{1} x_{2} -d_{1} x_{2} z_{2} +u_{2}(t), \\ {D_{t}^{q}} z_{2} &=&k_{1} x_{2} y_{2} -c_{1} y_{2} -g_{1} z_{2} +u_{3} (t), \end{array} $$
(5)

where z 2, y 2, x 2 are variables of the slave system, q represents the order of fractional derivation and a 1, b 1, c 1, d 1, g 1, k 1 are the unknown model parameters and the design control signal to synchronize two systems are defined by u 1, u 2, u 3.

The chaotic fractional-order Liu system is analysed and synthesized by an electronic circuit model of mixed shape unit. The components of the realization of chaotic fractional-order Liu system are resistor, capacitance, and operational amplifiers. For more details about the application and realization of chaotic fractional-order Liu system, see [20,22] and references therein.

4 Adaptive controller design

In this section, the synchronization of two chaotic systems with unknown parameters is studied.

Define

$$\begin{array}{@{}rcl@{}} && e_{x} =x_{{2}} -x_{{1}} {;} \quad e_{y} =y_{{2}} -y_{{1}} {;\quad} e_{z} =z_{{2}} -z_{{1}} {;} \quad \tilde{{a}}=a_{{1}} -a;\quad \tilde{{b}}=b_{{1}} -b \\ &&\tilde{{c}}=c_{{1}} -c{;} \quad {{d}}=d_{{1}} -d{;} \quad \tilde{{g}}=g_{{1}} -g{;}\quad \tilde{{k}}=k_{{1}} -k, \end{array} $$
(6)

where a 1,b 1,c 1, d 1, g 1, k 1 are the estimations for the parameters a,b,c,d,g,k.

By subtracting eq. (4) from eq. (5), the error dynamic equation is obtained as follows:

$$\begin{array}{@{}rcl@{}} D^{q}e_{x} &=&a({e_{z} -e_{x}})+\tilde{{a}}({z_{2} -x_{2}})+u_{1} (t), \\ D^{q}e_{y} &=&be_{x} -d({x_{2} z_{2} -x_{1} z_{1}})+\tilde{{b}}x_{2} -\tilde{{d}}x_{2} z_{2} +u_{2}(t), \\ D^{q}e_{z} &=&k({x_{2} y_{2} -x_{1} y_{1}} )-ce_{y} -ge_{z} +\tilde{{k}}x_{2} y_{2} -\tilde{{c}}y_{2} -\tilde{{g}}z_{2} +u_{3}(t ). \end{array} $$
(7)

Theorem 1.

If the control rule is

$$\begin{array}{@{}rcl@{}} u_{1} &=&ae_{x} -ae_{z} -\tilde{{a}}\left( {z_{2} -x_{2}} \right)-A_{1} { I}^{1-q}e_{x} + I^{1-q}\left( {\tilde{{a}}\left( {z_{2} -x_{2}} \right)} \right), \\ u_{2} &=&-be_{x} {}+{}d({x_{2} z_{2} -x_{1} z_{1}}){}-{}\tilde{{b}}x_{2}{}+{}\tilde{{d}}x_{2} z_{2} {}-{}A_{2} I^{1-q}e_{y} {\kern-1.5pt}+{\kern-1.5pt}I^{1-q}(\tilde{{b}}x_{2} {}+{}\tilde{{d}}x_{2} z_{2} ),\\ [5pt] u_{3} &=&-k\left( {x_{2} y_{2} -x_{1} y_{1}} \right)+ce_{y} +ge_{z} -\tilde{{k}}x_{2} y_{2} +\tilde{{c}}y_{2} +\tilde{{g}}z_{2} -A_{3} I^{1-q}e_{z}\\ [4pt] &&+ I^{1-q}(\tilde{{k}}x_{2} y_{2} +\tilde{{c}}y_{2} +\tilde{{g}}z_{2} ) \end{array} $$
(8)

and, the adaptation rules are

$$\begin{array}{@{}rcl@{}} \dot{a}_{1}=e_{x}(x_{2}-z_{2}); \quad\dot{b}_{1}=-e_{y}(x_{2});\quad\dot{c}_{1}=-e_{z}(y_{2}),\\ \dot{d}_{1}=-e_{y}(x_{2}z_{2});\quad\dot{g}_{1}=-e_{z}(z_{2});\quad\dot{k}_{1}=-e_{z}(x_{2}y_{2}), \end{array} $$
(9)

where A 1 , A 2 , A 3 are the positive coefficients, then the states of system in eq. ( 5 ) are asymptotically approximated to the states of system in eq. ( 4 ).

Proof.

To prove the synchronization of two systems in eqs (4) and (5), using the control rule shown in eq. (8) and the parameter updating rule in eq. (9), the stabilization of the system must be investigated. For this, the Lyapunov candidate function should be positive definite with negative definite derivation along the trajectory of the system.

The Lyapunov candidate function is defined as follows:

$$ V=\frac{{1}}{{2}}\left( {{e_{x}^{2}} +{e_{y}^{2}} +{e_{z}^{2}} +\tilde{{a}}^{2}+\tilde{{b}}^{2}+\tilde{{c}}^{2}+\tilde{{d}}^{2}+\tilde{{g}}^{2}+\tilde{{k}}^{2}} \right). $$
(10)

By differentiation from eq. (10), we derive

$$\begin{array}{@{}rcl@{}} \dot{V}&=&e_{x}\dot{e}_{x}+ e_{y}\dot{{e}}_{y} +e_{z} \dot{{e}}_{z} +\dot{{\tilde{{a}}}}\tilde{{a}}+\dot{{\tilde{{b}}}}\tilde{{b}}+\dot{{\tilde{{c}}}}\tilde{{c}}+ \dot{{\tilde{{d}}}}\tilde{{d}}+\dot{{\tilde{{g}}}}\tilde{{g}}+\dot{{\tilde{{k}}}}\tilde{{k}}\\ &=&e_{x} D^{1-q}(D^{q}e_{x} )+e_{y} D^{1-q}(D^{q}e_{y} )+e_{z} D^{1-q}(D^{q}e_{z} )\\ &&+\,\dot{{\tilde{{a}}}}\tilde{{a}}+\dot{{\tilde{{b}}}}\tilde{{b}}+\dot{{\tilde{{c}}}}\tilde{{c}}+\dot{{\tilde{{d}}}}\tilde{{d}}+\dot{{\tilde{{g}}}}\tilde{{g}}+\dot{{\tilde{{k}}}}\tilde{{k}}. \end{array} $$
(11)

Substituting eq. (7) in eq. (11), we have

$$\begin{array}{@{}rcl@{}} &=&e_{x}D^{1-q}(a(e_{z}-e_{x})+\tilde{a}(z_{2}-x_{2})+u_{1}(t))\\ &&+e_{y}D^{1-q}(be_{x}-d(x_{2}z_{2}-x_{1}z_{1})+\tilde{b}x_{2}-\tilde{d}x_{2}z_{2}+u_{2}(t))\\ &&+e_{z}D^{1-q}(k(x_{2}y_{2}-x_{1}y_{1})-ce_{y}-ge_{z}+\tilde{k}x_{2}y_{2}-\tilde{c}y_{2}-\tilde{g}z_{2}+u_{3}(t))\\ &&+\dot{\tilde{a}}\tilde{a}+\dot{\tilde{b}}\tilde{b}+\dot{\tilde{c}}\tilde{c}+\dot{\tilde{d}}\tilde{d}+\dot{\tilde{g}}\tilde{g}+\dot{\tilde{k}}\tilde{k}. \end{array} $$
(12)

The control inputs u 1, u 2, u 3 must be selected, so that the values of V and \(\dot {V}\) are the positive definite and negative respectively. Thus, by substituting u 1, u 2, u 3 from eq. (8) and the parameter estimation rules in eq. (9) into eq. (12), the following relation is achieved:

$$ \dot{V}=-A_{1}e_{x}^{2}-A_{2}e_{y}^{2}-A_{3}e_{z}^{2}<0. $$
(13)

Therefore, the available control rule is shown in eq. (8), the system states in eq. (5) are asymptotically approximated by the system states of eq. (4). □

Remark.

Analysis of stability against noise having master system of eq. (4) and slave system are as follows:

$$\begin{array}{@{}rcl@{}} {D_{t}^{q}} x_{2} &=&a_{1}({z_{2} -x_{2}})+n_{1} (t)+u_{1}(t), \\ {D_{t}^{q}} y_{2} &=&b_{1} x_{2} -d_{1} x_{2} z_{2} +n_{2} (t)+u_{2} \left( t \right), \\ {D_{t}^{q}} z_{2} &=&k_{1} x_{2} y_{2} -c_{1} y_{2} -g_{1} z_{2} +n_{3} (t)+u_{3}(t), \end{array} $$
(14)

where n 1(t), n 2(t), n 3(t) are norm bonded external noise signals. According to the definitions given in eq. (6) and by subtracting eq. (4) from eq. (14), the error dynamic equation is obtained as follows:

$$\begin{array}{@{}rcl@{}} D^{q}e_{x} &=&a({e_{z} -e_{x}})+\tilde{{a}}({z_{2} -x_{2}})+n_{1} (t)+u_{1}(t), \\ D^{q}e_{y} &=&be_{x} -d({x_{2} z_{2} -x_{1} z_{1}})+\tilde{{b}}x_{2} -\tilde{{d}}x_{2} z_{2} +n_{2} (t)+u_{2}(t), \\ D^{q}e_{z} &=&k({x_{2} y_{2} -x_{1} y_{1}}){\kern-1.3pt}-{\kern-1.3pt}ce_{y}{\kern-1.3pt}-{\kern-1.3pt}ge_{z} +\tilde{{k}}x_{2} y_{2}\\ &&-\tilde{{c}}y_{2} -\tilde{{g}}z_{2} +n_{3} (t)+u_{3} (t). \end{array} $$
(15)

Theorem 2.

If the control law is according to eq. (8) with suitable selection of positive coefficients A 1, A 2, A 3 and parameter estimation law is according to eq. (9) then, the states of the system in eq. (14) are approximated asymptotically to the states of system in eq. (4).

Proof.

According to eqs (10), (11), Lyapunov candidate function and differentiation are defined. By the placement of eq. (15) in eq. (11) we have

$$\begin{array}{@{}rcl@{}} \dot{{V}}&=&e_{x} D^{1-q}\left( {a({e_{z} -e_{x}})+\tilde{{a}}({z_{2} -x_{2}})+n_{1} (t)+u_{1} \left( t \right)} \right)\\ &&+e_{y} D^{1-q}\left( {be_{x} -d\left( {x_{2} z_{2} -x_{1} z_{1}} \right)+\tilde{{b}}x_{2} -\tilde{{d}}x_{2} z_{2} +n_{2} {(}t{)}+u_{2} \left( t \right)} \right) \\ &&+e_{z} D^{1-q}{}\left( {\kern-1.3pt}k({x_{2} y_{2} {\kern-1.3pt}-{\kern-1.3pt}x_{1} y_{1}} ){\kern-1.3pt}-{\kern-1.3pt}ce_{y} {\kern-1.3pt}-{\kern-1.3pt}ge_{z} {\kern-1.3pt}+{\kern-1.3pt}\tilde{{k}}x_{2} y_{2} {\kern-1.3pt}-{\kern-1.3pt}\tilde{{c}}y_{2} {\kern-1.3pt}-{\kern-1.3pt}\tilde{{g}}z_{2}{\kern-1.3pt}+{\kern-1.3pt}n_{3} (t){\kern-1.3pt}+{\kern-1.3pt}u_{3}(t)\right)\\ &&+\dot{{\tilde{{a}}}}\tilde{{a}}+\dot{{\tilde{{b}}}}\tilde{{b}}+\dot{{\tilde{{c}}}}\tilde{{c}}+\dot{{\tilde{{d}}}}\tilde{{d}}+\dot{{\tilde{{g}}}}\tilde{{g}}+\dot{{\tilde{{k}}}}\tilde{{k}}. \end{array} $$
(16)

If the following conditions are satisfied with suitable selection of positive coefficients A 1, A 2, A 3 by substituting u 1, u 2, u 3 from eq. (8) and the parameters estimation rules in eq. (9) into eq. (16),

$$\begin{array}{@{}rcl@{}} \left\| {A_{1} e_{x}} \right\|&>&\left\| {D^{1-q}n_{1} (t)} \right\|\Rightarrow \left\| {A_{1}} \right\|>\frac{\left\| {D^{1-q}n_{1} (t)} \right\|}{\left\| {e_{x}} \right\|}, \\ \left\| {A_{2} e_{y}} \right\|&>&\left\| {D^{1-q}n_{2} (t)} \right\|\Rightarrow \left\| {A_{2}} \right\|>\frac{\left\| {D^{1-q}n_{2} (t)} \right\|}{\left\| {e_{y}} \right\|}, \\ \left\| {A_{3} e_{z}} \right\|&>&\left\| {D^{1-q}n_{3} (t)} \right\|\Rightarrow \left\| {A_{3}} \right\|>\frac{\left\| {D^{1-q}n_{3} (t)} \right\|}{\left\| {e_{z}} \right\|}. \end{array} $$
(17)

Then, the inequality (13) holds. □

5 Numerical simulations

In this section, the efficiency of our proposed method is assessed. The simulation results are performed on the synchronization of Liu-fractional chaotic systems with different initial states. In this simulation, the sampling time and the order of fractional derivation are defined as h = 0.001 and q = 0.98 respectively. The initial states are as follows:

$$[d^{q-1}x_{1} (0),\,d^{q-1}y_{1} (0),\,d^{q-1}z_{1} (0)]^{T}=[0.5,\,0.5,\,0.5]^{T}, $$
$$[d^{q-1}x_{2} (0),\,d^{q-1}y_{2} (0),\,d^{q-1}z_{2} (0)]^{T}=[1,\,1,\,1]^{T}. $$

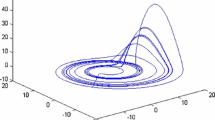
For some specific values of a, b, c, d, g, k, the system identified with eq. (3) is converted to be a chaotic system whose behaviour for a = 8, b = 40, c = 10/3, d = 1, g = 4, k = 1 are illustrated in figures 1 Footnote 1. In addition, its chaotic behaviour and butterfly effect treatment are depicted in the same figure. In figure 2, the synchronization performance of fractional-order chaotic systems in eqs (4) and (5) are presented for all possible states. From figure 3, it is evident that the synchronization error converges to zero. In figure 4, the control signal for three states is plotted.

6 Conclusion

In this paper, the synchronization issue of fractional-order chaotic systems using the adaptive control method has been investigated. According to the stabilization theory of Lyapunov and the adaptive control theory, a controller was designed to stabilize and synchronize fractional-order chaotic systems. In addition to an adaptive control rule, the synchronization rule for unknown parameters of the system was also presented. Finally, the simulation results demonstrated the appropriate performance of this method in order to synchronize the fractional-order chaotic systems.