1 Introduction

In the present paper, we shall consider the \((2+1)\)-dimensional generalized Kadomtsev–Petviashvili equation (\((2+1)\)-dimensional GKPE) [1] as follows:

$$\begin{aligned} (u_{t}+cuu_{x}+bu_{xxx})_x+\frac{c_{0}}{2}u_{yy}=0, \end{aligned}$$
(1)

where \(u=u(x,y,t)\) denotes a scalar function of the space variables x, y,  and time variable t, the parameters c is the nonlinear term coefficient, b is the dispersion coefficient along the x-axis, \(c_{0}\) is the velocity of the linear wave, and \({c_{0}}/{2}\) is the dispersion coefficient along the y-axis. It is worth noting that eq. (1) is sometimes referred to as the KP(II) equation or negative dispersion KP equation in y direction. If \({(c_{0}}/{2})u_{yy}\) is replaced by \(-({c_{0}}/{2})u_{yy}\) in eq. (1), then eq. (1) is called the KP(I) equation or positive dispersion KP equation in y direction. We know that the \((2+1)\)-dimensional KP equation can be used to model water waves of long wavelength with weakly nonlinear restoring forces and frequency dispersion. In recent years, some researchers have done a lot of research on \((2+1)\)-dimensional KP equation by different methods [2,3,4,5,6,7,8,9,10,11,12,13], and have obtained many useful conclusions.

When \(c=6, b=1\) and \(({c_{0}}/{2})=-1\), eq. (1) is reduced to the equation

$$\begin{aligned} u_{xt}+6(uu_{x})_{x}+u_{xxxx}-u_{yy}=0. \end{aligned}$$
(2)

Xu et al [3] obtained two-wave solution and rational breather-wave solution (also known as rogue wave solution) of eq. (2) by using the homoclinic (heteroclinic) breather limit method (HBLM). Ma [4] studied a class of lump solution of eq. (2) by selecting a special quadratic function with Hirota’s bilinear form, and they also analysed the rational localization of the lump solutions of eq. (2).

When \(c=-6, b=-1\) and \(({c_{0}}/{2})=\pm 3\), eq. (1) is reduced to equation

$$\begin{aligned} u_{xt}-3(u^2)_{xx}-u_{xxxx}\pm 3u_{yy}=0. \end{aligned}$$
(3)

Dai et al [5] obtained exact periodic soliton solution of eq. (3) by using the two-soliton and generalized Hirota methods. Guo and Ling [6] studied rogue wave solutions (lump solutions) and high-order lump solutions of eq. (3) by using generalized binary Darboux transformation method.

There are some distinct versions of the KP equation. When \(c=6, b=1\) and \(({c_{0}}/{2})=\pm 3\) in eq. (1), we can get the following normalized form:

$$\begin{aligned} (u_{t}+6uu_x+u_{xxx})_{x}\pm 3u_{yy}=0. \end{aligned}$$
(4)

Wang and Dai [7] obtained breather-type multisolitary wave solution with fission and fusion behaviours of eq. (4) by using Hirota’s bilinear method and generalized three-wave type of ansatz approach. Zha and Li [8] discussed N periodic-soliton solutions and 2N line-soliton solutions using Hirota’s bilinear method.

When \(c=6, b=1\) and \(({c_{0}}/{2})=0\), eq. (1) is reduced to the famous Korteweg–de Vries (KdV) equation

$$\begin{aligned} u_{t}+6(uu_{x})+u_{xxx}=0. \end{aligned}$$
(5)

Dai et al [9] obtained exact periodic solitary-wave solution of eq. (5) by using the extended homoclinic test technique. Sun et al [10] obtained blow-up solutions and non-singular solutions using a complex Miura transformation and Darboux transformation method.

Soliton solution of nonlinear partial differential equation (NLPDEs) play a very important role in nonlinear science fields such as nonlinear optics, thermodynamics, fluid dynamics, solid-state physics, etc. They can provide more information and more physical insight into the nonlinear aspects problems, which lead to further applications [14,15,16,17,18,19]. Therefore, the research and investigation of soliton solution for NLPDEs has become more and more important and attractive. Numerous methods have been proposed to obtain soliton solutions of NLPDEs [20,21,22,23]. Lump solution, also called the vortex and antivortex solution, is a specific type of soliton solution, and was introduced in 1976 by Zakharov [24] and later by Craik [25]. In contrast to other forms of soliton solutions, lump solution is a kind of rational function solution, decayed polynomially in all directions in the space. Very recently, lump solutions were presented for many nonlinear systems [26,27,28,29,30]. In this paper, a periodic breather-wave solution is obtained via Hirota’s bilinear method and homoclinic test technique [31] with a small perturbation parameter \(u_{0}\), and a lump solution based on periodic breather-wave solution is studied by a limit behaviour. More importantly, we have also discussed that the space–time structure changes of lump solution not only depends on the small perturbation parameter \(u_{0}\), but also has a relationship with the nonlinear term coefficient c, dispersion coefficient b, linear wave speed \(c_{0}\) and some other parameter. By changing the values of these parameters (\(u_{0},b, c, c_{0},\alpha , \alpha _{1}\)), we obtain a lump solution of three different forms of the space–time structures: bright lump structure, dark lump structure and linear lump structure. Finally, the mathematical reason of different space–time structures are analysed using the extreme value theory of multivariate function. Some new and interesting phenomena of the lump solution are discovered.

2 The emergence of lump solution

In eq. (2), Xu and his collaborators are using a transformation \(\xi =x+t\) to reduce the \((2+1)\)-dimensional KP equation to the \((1+1)\)-dimensional NLPDEs. Some two-wave solution and rational breather wave solution are derived by the application of the HBLM with bilinear form of \((1+1)\)-dimensional equation [3]. Here, a periodic breather-wave solution and a lump solution which is different from the paper [3, 4] for \((2+1)\)-dimensional GKPE are obtained using extended homoclinic test approach [32] and Hirota’s bilinear method. It is easy to note that \(u=u_{0}\) is a seed solution of eq. (1), where \(u_{0}\) is a free real number. Therefore, by Painlevé analysis, we assume that the solution of eq. (1) takes the form

$$\begin{aligned} u(x,y,t)=u_{0}+\frac{12b}{c}(\mathrm {ln}\,f)_{xx}, \end{aligned}$$
(6)

where f(x, y, t) is an unknown real function which will be selected later. Substituting eq. (6) into eq. (1), we have

$$\begin{aligned}&(\mathrm {ln}\,f)_{xxt}+cu_{0}(\mathrm {ln}\,f)_{xxx}+12b(\mathrm {ln}\,f)_{xx}(\mathrm {ln}\,f)_{xxx}\nonumber \\&\quad +\,b(\mathrm {ln}\,f)_{xxxxx}+\frac{c_{0}}{2}(\mathrm {ln}\,f)_{xyy}=0, \end{aligned}$$
(7)

which when integrated once with respect to x, yields

$$\begin{aligned}&(\mathrm {ln}\,f)_{xt}+cu_{0}(\mathrm {ln}\,f)_{xx}+6b(\mathrm {ln}\,f)_{xx}^2+b(\mathrm {ln}\,f)_{xxxx}\nonumber \\&\quad +\frac{c_{0}}{2}(\mathrm {ln}\,f)_{yy}=0. \end{aligned}$$
(8)

Therefore, eq. (8) can be converted into the following bilinear equation which is quite different from the work in [2,3,4,5,6,7,8,9,10,11,12,13]:

$$\begin{aligned} \left( D_{x}D_{t}+cu_{0}D_x^{2}+bD_{x}^{4}+\frac{c_{0}}{2}D_{y}^2\right) f\cdot f=0, \end{aligned}$$
(9)

where the D-operator is defined by [33]

$$\begin{aligned} D_x^mD_t^nf\cdot g= & {} \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x{'}}\right) ^m\left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t{'}}\right) ^n\nonumber \\&\times f(x,t)g(x{'},t{'})|_{x{'}=x,t{'}=t}. \end{aligned}$$
(10)

Now, with regard to eq. (9), by choosing a test function that is different from [3,4,5], using the extended heteroclinic test approach, we choose the test function of the form

$$\begin{aligned} f(x,y,t)={\mathrm {e}}^{-\xi }+b_{0}\cos (\eta )+b_{1}{\mathrm {e}}^{\xi }, \end{aligned}$$
(11)

where \(\xi =p(x+\alpha y+\beta t+\gamma ),\eta = p_1(x+\alpha _{1}y+\beta _{1}t+\gamma _{1})\) and \(\alpha , \beta , \alpha _{1},\beta _{1}, p, p_{1}, b_{0}, b_{1}, \gamma , \gamma _{1}\) are some free real numbers to be determined later. Substituting eq. (11) into eq. (9) and collecting the coefficients of \(\cos (\eta ), \sin (\eta ),\mathrm { e}^{\xi }\) and \(\mathrm {e}^{-\xi }\), then equating coefficients of these terms to zero, we obtain a set of algebraic equation about \(\alpha ,\beta ,\alpha _{1},\beta _{1}, p, p_{1}, b_{1} \) and \(b_{0}\). By using symbolic computation with Maple 16 to solve these algebraic equations, we can obtain the following relations:

$$\begin{aligned} \left\{ \begin{array}{l} \!\beta =b \!\left( 3{p_{{1}}^{2}-{p}^{2}} \right) \\ \quad -cu_{0}-{\dfrac{c_{0} \left( 2\,{p_{{1}}}^{2}\alpha _{{1}}\alpha -{p_{{1}}}^{2}{\alpha _{{1}}}^{2}+{p}^{2}{\alpha }^{2} \right) }{2({p}^{2}+{p_{{1}}}^{2})}},\\ \!\beta _{{1}}\!=\!b \!\left( {p_{{1}}}^{2}\!-\!3\,{p}^{2} \right) -cu_{0}\\ \quad +{\dfrac{c_{0} \left( {p}^{2}{\alpha }^{2}-2\,{p}^{2}\alpha _{{1}}\alpha -{p_{{1}}}^{2}{\alpha _{{1}}}^{2} \right) }{2 ({p}^{2}+{p_{{1}}}^{2}) }},\\ \!b_{{1}}={\dfrac{{b_{{0}}}^{2}{p_{{1}}}^{2} \left( \frac{1}{2}c_{0} {p}^{2} \left( \alpha -\alpha _{{1}} \right) ^{2}-3\,b \left( {p}^{2}+{p_{{1}}}^{2} \right) ^{2} \right) }{4 p^2 \left( \frac{1}{2} c_{0} {p_{{1}}}^{2} \left( \alpha -\alpha _{{1}}\right) ^{2} +3\,b \left( {p}^{2}+{p_{{1}}}^{2} \right) ^{2}\right) }}. \end{array} \right. \end{aligned}$$
(12)

Taking \(0<b_{1}\in R\), substituting eqs (12) with eq. (11) into eq. (6), an exact solution of eq. (1) was obtained as follows:

$$\begin{aligned} \begin{aligned}&u(x,y,t)=u_{0}\\&+\,\frac{12b}{c}{\frac{(2\sqrt{b_{1}}\cosh (\xi +\frac{1}{2}\ln (b_{1})){p}^{2}-b_{0}\cos (\eta ){p_{{1}}}^{2})}{2\sqrt{b_{1}}\cosh (\xi +\frac{1}{2}\ln (b_{1})) +b_{{0}}\cos (\eta )}} \\&-\,\frac{\left( 2\sqrt{b_{1}}\sinh \!\left( \xi +\frac{1}{2}\ln (b_{1})\right) \!p -b_{{0}}\sin (\eta )p_{{1}}\right) ^{2}}{\left( 2\sqrt{b_{1}}\cosh \!\left( \xi +\frac{1}{2}\ln (b_{1})\right) +b_{{0}}\cos (\eta )\right) ^{2}}. \end{aligned} \end{aligned}$$
(13)

In order to obtain the lump solution from the exact solution eq. (13) for the \((2+1)\)-dimensional GKPE, then taking \(p_{1}=p\) and \(b_{0}=-2\) in eq. (13). So, solution eq. (13) can be written as

$$\begin{aligned} \begin{aligned}&u(x,y,t)=u_{0}\\&\quad +\,\frac{12b}{c}\frac{(\sqrt{\Delta }\cosh (\xi +\frac{1}{2}\ln (\Delta )){p}^{2}+\cos (\eta )p^{2})}{{\sqrt{\Delta }}\cosh (\xi +\frac{1}{2}\ln (\Delta ))-\cos (\eta )} \\&\quad -\,\frac{(\sqrt{\Delta }\sinh (\xi +\frac{1}{2}\ln (\Delta ))p +\sin (\eta )p)^{2}}{(\sqrt{\Delta }\cosh (\xi +\frac{1}{2}\ln (\Delta ))-\cos (\eta ))^{2}}, \end{aligned} \end{aligned}$$
(14)

where

$$\begin{aligned} \Delta= & {} \frac{c_{0}(\alpha -\alpha _{1})^2-24 b p^2}{c_{0}(\alpha -\alpha _{1})^2+24 b p^2},\nonumber \\ \xi= & {} p\bigg (x+\alpha y+\bigg (2bp^2-cu_{0}\nonumber \\&+\,\frac{c_{0}}{2}\bigg (\frac{1}{2}\alpha _{1}^2-\alpha \alpha _{1}-\frac{1}{2}\alpha ^{2}\bigg )\bigg )t+\gamma \bigg ),\nonumber \\ \eta= & {} p\bigg ( x+\alpha _{1}y-\bigg ( 2b p^2+cu_{0}\nonumber \\&+\,\frac{c_{0}}{2}\bigg (\frac{1}{2}\alpha _{1}^2+\alpha \alpha _{1}-\frac{1}{2}\alpha ^2\bigg )\bigg ) t+\gamma _{1}\bigg ) \end{aligned}$$

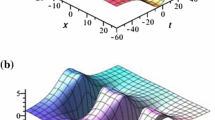
and \(u_{0}, b, c, c_{0}, p, \alpha ,\alpha _{1},\gamma ,\gamma _{1}\) are some free real numbers. The exact solution u(x, y, t) (eq. (13)) (or eq. (14)) is actually a periodic breather-wave solution, which includes a number of free parameters. That is to say, the homoclinic breather-wave solution is a homoclinic wave homoclinic to a fixed point \(u_{0}\) of eq. (14) when \(t\rightarrow \pm \infty \) [34], and is a periodic wave with period \(2\pi \) along \(X=\xi \) [35]. From figure 1 we can clearly see that amplitude periodically oscillates with the evolution of y or t. The space–time structure of the y–t plane of eq. (13) has changed, when the values of \(u_{0}, b, c, c_{0}, p, \alpha ,\alpha _{1},\gamma \) and \(\gamma _{1}\) are changed. Through deep analysis we know that homoclinic wave is hidden under the plane wave, when the nonlinear term coefficient \(c<0\) (see figure 1b); homoclinic wave is exposed on the plane wave, when \(c>0\) (see figure 1a).

Fig. 1
figure 1

Space–time structure of eq. (13) with \(u_{0}={1}/{10}, c_{0}=-6, b=1, \alpha =1\), \(\alpha _{1}=-{1}/{2}, b_{0}=-2,p={1}/{2}, \gamma =\gamma _{1}=t=0,\) when (a) \(c=1\) and (b) \(c=-1\). Curved lines drawn at the bottom of this figure are contour lines.

Full size image

Notice that

$$\begin{aligned} \Delta =\frac{c_{0}(\alpha -\alpha _{1})^2-24 b p^2}{c_{0}(\alpha -\alpha _{1})^2+24 b p^2} \rightarrow 1 \end{aligned}$$

in eq. (14), when \(p \rightarrow 0\). Therefore, if \(p\rightarrow 0\) in eq. (14), we can derive the following lump solution:

$$\begin{aligned} u(x,y,t)=u_{0}-\frac{12b \!\left( 8\theta \vartheta +\frac{192b}{c_{0}(\alpha -\alpha _{1})^2} \right) }{c\! \left( \theta ^2+\vartheta ^2-\frac{48b}{c_{0}(\alpha -\alpha _{1})^2} \right) ^2}, \end{aligned}$$
(15)

where

$$\begin{aligned} \theta= & {} x+\alpha \,y\\&+\left( -cu_{0}+\frac{c_{0}}{2}\bigg (\frac{1}{2}\alpha _{1}^2-\alpha \alpha _{1}-\frac{1}{2}\alpha ^2\bigg ) \right) t+\gamma ,\\ \vartheta= & {} x+\alpha _{1}y\\&-\left( cu_{0} +\frac{c_{0}}{2}\bigg (\frac{1}{2}\alpha _{1}^2+\alpha \alpha _{1}-\frac{1}{2}\alpha ^2\bigg ) \right) t+\gamma _{1}. \end{aligned}$$
Fig. 2
figure 2

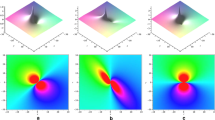
Space–time structure of eq. (15) with \(u_{0}=0, c_{0}=-2, b=1, c=6, \alpha =-{1}/{2},\alpha _{1}=1, \gamma =\gamma _{1}\!=x\!=0\): (a) Three-dimensional plot, (b) t-curves and (c) y-curves.

Full size image

Take \(bc_{0}<0\) and \(\alpha \ne \alpha _{1}\) in eq. (15) to avoid the singularity. Obviously, the exact solution eq. (15) represents a kind of exact solitary wave solution in the form of the rational function, and this kind of soliton solution is actually called lump solution [15]. Some researchers also call this as rogue wave solution [3], and the periodic feature has disappeared, as compared with solution eq. (13). Here, it is interesting to note that the amplitude pulse decays algebraically to the perturbation parameter \(u_{0}\). In fact, the asymptotic behaviour of the lump solution eq. (15) can be found \(u(x,y,t)\rightarrow u_{0}\), either \(x\rightarrow \pm \infty \) or \(y\rightarrow \pm \infty \) or \(t\rightarrow \pm \infty \). The lump solution (eq. (15)) with specific values of the involved parameters are plotted, as illustrative examples. The curves with different independent variables (\(u-t \) and \(u-y\) \()\) in figure 2b and 2c show that the solution in the form of eq. (15) has the properties of impulsive solutions. Meanwhile, we noticed that the lump solution (eq. (15)) has a number of free parameters \(\alpha , \alpha _{1}, \gamma , \gamma _{1}, b, c\) and \(c_{0}\), and when these free parameters take different values, the space–time structure of the lump solution is changed, and we get three different forms of lump structure: bright lump structure (see figure 2a), dark lump structure (see figure 3a) and linear lump structure (see figure 3b). From figure 2a we can clearly see that the bright lump structure has one upward peak and two small downward projections, the main peak forms a much higher hill, the two downward projections are hidden under the plane wave. On the contrary, the dark lump structure contains two small upward projections and one downward peak, the downward peak is hidden under the plane wave. These new and interesting phenomena of space–time structure of the \((2+1)\)-dimensional GKPE are discovered for the first time.

Fig. 3
figure 3

Space–time structure of eq (15) with \(c_{0}=-2, b=1,c=-6,\alpha =-{1}/{2},\alpha _{1}=1, \gamma =\gamma _{1}=x=0\): (a) \(u_{0}=0\), (b) \(u_{0}=-{5}/{48}.\) Curved lines drawn at the bottom of this figure are contour lines.

Full size image

For the KdV eq. (5), by variable transformation \(u(x,t)=u_{0}+2(\mathrm {ln}\,f)_{xx}\), where \(u_{0}\) is a free real number and

$$\begin{aligned} f(x,t)= & {} {\mathrm {e}}^{-p(x+\beta \,t+\gamma )}+b_{0}\cos (p_1(x+\beta _{1}t+\gamma _{1}))\nonumber \\&+\,b_{1}{\mathrm {e}}^{p(x+\beta \,t+\gamma )}. \end{aligned}$$
(16)

The calculation is similar to the \((2+1)\)-dimensional GKPE, and we can obtain the following relations:

$$\begin{aligned} b_{0}=-2\sqrt{b_{1}}, \quad p_{1}=ip, \quad \beta _{1}=-\beta -12u_{0}-8p^{2},\nonumber \\ \end{aligned}$$
(17)

where i is the imaginary unit and \(b_{1}, \beta ,\gamma ,\gamma _{1}, p\) are some free real numbers. So, we obtain a single soliton solution of \((1+1)\)-dimensional KdV

$$\begin{aligned} \begin{aligned}&u(x,t)=u_{0}+2p^{2} -\frac{2p^{2}\!\left( \sinh p\!\left( x+\beta t+\gamma +\frac{1}{2}\ln (b_{1})\right) +\sinh p(x- (\beta +12u_{0}+8p^2)t+\gamma _{1})\right) ^{2}}{\left( \cosh p\!\left( x+\beta t+\gamma +\frac{1}{2}\ln (b_{1})\right) -\cosh p(x-(\beta +12u_{0}+8p^2)t+\gamma _{1})\right) ^{2}}. \end{aligned} \end{aligned}$$
(18)

Letting \(b_{1}=1\), and taking \(p \rightarrow 0\) in eq. (18), we obtain a rational function solution

$$\begin{aligned} u(x,t)=u_{0}-\frac{8}{(2x-12u_{0}t+\gamma +\gamma _{1})^{2}}. \end{aligned}$$
(19)

3 Theoretical analysis of space–time structure changes

Here, we shall discuss the reason for space–time structure changes of the exact lump solution (eq. (15)) using the extreme discriminant theory of multivariate function. Through the analysis of the extreme value theory, we can know that the space–time structure of lump solutions are very rich and diverse. Now, consider the critical point of the two-element function \(U(y, t)=u(0, y, t)\). In order to obtain the extremum of the function U(y, t), we need to calculate the necessary condition

$$\begin{aligned} \left\{ \begin{array}{l} {\displaystyle \frac{\partial U \left( y,t \right) }{\partial y}}=0,\\ {\displaystyle \frac{\partial U \left( y,t \right) }{\partial t}}=0.\\ \end{array} \right. \end{aligned}$$
(20)

Thus, solving eq. (20) leads to a critical point p(y, t), where

$$\begin{aligned} \left\{ \begin{array}{l} y\!=\!\displaystyle \frac{2(\gamma _{1}\!-\!\gamma )(c_{0}\alpha \alpha _{1}\!+\!2cu_{0})\!+\! c_{0}(\gamma _{1}\!+\!\gamma )(\alpha ^2\!-\!\alpha _{1}^2)}{(\alpha -\alpha _{1})(c_{0}\alpha ^2+c_{0}\alpha _{1}^2-4cu_{0})},\\ t=\displaystyle \frac{4(\alpha _{1}\gamma -\alpha \gamma _{1})}{(\alpha -\alpha _{1})(c_{0}\alpha ^2+c_{0}\alpha _{1}^2-4cu_{0})}. \end{array} \right. \end{aligned}$$
(21)

Substituting eq. (21) into two-element function U(y, t), through complicated calculation, we can get the extreme value as

$$\begin{aligned} U(y, t)|_{p}=u_{0}-\frac{c_{0}(\alpha -\alpha _{1})^2}{c}. \end{aligned}$$
(22)

Furthermore, at the point p, the second-order derivative can be obtained as

$$\begin{aligned} \left\{ \begin{array}{l} \Delta \!=\!\displaystyle \frac{\partial ^{2}}{\partial y^{2}}U \left( y,t \right) \!=\!-\! \displaystyle \frac{c_{0}^2(\alpha \!-\!\alpha _{1})^4(\alpha ^2+\alpha _{1}^2+\alpha \alpha _{1})}{12bc},\\ H(U)=\left| \begin{array}{cc} \displaystyle \frac{\partial ^{2}}{\partial y^{2}}U(y,t) &{}\quad \displaystyle \frac{\partial ^{2}}{\partial y \partial t}U(y,t)\\ \displaystyle \frac{\partial ^{2}}{\partial t \partial y}U(y,t) &{}\quad \displaystyle \frac{\partial ^{2}}{\partial t^{2}}U(y,t) \end{array}\right| _{p}\\ \qquad \qquad \!\! \displaystyle =\frac{c_{0}^4(\alpha -\alpha _{1})^{10}(c_{0}\alpha ^2+c_{0}\alpha _{1}^2-4cu_{0})}{1536b^2c^2}.\\ \end{array} \right. \end{aligned}$$
(23)

Notice that \(\alpha ^2+\alpha _{1}^2+\alpha \alpha _{1}>0\) in eqs (23). We can get the following results by using the discriminant theory of the extreme value of the two-element function.

(i) If \(bc>0\) and \( c_{0}\alpha ^2+c_{0}\alpha _{1}^2-4cu_{0}>0\), that is, \( \Delta <0\) and \(H(U)>0\), the critical point p(y, t) is a maximum point and \(U(y,t)_{\mathrm {max}}=u_{0}-[{c_{0}(\alpha -\alpha _{1})^2}/{c]}\), U(y, t) shows single bright lump structure characteristics (see figure 2a).

(ii) If \(bc<0\) and \(c_{0}\alpha ^2+c_{0}\alpha _{1}^2-4cu_{0}>0\), that is, \( \Delta >0\) and \(H(U)>0\), the critical point p(y, t) is a minimum point and \(U(y,t)_{\mathrm {min}}=u_{0}-{[c_{0}(\alpha -\alpha _{1})^2}/{c}]\), U(y, t) shows dark lump structure characteristics (see figure 3a).

(iii) If \(c_{0}\alpha ^2+c_{0}\alpha _{1}^2\le 4cu_{0}\), that is, \(H(U)\le 0\), the test is inconclusive at p(y, t) via the extreme discriminant theory, U(y, t) shows linear lump structure characteristics (see figure 3b).

Through the above theoretical analysis, numerical simulation and three-dimensional image simulation, theoretical reasons for the change of space–time structure of lump solution for the \((2+1)\)-dimensional GKPE is clearly displayed. The space–time structure of the exact lump solution is mainly used to determine the value of the perturbation parameter \(u_{0}\), nonlinear term coefficient c, dispersion coefficient b and linear wave speed \(c_{0}\). Under different parameters conditions, we obtained three different forms of space–time structure of the lump solution: bright lump structure, dark lump structure and linear lump structure.

4 Conclusions

In summary, a class of lump solutions based on quadratic function has been analysed in refs [12, 14, 20] and [27] by Prof. Ma. But, in this manuscript, applying the extended homoclinic test approach and Hirota’s bilinear method with a perturbation parameter \(u_{0}\) to the \((2+1)\)-dimensional GKPE, we obtained a periodic breather-wave solution. Meanwhile, a lump solution was emerged from the periodic breather-wave solution by limit behaviour. The exact analytic solutions (periodic breather-wave solution and lump solution) contain some free parameters \(u_{0}\), b, c, \(\alpha \), \(\alpha _{1}\) and \(c_{0}\). Some new and interesting space–time structures of lump solution were investigated: bright lump structure, dark lump structure and linear lump structure varies with values of these parameters. Finally, we analysed the reasons for the change of space–time structure using the extreme discriminant theory of the two-element function. In addition, we obtained a single soliton solution and a rational function solution of the \((1+1)\)-dimensional KdV equation. Our results show the diversity of the spatial and space–time structures of solitary waves in nonlinear dynamic systems. Meanwhile, we also hoped that our results will provide some valuable information in the field of nonlinear science.