1 Introduction

In the recent years, seeking exact solution of nonlinear partial differential equations (NLPDEs) is of great significance, since the nonlinear complex phenomena related to the NLPDEs are involved in many physics, biology, mechanics, chemistry and engineering. Therefore, the investigation of exact solution for NLPDEs has become more and more important and attractive. Lump solution is also called the vortex and anti-vortex solution, as a specific type of exact solution, and it was found by Zakharov [1] and later by Craik [2]. In contrast to other exact solutions, lump solutions are a kind of rational function solutions, decayed polynomially in all directions in the space. Very recently, lump solutions were presented for many systems [3,4,5,6,7,8,9,10,11].

Now, we consider the (1 + 1)-dimensional Benjamin–Ono equation

$$\begin{aligned} u_{tt}+\beta (u^2)_{xx}+\gamma u_{xxxx}=0, \end{aligned}$$
(1)

where \(\beta \) is the nonlinear term coefficient and \(\gamma \) is dispersion coefficient. In mathematics, the Benjamin–Ono equation is an important nonlinear partial integro-differential equation that describes one-dimensional internal waves in deep water. It was introduced by Benjamin [12] and Ono [13]. Recently, Xu et al. [14] acquired its periodic solitary wave and doubly periodic solutions by using the bilinear method and extended homoclinic test approach. Fu et al. [15] studied its periodic wave solutions by using the Jacobi elliptic function expansion method and the F-expansion method. Wang et al. [16] discussed its traveling wave solutions of single variable by using Riccati equation method. Meng et al. obtained its multi-algebraic solitary wave solutions by applying the bilinear method [17], respectively. In work [18], Li et al. have applied the homoclinic (heteroclinic) limit method with a perturbation parameter \(u_{0}\) to obtain rational homoclinic wave solution (rogue wave solution). However, they did not discuss the influence of the perturbation parameter \(u_{0}\) on the structure of the exact solution in [18]. In this work, a periodically breather solitary solution is obtained by Hirota’s bilinear method, homoclinic test approach and parameter perturbation technique, and some lump solutions based on periodically breather solitary solution are studied by using homoclinic breather limit method (HBLM) [19]. Finally, a special quadratic function solution (lump solution) is found. What is more, we also discuss that the deflection of lump solution depends on not only the perturbation parameter \(u_{0}\), but also a relationship with the nonlinear term coefficient \(\beta \) and the dispersion coefficient \(\gamma \). By choice of the values of these parameters (\(u_{0}, \beta , \gamma \)), we obtain a lump solution with two different structures: bright lump structure and dark lump structure. Some novel and interesting phenomena are revealed.

2 From periodically breather solitary to lump solution

In this section, a periodically breather solitary solution and a lump solution for (1 + 1)-dimensional Benjamin–Ono equation are obtained by using HBLM and Hirota’s bilinear method. Obviously, an arbitrary constant \(u_{0}\) is a solution Eq. (1). Therefore, by Painlevé analysis, we assume that the solution of Eq. (1) as

$$\begin{aligned} u(x,t)=u_{0}+\frac{6\gamma }{\beta }(lnf)_{xx}, \end{aligned}$$
(2)

where f(x, t) is unknown real function. By substituting Eq. (2) into (1), the following bilinear equation is obtained

$$\begin{aligned} \left( D^{2}_{t}+2u_{0}\beta D_x^{2}+\gamma D_{x}^{4}\right) f\cdot f=0, \end{aligned}$$
(3)

where the \(D-\)operator is defined by [20]

$$\begin{aligned} D_{x}^{m}D_{y}^{k}f\cdot g= & {} \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x^{'}}\right) ^m\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y^{'}}\right) ^{k} f(x,y,t) \nonumber \\&\cdot g\left( x^{\prime },y^{\prime },t^{\prime }\right) |_{(x,y,t)=({x^{\prime },y^{\prime },t^{\prime }})}. \end{aligned}$$
(4)

In work [18], Li et al. have applied the homoclinic (heteroclinic) limit method with bilinear form Eq. (3) to obtain rational homoclinic wave solution (rogue wave solution) of the (1 + 1)-dimensional Benjamin–Ono equation. By choosing a special kind of homoclinic test function, they obtain rational homoclinic wave solution of Eq. (1) as follows

$$\begin{aligned} u(x,t)=u_{0}+\frac{24\gamma \left( R-2 \left( x-\frac{2\beta u_{0}}{w_{2}}t\right) (x+w_{2}t) \right) }{\beta \left( \left( x-\frac{2\beta u_{0}}{w_{2}}t\right) ^2+ (x+w_{2}t)^2+R \right) ^2 },\nonumber \\ \end{aligned}$$
(5)

where \(R=\frac{-6\gamma w_{2}^2}{2\beta ^2u_{0}^2+\beta u_{0} w_{2}^2}\). Obviously, this solution Eq. (5) represents a kind of exact solitary wave solution in the form of the rational solution; this kind of soliton solution is actually called lump solution also.

Here, with regard to Eq. (3), by choosing a test function that is different from [18], using the homoclinic test technique [21], we seek the test function of the form

$$\begin{aligned} f(x,t)=1+b_{1}({e}^{ipx}+{e}^{-ipx}){e}^{\varOmega \,t+\lambda }+b_{2}{e}^{2(\varOmega \,t+\lambda )},\nonumber \\ \end{aligned}$$
(6)

where \(p,\varOmega ,\lambda ,b_{1}\) and \(b_{2}\) are all real numbers to be determined below. Substituting Eqs. (6) into (2) yields the exact solution of Eq. (1)

$$\begin{aligned} u(x,t)= & {} u_{0}-\frac{12\gamma b_{1}p^2\mathrm{e}^{\varOmega \,t+\lambda }}{\beta } \nonumber \\&\cdot \frac{cos(px)+2b_{1}\hbox {e}^{\varOmega \,t+\lambda }+b_{2}cos(px)\hbox {e}^{2(\varOmega \,t+\lambda )}}{(1+2b_{1}\cos (px)\mathrm{e}^{\varOmega \,t+\lambda }+b_{2}\mathrm{\,\hbox {e}}^{2(\varOmega \,t+\lambda )})^2}.\nonumber \\ \end{aligned}$$
(7)

Substituting Eqs. (6) into (3) leads to

$$\begin{aligned}&4b_{1}b_{2} \left( \varOmega ^2-2u_{0}\beta p^2+ \gamma p^{4}\right) \cos (px){\mathrm{e}^{2(\varOmega \,t+\lambda )}} \nonumber \\&\quad +\,4b_{1}\left( \varOmega ^2-2u_{0}\beta p^2+\gamma p^{4}\right) \cos (px)\nonumber \\&\quad +\,8\left( \varOmega ^{2}b_{2}-2u_{0}\beta b_{1}^2p^2+4\gamma b_{1}^{2}p^{4}\right) {\mathrm{e}^{\varOmega \,t+\lambda }}=0.\nonumber \\ \end{aligned}$$
(8)

Equating all coefficients of different powers of \(\cos (px)\), \(\cos (px){\mathrm{e}^{2(\varOmega \,+\lambda )}},{\mathrm{e}^{\varOmega \,t+\lambda }}\) to zero, we get

$$\begin{aligned} \left\{ \begin{array}{l} \varOmega ^2-2u_{0}\beta p^2+\gamma p^{4}=0,\\ \varOmega ^{2}b_{2}-2u_{0}\beta b_{1}^2p^2+4\gamma b_{1}^{2}p^{4}=0. \end{array} \right. \end{aligned}$$
(9)

Solving above system of algebraic Eq. (9) with Maple, we get

$$\begin{aligned} \varOmega ^{2}=2\beta u_{0}p^{2}-\lambda p^{4},b_{2}=\frac{\left( 2\beta u_{0}-4\gamma p^{2}\right) b^{2}_{1}}{2\beta u_{0}-\gamma p^{2}},\nonumber \\ \end{aligned}$$
(10)

where \(p,\lambda \) and \(b_{1}\) are real numbers. At the same time, solution Eq. (7) can be written

$$\begin{aligned} u(x, t)= & {} u_{0}-\frac{6\gamma b_{1}p^2 }{\beta } \nonumber \\&\cdot \frac{\sqrt{b_{2}}\cos (px)\cosh (\varOmega \,t+\lambda +\frac{1}{2}\ln b_{2})+b_{1} }{ \left( \sqrt{b_{2}}\cosh (\varOmega \,t+\lambda +\frac{1}{2}\ln b_{2})+b_{1}\cos (px)\right) ^2}.\nonumber \\ \end{aligned}$$
(11)

Substituting Eqs. (10) into (11), we get an exact periodically breather solitary solution of Eq. (1) as follows

$$\begin{aligned}&u(x,t) =u_{0}\nonumber \\&\quad -\frac{6\gamma }{\beta }\frac{b_{1}p^2 \left( \sqrt{\frac{(2\beta u_{0}-4\gamma p^{2})b^{2}_{1}}{2\beta u_{0}-\gamma p^{2}}}\cos (px)\varTheta +b_{1} \right) }{\left( \sqrt{\frac{(2\beta u_{0}-4\gamma p^{2})b^{2}_{1}}{2\beta u_{0}-\gamma p^{2}}}\varTheta +b_{1}\cos (px) \right) ^2},\nonumber \\ \end{aligned}$$
(12)

where

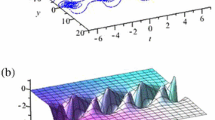
The solution u(x, t) represented by Eq. (12) is a periodically breather solitary solution, i.e., homoclinic breather-wave solution, which is a homoclinic wave homoclinic to a fixed point \(u_{0}\) of Eq. (12) when \(t\rightarrow \pm \infty \) [22], and meanwhile is a periodic wave with period \(\frac{2\pi }{p}\) along the x axis. From Fig. 1, we can clearly see that amplitude periodically oscillates with the evolution of x. At the same time, it is noted that this solution Eq. (12) contains six free parameters \(u_{0},\beta , \gamma , p, \lambda \) and \(b_{1}\). The spatiotemporal structure of the solution Eq. (12) has changed, when these parameters take different values. Through deep analysis, we know that these three parameters \(u_{0},\beta , \gamma \) play a critical role. The periodically breather solitary wave is hidden under the plane wave, when \(\beta u_{0} \gamma >0\) (see Fig. 1b). The periodically breather solitary wave is exposed above the wave plane, when \(\beta u_{0} \gamma <0\) (see Fig. 1a). This is a new nonlinear phenomenon up to now.

Fig. 1
figure 1

Spatiotemporal structure of solution Eq. (12) with a \(u_{0}=-1, \beta =-\frac{1}{32},\gamma =-1, p=\frac{1}{4}, \varOmega =1, b_{1}=1,\lambda =0\); b \(u_{0}=1, \beta =\frac{1}{32},\gamma =-1, p=\frac{1}{4}, \varOmega =1, b_{1}=1,\lambda =0\)

Full size image
Fig. 2
figure 2

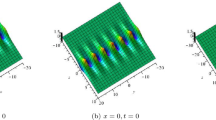
Spatiotemporal structure of solution Eq. (13) with a \(u_{0}=-1, \beta =-\frac{1}{32},\gamma =-1, p=\frac{1}{4}, \varOmega =1, b_{1}=1,\lambda =0\); b \(u_{0}=1, \beta =\frac{1}{32},\gamma =-1, p=\frac{1}{4}, \varOmega =1, b_{1}=1,\lambda =0\)

Full size image

Notice \(\varOmega \rightarrow 0\) and \(b_{2}\rightarrow b_{1}^2\) in Eq. (10), when \(p\rightarrow 0\). Therefore, letting \(p\rightarrow 0\) and taking \(\lambda =0,b_{1}=-\cos (kp)\) in Eq. (12), we can get a new lump solution as follows:

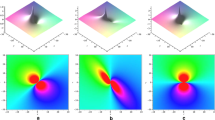
$$\begin{aligned} u(x,t)=u_{0}-\frac{12\gamma }{\beta }\frac{x^2-2\beta u_{0}t^2+\frac{3\gamma }{2\beta u_{0}}}{\left( x^2+2\beta u_{0}t^2-\frac{3\gamma }{2\beta u_{0}}\right) ^2}, \end{aligned}$$
(13)

where \(\beta u_{0}>0\) and \(\frac{\gamma }{\beta u_{0}}<0\). Obviously, this solution Eq. (13) represents a kind of exact solitary wave solution in the form of the rational solution, this kind of soliton solution is actually called lump solution and no longer has periodic feature. From Fig. 2b, we know that the lump solution has two small upward peak and a downward deep hole, and the downward deep hole is hidden below the plane wave. Therefore, the lump solution of this structure is called the dark lump solution. However, the structure of Fig. 2a is just the opposite; it is called the bright lump solution [5]. Meanwhile, the asymptotic behavior of the lump solution Eq. (13) can be found \(u(x,t)\rightarrow u_{0}\), either \(x\rightarrow \pm \infty \) or \(t\rightarrow \pm \infty \). The solution Eq. (13) has three free parameters \(u_{0}, \beta \) and \(\gamma \), and when these free parameters take different values, the spatiotemporal structure of the lump solution is changed. We get two different forms of lump structure: bright lump structure and the dark lump structure (see Fig. 2). This lump solution of bright and dark structures is obtained for the first time to the (1 + 1)-dimensional Benjamin–Ono equation.

3 Theoretical analysis of spatiotemporal structure of lump solution

In this section, we discuss why there are different spatiotemporal structure of the lump solution (Fig. 2a, b). Inspired by the lump solution of Eqs. (5) and (13), we choose the following quadratic function solution

$$\begin{aligned} f(x,t)= & {} a_{1}+(a_{2}x+a_{3}t+a_{4})^2\nonumber \\&+\,(a_{5}x+a_{6}t+a_{7})^2, \end{aligned}$$
(14)

where \(a_{i}, i = 1,\ldots ,7\) are some constants to be determined. Substituting Eq. (14) into bilinear form Eq. (3), through the long and tedious calculation, we can get the following relations among the parameters:

$$\begin{aligned}&a_{1}=\frac{3\gamma (a_{2}^2+a_{5}^2)}{-2\beta u_{0}}, a_{3}=a_{5}\sqrt{2\beta u_{0}},\nonumber \\&a_{6}=-a_{2}\sqrt{2\beta u_{0}}, \end{aligned}$$
(15)

where \(a_{2}, a_{4}, a_{5}\) and \(a_{7}\) are some free real numbers. Substituting Eqs. (15) with (14) into (2), we have

$$\begin{aligned} u(x,t)= & {} u_{0}+\frac{6\gamma }{\beta }\frac{2a_{2}^{2}+2a_{5}^{2}}{\vartheta ^{2}+\theta ^{2}-\frac{3\gamma (a_{2}^2+a_{5}^2)}{2\beta u_{0}}}\nonumber \\&-{\frac{ \left( 2\, \vartheta a_{{2}}+2\theta a_{{5}} \right) ^{2}}{ \left( \vartheta ^{2}+ \theta ^{2}-\frac{3\gamma (a_{2}^2+a_{5}^2)}{2\beta u_{0}} \right) ^{2 }}}. \end{aligned}$$
(16)

where \(\vartheta = a_{{2}}x+a_{5}\sqrt{2\beta u_{0}}t+a_{{4}}\) and \(\theta =a_{{5}}x-a_{2}\sqrt{2\beta u_{0}}t+a_{{7}}\). Similarly, solution Eq. (16) is also a lump solution, which contains seven free parameters \(\beta , u_{0}, \gamma , a_{2}, a_{4}, a_{5}\) and \(a_{7}\). When the values of these free parameters are changed, the spatiotemporal structure of lump solution is changed correspondingly. We got two different forms of lump structure of the bright and the dark lump structure (see Fig. 3). Now, we discuss the reason for structure change in lump solution Eq. (16) by using the extreme value theory of two element function. Consider the critical point of the function u(x, t). In order to obtain the extremum of the function Eq. (16), it is needed to calculate the necessary condition

$$\begin{aligned} \left\{ \begin{array}{l} {\frac{\partial u \left( x,t \right) }{\partial x}}=0,\\ {\frac{\partial u \left( x,t \right) }{\partial t}}=0.\\ \end{array} \right. \end{aligned}$$
(17)
Fig. 3
figure 3

Spatiotemporal structure of lump solution Eq. (16) with a \(u_{0}=-1, \beta =-1,\gamma =-4, a_{2}=1, a_{4}=1, a_{5}=3, a_{7}=1\); b \(u_{0}=1, \beta =1,\gamma =-4, a_{2}=1, a_{4}=1, a_{5}=3, a_{7}=1\)

Full size image

Thus, solving condition Eq. (17) leads to a critical point \(p(x, t)=p(-\frac{a_{2}a_{4}+a_{5}a_{7}}{a_{2}^2+a_{5}^2}, \frac{a_{2}a_{7}-a_{4}a_{5}}{\sqrt{2\beta u_{0}}(a_{2}^2+a_{5}^2)})\). After calculating, we can get the extreme value as \(u(x,t)|_{p}=-7u_{0}\). Furthermore, at the point p, the second-order derivative can be obtained

$$\begin{aligned} \left\{ \begin{array}{l} \varDelta =\frac{\partial ^{2}}{\partial x^{2}}u \left( x,t \right) =-\frac{32\beta u_{0}^2}{\gamma },\\ H(u)=\left| \begin{array}{cc} \frac{\partial ^{2}}{\partial t^{2}}u(x,t) &{} \frac{\partial ^{2}}{\partial x \partial t}u(x,t)\\ \frac{\partial ^{2}}{\partial t \partial x}u(x,t) &{} \frac{\partial ^{2}}{\partial t^{2}}u(x,t) \end{array}\right| _{p} =\frac{2048\beta ^3 u_{0}^5}{3\gamma ^{2}}.\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(18)

By using the discriminant method of extremum value for the two element function, from Eq. (18) we can obtain the following three possible cases:

  1. (i)

    If \(\beta \gamma >0\) and \(\beta u_{0}>0\), that is, \( \varDelta <0\) and \(H(u)>0\), the critical point p is a local maximum point and \(u(x,t)_{max}=-7u_{0}\), u(x, t) shows a single bright lump structure characteristics (see Figs. 2a, 3a).

  2. (ii)

    If \(\beta \gamma <0\) and \(\beta u_{0}>0\), that is, \( \varDelta >0\) and \(H(u)>0\), the critical point p is a local minimum point and \(u(x,t)_{min}=-7u_{0}\), u(x, t) shows dark lump structure characteristics (see Figs. 2b, 3b).

  3. (iii)

    If \(\beta u_{0}<0\), that is, \(H(u)<0\), the critical point p is not a local extremum point. There is no corresponding lump structure characteristics.

Through the above theoretical analysis, numerical simulation and three-dimensional image simulation, the reason for the spatiotemporal structure of lump solution for the (1 + 1)-dimensional Benjamin–Ono equation is clearly displayed. The structure of the lump solution is mainly determined by the value of the perturbation parameter \(u_{0}\), nonlinear term coefficient \(\beta \) and dispersion coefficient \(\gamma \). According to the different parameters condition, we obtained two different spatiotemporal structures of lump solution: bright lump structure and dark lump structure. Comparing our results and Lis’ work [18], we extend the result of the (1 + 1)-dimensional Benjamin–Ono equation.

4 Conclusions

In summary, applying the Hirota’s bilinear method and homoclinic test technique with a perturbation parameter \(u_{0}\) to the (1 + 1)-dimensional Benjamin–Ono equation, we obtain a periodically breather solitary and some lump solutions, which contain some free parameters such as \(u_{0}\), \(\gamma \) and \(\beta \). Some interesting spatiotemporal dynamics of lump solution obtained are investigated: Bright and dark lump structure varies with values of these parameters. In other words, a slight change with the parameter can lead to change in spatiotemporal structure of the lump solution. These results show the diversity of the structures of solitary waves in real dynamic systems. It is hoped that these results will provide some valuable information for ones in the field of nonlinear dynamics.