1 Introduction

As pointed out by Drazin and Johnson [1], it is not easy to give a comprehensive and precise definition of a soliton. However, one can associate the term with any solution of nonlinear partial differential equations (PDEs) which (i) represents a wave of permanent form, (ii) is localized, so that it decays or approaches a constant at infinity, and (iii) can undergo a strong interaction with other solitons preserving its identity. As the soliton phenomena were first observed in 1834 [2] and the Korteweg–de Vries (KdV) equation was solved by the inverse scattering method [3], finding soliton solutions of nonlinear PDEs has become one of the most exciting and extremely active areas of research. In the past several decades, many methods have been proposed for solving nonlinear PDEs, such as Bäcklund transformation [4], Darboux transformation [5], Hirota’s bilinear method [6], homogeneous balance method [7], function expansion methods [8–15] and some others [16–18]. Among them, Hirota’s bilinear method [6] is a purely algebraic method for constructing multisoliton solutions [19–25]. The key step of the method is to convert the given nonlinear PDE into the so-called bilinear form. For such bilinear forms, there is no general rule to follow and one often tries to take some transformations like rational transformation or logarithmic transformation [19].

Recently, Fokas [26] derived a new (4 + 1)-dimensional equation:

$$ u_{tx_{1} } - \frac{1}{4}u_{x_{1} x_{1} x_{1} x_{2} } + \frac{1}{4}u_{x_{2} x_{2} x_{2} x_{1} } + \frac{3}{2}(u^{2})_{x_{1} x_{2} } - \frac{3}{2}u_{y_{1} y_{2}} = 0 $$
(1)

in the process of extending the integrable Kadomtsev–Petviashvili (KP) and Davey–Stewartson (DS) equations to some higher-dimensional nonlinear wave equations. Yang and Yan [27] constructed Jacobi elliptic double periodic solutions, hyperbolic function solutions and rational solutions of eq. (1) by investigating its symmetries. Lee et al [28] obtained some exact solutions of eq. (1) by using modified tanh–coth method, extended Jacobi elliptic function method and the exp-function method. Kim and Sakthivel [29] obtained hyperbolic function solutions, trigonometric function solutions and rational solution of eq. (1) by applying \(G^{\prime }/G\)-expansion method. Zhang and Zhang [30] gave the space–time fractional derivative form of eq. (1) and obtained its generalized hyperbolic function solutions, generalized trigonometric function solutions and rational solution. More recently, He et al [31,32] obtained many new exact solutions of eq. (1) by using extended F-expansion method. To the best of our knowledge, eq. (1) has not been studied by Hirota’s bilinear method and multisoliton solutions of this equation have not been reported. Integrable nonlinear PDEs possess soliton solutions [33] and have important physical applications ranging from fluid mechanics and nonlinear optics to quantum gravity and field theories [26]. It is well known that both the celebrated KdV equation and the nonlinear Schrödinger (NLS) equation have (exist) n-soliton solutions [2]. As two extensions of the (1 + 1)-dimensional KdV and NLS equations into (2 + 1)-dimensional space, the integrable KP and DS equations also possess n-soliton solutions [2]. Does the (4 + 1)-dimensional Fokas equation (1) has multisoliton solutions? This paper will give a positive answer to this question.

The rest of this paper is organized as follows: In §2, following Hirota’s bilinear method, we first adopt some appropriate transformations to convert eq. (1) into the bilinear form and then construct its multisoliton solutions. In §3, we conclude this paper.

2 Multisoliton solutions

First, we take the following transformation:

$$ x = k_{1} x_{1} + k_{2} x_{2} , $$
(2)

where k 1 and k 2 are undetermined constants. Then eq. (1) becomes

$$ \left[ {u_{t} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )u_{xxx} + \frac{3}{2}k_{2} (u^{2})_{x} } \right]_{x_{1} } - \frac{3}{2}u_{y_{1} y_{2}} = 0. $$
(3)

Suppose k 1≠k 2 and let

$$ u = ({k_{2}^{2}} - {k_{1}^{2}} )(\ln f)_{xx} , \quad f = f(t,x_{1} ,x_{2} ,y_{1} ,y_{2} ). $$
(4)

Then substituting eq. (4) into eq. (3) and eliminating the common factor \({k_{2}^{2}} - {k_{1}^{2}} \), we have

$$\begin{array}{@{}rcl@{}} &&\left\{ {(\ln f)_{xxt} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(\ln f)_{xxxxx} + \frac{3}{2}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )\left[ {(\ln f)_{xx} } \right]_{x}^{2}} \right\}_{x_{1} }\\ &&\qquad\quad-\frac{3}{2}(\ln f)_{xxy_{1} y_{2} } = 0, \end{array} $$

which can be written as follows (when k 1≠0):

$$\begin{array}{@{}rcl@{}} &&\left\{(\ln f)_{xt} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(\ln f)_{xxxx} + \frac{3}{2}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )\left[ (\ln f)_{xx} \right]^{2}\right.\\ &&\quad\quad\left.-\frac{3}{2k_{1} }(\ln f)_{y_{1} y_{2} } \right\}_{xx} = 0. \end{array} $$
(5)

Integrating eq. (5) with respect to x twice and selecting the integration constants as zeros, we have

$$\begin{array}{@{}rcl@{}} &&(\ln f)_{xt} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(\ln f)_{xxxx} + \frac{3}{2}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )\left[ {(\ln f)_{xx} } \right]^{2} \\ &&\quad\quad -\frac{3}{2k_{1} }(\ln f)_{y_{1} y_{2} } = 0, \end{array} $$
(6)

and hence obtain the bilinear form of eq. (1):

$$ \left[ {D_{x} D_{t} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){D_{x}^{4}} - \frac{3}{2k_{1} }D_{y_{1} } D_{y_{2} } } \right]f \cdot f = 0, $$
(7)

where D x , D t , \(D_{y_{1}}\) and \(D_{y_{2}}\) are the Hirota’s differential operators [19] defined by

$${D}_{t}^{m} {D}_{x}^{n} f(t,x) \cdot g(t,x) = (\partial_{t} - {\partial}_{t}^{\prime} )^{m}(\partial_{x} - {\partial}_{x}^{\prime} )^{n} f(t,x)g (t^{\prime}, {x}^{\prime}) |_{t^{\prime} = t, x^{\prime} = x}. $$

Next we employ eq. (7) to construct multisoliton solutions of eq. (1). For this purpose, it is necessary to consider the boundary condition of eq. (5). As \(\tanh ^{2}\)-type solution [27] of eq. (1) can be rewritten using the relationship \(\text {sech}^{2}+\tanh ^{2}=1\), eq. (1) exists sech2-type solution with bell-shaped structure. Inspired by the structural features of such a sech2-type solution and eq. (4), in this paper we give an assumption of the boundary condition of eq. (5): ∀t, \((\ln f)_{xx}\rightarrow 0\) for \(\eta \rightarrow \pm \infty \). Here η is a linear function of spatial variables x, y 1 and y 2. In order to construct the single-soliton solution, we suppose

$$ f = 1 + f^{(1)}\varepsilon + f^{(2)}\varepsilon^{2} + f^{(3)}\varepsilon^{3} + {\cdots} , $$
(8)

substitute eq. (8) into eq. (7) and then collect the coefficients of the same order of ε. Then, this process yields a system of differential equations

$$ 2\!\left[ {\partial_{x}\partial_{t} + \frac{1}{4}({k_{2}^{2}} - {k_{1}^{2}} )k_{2} {\partial^{4}_{x}} - \frac{3}{2k_{1} }\partial_{y_{1} } \partial_{y_{2} } } \right]f^{(1)} =0, $$
(9)
$$\begin{array}{@{}rcl@{}} &&2\!\left[ {\partial_{x}\partial_{t} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){\partial^{4}_{x}} - \frac{3}{2k_{1} }\partial_{y_{1}} \partial_{y_{2}} } \right]f^{(2)}\\ &&\quad\quad = - \left[ {D_{x} D_{t} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){D_{x}^{4}} - \frac{3}{2k_{1} }D_{y_{1} } D_{y_{2} } } \right]f^{(1)} \cdot f^{(1)}, \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} &&2\!\left[ {\partial_{x}\partial_{t} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){\partial^{4}_{x}} - \frac{3}{2k_{1} }\partial_{y_{1}} \partial_{y_{2}} } \right]f^{(3)}\\ &&\quad\quad = - 2\left[ {D_{x} D_{t} + \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){D_{x}^{4}} - \frac{3}{2k_{1} }D_{y_{1} } D_{y_{2} } } \right]f^{(1)} \cdot f^{(2)}, \end{array} $$
(11)

and so forth. Let

$$ f^{(1)} = \text{e}^{\xi_{1} }, \quad \xi_{1} = r_{1} (\omega_{1} t + x + p_{1} y_{1} + q_{1} y_{2} ) + \xi_{1}^{(0)}, $$
(12)

be a solution of eq. (9). Here r 1, ω 1, p 1 and q 1 are constants to be determined, and \(\xi _{1}^{(0)}\) is an arbitrary constant. Insertion of eq. (12) into eq. (9) yields

$$ \omega_{1} = - \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){r_{1}^{2}} + \frac{3}{2k_{1} }p_{1} q_{1}. $$
(13)

Substituting eq. (13) into eqs (10) and (11), we can verify that

$$ f^{(n)} = 0, \quad n = 2, 3, \ldots. $$
(14)

In this case, we can write

$$ f_{1} = 1 + \text{e}^{\xi_{1} }, $$
(15)

and hence obtain the following single-soliton solution of eq. (1):

$$ u = ({k_{2}^{2}} - {k_{1}^{2}} )\left[ {\ln (1 + \mathrm{e}^{\xi_{1} })} \right]_{xx} = \frac{1}{4}{r_{1}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} )\text{sech}^{2}\frac{1}{2}\xi_{1} , $$
(16)

where

$$\begin{array}{@{}rcl@{}} \xi_{1} &=& r_{1} \left[ - \frac{1}{4}k_{2} {r_{1}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} )t + \frac{3}{2k_{1} }p_{1} q_{1} t + k_{1} x_{1} + k_{2} x_{2} \right.\\ &&+\!\left.p_{1} y_{1} + q_{1} y_{2} {\vphantom{\frac{1}{4}k_{2} {r_{1}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} )t + \frac{3}{2k_{1} }p_{1} q_{1} t + k_{1} x_{1} + k_{2} x_{2}}}\right] + \xi_{1}^{(0)} . \end{array} $$

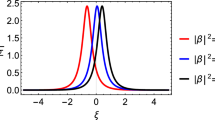
In figure 1, the single-soliton solution (16) is shown by selecting r 1=1, k 1=1, k 2=3, p 1=3, q 1=2, \(\xi _{1}^{(0)}=0\), y 1=0, y 2=0, from which we can see that the single-soliton propagating along the negative direction of x-axis possesses a bell-shaped structure.

Figure 1
figure 1

Evolutionary plots of the single-soliton solution (16).

Full size image

For the double-soliton solution, we suppose

$$ f^{(1)} = \mathrm{e}^{\xi_{1} } + \mathrm{e}^{\xi_{2} }, \quad \xi_{2} = r_{2} (\omega_{2} t + x + p_{2} y_{1} + q_{2} y_{2} ) + \xi_{2}^{(0)} , $$
(17)

and substitute eq. (17) into eq. (9). Here r 2, ω 2, p 2 and q 2 are constants to be determined, \(\xi _{2}^{(0)}\) is an arbitrary constant. We then obtain

$$ \omega_{2} = - \frac{1}{4}k_{2} {r_{2}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} ) + \frac{3}{2k_{1} }p_{2} q_{2} . $$
(18)

In view of eq. (10), we further suppose

$$ f^{(2)} = \mathrm{e}^{\xi_{1} + \xi_{2} + A_{12} }, $$
(19)

where A 12 is a constant to be determined. From eqs (10) and (19), we can obtain

$$ \mathrm{e}^{A_{12} } = \frac{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{2} - r_{1} )^{2} + 2(p_{2} - p_{1} )(q_{2} - q_{1} )}{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{2} + r_{1} )^{2} + 2(p_{2} - p_{1} )(q_{2} - q_{1} )}. $$
(20)

Substituting eqs (17)–(20) into eq. (11), we can verify that

$$ f^{(n)} =0, \quad n =3, 4, \ldots. $$
(21)

In this case, we can write

$$ f_{2} = 1 + \mathrm{e}^{\xi_{1} } + \mathrm{e}^{\xi_{2} } + \mathrm{e}^{\xi_{1} + \xi_{2} + A_{12} }, $$
(22)

and hence obtain the following double-soliton solution of eq. (1):

$$ u = ({k_{2}^{2}} - {k_{1}^{2}} )\left[ {\ln (1 + \mathrm{e}^{\xi_{1} } + \mathrm{e}^{\xi_{2} } + \mathrm{e}^{\xi_{1} + \xi_{2} + A_{12} })} \right]_{xx} , $$
(23)

where

$$\begin{array}{@{}rcl@{}} \xi_{i} = r_{i} \left[ - \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){r_{i}^{2}} t + \frac{3}{2k_{1} }p_{i} q_{i} t + k_{1} x_{1} + k_{2} x_{2} \right.\\[-15pt] \end{array} $$
$$\begin{array}{@{}rcl@{}} \left. ~~~~~~~+\!p_{1} y_{1} + q_{1} y_{2} {\vphantom{\frac{1}{4}k_{2} {r_{1}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} )t + \frac{3}{2k_{1} }p_{1} q_{1} t + k_{1} x_{1} + k_{2} x_{2}}}\right] + \xi_{i}^{(0)} , \quad i = 1,2. \end{array} $$

In figure 2, a double-soluton solution (23) is shown. Here, we select r 1=1, r 2=2, k 1=1, k 2=2, p 1=3, p 2=2, q 1=2, q 2=1, \(\xi _{1}^{(0)}=0\), \(\xi _{2}^{(0)}=0\), x 1=0, x 2=0. It is easy to see that collision between the pair of bell-shaped solitons has elastic characteristics. It must be noted that solitons do undergo elastic collision with colliding solitons coming out of collision without any change in shape. In case of solitary waves, this also can happen but is not general, for instance in [34].

Figure 2
figure 2

Evolutionary plots of the double-soliton solution (23).

Full size image

We continue to construct the three-soliton solution. We suppose

$$ f^{(1)} = \mathrm{e}^{\xi_{1} } + \mathrm{e}^{\xi_{2} } + \mathrm{e}^{\xi_{3} }, \quad \xi_{3} = r_{3} (\omega_{3} t + x + p_{3} y_{1} + q_{3} y_{2} ) + \xi_{3}^{(0)} , $$
(24)

and substitute eq. (24) into eq. (9). Here r 3, ω 3, p 3 and q 3 are constants to be determined, \(\xi _{3}^{(0)}\) is an arbitrary constant. We then obtain

$$ \omega_{3} = - \frac{1}{4}k_{2} {r_{3}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} ) + \frac{3}{2k_{1} }p_{3} q_{3} . $$
(25)

In view of eq. (10), we further suppose

$$ f^{(2)} = \mathrm{e}^{\xi_{1} + \xi_{2} + A_{12} } + \mathrm{e}^{\xi_{1} + \xi_{3} + A_{13} } + \mathrm{e}^{\xi_{2} + \xi_{3} + A_{23} }, $$
(26)
$$ f^{(3)} = \mathrm{e}^{\xi_{1} + \xi_{2} + \xi_{3} + A_{12} + A_{13} + A_{23} }, $$
(27)

where A 13 and A 23 are constants to be determined. From eqs (10), (26) and (27), we obtain

$$ \mathrm{e}^{A_{13} } = \frac{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{3} - r_{1} )^{2} + 2(p_{3} - p_{1} )(q_{3} - q_{1} )}{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{3} + r_{1} )^{2} + 2(p_{3} - p_{1} )(q_{3} - q_{1} )}, $$
(28)
$$ \mathrm{e}^{A_{23} } = \frac{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{3} - r_{2} )^{2} + 2(p_{3} - p_{2} )(q_{3} - q_{2} )}{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{3} + r_{2} )^{2} + 2(p_{3} - p_{2} )(q_{3} - q_{2} )}. $$
(29)

Substituting eqs (25)–(29) into eq. (11), we can verify that

$$ f^{(n)} = 0, \quad n=4, 5, \ldots. $$
(30)

In this case, we can write

$$\begin{array}{@{}rcl@{}} f_{3} &=& 1 + \mathrm{e}^{\xi_{1} } + \mathrm{e}^{\xi_{2} } + \mathrm{e}^{\xi_{3} } + \mathrm{e}^{\xi_{1} + \xi_{2} + A_{12} } + \mathrm{e}^{\xi_{1} + \xi_{3} + A_{13} }\\ &&+ \mathrm{e}^{\xi_{2} + \xi_{3} + A_{23} } + \mathrm{e}^{\xi_{1} + \xi_{2} + \xi_{3} + A_{12} + A_{13} + A_{23} }, \end{array} $$
(31)

and hence obtain the following three-soliton solution of eq. (1):

$$\begin{array}{@{}rcl@{}} u &=& ({k_{2}^{2}} - {k_{1}^{2}} )\left[ \ln \left( 1 + \mathrm{e}^{\xi_{1} } + \mathrm{e}^{\xi_{2} } + \mathrm{e}^{\xi_{3} } + \mathrm{e}^{\xi_{1} + \xi_{2} + A_{12} } + \mathrm{e}^{\xi_{1} + \xi_{3} + A_{13}} \right.\right.\\ &&+\! \left.\left.\mathrm{e}^{\xi_{2} + \xi_{3} + A_{23} } + \mathrm{e}^{\xi_{1} + \xi_{2} + \xi_{3} + A_{12} + A_{13} + A_{23} }\right) \right]_{xx} , \end{array} $$
(32)

where

$$\begin{array}{@{}rcl@{}} \xi_{i} = r_{i} \left[ - \frac{1}{4}k_{2} ({k_{2}^{2}} - {k_{1}^{2}} ){r_{i}^{2}} t + \frac{3}{2k_{1} }p_{i} q_{i} t + k_{1} x_{1} + k_{2} x_{2} \right.\\[-7pt] \end{array} $$
$$\begin{array}{@{}rcl@{}} ~~~~~~~\left.+ p_{1} y_{1} + q_{1} y_{2}{\vphantom{\frac{1}{4}k_{2} {r_{1}^{2}} ({k_{2}^{2}} - {k_{1}^{2}} )t + \frac{3}{2k_{1} }p_{1} q_{1} t + k_{1} x_{1} + k_{2} x_{2}}} \right] + \xi_{i}^{(0)} , \quad i = 1,2,3. \end{array} $$

In figure 3, we select r 1=1, r 2=2, r 3=−1, k 1=1, k 2=2, k 3=3, p 1=1, p 2=2, p 3=−1, q 1=2, q 2=1, q 3=−1, \(\xi _{1}^{(0)}=0\), \(\xi _{2}^{(0)}=0\), \(\xi _{3}^{(0)}=0\), x 1=0, y 1=0 and then show an elastic collision that happened among the three-soliton solution (32).

Figure 3
figure 3

Evolutionary plots of the three-soliton solution (32).

Full size image

Generally, by taking

$$ f_{n} = \sum\limits_{\mu = 0,1} { \mathrm{e}^{\sum {_{j = 1}^{n} \mu_{j} \xi_{j} + A\sum {_{1 \le j < l}^{n} \mu_{j} \mu_{l} A_{jl} } } }} , $$
(33)
$$ \mathrm{e}^{A_{jl} } = \frac{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{l} - r_{j} )^{2} + 2(p_{l} - p_{j} )(q_{l} - q_{j} )}{k_{1} k_{2} ({k_{2}^{2}} - {k_{1}^{2}} )(r_{l} + r_{j} )^{2} + 2(p_{l} - p_{j} )(q_{l} - q_{j} )}, $$
(34)

we can obtain the uniform formula of n-soliton solution of eq. (1):

$$ u = ({k_{2}^{2}} - {k_{1}^{2}} )\left[ {\ln \left( {\sum\limits_{\mu = 0,1} { \mathrm{e}^{\sum {_{j = 1}^{n} \mu_{j} \xi_{j} + A\sum {_{1 \le j < l}^{n} \mu_{j} \mu_{l} A_{jl} } } }} } \right)} \right]_{xx} , $$
(35)

where the summation \({\sum }_{\mu = 0,1} \) refers to all possible combinations of each \(\mu _{i} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} 1\) for \(i = 1,{\kern 1pt} 2,{\kern 1pt} {\ldots } ,n\).

To the best of our knowledge, the obtained double-soliton solution (23), three-soliton solution (32) and n-soliton solution (35) are new.

Remark 1.

As mentioned earlier, soliton solutions (16), (23), (32) and (35) have two constraints: k 1≠k 2 and k 1≠0. Otherwise, the bilinear form (7) does not exist. For k 1=k 2 or k 1=0, there are no soliton solutions as expected for eq. (1). If k 1=k 2, eq. (3) is reduced to

$$ k_{1}u_{tx} + \frac{3}{2}{k_{1}^{2}}(u^{2})_{xx} - \frac{3}{2}u_{y_{1} y_{2}} = 0. $$
(36)

According to the homogeneous balance method [7], we can easily see that eq. (36) has only trivial solutions. On the other hand, if k 1=0, eq. (3) becomes

$$ - \frac{3}{2}u_{y_{1} y_{2}} = 0, $$
(37)

which is a linear equation, and so has no soliton solution.

3 Conclusions

In summary, we have given bilinear form of the (4 + 1)-dimensional Fokas equation (1) and hence obtained its single-soliton solution, double-soliton solution, three-soliton solution and the new uniform formula of n-soliton solution through Hirota’s bilinear method. In the process of using Hirota’s bilinear method to solve eq. (1), one of the key steps is to convert eq. (1) into the bilinear form (7) by the appropriate transformations (2), (4)–(6) adopted in this work. Once a nonlinear PDE is converted into the bilinear form, then multisoliton solutions are usually obtained. In order to construct bilinear forms of nonlinear PDEs, some dependent variable transformations need to be taken. However, there is no general rule for the selection of such transformations. For the Fokas equation (1), not only the dependent variable transformation (4) but also the independent variable transformation (2) is taken. This paper shows that Hirota’s bilinear method with some appropriate transformations may provide us with an effective mathematical tool for constructing multisoliton solutions of some other new higher-dimensional nonlinear PDEs.