Improved NSAF Algorithms with Variable Control Parameter Against Impulsive Noises

Abstract

Some improved normalized subband adaptive filter algorithms derived from nonlinear cost functions, such as the logarithmic function and the arctangent function, have shown splendid robustness against the impulsive noises. However, due to the usage of the constant control parameter in their cost functions, these algorithms need to make a balance between the steady-state error and the convergence rate, especially when the unknown impulse response changes suddenly. For settling this trade-off issue, a way of obtaining the variable control parameter (VCP) recursively is constructed by an exponential function in this paper. In the contexts of system identification and acoustic echo cancellation, simulation results testified the improved performance of these proposed VCP algorithms in terms of the convergence rate, steady-state error, and tracking capability.

1 Introduction

Adaptive filtering has been extensively developed in numerous applications, such as system identification, active noise control, and acoustic echo cancellation [1, 13, 19, 25]. Among existing adaptive filtering algorithms, the normalized least-mean-square (NLMS) algorithm is distinguished for the merits of easy implementation and low computational cost. However, colored input signal bring about slow convergence rate. The subband adaptive filter (SAF) is an efficacious method to solve this issue resulting from colored input signal, due to the fact that colored input signal is decomposed into multiple mutually orthogonal white subband signals, thus quickening entire convergence rate [6]. The normalized SAF (NSAF) algorithm presented by Lee and Gan has faster convergence rate than the NLMS algorithm and owns similar computational complexity [4, 5]. The similarity between the NLMS and NSAF algorithms is that they are both derived by utilizing the L₂-norm optimization, and thus they have poor robustness against impulsive noises.

It is well known that such algorithms derived from lower-order-norm optimization criterion have tremendous ability for combating impulsive noises. By introducing the L₁-norm optimization into the subband structure, the sign subband adaptive filter (SSAF) algorithm and variable regularization parameter SSAF (VRP-SSAF) not only possess great robustness against impulsive noises but also obtain lower steady-state error [10]. In order to further accelerate convergence rate and decrease steady-state error of the SSAF algorithm, a series of variable step-size SSAF [3, 18, 21] and affine projection SSAF algorithms [11, 15] have been put forward. Besides, Yu et al. have analyzed the mean-square-deviation (MSD) performance of the SSAF algorithm [22]. More recently, some novel adaptive filter algorithms which are derived from nonlinear cost functions [7,8,9, 14, 16, 20, 23, 24, 26], such as normalized logarithmic SAF (NLSAF) [20], logarithm criterion SAF (LC-SAF) [23] and arctangent-based NSAF algorithms (Arc-NSAFs) [16], have developed with the outstanding robustness against impulsive noises. However, these nonlinear-function-based algorithms all have a constant control parameter, and they need to be properly chosen to make a trade-off between low steady-state error and fast convergence rate. In particular, a larger control parameter leads to a lower steady-state error but a relatively slower convergence rate. Besides, the tracking capability of these constant control parameter algorithms is depressed especially for the sudden change of the unknown impulse response.

To address this trade-off issue of these algorithms in the presence of impulsive noises, in this paper, an adaptive mechanism based on an exponential function is constructed to iteratively update variable control parameter (VCP). In fact, VCP technique is equivalent to imposing a variable step size on those original algorithms. When impulsive noises appear, the adaptive mechanism chooses a small step size to prevent the adverse influence resulting from impulsive noises on the performance of these algorithms, making the proposed VCP algorithms maintain robustness in non-Gaussian environment. On the contrary, when impulsive noises are absent, a large step size is preferred to speed up the convergence rate.

In system identification and acoustic echo cancellation scenarios, numerous simulation experiments verified that these proposed VCP algorithms not only inherit outstanding robustness against impulsive noises, but also obtain improved performance in terms of the convergence rate, steady-state error and tracking capability.

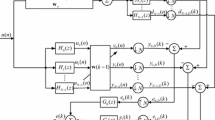
2 Review of the LC-SAF and Arc-NSAFs

The desired output signal $d(n)$ of the unknown system is modeled as

$$ d(n) = u^{\text{T}} (n)w_{o} + \vartheta (n) $$

(1)

where ${\mathbf{u}}(n) = \left[ {u\left( n \right),u(n - 1), \ldots ,u(n - L + 1)} \right]^{\text{T}}$ is input signal, the superscript T stands for the transposition, and ${\mathbf{w}}_{o}$ denotes an $L \times 1$ weight vector to be estimated. The additive noise $\vartheta (n)$ contains the Gaussian measurement noise $v(n)$ and the impulsive noises $\eta (n)$, i.e., $\vartheta (n) = v(n) + \eta (n)$. Figure 1 shows the multiband structure of the SAF with the number of subbands N. The input signal $u(n)$ and desired output signal $d(n)$ are partitioned into subband signals $u_{i} (n)$ and $d_{i} (n)$ by the analysis filter bank $\left\{ {H_{0} (z),H_{1} (z), \ldots ,H_{N - 1} (z)} \right\}$, respectively. The subband output signals $y_{i} (n)$ are obtained by filtering subband input signals $u_{i} (n)$ through an adaptive filter with its tap-weight vector ${\mathbf{w}}(k) = [w_{0} (k),w_{1} (k), \ldots ,w_{L - 1} (k)]^{\text{T}}$. Then, subband signals $d_{i} (n)$ and $y_{i} (n)$ are critically decimated to generate signals $d_{i,D} (k)$ and $y_{i,D} (k)$, respectively, where $y_{i, \, D} (k) = {\mathbf{u}}_{i}^{\text{T}} (k){\mathbf{w}}(k)$, ${\mathbf{u}}_{i} (k) = [u_{i} (kN),u_{i} (kN - 1), \ldots ,u_{i} (kN - L + 1)]^{\text{T}}$. Note that variables n and k are used to indicate the original sequences and the decimated orders, respectively. The ith decimated subband error signal is computed as

$$ e_{i, \, D} (k) = d_{i, \, D} (k) - y_{i, \, D} (k) $$

(2)

where $d_{i, \, D} (k) = d_{i} (kN)$.

Fig. 1

Multiband structure of the SAF

The LC-SAF algorithm is derived by minimizing the logarithmic cost function with respect to the normalized subband error signal [23]:

$$ J(\varvec{w}(k)) = \frac{1}{2\alpha }\sum\limits_{i = 0}^{N - 1} {\ln \left[ {1 + \alpha \frac{{e_{i,D}^{2} (k)}}{{\left\| {\varvec{u}_{i} (k)} \right\|^{2} }}} \right]} $$

(3)

where $\alpha > 0$ is a control parameter. By using the gradient descent method, the weight coefficient vector for the LC-SAF algorithm is updated:

$$ {\mathbf{w}}(k + 1) = {\mathbf{w}}(k) + \mu \sum\limits_{i = 0}^{N - 1} {\frac{1}{{1 + \alpha ({{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}})^{2} }}\frac{{{\mathbf{u}}_{i} (k)e_{i,D} (k)}}{{{\mathbf{u}}_{i}^{\text{T}} (k){\mathbf{u}}_{i} (k)}}} $$

(4)

where μ is the step size.

In order to further accelerate the convergence rate of the LC-SAF algorithm, two arctangent-based NSAF algorithms have been proposed in [16]. Both are derived from arctangent cost function, while the only distinction between them is the order of the arctangent computation and the summation operation of the normalized subband error signal in cost functions. Their cost functions are, respectively, expressed as:

$$ J({\mathbf{w}}(k)) = \frac{1}{2\alpha }\sum\limits_{i = 0}^{N - 1} {\arctan \left( {\alpha e_{i,D}^{2} (k)/\left\| {{\mathbf{u}}_{i} (k)} \right\|^{2} } \right)} , $$

(5)

$$ J({\mathbf{w}}(k)) = \frac{1}{2\alpha }\arctan \left( {\alpha \sum\limits_{i = 0}^{N - 1} {e_{i,D}^{2} (k)/\left\| {{\mathbf{u}}_{i} (k)} \right\|^{2} } } \right). $$

(6)

And then, by using the gradient descent method, the weight coefficient vector update formulas of these two Arc-NSAFs are summarized as follows:

$$ {\mathbf{w}}(k + 1) = {\mathbf{w}}(k){ + }\mu \sum\limits_{i = 0}^{N - 1} {\frac{1}{{1 + \alpha^{2} e_{i,D}^{4} (k)/\left\| {{\mathbf{u}}_{i} (k)} \right\|^{4} }}\frac{{{\mathbf{u}}_{i} (k)e_{i,D} (k)}}{{{\mathbf{u}}_{i}^{\text{T}} (k){\mathbf{u}}_{i} (k)}}} $$

(7)

$$ {\mathbf{w}}(k + 1) = {\mathbf{w}}(k){ + }\mu \sum\limits_{i = 0}^{N - 1} {\frac{1}{{1 + \alpha^{2} \left( {\sum\limits_{i = 0}^{N - 1} {e_{i,D}^{2} (k)/\left\| {{\mathbf{u}}_{i} (k)} \right\|^{2} } } \right)^{2} }}\frac{{{\mathbf{u}}_{i} (k)e_{i,D} (k)}}{{{\mathbf{u}}_{i}^{\text{T}} (k){\mathbf{u}}_{i} (k)}}} $$

(8)

For distinguishing them expediently, these two Arc-NSAF algorithms are referred to as the Arc-NSAF-1 and Arc-NSAF-2 algorithms, respectively [16]. Under the same impulsive noises circumstance, the Arc-NSAF-2 algorithm obtains better performance than the Arc-NSAF-1 algorithm.

The constant control parameter $\alpha$ is contained in the update equations of the LC-SAF and Arc-NSAFs algorithms. It affects the convergence rate and steady-state error of these algorithms simultaneously. Therefore, it should be selected appropriately to meet the conflicting needs of fast convergence rate and low steady-state error.

3 Proposed VCP Algorithms

Before presenting VCP algorithms, for the convenience of subsequent discussion, the above-mentioned LC-SAF and two Arc-NSAF algorithms can be summarized in a uniform form as follows:

$$ {\mathbf{w}}(k + 1) = {\mathbf{w}}(k) + \mu \sum\limits_{i = 0}^{N - 1} {h\left( {\alpha ,\frac{{e_{i,D} (k)}}{{{\mathbf{u}}_{i} (k)}}} \right)\frac{{{\mathbf{u}}_{i} (k)e_{i,D} (k)}}{{{\mathbf{u}}_{i}^{\text{T}} (k){\mathbf{u}}_{i} (k)}}} $$

(9)

where

$$ h_{\text{LC-SAF}} \left( {\alpha ,\frac{{e_{i,D} (k)}}{{{\mathbf{u}}_{i} (k)}}} \right) = \frac{1}{{1 + \alpha \left( {e_{i,D} (k)/{\mathbf{u}}_{i} (k)} \right)^{2} }} $$

(10)

$$ h_{\text{Arc-NSAF-1}} \left( {\alpha ,\frac{{e_{i,D} (k)}}{{{\mathbf{u}}_{i} (k)}}} \right) = \frac{1}{{1 + \alpha^{2} e_{i,D}^{4} (k)/\left\| {{\mathbf{u}}_{i} (k)} \right\|^{4} }} $$

(11)

$$ h_{\text{Arc-NSAF-2}} \left( {\alpha ,\frac{{e_{i,D} (k)}}{{{\mathbf{u}}_{i} (k)}}} \right) = \frac{1}{{1 + \alpha^{2} \left( {\sum\limits_{i = 0}^{N - 1} {e_{i,D}^{2} (k)/\left\| {{\mathbf{u}}_{i} (k)} \right\|^{2} } } \right)^{2} }} $$

(12)

To make these algorithms obtain fast convergence rate and low steady-state error simultaneously, motivated by the work in [2], by introducing an exponential function, an adaptive mechanism is proposed to iteratively update the control parameter $\alpha$ in $h\left( {\alpha ,{{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}}} \right)$

$$ \alpha_{i} (k) = k_{\alpha } {\text{e}}^{{ - k_{m} m_{i,e} (k)}} $$

(13)

where $k_{\alpha }$ and $k_{m}$ are both positive parameters, and they influence the steady-state error and convergence rate of the proposed VCP algorithms, respectively. The way of getting $m_{i,e} (k)$ is a common estimation method associated with the subband error signal $e_{i,D} (k)$

$$ m_{i,e} (k) = \lambda m_{i,e} (k - 1) + (1 - \lambda )C\hbox{min} (A_{i,e} (k)) $$

(14)

where $\lambda$ is a weighting factor, $C = 1.483(1 + 5/N_{\text{w}} - 1)$ is the finite sample correction factor [12, 18, 27], $N_{\text{w}}$ is the length of the estimation window, $\hbox{min} \,( \cdot )$ stands for the minimization and

$$ A_{i,e} (k) = \left[ {\left| {e_{i,D} (k)} \right|,\left| {e_{i,D} (k - 1)} \right|, \ldots ,\left| {e_{i,D} (k - N_{\text{w}} + 1)} \right|} \right]. $$

(15)

Combining (14) and (15), we know that the purpose of minimization of $A_{i,e} (k)$ is to obtain the minimum value of the past $N_{\text{w}}$ subband error signals. When the system encounters impulsive noises, the minimization of $A_{i,e} (k)$ could decrease the adverse influence caused by impulsive noises on the system updating, as a result, making the proposed VCP algorithms maintain the robustness against impulsive noises.

It is obvious that using $\alpha_{i} (k)$ instead of $\alpha$, Eq. (9) becomes the updating formula of the weight coefficient vector of the proposed VCP algorithms, and then the original LC-SAF and Arc-NSAF algorithms are modified to the corresponding VCPLC-SAF and VCPArc-NSAF algorithms as well

$$ {\mathbf{w}}(k + 1) = {\mathbf{w}}(k) + \mu \sum\limits_{i = 0}^{N - 1} {h\left( {\alpha_{i} (k),\frac{{e_{i,D} (k)}}{{{\mathbf{u}}_{i} (k)}}} \right)\frac{{{\mathbf{u}}_{i} (k)e_{i,D} (k)}}{{{\mathbf{u}}_{i}^{\text{T}} (k){\mathbf{u}}_{i} (k)}}} . $$

(16)

It is well known that the performance of the traditional NSAF algorithm will dramatically deteriorate in the presence of impulsive noises, i.e., it does not possess great robustness against impulsive noises. However, by observing (10)–(12), extremely small value of $\alpha_{i} (k)$ leads to $h\left( {\alpha_{i} (k),{{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}}} \right) \approx 1$, and then (16) reduces to the update formula of the NSAF algorithm, thus losing robustness against impulsive noises. Besides, considering that the iterative formula (13) of $\alpha_{i} (k)$ is a monotone decreasing exponential function, a constraint for the maximum value of $k_{m} m_{i,e} (k)$ circumvents this situation effectively. As long as we limit $k_{m} m_{i,e} (k)$ to have a maximum value m₊ (i.e., $m_{i,e} (k) < m_{ + } /k_{m}$), the demand that $\alpha_{i} (k)$ has a minimum value $k_{\alpha } e^{{ - m_{ + } }}$ could be guaranteed. For clarity, the proposed VCP algorithms are summarized in Table 1.

Table 1 Proposed VCP algorithms

Discussion 1

The scalar function $h( \cdot )$ of the proposed VCPLC-SAF algorithm with respect to the variable control parameter $\alpha_{i} (k)$ and the normalized subband error $e_{i,D} (k)/{\mathbf{u}}_{i} (k)$ is presented in Fig. 2. The curves of scalar functions of the proposed VCPArc-NSAF algorithms are similar and omitted for brevity. On the one hand, under the condition of the same normalized subband error value, a larger $\alpha_{i} (k)$ value is corresponding to a smaller function value. It reveals that the ability of decreasing the step size with a larger $\alpha_{i} (k)$ is stronger. On the other hand, when impulsive noises appear, a larger normalized subband error $e_{i,D} (k)/{\mathbf{u}}_{i} (k)$ is yielded. Since the scalar function $h( \cdot )$ is inversely proportional to the normalized subband error, a larger value of $e_{i,D} (k)/{\mathbf{u}}_{i} (k)$ brings about a smaller function value, which amounts to imposing a smaller step size on the proposed VCP algorithms. As a result, the adverse influence caused by impulsive noises can be restrained. When impulsive noise is absent, the value of $e_{i,D} (k)/{\mathbf{u}}_{i} (k)$ becomes small, and the proposed VCP adaptive mechanism adopts a larger step size to speed up the entire convergence rate. The essence of the proposed VCP adaptive mechanism is automatically choosing a proper step size according to the presence or absence of impulsive noises. Thus, the scalar function $h( \cdot )$ is just like a variable step size, so the scalar function $h( \cdot )$ can be considered as the variable-step-size-like scalar function.

Fig. 2

Variable-step-size-like scalar function of the proposed VCPLC-SAF algorithm

Discussion 2

As mentioned above, extremely small value of $\alpha_{i} (k)$ results in $h\left( {\alpha_{i} (k),{{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}}} \right) \approx 1$, and then (16) reduces to the update formula of the NSAF algorithm. Therefore, by observing (16), the proposed VCP algorithms can be viewed as imposing a variable individual step size $\mu h\left( {\alpha_{i} (k),{{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}}} \right)$ on the NSAF algorithm for each subband. For guaranteeing convergence of the NSAF algorithm in the mean-square sense, the step size should satisfy

$$ 0 < \mu_{\text{NSAF}} < 2. $$

(17)

Since $h\left( {\alpha_{i} (k),{{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}}} \right) < 1$, $\mu_{\text{VCP}} { = }\mu h\left( {\alpha_{i} (k),{{e_{i,D} (k)} \mathord{\left/ {\vphantom {{e_{i,D} (k)} {{\mathbf{u}}_{i} (k)}}} \right. \kern-0pt} {{\mathbf{u}}_{i} (k)}}} \right) \in \left( {0,2} \right)$ is evident, the convergence of the proposed VCP algorithms can be satisfied.

4 Computational Complexity

In Table 2, the computational complexities of the proposed VCPLC-SAF and VCPArc-NSAFs algorithms are compared with that of the SSAF [10], NLSAF [20], LC-SAF [23], and two Arc-NSAFs algorithms [16] in terms of the total number of additions, multiplications, comparisons, and exponents, where K means the length of the analysis filters. Obviously, when compared with the original algorithms, the proposed VCP algorithms need extra one addition, five multiplications, one comparison, and one exponent. Luckily, the slight increases in the proposed VCP algorithms in the computational complexity is worthy, because their performance achieve great improvement in terms of the convergence rate, steady-state error and tracking capability.

Table 2 Computational complexity of various SAF algorithms for each fullband input

5 Simulation Results

In the contexts of system identification and acoustic echo cancellation with impulsive noises, the performance of the proposed VCP algorithms is verified by Monte Carlo (MC) simulations. Together with the Gaussian measurement noise $v(n)$, the impulsive noises $\eta (n)$ are added to the system output, modeled as $\eta (n) = p(n)B(n)$, where $p(n)$ is a zero-mean white Gaussian process with variance $\sigma_{p}^{2} = 1000E[({\mathbf{u}}^{\text{T}} (n){\mathbf{w}}_{o} )^{2} ]$, and $B(n)$ stands for a Bernoulli process with the probability mass function expressed as $p(B(n) = 1) = P_{r}$ and $p(B(n) = 0) = 1 - P_{r}$ ($P_{r}$ denotes the occurrence possibility of the impulsive noises) [17]. The unknown impulse response ${\mathbf{w}}_{o}$ is a measured acoustic echo path with $L = 512$ taps. It is assumed that the length of adaptive filter is the same as that of the unknown vector. A white Gaussian measurement noise $v(n)$ is added to the unknown system output with a certain signal-to-noise (SNR) of 30 dB, except Fig. 9, whose SNR value is 10 dB. The cosine-modulated filter bank is used with $N = 4$. The normalized MSD (NMSD), defined as $20\log_{10} \left[ {\left\| {{\mathbf{w}}_{o} - {\mathbf{w}}(k)} \right\|_{2}^{2} /\left\| {{\mathbf{w}}_{o} } \right\|_{2}^{2} } \right]$, is used to measure the algorithms’ performance. All simulated learning curves are obtained by ensemble average over 30 independent trails.

5.1 System Identification

The input signal is a colored input generated by filtering a white Gaussian noise through an AR(1) system with a pole at 0.9. To assess the tracking capability of the algorithms, the unknown impulse response is changed to $- {\mathbf{w}}_{o}$ in the middle of iterations (except Figs. 8 and 10).

The performance of the original algorithms with different $\alpha$ values and that of the proposed VCP algorithms is compared in Figs. 3, 4, and 5 with $P_{r} = 0.001$. For a fair comparison, the step size of every pair of algorithms is the same, and other key parameter settings are given below the figure. For the original non-VCP algorithms, a larger $\alpha$ value results in a lower steady-state error but a slower convergence rate. Although their initial convergence speed is almost the same, the degree of convergence rate decrease is quite evident especially when unknown impulse response is changed suddenly, which reflects the tracking capability of the constant control parameter algorithms should be improved. The proposed VCP algorithms not only have fast convergence rate, great tracking capability of original algorithms with small $\alpha$ value, but also have low steady-state error of original algorithms with large $\alpha$ value. Therefore, the proposed VCP technique is effective in solving the trade-off problem of original non-VCP algorithms between fast convergence, low steady-state error, and good tracking capability.

Fig. 3

NMSD learning curves of the proposed VCPLC-SAF algorithm and the original LC-SAF algorithm for different $\alpha$ values with $P_{r} = 0.001$. LC-SAF: $\mu = 0.05$; VCPLC-SAF: $\mu = 0.05$, $N_{\text{w}} = 12$, $m_{ + } = 4$, $k_{m} = 25$, $k_{\alpha } = 1000$

Fig. 4

NMSD learning curves of the proposed VCPArc-NSAF-1 algorithm and the original Arc-NSAF-1 algorithm for different $\alpha$ values with $P_{r} = 0.001$. Arc-NSAF-1: $\mu = 0.1$; VCPArc-NSAF-1: $\mu = 0.1$, $N_{\text{w}} = 16$, $m_{ + } = 6$, $k_{m} = 35$, $k_{\alpha } = 1000$

Fig. 5

NMSD learning curves of the proposed VCPArc-NSAF-2 algorithm and the original Arc-NSAF-2 algorithm for different $\alpha$ values with $P_{r} = 0.001$. Arc-NSAF-2: $\mu = 0.2$; VCPArc-NSAF-2: $\mu = 0.2$, $N_{\text{w}} = 12$, $m_{ + } = 4$, $k_{m} = 35$, $k_{\alpha } = 1000$

Figures 6 and 7 show the NMSD learning curves of the standard SSAF [10], NLSAF [20], LC-SAF [23], Arc-NSAF-1 [16], Arc-NSAF-2 [16] and the proposed VCPLC-SAF, VCPArc-NSAF-1, VCPArc-NSAF-2 algorithms with $P_{r} = 0.001$ and $P_{r} = 0.01$, respectively. The step sizes of the SSAF, NLSAF, LC-SAF, Arc-NSAF-1, and Arc-NSAF-2 algorithms are chosen to make them obtain almost the same steady-state error. For a fair comparison, the step sizes of the proposed VCP algorithms are the same as those of their original algorithms. Other parameters of these algorithms are selected based on the recommended values in the literature. As expected, the proposed VCP algorithms achieve lower steady-state error and better tracking capability than their corresponding original algorithms with the same initial convergence rate.

Fig. 6

NMSD learning curves of the SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2 and the proposed VCPLC-SAF, VCPArc-NSAF-1, VCPArc-NSAF-2 algorithms with $P_{r} = 0.001$. SSAF: $\mu = 0.003$, $\delta = 0.01$; NLSAF: $\mu = 0.005$, $\alpha = 1500$; LC-SAF: $\mu = 0.05$, $\alpha = 80$; Arc-NSAF-1: $\mu = 0.1$, $\alpha = 80$; Arc-NSAF-2: $\alpha = 80$; VCPLC-SAF: $\mu = 0.005$; VCPArc-NSAF-1: $\mu = 0.1$; VCPArc-NSAF-2: $\mu = 0.2$.(Other corresponding parameter settings of the proposed VCP algorithms are the same as those of Figs. 3, 4 and 5)

Fig. 7

NMSD learning curves of the SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2 and the proposed VCPLC-SAF, VCPArc-NSAF-1, VCPArc-NSAF-2 algorithms with $P_{r} = 0.01$. SSAF: $\mu = 0.004$, $\delta = 0.01$; NLSAF: $\mu = 0.0045$, $\alpha = 1500$; LC-SAF: $\mu = 0.0025$, $\alpha = 80$; Arc-NSAF-1: $\mu = 0.08$, $\alpha = 200$; Arc-NSAF-2: $\mu = 0.4$, $\alpha = 200$; VCPLC-SAF: $\mu = 0.025$; VCPArc-NSAF-1: $\mu = 0.08$; VCPArc-NSAF-2: $\mu = 0.4$

Figure 8 illustrates the NMSD learning curves of the standard SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2, and the proposed VCP algorithms with $P_{r} = 0$. The VCPLC-SAF has similar performance to the LC-SAF algorithm, while the proposed VCPArc-NSAF algorithms achieve faster convergence rate than the original Arc-NSAFs in the absence of impulsive noises, which demonstrates that the proposed VCP algorithms perform better than the existing algorithms even in the impulsive-noise-free condition. The convergence rate of the Arc-NSAF-1 algorithm is faster than the Arc-NSAF-2 algorithm in this condition. This is because, for the Arc-NSAF-1 algorithm, $h_{\text{Arc-NSAF-1}} ( \cdot )$ in (11) is equivalent to providing a different step size for each subband according to their own different input signal information, while for $h_{\text{Arc-NSAF-2}} ( \cdot )$ of the Arc-NSAF-2 algorithm, each subband is allocated with the common step size.

Fig. 8

NMSD learning curves of the SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2 and the proposed VCPLC-SAF, VCPArc-NSAF-1, VCPArc-NSAF-2 algorithms with $P_{r} = 0$. SSAF: $\mu = 0.004$, $\delta = 0.01$; NLSAF: $\mu = 0.006$, $\alpha = 1500$; LC-SAF: $\mu = 0.08$, $\alpha = 80$; Arc-NSAF-1: $\mu = 0.08$, $\alpha = 200$; Arc-NSAF-2: $\mu = 0.08$, $\alpha = 200$; VCPLC-SAF: $\mu = 0.08$; VCPArc-NSAF-1: $\mu = 0.08$; VCPArc-NSAF-2: $\mu = 0.08$

To demonstrate the effectiveness of the proposed VCP algorithms under low-SNR condition, Fig. 9 depicts the NMSD learning curves of these algorithms with SNR = 10 dB. The parameter settings of all algorithms are the same as shown in Fig. 8. Evidently, the proposed VCP algorithms outperform their original algorithms with respect to the convergence rate, steady-state error, and tracking capability. All above simulation results confirm the outstanding performance of the proposed VCP algorithms.

Fig. 9

NMSD learning curves of the SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2 and the proposed VCPLC-SAF, VCPArc-NSAF-1, VCPArc-NSAF-2 algorithms with SNR = 10 dB. $P_{r} = 0.001$

5.2 Acoustic Echo Cancellation

The NMSD learning curves of the standard SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2, and the proposed VCP algorithms for speech input signal, depicted in Fig. 10a, is exhibited in Fig. 10b. The regularization parameter of the SSAF algorithm is $5\sigma_{u}^{2}$, where $\sigma_{u}^{2}$ is the power of the input signal. Clearly, the proposed VCP algorithms still outperform the existing algorithms in terms of the steady-state error, which demonstrates the outstanding performance of the proposed VCP algorithms in real-time data processing field.

Fig. 10

a Speech input signal for acoustic echo cancellation. b NMSD learning curves of the SSAF, NLSAF, LC-SAF, Arc-NSAF-1, Arc-NSAF-2 and the proposed VCPLC-SAF, VCPArc-NSAF-1, VCPArc-NSAF-2 algorithms for speech input. SSAF: $\mu = 0.01$; NLSAF: $\mu = 0.01$, $\alpha = 1500$; LC-SAF: $\mu = 0.05$, $\alpha = 80$; Arc-NSAF-1: $\mu = 0.01$, $\alpha = 80$; Arc-NSAF-2: $\mu = 0.2$, $\alpha = 80$; VCPLC-SAF: $\mu = 0.05$; VCPArc-NSAF-1: $\mu = 0.1$; VCPArc-NSAF-2: $\mu = 0.2$

6 Conclusion

The nonlinear-function-based algorithms with constant control parameter need to make a balance between fast convergence behavior and low steady-state error. In this paper, an adaptive mechanism to iteratively update the VCP has been proposed to address this problem. In the contexts of system identification and acoustic echo cancellation, simulation results demonstrated that the proposed VCP algorithms not only retain outstanding robustness against impulsive noises but also obtain improved performance as compared to their original versions.