Convergence analysis of the zero-attracting variable step-size LMS algorithm for sparse system identification

Abstract

The variable step-size least-mean-square algorithm (VSSLMS) is an enhanced version of the least-mean-square algorithm (LMS) that aims at improving both convergence rate and mean-square error. The VSSLMS algorithm, just like other popular adaptive methods such as recursive least squares and Kalman filter, is not able to exploit the system sparsity. The zero-attracting variable step-size LMS (ZA-VSSLMS) algorithm was proposed to improve the performance of the variable step-size LMS (VSSLMS) algorithm for system identification when the system is sparse. It combines the ${\ell _1}$-norm penalty function with the original cost function of the VSSLMS to exploit the sparsity of the system. In this paper, we present the convergence and stability analysis of the ZA-VSSLMS algorithm. The performance of the ZA-VSSLMS is compared to those of the standard LMS, VSSLMS, and ZA-LMS algorithms in a sparse system identification setting.

1 Introduction

Adaptive filtering has received a great deal of interest in signal processing [1, 2]. Many adaptive algorithms have been developed for applications such as system identification [1]. The least-mean-square (LMS) [1] is one of the most popular adaptive methods, but suffers from low convergence rate and high power consumption when a long impulse response of an unknown system contains many near-zero coefficients and a few large ones; that is, the impulse response of the system is sparse [3]. The VSSLMS method [4] aims to improve the convergence speed of the LMS algorithm, but fails to exploit the sparsity of the system.

Motivated by the LASSO [6] and the recent developments in the field of compressive sensing [7, 8], the sparsity is addressed by combining ${\ell _0}$-norm penalty function into the original cost function of the LMS algorithm [3]. Adding the ${\ell _0}$ norm to the cost function of the VSSLMS algorithm causes the optimization problem to be non-convex. In order to avoid this drawback, the ${\ell _1}$-norm is used as an approximation to the ${\ell _0}$ norm [7–9]. This gives the adaption process the ability of attracting zero (or nearly zero) filter coefficients. This process is called the zero attraction [3]. The zero-attracting variable step-size LMS (ZA-VSSLMS) [10] is proposed which was shown to outperform the standard VSSLMS when the system is highly sparse. In this paper, the convergence properties of the ZA-VSSLMS are analyzed when the input to the system is white. The stability condition of the aforementioned method is derived, and the performance of the proposed algorithm is compared with those of the standard LMS, VSSLMS, and ZA-LMS [3, 5] algorithms.

The paper is organized as follows: In Sect. 2, the recently proposed ZA-VSSLMS algorithm is briefly reviewed. In Sect. 3, the convergence analysis of the ZA-VSSLMS algorithm is developed and its stability condition is derived. In Sect. 4, simulation results that compare the performance of the ZA-VSSLMS with those of the standard LMS, VSSLMS, and ZA-LMS algorithms are provided. Finally, conclusions are drawn in Sect. 5.

2 ZA-VSSLMS algorithm

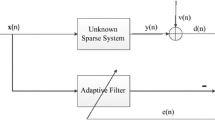
Consider the input–output relation of an linear time-invariant (LTI) system described by

$$\begin{aligned} y(k)=\mathbf{h}^{\mathrm{T}}\mathbf {x}(k)+ v(k), \end{aligned}$$

(1)

where $\mathbf{h}$ is the unknown tap weight vector of length $N,\,T$ is the transposition operator, $\mathbf{x}(k)$ is a white input signal, $\ y(k)$ is the output, and $v(k)$ is an additive noise process which is independent from $x(k)$.

Modifying the cost function in [4] by adding the $\ell _1$-norm penalty of the coefficient vector to the square of the prediction error results in

$$\begin{aligned} J_1(k)=\frac{1}{2}e^2(k) + \lambda \Vert \mathbf{w}(k)\Vert _1 , \end{aligned}$$

(2)

where $\mathbf{w}(k)$ corresponds to N-th order adaptive filter coefficients, and $\lambda$ is a positive constant. The error signal in (2) is defined by

$$\begin{aligned} e(k)=y(k)-\mathbf{w}^{\mathrm{T}}(k)\mathbf{x}(k). \end{aligned}$$

(3)

By the gradient method, the ZA-VSSLMS [10] update equation becomes

$$\begin{aligned} \mathbf{w}(k+1)=\mathbf{w}(k)+\mu (k) e(k)\mathbf{x}(k) -\rho (k)\mathrm{sgn}(\mathbf{w}(k)). \end{aligned}$$

(4)

where $\rho (k)=\lambda \mu (k),\,\hbox {sgn}(\cdot )$ is the pointwise sign function, and $\mu (k)$ is a variable step-size [4] which is given by

$$\begin{aligned} \mu (k) = \left\{ \begin{array}{ll} \mu _{\mathrm{max}} &{}\quad \text{ if }\,\mu '(k+1) > \mu _{\mathrm{max}}\\ \mu _{\mathrm{min}} &{}\quad \text{ if }\,\mu '(k+1) < \mu _{\mathrm{min}}\\ \mu '(k+1) &{}\quad \text{ otherwise }\end{array} \right. \end{aligned}$$

(5)

$\mu '(k+1)$ can be estimated in the following form

$$\begin{aligned} \mu '(k+1)=\alpha \mu '(k)+ \gamma e^2(k), \end{aligned}$$

(6)

with $0<\alpha <1$ and $\gamma >0$.

3 Convergence analysis of the ZA-VSSLMS algorithm

In this section, we analyze the convergence of the ZA-VSSLMS algorithm when the input to the system is white. We start by defining the filter misalignment vector, and then, the mean and the covariance of misalignment vector can be computed. Once all these parameters are well-defined, we use them to estimate the updated value of covariance matrix and hence deriving the stability condition based on the trace of this matrix. Here, we present the stability condition in terms of the input variance $\sigma ^2_x$ and filter length $N$. The filter’s misalignment vector can be defined as

$$\begin{aligned} \varvec{\delta }(k)=\mathbf{w}(k)-\mathbf{h}. \end{aligned}$$

(7)

The mean and covariance matrices of $\varvec{\delta }(k)$, respectively, as

$$\begin{aligned}&\varvec{\epsilon }(k)=E\{\varvec{\delta }(k)\}, \end{aligned}$$

(8)

$$\begin{aligned}&\mathbf{S}(k)=E\left\{ \mathbf{c}(k)\mathbf{c}^{\mathrm{T}}(k)\right\} , \end{aligned}$$

(9)

where $\mathbf{c}(k)$ is a zero mean vector defined as

$$\begin{aligned} \mathbf{c}(k)=\varvec{\delta }(k)-E\{\varvec{\delta }(k)\}. \end{aligned}$$

(10)

We also define the instantaneous mean-square-deviation (MSD) in the following form

$$\begin{aligned} J(k)=E\{||\varvec{\delta }(k)||^2_2\}=\sum \limits _{i=0}^{N-1}\varLambda _i(k) , \end{aligned}$$

(11)

where $\varLambda _i(k)$ represents the i-th tap MSD given by

$$\begin{aligned} \varLambda _i(k)&= E\{||\varvec{\delta }_i(k)||^2_2\}=S_{ii}(k)+\epsilon ^2_i(k),\nonumber \\&i=0,\ldots ,N-1. \end{aligned}$$

(12)

In Eq. (12), $S_{ii}(k)$ corresponds to the diagonal elements of the auto-covariance matrix $\mathbf{S}(k)$.

By combining (1), (3), (4), (7) and the independence assumption, we get

$$\begin{aligned} \varvec{\delta }(k+1)&= \left[ \mathbf{I}-\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k)\right] \varvec{\delta }(k)\nonumber \\&\quad +\mu (k)\mathbf{x}(k)v(k)-\rho (k) \hbox {sgn}[\mathbf{w}(k)], \end{aligned}$$

(13)

Taking the expectation of (13), we get

$$\begin{aligned} E\{\varvec{\delta }(k+1)\}&= E\left\{ \left[ \mathbf{I}-\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k)\right] \varvec{\delta }(k)\right. \nonumber \\&\quad \left. +\,\mu (k)\mathbf{x}(k)v(k)-\,\rho (k) \hbox {sgn}[\mathbf{w}(k)]\right\} \!. \end{aligned}$$

(14)

Due to the independence between $x$ and $v$, the expectation of the second term becomes zero. Thus, the expectation of (14) simplifies to

$$\begin{aligned} \epsilon (k+1)=(1-E\{\mu (k)\}\sigma ^2_x)\epsilon (k)-E\left\{ \rho (k) \mathrm{sgn}[\mathbf{w}(k)]\right\} \!.\nonumber \\ \end{aligned}$$

(15)

Subtracting $E\{\varvec{\delta }(k+1)\}$ from both sides of Eq. (13)gives

$$\begin{aligned} \mathbf{c}(k+1)&= \left( \mathbf{I}-\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k)\right) \varvec{\delta }(k)+\mu (k)\mathbf{x}(k)v(k)\nonumber \\&\quad -\,\rho (k)\mathrm{sgn}[\mathbf{w}(k)]-\epsilon (k+1)\nonumber \\&= \mathbf{A}(k)\varvec{\delta }(k)+\mu (k)\mathbf{x}(k)v(k)\nonumber \\&\quad -\left( 1-E\{\mu (k)\}\sigma ^2_x\right) \epsilon (k)+\mathbf{p}(k). \end{aligned}$$

(16)

Here

$$\begin{aligned} \mathbf{A}(k)&= \mathbf{I}-\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k), \end{aligned}$$

(17)

$$\begin{aligned} \mathbf{p}(k)&= E\{\rho (k)\}E\{\mathrm{sgn}[\mathbf{w}(k)]\}-\rho (k)\mathrm{sgn}[\mathbf{w}(k)]. \end{aligned}$$

(18)

Adding $\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k)\epsilon (k)$ to both side of (16) and rearranging the terms we get

$$\begin{aligned} \mathbf{c}(k+1)&= \mathbf{A}(k)\mathbf{c}(k)+\mu (k)\mathbf{x}(k)v(k)\nonumber \\&\quad +\mathbf{B}(k)\epsilon (k)+\mathbf{p}(k). \end{aligned}$$

(19)

In the above equation,

$$\begin{aligned} \mathbf{B}(k)=E\{\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k)\}-\mu (k)\mathbf{x}(k)\mathbf{x}^{\mathrm{T}}(k). \end{aligned}$$

(20)

Next, we estimate $\mathbf{S}(k+1)$ based upon the independence among $x(k),\,v(k)$, and $\varvec{\delta }(k)$ as follows:

$$\begin{aligned} \mathbf{S}(k+1)&= E\{\mathbf{c}(k+1)\mathbf{c}^{\mathrm{T}}(k+1)\}\nonumber \\&= E\{\mathbf{A}(k)\mathbf{c}(k)\mathbf{c}^{\mathrm{T}}(k)\mathbf{A}^{\mathrm{T}}(k)\} +2E\{\mathbf{A}(k)\mathbf{c}(k)\mathbf{p}^{\mathrm{T}}(k)\}\nonumber \\&\quad +\,E\{\mathbf{B}(k)\epsilon (k)\epsilon ^{\mathrm{T}}(k)\mathbf{B}(k)\}\nonumber \\&= (1-2E\{\mu (k\}\sigma ^2_x+2E\{\mu ^2(k)\}\sigma ^4_x)\mathbf{S}(k)\nonumber \\&\quad +E\{\mu ^2(k)\}\sigma ^4_x \hbox {tr}[\mathbf{S}(k)]\mathbf{I}\nonumber \\&\quad +\,2E\{\rho (k)\}(1-2E\{\mu (k\}\sigma ^2_x)E\{\mathbf{w}(k)\mathbf{p}^{\mathrm{T}}(k)\}\nonumber \\&\quad +E\{\mathbf{p}(k)\mathbf{p}^{\mathrm{T}}(k)\} +\,E\{\mu (k)^2\}\sigma ^4_x(\epsilon (k)\epsilon ^{\mathrm{T}}(k)\nonumber \\&\quad +\mathrm{tr}[\epsilon (k)\epsilon ^{\mathrm{T}}(k)]\mathbf{I})+E\{\mu (k)^2\}\sigma ^2_x\sigma ^2_v\mathbf{I}, \end{aligned}$$

(21)

The estimate in (21) is obtained by calculating input’s fourth moment [11–13] as well as using the symmetric behavior of the covariance matrix $\mathbf{S}(k)$. Finding the trace of (21)

$$\begin{aligned} tr[\mathbf{S}(k+1)]&= (1-2E\{\mu (k\}\sigma ^2_x+(N+2)E\{\mu ^2(k)\}\sigma ^4_x)\nonumber \\&\quad \times \,\hbox {tr}[\mathbf{S}(k)]+\hbox {tr}(E\{\mathbf{p}(k)\mathbf{p}^{\mathrm{T}}(k)\})\nonumber \\&\quad +\,NE\{\mu ^2(k)\}\sigma ^2_x\sigma ^2_v+2E\{\rho (k\}\nonumber \\&\quad \times (1-E\{\mu (k)\sigma ^2_x\})E\{\mathbf{w}(k)\mathbf{p}^{\mathrm{T}}(k)\}\nonumber \\&\quad +\,(N+1)E\{\mu ^2(k)\}\sigma ^4_x\epsilon ^{\mathrm{T}}(k)\epsilon ^{\mathrm{T}}(k). \end{aligned}$$

(22)

In Eq. (22), $\mathbf{p}(k),\,E\{\mathbf{w}(k)\},\,E\{\mathbf{w}(k)\mathbf{p}^{\mathrm{T}}(k)\}$, and $\epsilon (k)$ are all bounded. Thus, the adaptive filter is stable if the following holds

$$\begin{aligned} |2E\{\mu ^2(k)\}\sigma ^2_x-(N+2)E\left\{ \mu ^2(k)\right\} \sigma ^4_x|<1. \end{aligned}$$

(23)

This implies that as $k\longrightarrow \infty ,\,E\{\mu ^2(k)\}=E\{\mu (k)\}^2=\mu ^2(k)$. Hence, the above equation simplifies to

$$\begin{aligned} 0<\mu (\infty )<\frac{2}{(N+2)\sigma ^2_x}. \end{aligned}$$

(24)

This result shows that if $\mu$ stratifies (24), the convergence of the ZA-VSSLMS is guaranteed.

4 Simulation results

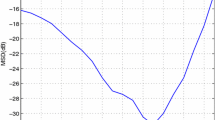
In this section, we evaluate the performance of the proposed adaptive filter for system identification problem. In our experiments, the input signal and the observed noise are both assumed to be white Gaussian random sequences with variances 1 and $10^{-3}$, respectively, which results in a 30 dB signal-to-noise ratio (SNR). In the first experiment, the performance of the ZA-VSSLMS algorithm is tested and compared to those of the standard VSSLMS, LMS, and ZA-LMS algorithms. We set the filter length $N=256$ with 10 % nonzero coefficients distributed randomly. In the first experiment, the following parameters were used : For the VSSLMS: $\mu _{\mathrm{min}}=0.008,\,\mu _{\mathrm{max}}=0.012,\,\gamma =0.0048$ and $\alpha =0.97$. For the ZA-VSSLMS: $\mu _{\mathrm{min}}=0.008,\,\mu _{\mathrm{max}}=0.012,\,\rho =0.0001$. For the ZA-LMS : $\mu =0.005$. The simulations are performed for 200 independent runs. Figure 1 shows the average MSD estimate of all algorithms. As shown, the ZA-VSSLMS algorithm converges to 2 and 9 dB lower MSDs compared to the VSSLMS, ZA-LMS algorithms respectively.

Fig. 1

MSDs of the VSSLMS, ZA-VSSLMS, LMS and ZA-LMS algorithms in AWGN with 10 % nonzero coefficients

In the second experiment, we investigate the effect of parameter $\rho$ on the performance of the ZA-VSSLMS algorithm. The parameter $\rho$ in the ZA-VSSLMS algorithm that was defined in the Eq. (4) controls the strength of zero attraction to small adaptive taps and pulls them toward the origin, which consequently increases the convergence speed and decreases the MSD. Its value is changing within an interval $0<\rho <1$. One can experimentally find the optimal value of $\rho$ that results in the best performance in terms of MSD.

We implement both ZA-VSSLMS and the standard VSSLMS algorithms in the same setting and the parameters given in the first experiment. As we see in Fig. 2, the performance of the ZA-VSSLMS algorithm keeps improving compared to the VSSLMS algorithm by changing the $\rho$ value until it reaches its minimum MSD at $\rho =4\times 10^{-4}$. At this point, the ZA-VSSLMS algorithm shows 4 dB improvement over the standard VSSLMS algorithm. By choosing $\rho$ value to be greater than its optimal value, the ZA-VSSLMS algorithm starts losing its ability of attracting the zero taps as it produces a higher MSD compared to the standard VSSLMS algorithm.

Fig. 2

MSDs of the ZA-VSSLMS and VSSLMS algorithms with $\rho$ varying

Fig. 3

MSDs of the VSSLMS, ZA-VSSLMS, LMS, and ZA-LMS algorithms in AWGN

Finally, to investigate the tacking ability and steady performance of the ZA-VSSLMS algorithm in a different scenario, we design a filter of 50 coefficients with abrupt changes at certain periods of time. Initially, a random tap of the unknown system is set to 1, and the rest are zeros. After each 1,500 iterations, 4 and 14 coefficients are set to ones and others to zeros, respectively. The performance of the ZA-VSSLMS algorithm is compared to those of the standard VSSLMS, LMS, and ZA-LMS algorithms. All the experiments are implemented with 200 independent runs.

The following parameters were used during this experiment: For the VSSLMS: $\mu _{\mathrm{min}}=0.009,\,\mu _{\mathrm{max}}=0.013,\,\gamma =0.0048$ and $\alpha =0.97$. For the ZA-VSSLMS: $\mu _{\mathrm{min}}=0.008,\, \mu _{\mathrm{max}}=0.012,\, \gamma =0.0048,\, \alpha =0.97$ and $\rho =0.0001$. For the LMS: $\mu =0.001$. For the ZA-LMS: $\mu =0.001$ and $\rho =0.0001$.

As it can be seen from Fig. 3, when the system is highly sparse (before 1,500th iteration), the ZA-VSSLMS algorithm has 5.5 dB lower MSD than over the LMS and VSSLMS algorithms and about 3.5 dB lower than ZA-LMS algorithm. After 1,500th iterations, as the number of nonzero taps increases, the performance difference between ZA-VSSLMS and the other three algorithms becomes smaller. In the last 1,500 iterations where the system is non-sparse, the ZA-VSSLMS reduces to the standard VSSLMS. However, it still performs comparably better than the VSSLMS.

5 Conclusions

In this paper, we presented the convergence analysis of the recently proposed ZA-VSSLMS algorithm, and we derived its stability condition. The stability result is consistent with the standard VSSLMS algorithm. The performance of the ZA-VSSLMS were studied when the parameter $\rho$ is changing. It is observed that when $\rho < 10^{-3}$, the ZA-VSSLMS outperforms the standard VSSLMS algorithm for sparse impulse response. We also investigated the MSD of ZA-VSSLMS algorithm for different sparsity orders. The results shows superiority of ZA-VSSLMS over the standard VSSLMS algorithm when the system is highly sparse.