Bivariate flood distribution analysis under parametric copula framework: a case study for Kelantan River basin in Malaysia

Abstract

Flood is becoming an intensive hydro-climatic issue at the Kelantan River basin in Malaysia. Univariate frequency analysis would be unreliable due to multidimensional behaviour of flood, which often demands multivariate flow exceedance probabilities. The joint distribution analysis of multiple interacting flood characteristics, i.e. flood peak, volume and duration, is very useful for understanding critical hydrologic behaviour at a river basin scale. In this paper, a copula-based methodology is incorporated for multivariate flood frequency analysis for the 50-year annual basis flood characteristics of Kelantan River basin at Guillemard bridge station in Malaysia. Investigation reveals that the Lognormal (2P), Johnson SB-4P and Gamma-3P are selected as marginal distributions for the flood peak flow, volume and duration series. Several bivariate families such as mono-parametric, bi-parametric (i.e. mixed version) and rotated version of Archimedean copulas and also the elliptical copula are introduced to cover a large dependence pattern of flood characteristics. The dependence parameter of bivariate copulas is estimated by the method of moments (MOM) based on the inversion of Kendall’s tau and maximum pseudo-likelihood estimator. To analytically validate and recognize most parsimonious copulas, GOF test and Cramer–von Mises distance statistics (S_n) with the parametric bootstrap method are employed. The Gaussian copula is identified as the most justifiable model for joint modelling of the flood peak–volume and peak–duration combination for MOM-based parameter estimation procedure. Similarly, the Frank copula is selected as the best-fitted structure for modelling peak–duration combination based on MPL estimators, but the MOM estimator recognized Gaussian copula as most suitable for peak–volume pair. Furthermore, the best-fitted copulas are used for obtaining the joint and conditional return periods of the flood characteristics.

Introduction

Probabilistic assessments of flood episodes for estimating the flow exceedance probability or design variable quantiles in the light of univariate or multivariate joint distribution framework often facilitate an insightful concern or design criteria in the planning and designing of hydraulic or flood defence infrastructure projects (i.e. dam spillway, river channel, dikes, etc.), urban drainage system or flood hazard mapping (Cunnane 1987; Bobee and Rasmussen 1994; Goel et al. 1998; Sen 1999; Rao and Hameed 2000; Katz et al. 2002; Poulin et al. 2007 and references therein). According to Rakhecha and Sigh (2009), flood signifies an inundation due to the river overflowing their banks in respect of heavy or intense rainfall structure or either melting of a large amount of snow. Flood is a multidimensional stochastics consequence usually characterized completely through its trivariate intercorrelated vectors such as flood peak discharge flow, volume and duration of flood hydrograph (Zhang 2005; Zhang and Singh 2006). Flood frequency analysis (FFA) statistically defines through an inter-association between flood quantiles with nonexceedance probabilities or return period by fitting the probability distribution functions or PDFs (Goel et al. 1998; Yue 1999; Yue 2001; Yue and Rasmussen 2002). In other words, it is an approach to relate the strength of extreme event quantiles to their frequency of occurrence in the light of probability distribution framework.

Hydro-meteorological simulations based on the extension of historical rainfall samples to recognize catchments profile or based on joint simulations in conjunction with univariate or multivariate statistical framework over the variables of interest are the two distinct ways to address the risk assessments for the extreme flood scenario. Numerous attempts such as Calver and Lamb (1995), Blazkova and Beven (2004) and Lawrence et al. (2014) retrieved flood frequency curve through integrating the hydrologic models in conjunction with probabilistic rainfall models for demonstrating catchment’s rainfall–runoff profile. Such incorporation usually adapted the conventional-based lumped and distributed models or either via the continuous or event-based hydro-climatic simulations. But, all such incorporations often required longer computational analysis to justify the demands of high spatial and temporal resolutions for revealing a satisfactory demonstration of flood stimulations procedure and thus would attribute for an ineffective characterization of catchments behaviour (Requena et al. 2016).

Earlier efforts frequently incorporated the univariate frequency analysis of flood series for estimating univariate return periods, i.e. either flood peak or volume as a function with their nonexceedance probabilities (Cunnane 1987, Bobee and Rasmussen 1994). But many studies highlighted the unreliability of univariate return period, which would be incapable to providing the full screen of flood or inflow hydrograph and also underestimation (i.e. low design value might increase the risk of failure) or overestimations (i.e. increasing the cost of hydraulic construction) of associated hydrologic risk of correlated flood characteristics (Yue et al. 1999; Yue and Wang 2004). For example, flood episodes with peak discharge value of 100-year return period would be less damaging than the same flood events describing through the joint concurrency of flood peak–volume/or peak–durations/or volume–durations. Actually, the potential damage could likely be a function of several associated flood variables and ignorance of spatial dependency among its multiple vectors might be attributed for underestimation of uncertainty distributed over the estimated design quantiles and thus often demands more flood variables (Graler et al. 2013), in particular, from the prospects of hydraulic designing procedures where accountability of multivariate design parameters could be a feasible desire based on their multivariate exceedance probabilities (Salvadori 2004; Reddy and Ganguli 2012a).

The necessity of estimating design hydrograph or multivariate return periods instead of just estimating the design quantiles derived from the single variable flood episodes motivated numerous literature towards the incorporation of joint distribution analysis among multiple flood characteristics, i.e. between peak–volume, or peak–duration, etc., through introducing a distinguished variety of traditional bivariate or few trivariate probability distribution functions, i.e. Krstanovic and Singh (1987), Escalante and Raynal (1998), Yue (1999), Yue (2000, 2001), Yue and Wang (2004), Nadarajah and Shiau (2005), Escalante and Raynal (2008) and references therein. But such distribution-based flood modelling approach or FFA often surrounded with several statistical constraints and limitations such as (1) each flood vector must assume to have Gaussian or normal distributions or either transformed to have normal distributions; (2) if the number of variables is increased, then mathematical formulation becomes more complex and complicated; (3) statistical parameter of univariate marginal structure is often employed to model their joint dependence structure; (4) limited space is available to justify joint dependence structure, etc., (Zhang 2005; Zhang and Singh 2006; Schmidt et al. 2007; Song and Singh 2010). Besides this, conventional multivariate models often attribute for the heavy dependency of flood exceedance on the right tail which might result for complexity during the demonstrations of observed samples; thus, it could be demanding for the separate modelling of margins from their joint dependence structure for securing their joint association significantly (Zhang and Singh 2006; Reddy and Ganguli 2012a).

Therefore, after encountering the above limitations it motivated firstly, the De Michele and Salvadori (2003) firstly incorporated copulas function, for establishing the joint dependence structure of storm intensity and duration series. The copula function is recognized as a highly flexible multivariate tool which segregated the modelling of individual univariate flood vectors and their joint dependence structure separately into two distinct stages and thus attributes the higher flexibility in the selection of best-fitted marginal distributions and their joint structure to capture a wider extent of mutual concurrency and preservation in their joint association (Saklar 1959; De Michele and Salvadori 2003; Salvadori 2004; Salvadori and De Michele 2004; Nelsen 2006). Genest and Favre (2007) provided an extended review of the application of copulas in the field of engineering and sciences. A series of literature incorporated copulas function ,for example, for flood samples (i.e. Salvadori and De Michele 2004; De Michele et al. 2005; Grimaldi and Serinaldi 2006; Poulin et al. 2007; Genest et al. 2007; Fan and Zheng 2016; and references therein), for rainfall characteristics (i.e. Salvadori and De Michele 2006), for drought modelling (i.e. Shiau 2006). Besides their extended applicability in extreme event modelling, copula-based joint distributions are significantly applied in the field of groundwater modelling (i.e. Reddy and Ganguli, 2012b) and also modelling of hydro-climatic samples (i.e. Cong and Brady 2011), etc. For the essential mathematical terminologies and theorems associated with copula function, readers are advised to follow the literature such as Saklar (1959) and Nelsen (2006), also ‘International Association of Hydrological Sciences (or IAHS)’ for extended details and lists of their applicability in the field of hydro-climatological observations.

The Kelantan River basin is one of the largest basins of Malaysia, which are known to be flood-prone. From the past few decades, it is often subjecting to the most severe monsoonal flooding and perceiving for increasing in terms of their frequency and magnitude (DID 2000, 2003, 2004; MMD 2007; Adnan and Atkinson 2011). Few studies, such as Chan (1997) and DID (2000, 2003, 2004), report the expectation of the occurrence of catastrophic flooding has increased from once in every 50–15 years from 2004 in Kelantan. For example, intense and prolonged precipitation in the year 2002 caused flooding of a total area of 1640 km² and affected the population of 714,287 (Adnan and Atkinson 2011). Similarly, in the early month of December 2014, much heavy precipitation occurred for many of days triggered the flood event in several parts of the east coast of the Kelantan river basin and it was the worst flood ever recorded in history and affected more than 200,000 people (Adnan and Atkinson 2011; Rahman et al. 2018). The maximum length and breadth of this catchment area are 150 km and 140 km, respectively, and it is about 248 km long and drains an area of 13,100 km², occupying more than 85% of the state of Kelantan. The basin has an annual rainfall of about 2500 mm much of which occurs during the north-east monsoon (or wet season) between mid-October and mid-January. Few studies are performed over this river basin; for example, according to Hussain and Ismail (2013) investigation, Guillemard Bridge, Lebir and Galas stations have highest in flood frequency rather than Nenggiri station and also the value of damaged property got increased according to the frequency of flood happening. Also, Abdulkareem and Sulaiman (2015) investigated the variability of precipitation in flood source area of Kelantan river basin through the trend analysis using the annual maximum series of 24-h precipitation data and annual maximum flood data and revealed that no statistically significant trend was detected in the annual maximum series of 24-h precipitation between for the period 1984–2014 while the AMF series were significant at 5% level at the targeted locations. Similarly, Nashwan et al. (2018) revealed that the downstream area of the Kelantan River basin is the highest risk of devastating flood events. Besides this, a lot of attention has been also pointed out in this region in the context of the impact of land-use changes which may affect the catchments response; for example, Hassan (2004) report revealed the substantial land-use changes in this region which might influence the rate of evapotranspiration and infiltrations (Wooldridge et al. 2001). Wan (1996) and Jamaliah (2007) literature also pointed the existence of rapid land-use changes from the year 1970 to 2000s, mainly due to deforestation and conversion from natural land into agriculture for oil palm and rubber.

The cause of frequent failure of hydrologic or flood defence infrastructure in Malaysia due to the impact of moderately severe of flood episodes might be attributed due to the lack of complete flood hydrograph or in other words, where only flood peak discharge samples often targeted in deriving flood frequency curve during the structural development. For example, according to Gaál et al. (2015) in the designing of retention basins and spillways of reservoirs or any other flood defence hydraulic structures where the storage is involved, in such circumstances the estimation of hydrograph volume must be required along with peak discharge, in order to calculate the impact of inflow on the storage. Therefore, multivariate designs and their associated return periods could be a comprehensive way of tackling such extreme issues through a defensive risk-based decision-making in this river basin.

In this study, the multivariate flood frequency analysis is performed for the Kelantan River basin at Guillemard bridge station in Malaysia, in order to overcome the limitations associated with univariate analysis, by introducing the bivariate copula distribution framework for partial series of flood characteristics, i.e. flood peak discharge flow (P), volume (V) and duration (D) series. At-site event-based or block (annual) maxima-based methodology is adopted for the 50-year (1961–2016) continuously distributed stream flow characteristics of this river basin. Evaluating the performance of parametric family functions for constructing univariate marginal distribution of flood characteristics, comparing two types of parameter estimation procedure, i.e. method of moment (MOM) and maximum pseudo-likelihood (MPL) estimations procedure, for fitting a distinguished variety of bivariate copula families such as the Archimedean copulas, elliptical copulas also, rotated version of Archimedean and mixed version of Archimedean copulas family which are introduced and tested to analyse and statistically evaluate the bivariate joint probability of the flood variables occurrence, i.e. between flood peak–volume and peak–duration series and also their associated joint and conditional return periods estimations are the main research concern which is addressed in this literature.

As a prerequisite, brief details on the theoretical aspect of copula functions, procedure for the estimations of copula dependence parameters, performance measure of copulas via the goodness-of-fit test statistics to selecting most parsimonious copulas for establishing joint relationship among flood characteristics as well as mathematical approach towards the return periods of flood characteristics are discussed in the next sections. In the third section, the copula-based methodology is applied to a case study to establish a joint distribution, conditional distributional distribution and their associated return periods of the flood attribute pairs (i.e. P–V and P–D). The fourth section provides the result and discussions, and the fifth section provides the research conclusion. Figure 1 illustrates the flow diagram indicating the steps of the analysis.

Fig. 1

Flow diagram of the copula-based bivariate joint analysis of flood characteristics

Theoretical research framework

Concept of copula function

The ideas of the copula method have been developed by Saklar (1959). According to Nelsen (2006), copula function connects multivariate probability distributions to their univariate marginal functions. According to Sklar’s theorem (Nelsen 2006), if (X, Y) be the bivariate random variables with continuous marginal distributions $u = F_{X} \left( x \right) = P\left( {X \le x} \right) \;{\text{and}}\; v = F_{Y} \left( y \right) = P\left( {Y \le y} \right)$, then it can be characterized uniquely by its associated dependence function called Copula or C which can be defined on the unit square and can be expressed as:

$$H_{X,Y} \left( {x,y} \right) = C\left[ {F_{X} \left( x \right), F_{Y} \left( y \right)} \right] = C\left( {u,v} \right)$$

(1)

where C = any type of bivariate copulas under consideration; $F_{X} \left( x \right) = F_{Y} \left( y \right) =$ cumulative distribution functions of random variables ‘X’ and ‘Y’; $H_{X,Y} \left( {x,y} \right)$ = bivariate joint distribution which can be expressed using bivariate copula function $C\left[ {F_{X} \left( x \right), F_{Y} \left( y \right)} \right]$, as revealed from Eq. (1). According to Shiau (2006) and Zhang and Singh (2006), the copula C must be unique if $F_{X} \left( x \right)\; {\text{and}} \;F_{Y} \left( y \right)$ are continuous, which can capture the wider extent of dependencies among random variables. Conversely, if $F_{X} \left( x \right)$, $F_{Y} \left( y \right)$ and the copula functions $C\left[ {x,y} \right]$ are given, then Eq. (1) must define the bivariate joint distribution functions with its marginal distributions $F_{X} \left( x \right)$ and $F_{Y} \left( y \right).$ Similarly, if $f_{X} \left( x \right) \;{\text{and}} \;f_{Y} \left( y \right)$ are the probability density function of variables X and Y, then the joint probability density of the two random variables can be expressed as:

$$f_{X,Y} \left( {x,y} \right) = c\left( {F_{X} \left( x \right), F_{Y} \left( y \right)} \right) f_{X} \left( x \right)f_{Y} \left( y \right)$$

(2)

where c is the density function of bivariate copula C, which can be defined as:

$$c\left( {u,v} \right) = \frac{{\partial^{2} c\left( {u,v} \right)}}{\partial u\partial v}$$

(3)

in which $u = F_{X} \left( x \right)$ and $v = F_{Y} \left( y \right)$.

For the extended mathematical details about copula functions, readers are advised to follow Genest and Rivest (1993) and Nelsen (2006).

In this study, we introduced the Archimedean copula families (i.e. Clayton, Gumbel, Frank, Joe), mixed version of two-parameter Archimedean copulas such as BB1 (i.e. Clayton–Gumbel copula) (i.e. Constantino et al. 2008), BB6 (i.e. Joe–Gumbel copula) (i.e. Manner 2010), BB7 (i.e. Joe–Clayton copula) (i.e. Li et al. 2016) and BB8 (i.e. Joe–Frank copula) (i.e. Tang et al. 2015), one elliptical copula family (i.e. Gaussian copula) (i.e. Zhang et al. 2016), one rotated version of Archimedean copula family (rotated Clayton by 90° of rotation for capturing negative dependence as well) (i.e. Manner 2007). The rotated Clayton copula is introduced to cover negative dependence structure and can’t be used for modelling positively correlated random pair. Actually, the bivariate Clayton copula is only capable of capturing positive dependency (i.e. $0 \le \theta < \infty$); this means by considering the rotation (i.e. by 90°), it becomes possible to capture negative dependency for the same random variables (i.e. $- \infty < \theta \le 0$). The consideration of the Joe copula would be a good decision in case of higher positive correlation exhibited between random variables (McNeil et al. 2015) which often plays an important role, especially for highlighting the upper tail dependence structure in extreme value analysis (Alina 2018). For the Clayton and Gumbel family, the Kendall’s tau  ≥ 0 and is only significant to capture the positive dependency while the Frank family exhibited higher versatility due to its capability in accommodating the entire range of dependencies (i.e. τθ ∈ [1, − 1]) and is the only member that justified radial symmetry as well (i.e. symmetric to  u + v = 1) (De Michele and Salvadori 2003; Favre et al. 2004; Nelsen 2006). Table 1 represents the summary description of the bivariate Archimedean copula functions incorporated in this study.

Table 1 Mathematical expressions for bivariate Archimedean copula families and their associated properties

Mathematically, the copula function (i.e. [C: [0,1]2 ⟶ [0,1]]) approximates the bivariate Archimedean class copula, if it justifies the representation as given below:

$$C\left( {u,v} \right) = \phi^{ - 1} \left( {\phi \left( u \right) + \phi \left( v \right)} \right) \;{\text{for}} \;u,v \in ,\left[ {0,1} \right]$$

(4)

where (∅(.) and ∅ − 1) signify the generator function of the specified Archimedean copulas and their inverse such that the generator (φ: I ⟶ R+) signifies for the positive, convex and decreasing function and could be approximated for (∅(1) = 0 and ∅(1) = ∞) (Nelsen 2006). The elliptical family-based Gaussian copula is also introduced for testing their adequacy in the establishment of bivariate distribution of flood characteristics and can capture both the positive and negative dependencies (Favre et al. 2004). The Gaussian copula is an implicit copula which can be expressed as an integral over the density of X and can be expressed mathematically as given below (Zhang et al. 2016):

$$C_{\theta } \left( {u,v} \right) = \mathop \int \limits_{ - \infty }^{{ - \phi^{ - 1\left( u \right)} }} \mathop \int \limits_{ - \infty }^{{ - \phi^{ - 1\left( v \right)} }} \frac{1}{{2\pi \left( {1 - \theta^{2} } \right)^{1/2} }}\exp \left[ { - \frac{{s^{2} - 2\theta st + t^{2} }}{{2\left( {1 - \theta^{2} } \right)}}} \right]{\text{d}}s{\text{d}}t$$

(5)

The Gaussian copula shows almost no dependence in the tails of distribution which is mostly distributed around centre (Zhang et al. 2016; Alina 2018).

Estimating copula dependence parameter

Several methods are often motivated such as the method of moment based rank-based nonparametric measures, i.e. Kendall’s tau $\left( \tau \right)$ or Spearman’s rho $\left( \rho \right)$ (i.e. Genest and Rivest 1993; Reddy and Ganguli 2012a), exact maximum likelihood or EML (i.e. Zhang et al. 2016), inference functions for marginal or IFM (i.e. Joe 1997), canonical maximum likelihood or CML (Genest et al. 1995), maximum pseudo-likelihood estimations (MPL) (Genest et al. 1995). In this experiment, both the MOM estimator based on the inversion of Kendall’s tau $\left( \tau \right)$ and MPL estimators are applied separately for estimating copula dependence parameter.

MOM estimators based on inversion of Kendall’s tau $\left( \tau \right)$ is quite popular and highly flexible for the Archimedean families of copula which often follows the definition of empirical copula. This method is based on the relationship between the copula parameter ‘$\theta$’ and sample rank correlation coefficient and if the corresponded between them exhibited then the copula parameter can be estimated by putting the empirical values of the rank correlation into the relation as given below (Nelsen 2006):

$$\hat{\theta } = f\left( {\hat{\tau }} \right)$$

(6)

According to Nelsen (2006) and Veronika and Halmova (2014), the mathematical relationship between Kendall’s tau $\left( \tau \right)$, copula function and generator function can be expressed as;

$$\tau = 4\int_{{\left[ {0,1} \right]^{2} }} C\left( {u,v} \right){\text{d}}C\left( {u,v} \right) - 1$$

(7)

and

$$\tau = 1 + 4\mathop \int \limits_{0}^{1} \frac{\phi \left( t \right)}{{\phi^{\prime}\left( t \right)}}{\text{d}}t$$

(8)

where $\phi \left( \cdot \right) =$ is the generator function of Archimedean copula family and $\phi^{\prime}\left( t \right) =$ is the first derivative of the generator function. Functional relationship of Kendall’s tau $\left( \tau \right)$ with copula parameter for various Archimedean families of copula, which are incorporated in this demonstration, is presented in Table 1.

Schweizer and Wolff (1981) explored that the two standard nonparametric correlation measuring statistics, i.e. Kendall’s correlation and Spearman’s correlation, can be expressed in terms of copula function. Mathematically, the Kendall’s tau $\left( \tau \right)$ statistics can be estimated by using the following equation:

$$\left( {\frac{n}{2}} \right)^{ - 1} \mathop \sum \limits_{i \triangleleft j} sign\left[ {\left( {x_{i} - x_{j} } \right)\left( {y_{i} - y_{j} } \right)} \right]$$

(9)

where sign = 1; if $\left[ {\left( {x_{i} - x_{j} } \right)\left( {y_{i} - y_{j} } \right) > 0} \right]$ and sign = − 1; if $\left[ {\left( {x_{i} - x_{j} } \right)\left( {y_{i} - y_{j} } \right) < 0} \right]$, for i = j = 1,2, …, n.

The mathematical range of Kendall’s tau $\left( \tau \right)$ is [− 1,1]; for example, $\tau = 1$ represents for concordant and $\tau = - 1$ for discordant and zero represents no concordance will be exhibited between random pairs. Therefore, determination of Kendall’s tau $\left( \tau \right)$ from the given bivariate random observations is firstly required to estimate unknown copula dependence parameters. MOM estimators can only be used for mono-parametric copulas functions, i.e. having single dependence parameter can’t be used for deriving more than one copula parameters.

The MPL estimators are a modified version of traditional maximum likelihood method where the rank-based empirical distributions are used for estimating copula parameters independently from their univariate marginal distribution functions and can be applied for both one- and multi-parameter copula functions (i.e. De Michele et al. 2005; Klein et al. 2010; Kojadinovic and Yan 2010; Reddy and Ganguli 2012a). Based on maximizing the pseudo-log-likelihood function, one can easily estimate the copula parameter as follows:

$$l\left( \theta \right) = \mathop \sum \limits_{i = 1}^{n} \log \left[ {c_{\theta } \left\{ {F_{1} \left( {X_{i,1} } \right),F_{1} \left( {X_{i,2} } \right) } \right\}} \right]$$

(10)

where $\theta$ is the copula parameter; $l\left( \theta \right)$is the pseudo-log-likelihood function; $F_{1} \left( {X_{i,1} } \right) = F_{1} \left( {X_{i,2} } \right)$is the empirical CDFs.

Goodness-of-fit test for bivariate copulas

In this demonstration, Cramer–von Mises test statistics is employed to evaluate adequacy of hypothesized copula fitted to bivariate flood characteristics which is often considered as one of the most powerful models for compatibility testing (Genest and Rémillard 2008; Genest et al. 2009). According to Genest et al. (2009), this test is based on parametric bootstrapping procedure and makes use of the Cramer–von Mises statistic S_n, which can be computed as follows:

$$\begin{aligned} S_{n} &= n\int_{{\left[ {0,1} \right]^{2} }} \left\{ {c_{n} \left( {u,v} \right) - C_{\theta } \left( {u,v} \right)} \right\}^{2} dC_{n} \left( {u,v} \right) \\&= \mathop \sum \limits_{i = 1}^{n} \left\{ {c_{n} \left( {U_{i,n} ,V_{i,n} } \right) - C_{\theta } \left( {U_{i,n} ,V_{i,n} } \right)} \right\}^{2} \end{aligned}$$

(11)

where $C_{n} =$ empirical copula estimated using n observational flood attribute pairs and $C_{\theta} =$ parametric copula derived under the null hypothesis. In this experiment, the p-values for each copula are estimated using the parametric bootstrapping procedure (i.e. followed by Genest and Rémillard (2008)) which can be mathematically formulated as given below:

$$p = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} 1\left( {S_{n,t} \ge S_{n} } \right)$$

(12)

where N = number of simulations.

This fitness statistics actually involve testing of null hypothesis $H_{0 }$ against the alternate hypothesis $H_{\text{a}}$ as given below. Null hypothesis ($H_{0 } ) = C \in C_{0} \{ {\text{where,}} C_{0} = C_{\theta } ;\theta \in O)$.Alternate hypothesis ($H_{\text{a}}$) = $C \notin C_{0}$.where O is the open subset of ${\Re }^{q}$ for some integer value q. The acceptance or rejection of the considered copulas is based on estimated p values. If the estimated p value is larger than a significance level $\left( \alpha \right)$, then the null hypothesis must be accepted, resulting that copula must be considered as satisfactory performance; otherwise, it will be liable for rejections. Therefore, from Eq. (11), it must be concluded that minimum value of S_n test value indicates minimum gap or distance between an empirical and derived parametric copula; in other words, it indicates the most justifiable copula for establishing bivariate joint relationship between flood variables.

Return periods of the flood characteristics and conditional distribution

Hydrology and hydraulic applications mostly interested in the evaluation of the mean inter-arrival period between two design events which usually are defined in a year called the return period (Shiau 2003; Salvadori 2004). In particular, the design quantiles define a higher return period that often seems a feasible practice in the hydraulic structure designs (Requena et al. 2016). Concurrence probability usually defines the probability of any extreme happening (i.e. flood episodes), which either characterizes through univariate (say flood peak discharge or ‘P’) or multivariate variables (say flood peak and volume series ‘P’, ‘V’…) exceeding certain a threshold level say ‘p’ (or ‘p’, ‘v’… for the multivariate structure) (Yue and Rasmussen 2002; Shiau 2003; Salvadori 2004). Yue and Rasmussen (2002) and Salvadori and De Michele (2004) thoroughly discussed the basic concept of return periods. Mathematically, univariate return period of the targeted flood characteristics that occurs once in a year can be defined from the univariate cumulative distribution function or CDF of the variable (say ‘X’) as given below:

$$\begin{aligned} T_{\text{Univariate}} &= \frac{\mu }{{{\text{total}}\; {\text{no}} .\; {\text{of}}\; {\text{flood}}\; {\text{per}} \;{\text{year}}}} \\&= \frac{1}{{P\left( {X \ge x} \right)}} = \frac{1}{{\left( {1 - F\left( x \right)} \right)}} = \frac{1}{{1 - {\text{CDF}}\left( y \right)}} \end{aligned}$$

(13)

where μ is the mean inter-arrival time between two consecutive episodes and that could be equal to unity (i.e. μ = 1) for annual maxima-based flood modelling (Yue and Rasmussen 2002).

Derivation of return periods from bivariate joint distribution of flood attribute pairs

The notation of return period under univariate concept (Eq. 13) might be useful only if the concentration of single hydrologic or flood attribute will justify the requirements of the design process, and in other words, it will also indicate the existence of no significant inter-association exhibited between multiple relevant vectors (Veronika and Halmova 2014). But for justifying much practical and effective risk analysis, accountability of multiple potential vectors for characterizing flood events based on joint probability density function or JPDF and joint cumulative distribution functions or JCDF could be the essential demands for hydrologist and water practitioner. Estimating multivariate design variable quantiles under different notations of return such as based on joint probability distribution functions, conditional distribution analysis or either based on the Kendall’s distribution (or survival functions) is often an essential concern in the hydrologic risk assessments (Salvadori 2004; Graler et al. 2013). In multidimensional risk framework, return periods can be derived from the exceedance probabilities of flood attributes pair, such as joint return period derived from the joint exceedance probabilities. Actually, each separate approach of return periods has their own significance, and that will be solely based on the nature of the undertaking problem, which cannot be interchanged and is also impossible to decide for the most consistent ways (Serinaldi 2015). Selection of return periods is depending upon the importance of undertaken structure as well as its consequences of failure where their appropriate selection often attributed an impact over the strength of design variables quantiles. Shiau (2003), Salvadori (2004), Salvadori and De Michele (2004, Salvadori and De Michele 2007), and Serinaldi (2015) pointed an extended mathematical framework towards the deriving of different notations of return periods under copula-based methodology.

The joint probability distributions for annual flood analysis can describe the following two situation such that in the first condition both the flood variables (say, P ≥ p AND V ≥ v) simultaneously exceed certain threshold during a flood event and their associated return period called AND joint period and it can be written in the form of:

$$\begin{aligned} T_{p,v}^{\text{AND}} &= \frac{1}{{P \left( {P \ge p \;{\text{AND}}\; V \ge v} \right)}} = \frac{1}{{(1 - F\left( p \right) - F\left( v \right) + H\left( {p,v} \right)}} \\ &= \frac{1}{{(1 - F\left( p \right) - F\left( v \right) + C\left( {F\left( p \right), F\left( v \right)} \right)}} \end{aligned}$$

(14)

Equation represents the joint return period of flood variable $P \ge p$ and $V \ge v$ where both variables simultaneously exceed threshold value. $H\left( {p,v} \right)$ is the joint cumulative distribution functions between flood variables (i.e. P and V) and that can be expressed using bivariate copula function C(F(p), F(v)).

In the second situation, the probability of either the first or second flood variable (say, $P \ge p$ OR $V \ge v$) exceeds given their threshold and thus their associated return period called OR joint return period which can be expressed as:

$$T_{P,V}^{\text{OR}} = \frac{1}{{P \left( {P \ge p\; {\text{OR}}\; V \ge v} \right)}} = \frac{1}{{\left( {1 - H\left( {p,v} \right)} \right)}} = \frac{1}{{(1 - C\left( {F\left( p \right), F\left( v \right)} \right)}}$$

(15)

Equation represents the OR joint return period of flood variable, i.e. $P \ge p$ OR $V \ge v$ for the bivariate events where either of the variables exceeds threshold value. Using the above two equations, it could be possible to derive the OR and AND joint return periods between flood peak flow–volume and peak flow–duration series.

Derivation of return periods from conditional distribution of flood attribute pairs

In most of the hydrologic design requirements, it would be demanding to define events through highlighting the significance or priority of one design variables over another design vectors, and thus, from this prospect several studies pointed out the necessity of conditional distributional framework for defining the concept of conditional return periods such as Salvadori and De Michele (2004), Shiau (2006), Zhang and Singh (2006), Zhang and Singh (2007a), Salvadori and De Michele (2010), Reddy and Ganguli (2012a, 2013), Veronika and Halmova (2014), Zhang et al. (2016) and Tosunglou and Kisi (2016). The conditional return period relies on a conditional probability relationship between flood characteristics given that some condition is fulfilled such as the conditional return period of flood peak series given various percentile values of flood volume or vice versa or in other words where the flood peak ‘P’ exceeds a threshold ‘p’ given that the volume ‘V’ series exceeds a threshold ‘v’. For example, probability of flood peak conditional to volume (or duration) or either the flood volume conditional to peak (or duration) or either flood duration conditional to flood peak (or volume) information would be benefited from the hydraulic design prospects. Therefore, using the bivariate copula functions, the conditional return periods between flood characteristics (say, P and V) can be obtained from the conditional probability distribution function as:

$$\begin{aligned} H_{{P\backslash V}}^{{\prime }} \left( {p\backslash v} \right) &= H\left( {p\backslash V \le v} \right) = \frac{{P\left( {P \le p,V \le v} \right)}}{{P\left( {V \le v} \right)}} \\ &= \frac{{H_{{P,V}} \left( {p,v} \right)}}{{F\left( v \right)}} = \frac{{C\left( {F\left( p \right),F\left( v \right)} \right)}}{{F\left( v \right)}} \\ \end{aligned}$$

(16)

and

$$T_{{\left( {P\backslash V} \right)}} \left( {p\backslash v} \right) = T_{{\left( {p\backslash V \le v} \right)}} = \frac{1}{{1 - H_{P\backslash V}^{'} \left( {p\backslash v} \right)}} = \frac{F\left( v \right)}{{F\left( v \right) - C\left( {F\left( p \right), F\left( v \right)} \right)}}$$

(17)

where $H_{P,V} \left( {p,v} \right)$ is the joint CDF of flood vector P and V which can be estimated using the bivariate copula functions $C(F\left( p \right), F\left( v \right)$) with $F\left( p \right)$ and $F\left( v \right)$ being the marginal distribution of flood peak and volume series. Actually, Eq. (16) represents the conditional distribution function of flood peak ‘$P$’ given volume ‘$V \le v$’. Thus, using Eq. (17), it could be possible to obtain return periods for various possible occurrences of flood characteristics (i.e. return period of volume condition to peak or either between volume–duration and peak–duration series).

Similarly, the conditional distribution of flood peak ‘P’ given ‘$V \ge v$’ or vice versa can be obtained using the following equations:

$$\begin{aligned} H_{{P\backslash V}}^{{\prime }} \left( {p\backslash v} \right) &= H\left( {p\backslash V \ge v} \right) = \frac{{P\left( {P \le p, V \ge v} \right)}}{{P\left( {V \ge v} \right)}} \\ &= \frac{{F\left( p \right) - H_{P,V} \left( {p,v} \right)}}{1 - F\left( v \right)} = \frac{{F\left( p \right) - C\left( {F\left( p \right), F\left( v \right)} \right)}}{1 - F\left( v \right)} \end{aligned}$$

(18)

and

$$T_{{\left( {P\backslash V} \right)}} \left( {p\backslash v} \right) = T_{{\left( {p\backslash V \ge v} \right)}} = \frac{1 - F\left( v \right)}{{1 - F\left( v \right) - F\left( p \right) + C\left( {F\left( p \right), F\left( v \right)} \right)}}$$

(19)

Therefore, by using the copula-based methodologies for estimating the joint and conditional distribution of the event-based or block (annual) maxima-based mutually correlated flood characteristics, the joint and conditional return periods are computed which can be an essential requirement for the Kelantan River basin for tackling several water-related queries.

Application

Details of study area

Monsoonal flood happening seems to be increased in the Kelantan River basin in Malaysia from the last few decades in terms of frequency as well as magnitude, according to the report of Drainage and Irrigation Department, Malaysia (DID 2000, 2003, 2004) and Malaysia Meteorological Department (MMD 2007). The geographical location of this river basin is ${\text{Lat}}\; 4{^\circ }\, 30^{{\prime }} \,{\text{N}}\; {\text{to}} \;6{^\circ } 15^{{\prime }} \; {\text{N}}\; {\text{and}}\;{\text{Long}}\; 101{^\circ }\,{\text{E}}\; {\text{to}}\; 102{^\circ } \,45^{{\prime }} \,{\text{E}}$, and it is the longest river of Kelantan state, which originates from the Tahan mountain range to the South China Sea in the north-eastern part of Peninsular Malaysia. The river is about 248 km long with a drain area of 13,100 km² occupying more than 85% of the state of Kelantan. The estimated runoff is about 500 m³ s⁻¹, and the variations in annual precipitations for this region are in between 0 mm (dry period) and 1750 mm (wet or north-eastern monsoonal period) (DID 2000). The major land use of this area is agriculture (i.e. paddy, rubber and oil palm) for midstream and downstream and forest for upstream (i.e. near to Gua Musang). Few studies over this region such as Chan (1997), Jamaliah (2007) and Adnan and Atkinson (2011) pointed that such extreme hydrologic consequences are mainly due to rapid human intervention from natural to land-use activities in the form of deforestations or land clearance either for promoting the agricultural activities through palm oil and rubber plantations or due to logging activities. In this literature, copula-based methodology is adopted for the 50 years (1961–2016) of daily basis streamflow discharge records for the Kelantan River basin which are collected and provided by the Drainage and Irrigation Department (DID), Malaysia, at the Guillemard Bridge gauge stations, at the downstream of Kelantan River near the Kuala Kari region.

Delineation of trivariate flood characteristics

Flood probability construction via the partial data series only focuses the extreme hydrograph portion, i.e. either high flow (for flood episodes) or low flow (for drought events), instead of visualizing the entire hydrograph (Correia 1987; Hosking et al. 1985; Rao and Hameed 2000). Annual (maximum) series (AM) also called block (annual) maxima and peak over threshold (or POT) are the two frequently modelling techniques widely accepted in the extreme probability simulations (Hosking et al. 1985; Madsen et al. 1997). The annual maximum flood peak discharge, volume and duration value of the flood episodes are retrieved from daily basis stream flow data. The characterizations of flood peak flow values are based on their maximum streamflow discharge records at an annual scale which means for each year there will be only one flood episode at the targeted site (Fig. 2) (Yue 2000; Yue and Rasmussen 2002; Xu et al. 2015). Similarly, corresponding to each flood peak value of the annual basis flood events, volume and duration series are derived from the streamflow hydrograph and using the algorithm reported by the literature such as Yue et al. (1999), Yue (2000) and Yue and Rasmussen (2002). Actually, flood duration (D) can be estimated by recognizing the time of rise and fall of the flood hydrograph as illustrated in Fig. 2 (i.e. points at Q_is and Q_ie) using Eq. (22). Flood peak discharge often attains their maximum value but not mandatory for hydrograph volume and duration series (Sraj et al. 2014; Xu et al. 2015). Mathematically, we are required to derive triplet flood characteristics for each of the ith years using the following equations:

$$\begin{aligned} P_{i} &= \hbox{max} \left\{ {Q_{ij} , j = {\text{SD}}_{i} + {\text{SD}}_{i} + 1, \ldots ,ED_{i} } \right\} \\ &= {\text{Annual}} \;{\text{flood}}\;{\text{peak }}\;{\text{series }} \end{aligned}$$

(20)

$${\text{Volume}} = V_{i} = V_{i}^{\text{total}} - V_{i}^{\text{Baseflow}} = \mathop \sum \limits_{{j = {\text{SD}}_{i} }}^{\text{ED}} Q_{ij} - \frac{{\left( {1 + D_{i} } \right)\left( {Q_{is} + Q_{ie} } \right)}}{2}$$

(21)

$${\text{Duration}} = D_{i} = {\text{ED}}_{i} - {\text{SD}}_{i}$$

(22)

where $Q_{ij}$ = jth days streamflow magnitude for the ith year and $Q_{is} \& Q_{ie} =$ streamflow magnitude for the start date ‘${\text{SD}}_{i}$’ and end date ‘${\text{ED}}_{i}$’ of the flood runoff. Once the flood characteristics are obtained from daily stream flow data using equations, it can be used for copula-based flood frequency analysis. Table 2 represents the descriptive statistics of triplet flood characteristics extracted from the daily streamflow discharge value at an annual scale (i.e. partial data series). Each univariate flood vector exhibited positively skewed distributions in which the duration series exhibited quite higher degree of unsymmetrical behaviour; Fig. 3a shows histogram distribution plot of flood characteristics. Figure 3b represents time series visualization of flood peak, volume and duration series.

Fig. 2

A typical hydrograph showing flood characteristic for the ith flood episodes

Table 2 Summary statistics of the flood event characteristics

Fig. 3

Visualizing the block (annual) maxima-based flood characteristics of the Kelantan River Basin at Guillemard Bridge station between the years 1960 and 2016 in the context of a histogram plot and b time series plot of peak, volume and duration series

Estimating marginal probability distribution of flood characteristics

Empirical univariate nonexceedance probabilities

The empirical nonexceedance probabilities or cumulative distribution, i.e. P(K ≤ k), for observed values of flood characteristics is derived from the commonly used Gringorten-based position-plotting formula (Gringorten 1963; Cunnane 1978; Zhang and Singh 2006; Karmakar and Simonovic 2008), which is usually compared with CDF of the fitted distributions for pointing the gaps and deviations between empirical and fitted samples and which can be mathematically formulated as:

$${\text{Empirical }}\;{\text{Cumulative }}\;{\text{frequency}} = P\left( {K \le k} \right) = \left( {k - 0.44} \right)/\left( {N + 0.12} \right)$$

(23)

where N = length of the sample (i.e. the total number of flood observations) and k = kth smallest observations in the data set arranged in ascending order.

Fitting univariate marginal distribution of flood characteristics

Selecting the most justifiable and parsimonious univariate probability distribution functions for defining flood marginal density is often a mandatory prerequisite desire before introducing random vectors into multivariate copula framework (Reddy and Ganguli 2013; Tosunoglu and Kisi 2016). In this study, the flood characteristics that are targeted are flood peak discharge flow, volume and its durations for the partial series of data called block (annual) maxima-based flood distribution analysis. Parametric distribution-based modelling is often based on the assumption that the undertaken samples must be following some specific distributions or having their predefined PDF. Actually, in hydrologic data modelling, no universally accepted distributions are assigned from any literature or in favour of any probability distribution functions to model any extreme series (Adamowaski 1985, 1989; Silverman 1986; Dooge 1986; Yue et al. 1999; Santhosh and Srinivas 2013). Several models often would fit the data equally well, but each would give different estimates of a given quantile, especially in the tails of the distribution, which is solely based on the goodness-of-fit procedure to visualize the compatibility of the fitted distributions (Karmakar and Simonovic 2008). An interactive set of 1-dimensional parametric functions with varying numbers of the unknown statistical parameter (i.e. 1 parameter, 2 parameters, 3 parameters and 4 parameters) are introduced as a candidate function in modelling univariate marginals of the flood characteristics. Table 3 lists the mathematical expressions (i.e. PDF) of distinct varieties of univariate parametric models and their associated vector of unknown statistical parameters or model parameters which are targeted for modelling marginal distribution of flood characteristics. The vector of the unknown statistical parameter of the fitted distributions for each flood characteristic is estimated based on the maximum likelihood estimation (MLE) (i.e. Owen 2008), method of moments (MOM) (i.e. Bain and Engelhardt 1991; Rao and Hameed 2000), least square method (LS) and L statistics-based method of L-moments (i.e. Hosking and Walis 1987). All the univariate distribution fitting procedures and their parameter estimation are carried out using Easyfit software (Mathwave Technologies 2004, 2017).

Table 3 Mathematical expressions for density functions and vector of unknown statistical parameters of different univariate probability distribution functions

Result and discussions

Test for stationarity within time series of flood characteristics

The individual flood characteristics need to be stationary or time independency behaviour before introducing into the univariate or multivariate copula distribution framework. Before modelling the joint dependency between floods using bivariate copula functions, it is mandatory to investigate whether the individual time series associated with each flood characteristic exhibits no serial correlations or stationary. For this, Ljung and box (1978)-based hypothesis testing also called Q-statistics is undertaken for investigating whether the individual series are time independent and no serial correlation (Cong and Brady 2011). Statistically, the Q-statistics usually follows a Chi-square distribution with ‘h’ degree of freedom under the null hypothesis H₀ (Ljung and Box 1978; Daneshkhan et al. 2016). Thus, Q-statistics for the sample size ‘n’ with ‘t’ is the total no. of lags being tested with sample autocorrelations at the specific lag, i.e. $\hat{\rho }_{t}$, as given below:

$$Q = n\left( {n + 2} \right)\mathop \sum \limits_{t = 1}^{h} \hat{\rho }_{t}^{2} /n - t$$

(24)

where null hypothesis (H₀) = zero autocorrelation or independent distributions and alternative hypothesis (H_a) = existence of serial correlation (or autocorrelation). The estimated Q-statistics and their associated p value for different lag sizes (i.e. 30, 20, 15, 10 and 5) are listed in Table 4 which points for almost negligible or zero first-order autocorrelations as their estimated statistics are below their critical value for each of the univariate series by accepting the null hypothesis (H₀) at 5% or 0.05 significance level against their alternative hypothesis (H_a) (Table 4). Figure 4a, b illustrates the graphical visualizations for investigating the existence of serial correlation within flood characteristics in the context of autocorrelation plot and sample autocorrelation plots. The nonparametric rank-based Mann–Kendall or M–K test is also incorporated for visualizing the monotonic trend within the historical series of flood characteristics under the null hypothesis H₀ against their alternative hypothesis H_a (Mann 1945; Kendall 1975), and their estimated values are listed in Table 5. The test is incorporated under two-tailed hypothesis attempts of the null hypothesis H₀ (i.e. zero trend with flood characteristics) against alternative hypothesis H_a which can be mathematically expressed as:

$$S = \mathop \sum \limits_{i = 1}^{n - 1} \mathop \sum \limits_{j = 1 + 1}^{n} \text{sgn} \left( {T_{j} - T_{i} } \right)$$

(25)

$$\text{sgn} \left( {T_{j} - T_{i} } \right) = \left\{ {\begin{array}{*{20}c} {1, } & { {\text{if}}\quad T_{j} > T_{i} } \\ {0,} & { {\text{if}}\quad T_{j} = T_{i} } \\ { - 1,} & { {\text{if}}\quad T_{j} < T_{i} } \\ \end{array} } \right.$$

(26)

where $T_{j} \;{\text{and}}\; T_{i }$ represent the annual value in year ‘j’ and ‘i’, respectively. Test statistics reveals the acceptance of null hypothesis (H₀) which points the existence of zero monotonic trend at the 5% or 0.05 level of significance level within flood series. In conclusion, no significant trends are detected for the flood characteristics; therefore, detrend or prewhitening procedure is not adopted (i.e. Razawi and Vogel 2018) before introducing the flood samples into univariate probability distribution framework.

Table 4 The Q-statistics and their corresponding p value for peak flow, volume and duration series

Fig. 4

a Autocorrelation plot and b sample autocorrelation plot of flood characteristics (P, V and D)

Table 5 Mann–Kendall (or M–K) test for identifying the existence of monotonic trend within time series of flood variables

Dependence measures of flood characteristics

The Pearson’s linear correlation (r) and two nonparametric dependence measures also called the rank-based correlations statistics such as Kendall’s tau (t) and Spearman’s rho (ρ) are used to measure the strength of dependency between flood characteristics and their estimated values are listed in Table 6. Actually, the Pearson coefficient only captures the linear dependencies and therefore might be incompatible for heavy-tailed distribution series (Tosunoglu and Kisi 2016). According to Favre et al. (2004), the Pearson correlation coefficient is not invariant to monotonic transformations to Kendall’s and Spearman’s correlation measures. Also, it can be strongly affected by outliers. On the other hand, the nonparametric measures of dependence called the Kendall’s tau and Spearman’s correlation measures are invariant under monotonic nonlinear transformations, without any assumption of underlying distribution structure, and thus frequently used as effective dependence measures for the nonlinear modelling in multivariate statistics. Both the Kendall’s tau and Spearman’s are calculated using ranking of random series; also both exhibited high resistance to outliers (Klein et al. 2011). From Table 6, it can be observed that flood peak and volume pair exhibited strong positive correlation. But the correlation structure between flood peak–duration pair and flood volume–duration pair is very weak where both are having negative dependence structure or negatively correlated.

Table 6 Correlation coefficient between flood peak flow–volume, volume–duration and peak flow–duration series

Several graphical tools such as scatter plot, chi plots (i.e. Fisher and Switzer 2001) and Kendall’s plots (i.e. Genest and Boies 2003) of the pair-wise flood characteristics are also presented for analysing the degree of inter-association and strength of dependency between flood attribute pairs, as illustrated in Figs. 5, 6 and 7. Chi-plot is actually a scatter plot of the pairs $(\lambda_{i} \chi_{i} )$, where it uses the data ranks, and $\lambda_{i}$ values is a measure of the distance of bivariate random observations (say $p_{i} v_{i} )$ from the centre of the data sets within the range of [− 1, 1]. Thus, for positively or negatively correlated random pairs, their values will tend to positive or negative. Also, the control limits $\chi_{i}$ are another measuring factor in chi-plot that are placed at $\chi = \pm c_{p} /\sqrt n$ (Fisher and Switzer 2001). Therefore, in case of stronger dependency the random pairs must be outside the control limit of chi-plot otherwise inside the control limit region which can be indicated for independence between random pairs. On the other hand, the Kendall’s plot is analogous to quantile–quantile (Q–Q) plot such that deviation of random pairs from the main diagonal of K-plot is the indication of inter-dependence otherwise it could be revealed for independence when the pot tends to be linear (Genest and Boies 2003; Genest and Favre 2007). The scatter plot between flood peak–volume pair of Fig. 5 clearly indicates the existence of positive and strong dependency because the increased density of points is located near the diagonal region (i.e. close to 45° angle). From Fig. 5, it reveals the existence of weak dependency between flood volume–duration and flood peak–duration pairs. Based on ranked chi-plot for flood peak–volume series, it indicated the evidence of strong dependency between these random pairs because a strong deviation from the control limit is observed for these random pairs. Between flood peak–duration and volume–duration pairs, very weak dependency is observed because most of the data samples are within the region of control limit. Similarly, based on kendall’s plot, it also indicates strong positive dependency between flood peak–volume pair because the data pairs are much deviated from the main diagonal, but the flood peak–volume and volume–duration random pairs are much closer to main diagonal, thus indicating negative and weak dependencies between these flood attribute pairs.

Fig. 5

Scatter plot of the multivariate flood characteristics

Fig. 6

Graphical interpretation of strength of dependence of pair-wise flood characteristics using Chi-plot between P–V, P–D and V–D

Fig. 7

Kendall’s plot (or K-plot) of the pair-wise flood characteristics such as between P–V (shows high and positive correlation structure), P–D (shows negatively correlated random pairs with weak dependency exhibited), V–D (negatively correlated random pairs)

Modelling of univariate flood marginal distributions

From Tables 4 and 5, it is already revealed that no significant trends are detected for the flood characteristics; therefore, the prewhitening procedure is not adopted (i.e. Razawi and Vogel 2018) before introducing the flood samples into univariate probability distribution framework.

A distinct variety of parametric probability distribution families (i.e. 1 parameter, 2 parameters, 3 parameters & 4 parameters) are introduced as a candidate model for demonstrating the univariate marginal distribution of each individual flood characteristic, and their PDFs are listed in Table 3. The vector of the unknown statistical parameters is estimated using maximum likelihood estimation (MLE), method of moments (MOM), least square method (LS) and method of L-moments, and the estimated parameter values of different univariate functions are listed in Table 7. Different analytical-based goodness-of-fit measures such as Kolmogorov–Smirnov (or K–S) (i.e. Conover 1999; Xu et al. 2015; Kong et al. 2015) and Anderson–Darling (or A–D) (i.e. Anderson and Darling 1954; Scholz and Stephens 1987; Farrel and Stewart 2006) distance criteria statistics, information criteria statistics such as Akaike Information criteria (or AIC) (i.e. Akaike 1974), Schwartz’s Bayesian Information criteria (or BIC) (i.e. Schwarz 1978) and Hannan–Quinn Information criteria (HQIC) (i.e. Hannan and Quinn 1979) and error indices statistics such as mean square error (or MSE) and root mean square error (or RMSE) (i.e. Singh and Demissie 2004; Moriasi et al. 2007) are incorporated for selecting the possible marginal structure of peak flow, volume and duration series based on the comparative assessments between their empirical cumulative and theoretical probabilities. The empirical nonexceedance probabilities are estimated from the Gringorten-based position-plotting formula using Eq. (23). Performance of different univariate models for fitting marginal distribution for flood characteristics is listed in Table 8a–c. It reveals that the performance of Lognormal (2P) distribution is much satisfactory for flood peak flow samples in comparison with other candidate functions such as the K–S value and A–D test statistics (${\text{KS}}_{n}$ (d-max) = 0.05293 with p value 0.9977) and (${\text{AD}}_{n}$ (d-max) = 0.19412) where the D-critical value for K–S and A–D test for sample size 50 is 0.1884 and 2.5018 at 5% significance level. Similarly, the performance of Johnson SB-4P and Gamma-3P is much consistent for representing flood volume and duration series such as K–S value and A–D test value for Johnson SB-4P distribution (${\text{KS}}_{n}$ (d-max) = 0.0522 with p value 0.99811) and (${\text{AD}}_{n}$ (d-max) = 0.17314), and for Gamma-3P distribution it is (${\text{KS}}_{n}$ (d-max) = 0.07865 with p value 0.89254) and (${\text{AD}}_{n}$ (d-max) = 0.37708). Statistically, if the estimated K–S and A–D values are below their critical level at the significance level ‘α’, then it often indicated better model performance with the observed flood characteristics. Information criteria-based statistics are also incorporated to find out the acceptability of the distribution functions which are pointed on the basis of K–S and A–D test and which indicates that the AIC, BIC and HQIC values are at minimum for Lognormal (2P) (i.e. AIC = − 379.344, BIC = − 375.52, HQC = − 377.89) for representing flood peak flow value, Johnson SB-4P distribution (i.e. AIC = − 381.821, BIC = − 374.173, HQC = − 378.91) for representing flood volume samples and Gamma-3P distribution (i.e. AIC = − 343.62, BIC = − 337.886, HQIC = − 259.089) for representing flood duration series. Minimum the AIC, BIC and HQIC value always indicates for the most suitable model. Error indices statistics such as based on RMSE and MSE measures are also in support of the distribution function selected from distance criteria statistics and information criteria statistics such as Lognormal (2P) distribution (MSE = 0.00046, RMSE = 0.02163) for flood peak, Johnson SB-4P (MSE = 0.0004112, RMSE = 0.02163) for volume and Gamma-3P distribution (MSE = 0.000918804, 0.030312) for representing duration samples. Overall, after summarizing all the analytical testing measures, it is pointing towards the Lognormal (2P) distributions for flood peak discharge flow, Johnson SB-4P for volume and Gamma-3P for modelling flood duration series. The probability density or PDFs plot and cumulative distribution or CDFs plot of the best-fitted marginal distribution of the flood characteristics are illustrated in Fig. 8a–c.

Table 7 Estimated parameters of marginal distribution of flood characteristics

Table 8 Performance of different univariate models for fitting marginal distribution for flood characteristics (a) based on K–S and A–D test distance statistics, (b) based on information criteria statistics such as AIC, BIC and HQC, (c) based on error indices statistics such as MSE and RMSE

Fig. 8

Fitted marginal distribution and their probability density functions (PDFs), cumulative distribution functions (CDFs), plot for flood characteristics a flood peak flow, b volume and c duration series

Modelling of joint dependence structure using bivariate copulas

In this demonstration, several bivariate copula families such as one elliptical family, i.e. Gaussian copula, mono-parametric and mixed version of bi-parametric Archimedean families, i.e. Clayton, Gumbel, Frank, Joe, BB1, BB6, BB7 and BB8 copulas, also rotated versions Archimedean copula families, i.e. rotated Gumbel by 90 degrees, are incorporated, and then, most appropriate copulas are selected for bivariate joint distribution analysis of flood characteristics. The rotated Archimedean copulas are included to cover negative dependence as well. In the modelling of flood peak–volume series, the rotated Clayton copula can’t be used because of positively dependent random variables between these random pairs which is only applicable to capture negative flood correlation structure (i.e. kendall’s tau < 0). Similarly, the Gumbel–Hougaard, Clayton, Joe, BB1, BB6, BB7, BB8 copulas can’t be used for negatively dependent data (i.e. Kendall’s tau < 0) such as between P–D, which is only applicable for positively correlated random variables such as between flood pair, P–V.

The vector of unknown statistical or dependence parameters of copula families fitted to observed flood attribute pairs is estimated using method of moment-like (MOM) estimators based on the inversion of Kendall’s tau and maximum pseudo-likelihood (MPL) estimators using Eqs. (6)–(9) for MOM estimator and based on Eq. (10) for MPL-based copula parameter estimation. The MOM estimators can’t be used for the estimation of bi-parametric copulas (i.e. having more than one dependence parameter) such as BB1, BB6, BB7 and BB8 copula, but MPL estimator can be used for estimating one parameter or more than one parameter copula. The estimated copula parameters fitted to P–V and P-D random pairs using both MPL and MOM estimators are listed in Tables 9a, b and 10a, b.

Table 9 Estimating copula dependence parameters based on the maximum pseudo-likelihood (MPL) estimator and their corresponding goodness-of-fit statistics via parametric bootstrap technique for (a) flood peak flow and volume and (b) peak flow and duration

Table 10 Dependence parameter estimates of copulas function based on the Inverse of Kendall’s tau [method of moment (or MOM)] and their corresponding goodness-of-fit statistics based on the parametric bootstrap technique for (a) flood peak flow and volume and (b) peak flow and duration pairs

To analytically validate and identify the most justifiable copula for describing joint distribution for both the estimators (i.e. MOM and MPL), it is investigated by means of Cramer–von Mises distance statistics with parametric bootstrap method which is employed using Eqs. (11) and (12). For this purpose, the test statistics ‘S_n’ and its associated p value have been computed from 1000 and 500 simulated random samples by means of parametric bootstrap procedure as given in Tables 9a, b (for MPL-based estimation procedure) and 10a, b (for MOM-based copulas estimation procedure). Table 9a, b shows the result based on MPL-based copula simulations; it reveals that the Gaussian copula exhibited minimum ‘S_n’ statistics (i.e. ‘S_n’ = 0.013444) and the highest p value (i.e. p value = 0.9356 for N = 1000 bootstrap samples and p value = 0.9411 for N = 500 random bootstrap samples) for flood peak–volume pair, as compared to another copula function. From the same table, it reveals that the frank copula is identified as the most suitable bivariate model for capturing joint structure of flood peak–duration (i.e. ‘S_n’ = 0.031215, p value = 0.4001 for N = 1000 bootstrap samples and p value = 0.3762 for N = 500 bootstrap samples). Similarly, Table 10a, b shows the estimations based on MOM estimators, the Gaussian copula recognized as most suitable for constructing joint distribution of flood peak–volume and peak–duration samples (i.e. ‘S_n’ = 0.01579, p value = 0.9156 for N = 1000 bootstrap samples and p value = 0.9012 for N = 500 bootstrap samples), for P–V random pairs, (i.e. ‘S_n’ = 0.030559, p value = 0.4101 for N = 1000 bootstrap samples and p value = 0.3982 for N = 500 bootstrap samples), for P–D random pairs. Also, the Kendall’s tau τ values estimated from the derived copulas fitted to flood attribute pairs are also listed in Tables 9 and 10 for each copula function. Besides the analytical fitness measures, graphical visual inspections are also carried out based on scatter plot (Fig. 9a, b) of the 1000 sample observations which are simulated from the joint distribution using copula functions which are recognized as most consistent (i.e. based on analytically goodness-of-fit measure) for both MPL- and MOM-based copula dependence parameter estimation procedures. The Kendall’s τ values of the simulated samples are also shown in Fig. 9a, b. Similarly, Fig. 10a, b illustrates the chi-plot and K-plot of the set of 1000 random samples drawn from the best-fitted bivariate copulas derived from MOM and MPL estimators for P–V and P–D combinations. From the comparison of scatter plots of simulated data (green colour) with overlapped observed flood characteristics (red colour), it can be revealed that the Gaussian copula performed satisfactorily for capturing the observed dependence of flood variables for P–V and P–D series in case of MOM-based estimators since the simulated data are adequately overlapped with the natural dependence of observed flood characteristics. Similarly, for MPL estimators, the performance of Gaussian copula (for P–V samples) and Frank copula (for P–D samples) is much satisfactorily and in support of analytical fitness test result.

Fig. 9

Scatter plot for comparing observed (red colour) flood peak–volume and peak–duration series with the set of 1000 sample observations simulated (green colour) from best-fitted bivariate copula functions for both MPL- and MOM-based dependence parameter estimation procedures

Fig. 10

Chi-plots and K-plots of the set of 1000 random sample drawn from best-fitted copulas using MOM and MPL-based dependence parameter estimation procedure fitted to a flood peak and volume (based on Gaussian copula) and b flood peak flow and duration series (Gaussian copula via MOM estimator and Frank copula via MPL estimator)

Joint and conditional distributions and their associated return periods

The univariate return period of the flood characteristics is derived from best-fitted univariate probability distribution functions (i.e. Lognormal (2P) for flood peak, Johnson SB-4P for flood volume and Gamma-3P for flood duration series) using Eq. (13) and represented in Fig. 11.

Fig. 11

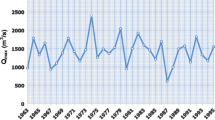
Univariate return period of the flood characteristics during the period of 1961–2016 (Kelantan river basin at Guillemard Bridge gauge station in Malaysia) derived from the Lognormal (2P) distribution for flood peak flow series, Johnson SB-4P for volume and Gamma-3P for duration series. Note: Brown circle in the Joint CDF contour plot represents observed flood peak and volume samples

Univariate return periods would attribute for underestimations or overestimations of hydrologic risk. This approach would be useful when only one flood characteristic is significant in design criteria, but in practical the considerations of multiple design variables are required for revealing effective risk practices. The best-fitted copulas which are identified in the previous section for both MOM and MPL estimators are employed for establishing joint distribution relationship, and their associated bivariate joint return between flood peak–volume and peak–duration pairs for both the ‘OR’ and ‘AND’ joint cases is estimated using Eqs. (14) and (15). Figures 12 and 13 represent the joint probability density function (JPDF) and joint cumulative distribution function (JCDF) plots (i.e. three-dimensional scatter plot, surface plot and contour plot) of flood peak–volume pairs using best-fitted Gaussian copula whose parameter is estimated using MOM and MPL estimator. Similarly, Figs. 14 and 15 represent the JPDFs and JCDFs of peak–duration pair using the Gaussian copula (i.e. best-fitted based on MOM estimator) and the Frank copula (best-fitted copula based on MPL estimator). The joint return periods of the flood characteristics, such as between flood peak–volume pair, and peak–duration pair for both OR and AND joint return cases, are estimated using Eqs. (14) and (15). It should be noted that for a given return period (or joint probability distribution), there may exhibit various possible combinations among flood characteristic combinations. Figure 16a, b represents the scatter plot for comparing observed (in red colour) flood peak–volume and peak–duration combinations with the set of 1000 sample observations simulated (in green colour) from the joint distribution of the best-fitted bivariate copula functions and their marginal distributions for both MPL- and MOM-based parametric estimators. Figure 17 illustrates the OR and AND joint return periods derived from the best-fitted Gaussian copula for flood peak–volume series whose parameter is estimated via MOM and MPL estimators. Similarly, Fig. 18 illustrates the OR and AND joint return periods for flood peak–duration combination using the Gaussian (based on MOM estimator) and Frank copula (based on MPL estimator). Actually, in most of the engineering-based water related issues, a flood episode may be considered as dangerous if its peak discharge flow value is larger either its volume or durations is also large. In other words, performing the flood risk by considering only the single variable return periods would be problematic which often demands the joint occurrence of multiple flood characteristics. Therefore, Tables 11 and 12 show the estimated values of joint return period for both the OR and AND joint cases for few combinations between flood peak–volume and peak–duration. From the estimated return periods, it is revealed that the OR joint return period is smaller than AND joint return periods for every possible combination of flood characteristic, i.e. T^OR < T^AND. For example, if a flood episode characterized by peak flow, P = 8089.2353 m³s⁻¹, volume, V = 13185.141 m³, the OR joint return period is $T^{\text{OR}}_{PV}$ = 1.765498249 years and the AND return period is $T^{\text{AND}}_{PV}$ = 4.521252343 years. Similarly, for P = 17,019.5015 m³ s⁻¹ and V = 53,420.634, the OR- joint return period is $T^{\text{OR}}_{PV}$ = 17.614561 years and the AND joint return period is $T^{\text{AND}}_{PV}$ = 50.919642 years (Table 11b). Similarly, if a flood episode with peak, P = 12639.4182 m³ s⁻¹, duration, D = 14.262899, the $T^{\text{OR}}_{PD}$ = 1.54 years and $T^{\text{AND}}_{PD}$ = 21.60 years and so on (Table 12a). Similar results are observed for joint return periods between flood peak–duration combinations which also reveals that the AND joint return is higher than OR joint return periods (i.e. $T^{\text{OR}}_{PD}$ < $T^{\text{AND}}_{PD}$). It is also revealed that univariate return periods are derived from either the flood peak series, T_P or volume series, T_V > $T^{\text{OR}}_{PV}$ but produces low return periods than $T^{\text{AND}}_{PV}$, i.e. both (T_P and T_V) > $T^{\text{AND}}_{{\left( {PV} \right)}}$ (Table 11a, b). Similarly, Table 12a, b, shows between the flood peak–duration pairs, both (T_P and T_D) > $T^{\text{OR}}_{PD}$ and (T_P and T_D) < $T^{\text{AND}}_{PD}$. Overall, based on the above results and the mathematical inequalities exhibited between univariate and bivariate joint return periods or between OR and AND joint return periods, it is concluded that for an effective risk-based flood risk analysis, it could be an essential concern and more practical to the hydrologist and water practitioner to take the accountability of both the cases of joint return periods, i.e. OR and AND joint cases, including the univariate return periods. In other words, considering just only the OR joint or AND joint return periods in the flood risk analysis might be problematic and might result for the underestimation or overestimation of hydrologic risk.

Fig. 12

Joint probability density function (JPDF) and joint cumulative distribution function (JCDF) of flood peak and volume pair using Gaussian copula derived from MOM estimator with Lognormal (2P) and Johnson SB-4P as a best-fitted marginal distribution to P and V. Note: Brown circle in the Joint CDF contour plot represents observed flood peak and volume samples

Fig. 13

Joint probability density function (JPDF) and joint cumulative distribution function (JCDF) of flood peak and volume series using best-fitted Gaussian copula derived from MPL estimators with Lognormal (2P) and Johnson SB-4P as a best-fitted marginal to P and V. Note: Brown circle in Joint CDF contour plot represents the observed flood peak and duration samples

Fig. 14

MOM-based Joint probability density function (JPDF) and joint cumulative distribution function (JCDF) of flood peak and duration series using best-fitted Gaussian copula with Lognormal (2P) and Gamma-3P as a best-fitted marginal to P and D series. Note: Brown circle in Joint CDF contour plot represents the observed flood peak and duration samples

Fig. 15

MPL-based Joint probability density function (JPDF) and joint cumulative distribution function (JCDF) of flood peak and duration series using best-fitted Frank copula with Lognormal (2P) and Gamma-3P as a best-fitted marginal to P (peak) and D (duration) series. Note. Brown circle in Joint CDF contour plot represents the observed flood peak and duration samples

Fig. 16

Scatter plot for comparing observed flood peak–volume, peak–duration and volume–duration series with the set of 1000 sample observations simulated from joint distribution using best-fitted copula functions and their marginal distributions for both MPL- and MOM-based dependence parameter estimation procedures a peak–volume and, b peak–duration pairs

Fig. 17

OR and AND joint return period derived from both MPL- and MOM-based bivariate joint distributions of the best-fitted copula functions, i.e. Gaussian copula for flood peak (variable = a) and volume (variable = b) series

Fig. 18

OR and AND joint return period derived from both MPL- and MOM-based bivariate joint distributions of the best-fitted copula functions, i.e. Gaussian copula via MOM estimator and Frank copula via MPL estimator) for flood peak (axis variable = a) and duration (axis variable = b) series

Table 11 Joint and conditional return period for the flood pairs P–V (a) using Gaussian copula via the MOM estimator (b) using Gaussian copula via the MPL estimator

Table 12 Joint and conditional return period for pairs P–D (a) using Gaussian copula via the MOM estimator (b) using Frank copula via the MPL estimator

Similarly, the bivariate conditional return periods of the flood peak given various percentile values of flood volume or duration, i.e. $\left( {T_{{\left( {p\backslash V \le v} \right) }} \;{\text{and}} \;T_{{\left( {V\backslash P \le p} \right)}} } \right)\;{\text{or}} \;\left( {T_{{\left( {p\backslash D \le d} \right) }} \;{\text{and}} \; T_{{\left( {D\backslash P \le p} \right)}} } \right)$ are estimated by using Eqs. (17) and (19), and their estimated values are listed in Tables 11 and 12. For example, if a flood episode is characterized with peak value, P = 8089.2353 m³ s⁻¹, and volume, V = 13,185.141 m³, then the conditional return periods $T\left( {P/V \le v} \right)$ = 58.33509 years and $T\left( {V/P \le p} \right)$ = 2.28404 years. From Table 11a, b it is also revealed that both the $T\left( {P/V \le v} \right)$ and $T\left( {V/P \le p} \right)$ conditional return periods are higher than the $T^{\text{OR}}_{PV}$, i.e. (($T\left( {P/V \le v} \right)$ and $T\left( {V/P \le p} \right)$) > $T^{\text{OR}}_{PV}$). The same mathematical inequality existed of return periods exhibited for flood pairs P–D, i.e. $T\left( {P/D \le d} \right) > T_{PD}^{\text{OR}}$ and $T\left( {D/P \le p} \right) > T_{PD}^{\text{OR}}$. But for the same flood pair, $T\left( {P/D \le d} \right) < T_{PD}^{\text{AND}}$ and $T\left( {D/P \le p} \right) < T_{PD}^{\text{AND}}$. From Table 11, it is also revealed that $T\left( {P/V \le v} \right)$ produced higher return periods than the return period derived from flood peak, T_P, and also, $T\left( {V/P \le p} \right)$ is higher than volume, T_V, series. Therefore, accounting both the case of joint return periods and the conditional return periods is an essential concern for tackling several water-related queries.

Research conclusions

Joint probability distribution analysis of multiple interacting flood is very useful for understanding critical hydrologic behaviour of flood episodes at a river basin scale, for tackling several water resources' planning, managements or either flood defence infrastructure designing projects. In actual, univariate flood frequency analysis or return periods would be problematic due to multidimensional characteristics of flood episodes and might be attributed for underestimation or overestimation of hydrologic risk. Therefore, estimating multivariate design quantiles under different notations of return periods, i.e. based on conditional distribution and joint distributions, could be an effective attempt for assessing the hydrologic risk. The Kelantan River basin in Malaysia is often subjecting to the most severe monsoonal flooding and perceiving for increasing in terms of their frequency and magnitude.

In this study, copula-based methodology is incorporated for establishing bivariate frequency analysis of flood characteristics, i.e. flood peak discharge flow (P), volume (V) and duration (D) of flood hydrograph, and applied for a case study of the Kelantan River basin at Guillemard bridge gauge station in Malaysia. At-site event-based or block (annual) maxima-based methodology is adopted for the 50-year (1961–2016) continuously distributed streamflow characteristics of this river basin. Based on the correlation measuring statistics, from both the analytical approach (i.e. Pearson, Kendall’s tau and Spearman rho correlation coefficient) and graphical visual inspection (i.e. based on rank-based scatter plot, K-plot and Chi-plot), it is found that flood peak–flow flood volume pair exhibited higher and positive dependence structure, but both flood volume–duration and peak–duration pairs are found to be negatively correlated random pairs with very weak correlation and thus considered for flood frequency analysis. A distinguished variety of probability distribution functions (i.e. 1 parameter, 2 parameters, 3 parameters and 4 parameters) are tested under parametric approach, for defining the univariate marginal distribution of each individual flood characteristic. The vector of the unknown statistical parameter of the fitted distributions is estimated based on maximum likelihood estimation (MLE), method of moments (MOM), least square method (LS) and L statistics-based method of L-moments. Based on fitness test statistics, best-fitted marginal distributions for each flood characteristic are introduced for copula dependence modelling. A distinguished variety of bivariate copula families such as the mono-parametric (or 1 parameter), Archimedean copulas (i.e. Clayton, Frank, Gumbel, Joe), mixed form of bi-parametric (i.e. 2 parameters) Archimedean copulas (i.e. BBI based on mixing between Clayton and Gumbel copula, BB6 mixing between Joe and Gumbel copula, BB7 mixing between Joe and Clayton copula, and BB8 mixing between Joe and Frank copula), elliptical family copula (i.e. Gaussian), and also rotated version of Archimedean copula (i.e. rotated Clayton by 90° of rotation) have been introduced and tested to model the bivariate joint probability distribution of flood variables occurrence, i.e. between flood peak–volume, and peak–duration pairs. The parameter of copulas function is estimated using the method of moment (MOM) based on inversion of Kendall’s tau $\left( \tau \right)$ and maximum pseudo-likelihood (MPL) estimators. The performance of each fitted copula is tested using both graphical and analytical approaches (i.e. based on Cramer–von Mises test statistics), and thus, best-fitted copulas are used for defining the joint and conditional return periods of flood characteristics.

From the present demonstrations, the following specific research conclusions are drawn, as given below:

• Based on the Q-statistics and their estimated p value for different lag sizes, it is concluded that the time series of each individual flood characteristic exhibited almost negligible or zero first-order autocorrelations. Also, based on nonparametric rank-based Mann–Kendall or M–K test, it reveals the acceptance of null hypothesis (H₀) which further points the existence of zero monotonic trends at the 5% or 0.05 level of significance within each flood series. In conclusion, no significant trends are detected for the flood characteristics.

• Based on parametric distribution fitting procedure for defining univariate flood marginals, it is pointing towards the Lognormal (2P) distributions for flood peak discharge flow, Johnson SB-4P for volume and Gamma-3P for modelling flood duration series.

• On performing the standard GOF test for each derived copula based on MOM and MPL estimators for each flood attribute pair, it is found that the Gaussian copula is the most parsimonious or best-fitted copula for flood peak–volume and peak–duration series using MOM-based parametric copula estimations. On the other hand, the Gaussian copula is recognized as best-fitted for defining flood peak–volume dependence structure and the frank copula is the most justifiable for both flood peak–duration pairs. The best-fitted copulas are employed for estimating the joint and conditional probability distributions, and their associated return periods for various possible combinations of flood characteristics (i.e. P–V and P–D combinations) are retrieved.

• Overall, copula function is found to be an effective way for establishing joint dependency simulation as well as preserving dependence structure of multiple flood characteristics, also revealing an effectiveness in retrieving both the conditional and joint return periods of the flood characteristics and thus could provide a better understanding of critical hydrologic behaviour at a river basin scale for assessing multivariate hydrologic risk.

• The present study investigated the adequacy of copula-based methodologies under the parametric setting for establishing the bivariate joint dependence structure of the flood characteristics, i.e. between flood peak–volume and flood peak–duration series. But no one could deny from the facts that the more comprehensive flood risk analysis can be achieved through accounting all the trivariate random vectors simultaneously instead of just the pair-wise joint analysis (i.e. Reddy and Ganguli 2013; Fan and Zheng 2016; Daneshkhan et al. 2016). Also, according to Graler et al. (2013) and Renard and Lang (2007), multiple relevant vectors of the specified hydrologic episodes could likely depend upon the potential damage where the ignorance of spatial dependency among these uncertain flood characteristics may responsible for the underestimation of uncertainty. On the other hand, the multivariate FFA either with or without copulas has been applied frequently with parametric distributions where the parametric functions are often employed to modelled their marginals and the parametric copula function for the joint dependence structure. But, the parametric functions always imposed an assumption that the random samples are coming from the known populations whose PDF are predefined, but, in actual, no universal rules and studies are imposed to model any hydrologic vectors through any fixed or predefined distribution functions, which would follow different distributions and desire to model separately (i.e. Adamowski 1989; Silverman 1986; Kim and Heo 2002; Karmakar and Simonovic 2008). Therefore, in the past few decades, an attempt via kernel density estimators (KDE) is recognized as a much flexible and stable nonparametric data smoothing procedure and thus implemented in conjuction with parametric copula function under the semiparametric settings (i.e. Karmakar and Simonovic 2009; Reddy and Ganguli 2012a). Also, if the targeted copulas and univariate marginal distributions belong to some specific parametric families, it might be problematic, if the underlying assumption is violated. Therefore, in such circumstances, the nonparametric copula distribution framework can ameliorate these modelling issues and can be able to produce a significant outcome without assuming a particular form for the univariate marginal or multivariate copula distributions. All the above raised issues can be considered as a future research purpose.