1 Introduction

Single-variable flood frequency analysis provides limited understanding and assessment of the true behaviour of flood phenomena, which are often characterised by a set of correlated random variables such as peak, volume and duration (Yue et al. 2001; Favre et al. 2004). Univariate frequency analysis methods cannot describe the random variable properties that are correlated (Sarhadi et al. 2016). This approach can lead to high uncertainty or failure of guidelines in water resources planning, operation and design of hydraulic structures or creating the flood risk mapping (Chebana and Ouarda 2011). Additionally, the flood is a multivariate natural calamity characterising peak, volume and duration. Hence, it is important to study the simultaneous, multivariate, probabilistic behaviour of flood characteristics.

Multivariate parametric distributions (e.g., bivariate normal, bivariate gamma and bivariate extreme value distributions), which have been extended from univariate distribution, is used to model the multivariate flood characteristics for different purposes (Adamson et al. 1999; Yue 1999; Yue et al. 2001). However, this approach has some drawbacks such as the dependence structure between the variables, which depends on the marginal distributions or the flood variables that have the same type of marginal distributions (Poulin et al. 2007; Zhang and Singh 2007).

In order to overcome the limitation of multivariate distributions, a copula is a very versatile approach for simulating joint distribution in a more realistic way (Favre et al. 2004). The main advantage of this method is that the dependence structure is independently modelled with the marginal distribution that allows for multivariate distribution with different margins and dependence structures to be built (Dupuis 2007; Zhang and Singh 2007). Several researchers have used copulas to perform the bivariate frequency analysis (Reddy and Ganguli 2012; Dung et al. 2015; Sraj et al. 2015). The most important step in the modelling process using copula is the selection of copula function which is the best fit for the data sample (Favre et al. 2004). The chosen copulas should include several classes of copulas and several degrees of tail dependence (Dupuis 2007; Poulin et al. 2007).

Tail dependence characteristics constitute important features that differentiate extreme value copulas from other copula structures (Chowdhary et al. 2011). Therefore, the extreme value copulas with upper tail dependence are considered to provide appropriate models for the dependence structure of the flood characteristics (Genest and Favre 2007; Poulin et al. 2007; Gudendorf and Segers 2011; Vittal et al. 2015). On the other hand, in the multivariate frequency analysis, the variables can be dependent or independent of each other. The relationship between the flood characteristics (i.e., peak, volume and duration) is analysed by several researchers. However, most of the results of the dependence between different pairs of flood variables were not consistent (Karmakar and Simonovic 2009; Reddy and Ganguli 2012; Sraj et al. 2015). Indeed, the identification of the degree of dependence between the flood variables is a difficult step, because the dependence of pairs of flood characteristics is controlled by different climate features and catchment properties (Viglione and Blöschl 2009; Gaál et al. 2015).

Most of the studies used Pearson’s linear correlation coefficient (r), Kendall’s (\(\tau \)) and Spearman’s rank correlation (\(\rho \)) for measuring the dependence among different flood variables. However, these measures are based on the association of the entire distributions, but do not reveal the dependence in the specific part of the distribution (Aghakouchak et al. 2010). When dealing with extreme events such as floods, extreme values will appear in the tail of the distributions. Hence, the tail dependence, which describes the dependence in the tail of a multivariate distribution, can be a suitable measure (Coles et al. 1999; Aghakouchak et al. 2010; Serinaldi et al. 2015; Hao and Singh 2016).

To describe the dependence in multivariate extreme values, there are two possible situations, namely, asymptotic dependence or asymptotic independence (Coles et al. 1999). Diagnostic analysis to determine whether the variables have asymptotic dependence or asymptotic independence is very important in multivariate extreme analysis. In fact, in a situation where diagnostic checks suggest data to be asymptotically independent, modelling with the classical families of bivariate extreme value distribution is likely to lead to misleading results (Ledford and Tawn 1996; Coles 2001). Different measures of extremal dependence have been developed. Coles et al. (1999) proposed two measures of extreme dependence (\(\chi \) and \(\bar{\chi }\)) for bivariate random variables. Nevertheless, recent studies show that there are still difficulties in detecting the asymptotic dependence and independence in many cases (Coles et al. 1999; Bacro et al. 2010; Weller et al. 2012; Serinaldi et al. 2015).

Apart from these, several parametric and non-parametric approaches are suggested to determine the tail dependence. Non-parametric tail dependence estimator (\(\uplambda _{\mathrm{U}}\)), namely, \(\uplambda _{\mathrm{U}}^{\mathrm{LOG}}\) (Coles et al. 1999; Frahm et al. 2005), \(\uplambda _{\mathrm{U}}^{\mathrm{SEC}}\) (Joe et al. 1992), \(\uplambda _{\mathrm{U}}^{\mathrm{CFG}}\) (Capéraà et al. 1997) and \(\uplambda _{\mathrm{U}}^{\mathrm{SS}}\) (Schmidt and Stadtmüller 2006) have been preferred by most researchers in hydrological analysis (Li et al. 2009; Requena et al. 2016). However, Villarini et al. (2008) indicated that these tail dependence estimators have some drawbacks (e.g., bias, uncertainty, etc.). Furthermore, all tail dependence estimators exhibit a very poor performance when the underlying upper tail dependence coefficient is null. It is, therefore, important to test for tail dependence before applying the estimator (Frahm et al. 2005; Poulin et al. 2007). Consequently, upper tail (in)dependence testing is a useful alternative approach. Serinaldi et al. (2015) suggested that test for tail (in)dependence is mandatory because: (i) samples exist which seem to fail dependency, but they are realisations of a tail-dependent distribution; (ii) the use of misspecified parametric marginals instead of empirical marginals may lead to wrong interpretations of the dependence structure; and (iii) the tail dependence estimators can be insensitive to upper tail dependence, thus indicating the upper tail dependence even if none exist. Similarly, if data are to be independent in the upper tail, then modelling with dependence will lead to overestimation of the probability of extreme joint events. Hence, Falk and Michel (2006) emphasised that testing for tail (in)dependence is essential in data analysis of extreme values.

Several recent studies indicated that Gumbel–Hougaard copula belonging to extreme value copulas works well when variables are asymptotically dependent (Zhang and Singh 2006; Poulin et al. 2007; Karmakar and Simonovic 2009; Dung et al. 2015). However, there are few studies which suggest what is the best copula for modelling the dependence structure where the variables have the strength of dependence but weaken at high levels or are asymptotically independent. Therefore, it is important to find the appropriate copula to derive the joint distribution of flood variables where the pair of flood characteristics has asymptotically independent or weak dependence at high thresholds.

The difference between the extreme value copulas and Gaussian copula is that the Gaussian copula becomes independent at the high threshold. Furthermore, Gaussian copula, which is characterised by correlation matrix, generates a wider range of dependence behaviour (Bortot et al. 2000). Studies by Renard and Lang (2007) also have proved the usefulness of the Gaussian copula in hydrological extreme events analysis. In fact, they suggested that the Gaussian copula can be reasonably well used for field significance determination, regional risk estimation, discharge–duration–frequency curves and regional frequency analysis. Frank and Clayton copulas, belonging to the Archimedean family, have been widely used in the hydrology analysis because they can be modelled with both negatively and positively associated variables. Furthermore, the Frank and Clayton copulas, which have zero dependencies in both tails, are suitable in case the tail dependence is not existing (Poulin et al. 2007; Dung et al. 2015; Sraj et al. 2015).

The previous studies have used parametric and non-parametric approaches to determine the tail dependence coefficient. However, these tail dependence estimators have some drawbacks. Consequently, tail dependence testing is a useful alternative approach. Therefore, this study assesses how tail dependence test can be useful in selecting the appropriate family of copula for modelling the joint dependence structure of flood characteristics. In order to identify the best copula family for each situation, the Clayton, Frank and Gaussian copulas are used for assessing the potential of their applications in case the variables are diagnosed as asymptotic independence. The hypothesised copulas (extreme value copulas) are applied to evaluate their suitability if there exists asymptotic independence in the tail for bivariate frequency analysis of flood in Trian watershed, Vietnam.

This study aims to address the following issues: (i) investigating the potential of performing the tail dependence tests for the pairs of flood characteristics; (ii) evaluating the performance of extreme value copula for asymptotic dependence variables and Clayton, Frank and Gaussian copulas for asymptotic independent variables; and (iii) estimating the joint return period of flood characteristics.

Fig. 1
figure 1

Study area.

Full size image

2 Study area and data

The Trian catchment, which is taken up for the study, is in the upper part of the Saigon–Dongnai River basin and it is one of the biggest subcatchments. The area of this catchment is \({\sim }14,200\,\hbox {km}^{2}\). The basin lies between the latitudes of \(10{^{\circ }}53^{\prime }46^{\prime \prime }{-}12{^{\circ }}22^\prime 08^{\prime \prime }\hbox {N}\) and longitudes of \(107{^{\circ }}01^{\prime }52^{\prime \prime }{-}108{^{\circ }}46^\prime 55^{\prime \prime }\hbox {E}\) (figure 1). There are two distinct seasons in this area, namely, rainy (April–November) and dry (December–April) seasons. The climate is controlled by the northeast and southwest monsoons. The annual average rainfall and temperature are about 2200 mm and \(20.6{^{\circ }}\hbox {C}\), respectively. There are two main tributaries of the Dongnai River (i.e., Dongnai and Langa). There are nine reservoirs, which are operating to supply water for drinking, irrigation, flood control and hydropower production, and were constructed upstream of Trian gauge. Most of them began to operate in recent years except for Hamthuan–Dami and Daininh reservoirs which were operated in 2001 and 2008, respectively. In the Dongnai tributary, Daininh and Dakrtik reservoirs provide energy with a capacity of 300 and 144 MW, respectively. Dongnai 2, Dongnai 3, Dongnai 4 and Dongnai 5 supply water to hydropower plants which have the installed capacity of 70, 180, 340 and 150 MW, respectively. Hamthuan and Dami reservoirs, located in the Langa tributary, are a cascade of two hydropower plants with the installed capacity of 300 and 175 MW. Tapao weir, located at the downstream of Hamthuan and Dami reservoirs, is constructed to supply water for drinking and for irrigation of around 20,340 ha (Government 2016). However, all reservoirs are located far away from the Trian gauge (figure 1). The flood from Trian station has significant impacts on the downstream areas (e.g., Bienhoa, Vungtau and Hochiminh cities). Therefore, this study mainly focused on the flood in the Trian gauge. Daily discharge data for the period 1978–2013 are available for the study from the Trian station on the Dongnai River, which is a part of the Saigon–Dongnai River basin and these data are used for flood frequency analysis. The Trian station is located at \(106{^{\circ }}59^\prime 08^{\prime \prime }\hbox {E}\) and \(11{^{\circ }}06^{\prime }16^{\prime \prime }\hbox {N}\) and it is at the confluence of two Dongnai and Langa rivers. Numerous researchers suggested that the length of data record should be at least 30 years for extreme value modelling (Bonnin et al. 2006; Kioutsioukis et al. 2010; Yilmaz et al. 2017). Further, there are several multivariate frequency analysis studies using the observed data of <35 yrs of data (Zhang and Singh 2006; Aissia et al. 2012; Jeong et al. 2014). Moreover, several researchers suggested that the main advantage of the POT approach, which is for smaller sample sizes, is also used to increase the sample sizes (Lang et al. 1999; Beguería 2005; Bezak et al. 2014). Based on the 35 years of observed data, the sample size of the flood variables is 68 in this study, which meets the minimum requirement of the sample size (\(n=30\)) for the extreme value modelling. Therefore, the length of the observed data is significant for the analysis of the tail dependence. The mean of daily discharge of Trian stream gauge from 1978 to 2013 is \(527.4\hbox { m}^{3}/\hbox {s}\) and the observed maximum daily discharge is \(3910\,\hbox {m}^{3}/\hbox {s}\). The daily time series of the river discharge data is collected from the National Hydro-Meteorological Service (NHMS) of Vietnam.

3 Methodology

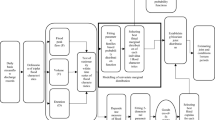
The methodology used in this study is shown in the form of a flowchart (figure 2). Firstly, identification of flood characteristics (peak, volume and duration) from the observed daily discharge time series is carried out. Secondly, check whether the flood variables time series are stationary or non-stationary. Thirdly, the tail dependence tests are then performed to diagnose whether the flood variables have asymptotic dependence or asymptotic independence. Finally, if the flood variables are having an asymptotic dependence, the extreme value copula is used for estimation of joint return periods. Otherwise, Gaussian, Frank and Clayton copulas are used.

Fig. 2
figure 2

Flowchart of methodology.

Full size image

3.1 Extracting flood characteristics

Block maxima (BM) and peak over threshold (POT) approaches are widely used to extract flood characteristics. However, the block maxima cannot consider multiple occurrences of flood events (Lang et al. 1999; Bezak et al. 2014). Unlike the block maxima, which only extracts one event per year, POT considers a wider range of events and provides more information than BM. The threshold estimation is the most difficult part of the POT approach (Lang et al. 1999; Scarrott and Macdonald 2012). Threshold choice involves balancing between the bias and variance. Too low a threshold may violate the asymptotic basis of the model, leading to bias, while too high a threshold will reduce the sample size, leading to high variance of the parameter estimates (Coles 2001). There are two common approaches for choosing a threshold, namely, fixed quantile corresponding to a high non-exceedance probability (95%, 99% or 99.5%) and graphical method (Vittal et al. 2015). Three different techniques belonging to the graphical method, namely, the mean residual life plot (MRL), threshold stability plots and fitting distribution diagnostics (Thompson et al. 2009; Solari and Losada 2012) are used in this study to decide the threshold value. In addition, the lag-autocorrelation plot is used to check the independent and identically distributed (IID) flood variables (i.e., peak, volume and duration) assumption.

3.2 Diagnostic test to examine non-stationary component

The extreme events, particularly flood events, are intensifying due to global climate change, urbanisation and anthropogenic activities. Therefore, the flood time series can have a non-stationary component. The flood frequency analysis, which considers time series as stationary, may lead to misleading results in the estimation of the flood quantile. Checking the non-stationary component of flood series in flood frequency analysis should be considered as an important initial step (Vittal et al. 2015). Trend analysis is normally used to detect the non-stationarities in the flood variables. The Mann–Kendall (M–K) test is a non-parametric statistical test which is used for examining the trends in time series and has been widely applied in the hydrological analysis (Villarini et al. 2009; Lima et al. 2015; Sun et al. 2015).

3.3 Tail dependence test

Coles et al. (1999) proposed two measures of extreme dependence (\(\chi \) and \(\bar{\chi }\)) for bivariate random variables, as shown below:

$$\begin{aligned} \chi =2-\frac{\hbox {log } P(F_1 \left( x \right)<u,F_2 \left( y \right) <u)}{\hbox {log }u}, \end{aligned}$$
(1)
$$\begin{aligned} \bar{\chi }=\frac{2\hbox {log }\left( {1-u} \right) }{\hbox {log } P(F_1 \left( x \right)>u,F_2 \left( y \right) >u)}-1. \end{aligned}$$
(2)

With a pair of complementary measure (\(\chi ,\bar{\chi }\)), a summary of multivariate extremal dependence can be determined:

  • If \(\bar{\chi }=1\) and \(0<\chi <1\), the variables are asymptotically dependent and \(\chi \) is a measure of the strength of dependence within the class of asymptotic dependence distribution.

  • If \(-1<\bar{\chi }<1\) and \(\chi =0\), the variables are asymptotically independent and \(\bar{\chi }\) is a measure of the strength of dependence within the class of asymptotically independent distribution.

There are still difficulties in detecting the asymptotic dependence and independence in many cases using these extremal dependencies (Coles et al. 1999; Bacro et al. 2010; Weller et al. 2012; Serinaldi et al. 2015). Hence, the coefficient of tail dependence (\(\eta \)) introduced by Ledford and Tawn (1996) is used to detect asymptotically dependent and independent variables. Ledford and Tawn (1996) assumed that the joint survivor function of the pair (X, Y) with unit Frechet distribution is a regularly varying function, as shown below:

$$\begin{aligned} P(X>z, Y>z)=\text {\pounds }(z)z^{-1/\eta }, \end{aligned}$$
(3)

where £(z) is a slowly varying function and \(\eta \) is the coefficient of tail dependence.

  • If \(\eta =1\) and \(\mathop {\lim }\nolimits _{z\rightarrow \infty }\) £ \(\left( z \right) =c\) for some \(0<c\le 1\), the variables are asymptotically dependent with a degree c.

  • If \(\eta <1\), the variables are asymptotically independent.

The coefficient of tail dependence can be estimated by univariate theory because the joint survivor function can be reduced to univariate survivor function \(T=\hbox {min}\)(X, Y). The coefficient of tail dependence will be equal to shape parameter if T is fitted with generalised Pareto distribution (GPD). The log-likelihood ratio (LLHR) test can be used for testing the asymptotic dependence against the asymptotic independence. The null hypothesis of asymptotic dependence is tested comparing the log-likelihood of the asymptotic dependence and asymptotic independence. Under the null hypothesis \(\eta =1\) vs. the alternative \(\eta <1\), the LLHR test statistic, based on twice the difference between the log-likelihood of asymptotic dependence and asymptotic independence, has the approximate \(\chi ^{2}\) distribution with the degree of freedom. The significance of asymptotic independence can be measured from the p-value of \(\chi ^{2}\) distribution. As mentioned earlier, threshold in GPD is selected based on the threshold stability plot.

Furthermore, tail (in)dependence test is used as an approach for detecting whether the flood variables have asymptotic dependence or independence, respectively. Tail independence test, proposed by Falk and Michel (2006), is normally suggested by many authors in extreme value analysis (Bel et al. 2008; Ribatet et al. 2009; Serinaldi et al. 2015). Frick et al. (2007) proposed a generalisation of Falk and Michel’s test, based on a second-order differential expansion of the spectral decomposition of non-degenerate distribution function. This test is based on the following equation:

$$\begin{aligned}&P\left( {X+Y>ct\,|X+Y>c} \right) \nonumber \\&\quad =\left\{ {{\begin{array}{l@{\quad }l} F\left( t \right) =t^{1+\rho },&{}\hbox {tail independence}, \\ F\left( t \right) =t, &{}\hbox {tail dependence}, \\ \end{array} }} \right. \end{aligned}$$
(4)

where \(c\rightarrow 0\) is the threshold, \(\rho \ge 0\) is the independence measure and \(F\left( t \right) \) is the standard uniform distribution with \(t \in \) [0,1]. According to the central limit theorem, the p-values of the optimal test are given below:

$$\begin{aligned} p=\varPhi \left( {\frac{\mathop \sum \nolimits _{i=1}^m \hbox {log } \bar{C}_i +m}{m^{1/2}}} \right) \end{aligned}$$
(5)

where \(\bar{C}_i =(X_{i }+Y_{i})/c\), \(i=1\), ..., m, and \(\varPhi \) is the standard normal density distribution function.

This test is quite sensitive to the threshold c. Hence, Frick et al. (2007) suggested that the threshold is chosen so that the number of exceedances is about 10–15% of the total number observed data.

3.4 Selection of marginal distribution

The work of Vittal et al. (2015) suggested that it is important to apply both parametric and non-parametric distributions for a selection of the best fit marginals for flood variables. There is more than one parametric distribution that can be fitted to the sample data. Hence, identifying the best fitting distribution to the sample needs to be tested with several distributions rather than assuming that the particular distribution will be sufficient to provide the necessary insight for flood variables (Lang et al. 1999; Vittal et al. 2015; Dong Nguyen et al. 2018). The log-normal (LN), Pearson type III (P3), log-Pearson type III (LP3), GPD, Gumbel and generalised extreme value (GEV) distributions, which have been widely used for modelling the extreme values (Lang et al. 1999; Saf 2009; Salas Jose et al. 2013; Bezak et al. 2014), are used.

For non-parametric distribution, the kernel density estimator with Epanechnikov, Gaussian, triangular and rectangular kernel functions is used in this study. Both parametric and non-parametric distributions are used to find the best marginal distribution for each flood variable in this study.

3.5 Extreme value copula and no tail dependence copula functions

A copula is defined as a joint distribution function of standard uniform random variables. If F(x, y) is any continuous bivariate distribution function with marginal distributions \(F_{1}(x)\) and \(F_{2}(y)\), the copula function can be expressed as:

$$\begin{aligned} F(x, y)=C[F_{1}(x), F_{2}(y)]. \end{aligned}$$
(6)
Table 1 Definition and upper tail dependence coefficient of the copula used in this study.
Full size table

If the \(F_{1}(x)\) and \(F_{2}(y)\) are continuous, the copula function C is unique and can be written as:

$$\begin{aligned} C(u, {\upsilon })=F[F_1^{-1} (u), F_2^{-2} ({\upsilon })], \end{aligned}$$
(7)

where the quantile functions \(F_1^{-1}\) and \(F_2^{-2}\) are defined by \(F_1^{-1} \left( u \right) = \hbox {inf}[x{:}\, F_{1}(x)\ge u]\) and \(F_2^{-1}( {\upsilon } ) = \hbox {inf}[x{:}\, F_{2}(y)\ge \upsilon ]\), respectively.

Among several families of copulas (Archimedean, Plackett, Farlie–Gumbel–Morgensten and Elliptical), extreme value copulas are more popular for hydrological application, particularly for extreme events. Indeed, the extreme value copulas with upper tail dependence are considered to be appropriate models for the dependence structure in extreme events. Extreme value copulas can be used as a convenient choice in modelling data with positive correlation and arise naturally in the domain of extreme events (Gudendorf and Segers 2011; Mirabbasi et al. 2012). The families of extreme value copulas considered in this study, including Gumbel–Hougaard, Husler–Reiss and Galambos. Besides, Gaussian, Frank and Clayton copulas, are also used in circumstances where diagnostic checks suggest data to be asymptotically independent. More details and descriptions can be found in Poulin et al. (2007), Gudendorf and Segers (2011) and Salvadori et al. (2013). The relevant expression for their dependence function and tail-dependent coefficient are presented in table 1.

Genest et al. (1995) and Cherubini et al. (2004) suggested the maximum pseudo-likelihood (MPL) and canonical maximum likelihood approaches in case of an unknown marginal distribution to estimate copula parameters. In order to allow marginal distribution to be free and not restricted by parametric families, the MPL method is suggested because the marginal distribution is considered to be the empirical distribution function. Furthermore, Genest and Favre (2007), Kim et al. (2007) and Kojadinovic and Yan (2010) showed that the MPL is the best choice for estimating copula parameters. Therefore, the MPL is used in this study.

Selection of appropriate copula is a complex process and needs to be considered through several different measures. Only one measure can fail to identify the suitable copulas that can lead to an inappropriate joint probability of flood characteristics (Fu and Butler 2014). There are several different methods to select the best copula, including graphical method, goodness-of-fit (GoF) tests and model selection criteria. The first two methods are used to measure the discrepancy between the theoretical distribution and empirical distribution, while the model selection criteria such as Akaike’s information criterion (AIC), which penalises the minimised negative log-likelihood function for the number of parameters estimated, would be more appropriate than repeated tests of significance whose outcomes lose their interpretability (Katz 2013).

Fig. 3
figure 3

(a) Mean residual life plot, (b) threshold stability plots and (c) diagnostic plots for observed daily flood data.

Full size image

In the graphical method, the theoretical non-exceedance joint probabilities obtained using copula functions are compared with the empirical non-exceedance joint probabilities, which can be estimated by Gringorten plotting position formula

$$\begin{aligned} F_{XY} \left( {x_i ,y_i } \right)= & {} P\left( {X\le x_i ,Y\le y_i } \right) \nonumber \\= & {} \frac{\mathop \sum \nolimits _{m=1}^i \mathop \sum \nolimits _{l=1}^i n_{ml} -0.44}{N+0.12}, \end{aligned}$$
(8)

where \(n_{ml}\) is the number of pairs (\(x_{j}, y_{j}\)) counted as \(x_{j}\le x_{i}\) and \(y_{j}\le y_{i }; i,j=1, {\ldots }, N\); \(1\le j\le i\) and N is the sample size. Besides the graphical method, the GoF test is also used to test the adequacy of the hypothesised copulas. Genest et al. (2009) reviewed and compared several GoF tests for copula. They proved that Cramer–von Mises (\(S_n^{\mathrm{I}}\)) test comparing the empirical and theoretical copulas is the best GoF test. However, there is no difference between the extreme value copulas in this test. In order to overcome this shortcoming, the test based on a Cramer–von Mises (\(S_n^{{\mathrm{II}}}\)) statistic, measuring the distance between parametric and non-parametric estimators of the Pickands dependence function, was introduced by Genest et al. (2011). This test is defined as:

$$\begin{aligned} S_n^{\mathrm{II}} =\mathop \int \nolimits _0^1 n\left| {A_n \left( t \right) -A_{\theta n} \left( t \right) } \right| ^{2}\hbox {d}t, \end{aligned}$$
(9)

where \(A_n ( t )\) and \(A_{\theta n} ( t )\) are the non-parametric and parametric estimators of Pickands dependence function A. Based on the objective and availability of data in this study, \(S_n^{\mathrm{II}} \) is used to find out the appropriate copula functions.

3.6 Joint return period estimation

The concepts of return period for flood events are widely used as criteria in the design of hydraulic structures and flood control facilities (Klein et al. 2010). The return period of hydrological extreme events is normally associated with a certain exceedance probability. In the bivariate case, the joint return periods called OR (\(X\ge x\) or \(Y\ge y\)) and AND (\(X\ge x\) and \(Y\ge y\)) have been commonly used:

$$\begin{aligned} T_{X,Y}^{\mathrm{AND}}= & {} \frac{\mu _T }{P\left( {X\ge x\hbox { and }Y\ge y} \right) }\nonumber \\= & {} \frac{\mu _T }{1-F_X \left( x \right) -F_Y \left( y \right) +F_{XY} \left( {x,y} \right) },\nonumber \\ \end{aligned}$$
(10)
$$\begin{aligned} T_{X,Y}^{\mathrm{OR}}= & {} \frac{\mu _T }{P\left( {X\ge x\hbox { or }Y\ge y} \right) }\nonumber \\= & {} \frac{\mu _T }{1-F_{XY} \left( {x,y} \right) }. \end{aligned}$$
(11)

The above equations are used for both block maxima and POT approaches, where \(\mu _T \) is the mean inter-arrival time (years). In the case of block maxima, \(\mu _T \) is equal to 1.0 (Shiau 2003; Vittal et al. 2015). Since POT is applied in this study, the mean inter-arrival time is determined based on the observed flood events.

Fig. 4
figure 4

The autocorrelation plot up to lag 10 for all the flood characteristics.

Full size image
Fig. 5
figure 5

Extremal measures for the dependence of observed flood peak and volume.

Full size image

4 Results and discussion

4.1 Identification of flood characteristics

The POT approach is used to extract flood characteristics in this study. The threshold is selected based on the three different approaches, namely, the mean residual life (MRL) plot, threshold stability plots and fitting distribution diagnostics. Figure 3(a) shows the MRL plot for observed daily discharge for Trian. It is clear that after the threshold value of \(u = 950\,\hbox {m}^{3}/\hbox {s}\), the MRL is consistent with a straight line. Furthermore, with the threshold value of \(u = 950\,\hbox {m}^{3}/\hbox {s}\), the shape and modified scale parameters begin to reach a plateau (figure 3b). Besides, the diagnostic plots (probability–probability (PP), quantile–quantile (QQ)) for the fitted PIII distribution with the threshold (\(950\hbox { m}^{3}/\hbox {s}\)) after declustering (\(r=10\) days) are shown in figure 3(c) and they show a good agreement between the model and empirical values.

Figure 4 shows that there is insignificant autocorrelation for all flood characteristics. The IID flood variables assumption is still maintained based on this threshold. Therefore, the threshold value of \(u = 950\hbox { m}^{3}/\hbox {s}\) is a suitable threshold for Trian. This threshold is used for all future flood characteristics. Flood duration and volume are also determined based on this threshold. The M–K test for peak, volume and duration of observed data showed that there is no significant trend for any of the flood variables observed at the Trian gauge. It indicates that the flood events in the present data are still stationary. Therefore, the stationary flood frequency analysis is used to estimate the joint return periods.

4.2 Tail independence test

The pair of extremal measures (\(\chi ,\bar{\chi }\)) is used to detect whether the flood variables are asymptotically dependent or not. Nevertheless, in this study, the value of \(\chi \)(u) is nearly equal to 0.5. It means that the pair of flood characteristics has asymptotic dependence for all u. However, the value of \(\bar{\chi }\) shows that the pair of flood characteristics is independent of many cases. For example, figure 5 shows the \(\chi \) and \(\chi \) bar plot for the pair of observed flood peak and volume. Therefore, it is difficult to identify between asymptotical dependence and independence based on these plots.

Table 2 Likelihood ratio and tail dependence test p-value.
Full size table
Table 3 AIC values for all marginal distributions.
Full size table
Fig. 6
figure 6

Theoretical and empirical joint non-exceedance probabilities of observed flood duration and volume (asymptotic independence).

Full size image

LLHR and tail dependence (TailDep) tests are used to decide the asymptotically (in)dependent variables in case the extremal measures do not work. The results from two tests are nearly similar. Table 2 shows the p-value of LLHR and tail dependence tests for all pairs of observed and future flood variables. Based on the extremal measures and these tests, the asymptotically dependence and independence are shown in table 2.

4.3 Marginal distribution of flood variables

To determine the most appropriate marginal distribution for all flood characteristics, GEV, Gumbel, LN, P3, GPD and LP3 distributions belonging to the parametric distribution and Epanechnikov, Gaussian, triangular and rectangular kernel functions belonging to non-parametric distribution are used in this study. The maximum likelihood estimation is used to estimate the parameters of the distributions. The selection of the appropriate distribution is based on the AIC value. The selected marginal distributions are presented in table 3, which provides a comparison of performances for all marginal distributions. The results indicate that the LP3 distribution is most appropriate for modelling the flood volume and duration while the P3 is found to be the best for flood peak.

4.4 Copula selection

Figure 6 shows the theoretical and empirical joint non-exceedance probabilities of asymptotic tail independence data. It is observed that the Frank and Gaussian copulas fit the dataset, which is diagnosed as an asymptotic independence better than extreme value copulas. Additionally, AIC value and GoF test also indicated that the copula function that has no tail dependence may work well when variables are asymptotically independent.

Fig. 7
figure 7

The joint return period of the pair of flood peak and volume modelling by Frank and Gumbel copulas.

Full size image
Table 4 Copula dependence parameters, AIC and corresponding GoF statistics.
Full size table
Fig. 8
figure 8

Theoretical and empirical joint non-exceedance probabilities of (a) observed duration and volume and (b) observed duration and peak.

Full size image

The joint return period (AND) of observed flood duration and peak pair is estimated by using the best fitted models of each group copulas. The Gumbel–Hougaard copula (extreme value copulas) and Frank copula (the no tail dependence copulas) are selected to estimate the joint return period of the observed flood duration and peak pair. Figure 7 shows the comparison of joint return period curves of the pairs of observed duration and peak which are estimated by the Frank copula (black) and Gumbel copula (blue). This plot indicates that there are huge differences between two copulas. For a lower return period, the two corresponding curves are very close to each other. However, there are large differences in the central part in the 50- and 100-yr return periods. Besides, the shape of the joint return period of each copula has significant differences. The bound limits shrink significantly for the Gumbel–Hougaard copula while this situation is not shown by the Frank copula. For example, at 5-year return period, the corresponding bound for the Gumbel-Hougaard copula is wider than that of the Frank copula. At 10-, 50- and 100-yr return periods, the phenomenon is opposite and the curve from the Gumbel–Hougaard becomes sharper. This result indicates that choosing the inappropriate copula function will lead to serious difference between the joint return period results. This study suggests that the copula function is selected based on the dependence structure of the variables. The result from the tail dependence test may provide useful additional information about the adequacy of the chosen copula functions.

Fig. 9
figure 9

The joint return periods of peak and volume (a) AND both peak and volume are exceeded and (b) OR either peak or volume is exceeded.

Full size image

On the basis of the above analysis, in this study, three extreme value families of copulas (Gumbel–Hougaard, Galambos and Husler–Reiss) are chosen to model the asymptotically dependence pair of flood characteristics. The Gaussian, Frank and Clayton copulas are used in modelling the asymptotically independence pair of flood characteristics. The dependence parameters of copulas are estimated using the MPL method. The copula dependence parameters, AIC and GoF statistics are given in table 4.

Figure 8(a) shows the PP plot of model and empirical joint non-exceedance probabilities for observed flood duration and volume. This plot indicates that the extreme value copulas (Gumbel–Hougaard, Galambos and Husler–Reiss) give the best fit to the dataset. However, identifying the differences among three copula functions is difficult. Therefore, the AIC and GoF tests are used to choose the best copula function. For example, the AIC value (− 165.013) and statistical test value (0.00579) are shown in table 4, which indicate that the Gumbel–Hougaard copula provides the best performance for the pair of observed flood duration and volume.

For asymptotically independence case, figure 8(b) shows the PP plot of the model and empirical joint non-exceedance probabilities for the pair of observed flood duration and peak. It is clear that all copulas (Gaussian, Clayton and Frank) give a good fit to the data. However, the Frank copula fits better than other copulas. Similarly, the best fit copula using the AIC (− 67.695) and statistical test values (0.285) is Frank copula (table 4). All measures indicate that the Frank copula is the best fit to the data sample (observed flood duration and peak). The best copula based on the AIC value and GoF test is used to estimate the joint return period for modelling the pair of flood characteristics.

4.5 Joint return period estimation

The joint return periods (AND and OR) of flood peak and volume for 5-, 10-, 50-, 75- and 100-year return periods are shown in figure 9. For example, the flood peak (\(\hbox {m}^{3}/\hbox {s}\))–volume (\(10^{6}\hbox { m}^{3}\)) pairs, (4011–11,020), (4119–11,432) and (42,965–11,674) are the joint return periods (OR) of 50, 75 and 100 years, respectively. The results from this figure also indicate that for all return periods, AND provide lower flood variable quantile than OR. Several combinations of flood peak and volume as well as other flood characteristics in the same return period are also obtained through bivariate frequency analysis. These results provide more possible choices for the decision maker to select the flood event for structure designing and water resources planning as well as assessing the variability of the obtained flood map inundation that cannot be achieved through the univariate frequency analysis.

5 Summary and conclusions

The main emphasis of this study is on the tail dependence test before the selection of copula function which best fits the data sample. Indeed, extremal measurement is a useful approach but in many cases, it cannot detect whether data are asymptotically dependent or not. The LLHR and tail dependence tests are used to identify the asymptotically (in)dependence of observed flood variables. Two pairs of flood characteristics (peak–volume and duration–peak) have asymptotically independence while flood duration and volume pair have asymptotically dependence in this study. Three extreme value families of copula, namely, Gumbel–Hougaard, Galambos and Husler–Reiss are evaluated to model the asymptotically dependence pair of flood characteristics. The extreme value copulas with upper tail dependence have proved that they are appropriate models for the dependence structure of the flood characteristics. However, identifying the differences among three copula functions is difficult. Therefore, the test based on a Cramer–von Mises (\(S_n^{\mathrm{II}} )\) statistic measuring the distance between parametric and non-parametric estimators of the Pickands dependence function is used and it is proved that it is highly efficient for extreme value copula. Similarly, Gaussian, Frank and Clayton copulas are the appropriate copula models in case of variables which are diagnosed as asymptotically independence. Then, the best fit copula models are used to calculate the joint return periods of flood characteristics. These results provide more possible choices for the decision maker to select the flood event for structure designing and water resources planning as well as assessing the variability of the obtained flood map inundation in the present situation that cannot achieve through the univariate frequency analysis.