Bivariate Flood Frequency Analysis of Upper Godavari River Flows Using Archimedean Copulas

Abstract

In this paper, a copula based methodology is presented for flood frequency analysis of Upper Godavari River flows in India. By using the specific advantages of copula method in modeling the joint dependence structure of uncertain variables, this study applies Archimedean copulas for frequency analysis of flood characteristics annual peak flow, flood volume and flood duration. To determine the best fit marginal distributions for flood variables, few parametric and nonparametric probability distributions are examined and the best fit model is adopted for copula modeling. Four Archimedean family of copulas, namely Ali-Mikhail-Haq, Clayton, Gumbel-Hougaard and Frank copulas are evaluated for modeling the joint dependence of annual peak flow-volume, and flood volume-duration pairs. The performance of two parameter estimation methods, namely method-of-moments-like estimator based on inversion of Kendall’s tau and maximum pseudo-likelihood estimator for copulas are investigated. On performing Monte Carlo simulation to assess the performance of copula distributions in modeling the joint dependence structure of flood variables, it is found that the developed copula models are well representing the observed flood characteristics. From standard statistical tests, Frank copula has been identified as the best fitted copula for both bivariate models. The Frank copula function is used for obtaining joint and conditional return periods of flood characteristics, which can be useful for risk based design of water resources projects.

1 Introduction

The flood frequency analysis is one of the most important and widely studied subjects in the field of hydrology and water resources. Since, floods have become most common natural hazards, increasingly posing a significant risk to human life and environment. At the drainage basin scale, consideration of flood risk plays an important role in planning of water infrastructure projects, for example in design of hydraulic structures (e.g., dam spillways, diversion canals, dikes and river channels), urban drainage systems, cross drainage structures (e.g., culverts and bridges), reservoir management, flood hazard mapping etc.

In general, a flood means inundation caused by rivers overflowing their banks on account of heavy rainfall and/or melting of large amounts of snow (Rakhecha and Singh 2009). The occurrence of hydrological extreme event, flood, involves lot of uncertainty, and its properties being stochastic in nature, are characterized by mutually correlated random variables such as flood peak, volume and duration of the flood hydrograph. Since flood is a multivariate stochastic phenomenon, so risk analysis of flood flows has to be modeled by an effective multivariate probabilistic approach.

Although single variable flood frequency analysis has been widely used in the past (Cunnane 1987; Bobée and Rasmussen 1994), it may not provide effective risk analyses to handle the associated risks of correlated flood properties. By recognizing the limitations of single variable flood frequency analysis, the multivariate frequency analysis was addressed by several researchers using conventional probability distributions. For example, bivariate generalized extreme value distribution (Raynal and Salas 1987; Yue et al. 1999; Yue and Wang 2004; Nadarajah and Shiau 2005; Escalante 2007), bivariate gamma distribution (Yue 2001), bivariate normal distribution (Goel et al. 1998; Yue 1999), bivariate lognormal distribution (Yue 2000), bivariate exponential distribution (Choulakian et al. 1990) etc. Most of these studies applied the bivariate probability distributions to obtain joint and conditional distribution of flood peak and volume. Some of these studies have considered the dependence among flood variables, but with restrictive assumptions, such as, assuming all flood properties were well represented by a single probability distribution (e.g., normal distribution). But in practice, the flood variables may follow different distributions and needs to be modeled separately. Also other issue is applying data transformations, such as taking natural logarithms or applying Box-Cox transformations to the flood variables, with an assumption of the transformed series will be invariant. But this may not be case all the time, as transformed marginals may deviate from original distributions. Moreover, several conventional multivariate distributions do not allow full coverage of dependence structure between the variables and they can represent only a very limited range of distributional shapes.

For modeling point of view, lower the dimensionality of the model, higher the reliability of the estimates. In this respect, any modeling approach that could decompose the multivariate estimation procedure into separate marginal distributions and functional form of dependence between the variables can effectively increase the reliability of the estimation process (Ané and Kharoubi 2003). Also, sometimes conventional methods are mathematically complicated and multivariate models may require linking to Pearson’s linear correlation coefficient as the dependence parameter. However, Pearson’s correlation coefficient is not an efficient measure of association when the dependence between the variables is nonlinear. Another classical approach to model joint distribution of random variables is the product of marginal and conditional distributions (Clemen and Reilly 1999). But the complexity of estimation process grows as the number of random variables increases. Thus conventional multivariate distributions are not flexible enough, and there is a greater necessity of sophisticated methods for flood frequency analysis.

In recent times, the use of copulas have become popular for multivariate analysis in various fields, viz., in financial studies (Frees and Valdez 1998; Cherubini et al. 2004), in hydrology and water resources for rainfall analysis (De Michele and Salvadori 2003; Shiau et al. 2006), for flood flow analysis (Favre et al. 2004; De Michele et al. 2005; Zhang and Singh 2006; Grimaldi and Serinaldi 2006; Genest and Favre 2007; Karmakar and Simonovic 2009; Wang et al. 2009; Klein et al. 2010; Chowdhary et al. 2011), for drought analysis (Kao and Govindaraju 2010; Song and Singh 2010; Janga Reddy and Ganguli 2012a), for groundwater analysis (Bárdossy 2006; Janga Reddy and Ganguli 2012b), and hydro-climatic variable analysis (Maity and Kumar 2008; Janga Reddy and Ganguli 2012b) etc. In the following, brief details of copula applications with relevance to the present study are discussed.

One of the early applications of copulas in hydrology is for rainfall analysis by De Michele and Salvadori (2003). They applied for a case study in Bisagno drainage basin, Italy, and modeled different combinations of negatively associated average storm intensity and duration using Frank Archimedean copula with heavy tailed Generalized Pareto as the marginal distribution for both storm duration and intensity data. Favre et al. (2004) investigated applicability of Clayton, Gumbel-Hougaard and Frank copulas for flood flow analysis for case studies in Québec, Canada. They found that Frank copula as the best model to capture dependence between flood variables. De Michele et al. (2005) employed Gumbel-Hougaard copula to model joint distribution of annual maximum flood peak and volume in Anza catchment, Northern Italy. They generated large number of synthetic observations with GEV marginals to check the behavior of reservoir during its expected design life and tested adequacy of dam spillways. Shiau et al. (2006) analyzed bivariate distribution of flood peak and volume in Jhuoshuei River basin, Taiwan using Ali-Mikhail-Haq, Clayton, Frank, Galambos, Gumbel-Hougaard and Plackett copulas. A comparative study is carried out between joint return period and univariate return period, and stressed the necessity of copulas for estimation of joint return periods.

Zhang and Singh (2006) modeled bivariate joint distributions of flood peak-volume, and flood volume-duration combinations using Archimedean copulas and applied to flood data from two different gauging stations, Ashuapmushuan River at Saguenay in Canada and Amite River at Denham springs in US, with marginal distribution as Extreme Value Type I and Log-Pearson Type III distributions. They found that Gumbel-Hougaard copula provides better fit to the both combinations of flood variables. Also the copula derived distributions were compared with Gumbel mixed model and Box-Cox transformed normal distributions, and found that copula derived distributions were much efficient to that of conventional multivariate distributions. Genest and Favre (2007) presented a comprehensive review of copula with their parameter estimation and inference procedures, with an application to a case study in Harricana watershed, Québec, Canada. Among various copula models considered in their study, they found that extreme value class of copulas—Gumbel-Hougaard, Galambos, Husler-Reiss, BB1 and BB5 as the plausible models for modeling flood peak and volume data. Karmakar and Simonovic (2009) applied three Archimedean copulas namely, Ali-Mikhal-Haq, Clayton and Gumbel-Hougaard for bivariate flood frequency analysis of flood flows of Red River at Grand Forks, Dakota, and found that Gumbel-Hougaard copula as the best model for representing flood properties.

Wang et al. (2009) presented copula method to estimate flood quantiles for a river at the downstream confluence point considering flood flows at two upstream tributaries, and demonstrated through an application to a case study in Des Moines River basin, Iowa and hinted that Frank copula performed satisfactorily. Klein et al. (2010) presented copula based bivariate probability analyses of flood flows in Unstrut River basin, Germany. In first application the spatial distribution of flood events within river basin is analyzed by joint probability of inflow peaks at two reservoirs located at the downstream of the main tributary. In second application copulas are used to obtain joint distribution of flood peak and volume in Unstrut catchment for risk assessment of individual flood detention structures. Chowdhary et al. (2011) employed Archimedean families of copulas namely Ali-Mikhail-Haq, Clayton, Farlie-Gumbel-Morgenstern, Frank, Galambos and Gumbel-Hougaard copulas to obtain joint distribution of flood peak and volume of Greenbrier River basin at Alderson, West Virginia, and found that Clayton copula was the best model for representing the flood properties.

Flood is a common phenomenon in many parts of India and studies have conducted for flood frequency analysis (FFA) using conventional probabilistic approaches in different parts of India. For example, L-moments based regional flood frequency analysis for developing flood frequency relationship for both gauged and ungauged catchments (Parida et al. 1998; Kumar et al. 2003; Kumar and Chatterjee 2005), LH-moments approach (Bhuyan et al. 2010). Most of these studies analyzed regional flood frequency relationship taking into account only annual maximum peak flow of the flood. Few studies considered bivariate analysis, for example bivarate FFA using bivariate normal distribution (Goel et al. 1998). As discussed in the above paragraphs regarding the limitations of conventional approaches, there is a greater necessity to adopt effective multivariate probabilistic approaches to properly assess the risks associated with the floods.

To overcome the problems associated with univariate probability analysis, which may lead to over and under estimation of associated hydrological risks, in this study, bivariate copula approach is presented for frequency analysis of floods in upper Godavari River basin in Maharashtra, India. The study aims to address the following issues: (i) evaluating the performance of parametric and non-parametric probability distributions for representing flood characteristics; (ii) Evaluating the performance of two types of parameter estimation methods for copula models; (iii) Testing the performance of four Archimedean copulas for flood frequency analysis by applying to a case study, and estimating joint return periods and conditional return periods of flood characteristics.

In the following, first brief details on theoretical aspects of copulas, procedure for estimation of copula parameter, and goodness-of-fit test and performance measures used for selection of best copula are presented. Afterward, copula methodology is applied to a case study and the obtained results are presented in a systematic way, which includes analysis of dependence structure of flood characteristics, selection of marginal distributions, fitting copulas, determining joint and conditional distribution of flood characteristics at various return periods. Finally a brief summary and conclusion is presented.

2 Theoretical Aspects of Copula

Copula is a function for capturing the dependence of two or more random variables. The Sklar’s theorem (Sklar 1959) states that the joint behavior of random variables (X, Y) with continuous marginals u = F _X (x) = P(X ≤ x) and v = F _Y (y) = P(Y ≤ y) can be characterized uniquely by its associated dependence function or copula C. For 2-dimensional case, for all (u, v) ϵ [0,1]² the relationship can be written as,

$$ \matrix{ {{F_{{X,Y}}}\left( {x,y} \right) = C\left[ {{F_X}(x),{F_Y}(y)} \right] = C\left( {u,v} \right),} \hfill &{\forall x,y \in \Re } \hfill \\ }<!end array> $$

(1)

where F _X,Y (x,y) is joint cumulative distribution function (CDF) of random variables X and Y.

Let I = [0,1]. A bivariate copula is distribution function C = I² → I, which normally satisfies the following basic properties:

• the boundary conditions: C(t, 0) = C(0, t) = 0 and C(t, 1) = C(1, t) = t, $\forall t \in {\mathrm{I}}$

• 2-increasing property: $C\left( {{u_2}, {v_2}} \right) - C\left( {{u_2}, {v_1}} \right) - C\left( {{u_1},{v_2}} \right) + C\left( {{u_1}, {v_1}} \right) \geqslant 0$, $\forall {u_1},{u_2},{v_1},{v_2}, \in {\text I}$ such that u ₁ ≤ u ₂ and v ₁ ≤ v ₂

The bivariate copula density c(u, v) is the double derivative of C with respect to its marginals and can be written as, $c\left( {u,v} \right) = \frac{{{\partial^2}C\left( {u,v} \right)}}{{\partial u\partial v}}$.

2.1 Archimedean Copulas

The copula function C: [0, 1]² → [0, 1] is called bivariate Archimedean copula, if it holds the representation (Nelsen 2006),

$$ \matrix{ {C\left( {u,v} \right) = {\phi^{{ - 1}}}\left( {\phi (u) + \phi (v)} \right)} \hfill &{u,v \in \left[ {0,1} \right]} \hfill \\ }<!end array> $$

(2)

where ϕ(•) is known as generator function of the copula and ϕ ⁻¹ is the inverse of ϕ(•). The generator $\phi :I \to {\Re^{ + }}$ is a continuous, decreasing, convex function such that ϕ(1) = 0 and $\phi (0) = \infty$.

In this study, four Archimedean families of copula functions are applied, namely, Ali-Mikhail-Haq, Clayton, Gumbel-Hougaard and Frank copula. The expressions for these copula families, generator functions, and other properties are given in Table 1 (Nelsen 2006). The applicability of each copula family is constrained by the association of the flood variables (e.g., by using the Kendall’s rank correlation (τ) dependence measure).

Table 1 Copula function, parameter space, generating function ϕ(t) and functional relationship of Kendall’s τ _θ with copula parameter for various Archimedean copulas

• The Ali-Mikhail-Haq family of copula is applicable for both negative and positive dependence, but has limitation that the copula parameter θ does not cover the entire range [−1, 1] of association measures, the dependence parameter is restricted for Kendall’s tau, τ _θ ϵ [−0.1817, 0.3333].

• Clayton copula and Gumbel-Hougaard copula are applicable only for positive dependence between random variables, τ _θ  ≥ 0.

• Frank copula can model both negative and positive dependence structure for entire range of association measures, τ _θ ϵ [−1, 1].

2.2 Estimation of Copula Parameter

The estimation of copula parameters is performed using two procedures: (1) method-of-moments-like (MOM) estimator based on inversion of Kendall’s τ (Genest and Rivest 1993) and (2) maximum pseudo likelihood (MPL) estimator (Genest et al. 1995).

2.2.1 Estimation Based on Inversion of Kendall’s τ

In MOM estimation, the relationship between sample rank correlation and the copula parameter θ is used. If there exists one-to-one correspondence between copula parameter $\widehat{\theta }$ and rank correlation, then by substituting the empirical values of the rank correlation into the relation $\widehat{\theta } = f\left( {\widehat{\tau }} \right)$ will yield the estimate of copula parameter.

For Archimedean family of copulas, the following relationships between Kendall’s τ, copula and the generator function holds (Nelsen 2006),

$$ \matrix{ {\tau = 4\int_{{{{\left[ {0,1} \right]}^2}}} {C\left( {u,v} \right)\,dC\left( {u,v} \right)} - 1;} \hfill &{\mathrm{and}} \hfill &{\tau = 1 + 4\int\limits_0^1 {\frac{{\phi (t)}}{{\phi \prime (t)}}dt} } \hfill \\ }<!end array> $$

(3)

Where ϕ (•) is the generator function of Archimedean family of copula; ϕ′ (•) is first derivative of the generator function. For Archimedean family of copulas, there exists explicit expressions for Kendall’s τ as a function of copula parameter $\widehat{\theta }$, which are given in Table 1 (Nelsen 2006).

The Kendall’s τ is defined as the difference between the probability of concordance and the probability of discordance. Let n paired samples (x ₁, y ₁), …, (x _n , y _n ) be observations of independent identically distributed random variables X and Y. Among the $\left( {\begin{array}{*{20}{c}} n \hfill \\ 2 \hfill \\ \end{array} } \right)$ distinct paired samples, two paired samples (x _i , y _i ) and (x _j , y _j ) are concordant if [(x _i -x _j )(y _i -y _j ) > 0] and otherwise those are discordant. The sample version of Kendall’s τ is defined as, $\tau = \left( {c - d} \right)/\left( {\begin{array}{*{20}{c}} n \hfill \\ 2 \hfill \\ \end{array} } \right)$, where n is sample size; c and d denote the number of concordant and discordant pairs respectively. The range of τ is [−1, 1], where 1 represents total concordance, −1 represents total discordance, and 0 represents zero concordance. Thus, the copula parameter $\widehat{\theta }$ can be estimated by using the given Kendall’s τ functional relation with θ for Archimedean family of copulas (Table 1).

2.2.2 Maximum Pseudo-Likelihood (MPL) Method

The MPL estimation method does not require any prior assumptions regarding marginal distributions of the dependent variables. The procedure consists of transforming the marginal variables into uniformly distributed vectors using its empirical distribution function. Then the copula parameters are estimated using maximization of pseudo log-likelihood function.

Let X ₁ = (X _1,1, X _1,2), …, X _n = (X _n,1, X _n,2)be n sample of observations in 2-dimensional space. The empirical CDF of variable X _k , for k ϵ {1,2} can be computed by,

$$ \matrix{ {{F_k}\left( {{X_{{i,k}}}} \right) = \frac{{{R_{{i,k}}}}}{{n + 1}}} \hfill &{i \in \left\{ {1, \ldots, n} \right\},k \in \left\{ {1,2} \right\}} \hfill \\ }<!end array>, $$

(4)

where R _i,k is rank, which is given by ${R_{{i,k}}} = \sum\limits_{{j = 1}}^n {I\left( {{X_{{j,k}}} \leqslant {X_{{i,k}}}} \right)}$. Here I(A) is a logical indicator function results in either 1 (if A is true) or 0 (if A is false).

The empirical distribution function is used as a surrogate for the unknown marginals. Substituting empirical CDFs into copula density and applying logarithm to the likelihood function of the copula yields the following form,

$$ \ell \left( \theta \right) = \sum\limits_{{i = 1}}^n {\log \left[ {{c_{\theta }}\left\{ {{F_1}\left( {{X_{{i,1}}}} \right),{F_2}\left( {{X_{{i,2}}}} \right)} \right\}} \right]} $$

(5)

Then the copula parameter $\widehat{\theta }$ can be obtained by maximizing this pseudo log-likelihood function $\ell \left( \theta \right)$.

From a computational perspective, estimation based on inversion of Kendall’s τ is generally faster than MPL method. However, in recent studies, it was noted that for the asymptotic relative efficiency point of view with finite samples, the MPL estimation method is more efficient (Kojadinovic and Yan 2010).

2.3 Selection of Appropriate Copula Family

Generally, there are more than one copula families that can model the dependence structure between the random variables. To identify the most appropriate copula family (among different copulas) for joint distribution of the flood variables, graphical methods as well as analytical goodness-of-fit tests are adopted in this study.

2.3.1 Graphical Methods

Graphical plots or comparison of the superimposed scatter plots of observed and simulated data (from copula) is a qualitative approach to assess the suitability of the assumed copulas. This method is more appropriate for bivaraite cases only, as visual inspection may become difficult for higher dimensional cases. The data generation is performed as Monte Carlo simulation, where it involves employing the conditional distributions for simulating fairly large number of samples (Nelsen 2006). The procedures for simulating random samples for chosen family of copulas are given in appendix A.

2.3.2 Statistical Test

Apart from graphical plots, an analytical goodness-of-fit (GOF) test is employed to formally test the adequacy of the hypothesized copulas. The test is based on parametric bootstrapping procedure and makes use of the Cramer-von Mises statistic S _n :

$$ {S_n} = \int_{{{{\left[ {0,1} \right]}^2}}} {n{{\left\{ {{C_n}\left( {u,v} \right) - {C_{{{\theta_n}}}}\left( {u,v} \right)} \right\}}^2}d{C_n}\left( {u,v} \right)} $$

(6)

Where C _n is the empirical copula calculated using n observational data, and ${C_{\theta }}_{{_n}}$ is the parametric copula (estimation under the null hypothesis). Genest et al. (2009) carried out a power study to evaluate the effectiveness of various GOF tests and recommended it for Archimedean copulas.

The GOF test helps to examine whether the unknown copula C actually belongs to the chosen parametric copula family C _θ or not. It involves testing null hypothesis H ₀:C ϵ C ₀, C ₀ = {C _θ :θ ϵ O}; against ${H_1}:C \notin C{}_0$. Where O is an open subset of ${\Re^q}$ for some integer q ≥ 1.

The step-by-step procedure for parametric bootstrap based GOF test is given below.

• 1. Compute empirical copula C _n from the pseudo-observations (U _1,n , V _1,n ), …, (U _n,n , V _n,n ),

$$ \matrix{ {{C_n}\left( {u,v} \right) = \frac{1}{n}\sum\limits_{{i = 1}}^n {1\left( {{U_{{i,n}}} \leqslant u,{V_{{i,n}}} \leqslant v} \right)}, } \hfill &{\left( {u,v} \right) \in \left[ {0,1} \right]} \hfill \\ }<!end array> $$

Where 1(•) is a logical indicator function; and (U _i,n , V _i,n ) are pseudo-observations from C computed from the data (X ₁, Y ₁), …, (X _n , Y _n ),

$$ \matrix{ {{U_{{i,n}}} = \frac{1}{{n + 1}}\sum\limits_{{j = 1}}^n {1\left( {{X_j} \leqslant {X_i}} \right)}, } \hfill &{{V_{{i,n}}} = \frac{1}{{n + 1}}\sum\limits_{{j = 1}}^n {1\left( {{Y_j} \leqslant {Y_i}} \right)}, } \hfill &{i \in \left\{ {1, \ldots, n} \right\},} \hfill \\ }<!end array> $$

and estimate dependence parameter θ using suitable estimator

• 2. Compute the Cramer-von Mises statistic

$$ {S_n} = \int_{{{{\left[ {0,1} \right]}^2}}} {n{{\left\{ {{C_n}\left( {u,v} \right) - {C_{{{\theta_n}}}}\left( {u,v} \right)} \right\}}^2}d{C_n}\left( {u,v} \right)} = \sum\limits_{{i = 1}}^n {{{\left\{ {{C_n}\left( {{U_{{i,n}}},{V_{{i,n}}}} \right) - {C_{{{\theta_n}}}}\left( {{U_{{i,n}}},{V_{{i,n}}}} \right)} \right\}}^2}} $$

(7)

• 3. For some large integer N, repeat the following steps for every k ϵ {1,…,N}:

• (a) Generate a random sample $\left( {U_1^k,V_1^k} \right), \ldots, \left( {U_n^k,V_n^k} \right)$from copula ${C_{\theta }}_{{_n}}$and deduce the associated pseudo-observations $\left( {U_{{1,n}}^k,V_{{1,n}}^k} \right), \ldots, \left( {U_{{n,n}}^k,V_{{n,n}}^k} \right)$

• (b) Let $C_n^{{(k)}}$ and $\theta_n^{{(k)}}$ stand for the versions of C _n and θ _n derived from the pseudo observations $\left( {U_{{1,n}}^k,V_{{1,n}}^k} \right), \ldots, \left( {U_{{n,n}}^k,V_{{n,n}}^k} \right)$.

• (c) Form an approximate realization of the test statistic under null hypothesis H ₀ as

$$ S_n^{{(k)}} = \sum\limits_{{i = 1}}^n {{{\left\{ {C_n^{{(k)}}\left( {U_{{i,n}}^{{(k)}},V_{{i,n}}^k} \right) - {C_{{\theta_n^{{(k)}}}}}\left( {U_{{i,n}}^{{(k)}},V_{{i,n}}^k} \right)} \right\}}^2}} $$

(8)

• 4. An approximate p-value for the test is finally given by $p = \frac{1}{N}\sum\limits_{{k = 1}}^N {1\left( {S_n^{{(k)}} \geqslant {S_n}} \right)}$

If the p-value is larger than a particular significance level (α), then the null hypothesis is accepted; otherwise, it is rejected. The larger the p-value, the more strongly the test accepts the null hypothesis.

2.4 Estimation of Return Periods

The return period of flood events is usually associated with a certain exceedance probability. For univariate case, the return period (T) is expressed as

$$ {T_X} = \frac{1}{{P\left( {X \geqslant x} \right)}} = \frac{1}{{\left( {1 - {F_X}(x)} \right)}} $$

(9)

2.4.1 Joint Return Period

For bivariate case, the joint return period can be characterized in two ways: (i) return period for X ≥ x AND Y ≥ y, let the corresponding return period represented by T _X,Y ; (ii) return period for X ≥ x OR Y ≥ y, let the corresponding return period represented by $T_{{X,Y}}^{\prime }$. Accordingly the joint return periods for copula based flood events can expressed (Shiau et al. 2006) as:

$$ \matrix{ {{T_{{X,Y}}} = \frac{1}{{P\left( {X \geqslant x\,AND\,Y \geqslant y} \right)}} = \frac{1}{{1 - {F_X}(x) - {F_Y}(y) + {F_{{X,Y}}}\left( {x,y} \right)}}} \\ { = \frac{1}{{1 - {F_X}(x) - {F_Y}(y) + C\left[ {{F_X}(x),{F_Y}(y)} \right]}}} \\ }<!end array> $$

(10)

$$ T_{{X,Y}}^{\prime } = \frac{1}{{P\left( {X \geqslant x\,OR\,Y \geqslant y} \right)}} = \frac{1}{{1 - {F_{{X,Y}}}\left( {x,y} \right)}} = \frac{1}{{1 - C\left[ {{F_X}(x),{F_Y}(y)} \right]}} $$

(11)

2.4.2 Conditional Return Period

The concern in flood risk analysis is not only just to determine whether flood peak flow, volume, and/or duration simultaneously exceed certain thresholds. But also to determine the probability of flood peak (or volume) given flood duration exceeding a certain threshold is vital, which can be estimated by copula modeling. The conditional probability for bivariate models can be expressed as:

$$ P\left( {X \leqslant x|Y \leqslant y} \right) = \frac{{P\left( {X \leqslant x,Y \leqslant y} \right)}}{{P\left( {Y \leqslant y} \right)}} = \frac{{{F_{{X,Y}}}\left( {x,y} \right)}}{{{F_Y}(y)}} = \frac{{C\left( {{F_X}(x),{F_Y}(y)} \right)}}{{{F_Y}(y)}} $$

(12)

$$ P(X \leqslant x|Y \geqslant y) = \frac{{P(X \leqslant x,Y \geqslant y)}}{{P(Y \geqslant y)}} = \frac{{{F_X}(x) - {F_{{X,Y}}}(x,y)}}{{1 - {F_Y}(y)}} = \frac{{{F_X}(x) - C({F_X}(x),{F_Y}(y))}}{{1 - {F_Y}(y)}} $$

(13)

By using above conditional distributions the corresponding return periods can be obtained (for given flood characteristics) by using the standard convention for return period (Eq. 10). In present study the capability of copula function to model joint dependence between annual flood peak flow, volume and/or duration has been evaluated for Godavari River basin near Nasik in India. By using copula based joint distributions of correlated flood variables, the joint and conditional return periods of flood events are computed, which can be useful for hydrologic design of water infrastructure.

3 Application

3.1 Study Area Details

The River Godavari ranks 34th and 32nd in terms of catchment area and water discharge respectively, amongst the 60 major rivers of the world. Figure 1 presents location map of the study region upper Godavari River basin. The River originates near Nasik at an elevation of 1,065 m in the Western Ghat, about 80 Km from the Arabian Sea. After descending from Western Ghats, it takes a South-Easterly course across the Southern part of Indian Peninsula and flows through 1,230 Km and falls into Bay of Bengal. The catchment area drained by the river is over an area of 31.3 Mha, which is nearly 9.5 % of the total geographical area of the country. Godavari basin is located between the latitudes of 16°16′ N and 22°36′N; longitudes of 73°26′E and 83°07′ E. The principal tributaries of the River are Manjara, Pranhita, Indravati, and Sabri. The Godavari basin receives an average rainfall of about 92.3 cm during monsoon season (June to September), which is about 85 % of the total annual rainfall (Rao 2001). The mean annual water discharge of Godavari River is 1.1 × 10⁵ Mm³, of which 93–96 % occurs during monsoon season. The flow in the river is mainly ephemeral in nature with high stream flow in monsoon season due to heavy rainfall. In non-monsoon season, there is low stream flow in the River and remains almost in dry state. Floods in Godavari are mostly associated with heavy rain in monsoon season.

Fig. 1

Location map of upper Godavari River basin

Geographical location of Nasik is 20°01′–20°02′ N and 73°30′–73°50′ E. Due to heavy rains, Nasik is frequently affected by floods in the monsoon season. In present study, stream gauge station located near Nasik City is considered, which is one of the heavy flood affected area in Nasik district. Daily stream flow data is collected from Hydrology Project Circle, Nasik for the period of 22 years (1987–2008). Due to sampling problem no measurements were available for the year 1995, 1998, 2000 and 2001. Hence those years are not considered and a total of 18 years daily stream flow record is available for the present analysis. The average monthly discharge data for monsoon period shows that stream flow is highest during the month of August (1255.65 m³/s).

3.2 Flood Characteristics

The flood characteristics such as flood peak (Q), flood volume (V) and flood duration (D) are obtained from daily stream flow data. The flood peak is defined as the maximum daily flow during the flood event; flood duration is defined as the total number of days the flood event occurred; while the flood volume is defined as the cumulative flow volume during the flood period. These are obtained for annual scale, which means that for each year there will be one flood characteristic. Other issue, which needs proper attention, is base flow consideration. The start of the surface runoff is marked by the sharp rise of the hydrograph and end of the flood runoff is identified by the inflection point on the receding limb of the hydrograph. If time of rise of the flood hydrograph is denoted by SD (day) and fall by ED (day), the flood volume (V) of each flood event is estimated as (Yue 2001):

$$ {V_i} = \left( {V_i^{{total}} - V_i^{{baseflow}}} \right) = \int\limits_{{SD}}^{{ED}} {{q_{{ij}}}dt - \frac{{{D_i}}}{2} \times \left( {{q_{{is}}} + {q_{{ie}}}} \right)} = \sum\limits_{{j = SD}}^{{ED}} {{q_{{ij}}} - \frac{{{D_i}}}{2}\left( {{q_{{is}}} + {q_{{ie}}}} \right)} \,\forall i = 1,2, \ldots, n $$

(14)

where, q _ij is the j ^th day observed stream flow value for i ^th year, q _is and q _ie are observed daily stream flow values on start and end day of the flood hydrograph for i ^th year.

The annual flood peak series is constructed by:

$$ \matrix{ {{Q_i} = \max \left\{ {{q_{{ij}}},j = S{D_i},S{D_i} + 1, \ldots, E{D_i}} \right\}} \hfill &{i = 1,2, \ldots, n} \hfill \\ }<!end array> $$

(15)

where SD _i and ED _i are start and end day of a flood event during the i ^th year.

The flood duration series is given by:

$$ \matrix{ {{D_i} = E{D_i} - S{D_i},} \hfill &{i = 1,2, \ldots, n} \hfill \\ }<!end array> $$

(16)

Once the flood characteristics are obtained from daily stream flow data, which can be used for flood frequency analysis.

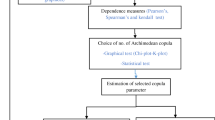
3.3 Step-Wise Procedure for Copula Based Flood Frequency Analysis

The steps involved in copula-based flood frequency analysis are given below:

• 1. Quantify the strength of dependence between the flood variables using standard dependence measures. Test whether the dependence is statistically significant using standard two-tailed t-test.

• 2. Fitting marginal (univariate) distribution of each variable using suitable probability distribution function.

• 3. Select copula families based on strength of dependence between flood variables.

• 4. Fitting copula, which requires estimating copula parameter using methods described above.

• 5. Identify appropriate copula model by using graphical plots, performance measures and statistical goodness-of-fit tests.

• 6. After selecting suitable copula family, the copula-based joint distribution can be used to estimate the joint and conditional return periods of flood events.

4 Results and Discussion

4.1 Dependence of Flood Variables

To measure the statistical dependence between random variables, the Pearson’s linear correlation (r), and two non-parametric dependence measures (rank correlations) such as Spearman’s rho (ρ) and Kendall’s tau (τ) are used. The Pearson’s linear correlation, measures the linear dependence between two random variables, but assumes that the underlying distribution is normal, and it is not invariant under monotonic non-linear transformation. The Spearman’s rho, and Kendall’s tau are calculated using ranking of variable values rather than actual values, so they are invariant under monotonic non-linear transformations; also there is no assumption on underlying distributions. Hence, these are more preferred and often used as effective dependence measures for the nonlinear modeling in hydrology.

Table 2 presents pair-wise association among flood variables—annual flood peak, volume and duration, along with their corresponding p-values of the estimate. It can be observed that the rank correlations for peak flow-volume and volume-duration pairs are statistically significant at 5 % significance level. The time series plots for flood characteristics are shown Fig. 2. The Fig. 2a and b give the visual or qualitative illustration of the dependence between annual flood peak-volume, and volume-duration pairs respectively. But the correlation between peak flow-duration pair is small and the estimate of corresponding Kendall’s τ and Spearman’s ρ is not statistically significant as confirmed by larger p-value of the estimate. Therefore, the null hypothesis of there is no dependence may be accepted and concluded that the corresponding flood variables are uncorrelated. So, in this study the dependence modeling is carried out for flood peak-volume, and volume-duration combinations only.

Table 2 Pair-wise association between flood characteristics flood peak, volume and duration

Fig. 2

Characteristics of observed bivariate annual flood flows: a peak flow and volume, b flood volume and duration pairs

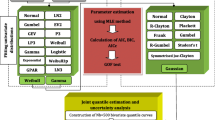
4.2 Marginal Distribution of Flood Variables

For fitting marginal distributions to flood variables, two parametric and two nonparametric probability distribution functions are tested. For parametric distributions, 2-parameter Gamma and 2-parameter Log-normal are used; whereas for nonparametric distributions, kernel density estimator with kernel type—Normal and Quadratic kernel functions are used. The expressions for probability density functions (PDFs) with their associated parameters of marginal distributions are presented in Table 3. The maximum likelihood estimation (MLE) method is applied to estimate the parameters of the distributions.

Table 3 Probability density function and parameters of marginal distribution

In parametric methods for estimating density function, it is assumed that the sample comes from a population with a given probability density function; whereas nonparametric method is developed directly from the data and it can reproduce attributes represented by the sample (Moon and Lall 1994). For validation, rank based Weibull plotting position formula $P\left( {X \leqslant {x_i}} \right) = {{i} \left/ {{\left( {n + 1} \right)}} \right.}$ is used as an estimate of empirical cumulative probability distribution. Where ‘i’ is the rank in ascending order, and x _i is the i ^th largest variate in a data series of size n.

The performance of each marginal distribution is evaluated against the empirical non-exceedance probability (i.e.,Weibull plotting position formula) using AIC criteria (mean square error form). The results are presented in Table 4, which provides a comparison of performances for various marginal distributions. From Table 4, the model results indicate that normal kernel is the best fit model for peak flow and duration, while quadratic kernel performed well for volume. Although the difference between relative performances of Normal and Quadratic kernel is very small, Normal kernel is chosen due to its lower AIC value for fitting flood duration data. The Kolmogorov-Smirnov (KS) goodness-of-fit test is used to detect whether the proposed models can be used to represent the observed data. The critical value of KS test statistic for sample size of 18, at 5 % significance level is d _critical =0.31. The maximum deviations (d _max) between observed data and the corresponding distributions are also reported in Table 5, which indicates that all the deviations are less than the critical value. Thus all the distributions are satisfactory. Figure 3 illustrates the fitted marginal distributions for the three flood variables. For empirical CDF, weibull plotting position formula is used. The PDFs, CDFs and corresponding probability (P-P) plots for the marginal distributions of flood variables (in Fig. 3) show good agreement between theoretical distributions and the empirical distributions. It can be noticed that normal kernel is the best fitted model for flood variables—peak flow and duration; whereas quadratic kernel is the best fitted model for flood volume.

Table 4 Performance of various parametric and non-parametric methods for fitting marginal distributions of flood variables

Table 5 Copula dependence parameter estimates based on the inversion of Kendall’s tau (MOM) and corresponding goodness-of-fit statistics. N = number of bootstrap sampling

Fig. 3

Illustration of fitted marginal distributions for flood characteristics: annual peak flow Q (first row), flood volume V (second row), and flood duration D (third row). First and second columns show the PDF and CDF of fitted distributions. Third column show the results for best fits models only

4.3 Joint Dependence Structure of Flood Variables Using Copulas

Four Archimedean families of copulas, viz., Ali-Mikhail-Haq, Clayton, Gumbel-Hougaard and Frank are chosen to model flood characteristics. To apply Ali-Mikhail-Haq copula for dependence modeling, the Kendall’s τ should be within the range of [−0.18, 0.33]. But for the present case study, the kendall’s τ of the flood variable pairs under consideration for dependence modeling i.e., flood peak-volume and volume-duration pairs, are found to be 0.76 and 0.46 respectively. Therefore, the Ali-Mikhail-Haq copula may not be applicable, and is not considered for further analysis.

The dependence parameter of copula families is estimated by method-of-moments-like (MOM) estimator based on inversion of Kendall’s tau, and maximum-pseudo likelihood (MPL) method. The copula dependence parameters estimated by MOM and MPL method are given in Tables 5 and 6 respectively. First observed flood data are compared with large number of generated or simulated samples from copulas. One thousand random pairs (u _i , v _i ) of data are generated from each families of copulas based on dependence parameters estimated by MOM and MPL methods, and then transformed back to their corresponding magnitudes of flood variables using marginal distributions. Then these simulated samples are compared with the observed flood variable data and the corresponding scatter plots, for flood peak-volume are shown in Fig. 4; and for flood volume-duration are shown in Fig. 5. The Kendall’s τ values of the simulated samples are also shown in the respective figures. The scatter plots in Figs. 4 and 5 show that most of the copula families are capturing the observed dependence of flood variables, overall Frank copula seems slightly better for modeling the dependence structure of flood variables. However, by just with visual illustration, it is very difficult task to make a choice on selection of a particular copula model over others.

Table 6 Copula dependence parameter estimates based on the Maximum Pseudo Likelihood (MPL) method and corresponding goodness-of-fit statistics

Fig. 4

Scatter plots of flood peak and volume, shows comparison of observed data with sets of 1,000 generated random samples based on dependence parameters obtained by MOM and MPL methods for different copula families: a Clayton, b Gumbel- Hougaard, c Frank copula. Solid circles in black color are observed data, and gray dots are simulated samples from copula models

Fig. 5

Scatter plots of flood volume and duration, shows comparison of observed data with sets of 1,000 generated random samples based on dependence parameters obtained by MOM and MPL methods for different copula families: a Clayton, b Gumbel- Hougaard, c Frank copula

To statistically validate and identify best suitable copula model, a formal GOF test statistics—Cramer von Mises distance with parametric bootstrap method is employed. The results of GOF test for the copulas fitted using MOM and MPL methods are presented in Tables 5 and 6 respectively. A parametric bootstrap procedure is employed for the simulated random samples of sizes 500 and 1,000. The values of Cramer von Mises distance statistics (S _n ), p-values of the estimate and critical values at 5 % significance level are given in Tables 5 and 6.

From Table 5 (results of MOM based copula models), it can be seen that the GOF test resulted in significantly higher p-values for Frank copula model as compared to other models. From Table 6 (results of MPL based copula models), it can be noted that the smaller p-values of GOF test for Clayton copula lead to rejection of Clayton copula at 5 % significance level for flood variable pairs; whereas for Frank copula model the test resulted in significantly higher p-values for peak flow-volume and volume-duration pairs (for both N = 500 and N = 1,000 bootstrapped samples). Hence Frank copula is found to be best copula model for dependence modeling of bivariate flood data.

Further to evaluate the performance of parameter estimation methods (MOM and MPL), the performance is evaluated in terms of root mean square error (RMSE) between the Frank copula CDF and the empirical non-exceedance probability or empirical CDF (ECDF) of flood variables. The ECDF is computed using Gringorten’s plotting position formula (Zhang and Singh 2006). For flood peak-volume, the resulting RMSE are 0.0441 and 0.0436 for MOM and MPL methods respectively; whereas for flood volume-duration dependence modeling, the resulting RMSE are 0.063 and 0.062 for MOM and MPL methods respectively. This shows that MPL based estimator gives slightly better performance over MOM method. Therefore, Frank copula model and the copula parameters obtained using MPL method are adopted for further analysis of flood characteristics.

4.4 Joint Return Periods

The joint return period of flood variables of interest, such as flood peak flow-volume pair (T _V,Q and $T_{{V,Q}}^{\prime }$), flood volume –duration pair (T _V,D and $T_{{V,D}}^{\prime }$) can be obtained using Eqs. 10 and 11. Here it should be noted that for a given joint probability (or return period), there may exist more than one possible flood variable combinations (e.g., flood volume and duration). Hence, the contour line of each particular return period is illustrated in Figs. 6 and 7. The contour plots of bivariate joint return periods associated with Eqs. 10 and 11 for flood characteristics are shown in separate figures. Figure 6a and b show the joint return periods of peak flow-volume pair for ‘AND’ and ‘OR’ cases respectively. Similarly, Fig. 7a and b show the joint return periods of flood volume-duration pair for ‘AND’ and ‘OR’ cases respectively. The contour lines for specific joint return periods, in which both peak flow and volume exceeded (T _VQ ), has inward bounds (Fig. 6a), whereas the joint return period, in which either peak flow or volume exceeded ($T_{{VQ}}^{\prime }$) has outward bounds (Fig. 6b). Similar inferences can be made from Fig. 7 for joint return periods of flood volume and duration pair.

Fig. 6

Joint return periods of peak flow and volume, for the case of (a) both peak flow and volume are exceeded, T _VQ (years); (b) either peak flow or volume are exceeded, $T_{{VQ}}^{\prime }$ (years)

Fig. 7

Joint return periods of flood volume and duration, for the case of (a) both volume and duration are exceeded, T _VD (years); (b) either volume or duration are exceeded, $T_{{VD}}^{\prime }$ (years)

From Fig. 6, it can be noticed that for the same values of peak flow and volume, the joint return period of T _VQ is much greater than that of $T_{{VQ}}^{\prime }$. For example, in the year 1997, for annual peak flow of 39.523 Mm³/day the corresponding flood volume was 107.2 Mm³. The joint return periods for this flood event T _VQ estimated using Eq. 10 and $T_{{VQ}}^{\prime }$ using Eq. 11 are 5.36 and 3.38 years respectively. Similar results are observed for joint return periods of volume and duration (i.e., T _V,D is greater than that of $T_{{V,D}}^{\prime }$). These results can be very useful for decision making in hydrologic design of water resource projects.

4.5 Conditional Return Periods

The conditional return periods of the flood volume V given the flood peak Q (T _V|Q≤q ), and return period of the flood peak Q given the flood volume V (T _Q|V≤v ) are computed by using the conditional probabilities estimated from Eq. 12, and the resultant conditional return periods are presented in Figs. 8 and 9. From Fig. 8(a-b), it is easy to know about return periods of the flood volume (flood peak) for a given value of flood peak (flood volume). Similarly, from Fig. 9(a-b), it is easy to determine return periods of the flood volume (flood duration) for a given value of flood duration (flood volume).

Fig. 8

Conditional return periods of flood characteristics: a return period of the flood volume given the flood peak (T _V|Q≤q ); b return period of the flood peak given flood volume (T _V|D≤d )

Fig. 9

Conditional return periods of flood characteristics: a return period of the flood duration given the flood volume (T _D|V≤v ); b return period of the flood volume given flood duration (T _V|D≤d )

From Fig. 8a(b), it can be noticed that the curves indicate smaller conditional return period of flood events at higher conditional peak flow values (volume) as compared to the lower conditional peak flows (volume) for the same specified value of flood volume (flood peak). At the same time, higher the flood volume (flood peak), higher is the return period of flood event. Similar kind of trend can be seen from Fig. 9, which shows conditional return period plots for flood volume and duration.

These results can be useful in hydrological risk assessment and design of hydraulic structures, such as design of spill way and construction of flood protection structures such as, levees, flood walls, diversion works and taking non- structural safety measures to control flood damage and developing flood mitigation strategies. Thus, the copula based methodology can be used as a potential tool for frequency analysis of flood flows.

5 Summary and Conclusions

In this study, a copula based methodology is presented for frequency analysis of flood flows and applied for a case study of Upper Godavari River flows in India. For bivariate frequency analysis, the flood flow characteristics such as annual flood peak flow (Q), flood volume (V) and flood duration (D) are considered. The correlation for flood peak flow-flood volume pair, and flood volume—duration pair are found to be statistically significant and considered for flood frequency analysis. Parametric and nonparametric methods are evaluated for fitting marginal distributions to flood variables and the best fit model is selected for copula modeling. Four Archimedean families of copulas namely, Ali-Mikhail-Haq (AMH), Clayton, Gumbel-Hougaard (GH), and Frank copula have been evaluated to model the joint distributions of correlated flood variables. The estimation of copula parameters is carried out using method-of-moments-like (MOM) estimator based on inversion of Kendall’s τ, and maximum pseudo likelihood (MPL) method. Based on dependence measures of flood data, it is noticed that Ali-Mikhail-Haq copula is not applicable for the data (as the correlation of flood variable pairs exceeded its allowable Kendall’s τ range). The remaining three copulas (Clayton, GH, Frank) are fitted for flood variables and evaluated their performances using graphical methods and goodness-of-fit (GOF) tests. Then, the best fit copula model is employed to obtain the joint and conditional return periods of flood characteristics.

The following specific conclusions can be drawn from the present study:

• The nonparametric kernel density functions are found to be best fit marginal distributions for flood variables.

• On performing standard goodness-of-fit tests for the Clayton, GH, Frank copula models, it is found that Frank copula is the best fitted copula for flood peak flow-volume, and flood volume-duration pairs.

• While comparing the copula parameter estimation methods, it is found that MPL method provided better estimates as compared to MOM method.

• The copula based joint distribution is found to be effective in preserving the dependence structure of flood variables and helping in better estimates of joint and conditional return periods of flood characteristics, which can be very useful for decision making in hydrologic design of water resource projects.

Appendix

1.1 A1 Simulation of Random Samples from Bivariate Archimedean Copulas

The generation of random variates (u, v) from Clayton and Frank copulas involves the following steps:

• 1. Generate two independent uniform U(0,1) random variates u and q.

• 2. Set $v = C_u^{{ - 1}}\left( {q|u} \right)$, where $C_u^{{ - 1}}\left( {q|u} \right)$ is the inverse of conditional distribution ${C_u}(v) = {{{\partial C\left( {u,v} \right)}} \left/ {{\partial u}} \right.}$. The functional relationships are given in Table 7.

  • Clayton and Frank copulas have closed form relationships for $C_u^{{ - 1}}\left( {q|u;\theta } \right)$, whereas Gumbel-Hougaard (G-H) copula does not has closed form relation, hence $C_u^{{ - 1}}\left( {q|u} \right)$ is solved numerically.

• 3. The pair (u, v) forms the random vector drawn from the respective copula family C(u, v; θ).

• 4. The desired (simulated) sample is given by $\left( {x,y} \right) = \left[ {F_X^{{ - 1}}(u),F_Y^{{ - 1}}(v)} \right]$, where $F_X^{{ - 1}}\left( \bullet \right)$ and $F_Y^{{ - 1}}\left( \bullet \right)$ are inverse of marginal distributions F _X (x) and F _Y (y) respectively.

Table 7 Functional relationships for conditional and inverse of conditional distributions for bivariate Archimedean copulas