1 Introduction

Estimates of flood quantiles for high return periods are essential for designing and assessing flood risk in hydraulic structures such as dams. Such quantiles are usually estimated by flood frequency analyses. There are many studies throughout the literature that involve univariate flood frequency analyses, usually focused on the study of the peak flow (e.g., Cunnane 1989; GREHYS 1996). Nevertheless, the multivariate nature of floods requires a multivariate flood frequency analysis (Chebana and Ouarda 2011) for certain applications. Lately, bivariate approaches studying the peak flow and hydrograph volume jointly have become widespread (e.g., Goel et al. 1998; Yue et al. 1999; Favre et al. 2004; Shiau et al. 2006). The more complex trivariate approach is considered in some studies by including the duration of the hydrograph (e.g., Serinaldi and Grimaldi 2007).

Long flood series are required to obtain accurate estimates of quantiles associated with high return periods (Saad et al. 2015), which in the case of a multivariate flood frequency analysis is even more important because of a higher uncertainty derived from a larger number of parameters involved in the study. Nevertheless, the available flood data series are short in practice, commonly between 30 and 80 years (e.g., Zhang and Singh 2007; Klein et al. 2010; Requena et al. 2015b). The need for extending observed data series to perform a proper flood frequency analysis can be addressed by either: (i) simulation via hydro-meteorological modelling, reproducing the catchment response by using long (observed or synthetic) rainfall series; or (ii) stochastic generation via a statistical analysis, such as by a multivariate model that represents the joint distribution of the studied variables.

Regarding hydro-meteorological simulation, Beven (1987) first proposed the idea of coupling a stochastic rainfall generator and a rainfall-runoff model to reproduce the flood frequency curve in a Welsh catchment, following the theoretical work presented by Eagleson (1972). Later, Cameron et al. (1999) elaborated on the idea of calibrating the predicted flood frequency curve by a model through the observed flood series for small return periods and using it to extrapolate flood magnitudes for larger return periods. Blazkova and Beven (1997, 2004) applied the procedure to several Czech catchments for dam safety evaluation. Calver and Lamb (1995) evaluated the proposed approach in ten catchments in the UK. Similar methodologies have been applied in Australia, (Boughton et al. 2002), US (England et al. 2007), France (Paquet et al. 2013), Norway (Lawrence et al. 2014), Russia (Kuchment et al. 2003), South Africa (Chetty and Smithers 2005) and other countries (Boughton and Droop 2003). These approaches are based on combining a stochastic rainfall generator and a hydrological model that reproduces the rainfall-runoff response in the catchment (Vrugt et al. 2002; Engeland et al. 2005). Such hydrological models can be classified into distributed or lumped, depending on whether the parameter values are spatially distributed or averaged in the catchment; and continuous or event-based, depending on whether a long time series, usually with a daily time step, or independent flood events, usually with around an hourly time step, are simulated. The underlying assumption is that a hydrological model calibrated with the observed data is able to simulate a set of feasible flood hydrographs that can be generated in a catchment, using synthetic rainfall events and the catchment characteristics as input. The main advantage of this approach is to provide not only the statistical characterisation of extreme values for the relevant variable, but also an ensemble of hydrographs that can force the structure under design, thus allowing for a better performance characterisation. A distributed event-based model with a high temporal and spatial resolution is required to represent correctly the variability of flood generation processes in the catchment. However, the higher is the model resolution, the longer is the computation time. Therefore, the required computation time can prevent the generation of arbitrarily long series with a good characterisation of the catchment response.

A multivariate distribution can be used for extending the available flood series, stochastically generating a larger series that keeps the statistical properties of the original sample and allows obtaining quantiles for high return periods. The shortcomings of the traditional multivariate distributions, such as the need for using the same marginal distribution for characterising all variables involved in the analysis, and the assumption of a linear relation between them, are overcome by using copulas (e.g., Salvadori et al. 2007). The use of copulas in hydrology and specially in multivariate flood frequency analysis is increasingly spreading (e.g., De Michele et al. 2005; Zhang and Singh 2006; Song and Singh 2010; Requena et al. 2013; Zhang et al. 2013). The multivariate distribution of several random variables can be obtained via the marginal distribution of each variable and a copula function, which is a multivariate distribution with uniform margins that characterises the dependence structure between them. The main advantages of the stochastic generation of flood data by a multivariate distribution based on copulas are twofold: (i) they only need a flood series as input; and (ii) the computation time required once the multivariate distribution is fitted is negligible. The drawback resides in the difficulty of properly selecting and fitting the multivariate distribution when the available data length is short. In this case, several copula families usually pass the goodness-of-fit test and a larger uncertainty is involved in fitting the parameters, which leads to larger uncertainties in estimates of the right tail of both copula and marginal distributions.

Some studies dealt with the idea of considering both approaches. Candela et al. (2014) applied a bivariate Archimedean copula-based distribution for characterising rainfall duration and intensity, in order to generate single synthetic rainfall events to be used as input in a conceptual fully distributed rainfall-runoff model based on the curve number method. The copula approach was then applied to the peak flow and hydrograph volume series of 5000 events synthetically generated from such a procedure, to obtain the flood design hydrograph related to a given joint return period. Klein et al. (2010) used 10,000 flood hydrographs generated from a distributed hydro-meteorological model as initial data for developing a copula-based flood frequency analysis in which dam safety was assessed. Dam safety was also evaluated by Giustarini et al. (2010), analysing the water level reached at a given dam by three sets of synthetic flood hydrographs. The first and second sets were obtained by generating peak-volume pairs from an Archimedean copula-based distribution fitted to observed data, and to several 1000-length synthetic data generated from a continuous hydro-meteorological model, respectively. The third set consisted of flood hydrographs generated directly from the continuous model. Dam-overtopping results were of the same order of magnitude for the three sets, although more dangerous events were obtained by the second set. On the basis of the drawbacks and advantages regarding the generation of each set, the notion of combining approaches was highlighted.

A long sample length was arbitrarily generated via hydro-meteorological modelling in the three aforementioned studies. The main aim of the present study is to determine the minimum number of flood hydrographs needed to be simulated by a hydro-meteorological model, in order to be used as input for a copula-based distribution. This is motivated by the need of obtaining a large synthetic series in short time, as the hydro-meteorological model is computationally very demanding because of entailing a high spatial and temporal resolution. The longer simulated sample improves the fitting of the distribution, as observed series are usually short and the hydro-meteorological model simulates the variability in the catchment response. Then, the flood series can be extended again by stochastically generating an (arbitrarily) long sample by the fitted copula-based distribution. The proposed mixed approach addresses the need for extending short observed peak-volume series, combining the ability to simulate the feasible catchment responses by a distributed rainfall-runoff model and the computational efficiency offered by statistical models. The hydro-meteorological modelling chain used in the present study consists of the RainSim stochastic rainfall generator, and the Real-time Interactive Basin Simulator (RIBS) hydrological rainfall-runoff model. The RainSim model is a spatial-temporal stochastic rainfall generator (Burton et al. 2008), while the RIBS model is an event-based distributed rainfall-runoff simulator of the catchment response under rainfall events that are spatially distributed (Garrote and Bras 1995a, b). The structure of the present paper is divided into the following sections: Methodology is presented in Sect. 2, Application consisting of the case study and results is shown in Sect. 3 and Conclusions are summarised in Sect. 4.

2 Methodology

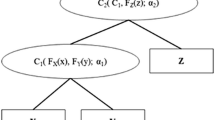
The present study focuses on a bivariate analysis of floods by using the maximum peak flow (Q) and its associated hydrograph volume (V). The methodology consists of the following steps (see Fig. 1 for an overview): (i) simulation of a set of flood hydrographs by a hydro-meteorological model calibrated with observed flood series, using synthetic rainfall series from a stochastic rainfall generator; (ii) sensitivity analysis to identify the minimum data length needed for keeping the statistical properties of the whole simulated data series when the marginal distribution and copula candidates are fitted; (iii) identification of the bivariate model based on copulas consisted of the marginal distribution that best fits each univariate variable and the copula that best represents the dependence structure between them, as well as the corresponding minimum data length to be fitted; and (iv) validation of the methodology by comparing the flood frequency curve (of each marginal distribution) and the copula level curves of a large sample simulated by the hydro-meteorological model, with those of a set of synthetic samples generated with the same size by the proposed mixed-approach. That is, synthetic samples generated via the bivariate distribution fitted to samples from the hydro-meteorological model with the data length identified in step (iii). Moreover, as an illustration of the results obtained by the application of the procedure, joint return period curves estimated by using the large simulated sample are compared with those obtained by a given synthetic sample. The proposed methodology allows reducing the computation time, while maintaining the statistical properties of the flood series simulated by the hydro-meteorological model. The methodology is applied to the Santillana reservoir catchment in the Manzanares River located in Spain.

Fig. 1
figure 1

Diagram of the steps forming the proposed methodology

Full size image

2.1 Simulation of flood hydrographs by a hydro-meteorological model

A set of flood hydrographs is generated by the hydro-meteorological modelling chain consisting of the RainSim rainfall simulator and the RIBS rainfall-runoff model. The RainSim V3 model is a stochastic rainfall generator based on the spatial-temporal Neyman-Scott rectangular pulses (NSRP) model (Cowpertwait 1994, 1995). This model allows the simulation of continuous series of rainfall of a number of years for a set of rain gauges in the catchment and with an arbitrary time step. The model details are described in Burton et al. (2008). The RIBS model simulates the catchment response to spatially distributed rainfall events and results in flood events at the catchment discharge point (Garrote and Bras 1995a, b). The RIBS model consists of two modules. The first is a runoff-generation module and the second simulates the runoff propagation. The runoff generation depends on the calibration parameter f (mm−1) that controls the decrease of saturated hydraulic conductivity with depth and the soil properties that have to be defined for each soil class. These properties are the saturated hydraulic surface conductivities in directions normal and parallel to the surface, the residual soil moisture content, the saturated moisture content and the index of soil porosity (Cabral et al. 1992). The runoff propagation depends on the hill-slope and the riverbed velocities. The latter is proportional to the coefficient C v (m s−1) that characterises the relation between riverbed velocity and discharge at the catchment outlet. Both velocities are considered uniform throughout the catchment at any time, and defined by their relationship to the dimensionless parameter K v . Event-based models need an estimate of the initial moisture content in the catchment at the beginning of the flood event. In the case of the RIBS, it corresponds to the water table depth that is in long term equilibrium with a constant recharge rate.

Once a large set of flood hydrographs is simulated, the associated Q–V series is extracted by identifying the maximum peak flow and the hydrograph volume (see Sect. 3.2.1). Such simulated Q–V series is divided into two samples: the model selection sample with a sample length n sel, for performing steps (ii) and (iii); and the simulated validation sample with a sample length n val, for carrying out step (iv). At this point it is important to verify if, as expected, the studied variables Q and V are dependent, in which case the joint analysis (by the marginal distributions and copula) is needed. This is done by the rank-based non-parametric Kendall’s tau (τ) measure, through which the independence between variables is rejected if the associated p-value is less than 0.05 (Genest and Favre 2007).

2.2 Sensitivity analysis: minimum data length needed

A prior step to the selection of the bivariate distribution of the Q–V series is the identification of the minimum data length (n) necessary for both marginal distribution and copula fits to be robust enough in terms of uncertainty of estimates. When marginal distributions are considered, the variable chosen for performing the sensitivity analysis is the univariate quantile (q T ) for a given return period value (T). Note that T is the inverse of (1 − p), where p is the non-exceedance probability of q T .

In the case of using copulas, the bivariate quantile is a curve in the Q–V space instead of a single value like in the univariate case. However, a single-value variable is needed for conducting the sensitivity analysis. The Kendall’s return period (Salvadori and De Michele 2004; Salvadori et al. 2011) could be a suitable variable to be used as a surrogate of the bivariate quantile, as each bivariate quantile curve is associated with a given Kendall’s return period value that depends on the copula. Moreover, the Kendall’s return period is the joint return period that provides an analogous definition of quantile to that considered in the univariate approach (Salvadori and De Michele 2010). Nevertheless, a long computation time is needed for performing the sensitivity analysis based directly on this variable. Consequently, as the aim of the proposed method is to reduce the computation time, the copula parameter (θ) is chosen to conduct the sensitivity analysis on the bivariate series. It should be noted that θ is needed for estimating the Kendall’s return period. In summary, the minimum required n is obtained by analysing the univariate quantile associated with a given T, q T , for marginal distributions, and the copula parameter, θ, for bivariate copulas.

The proposed procedure is the following: (i) 1000 bootstrap samples of varying length n = 25, 50,…, 1000 are obtained from the model selection sample of length n sel, without replacement; (ii) both q T and θ are estimated for the 1000 bootstrap samples associated with each n, considering the set of candidate marginal distributions and copulas; (iii) the sample distribution of either q T or θ for each n is displayed in a box plot where the 25th and 75th percentiles are shown as the borders of the box, hereafter such a statistical interval is named as confidence interval; (iv) the minimum length required for each either univariate distribution function (named as n m) or copula (named as n c) is determined as the smallest n for which the confidence interval of the bootstrap samples lies within boundaries related to the model selection sample. These boundaries are the sampling confidence interval of the model selection sample increased by 5 %, assuming that an increase of 5 % in the uncertainty of estimates at the expense of reducing the record length is acceptable. In the case of the marginal distributions, the sampling confidence interval is obtained by generating 10,000 samples by the distribution function fitted to the model selection sample, calculating the value of q T for each sample and obtaining the 25th and 75th percentiles. Note that in the case of copulas, only 1000 bootstrap samples are generated to avoid a long computation time for generating such a confidence interval in terms of the copula parameter θ.

As a result, the value of n m for each marginal distribution (named as n m,Q for Q and n m,V for V) as well as the value of n c for each copula is obtained. Note that in the case of two-parameter copulas, n c is identified as the maximum of the two values obtained by applying the procedure to each parameter. Also note that n m can be slightly different for a same distribution function for each variable, as the sampling uncertainty depends on its distribution parameters.

2.3 Identification of the bivariate model based on copulas

The bivariate model for accomplishing the stochastic generation of large Q–V samples is based on the Sklar’s Theorem (Sklar 1959), through which the bivariate joint cumulative distribution of the variables Q and V, H(q, v), is obtained as:

$$ H(q,v) = {\kern 1pt} {\kern 1pt} C(F_{Q} (q),F_{V} (v)),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} q,v{\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} \Re , $$
(1)

where F Q (.) is the cumulative marginal distribution of Q, q is a given value of such a variable (the same holds for V), and the copula function \( C(u_{1} ,u_{2} ):[0,1]{\kern 1pt}^{2} \to [0,1] \) is a bivariate joint cumulative distribution with uniform marginal distributions that can be expressed by using u 1 = F Q (q) and u 2 = F V (v). Thus, the estimate of H(q, v) requires the identification of the marginal distributions that best represent the univariate Q and V variables, as well as the copula that best characterises the dependence structure between them. The minimum sample length for fitting such a bivariate distribution, n b, is determined as the maximum of the minimum required lengths for fitting the marginal distributions, n m,Q and n m,V , and the copula, n c, i.e., n b = max (n m,Q , n m,V , n c). The procedure for identifying the bivariate distribution begins with the selection of the copula, since the copula is expected to require a larger data length than the marginal distributions because of its bivariate nature. As a result, the marginal distributions and copula to use for obtaining the bivariate distribution of Q and V are selected, and n b is identified.

2.3.1 Selection of the copula

The best copula is selected by considering 1000 bootstrap samples of the corresponding length n c obtained in Sect. 2.2, for each copula. One-parameter copulas, such as the Clayton, Frank, Gumbel and Plackett copula, and two-parameter copulas, such as the BB1 copula (Joe 1997), are considered as copula candidates in the present study.

The selection of the best copula among the candidates is not straightforward and different criteria should be considered (Chowdhary et al. 2011; Requena et al. 2013). Because of the nature of the present study, the procedure for selecting the best copula is based on three criteria, for which results are drawn in a box plot for each copula: the fit of the copula to the data, the adequacy of the estimate of a high Kendall’s return period value that is directly related to the bivariate quantile estimate, and the results of a model selection criterion that allows ranking the copulas.

The first criterion, related to the ability of the copula to characterise the data, is performed under the goodness-of-fit test based on the Cramér-von Mises statistic (Genest et al. 2009), S n :

$$ S_{n} = \sum\limits_{i = 1}^{{n_{\text{c}} }} {\left\{ {C_{n} \left( {\frac{{R_{i} }}{{n_{\text{c}} + 1}},\frac{{S_{i} }}{{n_{\text{c}} + 1}}} \right) - C_{\theta } \left( {\frac{{R_{i} }}{{n_{\text{c}} + 1}},\frac{{S_{i} }}{{n_{\text{c}} + 1}}} \right)} \right\}^{2} ,} $$
(2)

where (R i , S i ) are the ranks of the (Q i , V i ) pairs of each bootstrap sample, C θ is the copula fitted to such data estimating the parameter(s) by the maximum pseudo-likelihood method (Genest et al. 1995) and C n is the empirical copula:

$$ C_{n} (u_{1} ,u_{2} ) = \frac{1}{{n_{\text{c}} }}\sum\limits_{i = 1}^{{n_{\text{c}} }} {{\kern 1pt} {\kern 1pt} {\kern 1pt} } 1\left( {\frac{{R_{i} }}{{n_{\text{c}} + 1}} \le u_{1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{S_{i} }}{{n_{\text{c}} + 1}} \le u_{2} } \right),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u_{1} ,u_{2} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} [0,1], $$
(3)

where 1(A) is the indicator function of the set A (that equals 1 inside A and 0 otherwise). S n is indeed an error measure between the values of the empirical copula and those obtained by the fitted copula. Thus, the smaller is the (median) S n value, the better is the copula. The p-value associated with S n , estimated by a parametric bootstrap procedure (Genest and Remillard 2008) where 1000 simulations are employed in the present study because of computation time limitations, is also obtained to carry out the goodness-of-fit test itself. A copula is formally accepted when its (median) p-value is greater than 0.05. However, as it happens with other statistical tools, it is expected not to obtain suitable p-values in case of a large sample size is considered (see Vandenberghe et al. 2010; Requena et al. 2015a). In addition, a formal goodness-of-fit test is not performed in the copula selection process in some studies (e.g., Klein et al. 2010). In fact, the p-value is very useful to test if a sample comes from a given copula. However, in practice, observed flood series could not follow any of the existing copulas, due to the natural variability of floods. Consequently, the copula that best characterises the observed sample should be found, instead of the true copula that could represent the observed sample perfectly, as in some cases it does not exist.

The second criterion is related to the adequacy of the Kendall’s return period estimated by the copula, for a large copula value t ∊ [0, 1], which is based on the Kendall’s function K C (t) = P[C θ (u 1, u 2) ≤ t] (Genest and Rivest 1993). Its theoretical estimate (T K ) is expressed as:

$$ T_{K}^{{}} = \frac{1}{{1 - K_{\text{C}} (t)}} $$
(4)

The Kendall’s function has an analytical expression for Archimedean copulas (e.g., the Clayton, Frank and Gumbel copula), but simulation is required for the rest of copula families (Salvadori et al. 2011). The issue is that extreme value copulas (e.g., the Gumbel and Galambos copula) have associated the same Kendall’s function (Genest et al. 2006) and therefore the criteria based on the Kendall’s function is not able to distinguish among them. The value of the Kendall’s return period is also estimated and the results of each copula are plotted. In this case, the best copula is that with the closest (median) theoretical Kendall’s return period to the empirical Kendall’s return period (\( \dot{T}_{K}^{{}} \)), estimated by the Kendall’s function associated with the empirical copula of the whole model selection sample.

The third criterion is the Akaike Information Criterion (AIC) (e.g., Zhang and Singh 2006).

$$ {\text{AIC}} = - 2\sum\limits_{i = 1}^{{n_{\text{c}} }} {\ln \left[ {c_{\theta } \left( {\frac{{R_{i} }}{{n_{\text{c}} + 1}},\frac{{S_{i} }}{{n_{\text{c}} + 1}}} \right)} \right]} + 2k, $$
(5)

where c θ (.) is the density function of the fitted copula, and k is the number of copula parameters. The best copula for this criterion is that with the smallest (median) AIC value. The AIC penalises the copulas with more parameters, as it can be seen through the second term of its formula.

Note that although the median is the value considered to assess the performance of each criterion, the variability in the results (i.e., the height of the boxes) should also be considered in the decision process, as it makes reference to the uncertainty in the results given by the copula. As a result of taking into account all the information provided by these criteria, the best copula is selected and its minimum required sample length, \( n_{\text{c}}^{*} \), is identified. As illustration and in order to provide a visual support of the behaviour of the copulas, the empirical (i.e., based on C n ) and theoretical estimate of the Kendall’s function for the model selection sample is also provided.

2.3.2 Selection of the marginal distributions

If the minimum sample length required for the selected copula \( n_{\text{c}}^{*} \) is greater than any of the n m values obtained in Sect. 2.2, the minimum sample length required by the bivariate distribution is given by that of the copula, i.e., \( n_{\text{b}} = n_{\text{c}}^{*} \) and hence, the selection of the marginal distributions is done under 1000 bootstrap samples of size n b. Distributions usually used in hydrology, such as the Gumbel (G), generalised extreme value (GEV), generalised logistic (GLO) and log-normal (LNO) distribution, are the marginal distributions selected as candidates. Because of the nature of this study, the best marginal distribution is identified as that with the smallest distance between the median quantile estimate obtained by a given marginal distribution, \( \hat{q}_{T}^{{}} \) (named as \( \hat{q}_{T}^{Q} \) for Q and \( \hat{q}_{T}^{V} \) for V), and the median quantile estimate obtained by the empirical distribution, \( \dot{q}_{T}^{{}} \), both assessed by using 1000 bootstrap samples of size n b. Such a distance is expressed as the relative error (RE) in percentage:

$$ RE = 100\frac{{{\text{median}}(\hat{q}_{T}^{{}} ) - {\text{median}}(\dot{q}_{T}^{{}} )}}{{{\text{median}}(\dot{q}_{T}^{{}} )}} $$
(6)

As a result, the marginal distribution with the smallest absolute value of RE is selected for each variable (Q and V).

Note that in the (more unlikely) case that \( n_{\text{c}}^{*} \) is less than some n m, the selection of the marginal distributions is conducted by using 1000 bootstrap samples of the corresponding size n m. Then, as \( n_{\text{b}} = { \hbox{max} } \left( {n_{{{\text{m}},Q}}^{*} , n_{{{\text{m}},V}}^{*} , n_{\text{c}}^{*} } \right) \), the selection process should be repeated for the marginal distribution or copula for which \( n_{{{\text{m,}}Q}}^{*} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n_{{{\text{m,}}Q}}^{*} \) or \( n_{\text{c}}^{*} \) is different from n b (see Fig. 1 for a diagram of the process). As illustration, the fit of the marginal distributions to the model selection sample is also provided to visually check how the marginal distributions behave regarding the whole sample.

2.4 Validation of the methodology

The aim of this section is to check the adequacy of the proposed methodology by comparing the behaviour of a large sample obtained directly through the hydro-meteorological model (i.e., the simulated validation sample introduced in Sect. 2.1), with samples of the same length (called synthetic validation samples) stochastically generated by fitting the selected bivariate distribution to smaller samples of size n b belonging to such a simulated validation sample. The present section consists of the procedure needed to generate synthetic samples by the bivariate copula-based distribution, followed by the validation of the marginal distributions, the validation of the copula, and an example of the results provided by the application of the methodology in comparison to those obtained by only using the hydro-meteorological model.

The generation of synthetic validation samples is conducted by using the bivariate distribution identified in Sect. 2.3 based on the information provided by the model selection sample, and small bootstrap samples obtained from the simulated validation sample. The procedure is described below: (i) a bootstrap Q–V sample of size n b is obtained from the simulated validation sample without replacement; (ii) the selected copula is fitted to the bootstrap sample, generating a synthetic sample of size n val consisted of (u 1, u 2) pairs; (iii) the selected marginal distribution of Q and V are used for transforming the (u 1, u 2) pairs into (Q,V) pairs formed by the components q = F −1 Q (u 1) and \( v = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F_{V}^{ - 1} (u_{2} ) \), where F −1 Q (.) and F −1 V (.) are the inverses of the marginal distributions of Q and V, respectively. This synthetic Q–V sample of size n val is called synthetic validation sample. A new synthetic validation sample is generated each time the process is performed.

The validation of the marginal distributions is performed based on the following procedure: (i) the selected marginal distributions for Q and V are fitted to the whole simulated validation sample, obtaining their flood frequency curve; (ii) the selected marginal distributions are also fitted to each of the 10,000 synthetic validation samples generated by the procedure described above, obtaining their associated flood frequency curves; (iii) the confidence interval (i.e., the statistical interval consisted of the 25th and 75th percentiles) from the 10,000 synthetic flood frequency curves is obtained for given T values; and (iv) such a confidence interval is compared with the flood frequency curve obtained by the simulated validation sample in the first step of the present procedure.

An analogous process is carried out for the validation of the copula: (i) the copula selected is fitted to the whole simulated validation sample, obtaining the copula probability level curve for given p-values; (ii) the selected copula is also fitted to each of the 1000 synthetic validation samples generated by the procedure described at the beginning of the present section, obtaining their associated copula probability level curves formed by the (u 1, u 2) points that fulfil C(u 1, u 2) = p, for given probability values p. Only 1000 samples instead of 10,000 are used for avoiding a long computation time when the confidence intervals are estimated; (iii) For each u 1 value, the confidence interval of the u 2 values for the 1000 synthetic probability curves is obtained for each p; and (iv) the confidence interval associated with each probability value p is compared with the copula probability level curve obtained when fitted to the simulated validation sample.

As illustration of the results obtained by applying the proposed methodology, a given synthetic validation sample is plotted together with the simulated validation sample, and the Kendall’s return period curves for both samples are also estimated and drawn.

3 Application

The case study and the results obtained by the application of the proposed methodology are shown in the present section.

3.1 Case study

The application of the methodology is carried out on the gauging station of the Santillana reservoir in the Manzanares River, which belongs to the Tagus River catchment and is located in the centre of Spain (Fig. 2). The catchment drainage area of the Santillana reservoir gauging station is 325.6 km2. Mean daily outflow discharge and reservoir volume series are available at this gauging station for the period 1958–2002, from which the series of mean daily inflow discharges was extracted. This case study is chosen due to the previously available calibration of the hydro-meteorological model RainSim-RIBS. The rainfall simulator was calibrated by Flores et al. (2013) and the rainfall-runoff model by Mediero et al. (2011). The RainSim V3 model was calibrated through a set of observed daily series recorded at 15 rain-gauges with varying length between 11 and 118 years, where the largest series entails the period 1893–2011. As a result, a 9000-year length hourly rainfall series was generated by the calibrated model at each rain-gauge. The RIBS model was calibrated in the entire Manzanares River catchment with a drainage area of 1248 km2, where the Santillana reservoir catchment is its headwaters. The calibration process is based on a simultaneous minimisation of four objective functions (root mean square error, mean absolute error, coefficient of Nash–Sutcliffe efficiency and time to peak) that account for different hydrograph characteristics, resulting in a probability density function for characterising each of the model parameters subject to calibration. Validation of the probabilistic model was performed via simulations of the calibrated model for each validation event; assessing the bias of the results through a variation of the Nash–Sutcliffe efficiency coefficient, and the accuracy of the results by the inclusion coefficient.

Fig. 2
figure 2

Location of the case study: catchment of the Santillana reservoir gauging station

Full size image

3.2 Results

3.2.1 Simulation of flood hydrographs by a hydro-meteorological model

Storm events were then simulated individually from the 9000-year length hourly rainfall series generated in the 15 rain-gauges, as RIBS is an event-based model. Independent storm events were identified via the exponential method (Restrepo-Posada and Eagleson 1982), fixing a minimum dry period between events, in which rainfall is less than a given threshold (Bonta and Rao 1988). In order to reduce the number of simulations, a specific subset of five events was selected from each year, assuming that the event generating the maximum volume or peak flow hydrograph in a year is included among them.

Consequently, 45,000 synthetic flood events were generated through the calibrated RIBS rainfall-runoff model, accounting for random initial moisture content states among a representative set of 13 initial states in the catchment, in order to generate an ensemble of hydrographs that covers the range of totally dry to completely saturated soils. Each year, the hydrograph with the maximum peak flow was selected and its volume calculated, obtaining 9000 years of synthetic Q–V series. In order to validate the model in terms of the flood frequency curve, the observed and simulated frequency curves for 1-, 2-, 3- and 4-days accumulated inflow volumes were calculated and compared (Fig. 3). Validation was conducted by using inflow volumes for different durations, as information about the instantaneous peak flow of observed inflow hydrographs is not available at this site. It should be noted that the 1-day inflow volume series is used to validate the peak flow of observed inflow hydrographs, as it is characterised by the mean daily discharge. Results show that the model represents suitably the flood frequency curves. Therefore, the hydro-meteorological model can be used for extending the observed series to enable an accurate flood frequency analysis by selecting and fitting the bivariate copula-based distribution via the Q–V series extracted from the flood hydrographs simulated by the calibrated hydro-meteorological model, instead of via the short-length observed flood data.

Fig. 3
figure 3

Validation of the hydro-meteorological model. Observed data and empirical frequency curves of inflow volume for a one; b two; c three; and d four consecutive days

Full size image

As a result, the 9000 synthetic Q–V pairs obtained through the hydro-meteorological model, entailing a 1-h temporal and 100-m spatial resolution, were used. The computation time needed for its generation was approximately 20 days with a computer with a processor Intel Core i7-870 2.93 GHz with four cores. Such a (simulated) Q–V sample was divided into the model selection sample with n sel = 2000 (Q,V) pairs and the simulated validation sample with n val = 7000 (Q,V) pairs. Their scatter plots are shown in Fig. 4. The Kendall’s τ of both samples is 0.7 with a suitable p-value less than 0.05, indicating a positive dependence relation between variables.

Fig. 4
figure 4

Scatter plot of the (Q,V) pairs of the samples generated through the hydro-meteorological model divided into the model selection sample and the simulated validation sample

Full size image

3.2.2 Sensitivity analysis: minimum data length needed

The sensitivity analyses to identify the minimum sample length required for obtaining robust quantile estimates by each marginal distribution, in terms of the uncertainty of the quantile estimate by using the whole univariate either Q or V series, are shown in Fig. 5. The 100-year quantile was selected in this study (named as \( \hat{q}_{100} \)) as a trade-off between a high enough quantile and a quantile not entailing a large uncertainty. Following the procedure explained in Sect. 2.2, the box plots of the quantiles obtained from the bootstrap samples (from the model selection sample) of each length n are plotted along the x-axis. The boundaries associated with the confidence interval for the model selection sample are added as two horizontal lines. The minimum data length, n m, for which the confidence interval (i.e., the borders of the box) is inside such boundaries, i.e., n m,Q and n m,V , are marked by a dotted line in Fig. 5 for each marginal distribution. As expected, the n m required in the case of the two-parameter G distribution is less than that needed for the three-parameter (GEV, GLO and LNO) distributions. Moreover, the quantile related to Q requires the same or a similar data length than that related to V for each marginal distribution, with the exception of the GLO distribution for which the difference is larger (due to the randomness of the process and the data step considered).

Fig. 5
figure 5

Sensitivity analysis for identifying the minimum sample length required for the marginal distributions. The box plot of the quantiles estimated from the bootstrap samples of length n is plotted along the x-axis, where the points represent the outliers

Full size image

The results of the sensitivity analyses of the copula parameter estimate are shown in Fig. 6. In this case, the objective of the analysis is to identify the minimum record length, n c, required for assuming that the parameter estimated for each copula is robust enough in reference to uncertainty of the parameter estimate via the whole bivariate Q–V series. Analogously to the univariate case, the required n c, identified as the minimum data length for which the confidence interval is less than the boundaries associated with the confidence interval of the copula parameter for the model selection sample (i.e., the two horizontal lines), is marked in Fig. 6 for each copula. Note that for the BB1 copula n c = 525, which is the maximum of the two values obtained by applying the procedure to each copula parameter. As expected, the n c needed for the two-parameter copula BB1 is greater than that needed for the rest of the one-parameter (Clayton, Frank, Gumbel, Galambos and Plackett) copulas. Although in general and as expected, the minimum record length for a copula is greater than that needed for a marginal distribution, the value associated with the Gumbel copula is less than those associated with some marginal distributions.

Fig. 6
figure 6

Sensitivity analysis for identifying the minimum sample length required for each copula. The box plot of the copula parameter(s) estimated from the bootstrap samples of length n is plotted along the x-axis, where the points represent the outliers

Full size image

3.2.3 Identification of the bivariate model based on copulas

The identification of the bivariate distribution of Q and V, requiring the selection of the marginal distributions and the copula, is conducted by the procedure detailed in Sect. 2.3. First, the results obtained for the copula selection process are shown in Fig. 7. The assessment of the fit of each copula to the data is displayed in Fig. 7a, via the box plot of the S n values obtained by Eq. 2, considering the corresponding bootstrap sample of length n c obtained previously. As a result, the Clayton copula was identified as the worst copula in terms of fitting to the data, as both the median value of the S n and its variability represented by the height of the box are the largest. The values obtained for the rest of the copulas are smaller and similar to each other, obtaining the best results for the Frank and BB1 copula. Consequently, the Clayton copula is discarded, as it is not able to represent the dependence between the observed Q–V pairs.

Fig. 7
figure 7

Copula selection process based on 1000 bootstrap samples with a sample length n c for each copula. Box plots for each copula show a the assessment of the fit to the data via S n ; b the results of the formal goodness-of-fit test by the p-value of S n ; c the adequacy of the Kendall’s return period T K(0.99) in reference to the empirical Kendall’s return period \( \dot{T}_{K(0.99)} \); and d the evaluation of the AIC for ranking copulas. The points in the box plots represent the outliers

Full size image

The box plots of the p-values associated with the S n values are displayed in Fig. 7b. As expected, because of the use of large sample lengths (see Sect. 2.3.1 for more details), poor results were obtained by the goodness-of-fit-test. Only some p-values greater than 0.05, where such a threshold is indicated as a horizontal line, were obtained as outliers for the Frank, Gumbel, Galambos and BB1 copula. The results for a smaller sample length (n c = 50), which is in the range of the common observed data lengths recorded in practice (see Sect. 1), are also plotted in the upper right corner of Fig. 7b for illustration purposes. As expected, more suitable p-values were obtained. All copulas except the Clayton copula pass the goodness-of-fit test in this case. Consequently, the p-value is not used for identifying the suitable copulas in this study.

The adequacy of the Kendall’s return period estimate for a high copula value t = 0.99, T K(0.99) (Eq. 4), is analysed in Fig. 7c. The box plot of T K(0.99) for each copula is displayed together with the empirical value associated with the whole model selection sample as it was indicated in Sect. 2.3.1, \( \dot{T}_{{{\text{K(0}} . 9 9 )}} = 200 \) years, which is plotted as a horizontal line. It can be seen that besides the already discarded Clayton copula in terms of S n results, the Frank and Plackett copula show a large overestimate of the empirical value (in decreasing order). The Clayton and Frank copula also show a larger variability. Closer estimates to the empirical value, involving underestimate, were obtained by the Gumbel, Galambos and BB1 copula. For the first two copulas T K(0.99) = 150 years, while for the BB1 copula T K(0.99) = 192 years, being the last the best estimate. Note that an underestimate of the return period entails being on the safety side. As a result, the Frank and Plackett copulas are also discarded.

The results obtained by the AIC (Eq. 5) are shown in Fig. 7d. As it can be seen, the sample length affects the results, obtaining better values those copulas considering larger lengths. As a consequence, AIC results were obtained by using the same sample length for all copulas (not shown), resulting the BB1 copula the best copula in all cases. Hence, considering all the information provided by the copula selection process, the BB1 copula was chosen as the best copula for characterising the Q–V series, requiring a minimum sample length \( n_{\text{c}}^{*} = 5 2 5 \). A visual support of the behaviour of the copulas regarding the model selection sample (with n sel = 2000), by the comparison of the theoretical Kendall’s function of each copula and the empirical estimate, is plotted as an example in Fig. 8. It can be seen that the BB1 copula (Fig. 8b) involves the best fit.

Fig. 8
figure 8

Comparison among the empirical estimate of the Kendall’s function (for t copula values) and the theoretical estimate, regarding the model selection sample, obtained by a the Clayton, Frank and Gumbel copula; and b the Galambos, Plackett and BB1 copula. Results are divided into two figures for clarity

Full size image

As \( n_{c}^{*} \) is greater than any n m (see Fig. 5), \( n_{\text{b}} = n_{\text{c}}^{*} = 5 2 5 \) and hence, the selection of the marginal distributions is conducted under 1000 bootstrap samples of such a length, estimating the (median) quantile \( \hat{q}_{100}^{{}} \) for each marginal distribution, as well as the (median) empirical quantile \( \dot{q}_{100}^{{}} \). The distances between both quantiles are plotted in Fig. 9, and the RE values obtained via Eq. 6 are shown in Table 1. It was found that the best marginal distributions are the GEV for Q and the LNO for V, as they entail the minimum absolute value of RE in each case. The fit of the marginal distributions to the model selection sample is plotted in Fig. 10a as an illustration of the behaviour of the marginal distributions. It can be seen that the fit of the GEV distribution is the closest to the peak flow data, Q, and the fit of the LNO distribution is the closest to the volume data, V. In summary, the bivariate distribution selected to represent the Q–V series consists of the BB1 copula, the GEV distribution for Q and the LNO distribution for V, with a sample length of n b = 525.

Fig. 9
figure 9

Selection of the marginal distributions (for Q and V) based on 1000 bootstrap samples from the model selection sample. Box plots show the variability of the univariate quantile estimated for T = 100 years, \( \hat{q}_{100}^{{}} \), plotting its median value to be compared with its median empirical quantile estimate, \( \dot{q}_{100}^{{}} \), for bootstrap samples with a sample length equal to n m. Points in the box plots represent the outliers

Full size image
Table 1 Relative error (RE) of the (median) quantile estimated for 1000 bootstrap samples of length n b = 525
Full size table
Fig. 10
figure 10

a Fit of the marginal distributions of Q and V to the model selection sample; b Comparison between the flood frequency curve fitted to the simulated validation sample generated through the hydro-meteorological model, and the confidence interval obtained by the synthetic validation samples generated by the bivariate distribution

Full size image

3.2.4 Validation of the methodology

The methodology is then validated according to Sect. 2.4. Synthetic validation samples (of size n val = 7000) are generated by fitting the selected bivariate distribution to bootstrap samples of the identified length (n b = 525), obtained without replacement from the simulated validation sample. Regarding the marginal distributions, the flood frequency curve of the simulated validation sample is drawn together with the confidence interval related to the flood frequency curves of 10,000 synthetic validation samples (Fig. 10b). The flood frequency curve is tightly fitted by the confidence interval for small T values. The range slightly increases for larger values of T, as the uncertainty is larger. The simulated data remain inside the synthetic confidence interval in the case of V, and only two data points are outside in the case of Q, as the three largest peaks show similar values. The confidence interval in percentage is shown in Table 2 for several T values. The confidence intervals associated with the copula level curves of 1000 synthetic validation samples are almost equal to the corresponding curves obtained via the simulated validation sample (not shown).

Table 2 Confidence interval (in percentage) of the flood frequency curves obtained via 10,000 synthetic validation samples, for T = 10, 25, 100 and 500 years
Full size table

As an example of the results obtained by the application of the methodology, the simulated validation sample is plotted together with a given synthetic validation sample in Fig. 11. The Kendall’s return period curves estimated by the bivariate distribution fitted to each sample are also displayed (estimated parameters shown in Table 3). It can be seen that both scatter plots are visually similar and that the results regarding the Kendall’s return period curves are comparable. The Kendall’s return period curves are practically identical for small Kendall’s return period values, while as expected, such a difference becomes slightly larger the larger the return period value is, because of the increasing uncertainty.

Fig. 11
figure 11

Comparison between the Kendall’s return period curves estimated by the simulated validation sample generated through the hydro-meteorological model, and by a given synthetic sample generated by the bivariate distribution

Full size image
Table 3 Parameters of the fitted bivariate distribution (marginal distributions and copula) for the simulated validation sample, and a given bootstrap sample of size n b = 525 that belongs to the simulated validation sample, whereby the synthetic validation sample is generated
Full size table

4 Conclusions

In the present paper a bivariate procedure to extend flood series due to the need of achieving more appropriate flood frequency analyses is addressed, determining the minimum number of flood hydrographs required to be simulated by a hydro-meteorological model to be used as input for obtaining an extended flood series by a bivariate model based on copulas.

A previously calibrated distributed hydro-meteorological model is used for simulating a series of flood hydrographs, with the aim of extending the observed peak-volume series by a bivariate distribution consisting of two marginal distributions and a copula. The minimum data length needed to be simulated by the hydro-meteorological model is defined through a sensitivity analysis in order to obtain robust estimates from both marginal distributions and copula. The marginal distribution and copula selection process is performed, where the copula selection process is carried out by taking into account the fit of the copula to the data, the adequacy of high joint return period estimates (using the Kendall’s return period), and the results of a model selection criterion. As a result, the selected bivariate distribution fitted to a small sample simulated by the hydro-meteorological model is used for generating arbitrarily large synthetic samples. The adequacy of the procedure is checked by comparing the flood frequency curve (of each marginal distribution) and the copula level curves fitted to a large sample simulated by the hydro-meteorological model, with the corresponding confidence intervals obtained from a large amount of synthetic samples generated by the bivariate distribution.

The proposed methodology was applied to the Santillana reservoir gauging station in the Manzanares River located in Spain. It was found that a minimum data length of 525 flood hydrographs should be simulated through the hydro-meteorological model in order to accomplish a robust fit by a bivariate distribution based on the two-parameter BB1 copula, which was chosen as the best copula by the copula selection process. In this regard, it is suggested considering the BB1 copula as potential candidate for characterising peak-volume series in other catchments. As expected, a smaller data length (in the order of 200 data) should be required in the case of a one-parameter copula was selected. The generalised extreme value distribution for the peak flow and the log-normal distribution for the hydrograph volume were found to be the best marginal distributions for a record length of 525 years. As a result, large synthetic samples were stochastically generated by fitting the bivariate distribution to a random set of 525-length samples simulated by the hydro-meteorological model. The comparable performance of such synthetic samples in relation to a sample of the same length simulated by the hydro-meteorological model supported the use of the proposed methodology. The procedure provides an extended sample composed of 525 data from the simulation through a hydro-meteorological model and a much larger synthetic sample stochastically generated by fitting the bivariate distribution.

The proposed procedure allows cutting down the computation time required for generating a large sample of peak-volume pairs, in comparison to the time needed by a hydro-meteorological modelling chain (specifically, from a month scale to few days for the sample length generated for the case study), allowing the generation of a peak-volume sample as long as desired to enable more suitable flood risk assessment studies.