1 Introduction

The modern cellular communication network is a complex overlay of heterogeneous networks such as macrocells, microcells, picocells, and femtocells. The BS deployment for this network can be planned, unplanned, or uncoordinated. Even when planned, the BS placement in a region deviates from a regular hexagonal grid due to site-acquisition difficulties, variable traffic load, and terrain. The coexistence of heterogeneous networks have further added to these deviations [23]. As a result, the BS distribution appears increasingly irregular as the BS density grows and is outside standard performance analysis. Two approaches of modeling have been widely adopted in the literature. At one end, the BSs are located at the centers of regular hexagonal cells to form an ideal hexagonal cellular system. These ideal hexagonal cellular systems provide upper performance bound (upb). At the other end, the BS deployments are modeled according to a \(\tau \)-dimensional (\(\tau \)-D) Poisson point process with a parameter \(\lambda (r)\), as a function of the distances between BSs and the mobile station (MS) which is the average BS density for the SCS [23,24,25,26]. Note that throughout this paper we consider \(\tau =1, 2,\) and 3 for \(\tau \)-D SCS.

In the homogeneous \(\tau \)-D SCS, \(\tau =1\) is a model for the highway scenario, \(\tau =2\) models the planar deployment of BSs in suburbs, and \(\tau =3\) models the BS deployments within large multi-storey buildings and wireless LANs (WLANs) in mutistorey residential areas. Such systems provide lower performance bound (lpb).

Brown [6, 7] investigated the dynamic channel assignment in an SCS and the results were compared with hexagonal system. The difference between upper bound and lower bound is small under operating typical conditions in modern CDMA and TDMA cellular systems. The performance of wireless systems depends on using accurate statistical model to characterize the propagation channel. Depending on the environment, the propagation channel is susceptible to several physical problems such as path-loss, interference, multi-path, and shadow fading. For example, in a typical communication system, the effects of fading cause the received signal to fluctuate rapidly around its mean. Models that describe the effects of multi-path fading are known as short-term fading, whereas models that describe the effects of shadow fading are called long-term fading. In many real world scenarios, the effects of both multi-path and shadow fading are present in the system. Models that combine the effects of short and long term fading are known as composite fading models [4]. In an SCS, similar to each wireless system, the signal propagation is affected by path-loss, shadow fading (slow fading), and multi-path fading (fast fading). Many cellular deployments have significant randomness. Therefore, SCS is a system affected by random phenomena. The performance metric of interest is the signal quality at the MS. The performance in the SCS is defined as the ratio of the received signal power to the total interference power, and is denoted by \({ CIR}=\frac{P_C}{P_I}\) . The MS listens to the BS with the strongest received signal power \(P_C\), where the subscript C stands for the signal-carrying BS. The interference is the sum of the received power from all the other co-channel BSs and is denoted by \(P_I\), where the subscript I stands for the signal-interfering BSs. We know that the performance differs slightly between the uplink and downlink, but qualitatively they are similar and downlink may yield to at least much simpler analysis and simulations [7]. For these reasons, in this paper, similar to previous works, we only focus on the downlink. The SCS and its performance metrics have been studied under different channel models [5,6,7, 15, 21,22,23,24,25,26, 32]. In this paper, we study a \(\tau \)-D SCS over composite Rayleigh–Lognormal fading channels with random variables, by two methods.

First, in method 1, we analyze the effect of shadow fading and multi-path fading on the \(\tau \)-D SCS, separately, and then consider both effects together (composite Rayleigh and Lognormal fading) and determine expressions for the distribution of reverse CIR, and the probability density function (pdf) of CIR is calculated in an analytical form, and obtain the tail probability of CIR.

Second, in method 2, we analyze effect of shadow fading and multi-path fading on the \(\tau \)-D SCS together by using composite Rayleigh–Lognormal distribution and determine expressions for the distribution of reverse CIR, and the pdf of CIR is calculated in an analytical form, and obtain the tail probability of CIR. Because of complicated calculations, an approximation for the distribution of the reverse CIR over shadow fading and Rayleigh fading channels is proposed and its parameters are determined. So, a clear-tractable expression for the distribution of CIR is approximated. While reducing the mathematical complexity, this approximation provides fairly accurate pdf for the CIR. The paper is organized as follows. In Sect. 2, we explain system model. In Sect. 3, we review previous works. In Sect. 4, we explain main results. This section consists of two subsections. In Sect. 4.1, we use method 1 for analyzing \(\tau \)-D SCS over composite Rayleigh–Lognormal facing. In Sect. 4.2, we use method 2 for analyzing \(\tau \)-D SCS over composite Rayleigh–Lognormal fading. In Sect. 5, the details of simulation results are presented and finally Sect. 6 concludes the paper.

2 System model

In the SCS with fixed non-variable radio properties and no shadow fading, the BS closest to the MS will be chosen as the carrying or serving BS, and all the others are interfering BSs. When random radio properties and shadow fading are introduced to this system, the serving BS is not necessarily the BS closest to the MS. Since our focus is on the downlink, we consider the performance (i.e., CIR) of a single MS. This MS, without loss of generality, is assumed to be located at the origin and around this MS, BSs are placed according to a \(\tau \)-D Poisson point process with a parameter \(\lambda (r)\) which is the average BS density for the SCS [5,6,7, 21,22,23,24,25,26, 32]. In this paper, we assume a \(\tau \)-D SCS, which the BSs and MS are placed over the entire plane, according to a BS density function \(\lambda _\tau (r)\), where \(M\sim { Poisson} (\lambda _\tau (r))\). The received power at the MS from a BS is given by:

$$\begin{aligned} P_r=KP_TR^{-\varepsilon }\varPsi \phi \end{aligned}$$
(1)

where K is a radio factor and \(P_T\) is transmitter power. The path-loss is a function of the BS to MS separation R and follows an inverse power law with \(\varepsilon \), as the path-loss exponent. The multi-path fading factor and shadow fading factor are introduced with \(\phi \) and \(\varPsi \), respectively.

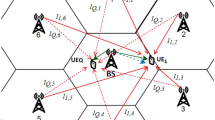
Shadow fading is usually modelled as a Lognormal random variable [5, 7,8,9, 12, 15, 21, 22, 24,25,26, 33]. Also, multi-path fading is modelled as a Rayleigh variable [1, 2, 4, 10, 13, 14, 16,17,18, 20, 28,29,30,31, 34,35,36]. The Rayleigh fading model is one of the simplest and most commonly used distribution to model short term-fading [4]. This model is an appropriate model for describing multi-path fading in urban environments with high buildings, when there is no direct line of sight (LOS) between the transmitter and the receiver, and the resultant signal at the receiver will be the sum of all the reflected and scattered waves (see Fig. 1).

Fig. 1
figure 1

The model fading is Rayleigh when there is no direct line of sight (LOS) between the transmitter and the receiver

Full size image

In the SCS, the MS communicates with only one BS. In a system with multiple channel reuse groups (CGs), each BS is assigned to one CG. The channels are assumed to be perfectly orthogonal to each other. All the interferences are due to co-channel radios. In Gaussian channels the received signal Y from transmitted signal X can be written as \(Y=hX+Z\), in which Z is noise of channel, and h is fading coefficient. In different channels, h can be modeled as different random variables (RVs) such as shadow fading \(\varPsi \) and multi-path fading \(\phi \). Therefore, assuming Gaussian channels in the SCS, the received power at the MS from a BS is given by Eq. 1.

The MS receives signals from all the BSs and chooses to communicate with the BS that corresponds to the strongest received signal power. This BS is referred to as the carrying BS, and all the other BSs are called the interfering BSs. Thus, the signal quality at the MS is defined as the ratio of the received power from the serving BS to the sum of the total interference power, i.e., carrier-to-interference ratio \(\frac{C}{I}=\frac{P_S}{P_I}\).

3 Previous works

In this section, we review the previous works. Madhusudhanan et al. [23] studied the performance of a \(\tau \)-D SCS with shadow fading modelled by i.i.d Lognormal random variables. A semi analytical expression for the CIR and the tail probability of CIR was obtained. Also, it was shown that an SCS affected by Lognormal shadow fading is equivalent to another SCS without shadow fading with different BS density function.

Madhusudhanan et al. [22] and Brown [6] considered a 2-D SCS, where the BSs were placed over the entire 2-D plane according to a 2-D Poisson point process with a constant BS density. They considered path-loss and shadow fading, while ignored multi-path fading and noise. They showed that the CIR random variable only depends on the distances between BSs and MS. So, they concluded that a uniform \(\tau \)-D SCS with a constant BS density \(\lambda \) is equivalent to a non-uniform one-sided 1-D SCS with a BS density function \(\lambda _\tau (r)=\lambda b_\tau r^{(\tau -1)}\)\(\forall r\ge 0\), where \(b_1 =2, b_2=2\pi \) and \(b_3=4\pi \). Therefore, all analyses and results are sufficient to be stated in terms of a 1-D SCS.

Brown [7] compared the performance of an SCS with hexagonal cellular system over shadow fading channels, and it was shown that the SCS is a useful system because its performance over very shadowed environment is close to hexagonal systems performance.

Madhusudhanan et al. [23, 26] investigated the performances of \(\tau \)-D SCSs with placing BSs as a non-homogenous Poisson distribution with random distances from origin. The authors in [26] also studied a 1-D SCS with BS density function \(\lambda (r)\), where shadow fading in the form of i.i.d non-negative random factors \(\varPsi \) was introduced. Also, it was shown that in a homogenous \(\tau \)-D SCS, shadow fading does not affect the performance at the MS and in noisy shadowed channels this term is completely captured in the noise power. They have numerically analysed effects of different fading factors in the performance of SCS. While they have not determined the distribution of performance in a closed form for all channel models.

Khodadoust and Hodtani [15] considered correlated shadowing paths between BS and MS pairs as a most important factor and analyzed the CIR in a 2-D SCS over this correlation and determined an expression for distribution of CIR and finally obtained the tail probability of the CIR.

4 Main results

4.1 Method 1

In this subsection, first, we obtain a generalized expression for the pdf of reverse CIR, \(x=\Big (\frac{C}{I}\Big )^{-1}\), on the \(\tau \)-D SCS over channels with only path-loss, and then we review the results that have been concluded in previous papers about the performance of an SCS over only shadow fading channels and we obtain an expression for the pdf of reverse CIR on the \(\tau \)-D SCS over channels with shadow fading. After that, we obtain an expression for the pdf of reverse CIR on the \(\tau \)-D SCS over channels with only Rayleigh fading. Finally, we calculate the pdf of performance of a \(\tau \)-D SCS by considering the path-loss, the shadow fading, and Rayleigh fading, and then we obtain the tail probability of performance.

The received power at the MS from a BS can be expressed in a more general form, based on Eq. 1. The radio factor K would be a random variable to capture the variations in antenna gains and antenna orientations, but here we just assume K as a constant. We model shadow fading factor \(\varPsi \) as a zero mean Lognormal random variable with variance \(\sigma \). Also multi-path fading factor \(\phi \) is modeled as a Rayleigh random variable. In such a case, we can write the CIR at the MS, in more general form as follows:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )=\frac{K{R_s}^{-\varepsilon }{\varPsi }_s{\phi }_s}{\sum _{i=1}^{\infty } K{R_i}^{-\varepsilon }{\varPsi }_i{\phi }_i} \end{aligned}$$
(2)

where subscript s denotes the serving BS and subscript i indexes the co-channel interferers and \(\{R_S\}\cup \{R_i\}_{i=1}^{\infty }\), where \(R_s\le R_1\le R_2\le R_3\le \cdots \), \(\{\varPsi _S\}\cup \{\varPsi _i\}_{i=1}^{\infty }\), and \(\{\phi _S\}\cup \{\phi _i\}_{i=1}^{\infty }\) are the separations, the shadow fading factors, and the Rayleigh fading factors between the corresponding BS to MS pairs, respectively.

First, we calculate a generalized expression for the distribution of reverse CIR on the \(\tau \)-D SCS over channels with only path-loss. As mentioned in Eqs. 1 and 2, we define \(x=\sum _{i=1}^{M}{\Big (\frac{R_i}{R_s}\Big )^{-\varepsilon }}\), where M is the number of interferer BSs, and is a Poisson random variable. In the SCS, the distances between BSs are exponential random variables. The random variable \(g_i\) is defined as a function of random variables \(R_i\) and \(R_s\) as \(g_i=\big (\frac{R_i}{R_s}\big )^{-\varepsilon }\). Now, we can calculate the distribution of \(g_i\).

In the \(\tau \)-D homogenous SCS, the random variables \(R_i\) and \(R_s\) are independent exponential with \(f_R(r)=\lambda b_\tau r^{\tau -1}exp\big (\frac{-\lambda b_\tau r^\tau }{\tau }\big )\)[23], where \(f_R(r)\) is pdf of R. To calculate pdf of \(g_i\), we use the usual relations for the joint and marginal distribution functions from [27]. Therefore, we define \(m_i=\frac{R_i}{R_s}\) and \(u=R_i\rightarrow R_S=\frac{u}{m_i}\) to use the joint distribution. Then, we write:

$$\begin{aligned} \mathfrak {I}(R_i,R_s)=\begin{vmatrix} \frac{\partial m_i}{\partial R_i}&\frac{\partial m_i}{\partial R_s}\\ \frac{\partial u}{\partial R_i}&\frac{\partial u}{\partial R_s} \end{vmatrix}=\frac{R_i}{{R_s}^2}=\frac{{m_i}^2}{u} \end{aligned}$$
(3)

where \(\mathfrak {I}(.,.)\) denotes the Jacobian matrix. According to [27], the joint density function of random variables \(m_i\) and u is written as:

$$\begin{aligned} f_{m_i,u}(m_i,u)= & {} \frac{f_{R_i,R_s}(u,\frac{u}{m_i})}{\big |\mathfrak {I}(R_i,R_s)\big |}\nonumber \\= & {} \left( \frac{u}{m_i^2}\right) \frac{\big (\lambda b_\tau u^{\tau -1}\big )^2}{{m_i}^{\tau -1}}\nonumber \\&\quad \exp \left\{ {-\,{u^\tau }\left( \frac{\lambda b_\tau }{\tau }+\frac{\lambda b_\tau }{\tau m_i^\tau }\right) }\right\} \nonumber \\= & {} \frac{\big (\lambda b_\tau \big )^2u^{2\tau -1}}{{m_i}^{\tau +1}}\exp \Bigg \{{-\,{u^\tau }\Bigg (\frac{\lambda b_\tau }{\tau }+\frac{\lambda b_\tau }{\tau m_i^\tau }\Bigg )}\Bigg \}\nonumber \\ \end{aligned}$$
(4)

Therefore the distribution of random variable \(m_i\) is calculated as:

$$\begin{aligned} f_{m_i}(m_i)=\int _{0}^{\infty }f_{m_i,u}(m_i,u)du=\frac{\bigg (\frac{\lambda ^2b_\tau ^2}{{m_i}^{\tau +1}}\bigg )}{\tau \bigg (\frac{\lambda b_\tau }{\tau }+\frac{\lambda b_\tau }{\tau m_i^\tau }\bigg )^2} \end{aligned}$$
(5)

By considering \(g_i=\Big (\frac{R_i}{R_s}\Big )^{-\varepsilon }=m_i^{-\varepsilon }\) , the distribution of \(g_i\) is calculated as:

$$\begin{aligned} f_{g_i}(g_i)=\frac{\tau \lambda ^2b_\tau ^2}{\varepsilon g_i^{\frac{\tau }{\varepsilon }+1}{\bigg (\lambda b_\tau g_i^{-\frac{\tau }{\varepsilon }}+\lambda b_\tau \bigg )^2}}=\frac{n}{\varepsilon g_i^{1+\frac{n}{\varepsilon }}{\bigg (1+g_i^{-\frac{n}{\varepsilon }}\bigg )^2}} \end{aligned}$$
(6)

Then, to calculate the pdf of random variable x with respect to M, we write:

$$\begin{aligned} f_{x|M}(x)=f_{g_1}(x)*\cdots *f_{g_M}(x) \end{aligned}$$
(7)

where \(*\) denotes convolution. Now, we write the expression for the pdf of x as:

$$\begin{aligned} f_x(x)=\sum _{\eta =1}^\infty f_{(x|M)}(x).p\{M=\eta \} \end{aligned}$$
(8)

where M is a Poisson random variable with parameter \(\lambda _\tau (r)\). Therefore, we write:

$$\begin{aligned} p\{M=\eta \}=e^{-\lambda _\tau (r)}\frac{\big (\lambda _\tau (r)\big )^\eta }{\eta !} \end{aligned}$$
(9)

For example, when \(\varepsilon =1\) and \(\lambda _\tau (r)=\lambda \), we can write the expression for the pdf of x as:

$$\begin{aligned} f_x(x)=\sum _{\eta =1}^\infty e^{-\lambda }\frac{(2\pi \lambda )^\eta }{\eta !}\sum _{n=0}^\eta {\eta \atopwithdelims ()n}\sum _{i=0}^n \frac{g^i(\delta (x))}{dx^i} \end{aligned}$$
(10)

where \(\delta (x)\) is delta Dirac function of random variable x. In the following, we review the results that have been concluded in previous papers about the performance of an SCS over only shadow fading channels. Brown [7] compared performance of an SCS with hexagonal cellular system over shadow fading channels , and was shown that SCS is useful for this channels, because its performance over very shadowed environments is close to hexagonal systems performance. Madhusudhanan et al. [23] studied the performance of a 1-D SCS over shadow fading channels , that have been modeled by i.i.d Lognormal random variables and a semi-analytical expression for the CIR, and the tail probability of CIR, that means probability that the CIR level is over a threshold level \(\gamma \), \(\gamma \ge 1\), has been concluded as:

$$\begin{aligned} prob\Bigg \{\frac{C}{I}>\gamma \Bigg \}=\int _{\omega =-\infty }^{\infty } \varPhi _{{\big (\frac{C}{I}\big )}^{-1}}(\omega )\Bigg (\frac{1-e^{\big (\frac{-i\omega }{\gamma }\big )}}{i\omega }\Bigg ) \frac{d\omega }{2\pi } \end{aligned}$$
(11)

In which for characteristic function of reverse CIR, we have:

$$\begin{aligned} \varPhi _{\bigg ({\frac{C}{I}\bigg )}^{-1}}(\omega )=E_{R_S}\Bigg [\exp \Bigg (R_S\int _{u=1}^{\infty }\big (\exp (i\omega u^{-\varepsilon })-1\big )\lambda (uR_S)du\Bigg )\Bigg ]\end{aligned}$$
(12)

Then, the pdf of \(R_S\) is modeled as exponential random variable [23], with the following distribution:

$$\begin{aligned} f_{R_S}(r_S)=\lambda (r_S).\exp \Bigg (\int _{s=0}^{r_S}\lambda (s)ds\Bigg ), \forall ~r_S\ge 0 \end{aligned}$$
(13)

and also \(E_{R_S}[.]\) denotes the static expectation with respect to \(R_S\) random variable. Madhusudhanan et al. [23, 26] shown that an SCS affected by Lognormal random shadow fading is equivalent to another SCS without shadow fading and a different BS density function. According to [23], we shown that when shadow fading in the form of i.i.d non-negative random factors \(\{\varPsi _S\}\cup \{\varPsi _i\}_{i=1}^{\infty }\) are introduced to a \(\tau \)-D SCS with BS density function \(\lambda _\tau (r)\), such that the random variables are independent of the BSs replacing, with Poisson point process, the resulting system is equivalent to another \(\tau \)-D SCS with a different BS density:

$$\begin{aligned} \bar{\lambda }_\tau (r)=E_{\varPsi }\Bigg [{\varPsi }^\frac{\tau }{\varepsilon }\lambda _\tau \Big (r{\varPsi }^{\frac{\tau }{\varepsilon }}\Big )\Bigg ] \end{aligned}$$
(14)

Such an equivalence is valid as long as \(E_\varPsi \Big [\varPsi ^{(\frac{\tau }{\varepsilon })} \lambda _\tau \Big (r\varPsi ^{(\frac{\tau }{\varepsilon })} \Big )\Big ]<\infty \), where \(E_{\varPsi }[.]\) denotes statistical expectation with respect to \(\varPsi \) random variable with the following distribution:

$$\begin{aligned} f_{\varPsi }(\varPsi )=\frac{1}{\varPsi \sqrt{2\pi }\sigma } e^{\frac{-\left( \frac{\ln {(\varPsi )}}{\sigma }\right) ^2}{2}} \end{aligned}$$
(15)

By entering Eq. 15 in Eq. 14, BS density function of \(\tau \)-D SCS is equal to \(\bar{\lambda }=\lambda e^{\big (\frac{\tau \sigma ^2}{\varepsilon ^2}\big )}\). Also, the authors in [23] were shown that in a homogenous \(\tau \)-D SCS, shadow fading does not affect the performance at the MS and in noisy shadowed channels this term is completely captured in the noise power. Previous works introduced only tail probability of distribution of performance over shadow fading and additive white Gaussian noise (AWGN) channels, and distribution of performance was not calculated. Also, multi-path fading has not been studied in the CIR performance of SCS. In this paper, we calculate the performance of an SCS over shadow fading and Rayleigh fading channels and calculate the reverse CIR distribution and tail probability of this random variable, too. Now, we just assume a \(\tau \)-D, non-noisy, and fading channels SCS. Also, in this case, we do not consider path-loss. First, equivalent system is introduced , then the distribution of reverse CIR and tail probability for the CIR in such a system are calculated. The effect of multi-path fading on the CIR in expression Eq. 2 can be expressed by multi-path fading factor \(\phi \), which is modeled as a Rayleigh random variable. The Rayleigh fading model is characterized by a single parameter, i.e., \(\sigma \). The pdf of the channel fading amplitude \(\phi \) in a Rayleigh fading environment is given by:

$$\begin{aligned} f_{\phi }(\phi )=\frac{\phi }{{\sigma }^2} e^{\frac{-\left( \frac{\phi }{\sigma }\right) ^2}{2}} \end{aligned}$$
(16)

In the presence of fading, the amplitude of the received signal is attenuated by the fading amplitude \(\phi \), which is a random variable with meansquare value \(\sigma \). Such that we can write:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )=\frac{{R_s}^{-\varepsilon }\phi _s}{\sum _{i=1}^\infty {R_i}^{-\varepsilon }\phi _i} \end{aligned}$$
(17)

where \(\{\phi _S\}\cup \{\phi _i\}_{i=1}^{\infty }\) are the nonnegative random Rayleigh fading factors with parameter \(\sigma \). Due to the complexity of the sentences in the direct calculation of the CIR, for the simplicity of the calculus, we use its reverse and calculate the following distribution:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )^{-1}=\sum _{i=1}^{\infty } \Bigg (\frac{{R_i}^{-\varepsilon }}{{R_s}^{-\varepsilon }}\Bigg ) \Bigg (\frac{\phi _i}{\phi _s}\Bigg ) \end{aligned}$$
(18)

According to [23], related to shadow fading, when multi-path fading in the form of i.i.d nonnegative random factors \(\{\phi _S\}\cup \{\phi _i\}_{i=1}^{\infty }\) are introduced to the \(\tau \)-D SCS with BS density function \(\lambda _\tau (r)\), we calculate BS density for a \(\tau \)-D SCS over Rayleigh fading in the following.

The expression for the CIR can equivalently be written as:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )=\frac{{\bar{R_s}}^{-\varepsilon }}{\sum _{i=1}^\infty {\bar{R_i}}^{-\varepsilon }} \end{aligned}$$
(19)

where \({\bar{R_s}}=R_s \phi _s^{\frac{-\tau }{\varepsilon }}\) and \({\bar{R_i}}=R_i \phi _i^{\frac{-\tau }{\varepsilon }}\), that subscripts s and i denote server and interferer, respectively, and R is the random variable representing the radial distance from the MS to a BS in the non-uniform SCS with a BS density function \(\lambda _\tau (r)\), and \(\phi _i\) is the multi-path fading factor corresponding to the BS, and \(\bar{R}\) is the corresponding equivalent radial distance. \(\bar{R}\) also follows a Poisson process with a BS density function derived in the following paragraph. For each non-homogeneous Poisson process, \(E[ N(t+s)-N(t)]\), the expected number of occurrences in the interval \((t,t+s)\) is called the mean function and can be written in terms of the BS density function as follows:

$$\begin{aligned} E[N(t+S)-N(t)]=E_\phi \Bigg [\int _{r{\phi }^{\frac{\tau }{\varepsilon }}}^{(r+s)\phi ^{\frac{\tau }{\varepsilon }}} \lambda _\tau (k)dk\Bigg ] \end{aligned}$$
(20)

where \(\lambda _\tau (k)\) is the density function of the Poisson process. Consider \(E [Number~of~BSs~with~\bar{R}\in (r ,r+s)]= E[ N(r+s)-N(r)]\).

Thus, we can write \(k\rightarrow k\phi ^{\frac{-\tau }{\varepsilon }}\) and obtain the following equation:

$$\begin{aligned} E[N(r+S)-N(r)]&\overset{a}{=}&E_\phi \Bigg [\int _{r{\phi }^{\frac{\tau }{\varepsilon }}}^{(r+s)\phi ^{\frac{\tau }{\varepsilon }}} \lambda _\tau (k)dk\Bigg ]\nonumber \\&\overset{b}{=}&\int _{r}^{r+s}E_{\phi }\Bigg [\phi ^{\frac{\tau }{\varepsilon }}\lambda _\tau \Big (k\phi ^{\frac{\tau }{\varepsilon }}\Big )\Bigg ]dk \end{aligned}$$
(21)

where (a) is obtained by rewriting the expectation with respect to every realization of the Rayleigh fading factor and R is generated from a non-homogeneous Poisson process with a density function \(\lambda _\tau (r)\) and (b) follows easily. Hence, \(\bar{R}\)s are generated from another non-homogeneous Poisson process with a density function \(E_\phi \Big [\phi ^{(\frac{\tau }{\varepsilon })} \lambda _\tau \Big (r\phi ^{(\frac{\tau }{\varepsilon })}\Big )\Big ]<\infty \).

When multi-path fading in the form of i.i.d nonnegative random factors \(\{\phi _S\}\cup \{\phi _i\}_{i=1}^{\infty }\) are introduced to the \(\tau \)-D SCS with a BS density function \(\lambda _\tau (r)\), the resulting system is equivalent to another \(\tau \)-D SCS with a different BS density:

$$\begin{aligned} \bar{\lambda }_\tau (r)=E_{\phi }\Bigg [{\phi }^{\frac{\tau }{\varepsilon }}\lambda _\tau \Big (r{\phi }^{\frac{\tau }{\varepsilon }}\Big )\Bigg ] \end{aligned}$$
(22)

where \(E_{\phi }[.]\) denotes statistical expectation with respect to \(\phi \). Such an equivalence is valid as long as \(E_\phi \Big [\phi ^{(\frac{\tau }{\varepsilon })} \lambda _\tau \Big (r\phi ^{(\frac{\tau }{\varepsilon })}\Big )\Big ]<\infty \).

Now, by entering Eq. 22 in Eq. 1 and using Eq. 8, we can find the distribution function of reverse CIR, and then calculate the tail probability of CIR for an SCS over Rayleigh fading channels, by using the result in Eq. 11.

In the following, we calculate the distribution of reverse CIR over this channel. To calculate the performance of a \(\tau \)-D SCS over fading channel, we can write \(\Big (\frac{C}{I}\Big )=\frac{R_s^{-\varepsilon }\phi _s}{\sum _{i=1}^\infty R_i^{-\varepsilon }\phi _i}\). Due to the complexity of the sentences in the direct calculation of the CIR, for the simplicity of the calculus, we use its reverse and calculate the distribution \(\Big (\frac{C}{I}\Big )^{-1}=\sum _{i=1}^M\Big (\frac{R_i^{-\varepsilon }}{R_s^{-\varepsilon }}\Big )\Big (\frac{\phi _i}{\phi _s}\Big )\), where \(\{\phi _S\}\cup \{\phi _i\}_{i=1}^{\infty }\) are i.i.d Rayleigh random variables. Then we can use symbol \(m_i\) for changing the variables as follows:

$$\begin{aligned} m_i=\Bigg (\frac{\phi _i}{\phi _s}\Bigg ) \end{aligned}$$
(23)

First, we obtain the distribution of \(m_i\) and then calculate the reverse CIR distribution by using the results. In first step, by using Jacobian matrix, we can calculate the distribution of \(m_i\), therefore define random variable u to use joint distribution as \(u=\phi _i\rightarrow \phi _s=\frac{u}{m_i}\) and we can write:

$$\begin{aligned} \mathfrak {I}(\phi _i,\phi _s)=\begin{vmatrix} \frac{\partial m_i}{\partial \phi _i}&\frac{\partial m_i}{\partial \phi _s}\\ \frac{\partial u}{\partial \phi _i}&\frac{\partial u}{\partial \phi _s} \end{vmatrix}=-\frac{\phi _i}{{\phi _s}^2}=-\frac{{m_i}^2}{u} \end{aligned}$$
(24)

According to [27], the joint density function of random variables \(m_i\) and u is written as:

$$\begin{aligned} f_{m_i,u}(m_i,u)= & {} \frac{f_{\phi _i,\phi _s}(u,\frac{u}{m_i})}{\big |\mathfrak {I}(\phi _i,\phi _s)\big |}\nonumber \\= & {} \frac{1}{\frac{m_i^2}{u}}f_{(\phi _i)}(u)f_{(\phi _s)}\bigg (\frac{u}{m_i}\bigg )\nonumber \\= & {} \frac{u}{m_i^2}\Bigg (\frac{u}{\sigma ^2}e^{\frac{-\big (\frac{u}{\sigma }\big )^2}{2}}\Bigg ) \Bigg (\frac{\big (\frac{u}{m_i}\big )}{\sigma ^2}e^{\frac{-\Big (\frac{\big (\frac{u}{m_i}\big )}{\sigma }\Big )^2}{2}}\Bigg )\nonumber \\= & {} \frac{u^3}{m_i^3\sigma ^4}e^{\Bigg (\frac{-\big (\frac{u}{\sigma }\big )^2}{2}+{\frac{-\Big (\frac{\big (\frac{u}{m_i}\big )}{\sigma }\Big )^2}{2}}\Bigg )}\nonumber \\= & {} \frac{u^3}{m_i^3\sigma ^4}e^{{-u^2}\Big (\frac{1}{2\sigma ^2}+\frac{1}{2\sigma ^2m_i^2}\Big )} \end{aligned}$$
(25)

Therefore the distribution of \(m_i\) can be calculated by:

$$\begin{aligned} f_{m_i}(m_i)= & {} \int _{0}^{\infty }f_{m_i,u}(m_i,u)du =\int _{0}^{\infty }Au^3e^{(-Bu^2)}du\nonumber \\= & {} A\int _{0}^{\infty }u^3e^{(-Bu^2)}du \end{aligned}$$
(26)

where the parameters A and B are defined: \(A=\frac{1}{m_i^3\sigma ^4}\) and \(B=\Big (\frac{1}{2\sigma ^2}+\frac{1}{2m_i^2\sigma ^2}\Big )\), and by using the following equation, i.e., Eq. 27, we obtain Eq. 28.

$$\begin{aligned} \int _{0}^{\infty }u^ne^{-au^2}du=\frac{K!}{2a^{K+1}} \end{aligned}$$
(27)

\(n=2K+1\) and \(a>0\).

$$\begin{aligned} f_{m_i}(m_i)= & {} \frac{A}{2B^2}=\frac{\frac{1}{{m_i}^3\sigma ^4}}{2\Big (\frac{1}{2\sigma ^2}+\frac{1}{2\sigma ^2{m_i}^2}\Big )^2}\nonumber \\= & {} \frac{\frac{1}{{m_i}^3\sigma ^4}}{2\Big (\frac{1}{4\sigma ^4}+\frac{1}{4\sigma ^4{m_i}^4}+\frac{2}{4\sigma ^4{m_i}^2}\Big )}=\frac{2m_i}{\big (1+{m_i}^2\big )^2}\nonumber \\ \end{aligned}$$
(28)

and by using the results, we can calculate an expression for the reverse CIR as follows:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )^{-1}=&\sum _{i=1}^M\Bigg (\frac{R_i^{-\varepsilon }}{R_s^{-\varepsilon }}\Bigg )\Bigg (\frac{\phi _i}{\phi _s}\Bigg )\nonumber \\ =&\sum _{i=1}^M\Bigg (\frac{R_i}{R_s}\Bigg )^{-\varepsilon }m_i =\sum _{1}^Mg_im_i=\sum _{1}^M Q_i \end{aligned}$$
(29)

Now, by having the pdf for \(m_i\), in Eq. 28, and the pdf for \(g_i\), in Eq. 6, and use of Jacobian matrix, we can determine the distribution of \(Q_i\). Therefore, we define random variable u to use the joint distribution as \(u=g_i\rightarrow m_i=\frac{Q_i}{u}\) and we can write:

$$\begin{aligned} \mathfrak {I}(g_i,m_i)=\begin{vmatrix} \frac{\partial Q_i}{\partial m_i}&\frac{\partial Q_i}{\partial g_i}\\ \frac{\partial u}{\partial m_i}&\frac{\partial u}{\partial g_i} \end{vmatrix}=g_i=u \end{aligned}$$
(30)

Then according to [27], the joint density function of random variables \(Q_i\) and u is written as:

$$\begin{aligned} f_{Q_i,u}(Q_i,u)= & {} \frac{f_{m_i,g_i}(\frac{Q_i}{u},u)}{\big |\mathfrak {I}(g_i,m_i)\big |}=\frac{1}{u}f_{m_i}\Big (\frac{Q_i}{u}\Big )f_{g_i}(u)\nonumber \\= & {} \frac{1}{u}\left( \frac{2\big (\frac{Q_i}{u}\big )}{\big (1+\big (\frac{Q_i}{u}\big )^2\big )^2}\right) \Big (f_{g_i}(g_i) \Big )\nonumber \\= & {} \frac{1}{u}\left( \frac{2\big (\frac{Q_i}{u}\big )}{1+\frac{{Q_i}^4}{u^4}+\frac{2{Q_i}^2}{u^2}}\right) \Big (f_{g_i}(g_i) \Big )\nonumber \\= & {} \frac{2Q_iu^2}{\big (u^2+{Q_i}^2\big )^2}\Big (f_{g_i}(g_i)\Big ) \end{aligned}$$
(31)

The distribution of \(Q_i\) is calculated as follows:

$$\begin{aligned} f_{Q_i}(Q_i)= & {} \int _{g_i=0}^{\infty }f_{Q_i,g_i}(Q_i,g_i)d_{g_i}\nonumber \\= & {} \int _{g_i=0}^{\infty }\left( \frac{2Q_i{g_i}^2}{{\big ({g_i}^2+{Q_i}^2\big )}^2}\right) \Big (f_{g_i}(g_i)\Big )d_{g_i}\nonumber \\= & {} 2{Q_i}\int _{g_i=0}^{\infty }\frac{{g_i}^2}{\big ({g_i}^2+{Q_i}^2\big )^2}\Big (f_{g_i}(g_i)\Big )d_{g_i} \end{aligned}$$
(32)

By comparing Eq. 32 and statistical expectation definition, we can write:

$$\begin{aligned} f_{Q_i}(Q_i)=2{Q_i}E_{g_i}\Bigg [\frac{{g_i}^2}{\big ({g_i}^2+{Q_i}^2\big )^2}\Bigg ] \end{aligned}$$
(33)

The distribution of y with respect to M can be written as follows:

$$\begin{aligned} f_{y|M}(y)=f_{Q_1}(y)*\cdots *f_{Q_M}(y) \end{aligned}$$
(34)

where M was showed in Eq. 9. Now, the expression for distribution of y can be calculated as follows:

$$\begin{aligned} f_y(y)= & {} \sum _{\eta =1}^{\infty }f_{y|(M=\eta )}(y).p\{M=\eta \}\nonumber \\= & {} \sum _{\eta =1}^{\infty }\big (f_{Q_1}(y)*\dots *f_{Q_M}(y)\big ).p\{M=\eta \}\nonumber \\= & {} \sum _{\eta =1}^{\infty }2^\eta e^{-\lambda _\tau (r)} \frac{{\lambda _\tau (r)}^\eta }{\eta !}\nonumber \\&\quad \times \Bigg (yE_{g_1}\Bigg [\frac{{g_1}^2}{\big ({g_1}^2+y^2\big )^2}\Bigg ]*\dots *\nonumber \\&\quad yE_{g_{\eta }}\Bigg [\frac{{g_\eta }^2}{\big ({g_{\eta }}^2+y^2\big )^2}\Bigg ]\Bigg ) \end{aligned}$$
(35)

Then we can calculate the tail probability of CIR for a \(\tau \)-D SCS over multi-path fading channels as follows:

$$\begin{aligned} p\Bigg \{\Bigg (\frac{C}{I}\Bigg )\ge \gamma \Bigg \}= & {} K_{\frac{\varepsilon }{\tau }}\gamma ^{\frac{-\tau }{\varepsilon }}\nonumber \\= & {} p\Bigg \{\Bigg (\frac{C}{I}\Bigg )^{-1}\le \frac{1}{\gamma }\Bigg \}=\int _{0}^{\frac{1}{\gamma }}f_y(y)dy \end{aligned}$$
(36)

where \(K_{\frac{\varepsilon }{\tau }}\) is a constant parameterized by \({\frac{\varepsilon }{\tau }}\) and \(\varepsilon \) is the path-loss exponent. Therefore the tail probability of reverse CIR, by using \(f_y (y)\), is given by:

$$\begin{aligned} p\Bigg \{\Bigg (\frac{C}{I}\Bigg )^{-1}\le \frac{1}{\gamma }\Bigg \}= & {} \int _{0}^{\frac{1}{\gamma }}\sum _{\eta =1}^{\infty }f_{y|(M=\eta )}(y).p\{M=\eta \}dy\nonumber \\= & {} \sum _{\eta =1}^{\infty }2^\eta e^{-\lambda _\tau (r)}\frac{{\lambda _\tau (r)}^\eta }{\eta !}\nonumber \\&\quad \int _{0}^{\frac{1}{\gamma }}\Bigg (yE_{g_1}\Bigg [\frac{{g_1}^2}{\big ({g_1}^2+y^2\big )^2}\Bigg ]\nonumber \\&\quad *\dots * yE_{g_{\eta }}\Bigg [\frac{{g_\eta }^2}{\big ({g_{\eta }}^2+y^2\big )^2}\Bigg ]\Bigg )dy\nonumber \\ \end{aligned}$$
(37)

Now, we will show the effect of shadow fading and Rayleigh fading on the \(\tau \)-D SCS and an expression for pdf of the reverse CIR in this system would be introduced. Moreover, the tail probability for this random variable, by using the results, would be calculated. The effect of shadow fading on a uniform 2-D SCS was studied in [15, 21, 22, 26]. It was shown that the performance of the uniform 2-D SCS is independent of the BS density, the performance of such a cellular system is the same as the performance of any other uniform 2-D SCS. Furthermore, in [23] it has been proved that when shadow fading in the form of i.i.d non-negative random factors \(\{\varPsi _S\}\cup \{\varPsi _i\}_{i=1}^{\infty }\) are introduced to the 1-D SCS with BS density function \(\lambda (r)\), the resulting system is equivalent to another 1-D SCS with a different BS density \(\bar{\lambda }(r)=E_\varPsi \Big [\varPsi ^{(\frac{1}{\varepsilon })} \lambda \big (r\varPsi ^{(\frac{1}{\varepsilon })} \big )\Big ]\). Now, by using this equivalent, Eqs. 8 and 14, we can calculate the pdf of reverse CIR affected by shadow fading and hence we can conclude that:

$$\begin{aligned} f_y(y)=\Bigg \{\sum _{\eta =1}^{\infty }f_{y|(M=\eta )}(y).p\{M=\eta \}\big |\bar{\lambda }_\tau (r)\Bigg \} \end{aligned}$$
(38)

and

$$\begin{aligned}&p\Bigg \{\Bigg (\frac{C}{I}\Bigg )^{-1}\le \frac{1}{\gamma }\Bigg \}\nonumber \\&\qquad =\Bigg \{\Bigg \{\int _{0}^{\frac{1}{\gamma }}\sum _{\eta =1}^{\infty }f_{y|(M=\eta )}(y).p\{M=\eta \}dy\Bigg \}\big |\bar{\lambda }_\tau (r)\Bigg \}\nonumber \\&\qquad =\Bigg \{\Bigg \{\sum _{\eta =1}^{\infty }2^\eta e^{-\lambda _\tau (r)}\frac{{\lambda _\tau (r)}^\eta }{\eta !}\int _{0}^{\frac{1}{\gamma }}\Bigg (yE_{g_1}\Bigg [\frac{{g_1}^2}{({g_1}^2+y^2)^2}\Bigg ]*\dots *\nonumber \\&\qquad \quad \quad yE_{g_{\eta }}\Bigg [\frac{{g_\eta }^2}{({g_{\eta }}^2+y^2)^2}\Bigg ]\Bigg )dy\Bigg \}\big |\bar{\lambda }_\tau (r)\Bigg \} \end{aligned}$$
(39)

According to [23, 26] and our results in Eq. 14, shadow fading affects on the BS density function, so, the distributions of M in Eq. 9 is changed with respect to previous assumed channels modelled without shadow fading. Therefore, we have:

$$\begin{aligned} p\{M=\eta \big |\bar{\lambda }_\tau (r)\}=e^{-\bar{\lambda }_\tau (r)} \frac{\bar{\lambda }_\tau (r)^\eta }{\eta !} \end{aligned}$$
(40)

By entering Eq. 40 in Eq. 39, the tail probability of reverse CIR in the \(\tau \)-D SCS over composite Rayleigh–Lognormal fading is:

$$\begin{aligned}&p\Bigg \{\Bigg (\frac{C}{I}\Bigg )^{-1}\le \frac{1}{\gamma }\Bigg \}\nonumber \\&\quad =\Bigg \{\sum _{\eta =1}^{\infty }2^\eta e^{-\bar{\lambda }_\tau (r)}\frac{{\bar{\lambda }_\tau (r)}^\eta }{\eta !}\int _{0}^{\frac{1}{\gamma }}\Bigg (yE_{g_1}\Bigg [\frac{{g_1}^2}{({g_1}^2+y^2)^2}\Bigg ]*\dots *\nonumber \\&\qquad yE_{g_{\eta }}\Bigg [\frac{{g_\eta }^2}{({g_{\eta }}^2+y^2)^2}\Bigg ]\Bigg )dy\Bigg \} \end{aligned}$$
(41)

4.2 Method 2

In this subsection, we analyze effect of both shadow fading and multi-path fading on the \(\tau \)-D SCS by considering composite Rayleigh–Lognormal distribution as the most employed composite distribution [3, 11, 19, 28] and determine expressions for the distribution of inverse CIR and the pdf of CIR is calculated in an analytical form and obtain the tail probability of CIR. Atapattu et al. [3] introduced a simple and new form of distribution which can accurately represent both the Rayleigh fading and Lognormal shadow fading effects. The pdf of the composite Rayleigh–Lognormal fading channel \(\mathfrak {R}\) is given by:

$$\begin{aligned} f_\mathfrak {R}(\mathfrak {R})\approx \frac{2\mathfrak {R}}{\sqrt{\pi }}\sum _{i=1}^{N}w_i h(p_i) \end{aligned}$$
(42)

In this equation, \(p=\frac{ln\varPsi }{\sqrt{2}\sigma }\) and \(h(p)=e^{-\big (\sqrt{2}\sigma p+\mathfrak {R}^2e^{-(\sqrt{2}\sigma p)}\big )}\), where \(\varPsi \) is Lognormal shadow fading with mean and variance 0 and \(\sigma \), respectively. \(p_i\) and \(w_i\) are abscissas and weight factors for the Gaussian-Hermite integration [3]. \(p_i\) and \(w_i\) for different N values are available in [3] or can be calculated by a simple MATLAB program.

By considering \(\mathfrak {R}\), in the SCS, we can write the CIR at the MS, in more general form as follows:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )=\frac{K{R_s}^{-\varepsilon }\mathfrak {R}_s}{\sum _{i=1}^{\infty } K{R_i}^{-\varepsilon }\mathfrak {R}_i} \end{aligned}$$
(43)

Due to the simplicity of the calculus we use reverse CIR and calculate the distribution \(\Big (\frac{C}{I}\Big )^{-1}=\sum _{i=1}^M\Big (\frac{R_i^{-\varepsilon }}{R_s^{-\varepsilon }}\Big )\Big (\frac{\mathfrak {R}_i}{\mathfrak {R}_s}\Big )\), where \(\{\mathfrak {R}_S\}\cup \{\mathfrak {R}_i\}_{i=1}^{\infty }\) are composite Rayleigh–Lognormal fading variables. Then, we can use symbol \(m_i\) for changing the variables as follows:

$$\begin{aligned} m_i=\Bigg (\frac{\mathfrak {R}_i}{\mathfrak {R}_s}\Bigg ) \end{aligned}$$
(44)

First, we obtain the distribution of \(m_i\) and then calculate the reverse CIR distribution by using the result. In first step, by using Jacobian matrix, we can calculate the distribution of \(m_i\), therefore we define random variable u to use joint distribution as \(u=\mathfrak {R}_i\rightarrow \mathfrak {R}_s=\frac{u}{m_i}\) and we can write:

$$\begin{aligned} \mathfrak {I}(\mathfrak {R}_i,\mathfrak {R}_s)=\begin{vmatrix} \frac{\partial m_i}{\partial \mathfrak {R}_i}&\frac{\partial m_i}{\partial \mathfrak {R}_s}\\ \frac{\partial u}{\partial \mathfrak {R}_i}&\frac{\partial u}{\partial \mathfrak {R}_s} \end{vmatrix}=-\frac{\mathfrak {R}_i}{{\mathfrak {R}_s}^2}=-\frac{{m_i}^2}{u} \end{aligned}$$
(45)

Then according to [27], the joint density function of random variables \(m_i\) and u is written as:

$$\begin{aligned} f_{m_i,u}(m_i,u)= & {} \frac{f_{\mathfrak {R}_i,\mathfrak {R}_s}(u,\frac{u}{m_i})}{\big |\mathfrak {I}(\mathfrak {R}_i,\mathfrak {R}_s)\big |}\nonumber \\= & {} \frac{1}{\bigg (\frac{m_i^2}{u}\bigg )}f_{(\mathfrak {R}_i)}(u)f_{(\mathfrak {R}_s)}\bigg (\frac{u}{m_i}\bigg )\nonumber \\= & {} \bigg (\frac{u}{m_i^2}\bigg )\bigg (\frac{2u}{\sqrt{\pi }}\sum _{j=1}^{N}w_j h(p_j)\bigg )\left( \frac{2{\big (\frac{u}{m_i}\big )}}{\sqrt{\pi }}\sum _{k=1}^{N}w_k h(p_k)\right) \nonumber \\&\quad \bigg (\frac{4u^3}{\pi m_i^3}\bigg )\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_kh(p_j)h(p_k) \end{aligned}$$
(46)

where \(h(p_j)=e^{-\big (\sqrt{2}\sigma p_j+u^2e^{-(\sqrt{2}\sigma p_j)}\big )}\) and \(h(p_k)=e^{-\big (\sqrt{2}\sigma p_k+(\frac{u}{m_i})^2e^{-(\sqrt{2}\sigma p_k)}\big )}\).

Therefore

$$\begin{aligned}&f_{m_i,u}(m_i,u)=\bigg (\frac{4u^3}{\pi m_i^3}\bigg )\nonumber \\&\quad \sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_ke^{-\big (\sqrt{2}\sigma (p_j+p_k)+u^2\big (e^{(-\sqrt{2}\sigma p_j)}+m_i^{-2}e^{(-\sqrt{2}\sigma p_k)}\big )\big )} \end{aligned}$$
(47)

Therefore, the distribution of random variable \(m_i\) can be calculated by:

$$\begin{aligned} f_{m_i}(m_i)= & {} \int _{0}^{\infty }f_{m_i,u}(m_i,u)du\nonumber \\= & {} \bigg (\frac{4}{\pi m_i^3}\bigg )\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_ke^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}\nonumber \\&\quad \int _{0}^{\infty }u^3e^{-u^2\big (e^{(-\sqrt{2}\sigma p_j)}+m_i^{-2}e^{(-\sqrt{2}\sigma p_k)}\big )} du \end{aligned}$$
(48)

By using Eq. 27, we have:

$$\begin{aligned} f_{m_i}(m_i)=\bigg (\frac{2}{\pi m_i^3}\bigg )\sum _{j=1}^{N} \sum _{k=1}^{N}w_jw_k \frac{e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}}{\big (e^{(-\sqrt{2}\sigma p_j)}+m_i^{-2}e^{(-\sqrt{2}\sigma p_k)}\big )^2} \end{aligned}$$
(49)

and by using the results, we can calculate an expression for reverse CIR as follows:

$$\begin{aligned} \Bigg (\frac{C}{I}\Bigg )^{-1}=&\sum _{i=1}^M \Bigg (\frac{R_i^{-\varepsilon }}{R_s^{-\varepsilon }}\Bigg ) \Bigg (\frac{\mathfrak {R}_i}{\mathfrak {R}_s}\Bigg )\nonumber \\ =&\sum _{i=1}^M\Bigg (\frac{R_i}{R_s}\Bigg )^{-\varepsilon }m_i =\sum _{i=1}^Mg_im_i=\sum _{i=1}^M Q_i \end{aligned}$$
(50)

Now, by having the Eqs. 6 and 49 and by using Eq. 30 we can determine the distribution of \(Q_i\). By using Eq. 30 and according to [27], the joint density function of random variables \(Q_i\) and u is written as:

$$\begin{aligned} f_{Q_i,u}(Q_i,u)= & {} \frac{f_{m_i,g_i}(\frac{Q_i}{u},u)}{\big |\mathfrak {I}(g_i,m_i)\big |}\nonumber \\= & {} \frac{1}{u}\bigg (\frac{2}{\pi \big (\frac{Q_i}{u}\big )^3}\bigg )\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_k\nonumber \\&\quad \frac{e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}}{\big (e^{(-\sqrt{2}\sigma p_j)}+\big (\frac{Q_i}{u}\big )^{-2}e^{(-\sqrt{2}\sigma p_k)}\big )^2}f_{g_i}(u)\nonumber \\ \end{aligned}$$
(51)

The distribution of \(Q_i\) is calculated as follows:

$$\begin{aligned} f_{Q_i}(Q_i)= & {} \int _{g_i=0}^{\infty }f_{Q_i,g_i}(Q_i,g_i)d_{g_i}\nonumber \\= & {} \int _{g_i=0}^{\infty }\frac{1}{u}\bigg (\frac{2}{\pi \big (\frac{Q_i}{u}\big )^3}\bigg )\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_k\nonumber \\&\frac{e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}}{\big (e^{(-\sqrt{2}\sigma p_j)}+\big (\frac{Q_i}{u}\big )^{-2}e^{(-\sqrt{2}\sigma p_k)}\big )^2}\Big (f_{g_i}(g_i)\Big )d_{g_i}\nonumber \\= & {} \frac{2}{\pi Q_i^3}\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_k{e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}}\nonumber \\&\quad \int _{g_i=0}^{\infty }\frac{g_i^2}{\big (e^{(-\sqrt{2}\sigma p_j)}+\big (\frac{g_i}{Q_i}\big )^{2} e^{(-\sqrt{2}\sigma p_k)}\big )^2}\Big (f_{g_i}(g_i)\Big )d_{g_i}\nonumber \\ \end{aligned}$$
(52)

By comparing Eq. 52 and statistical expectation definition, we can write:

$$\begin{aligned}&f_{Q_i}(Q_i)=\frac{2}{\pi Q_i^3}\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_k\nonumber \\&\quad {e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}}E_{g_i}\Bigg [\frac{g_i^2}{\big (e^{(-\sqrt{2}\sigma p_j)}+\big (\frac{g_i}{Q_i}\big )^{2}e^{(-\sqrt{2}\sigma p_k)}\big )^2}\Bigg ]\nonumber \\ \end{aligned}$$
(53)

The distribution of y with respect to M can be written as Eq. 34, then we can calculate the tail probability of CIR for a \(\tau \)-D SCS over composite Rayleigh–Lognormal fading channels as Eq. 36. Therefore the tail probability of reverse CIR, by using \(f_y (y)\), is given by:

$$\begin{aligned}&p\Bigg \{\Bigg (\frac{C}{I}\Bigg )^{-1}\le \frac{1}{\gamma }\Bigg \}=\int _{0}^{\frac{1}{\gamma }}\sum _{\eta =1}^{\infty }f_{y|(M=\eta )}(y).p\{M=\eta \}dy\nonumber \\&=\sum _{\eta =1}^{\infty }\Big (\frac{2}{\pi }\Big )^\eta e^{-\lambda _\tau (r)}\frac{{\lambda _\tau (r)}^\eta }{\eta !}\sum _{j=1}^{N}\sum _{k=1}^{N}w_jw_k\nonumber \\&\quad \int _{0}^{\frac{1}{\gamma }}\Bigg (\Bigg (y^{-3}{e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}}E_{g_1}\Bigg [\frac{g_1^2}{\big (e^{(-\sqrt{2}\sigma p_j)}+\big (\frac{g_1}{y}\big )^{2}e^{(-\sqrt{2}\sigma p_k)}\big )^2}\Bigg ]\Bigg )\nonumber \\&\quad *\dots *\Bigg (y^{-3}{e^{-\big (\sqrt{2}\sigma (p_j+p_k)\big )}} E_{g_\eta }\Bigg [\frac{g_\eta ^2}{\big (e^{(-\sqrt{2}\sigma p_j)}+\big (\frac{g_\eta }{y}\big )^{2}e^{(-\sqrt{2}\sigma p_k)}\big )^2}\Bigg ]\Bigg )\Bigg )dy\nonumber \\ \end{aligned}$$
(54)
Fig. 2
figure 2

The comparison of the tail probability of CIR for homogeneous \(\tau \)-D SCS on the BS density in \(\tau =1, 2,\) and 3 dimensions. (\(\varepsilon = 4\))

Full size image

5 Simulation results

In this section, the details of simulating the \(\tau \)-D SCS are presented. In every single trial a random number \(M\sim Poisson(\lambda _\tau (r))\) is generated, and then the BSs are placed over our region. The received power at the MS for each BS is computed by considering the path-loss exponent \(\varepsilon \), the shadow fading, multi-path fading, and composite fading, in the \(\tau \)-D SCS. For calculating the numerical results, in every trial, the received power at the MS from each BS is computed by generating random variables for shadow fading, multi-path fading, and composite fading according to the \(Log-N(0,\sigma _\varPsi ^2)\), Rayleigh fading and composite Rayleigh–Lognormal (Susuki) fading, respectively. Finally, the CIR random variable is generated according to Eqs. 2 and 43. The trial is repeated 10,000 times and the tail probability of \(\Big \{\Big (\frac{C}{I}\Big )>1\Big \}\) according to Eqs. 41 and 54 is simulated. For simulation \(f_{y}(y)\), we use central limit theorem for approximation of it as a normal random variable. Mont-Carlo method is used with number of iteration 10,000 times.

Fig. 3
figure 3

The tail probability of CIR at different BS densities, in a \(\tau \)-D SCS over different channel models. \((\varepsilon = 4, \tau =2)\)

Full size image
Fig. 4
figure 4

The comparison of the approximate distributions of reverse CIR for three different BS densities in \(\tau \)-D SCS by considering the shadow fading and Rayleigh fading. \((\varepsilon = 4, \tau =2)\)

Full size image

In Fig. 2, we compare the tail probability of CIR as a function of BS density for \(\tau \)-D SCS with \(\tau =1, 2,\) and 3, and it shows the 1-D SCS has a better CIR tail probability than the 2-D and 3-D SCS. Also, it shows that a 2-D and 3-D SCS is same as of a 1-D SCS with path-loss exponents \(\frac{\varepsilon }{2}\) and \(\frac{\varepsilon }{3}\), respectively.

In Fig. 3, the tail probability of CIR for a \(\tau \)-D SCS, over different channel models, at different BS densities is compared. By considering of shadow fading and Rayleigh fading together, the tail probability will be increased, as was concluded in [22] with shadow fading effect. Also, increasing the BS density, reduces the tail probability for all channel models; that it is because of increasing the interferer BSs. But when the number of BSs goes up, the tail probability gets approximately fixed, because the ratios of interferer distances to server distance get very high; hence the path-loss gets approximately fix. It is the same as calculated results for path-loss channels in [22, 26]. The pdf of reverse CIR, for different BS densities, is shown in Fig. 4. We can conclude that, when \(\lambda \) is grown the variance and mean of reverse CIR are increased. It means that the variance and mean of CIR decreases with growing BS density.

In Fig. 5, the tail probability of CIR for a \(\tau \)-D SCS over composite fading by using methods 1 and 2, at different BS densities, are compared.

In Fig. 6, the approximate distributions of \(y=\bigg (\frac{C}{I}\bigg )^{-1}\) by using methods 1 and 2 for two different BS densities in \(\tau \)-D SCS over composite fading are compared. Also, in this figure we compare the approximate distribution of reverse CIR and the numerical result which is calculated from Monte Carlo method for two different BS densities. This plot shows the ability of the approximation which obtains results close to the numerical results. Figures 5 and 6 show that analysing \(\tau \)-D SCS over composite fading, by using methods 1 and 2, are very similar. Therefore, we can use methods 1 or 2 to analyze \(\tau \)-D SCS over composite fading.

Fig. 5
figure 5

The comparison of the tail probability of CIR at different BS densities, in a \(\tau \)-D SCS over composite fading by using methods 1 and 2. \((\varepsilon = 4, \tau =2)\)

Full size image
Fig. 6
figure 6

The comparison of the approximate distributions of reverse CIR by using methods 1 and 2, and numerical result which is calculated from Monte Carlo method, for two different BS densities in \(\tau \)-D SCS by considering the composite fading. \((\varepsilon = 4, \tau =2)\)

Full size image

6 Conclusion

In this paper, we studied the generalized downlink CIR performance for an SCS in multiple dimensions (1, 2, and 3 dimensions). We considered path-loss, Lognormal shadow fading, Rayleigh fading, and composite Rayleigh–Lognormal (Suzuki) fading to model the BSs to MS channels. The generalized distribution of downlink CIR performance was calculated and then the performance of composite fading channels by using two methods was calculated and the tail probability of CIR was obtained. We compared the approximate and the exact distributions, which were obtained by using methods 1 and 2, and also exploited the Monte Carlo results by simulations, in order to show the ability of approximation and correctness of the analytical expression. The comparisons showed the effectiveness of the approximations. Also, the simulations illustrated that the Rayleigh fading and the composite Rayleigh–Lognormal fading both provide better metric performances, i.e., it increases the tail probability in the \(\tau \)-D SCSs.