A New Closed-Form Expressions of Channel Capacity with MRC, EGC and SC Over Lognormal Fading Channel

Abstract

In this work, we derive the closed-form expressions of channel capacity with maximal ratio combining, equal gain combining and selection combining schemes under different transmission policies such as optimal power and rate adaptation, optimal rate adaptation, channel inversion with fixed rate (CIFR) and truncated CIFR. Various approximations to the intractable integrals have been proposed using methods such as Holtzman and Gauss–Hermite approximations and simpler expressions are suggested. Moreover, as an application, the channel capacity of lognormally distributed fading channel in the interference-limited environment is discussed. The obtained closed-form expressions have been validated with the exact numerical results.

1 Introduction

Channel capacity over a fading channel gives an estimation of maximum possible transmission rate with minimal error and thus, is important from both information theoretic as well as practical view point. This parameter has been investigated in [1, 2] over lognormal (LN) shadowing under various power allocation schemes. In [1], Gaofeng et al. have analysed the channel capacity under schemes such as optimal power and rate adaptation (OPRA), optimal rate adaptation (ORA), and channel inversion with fixed rate (CIFR) only for single input- single output (SISO) channel. In [2], Karmeshu et al. have derived closed-form expressions of the channel capacity for ORA, OPRA, CIFR and truncated CIFR using moment generating function (MGF) approach without any diversity schemes and claimed to achieve simpler closed-form expressions compared to [1].

The goal of the present work is to derive the closed-form expressions for channel capacity under various definitions such as ORA, OPRA, CIFR and truncated CIFR with various diversity schemes, as maximal ratio combining (MRC), equal gain combining (EGC) and selection combining (SC). The expressions are shown to be mathematically very simple compared to [1, 2] enabling them to explain clearly the behaviour of system over lognormal fading parameters. Moreover, the results are shown to be accurate for entire range of shadowing (2–12 dB) for various wireless applications. In the last, a case of channel capacity in a co-channel interference (CCI) limited environment is discussed and compared for various transmission schemes.

The outline of the paper is as follows. In Sect. 2, closed-form expressions of channel capacity are derived for different diversity schemes. The numerical results and discussions are presented in Sect. 3. In Sect. 4, as an application, a cellular system with CCI environment is considered and the channel capacity is analysed for various transmission schemes. Section 5 concludes the work.

2 Closed Form Expressions for Channel Capacity with Diversity

2.1 MRC and EGC

The instantaneous signal-to-noise ratio (SNR) of maximal ratio combiner and equal gain combiner output are, respectively, given as

$$\begin{aligned} \gamma _{MRC}=\sum \limits _{k=1}^{L}\gamma _{k} ,\quad \gamma _{EGC}={\frac{1}{L}}\left( \sum \limits _{k=1}^{L}\sqrt{\gamma _{k}}\right) ^2 \end{aligned}$$

where L is the diversity order and $\gamma _{k}$ is the instantaneous SNR of kth branch. Sum of lognormal random variable(RV) may be approximated by another lognormal RV, hence mean and standard deviation for MRC and EGC are given by Laourine et al. [3, Section III]

$$\begin{aligned} \mu _{MRC} &= {} \xi \ln (L\Gamma )-\frac{\sigma _{MRC}^2}{2\xi },\quad \sigma ^2_{MRC}=\xi ^2\ln \Bigg (\frac{L-1+e^{\frac{\sigma ^2}{\xi ^2}}}{L}\Bigg )\\ \mu _{EGC} &= {} \xi \ln \Bigg (\Gamma +\Gamma (L-1)e^{-\frac{\sigma ^2}{4\xi ^2}}\Bigg )-\frac{\sigma _{EGC}^2}{2\xi },\quad \sigma ^2_{EGC}=4\xi ^2\ln \Bigg (\frac{L-1+e^{\frac{\sigma ^2}{4\xi ^2}}}{L}\Bigg ) \end{aligned}$$

where $\xi =10/\ln 10$, each branch has average SNR $\Gamma$, mean $\mu$ and standard deviation $\sigma$.

2.2 Selection Combining

For independent and identically distributed (i.i.d.) channel scenario, the cumulative distribution function (CDF) of SC output is given by

$$\begin{aligned} F_{sc}(\gamma )=(F(\gamma ))^{L} \end{aligned}$$

(1)

where $F(\gamma )$ is CDF of individual branch output SNR, is given as $Q[(\mu -\ln \gamma )/\sigma ]$ and L is the diversity order. This can be further simplified using [4, Eq. (2) and Table II] as

$$\begin{array}{ll} F_{sc}(\gamma )\approx {\left\{ \begin{array}{ll} \sum \limits _{r=0}^{L}\sum \limits _{r_1=0}^{r}\Bigg [{L\atopwithdelims ()r}(-1)^r{r\atopwithdelims ()r_1}\bigg (\dfrac{a_1}{2}\bigg )^{r-r_1}\bigg (\dfrac{a_2}{2}\bigg )^{r_1}\\ \times exp\Bigg (-\left( \sqrt{b(r+r_1)}\frac{(\ln \gamma -\mu )}{\sqrt{2}\sigma }\right) ^2\Bigg )\Bigg ]&{} \quad \text {if } \quad\gamma \ge e^\mu \\ \sum \limits _{r=0}^{L}{L\atopwithdelims ()r}\bigg (\dfrac{a_1}{2}\bigg )^{L-r}\bigg (\dfrac{a_2}{2}\bigg )^{r} exp\Bigg (-\left( \sqrt{b(L+r)}\frac{(\ln \gamma -\mu )}{\sqrt{2}\sigma }\right) ^2\Bigg ) &{} \quad \text {if } \quad\gamma < e^\mu \end{array}\right. } \end{array}$$

(2)

Probability distribution function (PDF) of SC is obtained by differentiating (2) with respect to $\gamma$ yields

$$\begin{aligned} f_{sc}(\gamma )\approx {\left\{ \begin{array}{ll} \dfrac{L}{\sigma \gamma \sqrt{2\pi }}\sum \limits _{r=0}^{L-1}\sum \limits _{r_1=0}^{r}A_1 \exp\left[-\bigg (\dfrac{\ln \gamma -\mu }{\sigma \sqrt{2p}}\bigg )^2\right] &{}\quad \text {if } \quad \gamma \ge e^\mu \\ \dfrac{L}{\sigma \gamma \sqrt{2\pi }}\sum \limits _{r=0}^{L-1}A_2 exp[-\bigg (\dfrac{\ln \gamma -\mu }{\sigma \sqrt{2p_1}}\bigg )^2] &{}\quad \text {if } \quad \gamma < e^\mu \end{array}\right. } \end{aligned}$$

(3)

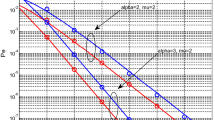
where $A_1={L-1\atopwithdelims ()r}(-1)^r{r\atopwithdelims ()r_1}\bigg (\dfrac{a_1}{2}\bigg )^{r-r_1}\bigg (\dfrac{a_2}{2}\bigg )^{r_1}$, $A_2={L-1\atopwithdelims ()r}\bigg (\dfrac{a_1}{2}\bigg )^{L-1-r}\bigg (\dfrac{a_2}{2}\bigg )^{r}$, $p=(b(r+r_1)+1)^{-1}$ and $p_1=(b(L+r-1)+1)^{-1}$. In Fig. 1, outage probability analysis is presented for different diversity schemes with shadowing 4 dB and diversity order, L = 2, 10.

Fig. 1

Comparison of outage probability of signal in lognormal channel using different diversity schemes

2.3 Channel Capacity

In this section, we analyse the channel capacity with various definitions such as OPRA, ORA, CIFR and truncated CIFR and we consider the following possibilities: (1) channel state information (CSI) is known only to the receiver (Rx) (2) it is known to both the transmitter (Tx) and the Rx.

2.3.1 Optimum Power and Rate Adaptation

In this scheme, knowing the CSI, the Tx can adapt its power and transmission rate such that to maximize the capacity. The policy is to allocate the higher power to more deterministic channel and lesser power to the channel having low average SNR, based on water-filling algorithm. The capacity under this category is defined as [5]

$$\begin{aligned} \dfrac{C_{OPRA}}{B}= \int \limits _{\gamma _0}^{\infty }\log _2\bigg (\frac{\gamma }{\gamma _0}\bigg )f_D(\gamma )d\gamma \end{aligned}$$

(4)

where B is bandwidth in Hz, $f_D(\gamma )$ is lognormal PDF and subscript D is used to define EGC, MRC and SC diversity techniques. The PDF of EGC and MRC combiner output SNR, is given as

$$\begin{aligned} f_{EGC, MRC}(\gamma )=\frac{1}{\gamma \sigma _d \sqrt{(}2\pi )} exp\bigg [-\bigg (\frac{\ln \gamma -\mu _d}{ \sqrt{2} \sigma _d}\bigg )^2\bigg ] \end{aligned}$$

(5)

where $\mu _d$ and $\sigma _d$ are parameters of EGC and MRC defined in Sect. 2.1, as $\mu _{EGC}$, $\mu _{MRC}$, $\sigma _{EGC}$ and $\sigma _{MRC}$. The expected value $E[\gamma ]$, is $\gamma _{Avg}=exp(\mu _d+\sigma _{d}^2/2)$ and the variance is var$(\gamma ) = [ exp (\sigma _{d}^2)-1 ] exp(2\mu _{d}+\sigma _{d}^2)$. We can express the mean in terms of $\gamma _{Avg}$ and shadowing parameter, as $\mu _d=[\ln \gamma _{Avg}-0.5\sigma _{d}^2]$. Optimal cutoff SNR $\gamma _o$ must satisfy the equation $p(\gamma _o)=0$, with p(.) is defined as

$$\begin{aligned} p(x)=\int \limits _{\gamma _o}^{\infty } \Bigg (\frac{1}{x}-\frac{1}{\gamma }\Bigg )f_D(\gamma )d\gamma -1 \end{aligned}$$

(6)

The integral in Eq. (4) can be split in two parts and is written as

$$\begin{aligned} \frac{C_{OPRA}}{B}=1/\ln 2\int \limits _{\gamma _o}^{\infty }\ln (\gamma ) f_D(\gamma ) d\gamma -\ln (\gamma _o)/\ln 2\int \limits _{\gamma _o}^{\infty } f_D(\gamma ) d\gamma \end{aligned}$$

(7)

In case of maximal ratio and equal gain diversity, the second integral of Eq. (7) is easily computed using outage probability of EGC and MRC combiner output SNR with lognormal distribution as $P_{out}(\gamma _{0})=1-Q(\frac{\ln \gamma _{0}-\mu _d}{\sigma _d})$. Substituting Eq. (5) in the first integral of Eq. (7), making a change of variable $t=\frac{\ln \gamma -\mu _d}{\sigma _d}$, we obtain the closed-form of the capacity, given as

$$\begin{aligned} \frac{C_{OPRA}}{B}=\dfrac{1}{\ln 2}\left[ \dfrac{\sigma _d exp(-\phi ^2/2)}{\sqrt{2\pi }}+(\mu _d-\ln \gamma _o)Q(\phi )\right] \end{aligned}$$

(8)

Equation (6) can be simplified using Eq. (5) as $p(x)= \frac{Q(\phi )}{x}-kQ(\sigma +\phi )-1$, where $k=exp(-\mu _d+(\sigma _d^2/2))$, $\varphi =(\ln x -\mu _d)/\sigma _d$ and $\phi =(\ln \gamma _0-\mu _d)/\sigma _d$. Equation (8) can further be simplified using an approximation of erfc(x) in [6, Eq. 6] and is given as

$$\begin{array}{ll} \frac{C_{OPRA}}{B}= {\left\{ \begin{array}{ll} \sigma _d \exp (-0.5\phi ^2)(\alpha +\beta \exp (-1.4\phi )) &{}\quad \text {if }\quad \phi >0 \\ 0.5745\sigma _d &{}\quad \text {if }\quad \phi =0 \\ \sigma _d [\exp (-0.5\phi ^2)(\alpha +\beta \exp (1.4\phi ))-c\phi ]&{}\quad \text {if }\quad \phi <0 \end{array}\right. } \end{array}$$

(9)

where $\alpha =0.0685$, $\beta =0.5071$, and c $=$ 1.44.

In order to evaluate OPRA channel capacity for SC, one can substitute Eq. (3) in Eq. (4) and after some mathematical manipulations, the approximate form is given as

$$\begin{aligned} \frac{C_{OPRA}}{B}\approx \frac{L}{\ln {2}} {\left\{ \begin{array}{ll} \sum \limits _{r=0}^{L-1}\Bigg [\Bigg (\sum \limits _{r_1=0}^{r}\frac{A_1}{2}\sqrt{p}\left( \frac{\sigma \sqrt{2p}}{\sqrt{\pi }}+\mu -\ln \gamma _0\right) \Bigg )\\ +\frac{A_2}{2}\sqrt{p_1}\left( \frac{\sigma \sqrt{2p_1}}{\sqrt{\pi }}\left( \exp (-t_2^2)-1\right) \right. \\ \left. -(\mu -\ln \gamma _0)erf(t_2)\right) \Bigg ] &{}\quad \text {if }\quad \gamma _0 \le e^\mu \\ \sum \limits _{r=0}^{L-1}\sum \limits _{r=0}^{r_1}\left[ \frac{A_1}{2}\sqrt{p}\left( \left( \frac{\sigma \sqrt{2p}}{\sqrt{pi}}\exp (-t_1^2)\right) \right. \right. \\ \left. \left. +(\mu -\ln \gamma _0)erfc(t_1)\right) \right] &{}\quad \text {if } \quad \gamma _0 > e^\mu \end{array}\right. } \end{aligned}$$

(10)

where $t_1=(\ln \gamma _0-\mu )/(\sigma \sqrt{2p})$ and $t_2=(\ln \gamma _0-\mu )/(\sigma \sqrt{2p_1})$. For SC diversity, Eq. (6) becomes

$$\begin{aligned} p(x)\approx {\left\{ \begin{array}{ll} \sum \limits _{r=0}^{L-1}\Bigg [\Bigg (\sum \limits _{r_1=0}^{r}\frac{A_1}{2}\sqrt{p}\left( \frac{1}{x}-\exp \left( -\mu +\frac{\sigma ^{2}p}{2}\right) erfc\left( \sigma \sqrt{\frac{p}{2}}\right) \right) \Bigg )\\ +\frac{A_2}{2}\sqrt{p_1}\left( -\frac{1}{x}-\exp \left( -\mu +\frac{\sigma ^{2}p_1}{2}\right) \left( erfc(z_2)-erfc\left( \sigma \sqrt{\frac{p_1}{2}}\right) \right) \right) \Bigg ] &{}\quad \text {if } \quad x \le e^\mu \\ \sum \limits _{r=0}^{L-1}\sum \limits _{r=0}^{r_1}\frac{A_1}{2}\sqrt{p}\left( \left( \frac{erf(s_1)}{x}\right) -\exp \left( -\mu +\frac{\sigma ^{2}p}{2}\right) erfc(z_1)\right) &{}\quad \text {if }\quad x > e^\mu \end{array}\right. } \end{aligned}$$

where $s_1=(\ln x-\mu )/(\sigma \sqrt{2p})$, $s_2=(\ln x-\mu )/(\sigma \sqrt{2p_1})$, $z_1=s_1+\sigma \sqrt{p/2}$ and $z_2=s_2+\sigma \sqrt{p_1/2}$.

2.4 Optimal Rate Adaptation

In this approach the CSI is known only to the Rx. Thus, the Tx does not have any policy to adapt the allocation of its power. The definition of average channel capacity is given by [5]

$$\begin{aligned} \dfrac{C_{ORA}}{B}=\int \limits _{0}^{\infty }\log _2(1+\gamma )f_D(\gamma )d\gamma \end{aligned}$$

(11)

Substitution of Eq. (5) in Eq. (11) and resorting to Gauss Hermite (G–H) [7], the closed-form for MRC and EGC schemes can be expressed as

$$\begin{aligned} \dfrac{C_{ORA}}{B}\approx \frac{1}{\sqrt{\pi }}\sum \limits _{i=0}^{N}\omega _i \log _2(1+\eta _i) \end{aligned}$$

(12)

where $\eta _i=exp(\sigma _d \nu _i\sqrt{2}+\mu _d)$, $\omega$ and $\nu$ are weights and abscissas of G–H integration [7, 8]. It may be noted that N terms series of Eq. (12) can be truncated to just five terms to closely match the exact results with mean square error $({\approx } 10^{-4})$ (see Fig. 3). The integral in Eq. (11), can also be solved using an efficient approach given by Holtzman [9], [10, Eq. (18)] that gives the closed-form in terms of just three terms as follows.

2.4.1 Simpler and Accurate Approximations

If z is Gaussian-distributed RV with mean $\mu$ and variance $\sigma ^2$, then, we can have the following approximation [9]

$$\begin{aligned} \begin{aligned} E[f(z)]=\int \limits _{-\infty }^{\infty } \frac{f(z)}{\sigma \sqrt{2\pi }}exp\Bigg [-\bigg (\dfrac{z-\mu }{\sqrt{2}\sigma }\bigg )^2\Bigg ],\\ E[f(z)]\approx \frac{2}{3}f(\mu )+\frac{1}{6}f(\mu +\sigma \sqrt{3})+\frac{1}{6}f(\mu -\sigma \sqrt{3}) \end{aligned} \end{aligned}$$

(13)

Substituting Eq. (5) in Eq. (11), making a change of variable $\ln (\gamma )=z$ and using Eq. (13), we can write

$$\begin{aligned} \dfrac{C_{ORA}}{B}\approx \frac{2}{3}\log _2\left( 1+e^{\mu _d}\right) +\frac{1}{6}\log _2\left( 1+e^{\mu _d+\sigma _d\sqrt{3}}\right) +\frac{1}{6}\log _2\left( 1+e^{\mu _d-\sigma _d\sqrt{3}}\right) \end{aligned}$$

(14)

Noting that, at higher average SNR of the channel, $\mu _d$ is high. As a result, $e^{\mu _d} \gg 1$ and we can write

$$\begin{aligned} \dfrac{C_{ORA}}{B}\approx \frac{2}{3}\mu _d+\frac{1}{6}\left( \mu _d+\sigma _d\sqrt{3}\right) +\frac{1}{6}\left( \mu _d-\sigma _d\sqrt{3}\right) =\mu _d=\left[ \ln \gamma _{Avg}-0.5\sigma _{d}^2\right] \end{aligned}$$

(15)

This result clearly indicates that the average channel capacity is proportional to the channel SNR on logarithmic basis and the capacity deteriorates with increase in the shadowing which is an obvious impact of shadowing on channel capacity. This is in the tune with the results in [3, Eq.12].

ORA channel capacity with SC diversity is found out by putting Eq. (3) in Eq. (11) and applying Gaussian Quadratures for integral [11], the closed-form yields

$$\begin{aligned} \dfrac{C_{ORA}}{B}\approx \frac{1}{\sqrt{\pi }}\sum \limits _{i=0}^{K}\Omega _i\sum \limits _{r=0}^{L-1}\left[ \left( \sum \limits _{r_1=0}^{r}A_1\sqrt{p}\log _2(1+\Delta _i)\right) +A_2\sqrt{p_1}\log _2(1+\tau _i)\right] \end{aligned}$$

(16)

where $\Delta _i=\exp (\sigma \delta _i\sqrt{2p}+\mu ), \tau _i=\exp (-\sigma \delta _i\sqrt{2p_1}+\mu )$, $\Omega$ and $\delta$ are weights and abscissas of Gaussian Quadratures for integration for 0 to $\infty$ [11]. It may be noted that K terms series of Eq. (8) can be truncated to just five terms to match with the exact results with accuracy of $({\approx } 10^{-3})$ (see Fig. 7).

2.5 CIFR

Channel inversion with fixed rate is based on the fact that the Tx allocates the power inversely proportional to the channel SNR such that the transmission rate remains constant. The formula for this adaptive scheme is given by [5]

$$\begin{aligned} \dfrac{C_{CIFR}}{B}=\log _2\Bigg (1+\frac{1}{E[1/\gamma ]}\Bigg ) \end{aligned}$$

(17)

For MRC and EGC diversity schemes, considering only the term $E[1/\gamma ]$ of Eq. (17), using Eq. (5) and applying G–H integration, we get

$$\begin{aligned} E[1/\gamma ]=\int \limits _{0}^{\infty }\frac{f_D(\gamma )}{\gamma }d\gamma \approx \dfrac{e^{-\mu _d}}{\sqrt{\pi }}\sum \limits _{i=1}^{N}\omega _ie^{-\sigma \nu _i\sqrt{2}} \end{aligned}$$

(18)

where $\omega$ and $\nu$ are weights and abscissas of G–H integration. After substituting Eq. (18) in Eq. (17), we obtained

$$\begin{aligned} \dfrac{C_{CIFR}}{B}\approx \log _2\left( 1+\frac{\sqrt{\pi }e^{\mu _d}}{\sum \nolimits _{i=1}^{N}\omega _ie^{-\sigma _d \nu _i\sqrt{2}}}\right) \end{aligned}$$

(19)

Further using [9] we can approximate $E[\frac{1}{\gamma }]$ as

$$\begin{aligned} E[1/\gamma ]\approx \frac{2}{3}e^{-\mu _d}+\frac{1}{6}e^{-(\mu _d+{\sigma _d \sqrt{3}})}+\frac{1}{6}e^{-(\mu _d-{\sigma _d \sqrt{3}})} \end{aligned}$$

(20)

Further simplifying Eq. (20), we get

$$\begin{aligned} E[1/\gamma ]\approx \frac{1}{6}e^{-(\mu _d+\sigma _d\sqrt{3})}(e^{\sigma _d \sqrt{3}}+3.732)(e^{\sigma _d \sqrt{3}}+0.268) \end{aligned}$$

(21)

Substituting Eq. (21) in Eq. (17), we get,

$$\begin{aligned} \dfrac{C_{CIFR}}{B}\approx \log _2\Bigg (1+\frac{6e^{(\mu _d+\sigma _d\sqrt{3})}}{(e^{\sigma _d \sqrt{3}}+3.732)(e^{\sigma _d \sqrt{3}}+0.268)}\Bigg ) \end{aligned}$$

(22)

For higher values of shadowing $\sigma _d$ (5–12 dB), $\exp (\sigma _d\sqrt{3})\gg0.268$, so the denominator part of Eq. (22) can further be simplified by neglecting 0.268. Finally, we get a simple expression which is valid for shadowing in the range of 5–12 dB having wireless applications and the closed-form is given as

$$\begin{aligned} \dfrac{C_{CIFR}}{B}\approx \log _2\Bigg (1+\frac{6e^{\mu _d}}{(e^{\sigma _d\sqrt{3}}+3.732)}\Bigg ) \end{aligned}$$

(23)

Further, we note that for higher values of $\sigma _d$ (9–12 dB), $e^{\sigma _d\sqrt{3}}\gg 3.732$ (Fig. 1). This further simplifies the expression Eq. (23), as

$$\begin{aligned} \dfrac{C_{CIFR}}{B}\approx \log _2(1+6e^{\mu _d-\sigma _d\sqrt{3}}) \end{aligned}$$

(24)

The expressions in Eqs. (22)–(24) have the great advantage as they are very simple and are in closed-form. They clearly explain the behaviour of the system with respect to LN parameters.

Figure 2 depicts the plots of channel capacity versus shadowing for several values of average SNR under CIFR policy. It is noted that the approximated expression Eq. (19) has an excellent agreement with exact expression Eq. (17) for all range of average SNR and shadowing parameter. This result also indicates that either on increasing average SNR or decreasing shadowing parameter CIFR channel capacity is increasing. The plot includes the upper bounds developed in Eqs. (23) and (24). Equations (23) and (24) show the tight bound, and loose bound respectively, at lower shadowing range whereas at higher shadowing they behave as a tight upper bound to CIFR capacity.

Fig. 2

Channel capacity under CIFR for different values of average SNR with diversity branch, L $=$ 1

Moreover, using Eq. (3) we can derive approximate form of $E\left[1/\gamma \right]$ of Eq. (18) for SC, as

$$\begin{aligned} E\left[\frac{1}{\gamma }\right]\approx L\sum \limits _{r=0}^{L-1}\left[ \sum \limits _{r_1=0}^{r}\bigg ( A_1\sqrt{p}\exp (T_1)Q(\sigma \sqrt{p})\bigg )+A_2\sqrt{p_1}\exp (T_2)(Q(-\sigma \sqrt{p_1}))\right] \end{aligned}$$

(25)

where $T_1=0.5\sigma ^{2}p-\mu$ and $T_2=0.5\sigma ^{2}p_1-\mu .$ Substituting Eq. (25) in Eq. (17) completes the closed-form of CIFR channel capacity.

2.6 TIFR

This policy is adopted to avoid the certain aspect of earlier discussed CIFR strategy where even the poorest channel is also taken into consideration and maximum power is allocated to maintain a constant transmission rate. Here, this condition is avoided which naturally improves the capacity. Channel capacity under this scheme is defined by [5]

$$\begin{aligned} \dfrac{C_{out}}{B}=\log _2\left( 1+\frac{1}{\int \nolimits _{\gamma _o}^{\infty }\frac{1}{\gamma }f_D(\gamma ) d\gamma }\right) [1-F_{D}(\gamma _o)] \end{aligned}$$

(26)

Substituting Eq. (5) in Eq. (26) and considering only the integral part of Eq. (26) and after some manipulations, we obtain

$$\begin{aligned} {\int \limits _{\gamma _o}^{\infty }\frac{1}{\gamma }f_d(\gamma ) d\gamma }=kQ(\sigma _d+\tau )=\frac{k}{2}erfc\bigg (\frac{\sigma _d+\tau }{2}\bigg ) \end{aligned}$$

(27)

where, $k= e^{-\mu _d+\sigma _d^2/2}$, $\tau =(\ln \gamma _o-\mu _d)/\sigma _d$. Substituting Eq. (27) in Eq. (26), we finally get the closed-form of capacity under truncated CIFR for EGC and MRC, as

$$\begin{aligned} \dfrac{C_{out}}{B}=\log _2\Bigg (1+\frac{e^{\mu _d-\sigma _d^2/2}}{Q(\sigma _d+\tau )}\Bigg )Q(\tau ) \end{aligned}$$

(28)

Assuming higher average SNR (i.e. $\gamma _{Avg}\gg 20\,\mathrm{dB}$), $\frac{exp(\mu _d-\sigma _d^2/2)}{Q(\sigma _d+\tau )}\gg 1$ for all range of $\sigma _d$, Eq. (28) becomes

$$\begin{aligned} \dfrac{C_{out}}{B}\approx 1.44 Q(\tau )\left[ \mu _d-\frac{\sigma _d^2}{2}-\ln (Q(\sigma _d+\tau ))\right] \end{aligned}$$

(29)

$$\begin{aligned} C_{TIFR} = max_{\gamma _0} C_{out} \end{aligned}$$

Intergral part of Eq. (26) is obtained by using Eq. (3) for SC diversity scheme, as

$$\begin{aligned} \int \limits _{\gamma _0}^{\infty }\frac{f(\gamma )}{\gamma }d\gamma \approx {\left\{ \begin{array}{ll} \sum \limits _{r=0}^{L-1}\Bigg [\Bigg (\sum \limits _{r_1=0}^{r}\frac{A_1}{2}\sqrt{p}\left( \exp \left( -\mu +\frac{\sigma ^{2}p}{2}\right) erfc\left( \sigma \sqrt{\frac{p}{2}}\right) \right) \Bigg )\\ +\frac{A_2}{2}\sqrt{p_1}\left( \exp \left( -\mu +\frac{\sigma ^{2}p_1}{2}\right) \left( erfc(v_2)-erfc\left( \sigma \sqrt{\frac{p_1}{2}}\right) \right) \right) \Bigg ] &{}\quad \text {if } \quad \gamma _0 \le e^\mu \\ \sum \limits _{r=0}^{L-1}\sum \limits _{r=0}^{r_1}\frac{A_1}{2}\sqrt{p}\left( \exp \left( -\mu +\frac{\sigma ^{2}p}{2}\right) erfc(v_1)\right) &{}\quad \text {if } \quad \gamma _0 > e^\mu \end{array}\right. } \end{aligned}$$

(30)

where $v_1=t_1+\sigma \sqrt{p/2}$, and $v_2=t_2+\sigma \sqrt{p_1/2}$. Substituting Eqs. (30) and (2) in Eq. (26) results in closed-form of $c_{out}$ and after maximizing it, we get capacity under truncated CIFR.

Figure 3 depicts the channel capacity under OPRA, ORA and TIFR schemes with respect to shadowing parameter in the range of 2–12 dB. The results include exact plot, closed-forms and approximated closed-form. It is observed that the capacity decreases with the increase in the shadowing indicating deleterious effect of shadowing and the plot is getting shifted upward by increasing the average SNR of the channel which is as expected. The closed-form expression using OPRA scheme Eq. (8) and simplified form Eq. (9) have an excellent agreement with the exact plot for all values of shadowing parameters and average SNR. The closed-form expression using ORA scheme Eq. (12) with N equals to five terms has an excellent agreement with the exact plot. The simplified form Eq. (15) also is noted to have an excellent agreement with exact plot for higher values of average SNR. The closed-form expression using TIFR scheme Eq. (28) and simplified form of Eq. (28) using [6, Eq.6] have an excellent agreement with the exact plot. It is observed that the simplified form Eq. (29) has a slight deviation from the exact result at lower SNR and lower values of shadowing parameter but has an excellent agreement for higher values of average SNR.

Fig. 3

Channel capacity using OPRA, ORA and TIFR policy with diversity branch, L $=$ 1

3 Numerical Result

This section present the different performance evaluation results explaining the behaviour of slow fading channel under various channel conditions.

Figures 4, 5 and 6 plot, respectively, the capacity under ORA, TIFR, and CIFR adaptive schemes with SC, EGC, MRC diversity techniques. Figure 7 shows comparative analysis of all the four definitions of channel capacity with respect to average SNR for shadowing parameter 6 dB and SC diversity branches ${\mathrm{L}}=1,10$. As expected, on increasing average SNR and diversity order, the capacity increases. It is interesting to observe that the TIFR has higher throughput than CIFR and both seems to be converge at higher average SNR. This convergence happens quiet early rather than large average SNR for higher diversity order. In CIFR policy, large capacity loss is observed with and without diversity. On increasing the diversity branches, all the four capacity plots show improvement whereas quite significant improvement is observed in CIFR as compared to others.

Fig. 4

Comparison of diversity techniques over ORA scheme

Fig. 5

Comparison of diversity techniques over CIFR scheme

Fig. 6

Comparison of diversity techniques over TIFR scheme

Fig. 7

Comparison of various average channel capacity with selection diversity for ($\sigma =6$ dB, L $=$ 1, 10)

4 Application

This section deals with the application of evaluating the transmission rate under different adaptive schemes in the presence of lognormal distributed co-channel interference which arise in the cellular system due to frequency reuse scheme. The received Signal to Interference Ratio (SIR) will be as

$$\begin{aligned} \gamma _{SIR}=\frac{\gamma _r}{\sum \nolimits _{i=1}^{M_I}\gamma _i} \end{aligned}$$

(31)

where $\gamma _r$ is the received power from the desired base station, $\gamma _i$ is the received power from the ith co-channel interferer and $M_I$ represents the number of interferers. Here all the interferers are considered to be i.i.d. lognormal RVs and according to [3, 12] sum of $M_I$ lognormal distributed RV are approximated by another lognormal RV. Hence $\gamma _{SIR}$ is a lognormal RV and by applying Eq. (31) on Eqs. (1, 7, 12, 20), we can evaluate transmission rate under different adaptive schemes as shown in Fig. 8. It is evident from the figure that increase in number of interferers have adverse effect on channel capacity.

Fig. 8

Comparison of various average channel capacity with number of interferers having shadowing parameter of signal and interferer ($\sigma _{S}=2$ dB, and $\sigma _{I}=5$ dB) respectively

5 Conclusion

In this work, we have presented accurate closed-form expressions of channel capacity under various adaptive schemes with diversity schemes. The results, thus obtained, are approximated to simple forms under various SNR and shadowing conditions, thus, enabling them to be used directly in several wireless applications. The derived results have the great advantage in terms of easy implementation and have the capability to interpret the system behaviours in lognormal fading conditions.