Statistical Characterization and Performance Evaluation of $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma Channels

Abstract

In this paper, two new shadowed fading distributions $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma are proposed to model wireless communication channel. Probability density functions (pdf), tth-moments and moment generating functions (MGF) of the instantaneous SNR for these channels have also been determined. Obtained statistics are applied to ascertain Amount of Fading (AoF), channel capacity per unit bandwidth and Average Symbol Error Rate (ASER). To judge the performance of multi-hop communication, Source to Sink Average Bit Error Rate (S2S-ABER) have been determined where independent and identical distributed and independent and non-identical distributed multi-hop links have been considered. The performance of these matrices are studied under various channel parameters and Monte Carlo simulations have been performed to validate the analytical expressions. Moreover, performance of multi-hop IEEE 802.15.4 Zigbee and IEEE 802.15.1 Bluetooth radios have also been analyzed over these channels.

1 Introduction

Recent developments in wireless technologies has created various applications such as Machine-to-Machine communication, vehicular communication, IoT applications, Ad-hoc and Sensor Networks, etc., which require thorough study of communication channel to fulfill stringent requirements. Information propagates through these unpredictable communication channels where it may suffer fading, shadowing or combination of both. Numerous channel distributions have been proposed in literature to judge the behavior of the combined effect of both fading and shadowing. These channel distributions are known as shadowed fading channel distributions. Nakagami-Lognormal [25] is most commonly used shadowed fading channel distribution. K-distribution [1], G-distribution [12] and Nakagami-N-Gamma [18] are few other composite channel distributions which have been proposed in literature. Moreover, researchers are also focusing on dual shadowing of generalized fading models [2, 19]. But, due to ever increasing constraints on wireless channels, there is dire need to explore more such channels and analyze the performance of wireless communication systems over these channels so that wireless systems perform as per design. In recent years, a family of distributions based on $\alpha -\mu$, $\eta -\mu$ and $\kappa -\mu$ fading and their variants such as $\kappa -\mu$/gamma [21], $\kappa -\mu$ shadowed fading [15] and their variants [3,4,5, 7, 13, 22, 23, 28] have been proposed. Besides these some channel models that considered effect of nonlinearities in fading have also been reported in literature such as $\alpha -\eta -\mu /gamma$ [24] and $\alpha -\kappa -\mu /gamma$ [20] channels.

Recently two new composite distributions i.e., $\eta -\mu$/Inverse Gamma and $\kappa -\mu$/Inverse Gamma have also been proposed [26, 27, 29]. These channels assumes $\eta -\mu$ or $\kappa -\mu$ fading along with inverse gamma shadowing, which is a good alternative for log-normal and gamma shadowing distributions [17, 30]. The suitability of these models have also be empirically validated through field measurements in wearable, vehicular as well as cellular networks [29]. But these channel models have not considered the effect of nonlinearities in fading which may be an important factor for recently developed and future communication environments. In this paper, more generalized forms of $\eta -\mu$/Inverse Gamma and $\kappa -\mu$/Inverse Gamma distributions are proposed which consider the effect of nonlinear fading. These distributions are $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma distributions. $\eta -\mu$/Inverse Gamma and $\kappa -\mu$/Inverse Gamma distributions can be considered as a special cases of these proposed distributions with $\alpha =2$. Expressions of pdfs, tth-moments and MGFs of the proposed distributions have been determined in this paper which signifies the error probability calculations prior to physical deployment of communication system. The performance of wireless communication systems over these proposed channels have also been analyzed. For multi-hop wireless communication systems, expressions for S2S-ABER have been derived for two cases i.e., 1. links with independent and identical distribution (iid) and, 2. links with independent and nonidentical distributions (inid)

[14]. Additionally to judge the performance of Wireless Sensor Networks (WSN)s, performance of multi-hop IEEE 802.15.4 Zigbee and IEEE 802.15.1 Bluetooth radios have also been analyzed over these channels. Monte Carlo simulation have also been performed to validate the obtained expressions.

Rest of the paper is organized as: in Sect. 2, expressions for the pdf of instantaneous SNR, tth-moment and MGF for $\alpha -\eta -\mu$/Inverse Gamma shadowed fading channel are determined. In Sect. 3, stated statistics are determined for $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channel. In Sect. 4, expressions for AoF, Channel Capacity per unit bandwidth and ASER are determined. Results and discussions are presented in Sect. 5. Section 6 concludes the paper.

2 The $\alpha -\eta -\mu$/Inverse Gamma Shadowed Fading Channel

If r be the received signal envelope which follows $\alpha -\kappa -\mu$ fading, then conditional probability density¹ of random variable $p=r^{\alpha }$, where $\alpha$ is non-linearity parameter, with shadowing power $\tau$ can be obtained as [8]:

$$\begin{aligned} f_{P_{\alpha -\eta -\mu }|\tau }(p,\tau )= \,& \frac{2\sqrt{\pi }\mu ^{\mu +\frac{1}{2}}h^\mu }{\tau \overline{p}\Gamma (\mu )H^{\mu -\frac{1}{2}}}\left( \frac{p}{\tau \overline{p}}\right) ^{\mu -\frac{1}{2}}\nonumber \\&\times \,e^{-\frac{2\mu hp}{\tau \overline{p}}}I_{\mu -\frac{1}{2}}\left( \frac{2\mu Hp}{\tau \overline{p}}\right) \end{aligned}$$

(1)

where $\mu$, h and H are the parameters of $\eta -\mu$ distribution and $\overline{p}=E[r^{\alpha }]$. h and H depend on the value of $\eta$ and can be defined either for format 1 or for format 2 [8]. We have followed format 1 for which h and H are defined as

$$\begin{aligned} h=\frac{(1+\eta )^2}{4\eta }\quad \text {and}\quad H=\frac{1-\eta ^2}{4\eta } \end{aligned}$$

(2)

respectively. $I_{\nu }(\cdot )$ is modified Bessel function of first kind and $\Gamma (\cdot )$ is Euler gamma function [16].

If $\gamma$ and ${\overline{\gamma }}$ be instantaneous and mean Signal to Noise Ratios (SNR)s, then pdf of $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channel can be obtained by transforming above pdf to conditional instantaneous SNR pdf through definition $\gamma ={\overline{\gamma }}\left( \frac{p}{\overline{p}}\right) ^{2/\alpha }$ and averaging it with inverse gamma distribution. This can be written as

$$\begin{aligned} f_{\gamma _{\alpha -\eta -\mu /\text {Inverse Gamma}}}(\gamma )= \,& \int _{0}^{\infty } \frac{\alpha \sqrt{\pi }\mu ^{\mu +\frac{1}{2}}h^\mu \beta ^{c}}{\tau ^{\mu +c+\frac{3}{2}}{\overline{\gamma }}\Gamma (\mu )\Gamma (c)H^{\mu -\frac{1}{2}}}\nonumber \\&\times \,\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\frac{\alpha }{2}\left( \mu +\frac{1}{2}\right) -1}e^{-\left( \frac{2\mu h}{\tau }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}+\frac{\beta }{\tau }\right) }\nonumber \\&\times \,I_{\mu -\frac{1}{2}}\left( \frac{2\mu H}{\tau }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}\right) ~ d\tau \end{aligned}$$

(3)

where $\gamma$ and ${\overline{\gamma }}$ are the instantaneous and average Signal to Noise Ratio, c and $\beta$ are the respective shape and scale parameters of inverse gamma distribution. $\beta =c-1$, as mean of inverse gamma variable has been set equal to 1.

The following lemmas give expressions of pdf, tth-moment and MGF for $\alpha -\eta -\mu$/Inverse Gamma shadowed fading Channel. Pdf can be obtained by solving the above integration whereas, tth-moment and MGF can be obtained by their respective definitions, i.e., expected values of $\gamma ^t$ and $e^{s\gamma }$ respectively.

Lemma 1

If $\gamma$ and ${\overline{\gamma }}$ are the instantaneous and average Signal to Noise Ratio, then pdf of instantaneous SNR for $\alpha -\eta -\mu$/Inverse Gamma distribution can be given as

$$\begin{aligned} f_{\gamma _{\alpha -\eta -\mu /\text {Inverse Gamma}}}(\gamma )=\, & K_a\sum _{i=0}^{N} \frac{w_i\alpha \sqrt{\pi }\mu ^{\mu +\frac{1}{2}}h^\mu x_i^{\mu +c-\frac{1}{2}}}{\beta ^{\mu +\frac{1}{2}}{\overline{\gamma }}\Gamma (\mu )\Gamma (c)H^{\mu -\frac{1}{2}}}\nonumber \\&\times \,\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\frac{\alpha }{2}\left( \mu +\frac{1}{2}\right) -1}e^{-\frac{2\mu hx_i}{\beta }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}}\nonumber \\&\times \,I_{\mu -\frac{1}{2}}\left( \frac{2 \mu Hx_i}{\beta } \left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}\right) \end{aligned}$$

(4)

where, $\alpha$, h, H and $\mu$are the parameters of $\alpha -\eta -\mu$ fading channel, c is shadowing parameter and $\beta =c-1$, $w_i$’s and $x_i$’s are weights and nodes for Gauss–Laguerre integral approximation and N is number of terms. $K_a$ is normalization constant given by

$$\begin{aligned} K_a=\, & \left[ \frac{\sqrt{\pi }}{2^{\mu -\frac{1}{2}}\Gamma (\mu )\Gamma (c)\sqrt{h}H^{\mu -\frac{1}{2}}}\sum _{i=0}^{N}w_ix_i^{c-1}\right. \nonumber \\&\left. \times \,\sum _{j=0}^{M}w_jy_j^{\mu -\frac{1}{2}} I_{\mu -\frac{1}{2}}\left( \frac{Hy_j}{h} \right) \right] ^{-1} \end{aligned}$$

(5)

Proof

Substituting $x=\beta /\tau$ in Eq. (3) and using Gauss–Laguerre integral approximation the required result in Eq. (4) is obtained. $K_a$ is normalization constant to ensure $\int _{0}^{\infty }f_{\gamma }(x)dx=1$, which is equal to zeroth moment of the distribution and can be obtained by substituting $t=0$ in Eq. (6) and given as Eq. (5).$\square$

Lemma 2

The tth-moment of $\alpha -\eta -\mu$/Inverse Gamma Shadowed Fading Channel can be given as

$$\begin{aligned} m_{t,\alpha -\eta -\mu /\text {Inverse Gamma}}= \,& \frac{K_a{\overline{\gamma }}^t\beta ^{2t/\alpha }\sqrt{\pi }}{2^{\mu +\frac{2t}{\alpha }-\frac{1}{2}}\mu ^{2t/\alpha }\Gamma (\mu )\Gamma (c)h^{\frac{2t}{\alpha }+\frac{1}{2}}H^{\mu -\frac{1}{2}}}\nonumber \\&\times \,\sum _{i=0}^{N}w_ix_i^{c-\frac{2t}{\alpha }-1}\nonumber \\&\times \,\sum _{j=0}^{M}w_jy_j^{\mu +\frac{2t}{\alpha }-\frac{1}{2}} I_{\mu -\frac{1}{2}}\left( \frac{Hy_j}{h} \right) \end{aligned}$$

(6)

where symbols have their usual meanings.

Proof

Following the definition of tth-moment, i.e $E(\gamma ^t)$, where $E(\cdot )$ is expectation, substituting $y=\frac{2\mu hx_i}{\beta }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}$ and using Gauss-Laguerre integral approximation the tth-moment of $\alpha -\eta -\mu$/Inverse Gamma distribution can be obtained as Eq. (6).$\square$

Lemma 3

The MGF of $\alpha -\eta -\mu$/Inverse Gamma Shadowed Fading Channel can be given as

$$\begin{aligned} \Psi _{\alpha -\eta -\mu /\text {Inverse Gamma}}(s)= \,& \frac{K_a\sqrt{\pi }}{2^{\mu -\frac{1}{2}}\Gamma (\mu )\Gamma (c)\sqrt{h}H^{\mu -\frac{1}{2}}}\sum _{i=0}^{N}w_ix_i^{c-1}\nonumber \\&\times \,\sum _{j=0}^{M}w_jy_j^{\mu -\frac{1}{2}}\nonumber \\&\times \, e^{s{\overline{\gamma }}y_j^{2/\alpha }\left( \frac{\beta }{2\mu hx_i}\right) ^{2/\alpha }}I_{\mu -\frac{1}{2}}\left( \frac{Hy_j}{h} \right) \end{aligned}$$

(7)

where symbols have their usual meanings.

Proof

From the definition of MGF, i.e $E(e^{\gamma })$, and following same procedure as in the proof of tth-moment of $\alpha -\eta -\mu$/Inverse Gamma distribution, MGF of $\alpha -\eta -\mu$/Inverse Gamma distribution can be obtained as Eq. (7).$\square$

3 The $\alpha -\kappa -\mu$/Inverse Gamma Shadowed Fading Channel

If r be the received signal envelope which follows $\alpha -\kappa -\mu$ fading, then conditional density of random variable $p=r^{\alpha }$ with shadowing power $\tau$ can be obtained as [8]:

$$\begin{aligned} f_{P_{\alpha -\kappa -\mu }|\tau }(p,\tau )= \,& \frac{\mu (1+\kappa )^{\frac{\mu +1}{2}}}{\tau \overline{p}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\left( \frac{p}{\tau \overline{p}}\right) ^{\frac{\mu -1}{2}}e^{-\frac{\mu (1+\kappa )p}{\tau \overline{p}}}\nonumber \\&\times \,I_{\mu -1}\left( 2\mu \sqrt{\frac{\kappa (1+\kappa )p}{\tau \overline{p}}}\right) , \end{aligned}$$

(8)

where $\kappa$ and $\mu$ are the parameters of $\eta -\mu$ distribution and $\overline{p}=E[r^{\alpha }]$.

If $\gamma$ and ${\overline{\gamma }}$ be instantaneous and mean Signal to Noise Ratios (SNR)s, then pdf of $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channel can be obtained by transforming the conditional power density pdf to conditional instantaneous SNR pdf through similar definition as in previous section i.e, $\gamma ={\overline{\gamma }}\left( \frac{p}{\overline{p}}\right) ^{2/\alpha }$ and averaging it with inverse gamma distribution. This can be written as:

$$\begin{aligned} f_{\gamma _{\alpha -\kappa -\mu /\text {Inverse Gamma}}}(\gamma )= \,& \int _{0}^{\infty } \frac{\alpha \mu (1+\kappa )^{\frac{\mu +1}{2}}\beta ^{c}}{2\Gamma (c)\tau ^{\frac{\mu +1}{2}+c+1}{\overline{\gamma }}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\nonumber \\&\times \,\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\frac{\alpha (\mu +1)}{4}-1}e^{-\left( \frac{\mu (1+\kappa )}{\tau }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}+\frac{\beta }{\tau }\right) }\nonumber \\&\times \,I_{\mu -1}\left( 2\mu \sqrt{\frac{\kappa (1+\kappa )}{\tau }}\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /4}\right) d\tau \end{aligned}$$

(9)

where $\gamma$ and ${\overline{\gamma }}$ are the instantaneous and average Signal to Noise Ratio, c and $\beta$ are the respective shape and scale parameters of inverse gamma distribution. Also $\beta =c-1$, as mean of inverse gamma variable has been set equal to 1.

The following lemmas give the expressions of pdf, tth-moment and MGF for $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading Channel.

Lemma 4

If $\gamma$ and ${\overline{\gamma }}$ are the instantaneous and average Signal to Noise Ratio, then pdf of instantaneous SNR for $\alpha -\kappa -\mu$/Inverse Gamma distribution can be given as

$$\begin{aligned} f_{\gamma _{\alpha -\kappa -\mu /\text {Inverse Gamma}}}(\gamma )=\, & K_b\sum _{i=0}^{N} \frac{w_i\alpha \mu (1+\kappa )^{\frac{\mu +1}{2}}x_i^{\frac{\mu -1}{2}+c}}{2\Gamma (c)\beta ^{\frac{\mu +1}{2}}{\overline{\gamma }}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\nonumber \\&\times \,\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\frac{\alpha (\mu +1)}{4}-1}e^{-\frac{\mu (1+\kappa )x_i}{\beta }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}}\nonumber \\&\times \,I_{\mu -1}\left( 2\mu \sqrt{\frac{\kappa (1+\kappa )x_i}{\beta }}\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /4}\right) \end{aligned}$$

(10)

where, $\alpha$, $\kappa$ and $\mu$ are the parameters of $\alpha -\kappa -\mu$ fading channel, c is shadowing parameter and $\beta =cc-1$, $w_i$’s and $x_i$’s are weights and nodes for Gauss–Laguerre integral approximation and N is number of terms. $K_b$ is normalization constant given by

$$\begin{aligned} K_b= \,& \left[ \frac{1 }{\Gamma (c)\mu ^{\frac{\mu -1}{2}}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\sum _{i=0}^{N} w_ix_i^{c-1}\right. \nonumber \\&\times \,\left. \sum _{j=0}^{M} w_jy_j^{\frac{\mu -1}{2}} I_{\mu -1}\left( 2\mu \sqrt{\frac{\kappa y_j}{\mu }}\right) \right] ^{-1} \end{aligned}$$

(11)

Proof

Substituting $x=\beta /\tau$ in Eq. (3) and using Gauss–Laguerre integral approximation, the required result in Eq. (10) is obtained. $K_b$ is again normalization constant which ensure $\int _{0}^{\infty }f_{\gamma }(x)dx=1$ and equal to zeroth moment of the distribution. It can be obtained by substituting $t=0$ in Eq. (12) and given as Eq. (11).$\square$

Lemma 5

The tth-moment of $\alpha -\kappa -\mu$/Inverse Gamma Shadowed Fading Channel can be given as

$$\begin{aligned} m_{t,\alpha -\kappa -\mu /\text {Inverse Gamma}}= \,& \frac{K_b{\overline{\gamma }}^t\beta ^{2t/\alpha } }{\Gamma (c)(1+\kappa )^{2t/\alpha }\mu ^{\frac{\mu -1}{2}+\frac{2t}{\alpha }}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\nonumber \\&\times \,\sum _{i=0}^{N} w_ix_i^{c-\frac{2t}{\alpha }-1} \sum _{j=0}^{M} w_jy_j^{\frac{\mu -1}{2}+\frac{2t}{\alpha }} \nonumber \\&\times \,I_{\mu -1}\left( 2\mu \sqrt{\frac{\kappa y_j}{\mu }}\right) \end{aligned}$$

(12)

where symbols have their usual meanings.

Proof

Following the definition of tth-moment, substituting $y=\frac{\mu (1+\kappa )x_i}{\beta }\left( \frac{\gamma }{{\overline{\gamma }}}\right) ^{\alpha /2}$ and using Gauss–Laguerre integral approximation the tth-moment of $\alpha -\kappa -\mu$/Inverse Gamma can be obtained as Eq. (12).$\square$

Lemma 6

The MGF of $\alpha -\kappa -\mu$/Inverse Gamma Shadowed Fading Channel can be given as

$$\begin{aligned} \Psi _{\alpha -\kappa -\mu /\text {Inverse Gamma}}(s)=\, & \frac{K_b}{\Gamma (c)\mu ^{\frac{\mu -1}{2}}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\sum _{i=0}^{N}w_ix_i^{c-1}\sum _{j=0}^{M} w_j y_j^{\frac{\mu -1}{2}}\nonumber \\&\times \,e^{s{\overline{\gamma }}y_j^{2/\alpha }\left( \frac{\beta }{\mu (1+\kappa )x_i}\right) ^{2/\alpha }}\nonumber \\&\times \,I_{\mu -1}\left( 2\sqrt{\mu \kappa y_j}\right) \end{aligned}$$

(13)

where symbols have their usual meanings.

Proof

Following the definition of MGF and same procedure as in the proof of tth-moment of $\alpha -\kappa -\mu$/Inverse Gamma distribution, MGF of $\alpha -\kappa -\mu$/Inverse Gamma distribution can be obtained as Eq. (13).$\square$

4 Performance Measures in Wireless Communication Systems

4.1 AoF

AoF for any arbitrary fading channel is defined as

$$\begin{aligned} AoF=\frac{m_2-m_1^2}{m_1^2}=\left( \frac{m_2}{m_1^2}\right) -1 \end{aligned}$$

(14)

where $m_1$ and $m_2$ are the $1^{st}$ and $2^{nd}$ moments of instantaneous SNR. AoF for $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channels can be obtained by calculating their respective $1^{st}$ and $2^{nd}$ moments and substituting in Eq. (14).

4.2 ASER

ASERs for different modulations schemes can be obtained using alternate representation of Q function [9] and [6, Eq. 17] and given as

$$\begin{aligned} \Lambda ({\bar{\gamma }})= \,& \frac{2A_c}{\pi }\int _{0}^{\pi /2}\Psi \left( -\frac{B_c}{\sin ^2(\delta )}\right) d\delta \end{aligned}$$

(15)

where $\Psi (\cdot )$ is MGF of the channel and values of $A_c$s and $B_c$s for different modulation schemes can be obtained from [6, Table I]. ASERs for various modulations schemes can be given by following lemmas.

Lemma 7

ASER for $\alpha -\eta -\mu /$ Inverse Gamma shadowed fading channel can be given as:

$$\begin{aligned} \Lambda _{\alpha -\eta -\mu /\text {Inverse Gamma}}({\overline{\gamma }})=\, & \frac{A_cK_a\sqrt{\pi }}{2^{\mu -\frac{1}{2}}\Gamma (\mu )\Gamma (c)\sqrt{h}H^{\mu -\frac{1}{2}}} \sum _{i=0}^{N}w_ix_i^{c-1} \nonumber \\&\times \, \sum _{j=0}^{M}w_jy_j^{\left( \mu +\frac{1}{2}\right) -1} I_{\mu -\frac{1}{2}}\left( \frac{Hy_j}{h} \right) \nonumber \\&\times \,\left[ 1-\text {erf}\left( \sqrt{B_c{\overline{\gamma }}}\left( \frac{\beta y_j}{2\mu hx_i}\right) ^{1/\alpha }\right) \right] \end{aligned}$$

(16)

where symbols have their usual meanings.

Proof

Substituting MGF of $\alpha -\eta -\mu /$Inverse Gamma channel and using [10, Eq. 3.363.2] Eq.16 follows.$\square$

Lemma 8

ASER for $\alpha -\kappa -\mu /$ Inverse Gamma shadowed fading channel can be given as:

$$\begin{aligned} \Lambda _{\alpha -\kappa -\mu /\text {Inverse Gamma}}({\overline{\gamma }})=\, & \frac{A_cK_b}{\Gamma (c)\mu ^{\frac{\mu -1}{2}}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\sum _{i=0}^{N}w_ix_i^{c-1} \nonumber \\&\times \, \sum _{j=0}^{M} w_j y_j^{\frac{\mu -1}{2}} I_{\mu -1}\left( 2\sqrt{\mu \kappa y_j}\right) \nonumber \\&\times \,\left[ 1-\text {erf}\left( \sqrt{B_c{\overline{\gamma }}}\left( \frac{\beta y_j}{\mu (1+\kappa )x_i}\right) ^{1/\alpha }\right) \right] \end{aligned}$$

(17)

where symbols have their usual meanings.

Proof

Substituting MGF of $\alpha -\kappa -\mu /$Inverse Gamma channel and using [10, Eq. 3.363.2] Eq.17 follows.$\square$

4.3 Average Channel Capacity

Average Channel Capacity per unit bandwidth (${\mathcal {C}}$) for any arbitrary channel can be defined as the expected value of $\log _2(1+\gamma )$, i.e., $E[\log _2(1+\gamma )]$, where $\gamma$ is instantaneous SNR. Next two lemmas give the expressions of Average Channel Capacity per unit bandwidth for $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channels respectively.

Lemma 9

Average Channel Capacity per unit bandwidth (${\mathcal {C}}$) for $\alpha -\eta -\mu$/Inverse Gamma shadowed fading channel can be given as

$$\begin{aligned} {\mathcal {C}}_{\alpha -\eta -\mu /\text {Inverse Gamma}}=\, & \frac{K_a\sqrt{\pi }}{2^{\mu -\frac{1}{2}}\Gamma (\mu )\Gamma (c)\sqrt{h}H^{\mu -\frac{1}{2}}} \sum _{i=0}^{N}w_ix_i^{c-1} \nonumber \\&\times \, \sum _{j=0}^{M}w_jy_j^{\left( \mu +\frac{1}{2}\right) -1} I_{\mu -\frac{1}{2}}\left( \frac{Hy_j}{h} \right) \nonumber \\&\times \,\log _2\left( 1+{{\overline{\gamma }}y_j^{2/\alpha }\left( \frac{\beta }{2\mu hx_i}\right) ^{2/\alpha }}\right) \end{aligned}$$

(18)

where symbols have their usual meanings.

Proof

Following the definition of Average Channel Capacity per unit bandwidth and same procedure as in the derivations of tth-moment and MGF, Average Channel Capacity per unit bandwidth for $\alpha -\eta -\mu$/Inverse Gamma distribution can be obtained and given in Eq. (18).$\square$

Lemma 10

Average Channel Capacity per unit bandwidth (${\mathcal {C}}$) for $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channel can be given as

$$\begin{aligned} {\mathcal {C}}_{\alpha -\kappa -\mu /\text {Inverse Gamma}}=\, & \frac{K_b}{\Gamma (c)\mu ^{\frac{\mu -1}{2}}\kappa ^{\frac{\mu -1}{2}}e^{\mu \kappa }}\sum _{i=0}^{N}w_ix_i^{c-1} \nonumber \\&\times \, \sum _{j=0}^{M} w_j y_j^{\frac{\mu -1}{2}} I_{\mu -1}\left( 2\sqrt{\mu \kappa y_j}\right) \nonumber \\&\times \,\log _2\left( 1+{{\overline{\gamma }}y_j^{2/\alpha }\left( \frac{\beta }{\mu (1+\kappa )x_i}\right) ^{2/\alpha }}\right) \end{aligned}$$

(19)

where symbols have their usual meanings.

Proof

Following the definition of Average Channel Capacity per unit bandwidth and same procedure as in the derivations of tth-moment and MGF, Average Channel Capacity per unit bandwidth for $\alpha -\kappa -\mu$/Inverse Gamma distribution can be obtained and given in Eq. (19).$\square$

4.4 S2S-ABER

Fig. 1

A typical multi-hop communication scenario

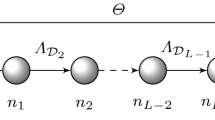
Figure 1 shows a typical multi-hop communication scenario with $L+1$ nodes where message passes from source to sink node in multiple hops using decode and forward technique. Each individual link is modeled as BPSK modulated system. Average BER of ith hop having any arbitrary distribution ${\mathcal {D}}$ is assumed to be $\Lambda _{{\mathcal {D}}_i}$ $\forall i\in [1,L]$. $\Theta$ is the S2S-ABER from source to sink node having L hops. Since message passes through multiple hops, every individual channel can be modeled independently either with identical or non-identical distributions.

For a multi-hop path in a network with L hops where all the links are independent and identically distributed with distribution ${\mathcal {D}}$ and equal received average SNR ${\overline{\gamma }}$, the S2S-ABER is given by [14]

$$\begin{aligned} \Theta=\, & \frac{1}{2}\left( 1-(1-2\Lambda _{{\mathcal {D}}}({\overline{\gamma }}))^L\right) . \end{aligned}$$

(20)

whereas, S2S-ABER for a multi-hop path in a network with L hops having independent but non identically distributed links is given by [14]

$$\begin{aligned} \Theta= \,& \sum _{i=1}^L\Lambda _{{\mathcal {D}}_i}({\overline{\gamma }}_i)\left( \prod _{j=i+1}^L (1-2\Lambda _{{\mathcal {D}}_j}({\overline{\gamma }}_j))\right) , \end{aligned}$$

(21)

where $\Lambda _{{\mathcal {D}}_i}({\overline{\gamma }}_i)$ is Average BER of ith hop(link) having distribution ${\mathcal {D}}_i$ and average SNR ${\overline{\gamma }}_i$. Considering a simpler network of L hops with only two types of links i.e., having $\nu$ links with distribution ${\mathcal {D}}_1$ and rest $L-\nu$ links with ${\mathcal {D}}_2$ and also assuming equal average SNR ${\overline{\gamma }}$, then Eq. (21) can be simplified to

$$\begin{aligned} \Theta=\, & \frac{1}{2}\left( 1-\left( 1-2\Lambda _{{\mathcal {D}}_1}({\overline{\gamma }})\right) ^\nu \left( 1-2\Lambda _{{\mathcal {D}}_2}({\overline{\gamma }})\right) ^{(L-\nu )}\right) \end{aligned}$$

(22)

where symbols have their usual meanings.

4.5 Application in IEEE 802.15.4 Zigbee and IEEE 802.15.1 Bluetooth Radios

Average BER for IEEE 802.15.4 Zigbee and IEEE 802.15.1 Bluetooth Radios over any arbitrary channel with distribution ${\mathcal {D}}$ can be given as [11]

$$\begin{aligned} \Lambda _{{\mathcal {D}}}^{wsn}(\gamma )= \,& \frac{8}{15}\frac{1}{16}\sum _{z=2}^{16}(-1)^z\left( {\begin{array}{c}16\\ z\end{array}}\right) \Psi _{{\mathcal {D}}}(s_{wsn}) \end{aligned}$$

(23)

and

$$\begin{aligned} \Lambda _{{\mathcal {D}}}^{BT}(\gamma )= \,& \frac{1}{2}\Psi _{{\mathcal {D}}}(s_{BT}) \end{aligned}$$

(24)

respectively, where $s_{wsn}=20(1-\frac{1}{z})$, $s_{BT}=\frac{1}{2}$ and $\Psi _{{\mathcal {D}}}(s)$ is the MGF of distribution ${\mathcal {D}}$. Substituting the expression of MGFs for $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma distributions for both links, the average BER for these distributions can be obtained. S2S-ABER for multi-hop iid and simpler case of inid networks can be obtained on substituting Average BERs in Eqs. (20) and (22) respectively.

5 Results and Discussion

Accuracy of numerical results with typical choice of parameters of the channels depend on number of terms N and M. As value of N and M increases results become more and more accurate. However, higher values of N and M increases the computation burden. Therefore choice of N and M need to be optimized based on the required accuracy and available computational resources. Number of terms (N, M) required in calculation of channel capacity and average BER for accuracy up to 4th significant digit for $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma channels with typical parameter sets $\zeta =[\alpha , \eta , \mu , c]=[3,3,6,2]$ and $\zeta =[\alpha , \kappa , \mu , c]=[4,3,3,3]$ respectively are shown in Table 1. Number of terms Ns and Ms required for other parameter sets can also be obtained in similar manner. Values of $w_i$’s, $x_i$’s and $y_i$’s in various expressions can be obtained directly from online resource https://keisan.casio.com/exec/system/1280624821.

Table 1 Number of terms N and M required for accuracy up to 4th significant digits in Channel Capacity, Average BER, and AoF for $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma channels with typical parameter sets $\zeta =[\alpha , \eta , \mu , c]=[3,3,6,2]$ and $\zeta =[\alpha , \kappa , \mu , c]=[4,3,3,3]$ respectively

5.1 Analysis Over Single-Hop Communication

Fig. 2

ASER over $\alpha -\eta -\mu /$Inverse Gamma and $\alpha -\kappa -\mu /$Inverse Gamma shadowed fading channels for various modulation schemes $\zeta$

Fig. 3

ABER over $\alpha -\eta -\mu /$Inverse Gamma and $\alpha -\kappa -\mu /$Inverse Gamma shadowed fading channels for various parameters $\zeta$

Figure 2 shows the variation of ASER with respect to Average SNR for different coherent modulation schemes over $\alpha -\eta -\mu /$Inverse Gamma and $\alpha -\kappa -\mu /$Inverse Gamma channels with typical parameter sets $\zeta =[\alpha , \eta , \mu , c]=[3,3,6,3]$ and $\zeta =[\alpha , \kappa , \mu , c]=[6,8,6,3]$ respectively. It can be easily seen from Fig. 2 that best performance is obtained through BPSK modulation system whereas performance degrades for higher constellations. For example at 10 dB Average SNR, ASER for BPSK modulation over $\alpha -\eta -\mu /$Inverse Gamma and $\alpha -\kappa -\mu /$Inverse Gamma channels are $4.5\times 10^{-4}$ and $3.2\times 10^{-5}$ respectively. For QPSK modulation these are $1.2\times 10^{-2}$ and $3.6\times 10^{-3}$, for 8PSK modulation these are $1.4\times 10^{-1}$ and $1.1\times 10^{-1}$ and for 16PSK modulation these are $4.3\times 10^{-1}$ and $4\times 10^{-1}$ respectively.

Figure 3 shows the variation of ABER with respect to Average SNR for BPSK modulated system over $\alpha -\eta -\mu /\text {Inverse Gamma}$ and $\alpha -\kappa -\mu /\text {Inverse Gamma}$ channels with various channel parameters. From Fig. 3, it can be easily seen that for $\alpha -\eta -\mu /\text {Inverse Gamma}$ channel, ABER increases if $\eta$ increases whereas it decreases if $\alpha$, $\mu$ and c increases. For $\alpha -\kappa -\mu /\text {Inverse Gamma}$ channel, ABER decreases with increase in all the channel parameters. For example at 12 dB Average SNR over $\alpha -\eta -\mu /$Inverse Gamma, ABER decreases from $1.12\times 10^{-4}$ to $1.99\times 10^{-5}$ if $\alpha$ increases from 3 to 4. It increases from $1.99\times 10^{-5}$ to $2.73\times 10^{-5}$ if $\eta$ increases from 3 to 6. It again decreases from $2.73\times 10^{-5}$ to $9.34\times 10^{-6}$ if $\mu$ increases from 3 to 6 and $9.34\times 10^{-6}$ to $2.16\times 10^{-6}$ if c increases from 3 to 6. Similarly at 12 dB Average SNR over $\alpha -\kappa -\mu /$Inverse Gamma channel, ABER decreases from $1.66\times 10^{-6}$ to $6.60\times 10^{-7}$, $6.6\times 10^{-7}$ to $5.85\times 10^{-7}$, $5.85\times 10^{-7}$ to $4.48\times 10^{-7}$ and $4.48\times 10^{-7}$ to $1.03\times 10^{-7}$ if $\alpha$ increases from 5 to 6, $\kappa$ increases from 8 to 10, $\mu$ increases from 3 to 6 and $\lambda$ increases from 3 to 6 respectively.

Fig. 4

AoF over $\alpha -\eta -\mu /$Inverse Gamma and $\alpha -\kappa -\mu /$Inverse Gamma shadowed fading channels with respect to $\mu$ for various parameters

Figure 4 shows the variation of AoF with respect to $\mu$ over $\alpha -\eta -\mu /\text {Inverse Gamma}$ and $\alpha -\kappa -\mu /\text {Inverse Gamma}$ channels with various channel parameters. From Fig. 4, it can be easily seen that for $\alpha -\eta -\mu /\text {Inverse Gamma}$ channel, AoF increases if $\eta$ increases whereas it decreases if $\alpha$, $\mu$ and $\lambda$ increases. For $\alpha -\kappa -\mu /\text {Inverse Gamma}$ channel, ABER decreases with increase in all the channel parameters. For example with $\mu =11$ AoF over $\alpha -\eta -\mu /$Inverse Gamma decreases from 0.6755 to 0.2889 if $\alpha$ increases from 3 to 4. It increases from 0.2889 to 0.2925 if $\eta$ increases from 3 to 6. It again decreases from 0.2925 to 0.1050 if $\lambda$ increases from 2 to 4. Similarly with $\mu =11$ AoF over $\alpha -\kappa -\mu /$Inverse Gamma decreases from 0.1517 to 0.0971, 0.0971 to 0.0967 and 0.0967 to 0.0356 if $\alpha$ increases from 5 to 6, $\kappa$ increases from 8 to 10, and $\lambda$ increases from 2 to 4 respectively.

Table 2 Capacity over $\alpha -\eta -\mu /$Inverse Gamma and $\alpha -\kappa -\mu /$Inverse Gamma channels with various channel parameters

Table 2 shows the variation of channel capacity per unit bandwidth with respect to Average SNR over $\alpha -\eta -\mu /\text {Inverse Gamma}$ and $\alpha -\kappa -\mu /\text {Inverse Gamma}$ channels with various channel parameters. From Table 2, it can be easily seen that for $\alpha -\eta -\mu /\text {Inverse Gamma}$ channel, channel capacity decreases if $\eta$ increases whereas it increases if $\alpha$, $\mu$ and c increases. For $\alpha -\kappa -\mu /\text {Inverse Gamma}$ channel, channel capacity increases with increase in all the channel parameters. For example at 8 dB Average SNR over $\alpha -\eta -\mu /$Inverse Gamma channel, channel capacity increases from 2.4838 to 2.5695 if $\alpha$ increases from 3 to 4. It decreases from 2.5695 to 2.5581 if $\eta$ increases from 3 to 6. It again increases from 2.5581 to 2.5916 if $\mu$ increases from 3 to 6 and 2.5916 to 2.7430 if $\lambda$ increases from 2 to 4. Similarly at 8 dB Average SNR over $\alpha -\kappa -\mu /$Inverse Gamma channel, channel capacity increases from 2.6551 to 2.6888, 2.6888 to 2.6913, 2.6913 to 2.6956 and 2.6956 to 2.8002 if $\alpha$ increases from 5 to 6, $\kappa$ increases from 8 to 10, $\mu$ increases from 3 to 6 and $\lambda$ increases from 2 to 4 respectively.

5.2 Analysis Over Multi-hop Communication

Fig. 5

S2S-ABER for multi-hop wireless communication system over $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma Composite Channels with typical parameter sets $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively

Fig. 6

S2S-ABER with respect to Average SNR for inidd multi-hop communication network with $L = 20$ Hops and $\nu$ varies from 2 to 15

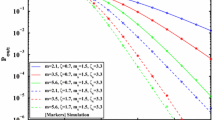
Figure 5 shows S2S-ABER for multi-hop wireless communication system over $\alpha -\eta -\mu$/Inverse Gamma and $\eta -\kappa -\mu$/Inverse Gamma composite channels with typical parameter sets $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively. From the figure, it is evident that for both the channels, to achieve a specific S2S-ABER, if number of hops increases, required Average SNR also increases. For example in $\alpha -\eta -\mu$/Inverse Gamma composite channel, to achieve S2S-ABER of $10^{-5}$, there is an increment of approximately 1.3 dB Average SNR is required, i.e., from 13.4 to 14.7 dB, if number of hops increased from 2 to 20. Similarly for $\alpha -\kappa -\mu$/Inverse Gamma composite channel, the required increment in Average SNR is approximately 3.1 dB i.e., from 12.8 to 14.1 dB, to achieve S2S-ABER of $10^{-5}$, if number of hops increased from 2 to 20.

Figure 6 shows S2S-ABER for multi-hop network with independent but two different types of distribution links i.e, ${\mathcal {D}}_1$ and ${\mathcal {D}}_2$ respectively. It was assumed that Average BER performance over ${\mathcal {D}}_2$ distributed links are better than Average BER performance over ${\mathcal {D}}_1$ distributed links. Therefore with our typical case ${\mathcal {D}}_1$ is assumed to be $\alpha -\eta -\mu$/Inverse Gamma composite channel and ${\mathcal {D}}_2$ is assumed to be $\alpha -\kappa -\mu$/Inverse Gamma composite channel with parameter $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively. Graphs of S2S-ABER has been plotted by fixing total number of hops $L = 20$ and varying number of links of distribution ${\mathcal {D}}_1$ from $\nu = 2$ to $\nu = 15$. It is evident from the figure that S2S-ABER increases as $\nu$ increases. For example, it increases from approximately $2.1\times 10^{-4}$ to $2.9\times 10^{-4}$ as $\nu$ increases from 2 to 15 at 13 dB Average SNR.

5.3 Performance Over IEEE 802.15.4 Zigbee and IEEE 802.15.1 Bluetooth Radios

Fig. 7

Average BER ($L=1$) and S2S-ABER ($L=10,20$) for multi-hop IEEE 802.15.4 zigbee radio over $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma Channels with typical parameter sets $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively

Fig. 8

S2S-ABER with respect to Average SNR for inidd multi-hop WSN with $L = 20$ Hops and $\nu$ varies from 2 to 15

Figure 7 shows Average BER ($L=1$) and S2S-ABER ($L=10,20$) for iid multi-hop Zigbee radio over $\alpha -\eta -\mu$/Inverse Gamma and $\eta -\kappa -\mu$/Inverse Gamma composite channels with typical parameter sets $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively. From the figure, it is evident that for both the channels, to achieve a specific S2S-ABER, if number of hops increases, required Average SNR also increases. For example in $\alpha -\eta -\mu$/Inverse Gamma channel, at 5 dB average SNR, S2S-ABER increases from $1.2\times 10^{-5}$ to $2.4\times 10^{-4}$ if number of hops increased from 1 to 20. Similarly for $\alpha -\kappa -\mu$/Inverse Gamma channel, at 5 dB average SNR, S2S-ABER increases from $2.8\times 10^{-6}$ to $6.5\times 10^{-5}$ if number of hops increased from 1 to 20.

Figure 8 shows S2S-ABER for multi-hop Zigbee radio with independent but two different types of distribution links i.e, ${\mathcal {D}}_1$ and ${\mathcal {D}}_2$ respectively. It was assumed that Average BER performance over ${\mathcal {D}}_2$ distributed links are better than Average BER performance over ${\mathcal {D}}_1$ distributed links. Therefore with our typical case ${\mathcal {D}}_1$ is assumed to be $\alpha -\eta -\mu$/Inverse Gamma composite channel and ${\mathcal {D}}_2$ is assumed to be $\alpha -\kappa -\mu$/Inverse Gamma composite channel with parameter $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively. Graphs of S2S-ABER has been plotted by fixing total number of hops $L = 20$ and varying number of links of distribution ${\mathcal {D}}_1$ from $\nu = 2$ to $\nu = 15$. It is evident from the figure that S2S-ABER increases as $\nu$ increases. For example, it increases from approximately $1.6\times 10^{-4}$ to $2.8\times 10^{-4}$ as $\nu$ increases from 2 to 15 at 5 dB Average SNR.

Fig. 9

Average BER ($L=1$) and S2S-ABER ($L=10,20$) for multi-hop IEEE 802.15.1 bluetooth radio over $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma Channels with typical parameter sets $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively

Fig. 10

S2S-ABER with respect to Average SNR for inidd multi-hop Bluetooth communication network with $L = 20$ Hops and $\nu$ varies from 2 to 15

Figure 9 shows Average BER ($L=1$) and S2S-ABER ($L=10,20$) for multi-hop IEEE 802.15.1 bluetooth radio over $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma composite channels with typical parameter sets $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively. From the figure, it is evident that for both the channels, at a typical average SNR, S2S-ABER increases if number of hops increases. For example in $\alpha -\eta -\mu$/Inverse Gamma channel, at 14 dB average SNR, S2S-ABER increases from $6.5\times 10^{-4}$ to $1.3\times 10^{-2}$, if number of hops increased from 1 to 20. Similarly for $\alpha -\kappa -\mu$/Inverse Gamma channel, S2S-ABER increases from $6.2\times 10^{-5}$ to $1.3\times 10^{-3}$, if number of hops increased from 1 to 20.

Figure 10 shows S2S-ABER for multi-hop bluetooth network with independent but two different types of distribution links i.e, ${\mathcal {D}}_1$ and ${\mathcal {D}}_2$ respectively. With our typical case ${\mathcal {D}}_1$ is assumed to be $\alpha -\eta -\mu$/Inverse Gamma channel and ${\mathcal {D}}_2$ is assumed to be $\alpha -\kappa -\mu$/Inverse Gamma composite channel with parameter $\zeta =[3,3,6,3]$ and $\zeta =[3,8,6,3]$ respectively. Graphs of S2S-ABER has been plotted by fixing total number of hops $L = 20$ and varying number of links of distribution ${\mathcal {D}}_1$ from $\nu = 2$ to $\nu = 15$. It is evident from the figure that S2S-ABER increases as $\nu$ increases. For example, it increases from approximately $2.4\times 10^{-5}$ to $4.6\times 10^{-5}$ as $\nu$ increases from 2 to 15 at 18 dB Average SNR.

6 Conclusion

This paper derives the expressions of pdfs, tth-moments and MGFs of instantaneous SNR for two new proposed $\alpha -\eta -\mu$/Inverse Gamma and $\alpha -\kappa -\mu$/Inverse Gamma shadowed fading channels. AoF, Channel Capacity per unit bandwidth and Average BER for wireless communication Systems over these channels have also been determined. The variation in the performance matrices with respect to change in various channel parameters have been plotted and discussed. Moreover, to judge the performance of multi-hop communication systems Source to Sink Average BER has been determined. Obtained statistics has also been analyzed to judge the performance of IEEE 802.15.4 zigbee and IEEE 802.15.1 bluetooth radios over stated channels. Monte Carlo Simulations have also been performed to validate the derived expressions. However expressions derived in this paper can also be derived through other ways to get closed form expressions but closed form expressions are quite complex to compute due to presence of complex mathematical operations/functions and is an open future scope.