Carrier to interference ratio analysis in shotgun cellular systems over a generalized shadowing distribution

Abstract

Shotgun cellular systems (SCSs) are wireless communication systems with randomly placed base stations (BSs) over the entire plane according to a two-dimensional Poisson point process. Such a system can model a dense cellular or wireless data network deployment, where the BS locations end up being close to random due to constraints other than optimal coverage. SCSs have been studied by considering path-loss and independent shadowing paths between BS to mobile station (MS) pairs in the channel models. In this paper, we consider correlated shadowing paths between BS to MS pairs as a most important factor, and analyze the carrier to interference ratio (CIR), in a SCS over this correlation, and determine an expression for distribution of CIR, and obtain the tail probability of the CIR.

1 Introduction

Cellular communication consists of a set of radio BSs distributed over a region that communicate with MS. Optimal planar cellular systems place BS in uniform size hexagonal grids. These ideal hexagonal cellular systems provide upper performance bound (upb). In contrast to hexagonal cellular systems with regular BS placement, in many wireless systems such as LANs and femtocells [1], due to site acquisition difficulties, BSs are placed randomly over the deployment region. In these systems called Shotgun cellular systems (SCSs), the BSs are placed randomly over the entire plane according to a two-dimensional (2-D) Poisson point process with a parameter $\lambda$ which is the average BS density for the SCS [2, 3]. Such systems provide lower performance bound (lpb). The difference between upper bound and lower bound is small under operating typical conditions in modern CDMA and TDMA cellular systems. Furthermore, in the strong shadowing limit the bounds converge [3]. In a SCS the signal propagation is affected by path-loss, log-normal shadowing (slow fading), and multi-path fading (fast fading). In this paper we only consider path-loss and shadow fading. Many cellular deployments have significant randomness. Therefore, SCS is a system affected by random phenomena. The performance in the SCS that we are concerned about is the signal quality at the MS. The performance in the SCS is defined as the ratio of the received signal power to the total interference power, and is denoted by $\textit{CIR}=\frac{P_S}{P_I}$. The MS listens to the BS with the strongest received signal power $P_S$, where the subscript S stands for the signal-carrying BS. The interference is the sum of the received power from all the other co-channel BSs and is denoted by $P_I$, where the subscript I stands for the signal-interfering BS. We know that the performance differs slightly between the uplink and downlink, but qualitatively they are similar and downlink may yield to at least much simpler analysis and simulations [3]. For these reasons, previous works and this paper focus only on the downlink. The SCS and its downlink performance metrics with shadowing and without shadowing [2,3,4] and downlink performance for a generalized SCS [1, 5] have been studied.

The previous works to study the SCS have considered independent signal propagation paths between BS to MS pairs, and have not considered the correlation between signal propagation paths BS to MS pairs [6,7,8,9,10,11,12,13]. Correlation between signal propagation paths is defined with correlation between their multi-path fading [7] and/or shadow fading factors [6,7,8,9,10,11,12,13]. In  [8] a spatial correlation coefficient (for both the shadow and the multi-path fading environments) was proposed to express the correlation characteristics of mobile cognitive radio (CR) users in different environments. Cacciapuoti et al. [7] analyzed TV white spases (TVWSs) in presence of correlation among the primary user (PU) traffic patterns through a Markov process. Szyszkowicz et al. [6] explained completely the correlated shadowing paths BS to MS pairs. Correlation in wireless shadowing is a significant step in obtaining more realistic channel propagation models. They also showed that shadowing correlation significantly affects handover behavior, interference power (and consequently system performance), and the performance of macrodiversity schemes. Shadowing correlation can also be positively exploited in some algorithms or protocols, e.g., for wireless positioning, cognitive radio and spectrum sensing or neighbor discovery applications. Therefore, in fact signal propagation in a SCS from BSs to MS is affected by path-loss and correlated shadowing. In this paper, by considering this correlation between signal propagation paths, we determine an expression for the distribution of CIR, and then obtain the tail probability of the CIR.

The paper is organized as follows: in Sect. 2, we explain system model. In Sect. 3, we describe important definitions and main results. This Sect. consists of three subsections. Section 3.1 describes important definitions. In Sect. 3.2, we explain main results. This Subsection consists of three subsections. In this subsection by considering the correlation between shadowing of BS to MS path pairs, we at first determine the probability distribution of C (carrier signals power received at the MS) in Sect. 3.2.1 and then we calculate the probability distribution of I (sum of the received powers at the MS from all the other co-channel BSs) in Sect. 3.2.2. Finally, in Sect. 3.2.3, we derive the probability distribution and tail probability for the CIR. In Sect. 3.3, to better understand our idea, we show simple numerical example. In Sect. 4, the details of simulation results are presented and lastly, in Sect. 5 concludes the paper.

Fig. 1

SCS

2 System model

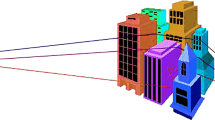
In the SCS with fixed non-variable radio properties and no shadowing, the BS closest to the MS will be chosen as the carrying or serving BS, and all the others are interfering BSs. When random radio properties and shadow fading are introduced to this system, the serving BS is not necessarily the BS closest to the MS. Since our focus is on the downlink, we consider the CIR performance of a single MS. This MS, without loss of generality, is assumed to be located at the origin and around this MS, BSs are placed according to 2-D Poisson point process with a parameter $\lambda$, which is the average BS density for the SCS [2, 3] (see Fig. 1). In this figure, $R_n$ is the separation between the $BS_n$ and the MS, where $n=1, 2, 3,\ldots , N$ and $R_1<R_2<R_3<\cdots <R_N$. In Gaussian channels with transmitted signal x, the received signal Y can be written as $Y=hx+Z$, in which Z is noise of channel and h is fading coefficient. In different channels, h can be modeled as different random variables such as shadowing $\varPsi$ and multi-path fading ${\alpha }$. Therefore assuming Gaussian channels in the SCS, the received power at the MS (without considering multi-path fading) from a BS is given by $P_r=KP_T\varPsi R^{-\varepsilon }$, where K is a radio factor and $P_T$ is transmitter power. The path-loss is a function of the BS to MS separation R, and follows an inverse power law with $\varepsilon$ as the path-loss exponent. The shadowing factor $\varPsi$, is usually modeled as a log-normal random variable [1,2,3,4,5,6,7, 10,11,12]. The MS receives signals from all BSs, and chooses to communicate with the BS that corresponds to the strongest received signal power. This BS is referred to as the carrying BS, and all the other BSs are called the interfering BSs. Thus, the signal quality at the MS is defined as the ratio of the received power from the serving BS (denoted by C or $P_S$) to the sum of the total interference power (denoted by I or $P_I$), i.e. carrier to interference ratio $\frac{C}{I}=\frac{P_S}{P_I}$. For a typical cellular system, the CIR at the MS is given by

$$\begin{aligned} \frac{C}{I}=\frac{P_TK_S\varPsi _S{R_1}^{-\varepsilon }}{P_T\left( \sum _{i=2}^N K_i\varPsi _i{R_i}^{-\varepsilon }\right) } \end{aligned}$$

(1)

where $K_S$ and $\{K_i\}_{i=2}^N$ are the radio factors of the signal-carrying BS and the interfering BSs respectively, $P_T$ is transmitter power, $\{R_j\}_{j=1}^N$ are the separations between the corresponding BS to MS pairs, and $\varPsi _S$ and $\{\varPsi _i\}_{i=2}^N$ are the shadow fading factors corresponding to the signal-carrying BS and the interfering BSs, respectively. The SCS and its performance without considering the correlation between BS to MS path pairs is described in [1,2,3,4,5].

Fig. 2

a Shadowing auto-correlation for a mobile Y(t). b Shadowing cross-correlation for a mobile X

3 Definitions and main results

This section describes important definitions and model of cellular system used for analyzing the SCS with correlation between signal propagation paths from BS to MS pairs.

Fig. 3

Pair of auto-correlated cross-correlated paths with the most relevant dimensional variable d, $R_1, R_2, \theta$

3.1 Definitions

3.1.1 Correlation between paths

In fact, there is correlation between signal propagation paths from BS to MS [6,7,8,9,10,11,12,13]. While all previous works about SCS, have not considered this correlation. Correlation is defined with correlation between their multi-path fading  [7] and/or shadow fading factors [6,7,8,9,10,11,12,13]. Szyszkowicz et al. [6] explained completely the correlated shadowing paths BS to MS pairs. It should be noted however that most of the literature on correlation in shadowing is driven by cellular scenarios, where the BS or MS, and uplink or downlink dualities apply. Also they concerned auto-correlation, cross-correlation, generalized-correlation, time-correlation, uplinkdownlink correlation. We specially consider auto-correlation and cross-correlation.

3.1.2 Auto-correlation (serial correlation)

This model considers a transmitting base station X received by the same moving mobile (i.e. MS) Y at two moments in time $t_1$ and $t_2$ and at distinct locations $Y_1= Y(t_1)$ and $Y_2= Y(t_2)$. Alternatively, the signal may be received by two distinct mobiles $Y_1$ and $Y_2$ at the same moment in time. These scenarios may also be reversed to consider the uplink. Auto-correlation is illustrated in Fig. 2(a).

3.1.3 Cross-correlation (site-to-site correlation)

Cross-correlation, considers two transmitting base stations $Y_1$ and $Y_2$ that transmit to a common mobile receiver (i.e. MS) X. Alternatively, cross-correlation can consider a mobile transmitter X whose signal is picked up by two base stations $Y_1$ and $Y_2$. These are illustrated in Fig. 2(b). Assume that X is the common node to all paths, and located at the origin for simplicity, and all links are between X and the points $Y_i,$ i = 1 and 2, cross-correlation is the central object of study in [6].

3.1.4 Correlation coefficient

Consider two directed paths $\overrightarrow{XY_1}$ and $\overrightarrow{XY_2}$ with shadowing values $\varPsi _1$ and $\varPsi _2$, respectively. Their correlation coefficient is $\rho$. According to [6] the best model for correlation between shadowing paths is Eqs. 2, 3 and 4, with two tunable parameters $\theta _0$$( 0^\circ <\theta _0\le 180^\circ )$ and $\varOmega _0$ ($\varOmega _0$ usually in [6 dB, 20 dB]), it may be tuned to approximate many other correlation models that might have less-desirable properties.

$$\begin{aligned} \rho =h(\theta ,\varOmega )=h_\theta (\theta )h_\varOmega (\varOmega ) \end{aligned}$$

(2)

$$\begin{aligned} h(\theta ) = {\left\{ \begin{array}{ll} 1-\frac{\theta }{\theta _0} &{} \qquad \theta \le \theta _0\\ 0 &{} \qquad \theta >\theta _0 \end{array}\right. } \end{aligned}$$

(3)

$$\begin{aligned} h_\varOmega (\varOmega )=\max \left( 0,1-\frac{\varOmega }{\varOmega _0}\right) \end{aligned}$$

(4)

where $\varOmega =\frac{10}{ln 10}|ln\frac{R_1}{R_2}|$.

Fig. 4

SCS at the first moment $t_1$

Fig. 5

SCS at the next moment $t_2$

Fig. 6

SCS at the two moments $t_1$ and $t_2$ together

The quantities $\theta$, $R_1$, $R_2$, and d are illustrated in Fig. 3.

According to the cross-correlation shadowing that was explained in Sect. 3.1.3 for hexagonal cellular systems and by considering its similarity with SCS, that all the BSs are moving and transmit to a common MS, we can define cross-correlation for SCS.

3.1.5 Cross-correlation in the SCS

Consider random BSs placement at the moment $t_1$ in the SCS (see Fig. 4). The BSs, according to 2-D Poisson point process, are moving in the SCS thus random BSs placement at the next moment $t_2$ is different (see Fig. 5).

In Figs. 4 and 5, the subscript $t-n$ in $BS_{t-n}$ and $R_{t-n}$ stands for random BSs placement with $R_{t-n}$ (the separation between the $BS_{t-n}$ and the MS) at the moments $t=1$ and 2 (1 is one moment and 2 is next moment), where $n = 1,2,3,\ldots ,N$.

The moving of BSs, at the moment, causes the changing of distance between BS to MS pairs. Since the shadowing is function of distance between BS to MS pair [6], therefore MS, in transmit paths whit BSs, is affected by different shadowing factors. Recall that the shadow fading in the SCS is well modeled by a log-normal distribution [1,2,3,4,5,6,7, 10,11,12].

For more understanding of the random moving of BSs and defining of the cross-correlation between path pairs, we assume random BSs placement at the two sequential moments $t_1$ and $t_2$ together at the moment (because difference between $t_1$ and $t_2$ in two states of random BSs placement is very small). They are illustrated in Fig. 6 (composite random BSs placement in Figs. 4, and 5, is shown in the Fig. 6). According to Fig. 6, carrier server at the first the moment $t_1$, i.e. $BS_{1-1}$, moving to other placement at the next moment $t_2$, i.e. $BS_{2-1}$, and also interference servers at the first the moment $t_1$, i.e. $\{BS_{1-i}\}_{i=2}^N$, moving to other placement at the next moment $t_2$, i.e. $\{BS_{2-i}\}_{i=2}^N$. By considering Fig. 6 and defined cross-correlation in Sect. 3.1.3, we can define cross-correlation for SCS.

The received power at the MS from BSs is equal the sum of received powers at the MS at the two moments together. It is given by $P_r=KP_T\varPsi _1{R_1}^{-\varepsilon }+KP_T\varPsi _2{R_2}^{-\varepsilon }$, where K is a radio factor, and $P_T$ is transmitter power, $R_1$ is the BS to MS separation at the first moment, $R_2$ is the BS to MS separation at the next moment, ${R_1}^{-\varepsilon }$ is path-loss at the first moment, ${R_2}^{-\varepsilon }$ is path-loss at the next moment, $\varPsi _1$ is the shadowing factor at the first moment and $\varPsi _2$ is shadowing factor at the next moment. According to Sect. 3.1.3 there is correlation between $\varPsi _1$ and $\varPsi _2$.

3.2 Main results

In this section, by considering the model described in Sect. 3.1.5, we calculate an expression for probability distribution of C and I separately and finally we obtain probability distribution and tail probability for the CIR. The received power at the MS from BSs can be expressed in a more general form as $P_r=KP_T\varPsi _1{R_1}^{-\varepsilon }+KP_T\varPsi _2{R_2}^{-\varepsilon }$. The radio factor K would be a random variable to capture the variations in antenna gains and antenna orientations, but we assume K as a constant. Shadowing factor is modeled as a zero mean log-normal random variable with variance $\sigma ^2$. In probability theory, a log-normal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed with mean m and variance $\sigma ^2$, and the mean and variance of log-normal distribution are computed in term of normal distribution parameters. Thus, if the random variable $\varPsi$ is log-normally distributed, then $Z=ln(\varPsi )$ has a normal distribution. Likewise, if Z has a normal distribution, then the $\varPsi =e^Z$, has a log-normal distribution. In such case, we can write the CIR at the MS, in more general form as

$$\begin{aligned} \frac{C}{I}=\frac{P_T(\varPsi _{1-1}{R_{1-1}}^{-\varepsilon }+\varPsi _{2-1}{R_{2-1}}^{-\varepsilon })}{P_T\left( \sum _{i=2}^N (\varPsi _{1-i}{R_{1-i}}^{-\varepsilon }+\varPsi _{2-i}{R_{2-i}}^{-\varepsilon })\right) } \end{aligned}$$

(5)

where $R_{1-1}$ is the BS (carrier server) to MS separation at the first moment and $R_{2-1}$ is the BS (carrier server) to MS separation at the next moment. Then ${R_{1-1}}^{-\varepsilon }$ is path-loss between BS (carrier server) to MS at the moment and ${R_{2-1}}^{-\varepsilon }$ is path-loss between BS (carrier server) to MS at the next moment. The shadowing factor between BS (carrier server) to MS at the first moment was introduced with $\varPsi _{1-1}$ and shadowing factor between BS (carrier server) to MS at the next moment was introduced with $\varPsi _{2-1}$. $\{R_{1-i}\}_{i=2}^N$ are the BSs (interference servers) to MS separation at the first moment and $\{R_{2-i}\}_{i=2}^N$ are the BSs(interference servers) to MS separation at the next moment. Then $\{{R_{1-i}}^{-\varepsilon }\}_{i=2}^N$ are path-loss between BSs (interference servers) to MS at the first moment and $\{{R_{2-i}}^{-\varepsilon }\}_{i=2}^N$ are path-loss between BSs (interference servers) to MS at the next moment. The shadowing factors between BSs (interference servers) to MS at the first moment were introduced with $\{\varPsi _{1-i}\}_{i=2}^N$ and shadowing factors between BSs (interference servers) to MS at the next moment were introduced with $\{\varPsi _{2-i}\}_{i=2}^N$. By considering random BSs placement at the moment, the separation BS to MS pairs at the same moment is constant. Therefore, for simplicity of calculations, we consider path-loss between each BS to MS pair as constant $a=R^{-\varepsilon }$, thus

$$\begin{aligned} \frac{C}{I}=\frac{a_{1-1}\varPsi _{1-1}+a_{2-1}\varPsi _{2-1}}{\sum _{i=2}^N (a_{1-i}\varPsi _{1-i}+a_{2-i}\varPsi _{2-i})} \end{aligned}$$

(6)

To determine the probability distribution of CIR, we need to determine the probability distribution of C and I separately.

3.2.1 The probability distribution of carrier (C) by considering correlation between shadowing BS to MS path pairs

According to Eq. 6, MS receives carrier signal from two main servers (i.e. $BS_{1-1}$ and $BS_{2-1}$) that there is correlation between their shadowing BS to MS path pairs, therefore

$$\begin{aligned} C=a_{1-1}\varPsi _{1-1}+a_{2-1}\varPsi _{2-1} \end{aligned}$$

(7)

We know that multiply a constant number by log-normal random variable produces an another log-normal variable with different mean and variance, therefore in Eq. 7 we have the sum of two log-normal random variables. Nevertheless, no exact closed form formula for the distribution of the sum of several log-normal variables is known. Even the characteristic function of a log-normal random variable is not known in closed form. Therefore, several approximations have been developed such as moment matching [14], recursive methods [15], and Laplas transform method [16]. Abu-Dayya et al. [17] specifically studied Wilkinson’s approach [14] and an extension to Schwartz and Yeh’s approach [15]; their results show that among the three methods considered in this paper, wilkinson’s approach may be the best method to compute the distribution of sums of correlated log-normal random variables. Therefore, in this paper we use Wilkinson’s method to achieve probability distribution of C. In this approximation (Fenton-Wilkinson (FW)), sum of N correlated log-normal random variables is approximated with a log-normal random variable. The sum of two correlated log-normal random variables can be represented by Eq. 7. By using approximation FW, the sum of two correlated log-normal random variables is approximated with a log-normal random variable

$$\begin{aligned} C=a_{1-1}\varPsi _{1-1}+a_{2-1}\varPsi _{2-1}=a_{1-1}e^{Y_{1-1}}+a_{2-1}e^{Y_{2-1}}\cong e^Z \end{aligned}$$

(8)

where terms $Y_{1-1}$, $Y_{2-1}$ and Z are Gaussian random variables. In FW approximation [17], the mean $m_z$ and the standard deviation $\sigma _z$ of Z in Eq. 8 are derived by matching the first two moments of the both sides of Eq. 8. The first moment of C is denoted by $u_1$. Matching the first moment, one obtains

$$\begin{aligned} u_1&=E\left\{ C\right\} =E\left\{ e^Z\right\} =E\left\{ a_{1-1}e^{Y_{1-1}}+a_{2-1}e^{Y_{2-1}}\right\} =e^{m_z+\frac{{\sigma _z}^2}{2}} \\&=a_{1-1}e^{m_{y_{1-1}}+\frac{{\sigma _{y_{1-1}}}^2}{2}}+a_{2-1}e^{m_{y_{2-1}}+\frac{{\sigma _{y_{2-1}}}^2}{2}} \end{aligned}$$

(9)

where $m_z$ and ${\sigma _z}^2$ are in decibels (dB) [17]. The second moment of C is denoted by $u_2$. Matching the second moment gives

$$\begin{aligned} u_2&=E\left\{ C^2\right\} =E\left\{ e^{2Z}\right\} =E\left\{ {(a_{1-1}e^{Y_{1-1}}+a_{2-1}e^{Y_{2-1}})}^2\right\} \\&=e^{2m_z+2{\sigma _z}^2}=E\left\{ {(a_{1-1}e^{Y_{1-1}})}^2\right\} +E\left\{ {(a_{2-1}e^{Y_{2-1}})}^2\right\} \\&\quad +2a_{1-1}a_{2-1}E\left\{ e^{Y_{1-1}+Y_{2-1}}\right\} \\&={a_{1-1}}^2e^{2m_{y_{1-1}}+2{\sigma _{y_{1-1}}}^2}+{a_{2-1}}^2e^{2m_{y_{2-1}}+2{\sigma _{y_{2-1}}}^2} \\&\quad +2a_{1-1}a_{2-1}\left( e^{m_{y_{1-1}}+m_{y_{2-1}}}e^{\frac{1}{2}\left( {\sigma _{y_{1-1}}}^2+{\sigma _{y_{2-1}}}^2+2({\rho _{y_{1-1},y_{2-1}}})\sigma _{y_{1-1}}\sigma _{y_{2-1}}\right) }\right) \end{aligned}$$

(10)

Solving Eqs. 9 and 10 for mean and standard deviation of Z yields

$$\begin{aligned}&m_z=2ln(u_1)-\frac{1}{2}ln(u_2) \end{aligned}$$

(11)

$$\begin{aligned}&{\sigma _z}^2=ln(u_2)-2ln(u_1) \end{aligned}$$

(12)

Thus, we can approximate the sum of two correlated log-normal random variables with a log-normal random variable $C=e^Z$ with parameters ($m_z,{\sigma _z}^2$). The probability distribution of C is

$$\begin{aligned} f_C(C)=\frac{e^{\frac{-{\left( \frac{ln(C)-m_z}{\sigma _z}\right) }^2}{2}}}{C\sqrt{2\pi }\sigma _z} \end{aligned}$$

(13)

3.2.2 The probability distribution of interference (I) by considering correlation between shadowing BS to MS path pairs

MS receives interference signals from interference servers at the first the moment $t_1$, i.e. $\{BS_{1-i}\}_{i=2}^N$, and interference servers at the next moment $t_2$, i.e. $\{BS_{2-i}\}_{i=2}^N$, together, that there is correlation between their shadowing BS to MS path pairs, therefore

$$\begin{aligned} I&=(a_{1-2}\varPsi _{1-2}+a_{2-2}\varPsi _{2-2})+(a_{1-3}\varPsi _{1-3}+a_{2-3}\varPsi _{2-3})+\cdots \\&\quad +(a_{1-N}\varPsi _{1-N}+a_{2-N}\varPsi _{2-N}) \end{aligned}$$

(14)

where I is sum of N-1 correlated log-normal random variables. Similar to C in Sect. 3.2.1, we use FW approximation, therefore I is approximated with a log-normal random variable $I=e^w$. The sum of N correlated log-normal random variables can be represented by the expression

$$\begin{aligned} I=\sum _{i=2}^N \left( a_{1-i}\varPsi _{1-i}+a_{2-i}\varPsi _{2-i}\right) \end{aligned}$$

(15)

By using approximation FW

$$\begin{aligned} I&=\sum _{i=2}^N \left( a_{1-i}\varPsi _{1-i}+a_{2-i}\varPsi _{2-i}\right) \\&=\sum _{i=2}^N \left( a_{1-i}e^{Y_{1-i}}+a_{2-i}e^{Y_{2-i}}\right) \cong e^W \end{aligned}$$

(16)

The mean $m_w$ and the standard deviation $\sigma _w$ of W in Eq. 16 are derived by matching the first two moments of the both sides of Eq. 16. The first moment of I is denoted by $u_1$. Matching the first moment, one obtains

$$\begin{aligned} u_1&=E\left\{ I\right\} =E\left\{ e^W\right\} = E\left\{ (a_{1-2}\varPsi _{1-2}+a_{2-2}\varPsi _{2-2})+\cdots \right. \\&\quad + \left. (a_{1-N}\varPsi _{1-N}+a_{2-N}\varPsi _{2-N})\right\} =E\left\{ \sum _{i=2}^N \left( a_{1-i}e^{Y_{1-i}}+a_{2-i}e^{Y_{2-i}}\right) \right\} \\&= e^{m_w+{\frac{{\sigma _w}^2}{2}}}=\sum _{i=2}^N\left( a_{1-i}e^{m_{y_{1-i}}+\frac{{\sigma _{y_{2-i}}}^2}{2}}+a_{2-i}e^{m_{y_{2-i}}+\frac{{\sigma _{y_{2-i}}}^2}{2}}\right) \end{aligned}$$

(17)

where $m_w$ and ${\sigma _w}^2$ are in dB [17]. The second moment of I is denoted by $u_2$. Matching the second moment gives

$$\begin{aligned} u_2&=E\left\{ I^2\right\} =E\left\{ e^{2W}\right\} \\&=E\left\{ \left( (a_{1-2}\varPsi _{1-2}+a_{2-2}\varPsi _{2-2})+\cdots +(a_{1-N}\varPsi _{1-N}+a_{2-N}\varPsi _{2-N})\right) ^2\right\} \\&=E\left\{ \left( \sum _{i=2}^N (a_{1-i}e^{Y_{1-i}} +a_{2-i}e^{Y_{2-i}})\right) ^2\right\} =e^{2m_w+{2\sigma _w}^2} \\&= \sum _{i=2}^N E\left\{ \left( a_{1-i}e^{Y_{1-i}}+a_{2-i}e^{Y_{2-i}}\right) ^2\right\} \\&\quad +2\sum _{i=2}^{N-1}\sum _{j=i+1}^{N} E\left\{ \left( (a_{1-i}e^{Y_{1-i}}+a_{2-i}e^{Y_{2-i}})\left( a_{1-j}e^{Y_{1-j}}+a_{2-j}e^{Y_{2-j}}\right) \right) \right\} \\&=\mathbf{A} +\mathbf{B} \end{aligned}$$

(18)

where

$$\begin{aligned} \mathbf{A}&=\sum _{i=2}^N E\left\{ \left( a_{1-i}e^{Y_{1-i}}+a_{2-i}e^{Y_{2-i}}\right) ^2\right\} \\&=\sum _{i=2}^N E\left\{ \left( a_{1-i}e^{Y_{1-i}}\right) ^2+\left( a_{2-i}e^{Y_{2-i}}\right) ^2+2\left( (a_{1-i}e^{Y_{1-i}})(a_{2-i}e^{Y_{2-i}})\right) \right\} \\&=\sum _{i=2}^N E\left\{ \left( a_{1-i}e^{Y_{1-i}}\right) ^2+\left( a_{2-i}e^{Y_{2-i}}\right) ^2+2\left( a_{1-i}a_{2-i}e^{Y_{1-i}+Y_{2-i}}\right) \right\} \\&=\sum _{i=2}^N \left( {a_{1-i}}^2e^{2m_{y_{1-i}}+2{\sigma _{y_{1-i}}}^2}+{a_{2-i}}^2e^{2m_{y_{2-i}}+2{\sigma _{y_{2-i}}}^2}\right. \\&\quad +\left. 2a_{1-i}a_{2-i}\left( e^{m_{y_{1-i}}+m_{y_{2-i}}}e^{\frac{1}{2}({\sigma _{y_{1-i}}}^2+{\sigma _{y_{2-i}}}^2+2({\rho _{y_{1-i},y_{2-i}}})\sigma _{y_{1-i}}\sigma _{y_{2-i}})}\right) \right) \end{aligned}$$

(19)

$$\begin{aligned} \mathbf{B}&=2\sum _{i=2}^{N-1}\sum _{j=i+1}^{N} E\left\{ \left( (a_{1-i}e^{Y_{1-i}}+a_{2-i}e^{Y_{2-i}})(a_{1-j}e^{Y_{1-j}}+a_{2-j}e^{Y_{2-j}})\right) \right\} \\&=2\sum _{i=2}^{N-1}\sum _{j=i+1}^{N} E\left\{ (a_{1-i}a_{1-j}e^{Y_{1-i}+Y_{1-j}})+(a_{1-i}a_{2-j}e^{Y_{1-i}+Y_{2-j}})\right. \\&\quad \left. + (a_{2-i}a_{1-j}e^{Y_{2-i}+Y_{1-j}})+(a_{2-i}a_{2-j}e^{Y_{2-i}+Y_{2-j}})\right\} =2\sum _{i=2}^{N-1}\sum _{j=i+1}^{N} \\&\left( a_{1-i}a_{1-j}\left( e^{m_{y_{1-i}}+m_{y_{1-j}}}e^{\frac{1}{2}\left( {\sigma _{y_{1-i}}}^2+{\sigma _{y_{1-j}}}^2+2({\rho _{y_{1-i},y_{1-j}}})\sigma _{y_{1-i}}\sigma _{y_{1-j}}\right) }\right) \right. \\&\quad + a_{1-i}a_{2-j}\left( e^{m_{y_{1-i}}+m_{y_{2-j}}}e^{\frac{1}{2}\left( {\sigma _{y_{1-i}}}^2+{\sigma _{y_{2-j}}}^2+2({\rho _{y_{1-i},y_{2-j}}})\sigma _{y_{1-i}}\sigma _{y_{2-j}}\right) }\right) \\&\quad + a_{2-i}a_{1-j}\left( e^{m_{y_{2-i}}+m_{y_{1-j}}}e^{\frac{1}{2}\left( {\sigma _{y_{2-i}}}^2+{\sigma _{y_{1-j}}}^2+2({\rho _{y_{2-i},y_{1-j}}})\sigma _{y_{2-i}}\sigma _{y_{1-j}}\right) }\right) \\&\quad + \left. a_{2-i}a_{2-j}\left( e^{m_{y_{2-i}}+m_{y_{2-j}}}e^{\frac{1}{2}\left( {\sigma _{y_{2-i}}}^2+{\sigma _{y_{2-j}}}^2+2({\rho _{y_{2-i},y_{2-j}}})\sigma _{y_{2-i}}\sigma _{y_{2-j}}\right) }\right) \right) \end{aligned}$$

(20)

Therefore, we have $u_2=\mathbf{A} +\mathbf{B}$ ( Eq. 18$=$ Eq. 19$+$ Eq. 20). Solving Eqs. 17 and 18 for mean and standard deviation of W yields

$$\begin{aligned} m_w=2ln(u_1)-\frac{1}{2}ln(u_2) \end{aligned}$$

(21)

$$\begin{aligned} {\sigma _w}^2=ln(u_2)-2ln(u_1) \end{aligned}$$

(22)

Thus, we can approximate the sum of N-1 correlated log-normal random variables with a log-normal random variable $I= e^W$ with parameters ($m_w,{\sigma _w}^2$). The probability distribution of I is

$$\begin{aligned} f_I(I)=\frac{e^{\frac{-\left( \frac{ln(I)-m_w}{\sigma _w}\right) ^2}{2}}}{I\sqrt{2\pi }\sigma _w} \end{aligned}$$

(23)

3.2.3 The probability distribution of CIR by considering correlation between shadowing BS to MS path pairs

Now by obtaining the probability distribution of U, the probability distribution of CIR is found.

$$\begin{aligned} U=\frac{C}{I}=\frac{e^Z}{e^W} \end{aligned}$$

(24)

By considering Eq. 24, the probability distribution of U is

$$\begin{aligned} f_U(U)=e^{Z-W} \end{aligned}$$

(25)

where Z and W are Gaussian random variables. We consider $K=Z-W$ then

$$\begin{aligned} f_U(U)=e^K \end{aligned}$$

(26)

To calculate $f_U (U)$ (i.e. the probability distribution of CIR), first, we calculate distribution of K.

The probability distribution of subtract of two normally distributed variables Z and W with means and variances $(m_z,{\sigma _z}^2)$ and $(m_w,{\sigma _w}^2)$, respectively, is another normal distribution (i.e. $f_K(K)$) and given by

$$\begin{aligned} f_K(K)&=\int _{-\infty }^\infty \frac{e^{\frac{-Z^2}{2{\sigma _z}^2}}}{\sigma _z\sqrt{2\pi }}.\frac{e^{\frac{-W^2}{2{\sigma _w}^2}}}{\sigma _w\sqrt{2\pi }}\delta ((Z-W)-K)d_Zd_W \\&=\frac{e^{\frac{-\left( \frac{K-m_{z-w}}{\sigma _{z-w}}\right) ^2}{2}}}{\sqrt{2\pi {\sigma _{z-w}}^2}} \end{aligned}$$

(27)

where $\delta (x)$ is a delta function and

$$\begin{aligned} m_{z-w}&=m_k=m_z-m_w \end{aligned}$$

(28)

$$\begin{aligned} {\sigma _{z-w}}^2&={\sigma _k}^2={\sigma _z}^2+{\sigma _w}^2 \end{aligned}$$

(29)

Therefore, probability distribution of K is

$$\begin{aligned} f_K(K)=\frac{e^{\frac{-\left( K-(m_z-m_w)\right) ^2}{2(\sigma _z^2+\sigma _w^2)}}}{\sqrt{2\pi {(\sigma _z^2+\sigma _w^2)}}} \end{aligned}$$

(30)

Then, the probability distribution of $U=\frac{C}{I}=e^K$ (i.e. $f_U(U)$), is a log-normal with parameters ($m_k,{\sigma _k}^2$).

$$\begin{aligned} f_U(U)=f_{\textit{CIR}}(\textit{CIR})=\frac{e^\frac{-\left( \frac{ln(U)-m_k}{\sigma _k}\right) ^2}{2}}{U\sqrt{2\pi }\sigma _k} \end{aligned}$$

(31)

In [1,2,3,4,5], tail probability of the CIR performance metric is given by $prob\left\{ \frac{C}{I}>y\bigg|y\ge 1,\varepsilon \right\} =K_\varepsilon y^{\frac{-2}{\varepsilon }}$, where the constant $K_\varepsilon =prob\left\{ \frac{C}{I}>1\bigg|\varepsilon \right\}$ and $\varepsilon$ is the path-loss exponent. Therefore, we can easily calculate the tail probability of CIR, for a SCS over a generalized shadowing distribution.

$$\begin{aligned} prob\left\{ \frac{C}{I}>y\right\} =\int _{U=y}^\infty f_U(U)dU=\int _{U=1}^\infty f_U(U)dU \end{aligned}$$

(32)

By using Eq. 31 in Eq. 32, the tail probability of CIR is given by

$$\begin{aligned} prob\left\{ \frac{C}{I}>y\right\}&=\int _{U=y}^\infty \frac{e^\frac{-\left( \frac{ln(U)-m_k}{\sigma _k}\right) ^2}{2}}{U\sqrt{2\pi }\sigma _k}dU \\&=\int _{U=1}^\infty \frac{e^\frac{-\left( \frac{ln(U)-m_k}{\sigma _k}\right) ^2}{2}}{U\sqrt{2\pi }\sigma _k}dU \end{aligned}$$

(33)

3.3 Numerical example

In this section, to better understand our work, we show simple numerical example. To simplify of calculations, we only consider four BSs at any moment, that first nearest BS is main server (carrier server) and next BSs are interference servers. We assume random BSs placement distribution in at the moment $t_1$ be according to Fig. 4 with $N=4$. Moreover, the BSs, according to 2-D Poisson point process, are moving in the SCS thus random BSs placement at the next moment $t_2$ is different (see Fig. 5 with $N=4$). For more understanding of the random moving of BSs and defining of the cross-correlation between path pairs, we assume random BSs placement at the two sequential moments $t_1$ and $t_2$ together at the moment. They are illustrated in Fig. 6 (composite random BSs placement in Figs. 4 and 5, is shown at the Fig. 6).

Table 1 Parameters R, $\sigma$, a and $\varPsi$ in the numerical example

In this example, we consider values of column R in Table 1 for Fig. 6. Recall that the shadow fading in the SCS is well modeled by a log-normal distribution. Shadowing (variance of log-normal random variable) is a function of the separation between paths BS to MS pairs [6]. Then, for calculating $\sigma$ in dB using

$$\begin{aligned} \sigma (R)=10\left( 1-e^{\frac{-3R}{200}}\right) \end{aligned}$$

(34)

where R is distance between BS to MS. According to Eq. 34 and values of column R in Table 1, we obtain values of column $\sigma$s in Table 1.

According to Sect. 3.2, to calculate the CIR by considering correlation between shadowing paths we use Eq. 6 with $N=4$, where $\varPsi$s are shown in Table 1.

In this example, we assume path-loss power $\varepsilon$ is 3, then obtain values a according to column a in Table 1. For calculating correlation between shadowing paths between main server to MS path pair, i.e. $\varPsi _{1-1}$ and $\varPsi _{2-1}$, using Eqs. 2, 3, and 4.

If we assume the angle of between path pair $\theta _{1-1,2-1}={10}^\circ$, by using Eq. 3 we have $h(\theta )= 0.8333$.

According to description of Sect. 3.1.4, we have

$$\begin{aligned} \varOmega =\frac{10}{ln10}\left| ln{\frac{R_{2-1}}{R_{1-1}}}\right| = \frac{10}{ln10}\left| ln{\frac{105m}{100m}}\right| =0.5115 \end{aligned}$$

(35)

By using Eq. 4 we obtain

$$\begin{aligned} h_\varOmega (\varOmega )=\max \left( 0,1-\frac{\varOmega }{6}\right) =0.9647 \end{aligned}$$

(36)

Then by entering Eqs. 3 and 4 in Eq. 2, correlation coefficient between path pair is

$$\begin{aligned} \rho =h(\theta ,\varOmega )=h_\theta (\theta )h_\varOmega (\varOmega )=0.8333\times 0.9647=0.8039 \end{aligned}$$

(37)

For calculating probability distribution of $C=(a_{1-1}\varPsi _{1-1}+a_{2-1}\varPsi _{2-1})$, we use Eqs. 8, 9, 10, 11, and 12. Therefore $m_C=-13.4009$ dB and ${\sigma _C}^2= 62.3270$ dB.

For calculating correlation between shadowing interfering server to MS path pairs $I=\sum _{i=2}^4 (a_{1-i}\varPsi _{1-i}+a_{2-i}\varPsi _{2-i})$, we use Eqs. 2, 3, and 4. If the angle between path pairs is similar to the column $\theta$ in Table 2, then by using Eqs. 2, 3, 4, correlation between path pairs are obtained similar to the column $\rho$ in Table 2.

Table 2 Angle $\theta$ and correlation $\rho$ between path pairs in the numerical example

Also, for calculating probability distribution of I, we use Eqs. 16, 17, 18, 21, and 22.

Therefore

$m_I=-13.5681$ dB and ${{\sigma}_I}^2=74.2140$ dB. Finally for calculating the probability distribution of CIR, we enter Eqs. 28 and 29 in Eq. 31. Therefore, the distribution of CIR is a log-normal random variable with parameters $m_k= 0.1672$ dB and ${\sigma _k}^2=11.6851^2$ dB, thus CIR$\sim log-N(0.1672, 11.6851^2)$.

The tail-probability of CIR for a SCS over a generalized shadowing distribution by using Eq. 33 is

$$\begin{aligned} prob\left\{ \frac{C}{I}>y|y\ge 1\right\}&=\int _{U=y}^\infty f_U(U)dU \\&=\int _{1}^\infty \frac{1}{U\times 11.6851\sqrt{2\pi }}e^{\frac{-\left( ln(U)-0.1672\right) ^2}{2\times 11.6851^2}}dU \end{aligned}$$

(38)

4 Simulation results

In this section, the details of simulating the SCS are presented. In every single trial a random number $M\sim Poisson(\lambda )$ is generated for the number of interferer BSs, and then the BSs are placed around MS (this MS without loss of generality, is assumed to be located at the origin). The received power at the MS for each BS is computed by using the path-loss exponent $\varepsilon$ and the shadow fading. For calculating the numerical results, in every trial, the received power at the MS from each BS is computed by generating random variables for shadowing according to the $log-N(0,{\sigma _\varPsi }^2)$. Finally the CIR random variable by considering correlated shadowing and independent shadowing paths between BS to MS pairs is generated according to Eq. 5. The trial is repeated $T=10{,}000$ times and the tail probability of $\left\{ \frac{C}{I}>1\right\}$ is simulated. Mont-Carlo method is used with number of iteration $T=10{,}000$ times. Figure 7 shows the plot of $K_\varepsilon$ vs $\varepsilon$ comparing the semi analytical expression with the Monte-Carlo simulations by considering correlated shadowing and independent shadowing paths between BS to MS pairs. This shows that this work is consistent with the previous attempts (cf. Fig. 2 of [1]). As with any cellular system covering the plane, communication is impossible when the path-loss exponent is less than or equal to 2. Conversely, CIR only improves with greater attenuation. In Fig. 8, the tail probability of CIR for a SCS, over different channel models, at different BS densities are compared. Correlated shadowing increases the tail probability, as was concluded in  [2] with independent shadowing effect. Also, increasing the BS density, reduces the tail probability for all channel models; that it is because of increasing the interferer BSs. But when the number of BSs goes up, the tail probability gets approximately fixed, because the ratios of interferer distances to server distance get very high; hence the path-loss gets approximately fix. It is the same as results in [2, 5], calculated for path-loss channels. We compare the distributions of CIR for two different BS densities by considering correlated shadowing and independent shadowing paths between BS to MS path pairs, in Fig. 9. It shows that, when we consider correlated shadowing, the average of CIR is increased. Also, it is obvious that increasing the BS density leads to upper interference, and reduces the average of CIR.

Fig. 7

Comparison of the $K_\varepsilon$ obtained through Monte-Carlo simulations with that obtained from the semi-analytical expression by considering correlated shadowing and independent shadowing paths between BS to MS pairs for various path-loss exponent values $(\varepsilon )$

Fig. 8

The CIR tail probability at different BS densities, in a 2-D SCS over correlated shadowing and independent shadowing paths between BS to MS pairs $(\varepsilon = 4)$

Fig. 9

The comparison of approximate distributions of CIR for two different BS densities by considering correlated shadowing and independent shadowing paths between BS to MS pairs ($\varepsilon$ = 4)

5 Conclusion

We know that in reality between signal propagation paths there is correlation. This correlation is defined with correlation between their shadowing factors. In this paper, by considering this correlation as an important factor between BS to MS pairs, we have analyzed the performance of SCS, i.e. CIR, and determined an expression for the distribution of CIR, and then obtained the tail probability of the CIR. We compared the calculated distributions and exploited the Monte-Carlo results by simulations, in order to show the ability of approximation and correctness of the analytical expression. Also, the simulations illustrated that the correlated shadowing provides better metric performances in the SCS.