Introduction. The problem of oscillations of elastic thin-walled shells of variable thickness is one of the most pressing problems in the mechanics of deformable solids. Solutions to such problems are necessary for developing aircraft, rocketry, shipbuilding, and many other branches of engineering and construction. To date, significant progress has been made in studying dynamic processes in elements of conical structures. However, the problems of the dynamic interaction of homogeneous and inhomogeneous conical shell structures with elastic media still need to be sufficiently investigated [1,2,3]. Many publications have been devoted to studying the dynamics of conical elements with variable thickness by analytical methods. Thus, the work [4] investigated the stress-strain state of nonthin conical shells with variable thickness in two coordinate directions. The displacement and stress fields in such shells were determined and analyzed. Paper [5] presented the results of a study of the natural frequencies of a truncated cone whose thickness varies according to different laws. The minimum vibration frequencies’ dependences on the shells’ thickness are subject to a power law change (linear and quadratic, with symmetrical and asymmetrical shapes). The paper [6] investigated the bending of an elastic truncated conical shell with a meridional thickness expressed by an arbitrary function. The vibration of composite conical shells consisting of three and five layers, each consisting of different materials, is analyzed.

Study [7] analyzed the longitudinal strength of a truncated cone under hinged support. A truncated conical shell of functionally graded materials (FGM) is subjected to axial compressive loading and supported on Winkler– Pasternak elastic bases. The properties of such a shell continuously change along its thickness. Parametric studies of the power law and exponential distribution of FGM, the Winkler–Pasternak bed modulus, and the aspect ratio of the shells were performed. Paper [8] investigated the characteristics of free oscillations of a truncated conical shell of variable thickness using the Haar wavelet method, where the shell thickness varied linearly or parabolically. The influence of geometric parameters and boundary conditions on the vibration characteristics of conical shells of variable thickness was analyzed. Paper [9] studied the vibration of complete conical shells with variable thickness. In [10], an analytical approach is proposed to analyze the influence of inhomogeneity, material orthotropy, cone half-vertex angle, and other geometric parameters on the value of the critical combined load when supported on a Pasternak elastic bed. Numerical results indicate the influence of the shell characteristics, porosity distribution, porosity coefficient, and the elastic bed on the critical bending load. Paper [11] investigated the bending of an orthotropic composite truncated conical shell with a continuously varying thickness subjected to a homogeneous external pressure, a power function of time. The effects of power variations in thickness, half-top angle, power in time of external pressure, and the Young modulus ratio on critical parameters were determined. In [12], the problem of the stability of a truncated conical shell made of FGM subjected to axial compressive loading and supported by elastic beds of the Winkler-Pasternak type was analytically solved. In [13], the free vibrations of a truncated conical shell of variable thickness were investigated by two methods, and in [14], the influence of boundary conditions and variable thickness of the conical shell on the vibration behavior of composite conical shells reinforced with a mesh was determined. Paper [15] investigated the free vibrations of symmetrical and asymmetrical cross-layer composite shells of a truncated conical layer using the spline function method. The effect of transverse shear strain on frequency and taper angle parameters under different boundary conditions was analyzed.

In [16], the stability of conical shells made of FGM was investigated under a homogeneous external pressure, which is a power function of time. Assuming that the properties of FGM shells continuously changed depending on their thickness based on the power law of the distribution of the volume fractions of the components, general formulas for critical parameters were obtained. The results showed that the critical parameters were affected by the constituent materials’ configurations, loading parameter variations, taper angle variations, and external pressure changes over time. In [17], the finite element method (FEM) was used to analyze free vibrations of axisymmetric shells of variable thickness, including shear deformation and the effect of rotational inertia. In [18], a three-dimensional (3D) analysis method was presented to determine the free vibration frequencies of complete (untruncated) conical shells with linearly variable thickness. Full conical shells, free or clamped at the lower edge with a free top, were studied. Study [19] analyzed the transient dynamic and free vibration of axisymmetric truncated conical shells with FGM with uneven thickness. Two numerically efficient and accurate methods for studying the transient dynamic responses of FGM shells subjected to internal or external mechanical shock loading were introduced. The material properties were continuously evaluated in the thickness direction according to the power law distribution of the volume fraction. The influence of various geometric and material parameters on the unsteady dynamic behavior of FGM shells was investigated using ANSYS.

In works [2, 20], the axisymmetric dynamic behavior of reinforced conical shells on a Winkler elastic bed under nonstationary loads was solved by the finite-difference method, and in [21], the problem of nonaxisymmetric vibrations of a heterogeneous conical shell of variable thickness under the action of a nonstationary load was solved. A finite difference algorithm for solving this problem was presented. For a specific example, the dynamic behavior of a conical panel of variable thickness under the action of a nonstationary load was analyzed.

There are few studies of free vibrations of conical shells of variable thickness resting on a Winkler–Pasternak elastic bed [22]. After an extensive literature review, we found only one article, which analyzed the dynamic behavior of a conical shell of variable thickness under unsteady loading on a Winkler elastic bed [23], which presented the problem statement and developed a finite-difference algorithm for its solution. The differential equations of the motion system were based on applying the Timoshenko-type shell theory. The dynamic characteristics of axisymmetric conical shells of variable thickness on a Winkler elastic bed under the action of an internal pulse load in the form of a semi- sinusoid were studied.

The Winkler model [24] is the simplest model of an elastic bed, for the description of which a single elastic bed coefficient C1 (kN/m3), which determines the relationship between the response of the elastic bed and the radial displacements of points on the median surface of the conical shell. A closer approximation of the elastic bed is the two-parameter Pasternak model of the elastic bed [25], in which the elastic bed’s second coefficient C2 (kN/m) characterizes the work of the elastic bed under shear.

This situation stimulates the study of the dynamic characteristics of conical shells of variable thickness on a Pasternak elastic bed under nonstationary loads.

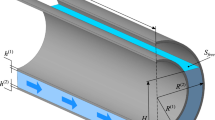
Problem Formulation and Basic Equations. Consider a sheared conical shell of variable thickness on a Pasternak elastic bed. The conical shell, which is inhomogeneous in thickness, is subjected to an internal distributed load P3(s1, t), where s1 and t are the spatial and temporal coordinates.

When considering axisymmetric vibrations of conical shells, the coordinate system is used s, t, where the coordinate s coordinate is taken from the cone vertex. In some cases, in particular, for cut conical shells, it is rational to use the coordinate s1 coordinate, calculated from the shell’s cut edge. We will assume that the general coordinate system refers to the shell’s median surface with a thickness h = h(s1). The coordinate z will be counted to increase the length of the outer normal to the original surface.

The coefficients of the first quadratic form and curvature of the coordinate surface are written as follows: A1 = 1, A2 = Rs, k1 = 0, k2 = cos θ/Rs, where 0 is the taper angle, Rs = R0 + s1 sin θ, and s1 is the current coordinate.

Based on the theory of shear deformation in shells [26], the displacements u1(s1) and u3(s1) in a conical shell of variable thickness in the direction s1 (longitudinal), z-coordinate and t (time) at small linear displacements are expressed by the following relationships:

$$\begin{array}{c}{u}_{l}\left({s}_{1},z,t\right)={u}_{1}\left({s}_{1},t\right)+z{\varphi }_{1}\left({s}_{1},t\right),\\ {u}_{3}\left({s}_{1},z,t\right)={u}_{3}\left({s}_{1},t\right),\end{array}$$
(1)

where <φ1(s1, t) is the normal rotation angle to the conical shell’s median surface.

The following formulas describe the deformations:

$$\begin{array}{c}{\varepsilon }_{11}=\frac{\partial {u}_{1}}{\partial {s}_{1}}, {\varepsilon }_{22}=\frac{1}{{A}_{2}}\frac{\partial {A}_{2}}{\partial {s}_{1}}{u}_{1}+{k}_{1}{u}_{3}, {\varepsilon }_{11}={\varphi }_{1}+\frac{\partial {u}_{3}}{\partial {s}_{1}}\\ {K}_{11}=\frac{\partial {\partial }_{1}}{\partial {s}_{1}}, {K}_{22}=\frac{1}{{A}_{2}}\frac{\partial {A}_{2}}{\partial {s}_{1}}{\varphi }_{1}.\end{array}$$
(2)

The Hamilton–Ostrogradsky variational principle was used to derive the following equation of vibration of the shell structure:

$${\int }_{{t}_{1}}^{{t}_{2}}\left[\delta \left(\Pi -T\right)\delta A\right]=0,$$
(3)

where П is the potential energy of the system, taking into account Pasternak’s external environment, T is kinetic energy, A is the work of external forces, and t1 and t2 are fixed moments of time.

The expressions for the variations of the total potential and kinetic energy of these components are written in the form:

$$\begin{array}{c}\delta\Pi ={\int }_{S}\left[{\int }_{-\frac{h}{2}}^\frac{h}{2}\left(\begin{array}{c}\delta {T}_{11}{\varepsilon }_{11}+\delta {T}_{22}{\varepsilon }_{22}+{T}_{13}\delta {\varepsilon }_{13}+{M}_{11}\delta {\upkappa }_{11}+{M}_{22}\delta {\upkappa }_{13}\\ +{C}_{1}{u}_{3}\delta {u}_{3}+{C}_{2}\frac{{\partial u}_{3}}{{\partial s}_{1}}\delta \frac{{\partial u}_{3}}{{\partial s}_{1}}\end{array}\right)dz\right]dS,\\ \delta T={\int }_{S}\left[{\int }_{-\frac{h}{2}}^\frac{h}{2}\rho h\left({s}_{1}\right)\left(\frac{{\partial }^{2}{u}_{1}}{\partial {t}^{2}}\partial {u}_{1}+\frac{{\partial }^{2}{u}_{3}}{\partial {t}^{2}}\partial {u}_{3}\right)+\rho \frac{h{\left({s}_{1}\right)}^{3}}{12}\left(\frac{{\partial }^{2}{u}_{1}}{\partial {t}^{2}}\partial {\varphi }_{1}\right)dz\right]dS.\end{array}$$
(4)

After the standard transformations in the variational equation (3), taking into account the relations (4), we obtain the hyperbolic equations of motion of a conical shell of variable thickness located in the Pasternak elastic bed under the action of an axisymmetric pulse load, boundary, and initial conditions:

$$\begin{array}{c}\frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{T}_{11}\right)-\frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{T}_{22}\right)=\rho h\left({s}_{1}\right)\frac{{\partial }^{2}{u}_{1}}{\partial {t}^{2}},\\ \frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{T}_{13}\right)-{k}_{2}{T}_{22}+{C}_{1}{u}_{3}-{C}_{2}\frac{{\partial }^{2}{u}_{3}}{\partial {s}_{1}^{2}}{P}_{3}\left({s}_{1}\right)=\rho h\left({s}_{1}\right)\frac{{\partial }^{2}{u}_{3}}{\partial {t}^{2}},\\ \frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{M}_{22}\right)-{T}_{13}=\rho \frac{{h}^{3}\left({s}_{1}\right)}{12}\frac{{\partial }^{2}{\varphi }_{1}}{\partial {t}^{2}}.\end{array}$$
(5)

The ratios for forces and moments are determined according to the formulas:

$$\begin{array}{c}{T}_{11}={B}_{11}\left({s}_{1}\right)\left({\varepsilon }_{11}+v{\varepsilon }_{11}\right),{T}_{22}={B}_{22}\left({s}_{1}\right)\left({\varepsilon }_{22}+v{\varepsilon }_{11}\right),{T}_{13}={B}_{13}\left({s}_{1}\right){\varepsilon }_{11},\\ {M}_{11}={D}_{11}\left({s}_{1}\right)\left({\kappa }_{11}+v{\kappa }_{11}\right);{M}_{22}={D}_{22}\left({s}_{1}\right)\left({\kappa }_{22}+v{\kappa }_{11}\right),\\ \begin{array}{c}{B}_{11}\left({s}_{1}\right)=\frac{Eh\left({s}_{1}\right)}{1-{v}^{2}},{B}_{13}\left({s}_{1}\right)={G}_{13}h\left({s}_{1}\right),\\ {B}_{11}\left({s}_{1}\right)=\frac{{Eh}^{3}\left({s}_{1}\right)}{12\left(1-{v}^{2}\right)},{D}_{22}\left({s}_{1}\right).\end{array}\end{array}$$
(6)

In formulas (1)-(6), u1(s1, t), u3(sq, t), φ1(s1, t) are the components of the generalized displacement vector of the middle surface of the shell, h(s1) is the variable thickness of the shell, ρ is the density of the shell material, E and v are the physical and mechanical parameters of the shell material, Pasternak elastic bed parameters are C1 = 0.25×l08 N/m3 and C2 = 0.25×l06 N/m.

To calculate the stiffness characteristics of the shell, the thickness h is defined as a linear function of the coordinate s1:

$$\begin{array}{c}h\left({s}_{1}\right)=h\left({s}_{10}\right)+\left[h\left({s}_{1N}\right)-h\left({s}_{10}\right)\right]\frac{{s}_{1}}{L},\\ {s}_{1N}-{s}_{10}=L, {s}_{10}\le {s}_{1}\le {s}_{1N}.\end{array}$$
(7)

The corresponding boundary and initial conditions supplement equation (5).

In the case of a rigidly fixed edge at s1 = s10 and s1 = s1N, the boundary conditions are as follows:

$${u}_{1}={u}_{3}={\varphi }_{1}=0.$$
(8)

The initial conditions are written as follows:

$$\begin{array}{c}{u}_{1}={u}_{3}={\varphi }_{1}=0.\\ \frac{{\partial u}_{1}}{\partial t}=\frac{{\partial u}_{3}}{\partial t}=\frac{{\partial \varphi }_{1}}{\partial t}=0.\end{array}$$
(9)

Numerical Algorithm for Solving the Equations of Axisymmetric Vibrations of Conical Shells of Variable Thickness on an Elastic Bed. Initial boundary-value problems of the theory of conical shells of variable thickness will be solved using numerical methods, and their subsequent numerical implementation will be done on computers. In particular, the method of finite differences is used for the tasks at hand. To create a numerical algorithm, we use the integral-interpolation method of constructing difference schemes in spatial coordinates and an explicit finite difference scheme for integrating in the time coordinate [1].

Thus, equations (5)–(9) represent the formulation of the problem of vibrations of conical shells of variable thickness, which are located on a Pasternak elastic bed under nonstationary axisymmetric loading.

The construction of a numerical algorithm begins with constructing a difference grid. let’s divide the interval [s10, s1N] (s10 = 0, s1N = L) into N equal parts with a step ∆s1 = L/N and get a grid with discrete nodes, ∆s1l = ∆s10 + ∆s1l, l = \(\stackrel{-}{l,N}.\) Along with the main difference grid, an auxiliary difference grid is introduced s1l±1/2, corresponding to the values of s1 in the half-nodes. At the time coordinate t, a similar grid is introduced on the interval [0; T] with a breakdown into N1 equal subintervals with a step τ = T/N1, τn = nτ. An auxiliary time grid is also introduced τn∓1/2 corresponding to the values t in the half-nodes. Using an explicit “cross” scheme in the time coordinate allows one to preserve the divergent form of the difference representation of differential equations and fulfill the law of conservation of total mechanical energy at the difference level [l].

In the following, we denote the displacements of the generalized vector of the conical shell as follows:

$${u}_{1},{u}_{3},{\varphi }_{1}\to {\left({u}_{1}\right)}_{1}^{n}, {\left({u}_{3}\right)}_{1}^{n}, {\left({\varphi }_{1}\right)}_{1}^{n}.$$
(10)

We will use the integral-interpolation method of creating finite-difference schemes for hyperbolic equations to construct difference schemes of the vibration equations of conical shells of variable thickness under unsteady loads [2]. According to this approach, we write equations (5) as follows in the domain:

$$\begin{array}{c}{s}_{1i-l/2}\le {s}_{1}\le {s}_{1i+1/2}, {t}^{n-\frac{1}{2}}\le t\le {t}^{n+\frac{1}{2}},\\ {s}_{1i-1/2}={s}_{it}-\Delta {s}_{1/2}, {s}_{1i+1/2}={s}_{1i}+\Delta {s}_{1/2},\\ \begin{array}{c}\underset{{s}_{1i-1/2}}{\overset{{s}_{1i+1/2}}{\int }}\left[\frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{T}_{11}\right)-\psi {T}_{22}\right]{ds}_{1}=\underset{{s}_{1i-1/2}}{\overset{{s}_{1i+1/2}}{\int }}\left[\frac{{\partial }^{2}{u}_{1}}{\partial {t}^{2}}\right]{ds}_{1},\\ \underset{{s}_{1i-1/2}}{\overset{{s}_{1i+1/2}}{\int }}\left[\frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{T}_{13}\right)-{k}_{2}{T}_{22}+{C}_{1}{u}_{3}-{C}_{2}\frac{{\partial }^{2}{u}_{3}}{\partial {s}_{1}^{2}}+{P}_{3}\left({s}_{1},t\right)\right]{ds}_{1}=\underset{{s}_{1i-1/2}}{\overset{{s}_{1i+1/2}}{\int }}\left[\rho h\frac{{\partial }^{2}{u}_{1}}{\partial {t}^{2}}\right]{ds}_{1},\\ \underset{{s}_{1i-1/2}}{\overset{{s}_{1i+1/2}}{\int }}\left[\frac{1}{{A}_{2}}\frac{\partial }{\partial {s}_{1}}\left({A}_{2}{M}_{11}\right)-\psi {M}_{22}-{T}_{13}\right]{ds}_{1}=\underset{{s}_{1i-1/2}}{\overset{{s}_{1i+1/2}}{\int }}\left[\rho h\frac{{h}^{3}}{12}\frac{{\partial }^{2}{u}_{2}}{\partial {t}^{2}}\right]{ds}_{1}.\end{array}\end{array}$$
(11)

After standard transformations in relations (11), we obtain the following difference approximations of equations (5):

$$\begin{array}{c}\frac{1}{{A}_{2i}}\frac{{\left({A}_{2}{T}_{11}^{n}\right)}_{i+1/2}-{\left({A}_{2}{T}_{11}^{n}\right)}_{i-1/2}}{{As}_{1}}-{\psi }_{1}\frac{{T}_{22i+1/2}^{n}+{T}_{22i-1/2}^{n}}{2}=\rho h\left({s}_{1i}\right){\left({u}_{1i}^{n}\right)}_{t\overline{t} },\\ \frac{1}{{A}_{2i}}\frac{{\left({A}_{2}{T}_{13}^{n}\right)}_{i+1/2}-{\left({A}_{2}{T}_{13}^{n}\right)}_{i-1/2}}{{As}_{1}}-{k}_{2i}\frac{{T}_{22i+1/2}^{n}+{T}_{22i-1/2}^{n}}{2}+{P}_{3}\left({s}_{1},{t}^{n}\right)+{C}_{1}{u}_{3i}^{n}-{C}_{2}\frac{{u}_{3,i+1}^{n}-{u}_{3,i}^{n}+{u}_{3,i-1}^{n}}{\Delta {s}_{1}^{2}}\\ \begin{array}{c}=\rho h\left({s}_{1i}\right){\left({u}_{3i}^{n}\right)}_{t\overline{t} },\\ \frac{1}{{A}_{2i}}\frac{{\left({A}_{2}{M}_{11}^{n}\right)}_{i+1/2}-{\left({A}_{2}{M}_{11}^{n}\right)}_{i-1/2}}{{\Delta s}_{1}}-{\psi }_{1}\frac{{M}_{22i+1/2}^{n}+{M}_{22i-1/2}^{n}}{2}-\frac{{T}_{13i+1/2}^{n}+{T}_{13i-1/2}^{n}}{2}=\rho \frac{{h}^{3}\left({s}_{1i}\right)}{12}{\left({\varphi }_{1i}^{n}\right)}_{t\overline{t} }.\end{array}\end{array}$$
(12)

In equations (12), discrete functions and derivatives are notated according to [2]. As follows from equations (12), the magnitudes of forces and moments are correlated with the difference points in semi-integer nodes in the spatial coordinate and in integer nodes in the time coordinate:

$$\left({T}_{11},{T}_{13},{T}_{22},{M}_{11},{M}_{22},\right)\to \left({T}_{11{s}_{1}+1/2}^{n},{T}_{13{s}_{1}+1/2}^{n},{T}_{22{s}_{1}+1/2}^{n},{M}_{11{s}_{1}+1/2}^{n},{M}_{11{s}_{1}+1/2}^{n}\right).$$

Given this, the difference relations for forces and moments (6) are as follows:

$$\begin{array}{c}{T}_{11{s}_{1}+1/2}^{n}={B}_{11}\left({S}_{1i+1/2}^{n}\right)\left({\varepsilon }_{11i+1/2}^{n}+{\mu }_{2}{\varepsilon }_{22i+1/2}^{n}\right),\\ {T}_{22{s}_{1}+1/2}^{n}={B}_{22}\left({S}_{1i+1/2}^{n}\right)\left({\varepsilon }_{11i+1/2}^{n}+{\mu }_{1}{\varepsilon }_{11i+1/2}^{n}\right),\\ \begin{array}{c}{T}_{13i+1/2}^{n}={B}_{13}\left({S}_{1i+1/2}^{n}\right){\varepsilon }_{13i+1/2}^{n},\\ {M}_{11{s}_{1}+1/2}^{n}={D}_{11}\left({S}_{1i+1/2}^{n}\right)\left({k}_{11i+1/2}^{n}+{\mu }_{2}{k}_{22i+1/2}^{n}\right),\\ {M}_{22i+1/2}^{n}={D}_{22}\left({S}_{1i+1/2}^{n}\right)\left({k}_{22i+1/2}^{n}+{\mu }_{2}{k}_{22i+1/2}^{n}\right),\end{array}\end{array}$$
(13)

and for equations (2):

$$\begin{array}{c}{\varepsilon }_{11i+1/2}^{n}=\frac{{u}_{1i+1,j}^{n}-{u}_{1i,j}^{n}}{\Delta {s}_{1}},{\varepsilon }_{11 i-2,j}^{n}=\frac{{u}_{1i+1,j}^{n}-{u}_{1i,j}^{n}}{\Delta {s}_{1}},\\ {\varepsilon }_{22 i+1/2}^{n}={\psi }_{i+1/2}\bullet {u}_{1i+1/2,j}^{n}+{k}_{2i+1/2}^{n}\bullet {u}_{3i+1/2,j}^{n},\\ \begin{array}{c}{\varepsilon }_{22 i-1/2}^{n}={\psi }_{i+1/2}\bullet {u}_{1i-1/2,j}^{n}+{k}_{2i-1/2}^{n}\bullet {u}_{3i-1/2,j}^{n},\\ {\varepsilon }_{13 i+1/2,j}^{n}=\frac{{u}_{3i+1,j}^{n}-{u}_{3i,j}^{n}}{\Delta {s}_{1}}+{\varphi }_{1i+1/2,j}^{n},\\ \begin{array}{c}{\varepsilon }_{13 i-1/2,j}^{n}=\frac{{u}_{3i,j}^{n}-{u}_{3i-1,j}^{n}}{\Delta {s}_{1}}+{\varphi }_{1i-1/2,j}^{n},\\ {k}_{11 i+1/2,j}^{n}=\frac{{u}_{1i+1,j}^{n}-{\varphi }_{3i,j}^{n}}{\Delta {s}_{1}},{k}_{11 i-1/2,j}^{n}=\frac{{\varphi }_{1i,j}^{n}-{\varphi }_{1i,j}^{n}}{\Delta {s}_{1}},\\ \begin{array}{c}{k}_{22 i+1/2,j}^{n}={\psi }_{i+1/2}\bullet {\varphi }_{1i-\frac{1}{n},j}^{n},\\ {k}_{22 i-1/2,j}^{n}={\psi }_{i-1/2}\bullet {\varphi }_{1i-\frac{1}{n},j}^{n}.\end{array}\end{array}\end{array}\end{array}$$
(14)

From the above formulas, it follows that the numerical algorithm for solving the problem consisted of a sequence of the following steps:

At the nth time interval, the values of the corresponding deformations, forces, and moments were calculated along the spatial coordinate;

The values of the generalized displacement vector component were calculated from the corresponding values of deformations, forces, and moments.

According to formulas (11)–(14), the difference scheme is explicit in the time coordinate. Thus, it is conditionally stable in spatial and temporal coordinates, i.e., there is a dependence between the quantities τ and ∆s1. The calculations also depend on the geometric, physical, and mechanical parameters of conical shells of variable thickness, under which the computational process is stable. In the future, when considering the numerical solution to the problems of axisymmetric vibrations of conical shells of variable thickness, we will proceed from the following formulas for the values of the difference steps ∆s1 and τ. Given that an explicit finite-difference scheme was used, the difference steps were chosen based on the following condition:

$$\tau \le K\Delta {s}_{1}/{c}_{1},$$

where \({c}_{1}^{2}=\frac{E}{\left[p\left(1-{v}^{2}\right)\right]},K\) is the Courant number, setting the time step requirements of a transient simulation. In the calculations, we assumed K = 0.3–0.5, given the practical convergence of the results.

In matrix-vector form, the difference equations (11)–(14) can be written as follows:

$$\left[C\right]\overline{U }+\left[M\right]\frac{{\partial }^{2}\overline{U}}{\partial {t }^{2}}=\overline{F }\left(t\right), \left[C\right]\overline{U }+\left[M\right]\frac{{\partial }^{2}\overline{U}}{\partial {t }^{2}}=\left(t\right),$$
(15)

where [M] and [C]are the mass and stiffness matrices of the discrete difference system, \(\left|\overline{U }\right|\) and \(\left|\overline{F }\right|\) are the vectors of discrete displacements and external load.

Assuming that the matrix [M] is non-degenerate, the last equation (15) is given in the form

$$\left[C\right]\overline{U }+\frac{{\partial }^{2}\overline{U}}{\partial {t }^{2}}={\left[M\right]}^{-1}\overline{F }\left(t\right), \left[D\right]\overline{U }+\left[M\right]\frac{{\partial }^{2}\overline{U}}{\partial {t }^{2}}=\left(t\right),$$
(16)

where the matrix [D] = [M]-1[C].

Earlier [2], it was established that when using an explicit finite difference scheme for integrating equations, a necessary condition for the stability of difference equations is the condition of the form

$$\tau \le \frac{2}{{\Omega }_{{\text{max}}}}=2,$$
(17)

where Ωmax is the maximum frequency of natural oscillations of the difference system, and β[D] is the upper limit of the matrix spectrum [D].

Using the Gershgorin theory to estimate the value of P[D) from above, using Gershgorin’s theorem, we obtain

$$\beta ={\Omega }_{max}^{2}\le {\text{max}}{\sum }_{i}\left|{d}_{iy}\right|,\beta ={{\Omega }_{{\text{max}}}}^{2}\le {\text{max}}\left|{d}_{ij}\right|,$$
(18)

where dij are the elements of the matrix [D].

The stability condition for the difference equations is as follows:

$$\tau \le 2{\Omega }_{max}.$$
(19)

Here Ωmax is determined from the following inequalities:

$$\begin{array}{c}{\Omega }_{max}^{2}\le {\text{max}}\left({\Omega }_{max0}^{2}\right),\\ {\Omega }_{max}^{2}\le {\text{max}}\left({\left[{\Omega }_{1}\right]}^{2},{\left[{\Omega }_{2}\right]}^{2},{\left[{\Omega }_{3}\right]}^{2}\right),\end{array}$$
(20)

where [Ω1]2, [Ω2]2, [Ω3]2 are determined by the following relations:

$$\begin{array}{c}{\left[{\Omega }_{1}\right]}^{2}=\frac{E}{\rho \left(1-{v}^{2}\right)}\left[\frac{4}{\Delta {\left({s}_{1}\right)}^{2}}+\left(\frac{1}{R\Delta {s}_{1}}\right)\right],\\ {\left[{\Omega }_{2}\right]}^{2}=\frac{E}{\rho \left(1-{v}^{2}\right)}\left\{\frac{12{G}_{13}\left(1-{v}^{2}\right)}{{\text{E}}}\left[\frac{1}{\Delta {s}_{1}h}+\frac{4}{\Delta {\left({s}_{1}\right)}^{2}}\right]+\left[\frac{4}{{R}^{2}}+v\left(\frac{1}{R\Delta {s}_{1}}\right)\right]\right\},\\ {\left[{\Omega }_{3}\right]}^{2}=\frac{E}{\rho \left(1-{v}^{2}\right)}\left\{\frac{4}{\Delta {\left({s}_{1}\right)}^{2}}+\frac{12{G}_{13}\left(1-{v}^{2}\right)}{{\text{E}}}\left[\frac{1}{\Delta {s}_{1}h}+\frac{4}{{h}^{2}}\right]\right\}.\end{array}$$
(21)

Numerical Results. As a numerical example for axisymmetric vibrations, consider the problem of the dynamic behavior of a sheared conical shell of variable thickness on the Pasternak elastic bed (5) with rigidly clamped edges under the action of a normally distributed load P3(s1, t).

The boundary and initial conditions are as follows:

$${u}_{1}={u}_{3}={\varphi }_{1}=0$$

at t = 0:

$${u}_{1}={u}_{3}={\varphi }_{1}=\frac{\partial {u}_{1}}{\partial t}=\frac{\partial {u}_{3}}{\partial t}=\frac{\partial {\varphi }_{1}}{\partial t}=0.$$
(22)

The geometric parameters of the shell thickness were set as follows: h(s10) = 0.5×10–2 m, h(s1N) = 10–2 m, R0 = 0.3 м, L = 0.4 m, and physico-mechanical parameters are E = 7×1010 Pa, v = 0.3, ρ = 2.7×103 kg/m3. Pasternak elastic bed parameters were C1 = 0.25×108 N/m3 and C2 = 0.25×106 N/m.

The nonstationary pulse load was set according to the formulas:

$${P}_{3}\left({s}_{1},t\right)=\left\{\begin{array}{cc}A\left(1-\frac{t}{T}\right)& \left(0\le t\le T\right),\\ 0& \left(t>T\right).\end{array}\right\}$$
(23)

where A = 106 Pa, T = L/c = 5 × 10-5 s, c is the longitudinal wave velocity in the metal of the conical shell.

An isotropic conical shell of variable thickness was considered with the following parameters.

Option 1: θ = π/6 at R0 = 0.3 m, L = 0.4 m. The conical shell’s first natural frequencies were 781.57 Hz (t = 14.7T) with no elastic bed, 851.91 Hz with the Winkler elastic bed, and 883.18 Hz with the Pasternak elastic bed.

Option 2: θ = π/4 at R0 = 0.3 m, L = 0.4 m. The conical shell’s first natural frequencies were 687.22 Hz (t = l8.3T) without an elastic bed, 769.69 Hz with the Winkler elastic bed, and 7833.43 Hz with the Pasternak elastic bed.

We assessed the dynamic behavior of a conical shell of variable thickness on the Pasternak elastic bed with the above parameters. Numerical calculations were performed for the time interval 0 ≤ t ≤ 40T.

Figure 1 shows the change in the maximum normal displacements u3 depending on the spatial coordinate s1 at the instant t = 14.7T (it is assumed that this instant corresponds to the achievement of the maximum value of u3 at the studied time interval) at θ = π/6. Hereafter, the displacements u3 are given in m.

Fig. 1.
figure 1

Dependence of maximum deflections u3 on the spatial coordinate s1 at t = 14.7T for θ = π/6. Here and in Figs. 2–8: (1) corresponds to the conical shell of variable thickness with no elastic bed, (2) with the Winkler elastic bed, and (3) with the Pasternak elastic bed.

Full size image

Thus, the maximum deflections u3 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 29 and 40%, respectively. In turn, the first natural frequency with no elastic bed was lower than those with the Winkler and Pasternak elastic beds by 12 and 14%, respectively.

Figure 2 shows the dependence of the maximum values of stresses σ22 on the spatial coordinate s1 at the instant t = 14.7T at 0 = π/6. Hereinafter, the stresses σ22 are given in Pa.

Fig. 2.
figure 2

Dependence of maximum stress values σ22 on the spatial coordinate s1 at t = 14.7T for θ = π/6.

Full size image

The maximum stresses σ22 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 23 and 35%, respectively.

Figure 3 shows the dependence of the maximum deflections u3 on the spatial coordinate s1 at the instant t = 18.3T at 0 = π/4.

Fig. 3.
figure 3

Dependence of maximum deflections u3 on the spatial coordinate s1 at t = 18.3T for θ = π/4.

Full size image

The maximum deflections u3 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 39% and 51%, respectively.

In turn, the first natural frequency with no elastic bed was lower than those with the Winkler and Pasternak elastic beds by 12 and 14%, respectively.

Figure 4 shows the dependence of the maximum stress values σ22 on the spatial coordinate s1 at the instant t = 18.3r at 0 = π/4.

Fig. 4.
figure 4

Dependence of maximum stress values σ22 on the spatial coordinate s1 at t = 18.3T for 0 = π/4.

Full size image

The maximum stresses σ22 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 28% and 55%, respectively.

The following geometric parameters of the shell thickness were set: h(s10) = 0.5×10–2 m, h(s1N) = 10–2 m, R0 = 0.1 m, L = 0.4 m, E = 7×1010 Pa, v = 0.3, ρ = 2.7×103 kg/m3. Pasternak elastic bed parameters were C1 = 0.25×108 N/m3 and C2 = 0.25×106 N/m.

An isotropic conical shell of variable thickness was considered with the following parameters.

Option 1: θ = π/6 at R0 = 0.1 m, L = 0.4 m. The conical shell’s first natural frequencies were 1169.70 Hz (t = 8.6T) with no elastic bed, 1268.4 Hz with the Winkler elastic bed, and 1381.9 Hz with the Pasternak elastic bed.

Option 2: θ = π/4 at R0 = 0.1 m, L = 0.4 m. The conical shell’s first natural frequencies were 976.34 Hz (t = 12.1T) with no elastic bed, l093.5 Hz with the Winkler elastic bed, and 1113.2 Hz with the Pasternak elastic bed.

Figure 5 shows the dependence of the maximum deflections u3 on the spatial coordinate s1 at the instant t = 8.6T.

Fig. 5.
figure 5

Dependence of maximum deflections u3 on the spatial coordinate s1 at t = 8.6T for θ = π/6.

Full size image

The maximum deflections u3 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 31 and 43%, respectively. In turn, the first natural frequency with no elastic bed was lower than those with the Winkler and Pasternak elastic beds by 12 and 14%, respectively.

Figure 6 shows the dependence of the maximum stress values σ22 on the spatial coordinate s1 at the instant t = 8.6T at 0 = π/6.

Fig. 6.
figure 6

Dependence of maximum stress values σ22 on the spatial coordinate s1 at t = 8.6T for θ = π/6.

Full size image

The maximum stresses σ22 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 35 and 43%, respectively.

Figure 7 shows the dependency of maximum deflections u3 on the spatial coordinate s1 at the instant t = 12.1T at θ = π/4.

Fig. 7.
figure 7

Dependence of maximum deflections u3 on the spatial coordinate s1 at t = 12.1T for θ = π/4.

Full size image

The maximum deflections u3 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 28% and 41%, respectively. In turn, the first natural frequency with no elastic bed was lower than those with the Winkler and Pasternak elastic beds by 8.4 and l8%, respectively.

Figure 8 shows the dependence of the maximum stress values σ22 on the spatial coordinate s1 at the instant t = 12,1T at 0 = π/4.

Fig. 8.
figure 8

Dependence of maximum stress values σ22 on the spatial coordinate s1 at t = 12.1T for θ = π/4.

Full size image

The maximum stresses σ22 with no elastic bed exceeded those with the Winkler and Pasternak elastic beds by 42 and 55%, respectively.

Thus, the above plots made it possible to analyze in detail the stress-strain state of a conical shell of variable thickness on an elastic bed at specified parameters under the action of a nonstationary load.

Conclusions. The finite-difference method analyzed transient processes in axisymmetric sheared conical shells of variable thickness under nonstationary loading. The integral-interpolation method of constructing difference schemes in spatial coordinates and an explicit finite-difference integration scheme in the time coordinate were used to create the numerical algorithm. Using the explicit cross scheme in the time coordinate allows for preserving the divergent form of the difference representation of the differential equations and fulfilling the law of conservation of total mechanical energy at the difference level. The stability conditions of the difference equations are investigated. Calculations show that maximum deflections u3 with no elastic bed exceeded those with the Pasternak elastic bed by 40% at R0 = 0.3 and θ = 30° and by 51% at R0 = 0.3 and θ = 45°. In the case of R0 = 0.1, the maximum deflections u3 drop by 43% at θ = 30° and by 41% at θ = 45°. The maximum compressive circumferential stresses σ22 are achieved in the region of the cut edge of the shell and tend to decrease by 43% at θ = 30° and by 55% at θ = 45° due to the influence of the Pasternak elastic bed. The change in R0 and the taper angle θ significantly affects the natural frequency of a conical shell of variable thickness: it amounts to 781.57 Hz at θ = 30° and R0 = 0.3 m, reaching 687.22 Hz at θ = 45°, while at R0 = 0.1 m, it increases by 50 and 42%. The presence of a Pasternak elastic bed contributes to the increase in the natural frequency of a conical shell of variable thickness. Consequently, it is possible to create a structure of a conical shell of variable thickness on a Pasternak elastic bed with predictable dynamic behavior under unsteady loading.

Conflict of Interests. All authors declare that they have no conflicts of interest.