1 Introduction

Liquid or gas containing coaxial cylindrical shells constitute, an integral part of many industrial applications and are used in various fields of engineering. For a long time, they have served as an object of numerous theoretical studies. Obviously, papers [1, 2] are the pioneer works in this field of research. The first is concerned with axisymmetric-free vibrations of a finite cylindrical shell, which is in contact with the layer of a quiescent fluid. The second determines the critical velocities of the gas flow between two infinite shells, one of which is perfectly rigid. These papers present the general formulation of the problem, in which the liquid is modeled in the acoustic approximation. Later, this formulation has been widely used by many authors. An extensive survey of the literature devoted to the analysis of coaxial shells, interacting with both quiescent and flowing fluids, is presented in monograph [3]. Below, there is a brief review of only those publications, in which various aspects of hydroelastic stability are investigated in the framework of the linear formulation.

The effect of the flowing fluid on the dynamic behavior of infinitely long coaxial shells was investigated in [4]. Here, for the first time, an analytical solution was proposed for such a system, in which an incompressible fluid flows not only in the annular channel, but also in the inner shell. Coaxial shells of finite length with a perfectly rigid or elastic outer shell were investigated more comprehensively for the shells clamped at two ends and for the cantilevered shells. In the analytical models [5, 6], the motion of the shells was described using the Flügge theory of thin shells. Generalized hydrodynamic forces were defined within the framework of the potential theory and calculated using the Fourier transform. The solution of the problem was found by the Galerkin method. The experimental data obtained in [7] demonstrate that in the case of a rigid outer shell the loss of stability occurs at flow velocities which are much smaller than the velocities predicted by the analytical model. The discrepancy between the analytical and experimental results is due to imperfections of the shell shape. In [8], it was suggested that for pinned-pinned shells a simple approximate theory be used to evaluate the dynamic behavior of a system of coaxial shells interacting with an incompressible fluid. It has been shown that in the case of a quiescent fluid the predicted natural vibration frequencies and the critical velocities responsible for the loss of stability are in good agreement with the available numerical results. In [9], the parametric analysis of the stability of coaxial shells interacting with two flows of an ideal compressible fluid was performed for different combinations of boundary conditions using the finite element method.

In some publications, different approaches were used to take into account the viscosity of a quiescent or flowing liquid. In [10], a solution of the three-dimensional linearized Navier–Stokes equations is sought as a sum of the scalar and vector potentials. A general solution for the system of coaxial, fluid-containing shells is obtained for the class of traveling waves. An analytical solution of the coupled problem of free and forced vibrations of coaxial shells separated by a viscous fluid, described by the linearized two-dimensional Navier–Stokes equations, was developed in [11]. It was demonstrated that the size of the annular gap and the viscosity of the fluid have the most significant effect on vibration damping. A similar approach was applied in [12] to the case of a flowing liquid. Here, the authors analyze the difficulties with realization of the no-slip conditions at the shell walls when performing numerical simulation of a viscous fluid. It was shown that, for simply supported shells, the influence of nonstationary viscous forces increases with decreasing width of the annular channel. The stationary viscous drag forces were taken into consideration for rigidly fixed and cantilevered shells in [13] and [6], respectively. These papers investigate the stability boundaries for different types of fluid flows and sizes of the annular gap between the inner and outer shells. It was found that the stationary viscous drag forces exert a significant influence on the critical fluid flow velocities. In [14], a similar model was used to study the effect of a number of system parameters on the stability of shells in the presence of an annular fluid flow. The model presented in [15] takes into account both the stationary and nonstationary viscous drag forces, which are determined from the linearized Navier–Stokes equations using the finite difference numerical method. It has been shown that this model provides better agreement with the experimental data presented in [7, 16] compared to the model which takes into account only the stationary viscous drag forces. An investigation of vibrations of shells with nonuniform constraints conveying or immersed in an annular axial flow of viscous or non-viscous liquids was carried out in [17, 18]. Here, the studies were carried out based on the Rayleigh – Ritz method, in which the linear modes of simply supported shells vibrating in vacuo were used as admissible functions. In Refs. [19, 20], the numerical solution of the problem obtained by the finite element method for non-viscous and viscous liquids revealed a significant discrepancy between the finite element solution and the known numerical and analytical solutions obtained for the system of coaxial shells, in which the loss of stability occurs at high vibration modes. The stability of coaxial shells with an ideal or viscous fluid flowing only in the annular channel was investigated in [21,22,23] with and without consideration of the temperature effects.

Note that in the works listed above the fluid completely fills not only the space between the two shells but also the interior space of the inner shell. In this situation, as in the case of partial filling of vertically oriented shells, the problem can be investigated in the framework of axisymmetric formulation. The partial filling of horizontally located shells with a fluid breaks the symmetry along the circumferential coordinate, which necessitates the employment of more complex spatial models. To our knowledge, such studies have not been published as yet. The purpose of this paper is to analyze the influence of the level of fluid in the annular gap between the shells on the hydroelastic stability boundary. It is suggested that the above problem be solved using the modified version of the finite element algorithm, which was used by the authors in their previous works to study the hydroelastic interaction of the shell structures of an arbitrary cross section completely or partially filled with liquid [24, 25].

2 Formulation of the problem/constitutive relations

We consider the system of elastic coaxial cylindrical shells of length L, thicknesses \(h^{(1)}\) and \(h^{(2)}\), and radii \(R^{(1)}\) and \(R^{(2)}\) with an ideal, compressible fluid, flowing with a velocity U through the annular gap between them (Fig. 1). Hereinafter, superscripts “(1)” and “(2)” denote the inner and outer shells, respectively. The aim of this study is to investigate the influence of the height of the liquid layer (filling level) H in the annular gap between the shells and its size on the boundaries of hydroelastic stability of the system, including the variant in which one of the shells is perfectly rigid.

Fig. 1
figure 1

A cross section of two coaxial cylindrical shells, with the fluid flowing in the annular gap between them in the case of partial filling

Full size image

The motion of an ideal compressible liquid in volume \(V_f\) is described in the framework of the potential theory, in which the wave equation for the velocity potential \(\phi \) in the Cartesian coordinates (x, y, z) is written as [26]

$$\begin{aligned} {\nabla ^2}\phi = \frac{1}{{{c^2}}}\frac{{{\partial ^2}\phi }}{{\partial {t^2}}} + \frac{{2U}}{{{c^2}}}\frac{{{\partial ^2}\phi }}{{\partial t \partial x}} + \frac{{{U^2}}}{{{c^2}}}\frac{{{\partial ^2}\phi }}{{\partial {x^2}}} \end{aligned}$$
(1)

where c is the speed of sound in a liquid medium.

The components of the velocity vector of the fluid \(\mathbf{v}\) in the perturbed state are determined as follows:

$$\begin{aligned} {v_x} = \frac{{\partial \varPhi }}{{\partial x}} = U + \frac{{\partial \phi }}{{\partial x}},\;\;\;{v_y} = \frac{{\partial \varPhi }}{{\partial y}} = \frac{{\partial \phi }}{{\partial y}},\;\;\;{v_z} = \frac{{\partial \varPhi }}{{\partial z}} = \frac{{\partial \phi }}{{\partial z}}, \end{aligned}$$

where \(\varPhi = Ux + \phi \) is the velocity potential.

It is assumed that the free surface of the liquid \(S_{free}\) does not move and is not under the action of dynamic pressure and surface tension. The corresponding boundary condition is given by [27]

$$\begin{aligned} \phi = 0. \end{aligned}$$
(2)

The perturbation velocity potential at the inlet and outlet of the annular channel between the shells obeys the following boundary conditions:

$$\begin{aligned} x = 0:\quad \phi = 0,\quad x = L:\quad {\partial \phi }/ {\partial x} = 0. \end{aligned}$$
(3)

On the wetted surfaces \(S_\sigma ^{(i)} = {S_f} \cap S_s^{(i)}\), we impose the impermeability conditions

$$\begin{aligned} \frac{{\partial \phi }}{{\partial \mathbf {n}}} = - \left( {\frac{{\partial {w^{(1)}}}}{{\partial t}} + U\frac{{\partial {w^{(1)}}}}{{\partial x}}} \right) \end{aligned}$$
(4)

and

$$\begin{aligned} \frac{{\partial \phi }}{{\partial \mathbf {n}}} = \left( {\frac{{\partial {w^{(2)}}}}{{\partial t}} + U\frac{{\partial {w^{(2)}}}}{{\partial x}}} \right) \end{aligned}$$
(5)

for the internal and external shell, respectively. Here, \(w^{(i)}\) are the normal components of the vectors of shell displacements; \(\mathbf {n}\) is the outward unit normal vector to the shell surfaces; \(S_f\), \(S_s^{(i)}\) are the surfaces that bound volumes of fluid \(V_f\) and shell \(V_s\). Hereinafter, \(i = \overline{1,2}\).

To calculate the hydrodynamic pressure p exerted by the liquid on the shells, we use the Bernoulli equation

$$\begin{aligned} {p^{(i)}} = \pm {\rho _f}\left( {\frac{{\partial \phi }}{{\partial t}} + U\frac{{\partial \phi }}{{\partial x}}} \right) \end{aligned}$$
(6)

where \(\rho _f\) is the fluid density, and the sign in front of the formula depends on the directions of the normals to the external surfaces of the shells.

Equation (1) together with the boundary conditions (2–5) is transformed to a weak form using the Bubnov–Galerkin method [28],

$$\begin{aligned} \begin{aligned}&\int \limits _{{V_f}} {\nabla F_n \nabla {\hat{\phi }} dV} + \int \limits _{{V_f}} {F_n \left( {\frac{1}{{{c^2}}}\frac{{{\partial ^2}{{\hat{\phi }}} }}{{\partial {t^2}}} + \frac{{2U}}{{{c^2}}}\frac{{{\partial ^2}{\hat{\phi }} }}{{\partial t \partial x}} + \frac{{{U^2}}}{{{c^2}}}\frac{{{\partial ^2}{\hat{\phi }} }}{{\partial {x^2}}}} \right) \hbox {d}V} \\&\quad + \int \limits _{S_\sigma ^{(1)}} {F_n \left( {\frac{{\partial {{\hat{w}}^{(1)}}}}{{\partial t}} + U\frac{{\partial {{\hat{w}}^{(1)}}}}{{\partial x}}} \right) \hbox {d}S} \\&\quad - \int \limits _{S_\sigma ^{(2)}} {F_n \left( {\frac{{\partial {{\hat{w}}^{(2)}}}}{{\partial t}} + U\frac{{\partial {{\hat{w}}^{(2)}}}}{{\partial x}}} \right) \hbox {d}S} = 0, \quad n=1,2, \ldots m_f, \end{aligned} \end{aligned}$$
(7)

where \({\hat{\phi }}\), \(\hat{w}^{(i)}\) are approximations of the perturbation velocity potential and the normal components of the vectors of shells displacements, \(F_n\) and \(m_f\) are the basic functions and number of them.

The basic relations, which describe the behavior of elastic shells, are written under the assumption that the curvilinear surface of the structure can be represented as a set of flat segments (Fig. 2) [29]. The strains in each of the segments are determined in the framework of the classical theory of thin plates [30, 31] in the Cartesian coordinate system \(\left( {{\bar{x}},{\bar{y}},{\bar{z}}} \right) \) associated with the lateral surface of the body,

$$\begin{aligned} {{\bar{\varvec{\varepsilon }}}^{(i)}}&= {\left\{ {\varepsilon _{{\bar{x}}{\bar{x}}}^{(i)},\;\varepsilon _{{\bar{y}}{\bar{y}}}^{(i)},\;\gamma _{{\bar{x}}{\bar{y}}}^{(i)}} \right\} ^\mathrm{{T}}} = {{\tilde{\varvec{\varepsilon }}}^{(i)}} + {{\bar{z}}^{(i)}}{{\varvec{\kappa }}^{(i)}},\quad i = \overline{1,2} ,\nonumber \\ {{\tilde{\varvec{\varepsilon }}}^{(i)}}&= {\left\{ {{\tilde{\varepsilon }}_{{\bar{x}}{\bar{x}}}^{(i)},\;\tilde{\varepsilon }_{{\bar{y}}{\bar{y}}}^{(i)},\;{{\tilde{\gamma }}} _{{\bar{x}}{\bar{y}}}^{(i)}} \right\} ^\mathrm{{T}}} = {\left\{ {\frac{{\partial {u^{(i)}}}}{{\partial {\bar{x}}}},\;\frac{{\partial {v^{(i)}}}}{{\partial {\bar{y}}}},\;\frac{{\partial {u^{(i)}}}}{{\partial {\bar{y}}}} + \frac{{\partial {v^{(i)}}}}{{\partial {\bar{x}}}}} \right\} ^\mathrm{{T}}},\nonumber \\ {{\varvec{\kappa }}^{(i)}}&= {\left\{ {\kappa _{{\bar{x}}{\bar{x}}}^{(i)},\;\kappa _{{\bar{y}}{\bar{y}}}^{(i)},\;\kappa _{{\bar{x}}{\bar{y}}}^{(i)}} \right\} ^\mathrm{{T}}} = {\left\{ { - \frac{{\partial ^2 {w^{(i)}}}}{{\partial {{{\bar{x}}}^2}}}, - \frac{{\partial ^2 {w^{(i)}}}}{{\partial {{{\bar{y}}}^2}}}, - 2\frac{{\partial ^2 {w^{(i)}}}}{{\partial {\bar{x}}\partial {\bar{y}}}}} \right\} ^\mathrm{{T}}}. \end{aligned}$$
(8)

In what follows, the over-bar denotes the quantities written in the coordinate system \(\left( {{\bar{x}},{\bar{y}},{\bar{z}}} \right) \), and \(u^{(i)}\), \(v^{(i)}\), \(w^{(i)}\) are the components of displacements of the middle surface of the plate (shell) in the direction of these axes.

Fig. 2
figure 2

Shell as a set of flat elements

Full size image

The physical relations between the vector of generalized forces and moments \({{\bar{\mathbf{T}}}^{(i)}}\) and the vector of generalized strains \({\tilde{\varvec{\varepsilon }}}^{(i)}\) are written in the following form:

$$\begin{aligned} {{\bar{\mathbf{T}}}^{(i)}} = {\left\{ {T_{{\bar{x}}{\bar{x}}}^{(i)},T_{{\bar{y}}{\bar{y}}}^{(i)}, T_{{\bar{x}}{\bar{y}}}^{(i)},M_{{\bar{x}}{\bar{x}}}^{(i)}, M_{{\bar{y}}{\bar{y}}}^{(i)},M_{{\bar{x}}{\bar{y}}}^{(i)}} \right\} ^\mathrm{{T}}} = {{\mathbf{D}}^{(i)}}{\bar{\varvec{\varepsilon }}^{(i)}}. \end{aligned}$$
(9)

For an isotropic material, the coefficients in the stiffness matrix \({\mathbf{D}}^{(i)}\) are determined from the expressions

$$\begin{aligned}&\left\{ {\begin{array}{*{20}{c}} {N_{{\bar{x}}{\bar{x}}}^{(i)}}\\ {N_{{\bar{y}}{\bar{y}}}^{(i)}}\\ {N_{{\bar{x}}{\bar{y}}}^{(i)}} \end{array}} \right\} = \int \limits _{ - h/2}^{h/2} {{\mathbf{{Q}}^{(i)}}\left\{ {\begin{array}{*{20}{c}} {\varepsilon _{{\bar{x}}{\bar{x}}}^{(i)}}\\ {\varepsilon _{{\bar{y}}{\bar{y}}}^{(i)}}\\ {\gamma _{{\bar{x}}{\bar{y}}}^{(i)}} \end{array}} \right\} d{\bar{z}}} = \left[ {\begin{array}{*{20}{c}} {A_{11}^{(i)}}&{}{A_{12}^{(i)}}&{}0\\ {A_{21}^{(i)}}&{}{A_{22}^{(i)}}&{}0\\ 0&{}0&{}{A_{66}^{(i)}} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {{\tilde{\varepsilon }} _{{\bar{x}}{\bar{x}}}^{(i)}}\\ {{\tilde{\varepsilon }} _{{\bar{y}}{\bar{y}}}^{(i)}}\\ {{\tilde{\gamma }} _{{\bar{x}}{\bar{y}}}^{(i)}} \end{array}} \right\} ,\nonumber \\&\left\{ {\begin{array}{*{20}{c}} {M_{{\bar{x}}{\bar{x}}}^{(i)}}\\ {M_{{\bar{y}}{\bar{y}}}^{(i)}}\\ {M_{{\bar{x}}{\bar{y}}}^{(i)}} \end{array}} \right\} = \int \limits _{ - h/2}^{h/2} {{\mathbf{{Q}}^{(i)}}\left\{ {\begin{array}{*{20}{c}} {\varepsilon _{{\bar{x}}{\bar{x}}}^{(i)}}\\ {\varepsilon _{{\bar{y}}{\bar{y}}}^{(i)}}\\ {\gamma _{{\bar{x}}{\bar{y}}}^{(i)}} \end{array}} \right\} {{\left( {{{{\bar{z}}}^{(i)}}} \right) }^2}d{\bar{z}} = \left[ {\begin{array}{*{20}{c}} {D_{11}^{(i)}}&{}{D_{12}^{(i)}}&{}0\\ {D_{21}^{(i)}}&{}{D_{22}^{(i)}}&{}0\\ 0&{}0&{}{D_{66}^{(i)}} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {\kappa _{{\bar{x}}{\bar{x}}}^{(i)}}\\ {\kappa _{{\bar{y}}{\bar{y}}}^{(i)}}\\ {\kappa _{{\bar{x}}{\bar{y}}}^{(i)}} \end{array}} \right\} } , \nonumber \\&A_{ij}^{(i)} = {h^{(i)}}Q_{ij}^{(i)},\;\;D_{ij}^{(i)} = \frac{{{{\left( {{h^{(i)}}} \right) }^3}}}{{12}}Q_{ij}^{(i)}, \quad {\mathbf{{Q}}^{\left( i \right) }} = \left[ {\begin{array}{*{20}{c}} {Q_{11}^{(i)}}&{}{Q_{12}^{(i)}}&{}0\\ {Q_{12}^{(i)}}&{}{Q_{22}^{(i)}}&{}0\\ 0&{}0&{}{Q_{66}^{(i)}} \end{array}} \right] ,\nonumber \\&Q_{11}^{(i)} = Q_{22}^{(i)} = \frac{{{E^{(i)}}}}{{1 - {{\left( {{\nu ^{(i)}}} \right) }^2}}}, \, Q_{12}^{(i)} = Q_{21}^{(i)} = \frac{{{\nu ^{(i)}}{E^{(i)}}}}{{1 - {{\left( {{\nu ^{(i)}}} \right) }^2}}}, \, Q_{66}^{(i)} = \frac{{{E^{(i)}}}}{{2\left( {1 - {\nu ^{(i)}}} \right) }} \end{aligned}$$
(10)

where \(E^{(i)}\) and \(\nu ^{(i)}\) are Young’s modulus and Poisson’s ratio, respectively, of the shell materials.

A mathematical formulation of the problem of the dynamics of elastic bodies is based on the variational principle of virtual displacements [32], which, taking into account the Bernoulli equation (6) and the work done by the inertia forces, can be written in matrix form as

$$\begin{aligned}&\int \limits _{S_s^{(i)}} {{{\left( {\delta {{\bar{\varvec{\varepsilon }}}^{(i)}}} \right) }^\mathrm{{T}}}{{\mathbf{D}}^{(i)}}{{\bar{\varvec{\varepsilon }}}^{(i)}}\hbox {d}S} \nonumber \\&\quad + \int \limits _{V_s^{(i)}} {\rho _s^{(i)}{{\left( {\delta {{{\bar{\mathbf{d}}}}^{(i)}}} \right) }^\mathrm{{T}}}{{{\bar{\ddot{\mathbf{d}}}}}^{(i)}}\hbox {d}V} - \int \limits _{S_\sigma ^{(i)}} { {{\left( {\delta {{{\bar{\mathbf{d}}}}^{(i)}}} \right) }^\mathrm{{T}}}{{\bar{\mathbf{P}}}^{(i)}}\hbox {d}S} = 0 \end{aligned}$$
(11)

where \(\rho _s^{(i)}\) are the densities of the shells materials; \({{\bar{\mathbf{d}}}^{(i)}} = {\left\{ {{u^{(i)}},{v^{(i)}},{w^{(i)}},\theta _{\bar{x}}^{(i)},\theta _{\bar{y}}^{(i)},\theta _{\bar{z}}^{(i)}} \right\} ^\mathrm{{T}}}\) are the vectors of displacements and rotation angles of the inner and outer shell; \({{\bar{\mathbf{P}}}^{(i)}} = {\{ 0,0,{p^{(i)}},0,0,0\} ^\mathrm{{T}}}\) are the vectors of loads acting on the shell surfaces.

3 Numerical implementation

The numerical solution of the problem is found by the finite element method [29]. To describe the perturbation velocity potential \(\hat{\phi }\), the basic functions \(F_n\) and the membrane displacements of shells (u, v), we use the Lagrange shape functions with a linear approximation, and for flexural motions of shells w we use the Hermite non-conformal shape functions. Discretization of the fluid and shells computational domains is based on the spatial 8-node brick and the 4-node plane rectangular finite elements, respectively.

The related system of equations, describing the interaction between the elastic shells and the liquid, can be formulated in a coordinate system \(\left( x,y,z\right) \) in matrix form as

$$\begin{aligned}&\left[ {\begin{array}{*{20}{c}} {\mathbf{M}}_s^{(1)}&{}\quad 0&{}\quad 0\\ 0&{}\quad {\mathbf{M}}_s^{(2)}&{}\quad 0\\ 0&{}\quad 0&{}\quad {\mathbf{M}}_{f} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {\ddot{\mathbf{d}}}^{(1)}\\ {\ddot{\mathbf{d}}}^{(2)}\\ {\ddot{\varvec{\phi }}} \end{array}} \right\} + \left[ {\begin{array}{*{20}{c}} 0&{}\quad 0&{}\quad - {\mathbf{C}}_{sf}^{(1)}\\ 0&{}\quad 0&{}\quad {\mathbf{C}}_{sf}^{(2)}\\ { - {\mathbf{C}}_{fs}^{(1)}}&{}\quad {\mathbf{C}}_{fs}^{(2)}&{}\quad {\mathbf{C}}_{f} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {{\dot{\mathbf{d}}}}^{(1)}\\ {{\dot{\mathbf{d}}}}^{(2)}\\ {\dot{\varvec{\phi }}} \end{array}} \right\} \nonumber \\&\quad + \left( {\left[ {\begin{array}{*{20}{c}} {\mathbf{K}}_s^{(1)}&{}\quad 0&{}\quad 0\\ 0&{}\quad {\mathbf{K}}_s^{(2)}&{}\quad 0\\ 0&{}\quad 0&{}\quad {\mathbf{K}}_{f} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0&{}\quad 0&{}\quad - {\mathbf{A}}_{sf}^{(1)}\\ 0&{}\quad 0&{}\quad {\mathbf{A}}_{sf}^{(2)}\\ { - {\mathbf{A}}_{fs}^{(1)}}&{}\quad {\mathbf{A}}_{fs}^{(2)}&{}\quad {\mathbf{A}}_{f} \end{array}} \right] } \right) \left\{ {\begin{array}{*{20}{c}} {\mathbf{d}}^{(1)}\\ {\mathbf{d}}^{(2)}\\ {\varvec{\phi }}\end{array}} \right\} = 0 \end{aligned}$$
(12)

where \(\mathbf{{d}}^{(1)}\), \(\mathbf{{d}}^{(2)}\), \({\varvec{\phi }}\) are the generalized vectors of displacements and rotation angles of the inner and outer shells and the perturbation velocity potential.

The typical matrices of stiffness \(\mathbf{K}\), mass \(\mathbf{M}\), damping \(\mathbf{C}\), and hydrodynamic rigidity \(\mathbf{A}\) for individual finite elements are formed using the expressions

$$\begin{aligned} {\bar{\mathbf{K}}}_s^{(i)}&= \int \limits _{V_s^{(i)}} {{{\left( {{\mathbf{{B}}^{(i)}}} \right) }^\mathrm{{T}}}{{\mathbf{D}}^{(i)}}{\mathbf{{B}}^ {(i)}}\hbox {d}V} ,\quad {\bar{\mathbf{M}}}_s^{(i)} = \int \limits _{V_s^{(i)}} {\rho _s^{(i)}{{\left( {{\mathbf{{N}}^{(i)}}} \right) }^\mathrm{{T}}}{\mathbf{{N}}^{(i)}}\hbox {d}V} ,\\ {\bar{\mathbf{C}}}_{sf}^{(i)}&= \int \limits _{S_\sigma ^{(i)}} {{\rho _f}{{\left( {\mathbf{{N}}_w^{(i)}} \right) }^\mathrm{{T}}}{\mathbf{F}}\hbox {d}S} ,\quad {\bar{\mathbf{A}}}_{sf}^{(i)} = \int \limits _{S_\sigma ^{(i)}} {{\rho _f}U{{\left( {{\mathbf{N}}_w^{(i)}} \right) }^\mathrm{{T}}}\frac{{\partial {\mathbf{F}}}}{{\partial x}}\hbox {d}S} ,\\ {{\mathbf{K}}_f}&= \int \limits _{{V_f}} {\left( {\frac{{\partial {{\mathbf{F}}^\mathrm{{T}}}}}{{\partial x}}\frac{{\partial {\mathbf{F}}}}{{\partial x}} + \frac{{\partial {{\mathbf{F}}^\mathrm{{T}}}}}{{\partial y}}\frac{{\partial {\mathbf{F}}}}{{\partial y}} + \frac{{\partial {{\mathbf{F}}^\mathrm{{T}}}}}{{\partial z}}\frac{{\partial {\mathbf{F}}}}{{\partial z}}} \right) \hbox {d}V} ,\quad {\mathbf{M}}_{f} = \int \limits _{{V_f}} {\frac{1}{{{c^2}}}{{\mathbf{F}}^\mathrm{{T}}}{\mathbf{F}}\hbox {d}V},\\ {{\mathbf{C}}_f}&= \int \limits _{{V_f}} {\frac{{2U}}{{{c^2}}}\frac{{\partial {{\mathbf{F}}^\mathrm{{T}}}}}{{\partial x}}{\mathbf{F}}\hbox {d}V} ,\quad {\mathbf{A}}_{f} = - \int \limits _{{V_f}} {\frac{{{U^2}}}{{{c^2}}}\frac{{\partial {{\mathbf{F}}^\mathrm{{T}}}}}{{\partial x}}\frac{{\partial {\mathbf{F}}}}{{\partial x}}\hbox {d}V} ,\\ {\bar{\mathbf{C}}}_{fs}^{(i)}&= - \int \limits _{S_\sigma ^{(i)}} {{{\mathbf{F}}^{\mathrm{T}}}{\mathbf{N}}_w^{(i)}\hbox {d}S} ,\quad {\bar{\mathbf{A}}}_{fs}^{(i)} =- \int \limits _{S_\sigma ^{(i)}} {U{{\mathbf{F}}^{\mathrm{T}}}\frac{{\partial {\mathbf{N}}_w^{(i)}}}{{\partial x}}\hbox {d}S} . \end{aligned}$$

Here, \({\mathbf{B}}^{(i)}\) is the gradient matrix, which links the deformation vector with the vector of nodal displacements of the shell finite element; \(\mathbf{F}\), \({\mathbf{N}}^{(i)}\), and \({\mathbf{N}}_w^{(i)}\) are the shape functions for the velocity potential of the fluid, the generalized vector of the nodal displacements of the shells, and its normal component. The constitutive relations (8) do not contain the equation for rotation about the axis \({\bar{z}}\). If the elements having a common node are coplanar, then the rigidity in this direction becomes zero. In this case, any perturbation contributing to the rotation will significantly affect the correctness of the solution. To eliminate this problem, one needs to introduce zero rows and columns and a fictitious moment \({M_{{\bar{z}}}}\) into the stiffness matrix of the finite element of the shell [29]. The matrices \({\bar{\mathbf{K}}}_s^{(i)}\) and \({\bar{\mathbf{M}}}_s^{(i)}\) are formed in the coordinate system \(\left( {{\bar{x}},{\bar{y}},{\bar{z}}} \right) \) associated with the lateral surface of the structure. The transformation of nodal displacements and rotation angles to the global Cartesian coordinate system (x, y, z) is performed for each node using the matrix of the directional cosines \({\varvec{\gamma }}\) of size \(3\times 3\) in the following way:

$$\begin{aligned} \mathbf{{d}}^{(i)}={{\left[ \begin{matrix} {\varvec{\gamma }} &{}\quad 0 \\ 0 &{}\quad {\varvec{\gamma }} \\ \end{matrix} \right] }^{\text {T}}}{{\bar{\mathbf{d}}}^{(i)}}. \end{aligned}$$

At each node of the shell finite element, six unknowns are defined (three displacements and three rotation angles), so the transformation of typical matrices is performed using a diagonal matrix \(\mathbf{{L}} = \mathrm{{diag}}\left( {{\varvec{\gamma }},{\varvec{\gamma }},{\varvec{\gamma }}, {\varvec{\gamma }},{\varvec{\gamma }},{\varvec{\gamma }}, {\varvec{\gamma }},{\varvec{\gamma }}} \right) \):

$$\begin{aligned} \mathbf{{K}}_{s}^{(i)}&={{\left( {\mathbf{{L}}^{(i)}} \right) }^{\text {T}}}{\bar{\mathbf{K}}}_{s}^{(i)}{\mathbf{{L}}^{(i)}},\quad \mathbf{{M}}_{s}^{(i)}={{\left( {\mathbf{{L}}^{(i)}} \right) }^{\text {T}}}{\bar{\mathbf{M}}}_{s}^{(i)}{\mathbf{{L}}^{(i)}},\\ \mathbf{{C}}_{fs}^{(i)}&={\bar{\mathbf{C}}}_{fs}^{(i)}{\mathbf{{L}}^{(i)}},\quad \mathbf{{C}}_{sf}^{(i)}={{\left( {\mathbf{{L}}^{(i)}} \right) }^{\text {T}}}{\bar{\mathbf{C}}}_{sf}^{(i)}. \end{aligned}$$

Let us write the system of equations (12) in a more compact form as

$$\begin{aligned}&\mathbf{{M}}{\left\{ {{{{\ddot{\mathbf{d}}}}^{(1)}},{{{\ddot{\mathbf{d}}}}^{(2)}},{\ddot{\varvec{\phi }}} } \right\} ^{\mathrm{T}}}+{\mathbf{C}}{\left\{ {{{{\dot{\mathbf{d}}}}^{(1)}},{{{\dot{\mathbf{d}}}}^{(2)}},{\dot{\varvec{\phi }}} } \right\} ^\mathrm{{T}}} + \left( {{\mathbf{K}} + {\mathbf{A}}} \right) {\left\{ {{{\mathbf{d}}^{(1)}},{\mathbf{{d}}^{(2)}},{\varvec{\phi }} } \right\} ^\mathrm{{T}}} = 0 \end{aligned}$$
(13)

and consider the perturbed motion of shells and fluid as \(\left( \mathbf{d}^{(1)},\mathbf{d}^{(2)},{\varvec{\phi }} \right) = \left( {{\tilde{\mathbf{d}}}}^{(1)},{{\tilde{\mathbf{d}}}}^{(2)},{\tilde{\varvec{\phi }}} \right) \exp (\lambda t)\), where \({{\tilde{\mathbf{d}}}^{(1)}},{{\tilde{\mathbf{d}}}^{(2)}}\), and \({\tilde{\varvec{\phi }}}\) are the vector functions of the coordinates and \(\lambda = \delta + \mathrm {i}\omega \) is the characteristic parameter (\({\mathrm{i}}= \sqrt{ - 1}\)). Here, it is assumed that \(\omega \) is the eigenfrequency of vibrations, and \(\delta \) is the quantity characterizing damping. Eventually, the initial system of equations (13) is transformed to a generalized eigenvalue problem written as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} \mathbf{{C}}&{}\quad {\mathbf{{K}} + \mathbf{{A}}}\\ { - \mathbf{{I}}}&{}\quad 0 \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {\lambda \mathbf{{x}}}\\ \mathbf{{x}} \end{array}} \right\} + \lambda \left[ {\begin{array}{*{20}{c}} \mathbf{{M}}&{}\quad 0\\ 0&{}\quad \mathbf{{I}} \end{array}} \right] \left\{ {\begin{array}{*{20}{c}} {\lambda \mathbf{{x}}}\\ \mathbf{{x}} \end{array}} \right\} = 0 \end{aligned}$$
(14)

where \(\mathbf{I}\) is the unit matrix, \(\mathbf{{x = }}{\left\{ {{{{\tilde{\mathbf{d}}}}^{(1)}},{{{\tilde{\mathbf{d}}}}^{(2)}},{\tilde{\varvec{\phi }}} } \right\} ^\mathrm{{T}}}\).

Complex eigenvalues for the system of equations (14) are calculated with the algorithm which is based on the implicitly restarted Arnoldi method [33]. The stability estimation is based on the analysis of the complex eigenvalues of the problem (14) obtained under the constraint of gradually increasing fluid velocity.

4 The results of computation

Below, we consider a few examples, which are concerned with the stability of the system of horizontally oriented coaxial shells (\(L = 1\) m, \({R^{(2)}} = 0.1\) m, \({h^{(1)}} = {h^{(2)}} = h = 5 \times {10^{ - 4}}\) m, \({E^{(1)}} = {E^{(2)}} = E = 2 \times {10^{11}}\)\(\hbox {N/m}^2\), \({\nu ^{(1)}} = {\nu ^{(2)}} = \nu = 0.3\), \(\rho _s^{(1)} = \rho _s^{(2)} = {\rho _s} = 7800\hbox { kg/m}^3\)), clamped at both ends (\(u = v = w = \theta _x = \theta _y = \theta _z = 0\)) and containing an ideal compressible fluid (\({\rho _f} = 1000\hbox { kg/m}^3\), \(c = 1500\hbox { m/s}\)) flowing in an annular channel between the shells. The computations were done for different values of the dimensionless annular gap between the inner and outer shell, which is defined as \(k = {{\left( {{R^{(2)}} - {R^{(1)}}} \right) } / {{R^{(1)}}}}\). In the analysis of the influence of the filling level H on the loss of stability, consideration is given only to such values of the fluid level at which both shells remain wetted, which corresponds to the following condition:

$$\begin{aligned} {R^{(2)}} - {R^{(1)}} \le H \le 2{R^{(2)}}. \end{aligned}$$
(15)

The obtained results are represented in terms of dimensionless quantities, such as the filling level \(\eta \), the critical velocities for the loss of stability \(\varLambda \) and the eigenvalues \(\varOmega \),

$$\begin{aligned} \eta&= H{(2{R^{(2)}})^{ - 1}},\quad \varLambda = U\psi \times {10^2}, \\ \varOmega&= \lambda {R^{(1)}}\psi \times {10^2},\quad \psi = {[{\rho _s}(1 - \nu ^2 )/E]^{0.5}}. \end{aligned}$$

Discretization of the liquid volume was performed under the constraint of finite element mesh matching at the fluid–structure interface and taking into account the level of shell filling. The parameters of the finite element mesh were determined by analyzing the asymptotic behavior of the solution as the number of nodal unknowns increases. In numerical simulation, the shell surfaces were approximated by 5040 elements (72 and 70 elements in circumferential and meridional direction, respectively). The coupled system in the case of complete filling with fluid had about 127,800 degrees of freedom.

4.1 Verification of the numerical model

The reliability of the developed model and its finite element realization for the system with a quiescent liquid is tested by comparing the obtained results with the results of [34]. We consider a system of coaxial shells rigidly clamped at both ends (\({E^{(1)}} = {E^{(2)}} = 6.9 \times {10^{10}}\) N/m\(^2\), \({\nu ^{(1)}} = {\nu ^{(2)}} = 0.3\), \(\rho _s^{(1)} = \rho _s^{(2)} = 2700\hbox { kg/m}^3\), \(L=0.3\hbox { m}\), \({R^{(1)}} = 0.1\hbox { m}\), \({R^{(2)}} = 0.15\hbox { m}\), \({h^{(1)}} = {h^{(2)}} = 2 \times {10^{ - 3}}\hbox { m}\)), and a quiescent compressible liquid flowing in the annular gap between the shells (\({\rho _f} = 1000\hbox { kg/m}^3\), \(c = 1483\hbox { m/s}\)). At the inlet and outlet of the annular channel for the perturbation velocity potential, we prescribe the following boundary conditions:

$$\begin{aligned} x = 0,L:\quad {\partial \phi } / {\partial x}= 0. \end{aligned}$$

Note that in [34] it was shown for the first time that for two elastic coaxial shells, along with the in-phase (direction and number of meridional half-waves m coincide) and out-of-phase (directions are opposite) modes, there are also mixed (the number of half-waves is different) modes. Table 1 presents the natural frequencies of vibrations \(\omega \) of the configuration described above, where j denotes the number of half-waves in the circumferential direction. In the studies performed in the framework of 3D formulation, the identification of a combination of wave numbers (j, m) necessitates the construction of mode shapes. In this case, the solution of the problem includes both the symmetric and antisymmetric components, which means that two vibration modes correspond to one frequency, differing only by the angle of rotation in the circumferential direction

Table 1 The natural frequencies of vibration \(\omega \) (Hz) of coaxial shells rigidly clamped at both ends and containing a quiescent fluid in the annular channel between them
Full size table

Based on the available information, we can conclude that the results obtained in the framework of the proposed model are in good agreement with the data of the analytical solution given in [34]. It should be noted that as the number of waves in the circumferential direction j increases, the difference in the results obtained within the framework of axisymmetric and three-dimensional formulation becomes more significant.

In the case when the fluid flow occurs only in the annular channel, the evaluation of the reliability of the algorithm is really a challenge due to the absence of publications, in which the reliability of the presented results has been verified. Instead, the obtained results are compared with the known data for the critical velocities of the annular flow in the presence of a quiescent liquid completely filling the interior space of the inner shell. The results are given in Table 2, which displays the dimensionless critical velocities of the annular fluid flow \(\varLambda \) for various configurations.

Table 2 Comparison of the dimensionless critical flow velocities \(\varLambda \) in the annular channel for various configurations and different methods of solution
Full size table

Based on the analysis of the results given in Table 2 for rigidly clamped coaxial shells, we can draw the following conclusion. The critical velocities calculated in the framework of the spatial formulation are in good agreement with both analytical and numerical data obtained with the help of axisymmetric models. For the configuration under consideration, the presence of a quiescent fluid in the inner shell has an insignificant effect on the critical velocities of the fluid flow in the annular channel. Moreover, this effect will further weaken with decrease in the annular gap size.

4.2 Stability analysis

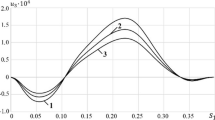
Figure 3 shows the plots of the real and imaginary parts of the dimensionless eigenvalues \(\varOmega \) versus the dimensionless velocity of the fluid flow in the annular channel \(\varLambda \) of the system, in which the inner shell is elastic and the outer shell is perfectly rigid. The data presented in Fig. 3a correspond to the case of complete filling of the annular gap with fluid. When the flow velocity is zero (\(\varLambda =0\)), the eigenvalues of the system are purely imaginary. An increase in the flow velocity causes a decrease in the imaginary parts of the eigenvalues until they become zero. At exactly the same time each mode acquires a pair of real parts, one of which is positive, which corresponds to a loss of stability by divergence. A further increase in the flow velocity leads to restabilization of the system, at which the eigenvalues again become purely imaginary.

Fig. 3
figure 3

The dimensionless eigenvalues \(\varOmega \) (\(m=1\)) versus the dimensionless fluid velocity \(\varLambda \) at different values of the fluid level for the system with rigid outer shell (\(k = 1/10\)): a\(\eta = 1\); b\(\eta = 0.25\)

Full size image
Fig. 4
figure 4

The dimensionless critical velocities \(\varLambda \) versus the dimensionless fluid level \(\eta \): a rigid outer shell and elastic inner shell; b both shells are elastic

Full size image
Fig. 5
figure 5

Mode shapes of the system with perfectly rigid outer shell at \(k = 1/10\), \(\eta = 1\), and different velocities of the flow in the annular channel: cross section \(x = L/2\) (a–c) and inner shell (d–f)

Full size image
Fig. 6
figure 6

Mode shapes of the system with perfectly rigid outer shell: cross section \(x = L/2\) (a–c) and inner shell (d–f) at \(k = 1/10\), \(\eta = 0.25\), and different values of the velocity of the fluid flow in the annular channel

Full size image
Fig. 7
figure 7

Mode shapes of coaxial shells interacting with the fluid at \(k = 1/10\), \(\eta = 1\), and different values of the velocity of the flow in the annular channel: cross section \(x = L/2\) (a–c), inner (d–f) and outer (g–i) shells

Full size image
Fig. 8
figure 8

Mode shapes of coaxial shells interacting with the fluid at \(k = 1/10\), \(\eta = 0.25\), and different values of the velocity of the flow in the annular channel: cross section \(x = L/2\) (a–c), inner (d–f) and outer (g–i) shells

Full size image
Fig. 9
figure 9

Mode shapes of coaxial shells interacting with the fluid at \(k = 1/2\), \(\eta = 0.4\), and \(\varLambda \ne 0\): a cross section \(x = L/2\); b inner shell; c outer shell

Full size image
Table 3 The effect of the ratio \(L/R^{(1)}\) on the dimensionless critical velocities \(\varLambda _\mathrm{cr}\) at different filling levels \(\eta \) and annular gap k
Full size table
Table 4 The effect of the ratio \(h/R^{(1)}\) on the dimensionless critical velocities \(\varLambda _\mathrm{cr}\) at different filling levels \(\eta \) and annular gap k
Full size table

As it was mentioned above, in the case when the annular gap is completely filled with fluid, the solution of the problem splits into symmetric and antisymmetric components. In this case, two modes of vibration correspond to a single frequency. The partial filling of horizontally located shells causes splitting of eigenfrequencies [24] with the result that the same mode, differing from each other by the angle of rotation in the circumferential direction, correspond to different frequencies. Figure 3b shows the evolution of such eigenvalues \(\varOmega \) that have the same set of wave numbers (j, m). From the above plots, it follows that in the case of partial filling of the annular channel there is no qualitative change in the behavior of the eigenvalues. Namely, the coalescence of the imaginary parts due to their proximity is not realized, and the type of stability loss remains unchanged.

At this point, it is also necessary to note the differences in the plots of the eigenvalues as a function of the flow velocity of the fluid obtained in the framework of the three-dimensional and axisymmetric formulations (for example, in [5]). Due to the fact that the spatial solution extends over the entire frequency spectrum, it is of interest to analyze the types of stability loss, which occur at lower modes and for the examined configurations correspond to instability by divergence. However, in this case the secondary loss of stability in the form of a coupled-mode flutter, which is commonly observed and analyzed within the framework of the axisymmetric solution, loses its significance.

Figure 4 shows plots of the dimensionless velocities of stability loss \(\varLambda _\mathrm{cr}\) versus the dimensionless fluid level \(\eta \) obtained for different values of the annular gap k between the rigid and elastic shells (Fig. 4a) and two elastic shells (Fig. 4b). As it is evident from the plots, a decrease in the fluid level leads to an increase in the critical velocities. This is due to a decrease in the area of the wetted surfaces and a decrease in the contribution of the added fluid mass. An abrupt change in the critical velocities responsible for the loss of stability is observed at low values of the fluid level \(\eta \) for a gap \(k=1/100\). Similar results were obtained in the case of partial filling of single shells [25]. This phenomenon is characteristic of only such systems that have narrow gaps between shells and is associated with the essential prerequisite for the existence of a wetted surface of the inner shell, which may be absent at a small amount of the fluid in a relatively wide annular gap, i.e., when the condition (15) is not satisfied. As in the case of complete filling, an increase in the gap size as well as of the stiffness of the outer shell leads to an increase in the critical velocities. At the same time, for small values of k, the level of filling has a negligible effect on \(\varLambda _\mathrm{cr}\) over a rather wide range of its variation.

Figures 5, 6, 7, and 8 show the mode shapes of vibrations of coaxial shells at \(k = 1/10\) and different values of the dimensionless flow velocities \(\varLambda \), filling level \(\eta \), including the case of a perfectly rigid outer shell. In the Figures depicting the cross sections of the system, the dashed lines denote the shells in the undeformed state, the contour lines correspond to the shells in the deformed state, the gray color represents the fluid, and the thick solid line denotes the perfectly rigid shell.

When constructing spatial modes of vibrations, we have scaled the displacements in order to provide the clarity of presentation of the results. The real values obtained from the solution of the spectral problem (14) are displayed on the color scale, which is common to both shells. On the spectral scale light gray (red) represents the displacement \({\bar{w}}\) in the direction normal to the external surface of the shell, and dark gray (blue) represents the displacement in the opposite direction. As the flow velocity approaches the critical value \(\varLambda _\mathrm{cr}\), at which the system loses stability, the displacements increase significantly. The obtained data allowed us to draw the conclusion that in the case of complete filling of the annular gap with the fluid the amplitude of displacements of the inner shell exceeds the amplitude of displacements of the outer shell, whereas partial filling leads to an opposite result. In addition, at \(\eta = 1\), the height of all half-waves in the circumferential direction is the same. In the case of partial filling, the maximum displacements will occur on the part of the lateral surface of the shell which interacts with the fluid.

The data presented in this paper also suggest that for the configurations under consideration the mode of the loss of hydroelastic stability does not depend on the fluid level in the annular channel, which is qualitatively similar to the behavior of the lowest frequency of a single shell containing a quiescent fluid [24].

The images shown in Fig. 9 demonstrate that, for partially filled coaxial shells with a sufficiently large inter-shell gap (\(k = 1/2\)), the classification of vibration modes proposed in [34] is found to be incomplete. Here, it is shown that apart from the mixed vibration modes in the meridional direction the mixed modes can also appear in the circumferential direction.

Tables 3 and 4 present the critical velocities for the loss of stability of coaxial shells interacting with the fluid flow in the annular gap for different linear dimensions and filling levels. The line below the critical values shows the combination of wave numbers (j, m) for which the loss of stability occurs. Here the symbol “*” denotes the mixed number of half-waves in the circumferential direction. The data obtained demonstrate that an increase in the length of the structure L (Table 3) and a decrease in its thickness h (Table 4) result in destabilization of the system, and, as a consequence, in a decrease in the critical flow velocity \(\varLambda _\mathrm{cr}\). This effect is also maintained when the gap is partially filled with a fluid. The results also confirm that the mode shape of loss of stability is more dependent on the linear dimensions of the shells than on the fluid level.

5 Conclusions

In this paper, we studied the dynamic behavior of coaxial cylindrical shells, interacting with a quiescent or flowing fluid, in a three-dimensional formulation based on the proposed mathematical model and its numerical implementation with the use of the finite element method. As an example, we considered the case when the fluid was contained only in the annular channel between the inner and outer shells. Using the developed numerical algorithm, we analyzed the effect of the filling level on the eigenfrequencies, vibrational modes, and boundaries of hydroelastic stability. The corresponding relationships and new qualitative dependencies were obtained for different annular gaps and geometrical parameters. In addition, we considered the case when the outer shell was perfectly rigid. It was found that for narrow annular gaps the character of decrease in the critical velocities for the onset of instability with increasing filling level was qualitatively similar to that observed previously for the single shells interacting with internal fluid flow. It was shown that the classification of vibration modes proposed in the axisymmetric analysis of coaxial shells should be extended, since at a certain size of the annular gap partially filled with fluid the number of half-waves appearing in the circumferential direction of the inner and outer shells is different.