Effect of Boundary Form Disturbances on the Frequency Response of Planar Vibrations of Piezoceramic Plates. Experimental Investigation

Experimental results for forced planar vibrations of parallelogram-shaped piezoceramic plates are presented. The concept of this study is to evaluate the potentials of controlling the spectrum of natural frequencies and electromechanical coupling coefficients of plates by changing their shape. The results permit of supporting the data on analytical and numerical investigations of dynamics of piezoceramic plates and establishing the consistency between the physical properties of a real plate and the assumptions of the ideal computational model in the solution of practical problems. Comparison of calculated and experimental data for the spectrum of natural frequencies of the plate over their rather wide range can demonstrate this consistency. The experimental procedure was tested in studying the vibration behavior of SM111 ceramic square and parallelogram-shaped plates with different side slopes. The frequency range of investigations is limited from above with 140 kHz, which provides effective excitation of a sufficient number of natural vibrations. The structure of an experimental complex and excitation mode of vibrations at actual values of the quality factor permit of considering the external voltage source as the infinite power one. The excitation of asymmetric vibration modes on the change in geometry of a rectangular plate is natural. As was shown, high-order modes (very low electromechanical coupling coefficients in rectangular plates) can be effectively excited in parallelogram-shaped plates with maintaining a uniform electrode coating. It needs the traditional estimates of electromechanical coupling coefficients in piezoelectric plates to be refined with regard to inhomogeneous stress and strain fields.

Introduction. Piezoceramic materials are widely used in the design of electromechanical transducers [1,2,3,4,5,6,7]. The spectrum of natural frequencies, natural vibration modes, and electromechanical coupling coefficients are their most important characteristics. Specified properties can be provided by varying the shape of a vibrating element and choosing the pattern of electrode coating [4].

Experimental studies on the amplitude-frequency response (AFR) of piezoceramic plates of uncanonical shape would corroborate the initial concepts of the mathematical model constructed with the method of superposition [8,9,10] that is applied to the derivation of planar vibration problem solutions. Moreover, the experiment can create a clear view of the natural vibration modes of those plates over a wide range of frequencies. Numerous problems stemming from different modes of vibration processes are observed in applied fields, e.g., in acoustics. The issue of parasitic vibrations in parallelogram-shaped resonators, in frequency filters or in MEMS (MicroElectroMechanical Systems) sensors, in wide-band acoustical emission transducers [17] is still currently central. The requirements and functions of those instruments dictate the material and shape of the resonator in use.

The method of studying the dynamic characteristics of a parallelogram-shaped piezoceramic plate under planar vibrations was proposed in [15].

As calculated data on different excitation levels of the boundary form (parallelogram angle) show, the proposed algorithms provide high accuracy of quantitative estimates.

Such algorithms can be effectively used in the solution of applied problems for designing mechanotronics equipment. In particular, they can be put to search of optimum electrode shapes to get high electromechanical coupling coefficients at certain vibration modes.

However, the solution of practical problems are always associated with the correspondence of physical properties of a real plate and the assumptions of the ideal computational model. In this case, the comparison of theoretical and experimental data for the spectrum of natural frequencies of the plate over their rather wide range can confirm the above correspondence. The comparison, performed in this study, shows that the properties of materials and quality of the electrode coating of real plates are in quite good agreement with the assumptions of the computational model. It is also important that the advanced experimental technique provides necessary accuracy of finding required dynamic characteristics.

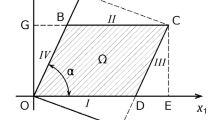
This study presents the results of experimental investigations of planar vibrations in piezoceramic plates that illustrate the potentials of controlling the above characteristics through the excitation of a square plate, which is transformed into the parallelogram-shaped ones by removing the portion of the material with different side slope angles, while the electrode coating covers the whole plate surface.

The square plate was chosen as the object of geometry transformation. The evolution of its frequency spectrum and normal modes was investigated during its successive transformation into parallelograms with 2 and 10° shear angles. The studies on those geometries are aimed at the search of vibration modes with the maximum intensive two-component motion kinematics of acute angles of plates to be used in piezoelectric ultrasonic friction engines.

1. Efficiency of Energy Conversion in the Plate at Resonant Vibrations. The most widespread methods of evaluating the electromechanical coupling coefficients (EMCC) of piezoceramic elements were comparatively assessed [18], in particular the Mason resonance method [19] and Ulitko accurate energy criterion valid for dynamic and static nonuniform strains of piezoelectric transducers [20].

Let ${k}_{d,n}^2$ represent the square of “dynamic” EMCC by Mason and ${k}_e^2$ be the square of a corresponding value by the Ulitko energy criterion, the so-called “energy” EMCC

$$ {k}_{d,n}^2=\frac{f_{A,n}^2-{f}_{R,n}^2}{f_{A,n}^2},\kern0.5em {k}_e^2=\frac{U^{(P)}-{U}^{(K)}}{U^{(P)}}. $$

(1)

Here ${f}_{R,n}^2$ and ${f}_{A,n}^2$ are the nth resonant and antiresonant vibration frequencies, U^(P) and U^(K) are the integrals of the internal deformation energy function for a given volume V of a piezoelectric element

$$ {\displaystyle \begin{array}{cc}u=\frac{1}{2}\left({\upsigma}_x{\upvarepsilon}_x+{\upsigma}_y{\upvarepsilon}_y+{\uptau}_{xy}{\upvarepsilon}_{xy}\right)+\frac{1}{2}{E}_z{D}_z,& U=\underset{V}{\iiint } udV,\end{array}} $$

(2)

calculated under electric boundary conditions for open (upper index P) and shorted (upper index K) electrodes, having the form, respectively [21]

$$ {\displaystyle \begin{array}{ccc}\frac{d}{dt}\underset{S_1^{+}}{\int}\int {D}_z dS=0,& {\uppsi}^{+}-{\uppsi}^{-}=0,& z=\pm h,\end{array}} $$

(3)

where σ_x, σ_y, and τ_xy are the stress components, ε_x, ε_y, and ε_xy are the strain components, and E_z and D_z are the z-components of electric intensity and electric induction vectors.

Notice that outcomes [18] are illustrated by the EMCC ${k}_{d,n}^2$ and ${k}_e^2$ calculations for the radial vibrations of a disk and ring-shaped plate as special cases of realizing an examined plane electroelastic state of the plate. At resonant frequencies of those piezoelectric plates, calculation results for the above coefficients were found to be coincident if the square of static planar EMCC of the material ${k}_p^2=2{d}_{31}^2/\left[\left(1-\upnu \right){s}_{11}^E{\upvarepsilon}_{33}^T\right]$ is assumed to be equal to 0.6. For real materials, this coefficient is much lower. For instance, for examined specimens, it equals ${k}_p^2\approx 0.31$, and exact ${k}_e^2$ at resonant frequencies is always at least 10% lower than ${k}_{d,n}^2$.

In practice, the energy EMCC ${k}_e^2$ assessment, requiring complete analytical description of all characteristics of the coupled electroelastic field, is not always possible. It should be noted that dynamic EMCC [18] are in agreement with the energy ones. With the number of a vibration mode, the difference between those coefficients at least does not increase, which in principle permits the dynamic EMCC ${k}_{d,n}^2$ to be used as the “local” estimate of the excitation performance for the normal modes of planar vibrations under successive changes of the plate geometry. The “local” estimate makes no physical sense for the exact calculation of a real energy transfer coefficient as the ratio of energy capable of conversion to the total accumulated energy of a piezoconverter at nonuniform dynamic strain.

2. Experimental Procedure. Parallelogram-shaped plate specimens were the objects of investigation. They were prepared from SM111 piezoceramic square plates with thickness polarization (modified PZT-4, STEMiNC), having 45.0 × 45.0 × 2.8 mm dimensions, by cutting them with a thin diamond disk under heating temperature control (no more than 65°C). Physical properties of SM111 piezoceramics are as follows: elastic modulus in the constant electric field, N/m²: ${c}_{11}^E=13.2\cdot {10}^{10}$, ${c}_{12}^E=7.1\cdot {10}^{10}$, ${c}_{13}^E=7.3\cdot {10}^{10}$, ${c}_{33}^E=11.5\cdot {10}^{10}$, and ${c}_{44}^E=3\cdot {10}^{10}$; piezoelectric constant, N/(V·m): e₃₁ = −4.1, and e₃₃ = 14.1, and e₁₅ = 10.5; relative dielectric constant at ε₀ = 8.854·10⁻¹², F/m: ${\upvarepsilon}_{11}^s/{\upvarepsilon}_0=804.6$ and ${\upvarepsilon}_{33}^s/{\upvarepsilon}_0=659.7$; material density, kg/m³: ρ = 7900; and mechanical Q-factor: Q_m = 1800.

The AFR was studied on a test bed, which includes a Kh1-46 curve tracer, consisting of a sweep generator and display unit, a U7-3 wide-band amplifier, G3-33 (high-voltage output) and G3-117 (spectral purity) audio-frequency generators, a vibration-damping stage with the test specimen, and shielded connectors, voltmeters for measuring effective amplitudes of input and output signals, oscillographs for observing signal modes, an N-306 XY-recorder for AFR registration.

The connecting diagram of a piezoceramic plate as well as the resistors R₁, R₂, and R₃ of 0.1, 1.0, and 10.0 Ω for measuring current at resonant frequencies and R₄ of 1 MΩ for measuring antiresonant frequencies is shown in Fig. 1. Here R_out is the output resistance of a generator or amplifier (R_out ≤ 5 Ω) and R_in is the input resistance of a meter (R_in ≥ 1 MΩ).

Fig. 1.

Simplified connecting diagram of a piezoceramic plate.

Since the Q-factor of examined piezoceramic plates Q_m = 1800, their impedance Z at resonant frequencies can reach several tens of ohms. Therefore, the resonance state registration by a current level is effected by connecting the piezoceramic plate via the resistor of several ohms. Under such experimental conditions, there is no need to consider power limitations of an external energy source.

Vibration modes are visualized with the method of Chladni figures. The sharp image of modes is reached only in the case of sufficiently intensive plate vibrations. Small electromechanical coupling coefficients can lead to undesirable plate overheating, which would require stringent temperature control on the excitation of vibrations at resonant frequencies.

Resonant frequencies were measured at room temperature (~ 20°C). Amplitude voltages applied to electrodes did not exceed 0.1 V and 10 mA current, which allowed dissipative plate heating to be avoided. The plates were fixed with thin wires 0.07 mm in diameter soldered to the electrodes with minimum solder quantities to insure against the effect of “attached weight.”

The frequency of measurements was restricted with f ≤ 140 kHz since the square plate (with account of dimensions) displays six resonant frequencies, and the parallelogram-shaped plates cut out from the former exhibit an essential increase in their number. For instance, a parallelogram with a 10° shear angle already shows about 20 resonant frequencies, which is caused by the effective excitation of asymmetric modes.

3. Amplitude-Frequency Response and Electromechamical Coupling Coefficient of a Square Plate and Parallelograms.

3.1. Amplitude-Frequency Response and EMCC of a Square Plate. Experimental AFR of a square piezoceramic plate is shown in Fig. 2. The resonant f_R,n and antiresonant f_A,n frequences and electromechanical coupling coefficients ${k}_{d,n}^2$ (Eq. 1), calculated by the Mason formula [19], which is an important characteristic of vibratory systems with piezoceramic elements [18,19,20], as well as the resonant frequencies ${f}_{R,n}^{comp}$, calculated by a method [15], are summarized in Table 1.

Fig. 2.

Amplitude-frequency response of the square piezoceramic plate. (Here and in Figs. 3 and 4: Numbers near resonance peaks refer to measured resonant frequencies, A_rel is the relative voltage amplitude at output (3) – Fig. 1.)

Table 1. Experimental Resonant and Antiresonant Frequencies, EMCC, and Calculated Resonant Frequencies of the Square Piezoceramic Plate

The first resonance is excited at a frequency of f_R,1 = 41.077 kHz, the closed nodal line is located in the center of the plate, which can correspond to the “quasiradial” mode typical of radial vibrations of a circular disk. The second intensive vibration mode occurs at a frequency of f_R,2 = 60.394 kHz, in this case, the nodal lines are diagonally distributed. The third vibration mode at a frequency of f_R,3 = 112.406 kHz possesses five nodal lines and is an overtone of the first mode, the fourth one at a frequency of f_R,4 = 116.964 kHz exhibits diagonal symmetry with nine nodal lines, and the fifth one at f_R,5 = 132.505 kHz displays central symmetry. As expected, the intensity of displacements u_x and u_y of the medium plane of the square plate is equal for all vibration modes, which gives rise to this sequence of modes with axial and diagonal symmetry.

The energy characteristics of those vibration modes can be described in the following way. The highest value ${k}_{d,1}^2\approx 0.27$ is reached at the first resonance, with this, the width of a resonance curve and both displacements u_x and u_y would be at their maximum. Then the ${k}_{d,n}^2$ values for the modes of higher order decrease essentially, except for the third mode with ${k}_{d,3}^2\approx 0.05$. This EMCC behavior corresponds to earlier results [18], and the differences in the intensity of vibration amplitudes at different frequencies correlate with the width of a resonance curve and ${k}_{d,n}^2$ value for each normal mode.

3.2. Amplitude-Frequency Response and EMCC of a Parallelogram-Shaped Plate (Case 1). The AFR of a parallelogram-shaped plate with an 88° acute angle, i.e., with a 2° shear angle is presented in Fig. 3. Accurate experimental evaluation of several antiresonant frequencies did not turn out well, which did not greatly influence the procedure. Comparison of data (Figs. 2 and 3) shows that the general structure of the resonant frequency spectrum was maintained, i.e., the most intensive resonances are observed near 40 and 60 kHz as well as in the range of 110–120 kHz. However, the frequency spectrum displays new resonances as compared to the square plate. The frequencies of resonances, antiresonances, and EMCC values as well as calculated resonant frequencies are summarized in Table 2.

Fig. 3.

Amplitude-frequency response of the parallelogram-shaped plate.

Table 2. Experimental Resonant, Antiresonant Frequencies, EMCC, and Calculated Resonant Frequencies of the Parallelogram-Shaped Plate (Case 1)

The three resonance peaks of inconsiderable intensity at f_R,1 = 28.6 kHz, f_R,2 = 32.39 kHz, and f_R,3 = 37.03 kHz with EMCC ${k}_{d,1}^2\approx 0.01$, ${k}_{d,2}^2\approx 0.007$, and ${k}_{d,3}^2\approx 0.005$ appeared below the most intensive resonance at a frequency of f_R,4 = 42.88 kHz, which corresponds to the first one of the square plate f_R,1 = 41.077 kHz. The resonance at a lower frequency f_R,1 = 28.6 kHz is consistent with the diagonal vibration mode.

It should be noted that the three low-frequency resonances of the parallelogram-shaped plate are most likely of metrological significance, associated, e.g., with experimental evaluation of elastic moduli of the piezomaterial. However, their practical application as any intensive modes, e.g., in actuators or frequency filters, is quite difficult.

The corresponding resonance at f_R,5 = 62.19 kHz with a very close value ${k}_{d,5}^2\approx 0.024$ is observed at a somewhat higher frequency as compared to the second resonance of the square plate f_R,2 = 60.394 kHz). Still further a weak resonance is revealed at f_R,6 = 74.8 kHz with a negligible ${k}_{d,6}^2\approx 0.006$.

The spectrum of very weak resonances f_R,7 = 92.73 kHz, f_R,8 = 95.77 kHz, f_R,9 = 97.93 kHz, and f_R,10 = 102.45 kHz does also appear over the range of ~90–100 kHz, unfortunately, antiresonant frequencies and EMCC could not be reliably determined. Moreover, the parallelogram-shaped plate exhibits resonances at f_R,11 = 110.98 kHz and f_R,13 = 114.83 kHz with very small values ${k}_{d,11}^2\approx 0.005$ and ${k}_{d,13}^2\approx 0.004$ as well as the resonance at f_R,12 = 111.93 kHz with a mach higher ${k}_{d,12}^2\approx 0.02$.

The vibration mode with f_R,14 = 119.05 kHz and ${k}_{d,14}^2\approx 0.016$ corresponds to the third resonance of the square plate at f_R,3 = 112.406 kHz. An adjacent resonance is located at f_R,15 = 120.43 kHz with practically the same ${k}_{d,15}^2\approx 0.017$.

Analysis of planar vibrations of the parallelogram-shaped plate and comparison of the results with those for the square plate demonstrate that the number of excited resonances for the former one grows greatly over the whole examined frequency range.

3.3. Amplitude-Frequency Response and EMCC of a Parallelogram-Shaped Plate (Case 2). The AFR of the parallelogram-shaped plate with a 10° shear angle, i.e., with an 80° acute angle is presented in Fig. 4. Comparison of the data with those in Fig. 3 shows that with an increase in the shear angle, all resonant frequencies are still somewhat increasing. The corresponding frequencies of resonances, antiresonanses, EMCC as well as calculated resonant frequencies are summarized in Table 3.

Fig. 4.

Amplitude-frequency response of the parallelogram-shaped plate.

Table 3. Experimental Resonant, Antiresonant Frequencies, EMCC, and Calculated Resonant Frequencies of the Parallelogram-Shaped Plate (Case 2)

The first mode frequency, corresponding to the first resonance of the square plate with f_R,1 = 41.077 kHz, grows to f_R,4 = 49.55 kHz and exhibits the highest EMCC ${k}_{d,4}^2\approx 0.168$, while the second resonance of the square plate with f_R,2 = 60.394 kHz is consistent with the mode of f_R,6 = 65.14 kHz and ${k}_{d,6}^2\approx 0.032$. Moreover, combined excited vibrations generate the mode with the resonant frequency f_R,5 = 55.72 kHz, which was not observed before. It possesses a rather high EMCC ${k}_{d,5}^2\approx 0.067$.

Comparison of the data for the three first resonances of the parallelogram-shaped plate with 2 and 10° shear angles (Figs. 3 and 4) demonstrates their upward frequency shift: for a 10° shear angle: f_R,1 = 31.05 kHz, f_R,2 = 34.35 kHz, and f_R,3 = 40.4 kHz and ${k}_{d,1}^2\approx 0.017$, ${k}_{d,2}^2\approx 0.037$, and ${k}_{d,3}^2\approx 0.011$, respectively, i.e., the intensity of the second resonance became more substantial in comparison with the neighboring ones. As a whole, the distribution of displacements for those three modes corresponds to those of the plate with a 2° shear angle.

In the range of frequencies of f_R,7 = 69.85 – f_R,13 = 102.67 kHz, the excitation of a large number of resonances with a relatively low efficiency is observed, coefficients with ${k}_{d,7}^2-{k}_{d,19}^2$ do not exceed several thousandth.

In the high-frequency region, the vibration modes have no specific features, the most intensive ones possess the following resonant frequencies f_R,14 = 107.49 kHz, f_R,15 = 112.03 kHz, f_R,16 = 114.84 kHz, and ${k}_{d,14}^2\approx 0.012$, ${k}_{d,15}^2\approx 0.016$, ${k}_{d,16}^2\approx 0.013$. The vibrations propagate mainly along the major diagonal of the parallelogram-shaped plate.

Thus, the parallelogram-shaped plates with a 10° shear angle exhibit the tendency of maintaining the same vibration modes, as those excited in the plate with a 2° shear angle. Many modes demonstrate rather significant form stability.

Conclusions

• 1. Experimental investigation results for square and parallelogram-shaped piezoceramic plates with uniformly continuous electrode coating under forced vibrations demonstrate that even a small change in the plate geometry alters abruptly the spectrum of excited planar resonant vibrations.

• 2. The modes of higher-order in parallelogram-shaped plates are established to be effectively excited with maintaining the uniformity of an electrode coating.

• 3. The data on measuring resonant and antiresonant frequencies were used to calculate dynamic electromechanical coupling coefficients for evaluating energy conversion efficiency at resonant plate vibrations.

• 4. Experimental results for square and parallelogram-shaped plates in measuring resonant vibration frequencies and calculated data obtained with an analytical method [15] are in good agreement. It corroborates efficiency of the analytical approach to simulation of planar vibrations of rectangular and uncanonical parallelogram-shaped piezoceramic plates.