1 Introduction

Recently, the development of piezoelectric materials has become an important objective since science and technology in this area are considerably increasing theoretical approaches and applications to meet the demands of social-technical and daily life requirements. Materials that have the piezoelectric effect can sense and adapt their response against external stimuli. Thanks to this excellent feature, their application areas are increasing day-by-day. In particular, structural systems described as smart are very popular in many engineering applications such as electromechanical systems and smart composites. For instance, piezoelectric materials are preferred for the layers instead of elastic ones while manufacturing smart composites. Their development is based on integration into the structure as sensors or actuators and in combination with appropriate electronics, modeling, and control mechanisms.

Up to the present, many articles have been governed related to the mechanical attitudes of piezoelectric structures; the reference in [1] may be read for more mechanical information. Let us briefly mention some of the relevant research. Alibeigloo solved the static problem of a simply supported functionally graded material (FGM) rectangular plate integrated with piezoelectric layers under the action of a transverse force, standing on the Winkler-Pasternak foundation [2]. Alibeigloo and Chen analyzed dynamic vibration by a normal load and electric excitation of an FGM cylindrical panel with simply supported edges [3]. Alibeigloo and Simintan presented their report regarding the axisymmetric analysis of an FGM circular/annular plate subjected to pressure and electrostatic excitation using the differential quadrature method [4]. Zhou et al considered the effect of the initial stress state on bulk wave propagation at the imperfect interface of a piezomagnetic/piezoelectric plate [5]. Gaur and Rana derived the dispersion relations in a piezoelectric composite strip of two different layers for two different wave propagations [6]. Cupiał proposed a numerical model for the natural vibrations of a piezoelectric slab and compared the perturbation solutions with the exact ones [7] Barati et al developed the refined plate model for the buckling response of a functionally graded piezoelectric (FGP) material with elastic faces [8]. Ezzin et al considered the SH wave propagations in laminated piezomagnetic/piezoelectric plates utilizing the stiffness matrix method [9]. Yue et al created a new numerical approach to investigate the dynamic behavior of the cantilever piezoelectric nanobeam for different initial configurations [10]. Andakhshideh et al investigated the piezoelectric electromechanical coupling effects on the interlaminar stresses of multi-layered piezoelectric plates subjected to uniform constant axial strain [11]. Hong studied the free vibration analysis of bidirectional functionally graded material (2D-FGM) for the case where mechanical properties vary continuously in both the thickness and one-edge directions [12]. Song et al solved the system of the partial differential equations regarding vibrations by the rigid flat or cylindrical punches of the piezoelectric half-space using the Fourier integral transform [13]. Qi et al studied SH wave propagation in a two-dimensional piezoelectric strip with infinite length on the basis of the multiple mirror superposition and wave function expansion methods [14]. Guha and Singh analytically analyzed the scattering of the SH wave along a piezoelectric fiber-reinforced material standing on a piezoelectric half-plane [15]. Kumar and Harsha considered the nonlinear static bending and free vibration of the functionally graded piezoelectric plate (FGPP) resting on the two/three-parameter foundation under a thermo-electro environment using the first-order shear deformation theory [16].

In some of the references cited above, there is a conspicuous concept; that is the "initial stress" in the problems. This factor is one of the most important features of the dynamic response of a system to be considered. Note that initial stresses may be exposed to layers of the body due to technological requirements or environmental conditions. Due to these and other similar factors, problems cannot be investigated according to the classical linear elastodynamic theory (CLTED) since stress distributions display nonlinear effects; as a result, the deformations in elastic bodies are governed in terms of nonlinear partial differential equations. However, when assuming (a) the initial stress state is exactly homogeneous and static and (b) the magnitude of the initial loading is considerably greater than that of the dynamic force subjected to the body, the corresponding problems can be investigated with the utilization of the three-dimensional linearized theory of elasticity for pre-stressed bodies. The recent studies by Guz [17], Shams et al [18], and Akbarov [19] can be considered quite popular papers related to the initial stress state.

Today, one can find many papers related to the influence of the initial stress. Akbarov et al studied the influence of the shear-spring imperfectness on the forced vibrations of a bi-layered plate-strip with initial stress under the action of a time-harmonic loading [20]. Kundu et al discussed oscillations of Love waves along fiber-reinforced anisotropic layer standing on an orthotropic half-plane numerically [21]. Li and Tao investigated the influence of the initial stress case on certain special types of wave propagation in a rock mass [22]. Shams considered the effect of initial stress on the propagation of Love waves in an incompressible material based on a half-space [23]. Daşdemir studied the forced vibration by a time-harmonic force of a finite-dimensional pre-stressed system with a piezoelectric core in contact perfectly with two elastic faces [24] and then extended the mentioned paper to the case where there exists incomplete contact at the interfaces of the layers [25]. Kocakaplan and Tassoulas presented formulations of the incremental equations of motion related to the frequency spectrum of a pre-stressed straight rod of circular cross-section [26]. Kumar et al analyzed shear (SH) waves in a horizontally polarized functional-graded piezoelectric body resting imperfectly on a functionally graded porous piezoelectric material half-space [27]. Mahanty et al studied shear acoustic waves in a piezoelectric cylinder boded imperfectly to an external functional-graded piezoelectric material [28]. Craciun et al developed a mathematical model to be able to investigate the influence of antiplane crack in a piezoelectric material in the existence of the static initial stress and initial polarization in terms of complex potentials [29]. Babych and Glukhov considered a vibration problem by moving force at the top surface in a multi-layered half-plane with initial stresses [30]. Panja and Mandal analytically solved the stress field problem related to several viscoelastic strips resting on a viscoelastic orthotropic half-plane with initial stresses using the finite difference method [31]. Daşdemir analyzed electromechanical vibrations of a pre-stressed piezoelectric plate under the action of an inclined dynamic force standing on a rigid ground [32].

Taking the current literature, to the author's knowledge, although great endeavor has been made on many electro-elastic problems of various forms regarding the dynamical behavior of the piezoelectric materials, there is no fundamental study for investigating the dynamical response of a bi-axially pre-stressed piezoelectric plate subjected to a time-harmonic force resting on a rigid ground. Research is needed to provide essential results in the characterization of the stated response. This is our motivation to attempt the aim to create an efficient mathematical model for the solution of dynamical stress field problems concerning a transversely isotropic and homogeneous piezoelectric plate with a finite length. For this aim, we develop the mechanical and electrical governing equations within the scope of the three-dimensional linearized theory of electro-elastic waves in initially stressed bodies (TLTEEWISB) and also derive relations between the mechanical and electrical initial stress. Note that the piezoelectric plate is poled in parallel to the lateral boundary. On the basis of the variational formulation and the virtual work principle, the three-dimensional finite element modeling (3D-FEM) under consideration is created. Great attention is given to the frequency response and dynamical behavior of the piezoelectric rectangular plate and the influence of both mechanical and electrical initial stress parameters on the resonance mode of the system.

2 Problem formulation

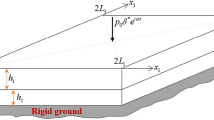
In the Cartesian coordinate system \(Ox_{1} x_{2} x_{3}\), consider a piezoelectric plate of finite lengths resting on a rigid foundation, with bi-axially initial stresses and poled in the perpendicular direction to the top surface. As summarized by figure 1, the horizontal lengths are \(2a_{1}\) and \(2a_{3}\), and the thickness is \(h\), respectively. While creating the present system, the body is first subjected to uniaxial static normal forces (i.e., either tensile or compression) along the \(Ox_{1}\) and \(Ox_{2}\)-axes; next, the plate is left on the rigid ground. In this case, the initial stress state can be determined by utilizing the linear theory of elasticity as

$$ \sigma _{{\ell \ell }}^{0} = q_{{\ell \ell }} ,\;\;{\text{and}}\;\;\sigma _{{ij}}^{0} = 0\;\;{\text{for}}\;\;ij \ne \ell \ell , $$

where \(i,j = 1,2,3\), \(\ell = 1,3\), \(q_{\ell \ell }\) is a known value for each direction, and the upper index “0” indicates the pre-state. It should be noted that these developments also lead to the construction of an initial electrical displacement in the plate; namely, they are self-consistent. It is well-known that the electric charge in the piezoelectric body is linearly proportional to the mechanical force. Consequently, considering the constitutive equations, the following interrelationship between the mechanical and electrical initial stress can be derived [32]:

$$ D_{1}^{0} = \frac{{e_{33} \left( {c_{11} + c_{12} } \right) - 2c_{13} e_{31} }}{{c_{33} \left( {c_{11} + c_{12} } \right) - 2c_{13}^{2} }}q_{11} \;\;{\text{and}}\;\;D_{3}^{0} = \frac{{\left( {c_{11} - 2c_{12} + c_{22} } \right)c_{13} e_{31} + \left( {c_{12}^{2} - c_{11} c_{22} } \right)e_{33} }}{{\left( {c_{11} - 2c_{12} + c_{22} } \right)c_{13}^{2} + \left( {c_{12}^{2} - c_{11} c_{22} } \right)c_{33} }}q_{33} . $$
Figure 1
figure 1

Skeleton of the problem.

Full size image

For simplicity, improving the related fields in the actual problem may be beneficial. First, because of the dynamic harmonic force varying with the time \(t\), all the components, such as displacement or stress, can be discretized from our problem such that \( \left[ \right]^{\left( m \right)} = \left[ {\hat{}} \right]^{\left( m \right)} e^{i\omega t}\), where \(i = \sqrt { - 1}\), and \(e\) is the famous Euler constant. We apply the coordinate transformation \(\hat{x}_{i} = x_{i} /h\) to move our problem to the simpler skeleton. For readability, we omit the hats over quantities after this. According to Guz [17] and Fulin et al [33], based on the foregoing assumptions, linear governing equations of motion can be given as

$$ \left( {\sigma_{ij} + \sigma_{kj}^{0} u_{i,k} } \right)_{,j} + \rho \omega^{2} h^{2} u_{i} = 0, $$
(1)
$$ \left( {D_{i} + D_{i}^{0} u_{j,i} } \right)_{,i} = 0, $$
(2)

where \(i,j,k = 1,2,3\), and the summation protocol over repeated indices is implemented. Here, \(\sigma_{ij}\) is the stress tensor, \(D_{i}\) is the electric displacement tensor, respectively, \(\rho\) is the mass density of the plate and the comma represents partial differentiation. For the present case, the constitutive relationships can be obtained as follows [1]:

$$ \left( {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{33} } \\ {\sigma_{23} } \\ {\sigma_{31} } \\ {\sigma_{12} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {c_{11} } & {c_{13} } & {c_{12} } & 0 & 0 & 0 \\ {c_{13} } & {c_{33} } & {c_{13} } & 0 & 0 & 0 \\ {c_{12} } & {c_{13} } & {c_{11} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {c_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{66} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {c_{44} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{33} } \\ {2\varepsilon_{23} } \\ {2\varepsilon_{13} } \\ {2\varepsilon_{12} } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} 0 & {e_{31} } & 0 \\ 0 & {e_{33} } & 0 \\ 0 & {e_{31} } & 0 \\ 0 & 0 & {e_{15} } \\ 0 & 0 & 0 \\ {e_{15} } & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \\ \end{array} } \right), $$
(3)
$$ \left( {\begin{array}{*{20}c} {D_{1} } \\ {D_{2} } \\ {D_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & {e_{15} } \\ {e_{31} } & {e_{33} } & {e_{31} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {e_{15} } & 0 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{33} } \\ {2\varepsilon_{23} } \\ {2\varepsilon_{13} } \\ {2\varepsilon_{12} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\gamma_{11} } & 0 & 0 \\ 0 & {\gamma_{33} } & 0 \\ 0 & 0 & {\gamma_{11} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {E_{1} } \\ {E_{2} } \\ {E_{3} } \\ \end{array} } \right), $$
(4)

where \(\varepsilon_{ij}\) is the strain component, \(E_{i}\) is the electric field component, and \(c_{ij}\), \(e_{ij}\), and \(\gamma_{ij}\) are the mechanic, piezoelectric and dielectric permittivity characteristics, respectively. The strain-displacement and electric field-electric potential relations are

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right)\;\;{\text{and}}\;\;E_{i} = - \varphi_{,i} . $$
(5)

Next, the following boundary-contact terms are held:

$$ \left. {\sigma_{21} } \right|_{{x_{2} = 0}} = \left. {\sigma_{32} } \right|_{{x_{2} = 0}} = 0,\;\;\left. {\sigma_{22} } \right|_{{x_{2} = 0}} = - p_{o} \delta^{*} , $$
(6)
$$ \left. {\left( {\sigma_{\ell \ell }^{0} u_{j,\ell } + \sigma_{\ell j} } \right)} \right|_{{x_{\ell } = 0,2a_{\ell } /h}} = 0, $$
(7)
$$ \left. {u_{j} } \right|_{{x_{2} = - 1}} = 0, $$
(8)
$$ \,\left. {\left( {D_{i} + D_{j}^{0} u_{i,j} } \right)} \right|_{{x_{\ell } = 0,2a_{\ell } }} = 0, $$
(9)
$$ \left. \varphi \right|_{{x_{2} = 0, - 1}} = 0, $$
(10)

where \(\ell = 1,3\) and \(\delta^{*}\) is the Dirac-like delta function as \(\delta^{*} = \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)\). While Eqs. (6) and (8) are the mechanical traction-free conditions, Eqs. (7) and (9) are mechanically and electrically open conditions. Also, Eq. (10) is electrically open conditions.

3 Solution procedure

As shown in figure 1, we study the harmonic vibration of the piezoelectric plate with finite lengths. For solving our problem, we, therefore, prefer to utilize the finite element method (FEM) according to the virtual work principle [34]. To accomplish the aim, we first introduce the test functions \(v_{i}\) and \(\psi\). Note that these functions satisfy the corresponding boundary-contact conditions given in Eqs. (6)–(10). Next, by integrating all the resultant equations over the unit cube \(V = \left[ { - 1,1} \right] \times \left[ { - 1,1} \right] \times \left[ { - 1,1} \right]\) after multiplying the equations of motion in Eqs. (1) and (2) by the test functions and summing them side by side, we obtain

$$ \int\limits_{V} {\left[ {T_{ij,j} v_{i} + \rho \omega^{2} h^{2} u_{i} v_{i} + S_{i,i} \psi } \right]dV} = 0, $$
(11)

and applying the famous Gauss-Ostrogradsky theorem into the last equation yields

$$ \int\limits_{V} {\left[ {T_{ij} v_{i,j} - \rho \omega^{2} h^{2} u_{i} v_{i} + S_{i} \psi_{,i} } \right]dV} - \int\limits_{S} {\left[ {T_{ij} v_{i} n_{j} + S_{i} n_{i} \psi } \right]dS} = 0, $$
(12)

where \(S\) denotes the boundary of the unit volume \(V\). Further, let us introduce the notations

$$ T_{ij} = \sigma_{ij} + \sigma_{kj}^{0} u_{i,k} = p_{ijkn} u_{n,k} + r_{ijk} \varphi_{,k} \;\;{\text{and}}\;\;S_{i} = D_{i} + D_{i}^{0} u_{j,i} = r_{ijk} u_{j,k} - s_{ik} \varphi_{,k} . $$
(13)

From the constitutive relationships in Eqs. (3) and (4), the notations used in Eq. (13) can explicitly be given as

$$ \begin{aligned} & p_{1111} = c_{11} + \sigma_{11}^{0} ,\,\,\,p_{1122} = c_{13} ,\,\,\,p_{1212} = c_{44} ,\,\,\,p_{1221} = c_{44} + \sigma_{11}^{0} ,\,\,\,p_{2112} = c_{44} , \\ & p_{2121} = c_{44} ,\,\,\,p_{2211} = c_{13} ,\,\,\,p_{2222} = c_{33} ,\,\,\,p_{1133} = c_{12} ,\,\,\,p_{1313} = c_{66} ,\,\,\,p_{1331} = c_{66} + \sigma_{11}^{0} , \\ & p_{3131} = c_{66} ,\,\,\,p_{3311} = c_{12} ,\,\,\,p_{2323} = c_{44} ,\,\,\,p_{2233} = c_{13} ,\,\,\,p_{3232} = c_{44} ,\,\,\,p_{3223} = c_{44} + \sigma_{33}^{0} , \\ & p_{3322} = c_{13} ,\,\,\,p_{3223} = c_{44} ,\,\,\,p_{3113} = c_{66} + \sigma_{33}^{0} ,\,\,\,p_{3333} = c_{11} + \sigma_{33}^{0} , \\ & r_{111} = D_{1}^{0} ,\,\,\,r_{112} = e_{15} ,\,\,\,r_{121} = e_{15} + D_{1}^{0} ,\,\,\,r_{131} = D_{1}^{0} ,\,\,\,r_{211} = e_{31} ,\,\,\,r_{222} = e_{33} , \\ & r_{233} = e_{31} ,\,\,\,r_{313} = D_{3}^{0} ,\,\,\,r_{323} = e_{15} + D_{3}^{0} ,\,\,\,r_{332} = e_{15} ,\,\,\,r_{333} = D_{3}^{0} , \\ & s_{11} = \gamma_{11} ,\,\,\,s_{22} = \gamma_{33} ,\,\,\,\,s_{33} = \gamma_{11} . \\ \end{aligned} $$
(14)

Note that all components not included in Eq. (14) are equal to zero.

Considering the partition of the plate surface and the boundary-contact terms in Eqs. (5)–(10), the integral statement in Eq. (12) over the unit volume \(V\) takes shape

$$ \int\limits_{V} {\left[ {T_{ij} v_{i,j} - \rho \omega^{2} h^{2} u_{i} v_{i} + S_{i} \psi_{,i} } \right]dV} - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {h^{2} \left\{ {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right\}} \right)v_{2} } \right]dS_{u} } = 0 $$
(15)

or in another way,

$$ \begin{aligned} & \int\limits_{V} {\left[ {\sigma_{ij} \varepsilon_{ij}^{v} + \theta_{ij}^{u} v_{i,j} + D_{i} \psi_{,i} + \theta_{ij}^{s} \psi_{,i} - \rho \omega^{2} h^{2} u_{i} v_{i} } \right]dV} \\ & - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } = 0, \\ \end{aligned} $$
(16)

where \(\varepsilon_{ij}^{v} = \left( {v_{i,j} + v_{j,i} } \right)/2\), \(\theta_{ij}^{u} = \sigma_{kj}^{0} u_{i,k}\), \(\theta_{ij}^{s} = D_{i}^{0} u_{j,i}\), and \(S_{u}\) denotes the upper surface of the plate. Thus, we have obtained the weak form of our problem.

Based on one of the weak forms given above, we can construct the variational formulation for the problem. For this purpose, let us replace the test functions \(v_{i}\) and \(\psi\) with the respective displacement functions \(\delta u_{i}\) and electric potential \(\delta \varphi\), which satisfy the governing equations in Eqs. (1)–(2) and the boundary-contact terms in Eqs. (6)–(10). As a result, Eq. (16) can be written as

$$ \begin{aligned} 0 & = \int\limits_{V} {\left[ {\sigma_{ij} \delta \varepsilon_{ij} + \theta_{ij}^{u} \delta u_{i,j} + D_{i} \delta \varphi_{,i} + \theta_{ij}^{s} \delta \varphi_{,i} - \rho \omega^{2} h^{2} u_{i} \delta u_{i} } \right]dV} \\ & \quad - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } \\ & = \int\limits_{V} {\left[ {\left( {\underline {\sigma }_{ij} + r_{kij} } \right)\delta \varepsilon_{ij} + \sigma_{kj}^{0} u_{i,k} \delta u_{i,j} + \left( {r_{kij} u_{i,j} - s_{kn} \varphi_{,n} } \right)\delta \varphi_{,k} - \rho \omega^{2} h^{2} u_{i} \delta u_{i} } \right]dV} \\ & \quad - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } \\ & = \int\limits_{V} {\left[ {\left( {\underline {\sigma }_{ij} + \sigma_{kj}^{0} u_{i,k} } \right)\delta u_{i,j} + r_{kij} \left( {\varphi_{,k} \delta u_{i,j} + u_{i,j} \delta \varphi_{,k} } \right) - s_{kn} \varphi_{,n} \delta \varphi_{,k} - \rho \omega^{2} h^{2} u_{i} \delta u_{i} } \right]dV} \\ & \quad - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } \\ & = \int\limits_{V} {\left[ {p_{mjkl} u_{k,l} \delta u_{i,j} + r_{kij} \left( {\varphi_{,k} \delta u_{i,j} + u_{i,j} \delta \varphi_{,k} } \right) - s_{kn} \varphi_{,n} \delta \varphi_{,k} - \rho \omega^{2} h^{2} u_{i} \delta u_{i} } \right]dV} \\ & \quad - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } \\ & = \delta \left[ \begin{gathered} \int\limits_{V} {\left[ {\frac{1}{2}p_{ijkl} u_{k,l} u_{i,j} + r_{kij} \varphi_{,k} u_{i,j} - \frac{1}{2}s_{kn} \varphi_{,n} \varphi_{,k} } \right]dV - \frac{1}{2}\int\limits_{V} {\rho \omega^{2} h^{2} u_{i}^{2} dV} } \\ - \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } \\ \end{gathered} \right] \\ \end{aligned} $$
(17)

Here, the underlined term \(\underline {\sigma }_{ij}\) denotes the mechanical part of the corresponding stress component. Let us use the following representations:

$$ \Pi = \int\limits_{V} {\left[ {\frac{1}{2}\left( {p_{ijkl} u_{k,l} u_{i,j} } \right) + r_{kij} \varphi_{,k} u_{i,j} - \frac{1}{2}s_{kn} \varphi_{,n} \varphi_{,k} } \right]dV} ,\;\;{\rm M} = \frac{1}{2}\int\limits_{V} {\rho h^{2} u_{i}^{2} dV} ,\;\;{\text{and}}\;\;{\rm P} = \int\limits_{{S_{u} }} {\left[ {p_{0} \delta \left( {\left( {x_{1} - a_{1} } \right)^{2} + \left( {x_{3} - a_{3} } \right)^{2} } \right)v_{2} } \right]dS_{u} } . $$

Consequently, our original problem related to the harmonic vibration of the piezoelectric plate is transformed into the total energy functional

$$ \delta \left( {\Pi - \omega^{2} {\rm M} - {\rm P}} \right) = 0, $$
(18)

where \(\Pi\), \({\rm M}\), and \({\rm P}\) are the potential, kinetic and virtual work energies, respectively.

For our numerical solution, we create the displacement-based FEM of our problem in view of the virtual work principle. For this purpose, let \(V_{h}\) be the region of a finite element mesh, i.e., \(V_{h} \subset V\) and \(V_{h} = \bigcup\nolimits_{m} {V^{em} }\). Following the classic finite element method, the displacements in \({\mathbf{u}} = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } \\ \end{array} } \right] \in V_{uh}\), the electrical fields in \({\mathbf{E}} = \left[ {\begin{array}{*{20}c} {E_{1} } & {E_{2} } & {E_{3} } \\ \end{array} } \right] \in V_{Eh}\), and their virtual structures can be approximated by

$$ {\mathbf{u}} \cong \sum\limits_{j = 1}^{M} {\mathbf{N}} {\tilde{\mathbf{u}}} ,\;\;\delta {\mathbf{u}} \cong \sum\limits_{j = 1}^{M} {{\mathbf{N}}\delta {\tilde{\mathbf{u}}}} ,\;\;{\mathbf{E}} \cong \sum\limits_{j = 1}^{M} {\mathbf{N}} {\tilde{\mathbf{E}}} ,\;\;{\text{and}}\;\;\delta {\mathbf{E}} \cong \sum\limits_{j = 1}^{M} {{\mathbf{N}}\delta {\tilde{\mathbf{E}}}} , $$
(19)

where \({\tilde{\mathbf{u}}}\), \(\delta {\tilde{\mathbf{u}}}\), \({\tilde{\mathbf{E}}}\), and \(\delta {\tilde{\mathbf{E}}}\) are nodal values of the displacements, the virtual displacements, the electrical fields and the virtual electrical fields, and \({\mathbf{N}}\left( {x_{1} ,x_{2} ,x_{3} } \right)\) are the conventional 3-D FE interpolation functions. In this paper, we use eight-noded smooth quadrilateral elements, so that the interpolation functions \({\mathbf{N}}\left( {x_{1} ,x_{2} ,x_{3} } \right)\) are identified to be quadratic polynomial functions. In [35], Hutton gave a list of the used interpolation functions.

All the fields obtained over the nodes of a typical finite element can be written in a single vector as follows:

$$ {\mathbf{u}}^{e} = \left[ {\begin{array}{*{20}c} {u_{1}^{e} } & {u_{2}^{e} } & {u_{3}^{e} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {u_{11}^{e} } & \ldots & {u_{18}^{e} } & | & {u_{21}^{e} } & \ldots & {u_{28}^{e} } & | & {u_{31}^{e} } & \ldots & {u_{38}^{e} } \\ \end{array} } \right]^{T} $$

and

$$ {\mathbf{E}}^{e} = \left[ {\begin{array}{*{20}c} {E_{1}^{e} } & {E_{2}^{e} } & {E_{3}^{e} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {E_{11}^{e} } & \ldots & {E_{18}^{e} } & | & {E_{21}^{e} } & \ldots & {E_{28}^{e} } & | & {E_{31}^{e} } & \ldots & {E_{38}^{e} } \\ \end{array} } \right]^{T} . $$

Substituting Eq. (19) into the total energy functional given in Eq. (18) and following the general process including so extensive operations and manipulations, the following matrix-vector system of equations is obtained:

$$ \left\{ {{\mathbf{K}}_{{uu}} - \omega ^{2} {\mathbf{M}}_{{uu}} } \right\}\varvec{\tilde{U}} + {\mathbf{K}}_{{uE}} \varvec{\bar{E}} = \varvec{F}_{u} $$
(20)
$$ {\mathbf{K}}_{uE} \tilde{\user2{U}} + {\mathbf{K}}_{EE} \overline{\user2{E}} = {\varvec{F}}_{E} , $$
(21)

where \({\mathbf{K}}_{uu} = \sum {{\mathbf{K}}_{uu}^{em} }\), \({\mathbf{K}}_{uE} = \sum {{\mathbf{K}}_{uE}^{em} }\), and \({\mathbf{K}}_{EE} = \sum {{\mathbf{K}}_{EE}^{em} }\) are the mechanical, electro-elastic, and electrical global stiffness matrices, respectively, and \({\mathbf{M}}_{uu} = \sum {{\mathbf{M}}_{uu}^{em} }\) is the global mass matrix. Note that the mentioned matrices are constructed with ensemble “\(\sum \square\)” of the corresponding local matrices. Further, \(\varvec{F}_{u}\) and \({\varvec{F}}_{E}\) are the nodal force vectors. It should be noted that, while the vector \({\varvec{F}}_{E}\) is null, \(\varvec{F}_{u}\) contains only a unique non-zero component due to the boundary-contact conditions in Eqs. (6)–(10). Considering Eq. (18), we get the explicit entries of the stiffness and mass matrices as

$$ {\mathbf{M}}_{uu}^{em} = \int\limits_{{V^{em} }} {\rho h^{2} {\mathbf{N}}_{uh}^{e} \cdot {\mathbf{N}}_{uh}^{e\;T} dV^{em} } ,\;\;{\mathbf{K}}_{uu}^{em} = \int\limits_{{V^{em} }} {{\mathbf{S}}_{uh}^{e\;T} \cdot {\mathbf{C}} \cdot {\mathbf{S}}_{uh}^{e} dV^{em} } , $$
(22)
$$ {\mathbf{K}}_{uE}^{em} = \int\limits_{{V^{em} }} {{\mathbf{N}}_{Eh}^{e\;T} \cdot {\mathbf{e}}^{T} \cdot {\mathbf{N}}_{Eh}^{e} dV^{em} } ,\;\;{\mathbf{K}}_{EE}^{em} = \int\limits_{{V^{em} }} {{\mathbf{S}}_{Eh}^{e\;T} \cdot {{\varvec{\upgamma}}} \cdot {\mathbf{S}}_{Eh}^{e} dV^{em} } , $$
(23)
$$ {\mathbf{S}}_{uh}^{e} = {\mathbf{L}}\left( \nabla \right) \cdot {\mathbf{N}}_{uh}^{e\;T} ,\;\;{\mathbf{S}}_{Eh}^{e} = \nabla {\mathbf{N}}_{Eh}^{e\;T} , $$
(24)
$$ {\mathbf{L}}\left( \nabla \right) = \left[ {\begin{array}{*{20}c} {\partial_{1} } & 0 & 0 & 0 & {\partial_{3} } & {\partial_{2} } \\ 0 & {\partial_{2} } & 0 & {\partial_{3} } & 0 & {\partial_{1} } \\ 0 & 0 & {\partial_{3} } & {\partial_{2} } & {\partial_{1} } & 0 \\ \end{array} } \right]^{T} $$
(25)

Inserting the approximations in Eq. (19) into Eq. (18) yields

$$ \left( {{\text{K}} - \omega^{2} {\mathrm{M}}} \right){\mathbf{U}} = {\mathbf{F}}, $$
(26)

where \({\text{K}}\) and \({\text{M}}\) are the global stiffness and mass matrices, which may include the components of the displacement in the plane stresses, \({\mathbf{U}}\) and \({\mathbf{F}}\) is the generalized displacement and force vectors. We can write the matrices and vectors in the forms of

$$ {\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{uu} } & {{\mathbf{K}}_{uE} } \\ {{\mathbf{K}}_{uE} } & {{\mathbf{K}}_{EE} } \\ \end{array} } \right],\;\;{\mathbf{M}} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{uu} } & 0 \\ 0 & 0 \\ \end{array} } \right],\;\;{\varvec{U}} = \left\{ {\begin{array}{*{20}c} {\tilde{\user2{U}}} \\ {\tilde{\user2{E}}} \\ \end{array} } \right\},\;\;{\text{and}}\;\;{\varvec{F}} = \left\{ {\begin{array}{*{20}c} {{\varvec{F}}_{u} } \\ {{\varvec{F}}_{E} } \\ \end{array} } \right\}, $$
(27)

respectively. Because of the positive definiteness of the variational form in Eq. (18), the global matrices \({\mathbf{K}}\) and \({\mathbf{M}}\) in Eq. (27) are symmetric, real, and positive definite. This means that the matrix-vector equation in Eq. (26) has a solution and, therefore, could be evaluated. Solving the above matrix equation leads to obtaining the displacements and electrical fields at nodes, and we can transform the obtained values to those of the relative stress and electrical displacement components according to constitutive equations.

4 Numerical findings and discussions

This section carries out numerical investigations for a three-dimensional piezoelectric plate with initial stress. The material to be used is Barium Titanate \(\left( {{\mathrm{BaTiO}}_{3} } \right)\) with \(c_{44} = 44\) \(GPa\), \(e_{15} = 11.4\) \(C/m^{2}\), and \(\gamma_{11} = 1.115\) \(nF/m\), which were taken from Ref. [36]. Define dimensionless frequency parameter, initial stress parameter, electrical initial stress parameter, aspect ratio, and thickness ratio as

$$ \Omega = \omega h\sqrt {\frac{\rho }{{c_{44} }}} ,\;\;\eta_{\ell } = \frac{{q_{\ell \ell } }}{{c_{44} }},\;\;\kappa_{\ell } = \frac{{D_{\ell }^{0} }}{{c_{44} }},\;\;{\text{a}} = \frac{{a_{1} }}{{a_{3} }},\;\;{\text{h}} = \frac{h}{{2{\text{a}}}}, $$
(28)

respectively. We split the domain of the problem into a number of isoparametric finite elements with eight-node. While the number of the components in the perpendicular direction is indicated by \(n\), the ones in the horizontal directions are equal and denoted by \(m\). It should be noted that throughout the paper, our results will be presented on the bottom surface of the plate under \({\text{a}} = 1\), \({\text{h}} = 0.2\), \(\Omega = 0\), \(\eta = \eta_{1} = \eta_{3}\), \(\eta = 0\), and \(\left( {m,n} \right) = \left( {50,12} \right)\). Here, it can be seen that the number of degrees of freedom (nDoFs) is equal to 135252 in total.

We shall first prove the accuracy of the PC program that will be used for numerical investigations. To do this, we will implement a two-stage strategy. For that, first, introduce the norm functions

$$ \left\| x \right\|_{\infty } = \mathop {\max }\limits_{i} \left\| {x_{i} } \right\|_{\infty } ,\;\;\left\| x \right\|_{1} = \sum\limits_{i} {\left\| {x_{i} } \right\|_{1} } ,\;\;{\text{and}}\;\;\left\| x \right\|_{0} = \sqrt {\sum\limits_{i} {\left\| {x_{i} } \right\|_{0}^{2} } } , $$
(29)

which are called the maximum norm, \(L_{1}\) norm, and the Frobenius norm, respectively. As it is known, as the number of finite elements increases, the amount of error made in numerical results should decrease. This statement motivates us to use the norm functions for the convergence analysis described above. We, therefore, can use these norms for testing relative errors between a reference solution and numerical solutions. Figure 2 shows the relative errors in norms given in Eq. (29) as a function of the total number of degrees of freedom (nDoFs). Note that, while the one in figure 2(b) has been produced for a mesh of \(24 \times 100 \times 24\) and the fixed value of \(m\), the reference solution in figure 2(a) has been obtained for a mesh of \(100 \times 5 \times 100\) and the fixed value of \(n\) via a special workstation. The graphs prove that the rates of relative errors in the stress values decrease gradually as the number of meshes increases. This means that the numerical results converge to a certain asymptotic value. As a result, we can obtain the numerical values at the desired accuracy rate by increasing the number of meshes as much as necessary. This indicates that our PC algorithm is valid.

Figure 2
figure 2

Convergence rates in error norms for the number of meshes in the directions of (a) horizontal and (b) vertical axes.

Full size image

For further validation, we consider the case where \({\text{a}} \to \infty\). This yields that the sketch of the plate looks like the one studied by Daşdemir [37] when the length \(a_{1}\) is a constant. In this situation, the numerical findings and results obtained for \(x_{3} /h = a_{3} /h\) under the same conditions must approach to the corresponding ones in [37] as \({\text{a}} \to \infty\). As seen, in figure 3(a), the distributions of the shear stress \(\sigma_{12} h/p_{0}\) versus the line \(x_{1} /h\) are displayed under \({\text{h}} = 0.1\) and \(x_{3} /h = a_{3} /h\). Further, in figure 3(b), the ones of the normal stress \(\sigma_{22} h/p_{0}\) versus the line \(x_{1} /h\) are located under \({\text{h}} = 0.2\) and \(x_{3} /h = a_{3} /h\). Here, the starred graphs imply the corresponding ones of Daşdemir [37]. The foresight above-stated is validated by the graphs of figures 3a and 3b. Further, the graphs of figure 3 are symmetric about line \(x_{1} /h\) since the dynamic force is perpendicular to the free surface of the plate. In addition, the normal stress \(\sigma_{22} h/p_{0}\) almost vanishes near the point where the shear stress \(\sigma_{12} h/p_{0}\) attains the extreme value. In [38], the authors also stated that this should be the case. This confirms the trustiness and accuracy of the PC algorithms and programs once again.

Figure 3
figure 3

Cross-compare of our results under \(x_{3} /h = a_{3} /h\) and the ones of Daşdemir [37]: (a) \({\text{h}} = 2\) and (b) \(\text{h} = 1\).

Full size image

Figure 4 shows the three-dimensional distributions of \(\sigma_{22} h/p_{0}\) on the plane \(x_{2} /h = - 1\) for various values of \(\eta\). The negative values of the initial stress parameter \(\eta\) indicate initial compression and positive values to initial tension. According to the graphs, the absolute values of \(\sigma_{22} h/p_{0}\) increase as the initial compression parameter \(\eta\) decreases but the corresponding values increase with the initial tension parameter \(\eta\). In summary, the absolute values of \(\sigma_{22} h/p_{0}\) decrease cordially with the values of the initial stress parameter \(\eta\). This means that increasing values of the initial stress parameter \(\eta\) give rise to the stiffness of the plate to increase. In view of the structural investigation of distributions, we can say that there are three domains; i.e., blue-, green-, and orange-colored domains. The first is the domain where stress formation is most intense. The latter is a relatively more peaceful area. In the last zone, the stress almost vanishes. We can term those as major, minor and dead domains, respectively. The numerical results prove that the increasing values of \(\eta\) lead to a decrease in the magnitudes of the major area but to increase in the magnitudes of the minor area. We, therefore, can say that the stress on the body is distributed more homogeneously as the values of \(\eta\) increase. In addition, according to the Robin boundary conditions in Eq. (7), the stress must vanish at the edge sides of the plate as \(\eta \to 0\). This is seen from the graphs in figures 3 and 4, confirming our algorithms.

Figure 4
figure 4

Three-dimensional distributions of \(\sigma_{22} h/p_{0}\) on the plane \(x_{2} /h = - 1\): (a) \(\eta = - 0.06\), (b) \(\eta = - 0.04\), (c) \(\eta = - 0.02\), (d) \(\eta = 0.02\), (e) \(\eta = 0.04\), (f) \(\eta = 0.06\), (g) color scale.

Full size image

Figure 5 displays three-dimensional graphs of \(\sigma_{22} h/p_{0}\) on the plane \(x_{2} /h = - 1\) for various values of the dimensionless frequency parameter \(\Omega\). An increase in the value of \(\Omega\) causes higher values of stress. This result is consistent with the present literature, i.e., see Daşdemir [39] and, Kuzeci and Akbarov [40]. It follows from the graphs that the greatest influence of the dimensionless parameter \(\Omega\) is seen near the point \(\left( {2.5,2.5} \right)\). Further, the magnitudes of both the major and minor domains expand with \(\Omega\). Note that the boundary of each domain can be seen from the graphs. Further, there are certain distortions in the dead domain for higher values of \(\Omega\), e.g., see figure 5(f). This is caused by the reflection of the stress waves striking the side edges of the plate. Figures 4 and 5 demonstrate that the 3D appearance of the stress caused by the dynamic loading in the plate is a right circular cone with the center at the point \(\left( {2.5,2.5} \right)\) of the plane \(x_{2} /h = - 1\). Alongside, in the case where \({\text{a}} \to 0\) and \(\Omega \to 0\) for fixed values of other problem parameters, the shape of our problem gradually begins to resemble the well-known Boussinesq problem considered by Timoshenko and Godier [38]. In this instance, the distributions of the graphs in figures 4 and 5 must qualitatively be similar to those of the mentioned paper. Both figures confirm this foresight. The excellent agreement of the numerical results provided confidence in the correctness of the present analysis once again.

Figure 5
figure 5

Three-dimensional distributions of \(\sigma_{22} h/p_{0}\) on the plane \(x_{2} /h = - 1\): (a) \(\Omega = 0.0\), (b) \(\Omega = 0.2\), (c) \(\Omega = 0.4\), (d) \(\Omega = 0.6\), (e) \(\Omega = 0.8\), (f) \(\Omega = 1.0\), (g) color scale.

Full size image

Figures 6 provides an opportunity to explain the relationships between \(\sigma_{22} h/p_{0}\) and \(\Omega\) for various values of \(\eta\). The values of \(\sigma_{22} h/p_{0}\) increase gradually with \(\Omega\) and after a certain value of \(\Omega\), the stress \(\sigma_{22} h/p_{0}\) suddenly reaches an extreme value that is called resonance value. Denote it by \(\Omega *\). After this point, the graphs have unstable distributions. It is clear that the influence of the parameter \(\eta\) on the dynamic response of the plate becomes more meaningful as \(\Omega \to \Omega *\). According to the distributions of the graphs, the resonance of the system under consideration appears near the point where \(\Omega \approx 1.3\). Furthermore, for certain values of \(\Omega\), the stress \(\sigma_{22} h/p_{0}\) also has local resonance values, which change with the ratio \(\eta\). Denote it by \(\Omega **\). Note that the values of \(\Omega *\) and \(\Omega **\) can be detected from the graphs. The location where these local resonances occur is indicated by an ellipse in the graph. The graphs show that increasing values of the initial tension shift the resonance values forward but increasing values of the initial compression becalm the corresponding resonance mode down. This establishes that when the plate was exposed to the higher initial stress, the stress \(\sigma_{22} h/p_{0}\) has more regular distributions and the system becomes more stable. According to the numerical results, initial compression increases the amount of particles falling on per unit volume of the body, accelerating the stress flow caused by the external force and increases the amount of vibration occurring in the environment. On the contrary, the initial tension causes the particles of the object to move away from each other, dampening the vibration of the environment. These expressions explain the physical effects of the initial stress parameter on the resonance mode of the system. As a result, the initial stress parameter \(\eta\) plays an important role in the frequency response of the plate.

Figure 6
figure 6

Dependency between \(\sigma_{22} h/p_{0}\) and \(\Omega\) for certain values of \(\eta\).

Full size image

Figures 7 shows the dependency between \(\sigma_{22} h/p_{0}\) and \(\Omega\) for various values of the aspect ratio \(\text{a}\). Note that while drawing the graphs, the length \(a_{3}\) is variable, but the length \(a_{1}\) is constant. It is deduced from the graphs that the absolute values of the stress \(\sigma_{22} h/p_{0}\) increase as the ratio \(\text{a}\) increases. But, the relationships between \(\sigma_{22} h/p_{0}\) and \(\Omega\) are non-monotonous, which is consistent with the current mechanical considerations, i.e., see the papers by Daşdemir [24], Eröz [41], and Akbarov [42]. This proves the validity of our algorithm and programs again. Further, an increase in the value of the ratio \(\text{a}\) prevents the resonance mode of \(\sigma_{22} h/p_{0}\), i.e., the values of \(\Omega *\) decrease as the ratio \(\text{a}\) increases. Since one of the horizontal lengths of the plate is chosen to be relatively small, it means that the stresses stored in the medium will affect each particle more. This causes the formation of a higher resonance mode in the medium. It is seen from the graphs that the influence of the aspect ratio \(\text{a}\) on the values of \(\Omega *\) have notable in both quantitative and qualitative.

Figure 7
figure 7

Dependency between \(\sigma_{22} h/p_{0}\) and \(\Omega\) for certain values of a.

Full size image

We can observe the influence of the thickness ratio \(\text{h}\) on the dependency between \(\sigma_{22} h/p_{0}\) and \(\Omega\) from figure 8. The absolute values of the stress \(\sigma_{22} h/p_{0}\) decrease as the ratio \(\text{h}\) increases. Further, the difference between the values of the stress \(\sigma_{22} h/p_{0}\) versus \(\Omega\) for two consecutive values of \(\text{h}\) decreases. This means that the influence of the ratio \(\text{h}\) on the stress \(\sigma_{22} h/p_{0}\) damps down. The graphs of figure 8 prove that the resonance mode of the external dynamic force exceeds as the ratio \(\text{h}\) increase. This is because the stress waves by the dynamic force hit more particles of the plate for a higher ratio \(\text{h}\) and increase the vibrations of the medium. To be clear, the values of \(\Omega *\) decrease for the increasing values of \(\text{h}\). We can say that the number of extremal values of the graphs of the stress \(\sigma_{22} h/p_{0}\) increases as \(\text{h}\) decreases. Hence, the stability of the system under consideration increases with decreasing values of the ratio \(\text{h}\). In addition, it can be said from figures 7 and 8 that both the aspect ratio \(\text{a}\) and the thickness ratio \(\text{h}\) have a significant influence on the frequency response of the piezoelectric plate, both quantitatively and qualitatively. The comparison of figures 7 and 8 shows that the thickness ratio \(\text{h}\) possesses a greater influence on the stress \(\sigma_{22} h/p_{0}\) than the aspect ratio \(\text{a}\). This can be explained by the fact that the total static force applied to the lateral sides of the plate is growing when the thickness ratio \(\text{h}\) increases.

Figure 8
figure 8

Dependency between \(\sigma_{22} h/p_{0}\) and \(\Omega\) for certain values of \(\text{h}\).

Full size image

In figure 9, the relationships between \(\sigma_{22} h/p_{0}\) and \(\eta\) for various values of the aspect ratio \(\text{a}\) are shown. Further, in figure 10, the influence of the thickness ratio \(\text{h}\) on the mentioned relationships is given. It is a common result from both figures that the graphs of \(\sigma_{22} h/p_{0}\) with respect to \(\eta\) are of linear distribution. The graphs in figures 4, 6, 9, and 10 prove that the initial tension displays an opposite effect on the oscillating character of the stress \(\sigma_{22} h/p_{0}\) according to that of the initial compression. As the ratio \(\text{a}\) increases, the slope of the graphs plotted for the stress \(\sigma_{22} h/p_{0}\) increases. Increasing values of the ratio \(\text{a}\) yield the influence of the initial stress parameter \(\eta\) on the stress \(\sigma_{22} h/p_{0}\) to increase. On the contrary, increasing values of the ratio \(\text{h}\) decrease the slope of the mentioned graphs. This means that the increase of the ratio \(\text{h}\) causes the influence of the initial stress parameter \(\eta\) on the stress \(\sigma_{22} h/p_{0}\) to reduce. These results show that the increase in the dimensions of the plate causes the influence of the initial stress parameter \(\eta\) on the stress \(\sigma_{22} h/p_{0}\) to damp. Apparently, the effect of the ratio \(\text{a}\) on the dynamic response of the plate is greater than that of \(\text{h}\). We can explain this situation as follows. When the ratio \(\text{a}\) is changed, the positions of the particles are more affected due to the static force applied to the lateral surfaces of the plate. This situation significantly affects the stress flow. Although changing the ratio \(\text{h}\) affects the amount of stress in the medium, its effect on the amount of stress emission of each particle is quite limited. Further, we can say that both ratios have a great role in the influence of \(\eta\) on stress distributions.

Figure 9
figure 9

Dependency between \(\sigma_{22} h/p_{0}\) and \(\eta\) for certain values of \(\text{a}\).

Full size image
Figure 10
figure 10

Dependency between \(\sigma_{22} h/p_{0}\) and \(\eta\) for certain values of \(\text{h}\).

Full size image

5 Conclusions

The work described the numerical characterization of forced vibration reasoned by a time-harmonic force of a pre-stressed piezoelectric plate in contact with a rigid foundation according to the piece-wise homogeneous body model. Our dynamic model was conducted according to the three-dimensional linearized theory of electro-elastic waves in initially stressed bodies (TLTEEWISB). The weak statement of the problem for arbitrary testing functions satisfying the corresponding boundary-contact conditions was derived. Based on weak expression, the variational statement of the pre-stressed piezoelectric plate was formulated, and the analytical solution to the forced vibration problem was obtained. We checked the validity and trustiness of the presented model and provided some numerical results related to the dynamical behavior of the piezoelectric plate.

We can summarize some outlines of the results achieved according to our numerical discussions as follows.

  • The distributions of the stress on the plate become more homogeneous as the values of \(\eta\) increase.

  • The aspect ratio \(\text{a}\) prevents the resonance of \(\sigma_{22} h/p_{0}\), but the thickness ratio \(\text{h}\) exceed this resonance mode.

  • The influence the parameter \(\eta\) has on the dynamical behavior of the plate is damped as the values of the thickness ratio \(\text{h}\) increases; but this influence increases with the aspect ratio \(\text{a}\).

  • For fixed values of the aspect ratio \(\text{a}\), the numbers of the extremal values of the stress versus the dimensionless frequency decrease with increasing the ratio \(\text{h}\).

  • The initial tension prevents resonance in the stress \(\sigma_{22} h/p_{0}\), but initial compression damps this resonance mode.

Although the results given throughout the paper were presented for a specific material, they also have general validity in a qualitative sense and are helpful for the designation and application of a pre-stressed piezoelectric plate resting on a rigid foundation in practice. Our model serves as a basis for mechanical investigations of different configurations, e.g., composite materials with imperfect interfaces, including various polarization directions.