Effect of Boundary Form Disturbances on the Frequency Response of Planar Vibrations of Piezoceramic Plates. Analytical Solution

The general solution of the boundary problem of planar vibrations of parallelogram-shaped piezoceramic plates is constructed. The solution is presented as infinite series, with each term satisfying the motion equations of a piezoceramic plate element. The series coefficients are determined with functional equations, generated by the boundary conditions of the problem. These equations can be solved using the two approaches, based on minimization of the standard deviation and the collocation method. In the case of practical application of finite sums, both approaches lead to the search of solving the systems of linear algebraic equations. Quantitative estimates of the dynamic characteristics of piezoceramic plates are obtained, their analysis permits of evaluating the plate geometry effect. This method provides high accuracy of calculation results.

Introduction. Piezoelectric effect-incorporated materials provide a means for easy excitation of vibrations in elastic solid bodies. Studies on such vibrations are of interest both for understanding the general behavior of elastic waves in bounded regions and for elaboration of recommendations on solving the design problems in the development of electromechanical transducers [1, 2]. At present particular emphasis is placed upon the development of microtransducers of various types termed as MEMS (Micro Electro Mechanical Systems) [3].

One way of controlling the dynamic characteristics of active MEMS elements is the piezoelectric element shape change, which makes the studies on elaboration of solution methods for the dynamic problems of electroelasticity currently central for the elements of different geometry. The analytical method of solving the boundary electroelasticity problems for parallelogram-shaped piezoelectric plates is presented below. The change in their shape may be considered as the excitation of the shape of rectangular plates.

Special attention is drawn to elaboration of the analytical solution method for boundary problems. The analytical solution provides the basis for an in-depth analysis of vibratory system properties. Such potentials may be illustrated by investigation results for the edge resonance phenomenon in elastic plates, including piezoceramic ones. The fact that all amplitudes of inhomogeneous waves reach their maximum at the edge resonance frequency is important for proper understanding of this phenomenon.

The construction of the analytical problem solution for a parallelogram-shaped plate makes use of the method based on the superposition of motion equation solutions represented as infinite series and set so to satisfy arbitrary conditions at the parallelogram boundary. The validity and efficiency of such an approach are outlined in [4,5,6,7].

Determining the coefficients of series, entering into the representation of general solutions of boundary problems, results in the infinite systems of algebraic equations. In addition to the direct accuracy evaluation of fulfilling the boundary conditions, the possibility of getting the numerical solution is realized and the results of two calculations are compared. Such a comparison is helpful both for additional verification of analytical estimates and elaboration of recommendations on the choice of necessary discretization steps in numerical calculations.

Basic Relations of the Theory of Planar Vibrations for Thin Electrodeposited Piezoelectric Plates with Thickness Polarization on the Electric Field Excitation. Planar vibrations of thin piezoceramic plates with thickness polarization are described with the vector equation of motion in displacements (Lame equation), which for the case of solid electrodes, coating face flat plate surfaces takes on the following form [2]:

$$ \frac{2}{1-v}\operatorname{grad} \operatorname {div}\;\mathbf{u}-\mathrm{rot}\;\mathrm{rot}\;\mathbf{u}=2\uprho {s}_{11}^E\left(1+v\right)\frac{\partial^2\mathbf{u}}{\partial {t}^2}, $$

(1)

where u is the two-dimensional displacement vector with the u_x and u_y components in the system of Cartesian

coordinates, u = u (x, y, t), the O_x and O_y axes lie in the plate plane, the Oz axis is normal to it, ρ is the density,

${s}_{11}^E$ and ${s}_{12}^E$ are the elastic compliances of the piezoelectric material, measured in the zero electric field, v is

Poisson’s ratio in the plane normal to the direction of material polarization (in the isotropy plane), $v=-{s}_{12}^E/{s}_{11}^E$:

$$ \operatorname{div}\;\mathbf{u}=\frac{\partial {u}_x}{\partial x}+\frac{\partial {u}_y}{\partial y},\kern0.5em {\left(\mathrm{rot}\;\mathbf{u}\right)}_z=\frac{\partial {u}_x}{\partial x}-\frac{\partial {u}_y}{\partial y},\kern0.5em {\left(\mathrm{rot}\;\mathbf{u}\right)}_x={\left(\mathrm{rot}\;\mathbf{u}\right)}_y\equiv 0. $$

(2)

The two-dimensional stress tensor components for thin piezoceramic plates are expressed as [2]

$$ \Big\{{\displaystyle \begin{array}{l}{\sigma}_x=\frac{1}{s_{11}^E\left(1-{v}^2\right)}\left[\left({\upvarepsilon}_x+{\upvarepsilon}_y\right)-\left(1-v\right){\upvarepsilon}_y-{d}_{31}\left(1+v\right){E}_z\right],\\ {}{\sigma}_y=\frac{1}{s_{11}^E\left(1-{v}^2\right)}\left[\left({\upvarepsilon}_x+{\upvarepsilon}_y\right)-\left(1-v\right){\upvarepsilon}_x-{d}_{31}\left(1+v\right){E}_z\right],\\ {}{\tau}_{xy}=\frac{1}{2{s}_{11}^E\left(1+{v}^2\right)}{\upvarepsilon}_{xy},\end{array}} $$

(3)

$$ {\displaystyle \begin{array}{ccc}{\upvarepsilon}_x=\frac{\partial {u}_x}{\partial x},& {\upvarepsilon}_y=\frac{\partial {u}_y}{\partial y},& {\upvarepsilon}_{xy}=\frac{\partial {u}_y}{\partial x}+\frac{\partial {u}_x}{\partial y}\end{array}}, $$

(4)

where ε_x , ε_y , and ε_xy are the strains [8], d₃₁ is the piezoelectric constant, E_z = E_z (t) is the component of the electric intensity vector E, which has only one nonzero component in the Oz axis direction normal to the electrode plate coatings.

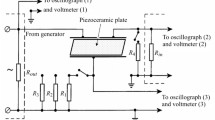
For excitation of plate vibrations 2h thick from the voltage generator with the output potential difference 2V₀ (t), applied to the electrode coatings on its face, we have

$$ {E}_z=-\frac{V_0(t)}{h}. $$

(5)

Correspondingly the stress vector components F_n on the elementary area with the unit normal n are expressed as [2]

$$ {\displaystyle \begin{array}{l}{F}_{nx}={\sigma}_x{n}_x+{\tau}_{xy}{n}_y,\\ {}{F}_{ny}={\tau}_{yx}{n}_x+{\tau}_y{n}_y.\end{array}} $$

(6)

When setting the stress conditions at the boundary, the normal and tangential stress vector components are usually considered

$$ {\displaystyle \begin{array}{l}{F}_{nx}={F}_{nx}{n}_x+{F}_{ny}{n}_y,\\ {}{F}_{\tau }=-{F}_{nx}{n}_y+{F}_{ny}{n}_x.\end{array}} $$

(7)

General Solutions in Potentials. Motion equation in displacements (1) is rather complicated, thus, in some cases, also in analytical studies, the elastic displacement field u = u(x, y, t) is convenient to calculate passing on to the Helmholtz representation via the scalar φ(x, y, t ) and vector ψ(x, y, t ) potentials [1]

$$ {\displaystyle \begin{array}{cc}\mathbf{u}=\mathrm{glad}\;\upvarphi +\mathrm{rot}\;\uppsi, & \operatorname{div}\;\uppsi =0\end{array}}. $$

(8)

In this two-dimensional case, the vector potential ψ possesses the only nonzero component ψ_z = ψ in the Oz axis direction. In terms of this, substituting (8) into (1) and considering that div grad φ = ∇²φ and rot rot ψ = grad div ψ − ∇²ψ as well as the identities rot grad φ ≡ 0 and div rot φ≡ 0 , we get the following wave equations relative to the scalar potential φ and nonzero component of the vector potential ψ

$$ {\displaystyle \begin{array}{cc}{\nabla}^2\upvarphi -\uprho {s}_{11}^E\left(1-{v}^2\right)\frac{\partial^2\upvarphi}{\partial {t}^2}=0,& {\nabla}^2\uppsi -2\uprho {s}_{11}^E\left(1-v\right)\frac{\partial^2\upvarphi \uppsi}{\partial {t}^2}=0,\end{array}} $$

(9)

where the first and second ones describe the propagation of longitudinal and transverse waves in the plate plane, respectively, with the velocities

$$ {\displaystyle \begin{array}{cc}{c}_1=\frac{1}{\sqrt{\uprho {s}_{11}^E\left(1-{v}^2\right)}},& {c}_2=\frac{1}{\sqrt{2\uprho {s}_{11}^E\left(1+v\right)}}.\end{array}} $$

(10)

In view of (10), Eqs. (9) take on the form

$$ {\displaystyle \begin{array}{cc}{\nabla}^2\upvarphi -\frac{1}{c_1^2}\frac{\partial^2\upvarphi}{\partial {t}^2}=0,& {\nabla}^2\uppsi -\frac{1}{c_2^2}\frac{\partial^2\uppsi}{\partial {t}^2}=0.\end{array}} $$

(11)

With the computation rules of vector operations grad(·) and rot(·) as well as with ψ = k (x, y) in the plane problem, where ψ (x, y)= ψ_z is the scalar function, ψ_x = 0, ψ_y = 0, and for the components of initial vector field of displacements u = i u_x + j u_x, we get expressions for the displacement components by Eq. (8)

$$ {\displaystyle \begin{array}{cc}{u}_x=\frac{\mathrm{\partial \upvarphi }}{\partial x}+\frac{\mathrm{\partial \uppsi }}{\partial y},& {u}_y=\frac{\mathrm{\partial \upvarphi }}{\partial y}+\frac{\mathrm{\partial \uppsi }}{\partial x}\end{array}}. $$

(12)

On the excitation of harmonic plate vibrations with the ac field from the voltage generator, assume the harmonic time dependence of the examined values

$$ {\displaystyle \begin{array}{ccc}\mathbf{u}=\mathbf{u}\left(x,y\right)\exp \left(i\upomega t\right),& \upvarphi =\upvarphi \left(x,y\right)\exp \left(i\upomega t\right)& \uppsi =\uppsi \left(x,y\right)\exp \end{array}}\left(i\upomega t\right), $$

(13)

where $i=\sqrt{-1}$ is the imaginary unit, ω = 2πf is the circular frequency (rad/s), and f is the natural (Hertzian) frequency, Hz.

Then the harmonic multiplier exp(i𝜔t) is omitted, and by the u, φ, ψ, etc. values are meant their amplitudes. Thus, substituting (13) into (11), we obtain the Helmholtz scalar equations

$$ {\displaystyle \begin{array}{cc}{\nabla}^2\upvarphi +{k}_1^2\upvarphi =0,& {\nabla}^2\uppsi +{k}_2^2\uppsi =0,\end{array}} $$

(14)

where k₁ and k₂ are the wave numbers of the longitudinal and transverse waves in the plate

$$ {\displaystyle \begin{array}{cc}{k}_1=\frac{\upomega}{c_1}=\sqrt{\upomega^2\rho {s}_{11}^E\left(1-{v}^2\right)},& {k}_2=\frac{\upomega}{c_2}=\sqrt{\upomega^2\rho {s}_{11}^E\left(1-v\right)}.\end{array}} $$

(15)

The transformation of stress tensor components for plane problem (3) in accordance with the representation of displacement vector components via Helmholtz potentials (12) in view of Cauchy formula for strains (4) and expression for the loading electric field (5) results in the equalities

$$ \Big\{{\displaystyle \begin{array}{l}{\sigma}_x=\frac{1}{s_{11}^E\left(1-{v}^2\right)}\left[\frac{\partial^2\upvarphi}{\partial {x}^2}+v\frac{\partial^2\upvarphi}{\partial {y}^2}+\left(1-v\right)\frac{\partial^2\uppsi}{\partial x\partial y}\right]+\frac{1}{s_{11}^E\left(1-v\right)}\left({d}_{31}\frac{V_0}{h}\right),\\ {}{\sigma}_y=\frac{1}{s_{11}^E\left(1-{v}^2\right)}\left[v\frac{\partial^2\upvarphi}{\partial {x}^2}+\frac{\partial^2\upvarphi}{\partial {y}^2}+\left(1-v\right)\frac{\partial^2\uppsi}{\partial x\partial y}\right]+\frac{1}{s_{11}^E\left(1-v\right)}\left({d}_{31}\frac{V_0}{h}\right),\\ {}{\tau}_{xy}=\frac{1}{2{s}_{11}^E\left(1-v\right)}\left[2\frac{\partial^2\upvarphi}{\partial x\partial y}-\frac{\partial^2\uppsi}{\partial {x}^2}+\frac{\partial^2\uppsi}{\partial y}\right].\end{array}} $$

(16)

On setting the normal ${\overline{F}}_n$ and tangential F_τ stresses at the plate contour, the boundary conditions take on the following form:

$$ {\displaystyle \begin{array}{c}2G\left[\left(\frac{1}{1-v}-{n}_y^2\right)\frac{\partial^2\upvarphi}{\partial {x}^2}+\left(\frac{1}{1-v}-{n}_x^2\right)\frac{\partial^2\upvarphi}{\partial {y}^2}+\frac{\partial^2\uppsi}{\partial x\partial y}\left({n}_x^2-{n}_y^2\right)+\left(2\frac{\partial^2\upvarphi}{\partial x\partial y}-\frac{\partial^2\uppsi}{\partial {x}^2}\right){n}_x{n}_y\right]\\ {}=-2G\frac{\left(1+v\right)}{\left(1-v\right)}{d}_{31}\frac{V_0}{h}+{\overline{F}}_n,\end{array}} $$

(17a)

$$ 2G\left[\left(\frac{\partial^2\upvarphi}{\partial x\partial y}-\frac{\partial^2\uppsi}{\partial {x}^2}+\frac{\partial^2\partial }{\partial {y}^2}\right)\left({n}_x^2-{n}_y^2\right)-\left(\frac{\partial^2\upvarphi}{\partial {x}^2}-\frac{\partial^2\upvarphi}{\partial {y}^2}+\frac{\partial^2\uppsi}{\partial x\partial y}\right){n}_x{n}_y\right]={\overline{F}}_{\tau }, $$

(17b)

where G is the shear modulus, ${\displaystyle \begin{array}{cc}G=\frac{1}{2{s}_{11}^E\left(1+v\right)},& -\end{array}}2G\frac{\left(1+v\right)}{\left(1-v\right)}{d}_{31}\frac{V_0}{h}$ in the right side of equality (17a) appears as a result of the relation between electric and mechanical fields, it is also proportional to the piezoelectric constant d₃₁ and amplitude of the external electric field intensity. Then denote it as ${\overline{F}}_n^{Veq}$. Notice that the terms in the left side of (17) correspond to the normal and tangential stress vector components related to elastic strain, which may be designated ${\sigma}_n^{def}$ and ${\sigma}_{\uptau}^{def}$.

Equation (17) may be rewritten in the reduced form as

$$ {\displaystyle \begin{array}{l}{\sigma}_n^{def}={\overline{F}}_n^{Veq}+{\overline{F}}_n,\\ {}{\sigma}_{\tau}^{def}={\overline{F}}_{\tau }.\end{array}} $$

(18)

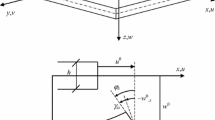
Statement of the Problem. Within the above model, examine the problem of harmonic vibrations of a thin piezoceramic plate with mechanical stress-free edges, OBCD parallelogram-shaped with the angles α in the O and C apexes and side sizes OD = BC = a, OB = CD = b (Fig. 1). The conditions for the stresses at the parallelogram boundary take the form (17) at

$$ {\displaystyle \begin{array}{cc}{\overline{F}}_n=0,& {\overline{F}}_{\tau }=0.\end{array}} $$

(19)

Fig. 1.

Parallelogram-shaped piezoceramic plate.

Enter the two systems of Cartesian coordinates Ox₁y₁ and Ox₂y₂ with their origin in the point O (Fig. 1). The relation between the coordinates in those systems has the form

$$ \Big\{{\displaystyle \begin{array}{l}{x}_1={x}_2\sin\;\upalpha +{y}_2\;\cos \upalpha, \\ {}{y}_1=-{x}_2\cos\;\upalpha +{y}_2\sin\;\upalpha, \\ {}{x}_2={x}_1\sin\;\upalpha -{y}_1\;\cos \upalpha, \\ {}{y}_2={x}_2\cos\;\upalpha +{y}_1\sin\;\upalpha .\end{array}} $$

(20)

The solution for φ and ψ may be presented as the sum (superpositions) of potentials that are the solutions of Helmholtz equations (14)

$$ {\displaystyle \begin{array}{l}\upvarphi ={\upvarphi}_1\left({x}_1,{y}_1\right)+{\upvarphi}_2\left({x}_1,{y}_1\right)+{\upvarphi}_3\left({x}_2,{y}_2\right)+{\upvarphi}_4\left({x}_2,{y}_2\right),\\ {}\uppsi ={\uppsi}_1\left({x}_1,{y}_1\right)+{\uppsi}_2\left({x}_1,{y}_1\right)+{\uppsi}_3\left({x}_2,{y}_2\right)+{\uppsi}_4\left({x}_2,{y}_2\right).\end{array}} $$

(21)

Each of the potentials φ_i and ψ_i is represented by the series as

$$ \Big\{{\displaystyle \begin{array}{l}{\upvarphi}_1\left({x}_1,{y}_1\right)=\sum \limits_{n=0}^{\infty }{A}_n^{(1)}\left({y}_1\right)\cos \frac{n\uppi}{a}{x}_1,\\ {}{\upvarphi}_2\left({x}_1,{y}_1\right)=\sum \limits_{n=0}^{\infty }{A}_n^{(2)}\left({y}_1\right)\cos \frac{n\uppi}{a}\left({x}_1-{\updelta}_1\right),\\ {}{\upvarphi}_3\left({x}_2,{y}_2\right)=\sum \limits_{m=0}^{\infty }{A}_m^{(3)}\left({x}_2\right)\cos \frac{m\uppi}{b}\left({y}_2-{\updelta}_2\right),\\ {}{\upvarphi}_4\left({x}_2,{y}_2\right)=\sum \limits_{m=0}^{\infty }{A}_m^{(3)}\left({x}_2\right)\cos \frac{m\uppi}{b}{y}_2,\\ {}{\uppsi}_1\left({x}_1,{y}_1\right)=\sum \limits_{m=0}^{\infty }{B}_n^{(1)}\left({y}_1\right)\cos \frac{n\uppi}{a}{x}_1,\\ {}{\uppsi}_2\left({x}_1,{y}_1\right)=\sum \limits_{n=0}^{\infty }{B}_n^{(1)}\left({y}_1\right)\cos \frac{n\uppi}{a}\left({x}_1-{\updelta}_1\right),\\ {}{\uppsi}_3\left({x}_2,{y}_2\right)=\sum \limits_{m=0}^{\infty }{B}_m^{(3)}\left({x}_2\right)\cos \frac{m\uppi}{b}\left({y}_2-{\updelta}_2\right),\\ {}{\uppsi}_4\left({x}_2,{y}_2\right)=\sum \limits_{m=0}^{\infty }{B}_m^{(4)}\left({x}_2\right)\cos \frac{m\uppi}{b}{y}_2,\end{array}} $$

(22)

where δ₁ = GB and δ₂ = FD (Fig. 1).

The form of series (22) was chosen so that at ith sides of the parallelogram, φ_i and ψ_i represented the series expanded by the complete trigonometric bases.

Substituting φ_j and ${\psi}_j\left(j=\overline{1,4}\right)$ into Helmholtz equations (14), we come to the system of independent homogeneous differential equations of second order with the constant coefficients relative to the functions ${A}_i^{(j)}$ and ${B}_i^{(j)}$ entering into representations (22). Solving these equations and choosing the solutions of the differential ones, from the considerations of independence of basis functions and exponent damping inwards from the parallelogram sides, we get the explicit expressions for ${A}_i^{(j)}$ and ${B}_i^{(j)}$ against the relations λ_n = n𝜋/a and μm=n𝜋/a and wave numbers k₁ and k₂ (15) for each n and m:

$$ \Big\{{\displaystyle \begin{array}{l}{A}_n^{(1)}\left({y}_1\right)={A}_{1n}\Big\{\begin{array}{l}\begin{array}{cc}\cos \sqrt{k_1^2-{\uplambda}_n^2}{y}_1,& {\uplambda}_n<{k}_1,\end{array}\\ {}\begin{array}{cc}\exp \left(-\sqrt{k_n^2-{k}_1^2}{y}_1\right),& {\uplambda}_n\ge {k}_1,\end{array}\end{array}\\ {}{A}_n^{(2)}\left({y}_1\right)={A}_{2n}\Big\{\begin{array}{l}\begin{array}{cc}\sin \sqrt{k_1^2-{\uplambda}_n^2}{y}_1,& \kern3em {\uplambda}_n<{k}_1,\end{array}\\ {}\begin{array}{cc}\exp \left(\sqrt{\lambda_n^2-{k}_1^2}\left({y}_1-h\right)\right),& {\uplambda}_n\ge {k}_1,\end{array}\end{array}\\ {}{A}_m^{(3)}\left({x}_2\right)={A}_{3m}\Big\{\begin{array}{l}\begin{array}{cc}\sin \sqrt{k_1^2-{\upmu}_m^2}{x}_2,& \kern3em {\upmu}_m<{k}_1,\end{array}\\ {}\begin{array}{cc}\exp \left(\sqrt{\upmu_m^2-{k}_1^2}\left({x}_2-a\right)\right),& {\upmu}_m\ge {k}_1,\end{array}\end{array}\\ {}{A}_m^{(4)}\left({x}_2\right)={A}_{4m}\Big\{\begin{array}{l}\begin{array}{cc}\cos \sqrt{k_1^2-{\upmu}_m^2}{x}_2,& \kern3em {\upmu}_m<{k}_1,\end{array}\\ {}\begin{array}{cc}\exp \left(-\sqrt{\upmu_m^2-{k}_1^2}{x}_2\right),& {\upmu}_m\ge {k}_1,\end{array}\end{array}\\ {}{B}_n^{(1)}\left({y}_1\right)={B}_{1n}\Big\{\begin{array}{l}\begin{array}{cc}\cos \sqrt{k_2^2-{\uplambda}_n^2}{y}_1,& \kern3em {\uplambda}_n<{k}_2,\end{array}\\ {}\begin{array}{cc}\exp \left(-\sqrt{\uplambda_n^2-{k}_2^2}{y}_1\right),& {\uplambda}_n\ge {k}_2,\end{array}\end{array}\\ {}{B}_n^{(2)}\left({y}_1\right)={B}_{2n}\Big\{\begin{array}{l}\begin{array}{cc}\sin \sqrt{k_2^2-{\uplambda}_n^2}{y}_1,& \kern3em {\uplambda}_n<{k}_2,\end{array}\\ {}\begin{array}{cc}\exp \left(-\sqrt{\uplambda_n^2-{k}_2^2}\left({y}_1-h\right)\right),& {\uplambda}_n\ge {k}_2,\end{array}\end{array}\\ {}{B}_m^{(3)}\left({x}_2\right)={B}_{3m}\Big\{\begin{array}{l}\begin{array}{cc}\sin \sqrt{k_2^2-\upmu m}{x}_2,& \kern3em {\upmu}_m<{k}_2,\end{array}\\ {}\begin{array}{cc}\exp \left(-\sqrt{\uplambda_n^2-{k}_2^2}\left({x}_2-a\right)\right),& {\upmu}_m\ge {k}_2,\end{array}\end{array}\\ {}{B}_m^{(4)}\left({x}_2\right)={B}_{4m}\Big\{\begin{array}{l}\begin{array}{cc}\cos \sqrt{k_2^2-{\upmu}_m^2}{x}_2,& \kern3em {\upmu}_m<{k}_2,\end{array}\\ {}\begin{array}{cc}\exp \left(-\sqrt{\upmu_m^2-{k}_2^2}{x}_2\right),& {\upmu}_m\ge {k}_2,\end{array}\end{array}\end{array}} $$

(23)

Thus, series (22) for φ_i and ψ_i in view of (23) are the series in terms of the two-dimensional basis functions, which would be denoted ,Φ_ij (x_k , y_k) and Ψ_ij (x_k , y_k) for short with the coefficients A_ij and ${B}_{ij}\left(i=\overline{1,4},k=1,2\right)$, respectively.

Computer Simulation of Plate Vibrations. The prime object of mathematical simulation of physical vibrations is evaluating their quantitative characteristics against the geometric parameters of the domain of their existence and boundary conditions. As a rule, it may be reached with several iterative processes, e.g., with an increase in the number of Fourier series terms used for the representation of a desired function. Effective realization of the iterative processes would require such characteristics that provide the process stability and getting reliable quantitative estimates. Note that the superposition method, allowing for the construction of general solutions of boundary problems, just exhibits such properties. The stability and convergence of computational procedures on its realization are effected by the completeness of fundamental properties used for representing the function values.

For obtaining the quantitative stress and displacement estimates for the plates, we go in representations (22) from the infinite series to the finite sums in terms of n and m to N − 1 and M − 1, respectively (reduction method) [9,10,11,12]. Further the problem solution is reduced to evaluating 4(N + M) unknown coefficients in reduced functional representations (22) based on approximate satisfying single collocation points or on the standard deviation minimization method (projection method) for the boundary conditions at the parallelogram sides OD (I), BC (II), CD (III), and OB (IV) (Fig. 1).

Collocation Method. The solution of the problem of planar vibrations for a parallelogram-shaped piezoceramic plate with the free edge with the collocation method would require to fulfill preset conditions for normal and tangential stresses (17), (19) in some boundary points (collocation points), they [8] may be chosen as mid-sections of uniform division into N parts of boundaries I and II and M parts of boundaries III and IV (Fig, 1). Thus, we have 2(N + M) collocation points with the coordinates $\left({x}_i^c,{y}_i^c\right)$ , in each of them the outward normal vector with the components n_x , n_y is preset. As a result, for each collocation point, the two linear algebraic equations are formed against the coefficients A_ij, B_ij of truncated series. Solving this system and substituting the computed values of the coefficients into corresponding representations for φ_i , ψ_i (22) as well as calculating their superposition by formulas (21), we get a required approximate solution of an examined boundary problem in potentials. After that, the necessary components of displacements and stresses are computed with (12) and (16). Similar transformations were performed earlier [13, 14].

Standard Deviation Minimization Method. Another method of approximate satisfying the boundary conditions for solving the boundary problem consists in successive multiplication of residuals of the conditions at boundaries I , II and III , IV (Fig. 1) by independent functions from the functional bases, used for the solution representation, and integration of the products over corresponding boundaries I–IV, i.e., computation of scalar products (projection) of residuals by the basis functions, equalled zero [12]. As a result, the system of linear algebraic equations is obtained against the coefficients of series expansions A_ij , B_ij . In this case, the trigonometric functions are chosen as the projected ones that enter as cofactors into the two-dimensional basis functions ${\varPhi}_{ij}\left({x}_y,{y}_y\right),{\varPsi}_{ij}\left({x}_y,{y}_y\right),\cos \frac{\tilde{n}\uppi}{a}{x}_1$ at boundary I, $\cos \frac{\tilde{n}\uppi}{a}\left({x}_1-{\updelta}_1\right)$ at boundary II ,$\tilde{n}=\overline{0,N-1},\cos \frac{\tilde{m}\uppi}{b}\left({y}_2-{\updelta}_2\right)$ at boundary III , and $\cos \frac{\tilde{m}\pi }{b}{y}_2$ at boundary $\tilde{m}=\overline{0,M-1}$ (Fig. 1). In the majority of cases, the accuracy of approximate solutions, obtained by this method, is somewhat higher than with the collocation method.

Theoretical models became the basis for software elaboration to numerically simulate the planar plate vibrations, realizing both the collocation and standard deviation minimization methods in approximate satisfying the boundary conditions. In many cases, it is convenient to pass on to dimensionless boundary conditions for stresses, normalizing them in (17) by the shear modulus G.

Numerical simulation was carried out for piezoceramic plates from a PZT-4 material, its characteristics are cited in [2, 15]: ${s}_{11}^E=12.3\cdot {10}^{-2}{\mathrm{m}}^2/\mathrm{N},{s}_{12}^E=4.05\cdot {10}^{-2}{\mathrm{m}}^2/\mathrm{N},v=-{s}_{12}^E/{s}_{11}^E=0.329268\dots \approx 0.33,\uprho =7500\mathrm{kg}/{\mathrm{m}}^3$.

For getting the amplitude-frequency characteristics of examined piezoceramic plates with solid two-sided electrodepositing, the dimensionless equivalent exciting load ${F}_n^{Veq}$ was assumed to be equal to -1.

Calculation results for the above characteristics of a parallelogram-shaped plate of the dimensions a = 34.54 mm, b = 45.69 mm and the angle α = / 80 by the collocation method for N = M = 60 are presented in Fig. 2.

Fig. 2.

Amplitude-frequency characteristics of a parallelogram-shaped piezoceramic plate (σ_Σ =  ∣ σ_x + σ_y∣ is the modulus of the sum of dimensionless principal stresses in the plate center).

The amplitude-frequency characteristics obtained by numerical simulation with the collocation method at N = M = 90 and the standard deviation minimization method at N = M = 60 and 90 as well as resonant frequencies do not practically differ from the data cited in Fig. 2.

The closeness of those values corroborates high accuracy of the analytical method and its efficiency in solving practical problems of dynamics research for piezoceramic plates of non-canonical shape.

Computation (f_comp) and experimental (f_exp) studies on the vibrations of a piezoelectric plate resulted in the following resonant frequency values (kHz): f_comp = 31.69, 34.93, 41.52, 51.54, 56.77, 66.69, 78.82, f_exp = 31.05, 34.35, 40.40, 49.55, 55.72, 65.14, 77.33.

When comparing calculation and experimental data on natural frequency spectra, the following should be considered. The computations were performed for the model of an ideally elastic material. In the experiment, the material exhibits its true properties, in particular internal damping. As regards the natural frequencies, the damping results in resonant frequency drift. Moreover, for such a case, the difference in natural frequencies by angular velocities and drifts should be considered since those are resonances of different types.

It is complicated by the fact that the damping is greatly dependent on the frequency. This should be taken into account in the comparison of results. It is also important that it is impossible to experimentally realize the boundary conditions preset exactly in the computation scheme.

For evaluating the accuracy of solution results, the errors of satisfying the boundary conditions are depicted in Figs. 3 and 4:

$$ {\displaystyle \begin{array}{l}{\sigma}_n^{err}={\sigma}_n^{def(comp)}-{\overline{F}}_n^{Veq},\\ {}{\sigma}_{\tau}^{err}={\sigma}_n^{def(comp)},\end{array}} $$

(24)

Fig. 3.

Comparison of errors of satisfying the boundary conditions for the normal ${\sigma}_n^{err}$ (a, b) and tangential ${\sigma}_{\tau}^{err}$ (c, d) stresses at boundary I of a parallelogram-shaped piezoceramic plate by the collocation method: (a, c)N = M = 60; (b, d)N = M = 90.

Fig. 4.

Comparison of errors of satisfying the boundary conditions for the normal ${\sigma}_n^{err}$ (a, b) and tangential ${\sigma}_{\tau}^{err}$ (c, d) stresses at boundary I of a parallelogram-shaped piezoceramic plate by the standard deviation minimization method: (a, c)N = M = 60; (b, d)N = M = 90.

where comp denotes computed values and err means error values.

In the construction of error spectra by the collocation method, the data in the vicinity of angular points in Fig. 3 are presented incompletely since here the error is somewhat growing, but does not surpass 10⁻³ loads preset at the boundary. Analysis of results demonstrates their good agreement since both methods neglect the contribution from higher harmonics in satisfying the boundary conditions, such residual behavior, viz high variability along the coordinate, is quite natural.

Comparison of results for the two systems of collocation points (60 and 90) shows that an increase in their number results in higher accuracy of satisfying the boundary conditions. The same is valid for an increase in the number of projection functions in the case of the standard deviation minimization method. However, with a similar number of terms, the accuracy of results is somewhat higher.

Of interest is a relatively high error within very narrow regions near the ends of boundary segments. This is apparently the specific feature of the collocation method (Fig. 3). However, the application, e.g., of the projection method eliminates this shortcoming (Fig. 4). In evaluating such integral characteristics of the vibratory system, as natural frequencies, both methods provide practically the same accuracy at a similar number of hold terms in infinite series.

Conclusions. Calculation results for the dynamic characteristics of parallelogram-shaped piezoelectric plates demonstrate that the method of analytical electroelasticity problem solution for the non-canonical domain provides their reliable quantitative estimates. The quantitative estimates of vibrating plate characteristics by both proposed algorithms are shown to be practically similar. At the same time, the collocation method would require a smaller body of analytical transformations.

Thus, expressions (22) offer an exact general solution of the boundary problem of planar vibrations of a piezoceramic plate in the form of infinite series. The number of hold terms is essential for a required accuracy level to get the quantitative estimates of physical values. For evaluating the necessary coefficients, the boundary problem conditions were used. The corresponding functional equations for the finite number (N and M) of hold terms may be transformed into algebraic relations by the two different methods. The two approaches to the solution of functional equations, expressing the boundary problem conditions, are proposed. One of them is known in applied mechanics as the collocation method [12] when the functional equation is transformed into the algebraic equalities for a certain system of points at the boundary. In terms of computability, it is a rather simple method of deriving the algebraic relations. From our viewpoint, another method of deducing the algebraic relations, more adequate for the traditional statement of boundary problems in mechanics, is based on the principle of standard deviation minimization in the fulfillment of boundary conditions. Quantitative estimates were obtained using both methods, with the comparison of the results.

Comparison of the results with experimental frequency characteristics of vibrations of parallelogram-shaped piezoceramic plates, which would be presented in the next study, corroborated a high accuracy of the proposed analytical approach to the investigation of planar vibrations of plates of non-canonical shape.