Directional characteristics of cylindrical radiators with an arc-shaped acoustic screen

Abstract

Directional sound radiation by a cylinder surrounded with an arc-shaped (open circular) acoustic screen is examined. The corresponding boundary problem is solved with the partial domain technique. The method of asymptotic solutions was used to verify the conditions of solving this problem using the method of simple reduction. As a result of the analysis, the quantitative characteristics of the acoustic field of the cylindrical radiator inside the arc-shaped screen were evaluated.

1 Introduction

Directional radiators of sound waves are widely used in various fields, for example, acoustic imaging, biomedical acoustics, and musical acoustics. The directivity of sound radiation is accomplished in two ways: either by phase matching of radiators in multicomponent systems (phased arrays) or by using different screens to obtain the desired directivity characteristics of the individual radiator.

The multifunctionality of modern radiators implies a precise control of parameters, in particular, the directional properties of their components. The effective method of controlling the directional parameters is radiator shielding. In this paper the problem of directional sound radiation by a cylinder surrounded by an arc-shaped (open circular) acoustic screen made of a sound-opaque material is considered. Cylindrical radiators, primarily owing to their processability and good strength properties, are widely employed in hydroacoustics in the design of high-power electroacoustic transducers and antennas, which are used in many applications [1–7].

The solution for the sound field generated by a shielded cylinder is constructed based on particular solutions of the Helmholtz equation for the velocity potential ${\varvec{\varPhi }}$.

The number of analytical solutions to similar applied problems is quite limited. For this reason, the approaches that extend the scope of subdomains, for which effective and instrumental solutions can be constructed for the quantitative assessment of physical field characteristics, have been devised in the last few decades. Such approaches include the so-called Schwarz algorithm [8–10], the T-matrix method [11], and the Shestopal method of solving the Riemann–Hilbert problem [12]. They are based on the decomposition of complex domains into relatively simple subdomains, for which the derived functions can be analytically represented as algebraic equations whose properties allow the method of simple reduction to be applied. In some cases, for example, the application of the T-matrix method, the derived solutions are valid only within a limited range of the domain geometry variation. This study presents a problem solution that illustrates the potentials of the new method of partial domains [13] for constructing analytical solutions for complex domains. Application of the alternative concept of the general solution opens new horizons for using the proposed approach to a wide range of problems of mathematical physics.

2 Problem statement

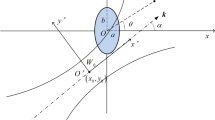
We examine the characteristics of sound radiation with a cylinder surrounded by an arc-shaped circular opaque layer with an acoustically soft surface (Fig. 1).

Fig. 1

Cylinder surrounded by an arc-shaped circular layer

The harmonic wave field is described by the Helmholtz equation for the velocity potential [3, 14]:

$$\begin{aligned} \varDelta {\varvec{\varPhi }} + k^2 {\varvec{\varPhi }} = 0, \end{aligned}$$

(1)

where $k=\omega /c$, $\omega$ is the angular frequency of harmonic waves, and c is the sound velocity. The following boundary conditions are evident from the assumption of physical layer properties:

$$\begin{aligned} \begin{array}{lll} {\varvec{\varPhi }} =0;&{}\quad r_0 \le r\le r_1,&{}\quad |\varphi |=\varphi _0 ; \\ {\varvec{\varPhi }} =0;&{}\quad r=r_1 ,&{}\quad \varphi _0 \le |\varphi |\le \pi . \end{array} \end{aligned}$$

(2)

Let a certain vibration velocity distribution $\upsilon _0 f(\varphi )$ be set on the open portion of the radiator surface. This distribution is assumed to be symmetric about the Oy axis to keep the problem from becoming too involved. Then the condition on the radiant surface takes on the following form:

$$\begin{aligned} -\frac{\partial {\varvec{\varPhi }} }{\partial (kr)}=\upsilon _0 f(\varphi );\quad r=r_0 ,\quad 0\le \left| \varphi \right| \le \varphi _0 . \end{aligned}$$

(3)

For the conceptual construction of the velocity potential over the domain of field existence, take the two partial domains (subdomains): $r_0 \le r\le r_1$, $\left| \varphi \right| \le \varphi _0$ (subdomain I) and $r\ge r_1$, $0\le \left| \varphi \right| \le \pi$ (subdomain II).

3 Problem solution

With the preceding boundary conditions, represent the field over each of the subdomains as

$$\begin{aligned} {\varvec{\varPhi }} _1= & {} \sum \limits _{q=0}^\infty {\left[ {A_q J_{\nu _q } (kr)+B_q N_{\nu _q } (kr)} \right] } \cos \nu _q \varphi ;\nonumber \\ {\varvec{\varPhi }} _2= & {} \sum \limits _{n=0}^\infty {S_n H_n^{(1)} (kr)\cos n\varphi .}\nonumber \end{aligned}$$

(4)

The expression for ${\varvec{\varPhi }} _1$ obeys the Helmholtz equation at an arbitrary $\nu _q$ value. The boundary conditions can be partially met over subdomain I by the proper choice of this value. Thus, assuming

$$\begin{aligned} \nu _q =\frac{(2q+1)\pi }{2\varphi _0 }, \end{aligned}$$

(5)

the first condition in (2) is satisfied at the layer edges $\varphi =\pm \varphi _0$. With such a $\nu _q$ choice, the solution for subdomain I involves two arbitrary functions on the surfaces $r=r_0$ and $r=r_1$, with $\left| \varphi \right| \le \varphi _0$ as the Fourier series with undetermined coefficients. The ${\varvec{\varPhi }} _2$ solution for exterior subdomain II, $r\ge r_1$, satisfies the Sommerfeld condition [15] and bears a sufficient degree of functional arbitrariness to satisfy the boundary conditions on the surface $r=r_1$, $0\le \varphi \le 2\pi$. These properties of the ${\varvec{\varPhi }} _1$ and ${\varvec{\varPhi }} _2$ expressions create the prerequisites for fulfilling boundary conditions (2) and (3) by the appropriate choice of their arbitrary constants.

Condition (3) allows the values of the $A_q$ and $B_q$ coefficients to be related. Substituting the expression for ${\varvec{\varPhi }} _1$ into (3), we can easily establish that

$$\begin{aligned} B_q =\frac{L_q -A_q {J}'_{\nu _q } (kr_0 )}{{N}'_{\nu _q } (kr_0 )}, \end{aligned}$$

(6)

where

$$\begin{aligned} L_q =-\frac{2\upsilon _0 }{k\varphi _0 }\int \limits _0^{\varphi _0 } f(\varphi )\cos \nu _q \varphi \,\mathrm {d}\varphi . \end{aligned}$$

With (6), the expression for ${\varvec{\varPhi }} _1$ is transformed into

$$\begin{aligned} {\varvec{\varPhi }} _1 =\sum \limits _{q=0}^\infty \left[ {A_q \varDelta _q (kr)+L_q \frac{N_{\nu _q } (kr)}{{N}'_{\nu _q } (kr_0 )}} \right] \cos \nu _q \varphi , \end{aligned}$$

(7)

where

$$\begin{aligned} \varDelta _q (kr)=J_{\nu _q } (kr)-{J}'_{\nu _q } (kr_0 )N_{\nu _q } (kr)/{N}'_{\nu _q } (kr_0 ) . \end{aligned}$$

To determine the remaining unknowns in (4), the functional equations that combine the sound field continuity condition at the subdomain boundary and the boundary condition on the surface $r=r_1$ should be applied:

$$\begin{aligned}&{\varvec{\varPhi }} _2 =\left\{ \begin{array}{ll} {\varvec{\varPhi }} _1 &{} \quad 0\le |\varphi | \le \varphi _0,\\ 0 &{} \quad \varphi _0 \le |\varphi | \le \pi , \end{array} \right. \nonumber \\&\frac{\partial {\varvec{\varPhi }} _2 }{\partial r}= \frac{\partial {\varvec{\varPhi }} _1 }{\partial r}\quad 0\le |\varphi |\le \varphi _0 .\nonumber \end{aligned}$$

(8)

Algebraization of functional equations (8) based on the properties of complete and orthogonal functions on the corresponding intervals leads to the following infinite system of linear algebraic equations of the second kind:

$$\begin{aligned} S_n H_n^{(1)} (kr_1 )-\frac{1}{\delta _n }\sum \limits _{q=0}^\infty A_q \varDelta _q (kr_1 )a_{nq}= & {} \frac{1}{\delta _n } \sum \limits _{q=0}^\infty a_{nq} L_q N_{\nu _q } (kr_1 )/{N}'_{\nu _q } (kr_0 ),\nonumber \\ A_q {\varDelta }'_q (kr_1 )-\frac{1}{\varphi _0 }\sum \limits _{n=0}^\infty S_n {H'}_n^{(1)} (kr_1 )a_{nq}= & {} -L_q {N}'_{\nu _q } (kr_1 )/{N}'_{\nu _q } (kr_0 ), \end{aligned}$$

(9)

where

$$\begin{aligned} \delta _n =\left\{ \begin{array}{ll} 2\pi &{}\quad n=0,\\ \pi &{}\quad n\ne 0, \end{array} \right. \qquad a_{nq} =\left\{ {{\begin{array}{ll} \displaystyle \frac{2\nu _q (-1)^{q+1}\cos n\varphi _0 }{n^2-\nu _q^2 }&{} n\ne \nu _q, \\ \varphi _0 &{} n=\nu _q, \end{array} }} \right. \end{aligned}$$

${\varDelta }'_q (kr_1 )$ is the derivative of $\varDelta _q (kr)$ with respect to kr at $r=r_1$.

Thus, we must seek the values of arbitrary constants from infinite system (9) entering into Eq. (4). In this connection, the existence of the boundary problem solution is reduced to the existence proof of such a solution for system (9), which provides the convergence of infinite series for the field components everywhere over an examined domain.

The commonly used approach to studying the solvability of such systems is to prove their regularity [16]. Embarking on a study of the regularity of system (9), enter the new unknowns:

$$\begin{aligned} \tilde{S}_n =S_n {H'}_n^{(1)} (kr_1 ), \quad \tilde{A}_q =A_q \varDelta _q (kr_1 ). \end{aligned}$$

(10)

With this, initial system (9) is transformed into

$$\begin{aligned}&\tilde{S}_n \frac{H_n^{(1)} (kr_1 )}{{H'}_n^{(1)} (kr_1 )}-\frac{1}{\delta _n }\sum \limits _{q=0}^\infty \tilde{A}_q a_{nq} =\frac{1}{\delta _n} \sum \limits _{q=0}^\infty L_q a_{nq} N_{\nu _q } (kr_1 )/{N}'_{\nu _q } (kr_0),\nonumber \\&\tilde{A}_q \frac{{\varDelta }'_q (kr_1 )}{\varDelta _q (kr_1 )}-\frac{1}{\varphi _0 }\sum \limits _{n=0}^\infty \tilde{S}_n a_{nq} =-L_q {N}'_{\nu _q } (kr_1 )/{N}'_{\nu _q } (kr_0). \end{aligned}$$

(11)

The complex functional dependence of the coefficients on their number in system (11) makes the analysis of its regularity more difficult. We now need to focus on the proof of the system’s quasi-regularity. In this case, it is permissible to simplify the matrix elements of the latter through the use of known asymptotic representations of the Bessel, Neumann, and Hankel functions taken as the functions of orders n and $\nu _q$. Based on those representations [17], we get

$$\begin{aligned} \frac{H_n^{(1)} (kr_1 )}{{H'}_{\!\!\!\! n}^{(1)} (kr_1 )}=\frac{kr_1 }{n}, \quad \frac{{\varDelta }'_q (kr_1 )}{\varDelta _q (kr_1 )}=\frac{\nu _q }{kr_1 }, \quad \frac{{N}'_{\nu _q } (kr_1 )}{{N}'_{\nu _q } (kr_0 )}=\left( {\frac{r_0 }{r_1 }} \right) ^{\nu _q +1}, \quad n,\nu _q \gg 1. \end{aligned}$$

(12)

With (12), the following infinite system is found, which is equivalent to initial system (11) in terms of its solvability:

$$\begin{aligned}&\tilde{S}_n^{(1)} -\frac{2n\cos ^2n\varphi _0}{\pi } \sum \limits _{q=0}^\infty A_q^{(1)} \frac{1}{n^2-\nu _q^2 }= \frac{2n\cos ^2n\varphi _0 }{\pi kr_1 } \sum \limits _{q=0}^\infty L_q a_{nq} N_{\nu _q } (kr_1 )/{N}'_{\nu _q } (kr_0 ),\nonumber \\&\tilde{A}_q^{(1)} -\frac{2\nu _q }{\varphi _0 } \sum \limits _{n=0}^\infty \tilde{S}_n^{(1)} \frac{1}{n^2-\nu _q^2 }= -L_q \left( {\frac{r_0 }{r_1 }} \right) ^{\nu _q +1}, \end{aligned}$$

(13)

where

$$\begin{aligned} \tilde{A}_q^{(1)} =\tilde{A}_q \frac{(-1)^{q+1}\nu _q }{kr_1 }, \quad \tilde{S}_n^{(1)} =\tilde{S}_n \cos n\varphi _0 . \end{aligned}$$

Since the coefficients $1/(n^2-\nu _q^2 )$ change their sign in each line of system (13), further analysis of the latter is quite difficult. Therefore, we proceed as follows: substitute the $\tilde{A}_q^{(1)}$ value obtained from the second equation of system (13) into the first one and determine $\tilde{S}_n^{(1)}$,

$$\begin{aligned} \tilde{S}_n^{(1)} =\frac{4n\cos ^2n\varphi _0 }{\pi }\sum \limits _{g=1}^\infty \tilde{S}_g^{(1)} a_{ng} +b_n \, , \end{aligned}$$

(14)

where

$$\begin{aligned} a_{ng} =\frac{1}{\varphi _0 }\sum \limits _{q=0}^\infty \frac{\nu _q }{\left( n^2-\nu _q^2 \right) \left( g^2-\nu _q^2 \right) } . \end{aligned}$$

The direct verification of fulfilling the quasi-regularity conditions of system (14) for arbitrary $\varphi _0$ values seems difficult. Therefore, we shall restrict our consideration to the specific, most unfavorable case, where $\varphi _0 =\pi$. Then the coefficients $a_{ng}$ take on the form

$$\begin{aligned} a_{ng} =\frac{1}{\pi }\sum \limits _{q=0}^\infty {\frac{q+1/2}{\left[ {(q+1/2)^2-n^2} \right] \left[ {(q+1/2)^2-g^2} \right] }} . \end{aligned}$$

(15)

The general term of infinite series (15) can be represented by the following integral:

$$\begin{aligned} \frac{q+1/2}{\left[ {(q+1/2)^2-n^2} \right] \left[ {(q+1/2)^2-g^2} \right] }=\frac{1}{n^2-g^2}\int \limits _0^\infty {\left[ \cosh (nt)-\cosh (gt) \right] \mathrm {e}^{-(q+1/2)t} \mathrm {d}t} . \end{aligned}$$

(16)

Thus, we succeed in convolving the infinite series in the expression for $a_{ng}$ and represent the coefficients of infinite system (14) as

$$\begin{aligned} a_{ng} =\frac{1}{\pi (n^2-g^2)} \int \limits _0^\infty \left[ \cosh (nt)-\cosh (gt) \right] \sum \limits _{q=0}^\infty \mathrm {e}^{-(q+1/2)t} \mathrm {d}t \nonumber \\ =\frac{1}{2\pi (n^2-g^2)} \int \limits _0^\infty \sinh ^{-1}(t/2) \left[ \cosh (nt)-\cosh (gt) \right] \mathrm {d}t . \end{aligned}$$

(17)

In accordance with known relations [18], the improper integrals in this expression may be represented via the special functions. Then we get

$$\begin{aligned} a_{ng} =\frac{1}{\pi (n^2-g^2)}\left[ {\psi (n+1/2)-\psi (g+1/2)} \right] , \end{aligned}$$

(18)

where $\psi (n+1/2)$ and $\psi (g+1/2)$ are the psi functions.

The psi functions [18, 19] were established to bear a constant sign. This significantly simplifies the computation of the sum of coefficient modules in system (14). With studies on quasi-regularity, for $a_{ng}$ the following asymptotic equation may be applied:

$$\begin{aligned} a_{ng} =\frac{1}{\pi }\left[ {\frac{\ln (n/g)}{n^2-g^2}-\frac{B_2}{4n^2g^2}} \right] , \quad g\ge G, \end{aligned}$$

(19)

which renders their value negligible as $1/n^4$ approaches unity. Here, $B_2$ is the Bernoulli number. G is a value of g beginning from which the asymptotic expressions may be already used for the system coefficients. To derive (19), the duplication formula and the asymptotic expansion for the psi function [19] were used.

With regard to (19), to study the quasi-regularity of (14) we have the following estimate:

$$\begin{aligned} F_n =\frac{4n}{\pi ^2}\sum \limits _{g=G}^\infty {a_{ng} \le } \frac{4n}{\pi ^2}\sum \limits _{g=G}^\infty {\left[ {\frac{\ln (n/g)}{n^2-g^2}-\frac{B_2 }{4n^2g^2}} \right] +O\left( {\frac{1}{n^4}} \right) } . \end{aligned}$$

(20)

For large n values, the sum of series (20) can be calculated using the methods of summability [20]. With this

$$\begin{aligned} \sum \limits _{g=G}^\infty {\frac{\ln (n/g)}{n^2-g^2}<-\frac{1}{n}\int \limits _0^\infty {\frac{\ln (n/g)}{1-(n/g)^2} \mathrm {d}(n/g)} } \end{aligned}$$

for large g values, the following estimate is assumed:

$$\begin{aligned} F_n \le 1-\frac{1}{36n}=1-Q(n). \end{aligned}$$

(21)

Thus, system (14) is quasi-regular. The existence of the bounded solution is now reduced to a comparison of descending orders of the function Q(n) and free terms in (14). Behavioral analysis of the free terms in (14) shows that they decrease as $1/n^2$, i.e., more rapidly than the function Q(n) in (21). It is indicative of the possibility of applying the method of simple reduction for finding the approximate solution of (14) and, thus, system (11).

Based on the existence of the bounded solution for system (11), it can be demonstrated that the infinite series in (4) and corresponding series for the vibration velocity converge in all the points of partial domains. This suggests the existence of the boundary problem solution in the adopted form. Nevertheless, in terms of actually finding the solution and further interpreting quantitatively the general formulas for the physical values that characterize the field, the regularity of the infinite system practically has little to offer. More comprehensive information on the potentials of the approach to the solution of boundary problems in complex domains can be gained from an analysis of the examined physical fields. In this connection, we analyze briefly the stages of solving the problem of cylinder sound radiation through an arc-shaped layer that preceded the derivation of infinite system (11).

To arrive at an unambiguous solution of the examined problem, the following conditions should be fulfilled: (1) boundary conditions on the cylinder and layer surfaces, (2) continuity conditions for the field components at the interface of partial domains, (3) radiation conditions at infinity, and (4) quite specific type of the vibration velocity in approaching the angular points (edges).

With respect to meeting the boundary conditions, $\nu _q$ can be uniquely determined and $A_q$ and $B_q$ values be related. The requirement of satisfying the radiation condition at infinity specified the form of radial functions in the expression for ${\varvec{\varPhi }} _2$. The satisfaction of mean-square continuity conditions resulted in an infinite system of algebraic equations for the coefficients of infinite series in ${\varvec{\varPhi }} _1$ and ${\varvec{\varPhi }} _2$.

This analysis makes it clear that the fourth condition has not been explicitly applied anywhere.

With the preceding method of representing the sound field, the existence of solutions with different vibration velocity singularities in the angular points may lead to the existence of several solutions for infinite system (11). In this case, the algorithm for reducing the infinite system to a finite one should offer the finding of a desired solution, i.e., one that is consistent with physically valid velocity field characteristics in the angular points.

A knowledge of the sound field characteristics near the angular points allows us to apply a theorem known in Fourier series theory [21]: if $f(x)=\sum \nolimits _{n=0}^\infty a_n \cos nx$ and $f(x) \sim 1/x^\alpha (x \rightarrow 0)$, then $a_n \sim 1/n^{1-\alpha } (n \rightarrow \infty )$. Just this allows for significant improvement in the procedure for solving infinite systems.

In the vicinity of the right angle formed by the surface $r=r_1$ and plane $\varphi =\varphi _0$, the vibration velocity exhibits a singularity of the $1/\tilde{r}^{1/3}$ type, where $\tilde{r}$ is the distance from the angle vertex. In this connection, the distribution of the radial vibration velocity component over the surface $r=r_1$ can be given as

$$\begin{aligned} \upsilon _r (\varphi )=\left\{ \begin{array}{ll} \displaystyle \frac{-ks}{(\cos \varphi -\cos \varphi _0 )^{1/3}} +\upsilon _1 (\varphi )&{} \quad 0\le \varphi \le \varphi _0, \\ \displaystyle -\frac{ks}{(\cos \varphi _0 -\cos \varphi )^{1/3} } +\upsilon _2 (\varphi )&{} \quad \varphi _0 \le \varphi \le \pi , \end{array} \right. \end{aligned}$$

(22)

where s is a certain constant, and $\upsilon _1 (\varphi )$ and $\upsilon _2 (\varphi )$ are regular functions. The principal terms in (22) examined on the complete interval $0\le \varphi \le \pi$ can be expressed as the Fourier series

$$\begin{aligned} \upsilon _r (\varphi )=\sum \limits _{n=0}^\infty a_n \cos n\varphi . \end{aligned}$$

(23)

Thus, the principal, slowest decreasing part of the coefficients $a_n$ is defined as

$$\begin{aligned} \tilde{a}_n =\frac{2}{\pi }\int \limits _0^{\varphi _0 } {\frac{ks\cos n\varphi }{\left( {\cos \varphi -\cos \varphi _0 } \right) ^{1/3}}} \mathrm {d}\varphi +\frac{2}{\pi }\int \limits _{\varphi _0 }^\pi {\frac{ks\cos n\varphi }{\left( {\cos \varphi _0 -\cos \varphi } \right) ^{1/3}}} \mathrm {d}\varphi . \end{aligned}$$

(24)

With the integral representations for the Legendre functions of the first and second kinds [22], it is easy to show that

$$\begin{aligned} \tilde{a}_n =ks\left[ {P_{n-1/2}^{-1/6} (\cos \varphi _0 )+\frac{2}{\pi }\frac{(n+1/3)}{(n+2/3)}Q_{n-1/2}^{1/6} (\cos \varphi _0 )} \right] . \end{aligned}$$

(25)

The asymptotic representations of the Legendre functions for large indices [17, 22] allow us to obtain the following asymptotic estimates for the coefficients of series (23):

$$\begin{aligned} \tilde{a}_n =A\frac{\cos n\varphi _0 }{n^{2/3}}, \quad n\gg 1. \end{aligned}$$

(26)

Based on the foregoing reasoning, one notices that relation (26) defines behavior with growth in a number of the unknowns $\tilde{S}_n$ in system (11). If one makes use of only the first part of the expression (which corresponds to $0\le \varphi \le \varphi _{0}$) for $\upsilon _r (\varphi )$ in (22) and develops it as series in the complete system of the functions $\cos \nu _q \varphi$ on the interval $0\le \varphi \le \varphi _0$, then the estimate of the asymptotic behavior of the unknowns $\tilde{A}_q$ in system (11) can be obtained:

$$\begin{aligned} \tilde{A}_q^{(0)} =B\frac{(-1)^{q+1}}{\nu _q^{5/3}},\quad q\gg 1 . \end{aligned}$$

(27)

Relations (26) and (27) define the assumed asymptotic properties of the unknowns in system (11), which were obtained from the analysis of the edge conditions necessary for the existence of the unique solution to the boundary problem. To support the existence of such a solution of infinite system (11), the consistency of asymptotic estimates (26) and (27) can be verified with the same relations of the infinite system.

From the properties of the unknowns $\tilde{A}_q$, determine the asymptotic properties $\tilde{S}_n$. At large n indices from the first equation of system (11), the following representation takes place:

$$\begin{aligned} \tilde{S}_n^{(0)} \frac{kr_1 }{n}=\frac{1}{\pi }\sum \limits _{q=0}^\infty \tilde{A}_q a_{nq} +O(n^{-2}),\quad n\gg 1 . \end{aligned}$$

(28)

Estimate the sum in the latter expression,

$$\begin{aligned} J=\frac{1}{\pi }\sum \limits _{q=0}^\infty \tilde{A}_q a_{nq}= & {} \frac{1}{\pi } \sum \limits _{q=0}^\infty \tilde{A}_q^{(0)} a_{nq} +\frac{1}{\pi } \left[ \sum \limits _{q=0}^{Q-1} \tilde{A}_q a_{nq} -\sum \limits _{q=0}^{Q-1} \tilde{A}_q^{(0)} a_{nq} \right] \nonumber \\= & {} \frac{1}{\pi }\sum \limits _{q=0}^\infty \tilde{A}_q^{(0)} a_{nq} + O(n^{-2}) , \end{aligned}$$

(29)

where Q is the minimum value of index q, for which the substitution of the Bessel and Neumann functions with their asymptotic representations is held valid, and $\tilde{A}_q^{(0)}$ is the asymptotic value of the coefficients $\tilde{A}_q$ at $q\gg 1$.

With (27), we get

$$\begin{aligned} J=B\cos n\varphi _0 \sum \limits _{q=0}^\infty \frac{1}{\nu _q^{2/3} \left( n^2-\nu _q^2 \right) } . \end{aligned}$$

(30)

The sum in this expression can easily be estimated with the method of summability of infinite series [20]:

$$\begin{aligned} \sum \limits _{q=0}^\infty \frac{1}{\nu _q^{2/3} (n^2-\nu _q^2 )}\le \frac{\varphi _0 }{\pi n^{5/3}} \int \limits _0^\infty \frac{\mathrm{d}x}{x^{2/3}(1-x^2)} =\frac{\varphi _0 }{\pi n^{5/3}} \cdot \frac{\pi }{2}\cot \frac{\pi }{6} =\frac{\varphi _0 \sqrt{3} }{2n^{5/3}} . \end{aligned}$$

(31)

Thus, with an accuracy to $O(n^{-5/3})$, we have

$$\begin{aligned} J=B\frac{\varphi _0 \sqrt{3} }{2}\frac{\cos n\varphi _0 }{n^{5/3}}. \end{aligned}$$

(32)

With estimates (32) from (28), we finally obtain

$$\begin{aligned} \tilde{S}_n^{(0)} =B\frac{\varphi _0 \sqrt{3} }{2kr_1 }\frac{\cos n\varphi _0 }{n^{2/3}}. \end{aligned}$$

(33)

The second relation in system (11) used for similar calculations permits of establishing the total consistency of estimates (26) and (27), derived from general considerations, with the properties of the coefficients in system (11).

The solution algorithm for system (11) should ensure such a solution whose asymptotic properties are determined by relations (26) and (27). In this connection, for the finite system with the N and Q unknowns, we assume

$$\begin{aligned}&\tilde{S}_n =\tilde{S}_N \frac{\cos n\varphi _0 }{\cos N\varphi _0}, \quad n\gg N,\nonumber \\&\tilde{A}_q =\tilde{A}_N \left( {\frac{\nu _Q }{\nu _q }} \right) ^{5/3}(-1)^{q-Q}, \quad q\gg Q . \end{aligned}$$

(34)

With relations (34), system (11) can be put in the form

$$\begin{aligned}&\tilde{S}_n \frac{H_n^{(1)} (kr_1 )}{{\tilde{H}'{}}_{\!\!\!\! n}^{(1)} (kr_1)} -\frac{1}{\delta _n } \sum \limits _{q=0}^{Q-1} {\tilde{A}_q a_{nq} -\frac{\tilde{A}_Q }{\delta _n }} \sum \limits _{q=Q}^\infty \left( \frac{\nu _Q }{\nu _q } \right) ^{5/3} a_{nq} = \frac{1}{\delta _n} \sum \limits _{q=0}^\infty L_q a_{nq} \frac{N_{\nu _q } (kr_1 )}{{N}'_{\nu _q } (kr_1)}, \nonumber \\&\tilde{A}_q \frac{{\varDelta }'_q (kr_1 )}{\varDelta _q (kr_1 )} -\frac{1}{\varphi _0 }\sum \limits _{n=0}^{N-1} {\tilde{S}_n a_{nq} -\frac{\tilde{S}_N }{\varphi _0 }\sum \limits _{n=N}^\infty {\left( {\frac{N}{n}} \right) } } ^{2/3}\frac{\cos n\varphi _0 }{\cos N\varphi _0} a_{nq} = L_q \frac{{N}'_{\nu _q } (kr_1 )}{{N}'_{\nu _q } (kr_0 )}. \end{aligned}$$

(35)

The foregoing data on a decrease in the coefficients of infinite series, which represent the sound fields in the partial domains, can be used to estimate the rates of their convergence. Thus, to study the characteristics of the far-zone field, one should apparently proceed from the following representation:

$$\begin{aligned} {\varvec{\varPhi }} _2 \approx {\varvec{\varPhi }} _0 \sum \limits _{n=0}^\infty {\bar{S}_n \cos n\varphi \quad {\varvec{\varPhi }} _0 =\left( {\frac{2}{\pi kr_1 }} \right) ^{1/2}} \mathrm {e}^{\mathrm{i}(kr-\pi /4)}. \end{aligned}$$

(36)

With (26), we find for $\bar{S}_n$

$$\begin{aligned} \bar{S}_n \approx \mathrm{const}\frac{(kr_1 )^n\cos n\varphi _0 \mathrm {e}^{\mathrm{i}n\pi /2}}{n^{2/3}(n-1)!},\quad n\gg 1. \end{aligned}$$

(37)

The Fourier series (36) with the coefficients $\bar{S}_n$ for the cylinder with a surrounding layer of not very large diameter-to-wavelength ratios converges very fast. This suggests that for a quantitative description of the far-zone field it would be sufficient to know the values of several first coefficients $\bar{S}_n$. A similar estimation can be performed for the near-zone field. With Eqs. (7) and (10), the velocity potential over domain I is given by the following series:

$$\begin{aligned} {\varvec{\varPhi }} _1 =\sum \limits _{q=0}^\infty \left[ A_q \frac{\varDelta _q (kr)}{\varDelta _q (kr_1 )}+ L_q \frac{N_{\nu _q } (kr)}{{N}'_{\nu _q } (kr_0 )} \right] \cos \nu _q \varphi . \end{aligned}$$

(38)

Based on the asymptotic properties of the coefficients $\tilde{A}_q$ (27), we notice that the convergence of series (38) at $r=r_0$ is the same as that of the Fourier series with the coefficients

$$\begin{aligned} \frac{2}{\pi }\frac{(-1)^{q+1}}{\nu _q^{5/3} }\left( {\frac{r_0 }{r_1 }} \right) ^{\nu _q }+\frac{(-1)^{q+1}kr_0 }{\nu _q^2 }. \end{aligned}$$

(39)

The analysis of convergence of infinite series shows that for quantitative estimation of engineering characteristics of a sound field, one need only have knowledge of several first coefficients in corresponding series. This is evidence that in a number of cases, system (11) can be solved with the method of simple reduction. The potentials of such an approach are corroborated by the additional quantitative data given in what follows. Noteworthy is that the application of the preceding method is acceptable if the following conditions are fulfilled: (1) with an increase in the number of unknowns in system (11), its solution would tend to that of a system with required asymptotic properties; (2) values of the unknowns with small numbers would be determined quite accurately with a comparatively small number of equations in a system obtained by the reduction of system (11). These conditions can be verified by comparing the solution results of system (11), gained by simple reduction, and of system (35), constructed with the asymptotic properties of unknowns (improved reduction method).

4 Results and discussion

4.1 Computational results

Table 1 lists several $\tilde{S}_n$ values computed at $N=6$ and $Q=6$ with the assumption of $kr_0 =1.6$, $kr_1 =2.89$, $\varphi _0 =\pi /2$, and $f(\varphi )=1$. The second column of Table 1 corresponds to the method of the simple reduction of system (11), and the third one contains the result for system (35), obtained using the improved reduction method.

Table 1 Computed $\tilde{S}_n$ values obtained using simple and improved reduction methods

The data in Table 1 are evidence in favor of the following assertions. First, the method of simple reduction used for finding the unknowns in system (11) actually gives the solution with their asymptotic properties corresponding to the essentials of the problem. Second, for deriving reliable values of several first unknowns, it suffices to consider a system holding about twice as many unknowns as those necessary for obtaining quantitative estimates of the field characteristics. The latter assertion is also corroborated by computational results for different geometric and wave parameters of a cylindrical radiator with an arc-shaped layer, as well as by data available in the literature [23, 24].

Thus, the analysis gives grounds for inferring that the far-zone field and radiation impedance can be evaluated to a good approximation from the solution results of infinite system (11) obtained by the method of simple reduction. However, to study the local field characteristics, especially on the surface $r=r_1$, where the series defining pressure and vibration velocity feature the slowest convergence, system (35) is used, employing known methods of improving the convergence of Fourier series [16].

4.2 Directional characteristics and radiation impedance of a cylinder surrounded by an arc-shaped circular layer

The computational results from the previous section allow us to proceed with a study of the quantitative characteristics of the sound field of a cylindrical radiator surrounded by an arc-shaped circular layer. Our prime interest is with the far-zone field of the radiator, which is conveniently characterized by the directional pattern and directivity [25]. The normalized directional pattern $R(\varphi )$ can easily be plotted on the basis of relation (4) defining the external field of the radiator, applying the asymptotic representation of the Hankel function for the large argument values:

$$\begin{aligned} R(\varphi )=\frac{\sum \nolimits _{n=0}^N {S_n \mathrm {e}^{\mathrm{i}n\pi /2}\cos n\varphi } }{\sum \nolimits _{n=0}^N {S_n \mathrm {e}^{\mathrm{i}n\pi /2}\cos n\varphi _1 } }, \end{aligned}$$

(40)

where N is dependent on the order of an actually solved finite system, and $\varphi _1$ is the direction relative to which normalization is done (hereinafter $\varphi _1 =0$).

In the strict sense, the directivity for the plane problem cannot be determined. Nevertheless, the value

$$\begin{aligned} K=\pi \left[ {\int \limits _0^\pi {R^2(\varphi ) \mathrm {d}\varphi } } \right] ^{-1} \end{aligned}$$

(41)

can be used; it is treated in [25] as the directivity per unit height of the cylindrical radiator and, in fact, characterizes the directional action only in the plane normal to its longitudinal axis.

Far- and near-zone field characteristics will be examined with the numerical solution of system (11). The order of truncation of this system was chosen on the basis of the foregoing analysis of series convergence.

For the data given in what follows, the number of unknowns $S_n$ was 12, and that of the unknowns $A_q$ was defined from the condition $\nu _q \approx 12$. In all the calculations, the vibration velocity was assumed to be uniformly distributed over the cylinder surface, i.e., $f(\varphi )=$ const.

Giving a general idea of the angular distribution of sound energy radiated by the cylinder in the far-zone field, one notices that it exhibits a clearly defined nonuniformity. The directional patterns for several angle $\varphi _0$ values are shown in Fig. 2. As is seen, most of the sound energy is radiated to the front half-space $|\varphi |\le \pi /2$, while only a small amount of energy falls on the rear one.

Fig. 2

Directional patterns for $kr_0 =4.52$ and $kr_1 =6.9$; curves 1, 2, 3, and 4 correspond to $\varphi _0 =\pi /6$, $\pi /4$, $\pi /3$, and $\pi /2$, respectively

The directional properties of an examined radiator will be further analyzed in more detail. The width of the main directional lobe $\varphi _{0,7}$, determined from a 0.7 level, versus the maximum value $R(\varphi )$ and the directivity K versus angle $2\varphi _0$ plots are given in Fig. 3. As follows from those data, at a relatively large thickness-to-wavelength ratio of the layer, there is a certain angle $\varphi _0$ such that the major lobe width is at a minimum, while the directivity is at its maximum. These patterns are attributable to the following reasons. At sufficiently minor $\varphi _0$, the aperture diameter-to-wavelength ratio (by aperture is meant the distance between the points $r=r_1$, $\varphi =\pm \varphi _0$) is small, which dictates a high $\varphi _{0.7}$ value and a low K value. With an increase in $\varphi _0$, the aperture/wavelength ratio and radiator directionality grow, which appears as a decrease in $\varphi _{0.7}$ and an increase in K. However, this process continues up to a certain limit where phase distortions caused by the cylindrical wave front in the aperture reach a significant value. This process alone retards a further narrowing of the major lobe, and at sufficiently large values even reverses, viz. the major lobe starts to widen again and, in some cases, bifurcate (e.g., curve 4 in Fig. 2). It may be expected that a decrease in the layer thickness-to-wavelength ratio (at a fixed $kr_0$ value) should give rise to a certain stabilization of the radiator directional properties. Actually, the calculations demonstrate that in the $(r_1 -r_0 )/\lambda \le 0.1$ range, either the directional pattern or the directivity does not practically change (curve 5 in Fig. 3b).

Fig. 3

Width of major a directional lobe and b directivity versus angle $2\varphi _0$ for $kr_0 =2.26$; curves 1, 2, 3, and 4 correspond to $kr_1 =2.89$, 4.14, 6.18, and 14.82, respectively; curve 5 corresponds to the case $(r_1 -r_0 )/\lambda \le 0.1$

Here, we dwell on the relations between the major characteristics of a cylindrical radiator with an arc-shaped circular layer and frequency response. A set of $\varphi _{0.7}$ and K versus frequency curves at different $\varphi _0$ values is presented in Fig. 4. These data reveal the existence of angles such that $\varphi _{0.7}$ and K values are practically frequency-independent. Thus, an examined radiator with certain geometrical parameters features the retention of the directional lobe position over a rather wide frequency band.

Fig. 4

Values a $\varphi _{0.7}$ and b K versus frequency response curves for $r_1 /r_0 =1.8$; curves 1, 2, and 3 correspond to angles $\varphi _0 =\pi /4$, $\pi /3$, and $\pi /2$

It is worth noting the limiting case where $\varphi _0 =\pi$ and the circular layer degenerates into a belt whose thickness tends to zero. In this case, the effective radiation of sound energy occurs over a wide range of angles (approximately from $0^\circ$ to $120^\circ$), and only in the range of larger angles does the field intensity start to decrease rapidly. Several typical directional patterns are shown in Fig. 5. These data clearly demonstrate the form of the directional pattern for the aforementioned specific case, as well as the efficiency of the belt shape in the suppression of the rear-side cylinder radiation (back lobe). In hydroacoustics, radiations with such directional properties are usually termed radiators with a sector-shaped pattern, which find extensive practical applications [25].

Fig. 5

Directional patterns for $\varphi _0 =\pi$ and $kr_1 =6.18$; curves 1, 2, and 3 correspond to $kr_0 =1.57$, 2.26, and 3.14

We now turn to the analysis of radiation impedance characteristics of a cylinder in the arc-shaped circular layer. With the general definition of radiation impedance and the expression for the sound field in subdomain I, the radiation impedance per unit height of the cylinder can be presented in the following form, conventionally used in acoustics:

$$\begin{aligned} Z=\rho c\bar{S}(R+\mathrm{i}X), \end{aligned}$$

(42)

where $\bar{S}=2r_0 \varphi _0$ is the radiant surface area of the radiator per unit height,

$$\begin{aligned} R= & {} \frac{1}{\pi r_0 }\sum \limits _{q=0}^\infty {\mathfrak {I}(A_q) \frac{L_q }{{N}'_{\nu _q } (kr_0 )}},\\ X= & {} -\frac{1}{2r_0 }\sum \limits _{q=0}^\infty {\left[ {\frac{2}{\pi } \mathfrak {R}(A_q) +r_0 L_q N_{\nu _q } (kr_0 )} \right] } \frac{L_q }{{N}'_{\nu _q } (kr_0 )}. \end{aligned}$$

The frequency dependence of radiation impedance components at different $\varphi _0$ angles is plotted in Fig. 6. Analyzing the frequency-dependent run of the curves, the following effects may be pointed out: with a decrease in the angle $\varphi _0$, the impedance components reach relatively large values at high $kr_0$ values, while R and X values within the extreme curve sections increase with a decrease in the $\varphi _0$ angle and growth of $r_1 /r_0$. The $r_1 /r_0$ effect was evaluated by comparing the data (Fig. 6) and calculation results for $r_1 /r_0 =1.1$. In this case, the slope of the curves characterising the R variation with $kr_0$ growth declines with a decrease in the general level of the radiant system reactivity.

Thus, the cylinder in an arc-shaped circular layer can effectively radiate sound energy only at certain frequencies depending on the $\varphi _0$ value. Below those frequencies, it quickly decreases in efficiency, with the rate of this decrease being determined by the $r_1 /r_0$ ratio.

Fig. 6

Radiation impedance of cylinder within arc-shaped layer for $r_1 /r_0 =2.5$; panels a and b show real and imaginary parts, respectively; curves 1, 2, 3, and 4 correspond to $\varphi _0 =\pi /2$, $\pi /4$, $\pi /6$, and $\pi /8$, respectively

Assuming $r_1 \rightarrow \infty$, we arrive at the case [26] of studying the radiation impedance of a cylinder mounted on an infinite fluid wedge with acoustically soft edges. This is equivalent to the case of the infinite thickness of an arc-shaped circular layer. Comparing the results [26] and the data (Fig. 6), it may be inferred that R and X values in both cases coincide within graphical accuracy.

5 Conclusions

Based on the foregoing analysis, the following conclusions can be drawn.

• 1. An acoustically soft arc-shaped layer makes it possible to effectively control the directional characteristics of a cylindrical radiator and its directivity. The proper choice of layer parameters can stabilize the directional pattern over a certain frequency range, i.e., provide a required frequency response of the radiator. At $r_1 /r_0 \ge 2.5$, the diffraction effects caused by the finite layer thickness do not significantly affect the impedance.

• 2. The results give insight into the major characteristics of cylindrical radiators with arc-shaped circular screens, which can be instrumental in the design of sonar antennas and other acoustic equipment.