A scheme for remote state preparation of a general pure qubit with optimized classical communication cost

Abstract

How to use shared entanglement and forward classical communication to remotely prepare an arbitrary (mixed or pure) state has been fascinating quantum information scientists. Berry has given a constructive scheme for remotely preparing a general pure state, using a pure entangled state and finite classical communication. To optimize the classical communication cost, Berry employed a coding of the high-dimensional target state. Though working in the high-dimensional cases, the coding method is inapplicable for low-dimensional systems, such as a pure qubit. Since qubit plays a central role in quantum information theory, here we propose an optimization procedure which can be used to minimize the classical communication cost in preparing a general pure qubit. Interestingly, our optimization procedure is linked to the uniform arrangement of $N$ points on the Bloch sphere, which provides a geometric description.

1 Introduction

In the field of quantum information processing, remote state preparation (RSP) is a kind of protocol that transmits a quantum state from a sender (“Alice”) to a receiver (“Bob”) using preshared entanglement and forward classical communication [1–6]. Unlike the teleportation protocols [7], in an RSP protocol the sender does not possess a copy of the target state, but has complete classical knowledge of the state, which she chooses from a given ensemble. RSP protocols can be divided into two categories: exactly (non-asymptotically) faithful and asymptotically faithful. The exactly faithful RSP produces the desired states one at a time, while the asymptotically faithful RSP only has an asymptotic efficiency. In the present paper, we are concerned with exactly faithful RSP.

The first RSP protocol is proposed for preparing a qubit chosen from a great circle on the Bloch sphere, using one maximally entangled state (ebit) and one classical bit (cbit) communication [2]. Later, Lo [1], Leung and Shor [8] showed that two cbits communication is necessary and sufficient for the RSP of an arbitrary pure qubit with one ebit preshared. Though the above investigations are based on presharing maximally entangled states, RSP can be performed with non-maximally entangled state. The imperfection of entanglement may occur when the quantum resource is delivered through a noisy channel or exposed to a noisy environment, which is common in the real world and leads the cbits cost to a higher level.

Ye et al. [9] proofed that it is possible to remotely prepare a general pure state using finite classical communication and one non-maximally entangled pure state. Soon after, Berry proposed a step-by-step scheme for performing this RSP [10]. Because the scheme is not optimized for classical communication cost, to minimize the cbits cost an extra optimization method needs to be included. When the system dimension $N$ is large, Berry employed a coding method for the scheme to minimize cbits cost. But when the system dimension $N$ is small, such as the qubit case ($N=2$), no optimization method is given, and thus, the cbits cost is still far from minimized.

To solve this optimization problem, we propose a novel optimization procedure for the remote preparation of a general pure qubit. Starting with giving a geometric description of the scheme, we link the optimization procedure to the construction of uniformly distributed points on the Bloch sphere. We introduce an algorithm called spiral points [11], which can be used for easy construction of considerably uniformly distributed points on a sphere. We use the spiral points to demonstrate the optimization procedure. In order to show that the cbits cost after the optimization has been certainly minimized, we calculate that the cbits versus ebits trade-off is between an upper bound and a lower bound of theoretical limit.

2 Remote preparation of a general pure qubit

Here, we describe Berry’s scheme for preparing a general pure qubit. Assume Alice and Bob share an entangled state of the form

$$\begin{aligned} \vert A\rangle =\sum _{k=0}^1 \alpha _k\vert k\rangle \vert k\rangle , \end{aligned}$$

(1)

$\alpha _k>0$, $\sum _{k=0}^1 \alpha _k^2=1$. Any two-qubit pure entangled state can be brought to this form via local unitary operations at Alice’s location. We also denote the target state Alice wants to prepare at Bob’s side by $\vert \beta \rangle$, which is known to her but unknown to Bob.

In Ref. [10], Berry summarizes this scheme as a three-step process. But we will prepend a Step 0 to these three steps and thus make the scheme to be a four-step process. The Step 0 is generalized from the state approximating scheme in Berry’s work [10]. Later, we will see that the Step 0 is the key step leading to the optimization procedure.

To avoid unnecessary elaboration, we will treat Step 1 and Step 2 briefly based on the following proposition. For more details, we refer to Ref. [10].

Proposition

By allowing Alice and Bob to perform local operations and communicate 2 bits of classical information, the possession of an entangled state in Eq. (1) guarantees Alice the ability to remotely prepare an arbitrary qubit of the form

$$\begin{aligned} \vert \psi \rangle =\sum _{k=0}^1 \psi _ke^{i \varphi _k}\vert k\rangle , \end{aligned}$$

(2)

where $\psi _0\ge \sqrt{1-r^2}$, $r=\min \{\alpha _i\}$.

We find that from the perspective of Bloch sphere, the ensemble of states satisfying Eq. (2) can be represented by a $\vert 0\rangle$-centered spherical cap, denoted by $c_0$. And the less entanglement [12] $\vert A\rangle$ has, the smaller spherical cap $c_0$ Alice can prepare. With this knowledge, we can restate the scheme for preparing a general pure qubit in a geometric way, instead of Berry’s formularized description.

Here is the four-step process:

Step 0. Construct a distribution of $N$ points (or states) $\vert \beta _i'\rangle$, $i=1, 2, \ldots , N$, on the Bloch sphere. $N$ should be large enough to make the set of spherical caps $C=\left\{ c_1, c_2, \ldots , c_N\right\}$, where $c_i=\{\vert e\rangle \ \vert \ |\langle \beta _i'\vert e\rangle |^2\ge 1-r^2\}$, a cover of the Bloch sphere. Further, define $N$ unitary transformations $U_i$, each transforms $c_0$ into $c_i$, respectively.

Step 1–2. Alice prepares at Bob’s location a state $\vert \psi \rangle$ in $c_0$ such that Bob can bring $\vert \psi \rangle$ to the desired state $\vert \beta \rangle$ in $c_i$ by some unitary transformation $U_i$. This can be done by an entanglement transformation followed by a disentangling measurement, and costs 2 bits of classical information [10, 13, 14].

Step 3. Alice send Bob $\log N$ bits classical information to indicate him which $U_i$ should be used to bring $\vert \psi \rangle$ to $\vert \beta \rangle$.

Step 0 has been generalized from Berry’s approximate scheme, and one can see clearly that the $\log N$ cbits cost in Step 3 depends on the point distribution given in Step 0. To optimize the scheme, one needs an algorithm for constructing suitable points’ distributions on the Bloch sphere. If we have an algorithm that can distribute the centers of the spherical caps more uniformly in Step 0, less number of spherical caps will be needed to cover the Bloch sphere on base of the same entanglement of $\vert A\rangle$, so more classical communication will be saved in Step 3. To minimize the cbits cost, what exactly one needs is an algorithm that constructs uniformly distributed points on the Bloch sphere.

Before we come to the algorithm which is suited to the optimization, we show the original algorithm (Berry’s approximate scheme) constructs non-uniform points’ distributions on the Bloch sphere, thus will lead to an unsatisfying classical communication cost. In the next section, we also make a quantitative comparison between the original scheme and the one we come up with for optimization.

Below is how Berry’s algorithm locates $N$ spherical caps. Assume the state located at the center of a spherical cap is expressed as

$$\begin{aligned} \vert \tilde{\beta '}\rangle =\sum _{k=0}^1 \beta _k\vert k\rangle , \end{aligned}$$

(3)

where $\beta _0$ is real, and $\beta _1$ is complex. The state $\vert \tilde{\beta '}\rangle$ is not necessarily normalized, and the corresponding normalized state will be denoted by $\vert \beta '\rangle$. Berry begins with finding on the interval $\left[ 0,1\right]$ $D$ uniformly distributed numbers

$$\begin{aligned} (2n-1)/D-1, \end{aligned}$$

(4)

$n=1,2, \ldots , D$. By picking 3 such numbers (repetition is allowed) as $\beta _0$, the real and imaginary parts of $\beta _1$, a spherical cap is located. The total number of spherical caps constructed by this algorithm satisfies $N=D^3$.

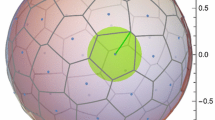
In the above algorithm, although the spherical caps are represented by $N$ points that are uniformly distributed in the unit box, the actual distribution of the spherical caps on the Bloch sphere is non-uniform. Worse, as two or more different $\vert \tilde{\beta '}\rangle$ may correspond to one the same $\vert \beta '\rangle$, lots of spherical caps coincide with each other. Figure 1 illustrates the case of $N=4^3$.

Fig. 1

Points distribution given the Berry’s algorithm in Ref. [10] in the case of $N=4^3$. Since some points coincide with each other, only 28 (instead of 64) points are distinguishable (view along the negative $z$ direction)

In this section, we have showed that the original scheme uses an algorithm for non-uniform points’ distributions, thus suffers from an unsatisfying classical communication cost. And to optimize the scheme, we need an algorithm for constructions of uniformly distributed points on the Bloch sphere. However, except for some special cases such as the arrangements of 4, 8, 6, 12, 20 points on a sphere, in which cases we can use the vertices of the Platonic solids due to their perfect symmetry, finding an algorithm that can uniformly arrange an arbitrary number of points on a sphere is still an open question. Fortunately, there is still a variety of algorithms that can construct quite uniform points distribution on a sphere. One simple way to describe and compute algorithm is spiral points, which we will use to demonstrate the optimization procedure in the next section.

3 Demonstrating the optimization procedure via spiral points

The problem of how to uniformly distribute points on a sphere has long been receiving attention in researches like searching for large stable carbon molecules and locating identical charged particles so that they are in equilibrium according to Coulomb’s law, etc. Spiral point is an algorithm proposed for the explicit construction of considerably uniformly distributed points on the sphere. It has the advantage of being simple to describe and compute, thus suitable for the demonstration of the optimization procedure in remote preparation of a pure qubit.

Just like the algorithm’s name, the construction of the spiral points is like drawing a spiral path along the surface of the unit ball. One begins from setting the first spiral point at the south pole of the sphere. To obtain the next spiral point, one proceeds upward from the current point along a meridian to the height that is $2/(n-1)$ higher and travels counterclockwise along a latitude for a fixed distance of $3.6/\sqrt{N}$ to arrive at the next point. The entire path will end up at the north pole. Using spherical coordinates, the $i$th spiral point $p_i$ is given by

$$\begin{aligned} \theta _i&= \arccos \left( z_i\right) ,\end{aligned}$$

(5)

$$\begin{aligned} z_i&= -1+\frac{2(i-1)}{N-1} \text {, } 1\le i\le N \text {, }\end{aligned}$$

(6)

$$\begin{aligned} \phi _1&= \phi _N=0 \text {, }\end{aligned}$$

(7)

$$\begin{aligned} \phi _i&= \left( \phi _{i-1}+\frac{3.6}{\sqrt{N}}\frac{1}{\sqrt{1-z_i^2}}\right) (\text {mod} 2\pi )\text {, } 2\le i\le N \text {.} \end{aligned}$$

(8)

In Fig. 2, one can see how uniform the distribution of 64 spiral points looks.

Fig. 2

Spiral points for $N=64$. The mesh on the sphere shows the Voronoi cells corresponding to spiral points (view along the negative z direction)

Now let us calculate the cbits versus ebits trade-off for the scheme using spiral points. But before we can calculate the trade-off, we must introduce the concept of Voronoi diagram [15]. A Voronoi diagram is a way of dividing space into numbers of regions. In the context of Voronoi diagram, the spiral points $p_i$ are called sites. For each site, there will be a corresponding polygon-shaped region consisting of all points closer to this site than to any other. These regions are called Voronoi cells, whose edges are equidistant from two sites, and vertices equidistant from three or more sites (Figure 2 gives an illustration of Voronoi cells corresponding to the 64 spiral points.). Let us denote by $v_{\{i,j\}}$ the $j$th vertex of the Voronoi cell corresponding to $p_i$.

Since every spherical cap $c_i$ is centered at the spiral point $p_i$, $C$ will not be a cover of the Bloch sphere until every $c_i$ covers the Voronoi cell corresponding to $p_i$. One can measure the size of $c_i$ by the infidelity radius $r_\text {I}$, which is defined by 1 minus the fidelity between the central state and a boundary state, i.e., $r_\text {I}=r^2$. Similarly, one can measure the size of the hardest to cover Voronoi cell by

$$\begin{aligned} \rho _\text {I}(N)=\max \left\{ 1-\left| \left\langle v_{\{i,j\}}\vert p_i\right\rangle \right| ^2 \vert \text { for } \text {any } p_i \text { and } \text {related }v_{\{i,j\}}\right\} . \end{aligned}$$

(9)

In order to make $C$ a cover of the Bloch sphere, $N$ should be large enough to ensure $\rho _\text {I}(N)\le r_F$. To compute $\rho _\text {I}(N)$, we need to obtain the coordinates of all $v_{\{i,j\}}$.

In the problem of generating a Voronoi diagram from a given set of points, except for some special points’ distributions, it is generally hard to find analytic solutions. One different approach that is commonly seen is to adopt a numerical solution. There are several algorithms developed for computing the spherical Voronoi diagram [15–17]. We write our program in Mathematica to implement the spherical version of the sweep line algorithm, which requires time $O(N \log N)$ for constructing Voronoi Diagram [17]. By taking the spiral points as input, the program is executed for the input size $N$ from 3 to 1,024. We list part of the result (for $N=2^n$, $n=1, 2, \ldots , 10$) in the table.

$N$	2	4	8	16	32
$\rho _\text {I}$	0.5	0.5	0.259739	0.120679	0.054644
$N$	64	128	256	512	1024
$\rho _\text {I}$	0.026443	0.013054	0.006607	0.003326	0.001669

Based on the obtained values of $\rho _\text {I}(N)$, we can compute the classical bits cost versus entanglement of the resource state. The smallest integer $N$ which satisfies the equation $r_F\ge \rho _\text {I}(N)$ is used to calculate the classical bits cost $\log N$, and the entanglement is calculated by $-r^2 \log r^2-(1-r^2)\log (1-r^2)$. We show the result in Fig. 3. Comparing with that of the original scheme proposed in Ref. [10], we can see that the classical bits cost after using spiral points is significantly reduced. Actually, the classical bits cost is reduced to a level very close to the limit for RSP scheme of this type, because it is between an upper bound and a lower bound of this limit (refer to Eqs. (23) and (24), respectively, of Ref. [10]).

Fig. 3

The cbits cost versus ebits for RSP of pure qubits using partially entangled state. The dotted curve is that based on the original scheme given in Ref. [10], and the solid curve is the result obtained when spiral points are used. The dashed-dotted curve and the dashed curve are an upper bound and a lower bound on the optimized classical communication cost for RSP scheme of this type. The red dots are drawn from the cases which are presented in table (Color figure online)

It must be emphasized that Fig. 3 only shows the classical bits cost in Step 3. The total classical bits cost for RSP schemes of this type should count the 2 bits in Step 2.

4 Conclusions

In this paper, we propose an optimization procedure which can be used to minimize the classical communication cost in remotely preparing a general pure qubit. By restating the RSP scheme in a geometric way, we related the optimization of the scheme to an algorithm that constructs uniformly distributed points on the Bloch sphere. Unlike an extra procedure adds to the scheme, the algorithm that the optimization needed can be integrated into the scheme directly.

To give a clear demonstration of this optimization procedure, we use an algorithm named spiral points, which gives a quite uniform points distribution with considerable simplicity. We calculate the cbits versus ebits trade-off, and the result shows that using a uniform points distribution algorithm like spiral points in the scheme reduced the classical bits cost to a level near optimal.