1 Introduction

In past the few years, nonlinear fractional order partial differential equations (NLFPDEs) have garnered considerable attention for their ability to demonstrate the core components that underpin real-life problems. In real-world research, fractional partial differential equations of the nonlinear type are expressing a wide variety of factors, including optical fiber, plasma physics, turbulence, finance, mechanical engineering, biological systems of nonlinear, control theory, and so on. It has been discovered to a wide range of physical objects, together with subordinate dissipative occupancy of components relapses, in a liquid, the movement of a huge meager surface, relaxation, and creeping characteristics are included in viscoelastic materials, and the \(P{I}^{\lambda }{D}^{\mu }\) controller for dynamic control systems and many other sectors (Uddin et al. 2021a, b). Thus, NLFPDEs are applied in several sectors, including modeling, describing, and predicting apparatuses related to engineering, bio-genetics, solid-state physics, optical fibers, physics of condensed material, elasticity, meteorology, electromagnetic, image and signal processing, plasma physics, chemical kinematics, oceanic spectacles, a neutron points kinematic model, electrical circuits, control and vibration, polymeric materials, finance, system identifications, quantum mechanics, landscape evolution, fluid dynamics and acoustics, medicine, and many more areas of applied mathematics and engineering (Arefin et al. 2022; Zaman et al. 2023).

The interest of this research is in wave motions towards the physical universe; the subject of traveling waves, which is very technical and well established, is also remarkable. The equations of nonlinear waves express dispersive systems of wave propagation such as elastic tubes, fluid flow, and liquid flow, as well as the ocean, rivers, gas bubbles, and lakes, along with the gravitational attraction of waves for a consistent domain and rescaling wave motion in nonlinear type. Traveling waves, their breaking on coasts, ship-generated waves on water, waves storm-generated in the ocean, riverine flooding, and limited oscillations in free liquid, such as lakes and ports, are all examples of wave difficulties (Uddin et al. 2018, 2019a).

The rapidly growing of computer programming and software-based tools like Maple or Mathematica, a variety of mathematical and analytical approaches for finding solutions of NLFPDEs have already been established, namely the extended rational sinh-cosh approach and extended Tanh–Coth approach (Rizvi et al. 2020), the tanh method (Wazwaz 2004), residual power series method (Alquran et al. 2017), first-integral approach (Eslami and Rezazadeh 2016), modified rational sine–cosine functions method (Alquran 2023a; Alquran and Al Smadi 2023; Alquran and Jaradat 2023), \(({G}{\prime}/{G}^{2})\)-expansion technique (Faridi et al. 2023a), Kudryashov method (Ali et al. 2023), Extended tanh-function technique (Zaman et al. 2022), New extended direct algebraic method (Majid et al. 2023; Faridi et al. 2023b, c), modified auxiliary expansion technique (Al Alwan et al. 2023), new auxiliary equation approach (Ur Rahman et al. 2023), Fractional Maclaurin series (Alquran 2023b), \({\Phi }^{6}\)-model expansion (Asjad et al. 2023), Sine–Gordon expansion approach (Yel et al. 2020), novel Homotopy perturbation method (Alquran 2023c), and many more. In each of these, the new generalized \(({G}{\prime}/G)\)-expansion technique gaining popularity in recent years. Wang et al. (2008) proposed a simple technique known as the \(({G}{\prime}/G)\)-expansion technique for generating the solutions of travelling wave of numerous NLFPDEs. Several researchers have utilized this strategy to solve a wide range of nonlinear issues involving traveling waves. After that, researchers gradually improved and developed this process, resulting in the extended \(({G}{\prime}/G)\)-expansion technique, improved \(({G}{\prime}/G)\)-expansion technique, and other approaches (Naher and Abdullah 2016). The new generalized \(({G}{\prime}/G)\)-expansion approach described by Naher and Abdullah (2013) is an original method for modifying \(({G}{\prime}/G)\)-expansion, and this approach can be used in a variety of physics contexts, particularly when dealing with fractional and integer nonlinear partial differential equations (PDEs) and mathematical physics. These techniques are frequently used to identify exact solutions to differential equations and nonlinear PDEs involved in a variety of physical phenomena. Nonlinear optics, quantum mechanics, fluid mechanics, and general mathematical physics are among specific areas where these techniques can be used and where perfect solutions to nonlinear PDEs are desired. It is significant to remember that the suitability of these methods may vary depending on the particulars of the equations being studied in terms of form and properties. Researchers often use these methods as part of their toolkit to find analytical solutions in various physical contexts.

The time fractional Gardner equation is a crucial NLFPDE which has significant impact in nonlinear science and engineering.

$$D_{t}^{\alpha } {\mathfrak{U}} + 6\left( {{\mathfrak{U}} - \varepsilon^{2} {\mathfrak{U}}^{2} } \right){\mathfrak{U}}_{x} + {\mathfrak{U}}_{xxx} = 0; 0\left\langle {\alpha \le 1,t} \right\rangle 0,$$
(1.1)

where \(\alpha\) denoted the fractional derivative and \(\varepsilon\) is a non-zero arbitrary constant. The proposed equation was linked to the modified KdV and Korteweg-de Vries equations. The improvement for the nonlinear equation of higher order defined to the equation in various physical plasmas is the focus of our investigation into the nonlinear characteristics of shallow water solitary waves, quantum mechanics, fluid mechanics, oceanic spectacles, and many more (Daghan and Donmez 2016). Many physicists and mathematicians have recently been intrigued by the demonstrates equation, as a result, numerous ways were used to solve it, such as Li et al. (2020) using suggested equation work with complete discrimination system method, exp \((-\Phi (\varepsilon ))-\) expansion approach was applied the proposed equation by Singh et al. (2021), using \((G^{\prime}/G)\)-expansion technique (Bayrak 2018) solved the suggested equation and many more.

The time fractional STO equation has piqued the interest of various mathematicians and physicists. Consider the time fractional STO equation becomes:

$${D}_{t}^{\alpha }\mathfrak{U}+3a{\mathfrak{U}}_{x}^{2}+3a{\mathfrak{U}}^{2}{\mathfrak{U}}_{x}+3a\mathfrak{U}{\mathfrak{U}}_{xx}+a{\mathfrak{U}}_{xxx}=0;\quad t>0, 0<\alpha \le 1,$$
(1.2)

where \(\alpha\) denoted the fractional order derivative and \(a\) is a non-zero arbitrary constant. The fusion and fission characteristic arising in of solitons, optical fibers, physics of condensed material, quantum relativistic atom theory in one particle, the relativistic relation for energy–momentum, and interactions of electromagnetic fields are all examined by this equation in mathematical physics and engineering (Uddin et al. 2019b). This equation was examined by several methods, such as the generalized Kudryashov technique was applied to solving the suggested equation by Sirisubtawee et al. (2020), Abdouet al. (2020) using extended F-expansion method, new Iterative method was using to solved this equations by Khan et al. (2018), Islam and Akter (2020) was using generalized Bernoulli equation method to solved the mentioned equation.

The main objective of this research is to create a visually pleasing exact analytic solution for the aforementioned equations using a new generalized \(({G}{\prime}/G)\)-expansion approach based on well-known conformable derivatives. The rest of the paper will be structured in the manner described below: the definition and the basic tools were announced in Sect. 2, In Sect. 3, the methodology for the new generalized \(({G}{\prime}/G)\)-expansion approach is demonstrated. We applied the mentioned approach, introduce previously to generate the accurate answer for the presented equation in Sect. 4. Section 5 holds physical explanation in brief. In the final portion, the summary is offered.

2 Definition and basic tools

Khalil et al. (2014) established the conformable derivative. Take up the function \(f:[0,\infty )\to {\mathbb{R}}\). The \(\alpha\)-order conformable derivative of \(f\) is determine as Khalil et al. (2014):

$${\mathcal{T}}_{\alpha }\left(f\right)\left(t\right)=\underset{\varepsilon \to 0}{\mathrm{lim}}\frac{f\left(t+\varepsilon {t}^{1-\alpha }\right)-f(t)}{\varepsilon } .$$
(2.1)

for all \(t>0, \alpha \in (\mathrm{0,1})\). If \(f\) is \(\alpha\)-differentiable for some \((0,\mathcal{a})\), \(\mathcal{a}>0\), and \(\underset{t\to {0}^{+}}{\mathrm{lim}}{f}^{(\alpha )}(t)\) seems to be exist, formerly to clarify \({f}^{\left(\alpha \right)}\left(0\right)=\underset{t\to {0}^{+}}{\mathrm{lim}}{f}^{(\alpha )}(t)\). The theorems that follow demonstrate how conformable derivatives should be used to establish a few principles.

On the derivatives of addition, quotients, and products for the functions of fractional differentiable, For time scales, the conformable derivative is necessary, and this is obtained using the abovementioned theorem (Benkhettou et al. 2016).

Rendering to the description supplied by Khalil et al. (2014), The following theorem is satisfied by the conformable derivative, which gives several important qualities.

Theorem 1

Take up \(\alpha \in (\mathrm{0,1}]\) and let that, \(f,g\) were \(\alpha\)-differentiable at each point i.e., \(t>0\).

Additionally

  1. (a)

    \({\mathcal{T}}_{\alpha }\left(cf+\mathcal{d}g\right)=\mathcal{c}{\mathcal{T}}_{\alpha }\left(f\right)+\mathcal{d}{\mathcal{T}}_{\alpha }\left(g\right)\), for all \(\mathcal{c},\mathcal{d}\in {\mathbb{R}}\).

  2. (b)

    \({\mathcal{T}}_{\alpha }\left({t}^{\mathcalligra{p}}\right)=p{t}^{\mathcal{p}-\alpha }\), for all \(\mathcalligra{p}\in {\mathbb{R}}\).

  3. (c)

    \({\mathcal{T}}_{\alpha }\left({c}\right)=0\), constant for all function \(f\left(t\right)={c}\).

  4. (d)

    \({\mathcal{T}}_{\alpha }\left(fg\right)=f{\mathcal{T}}_{\alpha }\left(g\right)+g{\mathcal{T}}_{\alpha }\left(f\right)\).

  5. (e)

    \({\mathcal{T}}_{\alpha }\left(\frac{f}{g}\right)=\frac{g{\mathcal{T}}_{\alpha }\left(f\right)-f{\mathcal{T}}_{\alpha }(g)}{{g}^{2}}\).

  6. (f)

    Therefore, if \(f\) be differentiable, so \({\mathcal{T}}_{\alpha }\left(f\right)\left(t\right)={t}^{1-\alpha }\frac{df}{dt}\).

Concerning the conformable derivative, Khalil et al. (2014) defines several more properties, such as the inequality of Gronwall's, law of chain rule, Laplace transform, integration techniques, several Tailor series expansions, and function of exponential.

Theorem 2

Suspect that the function \(f\) were an \(\alpha\)-differentiable function to conformable differentiable besides assume that the function \(g\) develop also differentiable and determine to the interval of \(f\). Thus

$${\mathcal{T}}_{\alpha }\left(f\circ g\right)\left(t\right)={t}^{1-\alpha }{g}{^\prime}\left(t\right){f}_{g}(t).$$
(2.2)

3 Execution of the methodology

Suppose the following is the basic NLFPDE formation:

$${\mathcal{Z}}\left( {{\mathfrak{U}},D_{t}^{\alpha } {\mathfrak{U}},D_{x}^{\beta } {\mathfrak{U}},D_{t}^{\alpha } D_{t}^{\alpha } {\mathfrak{U}},D_{t}^{\alpha } D_{x}^{\beta } {\mathfrak{U}},D_{x}^{\beta } D_{x}^{\beta } {\mathfrak{U}}, \ldots \ldots \ldots } \right) = 0,\;\;\;0 < \alpha \le 1, 0 < \beta \le 1$$
(3.1.1)

where \(\mathcal{Z}\) be seems a polynomial of \(\mathfrak{U}\), in this condition the undetermined function is \(\mathfrak{U}(x, y,t)=\mathfrak{U}(\zeta )\), and the partial derivatives, as well as the derivatives connecting nonlinear terms with subscripts.

Staircase 1 We gather\(x\), \(y\) and \(t\), which are real variables through a compound variable \(\zeta\)

$$\mathfrak{U}\left(x, y, t\right)=\mathfrak{U}\left(\zeta \right), \zeta =\mathcal{g}\frac{{x}^{\beta }}{\beta }+\mathcal{h}\frac{{y}^{\beta }}{\beta }-\mathcal{V}\frac{{t}^{\alpha }}{\alpha },$$
(3.1.2)

where the numbers of wave symbolize by \(\mathcal{g},\mathcal{h}\) and \(\mathcal{V}\) denote to velocity of wave traveling. The wave transformation of (3.1.2) changes to Eq. (3.1.1) to an ordinary differential equation (ODE) and if \(\mathfrak{U}=\mathfrak{U}\left(\zeta \right)\):

$$\mathcal{K}\left(\mathfrak{U},{\mathfrak{U}}{^\prime},{\mathfrak{U}}^{{\prime}{\prime}},{\mathfrak{U}}^{{\prime}{\prime}{\prime}}, \dots \dots \dots \right)=0,$$
(3.1.3)

where \(\mathcal{K}\) be the derivatives for \(\mathcal{Z}\), which is polynomial for \(\mathfrak{U}\), and the ordinary derivatives are superscripts with respect to \(\zeta\).

When \(\mathcal{h}=0\) and \(\mathcal{g}=1\), then the Eq. (3.1.2) turns into

$$\mathfrak{U}\left(x, t\right)=\mathfrak{U}\left(\zeta \right), \zeta =x-\mathcal{V}\frac{{t}^{\alpha }}{\alpha },$$
(3.1.4)

As a possible scenario, we integrate Eq. (3.1.3) one either more times, because of the complexity avoided, the integration constant(s) would be zero.

Staircase 2 The exact solution of wave for Eq. (3.1.3) was given bellow:

$$\mathfrak{U}\left(\zeta \right)=\sum_{l=0}^{\mathcal{N}}{\mathcal{a}}_{l}{(\mathcal{d}+\mathcal{S})}^{l}+\sum_{l=1}^{\mathcal{N}}{\mathcal{b}}_{l}{\left(\mathcal{d}+\mathcal{S}\right)}^{-l},$$
(3.1.5)

hence either \({\mathcal{a}}_{\mathcal{N}}\) or \({\mathcal{b}}_{\mathcal{N}}\) possible to be zero, however both \({\mathcal{a}}_{\mathcal{N}}\) and \({\mathcal{b}}_{\mathcal{N}}\) seems to be zero by the same time, \({\mathcal{a}}_{l}\) and \({\mathcal{b}}_{l}(\mathrm{for \, all}, l=\mathrm{1,2},\dots ,\mathcal{N})\) and \(\mathcal{d}\) are arbitrary constants that recognized subsequently and \(\mathcal{S}\left(\zeta \right)\) is presented by

$$\mathcal{S}\left(\zeta \right)=(G^{\prime}/G),$$
(3.1.6)

where \(G=G\left(\zeta \right)\) satisfies the ODE of nonlinear type was assumed beneath:

$$\mathcal{A}G{G}^{^{\prime\prime} }-\mathcal{B}GG^{\prime}-\mathcal{E}{G}^{2}-\mathcal{C}{(G^{\prime})}^{2}=0.$$
(3.1.7)

The key specifies for the derivative with respect to \(\zeta\); real parameters considered as \(\mathcal{A},\mathcal{B}, \mathcal{E}\) and \(\mathcal{C}\). To estimate \(\mathcal{N}\), which is the balance number and we use homogeneous balance technique to the higher order nonlinear term and the higher order derivatives term in Eq. (3.1.3).

Staircase 3 Substituting Eqs. (3.1.5) and (3.1.7) including Eq. (3.1.6) into Eq. (3.1.3) having \(\mathcal{N}\) achieved in Staircase 3, it gives a polynomial in \({(\mathcal{d}+\mathcal{S})}^{\mathcal{N}}\) and \({\left(\mathcal{d}+\mathcal{S}\right)}^{-\mathcal{N}}(\mathrm{for \, all}, \mathcal{N}=\mathrm{0,1},2,\dots \dots )\). Afterward, we specified every coefficient of the resulting polynomial to be zero, yielding a cluster of algebriace equations for \({\mathcal{a}}_{l}\), \({\mathcal{b}}_{l}(\mathrm{for all}, l=\mathrm{1,2},\dots \dots ,\mathcal{N})\), \(\mathcal{d}\) and \(\mathcal{V}\).

Staircase 4 In place of the general solution in Eq. (3.1.7) is common, introducing the values of \({\mathcal{a}}_{l}\), \({\mathcal{b}}_{l}(\mathrm{for \, all}, l=\mathrm{1,2},\dots ,\mathcal{N})\), \(\mathcal{d}\) and \(\mathcal{V}\) to Eq. (3.1.5), We get novel accurate solutions for traveling wave for the nonlinear PDE (3.1.1) that are of a more generic nature. Presenting the general solution of Eq. (3.1.7), now we take the next solutions of Eq. (3.1.6) were \(\Psi =\mathcal{A}-\mathcal{C}\):

Cluster 1 For \(\mathcal{B}\ne 0,\) then \(\Omega ={\mathcal{B}}^{2}+4\mathcal{E}(\mathcal{A}-\mathcal{C})>0\),

$$\mathcal{S}\left(\zeta \right)=\left({G}^{\prime}/G\right)=\frac{\mathcal{B}}{2\Psi }+\frac{\sqrt{\Omega }}{2\Psi }\frac{{C}_{1}\mathrm{sinh}\left(\frac{\sqrt{\Omega }}{2\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{cosh}\left(\frac{\sqrt{\Omega }}{2\mathcal{A}}\zeta \right)}{{C}_{1}\mathrm{cosh}\left(\frac{\sqrt{\Omega }}{2\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{sinh}\left(\frac{\sqrt{\Omega }}{2\mathcal{A}}\zeta \right)}.$$
(3.1.8)

Cluster 2 For \(\mathcal{B}\ne 0,\) then \(\Omega ={\mathcal{B}}^{2}+4\mathcal{E}(\mathcal{A}-\mathcal{C})<0\),

$$\mathcal{S}\left(\zeta \right)=({G}^{\prime}/G)=\frac{\mathcal{B}}{2\Psi }+\frac{\sqrt{-\Omega }}{2\Psi }\frac{-{C}_{1}\mathrm{sin}\left(\frac{\sqrt{-\Omega }}{2\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{cos}\left(\frac{\sqrt{-\Omega }}{2\mathcal{A}}\zeta \right)}{{C}_{1}\mathrm{cos}\left(\frac{\sqrt{-\Omega }}{2\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{sin}\left(\frac{\sqrt{-\Omega }}{2\mathcal{A}}\zeta \right)}.$$
(3.1.9)

Cluster 3 For \(\mathcal{B}\ne 0,\) then \(\Omega ={\mathcal{B}}^{2}+4\mathcal{E}(\mathcal{A}-\mathcal{C})=0\),

$$\mathcal{S}\left(\zeta \right)=\left({G}^{\prime}/G\right)=\frac{\mathcal{B}}{2\Psi }+\frac{{C}_{2}}{{C}_{1}+{C}_{2}\zeta }.$$
(3.1.10)

Cluster 4 For \(\mathcal{B}=0,\) then \(\Delta =\Psi \mathcal{E}>0\),

$$\mathcal{S}\left(\zeta \right)=\left({G}^{\prime}/G\right)=\frac{\sqrt{ \Delta }}{\Psi }\frac{{C}_{1}\mathrm{sinh}\left(\frac{\sqrt{ \Delta }}{\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{cosh}\left(\frac{\sqrt{ \Delta }}{\mathcal{A}}\zeta \right)}{{C}_{1}\mathrm{cosh}\left(\frac{\sqrt{ \Delta }}{\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{sinh}\left(\frac{\sqrt{ \Delta }}{\mathcal{A}}\zeta \right)}.$$
(3.1.11)

Cluster 5 For \(\mathcal{B}=0,\) then \(\Delta =\Psi \mathcal{E}<0\),

$$\mathcal{S}\left(\zeta \right)=\left({G}^{\prime}/G\right)=\frac{\sqrt{- \Delta }}{\Psi }\frac{-{C}_{1}\mathrm{sin}\left(\frac{\sqrt{-\Delta }}{\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{cos}\left(\frac{\sqrt{-\Delta }}{\mathcal{A}}\zeta \right)}{{C}_{1}\mathrm{cos}\left(\frac{\sqrt{-\Delta }}{\mathcal{A}}\zeta \right)+{C}_{2}\mathrm{sin}\left(\frac{\sqrt{-\Delta }}{\mathcal{A}}\zeta \right)}.$$
(3.1.12)

The benefits of the techniques employed over other ways in the literature, such as the exp-function method, tanh-function method, basic \(\left({G}^{\prime}/G\right)\)-expansion method, and so on. The proposed strategies provide further reliable traveling wave solutions with additional free parameters. These precise solutions are vital in revealing the underlying mechanics of physical phenomena. Having closed-form solutions for nonlinear evolution equations also makes it easier for numerical solvers to compare the accuracy of their results and aids in stability analysis. On the other hand, when solving reduced differential equations of third order or lower, using symbolic computation software such as Maple meaningfully rises the probability of finding valuable solutions to the corresponding algebraic equations. Nonetheless, as the order of the equations increases, ensuring the existence of solutions for the resulting algebraic equations becomes less viable in general. In such cases, the proposed approaches are especially useful since they can include a greater number of arbitrary constants than other existing methods. This feature enables these approaches to solve circumstances where other methods may fail.

4 Solutions proposing and analyzing causes

4.1 The time fractional gardner (FG) equation

By computer software such as Maple, we will create solutions of traveling wave for the time fractional FG equation in this sector. Let the equation looks like:

$${D}_{t}^{\alpha }\mathfrak{U}+6\left(\mathfrak{U}-{\varepsilon }^{2}{\mathfrak{U}}^{2}\right){\mathfrak{U}}_{x}+{\mathfrak{U}}_{xxx}=0; 0<\alpha \le 1,t>0.$$
(4.1.1)

The resulting nonlinear complex wave transformation is applied:

$$\zeta = \kappa x + \iota \frac{{t^{\alpha } }}{\alpha },\;{\mathfrak{U}}\left( {x,t} \right) = {\mathfrak{U}}\left( \zeta \right),$$
(4.1.2)

where \(\iota\) denoted traveling wave velocity, complex tnsformation is \(\zeta\), and \(\varepsilon , \kappa\) is a constant (arbitrary). To investigate the nonlinear properties of shallow water solitary waves, this equation is known as the equation for various physical plasmas. Using Eq. (4.1.2), to the Eq. (4.1.1) and by the phases bellow, this equation could be transformed to a nonlinear type ODE. Also, integrating with respect to \(\zeta\) once and considering integrating constant be zero and get:

$$\iota \mathfrak{U}+3\kappa {\mathfrak{U}}^{2}-2\kappa {\mathfrak{U}}^{3}+{\kappa }^{3}{\mathfrak{U}}^{{\prime}{\prime}}=0,$$
(4.1.3)

where \(^{\prime}=\frac{d}{d\zeta }\).

Taking balance to the order of uppermost nonlinear term \({\mathfrak{U}}^{3}\) and order of the uppermost linear term \({\mathfrak{U}}^{{\prime}{\prime}}\), produces homogeneous balance \(\mathcal{N}\) is one. So, the result of the Eq. (4.1.3) proceeds the formula bellow:

$$\mathfrak{U}\left(\zeta \right)=a_{0}+a_{1}{(d+\mathcal{S})}^{1}+{b}_{1}{\left(d+\mathcal{S}\right)}^{-1},$$
(4.1.4)

where evaluated constants are\({\mathcal{a}}_{0}\), \({\mathcal{a}}_{1}\) and \({\mathcal{b}}_{1}\). The leftward side turn to a polynomial in \((\mathcal{d}+\mathcal{S})\) by replacing (4.1.4) and (4.1.5) through (3.1.5). Tapping a null value in every of this polynomial's coefficients produces the sequential arithmetic equations of\({\mathcal{a}}_{0}\), \({\mathcal{a}}_{1}\) and \({\mathcal{b}}_{1}, \kappa , \iota \mathrm{and }\mathcal{d}\) (which we omit to show for clarity). The outcomes of our oversimplified set of equations are displayed below:

$$d = - \frac{{{\mathcal{A}} + \kappa {\mathcal{B}}}}{2\Psi }, \;\kappa = \kappa , \iota = - \frac{{\left( {4{\rm E}\Psi - {\mathcal{B}}^{2} } \right)}}{{{\mathcal{A}}^{2} }},a_{0} = 1, a_{1} = \frac{\kappa \Psi }{{\mathcal{A}}} ,\;and\;b_{1} = \frac{1}{4}\frac{{{\mathcal{A}}^{2} - \kappa^{2} \Omega }}{{\Psi {\mathcal{A}}\kappa }},$$
(4.1.5)

where \(\Omega ={\mathcal{B}}^{2}+4\mathcal{E}\left(\mathcal{A}-\mathcal{C}\right)={\mathcal{B}}^{2}+4\mathcal{E}\Psi\),\({\mathcal{a}}_{0}\), \({\mathcal{a}}_{1}\) and \({\mathcal{b}}_{1}\) are free parameters.

Phase 1

The following traveling wave solutions are obtained by replacing Eq. (4.1.5) to Eq. (4.1.4), with Eq. (3.1.8) and shortened (consider \({C}_{2}=0\) but \({C}_{1}\ne 0\) \(;{C}_{2}\ne 0\) but \({C}_{1}=0\)):

$${\mathfrak{U}}_{{1}_{1}}\left(x, t\right)=1+\frac{1}{4}\left[-2+\sqrt{\Omega }\mathrm{coth}\left\{\frac{\sqrt{\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-2+\sqrt{\Omega }\mathrm{coth}\left\{\frac{\sqrt{\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.1.6)
$${\mathfrak{U}}_{{1}_{2}}\left(x, t\right)=1+\frac{1}{4}\left[-2+\sqrt{\Omega }\mathrm{tanh}\left\{\frac{\sqrt{\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-2+\sqrt{\Omega }\mathrm{tanh}\left\{\frac{\sqrt{\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.1.7)

where \(\Omega, \mathrm{and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\kappa\) and \(\iota\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

Phase 2

Another two solutions from staircase-2 were obtained in a similar way, which are as follows:

$${\mathfrak{U}}_{{1}_{3}}\left(x, t\right)=1+\frac{1}{4}\left[-2+\sqrt{-\Omega }\mathrm{cot}\left\{\frac{\sqrt{-\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){[-2+\sqrt{-\Omega }\mathrm{cot}\left\{\frac{\sqrt{-\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}]}^{-1},$$
(4.1.8)
$${\mathfrak{U}}_{{1}_{4}}\left(x, t\right)=1+\frac{1}{4}\left[-2-\sqrt{-\Omega }\mathrm{tan}\left\{\frac{\sqrt{-\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){[-2-\sqrt{-\Omega }\mathrm{tan}\left\{\frac{\sqrt{-\Omega }}{4}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}]}^{-1},$$
(4.1.9)

where \(\Omega, \mathrm{ and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\kappa\) and \(\iota\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

Phase 3

From staircase 3 we obtain another solutions as

$${\mathfrak{U}}_{{1}_{5}}\left(x, t\right)=1+\frac{1}{4}\left[-2+\frac{{C}_{2}}{{C}_{1}+{C}_{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-2+\frac{{C}_{2}}{{C}_{1}+{C}_{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)}\right]}^{-1},$$
(4.1.10)

where \(\Omega, \mathrm{ and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\kappa\) and \(\iota\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

Phase 4

Get two more solutions by using the staircase-3

$${\mathfrak{U}}_{{1}_{6}}\left(x, t\right)=1+\frac{1}{2}\left[-1+\sqrt{ \Delta }\mathrm{cot}\left\{\frac{\sqrt{\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-1+\sqrt{ \Delta }\mathrm{cot}\left\{\frac{\sqrt{\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.1.11)
$${\mathfrak{U}}_{{1}_{7}}\left(x, t\right)=1+\frac{1}{2}\left[-1+\sqrt{ \Delta }\mathrm{tan}\left\{\frac{\sqrt{\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-1+\sqrt{ \Delta }\mathrm{tan}\left\{\frac{\sqrt{\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.1.12)

where \(\Omega ,\mathrm{and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\kappa\) and \(\iota\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

Phase 5

Finally, from the staircase 5 we achieved the following solutions

$${\mathfrak{U}}_{{1}_{8}}\left(x, t\right)=1+\frac{1}{2}\left[-1+\sqrt{-\Delta }\mathrm{cot}\left\{\frac{\sqrt{-\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-1+\sqrt{-\Delta }\mathrm{cot}\left\{\frac{\sqrt{-\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.1.13)
$${\mathfrak{U}}_{{1}_{9}}\left(x, t\right)=1+\frac{1}{2}\left[-1-\sqrt{-\Delta }\mathrm{tan}\left\{\frac{\sqrt{-\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{1}{16}\left(\frac{4-\Omega }{{\Psi }^{2}}\right){\left[-1-\sqrt{-\Delta }\mathrm{tan}\left\{\frac{\sqrt{-\Delta }}{2}\left(\kappa x+\iota \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.1.14)

where \(\Omega ,\mathrm{and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\kappa\) and \(\iota\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

4.2 The time fractional Sharma-Tasso-Olver (STO) equation

Consider the time fractional STO equation becomes:

$${D}_{t}^{\alpha }\mathfrak{U}+3a{\mathfrak{U}}_{x}^{2}+3a{\mathfrak{U}}^{2}{\mathfrak{U}}_{x}+3a\mathfrak{U}{\mathfrak{U}}_{xx}+a{\mathfrak{U}}_{xxx}=0; t>0, 0<\alpha \le 1,$$
(4.2.1)

where \(a\ne 0.\) We then apply the consequent complex nonlinear wave transformation:

$$\zeta =x+\omega \frac{{t}^{\alpha }}{\alpha }, \mathfrak{U}\left(x,t\right)=\mathfrak{U}\left(\zeta \right),$$
(4.2.2)

wherever \(\omega\) be the velocity of traveling wave. Numerous applications of the proposed equation are now used, such as the energy–momentum connection with relativistic energy, a quantum relativistic atom, and electromagnetic field interactions. Exploiting Eq. (4.2.2), to the Eq. (4.2.1) and this equation could be transformed to a nonlinear type ODE. Also, integrating with respect to \(\zeta\) one time and contemplating zero as constant for integration and obtained:

$$\omega \mathfrak{U}+3a\mathfrak{U}{\mathfrak{U}}^{\prime}+a{\mathfrak{U}}^{3}+a{\mathfrak{U}}^{{\prime}{\prime}}=0,$$
(4.2.3)

where \(^{\prime}=\frac{d}{d\zeta }\). Taking balance to the higher order nonlinear term \({\mathfrak{U}}^{3}\) and the higher order linear term \({\mathfrak{U}}^{{\prime}{\prime}}\), produces homogeneous balance \(\mathcal{N}\) is one. So, the result of Eq. (4.2.3) given the subsequent formula:

$$\mathfrak{U}\left(\zeta \right)={\mathcal{a}}_{0}+{\mathcal{a}}_{1}{(\mathcal{d}+\mathcal{S})}^{1}+{\mathcal{b}}_{1}{\left(\mathcal{d}+\mathcal{S}\right)}^{-1},$$
(4.2.4)

where evaluated constants denoted \({\mathcal{a}}_{0}\), \({\mathcal{a}}_{1}\) and \({\mathcal{b}}_{1}\). The leftward side turn to a polynomial in \((\mathcal{d}+\mathcal{S})\) by replacing (4.2.4) and (4.2.5) with (3.1.5). Tapping a null value in every of this polynomial's coefficients produces a sequential arithmetic equation for \({\mathcal{a}}_{0}\), \({\mathcal{a}}_{1}\) and \({\mathcal{b}}_{1}, \kappa , \iota \mathrm{and }\mathcal{d}\) (which we omit to show for clarity). The results of our oversimplified solution of the equations are displayed below:

$${d}=-\frac{\mathcal{B}}{2\Psi }, \omega =-\frac{4a\Omega }{{\mathcal{A}}^{2}}, { {a}}_{0}=0, {{a}}_{1}=\frac{2\Psi }{\mathcal{A}} ,\mathrm{ and }{{b}}_{1}=\frac{\Psi }{2\mathcal{A}\Psi } ,$$
(4.2.5)

where \(\Omega ={\mathcal{B}}^{2}+4\mathcal{E}\left(\mathcal{A}-\mathcal{C}\right)={\mathcal{B}}^{2}+4\mathcal{E}\Psi ,\Psi =\mathcal{A}-\mathcal{C}\),\({\mathcal{a}}_{0}\), \({\mathcal{a}}_{1}\) and \({\mathcal{b}}_{1}\) are free parameters.

Segment 1

The traveling wave solutions are produced by substituting Eq. (4.2.5) to the Eq. (4.2.4), amongst the Eq. (3.1.8), and simplifying the equations (consider \({C}_{2}=0\) but \({C}_{1}\ne 0\) \(;{C}_{2}\ne 0\) but\({C}_{1}=0\)):

$${\mathfrak{U}}_{{2}_{1}}\left(x, t\right)=\frac{\sqrt{\Omega }}{2}\mathrm{coth}\left\{\frac{\sqrt{\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\}+\frac{\sqrt{\Omega }}{2}\mathrm{tanh}\{\frac{\sqrt{\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\},$$
(4.2.6)
$${\mathfrak{U}}_{{2}_{2}}\left(x, t\right)=\frac{\sqrt{\Omega }}{2}\mathrm{tanh}\left\{\frac{\sqrt{\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\}+\frac{\sqrt{\Omega }}{2}\mathrm{coth}\{\frac{\sqrt{\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}$$
(4.2.7)

where \(\Omega, \mathrm{ and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\omega\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

Segment 2

Obtain the corresponding exact solutions by substituting Eq. (4.2.5) to the Eq. (4.2.4), adding Eq. (3.1.9), and shortening (consider \({C}_{2}=0\) but \({C}_{1}\ne 0\) \(;{C}_{2}\ne 0\) but \({C}_{1}=0\)):

$${\mathfrak{U}}_{{2}_{3}}\left(x, t\right)=\frac{\sqrt{-\Omega }}{2}\mathrm{cot}\left\{\frac{\sqrt{-\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}+\frac{\Omega }{4\Psi }{\left[\frac{\sqrt{-\Omega }}{2\Psi }\mathrm{cot}\left\{\frac{\sqrt{-\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1}$$
(4.2.8)
$${\mathfrak{U}}_{{2}_{4}}\left(x, t\right)=-\frac{\sqrt{-\Omega }}{2}\mathrm{tan}\left\{\frac{\sqrt{-\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}-\frac{\Omega }{4\Psi }{\left[\frac{\sqrt{-\Omega }}{2\Psi }\mathrm{tan}\left\{\frac{\sqrt{-\Omega }}{4}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.2.9)

where \(\Omega, \mathrm{ and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\omega\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

Segment 3

Equation (4.2.5) is substituted to Eq. (4.2.4) through Eq. (3.1.10) to simplify, and result is

$${\mathfrak{U}}_{{2}_{5}}\left(x, t\right)=\Psi \left\{\frac{{C}_{2}}{{C}_{1}+{C}_{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)}\right\}+\frac{\Omega }{4\Psi }\left\{{\frac{{C}_{2}}{{C}_{1}+{C}_{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)}}\right\}^{-1},$$
(4.2.10)

where \(\Omega, \mathrm{ and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\omega\) are conformable coefficient, let \(\alpha =\beta =\frac{1}{2}\).

Segment 4

Attain the solutions for the following traveling wave by replacement Eq. (4.2.5) into Eq. (4.2.4) and Eq. (3.1.11) (consider \({C}_{2}=0\) but \({C}_{1}\ne 0\) \(;{C}_{2}\ne 0\) but\({C}_{1}=0\)):

$${\mathfrak{U}}_{{2}_{6}}\left(x, t\right)=\left[\sqrt{\Delta }\mathrm{coth}\left\{\frac{\sqrt{\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{\Omega }{4\Psi }{\left[\frac{\sqrt{\Delta }}{\Psi }\mathrm{coth}\left\{\frac{\sqrt{\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.2.11)
$${\mathfrak{U}}_{{2}_{6}}\left(x, t\right)=\left[\sqrt{\Delta }\mathrm{tanh}\left\{\frac{\sqrt{\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{\Omega }{4\Psi }{\left[\frac{\sqrt{\Delta }}{\Psi }\mathrm{tanh}\left\{\frac{\sqrt{\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.2.12)

where \(\Omega, \mathrm{ and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\omega\) conformable coefficient, let \(\alpha =\beta =\frac{1}{2}\).

Segment 5

In order to simplify the given answers, Eq. (4.2.5) can be substituted to Eq. (4.2.4), with Eq. (3.1.12), (consider \({C}_{2}=0\) but \({C}_{1}\ne 0\) \(;{C}_{2}\ne 0\) but\({C}_{1}=0\)):

$${\mathfrak{U}}_{{2}_{8}}\left(x, t\right)=\left[\sqrt{-\Delta }\mathrm{cot}\left\{\frac{\sqrt{-\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]+\frac{\Omega }{4\Psi }{\left[\frac{\sqrt{-\Delta }}{\Psi }\mathrm{cot}\left\{\frac{\sqrt{-\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.2.14)
$${\mathfrak{U}}_{{2}_{9}}\left(x, t\right)=-\left[\sqrt{-\Delta }\mathrm{tan}\left\{\frac{\sqrt{-\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right] -\frac{\Omega }{4\Psi }{\left[\frac{\sqrt{-\Delta }}{\Psi }\mathrm{tan}\left\{\frac{\sqrt{-\Delta }}{2}\left(x+\omega \frac{{t}^{\alpha }}{\alpha }\right)\right\}\right]}^{-1},$$
(4.2.15)

where \(\Omega ,\mathrm{and} \, \Psi =\mathcal{A}-\mathcal{C}\) are using as free parameters, also \(\omega\) are conformable coefficient, let \(\alpha = \beta =\frac{1}{2}\).

5 Physical explanation

Utilizing fractional order derivatives and dynamical changes in the parameters, the graphical clarification and physical explanation of the exact traveling wave solutions for the three kinds of sketches using Mathematica for the given equations will be discussed in this part.

The 3D plotline is represented as a planar or curved surface using a three-dimensional cartesian coordinate system, as seen in (a). A curve linking the points where the formula (function) belongs equal value was also a function of the two-variable contour line, as shown in (b). Finally, by using the vector plot shown in (c), we may determine a waves direction. The plots describe a change of natures, like kink shape wave, singular-kink shape, single-soliton shape wave, double soliton shape, singular soliton wave shape, periodic soliton wave shape and few more types, which are made by choosing the right parameters and giving a physical explanation.

The diagrams below show many structures, together with the renowned solitons shape, such as the solutions of \({\mathfrak{U}}_{{1}_{7}}(x, t)\) (\(0<x<10\) to \(0<t<10\)) in Fig. 1 presented the kink shape solution of traveling wave that both sides have infinite wings. In this circumstance, we utilize \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=1 \mathrm{and}\Psi =1\) that remainders in Cluster-4. The result \({\mathfrak{U}}_{{1}_{9}}(x, t)\) (\(0<x<10\) to \(0<t<10\)) for (4.1.14) depicted similar figure to the Cluster-5. Kink waves are asymptotic waves that change asymptotic states in an upward or downward direction. The kink solution comes close to becoming a constant at infinity. For the time FG equations, those traveling wave solutions exist.

Fig. 1
figure 1

The solution of (4.1.12), display kink shape wave for \({\mathfrak{U}}_{{1}_{7}}(x, t)\) to (\(0<x<10\) and \(0<t<10\))

Full size image

The solution of \({\mathfrak{U}}_{{1}_{2}}(x, t) (0<x<60\) to \(0<t<150\)) showed a singular-kink shape wave result, depicted in Fig. 2 and \({\mathfrak{U}}_{{1}_{1}}(x, t)\) (\(0<x<60\) to \(0<t<340\)) for (4.1.6) depicted familiar figure for \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=1 \mathrm{and}\Psi =1\) that is in Cluster-1, also The result of \({\mathfrak{U}}_{{1}_{5}}(x, t) (0<x<10\) to \(0<t<10\)) presented same shape wave solution, depicted in Fig. 4 for Cluster-3 by \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=-1 \mathrm{and}\Psi =1\). In Fig. 3, we showed periodic-type singular-kink shape wave for \({\mathfrak{U}}_{{1}_{4}}(x, t)\) (\(0<x<12\) to \(0<t<12\)) for Cluster-2 by \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=-1 \mathrm{and}\Psi =1\). For time FG equations, those traveling wave solutions exist (Figs. 4 and 5).

Fig. 2
figure 2

Illustration of the solution (4.1.7), represented singular-kink shape wave for \({\mathfrak{U}}_{{1}_{2}}(x, t)\) to (\(0<x<60\) and \(0<t<150\))

Full size image
Fig. 3
figure 3

The solution of (4.1.9), shows the periodic-type singular-kink shape wave for \({\mathfrak{U}}_{{1}_{4}}(x, t)\) to (\(0<x<12\) and \(0<t<12\))

Full size image
Fig. 4
figure 4

The Illustration of the result (4.1.10), shows singular-kink shape wave for \({\mathfrak{U}}_{{1}_{5}}(x, t)\) to (\(0<x<10\) and \(0<t<10\))

Full size image
Fig. 5
figure 5

The image of the solution (4.2.7), represented double soliton shape wave with \({\mathfrak{U}}_{{2}_{2}}(x, t)\) to the duration (\(0<x<2900\) and \(0<t<3000\))

Full size image

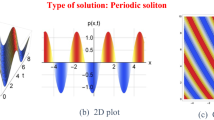
The profile of the solution \({\mathfrak{U}}_{{2}_{8}}(x, t)\) (\(0<x<20\) to \(0<t<0.80\)) showed a periodic solitary wave solution, presented in Fig. 6, here \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=1\mathrm{ and}\Psi =1\) that is in Cluster-4. Impulsive systems, self-reinforcing systems, diffusion–reaction- advection systems, etc. all depend heavily on periodic traveling waves. The periodic results are periodic solutions of traveling wave. Periodic solutions can be found using the conventional wave equation \({\mathfrak{U}}_{tt}\) = \({\mathfrak{U}}_{xx}\).

Fig. 6
figure 6

The solution of (4.2.14), display the periodic shape wave for \({\mathfrak{U}}_{{2}_{8}}(x, t)\) to (\(0<x<50\) and \(0<t<20\))

Full size image

Now, Fig. 5 depicts the portrayal of double solitons shape wave result of \({\mathfrak{U}}_{{2}_{2}}(x, t)\) (\(0<x<2900\) to \(0<t<3000\)). Here, we usage \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=1\mathrm{ and}\Psi =1\) in this scenario, that is still in Cluster-1 represented to the result (4.2.7) and the result (4.2.6) is also given the double solitons shape wave result of \({\mathfrak{U}}_{{2}_{1}}(x, t)\) (\(0<x<1000\) to \(0<t<1000\)).

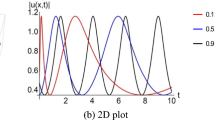
In addition, the depiction of Fig. 7 reveals the single-soliton shape wave for \({\mathfrak{U}}_{{2}_{9}}(x, t)\) (\(0<x<70\) to \(0<t<20\)) for Cluster-05 were as long as in the illustration of the result (4.2.14) here, we make use of \(\mathcal{A}=2, \mathcal{C}=1\), \(\mathcal{E}=-1 \mathrm{and}\Psi =1\) for the time fractional STO equations. The wave solution of \({\mathfrak{U}}_{{1}_{3}}(x,t)\) (\(0<x<40\) to \(0<t<50\)) for Cluster-02 in (4.1.8), \({\mathfrak{U}}_{{1}_{6}}(x,t)\) (\(0<x<900\) to \(0<t<400\)) for Cluster-4 in (4.1.11) and \({\mathfrak{U}}_{{1}_{8}}(x,t)\) (\(0<x<100\) to \(0<t<100\)) for Cluster-5 in (4.1.13) are also epitomized familiar traveling wave solution for the time FG equation. It is essential to inform that the solutions of wave \({\mathfrak{U}}_{{2}_{3}}(x,t)\) (\(0<x<0.10\) to \(0<t<0.40\)), \({\mathfrak{U}}_{{2}_{4}}(x,t)\) (\(0<x<0.10\) to \(0<t<2\)), \({\mathfrak{U}}_{{2}_{6}}(x,t)\) (\(0<x<1500\) to \(0<t<1500\)) and \({\mathfrak{U}}_{{2}_{7}}(x,t)\) (\(0<x<1300\) to \(0<t<3100\)) were showed the familiar figure with respectively (4.2.8), (4.2.9), (4.2.11) and (4.2.12) to time fractional STO equation.

Fig. 7
figure 7

The solution of (4.2.15), display the single-soliton shape wave for \({\mathfrak{U}}_{{2}_{9}}(x, t)\) to (\(0<x<70\) and \(0<t<20\))

Full size image

Solitons are special category of solitary wave. Solitary waves explain wave dynamics in diffraction and dissipative materials using evolution equations of nonlinear type by solutions like soliton. Solitons explain multiple-soliton solutions while solitons designate single-soliton solutions (Wazwaz 2009). At last, it is noteworthy to say that the wave results for \({\mathfrak{U}}_{{2}_{5}}(x,t)\) in Cluster-3 were undefined to time fractional STO equations.

The graphics to the suggested equations solution are established here. We express the many forms of images generated applying those mentioned equations while avoiding equal shape that intersections through the displayed image also.

6 Results comparison

This part demonstrates the novelty and effectiveness of our research. As a result of our investigation, we found that the obtained solutions have a substantial association with the ones that have already been created. In order to solve the aforementioned equations and obtain certain proven results, prior researchers used a number of techniques. The new generalized \(({G}^{\prime}/G)\)-expansion approach is applied to the aforementioned equations using the confirmable derivative, and we find numerous effective results that are both more general and fresher than those of the previous researchers.

In the beginning, the novelty of the space–time fractional Gardner equation is discussed. This problem was also studied by Zaman et al. (2023) and Korpinar et al. (2020). We compared their established solutions to our acquired solutions, which are shown in the picture below:

figure a

The solutions (4.1.7) and (4.1.12) in the aforementioned picture were shown to be comparable to the solutions (4.1.31) of Zaman et al. (2023), which are denoted by the blue tone. The suggested equation offers different results than those derived by Korpinar et al. (2020), which are shown by zero symbol in black box. It is also remarkable to note that some of our successful ideas are entirely original, highlighting our originality and displaying them in a green tone.

Additionally, we contrasted our findings from the space–time fractional STO equation with those from He et al. (2013) and Gómez (2015), which are depicted in the picture below:

figure b

According to the aforementioned graph, solutions (4.2.6) and (4.2.7) were comparable to solutions (23) of He et al. (2013), which were highlighted in blue. The red-colored solutions and (4.2.12) are equivalent to solutions (2.4.6) of Gómez (2015). Also, we can state that we have a few wholly original answers, which we labeled novel solutions and highlighted in green.

In the section on physical explanation, we depict Figs. 1, 2, 5, and 7, which are similar to the previously published results. Furthermore, Figs. 1, 2, 3, 4, 6 and 7 provided new solutions from previously established solutions. As a result, it is clear that we have some completely unique solutions, which we can refer to as novel solutions.

7 Conclusion

We have developed a large number of complete, advanced general solitary solutions of the wave to the time FG equation and fractional STO equations utilizing reliable generalized \(({G}^{\prime}/G)\)-expansion techniques using conformable derivative were presented in this study. We have generated closed-form solutions to the recommended equations, together with singular-kink wave shaped, periodic solitary formed, kink-shaped, periodic-type singular-kink shape, double soliton shaped, single-soliton formed, and some undefine soliton formed of travelling wave solutions with a change of free parameters. These flexible parameters have significant insinuations, for example the possibility to discovery specific results by changing the values of free parameter a single solution. The accuracy of the data obtained in this study was confirmed by converting them back to NLFPDEs and using the computational software Maple to find them. Visual representations of solitary wave behaviors in space and time are already made, proving the reliability and trustworthiness of the suggested methodologies. The attain solutions can be applying to the study of phase separation, optics, plasma physics, two-phase fluid flows, non-linear vibration, thermal science, analysis of image, nanofluids, fluid dynamics, mathematical biology, quantum physics, motion by mean curvature, and many other. The ability to fully comprehend the nonlinear water wave theory solutions that engineers and coastal researchers employ to construct harbors and coastlines is quite beneficial. So that, the approved technique is trustworthy, direct, effective, conformable, also it affords many solutions for the fresh physical model of NLFPDEs that developed in physical mathematics, applied mathematics, and engineering.