1 Introduction

The generalisation of conventional differentiation and integration to fractional order is fractional calculus. The fractional-order modelling provides a more well-grounded behaviour of the problem than the integer-order modelling. Over the past decades, fractional calculus had been broadly applied to quantum mechanics, plasma physics, fibre optics, quantum electronics, aerodynamics, ocean science, fluid dynamics and mathematical physics. A broad class of fractional models do not have analytical solutions. Hence, it is important to find the closed-form solutions of fractional models. With the advancement of symbolic computational packages, now it is possible to solve higher-order nonlinear fractional differential equations [1].

Several approaches are available in the literature to find exact solutions of these models, including the Hirota bilinear method [2] and ansatz approaches. The ansatz approaches such as first integral method [3,4,5], (\(G/G'\))-expansion method [6, 7], projective Ricatti and Ricatti–Bernoulli sub-ODE method [8, 9], extended trial equation method [10], the ansatz method [11], sub-equation method [12], sine-Gordon expansion method [13,14,15] and Hirota bilinear method [16,17,18,19,20] are successfully used to extract the exact solution of nonlinear differential equations. Among these methods, the ansatz approach, the exp\((- \Phi ( \varepsilon ))\)-expansion method which can be used to obtain a variety of exact solutions including hyperbolic, periodic and rational solutions, have attracted the interest of the researchers because of its ease and applicability. The exp(\(- \Phi ( \varepsilon ))\)-expansion approach had been used successfully to extract various solitary wave solutions of scalar (single-component) and vector (multicomponent/coupled) models and fractional models. By using the exp(\(- \Phi ( \varepsilon ))\)-expansion approach, the optical soliton of the coupled Lakshmanan–Porsezian–Daniel model is obtained in [21], the travelling wave solutions of the conformable time-fractional resonant nonlinear Schrödinger equation with Kerr law and parabolic nonlinearity is obtained in [22]; the solitary wave solutions of Gerdjikov–Ivanov equation is obtained in [23], and the travelling wave solutions of the time-fractional Boussinesq equation is obtained in [24]. Also, the solitary wave solution of the well-known Benjamin–Ono equation using exp(\(- \Phi ( \varepsilon ))\)-expansion approach is obtained in [25].

In this article, we consider the conformable time-fractional Gardner equation:

$$\begin{aligned} \dfrac{\partial ^ \alpha u}{\partial t ^ \alpha } + 6 u ( 1-u) \dfrac{\partial u}{\partial x} + \dfrac{\partial ^ 3 u}{\partial x ^ 3 } = 0, \quad 0 < \alpha \le 1 \end{aligned}$$
(1)

and conformable time-fractional Benjamin–Ono equation:

$$\begin{aligned}&\dfrac{\partial ^{2 \alpha }u(x,t)}{\partial t ^{2 \alpha } } + 2 \left( \dfrac{\partial u}{\partial x} \right) ^2 + 2 u \dfrac{\partial ^2 u}{\partial x^2 } \nonumber \\&\quad + \dfrac{\partial ^4 u(x,t)}{\partial x^4 } =0 , \quad 0 < \alpha \le 1 . \end{aligned}$$
(2)

The Gardner equation or the combined KdV and modified KdV equation describes numerous wave phenomena in plasma, hydrodynamics, solid-state and internal waves [26, 27]. The Benjamin–Ono equation describes many physical phenomena such as internal waves in deep water, percolation of water in the porous subsurface of horizontal layers, long internal gravity waves in deep stratified fluids [28,29,30,31] etc.

The \((G' / G, 1 / G)\) and \((1 / G')\)-expansion methods are utilised to solve Gardner equation arising in physical plasmas in [26], and the travelling wave solution of the time-fractional Gardner equation in the sense of Riemann–Liouville fractional derivative concerning Jacobi elliptic functions is extracted in [27]. The exact solutions of several other family of KdV equations are extracted in [32,33,34,35,36,37].

The one-dimensional internal waves in deep water are modelled using the Benjamin–Ono equation [28, 29]. Recently, the rogue wave and interaction solutions of the Benjamin–Ono equation is obtained in [30], and the (\(2+1\))-dimensional generalisation of the Benjamin–Ono equation is studied in [31], and several soliton solutions are extracted.

The main contribution of this paper are summarised as follows:

  • In this work, we have formulated the time-fractional Gardner and Benjamin–Ono equations in the conformable sense.

  • We obtained the exact solution of these two nonlinear partial fractional differential equations in polynomials of exp\((- \Phi ( \varepsilon ))\).

  • The obtained solutions are structured in hyperbolic, periodic and rational functions.

  • The investigation of symmetry analysis, nonlinear self-adjointness and conservation laws for the governing equations is done.

The article is organised in the following manner: Section 2 illustrates the conformable fractional derivative. In §3, the exp\( (- \Phi ( \varepsilon ))\)-expansion method is presented. In §4, exp\( (- \Phi ( \varepsilon ))\)-expansion method is utilised to find exact solutions of the time-fractional Gardner and Benjamin–Ono equations. In §5, symmetry analysis, nonlinear self-adjointness and conservation laws for the time-fractional Gardner and Benjamin–Ono equation are discussed and the conclusion is given at the end of the article.

2 Conformable fractional derivative

Many successful attempts have been made to define derivative and integral of fractional order, such as Riemann–Liouville, Caputo, Riesz, Gränwald–Letnikov [38,39,40], Atanngana–Baleanu [41], Caputo–Fabrizio [42] etc. Among many different definitions of fractional derivatives and integrals, Caputo and Riemann–Liouville are the much accepted definitions. It is well known that every fractional derivative has some drawbacks. Somewhere they challenge the physical significance of the models of fractional order because of their failures at fundamental properties of calculus such as chain rule and Leibnitz rule and many more. In [43], two examples are presented showing that Jumari’s Riemann–Liouville derivative does not satisfy the product and chain rules. Also, the drawback of the Caputo derivative is that the differentiation of the function is pre-assumed. An interesting article “What is fractional derivative?” provides a fascinating picture of fractional derivative, what criteria underlying the formulation of operator capable of being as fractional operator [44].

These operators have singular kernel, and the obtained solutions have tedious structure. Sometimes with these operators, it is tough to find the solutions also. To overthrow these drawbacks, a new explanation to fractional derivative and fractional integral, which is well behaved and obeying classical properties of known derivative named conformable fractional derivative and conformable fractional integral is proposed in [45].

DEFINITION 1

[45, 46]

Let \(f: (0, \infty ) \rightarrow \mathbb {R}\), then the conformable fractional derivative of function f of order \(\alpha \) of is defined as

$$\begin{aligned} (T_\alpha f)( t) = \lim \limits _{\varepsilon \rightarrow 0} \dfrac{f(t+ \varepsilon t ^{(1- \alpha )})- f(t)}{\varepsilon }, \quad 0< \alpha < 1, \end{aligned}$$

for all \(t > 0\).

Conformable derivatives enjoy the following properties:

  1. 1.

    Linearity:

    $$\begin{aligned}&T_\alpha ( a f_1 + b f_2 ) = a (T_\alpha f_1 ) + b(T_ \alpha f_2 ) \end{aligned}$$

    for all \(a,b \in \mathbb {R}\).

  2. 2.

    Leibniz rule:

    $$\begin{aligned}&T_\alpha (f_1 f_2) = f_1 T _ \alpha (f_2) + f_2 T_ \alpha (f_1). \end{aligned}$$
  3. 3.

    Quotient rule:

    $$\begin{aligned}&T _\alpha \left( \dfrac{f_1}{f_2} \right) = \dfrac{f_2 T_ \alpha (f_1) - f_1 T_ \alpha (f_2) }{f_2 ^2}, \end{aligned}$$

    If f is differentiable, then

    $$\begin{aligned} T_\alpha (f) (t) = t ^{1- \alpha } \left( \dfrac{\mathrm {d}f}{\mathrm {d}t} \right) . \end{aligned}$$

    Also \(T_\alpha ( t^r) = r t ^{r- \alpha }, \, r \in \mathbb {R}\), \( T_\alpha (K)=0\), where K is constant function.

  4. 4.

    Let \(f_1\) be an \(\alpha \)-conformable differentiable function \((0< \alpha < 1)\) and \(f_2\) be a derivable in the range of \(f_1\), then

    $$\begin{aligned}&T_\alpha (f_1\circ f_2)(t) = t ^{1-\alpha } f_2'(t) f_1'(f_2(t)). \end{aligned}$$

DEFINITION 2

[47]

For \(n=\lceil \alpha \rceil \), where \(\lceil \cdot \rceil \) is a ceiling function, the conformable time-fractional derivative of order \(\alpha \) of u(x, t) is defined as

$$\begin{aligned}&u^{\alpha }_{t} (x,t) =\frac{\partial ^ \alpha u(x,t)}{\partial t ^\alpha }\\&\quad = \lim \limits _{\varepsilon \rightarrow 0} \dfrac{u^{n-1}_{t} (x,t+ \varepsilon t ^{(n- \alpha )})- u^{n-1}_{t} (x,t)}{\varepsilon }, \quad t > 0.\, \end{aligned}$$

Clearly, by using the above definition, one can get

$$\begin{aligned} \frac{\partial ^ \alpha u(x,t)}{\partial t ^\alpha }= t^{n-\alpha } \frac{\partial ^ n u(x,t)}{\partial t ^n}. \end{aligned}$$

3 The exp\( (- \Phi ( \varepsilon ))\)-expansion method

In this section, we have outlined the exp\( (- \Phi ( \varepsilon )) \)-expansion approach for conformable time-fractional equations. Consider a fractional differential equation with time conformable derivatives [22]:

$$\begin{aligned} G(u, D_t^\alpha u, u_x , D_t^{2\alpha } u , u_{xx}, \ldots ) = 0 , \quad 0 < \alpha \le 1. \end{aligned}$$
(3)

To achieve the exact solution of eq. (3), we have used the wave transformation \(u(x,t) = g(\varepsilon )\), where \(\varepsilon = x -l (t^\alpha / \alpha ) \), l is a constant to be determined later. By this transformation, eq. (3) is converted into a nonlinear ordinary differential equation.

$$\begin{aligned} H(g,g',g'', \ldots ) = 0, \end{aligned}$$
(4)

where prime shows derivative with respect to \(\varepsilon \).

By the \(\exp (- \Phi (\varepsilon ))\) approach, the exact solution of eq. (4) is of the given form:

$$\begin{aligned} g(\varepsilon ) = \sum \limits _{n=0} ^{N} a_n (\exp ( - \Phi (\varepsilon )))^n, \end{aligned}$$
(5)

where \(a_n (a_n \ne 0) \) are the solution parameters which are to be found. \(\Phi (\varepsilon )\) satisfies the auxiliary equation given below:

$$\begin{aligned} \Phi ' (\varepsilon ) = \exp ( - \Phi (\varepsilon )) + \Theta \exp ( \Phi (\varepsilon )) + \Lambda . \end{aligned}$$
(6)

The above equation (eq. (6)) has different solution structures for the constraints over \(\Lambda \) and \(\Theta \), given in Cases I–V.

Case I: Hyperbolic function solution

When \(\Lambda ^2 - 4 \Theta > 0\) and \(\Theta \ne 0\)

$$\begin{aligned} \Phi _1 ( \varepsilon ) = \ln \left( \dfrac{{-} \sqrt{\Lambda ^2 {-} 4 \Theta } \tanh \left( \frac{\sqrt{\Lambda ^2 - 4 \Theta }}{2} (\varepsilon {+} c) \right) {-} \Lambda }{ 2 \Theta } \right) . \end{aligned}$$
(7)

Case II: Periodic solution

When \(\Lambda ^2 - 4 \Theta <0\) and \(\Theta \ne 0\)

$$\begin{aligned} \Phi _2 ( \varepsilon ) = \mathrm {ln} \left( \dfrac{\sqrt{4 \Theta - \Lambda ^2 } \tan \left( \frac{\sqrt{4 \Theta - \Lambda ^2 }}{2} (\varepsilon {+} c) \right) - \Lambda }{ 2\mu } \right) . \end{aligned}$$
(8)

Case III: Hyperbolic function solution

When \(\Lambda ^2 - 4 \Theta >0, \Theta =0\) and \(\Lambda \ne 0\),

$$\begin{aligned} \Phi _3(\varepsilon ) = - \mathrm {ln} \left( \dfrac{\Lambda }{ \cosh ( \Lambda (\varepsilon +c)) + \sin (h ( \varepsilon + c)) -1 }\right) . \end{aligned}$$
(9)

Case IV: Rational function solution

When \(\Lambda ^2 - 4 \Theta =0, \Theta \ne 0\) and \(\Lambda \ne 0\),

$$\begin{aligned} \Phi _4 ( \varepsilon ) = \mathrm {ln} \left( - \dfrac{2 ( \Lambda ( \varepsilon +c) +2) }{\Lambda ^2 (\varepsilon +c)} \right) . \end{aligned}$$
(10)

Case V: When \(\Lambda ^2 - 4 \Theta =0, \Theta =0\) and \(\Lambda =0\),

$$\begin{aligned} \Phi _5 (\varepsilon ) = \mathrm {ln} ( \varepsilon + c). \end{aligned}$$
(11)

Here c is the constant of integration. We follow Note 1 given below, to evaluate N.

Substituting eq. (5) into eq. (4), a polynomial in \((\exp (- \Phi (\varepsilon ))\) is obtained. After that, on collecting all coefficients of \((\exp ( - \Phi ( \varepsilon ) ) ^n, \, (n=0,1,2, \ldots )\), and equating to zero yields a system of algebraic equation in \(a_0, a_1, a_2, \ldots , l , \Lambda \) and \(\Theta \). Solving these equations, we get a variety of parameters of the exact solutions of eq. (3).

Note 1

We define the degree of \(g(\varepsilon )\) as \(D(g(\varepsilon ))=N\), and degree of derivatives of \(g(\varepsilon )\) turns out to be \(D[g^{(r)}]= N+r\), \(D[g^m (g^{(r)})^s ] = Nm + (r+N)s\). By balancing the highest-order derivative terms and the nonlinear terms, we can find N. This is also known as homogeneous balance principle.

Note 2

For \(N=2\), the values of derivatives of \(g(\varepsilon ), g'(\varepsilon )\) and \(g''(\varepsilon )\) are given below:

$$\begin{aligned} g'(\varepsilon )&= a_1 ( - \exp ( - 2 \Phi (\varepsilon )) - \Lambda \exp (- \Phi (\varepsilon ))-\Theta ) \\&\quad + 2 a_2 ( -\exp (- 3 \Phi (\varepsilon )) - \Lambda \exp (-2 \Phi (\varepsilon )) \\&\quad + l \exp (- \Phi (\varepsilon ))), \\ g''(\varepsilon )&= a_1 ( 2 \exp ( -3 \Phi (\varepsilon )) +( \Lambda ^2 + 2 \Theta ) \exp (- \Phi (\varepsilon )) \\&\quad + 3 \Lambda \exp ( -2 \Phi (\varepsilon )) + \Lambda \Theta ) \\&\quad + a_2 ( 6 \exp (-4 \Phi (\varepsilon )) + 10 \Lambda \exp ( - 3 \Phi (\varepsilon )) \\&\quad + 6 \Lambda \Theta \exp ( - \Phi (\varepsilon )) \\&\quad + ( 4 \Lambda ^2 + 8 \Theta ) \exp (-2 \Phi (\varepsilon ))) + 2 \Theta ^2 ). \end{aligned}$$

4 Solution of the time-fractional Gardner and Benjamin–Ono equations

In this section, a variety of exact travelling solutions of the time-fractional Gardner and Benjamin–Ono equations are extracted by applying the \(\exp ( - \Phi (\varepsilon ))\)-expansion method.

4.1 Time-fractional Gardner equation

By using wave transformation \(u(x,t)=g(\varepsilon ) \), where \(\varepsilon = x - l \left( {t^\alpha }/{\alpha } \right) \) to time-fractional Gardner equation (eq. (1)), we obtain an ordinary differential equation.

The Gardner equation is:

$$\begin{aligned} \dfrac{\partial ^ \alpha u}{\partial t ^ \alpha } + 6 u ( 1-u) \dfrac{\partial u}{\partial x} + \dfrac{\partial ^ 3 u}{\partial x ^ 3 } = 0, \quad 0 < \alpha \le 1. \end{aligned}$$
(12)

The transformation \(\varepsilon = x - l \left( {t^\alpha }/{\alpha } \right) \) converts eq. (12) into an ODE as

$$\begin{aligned} -lg' + 6 gg' -6g^2g' + g''' =0. \end{aligned}$$
(13)

Integrating eq. (13) and setting zero to the integration constant, we have

$$\begin{aligned} -lg + 3g^2 - 2g^3 + g'' =0. \end{aligned}$$
(14)

Now balancing \(g''\) and \(g^3\), we get \(N=1\). Hence the solution is of the following form:

$$\begin{aligned} g(\varepsilon ) = a_0 + a_1 \exp ( - \Phi ( \varepsilon )). \end{aligned}$$
(15)

By substituting \(g(\varepsilon )\) and \(g''(\varepsilon )\) in eq. (14), equating to zero, the coefficients of \((\exp (-\Phi (\varepsilon )))^n\), \(n=0,1,2,3\), we found the following nonlinear system of equations:

$$\begin{aligned}&a_1 \Lambda \Theta - 2a _0 ^3 + 3 a_0 ^2 - la_0 =0, \\&a_1 (\Lambda ^2 + 2 \Theta ) - 6 a_0 ^2 a_1 + 6 a_0 a_1 - la_1 =0, \\&3 \Lambda a_1 - 6 a_0 a_1 ^2 + 3a_1^2 =0, \\&2a_1 - 2a_1^3 =0. \end{aligned}$$

Solving this system of nonlinear equations, we obtain the following set of solutions:

Case I

$$\begin{aligned} a_0 = \dfrac{1+ \Lambda }{2}, \quad a_1=1, \quad l= \dfrac{3-\Lambda ^2+4\Theta }{2}. \end{aligned}$$

Substituting the above parameters, the nonlinear conformable time-fractional Gardner equation have travelling waves, periodic and rational waves as follows:

$$\begin{aligned} u_1(x,t)&= \left( \dfrac{1+\Lambda }{2} \right) + \dfrac{2 \Theta }{- \sqrt{\Lambda ^2 - 4 \Theta } \tanh \left( \frac{\sqrt{\Lambda ^2 - 4 \Theta }}{2} \left( x - \frac{1}{2} (3- \Lambda ^2 + 4 \Theta ) \frac{t^\alpha }{\alpha } +c\right) \right) - \Lambda } ,\\&\quad \Lambda ^2 - 4 \Theta>0, \Theta \ne 0, \\ u_2(x,t)&= \left( \dfrac{1+\Lambda }{2} \right) +\dfrac{\Lambda }{\cosh \left( \Lambda \left( x- \frac{1}{2} (3 - \Lambda ^2) \frac{t^\alpha }{\alpha }+c\right) \right) + \sinh \left( \Lambda \left( x- \frac{1}{2} (3 - \Lambda ^2) \frac{t^\alpha }{\alpha }+c \right) \right) -1 } ,\\&\quad \Lambda ^2 - 4 \Theta >0, \Theta =0, \Lambda \ne 0, \\ u_3(x,t)&= \left( \dfrac{1+\Lambda }{2} \right) + \dfrac{2 \Theta }{\sqrt{ 4 \Theta - \Lambda ^2 } \tan \left( \frac{\sqrt{4 \Theta - \Lambda ^2 }}{2} \left( x - \frac{1}{2} (3- \Lambda ^2 + 4 \Theta ) \frac{t^\alpha }{\alpha } +c\right) \right) - \Lambda },\\&\quad \Lambda ^2 - 4 \Theta <0, \Theta \ne 0, \end{aligned}$$
$$\begin{aligned} u_4 (x,t)&= \left( \dfrac{1+ \Lambda }{2} \right) - \dfrac{\Lambda ^2 \left( x- \left( \frac{3}{2} \right) \frac{t^\alpha }{\alpha } +c \right) }{2 \Lambda \left( x - \left( \frac{3}{2} \right) \frac{t^\alpha }{\alpha }+c\right) + 4 },\\&\quad \Lambda ^2 -4 \Theta =0, \Theta \ne 0 , \Lambda \ne 0, \\ u_5 (x,t)&= \dfrac{1}{2} + \dfrac{1 }{ \left( x - \left( \frac{3}{2} \right) \frac{t^\alpha }{\alpha }+c\right) },\\&\quad \Lambda ^2 -4 \Theta =0, \Theta = 0 , \Lambda = 0. \end{aligned}$$

Case II

$$\begin{aligned} a_0 = \dfrac{1 + \Lambda }{2}, \quad a_1=1, \quad l= \dfrac{2+3\Lambda -\Lambda ^3+4\Lambda \Theta }{2+2\Lambda }. \end{aligned}$$

For the above set of values, the obtained solution has singularity at \(\Lambda =-1\). Hence, we discard this set of solutions.

Fig. 1
figure 1

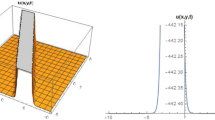
Physical features for \(u_1(x, t)\), \( u_2(x, t)\) and \( u_3(x, t)\). (a) 3D travelling wave picture of the solution \(u_1(x,t)\) of eq. (1) for \(\alpha =0.45\), \(\Theta =1\), \(C=3.5\), \(\Lambda =3\), (b) 3D travelling wave picture of the solution \(u_2(x,t)\) of eq. (1) for \(\alpha =0.45\), \(\Theta =1\), \(C=3.5\), \(\Lambda =3\) and (c) 2D periodic wave picture of the solution \(u_3(x,1)\) of eq. (1) for \(\alpha =0.75\), \(\Theta =2\), \(C=4\), \(\Lambda =1\).

Full size image

The nature of travelling waves satisfying the Gardner equation (eq. (1)) is shown in figures 1a–1c using 3D and 2D graphics. The travelling wave solutions \(u_1(x,t), u_2(x,t)\) and \(u_3(x,1)\) of eq. (1) are simulated for various values of physical parameters. The travelling wave solutions of eq. (1) are provided in figures 1a and 1b. Figures 1a and 1b show the 3D pictures for \(u_1(x,t)\) and \(u_2(x,t)\) for \(\Theta =1\), \(\Lambda =3\), \(c=3.5\), \(\alpha =0.45\). The 2D picture of the periodic wave solution \(u_3(x,t)\) of eq. (1) for \(\Theta =2\), \(\Lambda =1\), \(c=4\), \(\alpha =0.75\) is given in figure 1c for \(0\le x\le 40\) at \(t=1.\)

4.2 Time-fractional Benjamin–Ono equation

By using the wave transformation \(u(x,t)=g(\varepsilon ), \varepsilon =x - l(t^\alpha / \alpha ) \), to the time-fractional Benjamin–Ono equation (eq. (2)), we obtain an ordinary differential equation. The nonlinear time-fractional Benjamin–Ono equation is

$$\begin{aligned}&\dfrac{\partial ^{2 \alpha }u(x,t)}{\partial t ^{2 \alpha } } + 2 \left( \dfrac{\partial u}{\partial x} \right) ^2 + 2 u \dfrac{\partial ^2 u}{\partial x^2 } \nonumber \\&\quad + \dfrac{\partial ^4 u(x,t)}{\partial x^4 } =0 , \quad 0 < \alpha \le 1. \end{aligned}$$
(16)

The transformation \(\varepsilon =x - l(t^\alpha / \alpha ) \) converts the above equation into an ODE as

$$\begin{aligned} l^2 g'' + (2 g')^2 + 2gg'' + g'''' =0. \end{aligned}$$
(17)

Integrating eq. (17) twice and setting zero to the constant of integration, we have

$$\begin{aligned} g'' + g^2 + l^2 g=0. \end{aligned}$$
(18)

Balancing \(g''\) and \(g^2\), we get \(N=2\). Hence, the solution takes the form

$$\begin{aligned} g(\varepsilon ) = a_0 + a_1 \exp (-\Phi (\varepsilon ) ) + a_2 \exp (-2 \Phi (\varepsilon )). \end{aligned}$$
(19)

By substituting eq. (19) in eq. (18) and equating to zero, the coefficients of \((\exp (-\Phi (\varepsilon )))^n\), \(n=0,1,2,3,4\), we found the following nonlinear system of equations:

$$\begin{aligned}&l^2 a_0 + a_0^2 + 2 \Theta ^2 a_2 + \Lambda \Theta a_1 =0, \\&(\Lambda ^2 + 2 \Theta )a _1 + 6 \Lambda \Theta a_2 + 2 a_0 a_1 + l^2 a_1 = 0, \\&3 \Lambda a_1 + ( 4 \Lambda ^2 +8 \Theta ) a_2 + a_1 ^2 + 2 a_0 a_2 + l^2 a_2 = 0, \\&2a_1 + 10 \Lambda a_2 + 2 a_1 a_2 =0, \\&6 a_2 + a_2 ^2 =0. \end{aligned}$$

After solving this system, we have:

Case I

$$\begin{aligned}&a_0 = - \Lambda ^2 - 2 \Theta , \quad a_1 = - 6 \Lambda , \\&a_2= -6, \, l = \pm \sqrt{ \Lambda ^2 - 4 \Theta }. \end{aligned}$$

Through the above values of the parameters, the nonlinear conformable time-fractional Benjamin–Ono equation has the travelling wave solution, periodic solution as follows:

$$\begin{aligned} u_{1,2} (x,t)&= (- \Lambda ^2 -2 \Theta ) - \dfrac{12 \Theta \Lambda }{- \sqrt{\Lambda ^2 - 4 \Theta } \tanh \left( \frac{\sqrt{\Lambda ^2 - 4 \Theta }}{2} \left( x \mp \sqrt{\Lambda ^2 - 4 \Theta } \frac{t^\alpha }{\alpha } + c \right) \right) -\Lambda } \\&\quad - \dfrac{ 24 \Theta ^2 }{ \left( - \sqrt{\Lambda ^2 - 4 \Theta } \tanh \left( \frac{\sqrt{\Lambda ^2 - 4 \Theta }}{2} \left( x \mp \sqrt{\Lambda ^2 - 4 \Theta } \frac{t ^ \alpha }{\alpha } + c \right) \right) - \Lambda \right) ^2}, \\&\quad \Lambda ^2 - 4 \Theta>0, \Theta \ne 0 ,\\ u_{3,4}(x,t)&= - \Lambda ^2 - \dfrac{6 \Lambda ^2}{\cosh \left( \Lambda \left( x \mp \Lambda \frac{t ^ \alpha }{\alpha } +c \right) \right) + \sinh \left( \Lambda \left( x \mp \Lambda \frac{t ^ \alpha }{\alpha } +c \right) \right) -1 } \\&\quad - \dfrac{6 \Lambda ^2}{\left( \cosh \left( \Lambda \left( x \mp \Lambda \frac{t ^ \alpha }{\alpha } +c \right) \right) + \sinh \left( \Lambda \left( x \mp \Lambda \frac{t ^ \alpha }{\alpha } +c \right) \right) -1 \right) ^2 }, \\&\quad \Lambda ^2 - 4 \Theta >0, \Theta =0, \Lambda \ne 0,\\ u_{5,6} (x,t)&= ( -\Lambda ^2 - 2 \Theta ) - \dfrac{12 \Lambda \Theta }{\sqrt{4 \Theta - \Lambda ^2 } \tan \left( \frac{\sqrt{4 \Theta - \Lambda ^2}}{2} \left( x \mp \sqrt{\Lambda ^2 - 4 \Theta } \frac{t ^ \alpha }{\alpha } + c \right) \right) - \Lambda } \\&\quad - \dfrac{24 \Theta ^2}{\left( \sqrt{4 \Theta - \Lambda ^2 } \tan \left( \frac{\sqrt{4 \Theta - \Lambda ^2}}{2} \left( x \mp \sqrt{\Lambda ^2 - 4 \Theta } \frac{t ^ \alpha }{\alpha } + c \right) \right) - \Lambda \right) ^2},\\&\qquad \quad \qquad \Lambda ^2 - 4 \Theta <0, \Theta \ne 0. \end{aligned}$$

Case II

$$\begin{aligned} a_0 = - 6 \Theta , \ a_1 = - 6 \Lambda , \ a_2 =-6, \ l = \pm \sqrt{4 \Theta -\Lambda ^2 }. \end{aligned}$$

Through the above obtained parameters, the nonlinear conformable time-fractional Benjamin–Ono equation has travelling wave and periodic solutions as follows:

$$\begin{aligned}&u_{7,8} (x,t) = (- 6 \Theta ) - \dfrac{12 \Theta \Lambda }{- \sqrt{\Lambda ^2 - 4 \Theta } \tanh \left( \frac{\sqrt{\Lambda ^2 - 4 \Theta }}{2} \left( x \mp \sqrt{4 \Theta - \Lambda ^2 } \frac{t^\alpha }{\alpha } + c \right) \right) -\Lambda } \\&\quad - \dfrac{ 24 \Theta ^2 }{ \left( - \sqrt{\Lambda ^2 - 4 \Theta } \tanh \left( \frac{\sqrt{\Lambda ^2 - 4 \Theta }}{2} \left( x \mp \sqrt{4 \Theta - \Lambda ^2 } \frac{t ^ \alpha }{\alpha } + c \right) \right) - \Lambda \right) ^2}, \\&\qquad \Lambda ^2 - 4 \Theta>0, \Theta \ne 0 ,\\&u_{9,10}(x,t) = - \dfrac{6 \Lambda ^2}{\cosh \left( \Lambda \left( x \mp \sqrt{-\Lambda ^2} \frac{t ^ \alpha }{\alpha } +c \right) \right) + \sinh \left( \Lambda \left( x \mp \sqrt{-\Lambda ^2} \frac{t ^ \alpha }{\alpha } +c \right) \right) -1 } \\&\quad - \dfrac{6}{(\cosh \left( \Lambda \left( x \mp \sqrt{-\Lambda ^2} \frac{t ^ \alpha }{\alpha } +c \right) \right) + \sinh \left( \Lambda \left( x \mp \sqrt{-\Lambda ^2} \frac{t ^ \alpha }{\alpha } +c \right) \right) -1)^2 }, \\&\qquad \Lambda ^2 - 4 \Theta >0, \Theta =0, \Lambda \ne 0, \\ \end{aligned}$$
$$\begin{aligned} u_{11,12} (x,t)&= (-6 \Theta ) \\&\quad - \dfrac{12 \Lambda \Theta }{\sqrt{4 \Theta - \Lambda ^2 } \tan \left( \frac{\sqrt{4 \Theta - \Lambda ^2}}{2} \left( x \mp \sqrt{4 \Theta - \Lambda ^2 } \frac{t ^ \alpha }{\alpha } + c \right) \right) - \Lambda } \\&\quad - \dfrac{24 \Theta ^2}{\left( \sqrt{4 \Theta - \Lambda ^2 } \tan \left( \frac{\sqrt{4 \Theta - \Lambda ^2}}{2} \left( x \mp \sqrt{4 \Theta - \Lambda ^2 } \frac{t ^ \alpha }{\alpha } + c \right) \right) - \Lambda \right) ^2}, \\&\qquad \Lambda ^2 - 4 \Theta <0, \Theta \ne 0. \end{aligned}$$

For different parameters, the travelling wave solutions of eq. (2) are simulated in figures 2–4. The travelling wave solution of eq. (2) is given in figures 2a and 2b. The obtained solution \(u_1(x,t)\) and its 3D picture are given in figure 2a for \(\Theta =1\), \(\Lambda =3\), \(c=2\), \(\alpha =0.75\). For the same values of the physical parameters, the 2D picture is provided in figure 2b for \(0\le x\le 5\) at \(t=1\). The 3D picture of the established solution \(u_2(x,t)\) of eq. (2) for \(\Theta =1\), \(\Lambda =3\), \(c=2\), \(\alpha =0.75\) is given in figure 2c. The 2D picture of the same is provided in figure 3a for \(0\le x\le 5\) at \(t=1\). The periodic wave solutions of eq. (2) are given in figures 3b and 3c. 3D picture of the obtained periodic wave solution \(u_5(x,t)\) is pictured in figure 3b for \(\Theta =1\), \(\Lambda =1\), \(c=2\), \(\alpha =0.75\). The 2D picture for the same is given in figure 3c for \(0\le x\le 50\) at \(t=1\). 3D and 2D pictures of the obtained periodic wave solutions \(u_6(x,t)\) and \(u_6(x,1)\) are given in figures 4a–4c for \(\Theta =1\), \(\Lambda =3\), \(c=2\), \(\alpha =0.75\) for \(0\le x\le 50\). It is clear that 3D picture depicts the evolution of u for space and time variables, and 2D picture depicts the evolution of u and v in space for a fixed time \(t=1\). All calculations and graphics are implemented in Mathematica 11.3.

5 Symmetry analysis for the governing equations

This portion is dedicated to the investigation of symmetry analysis, nonlinear self-adjointness and conservation laws for eqs (12) and (16) [48,49,50,51,52,53,54]. The Lie point symmetries of eqs (12) and (16) are generated by a vector field of the form

$$\begin{aligned} \begin{aligned} \mathcal {X}=\xi _1(x,t,u)\frac{\partial }{\partial x}+\xi _2(x,t,u)\frac{\partial }{\partial t}+\eta (x,t,u)\frac{\partial }{\partial u}. \end{aligned} \end{aligned}$$
(20)

It can be shown by a well-established procedure that eqs (12) and (16) admit infinitesimals given below:

For (12) we have

$$\begin{aligned}&\xi _1(x,t,u)=\frac{1}{2}(1-2u)c_1,\, \nonumber \\&\xi _2(x,t,u) =xc_1+\frac{3t^\alpha c_1}{\alpha }+c_2,\,\nonumber \\&\eta (x,t,u)=t\left( \frac{3c_1}{\alpha }+t^{-\alpha }c_3\right) , \end{aligned}$$
(21)

where \(c_1, c_{2}, c_3\) are arbitrary constants. The associated algebra of the Lie point symmetries are given by

$$\begin{aligned} \begin{aligned} \mathcal {X}_1&=\frac{\partial }{\partial _x},\quad \mathcal {X}_2=t^{1-\alpha } \frac{\partial }{\partial _t}, \\ \mathcal {X}_3&=\frac{\partial }{\partial x} \left( \frac{6 t^{\alpha }}{\alpha }+2 x\right) +\left( \frac{6t}{\alpha } \frac{\partial }{\partial _t}+(1-2 u) \frac{\partial }{\partial _u}\right) . \end{aligned} \end{aligned}$$
(22)
Fig. 2
figure 2

Physical features for \(u_1(x,t)\) and \( u_2(x,t)\). (a) 3D travelling wave plot of the solution \(u_1(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =3\), (b) 2D travelling wave plot of the solution \(u_1(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =3\) and (c) 3D travelling wave plot of the solution \(u_2(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =3\).

Full size image
Fig. 3
figure 3

Physical features for \(u_2(x,t)\) and \(u_5(x,t)\). (a) 2D travelling wave plot of the solution \(u_2(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =3\), (b) 3D periodic wave plot of the solution \(u_5(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =1\) and (c) 2D periodic wave plot of the solution \(u_5(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =1\).

Full size image
Fig. 4
figure 4

Physical features for \(u_6(x,t)\). (a) 3D periodic wave plot of the solution \(u_6(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1.0\), \(C=2.0\), \(\Lambda =1.0\) and (b) 2D periodic wave plot of the solution \(u_6(x,t)\) of eq. (2) for \(\alpha =0.75\), \(\Theta =1\), \(C=2\), \(\Lambda =1\).

Full size image

For (16) we consider the following cases:

Case 1. When \(\alpha =\frac{1}{2}\), we have

$$\begin{aligned}&\xi _1(x,t,u) =c_1+\frac{xc_3}{2},\quad \xi _2(x,t,u)=c_2+tc_3,\nonumber \\&\eta (x,t,u) =-uc_3, \end{aligned}$$
(23)

where \(c_1, c_{2}, c_3\) are arbitrary constants. The associated algebra of the Lie point symmetries are given by

$$\begin{aligned} \mathcal {X}_1= & {} \frac{\partial }{\partial _x},\quad \mathcal {X}_2=\frac{\partial }{\partial _t},\nonumber \\ \mathcal {X}_3= & {} \left( (2 t) \frac{\partial }{\partial t}-(2 u) \frac{\partial }{\partial u}\right) +x \frac{\partial }{\partial x}. \end{aligned}$$
(24)

Case 2. When \(\alpha ={1}/{3}\), we have

$$\begin{aligned} \xi _1(x,t,u)=c_1,\quad \xi _2(x,t,u)=c_2,\quad \eta (x,t,u)=0, \end{aligned}$$
(25)

where \(c_1, c_{2}\) are arbitrary constants. The associated algebras of the Lie point symmetries are given by

$$\begin{aligned} \mathcal {X}_1=\frac{\partial }{\partial _x},\quad \mathcal {X}_2=\frac{\partial }{\partial _t}. \end{aligned}$$
(26)

Case 3. When \(\alpha ={2}/{3}\), we have

$$\begin{aligned}&\xi _1(x,t,u) =c_1+\frac{xc_2}{2}, \quad \xi _2(x,t,u)=tc_2,\nonumber \\&\eta (x,t,u) =-uc_2, \end{aligned}$$
(27)

where \(c_1, c_{2}\) are arbitrary constants. The associated algebras of the Lie point symmetries are given by

$$\begin{aligned} \mathcal {X}_1=\frac{\partial }{\partial _x},\quad \mathcal {X}_2=\left( (2 t) \frac{\partial }{\partial _t}-(2 u) \frac{\partial }{\partial _u}\right) +x \frac{\partial }{\partial _x}. \end{aligned}$$
(28)

5.1 Adjoint system and conditions for nonlinear self-adjointness

In this portion, we provide informations on the adjoint system and the condition for nonlinear self-adjointness. Consider the following theorem.

Theorem 1

A symmetry such as Lie point, Lie–Bäcklund and nonlocal symmetry given by

$$\begin{aligned} \mathcal {X}=\xi _i\frac{\partial }{\partial \bar{x}^i}+\eta _{\bar{\alpha }} \frac{\partial }{\partial \bar{u}^{\bar{\alpha }}}, \end{aligned}$$
(29)

for nonlinear partial differential equations

$$\begin{aligned} F_{\bar{\alpha }}(\bar{x},u,\ldots ,u_s)=0,\quad \bar{\alpha }=1,2,\ldots ,\bar{m}, \end{aligned}$$
(30)

with m dependent variables will have an adjoint equation

$$\begin{aligned} \mathcal {F}^*_{\bar{\alpha }}(\bar{x},u,\ldots ,u_s)=\frac{\delta (v^{\bar{\beta }}\mathcal {F}_{\bar{\beta }})}{\delta u^{\bar{\alpha }}},\,\,\bar{\alpha }=1,2,\ldots ,\bar{m} \end{aligned}$$
(31)

and Lagrangian given by

$$\begin{aligned} \mathcal {L}=Z^{\bar{\beta }}\mathcal {F}_{\bar{\beta }}(\bar{x},u,u_{(1)},\ldots ,u_{(s)}), \end{aligned}$$
(32)

with \(Z=Z(\bar{x},t)\) depicting a non-local dependent variables.

Considering eqs (12) and (16), the formal Lagrangian can be given by

$$\begin{aligned} \mathcal {L}_1= & {} \upsilon _1 (x,t) (6 u_{x} (1-u(x,t))u(x,t)\nonumber \\&+t^{1-\alpha } u_{t}+u_{xxx}),\nonumber \\ \mathcal {L}_2= & {} \upsilon _2 (x,t) (2 u_{xx} u(x,t)\nonumber \\&+(1-\alpha )(1-2 \alpha ) t^{1-3 \alpha } u_{t}\nonumber \\&+3 (1-\alpha ) u_{tt}+2 u_{x}^2+u_{xxxx}), \end{aligned}$$
(33)

where \(\upsilon _1\), \(\upsilon _2\) are new-dependent variables called the non-local variables for (12) and (16), respectively. The adjoint system can be obtained using

$$\begin{aligned} \mathcal {F}^*_1=\frac{\delta \mathcal {L}}{\delta p}=0,\,\quad \mathcal {F}^*_2=\frac{\delta \mathcal {L}}{\delta u}=0, \end{aligned}$$
(34)

where

$$\begin{aligned} \frac{\delta \mathcal {L}_1}{\delta u}= & {} \frac{\partial \mathcal {L}_1}{\partial u}-D_t\frac{\partial \mathcal {L}_1}{\partial u_t}-D_x\frac{\partial \mathcal {L}_1}{\partial u_x}+(D_x)^2\frac{\partial \mathcal {L}_1}{\partial u_{xx}}\nonumber \\&-(D_{xxx})^3\frac{\partial \mathcal {L}_1}{\partial u_{xxx}}, \nonumber \\ \frac{\delta \mathcal {L}_2}{\delta u}= & {} \frac{\partial \mathcal {L}_2}{\partial u}-D_t\frac{\partial \mathcal {L}_2}{\partial u_t}-D_x\frac{\partial \mathcal {L}_2}{\partial u_x}+(D_x)^2\frac{\partial \mathcal {L}_2}{\partial u_{xx}} \nonumber \\&-(D_{xxx})^3\frac{\partial \mathcal {L}_2}{\partial u_{xxx}}+(D_x)^4\frac{\partial \mathcal {L}_2}{\partial u_{xxxx}}. \end{aligned}$$
(35)

On the basis of Lagrangian reported in (33), one can get the adjoint system as

$$\begin{aligned} \mathcal {F}^*_1&=t^{-\alpha } ((\alpha -1) \upsilon (x,t) \nonumber \\&\quad + t^{\alpha } (6 \upsilon _{x} u(x,t)^2\!-\!6 \upsilon _{x} u(x,t)\!-\!\upsilon _{xxx})\!-\!t \upsilon _{t})\!=\!0,\nonumber \\ \mathcal {F}^*_2&=(6 \alpha ^3-11 \alpha ^2+6 \alpha -1) t^{-3 \alpha } \upsilon (x,t)\nonumber \\&\quad +2 \upsilon _{xx} u(x,t) -(2 \alpha ^2-3 \alpha +1) t^{1-3 \alpha } \upsilon _{t}\nonumber \\&\quad -3 (\alpha -1) \upsilon _{tt}+\upsilon _{xxxx}=0. \end{aligned}$$
(36)

DEFINITION 3

Equations (12) and (16) are nonlinear self-adjointness on the conditions of adjoint system if it satisfies

$$\begin{aligned} \mathcal {F}^*_1|_{z=Z(x,t,u)}=\Lambda _1 \mathcal {F}_1&=0, \nonumber \\ \mathcal {F}^*_2|_{z=Z(x,t,u)}=\Lambda _2 \mathcal {F}_2&=0 \end{aligned}$$
(37)

such that not all \(z=Z(x,t,u)\) are zero and \(\Lambda _i(i=1,2,\dots )\) are undetermined coefficients.

Therefore, from the coefficient of \(u_x, u_{xx}, u_t, u_{xxx}\), we attain

$$\begin{aligned} \Lambda _1=-Z_u,\quad \Lambda _2=-R_u. \end{aligned}$$
(38)

Substituting these into (37), we obtain a huge system of linear PDEs. Solving the system using SYM package [17], we obtain

$$\begin{aligned} H=t^{\alpha -1} \left( \mathbf {c}_2+\mathbf {c}_1 u\right) ,\quad R=xF_2(t)+F_1(t). \end{aligned}$$
(39)

Hence, eqs (12) and (16) are nonlinear self-adjointness. This property will give us the liberty to construct conservation laws for eqs (12) and (16) in the subsequent subsection.

5.2 Conservation laws

In this section, we establish the conservation laws of eqs (12) and (16). We recall the following theorem:

Theorem 2

System (30) with symmetry reported in (29) satisfies the conservation equation

$$\begin{aligned} D_i(C^i)|_{(30)=0}=0, \end{aligned}$$
(40)

where

$$\begin{aligned} C^i&=\xi _i \mathcal {L}+W^{\bar{\alpha }}\Bigg [\frac{\partial \mathcal {L}}{\partial u^{\bar{\alpha }}_{i}}-D_j\left( \frac{\partial \mathcal {L}}{\partial u^{\bar{\alpha }}_{ij}}\right) \nonumber \\&\quad +D_jD_k\left( \frac{\partial \mathcal {L}}{\partial u^{\bar{\alpha }}_{ijk}}\right) -\cdots \Bigg ] \nonumber \\&\quad + D_j\left( W^{\bar{\alpha }}\right) \Bigg [\frac{\partial \mathcal {L}}{\partial u^{\bar{\alpha }}_{ij}}-D_k\left( \frac{\partial \mathcal {L}}{\partial u^{\bar{\alpha }}_{ijk}}\right) +\cdots \Bigg ] \nonumber \\&\quad +D_jD_k\left( W^{\bar{\alpha }}\right) \Bigg [\frac{\partial \mathcal {L}}{\partial u^{\bar{\alpha }}_{ijk}}+\cdots \Bigg ] \end{aligned}$$
(41)

and \(W^{\bar{\alpha }}=\eta _{\bar{\alpha }}-\xi _{j}u^{\bar{\alpha }}_j\). The expression \(C^i\) represents the conserved vectors.

In accordance with (2) and the nonlinear self-adjoint substitution, we compute the conservation laws of eqs (12) and (16), using the obtained point symmetries:

For (12) we obtain

  1. (i)

    The symmetry \(\mathcal {X}_1=\partial _x\) admits the conserved vectors

    $$\begin{aligned}&C^x_1=u_{t} (A_1 u+A_2), \nonumber \\&C^t_1=u_{x} (-(A_1 u+A_2)). \end{aligned}$$
    (42)
  2. (ii)

    The symmetry \(\mathcal {X}_2=t^{1-\alpha }\partial _t\) admits the conserved vectors

    $$\begin{aligned} C^x_2&=(A_1 u+A_2) \nonumber \\&\quad \times \left( 6 u_{t} (u(x,t)-1) u(x,t)-u_{xxt}\right) ,\nonumber \\ C^t_2&=(A_1 u+A_2)) \nonumber \\&\quad \times \left( u_{xxx}-6 u_{x} (u(x,t)-1) u(x,t)\right) . \end{aligned}$$
    (43)
  3. (iii)

    The symmetry

    $$\begin{aligned} \mathcal {X}_3= & {} \frac{\partial }{\partial x} \left( \frac{6 t^{\alpha }}{\alpha }+2x \right) \\&+\left( \frac{6t}{\alpha } \frac{\partial }{\partial _t}+(1-2 u) \frac{\partial }{\partial _u}\right) \end{aligned}$$

    admits the conserved vectors

    $$\begin{aligned} C^x_3&=\frac{1}{t\alpha }2(A_1 u+A_2)\nonumber \\&\quad \times (3 t^{\alpha } (-3 u(x,t)^2(\alpha -2 t u_{t})\nonumber \\&\quad +u(x,t) (\alpha -6 t u_{t})+2 \alpha u(x,t)^3 \nonumber \\&\quad -t u_{xxt}+t u_{t}-\alpha u_{xx}) + \alpha t x u_{t}), \nonumber \\ C^t_3&=\frac{1}{\alpha }(A_1 u+A_2) \nonumber \\&\quad \times (-6 t^{\alpha }(u_{x} (6 (u(x,t)-1) u(x,t)+1)\nonumber \\&\quad -u_{xxx}) -2 \alpha (u(x,t)+x u_{x})+\alpha ). \end{aligned}$$
    (44)

For (16) we obtain

Case 1. For \(\alpha ={1}/{2}\),

  1. (i)

    The symmetry \(\mathcal {X}_1=\partial _x\) admits the conserved vectors

    $$\begin{aligned} C^x_1= & {} 2F_2(t) u_{x} u(x,t) \nonumber \\&+(\alpha -1) t^{-3 \alpha } ((2 \alpha -1) t u_{t} \nonumber \\&-3 t^{3 \alpha } u_{tt}) (F_1(t)\nonumber \\&+x F_2(t))+F_2(t) u_{xxx},\nonumber \\ C^t_1= & {} (\alpha -1) ((F_1(t)\nonumber \\&+xF_2(t)) ((t-2 \alpha t) t^{-3 \alpha } u_{x}\nonumber \\&+3 u_{xt})-3 u_{x} (F_1'+x F_2')). \end{aligned}$$
    (45)
  2. (ii)

    The symmetry \(\mathcal {X}_2=\partial _t\) admits the conserved vectors

    $$\begin{aligned} C^x_2= & {} -u_{t} (2 u_{x} (F_1(t)+xF_2(t))\nonumber \\&-2F_2(t)u(x,t)) \nonumber \\&-2 u(x,t) u_{xt} (F_1(t)+x F_2(t))\nonumber \\&-u_{xxxt} (F_1(t)+x F_2(t))+F_2(t) u_{xxt}, \nonumber \\ C^t_2= & {} (F_1(t)+x F_2(t)) \nonumber \\&\times (2 u_{xx} u(x,t)+2 u_{x}^2+u_{xxxx})\nonumber \\&-3 (\alpha -1) u_{t} (F_1'+x F_2'). \end{aligned}$$
    (46)
  3. (iii)

    The symmetry

    $$\begin{aligned} \mathcal {X}_3=(2 t) \frac{\partial }{\partial t}-(2 u) \frac{\partial }{\partial u}+x\partial _x \end{aligned}$$

    admits the conserved vectors

    $$\begin{aligned} C^x_3&=x (F_1(t) +x F_2(t)) (2 u_{xx} u(x,t)+(\alpha -1)\nonumber \\&\quad \times (2 \alpha -1) t^{1-3 \alpha } u_{t}-3 (\alpha -1) u_{tt}\nonumber \\&\quad +2u_{x}^2+u_{xxxx})\nonumber \\&\quad +(2 u(x,t)+2 t u_{t}+x u_{x}) (2F_2(t) u(x,t)\nonumber \\&\quad -2 u_{x} (F_1(t)+xF_2(t)))\nonumber \\&\quad -2 u(x,t) (2 t u_{xt}+3 u_{x}+x u_{xx}) \nonumber \\&\quad \times (F_1(t)+x F_2(t))-(2 t u_{xxxt}+5 u_{xxx}\nonumber \\&\quad +x u_{xxxx})(F_1(t)+x F_2(t)) +F_2(t)\nonumber \\&\quad \times (2 t u_{xxt}+4 u_{xx}+x u_{xxx}), \nonumber \\ C^t_3&=-(\alpha -1) t^{-3 \alpha } (2 u(x,t)+2 t u_{t}+x u_{x})\nonumber \\&\quad \times (3 t^{3 \alpha } (F_1'+x F_2')+(2 \alpha -1) t (F_1(t)\nonumber \\&\quad +xF_2(t)))+2 t (F_1(t)+x F_2(t)) \nonumber \\&\quad \times (2 u_{xx} u(x,t)+(\alpha -1) (2 \alpha -1) t^{1-3 \alpha } u_{t} \nonumber \\&\quad -3 (\alpha -1) u_{tt}+2 u_{x}^2+u_{xxxx})\nonumber \\&\quad +3 (\alpha -1) (x u_{xt}+4 u_{t}+2 t u_{tt}) (F_1(t)\nonumber \\&\quad +x F_2(t)). \end{aligned}$$
    (47)

Case 2. For \(\alpha ={1}/{3}\),

  1. (i)

    The symmetry \(\mathcal {X}_1=\partial _x\) admits the conserved vectors

    $$\begin{aligned} C^x_1&=2F_2(t) u_{x} u(x,t) \nonumber \\&\quad +(\alpha -1) t^{-3 \alpha } ((2 \alpha -1) t u_{t} \nonumber \\&\quad -3 t^{3 \alpha } u_{tt}) (F_1(t)+x F_2(t))\nonumber \\&\quad +F_2(t) u_{xxx}, \nonumber \\ C^t_1&=(\alpha -1) ((F_1(t)\nonumber \\&\quad +xF_2(t)) ((t-2 \alpha t) t^{-3 \alpha } u_{x} \nonumber \\&\quad +3 u_{xt})-3 u_{x} (F_1'+x F_2')). \end{aligned}$$
    (48)
  2. (ii)

    The symmetry \(\mathcal {X}_2=\partial _t\) admits the conserved vectors

    $$\begin{aligned} C^x_2&= -u_{t} (2 u_{x} (F_1(t)+xF_2(t))\nonumber \\&\quad -2F_2(t) u(x,t))-2 u(x,t) u_{xt} (F_1(t)\nonumber \\&\quad +x F_2(t)) -u_{xxxt} (F_1(t)\nonumber \\&\quad +xF_2(t))+F_2(t) u_{xxt},\nonumber \\ C^t_2&=(F_1(t)+x F_2(t)) \nonumber \\&\quad \times (2 u_{xx} u(x,t)+2 u_{x}^2+u_{xxxx})\nonumber \\&\quad -3 (\alpha -1) u_{t} (F_1'+xF_2'). \end{aligned}$$
    (49)

Case 3. For \(\alpha ={2}/{3}\),

  1. (i)

    The symmetry \(\mathcal {X}_1=\partial _x\) admits the conserved vectors

    $$\begin{aligned} C^x_1= & {} 2F_2(t) u_{x} u(x,t)\nonumber \\&+(\alpha -1) t^{-3 \alpha } ((2 \alpha -1) t u_{t}\nonumber \\&-3 t^{3 \alpha } u_{tt}) (F_1(t)\!+\!x F_2(t)) \!+\!F_2(t) u_{xxx},\nonumber \\ C^t_1= & {} (\alpha -1) ((F_1(t)\!+\!xF_2(t)) \nonumber \\&\times ((t-2 \alpha t) t^{-3 \alpha } u_{x}\nonumber \\&+3 u_{xt})\!-\!3 u_{x} (F_1'\!+\!x F_2')). \end{aligned}$$
    (50)
  2. (ii)

    The symmetry

    $$\begin{aligned} \mathcal {X}_2=(2 t) \frac{\partial }{\partial t}-(2 u) \frac{\partial }{\partial u}+x\partial _x \end{aligned}$$

    admits the conserved vectors

    $$\begin{aligned} C^x_2&=x (F_1(t)+x F_2(t)) (2 u_{xx} u(x,t)\nonumber \\&\quad +(\alpha -1) (2 \alpha -1) t^{1-3 \alpha } u_{t}\nonumber \\&\quad -3 (\alpha -1) u_{tt}+2 u_{x}^2+u_{xxxx})\nonumber \\&\quad +(2 u(x,t)+2 t u_{t}+x u_{x}) (2F_2(t) u(x,t)\nonumber \\&\quad -2 u_{x} (F_1(t)+xF_2(t)))-2 u(x,t)\nonumber \\&\quad \times (2 t u_{xt}+3 u_{x} +x u_{xx}) \nonumber \\&\quad \times (F_1(t)+x F_2(t))\nonumber \\&\quad -(2 t u_{xxxt}+5 u_{xxx} +x u_{xxxx})\nonumber \\&\quad \times (F_1(t)+x F_2(t))+F_2(t)\nonumber \\&\quad \times (2 t u_{xxt}+4 u_{xx}+x u_{xxx}) \nonumber \\ C^t_2&=-(\alpha -1) t^{-3 \alpha } (2 u(x,t)+2 t u_{t}+x u_{x}) \nonumber \\&\quad \times (3 t^{3 \alpha } (F_1'+x F_2')+(2 \alpha -1) t (F_1(t)\nonumber \\&\quad +xF_2(t)))+2 t (F_1(t)+x F_2(t))\nonumber \\&\quad \times (2 u_{xx} u(x,t)+(\alpha -1)(2 \alpha -1) t^{1-3 \alpha } u_{t} \nonumber \\&\quad -3 (\alpha -1) u_{tt}+2 u_{x}^2+u_{xxxx})\nonumber \\&\quad +3 (\alpha -1) (x u_{xt}+4 u_{t}+2 t u_{tt}) (F_1(t)\nonumber \\&\quad +x F_2(t)). \end{aligned}$$
    (51)

6 Conclusion

The time-fractional Gardner and Benjamin–Ono equations in the conformable sense are being discussed. The exp(\(- \Phi ( \varepsilon ))\)-expansion method is utilised for extracting exact solutions of the considered models. Several travelling wave solutions are obtained, and the achieved solutions are structured in terms of periodic, rational and hyperbolic functions. The obtained solutions critically depend on fractional-order \(\alpha \) of the models, and the arbitrary parameters of the obtained solutions can be used for controlling and manipulating the evolutionary dynamics of the models. Finally, the results confirm the reliability and applicability of the exp(\(-\Phi ( \varepsilon ))\)-expansion method for nonlinear partial fractional models. For the obtained solutions, 3D and 2D plots are provided in figures 1–4. Moreover, the symmetry analysis, nonlinear self-adjointness and conservation laws for the governing equations are also being discussed. The results obtained can be seen as potentially useful for application in mathematical physics, fluid dynamics, optics and engineering.