1 Introduction

The advent of fractional calculus had brought about a revolution in the research field by opening a new avenue of investigating analytical soliton solutions of the significant models. It is a wide branch of analysis, applied mathematics, and engineering that was initiated more than 300 years ago with a question, “Can the meaning of derivatives with integer order be generalized to derivatives with non-integer order?”. This question was queried by Leibniz to L’ Hospital in a correspondence between them in the seventeenth century. Any number (complex or real) may be taken into account as the order of differentiation in fractional nonlinear evolution equations (FNLEEs). As a result, numerous possible solutions are being resulted from any certain equation. FNLEEs are now used to model various constraints that occur in various scientific and technological fields, such as optics, fluid mechanics, control theory, bio-engineering, robotics, electrical engineering, and so on. Since its introduction, it has attracted diverse academics and has become a burning theme of research. So far, different academics have provided different definitions of fractional derivative, such as Riemann–Liouville (R–L) fractional derivative (FD) (Miller and Ross 1993), Conformable FD (Khalil et al. 2014), beta derivative (Atangana and Baleanu 2016), Caputo FD (Almeida 2017), etc. The newly defined beta fractional derivative is more reliable than the others, and that’s why the beta derivative has been taken into consideration in this article.

Kundu (1984) proposed a model describing the spread of ultra-short light pulse trough the dispersive medium such as optical fiber, ultrasonic devices, etc. which was named Kundu equation. The Kundu equation can be altered to nonlinear Schrödinger (NLS) equation and several integrable equations. Later, Eckhaus (1986) introduced a model which was obtained from the Kundu equation for the general case. This mathematical model is familiar as the nonlinear Kundu–Eckhaus (KE) equation. Another model known as Radhakrishnan–Kundu–Lakshmanan (RKL) was introduce by Radhakrishnan et al. (1999) from the Kundu equation. The time-fractional nonlinear Kundu–Eckhaus (KE) equation (Unal 2014) is of the form:

$$i D{}_{t}^{\beta }p+{p}_{xx}+{\left|p\right|}^{4}p+2{\left({\left|p\right|}^{2}\right)}_{x}p=0.$$
(1)

In Eq. (1), \(p=p(x,t)\) describes the wave function, \({D}_{t}^{\beta }p\) exhibits the fractional temporal evolution of the wave function, second term stands for the spacial dispersion, third and fourth term describe the nonlinear steeping.

However, looking into exact soliton solutions of FNLEEs is highly required with a view to understanding any phenomenon thoroughly. Solitary waves can travel a long distance with unaltered shape and constant intensity or energy. In optics, there are mainly three types of solitons such as bright, dark, and mixed bright-dark solitons. Bright solitons are seen in negative and anomalous group velocity dispersion (GVD) region in optical fiber whereas dark solitons occur in positive and normal GVD region. There are several well-functioned approaches to search out soliton solutions of the FNLPDEs. Several academics made their best attempt to develop a unique approach; yet, every technique has some particular drawbacks. Nevertheless, a good number of methods had been evolved like the sine–cosine method (Wazwaz 2004; Alquran 2012; Liang et al. 2022), the exp (\(-\phi (\xi )\))-expansion method (Rahman 2014; Arshed et al. 2018; Elboree 2021), the generalized Kudryashov method (Demiray and Bayrakci 2020), the extended tanh-function method (Fan 2000; Ni and Dai 2015), the modified extended tanh-function method (Elwakil et al. 2002; Zahran and Khater 2016; Alam et al. 2021), the improved modified extended tanh-function method (Yang and Hon 2006; Ahmed et al. 2022a), the sine–Gordon expansion scheme (Baskonus et al. 2019; Kundu et al. 2021; Mamun et al. 2022), the Jacobi elliptic function expansion method (Liu et al. 2001; Kumar et al. 2019; Ahmed et al. 2021), the \((G/G^{\prime})\)-expansion method (Bian et al. 2010; Aniqa and Ahmad 2022), the simple equation approach (Nofal 2016), the modified simple equation method (Jawad et al. 2010; Biswas et al. 2018), the improved \((G^{\prime}/G)\)-expansion method (Liu and Zeng 2015; Khater et al. 2021), the generalized \((G^{\prime}/G)\)-expansion method (Zhang et al. 2008), the auxiliary equation process (Akbulut and Kaplan 2018), the modified auxiliary equation technique (Mahak and Akram 2020; Akram et al. 2022), the \((G^{\prime}/G,1/G)\)-expansion method (Li et al. 2010; Miah et al. 2017; Duran 2021), the conformable Adomian decomposition method (Acan and Baleanu 2017), the modified variation iteration algorithm (Ahmed et al. 2022b), the generalized exponential rational function method (Ghanbari and Inc 2018), the \(({G}^{\prime}/{G}^{2})\)-expansion method (Bilal and Ahmad 2022; Bilal et al. 2022), and so on.

A straight-forward technique named the \(({G}^{\prime}/G)\)-expansion method was introduced by Wang et al. (2008) with a view to find out soliton solutions of nonlinear equations. In this method, trial solution is generated as \(q\left(\eta \right)=\sum_{j=0}^{n}{b}_{j}{\left({G}^{\prime}/G\right)}^{j}\) and \(G(\eta )\) satisfies the equation \({G}^{\prime\prime}+\gamma {G}^{\prime}+\delta G=0\), where \(\gamma \), \(\delta \), \({b}_{j}\) are arbitrary constants. Since the introduction of this approach, several researchers have made some modifications and improvements to this technique. As for example, extended \(({G}^{\prime}/G)\)-expansion method was suggested by Guo and Zhou (2010), where the trial solution has the form \(q\left(\eta \right)=\sum_{j=0}^{n}{b}_{j}{\left({G}^{\prime}/G\right)}^{j}+\sum_{j=1}^{n}{c}_{j}{\left({G}^{\prime}/G\right)}^{-j}\) and \(G(\eta )\) satisfies the same auxiliary equation as mentioned above. The improved \(({G}^{\prime}/G)\)-expansion method was presented by Zhang et al. (2010), where trial solution is generated in the form \(q\left(\eta \right)=\sum_{j=0}^{n}{b}_{j}{\left({G}^{\prime}/G\right)}^{j}\) and \(G(\eta )\) satisfies the equation \(G{G}^{\prime\prime}=L{G}^{2}+MG{G}^{\prime}+N{\left(G^{\prime}\right)}^{2}\). The generalized \(({G}^{\prime}/G)\)-expansion method was introduced by Zhang et al. (2008), where the trial solution is formulated in the form \(q\left(\eta \right)=\sum_{j=0}^{n}{b}_{j}{\left({G}^{\prime}/G\right)}^{j}\) and \(G(\eta )\) satisfies the equation \({\left(G^{\prime}\right)}^{2}=L+M{G}^{2}+N{G}^{4}/2\), the generalized and improved \(({G}^{\prime}/G)\)-expansion approach was offered by Akbar et al. (2012), where trial solution is expressed in the form \(q\left(\eta \right)=\sum_{j=-n}^{n}\frac{{c}_{-j}}{{\left(b+\left({G}^{\prime}/G\right)\right)}^{j}}\) and \(G(\eta )\) satisfies the subsidiary equation \({G}^{\prime\prime}+\gamma {G}^{\prime}+\delta G=0\), etc. The two variables (\({G}^{\prime}/G\),\(1/G\))-expansion method is one of the modifications of the \(({G}^{\prime}/G)\)-expansion method which was proposed and implemented to resolve the Zakharov equations by Li et al. (2010).

To search out the exact soliton solution of an equation, several techniques are taken into consideration by several academics. The concerned KE equation plays a significant role in nonlinear optical fibres communication. Many researchers have used several methods to visualize the soliton solutions of this equation like Smadi et al. (2020), Rezazadeh et al. (2019), Bekir and Zahran (2020), Kaplan (2021), Biswas et al. (2019), Manafian and Lakestani (2016), Ekici et al. (2016), and so on.

Since the Kundu–Eckhaus equation has yet not been studied using the \((G^{\prime}/G,1/G)\)-expansion approach, in this article, the new and wide-spectral soliton solutions of the stated equation are established using the above mentioned two variables \((G^{\prime}/G,1/G)\)-expansion method. Consequently, this article establishes several novel solutions that are comprised of hyperbolic, trigonometric, rational functions, and some arbitrary constants. In order to check the novelty of the solutions, the obtained solutions are compared with the existing results in the comparison section.

The structure of this article is organized as follows: In Sect. 2, the methodology of the stated approach has been described. Application of the method to the concerned equation is accomplished in Sect. 3. In Sect. 4, a comparison is made between the obtained results and previous results. Graphical visualization and description of the attained solitons have been presented in Sect. 5. In Sect. 6, we reach the conclusion.

2 Methodology

According to the procedure of the concerned method, a second order nonlinear equation in \(G(\eta )\) have to be resolved at first. The associated equation is

$${G}^{\prime\prime}\left(\eta \right)+\lambda G\left(\eta \right)=\mu .$$
(2)

We consider \(\varphi ={G}^{\prime}/G\), \(\chi =1/G\) and \(\lambda \), \(\mu \) are arbitrary constants.

In addition

$${\varphi }^{\prime}=-{\varphi }^{2}+\mu \chi -\lambda ,{\chi }^{\prime}=-\varphi \chi .$$
(3)

Now, there ascends three forms of general solution of Eq. (2) with the variation of the values of \(\lambda \).

When \(\lambda <0\): In this case, the general solution is comprised with hyperbolic functions as given below,

$$G\left(\eta \right)={n}_{1}\mathrm{sinh}\left(\sqrt{-\lambda } \eta \right)+{n}_{2}\mathrm{cosh}\left(\sqrt{-\lambda } \eta \right)+\frac{\mu }{\lambda }.$$
(4)

Together with

$${\chi }^{2}=-\frac{\lambda \left({\varphi }^{2}-2\mu \chi +\lambda \right)}{{\lambda }^{2}\gamma +{\upmu }^{2}}.$$
(5)

In Eq. (5), \(\gamma ={n}_{1}^{2}-{n}_{2}^{2}\) and \({n}_{1}, {n}_{2}\) are arbitrary parameters.

When \(\lambda >0\): In this case, the general solution is generated with the help of trigonometric functions as follows:

$$G\left(\eta \right)={n}_{1}\mathrm{sin}\left(\sqrt{\lambda } \eta \right)+{n}_{2}\mathrm{cos}\left(\sqrt{\lambda } \eta \right)+\frac{\mu }{\lambda }.$$
(6)

Along with

$${\chi }^{2}=\frac{\lambda \left({\varphi }^{2}-2\mu \chi +\lambda \right)}{{\lambda }^{2}\gamma -{\upmu }^{2}}.$$
(7)

Here, \(\gamma ={n}_{1}^{2}+{n}_{2}^{2}\) and \({n}_{1}, {n}_{2}\) are free parameters.

When \(\lambda =0\): In this case, the general solution contains rational functions as follows:

$$G\left(\eta \right)=\frac{\mu }{2}{\eta }^{2}+{n}_{1}\eta +{n}_{2}.$$
(8)
$$ {\text{Along with}}\,\,\,\chi^{2} = \frac{1}{{n_{1}^{2} - 2\mu n_{2} }}\left( {\varphi^{2} - 2\mu \chi } \right),\,\,n_{1} \,\,\,{\text{and}}\,\,n_{2} \,\,\,{\text{are arbitrary parameters}}. $$
(9)

Let us assume the equation which is to be solved contains the wave function \(p({x}_{1},{x}_{2},\ldots t)\) and its partial and fractional derivatives as given below:

$$L\left(p,p,{p}_{t},{p}_{{x}_{1}{x}_{2}},{p}_{t{x}_{1}},{p}_{tt},\ldots ,{D}_{t}^{\beta }p,{D}_{{x}_{1}}^{\beta }p,{D}_{tt}^{\beta \beta }p,{D}_{{x}_{1}{x}_{2}}^{\beta \beta }p,\ldots \right)=\mathrm{0,0}<\beta \le 1.$$
(10)

Here, \({D}_{t}^{\beta }p\), \({D}_{{x}_{1}}^{\beta }p\),… and \({p}_{t}\), \({p}_{{x}_{1}}\),… denote the fractional and partial derivatives of the wave function \(p\) with respect to spatial and temporal variables.

To look for the analytical exact soliton solution of the Eq. (10) through the mentioned method, the following steps have to be gone through.

1st step Direct approaches to investigating FNLEEs are rare. Equation (10) can be transformed using the beta wave transform into an ordinary differential equation:

$$p\left(t,{x}_{1},{x}_{2},\ldots \right)=r\left(\eta \right),$$

with

$$\eta =\frac{\nu }{\beta }{\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta }+\frac{{\tau }_{1}}{\beta }{\left({x}_{1}+\frac{1}{\Gamma \beta }\right)}^{\beta }+\frac{{\tau }_{2}}{\beta }{\left({x}_{2}+\frac{1}{\Gamma \beta }\right)}^{\beta }+\cdots .$$
(11)

Moreover, for complex equation, the transformation takes the form:

$$p\left(t,{x}_{1},{x}_{2},\ldots \right)=r(\eta ){e}^{i\omega }$$
(12)

with

$$\eta =\frac{v}{\beta }{\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta }+\frac{{\tau }_{1}}{\beta }{\left({x}_{1}+\frac{1}{\Gamma \beta }\right)}^{\beta }+\frac{{\tau }_{2}}{\beta }{\left({x}_{2}+\frac{1}{\Gamma \beta }\right)}^{\beta }+\cdots ,$$

and

$$\omega \left(t,{x}_{1},{x}_{2},\ldots \right)=\frac{\vartheta }{\beta }{\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta }+\frac{{\alpha }_{1}}{\beta }{\left({x}_{1}+\frac{1}{\Gamma \beta }\right)}^{\beta }+\frac{{\alpha }_{2}}{\beta }{\left({x}_{2}+\frac{1}{\Gamma \beta }\right)}^{\beta }+\cdots .$$

In these transformations, \(r(\eta )\) and \(\theta \left(t,{x}_{1},{x}_{2},\ldots \right)\) describe amplitude and the phase functions respectively. In addition, \(v\) is the velocity and \(\vartheta \) is the wave number. Here, \(v\), \(\vartheta \), \({\tau }_{1}\), \({\alpha }_{1}\), \(\ldots \) are arbitrary parameters which are to be ascertained.

By means of the above transformation, it leads to an ODE as follows:

$$U\left(r,{r}^{\prime},{r}^{\prime\prime},{r}^{\prime\prime\prime},\ldots \right)=0.$$
(13)

2nd step In consistent with the strategy of the mentioned method, the trial solution of Eq. (13) may be put forth in the subsequent form:

$$r\left(\eta \right)=\sum_{n=0}^{Z}{{h}_{n}\varphi }^{h}+\sum_{n=1}^{Z}{m}_{h}{\varphi }^{n-1}\chi ,\varphi ={G}^{\mathrm{^{\prime}}}/G,\chi =1/G.$$
(14)

In Eq. (14), \({m}_{n}\), \({h}_{n}\), and \(n\) are unknown constants which we are to be calculated. The value of \(n\) is resulted from the implication of the homogeneous principle of balance. If the outcome becomes negative or fractional, we will impose the subsequent formulae.

$$r\left(\eta \right)={w}^{n}\left(\eta \right).$$
(15)

Application of this transformation leads us to a new ODE which delivers a balanced variable with positive integer value.

3rd step Employing the trial solution from Eq. (14) in Eq. (13), a new polynomial, comprising \({\varphi }^{i}\), \({\chi }^{i}(i=\mathrm{0,1},\ldots z)\), their derivatives, and the arbitrary parameters \({m}_{n}\) and \({h}_{n}\), is generated. The derivatives of \(\varphi \), \(\chi \), and higher order of \(\chi \) is annihilated with the assistance of the values of \(\varphi ^{\prime}\), \(\chi ^{\prime}\), \({\chi }^{2}\). Furthermore, a system of algebraic equations is introduced by computing the components of \({\mathrm{\varphi }}^{j}{\chi }^{l}\) \(\left(j=\mathrm{0,1},\ldots z, l=\mathrm{0,1}\right)\) to zero.

4th step In conclusion, by solving the acquired equations, the required values of the arbitrary parameters \({m}_{n}\), \({h}_{n}\), \(v\), \(\vartheta \), \({\rho }_{1}\), \({\alpha }_{1}\), \(\ldots \), will be ascertained. Setting these attained values in trial solution, the desired soliton solutions will be formed.

3 Optical soliton solutions

Proceeding with the steps comprehended in methodology, governing Eq. (1) is alternated to a differential equation via the transformation:

$$p\left(x,t\right)=r\left(\eta \right){e}^{i\omega }.$$
(16)

Consequently, we attain

$$-\left({\tau }^{2}+\vartheta \right)r\left(\eta \right)+{r\left(\eta \right)}^{5}-i\left(v-2k\tau \right){r}^{\prime}\left(\eta \right)+4k{r\left(\eta \right)}^{2}{r}^{\prime}\left(\eta \right)+{k}^{2}{r}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\eta \right)=0.$$
(17)

Here, \(\eta =kx-\frac{v}{\beta }{\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta }\) and \(\omega =\tau x+\frac{\vartheta }{\beta }{\left(t+\frac{1}{\mathrm{\Gamma \beta }}\right)}^{\beta }.\)

Equating complex and real part of Eq. (17) to zero, the subsequent outcomes are offered.

$$v=2k\tau .$$
(18)
$$-\left({\tau }^{2}+\vartheta \right)r\left(\eta \right)+{r\left(\eta \right)}^{5}+4k{r\left(\eta \right)}^{2}{r}^{\prime}\left(\eta \right)+{k}^{2}{r}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\eta \right)=0.$$
(19)

Equation (18) provides the velocity of the wave function. However, Eq. (19) has been taken into consideration to be unraveled.

Therefore, from the homogeneous balancing principle it can be concluded that, \(+2=5n\) \(i.e.\), \(n=1/2\). The balanced value being fractional, we have to exert Eq. (15) in Eq. (19). Thus, it becomes

$$r\left(\eta \right)=\sqrt{w\left(\eta \right).}$$
(20)

Hence, Eq. (19) will be transformed to another equation in \(w(\eta )\) having the following form:

$$4{w(\eta )}^{4}-{k}^{2}{{w}^{\prime}\left(\eta \right)}^{2}-4{w\left(\eta \right)}^{2}\left({\tau }^{2}+\vartheta -2k{w}^{\prime}\left(\eta \right)\right)+2{k}^{2}w\left(\eta \right){w}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\eta \right)=0.$$
(21)

Equation (21) delivers the balanced value \(n=1\). Therefore, the trail solution of Eq. (21) is expressed as:

$$w\left(\eta \right)={h}_{0}+{h}_{1}\varphi \left(\eta \right)+{m}_{1}\chi \left(\eta \right).$$
(22)

Setting Eqs. (22) in (21) and proceeding with the steps depicted in methodology, several solutions have been acquired for the varied values of \(\lambda \).

For \(\lambda <0\) In this case, there are two sets of solutions, which have been expounded below:

Set 1 \({h}_{0}=\pm \frac{1}{2}k\sqrt{-\lambda }\), \({h}_{1}=\frac{k}{2}\), \({m}_{1}=0\), \(\mu =0\), \(\vartheta =-{\tau }^{2}-{k}^{2}\lambda \),\(v=2k\tau \).

Substitution of the above solution set in Eq. (22) provides

$$w\left(\eta \right)=\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{-\lambda }\{{n}_{1}\mathrm{cosh}\left(\sqrt{-\lambda }\eta \right)+{n}_{2}\mathrm{sinh}\left(\sqrt{-\lambda }\eta \right)\}}{2\{{n}_{1}\mathrm{sinh}\left(\eta \sqrt{-\lambda }\right)+{n}_{2}\mathrm{cosh}\left(\eta \sqrt{-\lambda }\right)\}}.$$

Thus, the required exact solution of Eq. (1), which is generated from Eq. (16), can be expressed as

$$p\left(x,t\right)={e}^{i\omega (x,t)}{\left\{\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{-\lambda }\left\{{n}_{1}\mathrm{cosh}\left(\sqrt{-\lambda }\eta \right)+{n}_{2}\mathrm{sinh}\left(\sqrt{-\lambda }\eta \right)\right\}}{2\left\{{n}_{1}\mathrm{sinh}\left(\eta \sqrt{-\lambda }\right)+{n}_{2}\mathrm{cosh}\left(\eta \sqrt{-\lambda }\right)\right\}}\right\}}^\frac{1}{2}.$$
(23)

Here, \(\omega \left(x,t\right)=\tau x+\frac{\left(-{\tau }^{2}-{k}^{2}\lambda \right){\left(t+\frac{1}{\Gamma \beta }\right)}^{\beta }}{\beta }\), \(\eta =kx-\frac{2k\tau {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\).

If we take \({n}_{1}=0\), solution (23) will be altered to

$$p\left(x,t\right)={e}^{i\omega (x,t)}\sqrt{\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{-\lambda }}{2}\mathrm{tanh}\left(\sqrt{-\lambda }\eta \right)}.$$
(24)

Similarly, for \({n}_{2}=0\), the solution (23) takes the form

$$p\left(x,t\right)={e}^{i\omega (x,t)}\sqrt{\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{-\lambda }}{2}\mathrm{coth}\left(\sqrt{-\lambda }\eta \right).}$$
(25)

Set 2 \({h}_{0}=\pm \frac{1}{4}k\sqrt{-\lambda }\), \({h}_{1}=\frac{k}{4}\), \({m}_{1}=\pm \frac{k\sqrt{({\mu }^{2}+{\lambda }^{2}\gamma )}}{4\sqrt{-\lambda }}\), \(\vartheta =\frac{1}{4}(-4{\tau }^{2}-{k}^{2}\lambda )\), \(v=2k\tau \).

Introducing the above-mentioned solution set 2 in Eq. (22), the acquisition solution is

$$w\left(\eta \right)=\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\sqrt{({\mu }^{2}+{\lambda }^{2}\gamma )}}{4\sqrt{-\lambda }\left(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sinh}(\eta \sqrt{-\lambda })+{n}_{2}\mathrm{cosh}(\eta \sqrt{-\lambda })\right)}+\frac{k\sqrt{-\lambda }({n}_{1}\mathrm{cosh}(\eta \sqrt{-\lambda })+{n}_{2}\mathrm{sinh}(\eta \sqrt{-\lambda }))}{4(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sinh}(\eta \sqrt{-\lambda })+{n}_{2}\mathrm{cosh}(\eta \sqrt{-\lambda }))}.$$

Therefore, Eq. (16) allowed us to develop the exact solution of Eq. (1) in the following form:

$$p\left(x,t\right)={e}^{i\omega \left(x,t\right)}{\left(\begin{array}{c}\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\sqrt{\left({\mu }^{2}+{\lambda }^{2}\gamma \right)}}{4\sqrt{-\lambda }\left(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sinh}\left(\eta \sqrt{-\lambda }\right)+{n}_{2}\mathrm{cosh}\left(\eta \sqrt{-\lambda }\right)\right)}\\ +\frac{k\sqrt{-\lambda }\left({n}_{1}\mathrm{cosh}\left(\eta \sqrt{-\lambda }\right)+{n}_{2}\mathrm{sinh}\left(\eta \sqrt{-\lambda }\right)\right)}{4\left(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sinh}\left(\eta \sqrt{-\lambda }\right)+{n}_{2}\mathrm{cosh}\left(\eta \sqrt{-\lambda }\right)\right)}\end{array}\right)}^\frac{1}{2},$$
(26)

with \(\omega \left(x,t\right)=\tau x+\frac{(-4{\tau }^{2}-{k}^{2}\lambda ){(t+\frac{1}{\Gamma \beta })}^{\beta }}{4\beta }\), \(\eta =kx-\frac{2k\tau {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\).

Here, \(k\), \(\tau \), \(\mu \) and \(\lambda \) are arbitrary parameters. If we impose zero value for \(\mu \) and \({n}_{1}\), solution (26) will be transformed into

$$p\left(x,t\right)={e}^{i\omega \left(x,t\right)}{\left(\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\lambda \sqrt{\gamma }}{4\sqrt{-\lambda }{n}_{2}}\mathrm{sech}(\eta \sqrt{-\lambda })+\frac{k\sqrt{-\lambda }}{4}\mathrm{tanh}(\eta \sqrt{-\lambda })\right)}^\frac{1}{2}.$$
(27)

Another form of solution (23) may be originated in the same way for \(\mu \), \({n}_{2}=0\):

$$p\left(x,t\right)={e}^{i\omega \left(x,t\right)}{\left(\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\lambda \sqrt{\gamma }}{4\sqrt{-\lambda }{n}_{1}}\mathrm{csch}(\eta \sqrt{-\lambda })+\frac{k\sqrt{-\lambda }}{4}\mathrm{coth}(\eta \sqrt{-\lambda })\right)}^\frac{1}{2}.$$
(28)

When \(\lambda >0\) For this condition, two different kinds of solution sets are attained which have been explained minutely in the subsequent context.

Set 1 \({h}_{0}=\pm \frac{1}{4}k\sqrt{-\lambda }\), \({h}_{1}=\frac{k}{4}\), \({m}_{1}=\pm \frac{k\sqrt{-{\mu }^{2}+{\lambda }^{2}\gamma }}{4\sqrt{\lambda }}\), \(\vartheta =\frac{1}{4}(-4{\tau }^{2}-{k}^{2}\lambda )\), \(v=2k\tau \).

Setting the values of parameters referred above, the pursuit result may be demonstrated from Eq. (22) as:

$$w\left(\eta \right)=\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\sqrt{-{\mu }^{2}+{\lambda }^{2}\gamma }}{4\sqrt{\lambda }(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sin}(\eta \sqrt{\lambda })+{n}_{2}\mathrm{cos}(\eta \sqrt{\lambda }))}+\frac{k\sqrt{\lambda }({n}_{1}\mathrm{cos}(\eta \sqrt{\lambda })-{n}_{2}\mathrm{sin}(\eta \sqrt{\lambda }))}{4(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sin}(\eta \sqrt{\lambda })+{n}_{2}\mathrm{cos}(\eta \sqrt{\lambda }))}.$$

Hence, the desired solution of Eq. (1) is derived as:

$$p\left(x,t\right)={e}^{i\omega }{\left\{\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\sqrt{-{\mu }^{2}+{\lambda }^{2}\gamma }}{4\sqrt{\lambda }\left(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)+{n}_{2}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)\right)}+\frac{k\sqrt{\lambda }\left({n}_{1}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)-{n}_{2}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)\right)}{4\left(\frac{\mu }{\lambda }+{n}_{1}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)+{n}_{2}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)\right)}\right\}}^{1/2},$$
(29)

together with \(\eta =kx-\frac{2k\tau {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \(\omega \left(x,t\right)=\tau x+\frac{(-4{\tau }^{2}-{k}^{2}\lambda ){(t+\frac{1}{\Gamma \beta })}^{\beta }}{4\beta }\).

By replacing \({n}_{1}\) and \(\mu \) with zero value, solution (29) can be written in the subsequent form:

$$p\left(x,t\right)={e}^{i\omega }{\left(\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\lambda \sqrt{\gamma }}{4\sqrt{\lambda }{\mathrm{n}}_{2}}\mathrm{sec}\left(\eta \sqrt{\lambda }\right)-\frac{k\sqrt{\lambda }}{4}\mathrm{tan}\left(\eta \sqrt{\lambda }\right)\right)}^\frac{1}{2}.$$
(30)

Similarly, the successive form of solution (29) can be attained for \({n}_{2}\), \(\mu =0\):

$$p\left(x,t\right)={e}^{i\omega }{\left(\pm \frac{1}{4}k\sqrt{-\lambda }\pm \frac{k\lambda \sqrt{\gamma }}{4\sqrt{\lambda }{\mathrm{n}}_{1}}\mathrm{csc}\left(\eta \sqrt{\lambda }\right)+\frac{k\sqrt{\lambda }}{4}\mathrm{cot}\left(\eta \sqrt{\lambda }\right)\right)}^\frac{1}{2}.$$
(31)

Set 2 \({h}_{0}=\pm \frac{1}{2}k\sqrt{-\lambda }\), \({h}_{1}=\frac{k}{2}\), \({m}_{1}=0\), \(\mu =0\), \(\vartheta =-{\tau }^{2}-{k}^{2}\lambda \), \(v=2k\tau \).

Substituting these values in Eq. (22), it is derived

$$w\left(\eta \right)=\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{\lambda }\left({n}_{1}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)-{n}_{2}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)\right)}{2\left({n}_{1}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)+{n}_{2}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)\right)}.$$

Now, setting value of \(w(\eta )\) in transformation (20) and exerting transformation (16) we attain exact soliton solution of Eq. (1).

$$p\left(x,t\right)={e}^{i\omega \left(x,t\right)}{\left(\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{\lambda }\left({n}_{1}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)-{n}_{2}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)\right)}{2\left({n}_{1}\mathrm{sin}\left(\eta \sqrt{\lambda }\right)+{n}_{2}\mathrm{cos}\left(\eta \sqrt{\lambda }\right)\right)}\right)}^\frac{1}{2},$$
(32)

Including \(\eta =kx-\frac{2k\tau {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \(\omega \left(x,t\right)=\tau x+\frac{(-{\tau }^{2}-{k}^{2}\lambda ){(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\).

Now, putting \({n}_{1}=0\), solution (32) yields

$$p\left(x,t\right)={e}^{i\omega (x,t)}\sqrt{\pm \frac{1}{2}k\sqrt{-\lambda }-\frac{k\sqrt{\lambda }\mathrm{tan}\left(\eta \sqrt{\lambda }\right)}{2}}.$$
(33)

Moreover, for \({n}_{2}=0\), the solution (32) takes the form,

$$p\left(x,t\right)={e}^{i\omega (x,t)}\sqrt{\pm \frac{1}{2}k\sqrt{-\lambda }+\frac{k\sqrt{\lambda }cot(\eta \sqrt{\lambda })}{2}}.$$
(34)

When \(\lambda =0\) Similarly, two sets of solution have been attained in this regard which have been brought out below:

Set 1 \({h}_{0}=0\), \({h}_{1}=\frac{lk}{4}\), \({m}_{1}=\pm \frac{l}{4}k\sqrt{{n}_{1}^{2}-2\mu {n}_{2}}\), \(\vartheta =-{\tau }^{2}\),\(v=2k\tau \),

Where \(l=1\) and \(3\).

Equation (22) permits us to generate a solution of Eq. (21) with the aid of the stated values of parameters.

$$w\left(\eta \right)=\frac{lk\left(\eta \mu +{n}_{1}\right)}{4\left(\frac{{\eta }^{2}\mu }{2}+\eta {n}_{1}+{n}_{2}\right)}\pm \frac{lk\sqrt{{n}_{1}^{2}-2\mu {n}_{2}}}{4\left(\frac{{\eta }^{2}\mu }{2}+\eta {n}_{1}+{n}_{2}\right)},$$

which bring out the travelling wave solution of Eq. (1) as:

$$q\left(x,t\right)=\frac{{e}^{i\omega \left(x,t\right)}\sqrt{lk}}{2\sqrt{(\frac{{\eta }^{2}\mu }{2}+\eta {n}_{1}+{n}_{2})}}\sqrt{\left(\eta \mu +{n}_{1}\right)\pm \sqrt{{n}_{1}^{2}-2\mu {n}_{2}}},$$
(35)

with \(\eta =kx-\frac{2k\tau {(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \(\omega \left(x,t\right)=\tau x-\frac{{\tau }^{2}{(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\), \({n}_{1}\), \({n}_{2}\), \(\mu \) is arbitrary constants.

Set 2 \({h}_{0}=0\), \({h}_{1}=k\), \({m}_{1}=-\frac{k{n}_{1}}{2}\), \(\mu =0\), \(\vartheta =-{\tau }^{2}\), \(v=2k\tau \).

Setting solution set 2 in Eq. (22), we attain

$$w\left(\eta \right)=\frac{k{n}_{1}}{2\left(\eta {n}_{1}+{n}_{2}\right)},$$

which provides the required solution of Eq. (1).

$$p\left(x,t\right)={e}^{i\omega (x,t)}\sqrt{\frac{k{n}_{1}}{2(\eta {n}_{1}+{n}_{2})}},$$
(36)

with \(\eta =kx-\frac{2k\tau {(t+\frac{1}{\mathrm{\Gamma \beta } })}^{\beta }}{\beta }\),\(\delta \left(x,t\right)=\tau x-\frac{{\tau }^{2}{(t+\frac{1}{\Gamma \beta })}^{\beta }}{\beta }\).

4 Comparison

In this section, we focus on the comparison between the results obtained in previous articles carried out by Kadkhoda and Jafari (2019) and Razazadeh et al. (2019) and the results attained in this study, which have been provided in Tables 1 and 2.

Table 1 Comparison between the results by Kadkhoda and Jafari (2019) and the results attained in this study
Full size table
Table 2 Comparison between the results by Razazadeh et al. (2019) and the results attained in this study
Full size table

Therefore, from Tables 1 and 2 it is observed that the stated solutions in the Tables are similar because of choosing zero value for several parameters. However, the original forms of solutions are novel and have yet to be achieved in any preceding article. Thus, it has been notified that the rest of the attained solutions are novel.

5 Visualization of the solitons and their descriptions

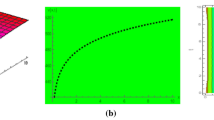
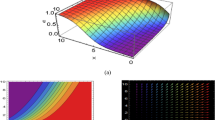
The characteristics and physical significance of the graphs plotted for the suitable values of parameters involving in attained solutions have been explained minutely in this section. Figure 1 disclose the feature of imaginary part of solution (23) which have been plotted for the values \(\beta =0.774\), \(\tau =-2\), \(k=-0.708\), \(\lambda =-4.67\), \({n}_{1}=0.89\), \({n}_{2}=-0.88\). Imaginary part of solution (23) exhibits a periodic soliton solution with velocity \(v=2.832\). From the contour plot it can be observed that the peak of the periodic soliton is occurred after a constant period. Periodic soliton can travel a long distance with the unaltered shape and velocity. Because of its significant characteristics, this type of soliton is used to transfer datum in remote area. This type of soliton is a potential and long-lasted soliton travelling a great distance with unchanged property. Figure 2 imparts the graphical attribute of real part of solution (23) while Fig. 3 is illustrated for the modulus of solution (23). Real part of solution (23) represents a periodic soliton for the values \(\beta =0.99\), \(\tau =-1.03\), \(k=-0.926\), \(\lambda =-0.23\), \({n}_{1}=0.53\), \({n}_{2}=1.715\) with velocity \(v=1.91\) and modulus of solution (23) represents a kink soliton for the values \(\beta =0.99\), \(\tau =-0.025\), \(k=-0.926\), \(\lambda =-5\), \({n}_{1}=1.136\), \({n}_{2}=1.445\) with velocity \(v=0.0463\). Solitons which alter from one asymptotic state to another and become stable in further propagation are acquainted as kink solitons. Hence, kink soliton provides constant value for \(t\to \infty \). In optical fiber study, kink soliton is also acquainted as dark soliton and it is used to transfer datum in long distance. Imaginary part of solution (26) presents a periodic soliton with velocity \(v=0.76\) which have been illustrated in Fig. 4 for the apt values \(\beta =0.368\), \(\tau =-1.45\), \(k=-0.264\), \(\lambda =-3.81\), \({n}_{1}=-3\), \({n}_{2}=1.36\), \(\mu =-5\). Moreover, modulus of solution (26) demonstrated a kink soliton with velocity \(v=0.19\) for the chosen values \(\beta =0.312\), \(\tau =-0.095\), \(k=-1\), \(\lambda =-5\), \({n}_{1}=0.53\), \({n}_{2}=-2\), \(\mu =-5\), which have been attached to Fig. 5. Figure 6 includes the graphical feather of imaginary part of solution (29) drawn for the values \(\beta =0.1\), \(\tau =3.64\), \(k=-0.1\), \(\lambda =4.838\), \({n}_{1}=5\), \({n}_{2}=1.975\), \(\mu =4.307\). Figure 6 exhibits physical characteristics of modulus of solution (29) which presents a periodic soliton with \(v=0.95\). Figure 6 is drawn for \(\beta =0.99\), \(\tau =2.07\), \(k=0.23\), \(\lambda =4.856\), \({n}_{1}=-0.05\), \({n}_{2}=-0.792\), \(\mu =4.429\). Figure 7 is illustrated for the real part of solution (32) with the aid of chosen values \(\beta =0.774\), \(\tau =1.5\), \(k=-0.02\), \(\lambda =4..404\), \({n}_{1}=0.17\), \({n}_{2}=0.75\). From Fig. 7 it is demonstrated that real part of solution (32) exhibits a periodic soliton of velocity \(v=0.06\). Though the imaginary as well as real parts of solution (35) present periodic soliton with velocities \(v=3.01\) and \(v=3.232\) respectively, they have the varied physical structure as shown in Figs. 8 and 9 respectively. Figure 8 is plotted for \(\beta =0.1\), \(\tau =-1.97\), \(k=0.764\), \(\mu =1.73\), \({n}_{1}=-3\), \({n}_{2}=2\) whereas Fig. 9 is plotted for \(\beta =0.729\), \(\tau =-2\), \(k=-0.808\), \(\mu =5\), \({n}_{1}=-3\), \({n}_{2}=0.41\). Figure 10 describes the graphical behavior of modulus of solution (35) for \(\beta =0.889\), \(\tau =-0.65\), \(k=-0.15\), \(\mu =-5\), \({n}_{1}=-4.71\), \({n}_{2}=-4\). From Fig. 10 we observe that modulus of solution (35) presents a compacton with \(v=0.195\). From the figure, it can be noted that it will be vanished after a short time of travel. As a result, compacton is a type of soliton where data propagate in compact area and is used to transfer datum in a nearby area.

Fig. 1
figure 1

Graphical exhibition of imaginary part of solution (23)

Full size image
Fig. 2
figure 2

Graphical exhibition of real part of solution (23)

Full size image
Fig. 3
figure 3

Graphical exhibition of modulus of solution (23)

Full size image
Fig. 4
figure 4

Graphical exhibition of imaginary part of solution (26)

Full size image
Fig. 5
figure 5

Graphical exhibition of modulus of solution (26)

Full size image
Fig. 6
figure 6

Graphical exhibition of modulus of solution (29)

Full size image
Fig. 7
figure 7

Graphical exhibition of real part of solution (32)

Full size image
Fig. 8
figure 8

Graphical exhibition of imaginary part of solution (35)

Full size image
Fig. 9
figure 9

Graphical exhibition of real part of solution (35)

Full size image
Fig. 10
figure 10

Graphical exhibition of modulus of solution (35)

Full size image

In this module, we exhibit the acquired solutions through the graphical representations. The exact soliton solutions have been picked out for the apposite values of arbitrary parameters comprising in attained analytical solutions and have been plotted within the ranges \(-5\le x\le 5\) and \(0\le t\le 10\).

6 Conclusion

In this article, we have established analytical soliton solution of the time-fractional Kundu-Eckhaus equation concerning beta derivative through the two variables \((G^{\prime}/G,1/G)\)-expansion approach. This method permits us to formulate soliton solutions comprising trigonometric, hyperbolic, rational functions with arbitrary parameters. Consequently, several kinds of soliton, like the periodic soliton, the kink, the singular periodic soliton, the compacton, the singular bell-shaped soliton, etc. have been formed for the suitable values of arbitrary parameters. Moreover, some consistent solutions of the concerned equation have been come out in this research work. The contour plot, two- and three-dimensional graphs illustrate the physical configuration of the attained results. The results of this article assure us about the reliability of the implemented method to investigate FNLEEs. Therefore, it is elucidated that this method can be considered for use in determining the useful and optimal soliton solutions to other significant FNLEEs.