1 Introduction

Nowadays, the nonlinear Schrödinger equation (NLSE) becomes an important model in numerous fields of science like quantum mechanics, nonlinear optics, ocean dynamics, plasma physics, etc. (El-Shiekh 2019; El-Shiekh and Gaballah 2021a, 2020a, b, c; El-Shiekh and Hamdy 2023; Gaballah et al. 2022).

Currently, the higher dimensional NLSE has attracted much attention since the high-dimensional NLSE model is more realistic and plentiful due to the increase of dimension. Moreover, other difficulties can be found by increasing the nonlinear terms like in the cubic and higher-order nonlinear Schrödinger equation which demonstrate the propagation of optical pulses in highly nonlinear optical systems (Alamri et al. 2019; Cheemaa et al. 2018; Li and Ma 2020; Wang 2021; Wazwaz 2021; Wazwaz and Mehanna 2021).

Recently, (Wang 2021) has introduced a new extended (3+1)-dimensional cubic NLSE built on the extended (3 + 1)-dimensional zero curvature equation as follows:

$$\begin{aligned} i\varphi _{t}-(\varphi _{xx}+\varphi _{yy}+\varphi _{zz}+2\varphi _{xy}-2\varphi _{yz}-2\varphi _{xz})+2\left| \varphi \right| ^{2}\varphi =0, \end{aligned}$$
(1)

Then, (Wazwaz and Mehanna 2021) generalized the extended (3+1)-dimensional cubic NLSE (1) in the following form:

$$\begin{aligned} i\varphi _{t}+p_{1}\varphi _{xy}+p_{2}\varphi _{yz}+p_{3}\varphi _{xz}+i\left( q_{1}\varphi _{x}+q_{2}\varphi _{y}+q_{3}\varphi _{z}\right) +r\varphi \left| \varphi \right| ^{2}-\varphi _{xx}-\varphi _{yy}-\varphi _{zz}=0, \end{aligned}$$
(2)

where \(\varphi (x,y,z,t)\) is the complex envelope of the wave and x,  y,  z are the spatial variables, where t is the temporal variable, also \(p_{j},q_{j},\) where \(j=1,2,3\) are constants and \(r=\pm 1\) is a parameter may representing self-focusing Kerr and self-defocusing nonlinearity, respectively. Equation (2) can be used to describe the pulse propagation in nonlinear optical fibers (Wang 2021; Wazwaz 2021; Wazwaz and Mehanna 2021).

From the previous importance of the extended (3+1)-dimensional cubic NLSE especially in the optics field, we are going to drive novel wave solutions for this equation using the generalized Jacobi elliptic function expansion (GJEE) method. The investigated solutions have different waveforms like kink, soliton, and periodic shapes and to discuss the novelty of the obtained solutions we will plot them in different structures and compare them with other obtained solutions before

2 Methodology

Nonlinear differential equations (NLDE) have an immense number of applications in numerous fields, especially in physics where they find widespread use in magnetohydrodynamics, ferrohydrodynamics, hydrostatic gravity waves, as well as the study of the electromagnetic spectrum, photons, and many other fields. To obtain exact solitary wave solutions to advanced NLDE that cause great concern in both physicists and mathematicians. These solutions are used to describe complex physical phenomena and dynamics, such as periodic wave solutions, solitons solutions, elliptic function solutions, dark solitary waves of the solution, and kink solitary waves of a solution, several methods have been constructed for this purpose, like the homogenous balance method, Hirota’s bilinear method, the hyperbolic function expansion method, auxiliary method, the sine cosine method, the Kudryashov method, the nonlinear transformation method, extended direct algebraic method and the trial function method (Cheemaa et al. 2019; El-Sayed et al. 2014; El-Shiekh et al. 2022; El-Shiekh 2021, 2018b, c, a, 2015; El-Sayed 2013; El-Shiekh et al. 2022; El-Shiekh and Gaballah 2023b, a; El-Shiekh et al. 2022; El-Shiekh and Gaballah 2021b; Gaballah et al. 2023; Li and Ma 2023b, a, 2022b, a, 2018, 2017; Ma et al. 2009, 2018; Ma and Li 2023; Moatimid et al. 2013; Seadawy 2016; Seadawy et al. 2019, 2018; Zkan et al. 2020). One of these powerful techniques is the generalized Jacobi elliptic function expansion technique (Gaballah et al. 2023, 2022; Zayed and Alngar 2020). In the following the main steps of the GJEE method:

Step1: Consider a nonlinear partial differential equation (NPDE)

$$\begin{aligned} P(x,y,z,t,\varphi _{x},\varphi _{y},\varphi _{z},\varphi _{xy},\varphi _{xz},...)=0, \end{aligned}$$
(3)

where \(\varphi =\varphi \left( x,y,z,t\right)\) is a complex function and x, y, z are the spatial variables and t is the temporal variable.

Step2: Use the following traveling wave transformation to transform Eq. (2) into a nonlinear ordinary equation (NODE)

$$\begin{aligned} \varphi (x,y,z,t)= & {} \Phi (\xi )e^{i\eta }, \end{aligned}$$
(4)
$$\begin{aligned} \xi= & {} k_{1}x+k_{2}y+k_{3}z+c_{1}t,\eta =\alpha x+\beta y+\gamma z+c_{2}t \end{aligned}$$
(5)

where \(k_{1},k_{2},k_{3},\) \(\alpha ,\beta ,\gamma ,c_{1}\) and \(c_{2}\) are real constants and \(\Phi\) is a real function on the wave variable \(\xi .\) Now, consider the new obtained NODE has a solution in the form:

$$\begin{aligned} \Phi (\xi )=\sum \limits _{l=0}^{l=M}(A_{l}\phi (\xi )^{l}+B_{l}\phi ^{\prime }(\xi )\phi (\xi )^{l-1}), \end{aligned}$$
(6)

where M is a positive integer determined from the balance procedure applied to the obtained NODE, \(A_{l},B_{l}\ (l=0,1,......,M)\)are real constants to be determined and \(\phi (\xi )\) satisfies the Jacobi elliptic function equation

$$\begin{aligned} \phi ^{\prime 2}(\xi )=a_{0}+a_{2}\phi (\xi )^{2}+a_{4}\phi (\xi )^{4}, \end{aligned}$$
(7)

where \(a_{0}\), \(a_{2},\) and \(a_{4}\) are parameters that have known values (Zayed and Alngar 2020). By inserting Eq. (6) and Eq. (7) into the obtained NODE after using the traveling wave transformation in Eq. (5) and by collecting different powers of \(\phi\) and \(\phi ^{\prime }\) equating it by zero, then an algebraic system is yielded, and by solving it the constants \(A_{l},B_{l}\) are determined. Finally, from the known values of the constants \(a_{0},a_{2},\) and \(a_{4}\) different functions like hyperbolic and periodic wave functions are arisen.

3 Novel wave solutions for the extended 3D-CNLSE

By inserting Eq. (4) and Eq. (5) into Eq. (2), considering the real and imaginary parts are separate, we get the real part as:

$$\begin{aligned}{} & {} (p_{1}k_{1}k_{2}+p_{2}k_{2}k_{3}+p_{3}k_{1}k_{3}-k_{1}^{2}-k_{2}^{2}-k_{3}^{2})\Phi ^{\prime \prime }\nonumber \\{} & {} \quad -\left( c_{2}+\alpha q_{1}+\beta q_{2}+\gamma q_{3}+p_{1}\alpha \beta +p_{2}\beta \gamma +p_{3}\alpha \gamma -\alpha ^{2}-\beta ^{2}-\gamma ^{2}\right) \Phi +r\Phi ^{3}=0, \end{aligned}$$
(8)

The imaginary part:

$$\begin{aligned}{} & {} \left( c_{1}+q_{1}k_{1}+q_{2}k_{2}+q_{3}k_{3}+p_{1}k_{1}\beta +p_{1}k_{2}\alpha +\gamma k_{2}p_{2}+\beta k_{3}p_{2}+p_{3}k_{1}\gamma +p_{3}k_{3}\alpha \right. \nonumber \\{} & {} \quad \left. -2\left( \alpha k_{1}+\beta k_{2}+\gamma k_{3}\right) \right) \Phi ^{\prime }=0, \end{aligned}$$
(9)

Assume that the imaginary part is finished so we have the following condition on the constants

$$\begin{aligned} c_{1}= & {} 2\left( \alpha k_{1}+\beta k_{2}+\gamma k_{3}\right) -(q_{1}k_{1}+q_{2}k_{2}+q_{3}k_{3}+p_{1}k_{1}\beta \nonumber \\{} & {} \quad +p_{1}k_{2}\alpha +\gamma k_{2}p_{2}+\beta k_{3}p_{2}+p_{3}k_{1}\gamma +p_{3}k_{3}\alpha ). \end{aligned}$$
(10)

Then, Eq. (8) becomes

$$\begin{aligned} \Phi ^{\prime \prime }+\lambda \Phi +\mu \Phi ^{3}=0, \end{aligned}$$
(11)

where

$$\begin{aligned} \lambda= & {} \frac{-\left( c_{2}+\alpha q_{1}+\beta q_{2}+\gamma q_{3}+p_{1}\alpha \beta +p_{2}\beta \gamma +p_{3}\alpha \gamma -\alpha ^{2}-\beta ^{2}-\gamma ^{2}\right) }{ p_{1}k_{1}k_{2}+p_{2}k_{2}k_{3}+p_{3}k_{1}k_{3}-k_{1}^{2}-k_{2}^{2}-k_{3}^{2} },\nonumber \\ \mu= & {} \frac{r}{p_{1}k_{1}k_{2}+p_{2}k_{2}k_{3}+p_{3}k_{1}k_{3}-k_{1}^{2}-k_{2}^{2}-k_{3}^{2}}. \end{aligned}$$
(12)

Now, we are going to solve Eq. (11) by using the GJEE method. Make the balance between the linear term \(\Phi ^{\prime \prime }\) and the nonlinear term \(\Phi ^{3}\) lead to \(M=1\) so that \(\Phi\) can be put in the form:

$$\begin{aligned} \Phi (\xi )=A_{0}+A_{1}\phi (\xi )+\frac{\phi ^{\prime }(\eta )}{\phi (\eta ) }B_{0}+B_{1}\phi ^{\prime }(\xi ), \end{aligned}$$
(13)

where \(\phi (\xi )\) verifying Eq. (7). By substituting Eq. (13) into Eq. (11) using Eq. (7), collecting the coefficients of \(\phi (\xi )\) and \(\phi ^{\prime }(\xi )\) and equating it with zero the following algebraic system is yielded:2

$$\left. \begin{gathered} 6\mu A_{0} B_{0} B_{1} a_{2} + 3\mu A_{1} B_{0}^{2} a_{2} + 3\mu A_{1} B_{1}^{2} a_{0} + 3\mu B_{0}^{2} B_{1} a_{2} + \mu a_{0} B_{1}^{3} + 3\mu A_{0}^{2} A_{1} + \lambda A_{1} + A_{1} a_{2} = 0, \hfill \\ 3\mu A_{0} B_{0}^{2} a_{2} + 3\mu A_{0} B_{1}^{2} a_{0} + 6\mu A_{1} B_{0} B_{1} a_{0} + \mu a_{2} B_{0}^{3} + 3\mu B_{0} B_{1}^{2} a_{0} + \mu A_{0}^{3} + \lambda A_{0} + 2B_{0} a_{2} = 0, \hfill \\ 3\mu A_{0} B_{0}^{2} a_{4} + 3\mu A_{0} B_{1}^{2} a_{2} + 6\mu A_{1} B_{0} B_{1} a_{2} + \mu B_{0}^{3} a_{4} + 3\mu B_{0} B_{1}^{2} a_{2} + 3\mu A_{0} A_{1}^{2} + 2B_{0} a_{4} = 0, \hfill \\ 6\mu A_{0} B_{0} B_{1} a_{4} + 3\mu A_{1} B_{0}^{2} a_{4} + 3\mu A_{1} B_{1}^{2} a_{2} + 3\mu B_{0}^{2} B_{1} a_{4} + \mu B_{1}^{3} a_{2} + \mu A_{1}^{3} + 2A_{1} a_{4} = 0, \hfill \\ 6\mu A_{0} B_{0} B_{1} a_{0} + 3\mu A_{1} B_{0}^{2} a_{0} + 3\mu B_{0}^{2} B_{1} a_{0} = 0, \hfill \\ 3\mu A_{0} B_{1}^{2} a_{4} + 6\mu A_{1} B_{0} B_{1} a_{4} + 3\mu B_{0} B_{1}^{2} a_{4} = 0, \hfill \\ 3\mu A_{0}^{2} B_{1} + 6\mu A_{0} A_{1} B_{0} + \lambda B_{1} + B_{1} a_{2} = 0, \hfill \\ 3\mu A_{0} B_{0}^{2} a_{0} + \mu B_{0}^{3} a_{0} + 2B_{0} a_{0} = 0, \hfill \\ 3\mu A_{1} B_{1}^{2} a_{4} + \mu a_{4} B_{1}^{3} = 0, \hfill \\ 6\mu A_{0} A_{1} B_{1} + 3\mu A_{1}^{2} B_{0} = 0, \hfill \\ 3\mu A_{0}^{2} B_{0} + \lambda B_{0} - 2B_{0} a_{2} = 0, \hfill \\ 3\mu A_{1}^{2} B_{1} + 6a_{4} B_{1} = 0. \hfill \\ \end{gathered} \right\}$$
(14)

System (14) is solved by the Maple program, and two different cases of solutions are given:

Case I: \(A_{1}=\pm \sqrt{\frac{-2a_{4}}{\mu }},A_{0}=B_{0}=B_{1}=0,\lambda =-a_{2}.\)

Novel Jacobi function solutions are yielded for the extended 3D-CNLSE equation as follows:

Group I:

$$\begin{aligned} \varphi _{1}= & {} \pm \sqrt{\frac{2\left( 1-\lambda \right) }{\mu }}\text { sn} \left( \xi ,\sqrt{\lambda -1}\right) e^{i\eta }, \end{aligned}$$
(15)
$$\begin{aligned} \varphi _{2}= & {} \pm \sqrt{\frac{2\left( 1-\lambda \right) }{\mu }}\text { cd} \left( \xi ,\sqrt{\lambda -1}\right) e^{i\eta }, \end{aligned}$$
(16)
$$\begin{aligned} \varphi _{3}= & {} \pm \sqrt{\frac{1-\lambda }{\mu }}\text { cn}\left( \xi ,\sqrt{ \frac{1}{2}(\lambda -1)}\right) e^{i\eta }, \end{aligned}$$
(17)
$$\begin{aligned} \varphi _{4}= & {} \pm \sqrt{\frac{2}{\mu }}\text { dn}\left( \xi ,\sqrt{\lambda +2} \right) e^{i\eta }, \end{aligned}$$
(18)
$$\begin{aligned} \varphi _{5}= & {} \pm \sqrt{\frac{-2}{\mu }}\text { ns}\left( \xi ,\sqrt{\lambda -1 }\right) e^{i\eta },\mu <0 \end{aligned}$$
(19)
$$\begin{aligned} \varphi _{6}= & {} \pm \sqrt{\frac{-2}{\mu }}\text { dc}\left( \xi ,\sqrt{\lambda -1 }\right) e^{i\eta },\mu <0, \end{aligned}$$
(20)
$$\begin{aligned} \varphi _{7}= & {} \pm \sqrt{\frac{-(1+\lambda )}{\mu }}\text { nc}\left( \xi , \sqrt{\frac{1}{2}(1-\lambda )}\right) e^{i\eta },\mu <0, \end{aligned}$$
(21)
$$\begin{aligned} \varphi _{8}= & {} \pm \sqrt{\frac{-2(1+\lambda )}{\mu }}\text { nd}\left( \xi , \sqrt{\lambda +2}\right) e^{i\eta },\mu <0, \end{aligned}$$
(22)
$$\begin{aligned} \varphi _{9}= & {} \pm \sqrt{\frac{2(1+\lambda )}{\mu }}\text { sc}\left( \xi , \sqrt{\lambda +2}\right) e^{i\eta }, \end{aligned}$$
(23)
$$\begin{aligned} \varphi _{10}= & {} \pm \sqrt{\frac{1-\lambda ^{2}}{2\mu }}\text { sd}\left( \xi , \sqrt{\frac{1}{2}\left( 1-\lambda \right) }\right) e^{i\eta }, \end{aligned}$$
(24)
$$\begin{aligned} \varphi _{11}= & {} \pm \sqrt{\frac{-2}{\mu }}\text { cs}\left( \xi ,\sqrt{\lambda +2}\right) e^{i\eta }, \end{aligned}$$
(25)
$$\begin{aligned} \varphi _{12}= & {} \pm \sqrt{\frac{-2}{\mu }}\text { ds}\left( \xi ,\sqrt{\frac{1}{ 2}\left( 1-\lambda \right) }\right) e^{i\eta }, \end{aligned}$$
(26)
$$\begin{aligned} \varphi _{13}= & {} \pm \sqrt{\frac{-1}{2\mu }}\left( \text {ns}\left( \xi ,\sqrt{ \frac{1}{2}\left( 1+2\lambda \right) }\right) \pm \text {cs}\left( \xi ,\sqrt{ \frac{1}{2}\left( 1+2\lambda \right) }\right) \right) e^{i\eta }, \end{aligned}$$
(27)
$$\begin{aligned} \varphi _{14}= & {} \pm \sqrt{\frac{-(1+\lambda )}{\mu }}\left( \text {nc}\left( \xi ,\sqrt{-\left( 1+2\lambda \right) }\right) \pm \text {sc}\left( \xi , \sqrt{-\left( 1+2\lambda \right) }\right) \right) e^{i\eta }, \end{aligned}$$
(28)
$$\begin{aligned} \varphi _{15}= & {} \pm \sqrt{\frac{-1}{2\mu }}\left( \text {ns}\left( \xi ,\sqrt{ 2\left( 1-\lambda \right) }\right) \pm \text {ds}\left( \xi ,\sqrt{2\left( 1-\lambda \right) }\right) \right) e^{i\eta }, \end{aligned}$$
(29)

where \(\lambda <1\) in most of the above Jacobi solutions.

If the modulus of the Jacobi elliptic function approches to 1,  the hyperbolic functions arise as:

Group II:

$$\begin{aligned} \varphi _{16}= & {} \pm \sqrt{\frac{-2}{\mu }}\tanh \left( \xi \right) e^{i\eta }, \text { if }\lambda =2, \end{aligned}$$
(30)
$$\begin{aligned} \varphi _{17}= & {} \pm \sqrt{\frac{2}{\mu }}\text {sech}\left( \xi \right) e^{i\eta },\text { if }\lambda =-1, \end{aligned}$$
(31)
$$\begin{aligned} \varphi _{18}= & {} \pm \sqrt{\frac{-2}{\mu }}\coth \left( \xi \right) e^{i\eta }, \text {with }\lambda =2, \end{aligned}$$
(32)
$$\begin{aligned} \varphi _{19}= & {} \pm \sqrt{\frac{-2}{\mu }}\text {csch}\left( \xi \right) e^{i\eta },\text { with }\lambda =-1, \end{aligned}$$
(33)
$$\begin{aligned} \varphi _{20}= & {} \pm \sqrt{\frac{-1}{2\mu }}\left( \coth \left( \xi \right) \pm \text {csch}\left( \xi \right) \right) e^{i\eta },\text { if }\lambda =\frac{1 }{2}, \end{aligned}$$
(34)

If the modulus of the Jacobi elliptic function approches to 0,  the triagnometric functions arise as:

Group III:

$$\begin{aligned} \varphi _{21}= & {} \pm \sqrt{\frac{-2}{\mu }}\tan \left( \xi \right) e^{i\eta }, \text { with }\lambda =-2, \end{aligned}$$
(35)
$$\begin{aligned} \varphi _{22}= & {} \pm \sqrt{\frac{-2}{\mu }}\text {sec}\left( \xi \right) e^{i\eta },\text { if }\lambda =1, \end{aligned}$$
(36)
$$\begin{aligned} \varphi _{23}= & {} \pm \sqrt{\frac{-2}{\mu }}\cot \left( \xi \right) e^{i\eta }, \text {if }\lambda =-2, \end{aligned}$$
(37)
$$\begin{aligned} \varphi _{24}= & {} \pm \sqrt{\frac{-2}{\mu }}\text {csc}\left( \xi \right) e^{i\eta },\text { with }\lambda =1, \end{aligned}$$
(38)
$$\begin{aligned} \varphi _{25}= & {} \pm \sqrt{\frac{-1}{2\mu }}\left( \cot \left( \xi \right) \pm \csc (\xi \right) e^{i\eta },\text { if }\lambda =\frac{-1}{2}, \end{aligned}$$
(39)
$$\begin{aligned} \varphi _{26}= & {} \pm \sqrt{\frac{-1}{2\mu }}\left( \sec \left( \xi \right) \pm \tan \left( \xi \right) \right) e^{i\eta },\text { if }\lambda =\frac{-1}{2}. \end{aligned}$$
(40)

Case II: \(\lambda =2a_{2},B_{0}=\pm \sqrt{\frac{-2}{\mu }},A_{0}=A_{1}=B_{1}=0.\)

By using the second case of solutions obtained for the algebric system (14), the follwoing novel Jacobi function solutions are created:

Group IV:

$$\begin{aligned} \varphi _{27}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\text {cn}\left( \xi , \sqrt{-(1+\frac{\lambda }{2})}\right) \text { dn}\left( \xi ,\sqrt{-(1+\frac{ \lambda }{2})}\right) }{\text {sn}\left( \xi ,\sqrt{-(1+\frac{\lambda }{2})} \right) }\right) e^{i\eta }, \end{aligned}$$
(41)
$$\begin{aligned} \varphi _{28}= & {} \mp \sqrt{\frac{-2}{\mu }}\left( \frac{(2+\frac{\lambda }{2}) \text { sn}\left( \xi ,\sqrt{-(1+\frac{\lambda }{2})}\right) }{\text {cn} \left( \xi ,\sqrt{-(1+\frac{\lambda }{2})}\right) \text { dn}\left( \xi , \sqrt{-(1+\frac{\lambda }{2})}\right) }\right) e^{i\eta }, \end{aligned}$$
(42)
$$\begin{aligned} \varphi _{29}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\text {dn}\left( \xi , \frac{1}{2}\sqrt{(2+\lambda )}\right) \text { sn}\left( \xi ,\frac{1}{2}\sqrt{ 2+\lambda }\right) }{\text {cn}\left( \xi ,\frac{1}{2}\sqrt{2+\lambda } \right) }\right) e^{i\eta }, \end{aligned}$$
(43)
$$\begin{aligned} \varphi _{30}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\lambda }{2}\mp 2\right) \left( \frac{\text {cn}\left( \xi ,\sqrt{\left( 2-\frac{\lambda }{2} \right) }\right) \text { sn}\left( \xi ,\sqrt{\left( 2-\frac{\lambda }{2} \right) }\right) }{\text {dn}\left( \xi ,\sqrt{\left( 2-\frac{\lambda }{2} \right) }\right) }\right) e^{i\eta }, \end{aligned}$$
(44)
$$\begin{aligned} \varphi _{31}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\text {dn}\left( \xi , \sqrt{\left( 2-\frac{\lambda }{2}\right) }\right) }{\text {cn}\left( \xi , \sqrt{\left( 2-\frac{\lambda }{2}\right) }\right) \text { sn}\left( \xi , \sqrt{\left( 2-\frac{\lambda }{2}\right) }\right) }\right) e^{i\eta }, \end{aligned}$$
(45)
$$\begin{aligned} \varphi _{32}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\text {cn}\left( \xi , \frac{1}{2}\sqrt{1+\lambda }\right) }{\text {dn}\left( \xi ,\frac{1}{2}\sqrt{ (1+\lambda )}\right) \text { sn}\left( \xi ,\frac{1}{2}\sqrt{1+\lambda } \right) }\right) e^{i\eta }, \end{aligned}$$
(46)
$$\begin{aligned} \varphi _{33}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\text {dn}\left( \xi , \sqrt{\frac{1}{2}(1-\lambda )}\right) }{\text {sn}\left( \xi ,\sqrt{\frac{1}{2 }(1-\lambda )}\right) }\right) e^{i\eta }, \end{aligned}$$
(47)
$$\begin{aligned} \varphi _{34}= & {} \pm \sqrt{\frac{-2}{\mu }}\left( \frac{\text {dn}\left( \xi , \sqrt{\lambda -1}\right) }{\text {cn}\left( \xi ,\sqrt{\lambda -1}\right) } \right) e^{i\eta }, \end{aligned}$$
(48)
$$\begin{aligned} \varphi _{35}= & {} \mp \sqrt{\frac{-2}{\mu }}\frac{\text {cn}\left( \xi ,\sqrt{ \lambda +2}\right) }{\text {sn}\left( \xi ,\sqrt{\lambda +2}\right) }e^{i\eta }, \end{aligned}$$
(49)

where \(\mu <0\) for Eqs. (16-46).

4 Results and discussion

Many natural phenomena can be described by nonlinear waves, so they exist in different fields of science as optics, hydrodynamics, plasma physics, etc. Nonlinear waves have two different types: solitary waves in a dispersion medium and waves in a dissipative dispersion medium. Solitons are nonlinear solitary waves that keep their shape according to propagation without change so it is very important and has many applications in physical science especially in optics. In this study many types of solitary waves are obtained therefore, in this section, we are going to plot three different solitary shapes, as an example of the change in the nonlinear wave behavior from one solitary wave solution to another as follows:

Fig. 1
figure 1

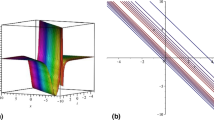
The different plots for the periodic solitary wave \(\left| \varphi _{1}\right| ^{2}\) through optical fiber, when \(p_{1}=0.5,p_{2}=p_{3}=k_{1}=k_{2}=k_{3}=q_{1}=q_{2}=q_{3}=\alpha =\beta =\gamma =r=1,c_{2}=-1\) and the values of \(c_{1}=-2\), \(\lambda =3,\) and \(\mu =-2\) according to equations (10) and (12). Moreover, the dimensions \(y=z=0\) but \(x\in [-10,10]\) and \(t\in [0,10]\) in figures (1-a) and (2-b), where \(t=1,2,3\) correspond to the blue, orange, and green lines respectively

Full size image
Fig. 2
figure 2

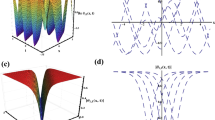
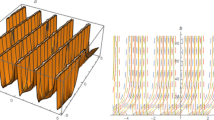
The different graphs of the optical kink soliton \(\left| \varphi _{16}\right| ^{2}\) in 3D, density, 2D respectively, where y=z=0 and the parameters are taken as: \(p_{1}=0.5,p_{2}=p_{3}=k_{1}=k_{2}=k_{3}=q_{1}=q_{2}=q_{3}=\alpha =\beta =\gamma =r=1,c_{2}=-1.5.\) Therefore, from Eqs. (10) and (12), \(c_{1}=-2\), \(\lambda =2,\) and \(\mu =-2,\) and hence, the periodic wave solution given by Eq. (15) transformed to the kink soliton solution \(\varphi _{16}\) given by Eq. (30). The graphs are in x range \(0\le x\le 10\) for all Fig. 2, and t range \(0\le t\le 5\) while the 2D lines are for the t values 1, 2, 3 respectively

Full size image
Fig. 3
figure 3

The 3D, density, and 2D plots for the bright optical soliton \(\left| \varphi _{17}\right| ^{2}\) where the constants are \(p_{1}=0.5,p_{2}=p_{3}=k_{1}=k_{2}=k_{3}=q_{1}=q_{2}=q_{3}=\alpha =\beta =\gamma =1,r=-1,c_{2}=-3\). So that, the other dependent constants are \(c_{1}=-2,\lambda =-1,\) and \(\mu =2,\) where \(y=z=0\), and \(x\in [0,10]\) and \(t\in [0,5]\)

Full size image

In Figs. 1 and 2, the periodic and kink soliton wave solutions were derived in a medium with self-focusing Kerr-nonlinearity as \(r=1\), but the bright soliton wave solution represented in Fig. 3 is driven in a medium with self-defocusing nonlinearity and it is clear that by changing the values of the parameters the soliton shape is changing and the dynamic behavior of the wave is affected.

5 Conclusion

In this paper, the extended 3D CNLSE was investigated by the GJEE method and according to that many distinct solitary wave solutions were obtained in the form of Jacobi elliptic functions, hyperbolic functions, and trigonometric functions. The obtained solutions covered some obtained solutions in the literature and there are many other novel solutions (Wang 2021; Wazwaz 2021; Wazwaz and Mehanna 2021). From the results, we can conclude that the GJEE is an effective, simple method and can be valid for other complicated complex systems. Moreover, the propagation of periodic, kink, and bright solitons was discussed in two different mediums self-focusing Kerr-nonlinearity and self-defocusing nonlinearity which have important applications in nonlinear optics.