Introduction

One of the most famous equations in mathematical physics is Burger’s equation. This equation yields because of merging both nonlinear wave motion with linear diffusion. The existence of viscous terms helps control wave-breaking, and smooth out shock discontinuities so that, we know that the obtained solutions will behave well and smoothly. Additionally, in the inviscid limit, as the diffusion term becomes very small, the smooth viscous solutions converge non-uniformly to the appropriate discontinuous shock wave. Many applications for Burger’s equations and their generalization can be found in weather problems, boundary layer behavior, acoustic transmission, shock weave formation, mass transport turbulence, and traffic flow [1,2,3,4,5]. Moreover, coupled Burger’s equations are one of the very important classes of systems of nonlinear parabolic and hyperbolic partial differential equations which models basic flow equations describing unsteady transport problems.

In this paper, we are going to use symmetry group analysis to investigate invariant transformations and exact solutions for one of those generalized Burgers systems; namely, the symmetric coupled Burgers equations (SCBE) [1,2,3]

$$\begin{aligned} \phi _{t}= & {} \frac{1}{2}\phi _{xx}+\frac{1}{2}\psi _{xx}+3\phi \phi _{x}+5\psi \phi _{x}+3\phi \psi _{x}+5\psi \psi _{x}\nonumber \\&-4\phi ^{3}-4\phi ^{2}\psi +4\phi \psi ^{2}+4\psi ^{3}, \nonumber \\ \psi _{t}= & {} \frac{1}{2}\phi _{xx}+\frac{1}{2}\psi _{xx}+3\psi \psi _{x}+5\phi \psi _{x}+3\psi \phi _{x}+5\phi \,\phi _{x}\nonumber \\&+4\phi ^{3}-4\psi ^{2}\phi +4\psi \phi ^{2}-4\psi ^{3}, \end{aligned}$$
(1)

where \(\phi =\phi (x,t)\) , \(\psi =\psi (x,t)\). The SCBE (1) was first discussed by Foursov in [1] as one of the symmetric integrable coupled Burgers type equations. Also, Wazwaz in [3] studied the SCBE system by using Hirota’s bilinear method to find its integrability property, and both kink and singular kink solutions were obtained.

The motivation of our work is to reduce system (1) by the symmetry method and obtain more novel solutions for it that also cover other solutions obtained before [1,2,3]. Moreover, some graphs for the obtained shock and kink wave solutions will given to illustrate the wave propagation behavior.

Methodology and Fundamental equations

Recently, many new methodologies constructed to solve nonlinear partial differential equations like Hirota’s bilinear method, Bäcklund transformation method, the Riccati equation method, the sine-Gordon equation method, and direct similarity reduction method, the symmetry reduction method etc. [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].

In this section we are going to apply the symmetry method to reduce the SCBE as follows [4, 5, 20, 22, 25], and [29]:

1- The SCBE system can be written in the form,

$$\begin{aligned} L_{1}(\phi ,\psi )= & {} \phi _{t}-\frac{1}{2}\phi _{xx}-\frac{1}{2}\psi _{xx}-3\phi \phi _{x}-5v\phi _{x}-3\phi \psi _{x}\nonumber \\&-5\psi \psi _{x}+4\phi ^{3}+4\phi ^{2}\psi -4\phi \psi ^{2}-4\psi ^{3}, \nonumber \\ L_{2}(\phi ,\psi )= & {} \psi _{t}-\frac{1}{2}\phi _{xx}-\frac{1}{2}\psi _{xx}-3\psi \psi _{x}-5\phi \psi _{x}-3\psi \phi _{x}\nonumber \\&-5\phi \,\phi _{x}-4\phi ^{3}+4\psi ^{2}\phi -4\psi \phi ^{2}+4\psi ^{3}, \end{aligned}$$
(2)

2- To find the invariant transformations of the SCBE system, put the following symmetry operators

$$\begin{aligned} S_{1}(\phi ,\psi )= & {} A\,\phi _{t}+B\,\phi _{x}-C \nonumber \\ S_{2}(\phi ,\psi )= & {} A\,\psi _{t}+B\,\psi _{x}-E. \end{aligned}$$
(3)

where \(A=A(x,t,\phi ,\psi )\), \(B=B(x,t,\phi ,\psi )\), \(C=C(x,t,\phi ,\psi )\) , and \(E=E(x,t,\phi ,\psi )\ \)are the infinitesimals to be found later.

3- To Calculate the Frèchet derivatives \(F_{1}(L_{1}\), \(\phi \), \(\psi ,\Phi ,\Psi )\) of \(L_{1}(\phi ,\psi )\) and \(F_{2}(L_{2}\), \(\phi \), \(\psi ,\Phi ,\Psi )\) of \(L_{2}(\phi ,\psi )\) in directions of \(\Phi \) and \(\Psi \), and replacing \(\Phi \) and \(\Psi \) in \(F_{1}\)and \(F_{2}\) by \( S_{1}(\phi \), \(\psi )\) and \(S_{2}(\phi \), \(\psi )\) respectively, we get

$$\begin{aligned} F_{1}(L_{1},\phi ,\psi ,S_{1}(\phi ,\psi ),S_{2}(u,v))= & {} [S_{1}(\phi ,\psi )]_{t}-\frac{1}{2}[S_{1}(\phi ,\psi ))]_{xx}-\frac{1}{2}[S_{2}(\phi ,\psi )]_{xx} \nonumber \\&-3\phi _{x}[S_{1}(\phi ,\psi )]-3\phi [S_{1}(\phi ,\psi )]_{x}-5\phi _{x}[S_{2}(\phi ,\psi )] \nonumber \\&-5\psi [S_{1}(\phi ,\psi )]_{x}-3\psi _{x}[S_{1}(\phi ,\psi )]-3\phi [S_{2}(\phi ,\psi )]_{x} \nonumber \\&-5\psi _{x}[S_{2}(\phi ,\psi )]-5\psi [S_{2}(\phi ,\psi )]_{x}+12\phi ^{2}[S_{1}(\phi ,\psi )] \nonumber \\&+8\phi \psi [S_{2}(\phi ,\psi )]+4\phi ^{2}[S_{2}(\phi ,\psi )]-4\psi ^{2}[S_{1}(\phi ,\psi )] \nonumber \\&-8\phi \psi [S_{2}(\phi ,\psi )]-12\psi ^{2}[S_{2}(\phi ,\psi )], \end{aligned}$$
(4)
$$\begin{aligned} F_{2}(L_{2},\phi ,\psi ,S_{1}(u,v),S_{2}(u,v))= & {} [S_{2}(\phi ,\psi )]_{t}- \frac{1}{2}[S_{1}(\phi ,\psi )]_{xx}-\frac{1}{2}[S_{2}(\phi ,\psi )]_{xx} \nonumber \\&-3\psi _{x}[S_{2}(\phi ,\psi )]-3\psi [S_{2}(\phi ,\psi )]_{x}-5\psi _{x}[S_{1}(\phi ,\psi )] \nonumber \\&-5\phi [S_{2}(\phi ,\psi )]_{x}-3\phi _{x}[S_{2}(\phi ,\psi )]-3\psi [S_{1}(\phi ,\psi )]_{x} \nonumber \\&-5\phi _{x}[S_{1}(\phi ,\psi )]-5\phi [S_{1}(\phi ,\psi )]_{x}+12\psi ^{2}[S_{2}(\phi ,\psi )] \nonumber \\&+4\psi ^{2}[S_{1}(\phi ,\psi )]+8\phi \psi [S_{2}(\phi ,\psi )]-8\phi \psi [S_{1}(\phi ,\psi )] \nonumber \\&-4\phi ^{2}[S_{2}(\phi ,\psi )]-12\phi ^{2}[S_{1}(\phi ,\psi )]. \end{aligned}$$
(5)

Substitute from (3) into Eqs. (4) and (5), then collect the coefficients of the derivatives of \(\phi \) and \(\psi \) in Eqs. (4) and (5) and equating it by zero, we get the following partial differential system

$$\begin{aligned}&A_{x}=0,A_{\phi }=0,A_{\psi }=0,B_{\phi }=0,B_{\psi }=0,E_{\phi \psi }+C_{\phi \psi }=0, \nonumber \\&\frac{1}{2}E_{\psi }-\frac{1}{2}C_{\phi }-B_{x}+\frac{1}{2}A_{t}=0, \nonumber \\&-\frac{1}{2}C_{\psi }+\frac{1}{2}A_{t}-B_{x}+\frac{1}{2}E_{\phi }=0, \nonumber \\&E_{\psi \psi }+C_{\psi \psi }=0, \nonumber \\&2(\psi -\phi )C_{\psi }+(5\psi +3\phi )E_{v}-\frac{1}{2}B_{xx}+E_{x\psi }+C_{x\psi }-(5\psi +3\phi )B_{x}+3C \nonumber \\&\quad +5E+(5\psi +3\phi ){\mathrm{A}}_{t}-(5\psi +3\phi )C_{\phi }+\frac{1}{2}E_{\phi \phi }+\frac{1}{2}C_{\phi \phi }=0, \nonumber \\&\frac{1}{2}C_{xx}+\frac{1}{2}E_{xx}+4(\phi \psi ^{2}-\phi ^{2}\psi +\psi ^{3}-\phi ^{3})A_{t}+4(\phi ^{2}\psi -\phi \psi ^{2}+\phi ^{3}-\psi ^{3})C_{\phi } \nonumber \\&\quad +4(\phi \psi ^{2}-\phi ^{2}\psi +\psi ^{3}-\phi ^{3})C_{\psi }+(5\psi +3\phi )C_{x}-4(3\phi ^{2}-\psi ^{2}+2\phi \psi )C \nonumber \\&-C_{t}+(5\psi +3\phi )E_{x}+4(3\psi ^{2}-\phi ^{2}+2\phi \psi )E=0, \nonumber \\&-(5\phi +3\psi )C_{\psi }+(5\psi +3\phi )E_{\phi }+3C+5E-\frac{1}{2} B_{xx}+E_{x\phi }+C_{x\phi }+B_{t} \nonumber \\&-(5\psi +3\phi )B_{x}+(5\psi +3\phi ){\mathrm{A}}_{t}=0, \nonumber \\&\frac{1}{2}C_{\psi }+\frac{1}{2}A_{t}-B_{x}-\frac{1}{2}E_{\phi }=0, \nonumber \\&\frac{1}{2}E_{\phi \phi }+\frac{1}{2}C_{\phi \phi }=0, \nonumber \\&-\frac{1}{2}B_{xx}+3E+C_{x\phi }+5C+E_{x\phi }+2\phi E_{\phi }+5\phi {\mathrm{A}} _{t}+3\psi A_{t}-3\psi B_{x}-5\phi B_{x} \nonumber \\&-2\psi E_{\phi }+5\phi C_{\phi }+3\psi C_{\phi }-3\psi E_{\psi }-5\phi E_{\psi }=0, \nonumber \\&\frac{1}{2}E_{xx}+\frac{1}{2}C_{xx}-E_{t}+4(\psi ^{3}-\phi ^{3}+\phi \psi ^{2}-\phi ^{2}\psi )E_{\psi }+4(\phi ^{2}\psi +\phi ^{3}-\phi \psi ^{2}-\psi ^{3})A_{t} \nonumber \\&\quad +4(\phi ^{3}-\psi ^{3}+\phi ^{2}\psi -\phi \psi ^{2})E_{\phi }+(3\psi +5\phi )C_{x}+4(2\phi \psi -\psi ^{2}+3\phi ^{2})C \nonumber \\&+(3\psi +5\phi )E_{x}+4(\phi ^{2}-3\psi ^{2}-2\phi \psi )E=0, \nonumber \\&-\frac{1}{2}B_{xx}+3E+E_{x\psi }+C_{x\psi }+B_{t}+5C-(5\psi +3\phi )E_{\phi }+(5\phi +3\psi )A_{t} \nonumber \\&+(5\phi +3\psi )C_{\psi }-(5\phi +3\psi )B_{x}=0, \nonumber \\&\frac{1}{2}C_{\phi }-\frac{1}{2}E_{\psi }+\frac{1}{2}A_{t}-B_{x}=0. \end{aligned}$$
(6)

By solving the above partial differential system, we get

$$\begin{aligned} A= & {} c_{1}t+c_{2}, \nonumber \\ B= & {} \frac{1}{2}c_{1}x+c_{3}, \nonumber \\ C= & {} (\psi -\phi )h(x)-\frac{1}{2}c_{1}\psi , \nonumber \\ E= & {} (\phi -\psi )h(x)-\frac{1}{2}c_{1}\phi , \end{aligned}$$
(7)

where \(c_{1},c_{2}\) and \(c_{3}\) are arbitrary constants, h(x) is an arbitrary function of x. Therefore, the Lie algebra generators of the SCBE system are given by

$$\begin{aligned} \chi _{1}= & {} t\frac{\partial }{\partial t}+\frac{1}{2}x\frac{\partial }{ \partial x}-\frac{1}{2}\psi \frac{\partial }{\partial \phi }-\frac{1}{2}\phi \frac{\partial }{\partial \psi }, \nonumber \\ \chi _{2}= & {} \frac{\partial }{\partial t}, \nonumber \\ \chi _{3}= & {} \frac{\partial }{\partial x},{ \ \ \ \ } \nonumber \\ \chi _{h}= & {} (\psi -\phi )\frac{\partial }{\partial \phi }+(\phi -\psi ) {\ }\frac{\partial }{\partial \psi }{.\ \ \ \ \ } \end{aligned}$$
(8)

By comparison with [5], the SCBE system is integrable if the symmetries obtained are of third (if \(h(x)=0\)) and fourth order symmetries, it means that the generator \(\chi _{h}\) should be zero. Therefore, \(h(x)=0\) and \(\phi =\psi \).

Further, from the infinitesimal symmetries given by Eqs. (8), the following possibilities exist for the reduction of system (1)

  1. (i)

    \(c_{1}\ne 0,\) \(c_{2}\ne 0,\) \(c_{3}\ne 0,\ \ \)

  2. (ii)

    \(c_{1}=0,\) \(c_{2}\ne 0,\) \(c_{3}\ne 0.\ \)

The new independent and dependent similarity variables corresponding to cases I and II can be obtained by solving the following equation

$$\begin{aligned} \frac{dt}{A\left( t,x,\phi ,\psi \right) }=\frac{dx}{B\left( t,x,\phi ,\psi \right) }=\frac{du}{C\left( t,x,\phi ,\psi \right) }=\frac{dv}{E\left( t,x,\phi ,\psi \right) }. \end{aligned}$$
(9)

Reductions and new solutions

In this section we are going to find the reductions of system (1) into nonlinear ordinary differential system in the independent similarity variable \(\zeta \) and the new dependent variable g

Case (i):

From Eq. (9) with conditions \(h(x)=0\) and \(\phi =\psi \)

$$\begin{aligned} \frac{dt}{c_{1}t+c_{2}}=\frac{dx}{\frac{1}{2}c_{1}x+c_{3}}=\frac{d\phi }{- \frac{1}{2}c_{1}\phi }=\frac{d\psi }{-\frac{1}{2}c_{1}\psi }. \end{aligned}$$
(10)

So that, we get

$$\begin{aligned} \zeta =\frac{(x+2\frac{c_{3}}{c_{1}})^{2}}{t+\frac{c_{2}}{c_{1}}}{,}\ {\ \ \ }\phi =\psi =\left( t+\frac{c_{2}}{c_{1}}\right) ^{-\frac{1}{2}}g(\zeta ). \end{aligned}$$
(11)

Inserting Eq. (11) into (1), the SCBE is reduced to the following nonlinear single ordinary differential equation:

$$\begin{aligned} \frac{1}{2}g+\zeta g^{\prime }+4\zeta g^{\prime }+2g^{\prime }+32\zeta ^{ \frac{1}{2}}gg^{\prime }=0. \end{aligned}$$
(12)

Assume that the solution of (12) takes the form

$$\begin{aligned} g=A_{1}\zeta ^{\frac{-1}{2}}+A_{2}\zeta ^{\frac{1}{2}}, \end{aligned}$$
(13)

where \(A_{1},A_{2}\) are constants to determine it, substitute from (13) into (12) and collect the powers of \(\zeta \), then equate it by zero, an algebraic system is obtained. Solve it by Maple program, the following values are given

$$\begin{aligned} A_{1}=\frac{1}{8},A_{2}=-\frac{1}{16}. \end{aligned}$$
(14)

By inserting (14) into (13) , then using it in (11), the SCBE has the new rational solution

$$\begin{aligned} \phi _{1}(x,t)=\psi _{1}(x,t)=\frac{1}{8\left( x+\frac{c_{3}}{c_{1}}\right) }-\frac{x+ \frac{c_{3}}{c_{1}}}{16\left( t+\frac{c_{2}}{c_{1}}\right) }, \ \ \text { with }c_{1}\ne 0 \end{aligned}$$
(15)

Case (ii)

From Eq. (9)

$$\begin{aligned} \frac{dt}{c_{1}t+c_{2}}=\frac{dx}{\frac{1}{2}c_{1}x+c_{3}}=\frac{d\phi }{0}= \frac{d\psi }{0} \end{aligned}$$
(16)

The associated new similarity variables are

$$\begin{aligned} \zeta =\frac{c_{2}}{c_{3}}x-t{,}\ \ \ \phi =\psi =g(\zeta ). \end{aligned}$$
(17)

The SCBE system is reduced to the following Ricatti equation

$$\begin{aligned} g^{\prime }+\frac{c_{2}^{2}}{c_{3}^{2}}g^{\prime \prime }+16\frac{c_{2}}{ c_{3}}gg^{\prime }=0. \end{aligned}$$
(18)

Integrating Eq. (18) with respect to \(\zeta ,\) we obtain

$$\begin{aligned} g+\frac{c_{2}^{2}}{c_{3}^{2}}g^{\prime }+8\frac{c_{2}}{c_{3}}g^{2}=c_{4}, \end{aligned}$$
(19)

where \(c_{4}\) is an arbitrary integration constant. Equation (19) can be rewritten as

$$\begin{aligned} g^{\prime }=c_{4}\frac{c_{3}^{2}}{c_{2}^{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}g-8 \frac{c_{3}}{c_{2}}g^{2}. \end{aligned}$$
(20)

Now, Eq. (20) has the following hyperbolic and periodic wave solutions

$$\begin{aligned} g_{2}(\zeta )= & {} \frac{1}{16}\left[ -\frac{c_{3}}{c_{2}}+\sqrt{\frac{c_{3}^{2}}{ c_{2}^{2}}+32\frac{c_{4}c_{3}}{c_{2}}}\tanh \left( \frac{1}{2}\frac{c_{3}}{c_{2}} \sqrt{\frac{c_{3}^{2}}{c_{2}^{2}}+32\frac{c_{4}c_{3}}{c_{2}}}(\zeta +\zeta _{0})\right) \right] ,{ \ }c_{4}<0, \end{aligned}$$
(21)
$$\begin{aligned} g_{3}(\zeta )= & {} \frac{1}{16}\left[ -\frac{c_{3}}{c_{2}}+\sqrt{\frac{c_{3}^{2}}{ c_{2}^{2}}+32\frac{c_{4}c_{3}}{c_{2}}}\coth \left( \frac{1}{2}\frac{c_{3}}{c_{2}} \sqrt{\frac{c_{3}^{2}}{c_{2}^{2}}+32\frac{c_{4}c_{3}}{c_{2}}}(\zeta +\zeta _{0})\right) \right] ,\,{ }c_{4}<0, \end{aligned}$$
(22)
$$\begin{aligned} g_{4}(\zeta )= & {} -\frac{1}{16}\left[ \frac{c_{3}}{c_{2}}+\sqrt{-32\frac{ c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}}\tan \left( \frac{1}{2}\frac{c_{3}}{ c_{2}}\sqrt{-32\frac{c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}}(\zeta +\zeta _{0})\right) \right] ,{\ }c_{4}>0, \end{aligned}$$
(23)
$$\begin{aligned} g_{5}(\zeta )= & {} -\frac{1}{16}\left[ \frac{c_{3}}{c_{2}}-\sqrt{-32\frac{ c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}}\cot \left( \frac{1}{2}\frac{c_{3}}{ c_{2}}\sqrt{-32\frac{c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}}(\zeta +\zeta _{0})\right) \right] {\ , }c_{4}>0, \end{aligned}$$
(24)
$$\begin{aligned} g_{6}(\zeta )= & {} -\frac{1}{16}\frac{c_{3}}{c_{2}}\left[ 1-\tanh \left( \frac{1}{2} \frac{c_{3}^{2}}{c_{2}^{2}}(\zeta +\zeta _{0})\right) \right] ,{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }c_{4}=0, \end{aligned}$$
(25)
$$\begin{aligned} g_{7}(\zeta )= & {} -\frac{1}{16}\frac{c_{3}}{c_{2}}\left[ 1-\coth \left( \frac{1}{2} \frac{c_{3}^{2}}{c_{2}^{2}}(\zeta +\zeta _{0})\right) \right] ,{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }c_{4}=0, \end{aligned}$$
(26)
$$\begin{aligned} g_{8}(\zeta )= & {} -\frac{c_{3}}{8c_{2}-c_{3}\zeta _{0}\exp \left[ \frac{c_{3}^{2}}{ c_{2}^{2}}\zeta \right] },{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }c_{4}=0. \end{aligned}$$
(27)

where \(\zeta _{0}\) is an arbitrary integration constant.

Fig. 1
figure 1

The rational solution (15) with \(c_{1}=c_{2}=c_{3}=1\)

Full size image
Fig. 2
figure 2

The shock wave solution (28) with \(c_{2}=1,c_{3}=c_{4}=-1,\varsigma _{0}=0\)

Full size image
Fig. 3
figure 3

Kink wave solution (29) with \(c_{2}=1,c_{3}=c_{4}=-1\) and \(\varsigma _{0}=0\)

Full size image
Fig. 4
figure 4

The periodic wave solution (30) with \( c_{2}=c_{4}=1,c_{3}=-1\) and \(\varsigma _{0}=0\)

Full size image
Fig. 5
figure 5

The periodic wave solution (31) with \(c_{2}=c_{4}=1,c_{3}=-1\) and \(\varsigma _{0}=0\)

Full size image
Fig. 6
figure 6

Plot of the shock wave solution (32) with \( c_{2}=c_{3}=1\) and \(\varsigma _{0}=0\)

Full size image
Fig. 7
figure 7

Plot of the dark kink wave solution (33) with \(c_{2}=c_{3}=1\) and \(\varsigma _{0}=0\)

Full size image
Fig. 8
figure 8

Plot of the traveling wave solution (34) with \( c_{2}=c_{3}=1\) and \(\varsigma _{0}=0\)

Full size image

By inserting Eqs. (21)–(27) into (17) , the following Kink soliton solutions and periodic wave solutions are constructed for the Coupled symmetric Burgers-Type Equations

$$\begin{aligned} \phi _{2}(x,t)= & {} \psi _{2}(x,t)=\frac{1}{16}\left[ -\frac{c_{3}}{c_{2}}+\sqrt{ \frac{c_{3}^{2}}{c_{2}^{2}}+32\frac{c_{4}c_{3}}{c_{2}}}\right. \nonumber \\&\left. \tanh \left( \frac{1}{2} \frac{c_{3}}{c_{2}}\sqrt{\frac{c_{3}^{2}}{c_{2}^{2}}+32\frac{c_{4}c_{3}}{ c_{2}}}\left( \frac{c_{2}}{c_{3}}x-t+\zeta _{0}\right) \right) \right] ,{ \ }c_{4}<0, \end{aligned}$$
(28)
$$\begin{aligned} \phi _{3}(x,t)= & {} \psi _{3}(x,t)=\frac{1}{16}\left[ -\frac{c_{3}}{c_{2}}+\sqrt{ \frac{c_{3}^{2}}{c_{2}^{2}}+32\frac{c_{4}c_{3}}{c_{2}}}\right. \nonumber \\&\left. \coth \left( \frac{1}{2} \frac{c_{3}}{c_{2}}\sqrt{\frac{c_{3}^{2}}{c_{2}^{2}}+32\frac{c_{4}c_{3}}{ c_{2}}}\left( \frac{c_{2}}{c_{3}}x-t+\zeta _{0}\right) \right) \right] ,\,c_{4}<0, \end{aligned}$$
(29)
$$\begin{aligned} \phi _{4}(x,t)= & {} \psi _{4}(x,t)=-\frac{1}{16}\left[ \frac{c_{3}}{c_{2}}+\sqrt{ -32\frac{c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}}\right. \nonumber \\&\left. \tan \left( \frac{1}{2} \frac{c_{3}}{c_{2}}\sqrt{-32\frac{c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{ c_{2}^{2}}}\left( \frac{c_{2}}{c_{3}}x-t+\zeta _{0}\right) \right) \right] ,\,{\ }c_{4}>0, \end{aligned}$$
(30)
$$\begin{aligned} \phi _{5}(x,t)= & {} \psi _{5}(x,t)=-\frac{1}{16}\left[ \frac{c_{3}}{c_{2}}-\sqrt{ -32\frac{c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{c_{2}^{2}}}\right. \nonumber \\&\left. \cot \left( \frac{1}{2} \frac{c_{3}}{c_{2}}\sqrt{-32\frac{c_{4}c_{3}}{c_{2}}-\frac{c_{3}^{2}}{ c_{2}^{2}}}\left( \frac{c_{2}}{c_{3}}x-t+\zeta _{0}\right) \right) \right] \,{\ , }c_{4}>0, \end{aligned}$$
(31)
$$\begin{aligned} \phi _{6}(x,t)= & {} \psi _{6}(x,t)=-\frac{1}{16}\frac{c_{3}}{c_{2}}\left[ 1-\tanh \left( \frac{1}{2}\frac{c_{3}^{2}}{c_{2}^{2}}\left( \frac{c_{2}}{c_{3}}x-t+\zeta _{0}\right) \right) \right] ,{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }c_{4}=0, \end{aligned}$$
(32)
$$\begin{aligned} \phi _{7}(x,t)= & {} \psi _{7}(x,t)=-\frac{1}{16}\frac{c_{3}}{c_{2}}\left[ 1-\coth \left( \frac{1}{2}\frac{c_{3}^{2}}{c_{2}^{2}}\left( \frac{c_{2}}{c_{3}}x-t+\zeta _{0}\right) \right) \right] ,{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }c_{4}=0, \end{aligned}$$
(33)
$$\begin{aligned} \phi _{8}(x,t)= & {} \psi _{8}(x,t)=-\frac{c_{3}}{8c_{2}-c_{3}\zeta _{0}\exp \left[ \frac{c_{3}^{2}}{c_{2}^{2}}\left( \frac{c_{2}}{c_{3}}x-t\right) \right] },{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }c_{4}=0.\nonumber \\ \end{aligned}$$
(34)

Results and discussion

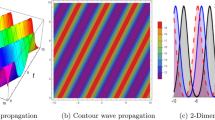
Burgers’ equation is yield because of merging both nonlinear wave motion with linear diffusion. Existence of viscous term helps control the wave-breaking, smooth out shock discontinuities so that, we know that the obtained will be well-behaved and smooth solution. Additionally, in the inviscid limit, as the diffusion term becomes very small, the smooth viscous solutions converge non-uniformly to the appropriate discontinuous shock wave. In the following are some graphs for the obtained solutions (28)–(34) to illustrate the shock and kink waves behavior for the obtained solutions.(See Figs. 1, 2, 3, 4, 5, 6, 7, and 8)

The above figures illustrate both discontinuously and smoothly wave propagation for the obtained shock, kink, and periodic wave solutions .

Conclusion

In this paper, the SCBE is studied by using the symmetry method due to Steinberg. The obtained symmetries are infinite symmetries, but according to Foursov in [1], the SCBE system is integrable and symmetric if it has a third and a fourth-order symmetry; therefore, \(h(x)=0\) and \(\phi \)=\(\psi \). After that, the SCBE under two different cases is transformed to only one reduced nonlinear ordinary differential equation. By obtaining solutions for the reduced differential equations, new exact solutions for the SCBE system are obtained. Furthermore, the graphs for the obtained shock, kink, and periodic wave solutions illustrate both discontinuously and smoothly wave propagation. Finally, we could conclude that the obtained solutions for the SCBE system are new and cover other solutions obtained before [3].