Novel solitary waves solutions of the extended cubic(3+1)-dimensional Schr$\ddot{o}$dinger equation via applications of three mathematical methods

Abstract

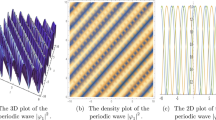
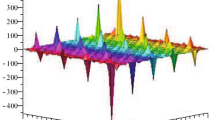
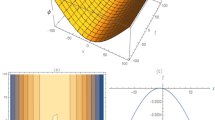
In this manuscript, solitary wave solution of the extended (3+1)-dimensional cubic Schr$\ddot{o}$dinger equation are constructed by application of three mathematical methods. These methods are namely called, extended simple equation method, modified extended auxiliary equation mapping method and $(G'/G)$-expansion method respectively. We have derived different types solutions in the form of trignometric, hypberbolic, exponential and rational functions. For the physical phenomena of the concern equation, some solutions are plotted 2-dimensional and 3-dimensional by assigning the particular values to the parameters under the constrain conditions with the assistance of Mathematica software. The extended (3+1)-dimensional cubic Schr$\ddot{o}$dinger equation is used to describe the propagation of pulses in highly nonlinear optical systems. Hence all results obtained by our proposed methods are novel and have not been yet reported in any literature. Moreover, this study will support physicists to envisage certain novel hypothesis and theories in nonlinear optical systems.

1 Introduction

Solitons are nonlinear solitary waves that keep their shape according to propagation without change so it is very important and has many applications in physical science especially in optics. A evolving attentiveness has been enthralled in the research of analytical and numerical solutions of nonlinear evolutions equations during the prior eras (Islam et al. 2020; Asaduzzaman and Ali 2022; Gharami et al. 2022; Ananna et al. 2022; Rozenman et al. 2020; Al-Ghafri et al. 2022). NLEEs are used to determine phenomena in divergent pitches of science and engineering such as plasmas, biology, fluid mechanics, acoustics, and numerous others (Houwe et al. 2020a; 2020b; 2020c; Kudryashov 2012; 2013a; b; Zayed and Arnous 2012; Ryabov et al. 2011; Wang et al. 2008; Ismail and Turgut 2009; Nestor et al. 2020a, b, c, d, e; Abbagari et al. 2020a). Exact and solitary wave solutions of nonlinear partial differential equations were made conceivable with the instigation of the choice of mathematical tools (Kudryashov 2012; 2013a; 2013b; Zayed and Arnous 2012; Houwe et al. 2020b; c; 2021; Ryabov et al. 2011; Wang et al. 2008; Ismail and Turgut 2009; Nestor et al. 2020a, b, c, d, e; Abbagari et al. 2020a, b, 2011, 2012, 2017; Mukam et al. 2018a; Yepez-Martinez et al. 2019; Mukam et al. 2018b; Inc et al. 2020). Presently, miscellaneous categories of nonlinear evolution equations have been established using an influential reductive perturbation method or a multiscale analysis (Wang et al. 2020a, b; Zhang and Yang 2021, 2019). Further specially, the investigation of exact solutions called soliton-like solutions has advanced quickly today, which is one of the important topics of nonlinear science. Solitons have enormous features because of their stuff (stability, robustness, and the ability to preserve their velocity and shape after interaction) (Nestor et al. 2020b, c, d, e; Abbagari et al. 2020a), and they occur in various forms such as bright, dark, kink, pulses, breather, and so on.Furthermore, latterly, novel forms of bright and dark solitons known as W-shape and M-shape have been exposed in Elsayed et al. (2019); El-Taibany et al. (2019); Sabry et al. (2008); El-Shiekh and Al-Nowehy (2013); Munro and Parkes (1999) and also many others methods to find the extact and travelling wave solutions of nonlinear problems discussed in Haci et al. (2021); Dipankar et al. (2020); Sadia et al. (2024); Khalid et al. (2020); Abdel-Gawad and Osman (2013, 2014); Sachin et al. (2022); Sania et al. (2023); Farhana et al. (2023); Ismael et al (2023); Rahman et al. (2024); Rehman et al. (2023); Akinyemi et al. (2023); Abdel-Gawad et al. (2016, 2013); Fahim et al. (2022); Islam et al. (2024); Chen et al. (2021). However, searching for the exact traveling wave solutions still carriages a problem at times due to not all the known methods can be applied to NLEEs.

The extended (3+1)-dimensional nonlinear Schr$\ddot{o}$dinger equation is used to describe the pulse propagation in nonlinear optical fibers and has the following mathematical form as mentioned in El-Shiekh et al. (2023); Wazwaz and Mehanna (2021);

$$\begin{aligned} iU_{t}+P_1 U_{xy}+P_2U_{yz}+P_3U_{xz}+i\left( Q_1U_{x}+Q_2U_{y}+Q_3U_{z}\right) +rU|U|^2-U_{xx}-U_{yy}-U_{yy}=0, \end{aligned}$$

(1)

This In this present research, we have discovered solitary wave solutions by applying three mathematical methods, Enhanced simple equation method, modified extended auxiliary equation mapping method and $(G'/G)$-expansion method (Seadawy and Lu 2018; Seadawy et al. 2021a, b). The derived solutions have great probable to handle nonlinear problems in mathematical physics.

The remaining part of work is prearranged as: In Sect. 2, demonstrate the fundamental steps of proposed three methos. In Sect. 3, we apply the declared methods to display wave solutions.Finally, Sect. 4 delivers abridgment for the current work.

2 Description of methods

Consider a nonlinear partial differential equation (NPDE)

$$\begin{aligned} F_1\left( U, U_{t}, U_{x},U_{y},U_{z},U_{xx},U_{yt},U{xz},U_{zz},... \right) =0, \end{aligned}$$

(2)

Let the traveling wave transformation

$$\begin{aligned} U(x,y,z,t)= V(\xi )~e^{i\eta }, ~~~~~~ \xi =\mu _1 x+\mu _2 y+\mu _3 z+\delta t,~~~\eta =\alpha x+\beta y+\gamma z+\omega t \end{aligned}$$

(3)

Subsituting Eq. (3) into Eq. (2),

$$\begin{aligned} F_{2}\left( V, V', V'',V''',...\right) e^{i\eta } \end{aligned}$$

(4)

2.1 Extended simple equation method

Assume that Eq. (4) has the following solutions form;

$$\begin{aligned} V = \sum ^N_ {i=-N}A_i\Psi ^i(\xi ) \end{aligned}$$

(5)

Let $\Psi '$ satisfy,

$$\begin{aligned} \Psi '= c_0+c_1\Psi + c_2\Psi ^2+c_3\Psi ^3 \end{aligned}$$

(6)

Putting Eq. (5) with Eq. (6) in Eq. (4). Solved the achieved system for solutions Eq. (2).

2.2 Modified extended auxiliary equation mapping method

Suppose that solution of Eq. (4) is,

$$\begin{aligned} V= \sum ^N_ {i=0}A_i\Psi ^i+\sum ^{-N}_ {i=-1}B_{-i}\Psi ^i+ \sum ^N_ {i=2}C_i\Psi ^{i-2}\Psi ^{'}+ \sum ^N_ {i=1}D_i\left( \frac{\Psi ^{'}}{\Psi }\right) ^i \end{aligned}$$

(7)

Let $\Psi '$ satisfiy,

$$\begin{aligned} \Psi ' = \sqrt{\beta _1\Psi ^2+\beta _2\Psi ^3+\beta _3\Psi ^4} \end{aligned}$$

(8)

Puttinh Eq. (7) with Eq. (8) in Eq. (4). Solved the achieved system for solutions Eq. (2) (Figs. 1, 2, 3, 4 and 5 ).

2.3 The $(G'/G)$-expansion method

Suppose that Eq. (4) has following solutiion form as;

$$\begin{aligned} V=A_{0}+\sum _{i=1}^N A_{i}\left( \frac{G'}{G}\right) \end{aligned}$$

(9)

Let

$$\begin{aligned} G''=-\lambda G'-\mu G \end{aligned}$$

(10)

Put Eq. (9) with Eq. (10) in Eq. (4). Solved the achieved system for solutions Eq. (2).

3 Applications

By putting Eq. (3) in Eq. (1), we have the real and imaginary parts as;

The real parts as;

$$\begin{aligned}&\left( -\mu _1^2-\mu _2^2-\mu _3^2+\mu _2 \mu _1 P_1+\mu _3 \mu _1 P_3+\mu _2 \mu _3 P_2\right) V''+rV^3\nonumber \\ {}&-\left( -\alpha ^2-\beta ^2-\gamma ^2+\alpha \beta P_1+\alpha \gamma P_3+\beta \gamma P_2+\alpha Q_1+\beta Q_2+\gamma Q_3+\omega \right) V=0, \end{aligned}$$

(11)

The imaginary parts as;

$$\begin{aligned}&V'\left( \delta +Q_1\mu _1+ Q_2\mu _2+Q_3\mu _3+P_1\mu _1\beta +P_1\mu _2\alpha +\gamma P_2\mu _2+\beta \mu _3P_2+P_3\mu _1\gamma +P_3\mu _3\alpha \right) \nonumber \\ {}&-2\left( \alpha \mu _1+\beta \mu _2+\gamma \mu _3\right) V'=0 \end{aligned}$$

(12)

Suppose that the imaginary part is finished so we have the following condition on the constants

$$\begin{aligned} \delta =&-\left( Q_1\mu _1+ Q_2\mu _2+Q_3\mu _3+P_1\mu _1\beta +P_1\mu _2\alpha +\gamma P_2\mu _2+\beta \mu _3P_2+P_3\mu _1\gamma +P_3\mu _3\alpha \right) \nonumber \\ {}&+2\left( \alpha \mu _1+\beta \mu _2+\gamma \mu _3\right) =0 \end{aligned}$$

(13)

Then, Eq. (11) has the following form as;

$$\begin{aligned}&V''-\left( \frac{ \left( -\alpha ^2-\beta ^2-\gamma ^2+\alpha \beta P_1+\alpha \gamma P_3+\beta \gamma P_2+\alpha Q_1+\beta Q_2+\gamma Q_3+\omega \right) }{-\mu _1^2-\mu _2^2-\mu _3^2+\mu _2 \mu _1 P_1+\mu _3 \mu _1 P_3+\mu _2 \mu _3 P_2}\right) V\nonumber \\ {}&\left( \frac{r }{-\mu _1^2-\mu _2^2-\mu _3^2+\mu _2 \mu _1 P_1+\mu _3 \mu _1 P_3+\mu _2 \mu _3 P_2}\right) V^3 \end{aligned}$$

(14)

3.1 Application of extended simple equation method

Suppose solution of Eq. (14) is,

$$\begin{aligned} V=A_1 \Psi +\frac{A_{-1}}{\Psi }+A_0 \end{aligned}$$

(15)

Putting Eq. (15) with (6) in (14), We the following solutions Cases as;

Case 1: $c_3=0$,

Family-I

$$\begin{aligned}&A_{-1}=0,~A_1=-\left( \frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) \nonumber \\ {}&A_0=-\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \nonumber \\ {}&\omega =\left( \alpha ^2+\beta ^2+\gamma ^2-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3\right) +\nonumber \\ {}&\frac{1}{2} \left( c_1^2-4 c_0 c_2\right) \left( \mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2\right) \end{aligned}$$

(16)

Put (16) in (15)

$$\begin{aligned} V_{1}=&-\left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2} \left( \sqrt{4 c_0 c_2-c_1^2} \tan \left( \frac{1}{2} \sqrt{4 c_0 c_2-c_1^2} \left( \xi +\xi _0\right) \right) +c_1\right) }{\sqrt{2} \sqrt{r}}\right) \nonumber \\ {}&-\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) ,~4c_0c_2>c_1^{2}. \end{aligned}$$

(17)

From Eq. (3) and Eq. (17) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{1}=&-\left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2} \left( \sqrt{4 c_0 c_2-c_1^2} \tan \left( \frac{1}{2} \sqrt{4 c_0 c_2-c_1^2} \left( \xi +\xi _0\right) \right) +c_1\right) }{\sqrt{2} \sqrt{r}}\right) e^{i\eta }\nonumber \\ {}&-\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta },~4c_0c_2>c_1^{2}. \end{aligned}$$

(18)

Fig. 1

The 3D and 2D plot of periodic waves of $U_{1}$ with $\alpha =0.1,~\beta =0,~c_0=1,~c_1=1.5,~c_2=1,~\gamma =0,~\delta =0.3,~\mu _1=2.3,~\mu _2=0.03,~\mu _3=0.2,~\xi _0=0.007,~P_1=0.3,~P_2=0.04,~P_3=0.4,~Q_1=2.3,~Q_2=2,~Q_3=3.1,~r=2.5,~y=1,~z=1.$

Family-II

$$\begin{aligned}&A_1=0,~A_0=\left( -\frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) ,~\nonumber \\ {}&A_{-1}=-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) \nonumber \\ {}&\omega =\frac{1}{2} \left( c_1^2-4 c_0 c_2\right) \left( \mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2\right) \nonumber \\ {}&+\left( \alpha ^2+\beta ^2+\gamma ^2-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3\right) \end{aligned}$$

(19)

Substitute Eq. (19) in Eq. (15)

$$\begin{aligned} V_{2}=&\left( -\frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \nonumber \\ {}&-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) \nonumber \\ {}&\left( \frac{2 c_2}{\sqrt{4 c_0 c_2-c_1^2} \tan \left( \frac{1}{2} \sqrt{4 c_0 c_2-c_1^2} \left( \xi +\xi _0\right) \right) +c_1}\right) ,~4c_0c_2>c_1^{2} \end{aligned}$$

(20)

From Eqs. (3 and 20) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{2}=&\left( -\frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \nonumber \\ {}&-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) e^{i\eta }\nonumber \\ {}&\left( \frac{2 c_2}{\sqrt{4 c_0 c_2-c_1^2} \tan \left( \frac{1}{2} \sqrt{4 c_0 c_2-c_1^2} \left( \xi +\xi _0\right) \right) +c_1}\right) e^{i\eta },~4c_0c_2>c_1^{2} \end{aligned}$$

(21)

Case 2:   $c_0=c_3=0$,

$$\begin{aligned}&A_{-1}=0,~A_1=\left( \frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) \nonumber \\ {}&A_0=\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \nonumber \\ {}&\omega =\frac{1}{2} \left( c_1^2 \mu _1^2+c_1^2 \mu _2^2+c_1^2 \mu _3^2-c_1^2 \mu _1 \mu _2 P_1-c_1^2 \mu _1 \mu _3 P_3-c_1^2 \mu _2 \mu _3 P_2\right) +\nonumber \\ {}&\left( \alpha ^2+\beta ^2+\gamma ^2-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3\right) \end{aligned}$$

(22)

Putting Eq. (22) in Eq. (15)

$$\begin{aligned} V_{3} =&\left( \frac{\left( c_1 \exp \left( c_1 \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{\sqrt{r} \left( 1-c_2 \exp \left( c_1 \left( \xi +\xi _0\right) \right) \right) }\right) +\nonumber \\ {}&\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) ,~c_1>0. \end{aligned}$$

(23)

From Eqs. (3 and 23) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{3} =&\left( \frac{\left( c_1 \exp \left( c_1 \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{\sqrt{r} \left( 1-c_2 \exp \left( c_1 \left( \xi +\xi _0\right) \right) \right) }\right) e^{i\eta }+\nonumber \\ {}&\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta },~c_1>0. \end{aligned}$$

(24)

$$\begin{aligned} V_{4} =&\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) +\left( -\frac{c_1 \exp \left( c_1 \left( \xi +\xi _0\right) \right) }{c_2 \exp \left( c_1 \left( \xi +\xi _0\right) \right) +1}\right) \nonumber \\ {}&\left( \frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) ,~c_1<0. \end{aligned}$$

(25)

From Eqs. (3 and 25) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{4} =&\left( \frac{c_1 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta }-\left( \frac{c_1 \exp \left( c_1 \left( \xi +\xi _0\right) \right) }{c_2 \exp \left( c_1 \left( \xi +\xi _0\right) \right) +1}\right) \nonumber \\ {}&\left( \frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) e^{i\eta },~c_1<0. \end{aligned}$$

(26)

Fig. 2

The 3D and 2D plot of bright waves of $U_{3}$ with $\alpha =0.3,~\beta =0.2,~c_1=1.5,~c_2=1,~\gamma =0.5,~\delta =0.3,~\mu _1=2.3,~\mu _2=0.03,~\mu _3=0.2,~\xi _0=0.006,~P_1=0.2,~P_2=0.04,~P_3=0.4,~Q_1=2.3,~Q_2=2,~Q_3=3.1,~r=2.5,~y=1;,~z=1.$

Case 3:    $c_1=0,~~c_3=0$,

Family-I

$$\begin{aligned}&A_{-1}=0,~A_1=\left( -\frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) ,~A_0=0,\nonumber \\ {}&\omega =\alpha ^2+\beta ^2+\gamma ^2-2 c_0 c_2 \mu _1^2+2 c_0 c_2 \mu _1 \mu _2 P_1-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3\nonumber \\ {}&-2 c_0 c_2 \mu _2^2-2 c_0 c_2 \mu _3^2+2 c_0 c_2 \mu _3 \mu _2 P_2+2 c_0 c_2 \mu _1 \mu _3 P_3 \end{aligned}$$

(27)

Put (27) in (15),

$$\begin{aligned} V_{5}=&-\left( \frac{\left( \sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) ,\nonumber \\ {}&~c_0c_2>0, \end{aligned}$$

(28)

From Eqs. (3 and 28) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{5}=&-\left( \frac{\left( \sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) e^{i\eta },\nonumber \\ {}&~c_0c_2>0, \end{aligned}$$

(29)

$$\begin{aligned} V_{6}=&\left( -\frac{\left( \sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) ,\nonumber \\ {}&~c_0c_2<0. \end{aligned}$$

(30)

From Eqs. (3 and 30) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{6}=&\left( -\frac{\left( \sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) e^{i\eta },\nonumber \\ {}&~c_0c_2<0. \end{aligned}$$

(31)

Family-II

$$\begin{aligned}&A_{-1}=-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) ,~A_1=0,~A_0=0,\nonumber \\ {}&\omega =\alpha ^2+\beta ^2+\gamma ^2-2 c_0 c_2 \mu _1^2+2 c_0 c_2 \mu _1 \mu _2 P_1-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3-\nonumber \\ {}&2 c_0 c_2 \mu _2^2-2 c_0 c_2 \mu _3^2+2 c_0 c_2 \mu _3 \mu _2 P_2+2 c_0 c_2 \mu _1 \mu _3 P_3 \end{aligned}$$

(32)

Put Eq. (32) in Eq. (15)

$$\begin{aligned} V_{7}=-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\frac{\sqrt{r} \left( \sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) \right) }{c_2}}\right) ,~c_0c_2>0, \end{aligned}$$

(33)

From Eq. (3) and Eq. (33) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{7}=-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\frac{\sqrt{r} \left( \sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) \right) }{c_2}}\right) e^{i\eta },~c_0c_2>0, \end{aligned}$$

(34)

$$\begin{aligned} V_{8}=-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\frac{\sqrt{r} \left( \sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) \right) }{c_2}}\right) ,~c_0c_2<0. \end{aligned}$$

(35)

From Eq. (3) and Eq. (35) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{8}=-\left( \frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\frac{\sqrt{r} \left( \sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) \right) }{c_2}}\right) e^{i\eta },~c_0c_2<0. \end{aligned}$$

(36)

Family-III

$$\begin{aligned}&A_1=-\left( \frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) ,~A_0=0,\nonumber \\ {}&\omega =\alpha ^2+\beta ^2+\gamma ^2+4 c_0 c_2 \mu _1^2-4 c_0 c_2 \mu _1 \mu _2 P_1-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3\nonumber \\ {}&+4 c_0 c_2 \mu _2^2+4 c_0 c_2 \mu _3^2-4 c_0 c_2 \mu _3 \mu _2 P_2-4 c_0 c_2 \mu _1 \mu _3 P_3\nonumber \\ {}&A_{-1}=\left( -\frac{\sqrt{2} c_0 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) \end{aligned}$$

(37)

Put Eq. (37) in Eq. (15),

$$\begin{aligned} V_{9}=&\left( -\frac{\left( \sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) \nonumber \\ {}&+\left( \frac{\left( -\frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) }{\frac{\sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) }{c_2}}\right) ,~c_0c_2>0, \end{aligned}$$

(38)

From Eq. (3) and Eq. (38) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{9}=&\left( -\frac{\left( \sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) e^{i\eta }\nonumber \\ {}&+\left( \frac{\left( -\frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) }{\frac{\sqrt{c_0 c_2} \tan \left( \sqrt{c_0 c_2} \left( \xi +\xi _0\right) \right) }{c_2}}\right) e^{i\eta },~c_0c_2>0, \end{aligned}$$

(39)

$$\begin{aligned} V_{10}=&\left( -\frac{\left( \sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) \nonumber \\ {}&+\left( \frac{\left( -\frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) }{\frac{\sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) }{c_2}}\right) ,~c_0c_2<0. \end{aligned}$$

(40)

From Eq. (3) and Eq. (40) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{10}=&\left( -\frac{\left( \sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) \right) \left( \sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) }{c_2 \sqrt{r}}\right) e^{i\eta }\nonumber \\ {}&+\left( \frac{\left( -\frac{\sqrt{2} c_2 \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) }{\frac{\sqrt{-c_0 c_2} \tanh \left( \sqrt{-c_0 c_2} \left( \xi +\xi _0\right) \right) }{c_2}}\right) e^{i\eta },~c_0c_2<0. \end{aligned}$$

(41)

3.2 Application of modified extended auxiliary equation mapping method

Assume Eq. (14) has solution,

$$\begin{aligned} V=A_1 \Psi +A_0+\frac{B_1}{\Psi }+D_1\left( \frac{ \Psi '}{\Psi }\right) \end{aligned}$$

(42)

Fig. 3

The 3D and 2D plot of bright waves of $U_{10}$ with $\alpha =0.2,~\beta =0.3,~c_0=-1.5,~c_2=1,~\gamma =0.6,~\delta =0.3,~\mu _1=2.3,~\mu _2=0.3,~\mu _3=0.3,~\xi =0.04,~P_1=0.3,~P_2=0.3,~P_3=0.7,~Q_1=2.4,~Q_2=2.1,~Q_3=3.2,~r=2.01,~y=1,~z=1.$

Put Eq. (42) with Eq. (8) in Eq. (14),

$$\begin{aligned}&A_0=0,~A_1=\left( \frac{\sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) ,~B_1=0,\nonumber \\ {}&\omega =\left( \alpha ^2+\beta ^2+\gamma ^2-\alpha \beta P_1-\alpha \gamma P_3-\beta \gamma P_2-\alpha Q_1-\beta Q_2-\gamma Q_3\right) +\nonumber \\ {}&\frac{1}{2} \left( \beta _1 \mu _1^2+\beta _1 \mu _2^2+\beta _1 \mu _3^2-\beta _1 \mu _2 \mu _1 P_1-\beta _1 \mu _3 \mu _1 P_3-\beta _1 \mu _2 \mu _3 P_2\right) \nonumber \\ {}&D_1=\frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}} \end{aligned}$$

(43)

Put Eq. (43) in Eq. (43)

Case I:

$$\begin{aligned} V_{11}=&\left( \frac{\left( \sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) \left( -\beta _1 \left( \epsilon \coth \left( \frac{1}{2} \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +1\right) \right) }{\beta _2 \left( \sqrt{2} \sqrt{r}\right) }\right) \nonumber \\ {}&\left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2} \left( \beta _1^{3/2} \epsilon \text {csch}^2\left( \frac{1}{2} \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) \right) }{\frac{\left( \sqrt{2} \sqrt{r}\right) \left( \left( 2 \beta _2\right) \left( -\beta _1 \left( \epsilon \coth \left( \frac{1}{2} \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +1\right) \right) \right) }{\beta _2}}\right) ,\nonumber \\ {}&~\beta _1>0,~~\beta _2^2-4\beta _1\beta _3=0. \end{aligned}$$

(44)

From Eq. (3) and Eq. (44) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{11}=&\left( \frac{\left( \sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}\right) \left( -\beta _1 \left( \epsilon \coth \left( \frac{1}{2} \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +1\right) \right) }{\beta _2 \left( \sqrt{2} \sqrt{r}\right) }\right) \nonumber \\ {}&\left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2} \left( \beta _1^{3/2} \epsilon \text {csch}^2\left( \frac{1}{2} \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) \right) }{\frac{\left( \sqrt{2} \sqrt{r}\right) \left( \left( 2 \beta _2\right) \left( -\beta _1 \left( \epsilon \coth \left( \frac{1}{2} \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +1\right) \right) \right) }{\beta _2}}\right) e^{i\eta },\nonumber \\ {}&~\beta _1>0,~~\beta _2^2-4\beta _1\beta _3=0. \end{aligned}$$

(45)

Case II:

$$\begin{aligned} V_{12}=&\left( -\frac{\sqrt{\frac{\beta _1}{\beta _3}} \left( \frac{\sqrt{\beta _1} \epsilon \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi }-\frac{\sqrt{\beta _1} \epsilon \sinh ^2\left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\left( \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi \right) ^2}\right) }{2 \left( -\sqrt{\frac{\beta _1}{4 \beta _3}} \left( \frac{\epsilon \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi }+1\right) \right) }\right) \left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}} \right) \nonumber \\ {}&+\left( \frac{\sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \left( -\sqrt{\frac{\beta _1}{4 \beta _3}} \left( \frac{\epsilon \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi }+1\right) \right) \nonumber \\ {}&,~\beta _1>0,~\beta _3>0, ~\beta _2=\left( 4\beta _1\beta _3\right) ^{1/2}. \end{aligned}$$

(46)

From Eq. (3) and Eq. (46) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{12}=&\left( -\frac{\sqrt{\frac{\beta _1}{\beta _3}} \left( \frac{\sqrt{\beta _1} \epsilon \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi }-\frac{\sqrt{\beta _1} \epsilon \sinh ^2\left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\left( \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi \right) ^2}\right) }{2 \left( -\sqrt{\frac{\beta _1}{4 \beta _3}} \left( \frac{\epsilon \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi }+1\right) \right) }\right) \left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}} \right) e^{i\eta }\nonumber \\ {}&+\left( \frac{\sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \left( -\sqrt{\frac{\beta _1}{4 \beta _3}} \left( \frac{\epsilon \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\chi }+1\right) \right) e^{i\eta }\nonumber \\ {}&,~\beta _1>0,~\beta _3>0, ~\beta _2=\left( 4\beta _1\beta _3\right) ^{1/2}. \end{aligned}$$

(47)

Case III:

$$\begin{aligned} V_{13}=&\left( -\frac{\beta _1 \left( \frac{\sqrt{\beta _1} \epsilon \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi }-\frac{\sqrt{\beta _1} \epsilon \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) \left( \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +P\right) }{\left( \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi \right) {}^2}\right) }{\frac{\beta _2 \left( -\beta _1 \left( \frac{\epsilon \left( \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +P\right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi }+1\right) \right) }{\beta _2}}\right) \nonumber \\ {}&\left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) +\left( \frac{\epsilon \left( \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +P\right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi }+1\right) \nonumber \\ {}&\left( \frac{\sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}} \right) ,~\beta _1>0. \end{aligned}$$

(48)

From Eq. (3) and Eq. (48) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{13}=&\left( -\frac{\beta _1 \left( \frac{\sqrt{\beta _1} \epsilon \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi }-\frac{\sqrt{\beta _1} \epsilon \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) \left( \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +P\right) }{\left( \cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi \right) {}^2}\right) }{\frac{\beta _2 \left( -\beta _1 \left( \frac{\epsilon \left( \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +P\right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi }+1\right) \right) }{\beta _2}}\right) \nonumber \\ {}&\left( \frac{\sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta }+\left( \frac{\epsilon \left( \sinh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +P\right) }{\cosh \left( \sqrt{\beta _1} \left( \xi +\xi _0\right) \right) +\sqrt{P^2+1} \chi }+1\right) \nonumber \\ {}&\left( \frac{\sqrt{\beta _3} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}} \right) e^{i\eta },~\beta _1>0. \end{aligned}$$

(49)

3.3 Application of $(G'/G)$-expansion method

Assume that Eq. (14) has solution form as,

$$\begin{aligned} V=A_1\left( \frac{ G'}{G}\right) +A_0 \end{aligned}$$

(50)

Put Eq. (50) with Eq. (10) in Eq. (14),

$$\begin{aligned}&A_0=\frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2}}{\sqrt{2 r}},~\nonumber \\ {}&A_1=\frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\nonumber \\ {}&\omega =\frac{1}{2} \left( 2 \alpha ^2+2 \beta ^2+2 \gamma ^2-2 \alpha \beta P_1-2 \alpha \gamma P_3-2 \beta \gamma P_2-2 \alpha Q_1-2 \beta Q_2-2 \gamma Q_3\right) +\nonumber \\ {}&\frac{1}{2}\left( \left( \lambda ^2 \mu _1^2+\lambda ^2 \mu _2^2-4 \mu \mu _1^2-4 \mu \mu _2^2-\lambda ^2 \mu _1 \mu _2 P_1-\lambda ^2 \mu _1 \mu _3 P_3+4 \mu \mu _1 \mu _2 P_1\right. \right) \end{aligned}$$

(51)

Put Eq. (51) in Eq. (50),

Fig. 4

The 3D and 2D plot of kink waves of $U_{11}$ with $\alpha =0.2,~\beta =0.01,~\beta _1=1,~\beta _2=2,~\beta _3=1,~\gamma =1.6,~\delta =1.3,~\mu _1=2.3,~\mu _2=0.3,~\mu _3=0.3,~\xi _0=-0.1,~P_1=0.3,~P_2=0.3,~P_3=0.7,~Q_1=2.4,~Q_2=2.1,~Q_3=0.02,~r=2.01,~y=1,~z=1,~\epsilon =1.$

Case I:          $\lambda ^2-4 \mu >0$

$$\begin{aligned} V_{14}=&\left( \frac{\sqrt{\lambda ^2-4 \mu } \left( L_1 \xi \sinh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) +L_2 \xi \cosh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) \right) }{2 \left( L_2 \xi \sinh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) +L_1 \xi \cosh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) \right) }-\frac{\lambda }{2}\right) \nonumber \\ {}&\left( \frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) +\nonumber \\ {}&\left( \frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \end{aligned}$$

(52)

From Eq. (3) and Eq. (52) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{14}=&\left( \frac{\sqrt{\lambda ^2-4 \mu } \left( L_1 \xi \sinh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) +L_2 \xi \cosh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) \right) }{2 \left( L_2 \xi \sinh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) +L_1 \xi \cosh \left( \frac{1}{2} \sqrt{\lambda ^2-4 \mu }\right) \right) }-\frac{\lambda }{2}\right) \nonumber \\ {}&\left( \frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) e^{i\eta }\nonumber \\ {}&+\left( \frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta } \end{aligned}$$

(53)

Case II:          $\lambda ^2-4 \mu <0$

$$\begin{aligned} V_{15}=&\left( \frac{\sqrt{4 \mu -\lambda ^2} \left( L_2 \xi \cos \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) -L_1 \xi \sin \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) \right) }{2 \left( L_2 \xi \sin \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) +L_1 \xi \cos \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) \right) }-\frac{\lambda }{2}\right) \nonumber \\ {}&\left( \frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) +\nonumber \\ {}&\left( \frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \end{aligned}$$

(54)

From Eq. (3) and Eq. (54) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{15}=&\left( \frac{\sqrt{4 \mu -\lambda ^2} \left( L_2 \xi \cos \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) -L_1 \xi \sin \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) \right) }{2 \left( L_2 \xi \sin \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) +L_1 \xi \cos \left( \frac{1}{2} \sqrt{4 \mu -\lambda ^2}\right) \right) }-\frac{\lambda }{2}\right) \nonumber \\ {}&\left( \frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{r}}\right) e^{i\eta }\nonumber \\ {}&+\left( \frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta } \end{aligned}$$

(55)

Fig. 5

The 3D and 2D plot of periodic waves of $U_{16}$ with $\alpha =0.6,\beta =0.01,~\gamma =1.6,~\delta =1.2,~\lambda =2,~\mu =1,~\mu _1=2.3,~\mu _2=0.3,~\mu _3=0.3,~L_1=2.03,~L_2=0.03,~P_1=0.3,~P_2=0.3,~P_3=0.7,~Q_1=2.4,~Q_2=2.1,~Q_3=0.02,~r=2.01,~y=1,~z=1.$

Case III:          $\lambda ^2-4 \mu =0$

$$\begin{aligned} V_{16}=&\left( \frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2} \left( \frac{L_2}{L_1+ \xi \text {L}_2}-\frac{\lambda }{2}\right) }{\sqrt{r}}\right) +\nonumber \\ {}&\left( \frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) \end{aligned}$$

(56)

From Eq. (3) and Eq. (56) the solution of Eq. (1) can be written as;

$$\begin{aligned} U_{16}=&\left( \frac{\sqrt{2} \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _1 \left( \mu _2 P_1+\mu _3 P_3\right) -\mu _2 \mu _3 P_2} \left( \frac{L_2}{L_1+ \xi \text {L}_2}-\frac{\lambda }{2}\right) }{\sqrt{r}}\right) e^{i\eta }+\nonumber \\ {}&\left( \frac{\lambda \sqrt{\mu _1^2+\mu _2^2+\mu _3^2-\mu _2 \mu _1 P_1-\mu _3 \mu _1 P_3-\mu _2 \mu _3 P_2}}{\sqrt{2} \sqrt{r}}\right) e^{i\eta } \end{aligned}$$

(57)

4 Conclusion

Solitons are nonlinear solitary waves that keep their shape according to propagation without change so it is very important and has many applications in physical science especially in optics. In this work, we have built abundant various solitary waves solutions of Eq. (1) by employing three mathematical methods (Seadawy and Lu 2018; Seadawy et al. 2021a, b) to obtain many distinct solitary wave solutions in the form of hyperbolic functions, trigonometric functions, exponential functions and rational functions. To represent the physical phenomena of Eq. (1), some solutions are plotted in 2-dimensional and 3-dimensional by assigning the specific value to the parameters. The whole calculations and figures are handling by assistance of Mathematica software.The offered mathematical methods are more powerful and investigated results have fruitful applications in optical fibers.