1 Introduction and problem statement

1.1 Scope

Incompressible viscous flows occur in various domains, surrounding and traversing porous media. These domains include the petroleum industry, automotive industry, underground water hydrology, biomedical engineering, and heat pipe modeling [1,2,3]. Typically, the Darcy model is useful for simulating slow flow problems [4, 5], but it does not perform well in describing cavity problems that arise in these applications. On the other hand, the Stokes–Darcy interface model can describe the flow of a viscous fluid in porous and cavity media. However, it is not practical due to the lack of accurate data regarding the number and locations of interfaces between the porous matrix and vugs. The Brinkman model, suggested by H. C. Brinkman [6] in 1949 [6], addresses this limitation and is employed to describe transport phenomena within porous media. The Brinkman model describes the flow of fluid within intricate porous media with highly variable permeability coefficients. In this model, the Darcy equation governs the flow in some areas, while the Stokes equation governs it in others. Unlike the Stokes–Darcy interface model, the Brinkman model can effectively model both Stokes and Darcy flows without relying on complicated interface conditions.

Furthermore, the Brinkman model can be understood mathematically as a combination of the Darcy and Stokes equations in a parameter-dependent form. The most significant challenge arises from the high variability in the coefficients of the partial differential equations (PDEs), which may take very large or very small values. This negatively impacts the conditioning of the discrete problem, posing a substantial challenge in designing an efficient and stable algorithm. Considerable works have been done in the literature to address this challenge, employing two different techniques: (i) modifying Darcy elements or Stokes elements to obtain new stable Brinkman elements and (ii) developing new numerical schemes to solve the Brinkman model. For an overview of the first approach, we refer to the relevant papers [7,8,9,10,11] and their references. Here, we focus on the second approach. Various numerical methods are employed within this approach, including pseudostress-based mixed finite element methods (see, e.g., [12,13,14,15,16]), weak Galerkin methods (see, e.g., [17,18,19]), the virtual element technique (see, e.g., [20, 21]), and the discontinuous Galerkin method (see, e.g., [22,23,24]). Recently, the development of specific mixed finite element methods (FEMs) has emerged as a new research field for solving both linear and nonlinear problems. These methods employ formulations based on velocity-pressure, velocity-pseudostress, and velocity-pressure-stress combinations. While the use of the velocity-pressure formulation for simulating incompressible Newtonian flows has been extensively discussed (see, e.g., [25, 26]), there is a growing focus on the development of numerical schemes grounded in pseudostress or stress formulations (see, e.g., [27,28,29,30]). This heightened attention is largely driven by the interest in addressing non-Newtonian flows. As a principal benefit, stress-based and pseudostress-based formulations offer a unified structure for general Newtonian flows. Moreover, physical quantities such as stress can be calculated directly, eliminating the need for taking derivatives of velocity, which can degrade precision.

On the other hand, the weak Galerkin method (WG), introduced in [31] for second-order elliptic equations, approximates the differential operators in the variational formulation through a framework that emulates the theory of distributions for piecewise polynomials. Additionally, the usual regularity of the approximating functions in this method is compensated by carefully designed stabilizers. In turn, the WG methods have been studied for solving various models [17, 18, 18, 19, 31,32,33,34,35,36,37], demonstrating their substantial potential as a formidable numerical method in scientific computing. The key distinction between WG methods and other existing finite element techniques lies in their utilization of weak derivatives and weak continuities in formulating numerical schemes based on conventional weak forms for the underlying PDE problems. Because of their significant structural pliability, WG methods are aptly suited for a broad class of PDEs, ensuring the requisite stability and accuracy in approximations. Although many research works have been studied and analyzed on the WG method for the Brinkman problem (cf. [17,18,19]), most existing schemes are extracted by the Stokes-type (or primal-mixed) formulation, where the velocity and pressure are principle unknowns. In the present paper, we are interested in continuing the research line drawn by Gatica et al. [13] and aim to develop a pseudostress-based weak Galerkin method for the Brinkman problem.

1.2 Outline and notations

The remainder of the paper is organized as follows. In the rest of this section, we recall the Brinkman model, provide notational preliminaries, and introduce the corresponding pseudostress-based mixed formulation for the problem under consideration. Section 2 presents the weak Galerkin discretization, introducing the mesh structure, the weak divergence operator, and the construction of the mixed WG space. In Section 3, we prove the existence and uniqueness of the discrete problem and establish error estimates for the pseudostress. In addition, we present the approximate velocity and pressure, along with the corresponding error estimates. Finally, in Section 4, a set of numerical tests is reported.

For any vector fields \( \textbf{v}=(v_1, v_2)^\texttt{t} \) and \( \textbf{w}=(w_1, w_2)^\texttt{t} \), we set the gradient and divergence operators as

$$ \varvec{\nabla }\textbf{v}:=(\nabla v_1, \nabla v_2)\,, {\quad \hbox {and}\quad }{\text {div}}(\textbf{v}):=\partial _x v_1 + \partial _y v_2 \,, $$

respectively. In addition, denoting by \(\mathbb {I}\) the identity matrix of \({\mathrm R}^2\), for any tensor fields \(\varvec{\tau }=(\tau _{ij}),~\varvec{\zeta }=(\zeta _{ij})\in \textrm{R}^{2\times 2}\), we write as usual

$$ \varvec{\tau }^{\texttt{t}}:=(\tau _{ji}), \quad {\text {tr}}(\varvec{\tau }):=\tau _{11}+\tau _{22},\quad \varvec{\tau }^{\texttt{d}}:= \varvec{\tau }-\dfrac{1}{2}{\text {tr}}(\varvec{\tau })\mathbb {I}\,, {\quad \hbox {and}\quad }\varvec{\tau }: \varvec{\zeta }:= \sum _{i,j=1}^{2}\tau _{ij}\zeta _{ij} \,, $$

which corresponds, respectively, to the transpose, the trace, and the deviator tensor of \( \varvec{\tau } \), and to the tensorial product between \( \varvec{\tau } \) and \( \varvec{\zeta } \).

Throughout the paper, given a bounded domain \(\Omega \), we let \(\mathcal {O}\) be any given open subset of \(\Omega \). By \((\cdot , \cdot )_{0,\mathcal {O}}\) and \(\Vert \cdot \Vert _{0,\mathcal {O}}\), we denote the usual integral inner product and the corresponding norm of \(\textrm{L}^{2}(\mathcal {O})\), respectively. For positive integers m and r, we shall use the common notation for the Sobolev spaces \(\textrm{W}^{m,r}(\mathcal {O})\) with the corresponding norm and semi-norm \(\Vert \cdot \Vert _{m,r,\mathcal {O}}\) and \(\vert \cdot \vert _{m,r,\mathcal {O}}\), respectively, and if \(r=2\), we set \(\textrm{H}^{m}(\mathcal {O}):=\textrm{W}^{m,2}(\mathcal {O})\), \(\Vert \cdot \Vert _{m,\mathcal {O}}:=\Vert \cdot \Vert _{m,2,\mathcal {O}}\), and \(\vert \cdot \vert _{m,\mathcal {O}}:=\vert \cdot \vert _{m,2,\mathcal {O}}\). If \(\mathcal {O}=\Omega \), the subscript will be omitted. Furthermore, \({\textbf {M}}\) and \(\mathbb {M}\) represent corresponding vectorial and tensorial counterparts of the scalar functional space \(\textrm{M}\). On the other hand, letting \( {\textbf{div}} \) be the usual divergence operator \( {\text {div}} \) acting along the rows of a given tensor, we introduce the standard Banach space

$$ \mathbb {H}({\textbf{div}};\Omega )\,:=\,\Big \{\varvec{\tau }\in \mathbb {L}^{2}(\Omega ):\quad {\textbf{div}}(\varvec{\tau })\in \textbf{L}^2(\Omega )\Big \}\,, $$

equipped with the usual norm

$$ \Vert \varvec{\tau }\Vert _{{\textbf{div}}; \Omega }\,:=\,\Vert \varvec{\tau }\Vert _{0,\Omega } + \Vert {\textbf{div}}(\varvec{\tau })\Vert _{0, \Omega }, \quad \quad \forall \,\varvec{\tau }\in \mathbb {H}({\textbf{div}}; \Omega ), $$

1.3 The model problem and its continuous formulation

Consider a spatially bounded domain \(\Omega \subset \textrm{R}^{2}\) with a Lipschitz continuous boundary \(\partial \Omega \) and an outward-pointing unit normal \({\textbf {n}}\). We focus on the Brinkman problem, which describes the flow of a fluid with velocity field \({\textbf{u}}\) and the pressure p in a porous medium characterized by dynamic viscosity \(\nu >0\), permeability coefficient \(\kappa >0\), following the problem setup from [18]. More precisely, given the body force term \({\textbf {f}}\in {\textbf {L}}^{2}(\Omega )\) and a suitable boundary data \({\textbf{g}}\in {\textbf {H}}^{1/2}(\partial \Omega )\), the problem is cast in the following strong form:

$$\begin{aligned} \begin{array}{rcll} \lambda \, {\textbf{u}}-\nu \,{\textbf{div}}(\varvec{\nabla } {\textbf{u}})+\nabla p \,&{}=&{}\,{\textbf {f}} &{} {\quad \hbox {in}\quad }\Omega \,, \\[2mm] {\textrm{div}}({\textbf{u}})\,&{}=&{}\,0 &{} {\quad \hbox {in}\quad }\Omega \,,\\[2mm] {\textbf{u}}\,&{}=&{}\, {\textbf{g}}&{} {\quad \hbox {on}\quad }\partial \Omega \,, \end{array} \end{aligned}$$
(1.1)

In addition, in order to guarantee the uniqueness of the pressure, this unknown will be sought in the space

$$\begin{aligned} L_0^{2}(\Omega )\,:=\, \Big \{q\in L^{2}(\Omega ):\quad \int _{\Omega }p \,=\, 0 \Big \}\,. \end{aligned}$$
(1.2)

Note that, due to the incompressibility of the fluid (cf. second row of (1.1)), \( {\textbf{g}}\) must satisfy

$$ \displaystyle \int _{\Omega }{\textbf{g}}\cdot {\textbf{n}}\,=\, 0 \,. $$

For the subsequent analysis, we assume that coefficients \( \nu \) and \( \lambda \) are piecewise constants and positive.

Next, to obtain a formulation independent of velocity and pressure variables, the first step is to rewrite (1.1) so that stress is the only unknown in the equation. To achieve this, we introduce a tensor field denoted by \({\varvec{\sigma }}\), represented as

$$\begin{aligned} {\varvec{\sigma }}\,:=\,\nu \varvec{\nabla } {\textbf{u}}-p\mathbb {I}{\quad \hbox {in}\quad }\Omega \,. \end{aligned}$$
(1.3)

In this way, applying the trace operator to both sides of the above equation, and utilizing the incompressibility condition \({\textrm{div}}({\textbf{u}})=0\), one arrives at

$$\begin{aligned} p \,=\,-\dfrac{1}{2}{\text {tr}}({\varvec{\sigma }}){\quad \hbox {in}\quad }\Omega \,. \end{aligned}$$
(1.4)

which allows us to eliminate the pressure variable from the formulation. In turn, according to (1.4), the assumption (1.2) becomes

$$\begin{aligned} \displaystyle \int _{\Omega }{\textrm{tr}}({\varvec{\sigma }})\,=\, 0\,. \end{aligned}$$
(1.5)

Hence, after replacing back (1.3) in (1.1), gathering the resulting equation and (1.5), we have the following problem, which contains unknowns \({\varvec{\sigma }}\) and \({\textbf{u}}\).

Problem 1

(Model problem) Find \({\varvec{\sigma }}\) and \({\textbf{u}}\) such that

$$\begin{aligned}{\left\{ \begin{array}{ll} ~\lambda \, {\textbf{u}}-{\textbf{div}}({\varvec{\sigma }})\,=\,{\textbf {f}} &{} {\quad \hbox {in}\quad }\Omega \,, \\ \hspace{1.5cm}~{\varvec{\sigma }}^{\texttt{d}}\,=\,\nu \,\varvec{\nabla } {\textbf{u}}&{} {\quad \hbox {in}\quad }\Omega \,,\\[1mm] \hspace{.8cm}~\displaystyle \int _{\Omega }{\textrm{tr}}({\varvec{\sigma }})\,=\, 0\,. \end{array}\right. } \end{aligned}$$

supplied with the following boundary condition

$$ {\textbf{u}}\,=\,{\textbf{g}}{\quad \hbox {on}\quad }\partial \Omega \,. $$

Here, in order to deal with the null mean value of \( {\textrm{tr}}({\varvec{\sigma }}) \) (cf. third row of Problem 1), we introduce the subspace of \( \mathbb {H}({\textbf{div}};\Omega ) \) given by

$$ \mathbb {H}_0({\textbf{div}};\Omega )\,:=\,\Big \{ {\varvec{\tau }}\in \mathbb {H}({\textbf{div}};\Omega ): \quad \displaystyle \int _{\Omega }{\textrm{tr}}({\varvec{\tau }})\,=\,0\Big \}\,. $$

Now, we are ready to extract the pseudostress formulation for Problem 1. This involves multiplying the second equation by \({\varvec{\tau }}\), integrating by parts, and utilizing the fact that \({\text {tr}}({\varvec{\tau }}^{\texttt{d}})=0\). Through these steps, we arrive at

$$\begin{aligned} \dfrac{1}{\nu }\int _{\Omega }{\varvec{\sigma }}^{\texttt{d}}: {\varvec{\tau }}^{\texttt{d}}+\int _{\Omega }{\textbf{u}}\cdot {\textbf{div}}({\varvec{\tau }})=\int _{\partial \Omega }{} {\textbf {g}}\cdot {\varvec{\tau }}{\textbf {n}}\qquad \forall \, {\varvec{\tau }}\in \mathbb {H}({\textbf{div}};\Omega ) \,. \end{aligned}$$
(1.6)

Hence, replacing \({\textbf{u}}\) by the first equation of Problem 1, that is,

$$\begin{aligned} {\textbf{u}}\,=\,\dfrac{1}{\lambda }\left( {\textbf{div}}({\varvec{\sigma }})+{\textbf {f}}\right) \,, \end{aligned}$$
(1.7)

in the (1.6) leads to the following pseudostress formulation.

Problem 2

(Variational problem) Find the tensor \({\varvec{\sigma }}\in \mathbb {H}_0({\textbf{div}};\Omega )\) such that

$$\begin{aligned} \mathcal {A}({\varvec{\sigma }}, {\varvec{\tau }})\,=\,\mathcal {L}({\varvec{\tau }})\qquad \quad \text {for all} ~{\varvec{\tau }}\in \mathbb {H}_0({\textbf{div}};\Omega )\,, \end{aligned}$$

where

$$\begin{aligned} \mathcal {A}(\cdot ,\cdot )&:&\mathbb {H}({\textbf{div}};\Omega )\times \mathbb {H}({\textbf{div}};\Omega )\rightarrow \textrm{R}\,,\qquad \mathcal {A}({\varvec{\zeta }}, {\varvec{\tau }})\,:=\,\dfrac{1}{\nu }\int _{\Omega }{\varvec{\zeta }}^{\texttt{d}}: {\varvec{\tau }}^{\texttt{d}}\nonumber \\{} & {} \quad +\dfrac{1}{\lambda }\int _{\Omega }{\textbf{div}}({\varvec{\zeta }})\cdot {\textbf{div}}({\varvec{\tau }})\,, \end{aligned}$$
(1.8)
$$\begin{aligned} \mathcal {L}(\cdot )&:&\mathbb {H}({\textbf{div}};\Omega )\rightarrow \textrm{R}\,,\qquad ~~~~ \mathcal {L}({\varvec{\tau }})\,:=\!\,-\dfrac{1}{\lambda }\int _{\Omega }{} {\textbf {f}}\cdot {\textbf{div}}({\varvec{\tau }})+\!\int _{\partial \Omega }{} {\textbf {g}}\cdot {\varvec{\tau }}{\textbf {n}}\,, \end{aligned}$$
(1.9)

The continuity and coercivity properties of the bilinear form that appeared in Problem 2 are briefly listed below. Before delving into that discussion, let us recall the following lemma.

Lemma 1.1

(A consequence of the Poincaré–Friedrichs inequality [26]) There exists \(c_{\Omega }>0\) depends on \(\Omega \), such that

$$\begin{aligned} c_{\Omega }\Vert {\varvec{\tau }}\Vert _{0,\Omega }^{2}\,\le \, \Vert {\varvec{\tau }}^{\texttt{d}}\Vert _{0,\Omega }^{2}+\Vert {\textbf{div}}({\varvec{\tau }})\Vert _{0,\Omega }^{2}\quad \quad \forall \,{\varvec{\tau }}\in \mathbb {H}({\textbf{div}};\Omega )\,. \end{aligned}$$

  • The bilinear form \(\mathcal {A}(\cdot ,\cdot )\) is continuous due to the Cauchy–Schwarz inequality:

$$\begin{aligned} \big |\mathcal {A}({\varvec{\zeta }},{\varvec{\tau }})\big |\,\le \, \max \bigg \{\dfrac{1}{\nu },\dfrac{1}{\lambda }\bigg \}\,\Vert {\varvec{\zeta }}\Vert _{{\textbf{div}};\Omega }\,\Vert {\varvec{\tau }}\Vert _{{\textbf{div}};\Omega } \quad \forall \,{\varvec{\zeta }},{\varvec{\tau }}\in \mathbb {H}({\textbf{div}};\Omega ) \,. \end{aligned}$$

  • The bilinear form \(\mathcal {A}(\cdot ,\cdot )\) is coercive on \(\mathbb {H}({\textbf{div}};\Omega )\) due to Lemma 1.1:

$$\begin{aligned} \mathcal {A}({\varvec{\zeta }},{\varvec{\zeta }})\ge \min \bigg \{c_{\Omega }\nu _{0},\dfrac{1}{2\lambda }\bigg \}\,\Vert {\varvec{\zeta }}\Vert _{{\textbf{div}};\Omega }^{2}\,,\quad \text {with}\quad \nu _{0}=\min \bigg \{\dfrac{1}{\nu },\dfrac{1}{2\lambda }\bigg \}\,. \end{aligned}$$

The standard results for the existence, uniqueness, and stability of the solution to Problem 2 can be stated as follows. The proof is a straightforward application of the Lax–Milgram lemma.

Theorem 1.2

Let \(\textbf{f}\) and \(\textbf{g}\) belong to spaces \(\textbf{L}^{2}(\Omega )\) and \(\textbf{H}^{1/2}(\partial \Omega )\), respectively. Then, there exists a unique solution \({\varvec{\sigma }}\in \mathbb {X}\) for the dual-mixed formulation Problem 2, and there holds

$$ \Vert {\varvec{\sigma }}\Vert _{{\textbf{div}};\Omega }\le C_{\texttt{stab}}\left( \Vert \textbf{f}\Vert _{0}+\Vert \textbf{g}\Vert _{1/2,\partial \Omega } \right) \,, $$

where \( C_{\texttt{stab}} \) is a positive constant, depending on \( c_{\Omega } \), \( \nu \), \( \lambda \).

2 Weak Galerkin approximation

The chief target of this section is to present the weak Galerkin spaces and discrete bilinear form that is required for creating a WG scheme. For simplicity of the presentation, we restrict the construction to the 2D case.

2.1 Various tools in weak Galerkin method

A key feature of the weak Galerkin method is the use of specifically defined weak derivatives instead of classical derivative operators. Here, our focus will be on the weak divergence operator, which is a fundamental step in introducing our WG technique. For this purpose, we first provide an overview of the mesh structure.

Mesh notation Let \(\mathcal {K}_{h}=\{K\}\) be a shape regular mesh of domain \(\Omega \) that consists of arbitrary polygon elements, where the mesh size \(h=\max \{h_{K}\}\), \(h_{K}\) is the diameter of element K. The interior and the boundary of any element \(K\in \mathcal {K}_{h}\) are represented by \(K^{0}\) and \(\partial K\), respectively. Denote by \(\mathcal {E}_{h}\) the set of all edges in \(\mathcal {K}_{h}\), and let \(\mathcal {E}_{h}^{0}=\mathcal {E}_{h}\backslash \partial \Omega \) be the set of all interior edges. Here is a set of normal directions on \( \mathcal {E}_{h}\):

$$\begin{aligned}\textrm{D}_{h}\,:=\,\Big \{{\textbf {n}}_{e}:\quad {\textbf {n}}_{e}\,\text {is unit and outward normal to}\, e \,\quad \text {for all}\, e\in \mathcal {E}_{h}\Big \}\,. \end{aligned}$$

Weak divergence operator and weak Galerkin space It is well known that the weak divergence operator is well-defined for weak functions \({\varvec{\tau }}=\{{\varvec{\tau }}_{0},{\varvec{\tau }}_{b}\}\) on the element K such that \({\varvec{\tau }}_{0}\in \mathbb {L}^{2}(K)\) and \({\varvec{\tau }}_{b}{} {\textbf {n}}_{e}\in \textbf{H}^{-1/2}(\partial K)\), where \({\textbf {n}}_{e}\in \textrm{D}_{h}|_{K}\). Components \({\varvec{\tau }}_{0}\) and \({\varvec{\tau }}_{b}\) can be understood as the values of function \({\varvec{\tau }}\) in \(K^{0}\) and on \(\partial K\), respectively. We follow [32], and introduce for each \(K\in \mathcal {K}_{h}\) the local weak tensor space

$$\begin{aligned} \mathbb {X}_{\texttt{w}}(K)\,:=\!\,\Big \{{\varvec{\tau }}\!=\!\{{\varvec{\tau }}_{0},{\varvec{\tau }}_{b}\}:\!\quad {\varvec{\tau }}_{0}\in \mathbb {L}^{2}(K)\!{\quad \hbox {and}\quad }{\varvec{\tau }}_{b}{} {\textbf {n}}_{e}\in \textbf{H}^{-1/2}(\partial K)\quad \!\forall \,{\textbf {n}}_{e}\in \textrm{D}_{h}|_{K}\Big \}\,. \end{aligned}$$
(2.1)

The global space \(\mathbb {X}_{\texttt{w}}\) is defined by gluing together all local spaces \(\mathbb {X}_{\texttt{w}}(K)\) for any \(K\in \mathcal {K}_{h}\).

Definition 2.1

[31] For any weak matrix-valued function \({\varvec{\tau }}\in \mathbb {X}_{\texttt{w}}(K)\) and element \(K\in \mathcal {K}_{h}\), the weak divergence operator, denoted by \({\textbf{div}}_{\texttt{w}}\), is defined as the unique vector-valued function \({\textbf{div}}_{\texttt{w}}({\varvec{\tau }})\in \textbf{H}^{1}(K)\) satisfying

$$\begin{aligned} ({\textbf{div}}_{\texttt{w}}({\varvec{\tau }}),~{\varvec{\zeta }})_{0,K}\,:=\,-({\varvec{\tau }}_{0},~\nabla {\varvec{\zeta }})_{0,K^{0}}\,+\,<{\varvec{\tau }}_{b}{} {\textbf {n}}_{e}, {\varvec{\zeta }}>_{0,\partial K}\,, \end{aligned}$$
(2.2)

for all \({\varvec{\zeta }}\in \textbf{H}^{1}(K)\).

Our focus will be on a subspace of \(\mathbb {X}_{\texttt{w}}\) in which \(({\varvec{\tau }}_{b}|_{e})=({\varvec{\tau }}|_{e}{} {\textbf {n}}_{e}){\textbf {n}}_{e}\). On the other hand, discrete weak divergence operator can be introduced using a finite-dimensional space \(\mathbb {X}_{h}\subset \mathbb {X}_{\texttt{w}}\), which will be stated in the next. First, for any mesh object \(\varpi \in \mathcal {K}_{h}\cup \mathcal {E}_{h}\) and for any \(r\in \textrm{N}\), let us introduce the space \(\textrm{P}_{r}(\varpi )\) to be the space of polynomials defined on \(\varpi \) of degree \(\le r\), with the extended notation \(\textrm{P}_{-1}(\varpi )=\{0\}\). Similarly, we let \(\textbf{P}_{r}(\varpi )\) and \(\mathbb {P}_{r}(\varpi )\) be the vectorial and tensorial versions of \(\textrm{P}_{r}(\varpi )\). Then, given \( k\in \textrm{N}_0 \), we define for any \( K\in \mathcal {K}_h \) the local weak Galerkin space

$$\begin{aligned} \begin{array}{c} \mathbb {X}_{h}(K)\,:=\,\Big \{{\varvec{\tau }}_{h}=\{{\varvec{\tau }}_{\textrm{0h}},{\varvec{\tau }}_{\textrm{bh}}\}\in \mathbb {X}_{\texttt{w}}(K):\quad {\varvec{\tau }}_{\textrm{0h}}|_{K}\in \mathbb { P}_{k}(K){\quad \hbox {and}\quad }\\[2ex] \qquad \qquad \qquad {\varvec{\tau }}_{\textrm{bh}}|_{e}=\tau _{b}\otimes {\textbf {n}}_{e}\,,\,\tau _{b}\in \textbf{P}_{k}(e) \,\,\,\, \forall \, e\subset \partial K \,,\,\,\forall \,{\textbf {n}}_{e}\in \textrm{D}_{h} \Big \}\,, \end{array} \end{aligned}$$
(2.3)

In addition, the global finite-dimensional space \(\mathbb {X}_{h}\), associated with the partition \(\mathcal {K}_{h}\), is defined so that the restriction of every weak function \({\varvec{\tau }}_{h}\) to the mesh element K belongs to \(\mathbb {X}_{h}(K)\).

Definition 2.2

[31] For any \({\varvec{\tau }}_{h}\in \mathbb {X}_{h}(K)\) and element \(K\in \mathcal {K}_{h}\), the discrete weak divergence operator, denoted by \({\textbf{div}}_{\texttt{w,h}}\), is defined as the unique vector-valued polynomial \({\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\in \textbf{P}_{k+1}(K)\) satisfying

$$\begin{aligned} ({\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h}),~{\varvec{\zeta }}_{h})_{0,K}\,:=\,-({\varvec{\tau }}_{\textrm{0h}},~\nabla {\varvec{\zeta }}_{h})_{0,K^{0}}\,+\,<{\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}_{e}, {\varvec{\zeta }}_{h}>_{0,\partial K}\,, \end{aligned}$$
(2.4)

for all \({\varvec{\zeta }}_{h}\in {\textbf {P}}_{k+1}(K)\).

L\(^{2}\)-orthogonal projections and approximation properties For any \(r\in \textrm{N}\), we introduce L\(^{2}\)-projection operators \(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_0^{K}:\mathbb {L}^{2}(K)\rightarrow \mathbb {P}_{r}(K)\) and \({\varvec{\mathcal P}}_{\texttt{b}}^{K}:\textbf{L}^{2}(\partial K)\rightarrow \textbf{P}_{r}(\partial K)\) which are type of interior and boundary, and are given by

$$\begin{aligned} \int _{K}\mathcal {P}\hspace{-1.5ex}\mathcal {P}_0^{K}({\varvec{\tau }}): \widehat{\textbf{q}}_r=\int _{K}{\varvec{\tau }}: \widehat{\textbf{q}}_r{\quad \hbox {and}\quad }\int _{\partial K}{\varvec{\mathcal P}}_{\texttt{b}}^{K}(\textbf{v})\cdot \textbf{q}_r=\int _{\partial K}\textbf{v} \cdot \textbf{q}_r \,, \end{aligned}$$
(2.5)

for all \(\{{\varvec{\tau }}, \textbf{v}\}\in \mathbb {L}^{2}(K)\times \textbf{L}^{2}(\partial K)\) and \(\{\widehat{\textbf{q}}_r,\textbf{q}_r\} \in \mathbb {P}_{r}(K)\times \textbf{P}_{r}(\partial K)\).

Now, we introduce projection operator \(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}^{K}\) into the tensorial weak space \(\mathbb {X}_{h}(K)\) as follows:

$$ \mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}^{K}{\varvec{\tau }}\,:=\,\big \{ \mathcal {P}\hspace{-1.5ex}\mathcal {P}_0^{K}{\varvec{\tau }}_0, {\varvec{\mathcal P}}_{b}^{K}(\tau _b)\otimes \textbf{n}_{e}\big \}\,,\qquad \text {for all} ~{\varvec{\tau }}\in \mathbb {X}_{h}(K)\,. $$

Also, for any element \(K\in \mathcal {K}_h\) and function \({\varvec{\tau }}\in \mathbb {X}_{h}\), the global projection operator \( \mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}\) on the global space \(\mathbb {X}_{h}\) is defined by

$$ \mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}({\varvec{\tau }})|_{K}\,=\,\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}^{{K}}({\varvec{\tau }}|_{K})\qquad \forall \, {\varvec{\tau }}\in \mathbb {X}_{h}\,. $$

It can be seen (see, e.g., [32]) that operator \(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}\) satisfies the following identity:

$$\begin{aligned} \varvec{\mathcal {P}}_{h} ({\textbf{div}}({\varvec{\tau }}))\,=\,{\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\tau }})\,, \end{aligned}$$
(2.6)

where \(\varvec{\mathcal {P}}_{h}|_{K}:=\varvec{\mathcal {P}}_{k+1}^{K}\) denotes the L\(^{2}\)-projection from \({\textbf {L}}^{2}(K)\) onto \({\textbf {P}}_{k+1}(K)\).

The approximation properties of \( \mathcal {P}\hspace{-1.5ex}\mathcal {P}_{0} \) and \( \varvec{\mathcal {P}}_{h} \) are stated as follows.

Lemma 2.3

Let \(\mathcal {K}_{h}\) be a finite element partition of \(\Omega \) satisfying the shape regularity assumptions \(\textbf{A1}\)-\(\textbf{A4}\) stated in [32]. Then, for \(k,s,m\in \textrm{N}_{0}\) such that \(m\in \{0,1\}\), there exist constants \(C_{1}, C_{2}\), independent of the mesh size h, such that

$$\begin{aligned} \sum \limits _{K\in \mathcal {K}_{h}}\Vert {\varvec{\tau }}-\mathcal {P}\hspace{-1.5ex}\mathcal {P}_0^{K}({\varvec{\tau }})\Vert _{m,0;K}^{2}&\,\le \, C_{1}\, h^{2(s-m)}\vert {\varvec{\tau }}\vert _{s}^{2}\qquad \forall \, s\le k +1\,,\end{aligned}$$
(2.7)
$$\begin{aligned} \sum \limits _{K\in \mathcal {K}_{h}}\Vert \textbf{v}-\varvec{\mathcal {P}}_{k+1}^{K}(\textbf{v})\Vert _{0;K}^{2}&\,\le \, C_{2}\, h^{2s}\vert \textbf{v}\vert _{s}^{2}\qquad \forall \, s\le k+2\,. \end{aligned}$$
(2.8)

2.2 Weak Galerkin scheme

In order to define our weak Galerkin scheme for Problem 2, we now introduce, when necessary, the discrete versions of the bilinear forms and functionals involving the weak spaces. Following the usual procedure in the WG setting, the construction of them is based on the weak derivatives to ensure computability for all weak functions.

Notice that, for arbitrary weak function in \(\mathbb {X}_{h}\), the bilinear form \(\mathcal {A}(\cdot ,\cdot )\) and the functional \( \mathcal {L}(\cdot ) \) are not computable because they involve the divergence operator which cannot be evaluated for weak functions. To overcome this matter, employing Definition 2.2 for any \({\varvec{\zeta }}_h, {\varvec{\tau }}_h\in \mathbb {X}_{h}(K)\), we define the discrete bilinear form

$$\begin{aligned} \mathcal {A}_{h}^{K}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\,:=\,\dfrac{1}{\nu }\displaystyle \int _{K}{\varvec{\zeta }}_{\textrm{0h}}^{\texttt{d}}:{\varvec{\tau }}_{\textrm{0h}}^{\texttt{d}}\,+\,\dfrac{1}{\lambda }\displaystyle \int _{K}{\textbf{div}}_{\texttt{w,h}}({\varvec{\zeta }}_{h})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,+\,\rho \,\mathcal {S}^{K}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\,, \end{aligned}$$
(2.9)

and the discrete linear functional

$$\begin{aligned} \mathcal {L}_{h}^{K}({\varvec{\tau }}_{h})\,:=\,-\dfrac{1}{\lambda }\displaystyle \int _{K}{} {\textbf {f}}\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,+\,\left\langle {\textbf {g}},\, {\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}_{e}\right\rangle _{0,(\partial K\cap \partial \Omega )}\,, \end{aligned}$$
(2.10)

where \(\rho \) is a piecewise constant on \(\mathcal {K}_h\) and the stabilization term \(\mathcal {S}^{K}(\cdot ,\cdot ): \mathbb {X}_{h}(K)\times \mathbb {X}_{h}(K)\rightarrow \textrm{R}\) is given by

$$\begin{aligned} \mathcal {S}^{K}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\,:=\, h_{K}\left\langle \mathcal {P}\hspace{-1.5ex}\mathcal {P}_b^K({\varvec{\zeta }}_{\textrm{0h}}{} {\textbf {n}})-{\varvec{\zeta }}_{\textrm{bh}}{} {\textbf {n}},\, \mathcal {P}\hspace{-1.5ex}\mathcal {P}_b^K({\varvec{\tau }}_{\textrm{0h}}{} {\textbf {n}})-{\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}\right\rangle _{0,\partial K}\,. \end{aligned}$$

In addition, the global bilinear form \(\mathcal {A}_{h}(\cdot ,\cdot )\) and the global linear functional \(\mathcal {L}_{h}(\cdot )\) can be derived by adding the local contributions, that is,

$$ \mathcal {A}_{h}(\cdot ,\cdot )\,:=\,\sum \limits _{K\in \mathcal {K}_{h}}\mathcal {A}_{h}^{K}(\cdot ,\cdot ){\quad \hbox {and}\quad }\mathcal {L}_{h}(\cdot )\,:=\,\sum \limits _{K\in \mathcal {K}_{h}}\mathcal {L}_{h}^{K}(\cdot )\,. $$

Let us introduce the discrete norm

$$ \Vert {\varvec{\tau }}_{h}\Vert _{h}^{2}\,:=\,\sum _{K\in \mathcal {K}_{h}}\Big [\Vert {\varvec{\tau }}_{\mathrm {0\,h}}\Vert _{0,K}^{2}+\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Vert _{0,K}^{2}+\mathcal {S}^{K}({\varvec{\tau }}_{h},{\varvec{\tau }}_{h})\Big ]\qquad \text {for all} ~{\varvec{\tau }}_{h}\in \mathbb {X}_{h}\,, $$

and the subspace of \(\mathbb {X}_{h}\) as follows:

$$ \mathbb {X}_{0,h}\,:=\,\Big \{ {\varvec{\tau }}_{h}=\{{\varvec{\tau }}_{\mathrm {0\,h}},{\varvec{\tau }}_{\textrm{bh}}\}\in \mathbb {X}_{h}:\quad \displaystyle \int _{\Omega }{\textrm{tr}}({\varvec{\tau }}_{\mathrm {0\,h}})\,=\,0 {\quad \hbox {in}\quad }\Omega \Big \}\,. $$

Finally, referring to the above space, the discrete bilinear form (2.9) and the discrete linear functional (2.10), the discrete weak Galerkin problem reads as follows.

Problem 3

(WG problem) Find \({\varvec{\sigma }}_h \in \mathbb {X}_{0,h}\) such that

$$\begin{aligned} \mathcal {A}_h({\varvec{\sigma }}_h, {\varvec{\tau }}_h)\,=\,\mathcal {L}_h({\varvec{\tau }}_h)\qquad \quad \text {for all} ~{\varvec{\tau }}_h\in \mathbb {X}_{0,h}\,. \end{aligned}$$

3 Solvability and a priori error analysis

The goal of this section is to investigate the solvability of the discrete weak Galerkin scheme stated in Problem 3 and derive an optimal order error estimate for the weak Galerkin approximation \({\varvec{\sigma }}_{h}\). First, we turn to discuss the stability properties of the discrete form in Problem 3. For this purpose, we begin with the following lemma a counterpart of Lemma 1.1 for the weak functions.

Lemma 3.1

There exists \(\hat{c}_{\Omega }>0\) depends on \(\Omega \) but independent of mesh size h, such that

$$\begin{aligned} \hat{c}_{\Omega }\Vert {\varvec{\tau }}_{0h}\Vert _{0,\Omega }^{2}\,\le \, \Vert {\varvec{\tau }}_{0h}^{\texttt{d}}\Vert _{0,\Omega }^{2}\,+\,\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_h)\Vert _{0,\Omega }^{2}\qquad \forall \, {\varvec{\tau }}_h\in \mathbb {X}_{h}\,. \end{aligned}$$
(3.1)

Proof

Given \(\varvec{\tau }_h=\{\varvec{\tau }_{0h},\varvec{\tau }_{bh}\}\in \mathbb {X}_h\), we know from [38, Corollary 2.4 in Chapter I] that there is a unique \(\textbf{z}\in \textbf{H}_0^1(\Omega )\) such that \({\text {div}}(\textbf{z})={\text {tr}}(\varvec{\tau }_{0h})\) and

$$\begin{aligned} \Vert \textbf{z}\Vert _{1,\Omega }\,\le \, c_{1}\Vert {\text {tr}}(\varvec{\tau }_{0h})\Vert _{0,\Omega }\,, \end{aligned}$$
(3.2)

where \(c_{1}>0\) is a constant independent of \(\textbf{z}\). Now, utilizing that fact \({\text {div}}(\textbf{z})=\nabla \textbf{z}:\mathbb {I}\) and the definition of deviatoric, we have that

$$\begin{aligned} \Vert {\text {tr}}(\varvec{\tau }_{0h})\Vert _{0,\Omega }^2&\,=\,\sum _{K\in \mathcal {K}_h}\int _{K} {\text {tr}}(\varvec{\tau }_{0h}){\text {div}}(\textbf{z})\,=\,\sum _{K\in \mathcal {K}_h}\int _{K} {\text {tr}}(\varvec{\tau }_{0h})\mathbb {I}:\nabla \textbf{z}\\&\,=\,2\sum _{K\in \mathcal {K}_h}\int _{K}(\varvec{\tau }_{0h}-\varvec{\tau }_{0h}^{\texttt{d}}):\nabla \textbf{z}\\&\,=\,2\sum _{K\in \mathcal {K}_h}\bigg \{\int _{\partial K\setminus \partial \Omega }\varvec{\tau }_{bh}\textbf{n}\cdot \textbf{z}-\int _{K}{{\textbf {div}}}_{\texttt{w,h}}(\varvec{\tau }_{h})\cdot \textbf{z}-\int _{K}\varvec{\tau }_{0h}^{\texttt{d}}:\nabla \textbf{z}\bigg \}\,, \end{aligned}$$

where in the last step, we have used the definition of discrete weak divergence (cf. (2.4)) and \(\textbf{z}\in \textbf{H}_0^1(\Omega )\). Note here that the first term on the right-hand side of the above equation vanishes since the weak functions are continuous across each interior edge e in the normal direction. Hence, applying Cauchy–Schwarz and Hölder inequalities, Sobolev embedding \(\textbf{H}^1\subset \textbf{L}^4\), and then inequality (3.2), we find that

$$\begin{aligned} \Vert {\text {tr}}(\varvec{\tau }_{0h})\Vert _{0,\Omega }^2&\,\le \, \sum _{K\in \mathcal {K}_h}\Big \{\Vert {{\textbf {div}}}_{\texttt{w,h}}(\varvec{\tau }_{h})\Vert _{0,4/3,K}\Vert \textbf{z}\Vert _{0,4,K} +\Vert \varvec{\tau }_{0h}^{\texttt{d}}\Vert _{0,K}\Vert \nabla \textbf{z}\Vert _{0,K}\Big \}\\&\,\le \, 2\max \{c_{\texttt{em}},1\}\Vert \textbf{z}\Vert _{1}\left( \sum _{K\in \mathcal {K}_h} \big (\Vert {{\textbf {div}}}_{\texttt{w,h}}(\varvec{\tau }_{h})\Vert _{0,4/3,K} +\Vert \varvec{\tau }_{0h}^{\texttt{d}}\Vert _{0,K}\big )^2\right) ^{1/2}\\&\,\le \, 2\max \{c_{\texttt{em}},1\}c_1\Vert {\text {tr}}(\varvec{\tau }_{0h})\Vert _{0,\Omega }\!\left( \sum _{K\in \mathcal {K}_h} \!\big (\Vert {{\textbf {div}}}_{\texttt{w,h}}(\varvec{\tau }_{h})\Vert _{0,4/3,K} \!+\!\Vert \varvec{\tau }_{0h}^{\texttt{d}}\Vert _{0,K}\big )^2\right) ^{1/2}\,, \end{aligned}$$

which gives

$$\begin{aligned} \Vert {\text {tr}}(\varvec{\tau }_{0h})\Vert _{0,\Omega }^2 \,\le \, 4 c_1\max \{c_{\texttt{em}},1\}\sum _{K\in \mathcal {K}_h} \Big \{\Vert {{\textbf {div}}}_{\texttt{w,h}}(\varvec{\tau }_{h})\Vert _{0,4/3,K}^2 +\Vert \varvec{\tau }_{0h}^{\texttt{d}}\Vert _{0,K}^2\Big \}\,. \end{aligned}$$

This inequality and the fact that

$$\Vert \varvec{\tau }_{0h}\Vert _{0,\Omega }^2 \,=\, \Vert \varvec{\tau }_{h}^{\texttt{d}}\Vert _{0,\Omega }^2+\frac{1}{2}\Vert {\text {tr}}(\varvec{\tau }_{0h})\Vert _{0,\Omega }^2 ,$$

complete the proof by letting \(\hat{c}_\Omega :=\,2 c_1\max \{c_{\texttt{em}},1\}+1\). \(\square \)

The below lemma confirms the continuity and the coercivity properties of \(\mathcal {A}_{h}(\cdot ,\cdot )\).

Lemma 3.2

There exist positive constants \(\alpha _1\) and \(\alpha _2\) (independent of K and h) verifying

$$\begin{aligned} \big |\mathcal {A}_{h}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\big |\,\le \, \alpha _1 \,\Vert {\varvec{\zeta }}_{h}\Vert _{h}\,\Vert {\varvec{\tau }}_{h}\Vert _{h}\,, \end{aligned}$$
(3.3)

and

$$\begin{aligned} \hspace{-.6cm}\mathcal {A}_{h}({\varvec{\tau }}_{h},{\varvec{\tau }}_{h})\,\ge \, \alpha _2 \,\Vert {\varvec{\tau }}_{h}\Vert _{h}^{2}\,, \end{aligned}$$
(3.4)

for all \({\varvec{\zeta }}_h\in \mathbb {X}_{h}\) and \({\varvec{\tau }}_h\in \mathbb {X}_{h}\).

Proof

Let us first notice that, by applying the Cauchy–Schwarz inequality and virtue of

$$ \Vert {\varvec{\tau }}_{\mathrm {0\,h}}^{\texttt{d}}\Vert _{0,K}^{2}\,=\,\Vert {\varvec{\tau }}_{\mathrm {0\,h}}\Vert _{0,K}^{2}-\dfrac{1}{2}\Vert {\text {tr}}({\varvec{\tau }}_{\mathrm {0\,h}})\Vert _{0,K}^{2}\,\le \, \Vert {\varvec{\tau }}_{\mathrm {0\,h}}\Vert _{0,K}^{2}\,, $$

the bilinear form \(\mathcal {A}_{h}(\cdot ,\cdot )\) is bounded:

$$\begin{aligned} \big |\mathcal {A}_{h}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\big |&\,\!=\!\,\bigg |\sum _{K\in \mathcal {K}_{h}}\Big [\dfrac{1}{\nu }\displaystyle \int _{K}{\varvec{\zeta }}_{\textrm{0h}}^{\texttt{d}}:{\varvec{\tau }}_{\textrm{0h}}^{\texttt{d}}\,+\,\dfrac{1}{\lambda }\displaystyle \int _{K} {\textbf{div}}_{\texttt{w,h}}({\varvec{\zeta }}_{h})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,\!+\!\,\rho \,\mathcal {S}^{K}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\Big ]\bigg |\nonumber \\&\,\le \, \sum _{K\in \mathcal {K}_{h}}\Big [\dfrac{1}{\nu }\Vert {\varvec{\zeta }}_{\textrm{0h}}\Vert _{0,K}\Vert {\varvec{\tau }}_{\textrm{0h}}\Vert _{0,K}+\dfrac{1}{\lambda }\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\zeta }}_{h})\Vert _{0,K}\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Vert _{0,K}\Big ]\nonumber \\&\hspace{.6cm}+\rho \sum _{K\in \mathcal {K}_{h}}\left( \mathcal {S}^{K}({\varvec{\zeta }}_{h},{\varvec{\zeta }}_{h})\right) ^{1/2}\left( \mathcal {S}^{K}({\varvec{\tau }}_{h},{\varvec{\tau }}_{h})\right) ^{1/2}\\&\,\le \, \max \big \{\dfrac{1}{\nu },\dfrac{1}{\lambda },\rho \big \}\,\Vert {\varvec{\zeta }}_{h}\Vert _{h}\,\Vert {\varvec{\tau }}_{h}\Vert _{h}\,. \end{aligned}$$

Moreover, as a consequence of Lemma 3.1, we have

$$\begin{aligned} \mathcal {A}_{h}({\varvec{\tau }}_{h},{\varvec{\tau }}_{h})&=\sum _{K\in \mathcal {K}_{h}}\left( \dfrac{1}{\nu }\Vert {\varvec{\tau }}_{\textrm{0h}}^{\texttt{d}}\Vert _{0,K}^{2}+\dfrac{1}{\lambda }\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Vert _{0,K}^{2}+\rho \,\mathcal {S}^{K}({\varvec{\tau }}_{h},{\varvec{\tau }}_{h})\right) \\&\ge \sum _{K\in \mathcal {K}_{h}}\Big (\min \big \{\dfrac{1}{\nu },\dfrac{1}{2\lambda }\big \}\left( \Vert {\varvec{\tau }}_{\textrm{0h}}^{\texttt{d}}\Vert _{0,K}^{2}+\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Vert _{0,K}^{2}\right) \\&\,\,\,\,+\,\dfrac{1}{2\lambda }\Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Vert _{0,K}^{2}+\rho \,\mathcal {S}^{K}({\varvec{\tau }}_{h},{\varvec{\tau }}_{h})\Big )\\&\ge \min \Big \{\hat{c}_{\Omega }\min \{\dfrac{1}{\nu },\dfrac{1}{2\lambda }\},\dfrac{1}{2\lambda },\rho \Big \}\Vert {\varvec{\tau }}_{h}\Vert _{h}^{2}\,, \end{aligned}$$

which together with setting

$$ \alpha _{1}\,:=\,\max \{\dfrac{1}{\nu },\dfrac{1}{\lambda },\rho \} {\quad \hbox {and}\quad }\alpha _{2}\,:=\,\min \Big \{\hat{c}_{\Omega }\min \{\dfrac{1}{\nu },\dfrac{1}{2\lambda }\},\dfrac{1}{2\lambda },\rho \Big \}\,, $$

complete the proof. \(\square \)

Moreover, we can easily conclude the boundedness of the linear functional form \(\mathcal {L}_h\) on \(\mathbb {X}_h\) by using the Cauchy–Schwarz inequality, adding zero in the form \(\pm \langle {\textbf {g}}, {\varvec{\mathcal P}}_b^K({\varvec{\tau }}_{\textrm{0h}}{} {\textbf {n}}_e)\rangle _{0,\partial \Omega }\), the continuity of the projection \({\varvec{\mathcal P}}_b^K\) and the definition of discrete norm given in Section 2.2 as follows:

$$\begin{aligned} \big |\mathcal {L}_{h}({\varvec{\tau }}_{h})\big |&\,=\,\bigg |-\sum _{K\in \mathcal {K}_h}\dfrac{1}{\lambda }\displaystyle \int _{K}{} {\textbf {f}}\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,+\,\langle {\textbf {g}}, {\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}_{e}\rangle _{0,\partial \Omega }\bigg |\nonumber \\&\,=\,\bigg |-\sum _{K\in \mathcal {K}_h}\dfrac{1}{\lambda }\displaystyle \int _{K}{} {\textbf {f}}\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,+\,\langle {\textbf {g}}, {\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}_{e}-{\varvec{\mathcal P}}_b^K({\varvec{\tau }}_{\textrm{0h}}{} {\textbf {n}}_e)\rangle _{0,\partial \Omega }\\&\qquad \,+\,\langle {\textbf {g}}, {\varvec{\mathcal P}}_b^K({\varvec{\tau }}_{\textrm{0h}}{} {\textbf {n}}_e)\rangle _{0,\partial \Omega }\bigg |\nonumber \\&\,\,\,\le \, \max \big \{\dfrac{1}{\lambda },1\big \}\Big (\Vert \textbf{f}\Vert _{0}+\Vert \textbf{g}\Vert _{1/2,\partial \Omega } \Big )\Vert {\varvec{\tau }}\Vert _h \nonumber \,. \end{aligned}$$
(3.5)

We are now in a position to establish the well-posedness of Problem 3.

Theorem 3.3

Let \(\textbf{f}\) and \(\textbf{g}\) belong to spaces \(\textbf{L}^{2}(\Omega )\) and \(\textbf{H}^{1/2}(\partial \Omega )\), respectively. Then, there exists a unique solution \({\varvec{\sigma }}_{h}\in \mathbb {X}_{0,h}\) to Problem 3. In addition, there exists a constant \(\hat{C}_{\texttt{stab}}>0\) independent of mesh size, such that

$$\begin{aligned} \Vert {\varvec{\sigma }}_{h}\Vert _{h}\,\le \, \hat{C}_{\texttt{stab}}\left( \Vert \textbf{f}\Vert _{0}+\Vert \textbf{g}\Vert _{1/2,\partial \Omega } \right) \,. \end{aligned}$$
(3.6)

Proof

It deduces straightly from Lemma 3.2, the boundedness (3.5), and Lax-Milgram lemma. \(\square \)

Our next step is to derive the corresponding a priori error estimate for Prolems 2 and 3. To this end, we first state the following lemma.

Lemma 3.4

For \({\varvec{\zeta }}\in \mathbb {H}^{r+1}(\Omega )\) and \(r\in N\) such that \(r\le k\), there exists a positive constant \(C_{\mathcal {S}}\) such that

$$\begin{aligned} \mathcal {S}^{K}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\zeta }},{\varvec{\tau }}_{h})\,\le \, C_{\mathcal {S}}\, h^{r+1}\Vert \varvec{\zeta }\Vert _{r+1}\Vert {\varvec{\tau }}_{h}\Vert _{h}\,, \end{aligned}$$
(3.7)

for all \({\varvec{\tau }}_{h}\in \mathbb {X}_{h}\).

Proof

The proof of vector version can be found in [36] and by following the similar arguments can easily conclude (3.7). \(\square \)

Thanks to the projection error estimate stated in Lemma 2.3, we only analyze the error function defined by

$$\begin{aligned} \varvec{\theta } \,:=\, \mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }}-{\varvec{\sigma }}_{h}\,=\,\big \{ \mathcal {P}\hspace{-1.5ex}\mathcal {P}_0^{K}{\varvec{\sigma }}-{\varvec{\sigma }}_{\textrm{0h}}, {\varvec{\mathcal P}}_{b}^{K}(({\varvec{\sigma }}-{\varvec{\sigma }}_{h})\textbf{n})\big \}\,. \end{aligned}$$

Lemma 3.5

Let \({\varvec{\sigma }}\in \mathbb {H}(\varvec{{\textrm{div}}};\Omega )\cap \mathbb {H}^{k+1}(\Omega ) \) such that \( {\textbf{div}}({\varvec{\sigma }})\in \textbf{H}^{k+2}(\Omega ) \) and \({\varvec{\sigma }}_{h}\in \mathbb {X}_{0,h}\) be solutions of Problems 1 and 3, respectively. Then, there hold

$$\begin{aligned}\big |\mathcal {A}_{h}(\varvec{\theta }, {\varvec{\tau }}_{h})\big |\,\le \, C_{\mathcal {A}}\, h^{k+1}\,\Big (\Vert {\varvec{\sigma }}\Vert _{k+2}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}\Big )\,\Vert {\varvec{\tau }}_{h}\Vert _{h}\,,\qquad \forall \, {\varvec{\tau }}_{h}\in \mathbb {X}_{h}. \end{aligned}$$

Proof

For any \({\varvec{\tau }}_{h}\in \mathbb {X}_{h}\) from Problem 3, we deduce

$$\begin{aligned} \mathcal {A}_{h}(\varvec{\theta }, {\varvec{\tau }}_{h})&\,=\,\mathcal {A}_{h}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }}, {\varvec{\tau }}_{h})-\mathcal {A}_{h}({\varvec{\sigma }}_{h}, {\varvec{\tau }}_{h})\nonumber \\&=\sum _{K\in \mathcal {K}_{h}}\Big [\dfrac{1}{\nu }\displaystyle \int _{K}\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{\textrm{0h}}{\varvec{\sigma }}^{\texttt{d}}:{\varvec{\tau }}_{\textrm{0h}}^{\texttt{d}}\,+\,\dfrac{1}{\lambda }\displaystyle \int _{K}{\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Big ]\\&+\rho \sum _{K\in \mathcal {K}_{h}}\mathcal {S}^{K}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }},{\varvec{\tau }}_{h})-\mathcal {L}_{h}({\varvec{\tau }}_{h})\nonumber \,. \end{aligned}$$
(3.8)

By testing the first and second equations of Problem 1 against \({\varvec{\tau }}_{\textrm{0h}}\) and \({\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\), respectively, one can have

$$\begin{aligned} \dfrac{1}{\nu }\displaystyle \int _{K}{\varvec{\sigma }}^{\texttt{d}}: {\varvec{\tau }}_{\textrm{0h}}\,=\,\displaystyle \int _{K}\nabla {\textbf{u}}: {\varvec{\tau }}_{\textrm{0h}}\,, \end{aligned}$$
(3.9)

and

$$\begin{aligned} \displaystyle \int _{K}{\textbf{u}}\cdot {\textbf{div}}_{\texttt{w,h}}{\varvec{\tau }}_{h}-\dfrac{1}{\lambda }\displaystyle \int _{K}{\textbf{div}}({\varvec{\sigma }})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,=\,\dfrac{1}{\lambda }\displaystyle \int _{K}{} {\textbf {f}}\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\,. \end{aligned}$$
(3.10)

First, we note that by employing the definition of the discrete divergence operator \({\textbf{div}}_{\texttt{w,h}}\) (cf. Definition 2.2) and fact \({\textbf{u}}\in {\textbf {H}}^{2}(\Omega )\), the right-hand of (3.9) can be rewritten as

$$ \dfrac{1}{\nu }\displaystyle \int _{K}{\varvec{\sigma }}^{\texttt{d}}: {\varvec{\tau }}_{\mathrm {0\,h}}\,=\,-\displaystyle \int _{K}{\textbf{u}}\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})-\langle {\textbf {g}}, {\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}_{e}\rangle _{\partial \Omega }\,, $$

from which, substituted back in (3.10) yields

$$\begin{aligned}\begin{array}{c} -\dfrac{1}{\nu }\displaystyle \int _{K}{\varvec{\sigma }}^{\texttt{d}}: {\varvec{\tau }}_{\textrm{0h}}-\dfrac{1}{\lambda }\displaystyle \int _{K}{\textbf{div}}({\varvec{\sigma }})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\\[2ex] \,=\,\dfrac{1}{\lambda }\displaystyle \int _{K}{} {\textbf {f}}\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})-\langle {\textbf {g}}, {\varvec{\tau }}_{\textrm{bh}}{} {\textbf {n}}_{e}\rangle _{\partial \Omega } \,=\,-\mathcal {L}_{h}({\varvec{\tau }}_{h})\,. \end{array} \end{aligned}$$

Now, substituting the above expression back into (3.8) and employing the commutative property (2.6), we arrive at

$$\begin{aligned} \mathcal {A}_{h}(\varvec{\theta }, {\varvec{\tau }}_{h})&=\sum _{K\in \mathcal {K}_{h}}\Big [\dfrac{1}{\nu }\displaystyle \int _{K}\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{\textrm{0h}}{\varvec{\sigma }}^{\texttt{d}}:{\varvec{\tau }}_{\textrm{0h}}^{\texttt{d}}+\dfrac{1}{\lambda }\displaystyle \int _{K}{\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})+\rho \,\mathcal {S}^{K}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }},{\varvec{\tau }}_{h})\Big ]\\&-\sum _{K\in \mathcal {K}_{h}}\Big [\dfrac{1}{\nu }\displaystyle \int _{K}{\varvec{\sigma }}^{\texttt{d}}: {\varvec{\tau }}_{\textrm{0h}}+\dfrac{1}{\lambda }\displaystyle \int _{K}{\textbf{div}}({\varvec{\sigma }})\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Big ]\\&=\sum _{K\in \mathcal {K}_{h}}\Big [\dfrac{1}{\nu }\displaystyle \int _{K}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{\textrm{0h}}{\varvec{\sigma }}^{\texttt{d}}-{\varvec{\sigma }}^{\texttt{d}}): {\varvec{\tau }}_{\textrm{0h}}+\dfrac{1}{\lambda }\displaystyle \int _{K}({\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }})-{\textbf{div}}({\varvec{\sigma }}))\cdot {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\Big ]\\&+\sum _{K\in \mathcal {K}_{h}}\rho \,\mathcal {S}^{K}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }},{\varvec{\tau }}_{h})\,. \end{aligned}$$

A direct application of the Cauchy–Schwarz inequality, the orthogonality and approximation properties of projections \(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{\textrm{0h}}\) and \(\varvec{\mathcal {P}}_{k}\) (cf. Lemma 2.3), respectively, and the estimate of stabilizer \(\mathcal {S}^{K}\) (cf. Lemma 3.4), yields

$$\begin{aligned} \big |\mathcal {A}_{h}(\varvec{\theta }, {\varvec{\tau }}_{h})\big |&\!\,\le \,\!\! \sum _{K\in \mathcal {K}_{h}}\!\bigg (\dfrac{1}{\lambda }\big \Vert \varvec{\mathcal {P}}_{k+1}({\textbf{div}}({\varvec{\sigma }}))\!-\!{\textbf{div}}({\varvec{\sigma }})\big \Vert _{0,K}\big \Vert {\textbf{div}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\big \Vert _{0,K}\!+\!\rho \, C_{\mathcal {S}}\, h^{k+1}\Vert {\varvec{\sigma }}\Vert _{k+1}\,\Vert {\varvec{\tau }}_{h}\Vert _{h} \!\bigg )\\&\le \left( \dfrac{C_{2}}{\lambda }+\rho \, C_{\mathcal {S}}\right) h^{k+1}\Big (\Vert {\varvec{\sigma }}\Vert _{k+1}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}\Big )\Vert {\varvec{\tau }}_{h}\Vert _{h}\,, \end{aligned}$$

which ends the proof by setting \(C_{\mathcal {A}}:=\max \bigg \{\dfrac{C_{1}}{\nu },\dfrac{C_{2}}{\lambda }\bigg \}+\rho \, C_{\mathcal {S}}\). \(\square \)

The main result of this section is summarized in the following theorem.

Theorem 3.6

Let \({\varvec{\sigma }}\in \mathbb {H}({\textbf{div}};\Omega )\cap \mathbb {H}^{k+1}(\Omega ) \) and \({\varvec{\sigma }}_{h}\in \mathbb {H}_{\texttt{h}}\) be solutions of Problems 1 and 3, respectively. Then, the following estimate holds

$$\begin{aligned} \Vert {\varvec{\sigma }}-{\varvec{\sigma }}_{\textrm{h}}\Vert _{h}\,\le \, \hat{C}_{1}\, h^{k+1}\Big (\Vert {\varvec{\sigma }}\Vert _{k+1}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}\Big )\,. \end{aligned}$$
(3.11)

Proof

It follows straightforwardly from the coercivity of \(\mathcal {A}_{h}\) (cf. Lemma 3.2) and Lemmas 2.3 and 3.5. \(\square \)

We end this section by remarking that (1.4) and (1.7) suggest the following post-processed approximation for the pressure p and \( {\textbf{u}}\)

$$\begin{aligned} p_{h}\,:=\,-\dfrac{1}{2}{\textrm{tr}}({\varvec{\sigma }}_{\textrm{0h}}){\quad \hbox {and}\quad }{\textbf{u}}_{h}\,:=\,\dfrac{1}{\lambda }\left( {\textbf{div}}_{\texttt{w,h}} ({\varvec{\sigma }}_{h})+\varvec{\mathcal {P}}_{h}(\textbf{f}) \right) \,. \end{aligned}$$
(3.12)

The rates of convergence for the above post-processed approximations are now provided by the following theorem.

Theorem 3.7

In addition to the hypothesis of Theorem 3.6, let \(\textbf{f}\in \textbf{H}^{k+2}(\Omega )\). Then, there exist positive constants \(\hat{C}_2\) and \(\hat{C}_{3}\), independent of h, such that

$$\begin{aligned} \Vert {\textbf{u}}-{\textbf{u}}_{h}\Vert _{0}\le \hat{C}_{2}h^{k+1}\Big (\Vert {\varvec{\sigma }}\Vert _{k+1}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}+\Vert \textbf{f}\Vert _{k+2}\Big ), \end{aligned}$$
(3.13)

and

$$\begin{aligned} \hspace{-1.4cm}\Vert p-p_{h}\Vert _{0}\le \hat{C}_{3}h^{k+1}\Big (\Vert {\varvec{\sigma }}\Vert _{k+1}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}\Big ). \end{aligned}$$
(3.14)

Proof

To derive (3.13), first, we subtract (1.7) from the second column of (3.12), and then add zero in form \(\pm {\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }})\) and use the commutative property (2.6):

$$\begin{aligned} {\textbf{u}}-{\textbf{u}}_{h}&\,=\,\dfrac{1}{\lambda }\bigg \{({\textbf{div}}({\varvec{\sigma }})-{\textbf{div}}_{\texttt{w,h}} ({\varvec{\sigma }}_{h}))+({\textbf {f}}-\varvec{\mathcal {P}}_{k+1}({\textbf {f}}))\bigg \}\nonumber \\&\,=\,\dfrac{1}{\lambda }\bigg \{\left( {\textbf{div}}({\varvec{\sigma }})-{\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }})\right) +{\textbf{div}}_{\texttt{w,h}}(\mathcal {P}\hspace{-1.5ex}\mathcal {P}_{h}{\varvec{\sigma }}- {\varvec{\sigma }}_{h})+({\textbf {f}}-\varvec{\mathcal {P}}_{k+1}({\textbf {f}}))\bigg \}\nonumber \\&\,=\,\dfrac{1}{\lambda }\bigg \{\left( {\textbf{div}}({\varvec{\sigma }})-\varvec{\mathcal {P}}_{k+1}({\textbf{div}}({\varvec{\sigma }}))\right) +{\textbf{div}}_{\texttt{w,h}}(\varvec{\theta })+({\textbf {f}}-\varvec{\mathcal {P}}_{k+1}({\textbf {f}}))\bigg \}\,, \end{aligned}$$
Fig. 1
figure 1

Example 1, samples of the kind of meshes utilized

Full size image
Fig. 2
figure 2

Example 1, snapshots of the first and second components of numerical stress (first row, left to right) and velocity magnitude and pressure (second row, left to right), computed with \(r = 0\) in the mesh made of hexagons with \(h = 3.030\)e-2

Full size image

A straightforward application of the approximation property of \(\varvec{\mathcal {P}}_{k}\) and the estimate of \(\varvec{\theta }\) stated in Lemmas 2.3 and 3.5, respectively, gives

$$\begin{aligned} \Vert {\textbf{u}}-{\textbf{u}}_{h}\Vert _0&\,=\,\dfrac{1}{\lambda }\bigg \{ \Vert {\textbf{div}}({\varvec{\sigma }})-\varvec{\mathcal {P}}_{k+1}({\textbf{div}}({\varvec{\sigma }}))\Vert _0 + \Vert {\textbf {f}}-\varvec{\mathcal {P}}_{k+1}({\textbf {f}})\Vert _0 + \Vert {\textbf{div}}_{\texttt{w,h}}(\varvec{\theta })\Vert _0\bigg \}\\&\,\le \, \dfrac{1}{\lambda }\bigg \{C_2 h^{k+2}\left( \Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}+\Vert {\textbf {f}}\Vert _{k+2}\right) +\Vert \varvec{\theta }\Vert _{h}\bigg \}\nonumber \\&\,\le \, \dfrac{1}{\lambda }\max \big \{C_2 , \alpha _2^{-1}C_{\mathcal {A}} \big \}h^{k+2}\Big (\Vert {\varvec{\sigma }}\Vert _{k+1}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}+\Vert {\textbf {f}}\Vert _{k+2}\Big )\,, \end{aligned}$$

which completes the proof (3.13) with constant \(\hat{C}_{2}:=\dfrac{1}{\lambda }\max \big \{c_2, \alpha _2^{-1}\hat{C} \big \}\). Next, in order to deal with (3.14), we observe from (1.4) and (3.12) that

$$\begin{aligned} p-p_{h}=-\dfrac{1}{2}{\text {tr}}({\varvec{\sigma }}-{\varvec{\sigma }}_{\textrm{0h}})\,, \end{aligned}$$
(3.15)
Table 1 Example 1, history of convergence using hexagon
Full size table
Table 2 Example 1, history of convergence using non-convex
Full size table
Table 3 Example 1, history of convergence using triangular
Full size table

which, together with Theorem 3.6, yields

$$\begin{aligned} \Vert p-p_{h}\Vert _{0}&\,\le \, \dfrac{1}{\sqrt{2}}\Vert {\varvec{\sigma }}-{\varvec{\sigma }}_{\textrm{0h}}\Vert _{0}\,\le \, \dfrac{1}{\sqrt{2}}\hat{C}_{1}h^{k+1}\Big (\Vert {\varvec{\sigma }}\Vert _{k+1}+\Vert {\textbf{div}}({\varvec{\sigma }})\Vert _{k+2}\Big )\,. \end{aligned}$$

Hence by setting \(\hat{C}_{3}:=\dfrac{1}{\sqrt{2}}\hat{C}_{1}\), the relation (3.14) is proved. \(\square \)

4 Numerical results

The purpose of this section is to illustrate the efficiency of the WG pseudostress-based mixed FEM for solving the Brinkman problem. In first example, we consider the WG subspace \(\mathbb {X}_{h}\) given in Section 2 with \(k\in \{0,1\}\). Like in Ref. [20], we use a real Lagrange multiplier to impose the zero integral mean condition for the only variable of the discrete scheme, that is, tensor in space \(\mathbb {X}_{h}\). As a result, Problem 3 is rewritten as follows: Find \(({\varvec{\sigma }}_{h},\eta )\in \mathbb {X}_{h}\times \textrm{R}\) such that

$$\begin{aligned} \begin{array}{ll} \mathcal {A}_{h}({\varvec{\sigma }}_{h},{\varvec{\tau }}_{h})+&{}\eta \displaystyle \int _{\Omega }{\text {tr}}({\varvec{\tau }}_{\textrm{0h}})\,=\,\mathcal {L}_{h}({\varvec{\tau }}_{h})\,,\\[2ex] &{}\xi \displaystyle \int _{\Omega }{\textrm{tr}}({\varvec{\sigma }}_{\textrm{0h}})\,=\,0\,, \end{array} \end{aligned}$$

for all \(({\varvec{\tau }}_{h},\xi )\in \mathbb {X}_{h}\times \textrm{R}\). Example 2 is utilized to evaluate the effectiveness of the discrete scheme by simulation of practical problems with different contrast permeability for which no analytical solutions. Also, for simplicity, we take \(\Omega =(0,1)^{2}\). We performed our computations using the MATLAB 2020 b software on an Intel Core i7 machine with 32 GB of memory.

Fig. 3
figure 3

Example 2, profiles for \(\kappa \)

Full size image
Fig. 4
figure 4

Example 2 with the first profile \(\kappa \); from left to right \(\kappa =\)1e-1,1e-3,1e-6: comparison of numerical velocity \(\{u_{1},u_{2}\}\) (the first and second rows) and numerical stress \(\{\sigma _{11},\sigma _{12}\}\) (the third and fourth rows)

Full size image

4.1 Example 1: accuracy assessment

We turn first to the numerical verification of the rates of convergence anticipated by Theorems 3.6 and 3.7. To this end, we consider parameters \(\nu =\lambda =0.1\) and design the exact solution as follows:

$$\begin{aligned}\begin{array}{c} {\textbf{u}}(x_1,x_2) \,\!=\!\,\!\begin{pmatrix} \sin (3\pi x_1)(\cos (3\pi x_2) \!-\! 1) \\ -\sin (3\pi x_2)(\cos (3\pi x_1) \!-\! 1) \end{pmatrix}\,,\qquad \!\!\!\!\! p(x_1,x_2) \,\!=\!\, \sin (2\pi x_1)\!-\!\sin (2\pi x_2)\,\!, \end{array} \end{aligned}$$

for all \( (x_1, x_2)^{\texttt{t}}\in \Omega \). The model problem is then complemented with the appropriate Dirichlet boundary condition.

Fig. 5
figure 5

Example 2 with the second profile \(\kappa \); from left to right \(\kappa =\)1e-2,1e-4: comparison of numerical velocity \(\{u_{1},u_{2}\}\) (the first and second rows) and numerical stress \(\{\sigma _{11},\sigma _{12}\}\) (the third and fourth rows)

Full size image

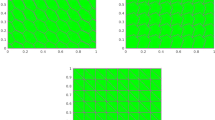
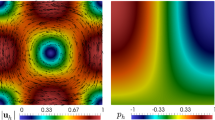
Using the weak Galerkin spaces given in Section 2 with polynomial degree \(k=0\), 1, we solve Problem 3 and obtain the approximated stress on a sequence of four successively refined polygonal meshes made of hexagons, non-convex, and triangular elements (see Fig. 1). In addition, the discrete velocity field and the discrete pressure are computed using the post-processing approach stated in Section 3. At each refinement level, we compute errors between approximate and smooth exact solutions in L\(^2\)-norm. The results of this convergence study are collected in Tables 1, 2 and 3. One can see that the rate of convergence of individual stress and pressure variables is \( O(h^{k+1}) \), whereas it is \( O(h^{k+2}) \) for the velocity, which both are in agreement with the theoretical analysis stated in Theorems 3.6 and 3.7. Moreover, in Fig. 2, we display some components of the approximate solution obtained with the polynomial degree k=0 in a hexagonal mesh to show the accuracy of the discrete scheme.

Fig. 6
figure 6

Example 2 with the third profile \(\kappa \); from left to right \(\kappa =\)1e-2,1e-4: comparison of numerical velocity \(\{u_{1},u_{2}\}\) (the first and second rows) and numerical stress \(\{\sigma _{11},\sigma _{12}\}\) (the third and fourth rows)

Full size image

4.2 Example 2: flow through porous media with discontinuous permeability

In our second example, inspired by [39], we focus on flows through porous media with the different profiles for permeability as shown in Fig. 3. In order to do that, we consider the permeability parameter in three cases: (i) \( \kappa \)=1e\(-\)1 in the orange circle area and \( \kappa \) =1 elsewhere; (ii) \( \kappa \)=1e\(-\)3 in the orange square area and \( \kappa \) =1 elsewhere; (iii) \( \kappa \)=1e\(-\)6 in the orange rectangular area and \( \kappa \) =1 elsewhere. Moreover, the body force and boundary condition are set as \({\textbf {f}}={\textbf {0}}\) and \({\textbf {g}}=(1,0)^{\texttt{t}}\), respectively.

For different values \(\kappa \), two components of the velocity and three components of stress for three different profiles of \(\kappa \) obtained by WG mixed FEM with mesh size \(h=1/32\) are presented in Figs. 4, 5 and 6. In Figs. 4, 5 and 6, we display the computed velocity and three components of stress for different profiles of \(\kappa \) displayed in Fig. 3 on polygonal mesh with mesh size \( h = 0.0213 \). As expected, because there is a greater increase in permeability in the blue region, the velocity of the fluid in the blue region is faster than in the orange region. This example illustrates the ability of our new mixed weak Galerkin method to fluid in complex porous media with a permeability coefficient highly varying.