A mixed virtual element method for a nonlinear Brinkman model of porous media flow

Abstract

In this work we introduce and analyze a mixed virtual element method for the two-dimensional nonlinear Brinkman model of porous media flow with non-homogeneous Dirichlet boundary conditions. For the continuous formulation we consider a dual-mixed approach in which the main unknowns are given by the gradient of the velocity and the pseudostress, whereas the velocity itself and the pressure are computed via simple postprocessing formulae. In addition, because of analysis reasons we add a redundant term arising from the constitutive equation relating the pseudostress and the velocity, so that the well-posedness of the resulting augmented formulation is established by using known results from nonlinear functional analysis. Then, we introduce the main features of the mixed virtual element method, which employs an explicit piecewise polynomial subspace and a virtual element subspace for approximating the aforementioned main unknowns, respectively. In turn, the associated computable discrete nonlinear operator is defined in terms of the $\mathbb {L}^2$-orthogonal projector onto a suitable space of polynomials, which allows the explicit integration of the terms involving deviatoric tensors that appear in the original setting. Next, we show the well-posedness of the discrete scheme and derive the associated a priori error estimates for the virtual element solution as well as for the fully computable projection of it. Furthermore, we also introduce a second element-by-element postprocessing formula for the pseudostress, which yields an optimally convergent approximation of this unknown with respect to the broken $\mathbb {H}(\mathbf {div})$-norm. Finally, several numerical results illustrating the good performance of the method and confirming the theoretical rates of convergence are presented.

1 Introduction

The numerical solution of diverse linear and nonlinear boundary value problems in fluid mechanics by means of the VEM technique has become a very promising research subject during recent years. In fact, we first refer to [2, 6, 17], where several virtual element methods, including stream function-based, divergence free, and non-conforming schemes, have been proposed for the classical velocity-pressure formulation of the Stokes equation. In turn, the method from [6] has been recently extended in [7] to the two-dimensional Navier–Stokes equations, thus yielding, up to our knowledge, the first VEM approach for this nonlinear model. On the other hand, and concerning the use of dual-mixed formulations, that is those in which the main unknown usually lives in either a vectorial $\mathbf H(\mathrm {div})$ or a tensorial $\mathbb H(\mathbf {div})$ space, we remark that several contributions have concentrated on the combination of VEM and pseudostress-based approaches, being the latter motivated by the need of circumventing the symmetry requirement of the usual stress-based methods. In particular, a mixed-VEM for the pseudostress-velocity formulation of the Stokes problem, in which the pressure is computed via a postprocessing formula, was introduced in [11]. The analysis in [11] is then extended in [12] to derive two mixed virtual element methods for the two-dimensional Brinkman problem. An interesting feature of both schemes in [12] refers to their robustness as the Stokes limit of the Brinkman model is approached. The corresponding pseudostress-based dual-mixed finite element methods for this model and its nonlinear version had been previously developed in [22, 23], respectively. More recently, another virtual element method for the Brinkman equations, though not employing the same dual-mixed approach from the aforementioned references, has been proposed in [30]. In addition, the approach from [11, 12] was extended in [13] to the case of quasi-Newtonian Stokes flows. More precisely, a virtual element method for an augmented mixed variational formulation of the class of nonlinear Stokes models studied in [21] (see also [18, 19]) is introduced and analyzed in [13]. Furthermore, in the recent work [26] we considered the same variational formulation from [16] (see also [14, 15]) and proposed, up to our knowledge, the first dual-mixed virtual element method for the Navier–Stokes equations. Indeed, the approach employed in [26] is based on the introduction of a nonlinear pseudostress linking the convective term with the usual pseudostress for the Stokes equations. We end this paragraph by highlighting that, besides the basic principles of the VEM philosophy (cf. [3, 10]), most of the aforedescribed works on mixed VEM for pseudostress-based variational formulations have made extensive use of the key contributions provided in [1, 4, 5]. In particular, the exact computations of the $\mathrm {L}^2$-projections onto suitable spaces of polynomials have certainly enriched the potential applications of the $\mathrm {H}^1$ and $\mathrm {H}(\mathrm {div})$ conforming cases.

According to the foregoing discussion, and in order to continue developing pseudostrees-based mixed virtual element methods for nonlinear models in fluid mechanics, we now aim to extend the analysis and results from [13, 26] to the case of the problem studied in [23]. In other words, the purpose of the present paper is to extend the analysis and results from [12] to a class of Brinkman models whose viscosity depends nonlinearly on the gradient of the velocity, which is a characteristic feature of quasi-Newtonian Stokes flows (see, e.g. [19,20,21, 27]). In order to deal with the aforedescribed nonlinearity, we follow [23] and introduce the gradient of the velocity as a new unknown. Moreover, we modify the resulting variational formulation by augmenting it with a redundant equation arising from the constitutive law relating the pseudostress and the velocity gradient, which allows us to apply known results from nonlinear functional analysis.

The rest of this work is organized as follows. In Sect. 2 we define the boundary value problem of interest, introduce its pseudostress-based mixed formulation, and provide the associated well-posedness result. Next, in Sect. 3 we follow [4, 5] to introduce the virtual element subspace that will be employed. This includes the basic assumptions on the polygonal mesh, the definition of the local virtual element space, and the projections and interpolants to be utilized together with their respective approximation properties. Further, we introduce a fully calculable local discrete nonlinear operator. Then, we set the corresponding mixed virtual element method, and apply the classical theory of nonlinear operators to conclude its well-posedness. In turn, in Sect. 4 we employ suitable bounds and identities satisfied by the nonlinear operator and the projectors and interpolators involved, to derive the a priori error estimates and corresponding rates of convergence for the virtual solution as well as for the computable projection of it. In addition, we follow the ideas from [24, 25] to construct a second approximation for the pseudostress variable ${\varvec{\sigma }}$, which yields an optimal rate of convergence in the broken $\mathbb {H}(\mathbf {div})$-norm. We remark that this new postprocessing formula can be used in general for any $\mathrm {H}(\mathrm {div})$-conforming VEM scheme. Finally, several numerical examples showing the good performance of the method, confirming the rates of convergence for regular and singular solutions, and illustrating the accurateness obtained with the approximate solutions, are reported in Sect. 5.

We end this section with several notations to be used throughout the paper. Firstly, we let $\mathbb {I}$ be the identity matrix in $\mathrm {R}^{2\times 2}$, and for any ${\varvec{\tau }}:=(\tau _{ij})$, ${\varvec{\zeta }}:=(\zeta _{ij})\in \mathrm {R}^{2\times 2}$, we set

$$\begin{aligned} {\varvec{\tau }}^{{\mathrm{t}}}:=(\tau _{ji}),\quad \mathrm{tr}({\varvec{\tau }}):=\sum _{i=1}^2\tau _{ii}, \quad {\varvec{\tau }}^{\mathrm{d}}:={\varvec{\tau }}-\frac{1}{2}\,\mathrm{tr}({\varvec{\tau }})\,\mathbb {I},\quad \text {and}\quad {\varvec{\tau }}{:}{\varvec{\zeta }}:=\sum _{i,j=1}^2\tau _{ij}\zeta _{ij}, \end{aligned}$$

which denote, respectively, the transpose, the trace, and the deviator of the tensor ${\varvec{\tau }}$, and the tensorial product between ${\varvec{\tau }}$ and ${\varvec{\zeta }}$. Next, given a bounded domain ${\mathcal {O}}\subseteq \mathrm {R}^2$, with polygonal boundary $\partial {\mathcal {O}}$, we utilize standard notations for Lebesgue spaces $\mathrm {L}^p({\mathcal {O}})$, $p > 1$, and Sobolev spaces $\mathrm {H}^s({\mathcal {O}})$, $s\in \mathrm {R}$, with norm $\Vert \cdot \Vert _{s,{\mathcal {O}}}$ and seminorm $|\cdot |_{s,{\mathcal {O}}}$. In particular, $\mathrm {H}^{1/2}(\partial {\mathcal {O}})$ is the space of traces of functions of $\mathrm {H}^1({\mathcal {O}})$ and $\mathrm {H}^{-1/2} (\partial {\mathcal {O}})$ denotes its dual. Moreover, by $\mathbf {M}$ and $\mathbb {M}$ we will refer to the corresponding vector and tensorial counterparts of the generic scalar functional space $\mathrm {M}$, and $\Vert \cdot \Vert$, with no subscripts, will stand for the natural norm of either an element or an operator in any product functional space. Furthermore, we recall that

$$\begin{aligned} \mathbb {H}(\mathbf {div};{\mathcal {O}}):= \big \{{\varvec{\tau }}\in \mathbb L^2({\mathcal {O}}):~\mathbf {div}({\varvec{\tau }})\in \mathbf L^2({\mathcal {O}})\big \}, \end{aligned}$$

equipped with the usual norm

$$\begin{aligned} \Vert {\varvec{\tau }}\Vert ^2_{\mathbf {div};{\mathcal {O}}}:=\Vert {\varvec{\tau }}\Vert ^2_{0,{\mathcal {O}}}+ \Vert \mathbf {div}({\varvec{\tau }})\Vert ^2_{0,{\mathcal {O}}} \quad \forall {\varvec{\tau }}\in \mathbb {H}(\mathbf {div};{\mathcal {O}}), \end{aligned}$$

is a Hilbert space. Finally, we employ ${\varvec{0}}$ to denote a generic null vector, null tensor or null operator, and use C and c, with or without subscripts to denote generic constants independent of the discretization parameters, which may take different values at different places.

2 The continuous problem

2.1 The model problem

Let $\Omega$ be a bounded domain in $\mathrm {R}^2$ with polygonal boundary $\Gamma$. Given a volume force $\mathbf {f}\in \mathbf {L}^2(\Omega )$ and a Dirichlet datum $\mathbf {g}\in \mathbf {H}^{1/2}(\Gamma )$, we seek a tensor ${\varvec{\sigma }}$ (pseudostress), a vector field $\mathbf {u}$ (velocity), and a scalar field p (pressure), such that

$$\begin{aligned} {\varvec{\sigma }}= & {} \mu (|\nabla \mathbf {u}|)\nabla \mathbf {u}-p\,\mathbb {I}{\quad \hbox {in}\quad }\Omega ,\quad \alpha \mathbf {u}-\mathbf {div}({\varvec{\sigma }})=\mathbf {f}{\quad \hbox {in}\quad }\Omega ,\nonumber \\ \mathrm {div}(\mathbf {u})= & {} 0{\quad \hbox {in}\quad }\Omega ,\quad \mathbf {u}=\mathbf {g}{\quad \hbox {on}\quad }\Gamma ,\quad \text {and}\quad \displaystyle \int _\Omega p=0, \end{aligned}$$

(2.1)

where $\mu :\mathrm {R}^+\rightarrow \mathrm {R}$ is the nonlinear kinematic viscosity function of the fluid, and $\alpha >0$ is a constant approximation of the viscosity divided by the permeability. In addition, note according to the incompressibility of the fluid, that $\mathbf {g}$ must satisfy the compatibility condition $\int _{\Gamma }\mathbf {g}\cdot {\varvec{\nu }}=0$, where ${\varvec{\nu }}$ is the unit outward normal on $\Gamma$, and that the uniqueness of a pressure solution is ensured by the last equation of (2.1).

In what follows, we let $\mu _{ij}:\mathrm {R}^{2\times 2}\rightarrow \mathrm {R}$ be the mapping given by $\mu _{ij}:=\mu (|{\mathbf {r}}|)r_{ij}$ for each ${\mathbf {r}}:=(r_{ij})\in \mathrm {R}^{2\times 2}$ and for each $i,j\in \lbrace 1,2\rbrace$. Then, throughout this paper we assume that $\mu$ is of class $C^1$ and that there exist $\gamma _0,\alpha _0>0$ such that for each ${\mathbf {r}}:=(r_{ij}),{\mathbf {s}}:=(s_{ij})\in \mathrm {R}^{2\times 2}$, there hold

$$\begin{aligned} |\mu _{ij}({\mathbf {r}})| \le \gamma _0|{\mathbf {r}}|,\quad \text {and}\quad \left| \frac{\partial }{\partial r_{kl}}\mu _{ij}({\mathbf {r}})\right| \le \gamma _0\quad \forall i,j,k,l\in \lbrace 1,2\rbrace , \end{aligned}$$

(2.2)

and

$$\begin{aligned} \sum _{i,j,k,l=1}^2\frac{\partial }{\partial r_{kl}}\mu _{ij}({\mathbf {r}})s_{ij}s_{kl} \ge \alpha _0|{\mathbf {s}}|^2. \end{aligned}$$

(2.3)

A classical example of nonlinear functions $\mu$ is given by the well-known Carreau law in fluid mechanics (see e.g. [28, 29])

$$\begin{aligned} \mu (s) := \rho _0 +\rho _1(1+s^2)^{(\beta -2)/2}\quad \forall s\ge 0, \end{aligned}$$

(2.4)

where $\rho _0,\rho _1>0$ and $\beta >1$. In particular, note that with $\beta =2$ we recover the usual linear Brinkman model. It is easy to check that (2.4) satisfies the assumptions (2.2) and (2.3) for all $\rho _0,\rho _1>0$ and for all $\beta \in [1,2]$, with

$$\begin{aligned} \gamma _0=\rho _0 +\rho _1\left\{ \frac{|\beta -2|}{2}+1\right\} \quad \text {and}\quad \alpha _0 =\rho _0. \end{aligned}$$

(2.5)

2.2 The continuous formulation

Here we proceed as in [23] to derive a weak formulation for (2.1). In fact, we begin by observing that the first equation of (2.1) together with the incompressibility condition are equivalent to the pair of equations given by

$$\begin{aligned} {\varvec{\sigma }}^\mathrm{d}=\mu (|\nabla \mathbf {u}|)\nabla \mathbf {u}{\quad \hbox {in}\quad }\Omega \quad \text {and}\quad p= -\frac{1}{2}\mathrm{tr}({\varvec{\sigma }}){\quad \hbox {in}\quad }\Omega , \end{aligned}$$

(2.6)

whence introducing the auxiliary unknown ${\mathbf {t}}:=\nabla \mathbf {u}$ in $\Omega$, we can rewrite (2.1) as follows:

$$\begin{aligned} {\mathbf {t}}= & {} \nabla \mathbf {u}{\quad \hbox {in}\quad }\Omega ,\quad {\varvec{\sigma }}^\mathrm{d}=\mu (|{\mathbf {t}}|) {\mathbf {t}}{\quad \hbox {in}\quad }\Omega ,\quad \alpha \mathbf {u}-\mathbf {div}({\varvec{\sigma }})= \mathbf {f}{\quad \hbox {in}\quad }\Omega ,\nonumber \\ \mathrm{tr}({\mathbf {t}})= & {} 0{\quad \hbox {in}\quad }\Omega ,\quad \mathbf {u}= \mathbf {g}{\quad \hbox {on}\quad }\Gamma ,\quad \text {and}\quad \displaystyle \int _\Omega \mathrm{tr}({\varvec{\sigma }})=0. \end{aligned}$$

(2.7)

In this way, we notice from the fourth and last equation of (2.7) that the unknowns ${\mathbf {t}}$ and ${\varvec{\sigma }}$ live in the spaces

$$\begin{aligned} \mathbb {L}_\mathrm{tr}^2(\Omega ) := \left\{ {\mathbf {s}}\in \mathbb {L}^2(\Omega ):\mathrm{tr}({\mathbf {s}})=0\right\} , \end{aligned}$$

and

$$\begin{aligned} \mathbb {H}_0(\mathbf {div};\Omega ) := \left\{ {\varvec{\zeta }}\in \mathbb {H}(\mathbf {div};\Omega ):\int _\Omega \mathrm{tr}({\varvec{\zeta }})=0\right\} , \end{aligned}$$

respectively. Then, testing the first and second equation of (2.7) with ${\varvec{\tau }}\in \mathbb {H}_0(\mathbf {div};\Omega )$ and ${\mathbf {s}}\in \mathbb {L}_\mathrm{tr}^2(\Omega )$, respectively, integrating by parts, using the Dirichlet condition for $\mathbf {u}$, and denoting by $\langle \cdot ,\cdot \rangle$ the duality pairing between $\mathbf {H}^{-1/2}(\Gamma )$ and $\mathbf {H}^{1/2}(\Gamma )$, we arrive at

$$\begin{aligned} \displaystyle \int _\Omega \mu (|{\mathbf {t}}|){\mathbf {t}}:{\mathbf {s}}-\displaystyle \int _\Omega {\mathbf {s}}:{\varvec{\sigma }}^\mathrm{d}= 0\quad \forall \;{\mathbf {s}}\in \mathbb {L}_\mathrm{tr}^2(\Omega ), \end{aligned}$$

(2.8)

and

$$\begin{aligned} \displaystyle \int _\Omega {\mathbf {t}}:{\varvec{\tau }}^\mathrm{d}+ \displaystyle \int _\Omega \mathbf {u}\cdot \mathbf {div}({\varvec{\tau }}) = \langle {\varvec{\tau }}{\varvec{\nu }},\mathbf {g}\rangle \quad \forall \;{\varvec{\tau }}\in \mathbb {H}_0(\mathbf {div};\Omega ), \end{aligned}$$

(2.9)

where we used the fact that ${\mathbf {t}}={\mathbf {t}}^\mathrm{d}$, which implies the equality $\int _\Omega {\mathbf {t}}:{\varvec{\tau }}=\int _\Omega {\mathbf {t}}:{\varvec{\tau }}^\mathrm{d}$. In turn, the velocity is replaced from the third equation of (2.7), that is

$$\begin{aligned} \mathbf {u}=\frac{1}{\alpha }\,\big \{\mathbf {f}+\mathbf {div}({\varvec{\sigma }}) \big \} {\quad \hbox {in}\quad }\Omega , \end{aligned}$$

(2.10)

whence (2.9) becomes

$$\begin{aligned} \displaystyle \int _\Omega {\mathbf {t}}:{\varvec{\tau }}^\mathrm{d}+ \frac{1}{\alpha }\displaystyle \int _\Omega \mathbf {div}({\varvec{\sigma }})\cdot \mathbf {div}({\varvec{\tau }})= -\frac{1}{\alpha }\displaystyle \int _\Omega \mathbf {f}\cdot \mathbf {div}({\varvec{\tau }})+ \langle {\varvec{\tau }}{\varvec{\nu }},\mathbf {g}\rangle \quad \forall {\varvec{\tau }}\in \mathbb {H}_0(\mathbf {div};\Omega ). \end{aligned}$$

The foregoing equation together with (2.8) yield at first instance the following variational formulation of (2.7): Find ${\mathbf {t}}\in X := \mathbb {L}_\mathrm{tr}^2(\Omega )$ and ${\varvec{\sigma }}\in H:=\mathbb {H}_0(\mathbf {div};\Omega )$ such that

$$\begin{aligned}&\displaystyle \int _\Omega \mu (|{\mathbf {t}}|){\mathbf {t}}:{\mathbf {s}}-\displaystyle \int _\Omega {\mathbf {s}}:{\varvec{\sigma }}^\mathrm{d}=0\quad \forall {\mathbf {s}}\in X,\nonumber \\&\displaystyle \int _\Omega {\mathbf {t}}:{\varvec{\tau }}^\mathrm{d}\!+\! \displaystyle \frac{1}{\alpha }\displaystyle \int _\Omega \mathbf {div}({\varvec{\sigma }})\cdot \mathbf {div}({\varvec{\tau }})\!=\!-\!\displaystyle \frac{1}{\alpha } \displaystyle \int _\Omega \mathbf {f}\cdot \mathbf {div}({\varvec{\tau }}) \!+\!\langle {\varvec{\tau }}{\varvec{\nu }},\mathbf {g}\rangle \quad \forall {\varvec{\tau }}\!\in \!H.\qquad \end{aligned}$$

(2.11)

However, in order to analyse the solvability of (2.11), we need to perform a suitable modification of it. More precisely, given a stabilization parameter $\kappa >0$ to be suitably chosen later on, we incorporate into (2.11) the following redundant Galerkin term:

$$\begin{aligned} \kappa \int _\Omega \left\{ {\varvec{\sigma }}^\mathrm{d}-\mu (|{\mathbf {t}}|){\mathbf {t}}\right\} :{\varvec{\tau }}^\mathrm{d}=0\quad \forall {\varvec{\tau }}\in \mathbb {H}_0(\mathbf {div};\Omega ), \end{aligned}$$

which leads to the augmented formulation: Find $({\mathbf {t}},{\varvec{\sigma }})\in X\times H$ such that

$$\begin{aligned}{}[\mathbf {A}({\mathbf {t}},{\varvec{\sigma }}),({\mathbf {s}},{\varvec{\tau }})]= [\mathbf {F},({\mathbf {s}},{\varvec{\tau }})]\quad \forall ({\mathbf {s}},{\varvec{\tau }})\in X\times H, \end{aligned}$$

(2.12)

where $[\cdot ,\cdot ]$ stands for the duality pairing between $(X\times H)^\prime$ and $X\times H$, $\mathbf {A}:X\times H\rightarrow (X\times H)^\prime$ is the nonlinear operator

$$\begin{aligned}{}[\mathbf {A}({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})]:= & {} \displaystyle \int _\Omega \mu (|{\mathbf {r}}|){\mathbf {r}}:{\mathbf {s}}-\displaystyle \int _\Omega {\mathbf {s}}:{\varvec{\zeta }}^\mathrm{d}+\int _\Omega {\mathbf {r}}:{\varvec{\tau }}^\mathrm{d}\nonumber \\&\displaystyle + \kappa \int _\Omega \left\{ {\varvec{\zeta }}^\mathrm{d}-\mu (|{\mathbf {r}}|){\mathbf {r}}\right\} :{\varvec{\tau }}^\mathrm{d}+\frac{1}{\alpha } \int _\Omega \mathbf {div}({\varvec{\zeta }})\cdot \mathbf {div}({\varvec{\tau }}),\qquad \end{aligned}$$

(2.13)

and $\mathbf {F}:X\times H\rightarrow \mathrm {R}$ is the bounded linear functional

$$\begin{aligned}{}[\mathbf {F},({\mathbf {s}},{\varvec{\tau }})] := -\frac{1}{\alpha } \int _\Omega \mathbf {f}\cdot \mathbf {div}({\varvec{\tau }})+\langle {\varvec{\tau }}{\varvec{\nu }},\mathbf {g}\rangle , \end{aligned}$$

(2.14)

for all $({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X\times H$. In addition, we also observe that we can write

$$\begin{aligned}{}[\mathbf {A}({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})]:= & {} [\mathbb {A}({\mathbf {r}}),{\mathbf {s}}-\kappa {\varvec{\tau }}^\mathrm{d}]-\int _\Omega {\mathbf {s}}:{\varvec{\zeta }}^\mathrm{d}+ \int _\Omega {\mathbf {r}}:{\varvec{\tau }}^\mathrm{d}\nonumber \\&\displaystyle + \kappa \int _\Omega {\varvec{\zeta }}^\mathrm{d}:{\varvec{\tau }}^\mathrm{d}+ \frac{1}{\alpha }\int _\Omega \mathbf {div}({\varvec{\zeta }})\cdot \mathbf {div}({\varvec{\tau }}), \end{aligned}$$

(2.15)

for each $({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X\times H$, where $\mathbb {A}:X\rightarrow X^\prime$ is the auxiliary nonlinear operator defined by

$$\begin{aligned}{}[\mathbb {A}({\mathbf {r}}),{\mathbf {s}}] := \displaystyle \int _\Omega \mu (|{\mathbf {r}}|){\mathbf {r}}:{\mathbf {s}}\quad \forall {\mathbf {r}},{\mathbf {s}}\in X. \end{aligned}$$

At this point we recall from [21, Lemma 2.1] that $\mathbb {A}$ is Lipschitz-continuous and strongly monotone, that is, with the constants $\gamma _0$ and $\alpha _0$ specified in (2.2) and (2.3), respectively, there hold

$$\begin{aligned} \Vert \mathbb {A}({\mathbf {r}})-\mathbb {A}({\mathbf {s}})\Vert _{X^\prime }\le \gamma _0\Vert {\mathbf {r}}-{\mathbf {s}}\Vert _{0,\Omega }, \end{aligned}$$

(2.16)

and

$$\begin{aligned}{}[\mathbb {A}({\mathbf {r}})-\mathbb {A}({\mathbf {s}}),{\mathbf {r}}-{\mathbf {s}}]\ge \alpha _0\Vert {\mathbf {r}}-{\mathbf {s}}\Vert _{0,\Omega }^2, \end{aligned}$$

(2.17)

for each ${\mathbf {r}},{\mathbf {s}}\in X$. In addition, employing the Cauchy–Schwarz inequality and the estimate (2.16), we deduce from (2.15) that $\mathbf {A}$ is Lipschitz-continuous with constant $L_\mathbf {A}:= \max \lbrace 1,\kappa ,\gamma _0,\frac{1}{\alpha }\rbrace$, that is

$$\begin{aligned} \Vert \mathbf {A}({\mathbf {t}},{\varvec{\sigma }})-\mathbf {A}({\mathbf {r}},{\varvec{\zeta }})\Vert _{(X\times H)'}\le L_\mathbf {A}\Vert ({\mathbf {t}},{\varvec{\sigma }})-({\mathbf {r}},{\varvec{\zeta }})\Vert _{X\times H} \quad \forall ({\mathbf {t}},{\varvec{\sigma }}), \, ({\mathbf {r}},{\varvec{\zeta }}) \in X\times H. \end{aligned}$$

(2.18)

Moreover, in what follows we show that $\mathbf {A}$ is strongly monotone as well. For this purpose, we need the following technical result.

Lemma 2.1

There exists $c(\Omega )>0$, depending only on $\Omega$, such that

$$\begin{aligned} c(\Omega )\,\Vert {\varvec{\tau }}\Vert _{0,\Omega }^2\le \Vert {\varvec{\tau }}^\mathrm{d}\Vert _{0,\Omega }^2+ \Vert \mathbf {div}({\varvec{\tau }})\Vert _{0,\Omega }^2\quad \forall {\varvec{\tau }}\in H. \end{aligned}$$

Proof

See [9, Chapter IV, Proposition 3.1]. $\square$

Then, the announced result on $\mathbf {A}$ is established as follows.

Lemma 2.2

Let $\mathbf {A}$ be the nonlinear operator defined in (2.13). Assume that, given $\delta \in \left( 0,\displaystyle \frac{2}{\gamma _0}\right)$, the parameter $\kappa$ lies in $\left( 0,\displaystyle \frac{2\delta \alpha _0}{\gamma _0}\right)$. Then, there exists a positive constant $C_{SM}$, independent of h, such that for all $({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X\times H$ there holds

$$\begin{aligned}{}[\mathbf {A}({\mathbf {r}},{\varvec{\zeta }})-\mathbf {A}({\mathbf {s}},{\varvec{\tau }}),({\mathbf {r}},{\varvec{\zeta }})-({\mathbf {s}},{\varvec{\tau }})]\ \ge \ C_{SM}\Vert ({\mathbf {r}},{\varvec{\zeta }})-({\mathbf {s}},{\varvec{\tau }})\Vert _{X\times H}^2. \end{aligned}$$

Proof

Given $({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X\times H$, we obtain from (2.15) that

$$\begin{aligned}&\displaystyle [\mathbf {A}({\mathbf {r}},{\varvec{\zeta }})-\mathbf {A}({\mathbf {s}},{\varvec{\tau }}),({\mathbf {r}},{\varvec{\zeta }})-({\mathbf {s}},{\varvec{\tau }})] =[\mathbb {A}({\mathbf {r}})- \mathbb {A}({\mathbf {s}}),{\mathbf {r}}-{\mathbf {s}}] \\&\quad \displaystyle -\,\kappa \, [\mathbb {A}({\mathbf {r}})- \mathbb {A}({\mathbf {s}}),({\varvec{\zeta }}-{\varvec{\tau }})^\mathrm{d}]+\kappa \Vert ({\varvec{\zeta }}-{\varvec{\tau }})^\mathrm{d}\Vert _{0,\Omega }^2+\frac{1}{\alpha } \Vert \mathbf {div}({\varvec{\zeta }}-{\varvec{\tau }})\Vert _{0,\Omega }^2, \end{aligned}$$

from which, using the Cauchy–Schwarz and Young inequalities, the Lipschitz-continuity and strong monotonicity properties of the operator $\mathbb {A}$, and Lemma 2.1, we find that

$$\begin{aligned}&\displaystyle [\mathbf {A}({\mathbf {r}},{\varvec{\zeta }})-\mathbf {A}({\mathbf {s}},{\varvec{\tau }}),({\mathbf {r}},{\varvec{\zeta }})-({\mathbf {s}},{\varvec{\tau }})] \ge \left( \alpha _0-\displaystyle \frac{\kappa \gamma _0}{2\delta }\right) \Vert {\mathbf {r}}-{\mathbf {s}}\Vert _{0,\Omega }^2\\&\qquad +\, \kappa \, \left( 1-\displaystyle \frac{\gamma _0\delta }{2}\right) \, \Vert ({\varvec{\zeta }}-{\varvec{\tau }})^\mathrm{d}\Vert _{0,\Omega }^2 \,+\, \frac{1}{\alpha } \, \Vert \mathbf {div}({\varvec{\zeta }}-{\varvec{\tau }})\Vert _{0,\Omega }^2\\&\quad \displaystyle \ge \left( \alpha _0-\displaystyle \frac{\kappa \gamma _0}{2\delta }\right) \, \Vert {\mathbf {r}}-{\mathbf {s}}\Vert _{0,\Omega }^2\,+\,c(\Omega )\,\min \left\{ \kappa \left( 1-\displaystyle \frac{\gamma _0\delta }{2}\right) ,\frac{1}{2\alpha } \, \right\} \Vert {\varvec{\zeta }}-{\varvec{\tau }}\Vert _{0,\Omega }^2\\&\qquad +\, \frac{1}{2\alpha }\Vert \mathbf {div}({\varvec{\zeta }}-{\varvec{\tau }})\Vert _{0,\Omega }^2. \end{aligned}$$

Finally, it suffices to choose

$$\begin{aligned} \displaystyle \, C_{SM} := \min \left\{ \left( \alpha _0 - \frac{\kappa \gamma _0}{2\delta }\right) , c(\Omega )\, \min \left\{ \kappa \left( 1-\displaystyle \frac{\gamma _0\delta }{2}\right) , \frac{1}{2\alpha } \,\right\} ,\frac{1}{2\alpha } \,\right\} . \end{aligned}$$

$\square$

Hence, the well-posedness of the variational formulation (2.12) is provided by the following theorem.

Theorem 2.1

Assume that $\mathbf {f}\in \mathbf {L}^2(\Omega ),\mathbf {g}\in \mathbf {H}^{1/2}(\Gamma )$, and that the parameter $\kappa$ satisfy the conditions required by Lemma 2.2. Then, there exists a unique $({\mathbf {t}},{\varvec{\sigma }})\in X\times H$ solution of (2.12). Moreover, there exists a positive constant C, depending only on $\Omega ,\alpha _0,\gamma _0,\kappa$ and $\alpha$, such that

$$\begin{aligned} \Vert ({\mathbf {t}},{\varvec{\sigma }})\Vert _{ X\times H}\ \le \ C\left\{ \Vert \mathbf {f}\Vert _{0,\Omega }\ +\ \Vert \mathbf {g}\Vert _{1/2,\Gamma }\right\} . \end{aligned}$$

Proof

Thanks to the Lipschitz-continuity and the strong monotonicity of the operator $\mathbf {A}$, the proof is a straightforward application of [31, Theorem 25.B]. $\square$

3 The mixed virtual element method

In this section we introduce and analyze a mixed virtual element scheme for the continuous formulation (2.12). An explicit piecewise polynomial subspace and a suitable virtual element subspace are employed for approximating ${\mathbf {t}}\in X$ and ${\varvec{\sigma }}\in H$, respectively. While all the definitions and results concerning the latter subspace, including its associated interpolation operator and main approximation properties, are available in [5, 13], most of the corresponding details are recalled in what follows for convenience of the reader. We begin with some preliminaries.

3.1 Preliminaries

Let $\{\mathcal {T}_h\}_{h>0}$ be a family of decompositions of $\Omega$ in polygonal elements. Then, for each $K\in \mathcal {T}_h$ we denote its diameter by $h_K$, and define, as usual, $h:=\max \{h_K : K\in \mathcal {T}_h\}$. Furthermore, in what follows we assume that there exists a constant $C_\mathcal {T}>0$ such that for each decomposition $\mathcal {T}_h$ and for each $K\in \mathcal {T}_h$ there hold:

• (a) the ratio between the shortest edge and the diameter $h_K$ of K is bigger than $C_\mathcal {T}$, and

• (b) K is star-shaped with respect to a ball B of radius $C_\mathcal {T}h_K$ and center $\mathbf {x}_B\in K$.

We recall here that, as consequence of the above hypotheses, one can show that each $K\in \mathcal {T}_h$ is simply connected, and that there exists an integer $N_\mathcal {T}$ (depending only on $C_\mathcal {T}$), such that the number of edges of each $K\in \mathcal {T}_h$ is bounded above by $N_\mathcal {T}$.

Now, given an integer $\ell \ge 0$ and ${\mathcal {O}}\subseteq \mathrm {R}^2$, we let $\mathrm {P}_\ell ({\mathcal {O}})$ be the space of polynomials on ${\mathcal {O}}$ of degree up to $\ell$, and according to Sect. 1, we set $\mathbf {P}_\ell ({\mathcal {O}}):=[\mathrm {P}_\ell ({\mathcal {O}})]^2$ and $\mathbb {P}_\ell ({\mathcal {O}}):=[\mathrm {P}_\ell ({\mathcal {O}})]^{2\times 2}$. Furthermore, given an edge e of $\mathcal T_h$ with barycentric $x_e$ and diameter $h_e$, we introduce the following set of $(\ell +1)$ normalized monomials on e

$$\begin{aligned} {\mathcal {B}}_\ell (e) := \left\{ \left( \frac{x-x_e}{h_e}\right) ^j\right\} _{0\le j\le \ell }, \end{aligned}$$

which certainly constitutes a basis on $\mathrm {P}_{\ell }(e)$. Similarly, given $K\in \mathcal {T}_h$ with barycenter $\mathbf {x}_K$, we define the following set of $\frac{1}{2}(\ell +1)(\ell +2)$ normalized monomials

$$\begin{aligned} {\mathcal {B}}_\ell (K) := \left\{ \left( \frac{\mathbf {x}-\mathbf {x}_K}{h_K}\right) ^{{\varvec{\alpha }}}\right\} _{0\le |{\varvec{\alpha }}|\le \ell }, \end{aligned}$$

which is a basis of $\mathrm {P}_{\ell }(K)$. Notice that in the definition of ${\mathcal {B}}_\ell (K)$ above, we have made use of the multi-index notation, that is, given $\mathbf {x}:=(x_1,x_2)^{{\mathrm{t}}}\in \mathrm {R}^2$ and ${\varvec{\alpha }}:=(\alpha _1,\alpha _2)^{{\mathrm{t}}}$, with non-negative integers $\alpha _1,\alpha _2$, we set $\mathbf {x}^{{\varvec{\alpha }}}:=x_1^{\alpha _1}x_2^{\alpha _2}$ and $|{\varvec{\alpha }}|:=\alpha _1+\alpha _2$. Furthermore, for e and K as indicated, we define

$$\begin{aligned} {\varvec{{\mathcal {B}}}}_{\ell }(e) := \Big \{(q,0)^{{\mathrm{t}}}:\, q\in {\mathcal {B}}_{\ell }(e)\Big \}\cup \Big \{(0,q)^{{\mathrm{t}}}\, :\, q\in {\mathcal {B}}_{\ell }(e)\Big \}, \end{aligned}$$

and

$$\begin{aligned} {\varvec{{\mathcal {B}}}}_{\ell }(K) := \Big \{(q,0)^{{\mathrm{t}}}:\, q\in {\mathcal {B}}_{\ell }(K)\Big \} \,\cup \,\Big \{(0,q)^{{\mathrm{t}}}:\, q\in {\mathcal {B}}_{\ell }(K)\Big \}. \end{aligned}$$

On the other hand, for each integer $\ell \ge 0$, we let ${\mathcal {G}}_{\ell }(K)$ be a basis of $\big (\nabla \mathrm {P}_{\ell +1}(K)\big )^{\perp }\cap \mathbf {P}_{\ell }(K)$, which is the $\mathbf {L}^2(K)$-orthogonal of $\nabla \mathrm {P}_{\ell +1}(K)$ in $\mathbf {P}_{\ell }(K)$, and denote its tensorial counterpart as follows:

$$\begin{aligned} {\varvec{{\mathcal {G}}}}_{\ell }(K) := \left\{ \left( \begin{array}{c} \mathbf {q}\\ {\varvec{0}}\end{array}\right) :\, \mathbf {q}\in {\mathcal {G}}_{\ell }(K)\right\} \cup \left\{ \left( \begin{array}{c} {\varvec{0}}\\ \mathbf {q}\end{array}\right) :\, \mathbf {q}\in {\mathcal {G}}_{\ell }(K)\right\} . \end{aligned}$$

While in what follows we use the aforedescribed decomposition of $\mathbf P_\ell (K)$ (and hence of its tensorial version $\mathbb P_\ell (K)$), we remark that, alternatively, one could also consider more modern choices, not necessarily orthogonal, that have been proposed recently, such as $\mathbf P_k(K)=\nabla \mathrm P_{k+1}\,\oplus \, \mathbf x^\perp \,\mathrm P_{k-1}(K)$, where, given $\mathbf x := (x_1,x_2)\in \mathrm {R}^2$, $\mathbf x^\perp$ denotes the rotated vector $(-x_2,x_1)$. Actually, it is not difficult to see that it suffices to choose any space $\mathcal G(K)$ such that $\mathbf P_\ell (K)= \nabla \mathrm P_{\ell +1}\,\oplus \, \mathcal G(K)$.

3.2 The virtual element spaces and its approximation properties

Given an integer $k\ge 0$, we define the finite dimensional subspaces of X and H, respectively, as

$$\begin{aligned} X_k^h:=\left\{ {\mathbf {s}}\in X:\quad {\mathbf {s}}\big \vert _K\in X_k^K\quad \forall \;K\in \mathcal {T}_h\right\} \end{aligned}$$

(3.1)

and

$$\begin{aligned} H_k^h:=\left\{ {\varvec{\tau }}\in H:\quad {\varvec{\tau }}\big \vert _K\in H_k^K\quad \forall \;K\in \mathcal {T}_h\right\} , \end{aligned}$$

(3.2)

where, given $K \in \mathcal T_h$, $X_k^K:=\mathbb {P}_k(K)$ and $H_k^K$ is the space introduced in [5, Section 3.1], namely

$$\begin{aligned} \displaystyle H_k^{K}:= & {} \Big \{{\varvec{\tau }}\in \mathbb {H}(\mathbf {div};K)\cap \mathbb {H}(\mathbf {rot};K)\,:\quad {\varvec{\tau }}{\varvec{\nu }}|_e\in \mathbf {P}_k(e)\quad \forall \ \text {edge }e\in \partial K,\nonumber \\&\displaystyle \mathbf {div}({\varvec{\tau }})\in \mathbf {P}_{k}(K)\quad \text {and}\quad \mathbf {rot}({\varvec{\tau }})\in \mathbf {P}_{k-1}(K)\Big \}. \end{aligned}$$

(3.3)

The degrees of freedom guaranteeing unisolvency for each ${\varvec{\tau }}\in H_k^K$ are defined by (see e.g. [4, Section 3.6], [5, 12])

$$\begin{aligned} \displaystyle \int _e{\varvec{\tau }}{\varvec{\nu }}\cdot \mathbf {q}&\qquad \forall \ \mathbf {q}\in {\varvec{{\mathcal {B}}}}_k(e) , \quad \forall \ \text{ edge }\ e\in \partial K,\nonumber \\ \displaystyle \int _K{\varvec{\tau }}:\nabla \mathbf {p}&\qquad \forall \, \mathbf {p}\in {\varvec{{\mathcal {B}}}}_{k}(K){\setminus }\lbrace (1,0)^{\mathbf {t}},(0,1)^{\mathbf {t}}\rbrace ,\nonumber \\ \displaystyle \int _K{\varvec{\tau }}:{\varvec{\rho }}&\qquad \forall \ {\varvec{\rho }}\in \varvec{\mathcal {G}}_k(K). \end{aligned}$$

(3.4)

In turn, we let ${\mathcal {P}}_k^K:\mathbf {L}^2(K)\rightarrow \mathbf {P}_k(K)$ and ${\varvec{{\mathcal {P}}}}_k^K:\mathbb {L}^2(K)\rightarrow \mathbb {P}_k(K)$ be the orthogonal projectors. Then, for each integer $m\in \lbrace 0,1,\ldots ,k+1\rbrace$ there hold the following approximation properties:

$$\begin{aligned} \Vert {\mathbf {v}}-{\mathcal {P}}_k^K({\mathbf {v}})\Vert _{0,K} \le Ch_K^m|{\mathbf {v}}|_{m,K} \qquad \forall \;{\mathbf {v}}\in \mathbf {H}^m(K), \end{aligned}$$

(3.5)

and

$$\begin{aligned} \Vert {\varvec{\tau }}-{\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})\Vert _{0,K}\ \le \ Ch_K^m|{\varvec{\tau }}|_{m,K} \qquad \forall \;{\varvec{\tau }}\in \mathbb {H}^m(K). \end{aligned}$$

(3.6)

We now introduce the interpolation operator $\mathbf {\Pi }_k^K:\mathbb {H}^1(K)\rightarrow H_k^K$, which is defined for each ${\varvec{\tau }}\in \mathbb {H}^1(K)$ as the unique $\mathbf {\Pi }_k^K({\varvec{\tau }})$ in $H_k^K$ such that

$$\begin{aligned} 0= & {} \int _e\left( {\varvec{\tau }}-\mathbf {\Pi }_k^K({\varvec{\tau }})\right) {\varvec{\nu }}\cdot \mathbf {q}\quad \forall \ \mathbf {q}\in {\varvec{{\mathcal {B}}}}_k(e), \quad \forall \ \text{ edge }\ e\in \partial K,\nonumber \\ 0= & {} \int _K\left( {\varvec{\tau }}-\mathbf {\Pi }_k^K({\varvec{\tau }})\right) : \nabla \mathbf {p}\quad \forall \; \mathbf {p}\in {\varvec{{\mathcal {B}}}}_{k}(K){\setminus }\lbrace (1,0)^{\mathbf {t}},(0,1)^{\mathbf {t}}\rbrace ,\nonumber \\ 0= & {} \int _K\left( {\varvec{\tau }}-\mathbf {\Pi }_k^K({\varvec{\tau }})\right) :{\varvec{\rho }}\quad \forall {\varvec{\rho }}\in \varvec{\mathcal {G}}_k(K). \end{aligned}$$

(3.7)

Concerning the approximation properties of $\mathbf {\Pi }_k^K$, we first recall from [5, eq. (3.19)] (see also [8, Lemma 6] for a closely related estimate) that for each ${\varvec{\tau }}\in \mathbb {H}^s(K)$, with $1\le s\le k+1$, there holds

$$\begin{aligned} \left\| {\varvec{\tau }}- \mathbf {\Pi }_k^K({\varvec{\tau }})\right\| _{0,K}\le C\,h_K^s\,|{\varvec{\tau }}|_{s,K}. \end{aligned}$$

(3.8)

In addition, for each $\mathbf {p}\in {\varvec{{\mathcal {B}}}}_{k}(K)$ we readily find that

$$\begin{aligned} \displaystyle \int _K\mathbf {div}\left( {\varvec{\tau }}-\mathbf {\Pi }_k^K({\varvec{\tau }})\right) \cdot \mathbf {p}= -\displaystyle \int _K\left( {\varvec{\tau }}-\mathbf {\Pi }_k^K({\varvec{\tau }})\right) :\nabla \mathbf {p}+\displaystyle \int _{\partial K}\left( {\varvec{\tau }}-\mathbf {\Pi }_k^K({\varvec{\tau }})\right) {\varvec{\nu }}\cdot \mathbf {p}= 0, \end{aligned}$$

which, thanks to the fact $\mathbf {div}(\mathbf {\Pi }_k^K({\varvec{\tau }}))\in \mathbf {P}_{k}(K)$, implies that

$$\begin{aligned} \mathbf {div}\left( \mathbf {\Pi }_k^K({\varvec{\tau }})\right) ={\mathcal {P}}_{k}^K(\mathbf {div}({\varvec{\tau }}))\quad \forall {\varvec{\tau }}\in \mathbb {H}^1(K). \end{aligned}$$

(3.9)

In this way, applying (3.9) and (3.5), we deduce that for each ${\varvec{\tau }}\in \mathbb {H}^1(K)$, such that $\mathbf {div}({\varvec{\tau }})\in \mathbf {H}^s(K)$, with $0 \le s\le k+1$, there holds

$$\begin{aligned} \left\| \mathbf {div}({\varvec{\tau }}) - \mathbf {div}\left( \mathbf {\Pi }_k^K({\varvec{\tau }})\right) \right\| _{0,K} \le C\,h_K^s\,|\mathbf {div}({\varvec{\tau }})|_{s,K}, \end{aligned}$$

(3.10)

which, together with (3.8), allows us to prove the following lemma.

Lemma 3.1

Let $K\in \mathcal T_h$, and let s be an integer such that $1 \le s \le k+1$. Then, there exists a constant $C>0$, independent of K, such that for each ${\varvec{\tau }}\in \mathbb {H}^s(K)$ such that $\mathbf {div}({\varvec{\tau }})\in \mathbf {H}^s(K)$, there holds

$$\begin{aligned} \left\| {\varvec{\tau }}- \mathbf {\Pi }_k^K({\varvec{\tau }})\right\| _{\mathbf {div};K}\le C\,h_K^s\, \Big \{|{\varvec{\tau }}|_{s,K}+|\mathbf {div}({\varvec{\tau }})|_{s,K}\Big \}. \end{aligned}$$

(3.11)

Proof

It follows straightforwardly from (3.8) and (3.10). $\square$

3.3 The discrete scheme

In what follows we define the mixed virtual element scheme itself for our nonlinear problem (2.12). In this regard, we first notice, thanks to (3.3), that the functional $\mathbf {F}$ (cf. (2.14)) is explicitly computable for all $({\mathbf {s}},{\varvec{\tau }})\in X_k^h\times H_k^h$, whereas for each $K\in \mathcal {T}_h$ the local version $\mathbf {A}^K:\left( X_k^K\times H_k^K\right) \rightarrow \left( X_k^K\times H_k^K\right) ^\prime$ of the nonlinear operator $\mathbf {A}$, which is defined for all $({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X_k^K\times H_k^K$ by

$$\begin{aligned}{}[\mathbf {A}^K({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})]:= & {} \displaystyle \int _K \mu (|{\mathbf {r}}|){\mathbf {r}}:{\mathbf {s}}- \int _K{\mathbf {s}}:{\varvec{\zeta }}^\mathrm{d}+\int _K{\mathbf {r}}:{\varvec{\tau }}^\mathrm{d}\nonumber \\&\displaystyle +\,\kappa \int _K\left\{ {\varvec{\zeta }}^\mathrm{d}-\mu (|{\mathbf {r}}|){\mathbf {r}}\right\} :{\varvec{\tau }}^\mathrm{d}\nonumber \\&+\frac{1}{\alpha }\,\int _K\mathbf {div}({\varvec{\zeta }})\cdot \mathbf {div}({\varvec{\tau }}), \end{aligned}$$

(3.12)

is not computable since ${\varvec{\zeta }}$ and ${\varvec{\tau }}$ are not known on the whole $K\in \mathcal {T}_h$. In order to deal with this difficulty, we now recall, as it was remarked in [5, Section 3.2], that the degrees of freedom introduced in (3.4) do allow the explicit calculation of ${\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})$ for each ${\varvec{\tau }}\in H_k^K$. Indeed, given $\mathbf {p}\in \mathbb {P}_k(K)$, we utilize the decomposition $\mathbb {P}_k(K)=\varvec{\mathcal {G}}_k^\perp (K) \oplus \varvec{\mathcal {G}}_k(K)$ to write $\mathbf {p}= \nabla \mathbf {q}+{\varvec{\rho }}$, with $\mathbf {q}\in \mathbf P_{k+1}(K)$ and ${\varvec{\rho }}\in \varvec{\mathcal {G}}_k(K)$, whence we find that

$$\begin{aligned} \int _K{\varvec{\tau }}:\mathbf {p}=\int _K{\varvec{\tau }}:\nabla \mathbf {q}+ \int _K{\varvec{\tau }}:{\varvec{\rho }}=-\int _K\mathbf {q}\cdot \mathbf {div}({\varvec{\tau }})+\int _{\partial K}{\varvec{\tau }}{\varvec{\nu }}\cdot \mathbf {q}+\int _K{\varvec{\tau }}:{\varvec{\rho }}. \end{aligned}$$

In this way, it readily follows from (3.3) and (3.4) that the foregoing expression, and hence ${\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})$, are both computable. Then, we now let $\mathbf {A}_h^K:\left( X_k^K\times H_k^K\right) \rightarrow \left( X_k^K\times H_k^K\right) ^\prime$ be the computable local discrete nonlinear operator approximating (3.12), which is defined by

$$\begin{aligned} \displaystyle \left[ \mathbf {A}_h^K({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\right]:= & {} \int _K \mu (|{\mathbf {r}}|)\,{\mathbf {r}}: \left( {\mathbf {s}}-\kappa ({\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }}))^\mathrm{d}\right) - \int _K\left( {\varvec{{\mathcal {P}}}}_k^K({\varvec{\zeta }})\right) ^\mathrm{d}:{\mathbf {s}}\nonumber \\&+\,\int _K\left( {\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})\right) ^\mathrm{d}:{\mathbf {r}}+\kappa \,\int _K\left( {\varvec{{\mathcal {P}}}}_k^K({\varvec{\zeta }})\right) ^\mathrm{d}:\left( {\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})\right) ^\mathrm{d}\nonumber \\&+\frac{1}{\alpha }\,\int _K\mathbf {div}({\varvec{\zeta }})\cdot \mathbf {div}({\varvec{\tau }})+\mathcal {S}^K\left( {\varvec{\zeta }}-{\varvec{{\mathcal {P}}}}_k^K({\varvec{\zeta }}),{\varvec{\tau }}-{\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})\right) ,\nonumber \\ \end{aligned}$$

(3.13)

for all $({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X_k^K\times H_k^K$, where $\mathcal {S}^K:H_k^K\times H_k^K\rightarrow \mathrm {R}$ is any symmetric and positive bilinear form verifying (see [3, Section 4.6] or [5, Section 3.3])

$$\begin{aligned} \widehat{c}_0\Vert {\varvec{\zeta }}\Vert _{0,K}^2\le \mathcal {S}^K({\varvec{\zeta }},{\varvec{\zeta }}) \le \widehat{c}_1\Vert {\varvec{\zeta }}\Vert _{0,K}^2\qquad \forall \;{\varvec{\zeta }}\in H_k^K, \end{aligned}$$

(3.14)

with constants $\widehat{c}_0$, $\widehat{c}_1>0$ depending only on $C_\mathcal {T}$. In particular, for the numerical results reported below in Sect. 5 we take $\mathcal {S}^K$ as the bilinear form whose associated matrix with respect to the canonical basis of $H_k^K$ determined by the degrees of freedom (3.4), is the identity matrix. Equivalently, letting $n^K_k$ be the dimension of $H^K_k$ and denoting by $m_{j,K}$, $j\in \big \{1,2,\ldots ,n^K_k\big \}$, the degrees of freedom given by (3.4), we set

$$\begin{aligned} \mathcal {S}^K({\varvec{\zeta }},{\varvec{\tau }}):=\sum _{j=1}^{n^K_k} m_{j,K}({\varvec{\zeta }})\, m_{j,K}({\varvec{\tau }}) \quad \forall \, ({\varvec{\zeta }},{\varvec{\tau }}) \,\in \, H_k^K\times H_k^K. \end{aligned}$$

According to (3.13), we now introduce the global discrete nonlinear operator $\mathbf {A}_h:(X_k^h\times H_k^h)\rightarrow (X_k^h\times H_k^h)^\prime$ as

$$\begin{aligned} \left[ \mathbf {A}_h({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\right] := \sum _{K\in \mathcal {T}_h}\left[ \mathbf {A}_h^K({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\right] \quad \forall \;({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X_k^h\times H_k^h. \end{aligned}$$

(3.15)

Therefore, the mixed virtual element scheme associated with the augmented formulation (2.12) reads: Find $({\mathbf {t}}_h,{\varvec{\sigma }}_h)\in X_k^h\times H_k^h$ such that

$$\begin{aligned} \left[ \mathbf {A}_h({\mathbf {t}}_h,{\varvec{\sigma }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)\right] = \left[ \mathbf {F},({\mathbf {s}}_h,{\varvec{\tau }}_h)\right] \quad \forall \;({\mathbf {s}}_h,{\varvec{\tau }}_h)\in X_k^h\times H_k^h. \end{aligned}$$

(3.16)

3.4 Analysis of the discrete scheme

In this section we develop the solvability analysis of our mixed virtual element scheme (3.16). First, recalling that the local orthogonal projectors ${\mathcal {P}}_k^K:\mathbf {L}^2(K)\rightarrow \mathbf {P}_k(K)$ and ${\varvec{{\mathcal {P}}}}_k^K:\mathbb {L}^2(K)\rightarrow \mathbb {P}_k(K)$ were introduced in Sect. 3.2, we now denote by ${\mathcal {P}}_k^h$ and ${\varvec{{\mathcal {P}}}}_k^h$, respectively, its global counterparts, that is, given ${\mathbf {v}}\in \mathbf {L}^2(\Omega )$ and ${\varvec{\zeta }}\in \mathbb {L}^2(\Omega )$, we let

$$\begin{aligned} {\mathcal {P}}_k^h({\mathbf {v}})\big \vert _K:={\mathcal {P}}_k^K({\mathbf {v}}\big \vert _K)\quad \text {and}\quad {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }})\big \vert _K:={\varvec{{\mathcal {P}}}}_k^K({\varvec{\zeta }}\big \vert _K)\quad \forall \;K\in \mathcal {T}_h. \end{aligned}$$

Further, given the local bilinear form $\mathcal {S}^K:H_k^K\times H_k^K\rightarrow \mathrm {R}$, we now define the symmetric and positive definite global bilinear form $\mathcal {S}_h:H_k^h\times H_k^h\rightarrow \mathrm {R}$ as

$$\begin{aligned} \mathcal {S}_h({\varvec{\zeta }},{\varvec{\tau }}):= \sum _{K\in \mathcal {T}_h}\mathcal {S}^K({\varvec{\zeta }}|_K,{\varvec{\tau }}|_K)\qquad \forall \;({\varvec{\zeta }},{\varvec{\tau }})\in H_k^h, \end{aligned}$$

which according to (3.14), satisfies

$$\begin{aligned} \widehat{c}_0\Vert {\varvec{\zeta }}\Vert _{0,\Omega }^2\ \le \ \mathcal {S}_h({\varvec{\zeta }},{\varvec{\zeta }})\ \le \ \widehat{c}_1\Vert {\varvec{\zeta }}\Vert _{0,\Omega }^2\qquad \forall \;{\varvec{\zeta }}\in H_k^h. \end{aligned}$$

(3.17)

Now, the Lipschitz-continuity of the discrete nonlinear operator $\mathbf {A}_h$ on $X_k^h\times H_k^h$ (cf. (3.15)) is established in the following lemma.

Lemma 3.2

There exists a constant $\gamma >0$, independent of h, such that

$$\begin{aligned} \Vert \mathbf {A}_h({\mathbf {t}},{\varvec{\sigma }})-\mathbf {A}_h({\mathbf {r}},{\varvec{\zeta }})\Vert _{(X\times H)^\prime }\ \le \ \gamma \Vert ({\mathbf {t}},{\varvec{\sigma }})-({\mathbf {r}},{\varvec{\zeta }})\Vert _{X\times H} \qquad \forall \, ({\mathbf {t}},{\varvec{\sigma }}),({\mathbf {r}},{\varvec{\zeta }})\in X_k^h\times H_k^h. \end{aligned}$$

(3.18)

Proof

Given $({\mathbf {t}},{\varvec{\sigma }}),({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\in X_k^h\times H_k^h$, we first observe that

$$\begin{aligned}&\displaystyle \left[ \mathbf {A}_h({\mathbf {t}},{\varvec{\sigma }})-\mathbf {A}_h({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})\right] =\left[ \mathbb {A}({\mathbf {t}})-\mathbb {A}({\mathbf {r}}),{\mathbf {s}}-\kappa \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }})\right) ^\mathrm{d}\right] \\&\displaystyle \quad -\displaystyle \int _\Omega {\mathbf {s}}:\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }}-{\varvec{\zeta }})\right) ^\mathrm{d}+ \int _\Omega ({\mathbf {t}}-{\mathbf {r}}):\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }})\right) ^\mathrm{d}+\kappa \int _\Omega \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }}-{\varvec{\zeta }})\right) ^\mathrm{d}:\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }})\right) ^\mathrm{d}\\&\displaystyle \quad +\, \mathcal {S}_h(({\varvec{\sigma }}-{\varvec{\zeta }})-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }}-{\varvec{\zeta }}),{\varvec{\tau }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }})) +\frac{1}{\alpha }\displaystyle \,\int _\Omega \mathbf {div}({\varvec{\sigma }}-{\varvec{\zeta }})\cdot \mathbf {div}({\varvec{\tau }}). \end{aligned}$$

Then, applying the Cauchy–Schwarz inequality, the Lipschitz-continuity of the operator $\mathbb {A}$ (cf. (2.16)), and the upper bound in (3.17), we find that

$$\begin{aligned}{}[\mathbf {A}_h({\mathbf {t}},{\varvec{\sigma }})-\mathbf {A}_h({\mathbf {r}},{\varvec{\zeta }}),({\mathbf {s}},{\varvec{\tau }})]\ \le \ \gamma \Vert ({\mathbf {t}},{\varvec{\sigma }})-({\mathbf {r}},{\varvec{\zeta }})\Vert _{X\times H}\Vert ({\mathbf {s}},{\varvec{\tau }})\Vert _{X\times H}, \end{aligned}$$

with $\gamma$ depending only on $\gamma _0$ (cf. (2.2), (2.16)), $\kappa$, $\frac{1}{\alpha }$, and $\widehat{c}_1$. In this way, the foregoing equation leads to (3.18), which ends the proof of the lemma. $\square$

The following result provides the discrete analogue of Lemma 2.2.

Lemma 3.3

Let $\mathbf {A}_h$ be the nonlinear operator defined in (3.15). Assume that the parameter $\kappa$ satisfy the conditions required by Lemma 2.2. Then, there exists a positive constant $\widetilde{C}_{SM}$, independent of h, such that for all $({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)\in X_k^h\times H_k^h$ there holds

$$\begin{aligned}{}[\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}_h({\mathbf {s}}_h,{\varvec{\tau }}_h),({\mathbf {r}}_h,{\varvec{\zeta }}_h)-({\mathbf {s}}_h,{\varvec{\tau }}_h)]\ge \widetilde{C}_{SM}\Vert ({\mathbf {r}}_h,{\varvec{\zeta }}_h)-({\mathbf {s}}_h,{\varvec{\tau }}_h)\Vert _{X\times H}^2. \end{aligned}$$

Proof

Given $({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)\in X_k^h\times H_k^h$, we have from (3.13) and (3.15) that

$$\begin{aligned} \displaystyle&[\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}_h({\mathbf {s}}_h,{\varvec{\tau }}_h),({\mathbf {r}}_h,{\varvec{\zeta }}_h)-({\mathbf {s}}_h,{\varvec{\tau }}_h)] =[\mathbb {A}({\mathbf {r}}_h)- \mathbb {A}({\mathbf {s}}_h),{\mathbf {r}}_h-{\mathbf {s}}_h]\\&\displaystyle \quad +\,\kappa \,\left\| \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\right\| _{0,\Omega }^2- \kappa \left[ \mathbb {A}({\mathbf {r}}_h)- \mathbb {A}({\mathbf {s}}_h),\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\right] \\&\displaystyle \quad +\, \frac{1}{\alpha }\Vert \mathbf {div}({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\Vert _{0,\Omega }^2 + \mathcal {S}_h\left( ({\varvec{\zeta }}_h-{\varvec{\tau }}_h)-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h),({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right. \\&\quad \left. -\,{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) . \end{aligned}$$

Then, using the Cauchy–Schwarz and Young inequalities, the Lipschitz-continuity and strong monotonicity properties of the operator $\mathbb {A}$ (cf. (2.16), (2.17)), and the lower bound in (3.17), we get

$$\begin{aligned}&\displaystyle [\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}_h({\mathbf {s}}_h,{\varvec{\tau }}_h),({\mathbf {r}}_h,{\varvec{\zeta }}_h)-({\mathbf {s}}_h,{\varvec{\tau }}_h)]\,\ge \, \left( \alpha _0-\displaystyle \frac{\kappa \gamma _0}{2\delta }\right) \,\Vert {\mathbf {r}}_h-{\mathbf {s}}_h\Vert _{0,\Omega }^2\nonumber \\&\displaystyle \quad + \, \kappa \,\left( 1-\displaystyle \frac{\gamma _0\delta }{2}\right) \,\left\| {\varvec{{\mathcal {P}}}}_k^h\left( ({\varvec{\zeta }}_h-{\varvec{\tau }}_h)^\mathrm{d}\right) \right\| _{0,\Omega }^2 \,+\, \frac{1}{\alpha }\,\Vert \mathbf {div}({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\Vert _{0,\Omega }^2\nonumber \\&\displaystyle \quad +\,\widehat{c}_0\,\Vert ({\varvec{\zeta }}_h-{\varvec{\tau }}_h)^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\Vert _{0,\Omega }^2\nonumber \\&\displaystyle \quad \ge \,\left( \alpha _0-\displaystyle \frac{\kappa \gamma _0}{2\delta }\right) \,\Vert {\mathbf {r}}_h-{\mathbf {s}}_h\Vert _{0,\Omega }^2 \,+\, \frac{1}{\alpha }\,\Vert \mathbf {div}({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\Vert _{0,\Omega }^2\nonumber \\&\displaystyle \qquad + \,\eta \,\left\{ 2\left\| \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\right\| _{0,\Omega }^2\,+\,2\,\left\| ({\varvec{\zeta }}_h-{\varvec{\tau }}_h)^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\right\| _{0,\Omega }^2\right\} ,\nonumber \\ \end{aligned}$$

(3.19)

where $\eta :=\displaystyle \frac{1}{2}\min \left\{ \kappa \left( 1-\displaystyle \frac{\gamma _0\delta }{2}\right) , \widehat{c}_0\right\}$. Next, applying the parallelogram law in the last term of the foregoing inequality, we arrive at

$$\begin{aligned}&2\left\| \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\right\| _{0,\Omega }^2\,+\,2\left\| ({\varvec{\zeta }}_h-{\varvec{\tau }}_h)^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h-{\varvec{\tau }}_h)\right) ^\mathrm{d}\right\| _{0,\Omega }^2\nonumber \\&\quad \ge \Vert ({\varvec{\zeta }}_h-{\varvec{\tau }}_h)^\mathrm{d}\Vert _{0,\Omega }^2, \end{aligned}$$

which replaced back into (3.19), and using Lemma 2.1, finishes the proof with the constant

$$\begin{aligned} \widetilde{C}_{SM}:=\min \left\{ \left( \alpha _0-\displaystyle \frac{\kappa \gamma _0}{2\delta }\right) ,\ c(\Omega )\min \left\{ \eta ,\frac{1}{2\alpha }\right\} ,\ \frac{1}{2\alpha }\right\} . \end{aligned}$$

(3.20)

$\square$

Now, looking again the definition (3.13), one could infer that the bilinear form $\mathcal S^K$, which is stabilizing the term $\displaystyle \kappa \,\int _K\left( {\varvec{{\mathcal {P}}}}_k^K({\varvec{\zeta }})\right) ^\mathrm{d}:\left( {\varvec{{\mathcal {P}}}}_k^K({\varvec{\tau }})\right) ^\mathrm{d}$, needs to be multiplied by $\kappa$ as well. Nevertheless, as shown by (3.20), the constant that really matters is not the one resulting from these two terms only, but the final one providing the strong monotonicity of the nonlinear operator $\mathbf A_h$, namely $\widetilde{C}_{SM}$, which also depends on $\alpha$ and the unknown constant $c(\Omega )$ (cf. Lemma 2.1). Perhaps, an alternative procedure to be considered is the multiplication of $\mathcal S^K$ by an arbitrary parameter $\xi$ to be chosen so as to maximize either $\widetilde{C}_{SM}$ or some of the three expressions defining it.

The unique solvability and stability of the actual Galerkin scheme (3.16) is established now

Theorem 3.1

Assume that given $\delta \in \left( 0,\displaystyle \frac{2}{\gamma _0}\right)$, the parameter $\kappa$ lies in $\left( 0,\displaystyle \frac{2\delta \alpha _0}{\gamma _0}\right)$. Then, there exists a unique $({\mathbf {t}}_h,{\varvec{\sigma }}_h)\in X_k^h\times H_k^h$ solution of (3.16), and there exists a positive constant C, independent of h, such that

$$\begin{aligned} \Vert ({\mathbf {t}}_h,{\varvec{\sigma }}_h)\Vert _{X\times H}\,\le \, C\, \Big \{ \Vert \mathbf {f}\Vert _{0,\Omega }\,+\,\Vert \mathbf {g}\Vert _{1/2,\Gamma } \Big \}. \end{aligned}$$

Proof

Thanks to Lemmas 3.2 and 3.3, the proof is a direct application of [31, Theorem 25.B]. $\square$

4 The a priori error estimates

We now aim to derive the priori error estimates for the continuous and discrete formulations (2.12) and (3.16). For this, given the local interpolation $\mathbf {\Pi }_k^K$ introduced in the Sect. 3.2, we denote by $\mathbf {\Pi }_k^h$ its global counterpart, that is, for all ${\varvec{\zeta }}\in \mathbb {H}(\mathbf {div};\Omega )$ such that ${\varvec{\zeta }}\big \vert _K\in \mathbb {H}^1(K)$ for all $K\in \mathcal {T}_h$, we let

$$\begin{aligned} \mathbf {\Pi }_k^h({\varvec{\zeta }})\big \vert _K:= \mathbf {\Pi }_k^K({\varvec{\zeta }}\big \vert _K)\quad \forall \;K\in \mathcal {T}_h. \end{aligned}$$

We begin our analysis with the following lemma.

Lemma 4.1

There exists a constant $c_1>0$, depending only on $\kappa$ and $\widehat{c}_1$ (cf. (3.14)), such that

$$\begin{aligned}&\displaystyle [\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)]\\&\quad \displaystyle \le \ c_1 \,\Big \{ \Vert {\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)\Vert _{0,\Omega } \,+\, \Vert \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h - {\varvec{{\mathcal {P}}}}_k^h \big (\mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h \big ) \Vert _{0,\Omega } \Big \}\, \Vert ({\mathbf {s}}_h,{\varvec{\tau }}_h)\Vert _{X\times H} \end{aligned}$$

for all $({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)\in X_k^h\times H_k^h$.

Proof

We first observe, according to the definitions of $\mathbf {A}_h$ (cf. (3.13), (3.15)) and $\mathbf {A}$ (cf. (2.13)), that

$$\begin{aligned}&\displaystyle [\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)]= \displaystyle \int _\Omega \left\{ {\varvec{\zeta }}_h^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)\right) ^\mathrm{d}\right\} :{\mathbf {s}}_h\\&\quad +\displaystyle \int _\Omega \left\{ \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) ^\mathrm{d}-{\varvec{\tau }}_h^\mathrm{d}\right\} :{\mathbf {r}}_h +\kappa \displaystyle \int _\Omega \left\{ {\varvec{\tau }}_h^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) ^\mathrm{d}\right\} : \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h \\&\quad +\,\kappa \,\int _\Omega \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)\right) ^\mathrm{d}:\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) ^\mathrm{d}-\kappa \, \int _\Omega {\varvec{\zeta }}_h^\mathrm{d}:{\varvec{\tau }}_h^\mathrm{d}\\&\displaystyle \quad +\,\, \mathcal {S}_h\left( {\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h),{\varvec{\tau }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) \!, \end{aligned}$$

for all $({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)\in X_k^h\times H_k^h$. Then, using that ${\mathbf {s}}_h\big \vert _K$ and ${\mathbf {r}}_h\big \vert _K$ belong to $\mathbb {P}_k(K)$ for each $K\in \mathcal {T}_h$, we deduce that the first two terms on the right hand side of the foregoing equation vanish. In turn, since it is clear that

$$\begin{aligned} \int _\Omega \left\{ {\varvec{\tau }}_h^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) ^\mathrm{d}\right\} : {\varvec{{\mathcal {P}}}}_k^h\big (\mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h\big )\,=\,0, \end{aligned}$$

the third term can be rewritten as

$$\begin{aligned} \kappa \displaystyle \int _\Omega \left\{ {\varvec{\tau }}_h^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) ^\mathrm{d}\right\} : \left\{ \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h - {\varvec{{\mathcal {P}}}}_k^h\left( \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h\right) \right\} , \end{aligned}$$

whereas the fourth one reduces to $\displaystyle \kappa \,\int _\Omega \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)\right) ^\mathrm{d}:{\varvec{\tau }}_h^\mathrm{d}$, and hence $\mathbf {A}_h$ becomes

$$\begin{aligned}&\displaystyle [\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)]= \kappa \,\int _\Omega \left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)- {\varvec{\zeta }}_h\right) ^\mathrm{d}:{\varvec{\tau }}_h^\mathrm{d}\\&\quad +\, \mathcal {S}_h\left( {\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h),{\varvec{\tau }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) \\&\quad \displaystyle + \, \kappa \displaystyle \int _\Omega \left\{ {\varvec{\tau }}_h^\mathrm{d}-\left( {\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h)\right) ^\mathrm{d}\right\} : \left\{ \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h - {\varvec{{\mathcal {P}}}}_k^h\left( \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h\right) \right\} .\qquad \end{aligned}$$

In this way, using the Cauchy–Schwarz inequality, the symmetry of $\mathcal {S}_h$, and the upper bound in (3.17), we find that

$$\begin{aligned}&\displaystyle [\mathbf {A}_h({\mathbf {r}}_h,{\varvec{\zeta }}_h)-\mathbf {A}({\mathbf {r}}_h,{\varvec{\zeta }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)]\\&\displaystyle \quad \le \kappa \, \left\{ \left\| {\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)\right\| _{0,\Omega } \,+\, \Vert \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h - {\varvec{{\mathcal {P}}}}_k^h (\mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h ) \Vert _{0,\Omega } \right\} \, \Vert {\varvec{\tau }}_h\Vert _{0,\Omega }\\&\displaystyle \qquad +\,\left\{ \mathcal {S}_h({\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h),{\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h))\right\} ^{1/2}\left\{ \mathcal {S}_h({\varvec{\tau }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h),{\varvec{\tau }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\tau }}_h))\right\} ^{1/2}\\&\displaystyle \quad \le c_1\, \left\{ \left\| {\varvec{\zeta }}_h-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\zeta }}_h)\right\| _{0,\Omega } \,+\, \left\| \mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h - {\varvec{{\mathcal {P}}}}_k^h (\mu (|{\mathbf {r}}_h|)\,{\mathbf {r}}_h) \right\| _{0,\Omega }\right\} \, \Vert ({\mathbf {s}}_h,{\varvec{\tau }}_h)\Vert _{X\times H}, \end{aligned}$$

with $c_1 \,:=\, 2\,\max \left\{ \kappa ,\widehat{c}_1 \right\}$, which completes the proof. $\square$

Then, we have the following main result.

Theorem 4.1

Let $({\mathbf {t}},{\varvec{\sigma }})\in X\times H$ and $({\mathbf {t}}_h,{\varvec{\sigma }}_h)\in X_k^h\times H_k^h$ be the unique solutions of the continuous and discrete schemes (2.12) and (3.16), respectively, and assume that ${\varvec{\sigma }}\big \vert _K\in \mathbb {H}^1(K)$ for all $K\in \mathcal {T}_h$. Then, there exists a positive constant $C>0$, independent of h, such that

$$\begin{aligned}&\Vert {\mathbf {t}}-{\mathbf {t}}_h\Vert _{0,\Omega }+\Vert {\varvec{\sigma }}-{\varvec{\sigma }}_h\Vert _{\mathbf {div};\Omega }\nonumber \\&\quad \le C\left\{ \Vert {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega }+\Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{\mathbf {div};\Omega }+\Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\right\} . \end{aligned}$$

(4.1)

Proof

We begin by observing, due to the triangle inequality, that

$$\begin{aligned}&\Vert {\mathbf {t}}-{\mathbf {t}}_h\Vert _{0,\Omega }+\Vert {\varvec{\sigma }}-{\varvec{\sigma }}_h\Vert _{\mathbf {div};\Omega }\nonumber \\&\quad \le \left\| {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\right\| _{0,\Omega }+\left\| {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\right\| _{\mathbf {div};\Omega }+\left\| \delta _h^{\mathbf {t}}\right\| _{0,\Omega }+\left\| \delta _h^{\varvec{\sigma }}\right\| _{\mathbf {div};\Omega }, \end{aligned}$$

(4.2)

where $\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) :=\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})-{\mathbf {t}}_h,\mathbf {\Pi }_k^h({\varvec{\sigma }})-{\varvec{\sigma }}_h\right) \in X_k^h\times H_k^h$. Then, applying the strong monotonicity of $\mathbf {A}_h$ (cf. Lemma 3.3) with $({\mathbf {r}}_h,{\varvec{\zeta }}_h):=\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right)$ and $({\mathbf {s}}_h,{\varvec{\tau }}_h):=({\mathbf {t}}_h,{\varvec{\sigma }}_h)$, and the Eqs. (3.16) and (2.12), we obtain that

$$\begin{aligned} \widetilde{C}_{SM}\left\| \left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right\| _{X\times H}^2\le & {} \displaystyle \left[ \mathbf {A}_h\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) -\mathbf {A}_h({\mathbf {t}}_h,{\varvec{\sigma }}_h),\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] \\= & {} \displaystyle \left[ \mathbf {A}_h\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) ,\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] - \left[ \mathbf {A}_h({\mathbf {t}}_h,{\varvec{\sigma }}_h),\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] \\ \displaystyle \quad= & {} \displaystyle \left[ \mathbf {A}_h\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) ,\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] - \left[ \mathbf {A}({\mathbf {t}},{\varvec{\sigma }}),\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] , \end{aligned}$$

from which, adding and subtracting $\left[ \mathbf {A}\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) ,\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right]$, we obtain

$$\begin{aligned} \widetilde{C}_{SM}\Vert (\delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }})\Vert _{X\times H}^2\le & {} \left[ \mathbf {A}_h\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) -\mathbf {A}\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})),(\delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] \nonumber \\&\displaystyle +\, \left[ \mathbf {A}\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) -\mathbf {A}({\mathbf {t}},{\varvec{\sigma }}),\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] . \end{aligned}$$

(4.3)

The two expressions on the right-hand side of (4.3) are bounded in what follows. Indeed, we first apply Lemma 4.1 to obtain

$$\begin{aligned}&\left[ \mathbf {A}_h\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) -\mathbf {A}\left( {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }})\right) ,\left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right] \le c_1\,\left\{ \left\| \mathbf {\Pi }_k^h({\varvec{\sigma }})-{\varvec{{\mathcal {P}}}}_k^h\left( \mathbf {\Pi }_k^h({\varvec{\sigma }})\right) \right\| _{0,\Omega }\right. \nonumber \\&\left. \displaystyle +\quad \left\| \mu \left( |{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|\right) \,{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}) - {\varvec{{\mathcal {P}}}}_k^h \left( \mu \left( |{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|\right) \, {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\right) \right\| _{0,\Omega }\right\} \,\left\| \left( \delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }}\right) \right\| _{X\times H}. \end{aligned}$$

(4.4)

Then, adding and subtracting ${\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})$, we find that

$$\begin{aligned}&\Vert \mathbf {\Pi }_k^h({\varvec{\sigma }})-{\varvec{{\mathcal {P}}}}_k^h\big (\mathbf {\Pi }_k^h({\varvec{\sigma }})\big )\Vert _{0,\Omega }\nonumber \\&\displaystyle \qquad \le \, \Big \{\Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\,+\, \Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\,+\, \Vert {\varvec{{\mathcal {P}}}}_k^h\big ({\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\big ) \Vert _{0,\Omega } \Big \}\nonumber \\&\displaystyle \qquad \le \, 2\, \Big \{\Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\,+\, \Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\Big \}. \end{aligned}$$

(4.5)

In turn, adding and subtracting $\mu (|{\mathbf {t}}|)\,{\mathbf {t}}- {\varvec{{\mathcal {P}}}}_k^h\big (\mu (|{\mathbf {t}}|)\,{\mathbf {t}}\big )$, we deduce that

$$\begin{aligned}&\Vert \mu (|{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|)\,{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}) - {\varvec{{\mathcal {P}}}}_k^h \big (\mu (|{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|)\, {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}) \big ) \Vert _{0,\Omega } \,\le \, \Vert \mu (|{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|)\,{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}) - \mu (|{\mathbf {t}}|)\,{\mathbf {t}}\Vert _{0,\Omega } \nonumber \\&\quad \displaystyle + \quad \Vert \mu (|{\mathbf {t}}|)\,{\mathbf {t}}- {\varvec{{\mathcal {P}}}}_k^h\big (\mu (|{\mathbf {t}}|)\,{\mathbf {t}}\big )\Vert _{0,\Omega } \,+\,\Big \Vert {\varvec{{\mathcal {P}}}}_k^h\Big (\mu (|{\mathbf {t}}|)\,{\mathbf {t}}\,-\, \mu (|{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|)\, {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Big )\Big \Vert _{0,\Omega }, \end{aligned}$$

(4.6)

from which, applying the boundedness of ${\varvec{{\mathcal {P}}}}_k^h$, the Lipschitz-continuity estimate (2.16), and the fact that $\mu (|{\mathbf {t}}|)\,{\mathbf {t}}\,=\, {\varvec{\sigma }}^\mathtt{d}$ (cf. (2.7)), we conclude the existence of a constant $c > 0$, depending on $\gamma _0$ (cf. (2.16)), such that

$$\begin{aligned}&\Vert \mu (|{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|)\,{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}) - {\varvec{{\mathcal {P}}}}_k^h \big (\mu (|{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})|)\, {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}}) \big ) \Vert _{0,\Omega }\nonumber \\&\quad \,\le \, c\,\Big \{ \Vert {\mathbf {t}}- {\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega }\,+\, \Vert {\varvec{\sigma }}- {\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\Big \}. \end{aligned}$$

(4.7)

Finally, the Lipschitz-continuity of $\mathbf {A}$ (cf. (2.18)) yields

$$\begin{aligned}&\displaystyle [\mathbf {A}({\mathcal {P}}_k^h({\mathbf {t}}),\mathbf {\Pi }_k^h({\varvec{\sigma }}))-\mathbf {A}({\mathbf {t}},{\varvec{\sigma }}),(\delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }})]\nonumber \\&\displaystyle \qquad \le \,\sqrt{2}\,L_\mathbf {A}\, \left\{ \Vert {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega } \,+\, \Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{\mathbf {div};\Omega }\right\} \, \Vert (\delta _h^{\mathbf {t}},\delta _h^{\varvec{\sigma }})\Vert _{X\times H}.\qquad \end{aligned}$$

(4.8)

In this way, (4.3), (4.4), (4.5), (4.7) and (4.8) yield the existence of $C := C(\widetilde{C}_{SM},c_1,\gamma _0,L_\mathbf {A}) > 0$, such that

$$\begin{aligned} \Vert \delta _h^{\mathbf {t}}\Vert _{0,\Omega }+\Vert \delta _h^{\varvec{\sigma }}\Vert _{\mathbf {div};\Omega }\le & {} C \,\left\{ \Vert {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega }\,+\, \Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{\mathbf {div};\Omega }\right. \\&\left. \,+\, \Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\right\} , \end{aligned}$$

which, together with (4.2), gives (4.1) and ends the proof of the theorem. $\square$

Having established the a priori error estimates for our unknowns, we now provide the corresponding rate of convergence.

Theorem 4.2

Let $({\mathbf {t}},{\varvec{\sigma }})\in X\times H$ and $({\mathbf {t}}_h,{\varvec{\sigma }}_h)\in X_k^h\times H_k^h$ be the unique solutions of the continuous and discrete schemes (2.12) and (3.16), respectively. Assume that for some $s\in [1,k+1]$ there hold ${\mathbf {t}}\big \vert _K$, ${\varvec{\sigma }}\big \vert _K\in \mathbb {H}^s(K)$, and $\mathbf {div}({\varvec{\sigma }})\big \vert _K\in \mathbf {H}^s(K)$ for each $K\in \mathcal {T}_h$. Then, there exists $C>0$, independent of h, such that

$$\begin{aligned} \Vert {\mathbf {t}}-{\mathbf {t}}_h\Vert _{0,\Omega }\,+\,\Vert {\varvec{\sigma }}-{\varvec{\sigma }}_h\Vert _{\mathbf {div};\Omega } \,\le \,C \,h^s\,\sum _{K\in \mathcal {T}_h}\Big \{|{\mathbf {t}}|_{s,K}+|{\varvec{\sigma }}|_{s,K}+|\mathbf {div}({\varvec{\sigma }})|_{s,K}\Big \}.\nonumber \\ \end{aligned}$$

(4.9)

Proof

It follows from (4.1) and a straightforward application of the approximation properties provided by (3.6) and (3.11). $\square$

4.1 Computable approximations of ${\varvec{\sigma }},p$ and $\mathbf {u}$

We now introduce the fully computable approximation of ${\varvec{\sigma }}_h$ given by

$$\begin{aligned} \widehat{{\varvec{\sigma }}}_h:= {\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }}_h), \end{aligned}$$

(4.10)

and establishes next the corresponding a priori error estimate in the $\mathbb {L}^2(\Omega )$-norm, which yields exactly the same rate of convergence given by Theorem 4.2.

Lemma 4.2

There exists a positive constant C, independent of h, such that

$$\begin{aligned} \Vert {\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h\Vert _{0,\Omega }\le C\left\{ \Vert {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega }+\Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{\mathbf {div};\Omega }+\Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\right\} . \end{aligned}$$

(4.11)

Proof

The proof is similar to [12, Lemma 5.2]. $\square$

Next, as suggested by (2.6) and (2.10), and proceeding as in [12, Section 5.2], we define

$$\begin{aligned} p_h:=-\frac{1}{2}\mathrm{tr}(\widehat{{\varvec{\sigma }}}_h)\quad \text {and}\quad \mathbf {u}_h:= \displaystyle \frac{1}{\alpha }\left\{ {\mathcal {P}}_{k}^h(\mathbf {f})+\mathbf {div}({\varvec{\sigma }}_h)\right\} , \end{aligned}$$

(4.12)

which constitute fully computable approximations of the pressure and velocity, respectively. Then, we notice from (2.6) and the first equation of (4.12) that there holds

$$\begin{aligned} \Vert p-p_h\Vert _{0,\Omega }\ =\ \frac{1}{2}\Vert \mathrm{tr}({\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h)\Vert _{0,\Omega }\ \le \ \frac{1}{\sqrt{2}}\Vert {\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h\Vert _{0,\Omega }, \end{aligned}$$

which, together with (4.11), gives the a priori error estimate for the pressure, that is

$$\begin{aligned} \Vert p-p_h\Vert _{0,\Omega }\le C\left\{ \Vert {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega }+\Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{\mathbf {div};\Omega }+\Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\right\} . \end{aligned}$$

(4.13)

In turn, starting from (2.10) and the second equation of (4.12), and then using again from (2.10) that $\mathbf {f}=\alpha \mathbf {u}-\mathbf {div}({\varvec{\sigma }})$, we arrive at

$$\begin{aligned} \Vert \mathbf {u}-\mathbf {u}_h\Vert _{0,\Omega }\le C\left\{ \displaystyle \Vert \mathbf {u}-{\mathcal {P}}_{k}^h(\mathbf {u})\Vert _{0,\Omega }+\Vert \mathbf {div}({\varvec{\sigma }})-{\mathcal {P}}_{k}^h(\mathbf {div}({\varvec{\sigma }}))\Vert _{0,\Omega }+\Vert \mathbf {div}({\varvec{\sigma }}-{\varvec{\sigma }}_h)\Vert _{0,\Omega }\right\} , \end{aligned}$$

from which, bounding $\Vert \mathbf {div}({\varvec{\sigma }}-{\varvec{\sigma }}_h)\Vert _{0,\Omega }$ by $\Vert ({\mathbf {t}},{\varvec{\sigma }})-({\mathbf {t}}_h,{\varvec{\sigma }}_h)\Vert _{X\times H}$, and employing the a priori error estimate (4.1) (cf. Theorem 4.1), we conclude that

$$\begin{aligned}&\displaystyle \Vert \mathbf {u}-\mathbf {u}_h\Vert _{0,\Omega } \,\le \, C \, \Big \{ \Vert \mathbf {u}-{\mathcal {P}}_{k}^h(\mathbf {u})\Vert _{0,\Omega }\,+\, \Vert \mathbf {div}({\varvec{\sigma }})-{\mathcal {P}}_{k}^h(\mathbf {div}({\varvec{\sigma }}))\Vert _{0,\Omega }\nonumber \\&\quad \displaystyle +\,\, \Vert {\mathbf {t}}-{\varvec{{\mathcal {P}}}}_k^h({\mathbf {t}})\Vert _{0,\Omega } \,+\, \Vert {\varvec{\sigma }}-\mathbf {\Pi }_k^h({\varvec{\sigma }})\Vert _{\mathbf {div};\Omega }\,+\, \Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_k^h({\varvec{\sigma }})\Vert _{0,\Omega }\Big \}. \end{aligned}$$

(4.14)

In this way, we are now able to provide the theoretical rates of convergence for $\widehat{{\varvec{\sigma }}}_h$, $p_h$, and $\mathbf {u}_h$.

Theorem 4.3

Let $({\mathbf {t}},{\varvec{\sigma }})\in X\times H$ and $({\mathbf {t}}_h,{\varvec{\sigma }}_h)\in X_k^h\times H_k^h$ be the unique solutions of the continuous and discrete schemes (2.12) and (3.16), respectively. In addition, let $\widehat{{\varvec{\sigma }}}_h$ and $(p_h,\mathbf {u}_h)$ be the discrete approximations introduced in (4.10) and (4.12), respectively. Assume that for some $s\in [1,k+1]$ there hold ${\mathbf {t}}\big \vert _K$, ${\varvec{\sigma }}\big \vert _K\in \mathbb {H}^s(K)$, $\mathbf {div}({\varvec{\sigma }})\big \vert _K\in \mathbf {H}^s(K)$, and $\mathbf {u}\big \vert _K\in \mathbf {H}^s(K)$ for each $K\in \mathcal {T}_h$. Then, there exist positive constants $C_1$ and $C_2$, independent of h, such that

$$\begin{aligned} \Vert {\varvec{\sigma }}\!-\!\widehat{{\varvec{\sigma }}}_h\Vert _{0,\Omega }\!+\!\Vert p-p_h\Vert _{0,\Omega } \,\le \, C_1 \, h^s \, \sum _{K\in \mathcal {T}_h}\Big \{ |{\mathbf {t}}|_{s,K}\!+\!|{\varvec{\sigma }}|_{s,K}\!+\!|\mathbf {div}({\varvec{\sigma }})|_{s,K}\Big \}, \end{aligned}$$

(4.15)

and

$$\begin{aligned} \Vert \mathbf {u}-\mathbf {u}_h\Vert _{0,\Omega } \,\le \,C_2 \, h^s \, \sum _{K\in \mathcal {T}_h}\Big \{ |\mathbf {u}|_{s,K}+ |{\mathbf {t}}|_{s,K}+|{\varvec{\sigma }}|_{s,K}+|\mathbf {div}({\varvec{\sigma }})|_{s,K}\Big \}. \end{aligned}$$

(4.16)

Proof

It follows from (4.11), (4.13), (4.14), and a straightforward application of the approximation properties provided by (3.5), (3.6) and (3.11). $\square$

4.2 A convergent approximation of ${\varvec{\sigma }}$ in the broken $\mathbb {H}(\mathbf {div})$-norm

In this section we proceed as in [12, Section 5.3] and construct a second approximation, denoted by ${\varvec{\sigma }}_h^{\star }$, for the pseudostress variable ${\varvec{\sigma }}$, which has an optimal rate of convergence in the broken $\mathbb {H}(\mathbf {div})$-norm. To this end, for each $K\in \mathcal {T}_h$ we let $(\cdot ,\cdot )_{\mathbf {div};K}$ be the usual $\mathbb {H}(\mathbf {div};K)$-inner product with induced norm $\Vert \cdot \Vert _{\mathbf {div};K}$, and let ${\varvec{\sigma }}_h^{\star }\big \vert _K:={\varvec{\sigma }}_{h,K}^{\star }\in \mathbb {P}_{k+1}(K)$ be the unique solution of the local problem

$$\begin{aligned} ({\varvec{\sigma }}_{h,K}^{\star },{\varvec{\tau }}_h)_{\mathbf {div};K}=\displaystyle \int _K\widehat{{\varvec{\sigma }}}_h:{\varvec{\tau }}_h\ +\ \int _K\mathbf {div}({\varvec{\sigma }}_h)\cdot \mathbf {div}({\varvec{\tau }}_h)\qquad \forall \;{\varvec{\tau }}_h\in \mathbb {P}_{k+1}(K). \end{aligned}$$

(4.17)

We stress that ${\varvec{\sigma }}_{h,K}^{\star }$ can be explicitly computed for each $K\in \mathcal {T}_h$, independently. Then, the rate of convergence for the broken $\mathbb {H}(\mathbf {div};\Omega )$-norm of ${\varvec{\sigma }}-{\varvec{\sigma }}_h^{\star }$ is established as follows.

Theorem 4.4

Assume that the hypotheses of Theorem 4.2 are satisfied. Then, there exists a positive constant C, independent of h, such that

$$\begin{aligned} \left\{ \!\sum _{K\in \mathcal {T}_h}\Vert {\varvec{\sigma }}\!-\!{\varvec{\sigma }}_{h,K}^{\star }\Vert _{\mathbf {div};K}^2\!\right\} ^{1/2} \le C\,h^s\,\sum _{K\in \mathcal {T}_h} \Big \{|{\mathbf {t}}|_{s,K}\!+\!|{\varvec{\sigma }}|_{s,K}+|\mathbf {div}({\varvec{\sigma }})|_{s,K}\Big \}. \end{aligned}$$

(4.18)

Proof

From [12, Lemma 5.3] and the first part in the proof of [12, Theorem 5.5], we find that there exists $C>0$, independent of h, such that for each $K\in \mathcal {T}_h$ there holds

$$\begin{aligned}&\displaystyle \Vert {\varvec{\sigma }}-{\varvec{\sigma }}_{h,K}^{\star }\Vert _{\mathbf {div};K} \,\le \, C\,\Big \{\Vert {\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h\Vert _{0,K}\,+\,\Vert \mathbf {div}({\varvec{\sigma }}-{\varvec{\sigma }}_h)\Vert _{0,K}\\&\quad \displaystyle \qquad + \, \Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_{k+1}^K({\varvec{\sigma }})\Vert _{0,K}\,+\, |{\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_{k+1}^K({\varvec{\sigma }})|_{1,K}\Big \}, \end{aligned}$$

which, after bounding $\Vert \mathbf {div}({\varvec{\sigma }}-{\varvec{\sigma }}_h)\Vert _{0,K}$ by $\Vert {\varvec{\sigma }}-{\varvec{\sigma }}_h)\Vert _{\mathbf {div},K}$, becomes

$$\begin{aligned}&\displaystyle \Vert {\varvec{\sigma }}-{\varvec{\sigma }}_{h,K}^{\star }\Vert _{\mathbf {div};K} \,\le \, C\, \Big \{\Vert {\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h\Vert _{0,K}\,+\,\Vert {\varvec{\sigma }}-{\varvec{\sigma }}_h\Vert _{\mathbf {div},K} \nonumber \\&\quad \displaystyle \qquad +\, \Vert {\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_{k+1}^K({\varvec{\sigma }})\Vert _{0,K}\,+\,|{\varvec{\sigma }}-{\varvec{{\mathcal {P}}}}_{k+1}^K({\varvec{\sigma }})|_{1,K}\Big \}. \end{aligned}$$

Next, summing up the squares of the foregoing equation over all $K\in \mathcal {T}_h$, and employing the estimates (4.9) and (4.15), and the approximation properties of ${\varvec{{\mathcal {P}}}}_{k+1}^K$ (cf. [11, Lemma 3.4]), we conclude (4.18), thus ending the proof. $\square$

At this point we remark that, while the use of Raviart–Thomas of order $k \ge 0$ instead of $\mathbb {P}_{k+1}(K)$ in (4.17) could seem more natural, it is not clear whether the approximation properties of the corresponding orthogonal projector with respect to the $\mathbb {H}(\mathbf {div};K)$-inner product, which up to the authors’ knowledge are unknown, would yield at least the same rates of convergence already guaranteed by Theorem 4.4. The advantage of employing $\mathbb {P}_{k+1}(K)$ is precisely that the respective approximation properties are well established in the literature.

5 Numerical results

In this section we present three numerical experiments illustrating the performance of the augmented mixed virtual element scheme (3.16) introduced and analized in Sects. 3.3 and 3.4, respectively. More precisely, in all the computations we consider the specific virtual element subspaces $X_k^h$ and $H_k^h$ (cf. (3.1)–(3.2)) and associated discrete nonlinear operator $\mathbf {A}_h$ (cf. (3.15)) determined by the definitions of the local subspaces $X_k^K$ and $H_k^K$, and the $\mathbb {L}^2$-orthogonal projector ${\varvec{{\mathcal {P}}}}_k^K$, respectively, with $k\in \lbrace 0,1,2\rbrace$. Here we recall, as already remarked in [13, Section 4.1], that the projector introduced in [11, Section 4] is applicable only when the viscosity $\mu$ is constant. In fact, this approach was utilized in [12] for the linear Brinkman problem. Now, as in [12, Section 6], the zero mean condition for tensors in the space $H_k^h$ is imposed via a real Lagrange multiplier, which means that, instead of (3.16), we solve the following modified discrete scheme: Find $(({\mathbf {t}}_h,{\varvec{\sigma }}_h),\lambda _h)\in (X_k^h\times H_k^h)\times \mathrm {R}$ such that

$$\begin{aligned}{}[\mathbf {A}_h({\mathbf {t}}_h,{\varvec{\sigma }}_h),({\mathbf {s}}_h,{\varvec{\tau }}_h)]+\lambda _h\displaystyle \int _\Omega \mathrm{tr}({\varvec{\tau }}_h)= & {} [\mathbf {F},({\mathbf {s}}_h,{\varvec{\tau }}_h)] \quad \forall \;({\mathbf {s}}_h,{\varvec{\tau }}_h)\in X_k^h\times H_k^h,\nonumber \\ \beta _h\displaystyle \int _\Omega \mathrm{tr}({\varvec{\sigma }}_h)= & {} 0 \quad \forall \;\beta _h\in \mathrm {R}, \end{aligned}$$

(5.1)

where $\lambda _h$ is an artificial unknown introduced just to keep the symmetry of (3.16). Concerning the decompositions of $\Omega$ employed in our computations, we consider quasi-uniform triangles, distorted squares, and distorted hexagons, where the term “distorted” refers here to perturbations of quadrilateral and hexagonal meshes, respectively.

We begin by introducing additional notations. In what follows, N stands for the total number of degrees of freedom (unknowns) of (5.1), that is

$$\begin{aligned} N:= & {} 2(k+1)\times \lbrace \text{ number } \text{ of } \text{ edges } e\in \mathcal {T}_h\rbrace \nonumber \\&+\displaystyle \frac{(k+2)(7k+3)}{2}\times \lbrace \text{ number } \text{ of } \text{ elements } K\in \mathcal {T}_h\rbrace +1. \end{aligned}$$

Also, the individual errors are defined by

$$\begin{aligned} \mathtt{e}({\mathbf {t}})\,:= & {} \, \Vert {\mathbf {t}}-{\mathbf {t}}_h\Vert _{0,\Omega },\quad \mathtt{e}_0({\varvec{\sigma }}):=\, \Vert {\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h\Vert _{0,\Omega },\\ \mathtt{e}(\mathbf {u})\,:= & {} \, \Vert \mathbf {u}-\mathbf {u}_h\Vert _{0,\Omega },\quad \mathtt{e}(p):=\, \Vert p-\widehat{p}_h\Vert _{0,\Omega },\\ \mathtt{e}_\mathrm {div}({\varvec{\sigma }})\,:= & {} \, \left\{ \displaystyle \sum _{K\in \mathcal {T}_h}\Vert {\varvec{\sigma }}-\widehat{{\varvec{\sigma }}}_h\Vert _{\mathbf {div};K}^2\right\} ^{1/2} \quad \text {and}\quad \\ \mathtt{e}({\varvec{\sigma }}^{\star })\,:= & {} \, \left\{ \displaystyle \sum _{K\in \mathcal {T}_h}\Vert {\varvec{\sigma }}-{\varvec{\sigma }}^{\star }_h\Vert _{\mathbf {div};K}^2\right\} ^{1/2}, \end{aligned}$$

where $\widehat{{\varvec{\sigma }}}_h,{\varvec{\sigma }}^{\star }_h$ and $(\widehat{p}_h,\mathbf {u}_h)$ are computed according to (4.10), (4.17), and (4.12), respectively, whereas the associated experimental rates of convergence are given by

$$\begin{aligned} \mathtt{r}(\cdot ):=\frac{\log (\mathtt{e}(\cdot )/\mathtt{e}^\prime (\cdot ))}{\log (h/h^\prime )}, \end{aligned}$$

where $\mathtt{e}$ and $\mathtt{e}^\prime$ denote the corresponding errors for two consecutive meshes with sizes h and $h^\prime$, respectively. In turn, the nonlinear algebraic systems arising from (5.1) are solved by the Newton method with a tolerance of $10^{-6}$ and taking as initial iteration the solution of the linear Brinkman problem with $\mu = 1$ (three iterations were required to achieve the given tolerance in each example). The numerical results presented below were obtained using a MATLAB code, in which all the resulting linear systems are solved by the usual instruction “\”.

In Example 1 we take the unit square $\Omega :=(0,1)^2$, set $\alpha =1$, and consider the nonlinear viscosity $\mu$ given by the Carreau law (2.4) with $\rho _0 = 2$, $\rho _1 = 1$, and $\beta = 5/3$, that is

$$\begin{aligned} \mu (s):= 2+(1+s^2)^{-1/6}\quad \forall \;s\ge 0. \end{aligned}$$

In addition, we choose the data $\mathbf {f}$ and $\mathbf {g}$ so that the exact solution is given by

$$\begin{aligned} \mathbf {u}(\mathbf {x}):= \left( \begin{array}{c} -\cos (\pi x_1)\sin (\pi x_2) \\ \sin (\pi x_1)\cos (\pi x_2)\\ \end{array} \right) \quad \text {and}\quad p(\mathbf {x}):=x_1^2-x_2^2 \end{aligned}$$

for all $\mathbf {x}:=(x_1,x_2)^{\mathbf {t}}\in \Omega$.

Table 1 Example 1, history of convergence using triangles

Table 2 Example 1, history of convergence using quadrilaterals

Table 3 Example 1, history of convergence using hexagons

Table 4 Example 2, history of convergence using triangles

Table 5 Example 2, history of convergence using quadrilaterals

Table 6 Example 2, history of convergence using hexagons

Table 7 Example 3, history of convergence using triangles

Table 8 Example 3, history of convergence using quadrilaterals

Table 9 Example 3, history of convergence using hexagons

In Example 2 we consider again $\Omega :=(0, 1)^2$, $\alpha =1$, and the nonlinear viscosity given by (2.4), but now with $\rho _0 = \rho _1 = 1/2$, and $\beta = 3/2$, that is

$$\begin{aligned} \mu (s):=\frac{1}{2}+\frac{1}{2}(1+s^2)^{-1/4}\quad \forall \;s\ge 0. \end{aligned}$$

In this case, the data $\mathbf {f}$ and $\mathbf {g}$ are chosen so that the exact solution is given by

$$\begin{aligned} \mathbf {u}(\mathbf {x}):= \left( \begin{array}{c} x_1^2(x_2+1)\exp (-x_1)\left( (x_2+1)\cos (x_2+1)+2\sin (x_2+1)\right) \\ x_1(x_1-2)(x_2+1)^2\exp (-x_1)\sin (x_2+1) \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} p(\mathbf {x}):=\sin (2\pi x_1)\sin (2\pi x_2) \end{aligned}$$

for all $\mathbf {x}:=(x_1,x_2)^{\mathbf {t}}\in \Omega$.

In Example 3 we take the L-shaped domain $\Omega :=(-1,1)^2\setminus [0,1]^2$, set again $\alpha = 1$, and consider the same nonlinearity $\mu$ from Example 2. Then, we choose the data $\mathbf {f}$ and $\mathbf {g}$ so that the exact solution is given by

$$\begin{aligned} \mathbf {u}(\mathbf {x}):= \left( \begin{array}{ccc} (1+x_1-\exp (x_1))(1-\cos (x_2)) \\ (1-\exp (x_1))(\sin (x_2)-x_2)\\ \end{array} \right) \quad \text {and}\quad p(\mathbf {x}):=(x_1^2+x_2^2)^{1/3}-p_0 \end{aligned}$$

for all $\mathbf {x}:=(x_1,x_2)^{\mathbf {t}}\in \Omega$, where $p_0\in \mathrm {R}$ is such that $\int _\Omega p=0$. Note in this example that the partial derivatives of p, and hence, in particular $\mathbf {div}({\varvec{\sigma }})$, are singular at the origin. More precisely, because of the power 1 / 3, there holds ${\varvec{\sigma }}\in \mathbb {H}^{5/3-\epsilon }(\Omega )$ and $\mathbf {div}({\varvec{\sigma }})\in \mathbf {H}^{2/3-\epsilon }(\Omega )$ for each $\epsilon >0$.

Finally, we remark that for all three examples the explicit constants $\gamma _0$ and $\alpha _0$ are defined according to (2.5), and that the stabilization parameter $\kappa$ is taken as suggested by the midpoints of the intervals specified in Lemma 2.2, that is $\delta = \dfrac{1}{\gamma }_0$ and $\kappa = \dfrac{\delta \,\alpha _0}{\gamma _0} = \dfrac{\alpha _0}{\gamma _0^2}$.

Fig. 1

Example 1, $\sigma _{h,11}$ (top), $p_h$ (middle) and $u_{h,1}$ (bottom)

Fig. 2

Example 3, $\sigma _{h,22}$ (top) and $p_h$ (bottom)

In Tables 1, 2, 3, 4, 5 and 6 we summarize the convergence history of the augmented mixed virtual element scheme (5.1) as applied to Examples 1 and 2. We notice there that the rate of convergence $O(h^{k+1})$ predicted by Theorems 4.3 and 4.4 (when $s = k + 1$) is achieved by all the unknowns for these smooth examples, for triangular as well as for quadrilateral and hexagonal meshes. In particular, these results confirm that our postprocessed stress ${\varvec{\sigma }}^{\star }_h$ improves in one power the non-satisfactory order provided by the first approximation $\widehat{{\varvec{\sigma }}}_h$ with respect to the broken $\mathbb {H}(\mathbf {div})$-norm. Next, in Tables 7, 8 and 9 we display the corresponding convergence history of Example 3. As predicted by the theory, and due to the limited regularity of p and ${\varvec{\sigma }}$ in this case, we observe that the orders $O(h^{\min \lbrace k+1,5/3\rbrace })$ and $O(h^{2/3})$ are attained by $({\varvec{\sigma }}_h, p_h)$ and ${\varvec{\sigma }}^{\star }_h$, respectively. However, the rates of convergence in Tables 8 and 9 oscillate more than expected, which, besides the singularity of this example, might be caused by the strong irregular character of the meshes. In addition, we observe that $\mathbf {u}_h$ shows a convergence rate of $O(h^{\min \lbrace k,5/3\rbrace +1})$. This behaviour of the error $\Vert \mathbf {u}-\mathbf {u}_h\Vert _{0,\Omega }$ is explained by the fact that, as shown by (4.14), it depends on the regularity of $\mathbf {u}$, ${\mathbf {t}}$, ${\varvec{\sigma }}$ and $\mathbf {div}({\varvec{\sigma }})$. A very common way to overcome this drawback is the use of adaptive algorithms based on suitable a posteriori error estimators. This issue will be addressed in a forthcoming work.

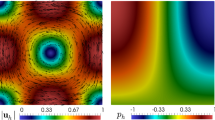
Finally, in order to graphically illustrate the accurateness of our discrete scheme, in Figs. 1 and 2 we display some components of the approximate solutions for Examples 1 and 3, respectively. They all correspond to those obtained with the first mesh of each kind (triangles, quadrilaterals and hexagons, respectively) and for the polynomial degree $k = 2$.