A priori and a posteriori error analysis of a mixed scheme for the Brinkman problem

Abstract

This paper deals with the analysis of new mixed finite element methods for the Brinkman equations formulated in terms of velocity, vorticity and pressure. Employing the Babuška–Brezzi theory, it is proved that the resulting continuous and discrete variational formulations are well-posed. In particular, we show that Raviart–Thomas elements of order $k \ge 0$ for the approximation of the velocity field, piecewise continuous polynomials of degree $k+1$ for the vorticity, and piecewise polynomials of degree k for the pressure, yield unique solvability of the discrete problem. On the other hand, we also show that families of finite elements based on Brezzi–Douglas–Marini elements of order $k+1$ for the approximation of velocity, piecewise continuous polynomials of degree $k+2$ for the vorticity, and piecewise polynomials of degree k for the pressure ensure the well-posedness of the associated Galerkin scheme. We note that these families provide exactly divergence-free approximations of the velocity field. We establish a priori error estimates in the natural norms with constants independent of the viscosity and we carry out the reliability and efficiency analysis of a residual-based a posteriori error estimator. Finally, we report several numerical experiments illustrating the behaviour of the proposed schemes and confirming our theoretical results on unstructured meshes. Additional examples of cases not covered by our theory are also presented.

1 Introduction

This paper is concerned with the numerical study of the generalized Stokes problem, also known as the linear Brinkman problem, differing from the classical Stokes system in the presence of a zeroth order term for the velocity in the momentum equation, and which is usually encountered after time discretizations of transient Stokes, or when considering a fluid in a mixture of porous and viscous regions and therefore ranging from Stokes to Darcy regimes. Our focus will be on the velocity–vorticity–pressure formulation of the mentioned problem.

There exist a great deal of numerical techniques available to solve these equations, each one of them with diverse features and, in general, being tested for many fundamental problems and industrial applications including for instance, filtering modelling, subsurface water treatment, oil recovery, and several others. Here, we concentrate on the development of mixed finite element formulations, as e.g. the variational problem in [16], which is recast as a twofold saddle point problem and it is analyzed based on the introduction of the flux and the tensor gradient of the velocity as further unknowns. In that contribution the flux is approximated by lowest order Raviart–Thomas elements, whereas the velocity and pressure fields are approximated by piecewise constant functions. In [32], the pseudostress and the trace-free velocity gradient are introduced as auxiliary unknowns and a pseudostress–velocity formulation is considered, existence, uniqueness, and error estimates are proposed. In addition, a mixed method associated to a pseudostress based formulation for the Brinkman problem has been introduced and analyzed in [27], in which the main unknown is given by the pseudostress, whereas the velocity and pressure fields are easily recovered through a simple postprocessing procedure.

Special interest lies in the case where the vorticity is introduced as an independent unknown (which is key in several applications), since no numerical differentiation of the velocity is needed to compute the additional field, boundary conditions for external flows can be treated in a natural way, and non-inertial effects can be readily included by simply modifying initial and boundary data [37]. Several numerical methods exploit these properties, as for instance, different formulations based on least-squares, stabilization techniques, mixed finite elements, spectral discretizations, and hybridizable discontinuous Galerkin methods (see for instance [3, 4, 8, 12, 14, 18, 19, 21–23, 26, 34–36], and the references therein). For the generalized Stokes problem written in velocity–vorticity–pressure variables, we mention [6] where an augmented mixed formulation based on $\mathbb {RT}_k-\mathbb P_{k+1}-\mathbb P_{k+1}$ (with continuous pressure approximation) finite elements has been developed and analyzed. Existence, uniqueness, and error estimates using the Lax–Milgram theorem have been established. Moreover, a dual mixed formulation has been introduced in [38] for the Brinkman problem. The well-posedness of the continuous and discrete formulations have been carried out using the Babuška theory, and optimal error estimates are proved, and preconditioners have been derived to solved efficiently the discrete linear system. In [7] a stabilized mixed method has been proposed for the axisymmetric Brinkman equations. We stress that the methods mentioned before do not deliver divergence-free approximations of the velocity.

In this article, we propose a finite element approximation of the Brinkman equations, written in terms of the vorticity, velocity, and pressure fields. A further goal of the present approach is to build different inf-sup stable families of finite elements to approximate the model problem, allowing a direct computation of the vorticity with optimal accuracy, and without the need of postprocessing. This appears to be quite difficult in mixed methods written only in terms of vector potential-vorticity [22, 30, 31]. In addition, the proposed method exhibits an exactly divergence-free approximation of the velocity, and thus, it exactly preserves an essential constraint of the governing equations. Moreover, our error estimates are established with constants independent of the viscosity. We also remark that the computational cost of the proposed method (in its lowest order configuration) is comparable with classical low-cost techniques as the so-called MINI element for velocity–pressure formulations.

On the other hand, adaptive mesh refinement strategies based on a posteriori error indicators play a relevant role in the numerical solution of flow problems, and partial differential equations in a general sense. For instance, they guarantee the convergence of finite element solutions, specially in the presence of complex geometries that could eventually lead to spurious solutions [39], and they provide substantial improvements in the accuracy of the approximations for given computational burden [1]. With this in mind, we also introduce a reliable and efficient residual-based a posteriori error estimator for the mixed problem, which can be computed locally, and hence, at a relatively low computational cost.

The proposed variational formulation is analyzed using standard tools in the realm of mixed problems and an a posteriori error estimator has been developed. To do this, we restrict our problem to the space of divergence-free velocities, and apply results from [15, 25, 28] to prove that the equivalent resulting saddle-point problem is well-posed. For the numerical approximation, we consider first the family of finite elements $\mathbb {RT}_k-\mathbb P_{k+1}-\mathbb P_{k}$, $k\ge 0$, i.e., Raviart–Thomas elements of order k for the velocity field, piecewise continuous polynomials of degree $k+1$ for the vorticity, and piecewise polynomials of degree k for the pressure. Since the proposed method provides an exactly divergence-free approximation of the velocity, we prove unique solvability of the discrete problem by adapting the same tools utilized for the continuous problem. In addition, the resulting finite element discretization turns to be convergent with optimal rate whenever the exact solution of the problem is regular enough. We mention that all the error estimates are fully independent of the viscosity. Next, we develop a reliable and efficient residual-based a posteriori error estimator for the proposed formulation. The proof of reliability makes use of the global continuous inf-sup condition of the variational formulation restricted to the space of divergence-free velocities, and the local approximation properties of the Clément and Raviart–Thomas operators, whereas for the efficiency we utilize inverse inequalities, and the localization technique based on element-bubble and edge-bubble functions. Moreover, numerical experiments with the family of finite elements considered in this paper perform satisfactorily for a variety of boundary conditions. We also introduce and comment the applicability of the present framework using other families of finite elements, as for instance Brezzi–Douglas–Marini elements of order $k+1$ for the velocity field, piecewise continuous polynomials of degree $k+2$ for the vorticity, and piecewise polynomials of degree k for the pressure. Finally, we stress that the proposed methodology can be used to analyze the extension to the three-dimensional case, and to study a larger class of problems, including the coupling with Darcy flows or with transport phenomena.

Outline. The remainder of the paper has been structured as follows. In what is left from this section, we introduce some standard notation, required functional spaces, and we describe the boundary value problem of interest. Section 2 presents the associate variational formulation, it provides an abstract framework where our formulation lies, and then we prove its unique solvability along with some stability properties. In Sect. 3, we present two mixed finite element schemes and we provide a stability result and obtain error estimates for the proposed methods. The derivation and analysis of a reliable and efficient residual-based a posteriori error estimator for this problem is carried out in Sect. 4. Several numerical results illustrating the convergence behaviour predicted by the theory and allowing us to assess the performance of the methods are collected in Sect. 5, and we close with some final remarks in Sect. 6.

Preliminaries. We will denote a simply connected polygonal Lipschitz bounded domain of $\mathbb {R}^2$ by $\Omega$ and $\varvec{n}=(n_i)_{1\le i\le 2}$ is the outward unit normal vector to the boundary $\partial \Omega$. The vector $\varvec{t}=(t_i)_{1\le i\le 2}$ is the unit tangent to $\partial \Omega$ oriented such that $t_1 =-n_2$, $t_2 = n_1$. Moreover, we assume that $\partial \Omega$ admits a disjoint partition $\partial \Omega =\Gamma \cup \Sigma$. For the sake of simplicity, we also assume that both $\Gamma$ and $\Sigma$ have positive measure. For any $s\ge 0$, the notation $\left\| \cdot \right\| _{s,\Omega }$ stands for the norm of the Hilbertian Sobolev spaces $\mathrm {H}^s(\Omega )$ or $\mathrm {H}^s(\Omega )^2$, with the usual convention $\mathrm {H}^0(\Omega ):=\mathrm {L}^2(\Omega )$. For $s\ge 0$, we recall the definition of the Hilbert space

$$\begin{aligned} \mathrm {H}^s(\mathop {\mathrm {div}}\nolimits ;\Omega ):=\{\varvec{v}\in \mathrm {H}^s(\Omega )^2:\mathop {\mathrm {div}}\nolimits \varvec{v}\in \mathrm {H}^s(\Omega )\}, \end{aligned}$$

endowed with the norm $\left\| \varvec{v}\right\| _{\mathrm {H}^s(\mathop {\mathrm {div}}\nolimits ;\Omega )}^2 :=\left\| \varvec{v}\right\| _{s,\Omega }^2+\left\| \mathop {\mathrm {div}}\nolimits \varvec{v}\right\| ^2_{s,\Omega }$, and we will denote $\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega ):={\mathrm {H}^0(\mathop {\mathrm {div}}\nolimits ;\Omega )}$.

Moreover, c and C, with or without subscripts, tildes, or hats, will represent a generic constant independent of the mesh parameter h, assuming different values in different occurrences. In addition, for any vector field $\varvec{v}=(v_i)_{i=1,2}$ and any scalar field $\theta$ we recall the differential operators:

$$\begin{aligned} \mathop {\mathrm {div}}\nolimits \varvec{v}\,{:=}\,\partial _1 v_1+\partial _2 v_2, \quad \mathop {\mathrm {rot}}\nolimits \varvec{v}\,{:=}\,\partial _1 v_2-\partial _2 v_1, \quad \nabla \theta \,{:=}\,\begin{pmatrix} \partial _1\theta \\ \partial _2\theta \end{pmatrix}, \quad \mathop {\mathbf {curl}}\nolimits \theta \,{:=}\,\begin{pmatrix} \partial _2\theta \\ -\partial _1\theta \end{pmatrix}. \end{aligned}$$

The model problem. We are interested in the Brinkman problem [31], formulated in terms of the velocity $\varvec{u}$, the scaled vorticity $\omega$ and the pressure p of an incompressible viscous fluid: given a force density $\varvec{f}$, vector fields $\varvec{a}$ and $\varvec{b}$, and scalar fields $p_0$ and $\omega _0$, we seek a vector field $\varvec{u}$, a scalar field $\omega$, and a scalar field p such that

$$\begin{aligned} \sigma \varvec{u}+\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega +\nabla p&= \varvec{f}\quad \text{ in } \Omega , \nonumber \\ \omega -\sqrt{\nu }\mathop {\mathrm {rot}}\nolimits \varvec{u}&= 0 \quad \text{ in } \Omega ,\nonumber \\ \mathop {\mathrm {div}}\nolimits \varvec{u}&= 0 \quad \text{ in } \Omega , \nonumber \\ \varvec{u}\cdot \varvec{t}&= \varvec{a}\cdot \varvec{t}\quad \text{ on } \Sigma ,\\ p&= p_{0} \quad \text{ on } \Sigma , \nonumber \\ \varvec{u}\cdot \varvec{n}&= \varvec{b}\cdot \varvec{n}\quad \text{ on } \Gamma ,\nonumber \\ \omega&= \omega _0 \quad \text{ on } \Gamma ,\nonumber \end{aligned}$$

(1.1)

where $\varvec{u}\cdot \varvec{t}$ and $\varvec{u}\cdot \varvec{n}$ stand for the normal and the tangential components of the velocity, respectively. In the model, $\nu >0$ is the kinematic viscosity of the fluid and $\sigma \in \mathrm {L}^{\infty }(\Omega )$ is the inverse permeability of the medium, here assumed isotropic and satisfying $0<\sigma _{\min }\le \sigma (\varvec{x})\le \sigma _{\max }$ a.e. in $\Omega$, for some positive bounds $\sigma _{\min },\sigma _{\max }$.

In addition, we assume that a boundary compatibility condition holds, i.e., there exists a velocity field $\varvec{w}\in \mathrm {L}^2(\Omega )^2$ satisfying $\mathop {\mathrm {div}}\nolimits \varvec{w}=0$ a.e. in $\Omega$, $\varvec{w}\cdot \varvec{t}=\varvec{a}\cdot \varvec{t}$ on $\Sigma$, and $\varvec{w}\cdot \varvec{n}=\varvec{b}\cdot \varvec{n}$ on $\Gamma$. For a detailed study on different types of standard and non-standard boundary conditions for incompressible flows, we refer to [13]. We observe that the boundary conditions considered here are relevant in the context of e.g. geophysical fluids and shallow water models [33].

For the sake of simplicity, we will work with homogeneous boundary conditions for the normal and the tangential velocity and, subsequently, for the vorticity, i.e., $\varvec{b}=\varvec{0}$, $\varvec{a}=\varvec{0}$ and $\omega _0=0$ on $\Gamma$. Nevertheless, these restrictions do not affect the generality of the forthcoming analysis.

2 A mixed velocity–vorticity–pressure formulation

2.1 Variational formulation and preliminary results

In this section, we propose a mixed variational formulation of system (1.1). First, we need to introduce the following spaces that we will consider in the sequel:

$$\begin{aligned} \mathrm {H}:= & {} \{\varvec{v}\in \mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega ):\varvec{v}\cdot \varvec{n}=0\,\,\text {on}\,\,\Gamma \}, \quad \mathrm {Z}:=\{\theta \in \mathrm {H}^1(\Omega ):\theta =0\,\,\text {on}\,\,\Gamma \}, \quad \text {and}\\ \mathrm {Q}:= & {} \mathrm {L}^2(\Omega ). \end{aligned}$$

We endow the spaces $\mathrm {H}$ and $\mathrm {Q}$ with their natural norms. However, for the functional space $\mathrm {Z}$ we will consider the following $\nu$-dependent norm:

$$\begin{aligned} |\!|\!| \theta |\!|\!|_{1,\Omega }^2:=\Vert \theta \Vert _{0,\Omega }^2 +\nu \Vert \mathop {\mathbf {curl}}\nolimits \theta \Vert _{0,\Omega }^2. \end{aligned}$$

Moreover, the symbol $\langle \cdot ,\cdot \rangle _{\Sigma }$ will denote the duality pairing between $\mathrm {H}^{-1/2}(\Sigma )$ and $\mathrm {H}^{1/2}(\Sigma )$ with respect to the $\mathrm {L}^2(\Sigma )$-inner product.

Now, by testing system (1.1) with adequate functions and imposing the boundary conditions, we end up with the following mixed variational formulation:

find $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ such that

$$\begin{aligned} \int _{\Omega }\sigma \varvec{u}\cdot \varvec{v}+\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \omega \cdot \varvec{v}-\int _{\Omega }p\mathop {\mathrm {div}}\nolimits \varvec{v}&= \int _{\Omega }\varvec{f}\cdot \varvec{v}-\langle \varvec{v}\cdot \varvec{n},p_0\rangle _{\Sigma } \quad \forall \varvec{v}\in \mathrm {H},\\ \sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \theta \cdot \varvec{u}-\int _{\Omega }\omega \theta&=0\quad \forall \theta \in \mathrm {Z},\\ -\int _{\Omega }q\mathop {\mathrm {div}}\nolimits \varvec{u}&=0\quad \forall q\in \mathrm {Q}. \end{aligned}$$

This variational problem can be rewritten as follows: find $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ such that

$$\begin{aligned} a(\varvec{u},\varvec{v})+\;b_{1}(\varvec{v},\omega )+\;b_2(\varvec{v},p)&=G(\varvec{v}) \quad \forall \varvec{v}\in \mathrm {H},\nonumber \\ b_{1}(\varvec{u},\theta )-d(\omega ,\theta )&=0 \quad \forall \theta \in \mathrm {Z},\\ b_2(\varvec{u},q)&=0 \quad \forall q\in \mathrm {Q},\nonumber \end{aligned}$$

(2.1)

where the bilinear forms $a:\mathrm {H}\times \mathrm {H}\rightarrow \mathbb {R}$, $b_1:\mathrm {H}\times \mathrm {Z}\rightarrow \mathbb {R}$, $d:\mathrm {Z}\times \mathrm {Z}\rightarrow \mathbb {R}$, $b_2:\mathrm {H}\times \mathrm {Q}\rightarrow \mathbb {R}$, and the linear functional $G:\mathrm {H}\rightarrow \mathbb {R}$ are defined by

$$\begin{aligned} a(\varvec{u},\varvec{v})&:=\int _{\Omega }\sigma \varvec{u}\cdot \varvec{v},\quad b_1(\varvec{v},\theta ):=\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \theta \cdot \varvec{v},\\ d(\omega ,\theta )&:=\int _{\Omega }\omega \theta ,\quad b_2(\varvec{v},q):=-\int _{\Omega }q\mathop {\mathrm {div}}\nolimits \varvec{v},\\ G(\varvec{v})&:=\int _{\Omega }\varvec{f}\cdot \varvec{v}-\langle \varvec{v}\cdot \varvec{n},p_0\rangle _{\Sigma }, \end{aligned}$$

for all $\varvec{u},\varvec{v}\in \mathrm {H}$, $\omega ,\theta \in \mathrm {Z}$, and $q\in \mathrm {Q}$.

With the analysis of (2.1) in mind, let us consider the Kernel of $b_2(\cdot ,\cdot )$

$$\begin{aligned} \mathrm {X}:= \{ \varvec{v}\in \mathrm {H}:b_2(\varvec{v},q)=0, \quad \forall q\in Q\} = \{ \varvec{v}\in \mathrm {H}:\mathop {\mathrm {div}}\nolimits \varvec{v}= 0\quad \mathrm{in}\; \Omega \}, \end{aligned}$$

and let us recall that the bilinear form $b_2$ satisfies the inf-sup condition:

$$\begin{aligned} \sup _{\mathop {\varvec{v}\ne 0}\limits ^{\scriptstyle \varvec{v}\in \mathrm {H}}}\frac{\vert b_{2}(\varvec{v},q)\vert }{\Vert \varvec{v}\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}\ge \beta _2\Vert q\Vert _{0,\Omega }\quad \forall q\in \mathrm {Q}, \end{aligned}$$

(2.2)

with an inf-sup constant $\beta _2>0$ only depending on $\Omega$ (cf. [25]).

In order to establish that our mixed variational problem is well-posed we will use the following abstract result (see e.g. [25, Theorem 1.3]):

Theorem 2.1

Let $(\mathcal X,\langle \cdot ,\cdot \rangle _{\mathcal X})$ be a Hilbert space. Let $\mathcal A:\mathcal X\times \mathcal X \rightarrow \mathbb {R}$ be a bounded symmetric bilinear form, and let $\mathcal G:\mathcal X\rightarrow \mathbb {R}$ be a bounded functional. Assume that there exists $\bar{\beta }> 0$ such that

$$\begin{aligned} \displaystyle \,\sup _{\mathop {y\ne 0}\limits ^{\scriptstyle y\in {\mathcal X}}}\frac{\mathcal A(x,y)}{\Vert y\Vert _{\mathcal X}}\ge \bar{\beta }\,\Vert x\Vert _{\mathcal X} \quad \forall x\in \mathcal X. \end{aligned}$$

(2.3)

Then, there exists a unique $x \in \mathcal X$, such that

$$\begin{aligned} \mathcal A(x,y)= \mathcal G(y)\quad \forall y\in \mathcal X. \end{aligned}$$

(2.4)

Moreover, there exists $C>0$, independent of the solution, such that

$$\begin{aligned} \Vert x\Vert _{\mathcal X}\le C\Vert \mathcal G\Vert _{\mathcal X'}. \end{aligned}$$

2.2 Analysis of the continuous formulation

In this section, we prove that the continuous variational formulation (2.1) is well-posed. To that end, it is enough to study the reduced counterpart of (2.1) defined on $\mathrm {X}\times \mathrm {Z}$: find $(\varvec{u},\omega )\in \mathrm {X}\times \mathrm {Z}$ such that

$$\begin{aligned} a(\varvec{u},\varvec{v})+\;b_{1}(\varvec{v},\omega )&=G(\varvec{v})\quad \forall \varvec{v}\in \mathrm {X},\nonumber \\ b_{1}(\varvec{u},\theta )- d(\omega ,\theta )&=0\quad \forall \theta \in \mathrm {Z}. \end{aligned}$$

(2.5)

In fact, the following result establishes the equivalence between (2.1) and (2.5).

Lemma 2.1

If $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ is a solution of (2.1), then $\varvec{u}\in \mathrm {X}$, and $(\varvec{u},\omega )\in \mathrm {X}\times \mathrm {Z}$ is also a solution of (2.5). Conversely, if $(\varvec{u},\omega )\in \mathrm {X}\times \mathrm {Z}$ is a solution of (2.5), then there exists a unique pressure $p\in \mathrm {Q}$ such that $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ is a solution of (2.1).

Proof

The proof follows basically from the inf-sup condition (2.2). We omit further details and refer to [31]. $\square$

According to the result above, we will now turn to prove that the continuous variational formulation (2.5) is well-posed.

Theorem 2.2

The variational problem (2.5) admits a unique solution $(\varvec{u},\omega )\in \mathrm {X}\times \mathrm {Z}$. Moreover, there exists $C>0$ independent of $\nu$ such that

$$\begin{aligned} \Vert \varvec{u}\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}+|\!|\!| \omega |\!|\!|_{1,\Omega }\le C(\Vert \varvec{f}\Vert _{0,\Omega }+\Vert p_0\Vert _{1/2,\Sigma }). \end{aligned}$$

(2.6)

Proof

First, we define $\mathcal X:=\mathrm {X}\times \mathrm {Z}$ (endowed with the corresponding product norm) and the following bilinear form and linear functional:

$$\begin{aligned} \mathcal A((\varvec{u},\omega ),(\varvec{v},\theta ))\,{:=}\,a(\varvec{u},\varvec{v})+\;b_{1}(\varvec{v},\omega )+b_{1}(\varvec{u},\theta )- d(\omega ,\theta ),\quad \mathcal G((\varvec{v},\theta )):=G(\varvec{v}). \end{aligned}$$

To continue, it suffices to verify the hypotheses of Theorem 2.1. First, we note that the linear functional $\mathcal G(\cdot )$ is bounded and as a consequence of the boundedness of $a(\cdot ,\cdot )$ $b_1(\cdot ,\cdot )$, and $d(\cdot ,\cdot )$, one has that the bilinear form $\mathcal A(\cdot ,\cdot )$ is bounded too with constants independent of $\nu$.

The next step consists in proving that the bilinear form $\mathcal A(\cdot ,\cdot )$ satisfies the inf-sup condition (2.3). In fact, given $(\varvec{u},\omega )\in \mathcal X$, we define

$$\begin{aligned} \tilde{\theta }:=-\omega \in \mathrm {Z},\quad \text {and}\quad \tilde{\varvec{v}}:=(\varvec{u}+\hat{c}\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega )\in \mathrm {X}, \end{aligned}$$

where $\hat{c}$ is a positive constant which will be specified later. Therefore, from the definition of bilinear form $\mathcal A(\cdot ,\cdot )$ we obtain

$$\begin{aligned} \mathcal A((\varvec{u},\omega ),({\tilde{\varvec{v}}},{\tilde{\theta }}))&=\int _{\Omega }\sigma \varvec{u}\cdot {\tilde{\varvec{v}}}+\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \omega \cdot {\tilde{\varvec{v}}} +\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits {\tilde{\theta }}\cdot \varvec{u}-\int _{\Omega }\omega {\tilde{\theta }}\\&\ge \sigma _{\min }\Vert \varvec{u}\Vert _{0,\Omega }^2+\hat{c}\sqrt{\nu }\int _{\Omega }\sigma \varvec{u}\cdot \mathop {\mathbf {curl}}\nolimits \omega +\sqrt{\nu }\int _{\Omega }\varvec{u}\cdot \mathop {\mathbf {curl}}\nolimits \omega \\&\quad +\hat{c}\nu \Vert \mathop {\mathbf {curl}}\nolimits \omega \Vert _{0,\Omega }^2-\sqrt{\nu }\int _{\Omega }\varvec{u}\cdot \mathop {\mathbf {curl}}\nolimits \omega +\Vert \omega \Vert _{0,\Omega }^2\\&\ge \sigma _{\min }\Vert \varvec{u}\Vert _{0,\Omega }^2-\frac{\sigma _{min}}{2}\Vert \varvec{u}\Vert _{0,\Omega }^2 -\frac{\hat{c}^2\sigma _{\max }^2}{2\sigma _{\min }}\nu \Vert \mathop {\mathbf {curl}}\nolimits \omega \Vert _{0,\Omega }^2\\&\quad +\hat{c}\nu \Vert \mathop {\mathbf {curl}}\nolimits \omega \Vert _{0,\Omega }^2+\Vert \omega \Vert _{0,\Omega }^2\\&=\frac{\sigma _{\min }}{2}\Vert \varvec{u}\Vert _{0,\Omega }^2+\hat{c}\left( 1-\frac{\hat{c}\sigma _{\max }^2}{2\sigma _{\min }}\right) \nu \Vert \mathop {\mathbf {curl}}\nolimits \omega \Vert _{0,\Omega }^2 +\Vert \omega \Vert _{0,\Omega }^2, \end{aligned}$$

and choosing $\hat{c}=\frac{\sigma _{\min }}{\sigma _{\max }^2}$, we can assert that

$$\begin{aligned} \mathcal A((\varvec{u},\omega ),({\tilde{\varvec{v}}},{\tilde{\theta }}))\ge C\Vert (\varvec{u},\omega )\Vert _{\mathcal X}^2, \end{aligned}$$

with C independent of $\nu$. On the other hand, we notice that

$$\begin{aligned} |\!|\!| \tilde{\theta } |\!|\!|_{1,\Omega }=|\!|\!| \omega |\!|\!|_{1,\Omega }\quad \text {and}\quad \Vert {\tilde{\varvec{v}}}\Vert _{0,\Omega }\le C\hat{c}(\Vert \varvec{u}\Vert _{0,\Omega }+|\!|\!| \omega |\!|\!|_{1,\Omega }), \end{aligned}$$

(2.7)

and consequently

$$\begin{aligned} \sup _{\mathop {(\varvec{v},\theta )\ne 0}\limits ^{\scriptstyle (\varvec{v},\theta )\in \mathcal X}}\frac{\mathcal A((\varvec{u},\omega ),(\varvec{v},\theta ))}{\Vert (\varvec{v},\theta )\Vert _{\mathcal X}}\ge \frac{\mathcal A((\varvec{u},\omega ),({\tilde{\varvec{v}}},{\tilde{\theta }}))}{\Vert ({\tilde{\varvec{v}}},{\tilde{\theta }})\Vert _{\mathcal X}} \ge C\Vert (\varvec{u},\omega )\Vert _{\mathcal X}\quad \forall (\varvec{u},\omega )\in \mathcal X, \end{aligned}$$

which finishes the proof. $\square$

The following result establishes the corresponding stability estimate for the pressure.

Corollary 2.1

Let $(\varvec{u},\omega )\in \mathrm {X}\times \mathrm {Z}$, be the unique solution of (2.5), with $\varvec{u}$ and $\omega$ satisfying (2.6). In addition, let $p\in Q$ be the unique pressure provided by Lemma 2.1, so that $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ is the unique solution of (2.1). Then, there exits $C>0$, independent of $\nu$ and the solution, such that

$$\begin{aligned} \Vert p\Vert _{0,\Omega }\le C(\Vert \varvec{f}\Vert _{0,\Omega }+\Vert p_0\Vert _{1/2,\Sigma }). \end{aligned}$$

Proof

From the inf-sup condition (2.2), and the first equation of (2.1), we obtain

$$\begin{aligned} \Vert p\Vert _{0,\Omega }\le \frac{1}{\beta _2}\sup _{\mathop {\varvec{v}\ne 0}\limits ^{\scriptstyle \varvec{v}\in \mathrm {H}}}\frac{\vert b_{2}(\varvec{v},p)\vert }{\Vert \varvec{v}\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}=\frac{1}{\beta _2}\sup _{\mathop {\varvec{v}\ne 0}\limits ^{\scriptstyle \varvec{v}\in \mathrm {H}}}\frac{\vert G(\varvec{v})-a(\varvec{u},\varvec{v})-b_1(\varvec{v},\omega )\vert }{\Vert \varvec{v}\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}, \end{aligned}$$

which together to (2.6), and the boundedness of G, a and $b_1$, complete the proof. $\square$

We end this section with the converse derivation of problem (2.1). More precisely, the following theorem establishes that the unique solution of (2.1) solves the original problem described in (1.1). This result will be used later on in Sect. 4.2 to prove the efficiency of our a posteriori error estimator.

Theorem 2.3

Let $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ the unique solution of (2.1). Then $\sigma \varvec{u}+{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega } +\nabla p=\varvec{f}$ in $\Omega$, $\omega -{\sqrt{\nu }\mathop {\mathrm {rot}}\nolimits \varvec{u}}=0$ in $\Omega$, $\mathop {\mathrm {div}}\nolimits \varvec{u}= 0$ in $\Omega$, $\varvec{u}\in \mathrm {H}^1(\Omega )^2$, $p\in \mathrm {H}^1(\Omega )$, and $\varvec{u}$, $\omega$, and p satisfy the boundary conditions described in (1.1).

Proof

It basically follows by applying integration by parts backwardly in (2.1) and using suitable test functions. Further details are omitted. $\square$

3 Mixed finite element schemes

In this section, we will construct two mixed finite element schemes associated to (2.1), we define explicit finite element subspaces yielding the unique solvability of the discrete schemes, derive the a priori error estimates, and provide the rate of convergence of the methods.

Let ${\mathcal T}_h$ be a regular family of triangulations of the polygonal region $\bar{\Omega }$ by triangles T of diameter $h_T$ with mesh size $h:= \max \{h_T:T\in {\mathcal T}_h\}$, and such that there holds $\bar{\Omega }=\cup \{T:T\in {\mathcal T}_h\}$. In addition, given an integer $k\ge 0$ and a subset S of $\mathbb {R}^2$, we denote by $\mathbb P_k(S)$ the space of polynomials in two variables defined in S of total degree less than or equal to k.

Let us introduce the local Raviart–Thomas space of order k

$$\begin{aligned} \mathbb {RT}_k(T):=\mathbb P_k(T)^2\oplus \mathbb P_k(T)\varvec{x}, \end{aligned}$$

where $\varvec{x}$ is a generic vector of $\mathbb {R}^{2}$, and let us define the following finite element subspaces:

$$\begin{aligned} \mathrm {H}_h&:=\{\varvec{v}_h \in \mathrm {H}:\varvec{v}_h|_{T} \in \mathbb {RT}_k(T), \quad \forall T \in {\mathcal T}_{h} \},\end{aligned}$$

(3.1)

$$\begin{aligned} \mathrm {Z}_h&:=\left\{ \theta _{h}\in \mathrm {Z}:\theta _h|_{T}\in \mathbb P_{k+1}(T),\quad \forall T \in {\mathcal T}_{h} \right\} , \end{aligned}$$

(3.2)

$$\begin{aligned} \mathrm {Q}_h&:=\{ q_h\in \mathrm {Q}:q_h|_{T} \in \mathbb P_k(T) , \quad \forall T \in {\mathcal T}_{h} \}. \end{aligned}$$

(3.3)

Then, the Galerkin scheme associated with the continuous variational formulation (2.1) reads as follows: Find $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ such that

$$\begin{aligned} a(\varvec{u}_h,\varvec{v}_h)+\;b_{1}(\varvec{v}_h,\omega _h)+\;b_2(\varvec{v}_h,p_h)&=G(\varvec{v}_h)\quad \forall \varvec{v}_h\in \mathrm {H}_h,\nonumber \\ b_{1}(\varvec{u}_h,\theta _h)- d(\omega _h,\theta _h)&=0\quad \forall \theta _h\in \mathrm {Z}_h,\\ b_2(\varvec{u}_h,q_h)&=0\quad \forall q_h\in \mathrm {Q}_h.\nonumber \end{aligned}$$

(3.4)

One of the key features of the scheme proposed in (3.4), besides the direct approximation of the vorticity, is that the approximate velocity $\varvec{u}_h$ is exactly divergence-free in $\Omega$. To discuss this property, we introduce the discrete kernel of $b_2$:

$$\begin{aligned} \mathrm {X}_h := \{ \varvec{v}_h \in \mathrm {H}_h:b_2(\varvec{v}_h,q_h)=0,\quad \forall q_h \in \mathrm {Q}_h\}. \end{aligned}$$

Since $\mathop {\mathrm {div}}\nolimits \mathrm {H}_h\subseteq \mathrm {Q}_h$, it can be readily seen that

$$\begin{aligned} \mathrm {X}_h := \{ \varvec{v}_h \in \mathrm {H}_h:\mathop {\mathrm {div}}\nolimits \varvec{v}_h\equiv 0\quad \mathrm{in}\ \Omega \}. \end{aligned}$$

(3.5)

Let us observe now that, similarly to the continuous case, the bilinear form $b_2$ satisfies the discrete inf-sup condition

$$\begin{aligned} \sup _{\mathop {\varvec{v}_h\ne 0}\limits ^{\scriptstyle \varvec{v}_h\in \mathrm {H}_h}}\frac{ b_{2}(\varvec{v}_h,q_h)}{\Vert \varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}\ge \tilde{\beta }_2\Vert q_h\Vert _{0,\Omega }\quad \forall q_h\in \mathrm {Q}_h, \end{aligned}$$

(3.6)

with the inf-sup constant $\tilde{\beta }_2$ independent of the discretization parameter h and of $\nu$; see [25] for instance.

Throughout the remainder of this section, we will show that the discrete variational formulation (3.4) is well-posed and that it satisfies the corresponding Céa estimate. In order to do this, we proceed as in Sect. 2.2, and introduce the following reduced version of (3.4) on the product space $\mathrm {X}_h\times \mathrm {Z}_h$: find $(\varvec{u}_h,\omega _h)\in \mathrm {X}_h\times \mathrm {Z}_h$ such that

$$\begin{aligned} \begin{aligned} a(\varvec{u}_h,\varvec{v}_h)+b_{1}(\varvec{v}_h,\omega _h)&=G(\varvec{v}_h)\quad \forall \varvec{v}_h\in \mathrm {X}_h,\\ b_{1}(\varvec{u}_h,\theta _h)-d(\omega _h,\theta _h)&=0\quad \forall \theta _h\in \mathrm {Z}_h. \end{aligned} \end{aligned}$$

(3.7)

The following result establishes the equivalence between (3.4) and (3.7), which is a direct consequence of the inf-sup condition (3.6).

Lemma 3.1

If $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ is a solution of (3.4), then $\varvec{u}_h\in \mathrm {X}_h$, and $(\varvec{u}_h,\omega _h)\in \mathrm {X}_h\times \mathrm {Z}_h$ is also a solution of (3.7). Conversely, if $(\varvec{u}_h,\omega _h)\in \mathrm {X}_h\times \mathrm {Z}_h$ is a solution of (3.7), then there exists a unique pressure $p_h\in \mathrm {Q}_h$ such that $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ is a solution of (3.4).

Remark 3.1

We point out that since $\mathrm {X}_h=\mathop {\mathbf {curl}}\nolimits (\mathrm {Z}_h),$ problem (3.7) is equivalent to the following formulation ($\sigma$-penalized) of a biharmonic problem (also known as the Ciarlet–Raviart formulation): find $(\omega _h,r_h)\in \mathrm {Z}_h\times \mathrm {Z}_h$ such that

$$\begin{aligned} \begin{aligned} \int _{\Omega }\omega _h\theta _h-\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits r_h\cdot \mathop {\mathbf {curl}}\nolimits \theta _h&=0\quad \forall \theta _h\in \mathrm {Z}_h,\\ -\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \omega _h\cdot \mathop {\mathbf {curl}}\nolimits \phi _h -\int _{\Omega }\sigma \mathop {\mathbf {curl}}\nolimits r_h\cdot \mathop {\mathbf {curl}}\nolimits \phi _h&=0\quad \forall \phi _h\in \mathrm {Z}_h, \end{aligned} \end{aligned}$$

(3.8)

which coincides with the mixed formulation of a thin Kirchhoff plate subject to simply supported boundary conditions on $\Gamma$. The present analysis could be therefore utilized to establish existence and uniqueness as well as error estimates for (3.8).

Keeping in mind Lemma 3.1, in what follows we will focus on the analysis of problem (3.7). To this end, let us first collect some previous results and notations to be used in the sequel. We start by introducing the discrete version of Theorem 2.1.

Theorem 3.1

Let $(\mathcal X,\langle \cdot ,\cdot \rangle _{\mathcal X})$ be a Hilbert space and let $\{\mathcal X_h\}_{h>0}$ be a sequence of finite-dimensional subspace of $\mathcal X$. Let $\mathcal A:\mathcal X\times \mathcal X \rightarrow \mathbb {R}$ be a bounded symmetric bilinear form, and let $\mathcal G:\mathcal X\rightarrow \mathbb {R}$ be a bounded functional. Assume that there exists $\bar{\beta }_h > 0$ such that

$$\begin{aligned} \displaystyle \,\sup _{\mathop {y\ne 0}\limits ^{\scriptstyle y_h\in {\mathcal X_h}}}\frac{\mathcal A(x_h,y_h)}{\Vert y_h\Vert _{\mathcal X}}\ge \bar{\beta }_h\,\Vert x_h\Vert _{\mathcal X} \quad \forall x_h\in {\mathcal X_h}. \end{aligned}$$

(3.9)

Then, there exists a unique $x_h \in {\mathcal X_h}$, such that

$$\begin{aligned} \mathcal A(x_h,y_h)= \mathcal G(y_h)\quad \forall y_h\in {\mathcal X_h}. \end{aligned}$$

(3.10)

Moreover, there exist $C_1,C_2>0$, independent of the solution, such that

$$\begin{aligned} \Vert x_h\Vert _{\mathcal X}\le C_1\Vert \mathcal G|_{\mathcal X_h}\Vert _{\mathcal X'_h}. \end{aligned}$$

and

$$\begin{aligned} \Vert x-x_h\Vert _{\mathcal X}\le C_2\inf _{y_h\in \mathcal X_h} \Vert x-y_h\Vert _{\mathcal X}, \end{aligned}$$

where $x\in \mathcal X$ is the unique solution of problem (2.4).

Proof

The proof follows from the continuous version given in Theorem 2.1 and the discrete inf-sup condition for $\mathcal A(\cdot ,\cdot )$ restricted to the finite-dimensional subspace.

We recall the Raviart–Thomas interpolation operator [15] ${\mathcal R}:\mathrm {H}^s(\Omega )^{2}\cap \mathrm {H}\rightarrow \mathrm {H}_h$ for all $s>0$, for which we review some properties to be used in the sequel: there exists $C>0$, independent of h, such that for all $s\in (0,k+1]$:

$$\begin{aligned} \Vert \varvec{v}-{\mathcal R}\varvec{v}\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}\le Ch^s\Vert \varvec{v}\Vert _{\mathrm {H}^s(\mathop {\mathrm {div}}\nolimits ;\Omega )}\quad \forall \varvec{v}\in \mathrm {H}^s(\mathop {\mathrm {div}}\nolimits ;\Omega )\cap \mathrm {H}. \end{aligned}$$

(3.11)

Secondly, for all $s>0$, let $\Pi :\mathrm {H}^{1+s}(\Omega )\rightarrow \mathrm {Z}_h$ be the usual Lagrange interpolant. This operator satisfies the following error estimate: there exists $C>0$, independent of h, such that for all $s\in (0,k+1]$:

$$\begin{aligned} \Vert \theta -\Pi \theta \Vert _{1,\Omega } \le Ch^{s}\Vert \theta \Vert _{1+s,\Omega }\quad \forall \theta \in \mathrm {H}^{1+s}(\Omega ). \end{aligned}$$

(3.12)

Let ${\mathcal P}$ be the orthogonal projection from $\mathrm {L}^2(\Omega )$ onto the finite element subspace $\mathrm {Q}_h$. We have that ${\mathcal P}$ satisfies the following error estimate for all $s\in (0,k+1]$:

$$\begin{aligned} \Vert q-{\mathcal P}q\Vert _{0,\Omega }\le Ch^{s}\Vert q\Vert _{s,\Omega }\quad \forall q\in \mathrm {H}^s(\Omega ). \end{aligned}$$

(3.13)

Moreover, the following commuting diagram property holds true:

$$\begin{aligned} \mathop {\mathrm {div}}\nolimits {\mathcal R}\varvec{v}={\mathcal P}(\mathop {\mathrm {div}}\nolimits \varvec{v})\quad \forall \varvec{v}\in \mathrm {H}^s(\Omega )^{2}\cap {\mathrm {H}(\mathrm {div};\Omega )}. \end{aligned}$$

We are now in a position of establishing the unique solvability and convergence of the reduced discrete problem (3.7).

Theorem 3.2

Let k be a non-negative integer and let $\mathrm {X}_h$ and $\mathrm {Z}_h$ be given by (3.5) and (3.2), respectively. Then, there exists a unique $(\varvec{u}_h,\omega _h)\in \mathrm {X}_h\times \mathrm {Z}_h$ solution of the Galerkin scheme (3.7). Moreover, there exist positive constants $\hat{C}_1,\,\hat{C}_2>0$ independent of h and $\nu$ such that

$$\begin{aligned} \Vert \varvec{u}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}+|\!|\!| \omega _h |\!|\!|_{1,\Omega }\le \hat{C}_1(\Vert \varvec{f}\Vert _{0,\Omega }+\Vert p_0\Vert _{1/2,\Sigma }), \end{aligned}$$

(3.14)

and

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega } \le \hat{C}_2\inf _{(\varvec{v}_h,\theta _h)\in \mathrm {X}_h\times \mathrm {Z}_h} (\Vert \varvec{u}-\varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}+|\!|\!| \omega -\theta _h |\!|\!|_{1,\Omega }), \end{aligned}$$

(3.15)

where $(\varvec{u},\omega )\in \mathrm {X}\times \mathrm {Z}$ is the unique solution to the variational problem (2.5).

Proof

We define $\mathcal X_h:=\mathrm {X}_h\times \mathrm {Z}_h$ and we consider $\mathcal A(\cdot ,\cdot )$ and $\mathcal G(\cdot )$ as in the proof of Theorem 2.2. The next step consists in proving that the bilinear form $\mathcal A(\cdot ,\cdot )$ satisfies the discrete inf-sup condition (3.9). In fact, given $(\varvec{u}_h,\omega _h)\in \mathcal X_h$, we define

$$\begin{aligned} \tilde{\theta }_h:=-\omega _h\in \mathrm {Z}_h,\quad \text {and}\quad \tilde{\varvec{v}}_h:=\left( \varvec{u}_h+\frac{\sigma _{\min }}{\sigma _{\max }^2}\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _h\right) \in \mathrm {X}_h. \end{aligned}$$

Then, repeating exactly the same steps used in the proof of Theorem 2.2 the proof follows. $\square$

We now establish the corresponding stability estimate for the discrete pressure and its approximation property.

Corollary 3.1

Let $(\varvec{u}_h,\omega _h)\in \mathrm {X}_h\times \mathrm {Z}_h$, be the unique solution of (3.7), with $\varvec{u}_h$ and $\omega _h$ satisfying (3.14). In addition, let $p_h\in Q_h$ be the unique discrete pressure provided by Lemma 3.1, so that $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ is the unique solution of (3.4). Then, there exist positive constants $\bar{C}_1,\,\bar{C}_2>0$, independent of h and $\nu$, such that

$$\begin{aligned} \Vert p_h\Vert _{0,\Omega }\le \bar{C}_1(\Vert \varvec{f}\Vert _{0,\Omega }+\Vert p_0\Vert _{1/2,\Sigma }), \end{aligned}$$

(3.16)

and

$$\begin{aligned} \Vert p-p_h\Vert _{0,\Omega }\le \bar{C}_2\inf _{(\varvec{v}_h,\theta _h,q_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times Q_h} (\Vert \varvec{u}-\varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}+|\!|\!| \omega -\theta _h |\!|\!|_{1,\Omega }+\Vert p-q_h\Vert _{0,\Omega }). \end{aligned}$$

(3.17)

Proof

Proceeding as in the proof of Corollary 2.1, we observe that from the discrete inf-sup condition (3.6), and the first equation of (3.4), there holds

$$\begin{aligned} \Vert p_h\Vert _{0,\Omega }\le \frac{1}{\tilde{\beta }_2}\sup _{\mathop {\varvec{v}_h\ne 0}\limits ^{\scriptstyle \varvec{v}_h\in \mathrm {H}_h}}\frac{\vert b_{2}(\varvec{v}_h,p_h)\vert }{\Vert \varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}=\frac{1}{\tilde{\beta }_2}\sup _{\mathop {\varvec{v}_h\ne 0}\limits ^{\scriptstyle \varvec{v}_h\in \mathrm {H}_h}}\frac{\vert G(\varvec{v}_h)-a(\varvec{u}_h,\varvec{v}_h)-b_1(\varvec{v}_h,\omega _h)\vert }{\Vert \varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}, \end{aligned}$$

which together to (3.14), and the boundedness of G, a and $b_1$, yield (3.16).

Next, given $q_h\in \mathrm {Q}_h$, from the first equation of (3.4) and the Galerkin orthogonality result, it follows that

$$\begin{aligned} b_2(\varvec{v}_h,p_h-q_h)=a(\varvec{u}-\varvec{u}_h,\varvec{v}_h)+b_1(\varvec{v}_h,\omega -\omega _h)+b_2(\varvec{v}_h,p-q_h)\quad \forall \varvec{v}_h \in \mathrm {H}_h. \end{aligned}$$

Then, applying again the inf-sup condition (3.6) and the boundedness of a, $b_1$ and $b_2$, we obtain

$$\begin{aligned} \Vert p_h-q_h\Vert _{0,\Omega }&\le \displaystyle \frac{1}{\tilde{\beta }_2}\sup _{\mathop {\varvec{v}_h\ne 0}\limits ^{\scriptstyle \varvec{v}_h\in \mathrm {H}_h}}\frac{\vert b_{2}(\varvec{v}_h,p_h-q_h)\vert }{\Vert \varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}\\&= \frac{1}{\tilde{\beta }_2}\sup _{\mathop {\varvec{v}_h\ne 0}\limits ^{\scriptstyle \varvec{v}_h\in \mathrm {H}_h}}\frac{\vert a(\varvec{u}-\varvec{u}_h,\varvec{v}_h)+b_1(\varvec{v}_h,\omega -\omega _h)+b_2(\varvec{v}_h,p-q_h)\vert }{\Vert \varvec{v}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}}\\&\le C(\Vert \varvec{u}-\varvec{u}_h\Vert _{{\mathrm {H}(\mathrm {div};\Omega )}}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega }+\Vert p-q_h\Vert _{0,\Omega }). \end{aligned}$$

Therefore, estimate (3.17) is a direct consequence of (3.15), the previous estimate and the triangle inequality. $\square$

The following theorem provides the rate of convergence of our mixed finite element scheme (3.4).

Theorem 3.3

Let k be a non-negative integer and let $\mathrm {H}_h,\mathrm {Z}_h$ and $\mathrm {Q}_h$ be given by (3.1)–(3.3). Let $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ and $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ be the unique solutions to the continuous and discrete problems (2.1) and (3.4), respectively. Assume that $\varvec{u}\in \mathrm {H}^s(\Omega )^2$, $\mathop {\mathrm {div}}\nolimits \varvec{u}\in \mathrm {H}^s(\Omega )$, $\omega \in \mathrm {H}^{1+s}(\Omega )$ and $p\in \mathrm {H}^s(\Omega )$, for some $s\in (0,k+1]$. Then, there exists $\hat{C}>0$ independent of h and $\nu$ such that

$$\begin{aligned}&\Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega }+\Vert p-p_h\Vert _{0,\Omega } \\&\quad \le \hat{C}h^s(\Vert \varvec{u}\Vert _{\mathrm {H}^s(\mathop {\mathrm {div}}\nolimits ;\Omega )}+\Vert \omega \Vert _{1+s,\Omega }+\Vert p\Vert _{s,\Omega }). \end{aligned}$$

Proof

The proof follows from (3.15), (3.17), and standard interpolation estimates satisfied by the operators ${\mathcal R}$, $\Pi$ and ${\mathcal P}$ (see (3.11)–(3.13), respectively). $\square$

Remark 3.2

As stated in the introduction, the present analysis can be easily adapted to study other families of mixed finite elements to solve (2.1). For instance, given an integer $k\ge 0$, we can employ finite element approximations based on piecewise continuous polynomials of degree $k+2$ for the vorticity, Brezzi–Douglas–Marini finite elements of order $k+1$ for the velocity, and piecewise polynomials of degree k for pressure.

Introducing the following finite element subspaces:

$$\begin{aligned} \mathcal {H}_h&:=\{\varvec{v}_h \in \mathrm {H}:\varvec{v}_h|_{T} \in \mathbb P_{k+1}(T)^2 , \quad \forall T \in {\mathcal T}_{h} \},\end{aligned}$$

(3.18)

$$\begin{aligned} \mathcal {Z}_h&:=\left\{ \theta _{h}\in \mathrm {Z}:\theta _h|_{T}\in \mathbb P_{k+2}(T), \quad \forall T \in {\mathcal T}_{h} \right\} ,\end{aligned}$$

(3.19)

$$\begin{aligned} \mathcal {Q}_h&:=\{ q_h\in \mathrm {Q}:q_h|_{T} \in \mathbb P_k(T) , \quad \forall T \in {\mathcal T}_{h} \}, \end{aligned}$$

(3.20)

we can state the following Galerkin scheme, which is the discrete counterpart of the continuous variational formulation (2.1): Find $(\varvec{u}_h,\omega _h,p_h)\in \mathcal {H}_h\times \mathcal {Z}_h\times \mathcal {Q}_h$ such that

$$\begin{aligned} a(\varvec{u}_h,\varvec{v}_h)+\;b_{1}(\varvec{v}_h,\omega _h)+\;b_2(\varvec{v}_h,p_h)&=G(\varvec{v}_h)\quad \forall \varvec{v}_h\in \mathcal {H}_h,\nonumber \\ b_{1}(\varvec{u}_h,\theta _h)- d(\omega _h,\theta _h)&=0\quad \forall \theta _h\in \mathcal {Z}_h,\\ b_2(\varvec{u}_h,q_h)&=0\quad \forall q_h\in \mathcal {Q}_h.\nonumber \end{aligned}$$

(3.21)

We further recall the Brezzi–Douglas–Marini interpolation operator $\tilde{{\mathcal R}}:\mathrm {H}^s(\Omega )^{2}\cap \mathrm {H}\rightarrow \mathcal {H}_h$ for all $s>0$ (see [15]), and we stress that an error estimate similar to (3.11) is valid for the operator $\tilde{{\mathcal R}}$.

Using the arguments considered in this section, it is straightforward to prove the following result regarding existence and uniqueness of solution, and convergence of the scheme defined by (3.21).

Theorem 3.4

Let k be a non-negative integer and let $\mathcal {H}_h\times \mathcal {Z}_h$ and $\mathcal {Q}_h$ be given by (3.18)–(3.20). Then there exists a unique $(\varvec{u}_h,\omega _h,p_h)\in \mathcal {H}_h\times \mathcal {Z}_h\times \mathcal {Q}_h$ solution of the Galerkin scheme (3.21). Assume further that the exact solution $(\varvec{u},\omega ,p)$ satisfies $\varvec{u}\in \mathrm {H}^s(\Omega )^2$, $\mathop {\mathrm {div}}\nolimits \varvec{u}\in \mathrm {H}^s(\Omega )$, $\omega \in \mathrm {H}^{1+s}(\Omega )$ and $p\in \mathrm {H}^s(\Omega )$, for some $s\in (0,k+1]$. Then, there exists $\hat{C}>0$ independent of h and $\nu$ such that

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega }+\Vert p-p_h\Vert _{0,\Omega }\le & {} \hat{C}h^s(\Vert \varvec{u}\Vert _{\mathrm {H}^s(\mathop {\mathrm {div}}\nolimits ;\Omega )}\\&+\left\| \omega \right\| _{1+s,\Omega }+\Vert p\Vert _{s,\Omega }), \end{aligned}$$

where $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ is the unique solution to the variational problem (2.1).

4 A posteriori error analysis

In this section we propose a residual-based a posteriori error estimator and we prove its reliability and efficiency. For sake of clarity, we restrict our analysis to a single type of boundary conditions, those defined on $\Gamma =\partial \Omega$. Therefore, the functional spaces consider in the sequel correspond to

$$\begin{aligned} \mathrm {H}:=\{\varvec{v}\in \mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega ):\varvec{v}\cdot \varvec{n}=0\quad \text {on}\,\Gamma \}, \quad \mathrm {Z}:=\mathrm {H}_{0}^1(\Omega ), \quad \text {and} \quad \mathrm {Q}:=\mathrm {L}_{0}^2(\Omega ). \end{aligned}$$

For each $T\in {\mathcal T}_h$ we let ${\mathcal E}(T)$ be the set of edges of T, and we denote by ${\mathcal E}_h$ the set of all edges in ${\mathcal T}_h$, that is

$$\begin{aligned} {\mathcal E}_h={\mathcal E}_h(\Omega )\cup {\mathcal E}_h(\Gamma ), \end{aligned}$$

where ${\mathcal E}_h(\Omega ):=\{e\in {\mathcal E}_h:e\subset \Omega \}$, and ${\mathcal E}_h(\Gamma ):=\{e\in {\mathcal E}_h:e\subset \Gamma \}$. In what follows, $h_e$ stands for the diameter of a given edge $e\in {\mathcal E}_h$, $\varvec{t}_{e}=(-n_2,n_1)$, where $\varvec{n}_{e}=(n_1,n_2)$ is a fix unit normal vector of e. Now, let $q\in \mathrm {L}^2(\Omega )$ such that $q|_{T}\in C(T)$ for each $T\in {\mathcal T}_h$, then, given $e\in {\mathcal E}_h(\Omega )$, we denote by [q] the jump of q across e, that is $[q]:=(q|_{T'})|_{e}-(q|_{T''})|_{e}$, where $T'$ and $T''$ are the triangles of ${\mathcal T}_{h}$ sharing the edge e. Moreover, let $\varvec{v}\in \mathrm {L}^2(\Omega )^2$ such that $\varvec{v}|_{T}\in C(T)^2$ for each $T\in {\mathcal T}_h$. Then, given $e\in {\mathcal E}_h(\Omega )$, we denote by $[\varvec{v}\cdot \varvec{t}]$ the tangential jump of $\varvec{v}$ across e, that is, $[\varvec{v}\cdot \varvec{t}]:=\left( (\varvec{v}|_{T'})|_{e}-(\varvec{v}|_{T''})|_{e}\right) \cdot \varvec{t}_e$, where $T'$ and $T''$ are the triangles of ${\mathcal T}_{h}$ sharing the edge e.

Next, let k be a non-negative integer and let $\mathrm {H}_h,\mathrm {Z}_h$ and $\mathrm {Q}_h$ be given by (3.1)–(3.3). Let $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ and $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ be the unique solutions to the continuous and discrete problems (2.1) and (3.4) with data satisfying $\varvec{f}\in \mathrm {L}^2(\Omega )^2$ and $\mathop {\mathrm {rot}}\nolimits \varvec{f}\in \mathrm {L}^2(T)$ for each $T\in {\mathcal T}_h$. We define for each $T\in {\mathcal T}_h$ the a posteriori error indicator

and we introduce the global a posteriori error estimator:

$$\begin{aligned} \varvec{\theta }:=\left\{ \sum _{T\in {\mathcal T}_h}\varvec{\theta }_{T}^2\right\} ^{1/2}. \end{aligned}$$

(4.1)

4.1 Reliability of the a posteriori error estimator

The main result of this section is stated as follows.

Theorem 4.1

There exists $C_{rel} > 0$, independent of h and $\nu$, such that

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega }+\Vert p-p_h\Vert _{0,\Omega }\le C_{rel}\varvec{\theta }. \end{aligned}$$

(4.2)

We begin the derivation of (4.2) by recalling that the continuous dependence result given by (2.6) is equivalent to the global inf-sup condition for the continuous reduced formulation (2.5). Then, applying this estimate to the total error $(\varvec{u}-\varvec{u}_h,\omega -\omega _h)\in \mathrm {X}\times \mathrm {Z}$, we obtain

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega } \le C\sup _{\mathop {(\varvec{v},\theta )\ne 0}\limits ^{\scriptstyle (\varvec{v},\theta )\in \mathrm {X}\times \mathrm {Z}}} \frac{\vert R(\varvec{v},\theta )\vert }{\Vert (\varvec{v},\theta )\Vert _{\mathcal X}}, \end{aligned}$$

(4.3)

where $R:\mathrm {X}\times \mathrm {Z}\rightarrow \mathbb {R}$ is the residual operator defined by

$$\begin{aligned} R(\varvec{v},\theta ):=a(\varvec{u}-\varvec{u}_h,\varvec{v})+b_{1}(\varvec{v},\omega -\omega _h)+b_{1}(\varvec{u}-\varvec{u}_h,\theta )-d(\omega -\omega _h,\theta ), \end{aligned}$$

for all $(\varvec{v},\theta )\in \mathrm {X}\times \mathrm {Z}$. Moreover, we have that

$$\begin{aligned} R(\varvec{v},\theta ):=R_{1}(\varvec{v})+R_{2}(\theta ), \end{aligned}$$

where

$$\begin{aligned} R_{1}(\varvec{v})&:=\int _{\Omega }\varvec{f}\cdot \varvec{v}-{\int _{\Omega }\sigma \varvec{u}_h\cdot \varvec{v}-\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \omega _{h}\cdot \varvec{v}},\\ R_{2}(\theta )&:=-{\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \theta \cdot \varvec{u}_h+\int _{\Omega }\omega _h\theta }. \end{aligned}$$

Hence, the supremum in (4.3) can be bounded in terms of $R_{i}, i\in \{1,2\}$, which yields

$$\begin{aligned} \Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega }\le C\left( \sup _{\mathop {\varvec{v}\ne 0}\limits ^{\scriptstyle \varvec{v}\in \mathrm {X}}}\frac{\vert R_{1}(\varvec{v})\vert }{\Vert \varvec{v}\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}}+ \sup _{\mathop {\theta \ne 0}\limits ^{\scriptstyle \theta \in \mathrm {Z}}}\frac{\vert R_{2}(\theta )\vert }{|\!|\!| \theta |\!|\!|_{1,\Omega }}\right) . \end{aligned}$$

(4.4)

In what follows, we provide suitable upper bounds for each term on the right hand side of (4.4). Some technical results are provided beforehand. Let us first recall the Clément interpolation operator $I_h:\mathrm {H}^1(\Omega )\rightarrow Y_h$, where

$$\begin{aligned} Y_h:=\{\theta _{h}\in \mathrm {H}^1(\Omega ):\theta _h|_{T}\in \mathbb P_{1}(T), \quad \forall T \in {\mathcal T}_{h}\}. \end{aligned}$$

This operator satisfies the following local approximation properties (cf. [20]).

Lemma 4.1

There exist positive constants $\tilde{c}$ and $\hat{c}$ such that for all $\theta \in \mathrm {H}^1(\Omega )$ there hold

$$\begin{aligned} \Vert \theta -I_h\theta \Vert _{0,T} \le \tilde{c}h_{T}\vert \theta \vert _{1,\Delta (T)} \quad \forall T\in {\mathcal T}_{h}, \end{aligned}$$

and

$$\begin{aligned} \Vert \theta -I_h\theta \Vert _{0,e} \le \hat{c}h_{e}^{1/2}\vert \theta \vert _{1,\Delta (e)} \quad \forall e\in {\mathcal E}_h, \end{aligned}$$

where $\Delta (T):=\cup \{T'\in {\mathcal T}_{h}:T'\cap T\ne 0\}$ and $\Delta (e):=\cup \{T'\in {\mathcal T}_{h}:T'\cap e\ne 0\}$.

The following lemma establishes the corresponding upper bound for $R_1$.

Lemma 4.2

There exists $C_1 > 0$, independent of h and $\nu$, such that

$$\begin{aligned} \displaystyle \sup _{\mathop {\varvec{v}\ne 0}\limits ^{\scriptstyle \varvec{v}\in \mathrm {X}}}\frac{\vert R_{1}(\varvec{v})\vert }{\Vert \varvec{v}\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}}&\le C_{1}\left\{ \sum _{T\in {\mathcal T}_h}h_{T}\Vert \mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})\Vert _{0,T}\right. \\&\qquad \qquad \quad +\left. \sum _{e\in {\mathcal E}_h(\Omega )}h_{e}^{1/2}\Vert [(\varvec{f}-\sigma \varvec{u}_h-{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})\cdot \varvec{t}]\Vert _{0,e} \right\} ^{1/2}. \end{aligned}$$

Proof

Given $\varvec{v}\in \mathrm {X}$ we know that $\mathop {\mathrm {div}}\nolimits \varvec{v}=0$ in $\Omega$ and $\varvec{v}\cdot \varvec{n}=0$ on $\Gamma$. Then, applying [31, Theorem3.1], we can assert that there exists a unique $\phi \in \mathrm {H}_0^1(\Omega )$, such that $\varvec{v}=\mathop {\mathbf {curl}}\nolimits \phi$ in $\Omega$, and

$$\begin{aligned} \vert \phi \vert _{1,\Omega }\le C\Vert \varvec{v}\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}. \end{aligned}$$

Hence, since $R_{1}(\varvec{v}_h)=0\quad \forall \varvec{v}_{h}\in \mathrm {X}_{h}$, which follows from the first equation of the Galerkin scheme (3.7), we obtain

$$\begin{aligned} R_{1}(\varvec{v})&=R_{1}(\mathop {\mathbf {curl}}\nolimits (\phi ))=R_{1}(\mathop {\mathbf {curl}}\nolimits (\phi -I_{h}\phi ))\\ {}&=\int _{\Omega }(\varvec{f}-\sigma \varvec{u}_h-{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})\cdot \mathop {\mathbf {curl}}\nolimits (\phi -I_{h}\phi ), \end{aligned}$$

and integrating by parts we easily get

$$\begin{aligned} R_{1}(\mathop {\mathbf {curl}}\nolimits (\phi -I_{h}\phi ))&=\sum _{T\in {\mathcal T}_h}\biggl [\int _{T} \mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h -{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})(\phi -I_{h}\phi )\\&\quad -\int _{\partial T}(\phi -I_{h}\phi )(\varvec{f}-\sigma \varvec{u}_h-{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})\cdot \varvec{t}\biggr ]\\&=\sum _{T\in {\mathcal T}_h}\int _{T} \mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})(\phi -I_{h}\phi )\\&\quad -\sum _{e\in {\mathcal E}_h(\Omega )}\int _{e}(\phi -I_{h}\phi )[(\varvec{f}-\sigma \varvec{u}_h-{\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}})\cdot \varvec{t}]. \end{aligned}$$

Therefore, the proof follows from the Cauchy–Schwarz inequality, Lemma 4.1, and the fact that the number of triangles in $\Delta (T)$ and $\Delta (e)$ is bounded. $\square$

Next we establish an upper bound for $R_2$.

Lemma 4.3

There exists $C_2 > 0$, independent of h and $\nu$, such that

$$\begin{aligned} \sup _{\mathop {\theta \ne 0}\limits ^{\scriptstyle \theta \in \mathrm {Z}}}\frac{\vert R_{2}(\theta )\vert }{|\!|\!| \theta |\!|\!|_{1,\Omega }} \le C_{2}\left\{ \sum _{T\in {\mathcal T}_h} h_{T} \biggl \Vert \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h} \biggr \Vert _{0,T} +\sum _{e\in {\mathcal E}_h(\Omega )}h_{e}^{1/2}\Vert [\varvec{u}_h\cdot \varvec{t}]\Vert _{0,e}\right\} ^{1/2}. \end{aligned}$$

Proof

We first observe that $R_{2}(\theta _h)=0\quad \forall \theta _{h}\in \mathrm {Z}_{h}$, which follows from the second equation in the Galerkin scheme (3.7). Then, for all $\theta \in \mathrm {H}^1_0(\Omega )$ it follows that

$$\begin{aligned} R_{2}(\theta )=R_{2}(\theta -I_h\theta )&= \int _{\Omega }\omega _{h}(\theta -I_h\theta ) -{\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits (\theta -I_h\theta )\cdot \varvec{u}_h}, \end{aligned}$$

and integrating by parts, we obtain

$$\begin{aligned} R_{2}(\theta -I_h\theta )&=\sum _{T\in {\mathcal T}_h}\int _{T}\frac{1}{\sqrt{\nu }}\omega _{h}\sqrt{\nu }(\theta -I_h\theta ) \\&\quad -{\sqrt{\nu }}\sum _{T\in {\mathcal T}_h}\left( \int _{T}(\theta -I_h\theta )\mathop {\mathrm {rot}}\nolimits \varvec{u}_h -\int _{\partial T}(\theta -I_{h}\theta )(\varvec{u}_h\cdot \varvec{t})\right) ,\\&=\sum _{T\in {\mathcal T}_h}\int _{T}\left( \frac{1}{\sqrt{\nu }}\omega _h-\mathop {\mathrm {rot}}\nolimits \varvec{u}_h\right) \sqrt{\nu }(\theta -I_h\theta )\\&\quad +{\sqrt{\nu }}\sum _{e\in {\mathcal E}_h(\Omega )}\int _{e}(\theta -I_{h}\theta )[\varvec{u}_h\cdot \varvec{t}]. \end{aligned}$$

Then, the proof readily follows by the Cauchy–Schwarz inequality, the approximation properties of the operator $I_h$ (see Lemma 4.1), and the fact that the number of triangles in $\Delta (T)$ and $\Delta (e)$ is bounded. $\square$

To conclude the derivation of (4.2) we need an estimate for $\Vert p-p_h\Vert _{0,\Omega }$, which follows from the following two results.

Lemma 4.4

Let $(\varvec{u},\omega ,p)\in \mathrm {H}\times \mathrm {Z}\times \mathrm {Q}$ and $(\varvec{u}_h,\omega _h,p_h)\in \mathrm {H}_h\times \mathrm {Z}_h\times \mathrm {Q}_h$ be the unique solutions of (2.1) and (3.4), respectively. Then for all $\varvec{v}\in \mathrm {H}$ and for all $\varvec{v}_h\in \mathrm {H}_h$, there holds

$$\begin{aligned} b_2(\varvec{v},p-p_h)=\displaystyle -a(\varvec{u}-\varvec{u}_h,\varvec{v})-b_1(\varvec{v},\omega -\omega _h)+L(\varvec{v}-\varvec{v}_h), \end{aligned}$$

(4.5)

with

$$\begin{aligned} L(\varvec{v}-\varvec{v}_h)=\int _\Omega \varvec{f}\cdot (\varvec{v}-\varvec{v}_h) -a(\varvec{u}_h,\varvec{v}-\varvec{v}_h)-b_1(\varvec{v}-\varvec{v}_h,\omega _h)-b_2(\varvec{v}-\varvec{v}_h,p_h). \end{aligned}$$

Proof

Let $\varvec{v}\in \mathrm {H}$ and $\varvec{v}_h\in \mathrm {H}_h$. The first equations in (2.1) and (3.4) yield

$$\begin{aligned} b_2(\varvec{v},p-p_h)&=\int _\Omega \varvec{f}\cdot \varvec{v}-a(\varvec{u},\varvec{v})-b_1(\varvec{v},\omega )-b_2(\varvec{v},p_h),\end{aligned}$$

(4.6)

$$\begin{aligned} b_2(\varvec{v}_h,p_h)&=\int _\Omega \varvec{f}\cdot \varvec{v}_h -a(\varvec{u}_h,\varvec{v}_h)-b_1(\varvec{v}_h,\omega _h), \end{aligned}$$

(4.7)

respectively. Then, adding and subtracting $a(\varvec{u}_h,\varvec{v})$, $b_1(\varvec{v},\omega _h)$ and $b_2(\varvec{v}_h,p_h)$ in the RHS of (4.6), we obtain

$$\begin{aligned} b_2(\varvec{v},p-p_h)&=\int _\Omega \varvec{f}\cdot \varvec{v}-a(\varvec{u}-\varvec{u}_h,\varvec{v})-b_1(\varvec{v},\omega -\omega _h)-a(\varvec{u}_h,\varvec{v})\\&\quad -b_1(\varvec{v},\omega _h)-b_2(\varvec{v}-\varvec{v}_h,p_h)-b_2(\varvec{v}_h,p_h). \end{aligned}$$

It then suffices to replace $b_2(\varvec{v}_h,p_h)$ by (4.7) in the last identity to conclude. $\square$

Before giving the upper bound for the pressure error, we recall the local approximation properties of the Raviart–Thomas interpolator $\mathcal {R} : \mathrm {H}^1(\Omega )^2 \,\rightarrow \, \mathrm {H}_h$ (see [15]): there exist $c_1, c_2 > 0$, independent of h, such that for all $\varvec{v}\in \mathrm {H}^1(\Omega )^2$, there hold

$$\begin{aligned} \Vert \varvec{v}-\mathcal {R}\varvec{v}\Vert _{0,T}&\le c_1\,h_T\, \Vert \varvec{v}\Vert _{1,T}\quad \forall T \in \mathcal {T}_h,\\ \Vert \varvec{v}\cdot \varvec{n}-\mathcal {R}\varvec{v}\cdot \varvec{n}\Vert _{0,e}&\le c_2\,h_e^{1/2}\, \Vert \varvec{v}\Vert _{1,T_e}\quad \forall e\in {\mathcal E}_h, \end{aligned}$$

where $T_e$ is a triangle of $\mathcal {T}_h$ containing e on its boundary.

Lemma 4.5

There exists $C_3>0$, independent of h and $\nu$, such that

$$\begin{aligned} \Vert p-p_h\Vert _{0,\Omega }&\le C_3\left( \Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )} +|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega } \right. \\&\quad +\left. \left\{ \sum _{T\in {\mathcal T}_h}h_{T}^2\Vert \varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}-\nabla p_h\Vert _{0,T}^2\right\} ^{1/2}\right) . \end{aligned}$$

Proof

First, let us notice that from the inf-sup condition (2.2), we have

$$\begin{aligned} \Vert p-p_h\Vert _{0,\Omega } \le \frac{1}{\beta _2}\sup _{\mathop {\varvec{v}\ne 0}\limits ^{\scriptstyle \varvec{v}\in \mathrm {H}}}\frac{\vert b_{2}(\varvec{v},p-p_h)\vert }{\Vert \varvec{v}\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}}. \end{aligned}$$

(4.8)

Then, it remains to bound the right hand side of (4.8) to conclude.

Let $\varvec{v}\in \mathrm {H}$. Since $\varvec{v}\cdot \varvec{n}=0$ on $\Gamma$, it follows that $\mathop {\mathrm {div}}\nolimits \varvec{v}\in L_0^2(\Omega )$, and then, applying [31, Corollary 2.4], we conclude that there exists a unique $\varvec{z}\in \mathrm {H}^1_0(\Omega )^2$, such that

$$\begin{aligned} \mathop {\mathrm {div}}\nolimits \varvec{z}= \mathop {\mathrm {div}}\nolimits \varvec{v}\quad \hbox {in }\Omega ,\quad \hbox {and}\quad \Vert \varvec{z}\Vert _{1,\Omega }\le C\Vert \varvec{v}\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}. \end{aligned}$$

(4.9)

Hence, we define $\varvec{z}_h=\mathcal {R}(\varvec{z})\in \mathrm {H}_h$, and apply identity (4.5) to obtain

$$\begin{aligned} b_2(\varvec{v},p-p_h)=b_2(\varvec{z},p-p_h)= -a(\varvec{u}-\varvec{u}_h,\varvec{z})-b_1(\varvec{z},\omega -\omega _h)+L(\varvec{z}-\varvec{z}_h).\ \end{aligned}$$

(4.10)

Now, recalling the definition of L, a, $b_1$ and $b_2$, we integrate by parts on each triangle, to obtain

$$\begin{aligned} L(\varvec{z}-\varvec{z}_h)&=\displaystyle \int _{\Omega }\varvec{f}\cdot (\varvec{z}-\varvec{z}_h) -{\int _{\Omega }\sigma \varvec{u}_h\cdot (\varvec{z}-\varvec{z}_h)}-\sqrt{\nu }\int _{\Omega }\mathop {\mathbf {curl}}\nolimits \omega _{h}\cdot (\varvec{z}-\varvec{z}_h)\nonumber \\&\quad +\int _{\Omega }p_h\mathop {\mathrm {div}}\nolimits (\varvec{z}-\varvec{z}_h),\nonumber \\&=\displaystyle \sum _{T\in {\mathcal T}_h}\int _{T}(\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}-\nabla p_h)\cdot (\varvec{z}-\varvec{z}_h). \end{aligned}$$

(4.11)

In this way, from (4.10) and (4.11), the definition of a, $b_1$, the local approximation properties of the interpolation operator $\mathcal R$, and the Cauchy–Schwarz inequality, we get

$$\begin{aligned} |b_2(\varvec{v},p-p_h)|&\le \displaystyle {\sigma _{\max }}\Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )} \Vert \varvec{z}\Vert _{1,\Omega } +\sqrt{\nu } \Vert \mathop {\mathbf {curl}}\nolimits (\omega -\omega _h)\Vert _{0,\Omega }\Vert \varvec{z}\Vert _{1,\Omega }\nonumber \\&\quad \displaystyle +\sum _{T\in {\mathcal T}_h}\Vert \varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}-\nabla p_h\Vert _{0,T}\Vert \varvec{z}-\varvec{z}_h\Vert _{0,T}\nonumber \\&\le \displaystyle \left( {\sigma _{\max }}\Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+\sqrt{\nu } \Vert \mathop {\mathbf {curl}}\nolimits (\omega -\omega _h)\Vert _{0,\Omega }\right) \Vert \varvec{z}\Vert _{1,\Omega }\nonumber \\&\quad \displaystyle +C\,\left\{ \sum _{T\in {\mathcal T}_h}h_T^2\Vert \varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}-\nabla p_h\Vert _{0,T}^2\right\} ^{1/2}\Vert \varvec{z}\Vert _{1,\Omega }. \end{aligned}$$

(4.12)

Therefore, the result follows from (4.8), (4.12) and the upper bound of $\varvec{z}$ in (4.9). $\square$

We end this section by observing that the reliability estimate (4.2) (cf. Theorem 4.1) is a direct consequence of Lemmas 4.2, 4.3 and 4.5.

4.2 Efficiency of the a posteriori error estimator

The main result of this section is stated next.

Theorem 4.2

There exists $C_{eff} > 0$, independent of h and $\nu$, such that

$$\begin{aligned} C_{eff}\varvec{\theta }\le \Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega } +\Vert p-p_h\Vert _{0,\Omega }+\text {h.o.t.}, \end{aligned}$$

where h.o.t. stands, eventually, for one or several terms of higher order.

In order to prove the efficiency of the a posteriori error estimator, we will bound each term defining $\varvec{\theta }_T$ in terms of local errors. We proceed similarly to [29] (see also [10, 17]): we apply inverse inequalities and the localization technique based on element-bubble and edge-bubble functions. We start by stating further notation and some preliminary results.

Given ${\mathcal T}_h$, $T\in {\mathcal T}_h$, and $e\in {\mathcal E}(T)$, let $\psi _T$ and $\psi _e$ be the usual triangle-bubble and edge-bubble functions, respectively [39, eqs.(1.5)–(1.6)]. In particular, $\psi _T\in \mathbb P_{3}(T)$, $supp(\psi _T)\subseteq T$, $\psi _T=0$ on $\partial T$, and $0\le \psi _T\le 1$ in T. Similarly, $\psi _e|_T\in \mathbb P_{2}(T)$, $supp(\psi _e)\subseteq \omega _e:=\cup \{T'\in {\mathcal T}_h:e\in {\mathcal E}(T')\}$, $\psi _e=0$ on $\partial T{\setminus } e$, and $0\le \psi _e\le 1$ in $\omega _e$. We recall (also from [39]) that, given $k\in \mathbb {N}\cup \{0\}$, there exists an extension operator $L:C(e)\rightarrow C(T)$ that satisfies $L(q)\in \mathbb P_{k}(T)$ and $L(q)|_{e}=q\quad \forall q\in \mathbb P_{k}(e)$. A component-wise application of L will be also considered. Additional properties of $\psi _T$, $\psi _e$ and L are collected in the following lemma (see [39]).

Lemma 4.6

Given $k\in \mathbb {N}\cup \{0\}$, there exist $c_1,c_2,c_3>0$, depending only on k and the shape regularity of the triangulations (minimum angle condition), such that for each triangle T and $e\in {\mathcal E}(T)$, there hold

$$\begin{aligned} \Vert q\Vert _{0,T}^2&\le c_1\Vert \psi _T^{1/2}q\Vert _{0,T}^2\quad \forall q\in \mathbb P_{k}(T),\\ \Vert q\Vert _{0,e}^2&\le c_2\Vert \psi _e^{1/2}q\Vert _{0,e}^2\quad \forall q\in \mathbb P_{k}(e),\\ \text {and}\quad \Vert \psi _e^{1/2}L(q)\Vert _{0,T}^2&\le c_3 h_{e} \Vert q\Vert _{0,e}^2\quad \forall q\in \mathbb P_{k}(e). \end{aligned}$$

The following classical result which states an inverse estimate will also be used.

Lemma 4.7

Let $k, l, m\in \mathbb {N}\cup \{0\}$ such that $l\le m$. Then, there exists $c_4>0$, depending only on k, l, m and the shape regularity of the triangulations, such that for each triangle T there holds

$$\begin{aligned} \vert q\vert _{m,T}\le c_4 h_{T}^{l-m}\vert q\vert _{l,T}\quad \forall q\in \mathbb P_{k}(T). \end{aligned}$$

The following lemmas provide the corresponding upper bounds for each term defining $\varvec{\theta }_T$.

Lemma 4.8

There exists $C > 0$, independent of h and $\nu$, such that for each $T\in {\mathcal T}_h$ there holds

$$\begin{aligned} h_{T}^2\left\| {\mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}}\right\| _{0,T}^2\le C\left( \Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}^2+\frac{h_{T}^2}{\nu }\Vert \omega -\omega _h\Vert _{0,T}^2\right) . \end{aligned}$$

Proof

First, from Lemma 4.6 and then, using that ${\sqrt{\nu }\mathop {\mathrm {rot}}\nolimits \varvec{u}-\omega =0}$ in $\Omega$ (see Theorem 2.3), integration by parts and the Cauchy–Schwarz inequality, we get

$$\begin{aligned} \left\| \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right\| _{0,T}^2&\le c_1\left\| \psi _T^{1/2}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \right\| _{0,T}^2\\&= c_1 \left( \int _{T}\psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \mathop {\mathrm {rot}}\nolimits (\varvec{u}_h-\varvec{u})\right. \\&\quad +\left. \int _{T}\psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \frac{1}{\sqrt{\nu }}(\omega -\omega _h)\right) \\&= c_1 \left( \int _{T}\mathop {\mathbf {curl}}\nolimits \left( \psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \right) \cdot (\varvec{u}_h-\varvec{u})\right. \\&\quad +\left. \int _{T}\psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \frac{1}{\sqrt{\nu }}(\omega -\omega _h)\right) \\&\le c_1 \left( \left\| \mathop {\mathbf {curl}}\nolimits \left( \psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \right) \right\| _{0,T}\Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}\right. \\&\quad +\left. \left\| \psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \right\| _{0,T}\frac{1}{\sqrt{\nu }}\Vert \omega -\omega _{h}\Vert _{0,T}\right) . \end{aligned}$$

Since $\psi _{T}(\mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h})$ is a polynomial on each $T\in {\mathcal T}_h$, from Lemma 4.7 we have

$$\begin{aligned} \left| \psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \right| _{1,T} \le c_{4}h_{T}^{-1}\left\| \psi _{T}\left( \mathop {\mathrm {rot}}\nolimits \varvec{u}_h-\frac{1}{\sqrt{\nu }}\omega _{h}\right) \right\| _{0,T}, \end{aligned}$$

which completes the proof. $\square$

Lemma 4.9

There exists $C > 0$, independent of h and $\nu$, such that for each $T\in {\mathcal T}_h$ there holds

$$\begin{aligned} h_{e}\Vert [\varvec{u}_h\cdot \varvec{t}]\Vert _{0,e}^{2}\le C\sum _{T\in \omega _e}(\Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}^2+\Vert \omega -\omega _h\Vert _{0,T}^2). \end{aligned}$$

Proof

It follows by a combination of the arguments in the proof of [17, Lemma 6.2], and Lemma 4.8. $\square$

Lemma 4.10

There exists $C > 0$, independent of h and $\nu$, such that for each $T\in {\mathcal T}_h$ there holds

$$\begin{aligned} h_{T}^2\Vert \mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})\Vert _{0,T}^2\le & {} C(\Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}^2+\nu \Vert \mathop {\mathbf {curl}}\nolimits ( \omega -\omega _h)\Vert _{0,T}^2\\&+\, h_{T}^2\Vert \mathop {\mathrm {rot}}\nolimits \varvec{f}-{\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits \varvec{f})\Vert _{0,T}^2), \end{aligned}$$

where ${\mathcal P}_{T}^{l}$ is the $L^2(T)^2$-orthogonal projection onto $\mathbb P_{l}(T)^2$, for $l\ge k$, with respect to the inner product $(\varvec{f},\varvec{g})_{0,T}:=\int _{T}\psi _{T}\varvec{f}\cdot \varvec{g}$ for each $\varvec{f},\varvec{g}\in L^2(T)^2$.

Proof

Adding and subtracting ${\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits \varvec{f})$, and using the triangle inequality we obtain

$$\begin{aligned}&\Vert \mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})\Vert _{0,T}^2 \\&\quad \le 2(\Vert \mathop {\mathrm {rot}}\nolimits \varvec{f}-{\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits \varvec{f})\Vert _{0,T}^2 +\Vert {\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits \varvec{f})-\mathop {\mathrm {rot}}\nolimits (\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})\Vert _{0,T}^2)\\&\quad = 2(\Vert \mathop {\mathrm {rot}}\nolimits \varvec{f}-{\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits \varvec{f})\Vert _{0,T}^2 +\Vert {\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}))\Vert _{0,T}^2). \end{aligned}$$

Next, from Lemma 4.6, we get

$$\begin{aligned}&\Vert {\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}))\Vert _{0,T}^2 \\&\quad \le \Vert \psi _T^{1/2}{\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}))\Vert _{0,T}^2\\&\quad = \int _{T}\psi _{T}{\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})) {\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}))\\&\quad = \int _{T}\psi _{T}{\mathcal P}_{T}^l(\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})) \mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}), \end{aligned}$$

where we have used the fact that ${\mathcal P}_{T}^{l}$ is the $L^2(T)^2$-orthogonal projection onto $\mathbb P_{l}(T)^2$. Then, since $\mathop {\mathrm {rot}}\nolimits (\varvec{f}-\sigma \varvec{u}-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega )=0$ in $\Omega$ (see Theorem 2.3), the proof follows by integration by parts, the Cauchy–Schwarz inequality and Lemma 4.7. $\square$

Lemma 4.11

There exists $C > 0$, independent of h and $\nu$, such that for each $T\in {\mathcal T}_h$ there holds

$$\begin{aligned}&h_{T}^2\Vert \varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}-\nabla p_h\Vert _{0,T}^2 \\&\quad \le C(h_{T}^2\Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}^2+h_{T}^2\nu \Vert \mathop {\mathbf {curl}}\nolimits (\omega -\omega _h)\Vert _{0,T}^2 +\Vert p-p_h\Vert _{0,T}^2\\ {}&\qquad +h_{T}^2\Vert \varvec{f}-{\mathcal P}_T^{l}(\varvec{f})\Vert _{0,T}^2),\end{aligned}$$

where ${\mathcal P}_{T}^{l}$ is defined as in Lemma 4.10.

Proof

The estimate follows after combining the arguments used in the proof of [17, Lemma 6.3] and the proof of Lemma 4.10. $\square$

Lemma 4.12

There exists $C > 0$, independent of h and $\nu$, such that for each $T\in {\mathcal T}_h$ there holds

$$\begin{aligned}&h_{e}\Vert [(\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})\cdot \varvec{t}]\Vert _{0,e}^{2} \\&\quad \le C\sum _{T\in \omega _e}(\Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}^2 +\nu \Vert \mathop {\mathbf {curl}}\nolimits (\omega -\omega _h)\Vert _{0,T}^2 +\Vert \varvec{f}-\tilde{{\mathcal P}}_{T}^l(\varvec{f})\Vert _{0,T}^2\\ {}&\qquad +h_T^2\vert \varvec{f}-\tilde{{\mathcal P}}^l(\varvec{f})\vert _{1,T}^2),\end{aligned}$$

where $\tilde{{\mathcal P}}_{T}^{l}$ is the usual $L^2(T)^2$-orthogonal projection onto $\mathbb P_{l}(T)^2$ with $l\ge k$.

Proof

Adding and subtracting $\tilde{{\mathcal P}}^l(\varvec{f})$, followed by a use of triangle inequality yields

$$\begin{aligned}&h_{e}^{1/2}\Vert [(\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})\cdot \varvec{t}]\Vert _{0,e}\nonumber \\&\quad \le h_{e}^{1/2}\Vert [(\varvec{f}-\tilde{{\mathcal P}}^l(\varvec{f}))\cdot \varvec{t}]\Vert _{0,e} +h_{e}^{1/2}\Vert [\tilde{{\mathcal P}}^l(\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h})\cdot \varvec{t}]\Vert _{0,e}.\qquad \quad \end{aligned}$$

(4.13)

The first term in the right hand side can be bound using the local trace inequality as follows:

$$\begin{aligned}&h_{e}^{1/2}\Vert [(\varvec{f}-\tilde{{\mathcal P}}^l(\varvec{f}))\cdot \varvec{t}]\Vert _{0,e}\nonumber \\&\quad \le h_{e}^{1/2}\left( h_{e}^{-1/2}\sum _{T\in \omega _e}\Vert \varvec{f}-\tilde{{\mathcal P}}^l(\varvec{f})\Vert _{0,T} +h_{e}^{1/2}\sum _{T\in \omega _e}\vert \varvec{f}-\tilde{{\mathcal P}}^l(\varvec{f})\vert _{1,T}\right) .\qquad \quad \end{aligned}$$

(4.14)

Now, we denote $\xi _h:=\varvec{f}-\sigma \varvec{u}_h-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega _{h}$. From Lemma 4.6, integration by parts, and the fact that $\nabla p=\varvec{f}-\sigma \varvec{u}-\sqrt{\nu }\mathop {\mathbf {curl}}\nolimits \omega :=\xi$ (see Theorem 2.3), we bound the second term in the right hand side of (4.13), as follows

$$\begin{aligned} \Vert [\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,e}^{2}&\le \Vert \psi _e^{1/2}[\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,e}^{2} =\int _{e}\psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}])[\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\\&= \sum _{T\in \omega _e}\left( \int _{T}\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \mathop {\mathbf {curl}}\nolimits (\psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]))\right. \\&\quad +\left. \int _{T}\psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}])\mathop {\mathrm {rot}}\nolimits \tilde{{\mathcal P}}_{T}^l(\xi _h)\right) \\&= \sum _{T\in \omega _e}\left( \int _{T}(\tilde{{\mathcal P}}_{T}^l(\xi _h)-\xi ) \cdot \mathop {\mathbf {curl}}\nolimits (\psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]))\right. \\&\quad +\left. \int _{T}\psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}])\mathop {\mathrm {rot}}\nolimits \tilde{{\mathcal P}}_{T}^l(\xi _h)\right) , \end{aligned}$$

where we have also used that $\nabla p\in \mathrm {H}(\mathop {\mathrm {rot}}\nolimits ;\Omega )$. Therefore, a direct application of Cauchy–Schwarz inequality and Lemma 4.7 implies that

$$\begin{aligned} \Vert [\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,e}^{2}&\le \sum _{T\in \omega _e}(h_{T}^{-1}\Vert \tilde{{\mathcal P}}_{T}^l(\xi _h)-\xi )\Vert _{0,T}\\&\quad +\Vert \mathop {\mathrm {rot}}\nolimits \tilde{{\mathcal P}}_{T}^l(\xi _h)\Vert _{0,T})\Vert \psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}])\Vert _{0,T}. \end{aligned}$$

Using that $0\le \psi _e\le 1$ and applying the third estimate of Lemma 4.6, we get

$$\begin{aligned} \Vert \psi _{e}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}])\Vert _{0,T}\le \Vert \psi _{e}^{1/2}L([\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}])\Vert _{0,T}\le Ch_{e}^{1/2}\Vert [\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,T}, \end{aligned}$$

and hence, we obtain that

$$\begin{aligned} \Vert [\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,e}\le&h_{e}^{1/2} \sum _{T\in \omega _e}(h_{T}^{-1}\Vert \tilde{{\mathcal P}}_{T}^l(\xi _h)-\xi \Vert _{0,T} +\Vert \mathop {\mathrm {rot}}\nolimits \tilde{{\mathcal P}}_{T}^l(\xi _h)\Vert _{0,T}). \end{aligned}$$

Therefore, using the fact that $h_e\le h_T$, we deduce that

$$\begin{aligned} h_{e}^{1/2}\Vert [\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,e}\le \sum _{T\in \omega _e}(\Vert \tilde{{\mathcal P}}_{T}^l(\xi _h)-\xi \Vert _{0,T} +h_T\Vert \mathop {\mathrm {rot}}\nolimits \tilde{{\mathcal P}}_{T}^l(\xi _h)\Vert _{0,T}). \end{aligned}$$

Now, repeating the arguments used in the proof of Lemma 4.10 allows us to prove that

$$\begin{aligned} \Vert \mathop {\mathrm {rot}}\nolimits \tilde{{\mathcal P}}_{T}^l(\xi _h)\Vert _{0,T}\le h_{T}^{-1}\Vert \tilde{{\mathcal P}}_{T}^l(\xi _h)-\xi \Vert _{0,T}. \end{aligned}$$

From the above inequality and the Cauchy–Schwarz inequality, we obtain that

$$\begin{aligned} h_{e}^{1/2}\Vert [\tilde{{\mathcal P}}_{T}^l(\xi _h)\cdot \varvec{t}]\Vert _{0,e}\le & {} C\sum _{T\in \omega _e}(\Vert \varvec{f}-\tilde{{\mathcal P}}_{T}^l(\varvec{f})\Vert _{0,T} +\Vert \varvec{u}-\varvec{u}_h\Vert _{0,T}\nonumber \\&+\sqrt{\nu }\Vert \mathop {\mathbf {curl}}\nolimits (\omega -\omega _h)\Vert _{0,T}). \end{aligned}$$

(4.15)

Thus, the proof follows combining (4.13)–(4.15). $\square$

We end this section by observing that the required efficiency of the a posteriori error estimator $\varvec{\theta }$ follows straightforwardly from Lemmas 4.8–4.12. In fact, from the estimates previously proved, we have that there exists $C>0$, independent of h and $\nu$, such that

$$\begin{aligned} \varvec{\theta }^2\le & {} C\left( \Vert \varvec{u}-\varvec{u}_h\Vert ^2_{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )}+|\!|\!| \omega -\omega _h |\!|\!|^2_{1,\Omega } +\Vert p-p_h\Vert ^2_{0,\Omega }+{\frac{h^2}{\nu }\Vert \omega -\omega _h\Vert _{0,\Omega }^2}\right. \nonumber \\&\qquad +\left. \sum _{T\in {\mathcal T}_h}\Vert \varvec{f}-{\mathcal P}_{T}^l(\varvec{f})\Vert _{0,T}^2 +h_{T}^2\vert \varvec{f}-{\mathcal P}_{T}^l(\varvec{f})\vert _{1,T}^2 +\Vert \varvec{f}-\tilde{{\mathcal P}}_{T}^l(\varvec{f})\Vert _{0,T}^2 \right. \nonumber \\&\qquad +\left. h_{T}^2\vert \varvec{f}-\tilde{{\mathcal P}}_{T}^l(\varvec{f})\vert _{1,T}^2\right) . \end{aligned}$$

(4.16)

First, we note that $\frac{h^2}{\nu }\Vert \omega -\omega _h\Vert _{0,\Omega }^2$ clearly corresponds to a higher order term. Moreover, if $\varvec{f}\in \mathrm {H}^{k+2}(T)$ and ${\mathcal P}_{T}^{l}$ is the $L^2(T)^2$-orthogonal projection onto $\mathbb P_{k+2}(T)^2$ with respect to the inner product $(\varvec{f},\varvec{g})_{0,T}:=\int _{T}\psi _{T}\varvec{f}\cdot \varvec{g}$, and $\tilde{{\mathcal P}}_{T}^{l}$ is the $L^2(T)^2$-orthogonal projection onto $\mathbb P_{k+2}(T)^2$, for each $T\in {\mathcal T}_h$, we obtain

$$\begin{aligned}&\sum _{T\in {\mathcal T}_h}\Vert \varvec{f}-{\mathcal P}_{T}^{k+2}(\varvec{f})\Vert _{0,T}^2 +h_{T}^2\vert \varvec{f}-{\mathcal P}_{T}^{k+2}(\varvec{f})\vert _{1,T}^2 +\Vert \varvec{f}-\tilde{{\mathcal P}}_{T}^l(\varvec{f})\Vert _{0,T}^2\\&\qquad +\, h_{T}^2\vert \varvec{f}-\tilde{{\mathcal P}}_{T}^l(\varvec{f})\vert _{1,T}^2\\&\quad \le C h^{2(k+2)}\sum _{T\in {\mathcal T}_h}\Vert \varvec{f}\Vert ^{2}_{k+2,T}, \end{aligned}$$

which corresponds to a higher order term as well. This inequality and (4.16) finalize the proof of Theorem 4.2.

5 Numerical results

In what follows, we present four numerical examples illustrating the performance of the FE methods described in Sect. 3, and which confirm the theoretical error bounds. Individual errors are denoted by

$$\begin{aligned} E_0(\omega ):= & {} \Vert \omega -\omega _h\Vert _{0,\Omega },\quad E_1(\omega ):=|\!|\!| \omega -\omega _h |\!|\!|_{1,\Omega },\quad E_{\mathop {\mathrm {div}}\nolimits }(\varvec{u}):=\Vert \varvec{u}-\varvec{u}_h\Vert _{\mathrm {H}(\mathop {\mathrm {div}}\nolimits ;\Omega )},\\ E_0(p):= & {} \Vert p-p_h\Vert _{0,\Omega }. \end{aligned}$$

In the numerical tests, we study the accuracy of the discretization by observing these errors on successively refined non-uniform partitions of $\Omega$. Convergence rates are defined as usual

$$\begin{aligned} r(\cdot ):=\frac{\log (E(\cdot )/\hat{E}(\cdot ))}{\log (h/\hat{h})}, \end{aligned}$$

(5.1)

where E and $\hat{E}$ denote errors associated to two consecutive meshes of sizes h and $\hat{h}$. The linear systems arising from the discrete formulations (3.4) and (3.21) have been solved using the multifrontal massively parallel sparse direct solver MUMPS [5].

5.1 Test 1: mesh convergence with respect to the Bercovier–Engelman solutions

As numerical validation of the convergence properties of our method, we first consider $\Omega =(0,1)^2$, and $\Gamma =\partial \Omega$, $\nu =0.01$, $\sigma =0.1$, and choose the data $\varvec{f},\varvec{b},\omega _0$ so that the solution of the problem is given by the Bercovier–Engelman functions [11]

$$\begin{aligned} \omega (x,y)&={\sqrt{\nu }}\, 256[x^2(x-1)^2(6y^2-6y+1) +y^2(y-1)^2(6x^2-6x+1)],\\ \varvec{u}(x,y)&=\begin{pmatrix} -256x^2(x-1)^2y(y-1)(2y-1)\\ 256y^2(y-1)^2x(x-1)(2x-1)\end{pmatrix}, \quad p(x,y)=(x-1/2)(y-1/2), \end{aligned}$$

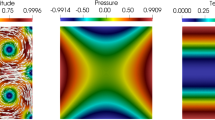
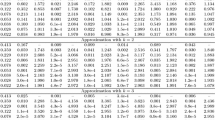
which are smooth in $\Omega$. Table 1 summarizes the convergence behaviour of two mixed finite element families corresponding to $k=0$ and $k=1$. Both mixed methods associated to different polynomial degrees attain optimal rates of convergence of order $O(h^{k+1})$ for vorticity in the $\mathrm {H}^1(\Omega )$-norm, for velocity in the ${\mathrm {H}(\mathrm {div};\Omega )}$-norm, and for pressure in the $\mathrm {L}^2(\Omega )$-norm as predicted by the theory. In addition, we observe that the vorticity $\omega _h$ converges with order $O(h^{k+2})$ to $\omega$ in the $\mathrm {L}^2(\Omega )$-norm. The last column of Table 1 illustrates that the velocity is practically divergence free for all refinement steps, and for both $k=0$ and $k=1$. Approximate solutions computed with a $\mathbb {RT}_1-\mathbb {P}_2-\mathbb {P}_1$ family on a mesh of 134,162 elements and 67,700 vertices are provided in Fig. 1. The same convergence rates have been observed on a set of additional tests with decreasing viscosity (down to $\nu =1$e$-$20), confirming the robustness of the method with respect to $\nu$. The case of varying $\sigma$ is postponed to Test 3, below.

Table 1 Test 1: convergence history for the mixed $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ (top rows) and $\mathbb {RT}_1-\mathbb {P}_2-\mathbb {P}_1$ (bottom rows) FE approximations of velocity–vorticity–pressure according to the Bercovier–Engelman test, on a sequence of non-uniformly refined triangulations of the unit square

Fig. 1

Test 1: approximated velocity field and velocity magnitude (top), vorticity (bottom left), and computed pressure (bottom right) with a $\mathbb {RT}_1-\mathbb {P}_2-\mathbb {P}_1$ family for the Bercovier–Engelman solutions to the generalized Stokes problem with $\sigma =0.1$, computed on an unstructured mesh of 134,162 elements and 67,700 vertices

5.2 Test 2: flow past a cylinder

Our next example focuses on the simulation of steady channel flow around a cylinder and confined between two parallel plates. The radius of the cylinder is $R=0.1$, and the length and height of the channel are $L=0.82,\,H=0.41$, respectively. The geometry and setting of the problem allows to consider the two-dimensional domain $\Omega =(0,L)\times (0,H){\setminus } B_R(x_c,y_c)$, where $B_R(x_c,y_c)$ is the disk of radius R centered in $(x_c,y_c)=(0.2,0.2)$ (see Fig. 2). There we also sketch the boundaries, where we specify the following data. On $\Gamma$ (left, top, bottom and “cylinder surface” boundaries) we set normal velocities and vorticity as

$$\begin{aligned}&\varvec{u}\cdot \varvec{n}=\varvec{b}\cdot \varvec{n},\quad \text {with } \varvec{b}(x,y)={\left\{ \begin{array}{ll} \varvec{0}&{} \text {on } \Gamma _{\mathrm {circ}},\\ \biggl (\frac{\displaystyle 4u_{\max }y(H-y)}{\displaystyle H^2},0\biggr )^\mathtt{t} &{} \text {on } \Gamma _{\mathrm {top}},\Gamma _{\mathrm {bot}},\Gamma _{\mathrm {left}}, \end{array}\right. }\\&\omega =\omega _0(x,y)=\sqrt{\nu }\,\mathop {\mathrm {rot}}\nolimits \varvec{b}={\left\{ \begin{array}{ll} 0 &{}\quad \! \text {on } \Gamma _{\mathrm {circ}},\\ \frac{\displaystyle -4\sqrt{\nu }\,u_{\max }(H-2y)}{\displaystyle H^2} &{}\quad \! \text {on } \Gamma _{\mathrm {top}},\Gamma _{\mathrm {bot}},\Gamma _{\mathrm {left}}, \end{array}\right. }\end{aligned}$$

and on $\Sigma$ (right boundary) we set zero tangential velocities and zero pressure

$$\begin{aligned} \varvec{u}\cdot \varvec{t}=\varvec{a}\cdot \varvec{t}=0,\quad \text {with }\varvec{a}(x,y) =\biggl (\frac{4u_{\max }y(H-y)}{H^2},0\biggr )^\mathtt{t},\quad p=p_0(x,y)=0. \end{aligned}$$

Table 2 Test 2: experimental convergence of the mixed $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ FE approximation of the steady flow around a cylinder with respect to a reference solution $(\varvec{u}_\mathrm {r},\omega _\mathrm {r},p_\mathrm {r})$ computed on a highly refined grid

We choose $u_{\max }=1.5$, $\nu =1$e$-$4, $\sigma =0.01$ and the approximate solutions obtained on a triangular mesh of 157,798 elements and 79,499 vertices (representing 474,594 degrees of freedom for the lowest order $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ family of finite elements) are presented in Fig. 3. In the lack of a known exact solution, we compute the $L^\infty$-norm of the velocity, and errors in different norms and on successively refined grids, with respect to a reference solution obtained on a highly refined mesh. These are reported in Table 2.

Fig. 2

Test 2: sketch of the geometry employed in the simulation of steady flow past a cylinder

Fig. 3

Test 2: approximated velocity field and velocity magnitude (top), vorticity (bottom left), and computed pressure (bottom right) with a $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ family for the steady flow past a cylinder

5.3 Test 3: The lid-driven cavity flow

In this example, we perform the classical lid-driven cavity test where we model the steady flow of an immiscible fluid in a box. The domain is again the unit square $\Omega =(0,1)^2$ and we consider an unstructured mesh with 81,738 elements. We first fix $\sigma =1$e$-$4, $\nu =0.001$, and take $\Gamma$ as the bottom, right, and left boundaries, and $\Sigma$ is the top lid of the domain. In this test the boundary conditions are not covered by the present analysis: on $\Gamma$ we set $\varvec{u}\cdot \varvec{n}=0$, whereas on $\Sigma$ we set $\varvec{u}\cdot \varvec{t}=1$, however the approximate velocities, pressure and vorticity (displayed in Fig. 4) remain stable and corner singularities are well resolved. Moreover, to assess the robustness of the method with respect to the choice of $\sigma$, we run several tests keeping fixed $\nu =0.001$ and varying $\sigma$ over several orders of magnitude. Plots of streamlines for each case are depicted in Fig. 5, confirming the stability of the approximations in all cases.

Fig. 4

Test 3: approximated velocity components (top), vorticity (bottom left), and computed pressure (bottom right) with a $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ family for the lid-driven cavity test

Fig. 5

Test 3: computed streamlines for different values of $\sigma$, obtained with a $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ approximation of the lid-driven cavity test

5.4 Test 4: Flow into a backwards facing step

Another classical benchmark test for Stokes and Navier–Stokes problems is the backwards facing step. In this example, the geometry consists on a channel of total height 2H and length 9H, with a backwards facing step of height is $H = 1$, where the reentrant corner is located at (H, H). No external forces are applied, whereas boundary data are set as follows: at the inlet region (left boundary) we impose a Poiseuille inflow (normal) velocity $\varvec{u}\cdot \varvec{n}=u_{\max }-\frac{1}{2}(y-\frac{3}{2}H)^2$ and a compatible vorticity $\omega _0=\sqrt{\nu }(y-\frac{3}{2}H)$, where the maximum speed of the inflow is $u_{\max } = 0.125$. At the outlet (right face) we apply a constant pressure $p_0=0$, and on the remaining segments conforming $\partial \Omega$ we impose slip velocity conditions ($\varvec{u}\cdot \varvec{n}=0$) and zero vorticity $\omega _0=0$. We generate an unstructured mesh consisting of 226,462 triangles and 113,202 vertices, and the model parameters are chosen to be $\sigma =\nu =0.0001$. Approximate solutions obtained with a $\mathbb {BDM}_1-\mathbb {P}_2-\mathbb {P}_0$ family are reported in Fig. 6, where some expected phenomena well-documented in the literature (including corner singularities, fluid recirculation zone, and vortex generation), can be observed.

Fig. 6

Test 4: velocity components (top panels), velocity vectors (middle left), zoomed velocity streamlines on the left bottom part of the channel (middle right panel), vorticity (bottom left) and pressure distribution (bottom right), computed with a $\mathbb {BDM}_1-\mathbb {P}_2-\mathbb {P}_0$ approximation for a generalized Stokes flow into a backwards facing step

5.5 Test 5: a posteriori error estimation

We close this section by numerically testing the efficiency of the a posteriori error estimator (4.1) and applying mesh refinement according to the local value of the indicator. In this case the convergence rates are no longer defined as in (5.1), but we consider instead

$$\begin{aligned} r(\cdot ):=\frac{\log (E(\cdot )/\hat{E}(\cdot ))}{- \frac{1}{2}\,\log (N/\hat{N})}, \end{aligned}$$

where N and $\hat{N}$ denote the corresponding degrees of freedom at each triangulation. We recall the definition of the so-called effectivity index as the ratio between the total error and the global error estimator, i.e.,

$$\begin{aligned} \mathtt{e}:= \{[E_{\mathop {\mathrm {div}}\nolimits }(\varvec{u})]^2+[E_1(\omega )]^2+[E_0(p)]^2\}^{1/2}, \quad \mathtt{r}:= \frac{\log (\mathtt{e}/\hat{\mathtt{e}})}{- \frac{1}{2}\,\log (N/\hat{N})}, \quad \mathtt{eff}:= \frac{\mathtt{e}}{\varvec{\theta }}. \end{aligned}$$

Here we employ $\mathbb {RT}_0$ approximations for velocities, piecewise linear elements for vorticity, and piecewise constant approximations for the pressure field. The computational domain is the nonconvex L-shaped domain $\Omega =(-1,1)^2{\setminus }(0,1)^2$, where problem (1.1) admits the following exact solution

$$\begin{aligned} \varvec{u}(x,y)&=\begin{pmatrix} -\pi \sin (\pi x)\cos (\pi y)\\ \pi \cos (\pi x)\sin (\pi y)\end{pmatrix}, \quad \omega (x,y)=-2\sqrt{\nu }\,\pi ^2\sin (\pi y)\sin (\pi x),\\ p(x,y)&=\frac{1-x^2-y^2}{(x-c)^2+(y-c)^2}-\int _{\Omega }\frac{1-x^2-y^2}{(x-c)^2+(y-c)^2}\,\text{ d }x\,\text{ d }y, \end{aligned}$$

satisfying $\varvec{u}\cdot \varvec{n}=0$ and $\omega =\omega _0=0$ on $\Gamma =\partial \Omega$ (and therefore falling into the framework where the a posteriori error analysis of Sect. 4 is valid). Model parameters are set to $\sigma =0.1$, $\nu =0.01$, $c=0.05$ and we notice that the pressure is singular near the reentrant corner of the domain and so we expect hindered convergence of the approximations when a uniform (or quasi-uniform) mesh refinement is applied. Such a degeneracy of the optimal convergence rates is indeed observed from the first rows in Table 3. In contrast, if we apply a classical adaptive mesh refinement procedure (here based on an equi-distribution of the discrete error indicators, where the diameter of each element in $\mathcal {T}_{h_{i+1}}$, which is contained in a generic element $T\in \mathcal {T}_{h_i}$ in the new step of the algorithm, is proportional to the diameter of T times the ratio $\hat{\varvec{\theta }}_T/\varvec{\theta }_T$, where $\hat{\varvec{\theta }}_T$ is the mean value of the estimator over $\mathcal {T}_h$, see also [1, 24, 39]) from the bottom rows of Table 3 we observe a recovering of the optimal convergence rates as predicted by the theory and a more stable effectivity index associated to the global error indicator. The resulting meshes after a few adaptation steps are reported in Fig. 7. We observe intensive refinement near the reentrant corner of the domain and a slight refinement near the zones of high vorticity and velocity gradients. Approximate solutions rendered on a fine mesh of 45,789 triangles and 28,765 vertices are presented in Fig. 8, where we can observe well-resolved profiles for all fields. As in Test 1, we have also performed a series of simulations considering a very small viscosity (down to $\nu =1$e$-$20). Again the method performs well, the accuracy is maintained, and the effectivity indexes remain stable.

Fig. 7

Test 5: snapshots of four grids adaptively refined according to the a posteriori error indicator defined in (4.1)

Fig. 8

Test 5: approximated velocity components (top), vorticity (bottom left), and computed pressure (bottom right) with a $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ family on an adaptive mesh for the L-shaped domain

Table 3 Test 5: convergence history, free-divergence of velocity, and effectivity indexes for the mixed $\mathbb {RT}_0-\mathbb {P}_1-\mathbb {P}_0$ FE approximations of velocity–vorticity–pressure computed on a sequence of quasi-uniformly (top rows) and adaptively (bottom rows) refined triangulations of the L-shaped domain

6 Concluding remarks

In this work, we have presented a mixed finite element method for the discretization of the vorticity–velocity–pressure formulation of the Brinkman equations. The key features of the proposed method are the liberty to choose different inf-sup stable finite element families, the direct and accurate access to vorticity without invoking any kind of postprocessing, the exactly divergence-free approximation of the velocity field, the proposed scheme has a computational cost which is comparable with those of other low-order schemes, and a natural analysis in the framework of the classical Babuška–Brezzi theory. We derived optimal convergence rates (and robust with respect to viscosity) in the natural norms. An a posteriori error analysis has been carried out, and some numerical tests have been presented to confirm the theoretically predicted decay of the error, and to illustrate the robustness, reliability and efficiency of the proposed method. We consider these capabilities as of great interest and foresee the application of the same framework in the study of some extensions, including: (a) the three-dimensional case, and (b) the coupling with Darcy flow and with transport phenomena.

Regarding (a), the same analysis carried out here applies if the structure of the embeddings can still be placed in the framework of Theorem 2.1. This is actually the case if the vorticity $\varvec{\omega }$ (in 3D, a vector field) would live in $\mathbf {H}(\mathop {\mathbf {curl}}\nolimits ;\Omega )$ (see e.g. the trace properties and Green formulas satisfied by the curl operator collected in [31, Sect. 2.3]). Therefore, according to the problem formulation the potential function $\mathop {\mathbf {curl}}\nolimits \varvec{\omega }$ would be uniquely defined if we restrict the vorticity space to $\mathbf {H}_0(\mathop {\mathbf {curl}}\nolimits ;\Omega )=\{\varvec{v}\in \mathbf {H}(\mathop {\mathbf {curl}}\nolimits ;\Omega ):\varvec{v}\times \varvec{n}=\varvec{0} \text { on }\Gamma \}$. The stability of the Galerkin approximation (here relying on Theorem 3.1) will then require that the curl of the finite element space for the approximation of vorticity be a subset of the space of velocity approximation. Therefore local edge elements of Nédélec type and Raviart–Thomas elements could be used for vorticity-velocity (see for instance, the recent augmented formulation of Brinkman equations coupled to Darcy flow introduced and analyzed in [2]). Nevertheless, the case of Dirichlet boundary data for velocity cannot be analyzed using the same tools without compromising the regularity of solutions and the convergence of the mixed approximations, as discussed in [9] for the approximation of the vector Laplacian, and in [38] for Brinkman equations.

With respect to generalization (b), we point again to [2], but we have in mind fully mixed approximations with different interface conditions between the viscous and porous domains.