Abstract
The present article introduces, mathematically analyzes, and numerically validates a new weak Galerkin mixed finite element method based on Banach spaces for the stationary Navier–Stokes equation in pseudostress–velocity formulation. Specifically, a modified pseudostress tensor, which depends on the pressure as well as the diffusive and convective terms, is introduced as an auxiliary unknown, and the incompressibility condition is then used to eliminate the pressure, which is subsequently computed using a postprocessing formula. Consequently, to discretize the resulting mixed formulation, it is sufficient to provide a tensorial weak Galerkin space for the pseudostress and a space of piecewise polynomial vectors of total degree at most ’k’ for the velocity. Moreover, the weak gradient/divergence operator is utilized to propose the weak discrete bilinear forms, whose continuous version involves the classical gradient/divergence operators. The well-posedness of the numerical solution is proven using a fixed-point approach and the discrete versions of the Babuška–Brezzi theory and the Banach–Nečas–Babuška theorem. Additionally, an a priori error estimate is derived for the proposed method. Finally, several numerical results illustrating the method’s good performance and confirming the theoretical rates of convergence are presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Scope
In recent decades, there has been a growing interest in developing approximation techniques based on general polygonal or polyhedral meshes, such as hybrid high-order (HHO) methods [13, 22], virtual element methods (VEMs) [5, 6], weak Galerkin (WG) methods (or weak Galerkin finite element methods) [54, 55], etc. Here we focus specifically on the weak Galerkin methods in more details. The Weak Galerkin finite element method, introduced by Wang and Ye in [54] for second-order elliptic problems, is a novel numerical technique for PDEs that approximates differential operators in the variational formulation using a framework that mimics the theory of distributions for piecewise polynomials. This innovation enables WG methods to provide multiple benefits, such as significant flexibility in polynomial approximations and mesh generation. Additionally, carefully-designed stabilizers compensate for the usual regularity of the approximating functions. Indeed, WG method may be viewed as a type of discontinuous Galerkin (DG) finite element method in some perspectives. However, unlike traditional DG methods, WG method produces more straightforward schemes and does not require the selection of sufficiently large parameters specified in the stabilization term. Moreover, by selecting appropriate function spaces for the weak functions, some WG method variants do not even need penalty terms (see e.g., [2, 58]). These advantages have led to WG methods being successfully applied to a variety of problems: Brinkman equations [47, 48, 62], Stokes equations [19, 46, 57], Navier-Stokes equations [44, 49, 59,60,61], Poisson-Nernst-Planck systems [36, 43], Boussinesq problem [24], coupled Cahn-Hilliard-Navier–Stokes phase-field model [36], etc. Several other notable works can be found in [38, 41, 50, 56] and references therein that deal with WG methods for Maxwell, Biot and elasticity equations.
On the other hand, to date, extensive mathematical studies have been carried out to solve the nonstationary Navier–Stokes equation [3, 33,34,35, 39, 42] and its coupling with other equations [1, 20, 23, 25] due to its extensive applications in physics, chemistry, and engineering. However, most of these works are from the classical families of finite elements which are based on velocity-pressure formulation and thus are not conservative methods. To overcome this issue of non-conservativity, numerous researchers have adopted alternative discretization techniques, including Finite Volumes and Discontinuous Galerkin methods, etc (see e.g., [11, 12, 52]). Recently, some researchers have developed one type of conservative classical approach by means of mixed finite element methods in the pseudostress–velocity-based formulations for flow problems (see for instance [14,15,16,17,18, 29, 30], and the references therein). In particular, in [28], a dual-mixed approach that proposes the velocity gradient tensor as the main unknown of the system is extended for solving the Navier–Stokes equations. In [16] the authors proposed and analyzed a new momentum conservative mixed finite element method for the Navier-Stokes problem posed in nonstandard Banach space. The approach in [16] involves introducing a pseudostress tensor relating the velocity gradient with the convective term, leading to a mixed formulation in pseudostress tensor and the velocity terms. Furthermore, they provide a solvability and convergence analysis, specifically demonstrating that the error decays with the optimal rate of convergence. Recently, Gatica et al. in [31] and Gharibi in [37] extended the conservative mixed FEM approach introduced in [16], adapting it to mixed virtual element and weak Galerkin frameworks for solving the Navier–Stokes and Brinkman equations, respectively.
According to the above discussion and aiming to broaden the application of the mixed-WG method to nonlinear fluid mechanics models, we now extend the novel approach proposed in [37] for the Brinkman equations, to address the Navier-Stokes problem. More precisely, we are particularly interested in the development of mixed formulations not involving any augmented terms (see e.g. [14, 15]). To this end, we now extend the applicability of the approach employed in [16] for the fluid model, in the framework weak Galerkin method. In fact, instead of using the primal or dual-mixed formulation of weak Galerkin method (see e.g. [36, 55]), we now employ a modified mixed formulation and adapt the approach from [37] to propose, up to our knowledge by the first time, a weak Galerkin mixed-FEM for Navier–Stokes, which consists of introducing the gradient of velocity and a vector version of the Bernoulli tensor as further unknowns. In this way, besides eliminating the pressure, which can be approximated later on via postprocessing, the resulting mixed variational formulation does not need to incorporate any augmented term, and it yields basically the same Banach saddle-point structure.
1.2 Outline and Notations
The remainder of the paper is organized as follows. In Sect. 2, we introduce the model of interest by referring to Ref. [16], summarize the dual-mixed variational formulation with the unknowns \({\varvec{\sigma }}\) and \({{\textbf{u}}}\) in appropriate Banach spaces, and present the main result demonstrating its well-posedness. We then introduce the WG discretization in Sect. 3, following Refs. [55] and [36]. This section comprises four main parts: first, we state basic assumptions on the mesh; second, we define the local WG space, projections, and weak differential operators; third, we discuss their approximation properties; and fourth, we derive the global WG subspace and the disceret scheme. In Sect. 4, we analyze the solvability of our discrete scheme using a fixed-point strategy. To accomplish this, we derive common estimates for the bilinear and trilinear forms, as well as the discrete inf-sup condition, so that the classical Banach theorem, along with the Babuška-Brezzi theory in Banach spaces, allows us to conclude, under a smallness assumption on the data, the existence of a unique solution. Sect. 5 is dedicated to deriving a priori error estimates for the numerical solution under a small data assumption. Finally, in Sect. 6, we present some numerical experiments to confirm the theoretical correctness and effectiveness of the discrete schemes.
For any vector fields \( {\textbf{v}}=(v_1, v_2)^\texttt {t} \) and \( {\textbf{w}}=(w_1, w_2)^\texttt {t} \), we set the gradient, divergence and tensor product operators as
respectively. In addition, denoting by \({\mathbb {I}}\) the identity matrix of \(\textrm{R}^2\), for any tensor fields \({\varvec{\tau }}=(\tau _{ij}),~{\varvec{\zeta }}=(\zeta _{ij})\in \textrm{R}^{2\times 2}\), we write as usual
which corresponds, respectively, to the transpose, the trace, and the deviator tensor of \( {\varvec{\tau }}\), and to the tensorial product between \( {\varvec{\tau }}\) and \( {\varvec{\zeta }}\).
Throughout the paper, given a bounded domain \(\Omega \), we let \({\mathcal {O}}\) be any given open subset of \(\Omega \). By \((\cdot , \cdot )_{0,{\mathcal {O}}}\) and \(\Vert \cdot \Vert _{0,{\mathcal {O}}}\) we denote the usual integral inner product and the corresponding norm of \(\textrm{L}^{2}({\mathcal {O}})\), respectively. For positive integers m and r, we shall use the common notation for the Sobolev spaces \(\textrm{W}^{m,r}({\mathcal {O}})\) with the corresponding norm and semi-norm \(\Vert \cdot \Vert _{m,r,{\mathcal {O}}}\) and \(\vert \cdot \vert _{m,r,{\mathcal {O}}}\), respectively; and if \(r=2\), we set \(\textrm{H}^{m}({\mathcal {O}}):=\textrm{W}^{m,2}({\mathcal {O}})\), \(\Vert \cdot \Vert _{m,{\mathcal {O}}}:=\Vert \cdot \Vert _{m,2,{\mathcal {O}}}\) and \(\vert \cdot \vert _{m,{\mathcal {O}}}:=\vert \cdot \vert _{m,2,{\mathcal {O}}}\). Furthermore, \({{\textbf {M}}}\) and \({\mathbb {M}}\) represent corresponding vectorial and tensorial counterparts of the scalar functional space \(\textrm{M}\). On the other hand, given \(t\in (1,+\infty )\), letting \( {\text {\textbf{div}}} \) be the usual divergence operator \( {\text {div}} \) acting along the rows of a given tensor, we introduce the standard Banach space
equipped with the usual norm
2 The Model Problem and its Continuous Formulation
Consider a spatial bounded domain \(\Omega \subset {\mathbb {R}}^{d}\) (\(d=2,3\)) with a Lipschitz continuous boundary \(\partial \Omega \) with outward-pointing unit normal \({\textbf{n}}\). We focus on solving the Navier–Stokes equation with viscosity \(\nu \), where, given the body force term \({{\textbf {f}}}\in {{\textbf {L}}}^{2}(\Omega )\) and suitable boundary data \({\textbf{g}}\in {{\textbf {H}}}^{1/2}(\partial \Omega )\), the objective is to find a velocity field \({\textbf{u}}:\Omega \rightarrow {\textbf{R}}\) and a pressure field \(p:\Omega \rightarrow \textrm{R}\) such that
In addition, in order to guarantee uniqueness of the pressure, this unknown will be sought in the space
Note that due to the incompressibility of the fluid (see the second row of (2.1)), \({\textbf{g}}\) must satisfy
For the subsequent analysis, we assume that the coefficient \(\nu \) is piecewise constant and positive.
Next, to obtain a velocity-pseudostress formulation, the first step is to rewrite equation (2.1) so that stress and velocity are the only unknowns in the equation. To achieve this, we introduce a tensor field denoted by \({\varvec{\sigma }}\), represented as
where
In this way, by applying the trace operator to both sides of (2.3) and utilizing the incompressibility condition \({\text {div}}({\textbf{u}})=0\), one arrives at
which allows us to eliminate the pressure variable from the formulation. In turn, according to (2.4), the assumption (2.2) becomes
Hence, after substituting (2.3) back into (2.1) and combining the resulting equation with (2.5), we have the following problem, which contains the unknowns \({\varvec{\sigma }}\) and \({{\textbf{u}}}\).
Problem 1
(Model problem) Find \(\varvec{\sigma }:\Omega \rightarrow {\mathbb {R}}, {\textbf{u}}:\Omega \rightarrow {\textbf{R}}\) such that
supplied with the following boundary condition
Next, to derive a velocity-pseudostress-based mixed formulation for Problem 1, we let \({\mathbb {X}}\) and \({\textbf{Y}}\) be the corresponding test spaces. We then proceed to multiply the first and second equations of Problem 1 by \({\varvec{\tau }}\) and \({{\textbf{v}}}\), respectively, and use the fact that \({\textrm{tr}}({\varvec{\tau }}^{\texttt{d}})=0\) to obtain
and
it is easy to notice that, thanks to Cauchy–Schwarz’s inequality, the first term on the left-hand side of (2.6) makes sense for \( {\varvec{\sigma }},{\varvec{\tau }}\in {\mathbb {L}}^{2}(\Omega ) \). In turn, regarding the term on the right-hand side of (2.6), assuming originally that \( {{\textbf{u}}}\in {\textbf{H}}^{1}(\Omega ) \), and given \( t,t'\in (1,\infty ) \), conjugate to each other, we can integrate by parts with \({\varvec{\tau }}\in {\mathbb {H}}({\textbf{div}}_t;\Omega )\), so that using the Dirichlet boundary condition provided in Problem 1, we obtain
where \(\langle \cdot ,\cdot \rangle \) stands for the duality \((\textbf{H}^{-1/2}(\partial \Omega ),{\textbf{H}}^{1/2}(\partial \Omega )\big )\). Now, from the first term on the right-hand side of the foregoing equation, along with the Sobolev embedding \( {\textbf{H}}^{1}(\Omega ){\hookrightarrow } {\textbf{L}}^{t'}(\Omega ) \), we realize that it actually suffices to look for \({{\textbf{u}}}\in {\textbf{L}}^{t'}(\Omega )\). However, it is clear from (2.6) that its second term is well-defined if \({{\textbf{u}}}\in {\textbf{L}}^{4}(\Omega )\), which yields \(t'= 4\) and thus \(t = 4/3\).
At this point, in order to deal with the null mean value of \( {\textrm{tr}}({\varvec{\sigma }}) \) (cf. third row of Problem 1), we introduce the subspace of \( {\mathbb {H}}({\textbf{div}}_{4/3};\Omega ) \) given by
Then, testing the new (2.6) against \( {\varvec{\tau }}\in {\mathbb {H}}({\text {\textbf{div}}}_{4/3};\Omega ) \) is equivalent to doing it against \( {\varvec{\tau }}\in {\mathbb {H}}_0({\text {\textbf{div}}}_{4/3};\Omega ) \), and taking into account the above discussion, we define the testing spaces as
and
Let us introduce the following bilinear (and trilinear) forms
and the linear functionals (associated to given data)
Then, with these forms at hand, the variational formulation of Problem 1 reads as follows:
Problem 2
Find the tensor \(\varvec{\sigma }\in {\mathbb {X}}\) and the velocity \({\textbf{u}}\in {\textbf{Y}}\) such that
The solvability result concerning Problem (2) is established as follows.
Theorem 2.1
Let \(\delta >0\) be the constant related to the inf-sup condition of the linear part of the left-hand side of Problem 2 (cf. Ref. [16, Eq. (3.29)]) and \(c_{g}\) be the upper bound of \({\mathcal {G}}(\cdot )\), define the ball
and assume that the given data satisfy
Then, there exists a unique solution \(({\varvec{\sigma }},{\textbf{u}})\in {\mathbb {X}}\times \widehat{{\textbf{Y}}}\) for Problem 2, and there holds the following stability estimate
Proof
See [16, proof of Theorem 3.8]. \(\square \)
3 Weak Galerkin Approximation
This section aims to introduce the weak Galerkin spaces and the discrete bilinear forms essential for introducing a weak Galerkin mixed FEM scheme.
3.1 Various Tools in Weak Galerkin Method
A fundamental aspect of the weak Galerkin method is the use of uniquely defined weak derivatives instead of traditional derivative operators. Our emphasis here is on the weak divergence operator, which is a crucial step in introducing our weak Galerkin technique. To facilitate this discussion, we begin with an overview of the mesh structure.
Mesh notation. Let \({\mathcal {K}}_{h}=\{K\}\) be a partition of domain \(\Omega \) that consists of arbitrary polygonal/polyhedral elements, where the mesh size \(h=\max \{h_{K}\}\), \(h_{K}\) is the diameter of element K. Assume that the partition \({\mathcal {K}}_{h}\) is WG shape regular - defined by a set of conditions as detailed in [55]. The interior and the boundary of any element \(K\in {\mathcal {K}}_{h}\), are represented by \(K^{0}\) and \(\partial K\), respectively. Denote by \({\mathcal {E}}_{h}\) the set of all edges/faces in \({\mathcal {K}}_{h}\), and let \({\mathcal {E}}_{h}^{0}={\mathcal {E}}_{h}\backslash \partial \Omega \) be the set of all interior edges/faces. Here is a set of normal directions on \( {\mathcal {E}}_{h}\):
Weak divergence operator and weak Galerkin space. It is well known that the weak divergence operator is well-defined for weak matrix-valued functions \({\varvec{\tau }}=\{{\varvec{\tau }}_{0},{\varvec{\tau }}_{b}\}\) on the element K such that \({\varvec{\tau }}_{0}\in {\mathbb {L}}^{2}(K)\) and \({\varvec{\tau }}_{b}{\textbf{n}}_{e}\in {\textbf{H}}^{-1/2}(\partial K)\), where \({\textbf{n}}_{e}\in \textrm{D}_{h}|_{K}\). Components \({\varvec{\tau }}_{0}\) and \({\varvec{\tau }}_{b}\) can be understood as the value of function \({\varvec{\tau }}\) in \(K^{0}\) and on \(\partial K\), respectively. We follow [55, Section 3], and introduce for each \(K\in {\mathcal {K}}_{h}\) the local weak tensor space
The global space \({\mathbb {X}}_{\texttt{w}}\) is defined by gluing together all local spaces \({\mathbb {X}}_{\texttt{w}}(K)\) for any \(K\in {\mathcal {K}}_{h}\). Now, we define the weak divergence operator for matrix-valued functions as follows.
Definition 3.1
([54]) For any weak matrix-valued function \({\varvec{\tau }}\in {\mathbb {X}}_{\texttt{w}}(K)\) and element \(K\in {\mathcal {K}}_{h}\), the weak divergence operator, denoted by \({\text {\textbf{div}}}_{\texttt{w}}\), is defined as the unique vector-valued function \({\text {\textbf{div}}}_{\texttt{w}}({\varvec{\tau }})\in {\textbf{H}}^{1}(K)\) satisfying
Our focus will be on a subspace of \({\mathbb {X}}_{\texttt{w}}\) in which \(({\varvec{\tau }}_{b}|_{e})=({\varvec{\tau }}|_{e}{\textbf{n}}_{e}){\textbf{n}}_{e}\). On the other hand, discrete weak divergence operator can be introduced using a finite-dimensional space \({\mathbb {X}}_{h}\subset {\mathbb {X}}_{\texttt{w}}\), which will be stated in the next. First, for any mesh object \(\varpi \in {\mathcal {K}}_{h}\cup {\mathcal {E}}_{h}\) and for any \(r\in \textrm{N}\) let us introduce the space \(\textrm{P}_{r}(\varpi )\) to be the space of polynomials defined on \(\varpi \) of degree \(\le r\), with the extended notation \(\textrm{P}_{-1}(\varpi )=\{0\}\). Similarly, we let \({\textbf{P}}_{r}(\varpi )\) and \({\mathbb {P}}_{r}(\varpi )\) be the vectorial and tensorial versions of \(\textrm{P}_{r}(\varpi )\). In addition, the jump of \({\varvec{\tau }}=\{{\varvec{\tau }}_{0},{\varvec{\tau }}_{b}\}\) on edge/face \(e\in {\mathcal {E}}_h \) is given by
Then, given \( k\in \textrm{N}_0 \), we define for any \( K\in {\mathcal {K}}_h \) the local discrete weak Galerkin space
In addition, the global finite dimensional space \({\mathbb {X}}_{h}\), associated with the partition \({\mathcal {K}}_{h}\), is defined so that the restriction of every weak function \({\varvec{\tau }}_{h}\) to the mesh element K belongs to \({\mathbb {X}}_{h}(K)\). Furthermore, let \(\widetilde{{\mathbb {X}}}_{h}\) be a subspace of \({\mathbb {X}}_{h}\) consisting of functions with zero jump on each interior boundary, that is
Definition 3.2
([54]) For any \({\varvec{\tau }}_{h}\in {\mathbb {X}}_{h}(K)\) and element \(K\in {\mathcal {K}}_{h}\), the discrete weak divergence operator, denoted by \({\text {\textbf{div}}}_{\texttt{w,h}}\), is defined as the unique vector-valued polynomial \({\text {\textbf{div}}}_{\texttt{w,h}}({\varvec{\tau }}_{h})\in {\textbf{P}}_{k+1}(K)\) satisfying
On the other hand, for approximating the velocity unknowns we simply consider the piecewise polynomial space of degree up to \(k+1\):
L\(^{2}\)-orthogonal projections and approximation properties. For any \(r\in \) N and \( K\in {\mathcal {K}}_h \), we introduce L\(^{2}\)-projection operators  and \({\varvec{{\mathcal {P}}}}_{b,r}^{K}:{\textbf{L}}^{2}(\partial K)\rightarrow {\textbf{P}}_{r}(\partial K)\) which are type of interior and boundary, and are given by
and \({\varvec{{\mathcal {P}}}}_{b,r}^{K}:{\textbf{L}}^{2}(\partial K)\rightarrow {\textbf{P}}_{r}(\partial K)\) which are type of interior and boundary, and are given by

for all \(({\varvec{\tau }}, {\textbf{v}})\in {\mathbb {L}}^{2}(K)\times {\textbf{L}}^{2}(\partial K)\) and \((\widehat{{\textbf{q}}}_r,{\textbf{q}}_r) \in {\mathbb {P}}_{r}(K)\times {\textbf{P}}_{r}(\partial K)\).
Now, we introduce projection operator  into the tensorial weak Galerkin space \({\mathbb {X}}_{h}(K)\) as:
into the tensorial weak Galerkin space \({\mathbb {X}}_{h}(K)\) as:

Also, for each element \(K\in {\mathcal {K}}_h\) and function \({\varvec{\tau }}\in {\mathbb {X}}_{h}\), the global projection operator  on the space \({\mathbb {X}}_{h}\) is defined by
on the space \({\mathbb {X}}_{h}\) is defined by

The approximation properties of  and \( \varvec{{\mathcal {P}}}_{h} \) are stated as follows.
and \( \varvec{{\mathcal {P}}}_{h} \) are stated as follows.
Lemma 3.3
Let \({\mathcal {K}}_{h}\) be a finite element partition of \(\Omega \) satisfying the shape regularity assumptions \(\textbf{A1}\)-\(\textbf{A4}\) stated in [55]. Then, for \(k,s,m\in \textrm{N}_{0}\) such that \(m\in \{0,1\}\) there exist constants \(C_{1}, C_{2}\), independent on the mesh size h, such that


3.2 Weak Galerkin Scheme
In order to define our weak Galerkin scheme for Problem 2, we introduce, where necessary, the discrete versions of the bilinear forms and functionals involving the weak spaces. Following the usual procedure in the WG setting, their construction is based on weak derivatives to ensure computability for all weak functions. Notice that, for each \( {\varvec{\zeta }},{\varvec{\tau }}\in {\mathbb {X}}_h \) and \( {{\textbf{z}}},{{\textbf{w}}},{{\textbf{v}}}\in {\textbf{Y}}_h \), the quantities
are computable, while the bilinear form \( {\mathcal {B}}|_{{\mathbb {X}}_h\times {\textbf{Y}}_h} \) is not computable because it involves the divergence operator, which cannot be evaluated for weak functions. To overcome this matter, employing Definition 3.2 we define the discrete bilinear form \( {\mathcal {B}}_{h}^{K}: {\mathbb {X}}_{h}(K)\times {\textbf{P}}_{k+1}(K)\rightarrow \textrm{R}\) by
On the other hand, despite the computability of \( {\mathcal {A}}|_{{\mathbb {X}}_h\times {\mathbb {X}}_h} \), this form needs an additional stabilization term to achieve the well-posedness of our weak Galerkin scheme. More precisely, we define the corresponding discrete bilinear form as follows:
where \(\rho \) is the piecewise constant on \({\mathcal {K}}_h\) and the stabilization form \({\mathcal {S}}^{K}(\cdot ,\cdot ): {\mathbb {X}}_{h}(K)\times {\mathbb {X}}_{h}(K)\rightarrow \textrm{R}\) is given by
In addition, the global bilinear forms \({\mathcal {A}}_{h}\) and \({\mathcal {B}}_{h}\) can be derived by adding the local contributions, that is,
Finally, let us introduce the subspace of \(\widetilde{{\mathbb {X}}}_{h}\) as
Referring to the above space and the discrete bilinear forms provided by (3.9) and (3.8), the discrete weak Galerkin problem reads as follow.
Problem 3
Find \({\varvec{\sigma }}_h \in {\mathbb {X}}_{0,h}\) and \({\textbf{u}}_h \in {\textbf{Y}}_h\) such that
4 Solvability Analysis
The goal of this section is to establish the well-posedness of Problem 3. We start by analyzing the stability properties of the forms \({\mathcal {A}}_h\) and \({\mathcal {B}}_h\). Next, we introduce resolvent operators for each decoupled equations of Problem 3 and reformulate the problem as an equivalent fixed-point equation. Finally, we demonstrate that these operators are well-defined and use the classical Banach theorem, together with the Babuška–Brezzi theory in Banach spaces to conclude the solvability of Problem 3.
4.1 Stability Properties
We begin by equipping the approximate pair spaces \({\widetilde{{\mathbb {X}}}_{h}}\) and \({\textbf{Y}}_h+{\textbf{H}}^{1}(\Omega )\) with the following discrete norms, respectively (see e.g., [55])
and
Note that the above suggests the following norm on \(\widetilde{{\mathbb {X}}}_{h}\times {\textbf{Y}}_h \)
Next, we provide the following result which is a counterpart of [16, Lemma 3.1] for the weak divergence operator.
Lemma 4.1
There exists \({\hat{c}}_{\Omega }>0\) depends on \(\Omega \) but independent of mesh size, such that
Proof
We extend the proof [32, Lemma 2.3, Chapter 3] in the discrete framework. Indeed, by recalling from [7, third proposition of eq. (2.11)] that the divergence operator \({\textrm{div}}\) is an isomorphism from \({\mathcal {R}}_{k+1}^{\perp }\) to the whole \(\textrm{P}_{k}\), where
Then, given \({\varvec{\tau }}_h=\{{\varvec{\tau }}_{0h},{\varvec{\tau }}_{bh}\}\in {\mathbb {X}}_h\), by knowing \({\varvec{\tau }}_{0h}|_{K}\in {\mathbb {P}}_{k}(K) \) we have \({\textrm{tr}}({\varvec{\tau }}_{0h}|_{K})\in \textrm{P}_{k}(K)\) and therefore there exist a unique \({{\textbf{z}}}_{k+1}\in {\mathcal {R}}_{k+1}^{\perp }\) such that \({\textrm{div}}({{\textbf{z}}}_{k+1})\,=\,{\textrm{tr}}({\varvec{\tau }}_{0h})\) in K and
where \(c_{1}>0\) is a constant independent of \({{\textbf{z}}}_{k+1}\). Now, utilizing that fact \({\textrm{div}}({{\textbf{z}}}_{k+1})=\nabla {{\textbf{z}}}_{k+1}:{\mathbb {I}}\) and the definition of deviatoric, we have that
where in the third step we have used the definition of discrete weak divergence (cf. (3.4)). Note here that the first term on the right-hand side of the above equation vanishes due to the definition of \(\widetilde{{\mathbb {X}}}_h\). Hence, applying Cauchy–Schwarz and Hölder inequalities, Sobolev embedding \({\textbf{H}}^1{\hookrightarrow } {\textbf{L}}^4\) and then (4.3), we find that
which gives
This inequality and the fact that
complete the proof by letting \({\hat{c}}_\Omega \,:=\,2 c_1\max \{c_{\texttt{em}},1\}+1\). \(\square \)
Then, some properties of \( {\mathcal {A}}_h \) (cf. (3.9)) are established as follows.
Lemma 4.2
The discrete bilinear form \({\mathcal {A}}_h\) defined in (3.9), satisfies the following properties:
-
consistency: for any \(\varvec{\xi }\in {\mathbb {H}}^{1}(\Omega )\), we have that
$$\begin{aligned} {\mathcal {A}}_h({\varvec{\zeta }}_{h}, \varvec{\xi })\,=\,{\mathcal {A}}({\varvec{\zeta }}_{h}, \varvec{\xi })\qquad \forall \,{\varvec{\zeta }}_{h}\in {\mathbb {X}}_{h} . \end{aligned}$$ -
stability and boundedness: there exists a positive constant \(c_{{\mathcal {A}}}\), independent of K and h, such that:
$$\begin{aligned} \big |{\mathcal {A}}_{h}({\varvec{\zeta }}_{h},{\varvec{\tau }}_{h})\big |\,\le \, c_{{\mathcal {A}}} \,\Vert {\varvec{\zeta }}_{h}\Vert _{{\mathbb {H}},h}\,\Vert {\varvec{\tau }}_{h}\Vert _{{\mathbb {H}},h}\qquad \forall \,{\varvec{\zeta }}_{h},{\varvec{\tau }}_{h}\in {\mathbb {X}}_{h} , \end{aligned}$$(4.4)and let \(\widehat{{\mathbb {X}}}_{h}\) be the discrete kernel of the bilinear form \({\mathcal {B}}_h\). Then, there exists constant \(\alpha >0\), independent of K, such that
$$\begin{aligned} {\mathcal {A}}_{h}({\varvec{\tau }}_h,{\varvec{\tau }}_h)\,\ge \, \alpha \, \Vert {\varvec{\tau }}_h\Vert _{{\mathbb {H}},h}^{2}\qquad \forall \,{\varvec{\tau }}_h\in \widehat{{\mathbb {X}}}_{h}. \end{aligned}$$(4.5)
Proof
By considering \(\varvec{\xi }\in {\mathbb {H}}^{1}(\Omega )\) and \({\varvec{\zeta }}_{h}\in {\mathbb {X}}_{h}\) and employing the definition of the discrete form \({\mathcal {A}}_{h}\) (cf. (3.9)), along with the observation that the stabilization term (cf. (3.10)) vanishes when one of the components is sufficiently regular, we deduce the "consistency" property. Next, to verify the boundedness of \({\mathcal {A}}_h\), we use the Cauchy–Schwarz inequality and, in virtue of
This gives
We now aim to establish the ellipticity of \({\mathcal {A}}_h\) on the discrete kernel of \({\mathcal {B}}_{h}|_{{\mathbb {X}}_h\times {\textbf{Y}}_h}\), that is,
which, together with fact \({\text {\textbf{div}}}_{\texttt{w,h}}({\varvec{\tau }}_h)\in {\textbf{Y}}_h\) (cf. Definition 3.2) implies that
Therefore, employing Lemma 4.1 and the fact that \({\varvec{\tau }}_h\) is the weak divergence-free, we obtain
which together with setting \(c_{{\mathcal {A}}} \,=\,\max \left\{ \dfrac{1}{\nu },\rho \right\} \) and \(\alpha \,=\,\min \left\{ \dfrac{{\hat{c}}_{\Omega }}{\nu },\rho \right\} \) completes the proof. \(\square \)
To establish the discrete inf-sup condition for the bilinear form \({\mathcal {B}}_h\), we require a preliminary result, as stated in the following lemma.
Lemma 4.3
For any \({\varvec{\tau }}_{h}\in {\mathbb {X}}_{h}\) and \({\textbf{v}}_{h}\in {\textbf{Y}}_{h}\), we have
Proof
It straightforwardly follows from the definition of \({\mathcal {B}}_h\), as given in (3.8), and the application of the discrete divergence operator (cf. Definition 3.2). \(\square \)
We are now in a position to establish the discrete inf-sup condition for the bilinear from \({\mathcal {B}}_h\).
Lemma 4.4
There exists a positive constant \({\widehat{\beta }}\), independent of h, such that
Proof
In what follows, we proceed similarly to the proof of [55, Lemma 3.3]. In fact, given \({\textbf{v}}_h\in {\textbf{Y}}_h\), we set
which satisfies
On the other hand, we use the definition of the discrete norm \(\Vert \cdot \Vert _{{\mathbb {H}},h}\) to the above chosen \({\varvec{\tau }}_{h}:=\,\{{\varvec{\tau }}_{0h},{\varvec{\tau }}_{bh}\}\) and the trace inequality, to obtain
Combining the above result with (4.9) concludes the desired inequality (4.8) with setting \({\widehat{\beta }}:=\frac{1}{\sqrt{\max \{1,(1+{\mathcal {C}}_{\texttt{tr}}) \}}}\). \(\square \)
The boundness property of the discrete bilinear form \( {\mathcal {B}}_h \) (cf. (3.8)) is established as follows.
Lemma 4.5
The discrete bilinear form \({\mathcal {B}}_h(\cdot ,\cdot )\) is bounded in \({\mathbb {X}}_{h}\times {\textbf{Y}}_h\). In other words, there exists a positive constant \(c_{{\mathcal {B}}}\) such that
Proof
An application of Lemma 4.3 and Cauchy–Schwarz inequality, yields
Our aim is now to show that
To attain the aforementioned inequality, we employ the trace inequality, resulting
Substituting the above result back into (4.11) finishes the proof of lemma. \(\square \)
Then, knowing from Lemmas 4.2,4.4 and 4.5, that the pair of bilinear forms \(({\mathcal {A}}_h, {\mathcal {B}}_h)\) satisfies the hypotheses of the discrete Babuška-Brezzi theory (see, e.g. [26, Proposition 2.42]), straightforward application of this result yields the discrete inf-sup condition for the bilinear form \({\mathscr {A}}_h:({\mathbb {X}}_h\times {\textbf{Y}}_h)\times ({\mathbb {X}}_h\times {\textbf{Y}}_h)\rightarrow \textrm{R}\) defined by
In other words, there exists the positive constant \(\alpha _{{\mathscr {A}},\texttt{d}}\), depending on \(c_{{\mathcal {A}}}, c_{{\mathcal {B}}}, \alpha , {\widehat{\beta }}\), such that
Furthermore, the boundedness of the trilinear form \({\mathcal {C}}(\cdot ;\cdot ,\cdot )\) on \({\textbf{Y}}_{h}\times {\textbf{Y}}_{h}\times {\mathbb {X}}_{h}\) can be readily inferred by utilizing the Hölder inequality, the Sobolev embedding \({\textbf{H}}^1{\hookrightarrow }{\textbf{L}}^4\) and inequality (4.6), as follows:
4.2 The Fixed-Point Strategy
We begin by introducing the associated fixed-point operator for any \({{\textbf {z}}}_{h}\in {\textbf{Y}}_{h}\) as \({\textbf{S}}_{\texttt{d}}({{\textbf {z}}}_{h})\,=\,{{\textbf{u}}}_{\star ,h}\), where \(({\varvec{\sigma }}_{\star ,h},{{\textbf{u}}}_{\star ,h})\in {\mathbb {X}}_{0,h}\times {\textbf{Y}}_h\) is the solution of the linearized version of Problem 3, that is,
Equivalently, given \( {{\textbf{z}}}_h\in {\textbf{Y}}_h \), introducing the bilinear form \({\mathscr {A}}_{h,{{\textbf{z}}}_h}:({\mathbb {X}}_h\times {\textbf{Y}}_h)\times ({\mathbb {X}}_h\times {\textbf{Y}}_h)\rightarrow \textrm{R}\) given by
and the linear functional \( {\mathscr {F}}: {\mathbb {X}}_{h}\times {\textbf{Y}}_h\rightarrow \textrm{R} \) as
for all \( ({\varvec{\zeta }}_h,{{\textbf{w}}}_h), ({\varvec{\tau }}_{h},{{\textbf{v}}}_{h})\in {\mathbb {X}}_{h}\times {\textbf{Y}}_h \), the linearized problem (4.15) can be rewritten as
It can be observed that solving Problem 3 is equivalent to seeking a fixed point of \({{\textbf {S}}}_{\texttt{d}}\), that is: Find \({{\textbf {u}}}_h\in {\textbf{Y}}_h\) such that
Next, we utilize the discrete version of classical Banach–Nečas–Babuška theorem (see e.g, [26, Theorem 2.22]) to demonstrate that, for any arbitrary \({{\textbf {z}}}_h\in {\textbf{Y}}_h\), the problem (4.15) (or equivalently (4.18)) is well-posed, implying the well-definedness of \( {\textbf{S}}_{\texttt{d}} \).
The following lemma demonstrates the global discrete inf-sup condition for \({\mathscr {A}}_{h,{{{\textbf {z}}}}_{h}}\) on space \({\mathcal {V}}_{h}:={\mathbb {X}}_{h}\times {\textbf{Y}}_{h}\).
Lemma 4.6
For any \({\textbf{z}}_{h}\in {\textbf{Y}}_{h} \) such that
there holds
where \(\alpha _{{\mathscr {A}},\texttt{d}}\) is the positive constant in (4.13).
Proof
Bearing in mind the definition of \({\mathscr {A}}_{h,{{\textbf{z}}}_{h}}\) (cf. (4.16)) for each \({{\textbf{z}}}_h \in {\textbf{Y}}_h\), and combining (4.13) with the effect of the extra term given by \({\mathcal {C}}({{\textbf{z}}}_h;\cdot ,\cdot )\), which means invoking the upper bound provided by (4.14), we arrive at
from which, under the assumption (4.19) we arrive at (4.20), which ends the proof. \(\square \)
Now we ready to show that map \({\textbf{S}}_{\texttt{d}}\) is well-defined or equivalently problem (4.15) is uniquely solvable.
Lemma 4.7
Let the assumption of Lemma 4.6 be satisfied. Then, there exists a unique \(({\varvec{\sigma }}_{\star ,h}, {{\textbf{u}}}_{\star ,h})\in {\mathbb {X}}_h\times {\textbf{Y}}_h\) solution to problem (4.15). In addition, there holds
Proof
A straightforward application of the classical Babuška–Brezzi theory and Lemma 4.6 implies that problem (4.15) is well-posed. For the second part of proof, by combining (4.18) and Lemma 4.6 with considering \(({\varvec{\zeta }}_{h},{\textbf{w}}_{h}):=\,({\varvec{\sigma }}_{\star ,h},{{\textbf{u}}}_{\star ,h})\), we readily obtain
where the boundness of \({\mathscr {F}}\) was used in the last step, and this finishes the proof. \(\square \)
We continue the analysis by establishing sufficient conditions under which \({\textbf{S}}_{\texttt{d}}\) maps a closed ball of \({\textbf{Y}}_{h}\) into itself. Let us define the set
and state the following result.
Lemma 4.8
Assume that the data are sufficiently small so that
Then, \({\textbf{S}}_{\texttt{d}}(\widehat{{\textbf{Y}}}_{h})\subseteq \widehat{{\textbf{Y}}}_{h}\).
Proof
It deduces straightly from a priori estimate stated by (4.21). \(\square \)
We now address the continuity property of \( {\textbf{S}}_{\texttt{d}}\).
Lemma 4.9
For any \( {\textbf{z}}_h, {\textbf{y}}_h \in {\textbf{Y}}_h \), there holds
Proof
Given \({{\textbf{z}}}_{h}, {{\textbf{y}}}_{h}\in \widehat{{\textbf{Y}}}_{h}\) we let \({\textbf{S}}_{\texttt{d}}({{\textbf {z}}}_{h})={{\textbf{u}}}_{\star ,h}\) and \({\textbf{S}}_{\texttt{d}}({{\textbf {y}}}_{h})={{\textbf{u}}}_{\circ ,h}\), where \(({\varvec{\sigma }}_{\star ,h}, {{\textbf{u}}}_{\star ,h})\) and \(({\varvec{\sigma }}_{\circ ,h}, {{\textbf{u}}}_{\circ ,h})\) are the corresponding solutions of equation (4.18). It follows from (4.18) that
from which, according to the definitions of \({\mathscr {A}}_{h,{{\textbf{z}}}_{h}}\) and \({\mathscr {A}}_{h,{{\textbf{y}}}_{h}}\) (cf. (4.16)), we have
This result, combined with (4.12) by setting \(({\varvec{\zeta }}_{h},{{\textbf {w}}}_{h}):=({\varvec{\sigma }}_{\star ,h}-{\varvec{\sigma }}_{\circ ,h}, {{\textbf{u}}}_{\star ,h}-{{\textbf{u}}}_{\circ ,h})\), yields
Now, we apply the discrete global inf–sup condition (4.20) to the left-hand side of the above equation and utilize the estimates (4.14) and (4.21), to get
So, thanks to the above inequality, we arrive at
and thus ends the proof. \(\square \)
The main result of this section is summarized in the following theorem.
Theorem 4.10
Assume that, in addition to the hypothesis of Lemma 4.8, the data satisfy
Then, there exists a unique solution \(({\varvec{\sigma }}_{h},{\textbf{u}}_{h})\in {\mathbb {X}}_{0,h}\times {\textbf{Y}}_{h}\) for Problem 3. Moreover, there holds
Proof
The compactness of \({\textbf{S}}_{\texttt{d}}\) on space \(\widehat{{\textbf{Y}}}_{h}\) and the Lipschitz-continuity of \({\textbf{S}}_{\texttt{d}}\) are guaranteed by Lemmas 4.8 and 4.9, respectively. Hence, by applying the Banach fixed-point theorem directly to Problem 3, one can conclude its existence and uniqueness. Furthermore, the stability result (4.23) is derived straightly from (4.21) stated in Lemma 4.7. \(\square \)
5 Convergence Analysis
In this section, we are interested in deriving a priori estimate for errors
where \( ({\varvec{\sigma }},{{\textbf{u}}})\in {\mathbb {X}}\times {\textbf{Y}} \) with \( {{\textbf{u}}}\in \widehat{{\textbf{Y}}} \), is the unique solution of Problem 2, and \( ({\varvec{\sigma }}_{h},{{\textbf{u}}}_h)\in {\mathbb {X}}_{0,h}\times {\textbf{Y}}_h \) with \( {{\textbf{u}}}_h\in \widehat{{\textbf{Y}}}_h \) is the unique solution of Problem 3. As a byproduct of this, we also derive a priori estimate for \( \Vert p -p_h\Vert _{0,\Omega } \), where \( p_h \) is the discrete pressure computed according to the postprocessing formula suggested by (2.4), that is
To this end, we divide our result into suboptimal and optimal convergence for the velocity.
5.1 Suboptimal Convergence
We begin by introducing the following lemmas, which will play an essential role in the error analysis.
Lemma 5.1
(trace inequality) Assume that the partition \({\mathcal {K}}_h\) satisfies the shape regularity assumptions \(\textbf{A1}\)-\(\textbf{A4}\) stated in [55]. Then, there exists a constant \({\mathcal {C}}_{\texttt{tr}}\) such that for any \(K\in {\mathcal {K}}_h\) and edge/face \(e\subset \partial K\), we have
Proof
See [55, proof of Lemma A.3]. \(\square \)
Lemma 5.2
(inverse inequality) Let \(K\subset \textrm{R}^d\) be a d-simplex which has diameter \(h_K\) and is shape regular. Assume that p and q be non-negative integers such that \(p\le q\). Then, there exists a constant \({\mathcal {C}}_{\texttt{inv}}\) such that
for any polynomial \(\varrho \) of degree no more than k.
Lemma 5.3
For \({\varvec{\sigma }}\in {\mathbb {H}}^{r+1}(\Omega )\) and \(r\in N\) such that \(r\le k\), there exist positive constants \( C_0 \) and \(C_{\texttt{s}}\) such that
and

for all \({\varvec{\tau }}_{h}\in {\mathbb {X}}_{h}\)
Proof
The result follows by proceeding analogously to the proof of [36, eqs. (33) and (34)] for the vector version. We omit further details. \(\square \)
Thanks to the projection error estimate stated in Lemma 3.3, we only need to analyze the error functions defined by

On the other hand, as the primary step in convergence analysis, we derive the error equation as follows.
-
For any \({\varvec{\tau }}_{h}\in {\mathbb {X}}_{h}\), from the first equation of Problem 2, we deduce

We test the first equation of Problem 1, i.e., \({\varvec{\sigma }}^{\texttt{d}}+({\textbf{u}}\otimes {\textbf{u}})^{\texttt{d}}-\nu \varvec{\nabla } {\textbf{u}}={{\textbf {0}}}\) against \({\varvec{\tau }}_{0\,h}\), where \({\varvec{\tau }}_{h}\in {\mathbb {X}}_{h}\), and add it on the right-hand side of the above equation,then use the L\(^{2}\)-orthogonality property of projections
 , \(\varvec{{\mathcal {P}}}_{h}\), along with the definition of discrete weak divergence operator (cf. Definition 3.2) and Green’s formula, to obtain
, \(\varvec{{\mathcal {P}}}_{h}\), along with the definition of discrete weak divergence operator (cf. Definition 3.2) and Green’s formula, to obtain 
-
An application of the second equation of Problem 1, that is, \({{\textbf {div}}} ({\varvec{\sigma }})+{\textbf{f}}=0\) with test function \({{\textbf{v}}}_{h}\in {\textbf{Y}}_{h}\), along with Definition 3.2 and Green’s formula, gives
 (5.6)
(5.6)
Hence, the error equation reads as follows.
Problem 4
Find error functions \({\varvec{\theta }}_h\in {\mathbb {X}}_h\) and \(\theta _h\in {\textbf{Y}}_h\) such that
in which

for all \({\varvec{\tau }}_{h}\in {\mathbb {X}}_{h}\) and \({\textbf{v}}_{h}\in {\textbf{Y}}_{h}\).
The following result states the estimate for the error terms that appear in Problem 4.
Lemma 5.4
Let \({\varvec{\sigma }}\in {\mathbb {X}}\cap {\mathbb {H}}^{r+1}(\Omega )\), \({\textbf{u}}\in {\textbf{Y}}\cap {\textbf{H}}^{r+2}(\Omega )\) and \( r\le k \). Then, there exist the constants \( {\mathcal {C}}_1 \) and \( {\mathcal {C}}_2 \) such that
Proof
The proof is analogous to that of [36, Lemma 4]. \(\square \)
Now we are in position of establishing the main result of this section, namely, the suboptimal rate of convergence for the weak Galerkin scheme provided by Problem 3.
Theorem 5.5
Assume that the data satisfy
and let \(({\varvec{\sigma }}_{h},{{\textbf{u}}}_{h})\in {\mathbb {X}}_{h}\times {\textbf{Y}}_{h}\) be the solution to Problem 3 and \(({\varvec{\sigma }},{{\textbf{u}}})\in {\mathbb {X}}\times {\textbf{Y}}\) be the solution of Problem 2 satisfying the regularity conditions \({\varvec{\sigma }}\in {\mathbb {H}}^{k+1}(\Omega )\) and \({\textbf{u}}\in {\textbf{H}}^{k+2}(\Omega )\). Then, there exists a positive constant \({\mathcal {C}}_{\texttt{sub}}\), independent of h, such that

Proof
Bearing in mind the definition of \( {\mathscr {A}}_{h,{{\textbf{u}}}_{h}} \) (cf. (4.16)), utilizing Problem 4 (cf. (5.7)), and some simple computations we obtain
Next, by adding and subtracting some suitable terms and recalling that \(\theta _h=\varvec{{\mathcal {P}}}_{h}{\textbf{u}}-{\textbf{u}}_{h}\), the first term on the right-hand side of the above equation can be rewritten as
Now, it suffices to substitute (5.11) back into (5.10) and employ the discrete global inf-sup of \({\mathscr {A}}_{h,{{\textbf {u}}}_{h}}\) (cf. Lemma 4.6, eq. (4.20)), the continuity property of \({\mathcal {C}}\) (cf. (4.14)) and the estimates of \({\mathcal {L}}_1\) and \({\mathcal {L}}_2\) (cf. Lemma 5.4), to arrive at
where \( {\mathcal {C}}_3 \) is a constant depending on \( {\mathcal {C}}_1 \), \( {\mathcal {C}}_2 \).
In this way, using the fact that \({\textbf{u}}\in \widehat{{\textbf{Y}}}\) and \({\textbf{u}}_h\in \widehat{{\textbf{Y}}}_h\), in particularly a priori bounds provided by (4.21) and (4.23), and the inequality (5.12) we deduce that
which, together with assumption (5.8), implies (5.9) by considering
and concludes the proof. \(\square \)
5.2 Optimal Convergence
To obtain an optimal order error estimate for the vector component \(\theta _h={\textbf{u}}_h -\varvec{{\mathcal {P}}}_h{{\textbf {u}}}\) in the usual \({\textbf{L}}^2\)-norm, we consider a dual problem that seeks \(\varvec{\vartheta }\) and \(\Phi \) satisfying
Assume that the usual \(\textrm{H}^2\)-regularity is satisfied for the dual problem; i.e., for any \(\theta _h\in {\textbf{L}}^{2}(\Omega )\), there exists a unique solution \((\varvec{\vartheta },\Phi )\in {\mathbb {H}}^{1}(\Omega )\times {\textbf{H}}^{2}(\Omega )\) such that
The main result of this section is stated in the following theorem.
Theorem 5.6
Let the assumption of Theorem 5.5 be satisfied. Also, assume that \((\varvec{\vartheta }, \Phi ) \in {\mathbb {H}}^{1}(\Omega )\times {\textbf{H}}^{2}(\Omega )\) be a solution of (5.13). Then, there exists a positive constant \({\mathcal {C}}_{\texttt{opt}}\), independent of h, such that
Proof
We divide the proof into three steps.
Step 1: discrete evolution equation for the error. First, for any \({\textbf{v}}\in {\textbf{H}}^{1}(\Omega )\) using Definition 3.2 and Green’s formula, we obtain the following result
Now, testing of Eq. (5.13) against \(({\varvec{\theta }}_h, \theta _h)\) yields
Then, by employing (5.16) and the fact that \(\Phi ={{\textbf {0}}}\) on \(\partial \Omega \), the term on the right-hand side of (5.17a) can be rewritten as:
from which, replacing the first term on the right-hand by the second row of (5.7) and using the fact that \(\Phi \in {\textbf{H}}^1(\Omega )\) and \(\Phi ={{\textbf {0}}}\) on \(\partial \Omega \) gives
On the other hand, by following the similar arguments of (5.6) the term on the left-hand side of (5.17b) can be rewritten by

where the first row of (5.7) and the definition of \({\mathcal {L}}_1\) (cf. Problem 4) were applied in the second and fourth lines, respectively.
Step 2: bounding the error terms \(\textrm{I}_1\)-\(\textrm{I}_7\). For the term \(\textrm{I}_1\), by applying the Cauchy-Schwarz inequality, the bound (5.4) stated in Lemma 5.3 and trace inequality (cf. Lemma 5.1) we estimate
As for the term \(\textrm{I}_2\), the Cauchy-Schwarz and trace inequalities, and the definition of discrete norm \(\Vert \cdot \Vert _{{\mathbb {H}},h}\) (cf. first paragraph of Sect. 4.1) imply that
For the term \(\textrm{I}_3\), we use the definition of \({\mathcal {S}}(\cdot ,\cdot )\) given by (3.10), the continuity and orthogonality properties of operator \({\varvec{{\mathcal {P}}}}_b^K\), and trace inequality to get

where the approximation property of the projector  (cf. Lemma 3.3) was used in the last step. Next, in order to estimate \(\textrm{I}_4\), we add zero in the form \(\pm {\mathcal {A}}_h({\varvec{\theta }}_h, \varvec{\vartheta })\) to find that
(cf. Lemma 3.3) was used in the last step. Next, in order to estimate \(\textrm{I}_4\), we add zero in the form \(\pm {\mathcal {A}}_h({\varvec{\theta }}_h, \varvec{\vartheta })\) to find that

The first term on the right-hand side of the above equation can be estimated using the continuity of \({\mathcal {A}}_h\) given in Lemma 4.2 and the approximation property of the projector  as follows:
as follows:

Also, an application of the consistency property of \({\mathcal {A}}_h\) (cf. Lemma 3.3) and testing the first row of (5.13) with \({\varvec{\theta }}_h\) yields
where the the equivalent expression of \(\int _{\Omega }\varvec{\nabla }\Phi : {\varvec{\theta }}_{0h}\) given by (5.18) was used in the last step. Then, thanks to (5.19) and (5.20) it suffices to estimate the last term on the right-hand side. For this purpose, we rewrite the associated term by adding and subtracting some suitable term as
To determine upper bounds for the right-hand side terms, we use Hölder’s inequality, the approximation and the continuity properties of the projector \(\varvec{{\mathcal {P}}}_h\), the Gagliardo-Nirenberg inequality, the inverse inequality and the Sobolev embedding \({\textbf{H}}^{2}{\hookrightarrow }{\textbf{W}}^{1,4}\). This gives
and
Combining the above bounds with (5.25) and (5.24), along with (5.19), (5.20) yields
which, together with estimate (5.23) gives
In what follow, we focus on the estimate of \(\textrm{I}_5\). To this end, using similar arguments as in the proof of Theorem 5.5 (cf. equation (5.11)), we obtain

and therefore, each of the terms above are estimated utilizing the approximation and the continuity properties of the projectors \(\varvec{{\mathcal {P}}}_h\) and  , Gagliardo-Nirenberg and inverse inequalities and the Sobolev embedding, \({\textbf{H}}^{1}{\hookrightarrow }{\textbf{L}}^{4}\) as follows:
, Gagliardo-Nirenberg and inverse inequalities and the Sobolev embedding, \({\textbf{H}}^{1}{\hookrightarrow }{\textbf{L}}^{4}\) as follows:

which leads to
On the other hand, by arguments similar to those used in the estimation term \(\textrm{I}_1\), we derive

Similarly, using (5.4) we have
Step 3: error estimate. We now insert the bounds on \(\textrm{I}_1\)-\(\textrm{I}_7\) in (5.17b), yielding
The sought result follows from Theorem 5.5 and employing regularity (5.14). \(\square \)
We end this section by establishing the error estimate for the pressure. By proceeding as in [30, Theorem 5.5, eqs. (5.38) and (5.39)] (see also [31, eq. 5.14]), we deduce the existence of a positive constant C, independent of h, such that
Therefore, thanks to Theorems 5.5 and 5.6 we get
6 Numerical Results
We examine the performance of the WG mixed-FEM for solving three examples of the Navier–Stokes problem governed by the Eq. (2.1) in two space dimension. Here, the weak Galerkin space \({\mathbb {X}}_{0,h}\) is used for the pseudostress \({\varvec{\sigma }}\) whereas the piecewise polynomial spaces \({\textbf{P}}_{k+1}({\mathcal {K}}_h) \) and \(\textrm{P}_{k+1}({\mathcal {K}}_h) \) are used for the velocity field \({{\textbf{u}}}\) and pressure solution p, respectively, with \(k\in \{0,1\}\). Also, like in Ref. [31], we use a real Lagrange multiplier to impose the zero integral mean condition for \( {\varvec{\sigma }}_h \) of the discrete scheme. As a result, Problem 3 is rewritten as follow: find \((({\varvec{\sigma }}_{h},{\textbf{u}}_{h}),\lambda )\in {\mathbb {X}}_{0,h}\times {\textbf{Y}}_{h}\times \textrm{R}\) such that
In addition, a fixed point strategy with a fixed tolerance \(\texttt{Tol}=1\)e-6 is utilized for solving the nonlinear equation (6.1). To that end, we begin with a vector of all zeros as an initial guess and stop iterations when the pseudostress’s and velocity’s errors between two consecutive iterations are adequately small, that is
We now introduce some additional notations. The individual errors associated to the main unknowns and the postprocessed pressure are denoted and defined, as usual, by
In turn, for all \( \star \in \{{\varvec{\sigma }},{{\textbf{u}}},p\} \), we let \(\texttt{r}(\star )~:=~\dfrac{\text {log}(\texttt {e}(\star )/\texttt{e}'(\star ))}{\text {log}(h/h')}\) be the experimental rates of convergence, where h and \( h^{'} \) denote two consecutive mesh sizes with errors \(\texttt {e}(\star )\) and \(\texttt {e}^{'}(\star )\), respectively.
The examples to be considered in this section are described next. In the first two examples, we solve a two-dimensional problem with manufactured exact solutions to validate the theoretical error estimates presented in the present study regarding the pseudostress, velocity, and pressure, and demonstrate the scheme’s robustness with respect to viscosity. Examples 3 and 4 are utilized to evaluate the effectiveness of the discrete scheme by simulation of practical problems for which no analytical solutions. We performed our computations using the \(\texttt{MATLAB}\) 2020b software on an Intel Core i7 machine with 32 GB of memory. In all our computation, the hexagonal partition, and the non-convex partition are generated by \(\texttt{PolyMesher}\) package [53] (see Fig. 1).
6.1 Example 1: Accuracy Assessment
We turn first to the numerical verification of the rates of convergence anticipated by Theorems 5.5 and 5.6. To this end, we consider parameter \(\nu =0.1\) and design the exact solution as follows:
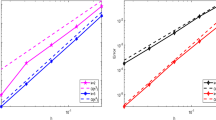
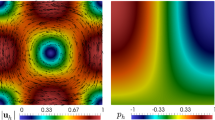
for all \( (x_1, x_2)^{\texttt{t}}\in \Omega =(0,1)^{2} \). The model problem is then complemented with the appropriate Dirichlet boundary condition. Using the weak Galerkin spaces given in Sect. 3 with polynomial degree k\(=0\), 1, we solve Problem 3 and obtain the approximated stress on a sequence of three successively refined polygonal meshes made of hexagons, non-convex and triangular elements (see Fig. 1) denoted by \({\mathcal {K}}_{1,h}\), \({\mathcal {K}}_{2,h}\) and \({\mathcal {K}}_{3,h}\), respectively. In addition, the discrete pressure is computed using post-processing approach stated in Sect. 5. At each refinement level we compute errors between approximate and smooth exact solutions. The results of this convergence study are collected in Tables 1, 2 and 3. One can see that the rate of convergence of individual stress and pressure variables is \( O(h^{k+1}) \), whereas it is \( O(h^{k+2}) \) for the velocity, which both are in agreement with the theoretical analysis stated in Theorems 5.5 and 5.6. On the other hand, in order to illustrate the accurateness of the discrete scheme, in Fig. 2 we display components of the approximate velocity, stress, pressure on polygonal mesh with \(h = 3.030\)e-2 and k\(=0\).
6.2 Example 2: Robustness with Respect to Viscosity
In this section, we focus on studying the scheme’s robustness concerning viscosity. Specifically, we investigate how the error behaves as the value of \(\nu \) decreases. For that end, we take \({\mathcal {K}}_h :=\, {\mathcal {K}}_{1,h}\) and consider the exact solution as
The computed errors and experimental rates of convergence are listed in Table 4 for \({k}=1\) and \(\nu \in \{10^{-3},10^{-6},10^{-9}\}\). One can observe that with the decrease in viscosity, small changes have occurred in the calculated errors, which do not affect the convergence rate.
6.3 Example 3 [40]: Lid-Driven Cavity Problem
The next example is chosen to illustrate the performance of the proposed method for modeling the lid-driven cavity flow in the square domain \(\Omega =(0,1)^{2}\) with different values of \( \nu \). For boundary conditions, we set the inflow \({{\textbf {g}}}=(1,0)^{\texttt{t}}\) at the top end of \( \Omega \) and no-slip condition everywhere on the boundary. In addition, the body force term is \({{\textbf {f}}}={{\textbf {0}}}\). In Fig. 3 we display the computed velocity components and pressure on hexagon mesh with \( h=3.03 \)e-2 and \( k=0 \), \(\nu \in \{1,10^{-2},10^{-3}\}\), which confirm the obtained results in [40].
6.4 Example 4: Fluid Flows with Heterogeneous Porous Inclusions
Mathematical modeling and simulation of fluid flows in the presence of single or multiple obstacles have been topics of interest for several decades due to their wide applicability in various practical circumstances across disciplines. Flow past solid bodies, such as cylinders and airfoils, has been investigated extensively for a long time using Navier–Stokes equations (see, for instance, [27, 45, 51]). Hence, we study the unsteady Navier–Stokes equation, which depends on the porosity parameter, within the exterior flow domain (\(\Omega _{f}\)), characterized by large porosity, and in the porous subdomains (\(\Omega _{p}\)), characterized by small porosity. A typical computational domain in the present problem is illustrated in Fig. 4a. Here, denoting domain by \(\Omega =(-1,1)^{2}\) and the final time by \( t_F \), we consider the unsteady Navier–Stokes equation with the porosity \(\phi \) using the following non-dimensionalization
Regarding the boundary condition, we prescribe an inflow velocity \({\textbf{u}}_{\texttt{in}}=(0,1)^{\texttt{t}}\) on the left boundary, while on the right boundary denoted by \(\Gamma _{out} \), we impose a zero normal Cauchy stress, which means that we need to set
and on the remainder of the boundary we set no-slip velocity \( {{\textbf{u}}}={\textbf{0}} \). In addition, we performed discretization of time by Backward Euler method and taken 24 circular inclusions with different radii at relatively random locations. The performance of the proposed method has been tested with the following data:
In Fig. 4b, we depicted the polygonal mesh of the computational domain. The results of the desired case simulation are presented in Fig. 5. It can be seen that the fluid is flowing faster in the area that has a large porosity; for the area that has a small porosity, the fluid is flowing slowly. In the area that has small porosity, we can see the gradation motion of the fluid clearly; this fact emphasizes that the proposed scheme can deal with the irregular pattern of porosity.
Data Availability
Data sets generated during the current study are available from the corresponding author on reasonable request.
References
Antonietti, P.F., Vacca, G., Verani, M.: Virtual element method for the Navier–Stokes equation coupled with the heat equation. IMA J. Numer. Anal. 43(6), 3396–3429 (2023)
Al-Taweel, A., Hussain, S., Lin, R., Zhu, P.: A stabilizer free weak Galerkin finite element method for general second-order elliptic problem. Int. J. Numer. Anal. Model. 18(3), 311–323 (2021)
Beirão da Veiga, L., Lovadina, C., Vacca, G.: Virtual elements for the Navier–Stokes problem on polygonal meshes. SIAM J. Numer. Anal. 56, 1210–1242 (2018)
Beirão da Veiga, L., Mora, D., Vacca, G.: The Stokes complex for virtual elements with application to Navier–Stokes flows. J. Sci. Comput. 81, 990–1018 (2019)
Beirão da Veiga, L., Brezzi, F., Cangiani, A., Manzini, G., Marini, L.D., Russo, A.: Basic principles of virtual element methods. Math. Models Methods Appl. Sci. 23, 199–214 (2013)
Beirão da Veiga, L., Brezzi, F., Marini, L.D., Russo, A.: Mixed virtual element methods for general second order elliptic problems on polygonal meshes. ESAIM Math. Model. Numer. Anal. 50(3), 727–747 (2016)
Beirão da Veiga, L., Brezzi, F., Marini, L.D., Russo, A.: \(H(\rm div )\) and \(H(\textbf{curl} )\)-conforming virtual element methods. Numer. Math. 133(2), 303–332 (2016)
Brezzi, F., Fortin, M.: Mixed and Hybrid Finite Element Methods. In: Springer Series in Computational Mathematics, vol. 15, Springer-Verlag, New York (1991)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications. In: Springer Series in Computational Mathematics, vol. 44, Springer, Heidelberg (2013)
Behr, M.A., Franca, L.P., Tezduyar, T.E.: Stabilized finite element methods for the velocity-pressure-stress formulation of incompressible flows. Comput. Methods Appl. Mech. Eng. 104(1), 31–48 (1993)
Cesmelioglu, A., Cockburn, B., Qiu, W.: Analysis of a hybridizable discontinuous Galerkin method for the steady-state incompressible Navier–Stokes equations. Math. Comput. 86, 1643–1670 (2017)
Cockburn, B., Kanschat, G., Schötzau, D.: A locally conservative LDG method for the incompressible Navier–Stokes equations. Math. Comput. 74(251), 1067–1095 (2005)
Cockburn, B., Di Pietro, D.A., Ern, A.: Bridging the hybrid high-order and hybridizable discontinuous Galerkin methods. ESAIM Math. Model. Numer. Anal. 50, 635–650 (2016)
Camaño, J., Oyarzúa, R., Tierra, G.: Analysis of an augmented mixed-FEM for the Navier–stokes problem. Math. Comput. 86(304), 589–615 (2017)
Camaño, J., Gatica, G.N., Oyarzúa, R., Tierra, G.: An augmented mixed finite element method for the Navier–Stokes equations with variable viscosity. SIAM J. Numer. Anal. 54(2), 1069–1092 (2016)
Camaño, J., García, C., Oyarzúa, R.: Analysis of a momentum conservative mixed-FEM for the stationary Navier–Stokes problem. Numer. Methods Partial Differ. Equ. 37, 2895–2923 (2021)
Camaño, J., Gatica, G.N., Oyarzúa, R., Ruiz-Baier, R.: An augmented stress-based mixed finite element method for the steady state Navier-Stokes equations with nonlinear viscosity. Numer. Methods Partial Differ. Equ. 33, 1692–1725 (2017)
Cai, Z., Wang, Y.: Pseudostress-velocity formulation for incompressible Navier–stokes equations. Int. J. Numer. Methods Fluids 63(3), 341–356 (2010)
Chen, G., Feng, M., Xie, X.: Robust globally divergence-free weak Galerkin methods for Stokes equations. J. Comput. Math. 34(5), 549–572 (2016)
Caucao, S., Gatica, G.N., Sandoval, F.: A fully-mixed finite element method for the coupling of the Navier–Stokes and Darcy–Forchheimer equations. Numer. Methods Partial Differ. Equations. 37(3), 2550–2587 (2021)
Cai, Z., Zhang, S.: Mixed methods for stationary Navier–Stokes equations based on pseudostress-pressure-velocity formulation. Math. Comput. 81(280), 1903–1927 (2012)
Di Pietro, D.A., Ern, A.: A hybrid high-order locking-free method for linear elasticity on general meshes. Comput. Methods Appl. Mech. Eng. 283, 1–21 (2015)
Dehghan, M., Gharibi, Z.: Numerical analysis of fully discrete energy stable weak Galerkin finite element scheme for a coupled Cahn–Hilliard–Navier–Stokes phase-field model. Appl. Math. Comput. 410, 126487 (2021)
Dehghan, M., Gharibi, Z.: An analysis of weak Galerkin finite element method for a steady state Boussinesq problem. J. Comput. Appl. Math. 406, 114029 (2022)
Dehghan, M., Gharibi, Z., Ruiz-Baier, R.: Optimal error estimates of coupled and divergence-free virtual element methods for the Poisson–Nernst–Planck/Navier–Stokes equations and applications in electrochemical systems, J. Sci. Comput. 94(72) (2023)
Ern, A., Guermond, J.-L.: Theory and practice of finite elements. Applied Mathematical Sciences, 159. Springer, New York (2004)
Fornberg, B.: A numerical study of steady viscous flow past a circular cylinder. J. Fluid Mech. 98(4), 819–855 (1980)
Farhloul, M., Nicaise, S., Paquet, L.: A priori and a posteriori error estimations for the dual mixed finite element method of the Navier–Stokes problem. Numer. Methods Partial Differ. Equations. 25(4), 843–869 (2009)
Gatica, G.N., Márquez, A., Sánchez, M.A.: Analysis of a velocity-pressure-pseudostress formulation for the stationary Stokes equations. Comput. Methods Appl. Mech. Engrg. 199(17–20), 1064–1079 (2010)
Gatica, G.N., Munar, M., Sequeira, F.A.: A mixed virtual element method for the Navier–Stokes equations. Math. Models Methods Appl. Sci. 28, 2719–2762 (2018)
Gatica, G.N., Sequeira, F.A.: An L\(^{p}\) spaces-based mixed virtual element method for the two-dimensional Navier–Stokes equations. Math. Models Methods Appl. Sci. 31(14), 2937–2977 (2021)
Gatica, G.N.: A Simple Introduction to the Mixed Finite Element Method: Theory and Applications, Springer Briefs in Mathematics (Springer, 2014)
Girault, V., Raviart, P.: Finite element methods for Navier–Stokes equations. Theory and Algorithms, Springer Series in Computational Mathematics, Vol. 5. Springer, Berlin (1986)
Girault, V., Raviart, P.-A.: An analysis of a mixed finite element method for the Navier–Stokes equations. Numer. Math. 33, 235–271 (1979)
Gunzburger, M.D., Lee, H.K.: An optimization-based domain decomposition method for the Navier–Stokes equations. SIAM J. Numer. Anal. 37(5), 1455–1480 (2000)
Gharibi, Z., Dehghan, M., Abbaszadeh, M.: Numerical analysis of locally conservative weak Galerkin dual-mixed finite element method for the time-dependent Poisson-Nernst–Planck system. Comput. Math. Appl. 92, 88–108 (2021)
Gharibi, Z.: A weak Galerkin pseudostress-based mixed finite element method on polygonal meshes: application to the Brinkman problem appearing in porous media. Numer. Algorithms, pp. 1–26 (2024)
Gharibi, Z., Dehghan, M., Abbaszadeh, M.: Optimal error bound for immersed weak Galerkin finite element method for elliptic interface problems. J. Comput. Appl. Math. 416, 114567 (2022)
Howell, J.S., Walkington, N.: Dual mixed finite element methods for the Navier–stokes equations. ESAIM: Math. Modell. Numer. Anal. 47, 789–805 (2013)
Hu, X., Mu, L., Ye, X.: A weak Galerkin finite element method for the Navier–Stokes equations. J. Comput. Appl. Math. 362, 614–625 (2019)
He, L., Feng, M., Guo, J.: A locking-free and mass conservative \(H(\operatorname{div})\) conforming DG method for the Biot’s consolidation model. Comput. Math. Appl. 136, 151–164 (2023)
Jamet, P., Raviart, P.A.: Numerical solution of the stationary Navier–Stokes equation by finite element methods, in Computing Methods in Applied Sciences and Engineering, Part 1. Lecture Notes in Computer Sciences, vol. 10. Springer, Berlin (1974)
Ji, G., Zhu, W.: A weak Galerkin finite element method for time-dependent Poisson–Nernst–Planck equations. J. Comput. Appl. Math. 416, 114563 (2022)
Liu, X., Li, J., Chen, Z.: A weak Galerkin finite element method for the Navier–Stokes equations. J. Comput. Appl. Math. 333, 442–457 (2019)
Li, G., Humphrey, J.A.C.: Numerical modelling of confined flow past a cylinder of square cross-section at various orientations. Int. J. Numer. Methods Fluids 20(11), 1215–1236 (1995)
Mu, L., Wang, X., Ye, X.: A modified weak Galerkin finite element method for the Stokes equations. J. Comput. Appl. Math. 275, 79–90 (2015)
Mu, L., Wang, J., Ye, X.: A stable numerical algorithm for the Brinkman equations by weak Galerkin finite element methods. J. Comput. Phys. 273, 327–342 (2014)
Mu, L.: A uniformly robust \(H(\operatorname{div})\) weak Galerkin finite element method for Brinkman problems. SIAM J. Numer. Anal. 58(3), 1422–1439 (2020)
Mu, L.: A pressure-robust weak Galerkin finite element method for Navier–Stokes equations. Numer. Methods Partial Differ. Equ. 39(3), 2327–2354 (2023)
Mu, L., Wang, J., Ye, X., Zhang, S.: A weak Galerkin finite element method for the Maxwell equations. J. Sci. Comput. 65(1), 363–386 (2015)
Sohankar, A., Norberg, C., Davidson, L.: Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. Int. J. Numer. Methods Fluids 26(1), 39–56 (1998)
Sifounakis, A., Lee, S., You, D.: A conservative finite volume method for incompressible Navier–Stokes equations on locally refined nested Cartesian grids. J. Comput. Phys. 326, 845–861 (2016)
Talischi, C., Paulino, G.H., Pereira, A., Menezes, I.F.: PolyMesher: a general-purpose mesh generator for polygonal elements written in Matlab. Struct. Multidiscip. Opt. 45, 309–328 (2012)
Wang, J., Ye, X.: A weak Galerkin finite element method for second-order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)
Wang, J., Ye, X.: A weak Galerkin mixed finite element method for second order elliptic problems. Math. Comput. 83, 2101–2126 (2014)
Wang, R., Wang, Z., Liu, J.: Penalty-free any-order weak Galerkin FEMs for linear elasticity on quadrilateral meshes. J. Sci. Comput. 95, 20 (2023)
Wang, Z., Wang, R., Liu, J.: Robust weak Galerkin finite element solvers for Stokes flow based on a lifting operator. Comput. Math. Appl. 125, 90–100 (2022)
Ye, X., Zhang, S.: A stabilizer-free weak Galerkin finite element method on polytopal meshes. J. Comput. Appl. Math. 372, 112699 (2020)
Zhang, T., Lin, T.: An analysis of a weak Galerkin finite element method for stationary Navier–Stokes problems. J. Comput. Appl. Math. 362, 484–497 (2019)
Zhang, B., Yang, Y., Feng, M.: A \({C^0}\)-weak Galerkin finite element method for the two-dimensional Navier–Stokes equations in stream-function formulation. J. Comput. Math. 38(2), 310–336 (2020)
Zhang, J., Zhang, K., Li, J., Wang, X.: A weak Galerkin finite element method for the Navier–Stokes equations. Commun. Comput. Phys. 23(3), 706–746 (2018)
Zhai, Q., Zhang, R., Mu, L.: A new weak Galerkin finite element scheme for the Brinkman model. Commun. Comput. Phys. 19(5), 1409–1434 (2016)
Acknowledgements
The authors are very grateful to the anonymous reviewers for carefully reading this paper and for their comments and suggestions, which have improved the paper.
Funding
No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Gharibi, Z., Dehghan, M. Analysis of Weak Galerkin Mixed Finite Element Method Based on the Velocity–Pseudostress Formulation for Navier–Stokes Equation on Polygonal Meshes. J Sci Comput 101, 12 (2024). https://doi.org/10.1007/s10915-024-02651-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-024-02651-w
Keywords
- Weak Galerkin
- pseudostress–velocity formulation
- Mixed finite element methods
- Navier–Stokes equation
- Well-posedness
- Error analysis




 ,
, 





