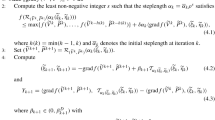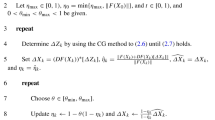Riemannian linearized proximal algorithms for nonnegative inverse eigenvalue problem

Abstract

We study the issue of numerically solving the nonnegative inverse eigenvalue problem (NIEP). At first, we reformulate the NIEP as a convex composite optimization problem on Riemannian manifolds. Then we develop a scheme of the Riemannian linearized proximal algorithm (R-LPA) to solve the NIEP. Under some mild conditions, the local and global convergence results of the R-LPA for the NIEP are established, respectively. Moreover, numerical experiments are presented. Compared with the Riemannian Newton-CG method in Z. Zhao et al. (Numer. Math. 140:827–855, 2018), this R-LPA owns better numerical performances for large scale problems and sparse matrix cases, which is due to the smaller dimension of the Riemannian manifold derived from the problem formulation of the NIEP as a convex composite optimization problem.

1 Introduction

The nonnegative inverse eigenvalue problem (NIEP) is a special kind of inverse eigenvalue problems which has been explored extensively in the literature and plays a key role in various areas such as control design, linear complementarity problems, Markov chains, and graph theory; see [2, 3, 9, 10, 19, 28] and references therein. Recall that a matrix $A\in {\mathbb {R}}^{n\times n}$ is said to be a nonnegative matrix if its entries are all greater than or equal to zero, that is, $A\in {\mathbb {R}}_+^{n\times n}$. An n-tuple $(\lambda _1,\lambda _2,\cdots ,\lambda _n)\in \mathbb {C}^n$ is said to be a realizable spectrum for nonnegative matrix if there is a matrix $A\in {\mathbb {R}}_+^{n\times n}$ such that its eigenvalues are $\lambda _1,\lambda _2,\cdots ,\lambda _n$. Then the NIEP is formulated as follows:

$$\begin{aligned} \begin{array}{ll} &{}\textrm{Given}\; (\lambda _1,\lambda _2,\cdots ,\lambda _{\textrm{n}})\; \mathrm {a\; realizable \;spectrum \;for \;nonnegative \;matrix,}\\ &{}\mathrm {find\; a \;nonnegative \;matrix}\; A\; \mathrm {such \;that \;its \;eigenvalues \;are}\; \lambda _1,\lambda _2,\cdots ,\lambda _\mathrm {n.} \end{array} \end{aligned}$$

(1.1)

Since $(\lambda _1,\lambda _2,\cdots ,\lambda _n)$ is a realizable spectrum, $\{\lambda _1,\lambda _2,\cdots ,\lambda _n\}$ is closed under complex conjugation. Without loss of generality, one can assume

$$\begin{aligned} \lambda _{2i-1}=a_i+b_i\sqrt{-1},\;\lambda _{2i}=a_i-b_i\sqrt{-1},\; i=1,\cdots ,s; \;\lambda _i\in \mathbb {R},\; i=2s+1,\cdots ,n, \end{aligned}$$

where $a_i,b_i\in \mathbb {R}$ with $b_i\ne 0$ for all $i=1,\cdots ,s$. Define the following block diagonal matrix

$$\begin{aligned} \varLambda :=\textrm{blkdiag}(\lambda _1^{[2]},\cdots ,\lambda _s^{[2]},\lambda _{2s+1},\cdots ,\lambda _n)\quad \mathrm {\;with \;each \;}\lambda _i^{[2]}:=\left[ \begin{array}{ll} a_i &{}b_i\\ -b_i&{} a_i \end{array}\right] . \end{aligned}$$

Let $\mathcal {O}(n)$ denote the set of all orthogonal matrices, i.e., $\mathcal {O}(n):=\{U\in \mathbb {R}^{n\times n}\;|\;U^TU=\mathbb {I}_{n\times n}\}$, and set

$$\begin{aligned} \mathcal {V}:=\{V\in \mathbb {R}^{n\times n}\;|\;V_{ij}=0 \mathrm { \;for \;all \;}(i,j)\; \textrm{ satisfying }\; i\ge j\;\mathrm {\; or \;}\varLambda _{ij}\ne 0 \}. \end{aligned}$$

(1.2)

Then A is a solution of (1.1) if and only if $A=U(\varLambda +V)U^T$ with $(U,V)\in \mathbb {R}^{n\times n}\times \mathbb {R}^{n\times n}$ being a solution of the following inclusion problem

$$\begin{aligned} (U,V)\in \mathcal {O}(n)\times \mathcal {V}\quad \textrm{and}\quad U(\varLambda +V)U^T\in \mathbb {R}_+^{n\times n}; \end{aligned}$$

(1.3)

see [28]. To solve problem (1.3), Zhao et al. [28] constructed a mapping $\varTheta : \mathbb {R}^{n\times n}\times \mathcal {O}(n)\times \mathcal {V}\rightarrow \mathbb {R}^{n\times n}$ by

$$\begin{aligned} \varTheta (W,U,V):=W\odot W-U(\varLambda +V)U^T\quad \mathrm { \;for \;each \;}(W,U,V)\in \mathbb {R}^{n\times n}\times \mathcal {O}(n)\times \mathcal {V}, \end{aligned}$$

(1.4)

where $W\odot W$ is the Hadamard product of W and W. Thus, solving problem (1.3) is equivalent to solving the following nonlinear matrix equation on the product manifold $\mathbb {R}^{n\times n}\times \mathcal {O}(n)\times \mathcal {V}$

$$\begin{aligned} \varTheta (W,U,V)=0. \end{aligned}$$

(1.5)

Zhao et al. [28] proposed a Riemannian inexact Newton-CG method for solving equation (1.5) and established its global convergence results under the assumption that the derivative operator of $\varTheta$ is surjective at a cluster point. Note that the dimension of the underlying space $\mathbb {R}^{n\times n}\times \mathcal {O}(n)\times \mathcal {V}$ of equation (1.5) is $n^2+\frac{n(n-1)}{2}+\textrm{dim}\mathcal {V}$ (cf. [28]). The Riemannian inexact Newton-CG method, as remarked in [28], has the following drawbacks or limitations:

• If the derivative operator at a cluster point is a sparse matrix, then it may fail to be surjective.

• In large scale cases, numerical tests illustrate that Newton-CG method spends most of computing times for solving the involved subproblem by CG method.

Observe that problem (1.3) is recast equivalently as the following optimization problem on the Riemannian manifold $M:=\mathcal {O}(n)\times \mathcal {V}$:

$$\begin{aligned} \min _{(U,V)\in M}f_p(U,V):=\frac{1}{p}\textrm{d}^{p}(U(\varLambda +V)U^T,\mathbb {R}_+^{n\times n}) \end{aligned}$$

(1.6)

(assuming that problem (1.3) is solvable), where $p\ge 1$ and $\textrm{d}^{p}(\cdot ,\mathbb {R}_+^{n\times n})$ is the distance function of the set $\mathbb {R}_+^{n\times n}$. Note also that the target function $f_p$ in problem (1.6) is of the special compositional structure with a convex outer function $h:{\mathbb {R}}^{n\times n} \rightarrow {\mathbb {R}}$ and a smooth inner function $F:M \rightarrow {\mathbb {R}}^{n\times n}$, that is, $f_p=h\circ F$ with h and F defined respectively by $h(\cdot ):=\frac{1}{p}\textrm{d}^{p}(\cdot ,\mathbb {R}_+^{n\times n})$ and

$$\begin{aligned} F(U,V):=U(\varLambda +V)U^T\quad \mathrm { \;for \;each \;}(U,V)\in M=\mathcal {O}(n)\times \mathcal {V}. \end{aligned}$$

(1.7)

Based on its special compositional structure, the development of efficient and rapid optimization algorithms for convex composite optimization problem on linear spaces such as Gauss-Newton method, Prox-descent algorithm and linearized proximal algorithms (LPAs) has been made with a great deal of attention; see [6, 11, 14, 15, 17, 25] and references therein.

With these observations, we develop a new type of efficient algorithms, i.e., Riemannian linearized proximal algorithms (R-LPA), to solve problem (1.3) by extending the LPA type algorithms of [14] in linear spaces to the Riemannian manifold setting. More precisely, we propose a R-LPA (i.e., Algorithm 4 in Section 4) together with its globalized version R-GLPA (i.e., Algorithm 5 in Section 4) to solve problem (1.6). Under a quasi-regular like condition for F given by (1.7), superlinear local convergence of the R-LPA is established (see Theorem 3 in Section 4). Furthermore, the global convergence of the R-GLPA is also provided (see Theorem 4 in Section 4). Notice that the dimension of the underlying manifold $\mathcal {O}(n)\times \mathcal {V}$ of the optimization problem (1.6) is $\frac{n(n-1)}{2}+\textrm{dim}\mathcal {V}$ which is $n^2$ less than that of (1.5). With utilizing this important property, numerical tests for the R-LPA and the R-GLPA are implemented. Compared with the Riemannian Newton-CG algorithm (R-NCGA), the R-GLPA has the following advantages:

• The R-GLPA costs less CPU time than the R-NCGA. This merit appears more clearly for large scale problems.

• For sparse matrix cases, the R-GLPA is much more efficient than the R-NCGA.

To furnish the tools to establish our main results, we study first in Section 3 the R-LPAs for general convex composite optimization problems on Riemannian manifolds. We establish local and global convergence results of the algorithms under the assumptions of local weak sharp minima of order p for outer function and the quasi-regularity condition for the inner function. The study of this issue is of independent interest. Applying the obtained results in Section 3 to the NIEP, we obtain in Section 4 a R-LPA, together with its global version, to solve the NIEP and establish their convergence results.

The organization of the present work is summarized as follows. We deal with the notation and preliminary results used in the present paper in Section 2, while in Section 3, the general forms of R-LPA for original convex composite optimization problems on Riemannian manifolds are proposed and their local and global convergence results are established under the assumptions of local weak sharp minima of order p and the quasi-regularity condition. In Section 4, we apply this general R-LPA to solve the NIEP and establish both local and global convergence results. Numerical experiments are reported in Section 5. The last section summarizes the conclusions.

2 Notation and preliminary results

We recall some notation and notions about smooth manifolds used in the present paper which are standard; see for example [8, 12]. Let M be a smooth complete connected n-dimensional Riemannian manifold with the Levi-Civita connection $\nabla$. Let $x\in M$, and let $T_{x}M$ denote the tangent space at x to M. Let $\langle \cdot ,\cdot \rangle _x$ be the scalar product on $T_{x}M$ with the associated norm $\Vert \cdot \Vert _{x}$, where the subscript x is sometimes omitted. Let $TM=\bigcup _{x\in M}T_xM$ be the tangent bundle of M, which is naturally a manifold. For any two points $x,\,y\in M$, let $c:[0,1]\rightarrow M$ be a piecewise smooth curve connecting x and y. Then the arc-length of c is defined by $l(c):=\int _{0}^{1}\Vert c'(t)\Vert \textrm{d}t$, and the Riemannian distance from x to y by $\textrm{d}(x,y):=\inf _{c}l(c)$, where the infimum is taken over all piecewise smooth curves $c:[0,1]\rightarrow M$ connecting x and y. Thus, the Riemannian distance $\textrm{d}(\cdot ,\cdot )$ induces the original topology on M. For a smooth curve c, a vector field X is said to be parallel along c if $\nabla _{c'}V=0$. In particular, if $c'$ is parallel along itself, then c is called a geodesic; thus, a smooth curve c is a geodesic if and only if $\nabla _{c'}{c'}=0$. A geodesic $c:[0,1]\rightarrow M$ joining x to y is minimal if its arc-length equals its Riemannian distance between x and y. By the Hopf-Rinow theorem [8], $(M,\textrm{d})$ is a complete metric space, and there is at least one minimal geodesic joining x to y for any points x and y.

Let Y be a Banach space or a Riemannian manifold. We use $\textbf{B}_Y(x,r)$ and ${\textbf{B}_Y[x,r]}$ to denote respectively the open metric ball and the closed metric ball at x with radius r, that is,

$$\begin{aligned} \textbf{B}_Y(x,r):=\{y\in Y|\;\textrm{d}(x,y)<r\}\quad \textrm{and}\quad {\textbf{B}_Y[x,r]}:=\{y\in Y|\;\textrm{d}(x,y)\le r\}. \end{aligned}$$

We often omit the subscript Y if no confusion occurs.

For each $x\in M$, the exponential map at x, $\exp _{x}:T_xM\rightarrow M$ is well-defined on $T_xM$. Recall a constant related to a point $x\in M$: the injectivity radius $r_{\textrm{inj}}(x)$

$$\begin{aligned} r_{\textrm{inj}}(x):=\sup \left\{ r>0:\exp _x(\cdot ) \mathrm {~is\; a \;diffeomorphism \;on}\; \textbf{B}(0,r)\subset {T}_xM\right\} . \end{aligned}$$

Let $c: \mathbb {R}\rightarrow M$ be a smooth curve and let $P_{c,\cdot ,\cdot }$ denote the parallel transport along c, which is defined by

$$\begin{aligned} P_{c,c(b),c(a)}(u)=X(c(b)),\quad \forall a,b\in \mathbb {R}\mathrm { \;and \;} u\in T_{c(a)}M, \end{aligned}$$

where X is the unique smooth vector field satisfying $\nabla _{c'(t)}X=0$ and $X(c(a))=u$. In particular, we write $P_{x,y}$ for $P_{c,x,y}$ in the case when c is the minimizing geodesic and no confusion arises.

We recall from [1, p. 55] the notion of retraction on M.

Definition 1

A $C^\infty$ mapping $R:TM\rightarrow M$ is said to be a retraction on M if the following assertion holds for each $x\in M$ ($R_x$ denotes the restriction of R to $T_xM$):

$R_x 0 =x$, and $\textrm{D}R_x 0 =\mathbb {I}_{T_xM}$, where $\mathbb {I}_{T_xM}$ denotes the identity mapping on $T_xM$.

Remark 1

The exponential map is a special retraction on M (cf. [1, p. 56]).

Let R be a retraction on M. Let $\bar{x}\in M$ and $r>0$. For simplicity, write

$$\begin{aligned} {\mathfrak {A}}(\bar{x},r):=\{ (y,u)\in TM |\; y\in \textbf{B}(\bar{x},r) \;\textrm{and}\; \Vert u\Vert <r\} \end{aligned}$$

and

$$\begin{aligned} \widehat{\mathfrak {A}}(\bar{x},r):= & {} \{ (y,u)\in TM |\; y\in \textbf{B}( \bar{x},r),\; \Vert u\Vert <r \\{} & {} \textrm{and }\; R_y(tu)\in \textbf{B} (\bar{x},r) \;\mathrm {for \;each}\; t\in [0,1]\}. \end{aligned}$$

Since R is $C^{\infty }$, for each $\bar{x}\in M$, there exist $\mu _{\bar{x}}>0$ and $\textbf{r}_{\bar{x}}>0$ such that

$$\begin{aligned} \textrm{d}(y, R_yu)\le \mu _{\bar{x}}\Vert u\Vert \quad \mathrm { for \;each \;} (y,u)\in {\mathfrak {A}}(\bar{x},\textbf{r}_{\bar{x}}). \end{aligned}$$

(2.1)

If R is the exponential map, then (2.1) holds with $\mu _{\bar{x}} = 1$.

Let $F:M \rightarrow {\mathbb {R}}^m$ be continuously differentiable. We recall the notion of Lipschitz continuity for the gradient $\textrm{D}F$. Let $U\subseteq M$ be such that for any two points $x,y\in U$ there is a unique minimal geodesic connecting x and y. Then $\textrm{D}F$ is said to be Lipschitz continuous on U with modulus $L>0$, if

$$\begin{aligned} \Vert \textrm{D}F(y)-\textrm{D}F(x)P_{x,y}\Vert \le L\textrm{d}(x,y)\quad \mathrm {for \;each \;x,y}\;\in \;\textrm{U}. \end{aligned}$$

(2.2)

$\textrm{D}F$ is said to be local Lipschitz continuous at $\bar{x}$ if there exists $0< r<r_{\textrm{inj}}(\bar{x})$ and $L_r>0$ such that $\textrm{D}F$ is Lipschitz continuous on $\textbf{B}(\bar{x}, r)$ with modulus $L_r$.

We close this section with the following useful lemma.

Lemma 1

Let $\bar{x} \in M$. Suppose that $\textrm{D} F$ is local Lipschitz continuous at $\bar{x}$. Then, there exist $r>0$ and $L>0$ such that for any $(x,u)\in \widehat{\mathfrak {A}}(\bar{x},r)$ it holds that

$$\begin{aligned} \Vert F(R_xu)-F(x)-\textrm{D}F(x)u\Vert \le \frac{L}{2}\Vert u\Vert ^2. \end{aligned}$$

(2.3)

Proof

By Lipschitz continuous assumption, there exist $0< r<r_{\textrm{inj}}(\bar{x})$ and $L_r>0$ such that

$$\begin{aligned} \Vert \textrm{D}F(y)P_{y,x}-\textrm{D}F(x)\Vert \le L_r\textrm{d}(x,y)\quad \mathrm {for \;each \;} x,y\in \textbf{B}(\bar{x},r). \end{aligned}$$

(2.4)

By (2.1), without loss of generality, we assume that there is $\mu _{\bar{x}}>0$ such that

$$\begin{aligned} \textrm{d}(x, R_xu)\le \mu _{\bar{x}}\Vert u\Vert \quad \mathrm {\; for \;each \;} (x,u)\in {\mathfrak {A}}(\bar{x},r). \end{aligned}$$

Let $L_1:=\sup _{(x,u)\in \widehat{\mathfrak {A}}(\bar{x},r)}\Vert \textrm{D}F(R_xu)\Vert$. Then by (2.4), one can check that $L_1<+\infty$. Since R is $C^\infty$, there exists $L_2>0$ such that $\Vert \textrm{D}R_xu-P_{R_xu,x}\textrm{D}R_x0\Vert \le L_2\Vert u\Vert$ for any $(x,u)\in \widehat{\mathfrak {A}}(\bar{x},r)$. Let $L=L_1L_2+ L_r\mu _{\bar{x}}$. Then r, L are the desired ones. Indeed, fix $(x,u)\in \widehat{\mathfrak {A}}(\bar{x},r)$. Note that

$$\begin{aligned} \Vert \textrm{D}F(R_xu)\textrm{D}R_xu-\textrm{D}F(R_xu)P_{R_xu,x}\Vert= & {} \Vert \textrm{D}F(R_xu)(\textrm{D}R_xu-P_{R_xu,x}\textrm{D}R_x 0)\Vert \\\le & {} L_1L_2\Vert u\Vert \end{aligned}$$

(due to $\textrm{D}R_x 0 =\mathbb {I}_{T_xM}$) and

$$\begin{aligned} \Vert \textrm{D}F(R_xu)P_{R_xu,x} -\textrm{D}F(x)\Vert \le L_r\textrm{d}(x,R_xu)\le L_r\mu _{\bar{x}}\Vert u\Vert . \end{aligned}$$

Thus, by triangle inequality, we have that

$$\begin{aligned} \Vert \textrm{D}F(R_xu)\textrm{D}R_xu-\textrm{D}F(x)\Vert \le L\Vert u\Vert . \end{aligned}$$

(2.5)

Note further that

$$\begin{aligned} F(R_xu)-F(x)-\textrm{D}F(x)u =\int _0^1\textrm{D} F(R_x(tu))\textrm{D}R_x(tu)u\textrm{d}t-\textrm{D} F(x)u. \end{aligned}$$

This, together with (2.5), implies that

$$\begin{aligned} \Vert F(R_xu)-F(x)-\textrm{D}F(x)u\Vert\le & {} \int _0^1\Vert \textrm{D} F(R_x(tu))\textrm{D}R_x(tu)-\textrm{D} F(x)\Vert \textrm{d}t\Vert u\Vert \\\le & {} \int _0^1 Lt\Vert u\Vert \textrm{d}t\Vert u\Vert . \end{aligned}$$

Hence, (2.3) is seen to hold.

3 Riemannian linearized proximal algorithms and convergence analysis

Throughout the whole section, we always assume that $p\in [1,2)$, unless otherwise specified. In this section, we shall study an inexact Riemannian linearized proximal algorithm to solve the general convex composite optimization problem on a manifold M:

$$\begin{aligned} \min _{x\in M}f(x):=h(F(x)), \end{aligned}$$

(3.1)

where the outer function $h:{\mathbb {R}}^m \rightarrow {\mathbb {R}}$ is convex, and the inner function $F:M \rightarrow {\mathbb {R}}^m$ is continuously differentiable. The local convergence results of the algorithm are established under the assumptions of the local weak sharp minima of order p for the outer function h and the quasi-regular condition for the inner function F. We also develop a globalization version for the algorithm by virtue of the backtracking line-search, and establish its convergence result.

We proceed with the (inexact) linearized proximal mapping and some basic properties. Associated to (3.1), we denote by $h_{\min }$ and C the minimum value and the set of minima for the function h respectively, that is,

$$\begin{aligned} h_{\min }:=\min _{y\in {\mathbb {R}}^m} h(y)\quad \textrm{and}\quad C:=\textrm{arg}\min _{y\in {\mathbb {R}}^m} h(y). \end{aligned}$$

(3.2)

Let $v>0$ and $x\in M$. The linearized proximal mapping $h_{x,v}:T_xM\rightarrow \mathbb {R}$ is defined by

$$\begin{aligned} h_{x,v}(d):=h(F(x)+\textrm{D}F(x)d)+\frac{1}{2v}\Vert d\Vert ^2\quad \mathrm { \;for \;each \;}d\in T_xM. \end{aligned}$$

(3.3)

Associated to problem (3.1), we consider the inclusion

$$\begin{aligned} F(x) \in C, \end{aligned}$$

(3.4)

where $C\subseteq {\mathbb {R}}^m$ is defined by (3.2). For $x\in M$, let ${\varGamma }(x)$ be defined by

$$\begin{aligned} \varGamma (x):=\{d\in T_xM:F(x)+\textrm{D}F(x)d\in C\}. \end{aligned}$$

(3.5)

The following lemma presents some useful properties of the linearized proximal mapping.

Lemma 2

Let $v>0$ and $\epsilon {\ge }\ 0$, and let $x\in M$ satisfying $\varGamma (x)\ne \emptyset$ and $d\in T_{x}M$ such that $h_{x,v}(d)\le \inf \limits _{y\in T_{x}M} h_{x,v}(y)+\epsilon$. Then the following statements hold:

• (i) $\Vert d\Vert ^2\le \textrm{d}^2(0,\varGamma (x))+2v\epsilon$,

• (ii) $h(F(x)+\textrm{D}F(x)d)\le h_{\min }+\frac{1}{2v}\textrm{d}^2(0,\varGamma (x))+\epsilon$.

Proof

Let $\tilde{d}\in \varGamma (x)$ and recall the definition of $h_{x,v}$. Then one has by assumption that

$$\begin{aligned} h(F(x)+\textrm{D}F(x)d)+\frac{1}{2v}\Vert d\Vert ^2\le h(F(x)+\textrm{D}F(x)\tilde{d})+\frac{1}{2v}\Vert \tilde{d}\Vert ^2+\epsilon . \end{aligned}$$

Since $h(F(x)+\textrm{D}F(x)\tilde{d})=h_{\min }$ (see (3.2) and (3.5)), it follows that

$$\begin{aligned} h(F(x)+\textrm{D}F(x)d)+\frac{1}{2v}\Vert d\Vert ^2\le h_{\min }+\frac{1}{2v}\Vert \tilde{d}\Vert ^2+\epsilon . \end{aligned}$$

Taking the infimum for $\tilde{d}$ over $\varGamma (x)$ on the right-hand side of the above inequality, we obtain

$$\begin{aligned} h(F(x)+\textrm{D}F(x)d)+\frac{1}{2v}\Vert d\Vert ^2\le h_{\min }+\frac{1}{2v}\textrm{d}^2(0,\varGamma (x))+\epsilon , \end{aligned}$$

(3.6)

or equivalently,

$$\begin{aligned} \frac{1}{2v}\Vert d\Vert ^2\le h_{\min }-h(F(x)+\textrm{D}F(x)d)+\frac{1}{2v}\textrm{d}^2(0,\varGamma (x))+\epsilon . \end{aligned}$$

Thus, (i) is seen to hold because $h_{\min }- h(F(x)+\textrm{D}F(x)d)\le 0$ (by the definition of $h_{\min }$ in (3.2)). Furthermore, (ii) follows from (3.6) directly. The proof is complete.

3.1 Riemannian linearized proximal algorithm

In view of practical computation, it could be very expensive to exactly solve the subproblem (3.3) in each iteration. In this section, we first extend the inexact version of the linearized proximal algorithm in linear space setting (i.e., [14, Algorithm 19]) to the Riemannian manifold settings for solving problem (3.1), where $\inf \limits _{d\in T_{x}M} h_{x,v}(d)$ is only solved approximately in each iteration (with progressively better accuracy), and study its local convergence behavior. In the following Riemannian linearized proximal algorithm for solving (3.1), we always assume that

$$\begin{aligned} 0< \theta< 1,\; K> 0,\; \alpha > 2\; \mathrm {\; and }\; 0< \underline{v}\le \overline{v} < + \infty . \end{aligned}$$

Algorithm 1

To establish the local convergence of Algorithm 1, we need the following two important notions: one is about weak sharp minima while the other is about quasi-regular point. The concepts of weak sharp minima were introduced by Burke and Ferris [7], and have been extensively studied and widely used to analyze the convergence properties of many algorithms; see [6, 17, 26, 27] and references therein. One natural extension of these concepts is that of weak sharp minima of order p ($p\ge 1$) (see [4, 13, 18, 23] and references therein): item (b) in the following definition was introduced by Studniarski and Ward [23]. The other is about the quasi-regularity condition which provides a local bound on the set $\varGamma (x)$. Recall that C is given by (3.2).

Definition 2

Let $S\subseteq {\mathbb {R}}^m$, $\eta >0$ and $p\ge 1$. C is said to be

• (a) the set of weak sharp minima of order p for h on S with modulus $\eta$ if

  $$\begin{aligned} \eta \, \textrm{d}^p(y,C)\le h(y)-h_{\min }\quad \mathrm{for~each}~ y\in S; \end{aligned}$$

  (3.7)

• (b) the set of local weak sharp minima of order p for h at $\bar{y}\in C$ if there exist $\epsilon >0$ and $\eta _\epsilon >0$ such that C is the set of weak sharp minima of order p for h on $\textbf{B}(\bar{y},\epsilon )$ with modulus $\eta _\epsilon$.

Definition 3

Let $\bar{x}\in M$. Then, $\bar{x}$ is said to be

• (a) a regular point for (3.4) if

  $$\begin{aligned} \textrm{ker}(\textrm{D}F(\bar{x})^*)\cap (C-F(\bar{x}))^\ominus =\{0\}, \end{aligned}$$

  where $\textrm{D}F(\bar{x})^*$ is the conjugate operator of $\textrm{D}F(\bar{x})$ and $(C-F(\bar{x}))^\ominus$ is the negative polar of $C-F(\bar{x})$ and defined by $(C-F(\bar{x}))^{\ominus }:= \{y:\langle y,c-F(\bar{x})\rangle \le 0,\ \text {for each}\ c\in C\}.$

• (b) a quasi-regular point for (3.4) if there exist $r>0$ and $\beta _r>0$ such that

  $$\begin{aligned} \textrm{d }(0,\varGamma (x))\le \beta _r\,\textrm{d}(F(x),C)\quad \mathrm{for~each}~ x\in \textbf{B}(\bar{x},r) \end{aligned}$$

  (3.8)

  (and so $\varGamma (x)\ne \emptyset$ for each $x\in \textbf{B}(\bar{x},r)$).

Remark 2

The notions of quasi-regular point and regular point were introduced and applied to establish the local convergence rate of the GNM for problem (3.1) in linear space setting, respectively, in Li and Ng [15], and Burke and Ferris [6], which have been extended to Riemannian setting in [24]. Furthermore, any regular point of inclusion (3.4) is a quasi-regular point (cf. [24, Proposition 4.1]).

The following lemma is about a useful property of the composition of a function, satisfying the weak sharp minima of order p, and a continuously differentiable function on M.

Lemma 3

Let $S\subseteq {\mathbb {R}}^m$, $\eta >0$ and $p\ge 1$. Let C be the set of weak sharp minima of order p for h on S with modulus $\eta$. Let $L>0$, $r>0$ and let $\bar{x}\in M$. Suppose that $\textrm{D} F$ is Lipschitz continuous on $\textbf{B}(\bar{x},r)$ with modulus L. Then, for all $x,y\in \textbf{B}(\bar{x},r)$ with $y=R_xu$ and $(x,u)\in \widehat{{\mathfrak {A}}}(\bar{x},r)$ such that $F(x)+\textrm{D}F(x)u\in S$, it holds that

$$\begin{aligned} \textrm{d }(F(y),C)\le \frac{1}{2} L \Vert u\Vert ^2+\eta ^{-\frac{1}{p}}\left( h(F(x)+\textrm{D}F(x)u)-h_{\min }\right) ^{\frac{1}{p}}. \end{aligned}$$

(3.9)

Proof

By Lemma 1 and (3.7), it follows that

$$\begin{aligned} \begin{array}{lll} \textrm{d }(F(y),C)&{}\le \Vert F(y)-F(x)-\textrm{D}F(x)u\Vert +\textrm{d}(F(x)+\textrm{D}F(x)u,C)\\ &{}\le \frac{1}{2} L \Vert u\Vert ^2+\eta ^{-\frac{1}{p}}\left( h(F(x)+\textrm{D}F(x)u)-h_{\min }\right) ^{\frac{1}{p}}. \end{array} \end{aligned}$$

The proof is complete.

Now we are ready to establish the following main theorem about local convergence of sequences generated by Algorithm 3.1. Our analysis, without loss of generality, focuses only on the special case when the stepsizes are chosen to be a constant, that is, $v_k\equiv v$, unless otherwise specified, as the corresponding convergence results for the general case can be established similarly.

Theorem 1

Let $\bar{x}\in M$ be such that $\bar{x}$ is a quasi-regular point for (3.4) and $F(\bar{x})\in C$. Suppose that C is the set of local weak sharp minima of order p for h at $F(\bar{x})$ and $\textrm{D} F$ is local Lipschitz continuous at $\bar{x}$. Then, for any $\delta >0$, there exist $r_\delta \in (0,\delta )$ and $r_1>0$ such that any sequence $\{x_k\}$ generated by Algorithm 1 with initial point $x_0\in \textbf{B}(\bar{x},r_\delta )$ and $\Vert d_{-1}\Vert \le r_1$, stays in $\textbf{B}(\bar{x}, \delta )$ and converges to some point $x^*$ satisfying $F(x^*)\in C$ at a rate of $q:=\min \left\{ \frac{\alpha }{2},\frac{2}{p}\right\}$.

Proof

Note by assumption that there exist $\beta$, $\eta$, $\bar{\delta }$ and $L\ge 1$ such that (2.3) holds with $\bar{\delta }$ in place of r,

$$\begin{aligned} \textrm{d}(0, \varGamma (x))\le \beta \textrm{d}(F(x),C) \quad \mathrm { \;for \;each\; }x\in \textbf{B}(\bar{x},\bar{\delta }) \end{aligned}$$

(3.10)

and

$$\begin{aligned} \eta \textrm{d}^p(y,C)\le h(y)-h_{\min } \quad \mathrm { \;for \;each }\;y\in \textbf{B}(F(\bar{x}),\bar{\delta }). \end{aligned}$$

(3.11)

Recalling from (2.1), we assume that there exists $\mu _{\bar{x}}>0$ such that

$$\begin{aligned} \textrm{d}(y, R_yu)\le \mu _{\bar{x}}\Vert u\Vert \quad \mathrm { \;for \;each \;} (y,u)\in \mathfrak {A}({\bar{x}},\bar{\delta })\end{aligned}$$

(3.12)

(choose smaller $\bar{\delta }$ if necessary). Furthermore, sine F is continuously differentiable on M, without loss of generality, we assume that

$$\begin{aligned} \Vert \textrm{D}F(x)\Vert \le L \quad \mathrm { \;for \;each \;}x\in \textbf{B}(\bar{x},\bar{\delta }). \end{aligned}$$

(3.13)

Let $\delta >0$ be arbitrary. Without loss of generality, one may assume that

$$\begin{aligned} \delta\le & {} \min \left\{ \frac{ \bar{\delta }}{2(\mu _{\bar{x}}+1)L}, \frac{1}{2}\left( \frac{1}{32vK}\right) ^{\frac{1}{\alpha -2}}\right\} \quad \mathrm { \;and \;}\quad \beta \left( L\delta +2\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\delta ^{\frac{2-p}{p}}\right) \nonumber \\\le & {} \frac{1}{2\sqrt{2}}. \end{aligned}$$

(3.14)

Set $r_\delta :=\delta \min \{1,\frac{1}{2\beta L}\}$ and $r_1:=\left( \frac{\delta ^2}{8vK}\right) ^{\frac{1}{\alpha }}$. We claim that $r_\delta$ and $r_1$ are as desired. To do this, let $x_0\in \textbf{B}(\bar{x}, r_\delta )$, $d_{-1}\in T_{x_0}M$ with $\Vert d_{-1}\Vert \le r_1$, and let $\{x_k\}$, together with $\{d_k\}$, be a sequence generated by Algorithm 1 with initial point $x_0$. Then,

$$\begin{aligned} \textrm{d }(F(x_0),C)\le \Vert F(x_0)-F(\bar{x})\Vert \le L\textrm{d}(x_0,\bar{x})\le \frac{\delta }{2\beta }. \end{aligned}$$

(3.15)

This, together with (3.10), implies that

$$\begin{aligned} \textrm{d}(0,{\varGamma }(x_0))\le \frac{\delta }{2}. \end{aligned}$$

(3.16)

Since $d_0$ satisfies Step 4 of Algorithm 1, Lemma 2(i) is applicable to concluding that

$$\begin{aligned} \Vert d_0\Vert \le \left( \textrm{d}^2(0,{\varGamma }(x_0))+2vK\Vert d_{-1}\Vert ^{\alpha }\right) ^{\frac{1}{2}}\le \frac{\sqrt{2}}{2}\delta \end{aligned}$$

(3.17)

(noting $\Vert d_{-1}\Vert \le r_1=\left( \frac{\delta ^2}{8vK}\right) ^{\frac{1}{\alpha }}$). We shall show by induction that the following estimates hold for each $i=0,1,2,\dots$:

$$\begin{aligned} \textrm{d}(x_i,\bar{x})< (2\mu _{\bar{x}}+1)\delta (<\bar{\delta }),\quad \textrm{d}(F(x_i),C)\le & {} \frac{\delta }{\beta }\left( \frac{1}{2}\right) ^{q^i+i}\quad \textrm{and}\nonumber \\ \Vert d_i\Vert\le & {} 2\delta \left( \frac{1}{2}\right) ^{q^i+i}(<\bar{\delta }). \end{aligned}$$

(3.18)

Note first that (3.18) holds for $i=0$ (thanks to the choice of $x_0$, (3.15) and (3.17)). Next, assume that (3.18) holds for each $i\le k-1$. Then it follows from (3.12) that

$$\begin{aligned} \textrm{d}(x_k,\bar{x})\le \mu _{\bar{x}}\sum \limits _{i=0}^{k-1}\Vert d_i\Vert +{\textrm{d}(x_0, \bar{x})} \le 2\mu _{\bar{x}}\delta \sum \limits _{i=0}^{k-1}\left( \frac{1}{2}\right) ^{q^i+i}+\delta < (2\mu _{\bar{x}}+1)\delta . \end{aligned}$$

(3.19)

Since $x_{k-1}\in \textbf{B}(\bar{x}, (2\mu _{\bar{x}}+1)\delta )$, one has from (3.13) that

$$\begin{aligned} \Vert F(x_{k-1})+\textrm{D}F(x_{k-1})d_{k-1}-F(\bar{x})\Vert\le & {} \Vert F(x_{k-1})-F(\bar{x})\Vert +L\Vert d_{k-1}\Vert \\ \le & {} 2(\mu _{\bar{x}}+1)L\delta < \bar{\delta } \end{aligned}$$

(due to (3.14)). Hence Lemmas 3 and 2(ii) are applicable to conclude that

$$\begin{aligned} \begin{array}{lll} \textrm{d}(F(x_k),C)&{}\le \frac{L}{2} \Vert d_{k-1}\Vert ^2+\left( \frac{1}{\eta }\right) ^{\frac{1}{p}} \left( h(F(x_{k-1})+\textrm{D}F(x_{k-1})d_{k-1})-h_{\min }\right) ^{\frac{1}{p}}\\ &{}\le \frac{L}{2} \Vert d_{k-1}\Vert ^2 +\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\left( \textrm{d}^2(0,{\varGamma }(x_{k-1}))+2vK\Vert d_{k-2}\Vert ^\alpha \right) ^{\frac{1}{p}}. \end{array} \end{aligned}$$

(3.20)

We now claim that

$$\begin{aligned} \textrm{d}(F(x_k),C)\le \frac{\delta }{\beta }\left( \frac{1}{2}\right) ^{q^k+k}. \end{aligned}$$

(3.21)

In fact, if $k=1$, then, (3.20), together with (3.16), (3.17) and the choice of $d_{-1}$, implies that

$$\begin{aligned} \begin{array}{lll} \textrm{d}(F(x_1),C)&{}\le \frac{L}{2} \Vert d_{0}\Vert ^2+\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\left( \textrm{d}^2(0,{\varGamma }(x_{0}))+2vK \Vert d_{-1}\Vert ^\alpha \right) ^{\frac{1}{p}}\\ &{}\le \frac{L}{2} \left( \frac{\sqrt{2}}{2}\delta \right) ^2+ \left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\left( \left( \frac{\delta }{2}\right) ^2+ \frac{\delta ^2}{4}\right) ^{\frac{1}{p}}\\ &{}= \frac{1}{4} L\delta ^2 +\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\left( \frac{1}{2} \delta ^2\right) ^{\frac{1}{p}}, \end{array} \end{aligned}$$

and so (3.21) is established because

$$\begin{aligned} \frac{1}{4} L\delta ^2 +\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\left( \frac{1}{2} \delta ^2\right) ^{\frac{1}{p}}= & {} \frac{\delta }{4} \left( \frac{1}{2} \right) ^{\frac{1}{p}-1}\left( \left( \frac{1}{2} \right) ^{1-\frac{1}{p}} L\delta +2\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\delta ^{\frac{2-p}{p}}\right) \\\le & {} \frac{\delta }{8\beta }\le \frac{\delta }{\beta } \left( \frac{1}{2}\right) ^{q +1}, \end{aligned}$$

where the first inequality is true by (3.14) and the facts that $\left( \frac{1}{2} \right) ^{\frac{1}{p}-1}\in [1,\sqrt{2})$ (noting $p\in [1,2)$). Now we consider the case when $k\ge 2$. Then, noting the following elementary inequality:

$$\begin{aligned} (a+b)^r\le a^r+b^r\quad \mathrm {for \;any \;} a\ge 0, \; b\ge 0 \mathrm { \;and \;} r\in (0,1], \end{aligned}$$

(3.22)

one has, from (3.20) and the induction assumption that (3.18) holds for each $i\le k-1$, that

$$\begin{aligned} \begin{array}{lll} \textrm{d}(F(x_k),C) &{}\le &{} \frac{L}{2} \Vert d_{k-1}\Vert ^2 +\left( \frac{1}{2\eta v}\right) ^{\frac{1}{p}}\left( \textrm{d}^{\frac{2}{p}}(0,{\varGamma }(x_{k-1}))+(2vK)^{\frac{1}{p}}\Vert d_{k-2}\Vert ^{\frac{\alpha }{p}}\right) \\ &{}\le &{} \frac{L}{2}(2\delta )^2\left( \frac{1}{2}\right) ^{2(q^{k-1}+k-1)}\\ &{}&{}+\left( \frac{1}{2\eta v}\right) ^\frac{1}{p}\left( \delta ^{\frac{2}{p}}\left( \frac{1}{2}\right) ^{\frac{2}{p}(q^{k-1}+k-1)} +(2vK)^\frac{1}{p}(2\delta )^{\frac{\alpha }{p}}\left( \frac{1}{2}\right) ^{\frac{\alpha }{p}(q^{k-2}+k-2)} \right) .\\ \end{array} \end{aligned}$$

(3.23)

Noting by $2vK\le \frac{1}{16}(2\delta )^{2-\alpha }$(that is, $\delta \le \frac{1}{2}\left( \frac{1}{32vK}\right) ^{\frac{1}{\alpha -2}}$ by (3.14)), we have that

$$\begin{aligned} (2vK)^\frac{1}{p}(2\delta )^{\frac{\alpha }{p}}\le \left( \frac{1}{16}(2\delta )^{2-\alpha }\right) ^{\frac{1}{p}}(2\delta )^{\frac{\alpha }{p}} =\left( \frac{1}{2} \delta \right) ^{\frac{2}{p}}, \end{aligned}$$

(3.24)

and also note that

$$\begin{aligned} 2(q^{k-1}+k-1)\ge q^k+k ,\quad \frac{2}{p}(q^{k-1}+k-1)\ge q^k+k-1 \end{aligned}$$

and

$$\begin{aligned} \frac{\alpha }{p}(q^{k-2}+k-2)\ge q^k+k-2 \end{aligned}$$

(as $q=\min \{\frac{\alpha }{2},\frac{2}{p}\}$, $\alpha >2$, $p\in [1,2]$ and $k\ge 2$). It follows from (3.23) that

$$\begin{aligned} \begin{array}{lll} \textrm{d}(F(x_k),C)&{}\le \frac{L}{2}(2\delta )^2 \left( \frac{1}{2}\right) ^{ q^{k}+k} +\left( \frac{1}{2\eta v}\right) ^\frac{1}{p}\left( \delta ^{\frac{2}{p}}\left( \frac{1}{2}\right) ^{q^{k }+k-1} +\left( \frac{1}{2} \delta \right) ^{\frac{2}{p}}\left( \frac{1}{2}\right) ^{ q^{k }+k-2} \right) \\ &{}= 2\delta \left( L\delta +\left( \frac{1}{2\eta v}\right) ^\frac{1}{p}\left( \delta ^{\frac{2-p}{p}}+ \left( \frac{1}{2}\right) ^{\frac{2}{p}-1} \delta ^{\frac{2-p}{p}} \right) \right) \left( \frac{1}{2}\right) ^{q^k+k}\\ &{}\le 2\delta \left( L\delta +2\left( \frac{1}{2\eta v}\right) ^\frac{1}{p}\delta ^{\frac{2-p}{p}}\right) \left( \frac{1}{2}\right) ^{q^k+k}\\ &{}< \frac{\delta }{\beta }\left( \frac{1}{2}\right) ^{q^k+k}, \end{array} \end{aligned}$$

where the last inequality holds because, by (3.14), $L\delta +2\left( \frac{1}{2\eta v}\right) ^\frac{1}{p}\delta ^{\frac{2-p}{p}}\le \frac{1}{2\sqrt{2}\beta }< \frac{1}{2 \beta }$. Hence (3.21) is established. Thus, by (3.10), we have that

$$\begin{aligned} \textrm{d}(0,{\varGamma }(x_k))\le \beta \textrm{d}(F(x_k),C)< \delta \left( \frac{1}{2}\right) ^{q^k+k}. \end{aligned}$$

(3.25)

In view of step 5 of Algorithm 3.1, it follows from Lemma 2(i) that

$$\begin{aligned} \Vert d_k\Vert \le \left( \textrm{d}^2(0,{\varGamma }(x_k))+2vK\Vert d_{k-1}\Vert ^{\alpha }\right) ^{\frac{1}{2}} \le \textrm{d}(0,D(x_k))+(2vK)^{\frac{1}{2}}\Vert d_{k-1}\Vert ^{\frac{\alpha }{2}} \end{aligned}$$

(thanks to (3.22)). Then, by (3.25) and the induction assumption that (3.18) holds for $i=k-1$, it follows that

$$\begin{aligned} \Vert d_k\Vert \le \delta \left( \frac{1}{2}\right) ^{q^{k}+k}+(2vK)^{\frac{1}{2}}(2\delta )^{\frac{\alpha }{2}}\left( \frac{1}{2}\right) ^{\frac{\alpha }{2}(q^{k-1}+k-1)}. \end{aligned}$$

Since $\frac{\alpha }{2}(q^{k-1}+k-1)\ge q^{k}+k-1$ (as $\frac{\alpha }{2}\ge q\ge 1$) and since $(2vK)^{\frac{1}{2}}(2\delta )^{\frac{\alpha }{2}}\le \frac{1}{2}\delta$ by (3.24) (with 2 in place of p), it follows that

$$\begin{aligned} \Vert d_k\Vert \le \delta \left( \frac{1}{2}\right) ^{q^{k}+k}+\frac{\delta }{2}\left( \frac{1}{2}\right) ^{q^{k}+k-1}= 2\delta \left( \frac{1}{2}\right) ^{q^{k}+k}. \end{aligned}$$

(3.26)

Hence, combining (3.19), (3.21) and (3.26), one checks that (3.18) holds for $i=k$ and so for each $i=0,1,2,\cdots$. Consequently, $\{x_k\}$ is a Cauchy sequence, and converges to a point $x^*$, which, by (3.18), satisfies that $F(x^*)\in C$, and

$$\begin{aligned} \textrm{d}(x_k,x^*)\le \sum _{i=k}^{+\infty } \Vert d_i\Vert \le 4\delta \left( \frac{1}{2}\right) ^{q^k+k}. \end{aligned}$$

Therefore, $\{x_k\}$ converges to $x^*$ at a rate of q $\left( =\min \left\{ \frac{\alpha }{2},\frac{2}{p}\right\} \right)$, and the proof is complete.

In the case when each $\epsilon _k=0$, we obtain the following exact R-LPA:

Algorithm 2

Then, the following corollary follows directly from Theorem 1 which shows the local convergence results of any sequence generated by Algorithm 2.

Corollary 1

Suppose that all assumptions of Theorem 1 hold. Then, for any $\delta >0$, there exists $r_\delta \in (0,\delta )$ such that any sequence $\{x_k\}$ generated by Algorithm 2 with initial point $x_0\in \textbf{B}(\bar{x},r_\delta )$, stays in $\textbf{B}(\bar{x}, \delta )$ and converges to some point $x^*$ satisfying $F(x^*)\in C$ at a rate of $\frac{2}{p}$.

3.2 Globalized Riemannian linearized proximal algorithm

By virtue of the backtracking line-search, this subsection is to propose a global version of Algorithm 2 and establish its global convergence theorem. The globalized Riemannian linearized proximal algorithm presented below is an extension of [14, Algorithm 17] to the Riemannian manifold settings.

Algorithm 3

The following proposition shows that any cluster point of a sequence generated by Algorithm 3 is a stationary point. Recall that F is continuously differentiable on M. For a convex function $g:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$, the subdifferential of g at $x\in {\mathbb {R}}^n$ is defined by

$$\begin{aligned} \partial g(x):=\{\xi \in {\mathbb {R}}^n:\; g(y)\ge g(x)+\langle \xi ,y-x\rangle , ~\mathrm {for \;each \;} y \in {\mathbb {R}}^n\}. \end{aligned}$$

Proposition 1

Let $\{x_k\}$ be a sequence generated by Algorithm 3 and assume that $\{x_k\}$ has a cluster point $\bar{x}$ such that $\textrm{D}F$ is local Lipschitz continuous at $\bar{x}$. hen, $\bar{x}$ is a stationary point: $0\in \textrm{D}F(\bar{x})^* \circ \partial h(F(\bar{x}))$, and $F(\bar{x})\in C$ if $\bar{x}$ is a regular point of inclusion (3.4).

Proof

By [14, Remark 16], it remains to show that $0\in \textrm{D}F(\bar{x})^* \circ \partial h(F(\bar{x}))$. To proceed, let $\{x_{k_{i}}\}$ be a subsequence of $\{x_k\}$ such that $\lim _{i\rightarrow \infty }x_{k_{i}}=\bar{x}$. Let $\{d_{k_i}\}$ be the associated sequence generated by Algorithm 3. For each $k_i$, there is $u_{k_i}\in T_{\bar{x}}M$ such that $x_{k_i}=\exp _{\bar{x}}u_{k_i}$. Since $u_{k_i}\rightarrow 0$ and $\textrm{D}\exp _{\bar{x}}0=\mathbb {I}_{T_{\bar{x}}M}$, without loss of generality, we assume that $(\textrm{D}\exp _{\bar{x}}u_{k_i})^{-1}$ exists for each ${k_i}$ and $\{\Vert (\textrm{D}\exp _{\bar{x}}u_{k_i})^{-1}\Vert \}$ is bounded. For each $k_i$, write $w_{k_i}:=(\textrm{D}\exp _{\bar{x}}u_{k_i})^{-1}d_{k_i}$. Noting that for each i,

$$\begin{aligned} \frac{1}{2v}\Vert d_{k_i}\Vert ^2\le h_{x_{k_i},v}(d_{k_i})-h_{ \min }\le h(F(x_{k_i}))-h_{ \min }, \end{aligned}$$

and $h(F(\cdot ))$ is continuous, one has that $\{d_{k_{i}}\}$ is bounded and so

$$\begin{aligned} \{ w_{k_i} \}\quad \mathrm {is \;bounded}. \end{aligned}$$

(3.28)

Set $\bar{d}:=\arg \min \limits _{d\in T_{\bar{x}}M} h_{\bar{x},v}(d)$. By the definition of $h_{ x,v}(\cdot )$ and the isometry $P_{x_{k_i},\bar{x}}$, we obtain

$$\begin{aligned} h_{ x_{k_i},v}(d_{k_i})-h_{\bar{x},v}(\bar{d})\le h(F(x_{k_i})+\textrm{D}F(x_{k_i})P_{x_{k_i},\bar{x}}\bar{d})-h(F(\bar{x})+\textrm{D}F(\bar{x})\bar{d}). \end{aligned}$$

(3.29)

For each ${k_i}$, write $\varDelta _{{k_i}}:=h_{x_{k_i},v}(d_{k_i})-h(F(x_{{k_i}})).$ Then, by the definition of $d_{k_i}$, we have that

$$\begin{aligned} h(F(x_{k_i})+\textrm{D}F(x_{k_i})d_{k_i})-h(F(x_{k_i}))\le \varDelta _{k_i}\le 0. \end{aligned}$$

(3.30)

We assert that

$$\begin{aligned} \lim _{i\rightarrow +\infty }\varDelta _{k_{i}}=0.\end{aligned}$$

(3.31)

Granting this, one has that

$$\begin{aligned} h(F(\bar{x}))=\lim _{i\rightarrow +\infty }h(F(x_{k_i}))=\lim _{i\rightarrow +\infty }h_{k_{i},v}(d_{k_i}), \end{aligned}$$

(3.32)

and then letting $i\rightarrow \infty$ in (3.29), by (3.32) and the fact that $h, F, \textrm{D}F, P_{\cdot ,\bar{x}}$ are respectively continuous at $\bar{x}$, one can check that

$$\begin{aligned} h(F(\bar{x})) =\lim _{i\rightarrow +\infty }h_{k_{i},v}(d_{k_i})\le h_{\bar{x},v}(\bar{d}). \end{aligned}$$

Combining this with the definitions of $\bar{d}$ and $h_{\bar{x},v}$ yields that $\bar{d}=0$. This, together with the optimal condition applied to $h_{\bar{x},v}(\cdot )$, gives that $0\in \textrm{D}F(\bar{x})^* \circ \partial h(F(\bar{x}))$.

Now we apply [5, Theorem 2.4] to show that (3.31) holds. To do this, for each $k_i$, write $D_{{k_i}}:=\{w_{k_i}\}.$ Define $\hat{F}_{\bar{x}}(\cdot ):=F\circ \exp _{\bar{x}}(\cdot )$. Fix ${k_i}$. Then, it follows from the definition of $u_{k_i}$ and (3.30) that

$$\begin{aligned} h(\hat{F}_{\bar{x}}(u_{k_i})+\textrm{D}\hat{F}_{\bar{x}}(u_{k_i})w_{k_i})-h(\hat{F}_{\bar{x}}(u_{k_i}))= & {} h(F(x_{k_i})+\textrm{D}F(x_{k_i})d_{k_i})-h(F(x_{k_i}))\\\le & {} \varDelta _{k_i}\le 0 \end{aligned}$$

and so

$$\begin{aligned}{}[0\in D_{k_i}]\Longleftrightarrow [w_{k_i}=0]\Longleftrightarrow [d_{k_i}=0]\Longleftrightarrow [\varDelta _{k_i}=0]. \end{aligned}$$

Note by the definition of $d_{k_i}$ and the optimal condition (applied to $h_{x_k,v}(\cdot )$) that

$$\begin{aligned}{}[d_{k_i}=0]\Longleftrightarrow [0\in \textrm{D}F(x_{k_i})^{*} \circ \partial h(F(x_{k_i}))]\Longleftrightarrow [0\in \textrm{D}\hat{F}_{\bar{x}}(u_{k_i})^{*} \circ \partial h(\hat{F}_{\bar{x}}(u_{k_i}))] \end{aligned}$$

(noting that $\textrm{D}\hat{F}_{\bar{x}}(u_{k_i})=\textrm{D} F(x_{k_i})\circ \textrm{D}\exp _{\bar{x}}u_{k_i}$ and $\textrm{D}\exp _{\bar{x}}u_{k_i}$ is invertible). Thus, one has

$$\begin{aligned}{}[0\in D_{k_i}]\Longleftrightarrow [\varDelta _{k_i}=0]\Longleftrightarrow [0\in \textrm{D}\hat{F}_{\bar{x}}(u_{k_i})^{*} \circ \partial h(\hat{F}_{\bar{x}}(u_{k_i}))]. \end{aligned}$$

Then, conditions (a)-(c) in [5, (2.2)] hold for $u_{k_i},w_{k_i},\hat{F}_{\bar{x}}$ in place of $x_i,d_i,f$ and so $\{u_{k_i}\}$ can be regarded as a sequence generated by algorithm [5, (2.1)]. Note further that $\{w_{k_i}\}$ is bounded by (3.28). Therefore, [5, Theorem 2.4] is applicable to concluding that (3.31) holds. The proof is complete.

We now establish in the following theorem a global superlinear convergence result for Algorithm 3 under the assumptions of local weak sharp minima of order p and the quasi-regular condition.

Theorem 2

Let $\{x_k\}$ be a sequence generated by Algorithm 3 and assume that $\{x_k\}$ has a cluster point $\bar{x}$ such that $\bar{x}$ is a quasi-regular point for (3.4), C is the set of local weak sharp minima of order p for h at $F(\bar{x})\in C$ and $\textrm{D} F$ is local Lipschitz continuous at $\bar{x}$.

Proof

Firstly, we show the following claim.

Claim For any subsequence $\{ x_{k_i} \}$ such that $x_{x_i}\rightarrow \bar{x}$, there exist $i_0\in {\mathbb {N}}$ and $\tau >0$ such that

$$\begin{aligned} h(F(R_{x_{k_i}}d_{k_i})))-h_{\min }\le \tau \textrm{d}^2(0,{\varGamma }(x_{k_i}))\quad \mathrm { \;for \;each \;}i\ge i_0. \end{aligned}$$

(3.33)

To do this, fix a subsequence $\{ x_{k_i} \}$ such that $x_{x_i}\rightarrow \bar{x}$. Then, by the continuity of F, it follows that

$$\begin{aligned} F(x_{k_i})\rightarrow F(\bar{x})\quad \textrm{and}\quad \textrm{d}(F(x_{k_i}),C)\rightarrow 0. \end{aligned}$$

(3.34)

Noting by the assumptions, there exist $\beta$, $\eta$, $\bar{\delta }$ and $L\ge 1$ such that (2.3) holds with $\bar{\delta }$ in place of r,

$$\begin{aligned} \eta \, \textrm{d}^p(z,C)\le h(z)-h_{\min }\quad \mathrm{for~each}~ z\in \textbf{B}(F(\bar{x}),\bar{\delta }), \end{aligned}$$

(3.35)

$$\begin{aligned} \textrm{d}(0,{\varGamma }(x))\le \beta \,\textrm{d}(F(x),C)\quad \mathrm{for~each}~ x\in \textbf{B}(\bar{x},\bar{\delta }). \end{aligned}$$

(3.36)

Combining (3.34) and (3.36), we apply Lemma 2(i) to obtain that

$$\begin{aligned} \textrm{d}(0,{\varGamma }(x_{k_i}))\rightarrow 0\quad \textrm{and}\quad \Vert d_{k_i}\Vert \rightarrow 0. \end{aligned}$$

(3.37)

Thus, there exists an integer $i_0$ such that, for all $i\ge i_0$, the following inequalities hold:

$$\begin{aligned} \textrm{d}(x_{k_i},\bar{x})< \frac{\bar{\delta }}{2},\quad \Vert d_{k_i}\Vert < \frac{\bar{\delta }}{2}, \end{aligned}$$

(3.38)

and

$$\begin{aligned} \quad \Vert F(R_{x_{k_i}}d_{k_i})-F(\bar{x})\Vert< \bar{\delta }, \quad \Vert F(x_{k_i})+\textrm{D}F(x_{k_i})d_{k_i}-F(\bar{x})\Vert < \bar{\delta }. \end{aligned}$$

(3.39)

Then, it follows from Lemmas 2(ii) that

$$\begin{aligned} h(F(R_{x_{k_i}}d_{k_i}))-h_{\min }\le h(F(R_{x_{k_i}}d_{k_i}))-h\left( F(x_{k_i})+\textrm{D}F(x_{k_i})d_{k_i}\right) +\frac{1}{2v}\textrm{d}^2(0,{\varGamma }(x_{k_i})). \end{aligned}$$

(3.40)

Without loss of generality, we assume that h is Lipschitz continuous on $\textbf{B}(F(\bar{x}),\bar{\delta })$ with Lipschitz constant l (using a smaller $\bar{\delta }$ if necessary). Then, by (3.39) and (3.38), we conclude from Lemmas 1 and 2(i) that

$$\begin{aligned} \begin{aligned} h(F(R_{x_{k_i}}d_{k_i}))\!-\!h\left( F(x_{k_i})\!+\!\textrm{D} F(x_{k_i})d_{k_i}\right)&\le l\Vert F(R_{x_{k_i}}d_{k_i}))\!-\!F(x_{k_i})-\textrm{D}F(x_{k_i})d_{k_i}\Vert \\&\le \frac{Ll}{2}\textrm{d}^2(0,{\varGamma }(x_{k_i})), \end{aligned} \end{aligned}$$

and so it follows from (3.40) that

$$\begin{aligned} h(F(R_{x_{k_i}}d_{k_i})))-h_{\min }\le \tau \textrm{d}^2(0,{\varGamma }(x_{k_i})), \end{aligned}$$

where $\tau :=\frac{Ll}{2}+\frac{1}{2v}<+\infty$. Thus the claim is seen to hold.

Secondly, we show that there exists $\delta >0$ such that the following implication holds for any k:

$$\begin{aligned} \textrm{d}(x_k, \bar{x})<\delta \Longrightarrow t_k= 1. \end{aligned}$$

(3.41)

Suppose on the contrary that, there exist a sequence $\{\delta _i\}\subseteq (0, 1)$ with $\delta _i \downarrow 0$ and a subsequence $\{ k_i \}\subseteq {\mathbb {N}}$ such that $x_{k_i}\in \textbf{B}(\bar{x},\delta _i)$ and $t_{k_i}\ne 1$. Then, $x_{k_i}\rightarrow \bar{x}$ and, for each $k_i$,

$$\begin{aligned} h(F(R_{x_{k_i}}d_{k_i}))-h(F(x_{k_i}))\!>\!c\left( h\left( F(x_{k_i})\!+\!\textrm{D}F(x_{k_i})d_{k_i}\right) \!+\!\frac{1}{2v}\Vert d_{k_i}\Vert ^2\!-\!h(F(x_{k_i}))\right) . \end{aligned}$$

(3.42)

Note by the above claim that there exist $i_0$ and $\tau >0$ such that (3.33) holds. This, together with (3.42), implies that

$$\begin{aligned} h_{\min }-h(F(x_{k_i}))+\tau \textrm{d}^2(0,{\varGamma }(x_{k_i}))\ge & {} h(F(R_{x_{k_i}}d_{k_i})))-h(F(x_{k_i}))\\> & {} c(h(F(x_{k_i})+\textrm{D}F(x_{k_i})d_{k_i})\\{} & {} +\frac{1}{2v}\Vert d_{k_i}\Vert ^2-h(F(x_{k_i})))\\\ge & {} c\left( h_{\min }+\frac{1}{2v}\Vert d_{k_i}\Vert ^2-h(F(x_{k_i}))\right) . \end{aligned}$$

Hence

$$\begin{aligned} (1-c)\left( h_{\min }-h(F(x_{k_i}))\right) +\tau \textrm{d}^2(0,{\varGamma }(x_{k_i}))\ge \frac{c}{2v}\Vert d_{k_i}\Vert ^2>0, \end{aligned}$$

(3.43)

(noting that $d_{k_i}\not =0$ by (3.42)). On the other hand, applying (3.35) and (3.36), we conclude that

$$\begin{aligned} (1-c)\left( h_{\min }-h(F(x_{k_i}))\right) \le (c-1)\eta \beta ^{-p} \textrm{d}^p(0,{\varGamma }(x_{k_i})). \end{aligned}$$

Hence it follows from (3.43) that

$$\begin{aligned} 0 < (c-1)\eta \beta ^{-p} +\tau \textrm{d}^{2-p}(0,{\varGamma }(x_{k_i})). \end{aligned}$$

Since $\textrm{d}(0,\varGamma (x_{k_i}))\rightarrow 0$ (see (3.37)) and that $p<2$, we arrive at (by taking the limit) $0<(c-1)\eta \beta ^{-p}$, which is clearly a contradiction. Thus, we establish the implication (3.41) for some $\delta >0$.

Finally, we show that $\{x_k\}$ converges to $\bar{x}$ at a rate of $\frac{2}{p}$. Let $\delta >0$ be such that the implication (3.41) holds for any k. Then, by Corollary 1, there exists $r_\delta \in (0,\delta )$ such that any sequence $\{\tilde{x}_k\}$ generated by Algorithm 2 with initial point $\tilde{x}_0\in \textbf{B}(\bar{x}, r_\delta )$ stays in $\textbf{B}(\bar{x}, \delta )$. Since $\bar{x}$ is a cluster point of $\{x_k\}$, there exists integer $j_0$ such that $\textrm{d}(x_{j_0},\bar{x})<r_\delta$. Let $\tilde{x}_0:=x_{j_0}\in \textbf{B}(\bar{x}, r_\delta )$, and let $\{\tilde{x}_k\}$ be generated by Algorithm 2 with $\tilde{x}_0$ being the initial point. Then we have that $\textrm{d}(\tilde{x}_k,\bar{x})<\delta$ for any $k=0,1,2,\cdots$ and $\{\tilde{x}_k\}$ is convergent. Moreover, since $\textrm{d}(x_{j_0},\bar{x})<r_\delta \le \delta$, it follows from (3.41) that $t_{j_0}=1$. This means that $\tilde{x}_1$ and $x_{j_0+1}$ are the same. Hence $\textrm{d} (x_{j_0+1},\bar{x})<\delta$, and we further have that $t_{j_0+1}=1$. Inductively, we conclude that $t_k=1$ for all $k\ge j_0$. Thus $\{x_k\}_{k\ge j_0}$ coincides with $\{\tilde{x}_k\}$ and so is convergent (to $\bar{x}$) at a rate of $\frac{2}{p}$ (as so is $\{\tilde{x}_k\}$ as noted earlier). Therefore the proof is complete.

4 The NIEP

This section is devoted to applying the R-LPA type algorithms to solve the NIEP (1.1). Recall that $\mathcal {O}(n)$ is an orthogonal Stiefel manifold (cf. [1]). Hence, $\mathcal {O}(n)\times \mathcal {V}$ is a product manifold where $\mathcal {V}$ is given by (1.2). Let $p\ge 1$. As mentioned in Section 1, solving the NIEP (1.1) is equivalent to solving (3.1) with

$$\begin{aligned} \left\{ \begin{array}{ll} M&{}:=\mathcal {O}(n)\times \mathcal {V},\\ F(U,V)&{}:=U(\varLambda +V)U^T\quad \mathrm { for\; each \;}(U,V)\in \mathcal {O}(n)\times \mathcal {V},\\ h(A)&{}:= \frac{1}{p}\textrm{d}^{p}(A,\mathbb {R}_+^{n\times n})\quad \mathrm { for \;each \;}A\in \mathbb {R}^{n\times n}; \end{array}\right. \end{aligned}$$

(4.1)

or equivalently,

$$\begin{aligned} \min _{(U,V)\in \mathcal {O}(n)\times \mathcal {V}}f_p(U,V):=h(F(U,V)). \end{aligned}$$

(4.2)

Note that F is analytic on $\mathcal {O}(n)\times \mathcal {V}$ (cf. [28]). Below, we recall a retraction R on $\mathcal {O}(n)\times \mathcal {V}$ and the differential of F; see [1, 28] for more details. To proceed, let $(U,V)\in \mathcal {O}(n)\times \mathcal {V}$. The tangent space at (U, V) to $\mathcal {O}(n)\times \mathcal {V}$ is given by

$$\begin{aligned} T_{(U,V)}(\mathcal {O}(n)\times \mathcal {V})=T_U\mathcal {O}(n)\times T_V\mathcal {V}, \end{aligned}$$

where $T_U\mathcal {O}(n)$ and $T_V\mathcal {V}$ are tangent spaces at U and V to $\mathcal {O}(n)$ and $\mathcal {V}$, respectively, and defined by

$$\begin{aligned} T_U\mathcal {O}(n):=\{U\varOmega |\; \varOmega ^T=-\varOmega ,\; \varOmega \in {\mathbb {R}}^{n\times n}\}\quad \textrm{ and }\;\quad T_V\mathcal {V}= \mathcal {V}. \end{aligned}$$

Let $R: T(\mathcal {O}(n)\times \mathcal {V})\rightarrow \mathcal {O}(n)\times \mathcal {V}$ be the retraction such that for each $(U,V)\in \mathcal {O}(n)\times \mathcal {V}$, the restriction of R to (U, V), that is, $R_{(U,V)}:T_{(U,V)}(\mathcal {O}(n)\times \mathcal {V}) \rightarrow \mathcal {O}(n)\times \mathcal {V}$, is given by

$$\begin{aligned} R_{(U,V)}(\xi _U,\eta _V):=(R_U\xi _U, R_V\eta _V)\quad \mathrm {for \;each \;}(\xi _U,\eta _V)\in T_{(U,V)}(\mathcal {O}(n)\times \mathcal {V}), \end{aligned}$$

(4.3)

where $R_U, R_V$ are retractions at $\mathcal {O}(n)$ and $\mathcal {V}$, respectively, and defined by

$$\begin{aligned} \left\{ \begin{array}{ll} R_U(\xi _U):&{}=\textrm{qf}(U+\xi _U)\quad \quad \mathrm {for \;each }\; \xi _U\in T_U\mathcal {O}(n);\\ R_V(\eta _V):&{}=V+\eta _V\quad \quad \mathrm {for \;each }\;\eta _V\in T_V\mathcal {V}.\end{array} \right. \end{aligned}$$

Here $\textrm{qf}(A)$ denotes the Q factor of the QR decomposition of a nonsingular matrix $A\in \mathbb {R}^{n\times n}$ in the form of $A=Q\tilde{R}$ with $Q\in \mathcal {O}(n)$ and $\tilde{R}$ an upper triangular matrix having strictly positive positive diagonal entries (see [1, p. 58–59] for more details). Now, we present the differential of F. Following [28], the differential $\textrm{D}F(U,V): T_{(U,V)}(\mathcal {O}(n)\times \mathcal {V})\rightarrow T_{F(U,V)}{\mathbb {R}}^{n\times n}\simeq {\mathbb {R}}^{n\times n}$ of F at $(U,V)\in \mathcal {O}(n)\times \mathcal {V}$ is given by

$$\begin{aligned} \textrm{D}F(U,V)(\xi _U,\eta _V):= & {} U\eta _VU^T-[U(\varLambda +V)U^T,\xi _UU^T]\nonumber \\{} & {} \mathrm { for \;each \;}(\xi _U,\eta _V)\in T_{(U,V)}(\mathcal {O}(n)\times \mathcal {V}), \end{aligned}$$

(4.4)

where $[A,B]=AB-BA$ is Lie Bracket of A and B.

Associated to h defined in (4.1), the linearized proximal mapping $h_{(U,V),v}$ for fixed $(U,V)\in \mathcal {O}(n)\times \mathcal {V}$ and $v>0$ in (3.3) is reduced to

$$\begin{aligned} h_{(U,V),v}(d):= & {} \frac{1}{p}\textrm{d}^{p}(F(U,V)+\textrm{D}F(U,V)d,\mathbb {R}_+^{n\times n})\nonumber \\{} & {} +\frac{1}{2v}\Vert d\Vert ^2\quad \mathrm { for \;each }~d\in T_{(U,V)} (\mathcal {O}(n)\times \mathcal {V}). \end{aligned}$$

(4.5)

For the remainder of this section, we assume that $1< p<2$. Then, solving the subproblem

$$\begin{aligned} \min \limits _{d\in T_{(U,V)}( \mathcal {O}(n)\times \mathcal {V})} h_{(U,V),v}(d) \end{aligned}$$

is equivalent to solving the following nonlinear equation due to first order optimality condition:

$$\begin{aligned} G_{(U,V),v}(d):= & {} h'_{(U,V),v}(d)\\= & {} \textrm{d}^{p-2}(F(U,V)+\textrm{D}F(U,V)d,\mathbb {R}_+^{n\times n})\textrm{D}F(U,V)^*\\{} & {} \circ (\mathbb {I}-\varPi _{\mathbb {R}_+^{n\times n}})(F(U,V)+\textrm{D}F(U,V)d)+2vd\\= & {} 0, \end{aligned}$$

where $\mathbb {I}$ denotes the identity operator and $\varPi _{\mathbb {R}_+^{n\times n}}$ is the projection onto $\mathbb {R}_+^{n\times n}$. Inspired by this, we propose the following algorithm for solving (4.2).

Algorithm 4

The corresponding global version of Algorithm 4 is as follows.

Algorithm 5

Remark 3

Clearly, the sequence generated by Algorithm 4 (resp. Algorithm 5) for solving (4.2) can also be regarded as a sequence generated by Algorithm 2 (resp. Algorithm 3) for solving (3.1) with (4.1).

To proceed, associated to problem (4.2), we consider the inclusion

$$\begin{aligned} F(U,V) \in {\mathbb {R}}_+^{n\times n}. \end{aligned}$$

(4.6)

For ensuring the regularity condition for inclusion (4.6), we will make use of the Robinson constraint qualification considered in [21, Definition 2]. To do this, as usual, we use $\textrm{cone}A$ (resp. $\textrm{int}A$) to denote the conic hull (resp. interior) of a subset A, while the image of a linear operator $T:\mathbb {R}^n\rightarrow \mathbb {R}^m$ is denoted by ${\text {im}} T$.

Proposition 2

Let $(\bar{U},\bar{V})\in \mathcal {O}(n)\times \mathcal {V}$ be such that $F(\bar{U},\bar{V})\in {\mathbb {R}}_+^{n\times n}$. Suppose that the Robinson constraint qualification for (4.6) holds at $(\bar{U},\bar{V})$:

$$\begin{aligned} 0\in \textrm{int}\{F(\bar{U},\bar{V})+{\text {imD}}F(\bar{U},\bar{V})+{\mathbb {R}}_-^{n\times n}\}. \end{aligned}$$

(4.7)

Then $(\bar{U},\bar{V})$ is a regular point for (4.6).

Proof

Since ${\text {imD}}F(\bar{U},\bar{V})$ is a linear subspace of ${\mathbb {R}}^{n\times n}$, it follows from (4.7) that

$$\begin{aligned} 0\in \textrm{int}\{{\text {imD}}F(\bar{U},\bar{V})+{\mathbb {R}}_+^{n\times n}-F(\bar{U},\bar{V})\}, \end{aligned}$$

and so

$$\begin{aligned} {\text {imD}}F(\bar{U},\bar{V}) +\textrm{cone}({\mathbb {R}}_+^{n\times n}-F(\bar{U},\bar{V}))={\mathbb {R}}^{n\times n}. \end{aligned}$$

(4.8)

Passing to the negative polar and using the basic properties on polars (cf. [16, Lemma 2.1(vii)]), we arrive at

$$\begin{aligned} \textrm{ker}(\textrm{D}F(\bar{U},\bar{V})^*)\cap ({\mathbb {R}}_+^{n\times n}-F(\bar{U},\bar{V}))^\ominus =\{0\} \end{aligned}$$

(noting that $({\text {imD}}F(\bar{U},\bar{V}))^\ominus =\textrm{ker}(\textrm{D}F(\bar{U},\bar{V})^*)$, that is, $(\bar{U},\bar{V})$ is a regular point for (4.6). The proof is complete.

The main theorems are as follows, which provide the convergence properties of Algorithms 4 and 5 for solving (4.2).

Theorem 3

Let $(\bar{U},\bar{V}) \in \mathcal {O}(n)\times \mathcal {V}$ be such that $F(\bar{U},\bar{V})\in {\mathbb {R}}_+^{n\times n}$ and (4.7) hold. Then, for any $\delta >0$, there exists $r_\delta \in (0,\delta )$ such that any sequence $\{(U_k,V_k)\}$ generated by Algorithm 4 with initial point $(U_0,V_0)\in \textbf{B}((\bar{U},\bar{V}),r_\delta )$, stays in $\textbf{B}((\bar{U},\bar{V}), \delta )$ and converges to some point $(U^*,V^*)$ satisfying $F(U^*,V^*)\in {\mathbb {R}}_+^{n\times n}$ at a rate of $\frac{2}{p}$.

Proof

Consider (3.1) with (4.1). Then $h_{\min }=0$, and $C:=\textrm{arg}\min _{y\in {\mathbb {R}}^{n\times n}} h(y)={\mathbb {R}}_+^{n\times n}$. By Proposition 2, together with Remark 2, $(\bar{U},\bar{V})$ is a quasi-regular point for (4.6): $F(U,V)\in C$. In terms of the definition of h, one sees that C is the set of local weak sharp minima of order p for h at $F(\bar{U},\bar{V})\in C$. Finally, $\textrm{D} F$ is local Lipschitz continuous at $(\bar{U},\bar{V})$ (noting that F is analytic as mentioned above). Thus, all assumptions of Theorem 1 are checked and so Corollary 1 is applicable. Thus, thank to Remark 3, the conclusion is seen to hold by Corollary 1. The proof is complete.

The proof for Theorem 4 below is similar (by applying Theorem 2 instead of Corollary 1) and so is omitted here.

Theorem 4

Let $\{(U_k,V_k)\}$ be a sequence generated by Algorithm 5 and assume that $\{(U_k,V_k)\}$ has a cluster point $(\bar{U},\bar{V}) \in \mathcal {O}(n)\times \mathcal {V}$ satisfying $F(\bar{U},\bar{V})\in {\mathbb {R}}_+^{n\times n}$ and (4.7). Then, $\{(U_k,V_k)\}$ converges to $(\bar{U},\bar{V})$ at a rate of $\frac{2}{p}$.

5 Numerical experiments

In this section, we present the numerical performance of the R-LPA and the R-GLPA for solving the NIEP (1.1), or equivalently, the convex composite optimization problem (4.2). To illustrate the efficiency of our algorithm, we compare the R-GLPA with the Riemannian inexact Newton-CG algorithm (R-NCGA) [28], which is one of typical state-of-the-art algorithms developed recently for solving the NIEP (1.1). All algorithms are implemented in MATLAB R2020b and the hardware environment is Intel Core i7-10750 H, @2.60 GHz (6 CPUs), 16.00 GB of RAM.

In the numerical experiments, the NIEP (1.1) is tested with various n. Let $A^\star \in \mathbb {R}_{+}^{n\times n}$ be a random dense matrix with each entry generated from the uniform distribution on the interval (0, 1) or a 1% sparse random matrix, and we choose the eigenvalues of $A^\star$ as prescribed spectrum $\varLambda$, which is derived from the block diagonal part of the upper triangular matrix generated by Schur decomposition using the built-in function schur. Let $W\in \mathcal {V}$ be such that

$$\begin{aligned} W_{ij}= {\left\{ \begin{array}{ll} 0, &{} \textrm{if} i\ge j \textrm{or} \varLambda _{ij}\ne 0, \\ 1,&{} \textrm{ otherwise} \end{array}\right. } \end{aligned}$$

The parameters of the R-GLPA and R-NCGA are set as follows:

• R-GLPA: $p=2$, $v_k\equiv 100$, $K=1$, $c =\gamma = 0.9$, $\theta =0.5$;

• R-NCGA: $\bar{\sigma }_{\max }=0.01$, $\bar{\eta }_{\max }=0.1$, $\hat{\eta }_{\max }=0.9$, $\theta =0.9$, $t=10^{-4}$.

We use the exponential map as the retraction on manifolds for both algorithms. The starting points $(U^0,V^0)$ (resp. $(R^0,U^0,V^0)$) for the R-GLPA (resp. R-NCGA) in Sects. 5.1 and 5.2 are generated randomly by the built-in function rand and schur:

$$\begin{aligned} R^0 \odot R^0={\textbf{rand}}(n,n),\quad [U^0, V]=\textbf{schur}(R^0 \odot R^0, '\textrm{real}'), \quad V^0=W\odot V. \end{aligned}$$

The accuracy of each algorithm is evaluated by the residual (RES) of the associated convex composite optimization problem:

$$\begin{aligned} \textrm{RES}:=\left\| [U_*(\varLambda +V_*) U_*^T]_{-}\right\| _{F}, \end{aligned}$$

where $X_{-}$ denotes the componentwise negative part of a matrix $X\in \mathbb {R}^{n\times n}$, and $U_*$, $V_*$ form the Schur decomposition of the solution estimated by the algorithm. The semismooth Newton (SN) method [20] is applied to solve the subproblems in the R-GLPA when $p=2$. We use the conjugate gradient (CG) method to solve the nonlinear equations associated to the semismooth Newton method for solving the subproblem of the R-GLPA and also the subproblem of the R-NCGA. The stopping criteria of the R-GLPA and R-NCGA are listed as follows:

• Outer iteration: the number of iterations is greater than 100, or $\text {RES}<10^{-4}$.

• SN iteration (for R-GLPA): the number of iterations is greater than 50 or

  $$\begin{aligned} G_{(U_k,V_k),v_k}(d)<\max \{\theta \Vert d_{k-1}\Vert ^{3},10^{-4}\}\ (\text {sparse case}: \max \{\theta \Vert d_{k-1}\Vert ^{3},10^{-3-(n/10)}\}). \end{aligned}$$

• CG iteration:

  • R-GLPA: RES of CG iteration is smaller than $10^{-4}$ (sparse matrix cases: $10^{-3-(n/10)}$) or the number of iterations is greater than 1000;

  • R-NCGA: (2.9) and (2.10) in [28] are satisfied or the number of iterations is greater than $n^2$.

5.1 Numerical performance of the R-GLPA

In our numerical tests, we repeat our experiments over 50 different starting points. For the dense matrix case of the NIEP (1.1), the results of averaged CPU time, averaged number of outer iterations (IT for short) and the averaged RES, are listed in Table 1.

Table 1 Numerical results of the NIEP (dense matrix case)

Fig. 1

RES — the number of outer iterations

We observe from Table 1 that both algorithms own a small averaged RES which means they converge to a solution. The R-GLPA costs less time than the R-NCGA under each scale of the problem determined by n from 10 to 1000, and the advantage is more obvious in the large scale cases. However, from the convergence result in [28] we know that R-NCGA converges quadratically while the R-GLPA converges only linearly when $p=2$ from our theoretical analysis in the previous section. The phenomenon can be illustrated by Fig. 1 which shows the RES on every outer iterations for $n=100$ and $n=1000$, respectively. The random initial points especially in the large scale case make the R-NCGA take several iterations at the initial stage, and consequently even with a higher accuracy requirement ($\text {RES}<10^{-8}$), the iteration complexity of the R-GLPA is better than that of the R-NCGA. Hence, only when starting from a sufficiently precise local initial point, the quadratical convergence rate of the R-NCGA may show its power.

In addition, Fig. 2 explicitly shows the CPU time consumed by the R-GLPA and R-NCGA when the dimension n varies. The cost of CPU time of the R-NCGA grows more rapidly than that of the R-GLPA with the increasing dimension n, which implies that the R-GLPA performs better for large scale problems due to the smaller dimension of the manifold determined by the problem formulation.

Fig. 2

CPU time — the dimension n

Finally, Table 2 lists the numerical results (also averaged by 50 random trials) of the R-GLPA and R-NCGA for the 1% sparse random matrices. It is observed that the R-GLPA is much more efficient than the R-NCGA in the sparse matrix case. It is due to the convergence theorem of the R-NCGA requiring the surjective assumption on the differential of a smooth mapping (associated to the NIEP) at the cluster point generated by the R-NCGA (see [28, Assumption 1]), which is likely to be satisfied in the dense matrix case but would fail in the sparse matrix case (see [28, Remark 3.9]); while the assumption for our convergence theorem of the R-GLPA is less restrictive than that of the R-NCGA.

Table 2 Numerical results of the NIEP (sparse matrix case)

In a word, it is revealed from the above numerical results that the R-GLPA is an efficient and robust algorithm for solving the NIEP (1.1), especially for the large scale problems.

5.2 Simulation of verification for the Robinson constraint qualification

From Theorems 3 and 4 we know that the Robinson constraint qualification (4.7) is important to derive the convergence result of the R-GLPA as well as the R-LPA. One sufficient condition ensuring (4.7) at $(\bar{U},\bar{V}) \in \mathcal {O}(n)\times \mathcal {V}$ is that $F(\bar{U},\bar{V})\in \mathbb {R}_{++}^{n\times n}$ (i.e., the derived matrix is elementwise strictly positive). We conduct in this subsection the simulation study to verify (4.7) at a cluster point when numerically solving the NIEP (1.1) by the R-GLPA.

Table 3 shows the result of numbers of the final step (i.e., reaching stopping criteria) satisfying $F(U_{\textrm{final}},V_{\textrm{final}})\in \mathbb {R}_{++}^{n\times n}$ for 100 replicates in various dimension scenario, where the given eigenvalues are derived from positive ground truth random matrices with elements generated from the standard uniform distribution on the open interval (0, 1) (i.e., rand(n, n)).

Table 3 Frequency of satisfaction of the condition (4.7) for 100 replicates

From the simulation results in Table 3 we observe that when the eigenvalues are generated from sufficient positive matrices (e.g., rand$(n,n)+0.5$ or rand$(n,n)+1.0$), the condition (4.7) holds with high probability at the final step.

5.3 Illustrative examples

This subsection is devoted to several numerical examples of the NIEP (1.1) to illustrate Theorems 1–4 for different cases: Example 1 provides the case when the assumptions of Theorems 3 and 4 (and so Theorem 1 and Theorem 2) are satisfied; Example 2 does the case when neither the assumptions of Theorem 3 nor those of Theorem 4 are satisfied, while Example 3 does the case when the assumptions of Theorem 2 are not satisfied.

Example 1

Consider the NIEP (1.1) with $n:=2$, $\lambda _1:=1$ and $\lambda _2:=2$. Take $\bar{U}:=\begin{pmatrix} 1 &{} 0\\ 0 &{} 1 \end{pmatrix}$, $\bar{V}:=\begin{pmatrix} 0 &{} 0\\ 0 &{} 0 \end{pmatrix}.$ Then $F(\bar{U},\bar{V})=\begin{pmatrix} 1 &{} 0\\ 0 &{} 2 \end{pmatrix}.$ By (4.4), one deduce that

$$\begin{aligned} \begin{aligned} {\text {imD}}F(\bar{U},\bar{V})= \left\{ \begin{pmatrix} 0 &{} a+b\\ b &{} 0 \end{pmatrix}\biggm | a,b\in {\mathbb {R}}\right\} . \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} F(\bar{U},\bar{V})+{\text {imD}}F(\bar{U},\bar{V})+{\mathbb {R}}_-^{2\times 2} =\left\{ \begin{pmatrix} 1+c_1 &{} a+b+c_2\\ b+c_3 &{} 2+c_4 \end{pmatrix}\biggm | a,b\in {\mathbb {R}}, c_1,c_2,c_3,c_4\in {\mathbb {R}}_{-} \right\} . \end{aligned}$$

From this, one checks by definition that

$$\begin{aligned} \begin{pmatrix} 0 &{} 0\\ 0 &{} 0 \end{pmatrix}\in \textrm{int}\{F(\bar{U},\bar{V})+{\text {imD}}F(\bar{U},\bar{V})+{\mathbb {R}}_-^{2\times 2}\}, \end{aligned}$$

that is, the Robinson constraint qualification (4.7) is satisfied at $(\bar{U},\bar{V})$. Then assumption of Theorem 3 is satisfied and so we apply Theorem 3 to concluding that for any $\delta >0$, there exists $r_\delta \in (0,\delta )$ such that any sequence $\{(U_k,V_k)\}$ generated by the R-LPA with initial point $(U_0,V_0)\in \textbf{B}((\bar{U},\bar{V}),r_\delta )$, stays in $\textbf{B}((\bar{U},\bar{V}), \delta )$ and converges to some point $(U^*,V^*)$ satisfying $F(U^*,V^*)\in {\mathbb {R}}_+^{n\times n}$ at a rate of $\frac{2}{p}$. In fact, we conduct 100 numerical experiments of the R-LPA with each initial point randomly generated by

$$\begin{aligned} U_0=\begin{pmatrix} \sin (\frac{\pi }{2}+\theta ) &{} \cos (\frac{\pi }{2}+\theta )\\ -\cos (\frac{\pi }{2}+\theta ) &{} \sin (\frac{\pi }{2}+\theta ) \end{pmatrix} \;\textrm{and }\; V_0=\begin{pmatrix} 0 &{} t\\ 0 &{} 0 \end{pmatrix}, \end{aligned}$$

where $\theta$ and t satisfy the standard uniform distribution on $(-\frac{\pi }{2},\frac{\pi }{2})$ and $(-1,1)$, respectively. The numerical results show that for each generated sequence $\{(U_k,V_k)\}$, the relative error $\sqrt{\Vert (U_k-U_{k-1}\Vert _F^2+\Vert V_k-V_{k-1})\Vert _F^2}$ is less than $10^{-6}$ within 10 steps.

Moreover, we also test the R-GLPA as showed in Table 4. From this table, one sees that the generated sequence numerically converges to $(\bar{U},\bar{V})$, at which the Robinson constraint qualification (4.7) is satisfied.

Table 4 The iterate of Example 1 by the R-GLPA

Table 5 Typical cases for the iterate of Example 2 by the R-GLPA

Table 6 The iterate of Example 3

Example 2

Consider the NIEP (1.1) with $n:=2$, $\lambda _1:=0$ and $\lambda _2:=2$. Take $\bar{U}:=\begin{pmatrix} 1 &{} 0 \\ 0 &{} 1 \end{pmatrix}$, $\bar{V}:=\begin{pmatrix} 0 &{} 0 \\ 0 &{} 0 \end{pmatrix}$. Then $F(\bar{U},\bar{V})=\begin{pmatrix} 0 &{} 0 \\ 0 &{} 2 \end{pmatrix}$. By (4.4), one deduce that

$$\begin{aligned} {\text {imD}}F(\bar{U},\bar{V})= \left\{ \begin{pmatrix} 0 &{} a-2b \\ -2b &{} 0 \end{pmatrix}\biggm | a,b\in {\mathbb {R}}\right\} . \end{aligned}$$

Thus, similar to what we have done in Example 1, one checks that

$$\begin{aligned} \begin{pmatrix} 0 &{} 0 \\ 0 &{} 0 \end{pmatrix}\notin \textrm{int}\{F(\bar{U},\bar{V})+{\text {imD}}F(\bar{U},\bar{V})+{\mathbb {R}}_-^{2\times 2}\}, \end{aligned}$$

that is, the Robinson constraint qualification (4.7) fails at $(\bar{U},\bar{V})$. As in Example 1, we also conduct 100 numerical experiments of the R-LPA with initial points generated randomly as in Example 1. The numerical experiments own the same convergence performance: the relative error $\sqrt{\Vert (U_k-U_{k-1}\Vert _F^2+\Vert V_k-V_{k-1})\Vert _F^2}$ of each generated sequence $\{(U_k,V_k)\}$ is less than $10^{-6}$ within 10 steps.

When the R-GLPA is tested for two initial points, the numerical results are given in Table 5 which illustrates that in Case I the R-GLPA terminates at a solution in finite steps, while in Case II, the R-GLPA numerically converges to $(\bar{U},\bar{V})$ even at which the Robinson constraint qualification (4.7) fails.

Example 3

Consider the NIEP (1.1) with $n:=3$, $\lambda _1:=1+\sqrt{-1}$, $\lambda _2:=1-\sqrt{-1}$ and $\lambda _3:=0$. From the numerical results of the R-GLPA for 100 random trials (one of which is listed in Table 6), we observe that each generated sequence does not converge to a point (U, V) such that F(U, V) is a solution of the NIEP (1.1). This means that the assumptions of Theorem 2 are not satisfied.

6 Conclusions

The present paper studied the issue of numerically solving the NIEP. At first, we reformulated the NIEP as a convex composite optimization problem on Riemannian manifolds. Then we developed a scheme of the R-LPA to solve the NIEP. Under some mild conditions, we presented the local and global convergence results of the R-LPA, respectively. Moreover, numerical experiments were provided. Compared with the Riemannian Newton-CG method in [28], this R-LPA owns better numerical performances for large scale problems and sparse matrix cases.