Abstract
In this paper, based on the Riemannian optimization approach we propose a Riemannian nonlinear conjugate gradient method with nonmonotone line search technique for solving the l parameterized original problem on generalized eigenvalue problems for nonsquare matrix pencils, which was first proposed by Chu and Golub (SIAM J Matrix Anal Appl 28:770–787, 2006). The new innovative approach is to reformulate the original optimization problem as a feasible optimization problem over a certain real product manifold. The global convergence of the proposed method is then established. Some numerical tests are given to demonstrate the efficiency of the proposed method. Comparisons with some latest methods are also given.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Given two matrices \(A, B\in {{\mathbb {C}}}^{m\times n}\) and \(m>n\), the set \(\{A-\lambda B; \lambda \in {{\mathbb {C}}}\}\) constitutes a nonsquare matrix pencil. The generalized eigenvalues of the nonsquare matrix pencil are those values \(\lambda \in {{\mathbb {C}}}\) so that for each \(\lambda \) there exists a nonzero vector \({\mathbf{v}}\in {{\mathbb {C}}}^n\), called a generalized eigenvector, such that the pair \((\lambda , \mathbf{v})\) satisfies
During recent years such problems (e.g., see [1,2,3,4,5] and references therein) have received considerable attention across various areas due to many potential applications.
The main challenge of the generalized eigenvalue problem for nonsquare pencils in practice is following: even if n linearly independent eigenpairs \((\lambda _k, \mathbf{v}_k), k=1,\ldots ,n,\) are known to exist in the noiseless case, these eigenpairs may fail to exist under some perturbations. To overcome this difficulty, Boutry et al. [1] considered an optimization problem by looking for the minimum perturbation of the given pair of matrices (A, B) such that the perturbed pair \(({\hat{A}}, {\hat{B}})\) still remains to be n linearly independent eigenvectors:
where \(\Vert M\Vert \) denotes the Frobenius norm of a complex matrix M which will be defined in the end of this section. Two special cases of (1.1) that allow for a simpler formulation of this optimization problem were studied in [1]. The first case is \(n=1\), i.e., \(A, B\in {{\mathbb {C}}}^{m}\), that was discussed. For this case Boutry et al. have showed that (1.1) is equivalent to a total least squares problem, and have derived a closed form solution. The second case with \(n > 1\) was further studied, under the assumption that a single finite eigenvalue is known to be existed. The simplified formulation of the minimal perturbation approach for this special case can then be characterized as
For this case an efficient numerical algorithm is proposed to seek the possible solutions. However, the authors in [1] pointed out that the general problem (1.1) is complicated and is still open in literature.
Subsequently, Chu and Golub [2] considered the more general case of the problem (1.1) with a positive integer l, \(1\le l\le n\), i.e.,
It is noted that the problem (1.3) is formulated more general than (1.1) and (1.2), since the case of \(l=n\) is (1.1) and that of \(l=1\) in (1.2). In [2], Chu and Golub have given the algebraic characterization for the infimum of the cost function in the problem (1.3), and they have also shown that this infimum can be obtained by solving the following optimization problem over a compact set of matrices,
where \(\sigma _i(M)\) is the ith singular value of \(M\in {{\mathbb {C}}}^{m\times n}\) with decreasing order, namely, \(\sigma _1(M)\ge \sigma _2(M)\ge \cdots \ge \sigma _{\min \{m,n\}}(M)\). Moreover, as pointed out in [2], the infimum of the objection function in (1.1) has a very concise algebraic characterization by (1.4) with \(l=n\), and some equivalent characterizations for the problem (1.2) given in [1] can also be rederived by (1.4) with \(l=1\). But no algorithm for solving the corresponding optimization problem (1.4) was given in [2]. Very recently, Ito and Murota [5] proposed a robust algorithm for the problem (1.1), which is based on the total least squares problem introduced by Golub and Van Loan [6]. They have shown by numerical examples that their algorithm is more robust against data noise than the algorithm given by Boutry et al in [1]. Further, they also point out in the conclusion part of [5]: “A challenging future work is to extend our results to the problem (1.3) containing a parameter l, which seems to be much more complicated than (1.1)”. To the best of our knowledge, the numerical algorithms for solving the problem (1.3) are still remaining open at this point.
Motivated by the aforementioned studies, in this paper, we are going to establish numerical approaches for solving the problem (1.3), by directly focusing on the optimization problem (1.4) from the numerical point of view. The main contributions of this paper are summarized in the following:
- 1.
We reformulate the problem (1.4) into a Riemannian optimization problem on the product of two complex Stiefel manifolds under the optimization framework. For the purpose of approach feasibility, we then consider the reformulated problem as an equivalent one on the product of two real manifolds, each of which is an intersection of the real Stiefel manifold and the “quasi-symplectic set”, which will be defined in Sect. 2. Our formulation leads to the numerical approach for solving (1.3) being not only feasible and approachable but also efficient in numerical implementation.
- 2.
We develop a Riemannian nonlinear conjugate gradient method for the optimization problem on the real product manifold, for which we generalize Dai’s nonmonotone conjugate gradient method [7] from the Euclidean space to Riemannian product manifolds. To make the algorithm be more transparent, we first translate the algorithm into a complex-value form, and then develope a complete algorithm for solving the original problem (1.3) efficiently.
Numerical results show that the proposed algorithm is quite efficient for solving the problem (1.3) with any \(1\le l\le n\). Detailed comparisons with Boutry et al.’s algorithm [1] for the problem (1.2) in the case \(l=1\), Ito and Murota’s algorithm [5] for the problem (1.1) in the case \(l=n\) are also given. For the case \(l=n\), the algorithm is less affected by the data noise and guaranteed to yield n eigenpairs, and the algorithm generated exactly the same optimal solution as Ito and Murota’s algorithm [5], which is essentially a direct method to solve the problem (1.1), and was proposed by Boutry et al. in [1]. Moreover, the algorithm runs faster than Boutry et al.’s algorithm [1] for the case \(l=1\), where the perturbed pair with minimal perturbation admits at least one engenpair.
The rest of this paper is organized as follows. In Sect. 2 we reformulate (1.4) as a Riemannian optimization problem on the product of two complex Stiefel manifolds, and then reformulate into a real optimization problem over a certain real product manifold for the purpose of feasibility. Sect. 3 studies the geometric properties of the resultant real product manifold. A Riemannian nonlinear conjugate gradient numerical method is developed in Sect. 4, and its global convergence is also established in this section. Finally, some numerical tests are reported in Sect. 5, and some concluding remarks are given in Sect. 6.
Notation Let \(M^T\), \(M^H\) and \(\text {tr}(M)\) represent the transpose, conjugate transpose and trace of a matrix M, respectively. \(I_n\) is the identity matrix of order n. Re(M) and Im(M) denote the real and imaginary parts of M. \(\text {sym}(M):=(M+M^T)/2\) denotes the symmetric part of a real matrix M. Let \({\mathbb {N}}^+\) be the set of positive integers. Let \({{\mathbb {R}}}^{p\times q}\) and \({{\mathbb {C}}}^{p\times q}\) be the set of all \(p\times q\) real matrices and the set of all \(p\times q\) complex matrices, respectively. Let \({\mathbb {S}}^{l\times l}\) and \(\mathbb {AS}^{l\times l}\) be the sets of all \(l\times l\) real symmetric and skew-symmetric matrices, respectively. For two complex matrices \(M, N\in {{\mathbb {C}}}^{p\times q}\), their inner product is defined by
Then \({{\mathbb {C}}}^{p\times q}\) is a Hilbert inner product space over \({{\mathbb {R}}}\) and the matrix norm induced by this inner product is
2 The Transformed Problem
In this section, we reformulate the problem (1.4) into a Riemannian optimization problem on the product of two complex Stiefel manifolds. For the purpose of feasibility, we further rewrite the reformulated problem as an equivalent problem on the product of two real manifolds, with each of them being an intersection of the real Stiefel manifold and the “quasi-symplectic set” to be defined later on.
First of all, we start with the following elementary lemma.
Lemma 2.1
(Theorem 3.3 of [8]) Let \(M\in {{\mathbb {C}}}^{m\times m}\) be a Hermitian matrix with eigenvalues \(\lambda _1\ge \cdots \ge \lambda _m\). Let \(U_l\in {{\mathbb {C}}}^{m\times l}\), \(U_l^HU_l=I_l\). Then \(\lambda _{m-l+1}+\cdots +\lambda _{m}=\min \limits _{U_l} \text {tr}(U_l^HMU_l)\).
Following from Lemma 2.1, the problem (1.4) can be rewritten as follows:
Note that a real Stiefel manifold is defined to be \(\text {St}(n, l, {{\mathbb {R}}}) =\{Y\in {{\mathbb {R}}}^{n\times l} | Y^T Y = I_l\}\). Because of the constraints, the set of all feasible points of the problem (2.1) naturally becomes the product manifold \(\text {St}(n,l,{{\mathbb {C}}}) \times \text {St}(2l,l,{{\mathbb {C}}})\), where \(\text {St}(n, l, {{\mathbb {C}}})\) is the complex Stiefel manifold defined by \(\text {St}(n, l, {{\mathbb {C}}}) =\{Y\in {{\mathbb {C}}}^{n\times l} | Y^H Y = I_l\}\). Then (2.1) can be equivalent to the following Riemannian optimization problem
When dealing with the complex-value optimization problem, we generally convert them to a real-value form. Motivated by Sato et al. [9, 10] for tackling the complex singular decomposition problem, we next give a real form of the problem (2.2). To identify a complex matrix with a real matrix, we consider the following correspondence. A complex matrix \(M=M_1+i M_2\in {\mathbb {C}}^{p\times q}\), where \(M_1\), \(M_2\in {{\mathbb {R}}}^{p\times q}\), has a one-to-one correspondence with a real matrix
Let \(\phi ^{(p,q)}\) denote the isomorphism of this correspondence: \(\phi ^{(p,q)}(M)={\widetilde{M}}\). Define the following quasi-symplectic set \({\mathcal {SP}}(p,q)\) for integers p, q by
It is easy to verify that a \(2p\times 2q\) real matrix \({\widetilde{M}}\) has the block form of (2.3) if and only if \({\widetilde{M}}\in {\mathcal {SP}}(p,q)\). On the other hand, the set \({\mathcal {SP}}(p,q)\) is a linear subspace of \({{\mathbb {R}}}^{2p\times 2q}\). Therefore, the complex vector space \({{\mathbb {C}}}^{p\times q}\) is isomorphic to the linear subspace \({\mathcal {SP}}(p,q)\), with the isomorphism \(\phi ^{(p,q)}\). Furthermore, for a complex \(M\in {{\mathbb {C}}}^{p\times q}\), one can easily prove that \(M\in \text {St}(p,q, {{\mathbb {C}}})\Leftrightarrow \phi ^{(p,q)}(M)\in \text {St}(2p,2q, {{\mathbb {R}}}) \).
Define the map \(\phi ^{(p,q)}|_{\text {St}(p,q, {{\mathbb {C}}})}\) as the restriction of \(\phi ^{(p,q)}\) to the complex Stiefel manifold \(\text {St}(p,q, {{\mathbb {C}}})\). Then, this map yields a real expression for \(\text {St}(p,q, {{\mathbb {C}}})\), which is denoted throughout this paper by
For simplicity, in what follows, we define the symbol \(\phi \) as the collection of \(\phi ^{(p,q)}\) for any integers p, q as:
That is, for a complex matrix M of any size, we have
We also use the notation \({\widetilde{M}}\) for the matrix \(\phi (M)\), i.e., \({\widetilde{M}}=\phi (M)\), for simplicity. Then, matrix operations on matrices without and with tilde are related as follows:
where M, N, E are complex matrices of appropriate sizes for the addition and multiplication operations. If \({\widetilde{M}}\in {\mathcal {SP}}(n,n)\) is nonsingular, then \(M=\phi ^{-1}({\widetilde{M}})\) is also nonsingular since the isomorphism of \(\phi \) together with \(\phi (M^{-1})\phi (M)= \phi (M^{-1}M) =\phi (I_n)=I_{2n}\) implies that \({\widetilde{M}}^{-1}=\phi (M^{-1})\in {\mathcal {SP}}(n,n)\). Additionally, traces of square complex matrices M and \({\widetilde{M}}\) are related by
and the Frobenius norm of M and \({\widetilde{M}}\) are connected by
Note that for any \({\widetilde{M}}\in {\mathcal {SP}}(p,q)\) and \({\widetilde{E}}\in {\mathcal {SP}}(q,s)\), one can easily verify that \({\widetilde{M}}{\widetilde{E}}\in {\mathcal {SP}}(p,s)\), that is to say, the set \({\mathcal {SP}}(\cdot , \cdot )\) is closed under the operations in the right-hand sides of (2.6).
With above preliminaries, we can rewrite the problem (2.2) on the product of two complex Stiefel manifolds into its real form by using \(\text {Stp}(n, l)\) given in (2.4). Define
and partition \(P\in {{\mathbb {C}}}^{2l\times l}\) in (2.2) as \(P=\begin{bmatrix}P_1\\ P_2\end{bmatrix}\) with \(P_1, P_2\in {{\mathbb {C}}}^{l\times l}\), then by using the following relation we have
Due to (2.7) and (2.9), the objective function \(f(V,P)=\Vert [AV~ BV]P\Vert ^2\) in (2.2) now can be rewritten as
Throughout this paper we will use the same symbol f to denote the function of \(({\widetilde{V}}, {\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\) on the right-hand side of (2.10), which leads to the following optimization problem on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\):
For convenience, we define the mapping \(F: \text {Stp}(n,l)\times \text {Stp}(2l,l)\rightarrow {\mathcal {SP}}(m,l)\) by
3 Riemannian Geometry of \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\)
Riemannian optimization refers to minimizing a function f(x) on a Riemannian manifold \({\mathcal {M}}\). A general iteration of Riemannian optimization has the scheme:
where \(\alpha _k\) is the step size at the kth iterate \(x_k\), \(\eta _k \in {{\mathbf {T}}}_{x_k}{\mathcal {M}}\) is a tangent vector, and where \({{\mathbf {T}}}_{x}{\mathcal {M}}\) denotes the tangent space at x on a manifold \({\mathcal {M}}\), and \({\mathcal {R}}\) is a retraction [11], which is a smooth map from the tangent bundle of \({\mathcal {M}}\) into \({\mathcal {M}}\) that approximates the exponential map to the first order. The construction of a conjugate gradient direction in the Euclidean space is associated with the numerical scheme:
This formula is meaningless for Riemannian manifolds since vectors in different tangent spaces do not permit the operation of additions. So we have to find a way to transport a vector from one tangent space to another, that is, the so-called vector transport [11]. The notion of vector transport \({\mathcal {T}}\) on a manifold \({\mathcal {M}}\), roughly speaking, specifies how to transport a tangent vector \(\xi \) from a point \(x\in {\mathcal {M}}\) to a point \({\mathcal {R}}_x(\eta )\in {\mathcal {M}}\). Given a vector transport, we can define a Riemannian conjugate gradient direction as follows:
According to previous discussions, we known that, in order to apply Riemannian conjugate gradient method to the problem (2.11), we need the Riemannian gradient of the objective function f, together with a retraction and a vector transport on the product manifold \(\text {Stp}(n,l) \times \text {Stp}(2l,l)\). For this purpose, we now study some basic geometric properties of \(\text {Stp}(n,l) \times \text {Stp}(2l,l)\), including tangent spaces, Riemannian metrics, orthogonal projections, retractions, as well as vector transports, and derive an explicit expression of the Riemannian gradient of the cost function. This is motivated by [9, 10, 12,13,14] for applying Riemannian optimization approaches to solve various kinds of eigenproblems during recent years and the latest development on Riemannian conjugate gradient methods [15, 16]. For the Riemannian geometry of the real Stiefel manifold \(\text {St}(n,l,{{\mathbb {R}}})\), the reader is referred to [11, 17] for more details.
3.1 Tangent Spaces and the Orthogonal Projection
Since the tangent space of the complex Stiefel manifold \(\text {St}(n,l,{{\mathbb {C}}})\) at \(V\in \text {St}(n,l,{{\mathbb {C}}})\) can be expressed as \({{{\mathbf {T}}}}_{V} \text {St}(n,l, {{\mathbb {C}}})=\{ \xi \in {{\mathbb {C}}}^{n\times p}| \xi ^HV+V^H\xi =0\}\) [11], the tangent space of \(\text {Stp}(n,l)\) at \({\widetilde{V}}\in \text {Stp}(n,l)\) is naturally given by
And the tangent space \({{\mathbf {T}}}_{({\widetilde{V}},{\widetilde{P}})}(\text {Stp}(n,l)\times \text {Stp}(2l,l))\) at \(({\widetilde{V}},{\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\) can be expressed as
where “\(\simeq \)” means the equivalent identification of two sets.
We now proceed to develop \(\text {Stp}(n,l) \times \text {Stp}(2l,l)\) with a Riemannian metric. The Euclidean space \({{\mathbb {R}}}^{2n\times 2l}\) is endowed with the standard inner product
When restricted to the linear subspace \({\mathcal {SP}}(n, l)\) of \({{\mathbb {R}}}^{2n\times 2l}\), to get rid of the factor 2 when applying the standard inner product directly, we define the inner product on \({\mathcal {SP}}(n,l)\) to be
for any \({\widetilde{M}}= {\begin{bmatrix} M_x&{}\quad M_y\\ -M_y&{}\quad M_x \end{bmatrix}}\), \({\widetilde{N}}= {\begin{bmatrix} N_x&{}\quad N_y\\ -N_y&{}\quad N_x \end{bmatrix}}\in {\mathcal {SP}}(n,l)\). Then, the manifold \(\text {Stp}(n,l )\) as a submanifold of \({\mathcal {SP}}(n,l)\) is endowed with the induced metric and its induced norm \(\Vert {\widetilde{M}}\Vert ^2=\langle {\widetilde{M}}, {\widetilde{M}}\rangle =\frac{1}{2}\text {tr}({\widetilde{M}}^T{\widetilde{M}})\) for any \({\widetilde{M}}\in {\mathcal {SP}}(n,l)\). Further, the product manifold \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) can also be viewed as an embedded Riemannian submanifold of \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\). Thus, it can be endowed with a induced Riemannian metric
for all \(({\widetilde{V}},{\widetilde{P}})\in \text {Stp}(n,l) \times \text {Stp}(2l,l)\) and \(({\widetilde{\xi }}_1, {\widetilde{\eta }}_1), ({\widetilde{\xi }}_2, {\widetilde{\eta }}_2)\in {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\). Without causing any confusion, in what follows we use \(\langle \cdot ,\cdot \rangle \) and \(\Vert \cdot \Vert \) to denote the Riemannian metric on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) and its induced norm.
The following proposition provides us an alternative characterization of \({{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\) which will be used in the sequel of this paper.
Proposition 3.1
For any \(({\widetilde{V}},{\widetilde{P}})\in { \text {Stp}(n,l)\times \text {Stp}(2l,l)}\), define the set \(\Omega _{({\widetilde{V}},{\widetilde{P}})}\) by
Then \({{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)=\Omega _{({\widetilde{V}},{\widetilde{P}})}\).
Proof
For any \(({\widetilde{\zeta }}, {\widetilde{\chi }})\in {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\), let us define \({\widetilde{W}}_{{\widetilde{\zeta }}}={\widetilde{\Pi }}_{{\widetilde{V}}}{\widetilde{\zeta }}{\widetilde{V}}^T-{\widetilde{V}}{\widetilde{\zeta }}^T{\widetilde{\Pi }}_{{\widetilde{V}}}\) and \({\widetilde{W}}_{{\widetilde{\chi }}}={\widetilde{\Pi }}_{{\widetilde{P}}}{\widetilde{\chi }}{\widetilde{P}}^T-{\widetilde{P}}{\widetilde{\chi }}^T{\widetilde{\Pi }}_{{\widetilde{P}}}\), where \({\widetilde{\Pi }}_{{\widetilde{V}}}={\widetilde{I}}_n-\frac{1}{2}{\widetilde{V}}{\widetilde{V}}^T\) and \({\widetilde{\Pi }}_{{\widetilde{P}}}={\widetilde{I}}_{2l}-\frac{1}{2}{\widetilde{P}}{\widetilde{P}}^T\), and \({\widetilde{I}}_n={\begin{bmatrix}I_n&{}\quad 0\\ 0&{}\quad I_n\end{bmatrix}}\in {\mathcal {SP}}(n,n)\). Clearly, \({\widetilde{W}}_{{\widetilde{\zeta }}}\) and \({\widetilde{W}}_{{\widetilde{\chi }}}\) are skew-symmetric matrices and \(({\widetilde{W}}_{{\widetilde{\zeta }}}, {\widetilde{W}}_{{\widetilde{\chi }}})\in {\mathcal {SP}}(n,n) \times {\mathcal {SP}}(2l,2l)\). By using the fact that \({\widetilde{\zeta }}^T{\widetilde{V}}=-{\widetilde{V}}^T{\widetilde{\zeta }}\) and \({\widetilde{\chi }}^T{\widetilde{P}}=-{\widetilde{P}}^T{\widetilde{\chi }}\), and \(({\widetilde{V}},{\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\), we have
Therefore, we conclude that \({{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\subset \Omega _{({\widetilde{V}},{\widetilde{P}})}\).
Conversely, consider \(({\widetilde{\zeta }},\ {\widetilde{\chi }}) \in \Omega _{({\widetilde{V}},{\widetilde{P}})}\), then there exist skew-symmetric matrices \({\widetilde{W}}_{{\widetilde{\zeta }}}\in {\mathcal {SP}}(n,n)\) and \({\widetilde{W}}_{{\widetilde{\chi }}}\in {\mathcal {SP}}(2l,2l)\) such that \(({\widetilde{\zeta }},\ {\widetilde{\chi }})=({\widetilde{W}}_{{\widetilde{\zeta }}}{\widetilde{V}}, {\widetilde{W}}_{{\widetilde{\chi }}}{\widetilde{P}})\). Note that
Thus, we have that \(\Omega _{({\widetilde{V}},{\widetilde{P}})}\subset {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\), which completes the proof. \(\square \)
We now derive the orthogonal projection of any \(({\widetilde{M}}, {\widetilde{N}})\in {\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\) onto \({{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\).
Proposition 3.2
For any \(({\widetilde{M}}, {\widetilde{N}})\in {\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\) and \(({\widetilde{V}},{\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\), the orthogonal projection operator \({{\mathbf {P}}}_{({\widetilde{V}}, {\widetilde{P}})}\) onto the tangent space \({{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\) is given by
where
Proof
Notice that the linear subspaces \({\mathcal {SP}}(n,l)\) and \({\mathcal {SP}}(2l,l)\) is closed under the operations in the right-hand sides of (2.6), due to the right-hand sides of (3.5), it is easy to verify that \({{\mathbf {P}}}_{({\widetilde{V}}, {\widetilde{P}})}({\widetilde{M}},{\widetilde{N}})\in {\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\).
From the fact that \({\widetilde{V}}^T{\widetilde{V}}={\widetilde{I}}_{l}\) and \({\widetilde{P}}^T{\widetilde{P}}={\widetilde{I}}_{l}\), we have
which implies \({{\mathbf {P}}}_{({\widetilde{V}}, {\widetilde{P}})}({\widetilde{M}},{\widetilde{N}})\in {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\). On the other hand, for any \(({\widetilde{\xi }}, {\widetilde{\eta }})\in {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\),
where in the last equality we have used the fact that the trace of the product of symmetric and skew-symmetric matrices is zero. The proof is thus complete. \(\square \)
3.2 A Retraction and a Vector Transport as the Differentiated Retraction
In this subsection we discuss a retraction and a vector transport on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\), which is quite critical to Riemannian optimization for the problem (2.11). For a given search direction \(({\widetilde{\xi }}, {\widetilde{\eta }})\in { {{{\mathbf {T}}}}_{({\widetilde{V}}, {\widetilde{P}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)}\) at a current point \(({{\widetilde{V}}}, {{\widetilde{P}}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\), a search should be performed on a curve emanating from \(({{\widetilde{V}}}, {{\widetilde{P}}})\) in the direction of \(({\widetilde{\xi }}, {\widetilde{\eta }})\). For this purpose, it is necessary to find a retraction on the product manifold \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) in question, which is a map from \({{{\mathbf {T}}}}_{({{\widetilde{V}}},{{\widetilde{P}}})}\text {Stp}(n,l) \times \text {Stp}(2l,l)\) to \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\).
In this paper, we adapt the Cayley transform for our retraction which is studied by [15]. The Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. Let W be any \(n\times n\) real skew-symmetric matrix. Then \(I_n-W\) is invertible. For any \(X\in {{\mathbb {R}}}^{n\times l}\) and any \(\alpha \in {{\mathbb {R}}}\), the matrix Y given in the following closed form:
is known as the Cayley transform [15]. Using the skew-symmetry of W and \((I-M)(I+M)=(I+M)(I-M)\) for any square matrix M, one can easily prove that \(Y^TY=X^TX\), which implies that Y preserves the same constrains as X.
From Proposition 3.1, for any \({\widetilde{\xi }}\in {{\mathbf {T}}}_{{\widetilde{V}}}\text {Stp}(n,l)\), it holds \({\widetilde{\xi }}={\widetilde{W}}_{{\widetilde{\xi }}}{\widetilde{V}}\), where \({\widetilde{W}}_{{\widetilde{\xi }}}={\widetilde{\Pi }}_{{\widetilde{V}}}{\widetilde{\xi }}{\widetilde{V}}^T-{\widetilde{V}}{\widetilde{\xi }}^T{\widetilde{\Pi }}_{{\widetilde{V}}}\) is a skew-symmetric matrix, and \({\widetilde{\Pi }}_{{\widetilde{V}}}={\widetilde{I}}_n-\frac{1}{2}{\widetilde{V}}{\widetilde{V}}^T\). This leads to a retraction based on the Cayley transform on the manifold \(\text {Stp}(n,l)\) of the form
for any \(\alpha \in {{\mathbb {R}}}\). It can be shown from [15] that the curve \(\Gamma (\alpha )={{\mathcal {R}}}_{{\widetilde{V}}}(\alpha {\widetilde{\xi }})\) is contained in \(\text {Stp}(n,l)\), and satisfies \(\Gamma (0)={\widetilde{V}}\) and \(\Gamma '(0)={\widetilde{W}}_{{\widetilde{\xi }}}{\widetilde{V}}={\widetilde{\xi }}\). In a similar manner, for any \({\widetilde{\eta }}\in {{\mathbf {T}}}_{{\widetilde{P}}}\text {Stp}(2l,l)\), we can derive a retraction based on the Cayley transform on the manifold \(\text {Stp}(2l,l)\) of the form
where \({\widetilde{\eta }}={\widetilde{W}}_{{\widetilde{\eta }}}{\widetilde{P}}\), and \({\widetilde{W}}_{{\widetilde{\eta }}}={\widetilde{\Pi }}_{{\widetilde{P}}}{\widetilde{\eta }}{\widetilde{P}}^T-{\widetilde{P}}{\widetilde{\eta }}^T{\widetilde{\Pi }}_{{\widetilde{P}}}\) with \({\widetilde{\Pi }}_{{\widetilde{P}}}={\widetilde{I}}_{2l}-\frac{1}{2}{\widetilde{P}}{\widetilde{P}}^T\). Therefore, a retraction \({{{\mathcal {R}}}}\) on the product manifold \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) is immediately defined as
where \(({\widetilde{V}}, {\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\) and \(({\widetilde{\xi }},{\widetilde{\eta }})\in {{\mathbf {T}}}_{({\widetilde{V}},{\widetilde{P}})}(\text {Stp}(n,l)\times \text {Stp}(2l,l))\).
Noting that the matrix inverse \(( {\widetilde{I}}_n-\frac{\alpha }{2}{\widetilde{W}}_{{\widetilde{\xi }}})^{-1}\) dominates the computation of \({{\mathcal {R}}}_{{\widetilde{V}}}(\alpha {\widetilde{\xi }})\) in (3.6). To overcome this difficulty, according to technique of [15], we can obtain a refined scheme by the following procedure. Rewriting \({\widetilde{W}}_{{\widetilde{\xi }}}\in {\mathcal {SP}}(n,n)\subset {{\mathbb {R}}}^{2n\times 2n}\) as \({\widetilde{W}}_{{\widetilde{\xi }}}=U_{{\widetilde{\xi }}}V_{{\widetilde{\xi }}}^T\), where \(U_{{\widetilde{\xi }}}=[{\widetilde{\Pi }}_{{\widetilde{V}}}{\widetilde{\xi }}~~ {\widetilde{V}}]\in {{\mathbb {R}}}^{2n\times 4l}\) and \(V_{{\widetilde{\xi }}}=[{\widetilde{V}}~ -{\widetilde{\Pi }}_{{\widetilde{V}}}{\widetilde{\xi }}]\in {{\mathbb {R}}}^{2n\times 4l}\), then apply the Sherman–Morrison–Woodbury(SMW) formula
we can derive the following refined scheme
Apparently, if \(l\ll n/2\), inverting \(I_{4l}-\frac{1}{2}V_{{\widetilde{\xi }}}^TU_{{\widetilde{\xi }}}\in {{\mathbb {R}}}^{4l\times 4l}\) is much easier than inverting \( {\widetilde{I}}_n-\frac{\alpha }{2}{\widetilde{W}}_{{\widetilde{\xi }}}\in {{\mathbb {R}}}^{2n\times 2n}\), hence (3.10) should be used to compute \({{\mathcal {R}}}_{{\widetilde{V}}}(\alpha {\widetilde{\xi }})\). However, if \(l \ge n/2\), then (3.10) has no advantage over (3.6), if this is the case, we still use (3.6) to compute \({{\mathcal {R}}}_{{\widetilde{V}}}(\alpha {\widetilde{\xi }})\). We also note that there is no need to refine \({{\mathcal {R}}}_{{\widetilde{P}}}(\alpha {\widetilde{\eta }})\) in (3.7) because \({\widetilde{I}}_{2l}-\frac{\alpha }{2}{\widetilde{W}}_{{\widetilde{\eta }}} \in {{\mathbb {R}}}^{4l\times 4l}\) but \({{\widetilde{\eta }}}\in {{\mathbb {R}}}^{4l\times 2l}\).
Remark 3.1
According to the refined formula (3.10), we can form the partition matrix
and then calculate
By using the following inverse formula of 2-by-2 block matrix
where \(A\in {{\mathbb {R}}}^{m\times n}\), \(B\in {{\mathbb {R}}}^{m\times m}\) is invertible, \(C\in {{\mathbb {R}}}^{n\times n}\), \(D\in {{\mathbb {R}}}^{n\times m}\) and \(C-DB^{-1}A\) is invertible, we have that, if
is invertible, then \((I_{4l}-\frac{\alpha }{2}V_{{\widetilde{\xi }}}^TU_{{\widetilde{\xi }}})^{-1}\) can be expressed as
Then we can further refine the computation of \({{\mathcal {R}}}_{{\widetilde{V}}}(\alpha {\widetilde{\xi }})\) for the case \(l\ll n/2\) as follows
where \(N_{{\widetilde{\xi }}}^1={\widetilde{V}}^T{\widetilde{\xi }}\), \(N_{{\widetilde{\xi }}}^2={\widetilde{I}}_l+\frac{\alpha }{4}N_{{\widetilde{\xi }}}^1\), \(N_{{\widetilde{\xi }}}^3={\widetilde{I}}_l-\frac{\alpha }{4}N_{{\widetilde{\xi }}}^1\) and \(N=\frac{\alpha }{2}{\widetilde{\xi }}^T{\widetilde{\xi }}-\frac{3\alpha }{8}{N_{{\widetilde{\xi }}}^1}^T N_{{\widetilde{\xi }}}^1+\frac{2}{\alpha }N_{{\widetilde{\xi }}}^2N_{{\widetilde{\xi }}}^3\). We observe from (3.11) that we only need to inverse \(N\in {{\mathbb {R}}}^{2l\times 2l}\), and there will be no high computational costs for computing (3.11) if we store the matrices \(N_{{\widetilde{\xi }}}^1\), \(N_{{\widetilde{\xi }}}^2\) and \(N_{{\widetilde{\xi }}}^3\) after \({\widetilde{\xi }}\) is obtained.
We use the differentiated retraction as a vector transport \({\mathcal {T}}_{({\widetilde{\xi }}, {\widetilde{\eta }})}({\widetilde{\zeta }}, {\widetilde{\chi }})\) on \(\text {Stp}(n, l)\times \text {Stp}(2l, l)\), defined as
for \(({\widetilde{\xi }}, {\widetilde{\eta }})\), \(({\widetilde{\zeta }}, {\widetilde{\chi }})\in {{\mathbf {T}}}_{({\widetilde{V}},{\widetilde{P}})}(\text {Stp}(n,l)\times \text {Stp}(2l,l))\). Consequently, we have
As in [16], we can derive computational formulas for the vector transport as the differentiated retraction of (3.6) and (3.7) by
and
Therefore, we have
and
Following from Lemma 2 in [16], we have that the vector transport formulas given by (3.12), (3.13) and (3.14) satisfy the following Ring-Wirth nonexpansive condition
where the last inequality makes use of the fact that both \({\widetilde{W}}_{{\widetilde{\xi }}}\) and \({\widetilde{W}}_{{\widetilde{\eta }}}\) are skew-symmetric, implying that their eigenvalues are zeros or pure imaginary numbers, and therefore \({\widetilde{I}}_{n}-\frac{\alpha ^2}{4}{\widetilde{W}}_{{\widetilde{\xi }}}^2\) and \({\widetilde{I}}_{2l}-\frac{\alpha ^2}{4}{\widetilde{W}}_{{\widetilde{\eta }}}^2\) are both symmetric matrices with all eigenvalues not less than 1.
For refining the computation of (3.13) for the case \(l\ll n/2\), as in [16], applying again the SMW formula (3.9), we can obtain the following refined scheme
where \(M_{{\widetilde{\xi }}}^1=V_{{\widetilde{\xi }}}^T{\widetilde{V}}\), \(M_{{\widetilde{\xi }}}^2=V_{{\widetilde{\xi }}}^TU_{{\widetilde{\xi }}}\) and \(M_{{\widetilde{\xi }}}^3=(I_{4l}-\frac{\alpha }{2}V_{{\widetilde{\xi }}}^TU_{{\widetilde{\xi }}})^{-1}V_{{\widetilde{\xi }}}^T{\widetilde{V}}\). One may refer to [16] for the details of derivations. We should observe that there will be no high computational costs for computing (3.12) if we store the matrices \(M_{{\widetilde{\xi }}}^1\), \(M_{{\widetilde{\xi }}}^2\) and \(M_{{\widetilde{\xi }}}^3\) after computing (3.10). For the case \(l\ge n/2\), we still use (3.13) to compute the vector transport \({\mathcal {T}}_{\alpha {\widetilde{\xi }}}({\widetilde{\xi }})\). Similar to \({{\mathcal {R}}}_{{\widetilde{P}}}(\alpha {\widetilde{\eta }})\), there is no reason to refine the computation of \({\mathcal {T}}_{\alpha {\widetilde{\eta }}}({\widetilde{\eta }})\) and we still use (3.14) to compute it.
3.3 Riemannian Gradient
We now derive explicit expression of the Riemannian gradient of the cost function \(f({\widetilde{V}},{\widetilde{P}})\) defined in (2.11). To do so, we define the mapping \({\overline{F}}: {\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\rightarrow {\mathcal {SP}}(m, l)\) and the cost function \({\overline{f}}: {\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\rightarrow {{\mathbb {R}}}\) by
Thus, the mapping F defined in (2.12) and the cost function \(f({\widetilde{V}},{\widetilde{P}})\) are the restrictions of \({\overline{F}}\) and \({\overline{f}}\) onto \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\). That is, \(F={\overline{F}}|_{\text {Stp}(n,l)\times \text {Stp}(2l,l)}\) and \(f={\overline{f}}|_{\text {Stp}(n,l)\times \text {Stp}(2l,l)}\). The Euclidean gradient of \({\overline{f}}\) at a point \(({\widetilde{V}},{\widetilde{P}})\in {\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\) is given by
By a simple computation, we have
Lemma 3.1
(p. 48 of [11]) Let \({\overline{h}}\) be a smooth function defined on a Riemannian manifold \(\overline{{\mathcal {M}}}\) and let h denote the restriction of \({\overline{h}}\) to a Riemannian submanifold \({\mathcal {M}}\). The gradient of h is equal to the projection of the gradient of \({\overline{h}}\) onto \({\mathcal {T}}_x{\mathcal {M}}\), that is, \( \text {grad}\ h(x) = {\mathbf {P}}_x \left( \text {grad}\ {\overline{h}}(x)\right) \).
Since \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) is a Riemannian submanifold of \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\) endowed with the induced metric. Applying Lemma 3.1, the Riemannian gradient of \(f({\widetilde{V}}, {\widetilde{P}} )\) at a point \(({\widetilde{V}}, {\widetilde{P}} )\in \text {Stp}(n,l) \times \text {Stp}(2l,l)\) is given by
Following from Proposition 3.2, we have
Together with (3.18) and the map \(\phi ^{-1}\), we can derive the first-order optimality conditions of the problem (2.2) as follows.
Corollary 3.1
Suppose that \((V^*, P^*)\) is a local minimizer of the problem (2.2). Then \((V^*, P^*)\) satisfies the following first-order optimality conditions:
where \(P^*={\begin{bmatrix} P_1^{*}\\ P_2^{*} \end{bmatrix}}\) with \(P_1^{*}, P_2^{*}\in {{\mathbb {C}}}^{l\times l}\).
Proof
The Lagrangian function of the problem (2.11) is given by
where \({\overline{f}}:={\overline{f}}({\widetilde{V}},{\widetilde{P}})\) is defined in (3.17) and \({\widetilde{\Lambda }}, {\widetilde{\Omega }}\in {\mathcal {SP}}(l,l)\) are symmetric matrices representing the Lagrange multipliers. The Lagrangian function leads to the first order optimality conditions for the problem (2.11):
where \({\frac{\partial }{\partial {\widetilde{V}}} {\overline{f}}}\) and \({\frac{\partial }{\partial {\widetilde{P}}} {\overline{f}}}\) are given in (3.18). From the first two equations in (3.22), we have \({\widetilde{\Lambda }}={\widetilde{V}}^T{\frac{\partial }{\partial {\widetilde{V}}} {\overline{f}}}\) and \({\widetilde{\Omega }}={\widetilde{P}}^T{\frac{\partial }{\partial {\widetilde{P}}} {\overline{f}}}\). Since \({\widetilde{\Lambda }}\) and \({\widetilde{\Omega }}\) must be symmetric matrices, we obtain \({\widetilde{\Lambda }}={\frac{\partial }{\partial {\widetilde{V}}} {\overline{f}}}^T{\widetilde{V}}\) and \({\widetilde{\Omega }}={\frac{\partial }{\partial {\widetilde{P}}} {\overline{f}}}^T{\widetilde{P}}\). Then the first-order optimality conditions of the problem (2.11) in the Euclidean sense satisfy
By using the map \(\phi ^{-1}\), the first-order optimality conditions of the problem (2.2) can be expressed as (3.21). \(\square \)
Next, we establish explicit formulas for the differential of \(F({\widetilde{V}},{\widetilde{P}})\) defined in (2.12) and the definition of pullback mappings which will be used in the sequel. For any given \(({\widetilde{V}},{\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\) and \(({\widetilde{\xi }}, {\widetilde{\eta }})\in {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l)\times \text {Stp}(2l,l)\), we obtain
Since \({\overline{F}}\) is a smooth mapping between two linear manifolds \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\) and \({\mathcal {SP}}(m, l)\), and F is the restriction of \({\overline{F}}\) to an embedded Riemannian submanifold \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) of \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\). Hence, the differential \(D F({\widetilde{V}},{\widetilde{P}}): {{\mathbf {T}}}_{({\widetilde{V}},{\widetilde{P}})} \text {Stp}(n,l)\times \text {Stp}(2l,l)\rightarrow {{\mathbf {T}}}_{F({\widetilde{V}},{\widetilde{P}})}{\mathcal {SP}}(m, l)\simeq {\mathcal {SP}}(m, l)\) (see p. 38 of [11]) of \(F({\widetilde{V}},{\widetilde{P}})\) at a point \(({\widetilde{V}},{\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\) is determined by
for any \(({\widetilde{\xi }}, {\widetilde{\eta }})\in {{{\mathbf {T}}}}_{({\widetilde{V}},{\widetilde{P}})} \text {Stp}(n,l)\times \text {Stp}(2l,l)\). Moreover, for the Riemannian gradient of \(f({\widetilde{V}},{\widetilde{P}})\) and the differential of \(F({\widetilde{V}},{\widetilde{P}})\), we have the following relationship (see p. 185 of [11])
where \((D F({\widetilde{V}},{\widetilde{P}}))^*\) denotes the adjoint of the operator \(D F({\widetilde{V}},{\widetilde{P}})\).
Let \({{\mathbf {T}}}\text {Stp}(n,l)\times \text {Stp}(2l,l)\) denote the tangent bundle of \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\). As in p.55 of [11], the pullback mappings \({\widehat{F}}: {{\mathbf {T}}}\text {Stp}(n,l)\times \text {Stp}(2l,l)\rightarrow {\mathcal {SP}}(m,l)\) and \({\widehat{f}}: {{\mathbf {T}}}\text {Stp}(n,l)\times \text {Stp}(2l,l)\rightarrow {{\mathbb {R}}}\) of F and f through the retraction \({{\mathcal {R}}}\) on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) can be defined by
for all \(({\widetilde{\xi }}, {\widetilde{\eta }})\in {{\mathbf {T}}}\text {Stp}(n,l)\times \text {Stp}(2l,l)\), where \({\widehat{F}}_{({\widetilde{V}},{\widetilde{P}})}\) and \({\widehat{f}}_{({\widetilde{V}},{\widetilde{P}})}\) are the restrictions of \({\widehat{F}}\) and \({\widehat{f}}\) to \({{\mathbf {T}}}_{({\widetilde{V}},{\widetilde{P}})} \text {Stp}(n,l)\times \text {Stp}(2l,l)\), respectively. Moreover, we have (see p. 55 of [11])
where \(0_{({\widetilde{V}},{\widetilde{P}})}\) is the origin of \({{\mathbf {T}}}_{({\widetilde{V}},{\widetilde{P}})} \text {Stp}(n,l)\times \text {Stp}(2l,l)\). For the Riemannian gradient of f and the Euclidean gradient of its pullback function \({\widehat{f}}\), we have (see p. 56 of [11])
4 A Riemannian Conjugate Gradient Algorithm
Recently, a few Riemannian optimization methods for solving eigenproblems have been proposed. For instance, in [18], a truncated conjugate gradient method was presented for the symmetric generalized eigenvalue problem. In [19], a Riemannian trust-region method was proposed for the symmetric generalized eigenproblem. In [20], a Riemannian Newton method was proposed for a kind of a nonlinear eigenvalue problem. In particular, in [12], Zhao, Jin and Bai presented a geometric Polak–Ribière–Polyak-based nonlinear conjugate gradient method for the inverse eigenvalue problem of reconstructing a stochastic matrix from the given spectrum data. In [13], Yao, Bai, Zhao and Ching proposed a Riemannian Fletcher–Reeves conjugate gradient method for the construction of a doubly stochastic matrix with the prescribed spectrum. In [14], Sato and Iwai presented a Riemannian conjugate gradient method for the problem of the singular value decomposition of a matrix. The complex singular value decomposition problem were also considered by Sato and Iwai [9] and Sato [10] based on a Riemannian Newton method and a Riemannian conjugate gradient method, respectively.
Very recently, in [16], Zhu developed a new Riemannian conjugate gradient method for optimization on the Stiefel manifold, which generalized Dai’s nonmonotone conjugate gradient method [7] from the Euclidean space to Riemannian manifolds. The author in [16] introduced two novel vector transports associated with the retraction constructed by the Cayley transform [15]. The first one is the differentiated retraction of the Cayley transform and the second one approximates the differentiated matrix exponential by the Cayley transform.
In this section, inspired by the work of [7, 16], we present a Riemannian nonmonotone conjugate gradient method with nonmonotone line search technique for solving the problem (2.11). We show the global convergence for the proposed algorithm, whose analytic framework can be regarded as an extension of the proof proposed in [7, 16]. In addition, to make the algorithm easy-to-perform, we translate the algorithm into the complex-value form. Finally, we provide a complete algorithm for the original problem (1.3) in the end of this section, which is to find a minimal perturbation for the pencil to have l eigenpairs with \(1\le l\le n\).
4.1 A Riemannian Conjugate Gradient Method for the Problem (2.11)
In Dai’s nonmonotone conjugate gradient method [7], the parameter \(\beta _{k+1}\) in (3.1) is given by
where \(y_k=\nabla f(x_{k+1})-\nabla f(x_{k})\). Aiming at the problem (2.11), the Riemannian generalization of this formula is given by
where \(Y_{k+1}=\langle \text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1}), \ \ {\mathcal {T}}_{\alpha _k({\widetilde{\xi }}_k,{\widetilde{\eta }}_k)}({\widetilde{\xi }}_k,{\widetilde{\eta }}_k)\rangle -\langle \text {grad} f({\widetilde{V}}^{k}, {\widetilde{P}}^{k}), ({\widetilde{\xi }}_{k}, {\widetilde{\eta }}_{k})\rangle \). Dai’s algorithm is globally convergent with a nonmonotone line search condition. The Riemannian generalization of this nonmonotone condition is
On the basis of these arrangements, the corresponding Riemannian nonmonotone conjugate gradient method for the problem (2.11) is described as follows.

We have several remarks for the above algorithm as follows.
Remark 4.1
In Algorithm 4.1, the initial steplength at the kth iteration is set to be \({\overline{\alpha }}_k\). We now derive a reasonable choice of this initial steplength. For the nonlinear mapping \({\widehat{F}}_{({\widetilde{V}}^k, {\widetilde{P}}^k)}({\widetilde{\xi }}, {\widetilde{\eta }}): {\mathbf {T}}_{({\widetilde{V}}^k, {\widetilde{P}}^k)}\text {Stp}(n,l)\times \text {Stp}(2l,l)\rightarrow {\mathcal {SP}}(m,l)\) defined in (3.26), we consider the first-order approximation of \({\widehat{F}}_{({\widetilde{V}}^k, {\widetilde{P}}^k)}\) at the origin \(0_{({\widetilde{V}}^k, {\widetilde{P}}^k)}\) along the search direction \(({\widetilde{\xi }}_k, {\widetilde{\eta }}_k)\):
for all \(\alpha \) close to 0. From (3.26) and (3.27), this is reduced to
for all \(\alpha \) close to 0. From (3.26) and (4.5), we have
where \((D{\widehat{F}}_{({\widetilde{V}}^k, {\widetilde{P}}^k)}(0_{({\widetilde{V}}^k, {\widetilde{P}}^k)}))^*\) denotes the adjoint of the operator \(D{\widehat{F}}_{({\widetilde{V}}^k, {\widetilde{P}}^k)}(0_{({\widetilde{V}}^k, {\widetilde{P}}^k)})\). Based on (3.26) and (3.27), this yields
From (3.25), we obtain the local approximation of \(f({\widetilde{V}},{\widetilde{P}})\) at \(({\widetilde{V}}^k, {\widetilde{P}}^k)\) along the direction \(({\widetilde{\xi }}_k, {\widetilde{\eta }}_k)\) as follows:
Let \(\varphi _k^{\prime }(\alpha )=0\), we arrive at
Then we have
Hence, from (3.24), we derive a suitable choice of the initial steplength as
Remark 4.2
Similar to unconstrained optimization in the Euclidean space, \(\Vert \text {grad} f({\widetilde{V}}^k, {\widetilde{P}}^k)\Vert < \epsilon \) for some constant \(\epsilon > 0\) is a reasonable stopping criterion for Riemannian optimization approaches to the problem (2.11). In fact, under the conditions \({\widetilde{V}}^T{\widetilde{V}}={\widetilde{I}}_l\) and \({\widetilde{P}}^T{\widetilde{P}}={\widetilde{I}}_l\), \(\frac{\partial }{\partial {\widetilde{V}}}{\mathcal {L}}=0\) and \(\frac{\partial }{\partial {\widetilde{P}}}{\mathcal {L}}=0\) in the proof of Corollary 3.1 are equivalent to \(\text {grad} f({\widetilde{V}}, {\widetilde{P}})=0\), since it follows from (3.19), (3.20), (3.22) and (3.23) that
Thus, first-order critical points in the Euclidean sense can be interpreted as stationary points in the Riemannian sense.
4.2 Global Convergence
In this subsection we study the convergence of Algorithm 4.1. Note that the convergence of the nonlinear conjugate gradient method with nonmonotone line search technique for unconstraint optimization has been well studied in the literature [7]. Considering that the problem (2.11) is a model with matrix variables while most of the nonmonotone CG-type literature is in the context of vectors, and to make the paper self-contained, we here provide more details about the convergence analysis of Algorithm 4.1 in solving the problem (2.2) for the purpose of completeness. The following analytic framework can be regarded as an extension of the proof proposed in [7, 16]. In particular, the author in [16] generalized Dai’s nonmonotone conjugate gradient method [7] from the Euclidean space to Riemannian manifold, while here we further extend to the Riemannian product manifolds, which appears to be more general.
Lemma 4.1
For any point \(({\widetilde{V}}^0, {\widetilde{P}}^0)\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\), the level set
is compact.
The proof to Lemma 4.1 can be found in “Appendix 7.1”. The following remark shows some basic properties of the involved product manifold \(\text {Stp}(n,l)\times \text {Stp}(l,l)\), and will provide the transparency in our coming convergence analysis.
Remark 4.3
One can see that \(\text {Stp}(n,l)\times \text {Stp}(l,l)\) is an embedded Riemannian submanifold of \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\). We may rely on the natural inclusion \({\mathbf {T}}_{({\widetilde{V}},{\widetilde{P}})} \text {Stp}(n,l)\times \text {Stp}(2l,l)\). Thus, the Riemannian gradient \(\text {grad}f({\widetilde{V}},{\widetilde{P}})\) can be viewed as a continuous nonlinear mapping between \(\text {Stp}(n,l)\times \text {Stp}(l,l)\) and \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\). Since \(\Phi \) is a compact set, then there exists a constant \(\gamma >0\) such that
Moreover, for any point \(({\widetilde{V}}_{1}, {\widetilde{P}}_1), ({\widetilde{V}}_{2}, {\widetilde{P}}_2)\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\), the operation \(\text {grad} f({\widetilde{V}}_{1}, {\widetilde{P}}_1)-\text {grad}f({\widetilde{V}}_{2}, {\widetilde{P}}_2)\) is meaningful since both \(\text {grad}f({\widetilde{V}}_{1}, {\widetilde{P}}_1)\) and \(\text {grad}f({\widetilde{V}}_{2}, {\widetilde{P}}_2)\) can be treated as vectors in \({\mathcal {SP}}(n,l)\times {\mathcal {SP}}(2l,l)\). Since \(\Phi \) is compact, then \(\text {grad}f({\widetilde{V}},{\widetilde{P}})\) is Lipschitz continuous on \(\Phi \), i.e., there exists a constant \({\widetilde{L}}>0\) such that
for all \(({\widetilde{V}}_{1}, {\widetilde{P}}_1), ({\widetilde{V}}_{2}, {\widetilde{P}}_2)\in \Phi \subset \text {Stp}(n,l)\times \text {Stp}(2l,l)\), where “dist” defines the Riemannian distance on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\).
The following lemmas show some properties of the nonmonotone line search. Their proofs can be found in “Appendix 7.2 and 7.3” respectively. Lemma 4.2 shows that Algorithm 4.1 produces a descent direction at each iteration. Lemma 4.3 shows that for Algorithm 4.1 using the technique the nonmonotone line search, the function need not decrease at every iteration, but there must be a reduction in the function every \(h-1\) iterations.
Lemma 4.2
Suppose Algorithm 4.1 does not terminate in finitely many iterations. Then we have, for all k,
Therefore \(\beta ^D_{k+1} > 0\) and \(\beta _{k+1}\in [0, \beta ^D_{k+1}]\) is well defined.
Lemma 4.3
There exists a positive constant \(\mu > 0\) for Algorithm 4.1 such that
where \({\overline{\alpha }}_k\) denotes the initial step length at iteration k. Further, we have
We now establish the global convergence of Algorithm 4.1 by the idea of the proof of Theorem 3.4 of [7] and Theorem 1 of [16]. The proof can be found in “Appendix 7.4”.
Theorem 4.1
Suppose Algorithm 4.1 does not terminate in finitely many iterations. Then the sequence \(\{ ({\widetilde{V}}^{k}, {\widetilde{P}}^{k}) \}\) generated by Algorithm 4.1 converges in the sense that
Hence there exists at least one accumulation point which is a first-order critical point.
4.3 A Riemannian Conjugate Gradient Method for the Problem (2.2)
In the implementation of Algorithm 4.1, as we can observe from (2.5), treating matrices on \(\text {Stp}(n, l)\) needs twice as much computer memory as those on \(\text {St}(n,l,{{\mathbb {C}}})\). Also, addition and multiplication of matrices on \(\text {Stp}(n,l)\) need about twice as much computation time as those on \(\text {St}(n, l, {{\mathbb {C}}})\). To avoid these difficulties, through the map \(\phi ^{-1}\), we now translate Algorithm 4.1 for the problem (2.11) into Riemannian conjugate gradient method for the problem (2.2) on \(\text {St}(n, l, {{\mathbb {C}}})\times \text {St}(2l, l, {{\mathbb {C}}})\).
In the process of translation, the relations (2.6) are used, together with the relation for \(E\in {{\mathbb {C}}}^{l\times l}\) and \({\widetilde{E}}=\phi (E)\in {\mathcal {SP}}(l,l)\),
where \(\text {her}(\cdot )\) denotes the Hermitian part of the matrix in the parentheses. Further, by using the relationships between matrix operations on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) and \(\text {St}(n, l, {{\mathbb {C}}})\times \text {St}(2l, l, {{\mathbb {C}}})\), the retraction \({\mathcal {R}}\) given in (3.8) on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) correspond to the retraction \({{{\mathcal {R}}}}^{{\mathbb {C}}}\) on \(\text {St}(n,l,{{\mathbb {C}}})\times \text {St}(2l,l,{{\mathbb {C}}})\) defined by
where
and
with
and
Similarly, the vector transport \({\mathcal {T}}\) given in (3.12) on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) correspond to the retraction \({{\mathcal {T}}}^{{\mathbb {C}}}\) on \(\text {St}(n,l,{{\mathbb {C}}})\times \text {St}(2l,l,{{\mathbb {C}}})\) defined by
where
Thus, Algorithm 4.1 is translated to Algorithm 4.2 for the problem (2.2), which provides a Riemannian conjugate gradient method for the problem (2.2). Here, we use the notation \(({\overline{\xi }}_k, {\overline{\eta }}_k)\) to express \(\phi ^{-1}(\text {grad} f({\widetilde{V}}^k,{\widetilde{P}}^k))\).

Remark 4.4
In the implementation of Algorithm 4.2, if \(l\ll n/2\), according to (3.10), the computation of \(V_{\alpha _k}\) in (4.16) is replaced by its refined scheme
where \(U_{{\xi _k}}=({\Pi }_{{V^k}}{\xi _k},\ {V^k})\in {{\mathbb {C}}}^{n\times 2l}\) and \(V_{{\xi _k}}=({V^k},\ -{\Pi }_{V^k}{\xi _k})\in {{\mathbb {C}}}^{n\times 2l}\). Similarly, if \(l\ll n/2\), according to (3.16), the computation of \({\mathcal {T}}^{{\mathbb {C}}}_{\alpha _k{\xi _k}}({\xi _k})\) in (4.20) is replaced by
where \(M_{{\xi _k}}^1=V_{{\xi _k}}^H{V^k}\), \(M_{{\xi _k}}^2=V_{{\xi _k}}^HU_{{\xi _k}}\) and \(M_{{\xi _k}}^3=(I_{2l}-\frac{\alpha _k}{2}V_{{\xi _k}}^HU_{{\xi _k}})^{-1}V_{{\xi _k}}^H{V^k}\).
4.4 An Algorithm for Solving the Problem (1.3)
Since our ultimate goal is to find an optimal pencil \(({\hat{A}},{\hat{B}})\) with minimal perturbation in the problem (1.3) in the sense that \(({\hat{A}}, {\hat{B}})\) has l distinct eigenvalues. In this subsection, we first review roughly how to obtain such an optimal pencil once the optimization problem (2.2) is solved, one may refer to pages 781–782 in [2] for more details, and then we present a complete algorithm for the problem (1.3). According to the Proofs of Theorems 1 and 4 and pages 781–782 in [2], such a pencil can be obtained by the following procedure.
Let \(V^*\in {{\mathbb {C}}}^{n\times l}\) with \(V^{*H}V^*=I_l\) and \(P^*={\begin{bmatrix}P^*_1\\ P^*_2\end{bmatrix}}\) with \(P^*_1, P^*_2\in {{\mathbb {C}}}^{l\times l}\) and \(P^{*H}_1P^*_1+P^{*H}_2P^*_2=I_l\) solve (2.2), i.e.,
If \(P^*_1\) is nonsingular, let
be unitary matrices. If \(P_1\) is singular, then as in page 781 of [2], we can construct \({\begin{bmatrix}\Delta P_1\\ \Delta P_2\end{bmatrix}}\) such that \(P^*_1+\Delta P_1\) is nonsingular and \(\Vert [A~~ B]\Vert \Vert {\begin{bmatrix}\Delta P_1\\ \Delta P_2\end{bmatrix}}\Vert \le \epsilon \) for \(\epsilon \) being small enough, then set \(P^*_1:=P^*_1+\Delta P_1\) and \(P^*_2:=P^*_2+\Delta P_2\). Moreover, since \(P^*_1\) is nonsingular, it follows from the cosine-sine decomposition that \(Q_2\) is also nonsingular. Then define
and
If all eigenvalues of \(\Lambda _0\) are distinct and \(\text {rank}({\overline{B}}_0)=n\), then \(({\hat{A}}, {\hat{B}})\) is the minimum perturbed pair of (A, B) that has l linearly independent eigenvectors. If all eigenvalues of \(\Lambda _0\) are not distinct, according to [2], we can also compute \(\Delta \Lambda _0\) such that all eigenvalues of \(\Lambda _0+\Delta \Lambda _0\) are distinct and \(\Vert B_0^{(1)}\Vert \Vert \Delta \Lambda _0\Vert \le \epsilon \), and then set \(\Lambda _0:=\Lambda _0+\Delta \Lambda _0\). Besides, let the spectral decomposition of \(\Lambda _0\) be
and
Then \(\{(\lambda _k, \mathbf{v }_k), k=1,\ldots , l\}\) are l linearly independent eigenpairs of pencil \({\hat{A}}-\lambda {\hat{B}}\).
From the above arguments, we now derive Algorithm 4.3 for solving the problem (1.3), which is to find a minimal perturbation for the pencil to have l eigenpairs with \(1\le l\le n\).

5 Numerical Experiments
In this section, we report some numerical results to illustrate the efficiency of the proposed algorithms. Because we focus on finding an optimal pencil \(({\hat{A}},{\hat{B}})\) in the problem (1.3) in the sense that \(({\hat{A}}, {\hat{B}})\) has l distinct eigenvalues with \(1\le l\le n\), in the first part we shall numerically compare Algorithm 4.3 with Boutry et al.’s algorithm [1] for the case \(l=1\), which is denoted by BEGM algorithm, and Ito and Murota’s algorithm [5] for the case \(l=n\), which is denoted by TLS-IM algorithm. In the second part we show more numerical results of Algorithm 4.2 in comparison with some other forms of Riemannian conjugate gradient methods proposed in [12,13,14] which are all applicable to the problem (2.2). All the numerical experiments were completed on a personal computer with a Intel(R) Core(TM)2 Quad of 2.33 GHz CPU and 3.00 GB of RAM.
5.1 Algorithmic Issues
According to Algorithm 4.2, the parameter \(\beta _{k+1}\) is chosen from the range \((0, \beta ^D_{k+1})\). In our implementation, we choose \(\beta _{k+1}\) by means of
where
is the Fletcher–Reeves parameter. From Remark 4.1, the initial steplength \({\overline{\alpha }}_{k}\) at iteration k is set to be
Here, we choose \({\overline{\alpha }}_k\) by means of
where \({\overline{\alpha }}_k^{BB}\) is a Riemannian generalization of the Barzilai–Borwein steplength [21], which is given by
with \(S_{\xi ,k-1} = \alpha _{k-1} \xi _{k-1}\) and \(S_{\eta ,k-1} = \alpha _{k-1} \eta _{k-1}\) being the displacement of the variables in the tangent space and \(Z_{\xi ,k-1} = {\overline{\xi }}_{k}-{\overline{\xi }}_{k-1}\) and \(Z_{\eta ,k-1} = {\overline{\eta }}_{k}-{\overline{\eta }}_{k-1}\) being the difference of gradients. Here we do not use a vector transport for \(Z_{\xi ,k-1}\) and \(Z_{\eta ,k-1}\) but just compute them as subtraction of two gradients in different tangent spaces because using a vector transport might increase CPU time.
To achieve high efficiency in the implementation of Algorithm 4.2, the actual stopping criterion is much more sophisticated than the simple one \(\Vert ({\overline{\xi }}_k, {\overline{\eta }}_k)\Vert \le \epsilon \). In our implementation we use the same stopping criterion as that in [15]: we let Algorithm 4.2 run up to K iterations and stop it at iteration \(k< K\) if \(\Vert ({\overline{\xi }}_k, {\overline{\eta }}_k)\Vert \le \epsilon \), or \(\text {rel}_{({V}, {P})}^k\le \epsilon _{vp}\) and \(\text {rel}_f^k\le \epsilon _f\), or
for some constants \(\epsilon \), \(\epsilon _{vp}\), \(\epsilon _{f}\in (0,1)\), and \(T,K\in {\mathbb {N}}^+\), where
For convenience, we summarize the default values and description for the parameters in our algorithms in Table 1. All starting points \(V^0\) and \(P^0\) were feasible and generated randomly by means of \(V^0 = \text {orth}(randn(n, l))\) and \(P^0 = \text {orth}(randn(2l, l))\) in Matlab style.
5.2 Comparison with the BEGM Algorithm and the TLS-IM Algorithm for Noisy Pencils
To start with our experiments, let us review roughly the following function defined by [1]
which can help us visualize the behaviors of the nonsquare pencil \(A-\lambda B\). This function is a mapping from the complex plane (values of \(\lambda \)) to the real and nonnegative numbers. If the matrix pair (A, B) has an eigenvalue \(\lambda _0\), the value of the function at \(\lambda _0\) is exactly zero. This is because, if the pencil \(A-\lambda _0B\) is rank deficient, it must have zero as its smallest singular value (and may have more than one zero singular value). For such a solvable pair the eigenvalues are the local minimum points of this function. If \(\lambda _0\) is perturbed, we get a full rank pencil that leads to a strictly positive minimal singular value and, in the case of a nonsolvable pair A and B, the function is strictly positive for all \(\lambda \). For a nonsquare matrix pair (A, B), if we describe the contour plots of the function \(h(\lambda )=\sigma _{\min }(A-\lambda B)\) on the complex plane, the local minimum of this function could help us to estimate how many eigenvalues the nonsquare pencil \(A-\lambda B\) have.
In our experiments, we generate the measured matrices \(A, B\in {{\mathbb {C}}}^{300\times 5}\)\((m=300,n=5)\) in the problem (1.3) by the following procedure employed in [1, 5]:
Choose random matrices \(\breve{A}, \breve{B}\in {\mathbb {C}}^{5\times 5}\), and \(\breve{Q}\in {\mathbb {C}}^{300\times 5}\) whose entries’ real and imaginary parts are drawn independently from Gaussian distribution with zero mean and standard deviation \(\sigma =1\).
Compute QR decomposition of \(\breve{Q}\), and define \(Q_0\) to be its Q part.
Define \(A_0\) and \(B_0\) by \(A_0=50*Q_0\breve{A}, B_0=50*Q_0\breve{B}\). Note that the nonsquare pencil \(A_0-\lambda B_0\) has the same eigenpairs as the square matrix pencil \(\breve{A}-\lambda \breve{B}\).
Define \(A =A_0 + N_A, B =B_0+N_B\), where \(N_A, N_B\) are matrices of random noise.
Real and imaginary parts of \(N_A, N_B\) are drawn independently from Gaussian distribution with zero mean and standard deviation equal to \(\sigma \). The parameter \(\sigma \) here represents the level of noise in inputs. We also used the relative errors \(\text {rel}_A:=\frac{\Vert N_A\Vert }{\Vert A\Vert }\) and \(\text {rel}_B:=\frac{\Vert N_B\Vert }{\Vert B\Vert }\) to measure the magnitude of the perturbation.
In our experiments, we used the matrices \(A_0, B_0\) with the pencil \(A_0-\lambda B_0\) having five engenvalues \(-0.0186-0.3735 i\), \(-0.2457 - 0.0982 i\), \(0.1503 + 0.7123 i\), \(0.9989 + 0.9233 i\), \(2.8651 +1.6573 i\). We prepared different noise \((N_A,N_B)\) with noise level \(\sigma =0, 0.25, 0.50, 0.75, 1.0, 1.25\). We note that, the exact eigenvalues of noiseless pencil \(A_0-\lambda B_0\) is not necessarily equal to the optimal solution to the problem (1.1) with noisy inputs.
5.2.1 Comparison with the TLS-IM Algorithm
We first compare Algorithm 4.3 with TLS-IM algorithm [5] for the case of \(l=n\), which is the case to find a minimal perturbation for the pencil \(A-\lambda B\) to have n eigenpairs. We show that our proposed algorithm can achieve exactly the same eigenvalues as TLS-IM algorithm, which is essentially a direct method to find n optimal eigenpairs. We also show that both of two algorithms are robust and less affected by the data noise. To do so, for the perturbed pair (A, B) with \(A =A_0 + N_A\) and \(B =B_0+N_B\), in Fig. 1, we first describe the contours of function \(h(\lambda )=\sigma _{\min }(A-\lambda B)\) in the \(\lambda \)-complex plane with different noise \(\sigma =0, 0.25, 0.50, 0.75, 1.0, 1.25\). We can see from Fig. 1 that, with \(\sigma =0\), the function \(h(\lambda )=\sigma _{\min }(A_0-\lambda B_0)\) have five minimum points, which match exactly the location of the exact eigenvalues (represented by “\(\circ \)” signs) of the unperturbed pair \((A_0, B_0)\). As the noise level \(\sigma \) increases, some of the local minima points of \(h(\lambda )\) vanished gradually. This implies that, with noisy inputs, the perturbed pair (A, B) may have less than five eigenvalues.
In Fig. 1, the red \(\times \)’s mark the optimal eigenvalues computed by Algorithm 4.3, and the blue \(+\)’s mark the optimal eigenvalues computed by TLS-IM algorithm. Our computational results show that, in the noiseless case, i.e., when \(\sigma = 0\), both of two algorithms capture the “exact solution”, i.e., eigenvalues of \(A_0-\lambda B_0\), accurately. The other figures in Fig. 1 show that, as the noise level \(\sigma \) increases, the discrepancy between numerical solutions and exact solution increases. However, in either case, the two algorithms can achieve exactly the same eigenvalues. On the other hand, most importantly, both of the two algorithms can always give five solutions even for the case when the measured pair (A, B) have less than five eigenvalues. This shows that both algorithms are robust and less affected by the noisy data.
We prepare 10 data sets with different noise \((N_A, N_B)\) with \(\sigma =0\), 0.25, 0.50, 0.75, 1.0, 1.25, respectively. Figure 2 shows numerically computed eigenvalues by the two compared algorithms. Since we used 10 data sets for each \(\sigma \), each figure has many points representing numerical solutions. Figure 2 shows again that, Algorithm 4.3 can achieve exactly the same eigenvalues as TLS-IM algorithm, and can capture five eigenpairs. Our computational results are also reported in Table 2, in which ’\(\sigma \)’ represents the level of noise in inputs, ’\(\hbox {rel}_A\)’ and ’rel\(_B\)’ denote the mean relative error of perturbation, ’IT.’, ’CT.’, ’Obj.’ and ’Res.’ denote the mean iteration numbers, the mean computational time in seconds, the mean value of \(\Vert A-{\hat{A}}\Vert ^2+\Vert B-{\hat{B}}\Vert ^2\) and the mean value of the residual \(\Vert {\hat{A}}X-{\hat{B}}X\Lambda \Vert \) for the computed optimal solution \(({\hat{A}}, {\hat{B}}, \{(\lambda _k, {\mathbf{v}}_k)\}_{k=1}^n)\) by Algorithm 4.3 with \(X=[\mathbf {v}_1~\cdots ~ \mathbf {v}_n]\), \(\Lambda =\text {diag}(\lambda _1,\ldots ,\lambda _n)\) based on 10 repeated tests, respectively. In particular, the last column in Table 2 shows the mean value of the error which is defined by
Here, the singular values of [A B] are arranged with decreasing order. Generally, it is meaningless to compare the iteration steps and computational time between two algorithms since TLS-IM algorithm is essentially a direct method. We here report the iteration steps only to emphasize that our proposed algorithm is very effective for finding a minimal perturbation for the pencil to have n eigenpairs. The results reported in the last column show that the computation results are in accordance with the theory established in the Corollary 2 in [2].
5.2.2 Comparison with the BEGM Algorithm
We then compare Algorithm 4.3 with BEGM algorithm [1] for the case of \(l=1\), i.e., the problem (1.2), in the sense that the perturbed pencil admits at least one eigenpair. As pointed out in [1], the optimization problem posed in (1.2) is equivalent to the optimization problem
A stable and convergent numerical algorithm is proposed in [1] which is guaranteed to converge to a local minimum of the function \(h(\lambda , \mathbf{v})\). Although, with different initial values, the BEGM algorithm may result in the optimization process converging at different local minima, and therefore, estimations of different eigenvalues. However, we here focus only on the case for finding one eigenpair. The initial \(\lambda \) in BEGM algorithm is set as the largest eigenvalue of \(B^\dagger A\) [1]. In Fig. 3, we describe the convergence trajectory of two algorithms on the contour plots of the function \(h(\lambda )=\min \limits _{\mathbf{v}} \frac{\Vert (A-\lambda B)\mathbf{v}\Vert ^2}{1+|\lambda |^2}\)(with given \(\lambda \), the optimal \({\mathbf{v}}\) is obtained by the right singular vector corresponding to the smallest singular value of \((A-\lambda B)^H(A-\lambda B)\)), which built using the perturbed pair (A, B) with \(\sigma =0,0.50,0.75,1.25\). In Fig. 3, the white \(\circ \)’s still mark the exact eigenvalues of the clear matrix pair \((A_0,B_0)\). The white dots and the red ’x’ sign present the iterative algorithm results and the optimal eigenvalue computed by Algorithm 4.3, respectively. The black dots and the pink ’+’ sign present the iterative algorithm results and the optimal eigenvalue computed by BEGM algorithm, respectively. Some more computational results are also reported in Table 3, in which the mean iteration numbers, the mean computational time in seconds, the mean value of \(\Vert A-{\hat{A}}\Vert ^2+\Vert B-{\hat{B}}\Vert ^2\) and the mean value of \(\Vert {\hat{A}}{\mathbf{v}}-\lambda {\hat{B}}{\mathbf{v}}\Vert \) for the computed optimal solution \(({\hat{A}}, {\hat{B}}, \{(\lambda , {\mathbf{v}})\})\) for the compared two algorithms are reported based on 10 repeated tests. We can see from Table 3 that, in most cases, Algorithm 4.3 runs faster that BEGM algorithm in terms of computational time and iteration steps.
An average of results of 10 random tests of Algorithm 4.3 for the case \(1\le l\le n\) is reported in Table 4, where parts of the items are the same as those of Tables 2 and 3. The items “\(\text {grad}_V f\)” and “\(\text {grad}_P f\)” represent the mean value of norm of gradient of f with respect to V and P based on 10 repeated tests, respectively. The case \(l=1\) and \(l=n\) are reported again in Table 4 just for comparison only, which show that Algorithm 4.3 is relatively less efficient for the case \(1<l<n\).
5.3 Further Numerical Performance
We compared the performance of Algorithm 4.2 with the Riemannian conjugate gradient methods used in [12,13,14, 16] which are all applicable to the problem (2.2) with necessary modifications. The known matrices \(A, B\in {{\mathbb {C}}}^{m\times n}\) in (2.2) are similar to the ones given in last example with \(\sigma =0.5\) but different problem size parameters (m, n, l). The numerical comparison results are reported in Table 5, where the terms “CT.”, “IT.”, “\(\text {grad}_V f\)” and “\(\text {grad}_P f\)” are the same as those in Table 4, “Obj.” means the objective function value \(\Vert [AV^k~~ BV^k]P^k\Vert \), “\(\text {feasi}_V\)” and “\(\text {feasi}_P\)” mean respectively the feasibility \(\Vert V^{kH}V^k-I_l\Vert \) and \(\Vert P^{kH}P^k-I_l\Vert \) at the final iterate by implementing the proposed algorithms. In Table 5,
“RCG-PR” stands for the Riemannian conjugate gradient method used in [14] designed to solve the problem (2.2), whose line search is the strong Wolfe line search, and the parameter \(\beta _{k+1}\) in (3.1) is the Riemannian version of the Polak–Ribière-type formula by combining the vector transport proposed. The retraction adapted in [14] is the QR-based retraction, and the vector transport is constructed by using the orthogonal projection operator onto the tangent space. On the real Stiefel manifold \(\text {St}(n,l,{{\mathbb {R}}})\), we often use a retraction \({{\mathcal {R}}}^{{{\mathbb {R}}}}\) based on the real QR decomposition. However, the map \({{\mathcal {R}}}^{{{\mathbb {R}}}}\) cannot be a retraction on \(\text {Stp}(n,l)\) and \(\text {Stp}(2l,l)\) (see [10] for more details). Alternatively, we can use a retraction \({{\mathcal {R}}}^{\text {Stp}}\) defined by
$$\begin{aligned} {{\mathcal {R}}}^{\text {Stp}}_{{\widetilde{V}}}({\widetilde{\xi }})=\phi \left( qf(\phi ^{-1}({\widetilde{V}}+{\widetilde{\xi }}))\right) =\phi (qf(V+{\xi })), \ \ {\widetilde{V}}\in \text {Stp}(n,l),\ \ {\widetilde{\xi }}\in {\mathcal {T}}_{{\widetilde{V}}}\text {Stp}(n,l), \end{aligned}$$where the \(qf(\cdot )\) denotes the Q-factor of the complex QR decomposition of the complex matrix in parentheses. That is, if a full-rank \(n\times l\) complex matrix M is decomposed into
$$\begin{aligned} M=QR,\ \ \ Q\in \text {St}(n,l,{{\mathbb {C}}}),\ \ R\in S^+_{upp}, \end{aligned}$$then \(qf(M) = Q\), where \(S^+_{upp}\) denotes the set of all \(l\times l\) upper triangular matrices with strictly positive diagonal entries. Therefore, a retraction \({{{\mathcal {R}}}}\) on the product manifold \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) is immediately defined as
$$\begin{aligned} {{{\mathcal {R}}}}_{({\widetilde{V}},{\widetilde{P}})}({\widetilde{\xi }},{\widetilde{\eta }})=\left( {{\mathcal {R}}}^{\text {Stp}}_{{\widetilde{V}}_l}({\widetilde{\xi }}),\ \ {{\mathcal {R}}}^{\text {Stp}}_{{\widetilde{P}}}({\widetilde{\eta }}) \right) \end{aligned}$$where \(({\widetilde{V}}_l, {\widetilde{P}})\in \text {Stp}(n,l)\times \text {Stp}(2l,l)\) and \(({\widetilde{\xi }},{\widetilde{\eta }})\in {\mathcal {T}}_{({\widetilde{V}}_l,{\widetilde{P}})}(\text {Stp}(n,l)\times \text {Stp}(2l,l))\). Further, the retraction on \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) corresponds to the retraction \({{\mathcal {R}}}\) on \(\text {St}(n,l,{{\mathbb {C}}})\times \text {St}(2l,l,{{\mathbb {C}}})\) defined by
$$\begin{aligned} {{\mathcal {R}}}_{(V,P)}(\alpha (\xi , \eta ))=({{\mathcal {R}}}^{{{\mathbb {C}}}}_V(\alpha \xi ),~~ {{\mathcal {R}}}^{{{\mathbb {C}}}}_P(\alpha \eta ))=(qf(V+\alpha \xi ), ~~qf(P+\alpha \eta )), \end{aligned}$$(5.2)for any \(\alpha \in {{\mathbb {R}}}\), where \(({V}, {P})\in \text {St}(n,l,{{\mathbb {C}}})\times \text {St}(2l,l,{{\mathbb {C}}})\) and \(({\xi },{\eta })\in {\mathcal {T}}_{({V},{P})}\text {St}(n,l,{{\mathbb {C}}})\times \text {St}(2l,l,{{\mathbb {C}}})\). The vector transport used in [14] is defined by
$$\begin{aligned} {{\mathcal {T}}}_{\alpha ({\xi }, {\eta })}({\zeta }, {\chi })= & {} {\mathbf {P}}_{{{{\mathcal {R}}}}_{({V}_l,{P})}(\alpha ({\xi },{\eta }))}({\zeta }, {\chi }) \nonumber \\= & {} \Big ( \zeta -qf(V+\alpha \xi )\text {her}(qf(V+\alpha \xi )^H\zeta ),~~ \chi -qf(P+\alpha \eta )\text {her}(qf(P+\alpha \eta )^H\chi ) \Big )\nonumber \\ \end{aligned}$$(5.3)where \(({\xi }, {\eta }), ({\zeta }, {\chi })\in {{{\mathbf {T}}}}_{({V}_l,{P})}\text {St}(n,l,{{\mathbb {C}}})\times \text {St}(2l,l,{{\mathbb {C}}})\).
“RCG-MPRP” stands for the Riemannian geometric modified Polak–Ribière–Polay conjugate gradient method used in [12] designed to solve to the problem (2.2), with the same QR-based retraction and vector transport as “RCG-PR”.
“RCG-FR” stands for the Riemannian Fletcher–Reeves conjugate gradient method used in [13] designed to solve the problem (2.2), with the same QR-based retraction and vector transport as “RCG-PR”.
“RCGQR” stands for a modification of Algorithm 4.2, by using the QR-based retraction (5.3) and the corresponding differentiated retraction as a vector transport (see p. 173 of [11]).
“RCGPol” stands for another modification of Algorithm 4.2, by the polar decomposition to construct a retraction (see p. 59 of [11]), and naturally using the corresponding differentiated retraction as a vector transport (see p. 173 of [11]).
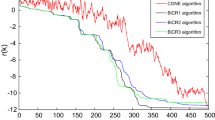
We see from Table 5 that, all the compared algorithms work very efficient for solving the problem (2.2) in the case \(l=1\), while the performance of Algorithm 4.2 is slightly better than that of the other algorithms in term of computational time and iteration steps. In the case \(1<l\le n\) Algorithm 4.2 perform much better than others. In addition, we present in Fig. 4 the plots of optimality (quadratic sum of norm of the gradient) versus iteration of one particular test to compare further the efficiency of these algorithms. We see that Algorithm 4.2 outperformed the other five competitors in general.
6 Concluding Remarks
In this paper, we have considered the generalized eigenvalue problem for nonsquare pencils, by finding the minimal perturbation to the pencil such that the perturbed pencil has l distinct eigenpairs with \(1\le l\le n\), which was first shown in theoretical study by Chu et al. [2] that can be reduced to a special form of optimization problem (1.4). We have focused on solving the general optimization problem (1.4) from numerical point of view, and proposed an efficient algorithm based on Riemannian nonlinear conjugate gradient method with nonmonotone line search technique. It is confirmed numerically that the proposed algorithm is effective for any \(1\le l\le n\). In particular, for the case \(l=n\), the algorithm is less affected by the data noise and guaranteed to yield n eigenpairs, and the algorithm generated exactly the same optimal solution as Ito and Murota’s algorithm [5], whose approach is essentially a direct method for designing for solving the problem (1.1), and was proposed by Boutry et al. in [1]. Moreover, the algorithm runs faster than Boutry et al.’s algorithm for the case with \(l=1\), in the sense that the perturbed pair with minimal perturbation admits at least one engenpair.
References
Boutry, G., Elad, M., Golub, G.H., Milanfar, P.: The generalized eigenvalue problem for nonsquare pencils using a minimal perturbation approach. SIAM J. Matrix Anal. Appl. 27(2), 582–601 (2005)
Chu, D., Golub, G.H.: On a generalized eigenvalue problem for nonsquare pencils. SIAM J. Matrix Anal. Appl. 28(3), 770–787 (2006)
Kressner, D., Mengi, E., Nakić, I., Truhar, N.: Generalized eigenvalue problems with specified eigenvalues. IMA J. Numer. Anal. 34(2), 480–501 (2013)
Lecumberri, P., Gómez, M., Carlosena, A.: Generalized eigenvalues of nonsquare pencils with structure. SIAM J. Matrix Anal. Appl. 30(1), 41–55 (2008)
Ito, S., Murota, K.: An algorithm for the generalized eigenvalue problem for nonsquare matrix pencils by minimal perturbation approach. SIAM J. Matrix Anal. Appl. 37(1), 409–419 (2016)
Golub, G.H., Loan, C.F.V.: An analysis of the total least squares problem. SIAM J. Numer. Anal. 17(6), 883–893 (1980)
Dai, Y.: A nonmonotone conjugate gradient algorithm for unconstrained optimization. J. Syst. Sci. Complex. 15, 139–145 (2002)
Sun, J.: Matrix Perturbation Analysis. Science Press, Beijing (2001)
Sato, H., Iwai, T.: A complex singular value decomposition algorithm based on the Riemannian Newton method. In: 52nd IEEE Conference on Decision and Control, pp. 2972–2978. IEEE (2013)
Sato, H.: Riemannian conjugate gradient method for complex singular value decomposition problem. In: 53rd IEEE Conference on Decision and Control, pp. 5849–5854. IEEE (2014)
Absil, P.A., Mahony, R., Sepulchre, R.: Optimization Algorithms on Matrix Manifolds. Princeton University Press, Princeton (2009)
Zhao, Z., Jin, X.Q., Bai, Z.J.: A geometric nonlinear conjugate gradient method for stochastic inverse eigenvalue problems. SIAM J. Numer. Anal. 54(4), 2015–2035 (2016)
Yao, T.T., Bai, Z.J., Zhao, Z., Ching, W.K.: A Riemannian Fletcher–Reeves conjugate gradient method for Doubly stochastic inverse eigenvalue problems. SIAM J. Matrix Anal. Appl. 37(1), 215–234 (2016)
Sato, H., Iwai, T.: A Riemannian optimization approach to the matrix singular value decomposition. SIAM J. Optim. 23(1), 188–212 (2013)
Wen, Z., Yin, W.: A feasible method for optimization with orthogonality constraints. Math. Program. 142(1–2), 397–434 (2013)
Zhu, X.: A Riemannian conjugate gradient method for optimization on the Stiefel manifold. Comput. Optim. Appl. 67(1), 73–110 (2017)
Edelman, A., Arias, T.A., Smith, S.T.: The geometry of algorithms with orthogonality constraints. SIAM J. Matrix Anal. Appl. 20(2), 303–353 (1998)
Absil, P.A., Baker, C., Gallivan, K.: A truncated-CG style method for symmetric generalized eigenvalue problems. J. Comput. Appl. Math. 189(1–2), 274–285 (2006)
Baker, C., Absil, P.A., Gallivan, K.A.: An implicit Riemannian trust-region method for the symmetric generalized eigenproblem. In: International Conference on Computational Science, pp. 210–217. Springer, Berlin (2006)
Zhao, Z., Bai, Z.J., Jin, X.Q.: A Riemannian Newton algorithm for nonlinear eigenvalue problems. SIAM J. Matrix Anal. Appl. 36(2), 752–774 (2015)
Barzilai, J., Borwein, J.M.: Two-point step size gradient methods. IMA J. Numer. Anal. 8(1), 141–148 (1988)
Acknowledgements
The authors would like to thank both reviewers for their very constructive suggestions that lead to the improvement of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research was supported in part by National Natural Science Foundation of China (11761024, 11671158, U1811464, 11561015, 11771159), MYRG2017-00098-FST from University of Macau, Natural Science Foundation of Guangxi Province (2016GXNSFAA380074, 2016GXNSFFA380009, 2017GXNSFBA198082), and in part by NSF-DMS 1419028, 1854638 of the United States.
Appendix
Appendix
1.1 Proof of Lemma 4.1
Proof
For any point \(({\widetilde{V}},{\widetilde{P}})\in \Phi \), we have \(\Vert {\widetilde{V}}\Vert =\Vert {\widetilde{P}}\Vert =\sqrt{l}\), which implies that the level set \(\Phi \) is bounded. This together with the fact that the objection function \(f({\widetilde{V}},{\widetilde{P}})\) is a continuous function with respect to \({\widetilde{V}}\) and \({\widetilde{P}}\), shows that \(\Phi \) is also closed. Thus the level set \(\Phi \) is compact.
\(\square \)
1.2 Proof of Lemma 4.2
Proof
We proceed by induction. Since \(({\widetilde{\xi }}_{0}, {\widetilde{\eta }}_{0}) = -\text {grad} f({\widetilde{V}}^{0}, {\widetilde{P}}^{0})\), (35) holds immediately for \(k = 0\). Suppose (4.11) holds for some k. Then \(\beta ^D_{k+1} > 0\) according to (32) and therefore \(\beta _{k+1}\) is well defined and the ratio \(r_{k+1}=\frac{\beta _{k+1}}{\beta ^D_{k+1}}\) lies in [0, 1]. By (4.2), (4.3) and (4.4), we have
If \(\langle \text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1}), \ \ {\mathcal {T}}_{\alpha _k({\widetilde{\xi }}_k,{\widetilde{\eta }}_k)}({\widetilde{\xi }}_k,{\widetilde{\eta }}_k)\rangle \ge 0\), it follows from the induction hypothesis and (7.1) that \(Y_{k+1}>0\) and
which show that \(\langle \text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1}), \ ({\widetilde{\xi }}_{k+1},{\widetilde{\eta }}_{k+1})\rangle <0\).
If \(\langle \text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1}), \ \ {\mathcal {T}}_{\alpha _k({\widetilde{\xi }}_k,{\widetilde{\eta }}_k)}({\widetilde{\xi }}_k,{\widetilde{\eta }}_k)\rangle <0 \), it follows from (7.1) that
which also gives \(\langle \text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1}), \ ({\widetilde{\xi }}_{k+1},{\widetilde{\eta }}_{k+1})\rangle <0\). Therefore (4.11) holds for \(k + 1\) in both cases. By induction, we conclude that (4.11) is true for all k. \(\square \)
1.3 Proof of Lemma 4.3
Proof
It follows from the nonmonotone linesearch step, Step 2, of Algorithm 4.1, that when k is sufficiently large, \(\rho ^{-1}\alpha _k\) does not satisfy (4.1). This means,
We note that the pullback function \({\widehat{f}}({\widetilde{\xi }}, {\widetilde{\eta }})\) defined in (3.26) is continuously differentiable since both the cost function \(f({\widetilde{V}},{\widetilde{P}})\) and the retraction mapping \({\mathcal {R}}_{({\widetilde{V}},{\widetilde{P}})}\) defined in (3.8) are continuously differentiable. Then there exist two constants \(\kappa > 0\) and \(L> 0\) such that
for any \(({\widetilde{V}},{\widetilde{P}})\in \Phi \) and \(({\widetilde{\xi }}, {\widetilde{\eta }}), ({\widetilde{\zeta }}, {\widetilde{\chi }})\in {\mathbf {T}}_{({\widetilde{V}},{\widetilde{P}})}\text {Stp}(n,l)\times \text {Stp}(2l,l)\) with \(\Vert ({\widetilde{\xi }}, {\widetilde{\eta }})\Vert ,\Vert ({\widetilde{\zeta }}, {\widetilde{\chi }})\Vert \le \kappa \).
By applying the mean-value theorem, together with (7.3), there exists a constant \(\omega _k\in (0,1)\) such that for all k sufficiently large,
Combining (7.2) with (7.4) together gives for all k sufficiently large,
Then we get (4.12) by setting \(\mu =(1-\delta )\rho /L\).
The proof of the second part is the same as that of Theorem 3.2 in [7]. To make this lemma self-contained, we prove it as follows.
For \(j\ge 0\), define
We show by induction that
for all \(i=1, \ldots , h\). In fact, due to (4.1), (7.5) holds for \(i=1\). Assume (7.5) holds for all \(i=1,\ldots , t\) for some \(1\le t \le h-1.\) Then it follows from (4.11) that
This, together with (4.1), implies that
Thus, (7.5) is true for \(t+1\). Therefore, (7.5) is true for \(i=1, \ldots , h\). By (7.5) and the definition of \(F_j\), we have
Since \({F_j}\) is bounded below, we deduce by summing (7.6) over j that (7.5) is true. \(\square \)
1.4 Proof of Theorem 4.1
Proof
We prove this theorem by contradiction. Suppose that \(\mathop {\text {lim inf}}_{k\rightarrow \infty }\Vert \text {grad} f({\widetilde{V}}^k, {\widetilde{P}}^k)\Vert \ne 0\) This means there exists a constant \(\gamma \in (0, 1)\) such that
From (7.1), we can see that the formula (4.4) of \(\beta ^D_{k+1}\) can be rewritten as
By (4.3), it is easy to prove that the denominator of \(\beta _{k+1}^D\) in (7.8) is equivalent to
Substituting (7.9) into the denominator of \(\beta _{k+1}^D\) in (7.8), together with the results of Lemma 4.2, we have
It follows from (4.2) that \(({\widetilde{\xi }}_{k+1}, {\widetilde{\eta }}_{k+1})+\text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1})=\beta _{k+1}{\mathcal {T}}_{\alpha _k({\widetilde{\xi }}_{k}, {\widetilde{\eta }}_{k})}({\widetilde{\xi }}_{k}, {\widetilde{\eta }}_{k})\). Hence
Dividing (7.11) by \(\langle \text {grad} f({\widetilde{V}}^{k+1}, {\widetilde{P}}^{k+1}), \ \ ({\widetilde{\xi }}_{k+1},{\widetilde{\eta }}_{k+1})\rangle ^2\), using (7.11), and together with the Ring-Wirth nonexpansive condition (3.15) of the presented vector transport defined in (3.12), we can get
Combining the recursion of (7.12) and the assumption (7.7) together gives
Then we have that
On the other hand, from the second inequality in (7.13) and (7.12), we have
which yields
If
then together with (7.15) gives
Therefore, by (4.11) and (7.7), we have
Using \({\overline{\alpha }}_k\ge \alpha _{min}\), together with (4.12), (7.14) and (7.16), we have
which contradicts with (4.13). This prove (4.14). The existence of a first-order critical accumulation point follows immediately from the compactness of the product manifold \(\text {Stp}(n,l)\times \text {Stp}(2l,l)\) in Lemma 4.1. \(\square \)
Rights and permissions
About this article
Cite this article
Li, Jf., Li, W., Vong, SW. et al. A Riemannian Optimization Approach for Solving the Generalized Eigenvalue Problem for Nonsquare Matrix Pencils. J Sci Comput 82, 67 (2020). https://doi.org/10.1007/s10915-020-01173-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-020-01173-5