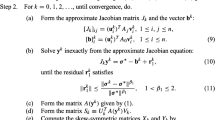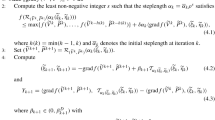Riemannian inexact Newton method for structured inverse eigenvalue and singular value problems

Abstract

Inverse eigenvalue and singular value problems have been widely discussed for decades. The well-known result is the Weyl-Horn condition, which presents the relations between the eigenvalues and singular values of an arbitrary matrix. This result by Weyl-Horn then leads to an interesting inverse problem, i.e., how to construct a matrix with desired eigenvalues and singular values. In this work, we do that and more. We propose an eclectic mix of techniques from differential geometry and the inexact Newton method for solving inverse eigenvalue and singular value problems as well as additional desired characteristics such as nonnegative entries, prescribed diagonal entries, and even predetermined entries. We show theoretically that our method converges globally and quadratically, and we provide numerical examples to demonstrate the robustness and accuracy of our proposed method.

1 Introduction

Let $|\lambda _1|\ge |\lambda _2|\ge \cdots \ge |\lambda _n| \ge 0$ and $\sigma _1 \ge \cdots \ge \sigma _n \ge 0$ be the eigenvalues and singular values of a given $n\times n$ real matrix A. In [45] Weyl showed that sets of eigenvalues and singular values satisfy the following necessary condition:

$$\begin{aligned}&\prod _{j=1}^k|\lambda _j| \le \prod _{j=1}^k \sigma _j, \quad k = 1,\ldots , n-1, \end{aligned}$$

(1.1a)

$$\begin{aligned}&\prod _{j=1}^n |\lambda _j| = \prod _{j=1}^n \sigma _j. \end{aligned}$$

(1.1b)

Moreover, Horn [29] proved that condition (1.1), called the Weyl-Horn condition, is also sufficient for constructing triangular matrices with prescribed eigenvalues and singular values. Research interest in inverse eigenvalue and singular value problems can be tracked back to the open problem raised by Higham in [28, Problem 26.3], as follows:

Develop an efficient algorithm for computing a unit upper triangular $n\times n$ matrix with the prescribed singular values $\sigma _1,\ldots ,\sigma _n$, where $\prod _{j=1}^n \sigma _j = 1$.

This problem, which was solved by Kosowski and Smoktunowicz [32], leads to the following interesting inverse eigenvalue and singular value problem (IESP):

(IESP) Given two sets of numbers ${\varvec{\lambda }} = \{\lambda _1, \ldots , \lambda _n\}$ and $\varvec{\sigma } = \{\sigma _1, \ldots ,\sigma _n\}$ satisfying (1.1), find a real $n\times n$ matrix with eigenvalues ${\varvec{\lambda }}$ and singular values ${\varvec{\sigma }}$.

The following factors make the IESP difficult to solve:

• Often the desired matrices are real. This problem was solved by the authors of [9] with prescribed real eigenvalues and singular values. The method for finding a general real-valued matrix with prescribed complex–conjugate eigenvalues and singular values was also investigated in [33]. In this work, we take an alternative approach to tackle this problem and add further constraints.

• Often the desired matrices are structured. Corresponding to physical applications, the recovered matrices often preserve some common structure such as nonnegative entries or predetermined diagonal entries [8, 46]. In this paper, specifically, we offer the condition of the existence of a nonnegative matrix provided that eigenvalues, singular values, and diagonal entries are given. Furthermore, solving the IESP with respect to the diagonal constraint is not enough because entries of the recovered matrices should preserve certain patterns, for example, non-negativity, which correspond to original observations. How to tackle this structured problem is the main thrust of this paper.

The IESP can be regarded as a natural generalization of the inverse eigenvalue problems, which is known for its a wide variety of applications such as the pole assignment problem [6, 20, 34], applied mechanics [15, 18, 19, 25, 38], and inverse Sturm–Liouville problem [3, 24, 26, 37]. Thus applications of the IESP could be found in wireless communication [17, 39, 43] and quantum information science [21, 30, 46]. Research results advanced thus far for the IESP do not fully address the above scenarios. Often, given a set of data, the IESP is studied in parts. That is, there have been extensive investigations of the conditions for the existence of a matrix when the singular values and eigenvalues are provided (i.e., the Weyl-Horn condition [29, 45]), when the singular values and main diagonal entries are provided (i.e., the Sing-Thompson condition [41, 42]), or when the eigenvalues and main diagonal entries are provided (i.e., the Mirsky condition [36]). Also, the above conditions have given rise to numerical approaches, as found in [5, 8, 9, 16, 22, 32, 48].

Our work here not only provides a way to solve the IESP but also immediately use the solution to address the IESP with the desired structure, for example, nonnegative entries and fixed diagonal elements. For one relatively close result, see [46], where the authors consider a new type of IESP that requires that all three constraints, i.e., eigenvalues, singular values, and diagonal entries, be satisfied simultaneously. Theoretically, Wu and Chu generalize the classical Mirsky, Sing-Thompson, and Weyl-Horn conditions and provide one sufficient condition for the existence of a matrix with prescribed eigenvalues, singular values, and diagonal entries when $n\ge 3$. Numerically, Wu and Chu establish a dynamic system for constructing such a matrix, in which real eigenvalues are given. In this work, we solve an IESP with complex conjugate eigenvalues and with entries fixed at certain locations. Note that, in general, the solution of the IESP is not unique or difficult to find once structured requirements are added. To solve an IESP with some specific feature, we combine techniques from differential geometry and for solving nonlinear equations.

We organize this paper as follows. In Sect. 2, we propose the use of the Riemannian inexact Newton method for solving an IESP with complex conjugate eigenvalues. In Sect. 3, we show that the convergence is quadratic. In Sect. 4, we demonstrate the application of our technique to an IESP with a specific structure that includes nonnegative or predetermined entries to show the robustness and efficiency of our proposed approaches. The concluding remarks are given in Sect. 5.

2 Riemannian inexact Newton method

In this section, we explain how the Riemannian inexact Newton method can be applied to the IESP. The problem of optimizing a function on a matrix manifold has received much attention in the scientific and engineering fields due to its peculiarity and capacity. Its applications include, but are not limited to, the study of eigenvalue problems [1, 2, 7, 10, 12,13,14, 46, 47, 49,50,51], matrix low rank approximation [4, 27], and nonlinear matrix equations [11, 44]. Numerical methods for solving problems involving matrix manifolds rely on interdisciplinary inputs from differential geometry, optimization theory, and gradient flows.

To begin, let ${\mathscr {O}}(n) \subset {\mathbb {R}}^{n\times n}$ be the group of $n\times n$ real orthogonal matrices, and let ${\varvec{\lambda }} = \{\lambda _1, \ldots , \lambda _n\}$ and $\varvec{\sigma } = \{\sigma _1, \ldots ,\sigma _n\}$ be the eigenvalues and singular values of an $n\times n$ matrix. We assume without loss of generality that:

$$\begin{aligned}&\lambda _{2i-1} = \alpha _i + \beta _i \sqrt{-1}, \quad \lambda _{2i} = \alpha _i - \beta _i \sqrt{-1}, \quad i = 1,\ldots , k, \\&\lambda _i\in {\mathbb {R}}, \quad i=2k+1,\ldots ,n, \end{aligned}$$

where $\alpha _i, \beta _i \in {\mathbb {R}}$ with $\beta _i\ne 0$ for $i = 1,\ldots , k$, and we define the corresponding block diagonal matrix

$$\begin{aligned} \begin{array}{ccl} {\varLambda } &{}=&{}\mathrm {diag}\left\{ \left[ \begin{array}{r@{\quad }r} \alpha _{1}&{} \beta _{1} \\ -\beta _{1} &{} \alpha _{1}\\ \end{array} \right] ,\ldots , \left[ \begin{array}{r@{\quad }r} \alpha _{k} &{} \beta _{k} \\ -\beta _{k} &{} \alpha _{k}\\ \end{array} \right] , {\lambda }_{2k+1},\ldots , {\lambda }_{n} \right\} \end{array} \end{aligned}$$

and the diagonal matrix

$$\begin{aligned} \begin{array}{ccl} {\varSigma }= & {} \mathrm {diag}\left\{ {\sigma }_{1},\ldots , {\sigma }_{n} \right\} . \end{array} \end{aligned}$$

Then the IESP, based on the real Schur decomposition, is equivalent to finding matrices $U,\, V,\, Q\in {\mathscr {O}}(n)$, and

$$\begin{aligned} W\in {\mathscr {W}}(n) := \{W\in {\mathbb {R}}^{n\times n} \,|\, W_{i,j} = 0 \text{ if } {\varLambda }_{i,j} \ne 0 \text{ or } i\ge j, \text{ for } \, 1\le i,j \le n \}, \end{aligned}$$

which satisfy the following equation:

$$\begin{aligned} F(U,V,Q,W) =U{\varSigma } V^\top - Q({\varLambda }+W)Q^\top = {\mathbf {0}}. \end{aligned}$$

(2.1)

Here, we may assume without loss of generality that Q is an identity matrix and simplify Eq. (2.1) as follows:

$$\begin{aligned} F(U,V,W) =U{\varSigma } V^\top - ({\varLambda }+W) = {\mathbf {0}}. \end{aligned}$$

(2.2)

Let $X = (U,V,W) \in {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)$. Upon using Eq. (2.2), we can see that we might solve the IESP by

$$\begin{aligned} \text{ finding } X \in {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n) \text{ such } \text{ that } F(X) = {\mathbf {0}}, \end{aligned}$$

(2.3)

where $F: {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n) \rightarrow {\mathbb {R}}^{n\times n}$ is continuously differentiable. By making an initial guess, $X_0$, one immediate way to solve Eq. (2.3) is to apply the Newton method and generate a sequence of iterates by solving

$$\begin{aligned} DF (X_{k}) [{\varDelta } X_k] = -F(X_k), \end{aligned}$$

(2.4)

for ${\varDelta } X_k \in T_{X_k}({\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n))$ and set

$$\begin{aligned} X_{k+1} = R_{X_k} ({\varDelta } X_k), \end{aligned}$$

where $DF (X_k)$ represents the differential of F at $X_k$ and R is a retraction on ${\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)$. Since Eq. (2.4) is an underdetermined system, it may have more than one solution. Let $DF (X_k)^*$ be the adjoint operator of $DF (X_k)$. In our calculation, we choose the solution ${\varDelta } X_k$ with the minimum norm by letting [35, Chap. 6]

$$\begin{aligned} {\varDelta } X_k = DF (X_k)^* [{\varDelta } Z_k], \end{aligned}$$

(2.5)

where ${\varDelta } Z_k \in T_{F(X_k)} ({\mathbb {R}}^{n\times n})$ is a solution for

$$\begin{aligned} \left( DF (X_k)\circ DF (X_k)^* \right) [{\varDelta } Z_k] = -F(X_k). \end{aligned}$$

(2.6)

Note that the notation $\circ$ represents the composition of two operators $DF (X_k)$ and $DF (X_k)^*$. This implies that the operator $DF (X_k)\circ DF (X_k)^*$ is symmetric and positive semidefinite. If, as is the general case, the operator $DF (X_k)\circ DF (X_k)^*$ from $T_{F(X_k)} ({\mathbb {R}}^{n\times n})$ to ${\mathbb {R}}^{n\times n}$ is invertible, we can compute the optimal solution in (2.5).

Note that solving for the solution of Eq. (2.6) could be unnecessary and computationally time-consuming, and that the linear model given by Eq. (2.6) is large-scale or the resulting iteration $X_k$ is far from the solution of condition (2.3) [40]. By analogy with the classical Newton method [23], we adopt the “inexact” Newton method on Riemannian manifolds, i.e., without solving Eq. (2.6) exactly, we repeatedly apply the conjugate gradient (CG) method to find ${\varDelta } Z_k\in T_{F(X_k)} ({\mathbb {R}}^{n\times n})$, such that:

$$\begin{aligned} \Vert ( DF (X_k)\circ DF (X_k)^*) [{\varDelta } Z_k] + F(X_k)\Vert \le \eta _k \Vert F(X_k)\Vert , \end{aligned}$$

(2.7)

for some constant $\eta _k \in [0,1)$, is satisfied. Then, we update $X_k$ corresponding to ${\varDelta } Z_k$ until the stopping criterion is satisfied. Here, the notation $\Vert \cdot \Vert$ is the Frobenius norm. Note that in our calculation, the elements in the product space ${\mathbb {R}}^{n\times n} \times {\mathbb {R}}^{n\times n}\times {\mathbb {R}}^{n\times n}$ are computed using the standard Frobenius inner product:

$$\begin{aligned} \langle (A_1, A_2,A_3), (B_1, B_2,B_3) \rangle _{F} := \langle A_1,B_1 \rangle + \langle A_2,B_2 \rangle + \langle A_3,B_3 \rangle , \end{aligned}$$

(2.8)

where $\langle A,B \rangle := \text{ trace }(AB^\top )$ for any $A, B\in {\mathbb {R}}^{n\times n}$ and the induced norm $\Vert X\Vert _{F} = \sqrt{\langle X,X \rangle _{F} }$ (or, simply, $\langle X,X\rangle$ and $\Vert X\Vert$ without the risk of confusion) for any $X \in {\mathbb {R}}^{n\times n} \times {\mathbb {R}}^{n\times n}\times {\mathbb {R}}^{n\times n}$.

Then, the mapping $DF (X_k)$ at ${\varDelta } X_k = ({\varDelta } U_k,{\varDelta } V_k, {\varDelta } W_k) \in T_{X_k}({\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n))$ is given by:

$$\begin{aligned} DF (X_k)[{\varDelta } X_k] = {\varDelta } U_k {\varSigma } V_k^\top + U_k{\varSigma } {\varDelta } V_k^\top - {\varDelta } W_k. \end{aligned}$$

Let $DF (X_k)^*: T_{F(X_k)} ({\mathbb {R}}^{n\times n}) \rightarrow T_{X_k}({\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n))$ be the adjoint of the mapping $DF (X_k)$. The adjoint $DF (X_k)^*$ is determined by the following:

$$\begin{aligned} \langle {\varDelta } Z_k, DF (X_k)[{\varDelta } X_k] \rangle = \langle DF (X_k)^*[{\varDelta } Z_k], {\varDelta } X_k \rangle \end{aligned}$$

and can be expressed as follows:

$$\begin{aligned} DF (X_k)^*[{\varDelta } Z_k] {=({\varDelta } U_k,{\varDelta } V_k,{\varDelta } W_k),} \end{aligned}$$

where

$$\begin{aligned} {\varDelta } U_k= & {} \frac{1}{2}({\varDelta } Z_k V_k {\varSigma }^\top -U_k {\varSigma } V_k^\top {\varDelta } Z_k^\top U_k ), \\ {\varDelta } V_k= & {} \frac{1}{2}( {\varDelta } Z_k^\top U_k{\varSigma } -V_k {\varSigma }^\top U_k^\top {\varDelta } Z_k V_k ), \\ {\varDelta } W_k= & {} -H\odot {\varDelta } Z_k, \end{aligned}$$

where the notation $\odot$ represents the Hadamard product and H is a matrix satisfying

$$\begin{aligned} H_{i,j} = \left\{ \begin{array}{l@{\quad }l} 0 &{} \text{ if } {\varLambda }_{i,j} \ne 0 \text{ or } i\ge j \\ 1 &{} \text{ otherwise } \end{array} \right. \end{aligned}$$

(see [12, 50] for a similar discussion).

There is definitely no guarantee that the application of the inexact Newton method can achieve a sufficient decrease in the size of the nonlinear residual $\Vert F(X_k)\Vert$. This provides motivation for deriving an iterate for which the size of the nonlinear residual is decreased. One way to do this is to update the Newton step ${\varDelta } X_k$ obtained from Eq. (2.5) by choosing $\theta \in [\theta _{\mathrm {min}}, \theta _{\mathrm {max}}]$, with $0<\theta _{\mathrm {min}}<\theta _{\mathrm {max}}<1$, and setting

$$\begin{aligned} \widehat{{\varDelta } X}_k = {\varDelta } X_k, \quad \hat{{\eta }}_k = \frac{\Vert F(X_k) + DF (X_k) [{{\varDelta } X}_k]\Vert }{\Vert F(X_k)\Vert }, \end{aligned}$$

(2.9)

and $\eta _k = {\hat{\eta }}_k$. Note that the definition of ${\hat{\eta }}_k$ is not well-defined if $F(X_k) = 0$. However, we can prevent this happening by assuming without loss of generality that $F(X_0)\ne 0$. Once $F(X_k) = 0$ is satisfied, we terminate our iterations and output the solution $X = X_k$. Otherwise, we update

$$\begin{aligned}&\eta _k \leftarrow 1-\theta (1-\eta _k) \text{ and } {\varDelta } X_k \leftarrow \frac{1-\eta _k}{1-{\hat{\eta }}_k} \widehat{{\varDelta } X}_k, \end{aligned}$$

(2.10)

while

$$\begin{aligned} \Vert F(X_k)\Vert - \Vert F(R_{X_k}({\varDelta } X_k))\Vert > t(1-{\eta }_k)\Vert F(X_k)\Vert , \end{aligned}$$

or, equivalently,

$$\begin{aligned} \Vert F(R_{X_k}({\varDelta } X_k))\Vert < [1-t(1-{\eta }_k)]\Vert F(X_k)\Vert , \end{aligned}$$

(2.11)

for some $t \in [0,1)$ [23]. Let $Q_f(\cdot )$ denote the mapping that sends a matrix to the Q factor of its QR decomposition with its R factor having strictly positive diagonal elements [1, Example 4.1.3]. For all $(\xi _U, \xi _V,\xi _W) \in T_{(U,V,W)} \left( {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)\right)$, we can compute the retraction R using the following formula:

$$\begin{aligned} R_{(U,V,W)} (\xi _U, \xi _V,\xi _W) = (R_U(\xi _U),R_V(\xi _V), R_W(\xi _W)), \end{aligned}$$

where

$$\begin{aligned} R_U(\xi _U) = {Q_f}(U+\xi _U), \quad R_V(\xi _V) = {Q_f}(V+\xi _V), \quad R_W(\xi _W) = W+\xi _W. \end{aligned}$$

We call this the Riemannian inexact Newton backtracking method (RINB) and formalize this method in Algorithm 1. To choose the parameter $\theta \in [\theta _{\mathrm {min}}, \theta _{\mathrm {max}}]$, we apply a two-point parabolic model [31, 50] to achieve a sufficient decrease among steps 6–9. That is, we use the iteration history to model an approximate minimizer of the following scalar function:

$$\begin{aligned} f(\lambda ) := \Vert F(R_{X_k} (\lambda {\varDelta } X_k))\Vert ^2 \end{aligned}$$

by defining a parabolic model, as follows:

$$\begin{aligned} p(\lambda ) = f(0) + f'(0)\lambda + (f(1)-f(0)-f'(0)) \lambda ^2, \end{aligned}$$

where

$$\begin{aligned} f(0)= & {} \Vert F(X_k)\Vert ^2,\,\,\\ f'(0)= & {} 2\langle DF (X_k) [{\varDelta } X_k], F(X_k) \rangle ,\,\, \text{ and }\,\, f(1) = \Vert F(R_{X_k}({\varDelta } X_k))\Vert ^2. \end{aligned}$$

It should be noted that the computational costs for constructing the parabolic $p(\lambda )$ are only ${O}(n^3)$ operations per iteration.

From (2.7), it can be shown that the function evaluation $f'(0)$ should be negative. Since $f'(0) < 0$, if $p''(\lambda ) = 2(f(1) - f(0) - f'(0)) > 0$, then $p(\lambda )$ has its minimum at:

$$\begin{aligned} \theta = \frac{-f'(0)}{2(f(1) - f(0) - f'(0))} > 0; \end{aligned}$$

otherwise, if $p''(\lambda ) < 0$, we choose $\theta = \theta _{\mathrm {max}}$. By incorporating two types of selection, we can choose the following:

$$\begin{aligned} \theta = {\min }\left\{ {\max }\left\{ \theta _{{\min }}, \frac{-f'(0)}{2(f(1) - f(0) - f'(0))}\right\} , \theta _{{\max }} \right\} . \end{aligned}$$

as the parameter $\theta$ in Algorithm 1 [31, 50]. In the next section, we mathematically investigate the convergence analysis of Algorithm 1.

3 Convergence analysis

By combining the classical inexact Newton method [23] with optimization techniques on matrix manifolds, Algorithm 1 provides a way to solve the IESP. However, we have yet to theoretically discuss the convergence analysis of Algorithm 1. In this section, we provide a theoretical foundation for the RINB method, and show that this RINB method converges globally and finally converges quadratically when Algorithm 1 does not terminate prematurely. We address this phenomenon in the following:

Lemma 3.1

Algorithm 1 does not break down at some $X_k$ if and only if $F(X_k)\ne {\mathbf {0}}$ and the inverse of $DF (X_k)\circ DF (X_k)^*$ exists.

Next, we provide an upper bound for the approximate solution $\widehat{{\varDelta } X}_k$ in Algorithm 1.

Theorem 3.1

Let ${\varDelta }{Z}_k\in T_{F(X_k)} ({\mathbb {R}}^{n\times n})$ be a solution that satisfies condition (2.7) and

$$\begin{aligned} \widehat{{\varDelta } X}_k = DF (X_k)^* [{\varDelta }{Z}_k]. \end{aligned}$$

Then,

$$\begin{aligned}&\mathrm {(a)}\, \Vert \widehat{{\varDelta } X}_k \Vert \le (1+ {{\hat{\eta }}_k} )\Vert DF (X_k)^\dagger \Vert \Vert F(X_k)\Vert , \end{aligned}$$

(3.1a)

$$\begin{aligned}&\mathrm {(b)}\, \Vert \sigma _k(\eta )\Vert \le \frac{ 1+\eta _{\mathrm {max}} }{1-{\eta }_{\mathrm {max}}} (1-\eta ) {\Vert DF (X_k)^\dagger \Vert } \Vert F(X_k)\Vert , \end{aligned}$$

(3.1b)

where $DF (X_k)^\dagger$ is the pseudoinverse of $DF (X_k)$, ${{\hat{\eta }}_k}$ is defined in Eq. (2.9), and $\sigma _k$ is the backtracking curve used in Algorithm 1, which is defined by the following:

$$\begin{aligned} \sigma _k(\eta ) = \frac{1-\eta }{1-{\hat{\eta }}_k} \widehat{{\varDelta } X}_k \end{aligned}$$

with ${\hat{\eta }}_k\le \eta \le 1$, and

$$\begin{aligned} \Vert DF (X_k)^\dagger \Vert := \max \limits _{\Vert {\varDelta } Z\Vert = 1} {\Vert DF (X_k)^\dagger [{\varDelta } Z]\Vert } \end{aligned}$$

represents the norm of the pseudoinverse of $DF (X_k)$.

Proof

Let $r_k = ( DF (X_k)\circ DF (X_k)^*) [{\varDelta } {Z}_k] + F(X_k)$. We see that

$$\begin{aligned} \Vert \widehat{{\varDelta } X}_k \Vert\le & {} \Vert DF (X_k)^* \circ [ DF (X_k)\circ DF (X_k)^*]^{-1}\Vert \Vert r_k - F(X_k)\Vert \\\le & {} (1+ {\hat{\eta }}_k)\Vert DF (X_k)^\dagger \Vert \Vert F(X_k)\Vert \end{aligned}$$

and

$$\begin{aligned} \Vert \sigma _k(\eta )\Vert= & {} \frac{1-\eta }{1-{\hat{\eta }}_k} \Vert DF (X_k)^\dagger (r_k-F(X_k)) \Vert \le \frac{ 1+{\hat{\eta }}_k }{1-{\hat{\eta }}_k} (1-\eta ) \Vert DF (X_k)^\dagger \Vert \Vert F(X_k) \Vert \\\le & {} \frac{ 1+\eta _{\mathrm {max}} }{1-{\eta }_{\mathrm {max}}} (1-\eta ) \Vert DF (X_k)^\dagger \Vert \Vert F(X_k) \Vert . \end{aligned}$$

$\square$

In our subsequent discussion, we assume that Algorithm 1 does not break down and the sequence $\{X_k\}$ is bounded. Let $X_*$ be a limit point of $\{X_k\}$. Since F is continuously differentiable, we have the following:

$$\begin{aligned} \Vert DF (X)^\dagger \Vert \le 2 \Vert DF (X_*)^\dagger \Vert \end{aligned}$$

(3.2)

whenever $X \in B_\delta (X_*)$ for a sufficiently small constant $\delta > 0$. Here, the notation $B_\delta (X_*)$ represents a neighborhood of $X_*$ consisting of all points X such that $\Vert X - X_*\Vert < \delta$. By condition (3.1), we can show without any difficulty that whenever $X_k$ is sufficiently close to $X_*$,

$$\begin{aligned} \Vert \widehat{{\varDelta } X}_k \Vert\le & {} (1+\eta _{\mathrm {max}} )\Vert DF (X_*)^\dagger \Vert \Vert {F(X_k)}\Vert , \nonumber \\ \Vert \sigma _k(\eta )\Vert\le & {} {\varGamma } (1-\eta ) \Vert {F(X_k)}\Vert , \quad {\hat{\eta }}_k\le \eta \le 1, \end{aligned}$$

(3.3)

where ${\varGamma }$ is a constant independent of k defined by

$$\begin{aligned} {\varGamma } = 2\frac{ 1+\eta _{\mathrm {max}} }{1-{\eta }_{ \mathrm { max}}} \Vert DF (X_*)^\dagger \Vert . \end{aligned}$$

Now, we show that the sequence of $\{F(X_k)\}$ eventually converges to zero.

Theorem 3.2

Assume that Algorithm 1 does not break down. If $\{X_k\}$ is the sequence generated in Algorithm 1, then

$$\begin{aligned} \lim _{k\rightarrow \infty } F(X_k) = {\mathbf {0}}. \end{aligned}$$

Proof

Observe that

$$\begin{aligned} \Vert F(X_k)\Vert= & {} \Vert F(R_{X_{k-1}}({\varDelta } X_{k-1}))\Vert \le (1-t(1-\eta _{k-1})) \Vert F(X_{k-1})\Vert \\\le & {} \Vert F(X_0)\Vert \prod \limits _{j=0}^{k-1}(1-t(1-\eta _j)) \le \Vert F(X_0)\Vert e^{-t\sum \limits _{j=0}^{k-1}(1-\eta _j)}. \end{aligned}$$

Since $t>0$ and $\lim \nolimits _{k\rightarrow \infty }\sum \nolimits _{j=0}^{k-1}(1-\eta _j) = \infty$, we have $\lim \nolimits _{k\rightarrow \infty } F(X_k) = {\mathbf {0}}$. $\square$

In our iteration, we implement the repeat loop among steps 6–9 by selecting a sequence $\{\theta _j\}$, with $\theta _j \in [\theta _{\mathrm {min}},\theta _{\mathrm {max}}]$. For each loop, correspondingly, we let $\eta _k^{(1)} = {\hat{\eta }}_k$ and ${\varDelta } X^{(1)} = \widehat{{\varDelta } X}_k$, and for $j = 2,\ldots ,$ we let

$$\begin{aligned} \eta _k^{(j)}= & {} 1-\theta _{j-1}(1-\eta _k^{(j-1)}), \nonumber \\ {\varDelta } X_k^{(j)}= & {} \frac{1-\eta _k^{(j)}}{1- {\hat{\eta }}_k}\widehat{{\varDelta } X}_k. \end{aligned}$$

(3.4)

By induction, then, we can easily show that:

$$\begin{aligned} {\varDelta } X_k^{(j)}= & {} {\varTheta }_{j-1} \widehat{{\varDelta } X}_k, \quad 1-\eta _k^{(j)} = {\varTheta }_{j-1} (1-{\hat{\eta }}_k), \end{aligned}$$

where

$$\begin{aligned} {\varTheta }_{j-1} = \prod \limits _{\ell =1}^{j-1} \theta _\ell , \quad j \ge 2. \end{aligned}$$

(3.5)

In other words, the sequence $\{\Vert {\varDelta } X_k^{(j)}\Vert \}_j$ is a strictly decreasing sequence satisfying $\lim \nolimits _{j\rightarrow \infty } {\varDelta } X_k^{(j)} = {\mathbf {0}}$, and $\{\eta _{k}^{(j)}\}_j$ is a sequence satisfying $\eta _{k}^{(j)} \ge {\hat{\eta }}_k$ for $j\ge 1$, and $\lim \nolimits _{j\rightarrow \infty } \eta _{k}^{(j)} = 1$. Based on these observations, next, we show that the repeat loop terminates after a finite number of steps.

Theorem 3.3

  Let $\{\widehat{{\varDelta } X}_k\}$ be the sequence generated from Algorithm 1, i.e.,

$$\begin{aligned} \Vert ( DF (X_k) [\widehat{{\varDelta } X}_k] + F(X_k)\Vert \le \eta _k \Vert F(X_k)\Vert . \end{aligned}$$

Then, once j is large enough, the sequence $\{\eta _{k}^{(j)}\}_j$ satisfies the following:

$$\begin{aligned} \Vert F(X_k) + DF (X_k) [{\varDelta }{X}_k^{(j)}]\Vert\le & {} \eta _k^{(j)} \Vert F(X_k)\Vert ,\nonumber \\ \Vert F(R_{X_{k}}( {\varDelta } X_k^{(j)} ) )\Vert\le & {} (1-t(1-\eta _k^{(j)}))\Vert F(X_k)\Vert . \end{aligned}$$

(3.6)

Proof

Let ${\hat{\eta }}_k$ be defined in Eq. (2.9) with ${\varDelta } X_k = \widehat{{\varDelta } X}_k$, and $\epsilon _k = \frac{(1-t)(1-{\hat{\eta }}_k)\Vert F(X_k)\Vert }{\Vert \widehat{{\varDelta } X}_k\Vert }$. Since F is continuously differentiable, for $\epsilon _k > 0$, there exists a sufficiently small $\delta > 0$ such that $\Vert {\varDelta } X\Vert < \delta$ implies that:

$$\begin{aligned} \Vert F(R_{X_{k}}({\varDelta } X) ) - F(R_{X_{k}}({\mathbf {0}}_{X_{k}})) -D F(R_{X_{k}}({\mathbf {0}}_{X_{k}})) [{\varDelta } X] \Vert \le \epsilon _k \Vert {\varDelta } X\Vert , \end{aligned}$$

where ${\mathbf {0}}_{X_{k}}$ is the origin of $T_{X_{k}}\left( {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)\right)$.

For $\delta > 0$, we let

$$\begin{aligned} \eta _{\mathrm {min}} = \mathrm {max} \left\{ {\hat{\eta }}_k, 1-\frac{(1-{\hat{\eta }}_k)\delta }{\Vert \widehat{{\varDelta } X}_k\Vert }\right\} . \end{aligned}$$

Note that once j is sufficiently large,

$$\begin{aligned} \eta _k^{(j)} - \eta _{\mathrm {min}} \ge \left( \frac{\delta }{\Vert \widehat{{\varDelta } X}_k\Vert } -{\varTheta }_{j-1} \right) (1-{\hat{\eta }}_k) {\ge } 0. \end{aligned}$$

(3.7)

For sufficiently large j, we consider the sequence $\{{\varDelta } X_k^{(j)}\}_j$ in Eq. (3.4) with $\eta _k^{(j)} \in [\eta _{\mathrm {min}},1)$. We can see that:

$$\begin{aligned} \Vert {\varDelta } X_k^{(j)} \Vert = \Vert \frac{1- \eta _k^{(j)}}{1- {\hat{\eta }}_k}\widehat{{\varDelta } X}_k \Vert \le \frac{1-\eta _{\mathrm {min}}}{1- {\hat{\eta }}_k}\Vert \widehat{{\varDelta } X}_k\Vert \le \delta . \end{aligned}$$

Note that

$$\begin{aligned} F(X_k) + DF (X_k) [{\varDelta }{X}_k^{(j)}]{=}\frac{ \eta _k^{(j)} - {\hat{\eta }}_k}{1- {\hat{\eta }}_k} F(X_k) {+} \frac{1- \eta _k^{(j)}}{1- {\hat{\eta }}_k} \left( DF (X_k) [\widehat{{\varDelta } X}_k] + F(X_k)\right) . \end{aligned}$$

From triangle inequality, we have

$$\begin{aligned} \Vert F(X_k) + DF (X_k) [{\varDelta }{X}_k^{(j)}]\Vert\le & {} \frac{ \eta _k^{(j)} - {\hat{\eta }}_k}{1- {\hat{\eta }}_k} \Vert F(X_k)\Vert + \frac{1- \eta _k^{(j)}}{1- {\hat{\eta }}_k} {\hat{\eta }}_k \Vert F(X_k)\Vert \\= & {} \eta _k^{(j)} \Vert F(X_k)\Vert , \end{aligned}$$

and

$$\begin{aligned} {\Vert F(R_{X_{k}}( {\varDelta } X_k^{(j)} ) )\Vert }\le & {} \Vert F(R_{X_{k}}( {\varDelta } X_k^{(j)}) - F(R_{X_{k}}({\mathbf {0}}_{X_{k}})) -D F(R_{X_{k}}({\mathbf {0}}_{X_{k}})) [ {\varDelta } X_k^{(j)}] \Vert \\&+\, \Vert F(X_k) + DF (X_k) [{\varDelta } X_k^{(j)}]\Vert \\\le & {} \epsilon _k \Vert {\varDelta } X_k^{(j)}\Vert + \eta _k^{(j)}\Vert F(X_k)\Vert \\= & {} \frac{(1-t)(1-{\hat{\eta }}_k)\Vert F(X_k)\Vert }{\Vert \widehat{{\varDelta } X}_k\Vert } \left\| \frac{1- \eta _k^{(j)}}{1- {\hat{\eta }}_k}\widehat{{\varDelta } X}_k \right\| + \eta _k^{(j)}\Vert F(X_k)\Vert \\= & {} (1-t(1-\eta _k^{(j)}))\Vert F(X_k)\Vert . \end{aligned}$$

$\square$

From the proof of Theorem 3.3, we can see that for each k, the repeat loop for the backtracking line search will terminate in a finite number of steps once condition (3.7) is satisfied. Moreover, Theorem 3.2 and condition (3.3) imply the following:

$$\begin{aligned} \lim \limits _{k\rightarrow \infty } \Vert \widehat{{\varDelta } X}_k\Vert = {\mathbf {0}}. \end{aligned}$$

That is, if k is sufficient large, i.e., $\Vert \widehat{{\varDelta } X}_k\Vert$ is small enough, then from the proof of Theorem 3.3 we see that condition (2.11) is always satisfied, i.e., $\eta _k ={\hat{\eta }}_k$ for all sufficient large k.

To show that Algorithm 1 is a globally convergent algorithm, we have one additional requirement for the retraction $R_X$, i.e., there exist $\nu >0$ and $\delta _{\nu } > 0$ such that:

$$\begin{aligned} \nu \Vert {\varDelta } X\Vert \ge \text{ dist }(R_X({\varDelta } X),X), \end{aligned}$$

(3.8)

for all $X \in {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)$ and for all ${\varDelta } X \in T_X\left( {\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)\right)$ with $\Vert {\varDelta } X\Vert \le \delta _{\nu }$ [1]. Here the notation “$\text{ dist }(\cdot ,\cdot )$” represents the Riemannian distance on ${\mathscr {O}}(n) \times {\mathscr {O}}(n) \times {\mathscr {W}}(n)$. Under this assumption, our next theorem shows the global convergence property of Algorithm 1. We have borrowed the strategy for this proof from that used in [23, Theorem 3.5] to prove the nonlinear matrix equation.

Theorem 3.4

Assume that Algorithm 1 does not break down. Let $X_*$ be a limit point of $\{X_k\}$. Then $X_k$ converges to $X_*$ and $F(X_*) = {\mathbf {0}}$. Moreover, $X_k$ converges to $X_*$ quadratically.

Proof

Suppose $X_k$ does not converge to $X_*$. This implies that there exist two sequences of numbers $\{k_j\}$ and $\{\ell _j\}$ for which:

$$\begin{aligned}&X_{k_j} \in N_{{\delta }/{j}} (X_*), \\&X_{k_j+\ell _j} \not \in N_{{\delta }} (X_*), \\&X_{k_j + i} \in N_{\delta } (X_*), \text{ if } i = 1,\ldots , \ell _{j-1}\\&k_j+\ell _j \le k_{j+1}. \end{aligned}$$

From Theorem 3.3, we see that the repeat loop among steps 6–9 of Algorithm 1 terminates in finite steps. For each k, let $m_k$ be the smallest number such that condition (3.6) is satisfied, i.e., ${\varDelta } X_k = {\varTheta }_{m_k} \widehat{{\varDelta } X}_k$ and $\eta _k = 1- {\varTheta }_{m_k}(1-{\hat{\eta }}_k)$ with ${\varTheta }_{m_k}$ being defined in Eq. (3.5). It follows from condition (3.1b) that:

$$\begin{aligned} \Vert {\varDelta } X_k\Vert \le { 2 {\varTheta }_{m_k} \left( \frac{ 1+\eta _{\mathrm {max}} }{1-{\eta }_{\mathrm {max}}} \right) } (1-{\eta _{k}}) \Vert DF (X_*)^\dagger \Vert \Vert F(X_k)\Vert , \end{aligned}$$

(3.9)

for a sufficiently small $\delta$ and $X_k \in B_\delta (X_*)$, so that condition (3.2) is satisfied. Let

$$\begin{aligned} {\varGamma }_{m_k} = {2 {\varTheta }_{m_k} \left( \frac{ 1+\eta _{\mathrm {max}} }{1-{\eta }_{\mathrm {max}}} \right) } \Vert DF (X_*)^\dagger \Vert . \end{aligned}$$

According to condition (3.8), there exist $\nu >0$ and $\delta _{\nu } > 0$ such that:

$$\begin{aligned} \nu \Vert {\varDelta } X\Vert \ge \text{ dist }\left( R_X({\varDelta } X), X\right) , \end{aligned}$$

when $\Vert {\varDelta } X\Vert \le {\delta _{\nu }}$. Since $F(X_k)$ approaches zero as k approaches infinity, for $\delta _{\nu }$, condition (3.9) implies that there exists a sufficiently large k such that:

$$\begin{aligned} \nu \Vert {\varDelta } X_k\Vert \ge \text{ dist }\left( R_{X_k}({\varDelta } X_k),X_k\right) \end{aligned}$$

(3.10)

is satisfied whenever $\Vert {\varDelta } X_k\Vert \le \delta _{\nu }$.

Then for a sufficiently large j, we can see from conditions (3.9) and (3.10) that:

$$\begin{aligned} \frac{\delta }{2}\le & {} \text{ dist }(X_{k_j+\ell _j},X_{k_j}) \le \sum _{k=k_j}^{k_j+\ell _j-1} \text{ dist }(X_{k+1},X_{k})\\= & {} \sum _{k=k_j}^{k_j+\ell _j-1} \text{ dist }(R_{X_k}({\varDelta } X_{k}),X_{k}) \le \sum _{k=k_j}^{k_j+\ell _j-1} \nu \Vert {\varDelta } X_k\Vert \\\le & {} \sum _{k=k_j}^{k_j+\ell _j-1} \nu {\varGamma }_{m_k}(1-\eta _k) \Vert F(X_k)\Vert \le \sum _{k=k_j}^{k_j+\ell _j-1} \frac{\nu {\varGamma }_{m_k}}{t}\left( \Vert F(X_k)\Vert - \Vert F(X_{k+1})\Vert \right) \\\le & {} \frac{\nu {\varGamma }_{m_k}}{t} \left( \Vert F(X_{k_j})\Vert - \Vert F(X_{k_{j + 1}}) \Vert \right) . \end{aligned}$$

This is a contraction, since Theorem 3.2 implies that $F(X_{k_j})$ converges to zero as j approaches infinity and ${\varGamma }_{m_k}$ is bounded. Thus, $X_k$ converges to $X_*$, and immediately, we have $F(X_*) = {\mathbf {0}}$. This completes the proof of the first part.

To show that $X_k$ converges to $X_*$ quadratically once $X_k$ is sufficiently close to $X_*$, we let $C_1$ and $C_2$ be two numbers satisfying the following:

$$\begin{aligned} \Vert F(X_{k+1}) - F(X_{k}) -D F(X_k) [ {\varDelta } X_k] \Vert\le & {} C_1 \Vert {\varDelta } X_k\Vert ^2,\\ \Vert F(X_{k}) \Vert\le & {} C_2 \text{ dist } (X_k,X_*), \end{aligned}$$

for a sufficiently large k. The above assumptions are true since F is second differentiable and $F(X_*) = {\mathbf {0}}$. We can also observe that:

$$\begin{aligned} \Vert F(X_{k+1}) \Vert\le & {} \Vert F(X_{k+1}) - F(X_{k}) -D F(X_k) [ {\varDelta } X_k] \Vert + \Vert F(X_k) + DF (X_k) [{\varDelta } X_k]\Vert \nonumber \\\le & {} C_1 \Vert {\varDelta } X_k\Vert ^2 + {\hat{\eta }}_k \Vert F(X_k)\Vert \le C_1 ({\varGamma }_{m_k} \Vert F(X_k)\Vert )^2 + \Vert F(X_k)\Vert ^2 \nonumber \\\le & {} \left( C_1 {\varGamma }^2 C_2^2+C_2^2\right) \text{ dist } (X_k,X_*)^2, \end{aligned}$$

(3.11)

where ${\varGamma } = {2 \left( \dfrac{ 1+\eta _{\mathrm {max}} }{1-{\eta }_{\mathrm {max}}} \right) } \Vert DF (X_*)^\dagger \Vert .$

Since $X_k$ converges to $X_*$ as k converges to infinity, for a sufficiently large k, it follows from conditions (3.9), (3.10), (3.6), and (3.11) that:

$$\begin{aligned} \text{ dist }(X_{k+1}, X_*)= & {} \lim _{p\rightarrow \infty } \text{ dist }(X_{k+1}, X_p) \le \sum _{s = k}^\infty \text{ dist }\left( X_{s+1}, R_{X_{s+1}}({\varDelta } X_{s+1}) \right) \\\le & {} \sum _{s = k}^\infty \nu \Vert {\varDelta } X_{s+1}\Vert \le \sum _{s=k}^{\infty } \nu {\varGamma }_{m_{s+1}}(1+\eta _{\mathrm {max}}) \Vert F(X_{s+1})\Vert \\\le & {} \nu {\varGamma } (1+\eta _{\mathrm {max}}) \sum _{j=0}^{\infty } (1-t(1-\eta _{\mathrm {max}}))^j\Vert F(X_{k+1})\Vert \\\le & {} C \text{ dist }(X_{k},X_*)^2, \end{aligned}$$

for some constant $C = \dfrac{ \nu {\varGamma } (1+\eta _{\mathrm {max}}) \left( C_1 {\varGamma }^2C_2^2+C_2^2\right) }{ t(1-\eta _{\mathrm {max}})}$. $\square$

It is true that we might assume without loss of generality that the inverse of $DF (X_k)\circ DF (X_k)^*$ always exists numerically. However, once $DF (X_k)\circ DF (X_k)^*$ is ill-conditioned or (nearly) singular, we choose an operator $E_k = \sigma _k \mathrm {id}_{T_{F(X_k)}}$, where $\sigma _k$ is a constant and $\mathrm {id}_{T_{F(X_k)}}$ is an identity operator on $T_{F(X_k)} ({\mathbb {R}}^{n\times n})$ to make $DF (X_k)\circ DF (X_k)^* + \sigma _k \mathrm {id}_{T_{F(X_k)}}$ well-conditioned or nonsingular. In the calculation, this replaces the calculation in Eq. (2.6) with the following equation:

$$\begin{aligned} ( DF (X_k)\circ DF (X_k)^* + \sigma _k \mathrm {id}_{T_{F(X_k)}}) [{\varDelta } Z_k] = -F(X_k). \end{aligned}$$

That is, Algorithm 1 can be modified to fit in this case by replacing the satisfaction of condition (2.7) with the following two conditions:

$$\begin{aligned}&\Vert ( DF (X_k)\circ DF (X_k)^* + \sigma _k \mathrm {id}_{T_{F(X_k)}}) [{\varDelta } {Z}_k]\Vert \le \eta _{k} \Vert F(X_k)\Vert , \end{aligned}$$

(3.12a)

$$\begin{aligned}&\Vert ( DF (X_k)\circ DF (X_k)^*) [{\varDelta } {Z}_k] + F(X_k)\Vert \le \eta _{\mathrm {max}} \Vert F(X_k)\Vert , \end{aligned}$$

(3.12b)

where $\sigma _k := \mathrm {min}\left\{ \sigma _{\mathrm {max}}, \Vert F(X_{k})\Vert \right\}$ is a selected perturbation determined by the parameter $\sigma _{\mathrm {max}}$ and $\Vert F(X_{k})\Vert$. Of course, we can provide the proof of the quadratic convergence under condition (3.12) without any difficulty (see [50] for a similar discussion). Thus, we ignore the proof here. However, we note that even if a selected perturbation is applied to an ill-conditioned problem, the linear operator $DF (X_k)\circ DF (X_k)^* + \sigma _k \mathrm {id}_{T_{F(X_k)}}$ in condition (3.12a) might become nearly singular or ill-conditioned once $\sigma _k$ is small enough. This will prevent the iteration in the CG method from converging in fewer than $n^2$ steps, and cause the value of $f'(0)$ to not be negative. This possibility suggests that we apply Algorithm 1 without performing any perturbation in our numerical experiments. If the CG method cannot terminate within $n^2$ iterations, it may be necessary to compute a new approximated solution ${{\varDelta } Z}_k$ by selecting a new initial value for $X_0$.

4 Numerical experiments

To test the capacity and efficiency of our method, we generate sets of eigenvalues and singular values from a series of randomly generated matrices. We performed all of the computations in this work in MATLAB version 2016a on a desktop with a 4.2 GHz Intel Core i7 processor and 32 GB of main memory. For our experiments, we set $\eta _{\mathrm {max}} = 0.9$, $\theta _{\mathrm {min}} = 0.1$, $\theta _{\mathrm {max}} = 0.9$, $t = 10^{-4}$, and $\epsilon = 10^{-10}$. Also, in our computation, we emphasize two things. First, once the CG method computed in Algorithm 1 cannot be terminated within $n^2$ iterations, restart Algorithm 1 with a different initial value $X_0$. Second, due to the rounding errors in numerical computation, care must be taken in the selection of $\eta _{k}$ so that the upper bound $\eta _k \Vert F(X_k)\Vert$ in condition (2.7) is not too small to cause the CG method abnormal. To this end, in our experiments, we use the condition

$$\begin{aligned} \text{ max }\{\eta _k \Vert F(X_k)\Vert , 10^{-12}\}, \end{aligned}$$

instead of $\eta _k \Vert F(X_k)\Vert$. The implementations of the Algorithm 1 are available online: http://myweb.ncku.edu.tw/~mhlin/Bitcodes.zip.

Example 4.1

To demonstrate the capacity of our approach for solving problems that are relatively large, we randomly generate a set of eigenvalues and a set of singular values of different size, say, $n = 20$, 60, 100, 150, 200, 500, and 700 from matrices given by the MATLAB command:

$$\begin{aligned} A = \mathtt{randn(n)}. \end{aligned}$$

For each size, we perform 10 experiments. To illustrate the elasticity of our approach, we randomly generate the initial value $X_0 = (U_0,V_0, W_0)$ in the following way:

$$\begin{aligned} W_0 = \mathtt{triu(randn(n))}, \, W_0\mathtt{(find({\varLambda }))} = {\mathbf {0}}, \text{ and } [ U_0,tmp,V_0 ] = \mathtt{svd}({\varLambda }+W_0). \end{aligned}$$

In Table 1, we show the average residual value $(\mathrm{Residual})$, the average final error $(\mathrm{Error})$, as defined by:

$$\begin{aligned} {\text{ final }\,\, \text{ error }} = \Vert \varvec{\lambda }(A_{{\mathrm {new}}}) - \varvec{\lambda }\Vert _2 + \Vert \varvec{\sigma }(A_{{\mathrm {new}}}) - \varvec{\sigma }\Vert _2, \end{aligned}$$

the average number of iterations within the CG method (CGIt)$\sharp$, the average number of iterations within the inexact Newton method (INMIt)$\sharp$, and the average elapsed time (Time), as performed by our algorithm. In Table 1, we can see that the elapsed time and the average number of iterations within the $\mathrm CG$ method increase dramatically as the size of the matrices increases. This can be explained by the fact that the number of degrees of freedom of the problem increases significantly. Thus, the number of the iterations required by the CG method and the required computed time increase correspondingly. However, it is interesting to see that the required number of iterations within the inexact Newton method remains almost the same for matrices of different sizes. One way to speed up the entire process of iterations is to transform the problem (2.6) into a form that is more suitable for the CG method, for example, apply the CG method with a preselected preconditioner. Still, this selection of the preconditioner requires further investigation.

Table 1 Comparison of the required CGIt$\sharp$, INMIt$\sharp$, Residual, Error values, and Time for solving the IESP by Algorithm 1

Example 4.2

In this example, we use Algorithm 1 to construct a nonnegative matrix with prescribed eigenvalues and singular values and a specific structure. We specify this IESP and call it the IESP with desired entries (DIESP). The DIESP can be defined as follows.

(DIESP) Given a subset ${\mathscr {I}} = \{(i_t,j_t)\}_{t=1}^\ell$ with double subscripts, a set of real numbers ${\mathscr {K}} = \{k_t\}_{t=1}^\ell$, a set of n complex numbers $\{\lambda _i\}_{i=1}^n$, satisfying $\{\lambda _i\}_{i=1}^n = \{{\bar{\lambda }}_i\}_{i=1}^n$, and a set of n nonnegative numbers $\{\sigma _i\}_{i=1}^n$, find a nonnegative $n\times n$ matrix A that has eigenvalues $\lambda _1, \ldots , \lambda _n$, singular values $\sigma _1,\ldots ,\sigma _n$ and $A_{i_t,j_t} = k_t$ for $t = 1,\ldots , \ell$.

Note that once $i_t= j_t = t$ for $t = 1,\ldots , n$, we investigate a numerical approach for solving the IESP with prescribed diagonal entries. As far as we know, the research result close to this problem is only available in [46]. However, for a general structure, no research has been conducted to implement this investigation. To solve the DIESP, our first step is to obtain a real matrix A with prescribed eigenvalues and singular values. Our second step is to derive entries of $Q^\top A Q$, where $Q\in {\mathscr {O}}(n)$, that satisfy the nonnegative property and desired values determined by the sets ${\mathscr {I}}$ and ${\mathscr {K}}$. We solve the first step in the same manner as in Example 4.1, but for the second step, we consider the following two sets ${\mathscr {L}}_1$ and ${\mathscr {L}}_2$, which are defined by:

$$\begin{aligned} {\mathscr {L}}_1= & {} \{A \in {\mathbb {R}}^{m\times n} \,|\, A_{i_t,j_t} = k_t,\,\, \text{ for }\,\, 1\le t\le \ell ; \text{ otherwise } A_{i,j} = 0 \}, \\ {\mathscr {L}}_2= & {} \{A \in {\mathbb {R}}^{m\times n} \,|\, A_{i,j} = 0,\,\, \text{ for }\,\, 1\le i,j \le n \,\, \text{ and } \,\, (i,j)\in {\mathscr {I}}\}, \end{aligned}$$

and then solve the following problem:

$$\begin{aligned} \text{ find } P \in {\mathscr {L}}_2 \text{ and } Q \in {\mathscr {O}}(n) \text{ such } \text{ that } H(P,Q) ={\hat{A}} + P\odot P - Q AQ^\top = {\mathbf {0}},\nonumber \\ \end{aligned}$$

(4.1)

with ${\hat{A}} \in {\mathscr {L}}_1$. Let $[A, B]:= AB - BA$ denote the Lie bracket notation. It follows from direct computation that the corresponding differential DH and its adjoint $DH^*$ have the following form [50]:

$$\begin{aligned} DH(P,Q)[({\varDelta } P, {\varDelta } Q)]= & {} 2 P\odot {\varDelta } P + [ Q A Q^\top , {\varDelta } Q Q^\top ],\\ DH(P,Q)^* [{\varDelta } Z]= & {} \left( 2P\odot {\varDelta } Z, \frac{1}{2}( [QA Q^\top , {\varDelta } Z^\top ] + [Q A^\top Q^\top , {\varDelta } Z] )Q \right) , \end{aligned}$$

and, for all $(\xi _P, \xi _Q) \in T_{(P,Q)} ({\mathscr {L}}_2 \times {\mathscr {O}}(n))$, we can compute the retraction R using the following formula:

$$\begin{aligned} R(P,Q) = (R_P(\xi _P),R_Q(\xi _Q)), \end{aligned}$$

where

$$\begin{aligned} R_P(\xi _P) = P+\xi _P, \quad R_Q(\xi _Q) = {Q_f}(Q+\xi _Q). \end{aligned}$$

For these experiments, we randomly generate nonnegative matrices $20\times 20$ in size by the MATLAB command “$A = rand(20)$” to provide the desired eigenvalues, singular values, and diagonal entries, i.e., to solve the DIESP with the specified diagonal entries. We record the final error, as given by the following formula:

$$\begin{aligned} \text{ final } \text{ error } = \Vert \varvec{\lambda }(A_{\mathrm {new}}) - \varvec{\lambda }\Vert _2 + \Vert \varvec{\sigma }(A_{\mathrm {new}}) - \varvec{\sigma }\Vert _2 + \Vert (A_{\mathrm {new}})_{i_t,j_t } - k_t \Vert _2. \end{aligned}$$

After randomly choosing 10 different matrices, Table 2 shows our results with the intervals (Interval) containing all of the residual values and final errors, and their corresponding average values (Average). These results provide sufficient evidence that Algorithm 1 can be applied to solve the DIESP with high accuracy.

Table 2 Records of final errors and residual values for solving the DIESP by Algorithm 1

Although Example 4.2 considers examples with a nonnegative structure, we emphasize that Algorithm 1 can work with entries that are not limited to being nonnegative. That is, to solve the IESP without nonnegative constraints but with another specific structure, Algorithm 1 can fit perfectly well by replacing H(P, Q) in problem (4.1) with

$$\begin{aligned} G(S,Q) := {\hat{A}} + S - QAQ^\top , \end{aligned}$$

where ${\hat{A}} \in {\mathscr {L}}_1$, $S\in {\mathscr {L}}_2$ and $Q\in {\mathscr {O}}(n)$.

5 Conclusions

In this paper, we apply the Riemannian inexact Newton method to solve an initially complicated and challenging IESP. We provide a thorough analysis of the entire iterative processes and show that this algorithm converges globally and quadratically to the desired solution. We must emphasize that our theoretical discussion and numerical implementations can also be extended to solve an IESP with a particular structure such as desired diagonal entries and a matrix whose entries are nonnegative. This capacity can be observed in our numerical experiments. It should be emphasized that this research is the first to provide a unified and effective means to solve the IESP with or without a particular structure.

However, the numerical stability for extremely ill-conditioned problems is a case that we should pay attention to, though reselecting the initial values could be a strategy to get rid of this difficulty. Another way to tackle this difficulty is to select a good preconditioner. But, the operator encountered in our algorithm is nonlinear and high-dimensional. Thus, the selection of the preconditioner could involve the study of tensor analysis, where further research is needed.