Research on vibration suppression of nonlinear energy sink with linear damping and geometrically nonlinear damping

Abstract

Nonlinear energy sink (NES) is a passive control device that can absorb a wide band, and it has the advantages of lightweight and strong robustness, which can play a very important role in vibration suppression. In this paper, the dynamic modeling and research on vibration suppression of NES with linear damping and geometrically nonlinear damping are carried out, and the effects of NES parameters on the vibration reduction effect are investigated. For the study of dynamic bifurcation, the slowly varying equation of the system is obtained by using the complex variable average method, and the effects of NES parameters on the number of fixed points and stability of the system are analyzed according to the slowly varying equation. At the same time, the effects of excitation amplitude and excitation frequency on the system response amplitude are also investigated. For the study of strongly modulated response (SMR), the slowly varying equation is further analyzed by using the multi-scale method, and the conditions for SMR phenomenon in the system are described by slow invariant manifold and phase portraits. By studying the slow manifold, the detuned parameter interval for the system to appear SMR is derived. For vibration reduction performance analysis, the effects of NES parameters on vibration reduction performance are analyzed from the perspectives of energy and amplitude-frequency response, and the influence laws of various parameters on vibration suppression are revealed. The vibration reduction performance of different NES is compared and analyzed, and it is concluded that the new NES proposed in this paper has better vibration reduction performance.

1 Introduction

There are many harmful vibration problems in the fields of building structures, aviation devices and precision machinery [1, 2], which will seriously affect the use and stability of system structures, so in recent decades, scholars have been exploring methods that can effectively suppress vibrations [3,4,5]. At present, the structural vibration suppression methods mainly include active control, semi-active control, hybrid control and passive control. Passive control has attracted wide attention because of its low cost and simple structure in practical applications [6,7,8]. As a classical passive control method, NES was first proposed by Roberson, who introduced nonlinear stiffness into the traditional linear vibration absorber to form a nonlinear vibration absorber with wider vibration reduction bandwidth and better robustness [9]. The traditional NES structure is composed of viscous damping, nonlinear spring and lightweight mass block. In practical application, it can provide a special energy transfer mechanism, which is called target energy transfer (TET). TET has high energy transfer efficiency and the transfer process is unidirectional and irreversible [10, 11]. With the deepening of research, scholars have proposed more and more abundant forms of NES, such as track NES, bi-stable NES, lever-type NES and non-smooth NES [12,13,14,15]. Due to the complexity of both the structures for vibration reduction and the environments in which they are located, most scholars often simplify the main system into a mathematical model composed of mass block, linear damping and linear stiffness in their analysis, and on this basis, add NES to be studied for theoretical analysis [16,17,18]. In this paper, the main system is simplified by this method, and a dynamic model of coupled geometrically nonlinear damping NES is established.

The researchers have found that the vibration reduction performance of NES is different when the system is subjected to different excitation forms. Wang et al. [19] analyzed the vibration reduction performance of NES under impulsive excitation through experiments, while Remick et al. [20, 21] analyzed the influence of NES on system vibration suppression under impulsive excitation from the numerical aspect. Both found that NES provided good vibration reduction effect when the main system was under impulsive excitation. Zhang et al. [22] analyzed the influence of different impulsive excitation intensities on the vibration reduction performance of NES, and found that under low impulsive excitation intensities, the vibration reduction performance of traditional NES was better than that of nonlinear damping NES. Although scholars have done a lot of research on nonlinear systems under impulsive excitation, the influence law of NES parameters on vibration suppression has not been revealed.

When the system is subjected to harmonic excitation, NES will show a special steady-state response, and the amplitude of the main system will be greatly modulated. Gendelman et al. [23,24,25] analyzed this special response by using the complex variable average method, and found that this special response is formed when the main system and NES have 1:1 resonance, he defined this special response as strongly modulated response. Then scholars try to use various methods to analyze whether SMR occurs in the system and the conditions that generate SMR. Starosvetsky et al. [26,27,28] used the multi-scale method to further analyze and used SIM to predict whether a nonlinear system would generate SMR, and found that SMR could only be generated if the system included nonlinear components. Some scholars have also found that the existence of SMR is affected by frequency detuning parameters, but the influence law has not been revealed. Kong et al. [29,30,31] used the main structure energy spectrum to study the vibration reduction effect of NES under harmonic excitation, focusing on the comparative analysis of the effects of different NES on the system vibration suppression. It is pointed out that NES has better vibration reduction performance than linear vibration absorber, but the effects of NES parameters on vibration suppression is not analyzed.

Previous scholars mainly focused on the effect of stiffness on the vibration reduction effect of NES, ignoring the influence of damping, so there were few studies on the analysis of NES damping [19, 32, 33]. Al-shudeifat et AL. [34] studied NES with nonlinear damping and found that under high-intensity impulsive excitation, the vibration reduction performance of NES with nonlinear damping is better than that of traditional NES, and also pointed out that nonlinear damping can improve the effective stiffness and damping of the system. Jing et al. [35] studied the effect of cubic damping NES on the vibration reduction of the main system and found that cubic damping can effectively suppress the peak value near the resonance frequency. Guo et al. [36] analyzed the effect of nonlinear damping NES on the system force transmissibility and found that nonlinear damping can expand the effective bandwidth of NES. The above results indicate that damping plays an important role in the vibration reduction effect of NES.

Although researchers have conducted a lot of research on NES systems, most of these research results are on the NES stiffness, lack of research on NES damping, and lack of analytical solution verification analysis when analyzing vibration reduction applications. Based on the shortcomings of the existing research results, the model of combined damping NES is established in this paper. Firstly, the slowly varying equations of the system are derived by using the complex variable average method. The bifurcation characteristics of the system and the effects of excitation amplitude and frequency on the response amplitude are analyzed by the slowly varying equations. Secondly, the effects of the detuning parameters on the existence of SMR are studied by analyzing the phase portrait and the slow manifold. Finally, the vibration suppression effect of NES system under impulsive excitation is analyzed according to energy change, and the vibration suppression effect of NES system under harmonic excitation is studied according to the energy spectrum and amplitude-frequency response curve, and the optimal parameter range of NES is pointed out. The structure of this paper is as follows: the second part analyzes the bifurcation characteristics of the NES system, the third part analyzes the SMR existence interval of the NES system, the fourth part analyzes the vibration reduction effect of the NES system under impulsive excitation and harmonic excitation, and the last part summarizes the main research results of this paper.

2 Dynamic bifurcation research

The schematic diagram of geometrically nonlinear damping is shown below:

The two linear damping c horizontally are arranged symmetrically, with one end fixed and the other end connected to a small mass block m. When the mass block is moved vertically by an external force, the force generated by the linear damping of the symmetrical arrangement is nonlinear. The specific derivation process is as follows:

Let the travel distance of $c$ under external force be $\delta$, then the force generated by each damping can be expressed as

$$ F_{1} = F_{2} = c\dot{\delta } $$

(1)

From Fig. 1, the following geometric relationship can be obtained

$$ \begin{aligned} \delta & = \sqrt {x^{2} + l^{2} } , \sin \theta & = \frac{x}{\delta } = \frac{x}{{\sqrt {x^{2} + l^{2} } }} \\ \end{aligned} $$

(2)

Fig. 1

Schematic diagram of geometrically nonlinear damping

Fig. 2

The system model of NES with linear damping and geometrically nonlinear damping

So we can get

$$ F_{c} = 2c\dot{\delta }\sin \theta = 2c\dot{x}\sin^{2} \theta $$

(3)

Considering that the Angle between c and the horizontal direction is particularly small, there are

$$ \sin \theta \approx \tan \theta = \frac{x}{l} $$

(4)

Put Eq. (4) into Eq. (3), we have

$$ F_{c} = \frac{2c}{{l^{2} }}x^{2} \dot{x} $$

(5)

Thus, the general form of geometrically nonlinear damping can be obtained as $x^{2} \dot{x}$. It is important to note that the $\delta$ should be small enough.

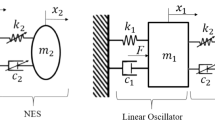
In this paper, a dynamic model of combined damping NES system, as shown in Fig. 2, is established. The model consists of two parts. The main system is composed of mass block $m_{1}$, linear damping $c_{1}$ and linear stiffness spring $k_{1}$. The nonlinear energy sink contains a smaller mass block $m_{2}$, linear damping $c_{2}$, geometrically nonlinear damping $c_{3}$[37, 38] and cubic stiffness $k_{2}$. $F(t)$ is the external excitation of the system, $x_{1}$ and $x_{2}$ are the displacements of the main system and the nonlinear energy sink, respectively.

According to Newton's second law, the corresponding dynamic equation is established as follows

$$ \left\{ \begin{aligned} & m_{1} \ddot{x}_{1} + c_{1} \dot{x}_{1} + k_{1} x_{1} + c_{2} (\dot{x}_{1} - \dot{x}_{2} ) + c_{3} (x_{1} - x_{2} )^{2} (\dot{x}_{1} - \dot{x}_{2} ) + k_{2} (x_{1} - x_{2} )^{3} = F\cos (\omega t) \\ & m_{2} \ddot{x}_{2} + c_{2} (\dot{x}_{2} - \dot{x}_{1} ) + c_{3} (x_{2} - x_{1} )^{2} (\dot{x}_{2} - \dot{x}_{1} ) + k_{2} (x_{2} - x_{1} )^{3} = 0 \\ \end{aligned} \right. $$

(6)

For the convenience of calculation, the following parameter transformations are introduced

$$ \begin{aligned} \overline{{x_{1} }} & = \frac{{x_{1} }}{l},\;\;\overline{{x_{2} }} = \frac{{x_{2} }}{l},\;\; \\ \omega_{0} & = \sqrt {\frac{{k_{1} }}{{m_{1} }}} ,\;\;\overline{t} = t\omega_{0} ,\;\;\overline{\omega } = \frac{\omega }{{\omega_{0} }}, \\ \varepsilon & = \frac{{m_{2} }}{{m_{1} }} < < 1,\;\;\varepsilon \lambda_{2} = \frac{{c_{2} }}{{m{}_{1}\omega_{0} }},\;\; \\ \varepsilon \lambda_{3} & = \frac{{c_{3} }}{{m{}_{1}\omega_{0} }},\;\;\varepsilon k = \frac{{k_{2} }}{{m{}_{1}\omega_{0}^{2} }},\;\;\varepsilon f = \frac{F}{{lk_{1} }} \\ \end{aligned} $$

(7)

Substituting Eq. (7) into Eq. (6), and setting $\,c_{1} = 0$. At the same time, for the convenience of subsequent writing, the overlines of ${\kern 1pt} \overline{{x_{1} }}$, $\overline{{x_{2} }}$, ${\kern 1pt} \overline{t} {\kern 1pt}$ and ${\kern 1pt} \overline{\omega } {\kern 1pt}$ are omitted, and Eq. (1) is transformed into

$$ \left\{ \begin{aligned} & \ddot{x}_{1} + x_{1} + \varepsilon \lambda_{2} (\dot{x}_{1} - \dot{x}_{2} ) + \varepsilon \lambda_{3} (x_{1} - x_{2} )^{2} (\dot{x}_{1} - \dot{x}_{2} ) + \varepsilon k(x_{1} - x_{2} )^{3} = \varepsilon f\cos (\omega t) \\ & \ddot{x}_{2} + \lambda_{2} (\dot{x}_{2} - \dot{x}_{1} ) + \lambda_{3} (x_{2} - x_{1} )^{2} (\dot{x}_{2} - \dot{x}_{1} ) + k(x_{2} - x_{1} )^{3} = 0 \\ \end{aligned} \right. $$

(8)

This paper studies the case where the ratio of external excitation frequency to the natural frequency of the system is 1:1, expressed as ${\kern 1pt} \omega = 1 + \varepsilon \sigma$, where the detuning parameter $\sigma$ can be used to describe the closeness between the external excitation frequency and the natural frequency of the system. Meanwhile, variable substitution is introduced into Eq. (8): $u = x_{1} + \varepsilon x_{2}$, $v = x_{1} - x_{2}$, $u$ represents the mass center motion and ${\kern 1pt} v{\kern 1pt}$ represents the relative motion between the NES and main system.

Then the equation is transformed into

$$ \left\{ \begin{aligned} &\ddot{u} + \frac{u + \varepsilon v}{{1 + \varepsilon }} = \varepsilon f\cos [(1 + \varepsilon \sigma )t] \\ & \ddot{v} + (1 + \varepsilon )\lambda_{2} \dot{v} + (1 + \varepsilon )\lambda_{3} v^{2} \dot{v} + (1 + \varepsilon )kv^{3} + \frac{u + \varepsilon v}{{1 + \varepsilon }} = \varepsilon f\cos [(1 + \varepsilon \sigma )t] \\ \end{aligned} \right. $$

(9)

It is not convenient to solve Eq. (9) directly, according to references [25, 30, 40], the Complex variable average method is used to solve the equation. Introduce the following complex variable transformations.

$$ \begin{aligned} \phi_{1} e^{i(1 + \varepsilon \sigma )t} & = \dot{u} + iu, \\ \phi_{2} e^{i(1 + \varepsilon \sigma )t} & = \dot{v} + iv \\ \end{aligned} $$

(10)

where.

$e^{i(1 + \varepsilon \sigma )t}$ indicates the fast vibrating part, $\phi_{i}$ indicates the slow modulation part.

According to Eq. (10), we have

$$ \begin{aligned} u & = \frac{{\phi_{1} e^{i(1 + \varepsilon \sigma )t} - \overline{\phi }_{1} e^{ - i(1 + \varepsilon \sigma )t} }}{2i(1 + \varepsilon \sigma )},\dot{u} = \frac{{\phi_{1} e^{i(1 + \varepsilon \sigma )t} + \overline{\phi }_{1} e^{ - i(1 + \varepsilon \sigma )t} }}{2}, \\ \ddot{u} & = \dot{\phi }_{1} e^{i(1 + \varepsilon \sigma )t} + i(1 + \varepsilon \sigma )\frac{{\phi_{1} e^{i(1 + \varepsilon \sigma )t} - \overline{\phi }_{1} e^{ - i(1 + \varepsilon \sigma )t} }}{2} \\ v & = \frac{{\phi_{2} e^{i(1 + \varepsilon \sigma )t} - \overline{\phi }_{2} e^{ - i(1 + \varepsilon \sigma )t} }}{2i(1 + \varepsilon \sigma )},\dot{v} = \frac{{\phi_{2} e^{i(1 + \varepsilon \sigma )t} + \overline{\phi }_{2} e^{ - i(1 + \varepsilon \sigma )t} }}{2}, \\ \ddot{v} & = \dot{\phi }_{2} e^{i(1 + \varepsilon \sigma )t} + i(1 + \varepsilon \sigma )\frac{{\phi_{2} e^{i(1 + \varepsilon \sigma )t} - \overline{\phi }_{2} e^{ - i(1 + \varepsilon \sigma )t} }}{2} \\ \end{aligned} $$

Substitute the parameter transformation into Eq. (9) and omit the fast variable part of the equation $e^{i(1 + \varepsilon \sigma )t}$, the slowly varying equation of the system can be obtained as

$$ \left\{ \begin{aligned} & \dot{\phi }_{1} + i\varepsilon \sigma \phi_{1} + \frac{{i\varepsilon (\phi_{1} - \phi_{2} )}}{2(1 + \varepsilon )} = \frac{\varepsilon f}{2} \\ & \dot{\phi }_{2} + i\varepsilon \sigma \phi_{2} + \frac{{i(\phi_{2} - \phi_{1} )}}{2(1 + \varepsilon )} + \frac{{(1 + \varepsilon )\phi_{2} }}{8}(4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} ) = \frac{\varepsilon f}{2} \\ \end{aligned} \right. $$

(11)

In order to obtain the fixed points equation of the system, the derivative term in Eq. (11) is equal to 0, which can be obtained

$$ \left\{ \begin{aligned} & i\varepsilon \sigma \phi_{10} + \frac{{i\varepsilon (\phi_{10} - \phi_{20} )}}{2(1 + \varepsilon )} = \frac{\varepsilon f}{2} \\ & i\varepsilon \sigma \phi_{20} + \frac{{i(\phi_{20} - \phi_{10} )}}{2(1 + \varepsilon )} + \frac{{(1 + \varepsilon )\phi_{20} }}{8}(4\lambda_{2} + \lambda_{3} \left| {\phi_{20} } \right|^{2} - 3ik\left| {\phi_{20} } \right|^{2} ) = \frac{\varepsilon f}{2} \\ \end{aligned} \right. $$

(12)

The $\phi_{10}$ and $\phi_{20}$ in the formula represent the fixed points of the system and the solution of Eq. (12) can be expressed as

$$ \left\{ \begin{aligned} & \phi_{10} = \frac{{\phi_{20} - i(1 + \varepsilon )f}}{2(1 + \varepsilon )\sigma + 1} \\ & \frac{{9k^{2} + \lambda_{3}^{2} }}{16}\left| {\phi_{20} } \right|^{6} + \frac{{\lambda_{2} \lambda_{3} - 6kM\sigma }}{2}\left| {\phi_{20} } \right|^{4} + (\lambda_{2}^{2} + 4M^{2} \sigma^{2} )\left| {\phi_{20} } \right|^{2} = M^{2} f^{2} \\ \end{aligned} \right. $$

(13)

where $M = (2\varepsilon \sigma + 1)/(2\varepsilon \sigma + 2\sigma + 1)$. The second equation in Eq. (13) is simplified as

$$ \alpha_{1} Z^{3} + \alpha_{2} Z^{2} + \alpha_{3} Z = f^{2} $$

(14)

where

$$ \begin{aligned} \alpha_{1} & = \frac{{9k^{2} + \lambda_{3}^{2} }}{{16M^{2} }}, \\ \alpha_{2} & = \frac{{\lambda_{2} \lambda_{3} - 6kM\sigma }}{{2M^{2} }}, \\ \alpha_{3} & = \frac{{\lambda_{2}^{2} + 4M^{2} \sigma^{2} }}{{M^{2} }}, \\ Z & = \left| {\phi_{20} } \right|^{2} \\ \end{aligned} $$

Taking the derivative of Eq. (14) yields

$$ 3\alpha_{1} Z^{2} + 2\alpha_{2} Z + \alpha_{3} = 0 $$

(15)

Equation (14) and Eq. (15) are combined to obtain the saddle-node(SN) bifurcation boundary equation of the system as follows

$$ \begin{aligned} f^{2} & = \alpha_{1} \left( {\frac{{ - \alpha_{2} \pm \sqrt {\alpha_{2}^{2} - 3\alpha_{1} \alpha_{3} } }}{{3\alpha_{1} }}} \right)^{3} \\ & + \alpha_{2} \left( {\frac{{ - \alpha_{2} \pm \sqrt {\alpha_{2}^{2} - 3\alpha_{1} \alpha_{3} } }}{{3\alpha_{1} }}} \right)^{2} \\ & \quad \alpha_{3} \left( {\frac{{ - \alpha_{2} \pm \sqrt {\alpha_{2}^{2} - 3\alpha_{1} \alpha_{3} } }}{{3\alpha_{1} }}} \right) \\ \end{aligned} $$

(16)

According to Eq. (16), the SN bifurcation of the system is drawn, as shown in Fig. 3. Where the parameters are selected as: $\varepsilon = 0.1$, $k = 4/3$, $\lambda_{2} = 0.1$ [25, 30, 40].

Fig. 3

SN bifurcation diagram ($\sigma = 3$)

As can be seen from Fig. 3, the SN bifurcation boundary curve of the combined damping NES system divides the plane $\;[\lambda_{3} ,\;f]\;$ into two parts, and the shape of the curve is approximately triangular. As shown in the figure above, taking points inside and outside the triangle, it can be found that there are three real roots inside the triangle and only one real root outside the triangle, indicating that there are three fixed points inside the triangle and only one fixed point outside the triangle. According to the analysis of the points taken, When ${\kern 1pt} f{\kern 1pt}$ is fixed, changing the value of ${\kern 1pt} \lambda_{3} {\kern 1pt}$ can get a different number of fixed points. Similarly, when ${\kern 1pt} \lambda_{3} {\kern 1pt}$ is fixed, changing the value of ${\kern 1pt} f{\kern 1pt}$ can also obtain a different number of fixed points.

Next, the effects of linear damping coefficient ${\kern 1pt} \lambda_{2}$, mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ and detuning parameter ${\kern 1pt} \sigma {\kern 1pt}$ on the SN bifurcation boundary curve of the system were studied. On the premise that other parameters remained unchanged, the SN bifurcation diagram of different combined damping NES parameters was obtained by changing the values of combined damping NES parameters, as shown in Fig. 4.

Fig. 4

SN bifurcation with combined damping NES parameters change

In Fig. 4a, the area of the SN bifurcation curve gradually decreases with the increase of the ${\kern 1pt} \lambda_{2} {\kern 1pt}$ value. In Fig. 4b, with the increase of the ${\kern 1pt} \varepsilon {\kern 1pt}$ value, the area of the SN bifurcation curve gradually increases. In Fig. 4c and d, the area of the SN bifurcation curve increases with the increase of ${\kern 1pt} \sigma$, regardless of whether the detuning parameter ${\kern 1pt} \sigma {\kern 1pt}$ is greater than or less than 0. According to the above analysis, changing the linear damping coefficient ${\kern 1pt} \lambda_{2}$, mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ and detuning parameter ${\kern 1pt} \sigma {\kern 1pt}$ can affect the number of fixed points.

SN bifurcation can only analyze the number of fixed points, and the stability of fixed points needs to be studied through Hopf bifurcation. Then Hopf bifurcation is used to analyze the stability of fixed points in the combined damping NES system. A small disturbance is applied to the combined damping NES system near the fixed points. Letting

$$ \phi_{1} = \phi_{10} + \Delta_{1} ,\quad \phi_{2} = \phi_{20} + \Delta_{2} $$

(17)

Then Eq. (12) can be simplified to

$$ \begin{aligned} \dot{\Delta }\;_{1} & = - i\varepsilon \sigma \Delta_{1} - \frac{i\varepsilon }{{2(1 + \varepsilon )}}(\Delta_{1} - \Delta_{2} ) \\ \dot{\Delta }_{1}^{*} & = i\varepsilon \sigma \Delta_{1}^{*} + \frac{i\varepsilon }{{2(1 + \varepsilon )}}(\Delta_{1}^{*} - \Delta_{2}^{*} ) \\ \dot{\Delta }_{2} & = - i\varepsilon \sigma \Delta_{2} - \frac{{i(\Delta_{2} - \Delta_{1} )}}{2(1 + \varepsilon )} - \frac{(1 + \varepsilon )}{2}\lambda_{2} \Delta_{2} - \frac{(1 + \varepsilon )}{4}\lambda_{3} \left| {\phi_{20} } \right|^{2} \Delta_{2} \\ \quad \;\;\; & + \frac{3ik(1 + \varepsilon )}{4}\left| {\phi_{20} } \right|^{2} \Delta_{2} - \frac{(1 + \varepsilon )}{8}\lambda_{3} \phi_{20}^{2} \Delta_{2}^{*} + \frac{3ik(1 + \varepsilon )}{8}\phi_{20}^{2} \Delta_{2}^{*} \\ \dot{\Delta }_{2}^{*} & = i\varepsilon \sigma \Delta_{2}^{*} + \frac{{i(\Delta_{2}^{*} - \Delta_{1}^{*} )}}{2(1 + \varepsilon )} - \frac{(1 + \varepsilon )}{2}\lambda_{2} \Delta_{2}^{*} - \frac{(1 + \varepsilon )}{4}\lambda_{3} \left| {\phi_{20} } \right|^{2} \Delta_{2}^{*} \\ \quad \;\;\; & - \frac{3ik(1 + \varepsilon )}{4}\left| {\phi_{20} } \right|^{2} \Delta_{2}^{*} - \frac{(1 + \varepsilon )}{8}\lambda_{3} \phi_{20}^{*2} \Delta_{2} - \frac{3ik(1 + \varepsilon )}{8}\phi_{20}^{*2} \Delta_{2} \\ \end{aligned} $$

(18)

The characteristic polynomial of the above equation can be expressed as

$$ \mu^{4} + \gamma_{1} \mu^{3} + \gamma_{2} \mu^{2} + \gamma_{3} \mu + \gamma_{4} = 0 $$

(19)

where

$$ \begin{aligned} \gamma_{1} & = \frac{(1 + \varepsilon )}{2}(2\lambda_{2} + \lambda_{3} Z) \\ \gamma_{2} & = \frac{{3(1 + \varepsilon )^{2} (9k^{2} + \lambda_{3}^{2} )}}{64}Z^{2} + \frac{{ - 3(1 + 2\sigma + 2\varepsilon^{2} \sigma )k + (1 + \varepsilon )^{2} \lambda_{2} \lambda_{3} }}{4}Z \\ & \frac{{1 + 4\varepsilon \sigma + 8\varepsilon^{2} \sigma^{2} + (1 + \varepsilon )^{2} \lambda_{2}^{2} }}{4} \\ \gamma_{3} & = \frac{\varepsilon }{8}(2\lambda_{2} + \lambda_{3} Z)(1 + 4\varepsilon \sigma + 4\varepsilon \sigma^{2} + 4\varepsilon^{2} \sigma^{2} ) \\ \gamma_{4} & = \frac{{3\varepsilon^{2} (1 + 2\sigma + 2\varepsilon \sigma )^{2} (9k^{2} + \lambda_{3}^{2} )}}{256}Z^{2} \\ & \quad + \left[ {\frac{{\varepsilon^{2} (1 + 2\sigma + 2\varepsilon \sigma )^{2} }}{16}\lambda_{2} \lambda_{3} - } \right.\;\left. {\frac{{3k\varepsilon^{2} \sigma (1 + 2\varepsilon \sigma )(1 + 2\sigma + 2\varepsilon \sigma )}}{8}} \right]Z \\ & \quad + \varepsilon^{2} \frac{{4\sigma^{2} (1 + 2\varepsilon \sigma )^{2} + \lambda_{2}^{2} (1 + 2\sigma + 2\varepsilon \sigma )^{2} }}{16} \\ Z & = \left| {\phi_{20} } \right|^{2} \\ \end{aligned} $$

(20)

When the stability of the fixed points changes, the eigenvalues of the system cross the imaginary part of the complex plane, so there is the following condition.

$$ \mu = \pm i\Omega $$

(21)

Substituting Eq. (21) into Eq. (19), we get

$$ v{}_{1}Z^{2} + v{}_{2}Z + v{}_{3} = 0 $$

(22)

where

$$ \begin{aligned} v_{1} & = 3(1 + \varepsilon )^{2} (9k^{2} + \lambda_{3}^{2} ) \\ v_{2} & = 16(1 + \varepsilon )[(1 + \varepsilon )\lambda_{2} \lambda_{3} - 3k(1 + 4\varepsilon \sigma )] \\ v_{3} & = 16[(1 + 4\varepsilon \sigma )^{2} + \lambda_{2}^{2} (1 + \varepsilon )^{2} ] \\ \end{aligned} $$

(23)

By solving Eq. (22), we can obtain

$$ Z_{1,2} = \frac{{ - v_{2} \pm \sqrt {v_{2}^{2} - 4v_{1} v_{3} } }}{{2v_{1} }} $$

(24)

Combined with Eq. (14), the Hopf bifurcation boundary equation of the system is obtained as follows

$$ \begin{aligned} f^{2} & = \alpha_{1} \left( {\frac{{ - v_{2} \pm \sqrt {v_{2}^{2} - 4v_{1} v_{3} } }}{{2v_{1} }}} \right)^{3} + \alpha_{2} \left( {\frac{{ - v_{2} \pm \sqrt {v_{2}^{2} - 4v_{1} v_{3} } }}{{2v_{1} }}} \right)^{2} \\ &\quad \alpha_{3} \left( {\frac{{ - v_{2} \pm \sqrt {v_{2}^{2} - 4v_{1} v_{3} } }}{{2v_{1} }}} \right) \\ \end{aligned} $$

(25)

According to Eq. (16) and (25), the bifurcation diagrams of the combined damping NES system are presented in Fig. 5.

Fig. 5

SN bifurcation and Hopf bifurcation diagrams of the system

In Fig. 5, the solid line represents the SN bifurcation curve and the dashed line represents the Hopf bifurcation curve. The region enclosed by the Hopf bifurcation curve of the system and the Y-axis is the unstable region of the fixed points, and the external region is the stable region. As can be seen from Fig. 5, the region where the SN bifurcation curve of the system intersects with the Hopf bifurcation curve, shows that the system is affected by two kinds of bifurcation in some areas. When the selected parameters are located outside the two bifurcation curves, only a single stable fixed point can appear in the system.

At the same time, this paper studies the effects of linear damping coefficient ${\kern 1pt} \lambda_{2}$, mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ and detuning parameter ${\kern 1pt} \sigma {\kern 1pt}$ on the Hopf bifurcation curve of the system. On the premise that other parameters remain unchanged, the Hopf bifurcation diagram of different combined damping NES parameters is obtained by changing the values of combined damping NES parameters, as shown in Fig. 6.

Fig. 6

Hopf bifurcation with combined damping NES parameters change

It can be seen from Fig. 6 that changes in the linear damping coefficient ${\kern 1pt} \lambda_{2}$, mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ and the detuning parameter ${\kern 1pt} \sigma {\kern 1pt}$ will result in changes in the Hopf bifurcation curve of the system similar to that of the SN bifurcation, indicating that the effects of changing combined damping NES parameters on the number and stability of fixed points is similar.

Figure 7 plots the effects of external excitation amplitude change and frequency change on the system response amplitude, respectively.

Fig. 7

System response amplitude

It can be seen from Fig. 7 that no matter whether the excitation frequency changes or the excitation amplitude changes, the state of the system changes from a stable state to an unstable state, and finally returns to a stable state, representing that the number of fixed points changes from a single to three stages, and finally returns to a single stage. In Fig. 7a, the response amplitude of the system has a high-amplitude response loop in the frequency range of (-1.14, -0.51), which is caused by SN bifurcation. SN bifurcation also occurs in the frequency range (0.77, 1.15), and Hopf bifurcation occurs in the frequency range (-0.48, 1.15). This diagram is a good validation of the bifurcation in Figs. 4 and 6.

Through the analysis of the bifurcation characteristics of the system, it can be seen that adjusting combined damping NES parameters can make the system in an unstable state and smaller response amplitude of the system, which is important for suppressing the system vibration.

3 Strongly modulated response analysis

The current research results show that SMR occurs at the resonance frequency of the system, and when SMR occurs, the vibration suppression effect of combined damping NES on the system can be greatly improved. The purpose of this section is to determine the frequency interval in which the system generates SMR.

According to Eq. (11), this system is a four-dimensional phase space $(\phi_{1} ,\dot{\phi }_{1} ,\phi_{2} ,\dot{\phi }_{2} )$, slow converter consists of 4 variables, where ${\kern 1pt} \phi_{2} {\kern 1pt}$ and ${\kern 1pt} \dot{\phi }_{2} {\kern 1pt}$ are fast variables,${\kern 1pt} \phi_{1} {\kern 1pt}$ and ${\kern 1pt} \dot{\phi }_{1} {\kern 1pt}$ are slow variables. In order to facilitate subsequent calculation, Eq. (11) is processed to reduce the number of variables in the phase plane of the equation. The reduced equation of this system is obtained as follows

$$ \begin{aligned} & \ddot{\phi }_{2} + \frac{d}{dt}\left[ {\frac{i(1 + 4\varepsilon \sigma )}{2}\phi_{2} + \frac{{(1 + \varepsilon )\phi_{2} }}{8}\left( {4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right)} \right] \\ & + \phi_{2} \left[ { - \frac{\varepsilon \sigma }{2}(1 + 2\varepsilon \sigma ) + \frac{i\varepsilon (1 + 2\sigma + 2\varepsilon \sigma )}{{16}}\left( {4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right)} \right] \\ & - \frac{i\varepsilon f}{4}(1 + 2\varepsilon \sigma ) = 0 \\ \end{aligned} $$

(26)

We use the multi-scale method to solve Eq. (11). Defining

$$ \begin{aligned} \phi_{2} & = \phi_{2} (t_{0} ,\;t_{1} ,\; \cdots ),\;t_{n} = \varepsilon^{n} t,\;n = 0,\;1,\; \cdots \\ D & = D_{0} + \varepsilon D_{1} + \cdots = \frac{\partial }{{\partial \tau_{0} }} + \varepsilon \frac{\partial }{{\partial t_{1} }} + \cdots \\ \end{aligned} $$

(27)

The Eq. (26) can be converted to

$$ \begin{aligned} & \varepsilon^{0} :D_{0}^{2} \phi_{2} + \frac{{D_{0} \phi_{2} }}{8}\left( {4i + 4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) = 0 \\ & \varepsilon^{1} :2D_{0} D_{1} \phi_{2} + \frac{{D_{0} \phi_{2} }}{8}\left( {16i\sigma + 4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) \\ & + \frac{{D_{1} \phi_{2} }}{8}\left( {4i + 4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) - \frac{\sigma }{2}\phi_{2} \\ & + \frac{{i(1 + 2\sigma )\phi_{2} }}{16}\left( {4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) - \frac{if}{4} = 0 \\ \end{aligned} $$

(28)

By integrating the first formula of the above equation, we can get

$$ D_{0} \phi_{2} + \frac{{\phi_{2} }}{8}\left( {4i + 4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) = C(t_{1} ,...) $$

(29)

Setting $D_{0} \phi_{2} = 0$, the equation of the system at the fixed point can be obtained as

$$ \frac{{\phi_{2} }}{8}\left( {4i + 4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) = C(t_{1} ) $$

(30)

Since ${\kern 1pt} \phi_{2} {\kern 1pt}$ is only related to $\,t_{1}$, introduce: $\phi_{2} (t_{1} ) = N(t_{1} )e^{{i\theta (t_{1} )}}$, put it into (30), there is

$$ \frac{{9k^{2} + \lambda_{3}^{2} }}{16}N^{6} + \frac{{\lambda_{2} \lambda_{3} - 3k}}{2}N^{4} + (1 + \lambda_{2}^{2} )N^{2} = 4\left| C \right|^{2} $$

(31)

Letting $Z = N_{2}$, substituting it into (31) and derivation, one obtains

$$ \frac{{27k^{2} + 3\lambda_{3}^{2} }}{16}Z^{2} + \left( {\lambda_{2} \lambda_{3} - 3k} \right)Z + \lambda_{2}^{2} + 1 = 0 $$

(32)

The solutions of Eq. (32) are as follows

$$ \begin{aligned} Z_{1,2} & = \frac{{4(6k - 2\lambda_{2} \lambda_{3} ) \mp 4\sqrt {k^{2} (9 - 27\lambda_{2}^{2} ) - 24k\lambda_{2} \lambda_{3} + \lambda_{3}^{2} ( - 3 + \lambda_{2}^{2} )} }}{{3(9k^{2} + \lambda_{3}^{2} )}} \Rightarrow \\ N_{1,2} & = \sqrt {\frac{{4(6k - 2\lambda_{2} \lambda_{3} ) \mp 4\sqrt {k^{2} (9 - 27\lambda_{2}^{2} ) - 24k\lambda_{2} \lambda_{3} + \lambda_{3}^{2} ( - 3 + \lambda_{2}^{2} )} }}{{3(9k^{2} + \lambda_{3}^{2} )}}} \\ \end{aligned} $$

(33)

According to the solutions of Eqs. (31) and (33), the corresponding coordinate equation of the starting and landing point of the system where the jump phenomenon occurs can be obtained as follows

$$ \begin{aligned} & \frac{{9k^{2} + \lambda_{3}^{2} }}{16}Z_{1,2}^{3} + \frac{{\lambda_{2} \lambda_{3} - 3k}}{2}Z_{1,2}^{2} + (1 + \lambda_{2}^{2} )Z_{1,2} \\ & = \frac{{9k^{2} + \lambda_{3}^{2} }}{16}Z_{u,d}^{3} + \frac{{\lambda_{2} \lambda_{3} - 3k}}{2}Z_{u,d}^{2} + (1 + \lambda_{2}^{2} )Z_{u,d} \\ \end{aligned} $$

(34)

The solutions of Eq. (34) are as follows

$$ \begin{aligned} Z_{u,d} & = \frac{{4(6k - 2\lambda_{2} \lambda_{3} ) \pm 8\sqrt {k^{2} (9 - 27\lambda_{2}^{2} ) - 24k\lambda_{2} \lambda_{3} + \lambda_{3}^{2} ( - 3 + \lambda_{2}^{2} )} }}{{3(9k^{2} + \lambda_{3}^{2} )}} \Rightarrow \\ N_{u,d} & = \sqrt {\frac{{4(6k - 2\lambda_{2} \lambda_{3} ) \pm 8\sqrt {k^{2} (9 - 27\lambda_{2}^{2} ) - 24k\lambda_{2} \lambda_{3} + \lambda_{3}^{2} ( - 3 + \lambda_{2}^{2} )} }}{{3(9k^{2} + \lambda_{3}^{2} )}}} \\ \end{aligned} $$

(35)

${\kern 1pt} N_{1,2} {\kern 1pt}$ indicate the extreme value point of the SIM of the system, which represents the return point of the SIM, and determines the position where the SIM of the system may jump. Combined with Eq. (31), select $k = 4/3$, $\lambda_{2} = \lambda_{3} = 0.2$ [19], and draw the SIM of the system as shown.

In Fig. 8, the dotted line with an arrow represents the jump trajectory between the left and right stable parts of the system. Since the slow-varying amplitude of the system is affected by manifold invariance, it can only move along the SIM curve. When the slow-varying amplitude moves along the curve of the left stable part to ${\kern 1pt} N_{1}$, because the dotted line between the two return points is the unstable part, the system will not move along the SIM to ${\kern 1pt} N_{2}$, but directly jump from ${\kern 1pt} N_{1} {\kern 1pt}$ to ${\kern 1pt} N_{u}$, and then continue to move along the right stable part. When moving to ${\kern 1pt} N_{2}$, for the same reason, the slow-varying amplitude of the system jumps directly to point ${\kern 1pt} N_{d}$, and then continues along the left stable part. This process creates a continuous jump, the jumping process is manifested as: $N_{1} \to N_{u} \to N_{2} \to N_{d} \to N_{1}$. This continuous jumping process makes it possible for SMR to appear in the system.

Fig. 8

SIM projection

Next, the first-order equation in Eq. (31) is further analyzed to study the dynamic characteristics of the system tending to stability on time scale $t_{0}$. When $t_{0} \to \infty$, the first order equation can be converted to

$$ \frac{{D_{1} \phi_{2} }}{8}\left( {4i + 4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) = T $$

(36)

where

$$ T = \frac{if}{4} + \frac{\sigma }{2}\phi_{2} - \frac{{i(1 + 2\sigma )\phi_{2} }}{16}\left( {4\lambda_{2} + \lambda_{3} \left| {\phi_{2} } \right|^{2} - 3ik\left| {\phi_{2} } \right|^{2} } \right) $$

(37)

Take complex conjugation of Eq. (36) and combine Eq. (34), we can get

$$ \frac{{\partial \phi_{2} }}{{\partial t_{1} }} = \frac{{T\left[ { - 2i + 2\lambda_{2} + (\lambda_{3} + 3ik)\left| {\phi_{2} } \right|^{2} } \right] - \frac{{T^{*} }}{2}(\lambda_{3} - 3ik)\phi_{2}^{2} }}{{\frac{{27k^{2} + 3\lambda_{3}^{2} }}{16}\left| {\phi_{2} } \right|^{4} + (\lambda_{2} \lambda_{3} - 3k)\left| {\phi_{2} } \right|^{2} + \lambda_{2}^{2} + 1}} $$

(38)

Introducing complex variables to Eq. (37) and Eq. (38), one has

$$ \left\{ \begin{aligned} & G(N)\frac{\partial N}{{\partial t_{1} }} = - \frac{{\lambda_{3} N^{3} }}{4} + \frac{{fN^{2} }}{4}(\lambda_{3} \sin \theta - 3k\cos \theta ) + \lambda_{2} (f\sin \theta - N) + f\cos \theta \\ & G(N)\frac{\partial \theta }{{\partial t_{1} }} = - \frac{{3N^{4} }}{16}(9k^{2} + \lambda_{3}^{2} )(1 + 2\sigma ) + \left[ {\frac{3k}{4}(1 + 8\sigma ) - (1 + 2\sigma )\lambda_{2} \lambda_{3} } \right]N^{2} + \\ \; & \frac{3fN}{4}(\lambda_{3} \cos \theta + 3k\sin \theta ) + \frac{f}{N}(\lambda_{2} \cos \theta - \sin \theta ) - \left[ {\lambda_{2}^{2} (1 + 2\sigma ) + 2\sigma } \right] \\ \end{aligned} \right. $$

(39)

where

$$ G(N) = 2\left[ {\frac{{27k^{2} + 3\lambda_{3}^{2} }}{16}N^{4} + (\lambda_{2} \lambda_{3} - 3k)N^{2} + \lambda_{2}^{2} + 1} \right] $$

(40)

When jumping occurs, fold line will appear in the system. In order to avoid singularity in the system, Eq. (39) is simplified as

$$ \left\{ \begin{aligned} & N^{\prime} = - \frac{{\lambda_{3} N^{3} }}{4} + \frac{{fN^{2} }}{4}(\lambda_{3} \sin \theta - 3k\cos \theta ) + \lambda_{2} (f\sin \theta - N) + f\cos \theta \\ & \theta^{\prime} = - \frac{{3N^{4} }}{16}(9k^{2} + \lambda_{3}^{2} )(1 + 2\sigma ) + \left[ {\frac{3k}{4}(1 + 8\sigma ) - (1 + 2\sigma )\lambda_{2} \lambda_{3} } \right]N^{2} + \\ & \frac{3fN}{4}(\lambda_{3} \cos \theta + 3k\sin \theta ) + \frac{f}{N}(\lambda_{2} \cos \theta - \sin \theta ) - \left[ {\lambda_{2}^{2} (1 + 2\sigma ) + 2\sigma } \right] \\ \end{aligned} \right. $$

(41)

Equation (41) defines the phase portrait of the system on plane $[\theta ,N]$, the parameters are selected as: $k = 4/3$, $\lambda_{2} = \lambda_{3} = 0.2$, $f = 1$, integrates the above equation, and draws the phase portraits of the system under different ${\kern 1pt} \sigma {\kern 1pt}$, as shown in Fig. 9. The two vertical lines in Fig. 9 define the initial phase angle interval for the SIM to jump, which is called the phase jump interval. ${\kern 1pt} \theta_{1} {\kern 1pt}$ and ${\kern 1pt} \theta_{2} {\kern 1pt}$ represent the initial phase angle of the ${\kern 1pt} N_{1} {\kern 1pt}$ and ${\kern 1pt} N_{2}$. The two horizontal lines correspond to the jump trajectory of the two return points in Fig. 8, and the blank area between them corresponds to the unstable part in Fig. 8. The arrow represents the future direction of the phase portrait motion.

Fig. 9

Phase portraits with ${\kern 1pt} \sigma {\kern 1pt}$ change

As can be seen from Fig. 9, the motion path of the phase portraits starts from ${\kern 1pt} N_{1} {\kern 1pt}$ within the jump interval, moves down along the arrow, and returns to ${\kern 1pt} N_{1} {\kern 1pt}$ outside the jump interval. However, a part of the phase portraits cannot return to ${\kern 1pt} N_{1} {\kern 1pt}$ due to the presence of attractors, as shown in Fig. 9a and c, which will converge this part of the phase portraits. Those that return to ${\kern 1pt} N_{1} {\kern 1pt}$ produce a jump, crossing the unstable part between the two horizontal lines to ${\kern 1pt} N_{2}$, then moving up the phase portrait and back to ${\kern 1pt} N_{2} {\kern 1pt}$ within the jump interval, and finally jumping from ${\kern 1pt} N_{2} {\kern 1pt}$ to ${\kern 1pt} N_{1}$, forming a complete jump process, which corresponds to the change in Fig. 8. The continuous motion process of the above phase portraits provide the possibility for SMR to occur in the system, but whether the system occur SMR needs further analysis.

Since the phase portraits cannot clearly indicate whether the system generates SMR, and the jumping process of the phase portrait is extremely complex and unstable, one-dimensional mapping is often used to analyze the detuning parameter interval of the system where SMR occurs [39]. However, one-dimensional mapping cannot intuitively distinguish the mapping lines that generate SMR phenomenon. At the same time, it is easy to produce errors when calculating jump points, so the slow manifold is used in this paper to intuitively study the detuning parameter interval of the system that generates SMR phenomenon.

Considering the first two orders of the time scale, setting

$$ \phi_{1} (t) = a_{1} (t) + ib_{1} (t),\quad \phi_{2} (t) = a_{2} (t) + ib_{2} (t) $$

(42)

By substituting Eq. (42) into Eq. (11) and taking ${\kern 1pt} \varepsilon^{0} {\kern 1pt}$ to separate the real and imaginary parts, the system of ordinary differential equations can be obtained as

$$ \left\{ \begin{aligned} \dot{a}_{1} & = \varepsilon \sigma b_{1} + \frac{{\varepsilon (b_{1} - b_{2} )}}{2(1 + \varepsilon )} + \frac{\varepsilon f}{2} \\ \dot{b}_{1} & = - \varepsilon \sigma a_{1} - \frac{{\varepsilon (a_{1} - a_{2} )}}{2(1 + \varepsilon )} \\ \dot{a}_{2} & = \varepsilon \sigma b_{2} + \frac{{(b_{2} - b_{1} )}}{2(1 + \varepsilon )} - \frac{{(1 + \varepsilon )[4\lambda_{2} + \lambda_{3} (a_{2}^{2} + b_{2}^{2} )]a_{2} }}{8} - \frac{{3k(1 + \varepsilon )(a_{2}^{2} + b_{2}^{2} )b_{2} }}{8} + \frac{\varepsilon f}{2} \\ \dot{b}_{2} & = - \varepsilon \sigma a_{2} - \frac{{(a_{2} - a_{1} )}}{2(1 + \varepsilon )} - \frac{{(1 + \varepsilon )[4\lambda_{2} + \lambda_{3} (a_{2}^{2} + b_{2}^{2} )]b_{2} }}{8} + \frac{{3k(1 + \varepsilon )(a_{2}^{2} + b_{2}^{2} )a_{2} }}{8} \\ \end{aligned} \right. $$

(43)

Using Matlab to solve Eqs. (43), parameters are selected as $k = 4/3$, $\lambda_{2} = \lambda_{3} = 0.2$, $f = 1$, and the slow manifolds of the system response are drawn, as shown in Fig. 10.

Fig. 10

Slow manifolds of the system response with ${\kern 1pt} \sigma {\kern 1pt}$ change

As can be seen from Fig. 10, when $\sigma = - 2$, although the slow manifold of the system increases from 0 to ${\kern 1pt} N_{1}$, it does not jump to ${\kern 1pt} N_{2}$. Instead, after experiencing several periodic changes, it is attracted by the lower attractor to the lower stable branch, forming a local cycle. At this time, the system was unable to generate SMR. When $\sigma = - 0.9$, although the slow manifold of the system can reach ${\kern 1pt} N_{1} {\kern 1pt}$ and jump to ${\kern 1pt} N_{2}$, it does not return from ${\kern 1pt} N_{2} {\kern 1pt}$ to ${\kern 1pt} N_{1}$, but is attracted by the attractor above and cannot form a complete cycle. At this time, the system is also unable to generate a complete SMR. When $\sigma = 1$, the slow manifold of the system can form a complete jump loop between ${\kern 1pt} N_{1} {\kern 1pt}$ and ${\kern 1pt} N_{2}$, and at this time, the system can exhibit stable SMR. When $\sigma = 2.1$, the changes of the slow manifold of the system, as shown in Fig. 10a, are all attracted to the lower stable branch by the lower attractor, which cannot form a complete jump loop, so the system cannot generate SMR.

In order to verify the correctness of using the slow manifold to analyze SMR in the system, this paper uses the time response diagram for comparison and verification. Under the premise of ensuring the same parameter selection, the time response diagrams of the main system under different ${\kern 1pt} \sigma {\kern 1pt}$ are drawn, as shown in Fig. 11.

Fig. 11

Time response diagrams with ${\kern 1pt} \sigma {\kern 1pt}$ change

The time response diagram in Fig. 11 corresponds to the slow manifold diagram in Fig. 10. Observing the above figure, it can be seen that it is reliable to analyze the occurrence of SMR in the system through the slow manifold. Because the calculation of the slow manifold is simpler and the observation of the slow manifold is easier than one-dimensional mapping, it is easy to determine the detuning parameter interval of SMR in the system by the slow manifold. After calculation, the interval of SMR in this example is ${\kern 1pt} [ - 0.19,\,1.52]$.

Figure 12 plots the slow manifold diagrams of the system response under different ${\kern 1pt} \varepsilon$.

Fig. 12

Slow manifolds of the system response with ${\kern 1pt} \varepsilon {\kern 1pt}$ change

As can be seen from Fig. 12, when ${\kern 1pt} \varepsilon {\kern 1pt}$ changes, the shape of the slow manifold of the system basically does not change, and with the decrease of ${\kern 1pt} \varepsilon$, the numerical solution of the slow manifold corresponds better with the analytical solution, with a higher degree of agreement. This indicates that it is easier to determine whether SMR occurs in the system by selecting a small ${\kern 1pt} \varepsilon$.

4 Vibration reduction performance analysis

4.1 Energy analysis

This section will study the vibration suppression effect of combined damping NES on the main system through the numerical solution, and the vibration reduction analysis and comparison will be carried out from the perspective of energy, further explaining the vibration reduction effect of the proposed combined damping NES in this paper. Firstly, the energy variation of a system containing combined damping NES under impulsive excitation is studied. According to Eq. (6), the dynamic equation under impulsive excitation can be obtained as

$$ \left\{ \begin{aligned} & \ddot{x}_{1} + x_{1} + \varepsilon \lambda_{2} (\dot{x}_{1} - \dot{x}_{2} ) + \varepsilon \lambda_{3} (x_{1} - x_{2} )^{2} (\dot{x}_{1} - \dot{x}_{2} ) + \varepsilon k(x_{1} - x_{2} )^{3} = \varepsilon A\delta (t) \\ & \ddot{x}_{2} + \lambda_{2} (\dot{x}_{2} - \dot{x}_{1} ) + \lambda_{3} (x_{2} - x_{1} )^{2} (\dot{x}_{2} - \dot{x}_{1} ) + k(x_{2} - x_{1} )^{3} = 0 \\ \end{aligned} \right. $$

(44)

According to the momentum theorem, applying impulsive excitation to the system is equivalent to an initial velocity provided to the main system, then the initial conditions of the combined damping NES system are $x_{1} (0) = x_{2} (0) = \dot{x}_{2} (0) = 0$, $\dot{x}_{1} (0) = Am/s$.

The energy of the main system is denoted by ${\kern 1pt} E_{1} {\kern 1pt}$ and is defined as

$$ E_{1} = \frac{1}{2}\dot{x}_{1}^{2} + \frac{1}{2}x_{1}^{2} $$

(45)

The energy of combined damping NES is denoted by ${\kern 1pt} E_{2} {\kern 1pt}$ and is defined as

$$ E_{2} = \frac{1}{2}\varepsilon \dot{x}_{2}^{2} + \frac{1}{4}\varepsilon k(x_{1} - x_{2} )^{4} $$

(46)

The total energy ${\kern 1pt} E{\kern 1pt}$ of the system consists of ${\kern 1pt} E_{1} {\kern 1pt}$ and ${\kern 1pt} E_{2}$. The expression is as

$$ E = E_{1} + E_{2} = \frac{1}{2}(\dot{x}_{1}^{2} + \varepsilon \dot{x}_{2}^{2} ) + \frac{1}{2}\left[ {x_{1}^{2} + \frac{1}{2}\varepsilon k(x_{1} - x_{2} )^{4} } \right] $$

(47)

By substituting the initial conditions into ${\kern 1pt} E$, the initial energy $E_{0}$ of the system under impulsive excitation can be obtained as

$$ E_{0} = \frac{1}{2}\dot{x}_{1}^{2} = \frac{1}{2}A^{2} $$

(48)

System parameters are selected as: $k = 4/3$, $\lambda_{2} = \lambda_{3} = 0.3$, $\varepsilon = 0.1$ [19]. The time response and energy of the main system with different damping NES under different impulsive excitation intensities are shown in Fig. 13.

Fig. 13

The time response and energy of the main system with different damping NES under different impulsive excitation intensities

In the figure above, L-NES represents linear damping NES, G-NES represents geometrically nonlinear damping NES, and LG-NES is a combined damping NES studied in this paper. As can be seen from Fig. 13, when the impulsive excitation intensity ${\kern 1pt} A{\kern 1pt}$ remains constant, the dissipation time of ${\kern 1pt} E_{1} {\kern 1pt}$ with additional combined damping NES is the shortest, and the vibration attenuation of the main system is the fastest, indicating that the vibration reduction performance of combined damping NES is better than that of L-NES and G-NES. It is worth noting that with the increase of the impulsive excitation intensity ${\kern 1pt} A$, the vibration reduction performance of G-NES gradually exceeds that of L-NES. It shows that L-NES is suitable for use in environments with lower impulsive excitation intensity, and G-NES is suitable for use in environments with higher impulsive excitation intensity. But overall, the vibration reduction performance of combined damping NES is the best.

Next, analyze the effects of cubic stiffness coefficient ${\kern 1pt} k$, linear damping coefficient ${\kern 1pt} \lambda_{2}$, and geometrically nonlinear damping coefficient ${\kern 1pt} \lambda_{3}$ on the vibration reduction performance of combined damping NES. Firstly, study the vibration reduction performances under different ${\kern 1pt} k$, and select the parameters as shown in the table below.

According to the parameters selected in Table 1, the energy variation curves of the main system and combined damping NES when A = 1 m/s are drawn, as shown in Fig. 14.

Table 1 Parameter value table

Fig. 14

${\kern 1pt} E_{1} {\kern 1pt}$ and ${\kern 1pt} E_{2} {\kern 1pt}$ with different k

As can be seen from Fig. 14a, when ${\kern 1pt} k{\kern 1pt}$ is small, the energy transferred by the main system to combined damping NES is very low, and almost no energy transfer occurs. With the increase of ${\kern 1pt} k$, the energy transferred by the main system to combined damping NES gradually increases, and the dissipation time of ${\kern 1pt} E_{1} {\kern 1pt}$ gradually becomes shorter, indicating that the vibration reduction performance of combined damping NES is gradually improved. However, when ${\kern 1pt} k{\kern 1pt}$ is too large, as shown in Fig. 13d, the energy transferred by the main system to combined damping NES will decrease, and the dissipation speed of ${\kern 1pt} E_{1} {\kern 1pt}$ will slow down, indicating that the vibration reduction performance of combined damping NES on the main system is deteriorating. Therefore, in order to make combined damping NES produce a good vibration suppression effect, it is necessary to select the appropriate ${\kern 1pt} k$.

To verify the conclusion of Fig. 14, define the energy proportion ${\kern 1pt} \eta {\kern 1pt}$ of the main system as follows

$$ \eta = \frac{{E_{1} }}{{E_{0} }} \times 100\% = \frac{{(\dot{x}_{1}^{2} + x_{1}^{2} )}}{{A^{2} }} \times 100\% $$

(49)

The energy proportion diagram of the main system under different ${\kern 1pt} k{\kern 1pt}$ is drawn as shown in the figure below.

In Fig. 15, with the increase of ${\kern 1pt} k$, the energy proportion curve of the main system shows a trend of first decreasing and then increasing, indicating that when ${\kern 1pt} k{\kern 1pt}$ is too small or too large, the energy transmitted by the main system to combined damping NES is less, and the energy dissipation speed of the main system is slower. At this time, combined damping NES does not have a good vibration reduction effect.

Fig. 15

Energy proportion of the main system with different k

Secondly, the effects of different linear damping coefficients ${\kern 1pt} \lambda_{2} {\kern 1pt}$ on the vibration reduction performance of combined damping NES are studied, and the parameters selection is shown in the table below.

According to the parameters selected in Table 2, the energy variation curves of the main system and combined damping NES when A = 1 m/s are drawn, as shown in the figure below.

Table 2 Parameter value table

As can be seen from Fig. 16a, when ${\kern 1pt} \lambda_{2} {\kern 1pt}$ is small, although the main system can transfer more energy to combined damping NES, combined damping NES will return energy to the main system, resulting in a longer energy dissipation time of the main system, which makes the main system unable to obtain good vibration reduction performance. With the increase of ${\kern 1pt} \lambda_{2}$, as shown in Fig. 15c, when the value is 0.3, the energy transmitted by the main system to combined damping NES is rarely returned to the main system by combined damping NES, and the energy of the main system will rapidly decrease. At this time, the main system can obtain a good vibration suppression effect. When the value of ${\kern 1pt} \lambda_{2} {\kern 1pt}$ is too large, as shown in Fig. 15d, the energy of the main system can hardly be transferred to combined damping NES, resulting in combined damping NES can not have a good vibration suppression effect.

Fig. 16

${\kern 1pt} E_{1} {\kern 1pt}$ and ${\kern 1pt} E_{2} {\kern 1pt}$ with different λ₂

Figure 17 plots the energy proportion of the main system under different linear damping coefficients.

Fig. 17

Energy proportion of the main system with different λ₂

As can be seen from Fig. 17, as ${\kern 1pt} \lambda_{2} {\kern 1pt}$ increases, the degree of rebound in the energy proportion curve of the main system decreases, and the dissipation time of the energy proportion curve is shorter and shorter. This indicates that the energy returned to the main system by combined damping NES is gradually decreasing, and the vibration reduction effect of combined damping NES is getting better and better. When ${\kern 1pt} \lambda_{2} {\kern 1pt}$ is too large, the energy proportion curve changes more gently and the dissipation time becomes longer, indicating that the main system almost does not transfer energy to combined damping NES, and the combined damping NES does not provide a good reduction effect on the main system.

Finally, the effects of different geometrically nonlinear damping coefficients ${\kern 1pt} \lambda_{3} {\kern 1pt}$ on the vibration reduction performance of combined damping NES are studied, and the parameters selected are shown in the following table.

According to the parameters selected in Table 3, the energy variation curves of the main system and combined damping NES when the A = 1 m/s are drawn, as shown in Fig. 18.

Table 3 Parameter value table

Fig. 18

${\kern 1pt} E_{1} {\kern 1pt}$ and ${\kern 1pt} E_{2} {\kern 1pt}$ with different λ₃

In Fig. 18, as ${\kern 1pt} \lambda_{3} {\kern 1pt}$ increases, the energy variation curve of the main system becomes more gentle and the dissipation time becomes shorter, indicating that the energy returned by combined damping NES to the main system is less and less, and the vibration reduction effect of combined damping NES is getting better and better. However, when ${\kern 1pt} \lambda_{3} {\kern 1pt}$ is too large, as shown in Fig. 18d, the dissipation time of the main system energy increases, and the energy transmitted to combined damping NES decreases to a certain extent, indicating that the combined damping NES's vibration reduction effect has decreased. Therefore, it is necessary to select an appropriate ${\kern 1pt} \lambda_{3} {\kern 1pt}$ to make the main system obtain a good vibration reduction effect.

Figure 19 shows the energy proportion of the main system under different geometrically nonlinear damping coefficients.

Fig. 19

Energy proportion of the main system with different λ₃

It can be seen from Fig. 19 that the change of ${\kern 1pt} \lambda_{3} {\kern 1pt}$ has a small impact on the energy proportion curve of the main system. By enlarging the figure, it is found that the energy proportion curve of the main system becomes more gentle with the increase of ${\kern 1pt} \lambda_{3}$, indicating that the energy returned by combined damping NES to the main system gradually decreases. When ${\kern 1pt} \lambda_{3} {\kern 1pt}$ reaches 1.5, the dissipation rate of the energy proportion curve decreases to a certain extent. This figure can effectively validate the conclusion of Fig. 18.

In order to analyze the vibration reduction effect of combined damping NES under harmonic excitation, the energy spectrum is used for comparative study in this part. According to Eq. (8), the average energy ${\kern 1pt} E_{a} {\kern 1pt}$ of the main system can be expressed as:

$$ E_{a} = \left\langle {\frac{1}{2}\dot{x}_{1}^{2} + \frac{1}{2}x_{1}^{2} } \right\rangle_{t} $$

(50)

This equation means the average value of ${\kern 1pt} E_{1} {\kern 1pt}$ over time period ${\kern 1pt} t$, and ${\kern 1pt} t{\kern 1pt}$ must be greater than the period T of harmonic excitation. According to the above equation, when the value of ${\kern 1pt} E_{a} {\kern 1pt}$ is the smallest, the combined damping NES has the best vibration suppression effect on the main system. For the convenience of comparing the vibration reduction effect of different damping NES, the parameter selection should be consistent with the literature results [19], and the values are: $t \in [2000,{\kern 1pt} 3000]$, $f = 0.3$.

Next, analyze the influence of mass ratio ${\kern 1pt} \varepsilon$, damping ratio ${\kern 1pt} \lambda_{3} {/}\lambda_{{2}} {\kern 1pt}$ and cubic stiffness coefficient $k$ on the vibration reduction effect of combined damping NES. Firstly, draw the energy spectrum of the main system with different ${\kern 1pt} \varepsilon {\kern 1pt}$ and ${\kern 1pt} \lambda_{3} {/}\lambda_{{2}} {\kern 1pt}$ as shown in the following figure.

As can be seen from Fig. 20, when ${\kern 1pt} \varepsilon {\kern 1pt}$ and ${\kern 1pt} \lambda_{3} {/}\lambda_{{2}} {\kern 1pt}$ remain constant, the energy spectrum area of the main system does not decrease with the increase of the damping coefficient of combined damping NES, indicating that the vibration reduction effect of combined damping NES does not develop in a good direction. On the contrary, when the damping coefficient of combined damping NES is smaller, the energy spectrum area of the main system is smaller, and the vibration reduction effect of combined damping NES is better. As shown in Fig. 21, near the resonance frequency, when the value of ${\kern 1pt} \lambda_{3} {\kern 1pt}$ is 0.3, the SMR phenomenon occurs in the system, and the amplitude of the main system is greatly modulated. At this time, combined damping NES has a better vibration reduction effect on the main system. When the value is 0.5, the system exhibits a weak modulation phenomenon, and the amplitude of the main system is subject to a certain degree of small modulation. When the value is 0.8, the main system presents a steady periodic response, which is not conducive to the vibration suppression of the main system. When ${\kern 1pt} \varepsilon {\kern 1pt}$ remains constant, the energy spectrum area of the main system decreases with the increase of ${\kern 1pt} \lambda_{3} {/}\lambda_{{2}} {\kern 1pt}$, indicating that the greater the difference between the linear damping coefficient and the geometrically damping coefficient, the better the vibration reduction effect of combined damping NES. When ${\kern 1pt} \lambda_{3} {/}\lambda_{{2}} {\kern 1pt}$ remains constant, increasing ${\kern 1pt} \varepsilon {\kern 1pt}$ will increase the energy spectrum area and bandwidth of the main system, which is not conducive to the vibration reduction of the main system by combined damping NES.

Fig. 20

Energy spectrum of the main system with ${\kern 1pt} \varepsilon {\kern 1pt}$ and λ₃ λ₂ change

Fig. 21

Poincare map and time response of different λ₃

According to the previous analysis, the greater the ${\kern 1pt} \lambda_{3} {/}\lambda_{{2}}$, the better the vibration reduction effect of combined damping NES on the main system. Based on this, the damping ratio is taken as 5, and the energy spectrum of the main system with different ${\kern 1pt} \varepsilon {\kern 1pt}$ and ${\kern 1pt} k{\kern 1pt}$ is plotted as shown in the following figure.

According to Fig. 22, when ${\kern 1pt} \varepsilon {\kern 1pt}$ remains constant, as ${\kern 1pt} k{\kern 1pt}$ continues to increase, the energy spectrum area of the main system gradually decreases, and the bandwidth of vibration reduction continues to increase. At this time, the main system will generate SMR phenomenon, and its amplitude will be greatly modulated, as shown in Fig. 23a and b. However, when ${\kern 1pt} k{\kern 1pt}$ is too large, the energy spectrum of the main system will appear a resonance peak near the resonance frequency, causing the energy spectrum area to become very large. Drawing the Poincare map and time response here, as shown in Fig. 23c, it can be found that the main system presents a steady periodic response without occuring SMR phenomenon, in which case the vibration reduction effect of combined damping NES is poor. The effect of ${\kern 1pt} \varepsilon {\kern 1pt}$ change is the same as above, and increasing ${\kern 1pt} \varepsilon {\kern 1pt}$ is not conducive to the vibration reduction effect of combined damping NES.

Fig. 22

Energy spectrum of the main system with ${\kern 1pt} \varepsilon {\kern 1pt}$ and k change

Fig. 23

Poincare map and time response of different k and ${\kern 1pt} \sigma {\kern 1pt}$

In summary, when designing combined damping NES parameters, it is necessary to select appropriately large stiffness coefficient ${\kern 1pt} k$, smaller mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ and larger damping ratio ${\kern 1pt} \lambda_{3} {/}\lambda_{2} {\kern 1pt}$ to obtain smaller energy spectrum area and bandwidth, so as to achieve the optimal vibration reduction effect of combined damping NES on the main system.

In this paper, there are two standards to evaluate the vibration reduction effect of combined damping NES, the main standard is the energy spectrum area of the main system, and the secondary standard is the peak value at each position of the energy spectrum. According to these two standards, the parameters of combined damping NES are optimized. In the optimization process, considering that the energy spectrum of the main system is mainly concentrated near the resonance frequency, the frequency range is selected as $\omega = [0.8,1.2]$, the weight allocation ratio is 80% of the energy spectrum area and 20% of the peak variance of the energy spectrum. After optimization, the optimal parameters are obtained as: $\lambda_{2} = 0.05$, $\lambda_{3} = 1.7$, $k = 5.31$, and compared with NES studied in the literature [40], the comparison diagram of the optimal energy spectrum is shown in Fig. 24.

Fig. 24

Optimal energy spectrum comparison diagram

In the figure, LN-NES represents NES with linear damping and cubic damping, while LG-NES represents NES with combined damping studied in this paper. As shown in Fig. 23, the energy spectrum area of the main system of LG-NES is smaller than that of LN-NES, and the peak in most positions is lower than that of LN-NES. Therefore, it can be concluded that the vibration reduction effect of LG-NES is better than that of LN-NES.

4.2 Amplitude-frequency response analysis

This section studies the vibration reduction effect of combined damping NES on the main system from the perspective of analytical solution, and analyzes the influence of NES parameters on the vibration reduction performance by using the amplitude-frequency response curve. Introduce a new complex variable to Eq. (9).

$$ \gamma_{1} e^{i\omega t} = \dot{u} + i\omega u,\quad \gamma_{2} e^{i\omega t} = \dot{v} + i\omega v $$

(51)

Then Eq. (9) is transformed into

$$ \left\{ \begin{aligned} & \dot{\gamma }_{1} + i\frac{{[ - 1 + (1 + \varepsilon )\omega^{2} ]\gamma_{1} - \varepsilon \gamma_{2} }}{2(1 + \varepsilon )\omega } = \frac{\varepsilon f}{2} \\ & \dot{\gamma }_{2} + \frac{1}{2}(i\omega + \lambda_{2} + \varepsilon \lambda_{2} )\gamma_{2} + \frac{1 + \varepsilon }{{8\omega^{2} }}\lambda_{3} \left| {\gamma_{2} } \right|^{2} \gamma_{2} - \frac{3ik(1 + \varepsilon )}{8}\left| {\gamma_{2} } \right|^{2} \gamma_{2} \\ & \quad - \frac{{i(\gamma_{1} + \varepsilon \gamma_{2} )}}{2(1 + \varepsilon )\omega } = \frac{\varepsilon f}{2} \\ \end{aligned} \right. $$

(52)

In order to obtain the steady solution of the system, letting $\dot{\gamma }_{1} = \dot{\gamma }_{2} = 0$, and perform the following transformations on ${\kern 1pt} \gamma_{1} {\kern 1pt}$ and ${\kern 1pt} \gamma_{2}$.

$$ \gamma_{1} = \beta_{1} e^{{i\alpha_{1} }} ,\quad \gamma_{2} = \beta_{2} e^{{i\alpha_{2} }} $$

(53)

By substituting Eqs. (53) into (52), we can yield

$$ \left\{ \begin{aligned} & \frac{{[ - 1 + (1 + \varepsilon )\omega^{2} ]\beta_{1} \sin \alpha_{1} - \varepsilon \beta_{2} \sin \alpha_{2} + \varepsilon f(1 + \varepsilon )\omega }}{2(1 + \varepsilon )\omega } = 0 \\ & \frac{{[ - 1 + (1 + \varepsilon )\omega^{2} ]\beta_{1} \cos \alpha_{1} - \varepsilon \beta_{2} \cos \alpha_{2} }}{2(1 + \varepsilon )\omega } = 0 \\ & \frac{1}{8}\left[ { - 4\varepsilon f + \frac{{(1 + \varepsilon )\lambda_{3} }}{{\omega^{2} }}\beta_{2}^{3} \cos \alpha_{2} + \frac{3k(1 + \varepsilon )}{{\omega^{3} }}\beta_{2}^{3} \sin \alpha_{2} + \frac{{4\beta_{1} \sin \alpha_{1} }}{(1 + \varepsilon )\omega }} \right] \\ & + \frac{{(1 + \varepsilon )^{2} \lambda_{2} \omega \beta_{2} \cos \alpha_{2} + [\varepsilon - (1 + \varepsilon )\omega^{2} ]\beta_{2} \sin \alpha_{2} }}{2(1 + \varepsilon )\omega } = 0 \\ & \frac{1}{8}\left[ {\frac{{(1 + \varepsilon )\lambda_{3} }}{{\omega^{2} }}\beta_{2}^{3} \sin \alpha_{2} - \frac{3k(1 + \varepsilon )}{{\omega^{3} }}\beta_{2}^{3} \cos \alpha_{2} - \frac{{4\beta_{1} \cos \alpha_{1} }}{(1 + \varepsilon )\omega }} \right] \\ & + \frac{{(1 + \varepsilon )^{2} \lambda_{2} \omega \beta_{2} \sin \alpha_{2} + [(1 + \varepsilon )\omega^{2} - \varepsilon ]\beta_{2} \cos \alpha_{2} }}{2(1 + \varepsilon )\omega } = 0 \\ \end{aligned} \right. $$

(54)

According to the paper studied by Fang et al. [41], it can be obtained

$$ u(t) \approx \frac{{\beta_{1} }}{\omega }\sin (\omega t + \alpha_{1} ),\quad v(t) \approx \frac{{\beta_{2} }}{\omega }\sin (\omega t + \alpha_{2} ) $$

(55)

The steady-state response of the system is obtained as

$$ \left\{ \begin{aligned} & x_{1} (t) \approx \frac{1}{1 + \varepsilon }\left[ {\frac{{\beta_{1} }}{\omega }\sin (\omega t + \alpha_{1} ) + \varepsilon \frac{{\beta_{2} }}{\omega }\sin (\omega t + \alpha_{2} )} \right] \\ & x_{2} (t) \approx \frac{1}{1 + \varepsilon }\left[ {\frac{{\beta_{1} }}{\omega }\sin (\omega t + \alpha_{1} ) - \frac{{\beta_{2} }}{\omega }\sin (\omega t + \alpha_{2} )} \right] \\ \end{aligned} \right. $$

(56)

Solve Eq. (54) and bring the results into Eq. (56) to obtain the analytical solution of the response amplitude. Meanwhile, using the Runge Kutta method to solve Eq. (8) to obtain the numerical solution of the response amplitude. Draw the amplitude-frequency response curves of the main system and combined damping NES, as shown in Fig. 25.

Fig. 25

Comparison of the amplitude-frequency response curves

It can be seen from Fig. 25 that the analytical solution and the numerical solution agree well, which verifies the correctness of the complex variable average method to solve the response amplitude.

Figure 26 shows the amplitude-frequency response curves of the main system for different NES under different external excitation amplitudes. From Fig. 26, it can be seen that when the two NES selected the same parameters, the resonance amplitude of LG-NES is lower than that of LN-NES. Moreover, when the external excitation amplitude increases, the difference in resonance amplitude between LG-NES and LN-NES is more significant, indicating that the vibration reduction effect of LG-NES is better than that of LN-NES. Moreover, when the external excitation amplitude is larger, the vibration reduction advantage of LG-NES is more obvious.

Fig. 26

Amplitude-frequency response curves of different NES at different f

Next, analyze the influence of NES parameter changes on the vibration reduction performance of combined damping NES. Firstly, analyze the influence of mass ratio ${\kern 1pt} \varepsilon$, damping ratio ${\kern 1pt} \lambda_{3} {/}\lambda_{2} {\kern 1pt}$ and damping coefficient on the vibration reduction effect. Parameters selected as: $k = 4/3$, $f = 0.3$ [31], and draw the amplitude-frequency response curves of the main system with different ${\kern 1pt} \varepsilon {\kern 1pt}$ and ${\kern 1pt} \lambda_{3} {/}\lambda_{2} {\kern 1pt}$ as shown in the following figure.

As can be seen from Fig. 27, when ${\kern 1pt} \varepsilon {\kern 1pt}$ and $\lambda_{3} {/}\lambda_{2}$ remain constant, the steady-state response amplitude near the resonance frequency of the main system increases with the increase of the damping coefficient, which indicates that the vibration reduction performance of combined damping NES gradually decreases with the increase of the damping coefficient. Therefore, when choosing the damping coefficient, we should choose a smaller damping coefficient to make the main system get a good vibration reduction effect. When the damping coefficient and ${\kern 1pt} \varepsilon {\kern 1pt}$ remain constant, with the increase of $\lambda_{3} {/}\lambda_{2}$, although the steady-state response amplitude of the main system near the resonance frequency increases to a certain extent, the frequency band of resonance becomes narrower. Therefore, when selecting the damping ratio, it is necessary to choose an appropriately large damping ratio. When the damping coefficient and $\lambda_{3} {/}\lambda_{2}$ remain constant, both the resonant frequency band and steady-state response amplitude of the main system increase with the increase of ${\kern 1pt} \varepsilon$, indicating that the vibration reduction performance of combined damping NES is gradually declining. Therefore, it is necessary to choose a smaller ${\kern 1pt} \varepsilon$.

Fig. 27

Amplitude-frequency response curves with ${\kern 1pt} \varepsilon {\kern 1pt}$ and λ₃ λ₂ change

In order to further study the optimal range of the above parameters, 3D and 2D contour maps with different $\lambda_{3} {/}\lambda_{2}$ and ${\kern 1pt} \varepsilon {\kern 1pt}$ are drawn, as shown in Figs. 28 and 29. The parameter selection is the same as above.

Fig. 28

Amplitude-frequency response curves with λ₃ change

Fig. 29

Amplitude-frequency response curves with ${\kern 1pt} \varepsilon {\kern 1pt}$ change

As can be seen from Fig. 28, when $\lambda_{3} {/}\lambda_{2}$ is about 3.5, the amplitude-frequency response curve of the main system not only does not show a high steady-state response amplitude, but also has a narrow resonance frequency band. Therefore, in the subsequent analysis, the damping ratio is selected as 3.5.

Figure 29 shows the amplitude-frequency response curves of the main system with different ${\kern 1pt} \varepsilon$.

It can be observed from Fig. 29 that when ${\kern 1pt} \varepsilon {\kern 1pt}$ is 0.21, there is obviously a large response amplitude near the main resonance frequency, which is not conducive to the vibration reduction of the main system. Meanwhile, it is also found that the larger ${\kern 1pt} \varepsilon$, the wider the frequency range of the system resonance. Therefore, a smaller ${\kern 1pt} \varepsilon {\kern 1pt}$ should be selected to obtain a good vibration reduction effect for the main system.

According to the conclusions of Figs. 28 and 29, the damping ratio $\lambda_{3} {/}\lambda_{2}$ is 3.5 and the mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ is 0.1. The amplitude-frequency response curves of the main system with different ${\kern 1pt} \varepsilon {\kern 1pt}$ and stiffness coefficient ${\kern 1pt} k{\kern 1pt}$ are drawn, as shown in Fig. 30:

Fig. 30

Amplitude-frequency response curves with ${\kern 1pt} \varepsilon {\kern 1pt}$ and k change

It can be seen from Fig. 30 that the influence of ${\kern 1pt} \varepsilon {\kern 1pt}$ is the same as above, and it will not be repeated here. When ${\kern 1pt} \varepsilon {\kern 1pt}$ is unchanged, the steady-state response amplitude of the main system gradually decreases with the increase of $\,k$. However, when ${\kern 1pt} k{\kern 1pt}$ is too large, a resonance peak will appear near the resonance frequency, which is not conducive to LN-NES to reduce the vibration of the main system.

In order to further determine the range of $\,k$, 3D and 2D contour maps of different ${\kern 1pt} k{\kern 1pt}$ are drawn in Fig. 31. According to the figure below, when the value of ${\kern 1pt} k{\kern 1pt}$ is greater than 6.9, the steady-state response amplitude of the main system is relatively small, basically at the same height. When the value exceeds 11.8, a resonance peak begins to appear near the resonance frequency, which is not conducive to the system vibration reduction. Therefore, under this set of parameters, the value range of $\,k{\kern 1pt}$ is $(6.9,11.8)$.

Fig. 31

Amplitude-frequency response curves with k change

5 Conclusion

In this study, the bifurcation characteristics and strongly modulated response of the combined damping NES are studied, and the vibration suppression effect of the combined damping NES under different excitation is analyzed.

For the study of bifurcation characteristics, by analyzing the influence of NES parameters on SN bifurcation and Hopf bifurcation, it is found that the smaller the linear damping coefficient ${\kern 1pt} \lambda_{2}$, the larger the mass ratio ${\kern 1pt} \varepsilon {\kern 1pt}$ and the detuning parameter ${\kern 1pt} \sigma$, the larger the area of the system to obtain the three unstable fixed points. Meanwhile, by analyzing the influence of excitation amplitude and excitation frequency on the system response amplitude, It is found that the system is unstable only in the vicinity of $f = 3.2$ and $\sigma = 0$.

For the study of strongly modulated response, by analyzing the slow invariant manifold and phase portrait of the system, it is found that continuous jumps can provide the possibility for the system to have SMR phenomenon. Then, the slow manifold is used to analyze the detuning parameter range of SMR in the system from a numerical perspective, and it is concluded that the detuning parameter interval for the occurrence of SMR in the system is ${[ - 0}{\text{.19,}}{\kern 1pt} {1}{\text{.52]}}$.

For the analysis of vibration reduction performance, On the one hand, the damping effect of the combined damping NES under pulse excitation and harmonic excitation is studied. By analyzing the amplitude and energy spectrum of the main system, it is found that the vibration suppression effect of the combined damping NES is better than that of the linear damping NES and the geometrically nonlinear damping NES. On the other hand, the parameters of the system are optimized by the amplitude-frequency response and the maximum amplitude, and the optimal parameters of the combined damping NES are pointed out.