Dynamic analysis of 1-dof and 2-dof nonlinear energy sink with geometrically nonlinear damping and combined stiffness

Abstract

Nonlinear energy sink (NES) refers to a typical passive vibration device connected to linear or weakly nonlinear structures for vibration absorption and mitigation. This study investigates the dynamics of 1-dof and 2-dof NES with nonlinear damping and combined stiffness connected to a linear oscillator. For the system of 1-dof NES, a truncation damping and failure frequency are revealed through bifurcation analysis using the complex variable averaging method. The frequency detuning interval for the existence of the strongly modulated response (SMR) is also reported. For the system of 2-dof NES, it is reported in a similar bifurcation analysis that the mass distribution between NES affects the maximum value of saddle-node bifurcation. To obtain the periodic solution of the 2-dof NES system with the consideration of frequency detuning, the incremental harmonic balance method (IHB) and Floquet theory are employed. The corresponding response regime is obtained by Poincare mapping, it shows that the responses of the linear oscillator and 2-dof NES are not always consistent, and 2-dof NES can generate extra SMR than 1-dof NES. Finally, the vibration suppression effect of the proposed NES with nonlinear damping, and combined stiffness is analyzed and verified by the energy spectrum, and it also shows that the 2-dof NES system demonstrates better performance.

1 Introduction

The suppression of unwanted vibration has attracted significant attention in various engineering applications for many years. Structural vibration suppression applications can be divided into active, semi-active, passive and hybrid control systems [1,2,3,4]. Passive vibration mitigation devices are popular vibration reduction approaches as they are convenient in practice. A classical passive vibration device is a tuned vibration absorber (TVA) proposed by Frahm [5]. TVA has been widely proved to be simple and efficient to mitigate unwanted vibrations [6, 7]. However, it can only be effective in a narrow frequency range. To effectively dissipate the vibration energy within a wide range of frequencies, Roberson introduced a nonlinear system into TVA, which could be called a nonlinear vibration absorber [8]. A typical nonlinear vibration absorber is the nonlinear energy sink (NES), which is a relatively small and spatially localized nonlinear attachment connected to the primary linear or weakly nonlinear system to play a passive energy absorption role [9, 10]. It is generally considered that nonlinearity is harmful, but most of the studies show that NES is more effective than linear absorbers in suppressing vibration [11,12,13]. NES can passively absorb and dissipate vibrational energy in a wide range of frequencies [14]. NES have received enough attention and research, such as piecewise stiffness, bi-stable NES, and internal rotational NES [15,16,17]. The effectiveness of NES in vibration absorption has been verified by many real engineering systems, such as beams, buildings, and aeroelastic system [18,19,20]. Due to the complexity of real engineering system equations, many scholars simplified the linear main structure into a simple oscillator for theoretical research of discrete model [21,22,23]. In this paper, the discrete model will be applied to conduct related theoretical research on the system with NES. Therefore, the present study will be carried out on corresponding simplified oscillators.

Gendelman et al. [24,25,26] investigated the energy transfer when the main structure of NES was subjected to harmonic excitation, it was found that SMR of the system appeared near the resonance frequency, and SMR can be explained as the jumping of the slow invariant manifold in different stable branches. A further study on the conditions of SMR generation and the vibration suppression effect of NES have been carried out. It is revealed that the generation of SMR requires the system to contain nonlinearity and the ratio of NES to linear main structure is small enough; SMR has a better effect in suppressing vibration than steady-state periodic response [26]. SMR has received extensive attention and researched in Refs. [27,28,29]. It has special advantages in vibration suppression, which also provides a new idea and reference index for optimizing the design of NES [30, 31].

Literature [32] considers the influence of frequency detuning on the vibration suppression of the coupled NES system. It is indicated that the value of the frequency detuning coefficient is related to the existence of SMR; however, no specific expression is given. Some scholars have found that the stiffness of nonlinear vibration absorbers is not purely cubic; they believe that the combined stiffness of some nonlinear vibration absorbers is more realistic [33,34,35]. However, their research is not thorough enough.

Despite the fruitful success that has been achieved in previous studies on NES, most studies only consider the stiffness nonlinearity of NES and the damping nonlinearity is received less attention. Starosvetsky and Gendelman studied the nonlinear damping NES system with piecewise quadratic characteristics and drawn that nonlinear damping can eliminate the unwanted periodic response near the main resonance frequency of the system [36]. Andersen revealed that a system coupled with geometrically nonlinear damping NES could lead to dynamical instability [37]. Some studies also considered the effects of energy exchange and amplitude decay caused by nonlinear damping [38, 39]. In general, most NES studies have ignored the effect of nonlinear damping. However, nonlinear damping plays an important role in suppressing the vibration of the system through the research of these scholars. In the research of nonlinear damping NES, most of them considered only the case of 1-dof NES to suppress system vibration.

Therefore, in light of the research achievements and existing drawbacks of previous scholars. In order to be more in line with engineering reality and consider more comprehensive, this study focuses on the analysis of the dynamic behavior of the system with nonlinear damping and combined stiffness NES considering frequency detuning under harmonic excitation. By analyzing the bifurcation and SMR of the system with NESs, and comparing the energy of different structural systems, the effects of the system frequency detuning, nonlinear damping and combined stiffness are shown. The effect of 2-dof NES on the system response regimes and vibration suppression is also paid special attention. The structure of the study is as follows: Section 2 introduces the dynamics of the linear oscillator coupled with 1-dof NES, which mainly analyzes its bifurcation and SMR, while considering the influence of frequency detuning. Section 3 investigates the bifurcation of the linear oscillator with 2-dof NES. First, the same method as 1-dof NES is applied for response analysis, and then, the response of the overall model is further analyzed by IHB. In addition, the numerical simulation is also utilized to study the relevant modulation response. In Sect. 4, the applications of 1-dof and 2-dof NES systems in vibration suppression are introduced. The main concluding remarks of this paper are summarized in Sect. 5.

Fig. 1

Model diagram of the linear oscillator with 1-dof NES

2 Dynamic analysis of a linear oscillator with a 1-dof NES under harmonic forcing

2.1 Research on system mathematical model

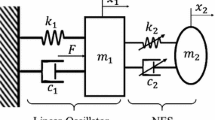
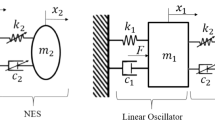
The system model is a linear oscillator with 1-dof NES as depicted in Fig. 1. Where $k_{nl}$ is composed of linear stiffness $k_{21}$ and nonlinear stiffness $k_{23}$, $c_2$ represents the nonlinear damping of the NES [40], letting $F = F_0 cos(wt)$. The simplified system equation is expressed as

$$\begin{aligned} \begin{aligned}&{{{\ddot{x}}}_{1}}+{{x}_{1}}+\varepsilon {{k}_{221}}({{x}_{1}}-{{x}_{2}})+\varepsilon {{k}_{223}}{{({{x}_{1}}-{{x}_{2}})}^{3}} \\&\quad +\varepsilon \lambda {{({{{{\dot{x}}}}_{1}}-{{{\dot{x}}}_{2}})}^{3}}=\varepsilon A\cos (wt) \\&\quad {{{\ddot{x}}}_{2}}+{{k}_{221}}({{x}_{2}}-{{x}_{1}})+{{k}_{223}}{{({{x}_{2}}-{{x}_{1}})}^{3}}\\&\quad +\lambda {{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})}^{3}}=0 \end{aligned} \end{aligned}$$

(1)

Two assumptions in Eq. (1) should be emphasized here. Firstly, it is assumed in this system that $0<\varepsilon \ll 1$, which means the NES is lightweight compared to the linear oscillator. Secondly, as a matter of 1:1 resonance condition, the frequency of the harmonic excitation is assumed to be at the near neighborhood of the eigenfrequency of the linear oscillator in the order of $\varepsilon ^1$, setting $w = 1+\varepsilon \delta$, where $\delta$ stands for the frequency detuning parameter [41], u and v represent the displacement of the center of the system mass and the relative displacement between the linear oscillator and NES, as shown in Eq. (2). By substituting Eqs. (2) into (1), we can derive Eq. (3).

$$\begin{aligned}&u={{x}_{1}}+\varepsilon {{x}_{2}},v={{x}_{1}}-{{x}_{2}} \end{aligned}$$

(2)

$$\begin{aligned}&\ddot{u}+\frac{u+\varepsilon v}{1+\varepsilon }=\varepsilon A\cos (1+\varepsilon \delta )t \nonumber \\&\ddot{v}+(1+\varepsilon ){{k}_{221}}v+(1+\varepsilon ){{k}_{223}}{{v}^{3}} +\lambda (1+\varepsilon ){{{\dot{v}}}^{3}} \nonumber \\&\ +\frac{u+\varepsilon v}{1+\varepsilon }=\varepsilon A\cos (1+\varepsilon \delta )t \end{aligned}$$

(3)

This study uses the complex variable averaging method to approximate the system dynamics, by making the following complex variable changes

$$\begin{aligned} {{\varphi }_{1}}{{e}^{i(1+\varepsilon \delta )t}}=\dot{u}+iu,{{\varphi }_{2}}{{e}^{i(1+\varepsilon \delta )t}}=\dot{v}+iv \end{aligned}$$

(4)

we could obtain the slow flow equation of the research system as

$$\begin{aligned} \begin{aligned}&{{{\dot{\varphi }}}_{1}}+i\varepsilon \delta {{\varphi }_{1}}+\frac{i\varepsilon }{2(1+\varepsilon )}({{\varphi }_{1}}-{{\varphi }_{2}})=\frac{\varepsilon A}{2} \\&{{{\dot{\varphi }}}_{2}}+i\varepsilon \delta {{\varphi }_{2}}+\frac{i}{2(1+\varepsilon )}({{\varphi }_{2}}-{{\varphi }_{1}}) +\frac{{{\varphi }_{2}}}{8}(3|{{\varphi }_{2}}{{|}^{2}}\lambda \\&\quad -4i{{k}_{221}}-3i{{k}_{223}}|{{\varphi }_{20}}{{|}^{2}}i)(1+\varepsilon )=\frac{\varepsilon A}{2} \end{aligned} \end{aligned}$$

(5)

2.2 Bifurcation analysis

By substituting fixed point ${{\varphi }_{10}}$ and ${{\varphi }_{20}}$ into Eq. (5), we can derive

$$\begin{aligned} \begin{aligned}&i\varepsilon \delta {{\varphi }_{10}}+\frac{i\varepsilon }{2(1+\varepsilon )}({{\varphi }_{10}}-{{\varphi }_{20}})=\frac{\varepsilon A}{2} \\&i\varepsilon \delta {{\varphi }_{20}}+\frac{i}{2(1+\varepsilon )}({{\varphi }_{20}}-{{\varphi }_{10}})+\frac{{{\varphi }_{20}}}{8}(3|{{\varphi }_{20}}{{|}^{2}}\lambda \\&\quad -4i{{k}_{221}}-3i{{k}_{223}}|{{\varphi }_{20}}{{|}^{2}})(1+\varepsilon )=\frac{\varepsilon A}{2} \end{aligned} \end{aligned}$$

(6)

Eq. (6) could be rewritten as

$$\begin{aligned} \begin{aligned}&\frac{9({{\lambda }^{2}}+k_{223}^{2})}{16}|{{\varphi }_{20}}{{|}^{6}}+\frac{3}{2}{{k}_{223}}({{k}_{221}}-2\delta M)|{{\varphi }_{20}}{{|}^{4}}\\&\quad +{{(2\delta M-{{k}_{221}})}^{2}}|{{\varphi }_{20}}{{|}^{2}}={{A}^{2}}{{M}^{2}} \end{aligned} \end{aligned}$$

(7)

with $M = (2\varepsilon \delta +1)/(2\varepsilon \delta + 2\delta +1)$, Eq. (7) can be expressed as

$$\begin{aligned} {{\alpha }_{0}}+{{\alpha }_{1}}Z+{{\alpha }_{2}}{{Z}^{2}}+{{\alpha }_{3}}{{Z}^{3}}=0 \end{aligned}$$

(8)

where ${{\alpha }_{1}} = ((2\delta M-k_{221})/M)^2, {{\alpha }_{2}} = (3k_{223}(k_{221}-2\delta M))/(2{M}^2 ), {{\alpha }_{3}} = (9({{\lambda }^{2}}+k_{223}^{2}))/(16 {{M}^{2}} ), {{\alpha }_{0}} = -A^2,$ $Z = |{{\varphi }_{20}}{{|}^{2}}.$ Taking the derivative of Eq. (8) with respect to Z leads to

$$\begin{aligned} {{\alpha }_{1}}+2{{\alpha }_{2}}Z+3{{\alpha }_{3}}{{Z}^{2}}=0 \end{aligned}$$

(9)

eliminating Z from Eqs. (8) and (9), one has

$$\begin{aligned} \begin{aligned} {{\alpha }_{0}}=&-{{\alpha }_{1}}(-\frac{{{\alpha }_{2}}}{3{{\alpha }_{3}}}\pm \frac{\sqrt{\alpha _{2}^{2}-3{{\alpha }_{1}}{{\alpha }_{3}}}}{3{{\alpha }_{3}}})-{{\alpha }_{2}}\left( -\frac{{{\alpha }_{2}}}{3{{\alpha }_{3}}}\right. \\&\left. \pm \frac{\sqrt{\alpha _{2}^{2}-3{{\alpha }_{1}}{{\alpha }_{3}}}}{3{{\alpha }_{3}}}\right) ^{2}\\&- {{\alpha }_{3}}{{(-\frac{{{\alpha }_{2}}}{3{{\alpha }_{3}}}\pm \frac{\sqrt{\alpha _{2}^{2}-3{{\alpha }_{1}}{{\alpha }_{3}}}}{3{{\alpha }_{3}}})}^{3}} \end{aligned} \end{aligned}$$

(10)

Equation (10) gives an equation of the form $A = f(\lambda ,\delta )$, which can represent the saddle-node bifurcation boundary curve on the $[\lambda , A]$ plane; the parameters are selected as $\varepsilon = 0.1, k_1 = 1/3, k_3 = 4/3$ [14, 25, 35], as shown in Fig. 2.

Fig. 2

Saddle-node bifurcation for $\delta = 3$

In Fig. 2, the shape of the saddle-node bifurcation boundary curve is approximately triangular and the $[\lambda ,A]$ plane is divided into two parts to determine the number of the real periodic solutions. Spot checks are performed on different areas in Fig. 2. According to Fig. 2, for $\lambda ~ =~ 0.3, A = 1.3$ falls within the region of the three real periodic solutions. However, for the parameters outside this area region, for example, choosing $\lambda = 0.3, A = 1.8$ or $\lambda = 0.3, A = 0.5,$ only one real solution is defined.

Then, we study the influence of the frequency detuning coefficient on the saddle-node bifurcation; the diagram for different $\delta$ is described in Fig. 3. It is obvious from Fig. 3, for $\delta > 0$, with the increase of $\delta$ the maximum value of A gradually increases, when $-3.35 \le \delta <0$, with the decreases of $\delta$ the maximum value of A progressively decreases. For $\delta = 0$ or $\delta < -3.35$, the saddle-node bifurcation does not exist.

Fig. 3

Saddle-node bifurcation diagram with $\delta$ change

All saddle-node bifurcation shapes in the above study are triangular-like. The right vertices of each saddle-node bifurcation curve are on the same line damping line, which is about $\lambda =0.77$. After this damping is exceeded, the saddle-node bifurcation boundary line vanished and the number of the real periodic solution is unique. We call this value truncation damping and record it as $\lambda _t$; its value is as follows:

$$\begin{aligned} {{\lambda }_{\text { }t}}=\frac{\sqrt{3}}{3}{{k}_{223}} \end{aligned}$$

(11)

From Eq. (11), it can be noted that $\lambda _t$ is proportional to $k_{223}$, we can adjust the size of $\lambda _t$ by selecting different $k_{223}$ and adjust the range of the saddle-node bifurcation curve area. In this study, we use the Hopf bifurcation to determine the stability of the periodic solution. Considering the perturbation motion of the dynamic system near the fixed point, letting

$$\begin{aligned} {{\varphi }_{1}}={{\varphi }_{10}}+{{o}_{1}},\text { }{{\varphi }_{2}}={{\varphi }_{20}}+{{o}_{2}} \end{aligned}$$

(12)

substituting into the slow flow Eq. (5), we have

$$\begin{aligned} \begin{aligned} {{{\dot{o}}}_{1}}&=-i\varepsilon \delta {{o}_{1}}-\frac{i\varepsilon }{2(1+\varepsilon )}({{o}_{1}}-{{o}_{2}}) \\ \dot{o}_{1}^{*}&=i\varepsilon \delta o_{1}^{*}+\frac{i\varepsilon }{2(1+\varepsilon )}(o_{1}^{*}-o_{2}^{*}) \\ {{{\dot{o}}}_{2}}&=-i\varepsilon \delta {{o}_{2}}-\frac{i}{2(1+\varepsilon )}({{o}_{2}}-{{o}_{1}})-\frac{1+\varepsilon }{8}(3(2{{o}_{2}}|{{\varphi }_{20}}{{|}^{2}} \\&\quad +o_{2}^{*}\varphi _{20}^{2})\lambda -4i{{k}_{221}}{{o}_{2}}-3i{{k}_{223}}(2{{o}_{2}}|{{\varphi }_{20}}{{|}^{2}}+o_{2}^{*}\varphi _{20}^{2})) \\ \dot{o}_{2}^{*}&=i\varepsilon \delta o_{2}^{*}+\frac{i}{2(1+\varepsilon )}(o_{2}^{*}-o_{1}^{*})-\frac{1+\varepsilon }{8}(3(2o_{2}^{*}|{{\varphi }_{20}}{{|}^{2}} \\&\quad +{{o}_{2}}\varphi {{_{20}^{*}}^{2}})\lambda +4i{{k}_{221}}o_{2}^{*}+3i{{k}_{223}}(2o_{2}^{*}|{{\varphi }_{20}}{{|}^{2}}+{{o}_{2}}\varphi {{_{20}^{*}}^{2}})) \\ \end{aligned} \end{aligned}$$

(13)

The characteristic polynomial of Eq. (13) can be expressed as

$$\begin{aligned} {{\mu }^{4}}+{{\gamma }_{1}}{{\mu }^{3}}+{{\gamma }_{2}}{{\mu }^{2}}+{{\gamma }_{3}}\mu +{{\gamma }_{4}}=0 \end{aligned}$$

(14)

where $\mu$ is the eigenvalues, and the coefficient ${{\gamma }_{i}} (i =1,\ldots ,4)$ are given as

$$\begin{aligned} \begin{aligned} {{\gamma }_{1}}&=\frac{3\lambda (1+\varepsilon )}{2}Z \\ {{\gamma }_{2}}&=\varepsilon \delta -\frac{{{k}_{221}}}{2}+\frac{\varepsilon k_{221}^{2}}{2}+\frac{k_{221}^{2}}{4}+\frac{{{\varepsilon }^{2}}k_{221}^{2}}{4}\text {+}2{{\varepsilon }^{2}}{{\delta }^{2}}\\&\quad + \frac{9{{(1+\varepsilon )}^{2}}(k_{223}^{2}+{{\lambda }^{2}})}{16}{{Z}^{2}}-{{k}_{221}}\varepsilon \delta -\frac{9{{\lambda }^{2}}{{Z}^{2}}}{64} \\&\quad +\frac{3{{k}_{223}}({{k}_{221}}+2\varepsilon {{k}_{221}}-2\varepsilon \delta +{{\varepsilon }^{2}}{{k}_{221}}-2{{\varepsilon }^{2}}\delta -1)}{4}Z \\&\quad -{{\varepsilon }^{2}}\delta {{k}_{221}}-\frac{9k_{223}^{2}\varepsilon {{Z}^{2}}}{32}-\frac{9\varepsilon {{\lambda }^{2}}{{Z}^{2}}}{32}-\frac{9k_{223}^{2}{{Z}^{2}}}{64}\\&\quad -\frac{9{{\varepsilon }^{2}}k_{223}^{2}{{Z}^{2}}}{64}-\frac{9{{\varepsilon }^{2}}{{\lambda }^{2}}{{Z}^{2}}}{64}+\frac{1}{4} \\ {{\gamma }_{3}}&=\frac{3\varepsilon \lambda (4{{\varepsilon }^{2}}{{\delta }^{2}}+4\varepsilon {{\delta }^{2}}+4\varepsilon \delta +1)}{8}Z \\ {{\gamma }_{4}}&={{\varepsilon }^{2}}{{({{k}_{221}}-2\delta +2{{k}_{221}}\delta -4{{\delta }^{2}}\varepsilon +2{{k}_{221}}\delta \varepsilon )}^{2}}/16 \\&\quad +27{{Z}^{2}}{{\varepsilon }^{2}}(k_{223}^{2}+{{\lambda }^{2}}){{(2\delta +2\delta \varepsilon +1)}^{2}}/256 \\&\quad +3{{k}_{223}}Z{{\varepsilon }^{2}}(2\delta +2\delta \varepsilon +1)({{k}_{221}}-2\delta +2{{k}_{221}}\delta \\&\quad -4{{\delta }^{2}}\varepsilon +2{{k}_{221}}\delta \varepsilon )/16 \end{aligned} \end{aligned}$$

(15)

where

$$\begin{aligned} Z=|{{\varphi }_{20}}{{|}^{2}},\text { }{{Z}^{2}}=\varphi _{20}^{2}\varphi {{_{20}^{*}}^{2}} \end{aligned}$$

(16)

When the Hopf bifurcation occurs, the fixed point passes through the positive and negative imaginary axes of the complex plane; this implies

$$\begin{aligned} \mu = \pm i\varOmega \end{aligned}$$

(17)

By substituting Eqs. (17) into (14), we can yield

$$\begin{aligned} {{\varOmega }^{4}}-{{\gamma }_{2}}{{\varOmega }^{2}}+{{\gamma }_{4}}=0,\text { }\varOmega ({{\gamma }_{1}}{{\varOmega }^{2}}-{{\gamma }_{3}})=0 \end{aligned}$$

(18)

Then, eliminating $\varOmega$ in the above equation, we have

$$\begin{aligned} {{\nu }_{1}}{{Z}^{2}}+{{\nu }_{2}}Z+{{\nu }_{3}}=0 \end{aligned}$$

(19)

the coefficient ${{\nu }_{i}}(i =1,2,3)$ are shown as

$$\begin{aligned} \begin{aligned} {{\nu }_{1}}&=-\frac{243\varepsilon {{\lambda }^{2}}(\varepsilon +1)(k_{223}^{2}+{{\lambda }^{2}})}{1024} \\ {{\nu }_{2}}&=-\frac{27{{k}_{223}}\varepsilon {{\lambda }^{2}}(1+\varepsilon )({{k}_{221}}+{{k}_{221}}\varepsilon -4\varepsilon \delta -1)}{64} \\ {{\nu }_{3}}&=-\frac{9\varepsilon {{\lambda }^{2}}{{({{k}_{221}}+{{k}_{221}}\varepsilon -4\varepsilon \delta -1)}^{2}}}{64} \end{aligned} \end{aligned}$$

(20)

Furthermore, solving Eq. (19) to get

$$\begin{aligned} {{Z}_{1,2}}=\frac{-{{\nu }_{2}}\pm \sqrt{\nu _{2}^{2}-4{{\nu }_{1}}{{\nu }_{3}}}}{2{{\nu }_{1}}} \end{aligned}$$

(21)

From Eq. (8), the boundary of the stable region of the Hopf bifurcation is given by

$$\begin{aligned} {{\alpha }_{0}}+{{\alpha }_{1}}{{Z}_{i}}+{{\alpha }_{2}}{{Z}_{i}}^{2}+{{\alpha }_{3}}{{Z}_{i}}^{3}=0 \end{aligned}$$

(22)

The saddle-node bifurcation and Hopf bifurcation of the system are presented in Fig. 4. The solid line represents the Hopf bifurcation and the dashed line represents the saddle-node bifurcation; it can also be observed that they coexist in certain regions.

Fig. 4

Saddle-node bifurcation and Hopf bifurcation for $\delta =3, \varepsilon =0.1, {k_{221}}=1/3, {k_{223}}=4/3$

Fig. 5

Amplitude response for $\delta =3, \varepsilon =0.1, {k_{221}}=1/3, {k_{223}}=4/3, \lambda =0.3, {N_{20}} = |{{\varphi }_{20}}{{|}}$, solid line: stable branch, asterisk: unstable branch

Fig. 6

Frequency response for $A=1, \varepsilon =0.1, {k_{221}}=1/3, {k_{223}}=4/3, \lambda =0.3, {N_{20}} = |{{\varphi }_{20}}{{|}}$, solid line: stable branch, asterisk: unstable branch

The amplitude response and frequency response of the system are shown in Figs. 5 and  6; meanwhile, the stability of the solution of random check parameters is also analyzed. According to Fig. 5, with the increase of A, the fixed point is first in a stable state, then turn to an unstable state, and finally back to a stable state. According to Fig. 6, the difference between Figs. 6 and  5 is that it contains a peak of the stable state in the unstable state. The peak value makes NES lose its effect on the vibration suppression of the system; therefore, it should be avoided as much as possible in the practical application of NES. The frequency that causes the failure of NES vibration reduction is called the failure frequency, and the interval to which it belongs is called the failure interval where it is $\delta \in [-0.75,-0.49]$ in Fig. 6.

2.3 SMR analysis for the system with 1-dof NES

Based on the research results of Starosvetsky and Gendelman, the combination of essential nonlinearity and strong mass asymmetry brings about a possible response mechanism called SMR [24,25,26]. SMR is different from the steady-state and weakly modulated response under the condition of 1:1 resonance, and has a better performance in suppressing vibration. The goal of this section is to determine the range of frequency detuning coefficients where SMR exists. Equation (5) can be reduced to a function of ${{\varphi }_{2}}$ as follows:

$$\begin{aligned} \begin{aligned}&{{{\ddot{\varphi }}}_{2}}+\frac{d}{dt}[\frac{i(4\varepsilon \delta +1)}{2}{{\varphi }_{2}}+\frac{1\text {+}\varepsilon }{8}(3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}{{\varphi }_{2}}i\\&\quad -3{{k}_{223}}{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}i)]+{{\varphi }_{2}}[ \frac{i\varepsilon (2\delta +2\varepsilon \delta +1)}{16}(3{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda \\&\quad -4{{k}_{221}}i-3{{k}_{223}}{{\left| {{\varphi }_{2}} \right| }^{2}}i)-\frac{\varepsilon \delta (2\varepsilon \delta +1)}{2}]-\frac{i\varepsilon A}{4}(1\\&\quad +2\varepsilon \delta )=0 \end{aligned} \end{aligned}$$

(23)

Since this study assumes that $\varepsilon ( 0 < \varepsilon \ll 1)$ is sufficiently small, the multi-scale method can be used to solve Eq. (23). Defining

$$\begin{aligned} \begin{aligned} {{\varphi }_{2}}&={{\varphi }_{2}}({{t}_{0}},{{t}_{1}},\cdot \cdot \cdot ),{{t}_{m}}={{\varepsilon }^{m}}t,m=0,1,\cdot \cdot \cdot \\ D&={{D}_{0}}+\varepsilon {{D}_{1}}+\cdot \cdot \cdot =\frac{\partial }{\partial {{t}_{0}}}+\varepsilon \frac{\partial }{\partial {{t}_{1}}}+\cdot \cdot \cdot =\frac{d}{dt} \\ \end{aligned} \end{aligned}$$

(24)

By substituting Eqs. (24) into (23) and separating the $\varepsilon ^0, \varepsilon ^1$ order scale, we can get

$$\begin{aligned} \begin{aligned}&{{\varepsilon }^{0}}:\text { }D_{0}^{2}{{\varphi }_{2}}+{{D}_{0}}(\frac{3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}{{\varphi }_{2}}i-3{{k}_{223}}{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}i}{8}\\&\quad +\frac{i{{\varphi }_{2}}}{2})=0 \\&{{\varepsilon }^{1}}:{{D}_{0}}(2\delta {{\varphi }_{2}}i+\frac{3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}{{\varphi }_{2}}i-3{{k}_{223}}{{\left| {{\varphi }_{2}} \right| }^{2}}i}{8}) \\&\quad +{{D}_{1}}(\frac{i}{2}{{\varphi }_{2}}+\frac{3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}{{\varphi }_{2}}i-3{{k}_{223}}{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}i}{8}) \\&\quad +\frac{{{\varphi }_{2}}(2\delta +1)i}{16}(3{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}i-3{{k}_{223}}{{\left| {{\varphi }_{2}} \right| }^{2}}i)\\&\quad -\frac{\delta }{2}{{\varphi }_{2}}-\frac{iA}{4}+\text { }2{{D}_{0}}{{D}_{1}}{{\varphi }_{2}}=0 \\ \end{aligned} \end{aligned}$$

(25)

Furthermore, by integrating the equation of ${{\varepsilon }^{0}}$ order respect to ${t_0}$, we could obtain

$$\begin{aligned} \begin{aligned}&{{D}_{0}}{{\varphi }_{2}}+\frac{3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}{{\varphi }_{2}}i-3{{k}_{223}}{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}i}{8}\\&\quad +\frac{i{{\varphi }_{2}}}{2}=C({{t}_{1}},\cdot \cdot \cdot ) \end{aligned} \end{aligned}$$

(26)

Since the derivative at the fixed point is zero, Eq. (25) only considers two independent variables $t_0, t_1$. Then, Eq. (26) is reformulated as

$$\begin{aligned} \frac{i{{\varphi }_{2}}}{2}+\frac{3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}{{\varphi }_{2}}i-3{{k}_{223}}{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}i}{8}=C({{t}_{1}}) \end{aligned}$$

(27)

Hence, ${\varphi }_{2}$ is only a function of $t_1$, setting

$$\begin{aligned} {\varphi }_{2} = N(t_1)e^{i\theta (t_1)} \end{aligned}$$

(28)

substituting Eqs. (28) into (27), one has

$$\begin{aligned} \left( \frac{iN}{2}+\frac{3{{N}^{3}}\lambda -4{{k}_{221}}Ni-3{{k}_{223}}{{N}^{3}}i}{8}\right) {{e}^{i\theta }}=C \end{aligned}$$

(29)

Taking the magnitude of Eq. (29), letting $Z = N^2$, Eq. (29) could be rewritten as

$$\begin{aligned} \begin{aligned}&\frac{9}{16}({{\lambda }^{2}}+k_{223}^{2}){{Z}^{3}}-\frac{3}{2}{{k}_{223}}(1-{{k}_{221}}){{Z}^{2}}\\&\quad +{{(1-{{k}_{221}})}^{2}}Z=4{{\left| C \right| }^{2}} \end{aligned} \end{aligned}$$

(30)

Then, taking the derivative of Z on both sides of Eq. (30), one can derive

$$\begin{aligned} \begin{aligned}&\frac{27}{16}({{\lambda }^{2}}+k_{223}^{2}){{Z}^{2}}-3{{k}_{223}}(1-{{k}_{221}})Z \\&\quad +{{(1-{{k}_{221}})}^{2}}=0 \end{aligned} \end{aligned}$$

(31)

The roots of Eq. (31) are as follows:

$$\begin{aligned} \begin{aligned}&{{Z}_{1,2}}=\frac{4(2{{k}_{223}}\mp \sqrt{k_{223}^{2}-3{{\lambda }^{2}}})(1-{{k}_{221}})}{9({{\lambda }^{2}}+k_{223}^{2})}\\&\Rightarrow {{N}_{1,2}}=\sqrt{\frac{4(2{{k}_{223}}\mp \sqrt{k_{223}^{2}-3{{\lambda }^{2}}})(1-{{k}_{221}})}{9({{\lambda }^{2}}+k_{223}^{2})}} \end{aligned} \end{aligned}$$

(32)

At the jumping point, Eq. (30) can be described as

$$\begin{aligned} \begin{aligned}&\frac{9}{16}({{\lambda }^{2}}+k_{223}^{2}){{Z}_{1,2}}^{3}-\frac{3}{2}{{k}_{223}}(1-{{k}_{221}}){{Z}_{1,2}}^{2}\\&\quad +{{(1-{{k}_{221}})}^{2}}{{Z}_{1,2}}=\frac{9}{16}({{\lambda }^{2}}+k_{223}^{2}){{Z}_{u,d}}^{3}\\&\quad -\frac{3}{2}{{k}_{223}}(1-{{k}_{221}}){{Z}_{u,d}}^{2}+{{(1-{{k}_{221}})}^{2}}{{Z}_{u,d}} \\ \end{aligned} \end{aligned}$$

(33)

The solutions of Eq. (33) are given by

$$\begin{aligned} \begin{aligned}&{{Z}_{u,d}}=\frac{8({{k}_{223}}\pm \sqrt{k_{223}^{2}-3{{\lambda }^{2}}})(1-{{k}_{221}})}{9({{\lambda }^{2}}+k_{223}^{2})}\\&\Rightarrow {{N}_{u,d}}=\sqrt{\frac{8({{k}_{223}}\pm \sqrt{k_{223}^{2}-3{{\lambda }^{2}}})(1-{{k}_{221}})}{9({{\lambda }^{2}}+k_{223}^{2})}} \end{aligned} \end{aligned}$$

(34)

Equation (30) defines the slow invariant manifold (SIM) of the system on the $(N,4{{\left| C \right| }^{2}})$ plane shown in Fig. 7. The dashed line with an arrow indicates the trajectory for the jumps from one stable branch of the SIM to another. $N_u$ and $N_d$ are the jumping target points on the SIM with the same value of C as $N_1$ and $N_2$. One of the trajectories of the system is to run from the left stable branch to $N_1$, then jump to $N_u$ and continue to move on the right stable branch. Similarly, the other starts at point $N_2$ on the right stable branch, then jumps to $N_d$ and continues at the left stable branch. The jump between different stable branches provides conditions for the existence of SMR and is also the most important mechanism to produce SMR.

Fig. 7

SIM projection for $\lambda =0.3, {k_{221}}=1/3, {k_{223}}=4/3$, solid line: stable branch, dashed line: unstable branch

Equation (25) continued to be analyzed at the $\varepsilon ^1$ order, taking $t_0 \rightarrow +\infty$, we have

$$\begin{aligned} \begin{aligned}&{{D}_{1}}\left( \frac{i}{2}{{\varphi }_{2}}+\frac{1}{8}(3{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -3{{k}_{223}}{{\varphi }_{2}}{{\left| {{\varphi }_{2}} \right| }^{2}}i\right. \\&\left. \quad -4{{k}_{221}}{{\varphi }_{2}}i)\right) -\frac{\delta }{2}{{\varphi }_{2}} +\frac{{{\varphi }_{2}}(2\delta +1)i}{16}(3{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda \\&\quad -4{{k}_{221}}i-3{{k}_{223}}{{\left| {{\varphi }_{2}} \right| }^{2}}i)-\frac{iA}{4}=0 \end{aligned} \end{aligned}$$

(35)

Letting

$$\begin{aligned} \begin{aligned}&M=\frac{iA}{4}-\frac{{{\varphi }_{2}}(2\delta +1)i}{16}(3{{\left| {{\varphi }_{2}} \right| }^{2}}\lambda -4{{k}_{221}}i\\&\quad -3{{k}_{223}}{{\left| {{\varphi }_{2}} \right| }^{2}}i)+\frac{\delta }{2}{{\varphi }_{2}} \end{aligned} \end{aligned}$$

(36)

Equation (35) can be simplified as

$$\begin{aligned} \begin{aligned}&\frac{\partial {{\varphi }_{2}}}{\partial {{t}_{1}}}\left( \frac{1-{{k}_{221}}}{2}i+\frac{3(\lambda -{{k}_{223}}i)}{4}{{\left| {{\varphi }_{2}} \right| }^{2}}\right) \\&\quad +\frac{3(\lambda -{{k}_{223}}i)}{8}{{\varphi }_{2}}^{2}\frac{\partial \varphi _{2}^{\text {*}}}{\partial {{t}_{1}}}=M \end{aligned} \end{aligned}$$

(37)

Taking the complex conjugate and making substitution to Eq. (37), it can be written as

$$\begin{aligned} \begin{aligned} \frac{\partial {{\varphi }_{2}}}{\partial {{t}_{1}}}&=\{M(-2(1-{{k}_{221}})i+3(\lambda +{{k}_{223}}i){{\left| {{\varphi }_{2}} \right| }^{2}})\\&\quad \ -\frac{3}{2}(\lambda -{{k}_{223}}i)\varphi _{2}^{2}{{M}^{*}}\}/\{[{{(1-{{k}_{221}})}^{2}} \\&\quad -3{{\left| {{\varphi }_{2}} \right| }^{2}}(1-{{k}_{221}}){{k}_{223}}]+\frac{27}{16}({{\lambda }^{2}}+k_{223}^{2}){{\left| {{\varphi }_{2}} \right| }^{4}}\} \end{aligned} \end{aligned}$$

(38)

By substituting Eqs. (28) into (37) and Eq. (38), we can derive

$$\begin{aligned} \begin{aligned} \frac{\partial N}{\partial {{t}_{1}}}+iN\frac{\partial \theta }{\partial {{t}_{1}}}&=\{M{{e}^{-i\theta }}(-2(1-{{k}_{221}})i+3(\lambda \\&\quad +{{k}_{223}}i){{N}^{2}})\\&\quad -\frac{3}{2}(\lambda -{{k}_{223}}i){{N}^{2}}{{e}^{i\theta }}{{M}^{*}}\}/\{[{{(1-{{k}_{221}})}^{2}}\\&\quad -3{{N}^{2}}(1-{{k}_{221}}){{k}_{223}}]+\frac{27}{16}({{\lambda }^{2}}+k_{223}^{2}){{N}^{4}}\} \\ M{{e}^{-i\theta }}&=-\frac{3(2\delta +1)}{16}(\lambda i+{{k}_{223}}){{N}^{3}}+\frac{iA}{4}{{e}^{-i\theta }}\\&\quad -\frac{[{{k}_{221}}(2\delta +1)-2\delta ]}{4}N \\ {{M}^{*}}{{e}^{i\theta }}&=\frac{3(2\delta +1)}{16}(\lambda i-{{k}_{223}}){{N}^{3}}-\frac{iA}{4}{{e}^{i\theta }}\\&\quad -\frac{[{{k}_{221}}(2\delta +1)-2\delta ]}{4}N\\ \end{aligned} \end{aligned}$$

(39)

Furthermore, Eq. (39) can be simplified as

$$\begin{aligned} \begin{aligned} G(N)\frac{\partial N}{\partial {{t}_{1}}}=&\frac{-3\lambda {{N}^{3}}}{4}+A(1-{{k}_{221}})\cos \theta \\&+\frac{3A{{N}^{2}}(\lambda \sin \theta -{{k}_{223}}\cos \theta )}{4} \\ G(N)\frac{\partial \theta }{\partial {{t}_{1}}}=&-\frac{27(2\delta +1)({{\lambda }^{2}}+k_{223}^{2}){{N}^{4}}}{16}\\&+\frac{9AN(\lambda \cos \theta +{{k}_{223}}\sin \theta )}{4}\\&-\frac{A(1-{{k}_{221}})\sin \theta }{N} \\&+\frac{[(2\delta +1)(3{{k}_{223}}-12{{k}_{221}}{{k}_{223}})+18{{k}_{223}}\delta ]{{N}^{2}}}{4} \\&+[{{k}_{221}}(2\delta +1)-2\delta ](1-{{k}_{221}}) \\ \end{aligned} \end{aligned}$$

(40)

where

$$\begin{aligned} \begin{aligned} G(N)=&2[{{(1-{{k}_{221}})}^{2}}-3{{N}^{2}}(1-{{k}_{221}}){{k}_{223}}\\&\ +\frac{27}{16}({{\lambda }^{2}}+k_{223}^{2}){{N}^{4}}] \end{aligned} \end{aligned}$$

(41)

When $G(N) = 0$, the fold lines occur. Thus, in order to avoid singularities, Eq. (40) can be rescaled as

$$\begin{aligned} \begin{aligned} N'&=\frac{-3\lambda {{N}^{3}}}{4}+\frac{3A{{N}^{2}}(\lambda \sin \theta -{{k}_{223}}\cos \theta )}{4}\\&\quad +A(1-{{k}_{221}}\cos \theta ) \\ \theta '&=-\frac{27(2\delta +1)({{\lambda }^{2}}+k_{223}^{2}){{N}^{4}}}{16}+[{{k}_{221}}(2\delta +1)\\&\quad -2\delta ](1-{{k}_{221}})+\frac{9AN(\lambda \cos \theta +{{k}_{223}}\sin \theta )}{4}\\&\quad +\frac{[(2\delta +1)(3{{k}_{223}}-12{{k}_{221}}{{k}_{223}})+18{{k}_{223}}\delta ]{{N}^{2}}}{4} \\&\quad -\frac{A(1-{{k}_{221}})\sin \theta }{N} \\ \end{aligned} \end{aligned}$$

(42)

The phase portraits of the system, as seen in Fig. 8, can be described by numerical integration of Eq. (42). The phase portraits show stable trajectories on the SIM. Arrows denote the direction of the trajectories with time increase. The two horizontal lines at $N_1$ and $N_2$ in the phase trajectory represent the twofold lines in the SIM. $\theta _1$ and $\theta _2$ denote the initial phase angle; the value can be given by solving $\theta ' = 0$.

Fig. 8

Phase portraits of the SIM with $\delta$ varying for $\lambda =0.3, A=1, {k_{221}}=1/3, {k_{223}}=4/3$

Each case has its own characteristics in Fig. 8. According to Fig. 8b, the lower phase trajectory starts from the phase angle interval $[\theta _1,\theta _2]$ on the $N_1$ horizontal line, then moves downwards on the left and right sides, and finally can return to the $N_1$ horizontal line and jump to the upper branch to continue the movement. There are some phase trajectories near $\theta _1$ that cannot return to the horizontal line in Fig. 8a; this phenomenon also occurs near $\theta _2$ in Fig. 8c. The reason is that attractors appear in the stable branch of the system, and the partial phase trajectories converging to the attractor instead of the horizontal line. From inspection of Fig. 8d, the phase trajectory starting from the phase angle interval $[\theta _1,\theta _2]$ on the horizontal line of $N_1$ only moves downward to the left; it finally can return to the horizontal line of $N_1$ and jump to the upper branch. This phenomenon means that the movement of the phase trajectory can move unilaterally and not only move both sides simultaneously

All phase trajectories in the lower part of Fig. 8 start moving downward from the initial interval $[\theta _1,\theta _2]$, and mostly arrive at $N_1$. Then, the phase trajectories jump to the upper branch of the phase portraits, along with the upper trajectory move to the $N_2$. Finally, the phase trajectories jump to the initial interval $[\theta _1,\theta _2]$ of the $N_1$. In this process, the amplitude of the system is constantly changing, which provides the possibility for the emergence of SMR. The phase angle interval $[\theta _1,\theta _2]$ is also called the jump interval. On the one hand, the jump process between different stable branches is unstable and complicated. On the other hand, a complete jump process starts and ends within the jump interval. Therefore, to simplify the jumping process, a 1-D mapping from the defined jump interval to itself can be used. In this process, the frequency detuning interval for generating SMR is determined.

From Eq. (29), the phase angle of the fixed point can be expressed as

$$\begin{aligned} \arg C=\theta +{{\tan }^{-1}}\left( \frac{4-4{{k}_{221}}-3{{k}_{223}}Z}{3\lambda Z}\right) \end{aligned}$$

(43)

According to the SIM, the C values at $N_1$ and $N_u$, $N_2$ and $N_d$ are, respectively, equal, and the following relationship can be obtained

$$\begin{aligned} \begin{aligned} {{\theta }_{u,d}}&={{\theta }_{1,2}}+{{\tan }^{-1}}\left( \frac{4-4{{k}_{221}}-3{{k}_{223}}{{Z}_{1,2}}}{3\lambda {{Z}_{1,2}}}\right) \\&\quad -{{\tan }^{-1}}\left( \frac{4-4{{k}_{221}}-3{{k}_{223}}{{Z}_{u,d}}}{3\lambda {{Z}_{u,d}}}\right) \end{aligned} \end{aligned}$$

(44)

The 1-D mapping for various values of $\delta$ is illustrated in Fig. 9. It should be noted from Fig. 9 that the 1-D mapping trajectory of a jumping process in the jumping interval is represented by a straight line with an arrow and the interval in which SMR exists is $\delta \in [-10.04, 6.90]$ by varying $\delta$ value until the 1-D mapping disappears. We change the value of A to obtain the $\delta$ interval where SMR exists, as demonstrated in Table 1.

Fig. 9

1-D mapping with $\delta$ varying from −10.04 to 6.90 for $\lambda =0.3, A=1, {k_{221}}=1/3, {k_{223}}=4/3$

Table 1 The $\delta$ interval where SMR exists with varying A

According to Table 1, the start coordinates of the $\delta$ interval where SMR exists decrease with the increase of A, and the approximate linear trend is $y = -9.8754x - 0.8308$. The end coordinates increase with the increase of A; the approximate linear trend is $y = 4.972x + 1.9112$. The length of the interval increases with the increase of A, and the approximate linear trend is $y = 14.847x + 2.742$. It is worth mentioning that the existence interval of SMR obtained by 1-D mapping is only a necessary condition. Whether the specific SMR exists needs to be determined in combination with the dynamic response.

Fig. 10

System model of coupled with 2-dof NES

3 Dynamic analysis of a linear oscillator with a 2-dof NES under harmonic forcing

3.1 Description of considered system mathematical model

The system model considered in this section is a linear oscillator with 2-dof NES as shown in Fig. 10. The relationship among the mass of oscillators could be denoted as

$$\begin{aligned} \frac{{{m}_{2}}}{{{m}_{1}}}=\varepsilon \eta ,\frac{{{m}_{3}}}{{{m}_{1}}}=\varepsilon (1-\eta ) \end{aligned}$$

(45)

Carrying out a similar transformation as in the second section, the dimensionless form equation of the model considered in this section can be expressed as

$$\begin{aligned} \begin{aligned}&{{{\ddot{x}}}_{1}}+{{x}_{1}}+\varepsilon {{k}_{221}}({{x}_{1}}-{{x}_{2}})+\varepsilon {{k}_{223}}{{({{x}_{1}}-{{x}_{2}})}^{3}}\\&\quad +\varepsilon {{\lambda }_{1}}{{({{{\dot{x}}}_{1}}-{{{\dot{x}}}_{2}})}^{3}}=\varepsilon A\cos (wt) \\&\eta {{{\ddot{x}}}_{2}}+{{k}_{221}}({{x}_{2}}-{{x}_{1}})+{{k}_{223}}{{({{x}_{2}}-{{x}_{1}})}^{3}}+{{\lambda }_{1}}{{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})}^{3}} \\&\quad +{{k}_{331}}({{x}_{2}}-{{x}_{3}})+{{k}_{333}}{{({{x}_{2}}-{{x}_{3}})}^{3}}\\&\quad +{{\lambda }_{2}}{{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{3}})}^{3}}=0 \\&(1-\eta ){{{\ddot{x}}}_{3}}+{{k}_{331}}({{x}_{3}}-{{x}_{2}})+{{k}_{333}}{{({{x}_{3}}-{{x}_{2}})}^{3}}\\&\quad +{{\lambda }_{2}}{{({{{\dot{x}}}_{3}}-{{{\dot{x}}}_{2}})}^{3}}=0 \end{aligned} \end{aligned}$$

(46)

3.2 Analysis without considering frequency detuning

Let $w = 1$ and ${{\dot{x}}_{i}}+i{{x}_{i}}={{\psi }_{i}}{{e}^{it}}$, Eq. (46) can be written as

$$\begin{aligned} \begin{aligned}&{{{\dot{\psi }}}_{1}}-\frac{\varepsilon {{k}_{221}}{{\psi }_{u}}}{2}+\frac{3\varepsilon {{\left| {{\psi }_{u}} \right| }^{2}}{{\psi }_{u}}({{\lambda }_{1}}-{{k}_{223}}i)}{8}=\frac{\varepsilon A}{2} \\&{{{\dot{\psi }}}_{u}}+\frac{3{{\left| {{\psi }_{u}} \right| }^{2}}{{\psi }_{u}}(1+\varepsilon \eta )({{\lambda }_{1}}-{{k}_{223}}i)}{8\eta }\\&\quad -\frac{{{\psi }_{1}}-{{\psi }_{u}}}{2}i-\frac{(1+\varepsilon \eta ){{k}_{221}}{{\psi }_{u}}}{2\eta }i+\frac{{{k}_{331}}{{\psi }_{v}}}{2\eta }i \\&\quad -\frac{3{{\left| {{\psi }_{v}} \right| }^{2}}{{\psi }_{v}}({{\lambda }_{2}}-{{k}_{333}}i)}{8\eta }=\frac{\varepsilon A}{2} \\&{{{\dot{\psi }}}_{v}}+\frac{{{\psi }_{v}}}{2}i-\frac{3{{\left| {{\psi }_{u}} \right| }^{2}}{{\psi }_{u}}({{\lambda }_{1}}-{{k}_{223}}i)}{8\eta }+\frac{{{k}_{221}}{{\psi }_{u}}}{2\eta }i\\&\quad -\frac{{{k}_{331}}{{\psi }_{v}}}{2\eta (1-\eta )}i+\frac{3{{\left| {{\psi }_{v}} \right| }^{2}}{{\psi }_{v}}({{\lambda }_{2}}-{{k}_{333}}i)}{8\eta (1-\eta )}=0 \end{aligned} \end{aligned}$$

(47)

where ${{\psi }_{u}}={{\psi }_{1}}-{{\psi }_{2}},{{\psi }_{v}}={{\psi }_{2}}-{{\psi }_{3}}$. By substituting the fixed point, Eq. (47) could be rewritten as

$$\begin{aligned} \begin{aligned}&-{{k}_{221}}{{\psi }_{u}}i+\frac{3{{\left| {{\psi }_{u}} \right| }^{2}}{{\psi }_{u}}({{\lambda }_{1}}-{{k}_{223}}i)}{4}=A \\&i\eta {{\psi }_{v}}-\frac{{{k}_{331}}{{\psi }_{v}}}{1-\eta }i+\frac{3{{\left| {{\psi }_{v}} \right| }^{2}}{{\psi }_{v}}({{\lambda }_{2}}-{{k}_{333}}i)}{4(1-\eta )}=A \\&{{\psi }_{1}}i-{{\psi }_{u}}i-(1-\eta ){{\psi }_{v}}i=A \end{aligned} \end{aligned}$$

(48)

The first equation of Eq. (48) is the same as the 1-dof NES bifurcation equation when $\delta = 0$, which the saddle-node bifurcation does not exist according to the previous analysis. Analyzing the third equation of Eq. (48), we should note that the value of ${{\psi }_{1}}$ corresponds to the value of ${{\psi }_{u}}$ and ${{\psi }_{v}}$. Therefore, the number of fixed points in the system is determined by the second equation of Eq. (48). Further simplifying the second equation of Eq. (48), one has

$$\begin{aligned} \begin{aligned}&\frac{9(k_{333}^{2}+\lambda _{2}^{2}){{Z}^{3}}}{16{{(1-\eta )}^{2}}}+\frac{3{{k}_{333}}({{\eta }^{2}}-\eta +{{k}_{331}}){{Z}^{2}}}{2{{(1-\eta )}^{2}}}\\&\quad +({{\eta }^{2}}+\frac{2{{\eta }^{2}}{{k}_{331}}-2\eta {{k}_{331}}+k_{331}^{2}}{{{(1-\eta )}^{2}}})Z={{A}^{2}} \end{aligned} \end{aligned}$$

(49)

where $Z = {{\left| {{\psi }_{v}} \right| }^{2}}$ , the Cardano discriminant is used to determine the number of roots of Eq.(49), which can be described as

$$\begin{aligned} \begin{aligned} \varDelta&={{(\frac{q}{2})}^{2}}+{{(\frac{p}{3})}^{3}} \\ q&=\frac{128{{k}_{333}}(k_{333}^{2}+9\lambda _{2}^{2}){{({{\eta }^{2}}-\eta +{{k}_{331}})}^{3}}}{729{{(k_{333}^{2}+\lambda _{2}^{2})}^{3}}}\\&\quad +\frac{16{{A}^{2}}{{(\eta -1)}^{2}}}{9{{(k_{333}^{2}+\lambda _{2}^{2})}^{2}}} \\ p&=-\frac{16(k_{333}^{2}-3\lambda _{2}^{2}){{({{\eta }^{2}}-\eta +{{k}_{331}})}^{2}}}{27{{(k_{333}^{2}+\lambda _{2}^{2})}^{2}}} \end{aligned} \end{aligned}$$

(50)

The number of roots of Eq. (49) can be obtained from the discriminant: when $\varDelta < 0$, the equation has three unequal real roots. When $\varDelta > 0$, the equation has three roots, one of which is a real root and two are conjugate imaginary roots. According to the analysis of the discriminant, the saddle-node bifurcation boundary curve appears when $\varDelta = 0$. The saddle-node bifurcation with different values of $\eta$ is depicted in Fig. 11. The system with 2-dof NES selects parameters in Refs. [14, 25, 35].

Fig. 11

The saddle-node bifurcation with different values of $\eta$ in the $[\lambda _{2}, A]$ plane

From inspection of Fig. 11, the saddle-node bifurcation exists in the system with 2-dof NES, which is different from the 1-dof NES system. The 1-dof and 2-dof NES saddle-node bifurcations are similar in shape, and both of them have truncation damping. The 2-dof NES truncation damping $\lambda _{t2}$ can be expressed as

$$\begin{aligned} {{\lambda }_{t2}}=\frac{\sqrt{3}}{3}{{k}_{333}} \end{aligned}$$

(51)

In Fig. 11, for $\eta < 0.6$, the maximum value of A increases with the increase of $\eta$, and A reaches the maximum value when $\eta = 0.6$. For $\eta > 0.6$, the maximum value of A decreases as $\eta$ increases. Analyzing the stability of the fixed point and performing perturbation motion of the dynamic system near the fixed point, letting

$$\begin{aligned} {{\psi }_{1}}={{\psi }_{10}}+{{\varDelta }_{1}},\text { }{{\psi }_{u}}={{\psi }_{u0}}+{{\varDelta }_{u}},\text { }{{\psi }_{v}}={{\psi }_{v0}}+{{\varDelta }_{v}} \end{aligned}$$

(52)

and substituting Eqs. (52) into (47), we have

$$\begin{aligned} {{{\dot{\varDelta }}}_{1}}&=\frac{\varepsilon {{k}_{221}}{{\varDelta }_{u}}}{2}i-\frac{3\varepsilon }{8}(2{{\varDelta }_{u}}{{\left| {{\psi }_{u0}} \right| }^{2}}+\varDelta _{u}^{*}\psi _{u0}^{2})({{\lambda }_{1}}-{{k}_{223}}i) \nonumber \\ \dot{\varDelta }_{1}^{*}&=\frac{-\varepsilon {{k}_{221}}\varDelta _{u}^{*}}{2}i-\frac{3\varepsilon }{8}(2\varDelta _{u}^{*}{{\left| {{\psi }_{u0}} \right| }^{2}}+{{\varDelta }_{u}}\psi {{_{u0}^{*}}^{2}})({{\lambda }_{1}}+{{k}_{223}}i) \nonumber \\ {{{\dot{\varDelta }}}_{u}}&=\frac{({{\varDelta }_{1}}-{{\varDelta }_{u}})}{2}i-\frac{(1+a\varepsilon ){{k}_{221}}{{\varDelta }_{u}}}{2a}i-\frac{{{k}_{331}}{{\varDelta }_{v}}}{2a}i\nonumber \\&\quad -\frac{3(1+a\varepsilon )}{8a}(2{{\varDelta }_{u}}{{\left| {{\psi }_{u0}} \right| }^{2}}+\varDelta _{u}^{*}\psi _{u0}^{2})({{\lambda }_{1}}-{{k}_{223}}i) \nonumber \\&\quad +\frac{3({{\lambda }_{2}}-{{k}_{333}}i)}{8a}(2{{\varDelta }_{v}}{{\left| {{\psi }_{v0}} \right| }^{2}}+\varDelta _{v}^{*}\psi _{v0}^{2}) \nonumber \\ \dot{\varDelta }_{u}^{*}&=-\frac{(\varDelta _{1}^{*}-\varDelta _{u}^{*})}{2}i+\frac{(1+a\varepsilon ){{k}_{221}}\varDelta _{u}^{*}}{2a}i+\frac{{{k}_{331}}\varDelta _{v}^{*}}{2a}i\nonumber \\&\quad -\frac{3(1+a\varepsilon )}{8a}(2\varDelta _{u}^{*}{{\left| {{\psi }_{u0}} \right| }^{2}}+{{\varDelta }_{u}}\psi {{_{u0}^{*}}^{2}})({{\lambda }_{1}}+{{k}_{223}}i) \nonumber \\&\quad +\frac{3({{\lambda }_{2}}+{{k}_{333}}i)}{8a}(2\varDelta _{v}^{*}{{\left| {{\psi }_{v0}} \right| }^{2}}+{{\varDelta }_{v}}\psi {{_{v0}^{*}}^{2}}) \nonumber \\ {{{\dot{\varDelta }}}_{v}}&=-\frac{{{\varDelta }_{v}}}{2}i-\frac{{{k}_{221}}{{\varDelta }_{u}}}{2a}i+\frac{{{k}_{331}}{{\varDelta }_{v}}}{2a(1-a)}i+\frac{3}{8a}(2{{\varDelta }_{u}}{{\left| {{\psi }_{u0}} \right| }^{2}}\nonumber \\&\quad +\varDelta _{u}^{*}\psi _{u0}^{2})({{\lambda }_{1}}-{{k}_{223}}i) -\frac{3({{\lambda }_{2}}-{{k}_{333}}i)}{8a(1-a)}(2{{\varDelta }_{v}}{{\left| {{\psi }_{v0}} \right| }^{2}}\nonumber \\&\quad +\varDelta _{v}^{*}\psi _{v0}^{2}) \nonumber \\ \dot{\varDelta }_{v}^{*}&=\frac{\varDelta _{v}^{*}}{2}i+\frac{{{k}_{221}}\varDelta _{u}^{*}}{2a}i-\frac{{{k}_{331}}\varDelta _{v}^{*}}{2a(1-a)}i+\frac{3}{8a}(2\varDelta _{u}^{*}{{\left| {{\psi }_{u0}} \right| }^{2}}\nonumber \\&\quad +{{\varDelta }_{u}}\psi {{_{u0}^{*}}^{2}})({{\lambda }_{1}}+{{k}_{223}}i)-\frac{3({{\lambda }_{2}}+{{k}_{333}}i)}{8a(1-a)}(2\varDelta _{v}^{*}{{\left| {{\psi }_{v0}} \right| }^{2}}\nonumber \\&\quad +{{\varDelta }_{v}}\psi {{_{v0}^{*}}^{2}}) \end{aligned}$$

(53)

The characteristic polynomial of Eq. (53) can be written as

$$\begin{aligned} {{\mu }^{6}}+{{\gamma }_{1}}{{\mu }^{5}}+{{\gamma }_{2}}{{\mu }^{4}}+{{\gamma }_{3}}{{\mu }^{3}}+{{\gamma }_{4}}{{\mu }^{2}}+{{\gamma }_{5}}\mu +{{\gamma }_{6}}=0 \end{aligned}$$

(54)

where $\mu$ is the eigenvalues, and ${{\gamma }_{i}} (i = 1,2,\ldots ,6)$ are the calculation coefficients.

Fig. 12

The saddle-node and Hopf bifurcation of 2-dof NES, solid line: saddle-node bifurcation, dot line: Hopf bifurcation

In Fig. 12, $W^s$ and $W^u$ are applied to denote the stable region and the unstable region. There are three parts of the unstable region in Fig. 12, which are located in the upper part of the figure, the saddle-node bifurcation, and the upper part of the saddle-node bifurcation. Therefore, the three different real roots of the saddle-node bifurcation are almost unstable. By comparing with the Hopf bifurcation of 1-dof NES, the Hopf bifurcation of 2-dof NES has no boundary.

Fig. 13

Amplitude response for $\eta = 0.6, \varepsilon = 0.1, \lambda _1 = 0.3, {k_{221}} = 0.133, {k_{223}} = 1.333, {k_{331}} = 0.133, {k_{333}} = 1.333$, ${N_{v0}}~ = ~|{{\psi }_{v0}}{{|}}$

In this section, we choose two values of $\lambda _{2}$, one of which is less than $\lambda _{t2}$ and the other is greater than $\lambda _{t2}$. The amplitude response of the system is shown in Fig. 13. According to Fig. 13, the number of fixed points is different with different $\lambda _{2}$. When A is greater than a certain value and continues to increase, the system will be in an unstable state.

3.3 Application of incremental harmonic balance method for response analysis

In the previous section, the analytical method was carried out to analyze the dynamic characteristics of the system at $w =1$. This section will study the dynamic characteristics of the system when the frequency of excitation changes. Since IHB is simple and effective in solving such problems, IHB is applied to analyze the dynamic characteristics of the system when the excitation frequency changes in this section.

Letting $\tau = wt$, Eq. (46) can be rewritten as

$$\begin{aligned} {{w}^{2}}{\bar{{{\varvec{M}}}}}{\ddot{{{\varvec{X}}}}}+{{w}^{3}}{{\bar{{{\varvec{C}}}}}_{{{\varvec{N}}}}}{\dot{{{\varvec{X}}}}}+({\bar{{{\varvec{K}}}}}+{{{\bar{{{\varvec{K}}}}}_{{{\varvec{N}}}}}}){\varvec{X}}={\bar{{{\varvec{F}}}}}\cos \tau \end{aligned}$$

(55)

where

$$\begin{aligned} \begin{aligned} {\varvec{X}}&=\left[ \begin{array}{l} {{x}_{1}} \\ {{x}_{2}} \\ {{x}_{3}} \\ \end{array}\right] \text {, }{\bar{{{\varvec{M}}}}}=\left[ \begin{array}{l} \frac{1}{\varepsilon }\text { } \\ \text { }\quad \eta \\ \text { }\qquad 1-\eta \\ \end{array}\right] ,\text { } {\bar{{{\varvec{F}}}}}=\left[ \begin{array}{l} A \\ 0 \\ 0 \\ \end{array}\right] ,\\ {\bar{{{\varvec{K}}}}}&=\left[ \begin{array}{l} \frac{1}{\varepsilon }+{{k}_{221}}\text { }\quad -{{k}_{221}}\text { }\qquad 0\\ -{{k}_{221}}\text { }\quad {{k}_{221}}+{{k}_{331}}\text { }\quad -{{k}_{331}} \\ \text { 0 }\qquad \qquad -{{k}_{331}}\text { }\qquad {{k}_{331}} \\ \end{array}\right] \\ {{L}_{1}}&={{x}_{1}}-{{x}_{2}}, {{L}_{2}}={{x}_{2}}-{{x}_{3}},\\ \text { }{{\bar{{\varvec{C}}}}_{{\varvec{N}}}}&=\left[ \begin{array}{l} {{\lambda }_{1}}{{{{\dot{L}}}_{1}}^{2}}\text { } \qquad \quad -{{\lambda }_{1}}{{{{\dot{L}}}_{1}}^{2}}\text { }\qquad \qquad 0 \\ -{{\lambda }_{1}}{{{{\dot{L}}}_{1}}^{2}}\text { } \quad {{\lambda }_{1}}{{{{\dot{L}}}_{1}}^{2}}+{{\lambda }_{2}}{{{{\dot{L}}}_{2}}^{2}}\text { }\quad -{{\lambda }_{2}}{{{{\dot{L}}}_{2}}^{2}} \\ \text { }0\text { }\qquad \qquad \quad -{{\lambda }_{2}}{{{{\dot{L}}}_{2}}^{2}}\text { }\qquad \quad {{\lambda }_{2}}{{{{\dot{L}}}_{2}}^{2}} \\ \end{array}\right] \\ {{\bar{{\varvec{K}}}}_{{\varvec{N}}}}&=\left[ \begin{array}{l} {{k}_{223}}{{{L}_{1}}^{2}}\text { }\qquad \quad -{{k}_{223}}{{{L}_{1}}^{2}}\qquad \qquad \qquad \text { 0} \\ -{{k}_{223}}{{{L}_{1}}^{2}}\text {}\quad {{k}_{223}}{{{L}_{1}}^{2}}\text {+}{{k}_{\text {33}3}}{{{L}_{2}}^{2}}\text {}\quad -{{k}_{333}}{{{L}_{2}}^{2}} \\ \text { }0\text { }\quad \qquad \quad \quad \; -{{k}_{333}}{{{L}_{2}}^{2}}\text { }\qquad \qquad {{k}_{333}}{{{L}_{2}}^{2}} \\ \end{array}\right] \end{aligned} \end{aligned}$$

(56)

The first step of IHB is the incremental process, let $\varvec{X_0}$, $w_0$ and ${\bar{{{\varvec{F}}}}_\mathbf{0 }}$ be a set of solutions of Eq. (55), then the incremental form of neighboring states can be expressed as follows:

$$\begin{aligned} {\varvec{X}}={{{{{\varvec{X}}}}_{\mathbf{0 }}}}+\varDelta {\varvec{X}}, w={{w}_{0}}+\varDelta w, \bar{{\varvec{F}}}={{{\bar{{{\varvec{F}}}}}_{\mathbf{0 }}}}+\varDelta {\varvec{F}} \end{aligned}$$

(57)

Substituting Eqs. (57) into (55) and omitting the high-order small terms, we have

$$\begin{aligned} \begin{aligned}&w_{0}^{2}{\bar{{{\varvec{M}}}}}\varDelta {\ddot{{{\varvec{X}}}}}+3w_{0}^{3}{{{\bar{C}}}_{N0}}\varDelta {\dot{{\varvec{X}}}}+({\bar{{{\varvec{K}}}}}+3{{\bar{{\varvec{K}}}}_{{\varvec{N}}{} \mathbf{0}}})\varDelta {\varvec{X}}\\&\quad =\bar{{\varvec{R}}}-(2{{w}_{0}}{\bar{{{\varvec{M}}}}}{{\ddot{{{\varvec{X}}}}}_{\mathbf{0 }}}+3w_{0}^{2}{{{{\bar{{{\varvec{C}}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}{{{\dot{{{\varvec{X}}}}}}_{\mathbf{0 }}}})\varDelta w+\varDelta {\varvec{F}}\cos \tau \\ \end{aligned} \end{aligned}$$

(58)

with

$$\begin{aligned} \begin{aligned} {\bar{{{\varvec{R}}}}}&={{{{\bar{{{\varvec{F}}}}}}_{\mathbf{0 }}}}\cos \tau -w_{0}^{2} {\bar{{{\varvec{M}}}}{{{\ddot{{{\varvec{X}}}}}}_{\mathbf{0 }}}}-w_{0}^{3}{{{{\bar{{{\varvec{C}}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}{{{\dot{{{\varvec{X}}}}}}_{\mathbf{0 }}}}-({\bar{{{\varvec{K}}}}}+{{\bar{{\varvec{K}}}}_{{\varvec{N}}{} \mathbf{0}}}){{{{{\varvec{X}}}}_{\mathbf{0 }}}} \\ {{\bar{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}}&={{\bar{{\varvec{C}}}}_{{\varvec{N}}}}({{{{{\varvec{X}}}}_{\mathbf{0 }}}}),\text { }{{\bar{{\varvec{K}}}}_{{\varvec{N}}{} \mathbf{0}}}={{{{{\varvec{K}}}}_{{{\varvec{N}}}}}} ({{{{{\varvec{X}}}}_{\mathbf{0 }}}}) \end{aligned} \end{aligned}$$

(59)

It can be concluded from the expression of ${\bar{{{\varvec{R}}}}}$ that when ${{{{{\varvec{X}}}}_{\mathbf{0 }}}}$, $w_0$ and ${{{\bar{{{\varvec{F}}}}}_{\mathbf{0 }}}}$ are precise solutions, one has ${\bar{{{\varvec{R}}}}} = 0$. The second step of IHB is the process of harmonic balance; the periodic solution of Eq. (55) is assumed to be

$$\begin{aligned} \begin{aligned} {{x}_{j}}&=\sum \limits _{k=1}^{n}{{{a}_{jk}}\cos (2k-1)\tau +\sum \limits _{k=1}^{n}{{{b}_{jk}}\sin (2k-1)\tau =\varvec{B{{D}_{j}}}}} \\ \varDelta {{x}_{j}}&=\sum \limits _{k=1}^{n}\varDelta {{a}_{jk}}\cos (2k-1)\tau \\&\quad +\sum \limits _{k=1}^{n}\varDelta {{b}_{jk}}\sin (2k-1)\tau \\&={\varvec{B}}\varDelta {{{{{\varvec{D}}}}_{{{\varvec{j}}}}}} \end{aligned} \end{aligned}$$

(60)

where

$$\begin{aligned} \begin{aligned} {\varvec{B}}&=[\cos \tau ,\cos 3\tau ,...,\sin \tau ,\sin 3\tau ,...] \\ {{{{{\varvec{D}}}}_{{{\varvec{j}}}}}}&={{[{{a}_{j1}},{{a}_{j2}},...,{{a}_{jn}},{{b}_{j1}},{{b}_{j2}},...,{{b}_{jn}}]}^{T}} \\ \varDelta {{{{{\varvec{D}}}}_{{{\varvec{j}}}}}}&={{[\varDelta {{a}_{j1}},...,\varDelta {{a}_{jn}},\varDelta {{b}_{j1}},...,\varDelta {{b}_{jn}}]}^{T}} \end{aligned} \end{aligned}$$

(61)

Equation (60) can be described in matrix form as

$$\begin{aligned} {{{{{\varvec{X}}}}_{\mathbf{0 }}}}=\varvec{SD},\text { }\varDelta {\varvec{X}}={\varvec{S}}\varDelta {\varvec{D}} \end{aligned}$$

(62)

with

$$\begin{aligned} \begin{aligned} {\varvec{D}}&=[{{{{{\varvec{D}}}}_{{{\varvec{1}}}}}}\text {,}{{{{{\varvec{D}}}}_{{{\varvec{2}}}}}},\text { }...\text { }, {{{{{\varvec{D}}}}_{{{\varvec{n}}}}}}],{\varvec{S}}=[{\varvec{B}};{\varvec{B}};\text { }...\text { };{\varvec{B}}]\\ \varDelta {\varvec{D}}&=[\varDelta {{{{{\varvec{D}}}}_{{{\varvec{1}}}}}}\text {,}\varDelta {{{{{\varvec{D}}}}_{{{\varvec{2}}}}}},\text { }...\text { },\varDelta {{{{{\varvec{D}}}}_{{{\varvec{n}}}}}}] \end{aligned} \end{aligned}$$

(63)

Inserting Eqs. (62) into Eq. (58) and employing the following integral

$$\begin{aligned} \begin{aligned}&\int _{0}^{2\pi }\delta {{(\varDelta {\varvec{X}})}^{T}}[w_{0}^{2}{\bar{{{\varvec{M}}}}}\varDelta {\ddot{{{\varvec{X}}}}}+3w_{0}^{3}{{\bar{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}}\varDelta {\dot{{\varvec{X}}}}+({\bar{{{\varvec{K}}}}}\\&\quad +3{{\bar{{\varvec{K}}}}_{{\varvec{N}}{} \mathbf{0}}})\varDelta {\varvec{X}}]d\tau \text { }=\int _{0}^{2\pi }\delta {{(\varDelta {\varvec{X}})}^{T}}[{\bar{{{\varvec{R}}}}}\\&\quad -(2{{w}_{0}}{\bar{{{\varvec{M}}}}{{{\ddot{{{\varvec{X}}}}}}_{\mathbf{0 }}}}+3w_{0}^{2} {{{{\bar{{{\varvec{C}}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}{{{\dot{{{\varvec{X}}}}}}_{\mathbf{0 }}}})\varDelta w+\varDelta {\varvec{F}}\cos \tau ]d\tau \\ \end{aligned} \end{aligned}$$

(64)

one can be simplified as

$$\begin{aligned} {{{{{\varvec{K}}}}_{{{\varvec{mc}}}}}}\varDelta {\varvec{D}}={\varvec{R}}+ {{{{{\varvec{R}}}}_{{{\varvec{mc}}}}}}\varDelta w + {{{{{\varvec{R}}}}_{{{\varvec{f}}}}}}\varDelta {\varvec{F}} \end{aligned}$$

(65)

where

$$\begin{aligned} \begin{aligned} {{{{{\varvec{K}}}}_{{{\varvec{mc}}}}}}&=w_{0}^{2}{\varvec{M}}+3w_{0}^{3}{{{{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}+{\varvec{K}}+3 {{{{{\varvec{K}}}}_{{{\varvec{N}}{} \mathbf{0}}}}},\\ {{{{{\varvec{R}}}}_{{{\varvec{mc}}}}}}&=(-2{{w}_{0}}{\varvec{M}}+3w_{0}^{2} {{{{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}){\varvec{D}}, \\ {\varvec{R}}&={\varvec{F}}-(w_{0}^{2}{\varvec{M}}+w_{0}^{3} {{{{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}+ {\varvec{K}}+ {{{{{\varvec{K}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}){\varvec{D}},\\ {{{{{\varvec{R}}}}_{{{\varvec{f}}}}}}&=\int _{0}^{2\pi } {{{{{{\varvec{S}}}}^{{{\varvec{T}}}}}}}\cos \tau d\tau , {{{{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}=\int _{0}^{2\pi } {{{{{{\varvec{S}}}}^{{{\varvec{T}}}}}{{{\bar{{{\varvec{C}}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}\dot{{{\varvec{S}}}}}}d\tau ,\\ {\varvec{F}}&=\int _{0}^{2\pi }{{{{{{\varvec{S}}}}^{{{\varvec{T}}}}}{{{\bar{{{\varvec{F}}}}}}_{\mathbf{0 }}}}}\cos \tau d\tau ,\text { }{\varvec{M}}=\int _{0}^{2\pi } {{{{{{\varvec{S}}}}^{{{\varvec{T}}}}}{{{\bar{{{\varvec{C}}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}\ddot{{{\varvec{S}}}}}}d\tau ,\\ {\varvec{K}}&=\int _{0}^{2\pi } {{{{{{\varvec{S}}}}^{{{\varvec{T}}}}}\bar{{{\varvec{K}}}} {{\varvec{S}}}}}d\tau , {{{{{\varvec{K}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}=\int _{0}^{2\pi } {{{{{{\varvec{S}}}}^{{{\varvec{T}}}}}{{{\bar{{{\varvec{K}}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}{{\varvec{S}}}}d\tau \end{aligned} \end{aligned}$$

(66)

This study considers the frequency response of the system under a fixed external excitation amplitude. Hence, Eq.  (65) becomes

$$\begin{aligned} {{{{{\varvec{K}}}}_{{{\varvec{mc}}}}}}\varDelta {\varvec{D}}={\varvec{R}}+ {{{{{\varvec{R}}}}_{{{\varvec{mc}}}}}}\varDelta w \end{aligned}$$

(67)

The frequency response of the system is drawn in Fig. 14, where $D_1$ is the amplitude of the linear structure, $D_{21}$ is the amplitude of the first-order NES relative to the linear structure, and $D_{32}$ is the amplitude of the second-order NES relative to the first-order NES.

Fig. 14

Frequency response of the system for $\eta = 0.6, \varepsilon = 0.1, \lambda _1 = 0.3, \lambda _2 = 0.3, {k_{221}} = 0.133, {k_{223}} = 1.333,$ ${k_{331}} =~ 0.133, {k_{333}} = 1.333, A = 0.3$

In Fig. 14, the saddle-node bifurcation exists in the system near $w = 1$. The three frequency response curves are bent after they intersect, which shows hard characteristic nonlinearity. The curve bending phenomenon is extremely prominent in the linear oscillator, and the upward trend of amplitude is significantly reduced. To this extent, it can be demonstrated that the 2-dof NES system has a vibration suppression effect near the resonance frequency.

Then, the stability of the periodic solution of the system is studied by applying the multivariable Floquet theory. $\varvec{X_0}$ is set as the solution, and the perturbations near it can be derived

$$\begin{aligned} {\varvec{X}}={{{{{\varvec{X}}}}_{\mathbf{0 }}}}+\varDelta {\varvec{X}} \end{aligned}$$

(68)

By implementing the same simplification process as Eqs. (58, 55) can be reformulated as

$$\begin{aligned} {{w}^{2}}{\bar{{{\varvec{M}}}}}\varDelta {\ddot{{{\varvec{X}}}}}+3{{w}^{3}} {{{\bar{{{\varvec{C}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}}\varDelta {\dot{{\varvec{X}}}}+({\bar{{{\varvec{K}}}}}+3 {{{\bar{{{\varvec{K}}}}}_{{{\varvec{N}}{} \mathbf{0}}}}})\varDelta {\varvec{X}}=0 \end{aligned}$$

(69)

According to Floquet theory, Eq. (69) yields

$$\begin{aligned} {\dot{{\varvec{X}}}}={\varvec{Q}}(\tau ){\varvec{X}} \end{aligned}$$

(70)

with

$$\begin{aligned} \begin{aligned} {\varvec{X}}&=\left[ \begin{array}{l} \varDelta {\varvec{X}} \\ \varDelta {\dot{{\varvec{X}}}} \\ \end{array}\right] ,\text { }{\varvec{Q}}(\tau )=\left[ \begin{array}{l} {\varvec{0}}\text { }\quad {\varvec{I}} \\ {{{\varvec{Q}}}_{{\varvec{21}}}}\text { }{{{\varvec{Q}}}_{{\varvec{22}}}} \\ \end{array}\right] \\ {{{\varvec{Q}}}_{{\varvec{21}}}}&=\frac{-1}{{{w}^{2}}}{{{{\bar{{{\varvec{M}}}}}}}^{-{{\varvec{1}}}}}(\bar{{\varvec{K}}}+3{{\bar{{\varvec{K}}}}_{{\varvec{N}}{} \mathbf{0}}}),\\ {{{\varvec{Q}}}_{{\varvec{22}}}}&=-3w{{\bar{{\varvec{M}}}}^{-{{\varvec{1}}}}}{{\bar{{\varvec{C}}}}_{{{\varvec{N}}{} \mathbf{0}}}} \\ \end{aligned} \end{aligned}$$

(71)

where ${\varvec{0}}$, ${\varvec{I}}$ represent the zero matrix and the identity matrix, $\varvec{X_0}$ is a solution with period $T = 2\pi$, therefore, ${\varvec{Q}}(\tau )$ is also a function with period T. For Eq. (70), assuming that there is a fundamental matrix solution ${\varvec{Y}}(\tau )$, since ${\varvec{Q}}(\tau + T) = {\varvec{Q}}(\tau )$, ${\varvec{Y}}(\tau + T)$ is also a solution of Eq. (70), and consequently, the relation between the two solutions can be described as

$$\begin{aligned} {\varvec{Y}}(\tau +T)=\varvec{PY}(\tau ) \end{aligned}$$

(72)

with ${\varvec{P}}$ refers to the transition matrix. Hence, solving the transfer matrix ${\varvec{P}}$ becomes the key to analyze the stability of the system.

In this study, an effective method is implemented to numerically calculate ${\varvec{P}}$. The system period is equally divided into N intervals, for the kth interval $[\tau _k\quad \tau _{k-1}]$, the value of coefficient matrix ${\varvec{Q}}(\tau )$ is approximated by a constant matrix $\varvec{Q_k}$ , and the local transition matrix $\varvec{P_k}$ can be approximately presented in the following form:

$$\begin{aligned} {{{{{\varvec{P}}}}_{{{\varvec{k}}}}}}={{e}^{h{{{{{\varvec{Q}}}}_{{{\varvec{k}}}}}}}}={\varvec{I}}+\sum \limits _{j=1}^{N}{\frac{{{(h {{{{{\varvec{Q}}}}_{{{\varvec{k}}}}})}}^{j}}}{j!}} \end{aligned}$$

(73)

Therefore, the transition matrix ${\varvec{P}}$ can be expressed as

$$\begin{aligned} {\varvec{P}}=\underset{k=1}{\overset{N}{\mathop {\varPi }}}\,{{{{{\varvec{P}}}}_{{{\varvec{k}}}}}} \end{aligned}$$

(74)

Fig. 15

Stability analysis for the frequency response of the linear structure, solid line: stable periodic solutions, asterisk: unstable periodic solutions

The stability of the periodic solution is obtained by studying the spectral radius of the matrix ${\varvec{P}}$; the stability analysis of the linear oscillator is illustrated in Fig. 15. In order to study the response regimes near the main resonance frequency, take $P_1$, $P_2$, $P_3$, and $P_4$ in Fig. 15a, from $w = 1+\varepsilon \delta$, they correspond to $\delta = -0.5$, $\delta = 0$, $\delta = 0.5$, $\delta = 1$, respectively, and Poincare mapping is shown in Fig. 16. From Fig. 15(b), it can be concluded that proper selection of parameters can change the stability region and reduce the linear oscillator amplitude. Figure 15c illustrates that compared with the 1-dof NES, 2-dof NES can eliminate undesired response near the main resonance frequency. Figure 16 indicates that when $\delta = 0.5$ and $\delta = 0$, the responses of the linear oscillator and NES are both periodic. For $\delta = 0.5$, the whole system possesses a chaotic response. When $\delta = 1$, the response of the linear oscillator is chaotic, while the response of NES becomes periodic. In conclusion, the response of linear oscillator and NES can be inconsistent in the 2-dof NES system, which is significantly different from the 1-dof NES system.

Fig. 16

Poincare map for the system with red part refers to the system reaches steady state, $x_1 ,v_1$ : the displacement and velocity of the linear structure, $x_{Nc} ,v_{Nc}$: the displacement and velocity of the center of mass of the NES with two degrees of freedom

3.4 SMR analysis for the system with 2-dof NES

This section studies SMR of the system with 2-dof NES and compares their differences with 1-dof NES. Since the slow invariant manifold equation of the system with 2-dof NES is not solved, the analysis method of 1-dof NES cannot be applied. This section analyzes its numerical simulation results to conduct related SMR research.

As the system with 2-dof NES has rich dynamic phenomena, which provides the possibility for the emergence of SMR. This section investigates whether SMR can exist in a 2-dof NES system when there is no SMR in a 1-dof NES system. To achieve reasonable comparisons, a system composed of 2-dof NES is adopted, the mass distribution $\eta = 1.0$ is applied to represent 1-dof NES, and the initial conditions are zero.

Two examples of time response of the 1-dof and 2-dof NES system are presented as shown in Fig. 17. In Fig. 17a, the response regimes of 1-dof and 2-dof NES systems are the steady-state periodic (no modulation) and strongly modulated, respectively. In Fig. 17b, when the response regime of 1-dof NES system is weakly modulated, while the 2-dof NES system also exhibits strongly modulated. The reason for the above phenomenon could be explained as follows: on the one hand, the occurrence of SMR is strongly related to the dynamical instability of the system. On the other hand, according to the previous analysis in this study, the 2-dof NES can increase the instability near the resonance frequency of the system. Therefore, the system with 2-dof NES could generate additional SMR.

Fig. 17

Time response of the 1-dof and 2-dof NES system, $x_1$: displacement of the linear structure. The parameters of the system: a $\delta = 0.1,\lambda _1 = 0.5, \varepsilon = 0.1, {k_{221}}=0.133, {k_{223}}=1.333, \lambda _2 = 0.3, {k_{331}}=0.133, {k_{333}}=1.333, A = 1.0$ ;(b) $\delta = 0.7,\lambda _1 = 0.5, \varepsilon = 0.1, {k_{221}}=0.133, {k_{223}}=1.333, \lambda _2 = 0.1, {k_{331}}=0.133, {k_{333}}=1.333, A = 0.3$

In order to further verify that the system with 2-dof NES can generate additional SMR and analyze the effect of parameters on the generation of SMR, the response regimes of the1-dof and 2-dof NES system with different parameters are spot-checked in Table 2. The other relevant parameters are selected as $\varepsilon = 0.1, {k_{221}} = 0.133, {k_{223}} = 1.333, {k_{331}} = 0.133,$ ${k_{333}}~=~1.333, \lambda _1~=~0.3$, $\lambda _2~=~0.3$. It is evidently portrayed in Table 2 that the 2-dof NES can bring extra SMR. Most of these system response regimes are consistent; it implies that the mechanisms governing these system responses are highly similar.

Table 2 Response regimes of the 1-dof and 2-dof NES system with different parameters, S: strongly modulated, W: weakly modulated, P: the steady-state periodic (no modulation)

In order to better reveal the impact of the mass distribution $\eta$ on the response regime, a set of simulation results are illustrated in Fig. 18. We can observe from Fig. 18 that the time responses of the linear oscillator and NES significantly change with the variation of mass distribution $\eta$. For the case of $\eta = 0.8$, the response regime of linear oscillator is weakly modulated, but each NES is strongly modulated. It is further confirmed that the response mechanism of the linear oscillator and NES is no longer consistent, which is significantly different from 1-dof NES.

Fig. 18

Time response of each part for the 2-dof NES system with the change of the mass distribution $\eta , x_1, x_2, x_3$: the displacement of the linear oscillator, the first and second NES, system parameter: $A = 0.3,\delta = 0,\lambda _1 = 0.3,\varepsilon = 0.1$, ${k_{221}} = 0.133,{k_{223}} = 1.333,\lambda _2 = 0.3,{k_{331}} = 0.133,{k_{333}} = 1.333$

In summary, the following conclusions are emphasized: for one thing, the appropriate selection of the 2-dof NES parameter can generate extra SMR. For another, the mass distribution $\eta$ of 2-dof NES has a significant impact on the response regime of the system. Above all, the response mechanism of linear oscillator and NES are no longer consistent in the 2-dof NES system. These conclusions are helpful for solving the vibration suppression problem in the next section.

4 Vibration suppression applications for the NES system

This section concerns the application of the 1-dof and 2-dof NES in vibration suppression. The goal of this section is to discover the optimal vibration suppression parameters through the parameter tuning process of the strongly nonlinear vibration absorber, and to verify the system with 2-dof NES has better vibration suppression effects than 1-dof NES.

Since the NES system has rich response regimes in the vicinity of the main resonance frequency, the system amplitude is also related to time. Therefore, this study uses the energy spectrum to assess the vibration suppression efficiency of NES. The energy spectrum is generated by calculating the average energy of the linear structure in a period of time which is greater than one modulation period. According to Eq. (1) or (46), the energy of linear structure can be expressed as

$$\begin{aligned} E={{\left\langle \frac{1}{2}\dot{x}_{1}^{2}+\frac{1}{2}x_{1}^{2} \right\rangle }_{t}} \end{aligned}$$

(75)

where $<\cdot >_t$ means to calculate the average value in the time interval t. In this sense, the optimization of NES in vibration suppression can be equivalent to minimizing the value of the above formula E. To simplify the calculation, the fixed parameters are selected as $\varepsilon = 0.1, A = 0.3, {k_{221}} = 0.1, {k_{223}} = ~1, t \in [2000,3000]$.

Fig. 19

The energy spectrum of the linear oscillator with damping change

Fig. 20

Poincare map and time response of different damping systems, $x_1, v_1$: the displacement and velocity of the linear oscillator, $x_N, v_N$: the displacement and velocity of the NES

This section analyzes the vibration suppression of the 1-dof NES system under different damping and stiffness. First, the vibration suppression of 1-dof NES with different damping is studied to evaluate the importance of damping. The energy spectrum of the linear oscillator with different damping is shown in Fig. 19. Poincare mapping and time response are applied to analyze systems with $\lambda _1 = 0.7$ and $\lambda _1 = 0.2$ to obtain Fig. 20.

From the above analysis, it can be noted that the system truncation damping of 1-dof NES is 0.577. When $\lambda _1 = 0.7$, there is no bifurcation in the 1-dof NES system; Fig. 20a demonstrates that the system possesses a steady-state periodic response near the resonance frequency. For $\lambda _1 = 0.2$, SMR of the system in the vicinity of the resonance frequency can be obtained from Fig. 20b. Therefore, increasing the damping of the NES does not necessarily reduce the average energy of the system. SMR can greatly reduce the average energy of the system and make the system vibration suppression effect better.

Fig. 21

Energy spectrum of the linear oscillator with different stiffness

In this section, we further describe the effect of stiffness on the energy spectrum of the system, let $\varepsilon = 0.1$, $A = 0.3, \lambda _1 = 0.5, {k_{221}}/{k_{223}} = 0.1$, whose results are presented in Fig. 21. Poincare mapping and time response are applied in the study of the system with different stiffness; they are demonstrated in Fig. 22.

Figures 21 and 22 illustrate that the average energy of the system monotonically reduces and the vibration suppression bandwidth keeps growing when the stiffness increases in the SMR interval. However, when the value of ${k_{223}}$ continues to improve to 2.94, an undesired steady-state periodic response appears near the resonance frequency, and an abnormal peak appears in the energy spectrum. It is called a failure of efficiency and should be avoided when designing NES. In summary, increasing the stiffness of NES within a certain range can continuously improve the vibration suppression effect, but the vibration suppression fails when the stiffness is too large.

Fig. 22

Poincare mapping and time response of systems with different stiffness

By varying the value of damping $\lambda$ and stiffness k, the energy spectrum is applied to discover the parameters of the optimal vibration suppression effect of NES. The criterion to evaluate the vibration suppression effect is mainly that the area of E in the energy spectrum is the smallest. The minimum peak value at each position is also a reference indicator. When $k_{221} = 0$, according to the optimization standard, the optimal value of 1-dof NES can be obtained as $k_{223} = 5,\lambda _1 =1.2$. When $k_{221} \ne 0$, the best parameters of 1-dof NES can be got similarly as $k_{223} = 3.9, \lambda _1 = 0.7, k_{221} = 0.09$. To verify the effectiveness of NES vibration suppression, the energy spectrum is compared with the optimal vibration suppression of the linear damping NES in Ref. [14, 26]. The comparison result of the energy spectrum is shown in Fig. 23.

It is found that the energy amplitude of the single-stiffness nonlinear damping NES is higher than linear damping NES in individual positions; however, the overall area of E is smaller than linear damping NES. Therefore, the single-stiffness nonlinear damping NES overall vibration suppression effect is better than linear damping NES. The NES with combined stiffness and nonlinear damping has the smallest area in the energy spectrum, and it has the smallest peak everywhere. Therefore, it can provide the best vibration suppression effect.

Then, this study analyzes the influence of mass distribution $\eta$ on vibration suppression. As indicated in Fig. 24, by appropriately selecting the mass distribution $\eta$, 2-dof NES can effectively eliminate the undesired periodic response which occurred in 1-dof NES, and it can release some parameter limitations of the selected value of 1-dof NES. Therefore, this is of great significance for optimizing 2-dof NES to suppress vibration.

In this section, based on the best-tuned energy spectrum of 1-dof NES, the parameters of better vibration suppression of 2-dof NES can also be appropriately designed. For example, a set of satisfactory 2-dof NES parameters is $k_{221} = 0.14, k_{223} = 4.8, \lambda _1 = 0.7, \eta = 0.9, k_{331} = 0.01, k_{333} = 1.6, \lambda _2 = 0.5$. The system energy spectrum of 2-dof NES under satisfactory parameters is compared with the optimal tuning of 1-dof NES in Fig. 25.

According to Fig. 25, the vibration energy of 2-dof NES with geometrically nonlinear damping and combined stiffness at the near and small of the main resonance frequency is obviously reduced. Hence, the 2-dof NES researched in this study has a better vibration suppression effect than 1-dof NES.

5 Conclusion

This study has investigated a NES system with geometrically nonlinear damping and combined nonlinear stiffness under the harmonic excitation, and the rich dynamic characteristics are also demonstrated. First, for 1-dof NES, it has been found that there is a truncation damping in the saddle-node bifurcation. Through analyzing the amplitude–frequency response, the interval of the failure frequency should be avoided in the actual application of NES. SMR research is carried out by using phase trajectory diagram and 1-D map; the frequency detuning interval for the existence of SMR is also reported.

Next, the 2-dof NES system is analyzed. When $w = 1$, compared with 1-dof NES, the 2-dof NES system has the saddle-knot bifurcation, and Hopf bifurcation loses its range limitation. When $w = 1+\varepsilon \delta$, the value of NES mass distribution has a certain influence on the response regime of the system. It has found that 2-dof NES can generate extra SMR than 1-dof NES, which stressed that the response mechanism of linear oscillator and NES is no longer consistent.

Finally, the energy spectrum, Poincare mapping, and time response are applied to compare the vibration reduction of different NESs. Adjusting the mass distribution $\eta$ of 2-dof NES can eliminate some constraints on the selected value of 1-dof NES. It also demonstrates that nonlinear damping NES can provide better vibration suppression effect than linear damping NES, NES with combined stiffness is more preferable for the vibration mitigation than pure cubic stiffness NES, and 2-dof NES system has a much better vibration suppression effect than 1-dof NES system.

Fig. 23

The comparison of the energy spectrum of the best vibration suppression for different NESs

Fig. 24

The energy spectrum of 1-dof and 2-dof NES main structure through parameter variation to eliminate unwanted periodic responses

Fig. 25

Energy spectrum of 2-dof NES under satisfactory parameters and 1-dof NES with best-tuned parameters

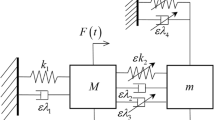
Appendix: Derivation of simplified system equations

The system equation is expressed as

$$\begin{aligned} \begin{aligned}&{{m}_{1}}{{{\ddot{x}}}_{1}}+{{k}_{1}}{{x}_{1}}+{{c}_{1}}{{{\dot{x}}}_{1}}+{{k}_{21}}({{x}_{1}}-{{x}_{2}}) \\&\quad +{{k}_{23}}{{({{x}_{1}}-{{x}_{2}})}^{3}}+{{c}_{2}}{{({{{\dot{x}}}_{1}}-{{{\dot{x}}}_{2}})}^{3}}={{F}_{0}}\cos (wt) \\&{{m}_{2}}{{{\ddot{x}}}_{2}}+{{k}_{21}}({{x}_{2}}-{{x}_{1}})+{{k}_{23}}{{({{x}_{2}}-{{x}_{1}})}^{3}}\\&\quad +{{c}_{2}}{{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})}^{3}}=0 \end{aligned} \end{aligned}$$

(A.1)

To transform Eq. (A.1) into a dimensionless form, the following coordinate transformations are introduced

$$\begin{aligned} \bar{t}=\sqrt{\frac{{{k}_{1}}}{{{m}_{1}}}}\text { }t,\text { }{{\bar{x}}_{i}}={{x}_{i}},\text { }\bar{w}=w\sqrt{\frac{{{m}_{1}}}{{{k}_{1}}}} \end{aligned}$$

(A.2)

Letting $c_1 = 0$, by defining the following variables

$$\begin{aligned} \begin{aligned}&\frac{{{k}_{21}}}{{{k}_{1}}}=\varepsilon {{k}_{221}},\quad \frac{{{k}_{23}}}{{{k}_{1}}}=\varepsilon {{k}_{223}},\quad \frac{{{c}_{2}}}{{{m}_{1}}}\sqrt{\frac{{{k}_{1}}}{{{m}_{1}}}}=\varepsilon \lambda \\&\frac{{{m}_{2}}}{{{m}_{1}}}=\varepsilon ,\quad \qquad \frac{{{F}_{0}}}{{{k}_{1}}}=\varepsilon A \end{aligned} \end{aligned}$$

(A.3)

and substituting Eqs. (A.2) and (A.3) into Eq. (A.1), we have

$$\begin{aligned} \begin{aligned}&{{{\ddot{x}}}_{1}}+{{x}_{1}}+\varepsilon {{k}_{221}}({{x}_{1}}-{{x}_{2}})+\varepsilon {{k}_{223}}{{({{x}_{1}}-{{x}_{2}})}^{3}} \\&\quad +\varepsilon \lambda {{({{{\dot{x}}}_{1}}-{{{\dot{x}}}_{2}})}^{3}}=\varepsilon A\cos (wt) \\&{{{\ddot{x}}}_{2}}+{{k}_{221}}({{x}_{2}}-{{x}_{1}})+{{k}_{223}}{{({{x}_{2}}-{{x}_{1}})}^{3}}+\lambda {{({{{\dot{x}}}_{2}}-{{{\dot{x}}}_{1}})}^{3}}=0 \\ \end{aligned} \end{aligned}$$

(A.4)