Analysis and control of three-link planar robot with active last link: property and energy-based approach

Abstract

This paper investigates the nonlinear control of a three-link planar robot, which includes a passive first link, a passive second link, and an active last link (subsequently referred to as the PPA robot). Notably, only the angle between the last link and the vertical axis is actuated. First, this paper presents and strictly proves a property of the PPA robot, unaffected by its mechanical parameters. This property reveals that the two passive links of the PPA robot maintain static positions when the active last link remains fixed under a constant control input. Different from previous studies, the proof for the PPA robot demonstrates new challenges and distinctions originated from actuator configuration. Second, leveraging this property, this paper studies the energy-based control corresponding to the PPA robot’s upright equilibrium point (UEP), where all links extend upward. Under the derived energy-based controller, this paper conducts a global motion analysis of the closed-loop system to show that if the control gains satisfy certain requirements, then all initial states, apart from those in a set of Lebesgue measure zero, converge to an invariant set in which the last link extends upward and the robot’s total mechanical energy coincides with its value at the UEP. Finally, this paper provides numerical simulation to validate the developed theoretical results and to demonstrate the effectiveness of applying the derived controller along with an LQR controller to the swing-up and stabilizing task of the PPA robot.

1 Introduction

Underactuated systems, which possess fewer actuators than degrees of freedom, take the form of various applications. Typical examples of such systems include cranes [21, 29], unmanned aircraft [24], underwater vehicles [5], flexible links [16, 30], gymnastic robots [13], and intentionally designed systems using reduced actuation. Currently, applications of underactuated systems in cutting-edge fields like high-performance robotics and biomimetics have attracted increasing attention. Reference [9] presented a motion optimization strategy for a planar spring-loaded monopod robot with single actuator executing double backflip. Reference [10] designed a minimalist underactuated brachiating robot composed of one actuator and two grippers, and realized brachiation with three different control schemes. Reference [4] proposed a novel path-following scheme for an underactuated robotic fish subjected to time-varying sideslip, which utilizes sliding-mode controllers and nonlinear disturbance observer. Reference [8] drew inspiration from birds, and investigated the control problem of tracking a trajectory while maintaining balance for an n-link manipulator with static friction at the unactuated first revolute joint. Reference [3] developed a biomimetic morphing wing made up of forty underactuated feathers and four controllable joints to study the morphing pattern of birds, providing insight for bioinspired aircraft design.

Within the advances and broad spectrum of underactuated systems, multi-link planar robots serve as typical models for studying underactuated dynamics. In the context of these robots, [14] defined the link angle as the angle between a link and the positive vertical direction. The joint angle is designated as the difference between the link angles of two adjacent links connected at a joint, with the first joint angle being identical to the first link angle. Consequently, a link (joint) is active if the corresponding link (joint) angle represents an actuated variable, and passive if that angle represents an unactuated variable [14].

For a three-link planar robot with passive first joint, [27] addressed the swing-up control by introducing the notion of virtual composite link, which combines the last two links as a single virtual link. In [13], this notion was further extended to tackle the set-point control for a folded configuration. Regarding stabilizing control, [11] estimated the region of attraction of an equilibrium point with sum of squares and trajectory reversing methods, and enlarged the estimation by using impulse manifold method. For a three-link planar robot with single active joint, prior works have mainly focused on achieving the swing-up control via trajectory planning. Reference [22] designed a two-segment trajectory for the active joint, and optimized the trajectory parameters with PSO algorithm to ensure the simultaneous convergence of the passive joints. Reference [2] introduced the time-reversal symmetry characteristic of such system and utilized this characteristic to design a swing-up trajectory by reversing a swing-down trajectory in time. However, these approaches require meticulous design or selection of suitable trajectories.

For underactuated systems exhibiting nonholonomic characteristics and complex dynamics, [6, 12] proposed an energy-based control approach, whose objective is to design a controller to stabilize the actuated variable(s) and regulate the system’s total mechanical energy to a predetermined value simultaneously. The feasibility of this objective has been examined for several systems with one underactuated variable [7, 12, 26].

However, it remains a challenging problem to investigate whether the energy-based control objective can be achieved for systems containing more than one underactuated variable, especially for multi-link planar robots. For the double pendulum on a cart, [25] demonstrated a parallel control of regulating the system’s total mechanical energy and stabilizing the cart’s horizontal displacement. For a three-link planar robot with active first link, [15] proved that the objective corresponding to the robot’s upright equilibrium point (UEP), where all links extend upward, can be achieved for almost all initial states. In either case, the closed-loop analysis under the energy-based controller was carried out with the aid of an important property; that is, if the actuated variable remains stationary under a constant control input, then the underactuated variables of the system remain stationary. Despite the physical intuition, an effective method was proposed in [15] to strictly prove this property, which involves the derivation and utilization of a holonomic constraint and does not require any prior assumption regarding the mechanical parameters of the system or the constant input.

Shifting focus to other actuator configuration, the feasibility of achieving the energy-based control objective for three-link planar robots with a single actuator acting on the last link has not yet been reported. Following the definition in [14], two distinct types of such robots exist. The directly driven type uses the joint angle of the last link as the actuated variable. In contrast, the remotely driven type treats the link angle of the last link as the actuated variable. The directly driven type can be compared to a simplified depiction of a gymnast performing on rings [20], thereby serving as platform for robotic and biomimetic investigation. However, controlling this type with energy-based control approach proves more challenging compared to its remotely driven counterpart.

For this reason, and as an initial focus, this paper investigates the remotely driven type of three-link planar robot, which comprises a passive first link, a passive second link, and an active last link. This robot is referred to as the PPA robot. The present work is based on the idea sketched in [23] and extended and proven in the general case here. First, we extend the method proposed in [15] to prove an essential property for the PPA robot, regardless of its mechanical parameters or the constant control input. This property states that if the active last link is held fixed under a constant control input, then the PPA robot stays at an equilibrium point. Due to inherent difference in actuator configuration, the strict proof for the PPA robot requires a deeper utilization of the aforementioned holonomic constraint, compared to its proximal-actuated counterparts in [15] and [25]. More complicated manipulations and extra discretion are thereby demanded. Next, we derive an energy-based controller for the PPA robot and explore the feasibility of achieving the control objective that corresponds to the UEP. Leveraging the above property, we analyze the global motion of the closed-loop system by examining the convergence of energy. Results show that the control objective can be achieved for almost all initial states. Finally, we verify the theoretical results via numerical simulation and demonstrate the effectiveness of the energy-based controller along with an LQR controller for the swing-up and stabilizing task [19], which involves swinging the robot to a vicinity of its UEP and stabilizing it at that point.

In summary, the contributions of this paper are as follows.

• (1) Strict proof of a property of the PPA robot that the system stays at an equilibrium point, if the active last link is held fixed under constant control input.

• (2) Global motion analysis of the closed-loop system under the energy-based controller, showing the feasibility of achieving the objective targeting the UEP.

• (3) Simulation demonstration of performing swing-up and stabilizing task with the energy-based control and the LQR control.

The structure of the remainder is as follows: The dynamics of the PPA robot and the control objective are given in Sect. 2. An important property of the robot is presented in Sect. 3. The energy-based controller is derived and the closed-loop solution is analyzed in Sect. 4, followed by numerical simulations in Sect. 5 and the conclusion in Sect. 6. Two proofs are included in the appendices to increase readability.

2 System dynamics and control objective

In this section, we revisit the dynamics of the three-link planar robot and state our control objective regarding the energy-based control approach.

2.1 System dynamics

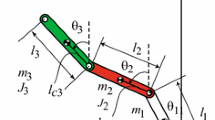
The three-link planar robot with active last link, as depicted in Fig. 1, is considered. The symbols involved are defined and collected in the Nomenclature section.

Fig. 1

PPA robot: three-link planar robot with active last link

The robot’s dynamics are derived in [28] and expressed as

$$\begin{aligned} \varvec{M}\left( \varvec{\theta }\right) \ddot{\varvec{\theta }}+\varvec{C}\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big ){\dot{\varvec{\theta }}}+\varvec{G}\left( \varvec{\theta }\right) =\varvec{B}u_{3}, \end{aligned}$$

(1)

where $(\theta _1,\theta _2)\in {\mathbb {S}}\times {\mathbb {S}}$ (a torus) and $\theta _3\in {\mathbb {R}}$ constitute the generalized coordinate vector $\varvec{\theta }=[\theta _1,\theta _2,\theta _3]^\textrm{T}$; $\varvec{M}(\varvec{\theta })\in {\mathbb {R}}^{3\times 3}$ is the symmetric positive definite inertia matrix $\varvec{M}(\varvec{\theta })=[\alpha _{ij}\cos (\theta _j-\theta _i)]$; $\varvec{C}(\varvec{\theta },{\dot{\varvec{\theta }}})\in {\mathbb {R}}^{3\times 3}$ is $\varvec{C}(\varvec{\theta },{\dot{\varvec{\theta }}})=[-\alpha _{ij}{\dot{\theta }}_j\sin (\theta _j-\theta _i)]$; $\varvec{G}(\varvec{\theta })\in {\mathbb {R}}^3$ is $\varvec{G}(\varvec{\theta })=[-\beta _i\sin \theta _i]$; and $\varvec{B}=[0,\ 0,\ 1]^\textrm{T}$. In these expressions,

$$\begin{aligned} \left\{ \begin{array}{l} \alpha _{ii}=J_{i}+m_{i}l_{ci}^2+l_i^2\sum \limits _{k=i+1}^{3}m_k,\ 1\le i\le 3,\\ \alpha _{ij}=\alpha _{ji}=m_jl_il_{cj}+l_il_j\sum \limits _{k=j+1}^{3}m_k,\ 1\le i < j \le 3,\\ \end{array} \right. \end{aligned}$$

(2)

$$\begin{aligned} \beta _i=\left( m_il_{ci}+l_i\sum \limits _{k=i+1}^{3}m_k\right) g,\ 1\le i\le 3. \end{aligned}$$

(3)

The PPA robot’s total mechanical energy is

$$\begin{aligned} E\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )=\frac{1}{2}{\dot{\varvec{\theta }}}^\textrm{T}\varvec{M}\left( \varvec{\theta }\right) {\dot{\varvec{\theta }}}+P\left( \varvec{\theta }\right) , \end{aligned}$$

(4)

where $P(\varvec{\theta })=\sum _{i=1}^3\beta _i\cos \theta _i$ is the potential energy. Direct computation gives

$$\begin{aligned} {\dot{E}}\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )={\dot{\theta }}_{3}u_3. \end{aligned}$$

(5)

2.2 Control objective

In this paper, we design an energy-based controller for the PPA robot in (1) that aims at achieving the following control objective:

$$\begin{aligned} \lim _{t\rightarrow \infty }E\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )=E_\textrm{r},\quad \lim _{t\rightarrow \infty }\theta _3=0,\quad \lim _{t\rightarrow \infty }{\dot{\theta }}_3=0, \end{aligned}$$

(6)

which corresponds to the UEP $(\theta _1,\theta _2,\theta _3,{\dot{\theta }}_1,{\dot{\theta }}_2,{\dot{\theta }}_3)=(0,0,0,0,0,0)$ with $E_\textrm{r}=\sum _{i=1}^3\beta _i$ being the potential energy of the robot at the UEP.

3 Property of PPA robot

In this section, we present an important property of the PPA robot, which is stated in Theorem 1 below and proved in “Appendix A”.

Theorem 1

Suppose that link 3 of the PPA robot satisfies constraints

$$\begin{aligned} \theta _3\equiv \theta _3^{*},\quad u_3\equiv u_3^{*}, \end{aligned}$$

(7)

with $\theta _3^{*}$ and $u_3^{*}$ being constants; that is, the angle of link 3 is held fixed under a constant control input. Then, links 1 and 2 of the PPA robot maintain static positions; that is,

$$\begin{aligned} {\dot{\theta }}_1\equiv 0,\quad {\dot{\theta }}_2\equiv 0, \end{aligned}$$

(8)

regardless of its mechanical parameters, $\theta _3^{*}$, and $u_3^{*}$. Equivalently, $\theta _1\equiv \theta _1^{*}$ and $\theta _2\equiv \theta _2^{*}$, with $\theta _1^{*}$ and $\theta _2^{*}$ being constants.

The essence of the property in Theorem 1 is that if the actuated variable remains still under a constant control input, then the whole system stays at an equilibrium configuration. We have tried to prove this property from a physical perspective by looking into the forces exerting on each joint; however, we cannot extract new information beyond the dynamics in (1). Even so, this property cannot be simply revealed by straightforward analysis of the dynamics, which are in the form of second-order nonholonomic constraints. Thus, we transform the dynamics with (7) into a holonomic constraint in terms of a $28\textrm{th}$-order polynomial. Under this particular constraint, we show that the PPA robot cannot move for any possible mechanical parameters in (2) and (3), any position of the actuated link 3, and any corresponding constant control input.

It is worth noting that the most difficult part of the proof is to prove the following result, which represents a special case of Theorem 1 with the constraint in (7) being further specified.

Corollary 1

Suppose that link 3 of the PPA robot is further constrained to the horizontal position, with $\theta _3\equiv \theta _3^{*}=\pm \pi /2$ and $u_3\equiv u_3^{*}$. Then, the motion of the PPA robot satisfies: $\textrm{i})$ the link 3 is parallel to X-axis with its distance to X-axis remains fixed, and $\textrm{ii})$ (8) holds.

Fig. 2

Illustrative example of the equilibrium configuration of the PPA robot, when link 3 is held in a horizontal position under a constant control input

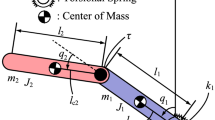
Similarly, Corollary 1 indicates a special equilibrium configuration for the PPA robot, such as the illustrative example shown in Fig. 2. The proof of Corollary 1 is given in Case 2.2 of “Appendix A”.

4 Energy-based control

In this section, we derive an energy-based controller targeting the UEP and analyze the global motion of the closed-loop system by utilizing the property in Theorem 1.

4.1 Design of energy-based controller

Take the Lyapunov candidate proposed in [28] as

$$\begin{aligned} V=\frac{1}{2}\left( E\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )-E_\textrm{r}\right) ^2 +\frac{k_D}{2}{\dot{\theta }}_3^2+\frac{k_P}{2}\theta _3^2, \end{aligned}$$

(9)

where $k_D\in {\mathbb {R}}^{+}$ and $k_P\in {\mathbb {R}}^{+}$ are constant control gains. Taking the time derivative of V along (1) with (5) gives

$$\begin{aligned} {\dot{V}}={\dot{\theta }}_3\Big (\big (E\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big ) -E_\textrm{r}\big )u_3+k_D\ddot{\theta }_3+k_P\theta _3\Big ). \end{aligned}$$

If we can design $u_3$ satisfying

$$\begin{aligned} \big (E\big (\varvec{\theta },\dot{\varvec{\theta }}\big ) -E_\textrm{r}\big )u_3+k_D\ddot{\theta }_3+k_P\theta _3=-k_V{\dot{\theta }}_3, \end{aligned}$$

(10)

where $k_V\in {\mathbb {R}}^{+}$ is a constant control gain, then we have

$$\begin{aligned} {\dot{V}}=-k_V{\dot{\theta }}_3^2\le 0. \end{aligned}$$

(11)

Since $\varvec{M}(\varvec{\theta })$ is a positive definite matrix, from (1), we have

$$\begin{aligned} \ddot{\theta }_3=\varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\theta }\right) \big (\varvec{B}u_3-\varvec{C}\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big ){\dot{\varvec{\theta }}}-\varvec{G}\left( \varvec{\theta }\right) \big ). \end{aligned}$$

(12)

Substituting (12) into (10) yields

$$\begin{aligned} \varLambda \big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )u_3{} & {} =k_D\varvec{B}^\textrm{T}\varvec{M}^{-1} \left( \varvec{\theta }\right) \big (\varvec{C}\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big ){\dot{\varvec{\theta }}}\\{} & {} \quad +\varvec{G}\left( \varvec{\theta }\right) \big )-k_P\theta _3-k_V{\dot{\theta }}_3, \end{aligned}$$

where

$$\begin{aligned} \varLambda \big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )=\big (E\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big ) -E_\textrm{r}\big )+k_D\varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\theta }\right) \varvec{B}. \end{aligned}$$

(13)

Hence, if $\varLambda (\varvec{\theta },{\dot{\varvec{\theta }}})$ is nonzero for any state $(\varvec{\theta },{\dot{\varvec{\theta }}})$, then we obtain

$$\begin{aligned} u_3=\frac{k_D\varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\theta }\right) \big (\varvec{C}\big (\varvec{\theta },{\dot{\varvec{\theta }}}\big ){\dot{\varvec{\theta }}}\ +\varvec{G}\left( \varvec{\theta }\right) \big )-k_P\theta _3 -k_V{\dot{\theta }}_3}{\varLambda \big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )}. \end{aligned}$$

(14)

We present Lemma 1 below regarding the controller in (14) and the behavior of the corresponding closed-loop system.

Lemma 1

Consider the closed-loop system consisting of the PPA robot in (1) and the energy-based controller in (14). The controller in (14) is free of singular points if and only if

$$\begin{aligned} k_D>k_{Dm}=\max _{\begin{array}{c} -\pi \le \theta _{i}\le \pi \\ \left( 1\le i \le 3\right) \end{array}}\Big (\big (E_\textrm{r}-P\left( \varvec{\theta }\right) \big ) \big (\varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\theta }\right) \varvec{B}\big )^{-1}\Big ). \end{aligned}$$

(15)

Consequently, any closed-loop trajectory approaches an invariant set described as:

$$\begin{aligned}{} & {} \frac{1}{2}\alpha _{11}{\dot{\theta }}_1^2+\alpha _{12}{\dot{\theta }}_1{\dot{\theta }}_2 \cos \left( \theta _2-\theta _1\right) \nonumber \\{} & {} \quad +\frac{1}{2}\alpha _{22} {\dot{\theta }}_2^2+P\left( \theta _1,\theta _2,\theta _3^{*}\right) \equiv E^{*}, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} W=\left\{ \big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )\big |\big (\theta _1,\theta _2,{\dot{\theta }}_1,{\dot{\theta }}_2\big )\ \textrm{satisfies}\ (28),\ \theta _3\equiv \theta _3^{*} \right\} ,\nonumber \\ \end{aligned}$$

(17)

with $E^{*}$ and $\theta _3^{*}$ being constants.

Proof

We say that the controller in (14) is free of singular points if $\varLambda (\varvec{\theta },{\dot{\varvec{\theta }}})\ne 0$. Owing to $E(\varvec{\theta },{\dot{\varvec{\theta }}})\ge P(\varvec{\theta })$ and $E_\textrm{r}\ge P(\varvec{\theta })$, if (15) holds, we obtain $\varLambda (\varvec{\theta },{\dot{\varvec{\theta }}})>0$ directly from (13). Thus, (15) is a sufficient condition such that the controller in (14) is free of singular points. Note that in (15) we have

$$\begin{aligned} \varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\theta }\right) \varvec{B}=\frac{\alpha _{11}\alpha _{22} -\alpha _{12}^2\cos ^2\left( \theta _1-\theta _2\right) }{\left| \varvec{M}\left( \varvec{\theta }\right) \right| }>0, \end{aligned}$$

(18)

since $\varvec{M}(\varvec{\theta })$ is positive definite.

We now show that (15) is also a necessary condition by revealing that for any specific $k_D$ satisfying $0<k_D\le k_{Dm}$, there exists a state $(\varvec{\theta },{\dot{\varvec{\theta }}})$ rendering $\varLambda (\varvec{\theta },{\dot{\varvec{\theta }}})=0$. To this end, let $\varvec{\zeta } \in {\mathbb {R}}^3$ be the value of $\varvec{\theta }$ at which the function in (15) takes its maximum value, then we have

$$\begin{aligned} k_{Dm}=\big (E_\textrm{r}-P\left( \varvec{\zeta }\right) \big )\big (\varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\zeta }\right) \varvec{B}\big )^{-1}. \end{aligned}$$

(19)

Take $\varvec{\zeta }_d \in {\mathbb {R}}^3$ such that

$$\begin{aligned} \frac{1}{2}\varvec{\zeta }_d^\textrm{T}\varvec{M}\left( \varvec{\zeta }\right) \varvec{\zeta }_d=\left( k_{Dm}-k_D\right) \left( \varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\zeta }\right) \varvec{B}\right) \ge 0. \end{aligned}$$

Then, by using (4) and (13), we have

$$\begin{aligned}{} & {} \varLambda \left( \varvec{\zeta },\varvec{\zeta }_d\right) =\frac{1}{2}\varvec{\zeta }_d^ \textrm{T}\varvec{M}\left( \varvec{\zeta }\right) \varvec{\zeta }_d \\{} & {} \quad +P\left( \varvec{\zeta }\right) -E_\textrm{r}+k_D\varvec{B}^\textrm{T}\varvec{M}^{-1}\left( \varvec{\zeta }\right) \varvec{B}=0. \end{aligned}$$

Thus, the controller in (14) is free of singular points if and only if (15) holds.

From (11), since ${\dot{V}}\le 0$, using LaSalle’s invariance principle with (9) and (11) shows that the closed-loop trajectory eventually approaches an invariant set W where $E(\varvec{\theta },{\dot{\varvec{\theta }}})$ and $\theta _3$ are constants denoted as $E^{*}$ and $\theta _3^{*}$, respectively. Finally, substituting $E=E^{*}$ and $\theta _3=\theta _3^{*}$ into (4) gives the characterization of W in (17). $\square$

4.2 Global motion analysis

We further analyze the closed-loop trajectory by studying the convergence of the system’s total mechanical energy.

Define the set

$$\begin{aligned}{} & {} \begin{aligned}&\frac{1}{2}\alpha _{11}{\dot{\theta }}_1^2+\alpha _{12}{\dot{\theta }}_1{\dot{\theta }}_2 \cos \left( \theta _2-\theta _1\right) +\frac{1}{2}\alpha _{22}{\dot{\theta }}_2^2\\&+\beta _1\left( \cos \theta _1-1\right) +\beta _2\left( \cos \theta _2-1\right) =0, \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned}{} & {} \begin{aligned} W_\textrm{r}=\left\{ \big (\varvec{\theta },{\dot{\varvec{\theta }}}\big )\big |\big (\theta _1,\theta _2,{\dot{\theta }}_1,{\dot{\theta }}_2\big )\ \textrm{satisfies}\ (20),\ \theta _3\equiv 0\right\} , \end{aligned}\nonumber \\ \end{aligned}$$

(21)

and the equilibrium set

$$\begin{aligned} \varOmega _\textrm{s}=\left\{ \left( \varvec{\theta }^{*}, \varvec{0}_3\right) \big |\varvec{\theta }^{*}\equiv \left[ \pi ,\pi ,0\right] ^\textrm{T},\ \left[ \pi ,0,0\right] ^\textrm{T},\ \left[ 0,\pi ,0\right] ^\textrm{T} \right\} , \end{aligned}$$

(22)

which comprises the down–down–up, down–up–up, and up–down–up equilibrium points. The terms “down” and “up” denote the downward ($\theta _i=\pi$) and upward ($\theta _i=0$) positions of link i, respectively. Define function

$$\begin{aligned}{} & {} f\left( \psi \right) =\frac{\left( -2\left( \beta _1+\beta _2\right) +\left( \cos \psi -1\right) \beta _3\right) \beta _3\sin \psi }{\psi }, \nonumber \\{} & {} \quad {\psi \in [\pi ,2\pi ].} \end{aligned}$$

(23)

We are ready to present another main result of this paper.

Theorem 2

Consider the closed-loop system consisting of the PPA robot in (1) and the energy-based controller in (14) with $k_D$ satisfying (15), $k_P>0$, and $k_V>0$. If $k_P$ further satisfies

$$\begin{aligned} k_P>k_{Pm}=\max _{\pi \le \psi \le 2\pi }f\left( \psi \right) , \end{aligned}$$

(24)

where $f(\psi )$ is defined in (23). Then, the following statements hold:

1 If $E^{*}=E_\textrm{r}$, then the closed-loop trajectory converges to the invariant set $W_\textrm{r}$ in (21), where the only equilibrium point UEP is strictly unstable.

2 If $E^{*}\ne E_\textrm{r}$, then the closed-loop trajectory converges to $\varOmega _\textrm{s}$ in (22), where all three equilibrium points are strictly unstable.

Proof

Substituting $\theta _3=\theta _3^{*}$ and $E(\varvec{\theta },{\dot{\varvec{\theta }}})=E^{*}$ into (10) yields

$$\begin{aligned} \left( E^{*}-E_\textrm{r}\right) u_3+k_P\theta _3^{*}=0. \end{aligned}$$

(25)

If $E^{*}=E_\textrm{r}$, we obtain $\theta _3^{*}=0$ from (25), which turns (17) into $W_\textrm{r}$ in (21). Substituting ${\dot{\theta }}_1=0$ and ${\dot{\theta }}_2=0$ into (21) gives $\theta _1=0$ and $\theta _2=0$. This suggests that $W_\textrm{r}$ contains the UEP as the unique equilibrium point.

If $E^{*}\ne E_\textrm{r}$, we obtain $u_3=u_3^{*}$ from (25). Since links 1 and 2 are stationary according to Theorem 1, using (1), (4), and (10) with $\varvec{\theta }^{*}=[\theta _1^{*},\theta _2^{*},\theta _3^{*}]^\textrm{T}$ then gives

$$\begin{aligned}{} & {} \sin \theta _i^{*}\equiv 0,\ i=1,2, \end{aligned}$$

(26)

$$\begin{aligned}{} & {} \beta _3\left( E_\textrm{r}-P\left( \varvec{\theta }^{*}\right) \right) \sin \theta _3^{*}+k_P\theta _3^{*}=0. \end{aligned}$$

(27)

From (26), we have $\theta _1^{*}$ and $\theta _2^{*}$ equal 0 or $\pi$ under modulo $2\pi$. In case where $\theta _3^{*}\ne 0$, (27) can be further expressed as

$$\begin{aligned} k_P=\frac{-\beta _3\left( E_\textrm{r}-P\left( \varvec{\theta }^{*}\right) \right) \sin \theta _3^{*}}{\theta _3^{*}}, \end{aligned}$$

where the numerator of the right-hand side is an even and periodic function with period of $2\pi$. Due to $E_\textrm{r}\ge P(\varvec{\theta }^{*})$ and $P(\varvec{\theta }^{*})\ge -\beta _1-\beta _2+\beta _3\cos \theta _3^{*}$, (27) has an unique solution $\theta _3^{*}=0$ if $k_P$ satisfies (24). This implies that the closed-loop trajectory converges to one of the three equilibrium points in $\varOmega _\textrm{s}$.

In what follows, we apply Routh–Hurwitz criterion to check the stability of equilibrium points in $W_\textrm{r}$ and $\varOmega _\textrm{s}$. By calculating the characteristic polynomial of the robot’s linearization at the UEP, we obtain

$$\begin{aligned} \left| s\varvec{I}-\varvec{J}_{uuu} \right| =s^6+a_1s^5+a_2s^4+a_3s^3+a_4s^2+a_5s+a_6, \end{aligned}$$

where $\varvec{J}_{uuu}$ is the corresponding Jacobian matrix, and

$$\begin{aligned}&a_1=\frac{k_V}{k_D},\ a_2=\frac{k_P}{k_D}-\frac{\alpha _{22}\beta _1 +\alpha _{11}\beta _2}{\alpha _{11}\alpha _{22}-\alpha _{12}^2},\\&{a_3=-\frac{k_V\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) }{k_D\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) },}\\&{a_4=\frac{k_D\beta _1\beta _2-k_P\left( \alpha _{22}\beta _1+\alpha _{11} \beta _2\right) }{k_D\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) },}\\&a_5=\frac{k_V\beta _1\beta _2}{k_D\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) }, \ a_6=\frac{k_P\beta _1\beta _2}{k_D\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) }. \end{aligned}$$

Using $\alpha _{11}\alpha _{22}-\alpha _{12}^2>0$ due to $M(\varvec{\theta })|_{\varvec{\theta }=\varvec{0_3}}>0$ shows that $a_3<0$, regardless of the control gains and mechanical parameters. Hence, it can be concluded that the UEP is strictly unstable, since $\varvec{J}_{uuu}$ possesses no less than one eigenvalue in the open right-half plane.

The proof of all the equilibrium points in $\varOmega _\textrm{s}$ being strictly unstable is given in “Appendix B”. $\square$

Fig. 3

Configurations of the PPA robot at all possible closed-loop equilibrium points described in Theorem 2

Figure 3 depicts the configurations of the PPA robot at all possible equilibrium points described in Theorem 2. We give the following remark about Theorem 2.

Remark 1

Since all three equilibrium points in $\varOmega _\textrm{s}$ are strictly unstable, the set of initial states from which the closed-loop trajectory converges to $\varOmega _\textrm{s}$ is of Lebesgue measure zero, see, e.g., [18] (p. 1225). Thus, under the energy-based controller in (14), every initial state apart from those in a set of Lebesgue measure zero converges to $W_\textrm{r}$. This indicates that the objective in (6) is achieved.

5 Simulation results

In this section, we provide simulation verification for the developed theoretical results, and demonstrate an application to the swing-up and stabilizing task. Notably, in addition to simulations without friction, we also conduct simulation in the presence of linear viscous friction to showcase the robustness of our proposed control approach. The mechanical parameters listed in Table 1 for simulation are extracted from the physical device of the three-link planar robot in [17]. The gravitational acceleration g is set to $9.81~\mathrm{m/s^2}$.

Table 1 Mechanical parameters of the physical device of a three-link planar robot in [17]

Since the PPA robot is linearly controllable at the UEP regardless of mechanical parameters [14], stabilization around the UEP, if the robot ever comes close under the controller in (14), can then be accomplished by switching to a local stabilizing controller:

$$\begin{aligned} u_3=-\varvec{F}\varvec{x}, \end{aligned}$$

(28)

where $\varvec{x}=[\theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3}]^\textrm{T}$ and $\varvec{F}$ is the state-feedback gain obtained by the LQR method. Using the MATLAB function “lqr” with

$$\begin{aligned} \varvec{Q}=\textrm{diag}\{1,1,1,0.1,0.1,0.1\},\quad R=1, \end{aligned}$$

we obtain

$$\begin{aligned} \varvec{F}{} & {} =[847.7247,\ -197.3587,\ 1.4521,\ \nonumber \\{} & {} \quad 109.9323,\ 10.6374,\ 0.9831]. \end{aligned}$$

(29)

The local stabilizing controller in (28) is switched when the PPA robot enters a vicinity of the UEP defined by

$$\begin{aligned} d= \big | \theta _1 \big | + \big | \theta _2 \big | + \big | \theta _3 \big | +0.3 \big | {\dot{\theta }}_1 \big | + \big | {\dot{\theta }}_2 \big | + \big | {\dot{\theta }}_3 \big |<0.5. \end{aligned}$$

(30)

5.1 Swing-up and stabilizing without friction

Under the mechanical parameters in Table 1, the conditions of the control gains in (15) and (24) are $k_D>0.3088$ and $k_P>3.1235$. Below are the results of the simulation conducted for three initial states. The dashed vertical line in the figures marks the switch from the energy-based controller to the local stabilizing controller.

The first simulation starts from initial state 1:

$$\begin{aligned} \left( \theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2}, {\dot{\theta }}_{3}\right) =\left( \frac{5\pi }{6},\frac{6\pi }{7},\frac{7\pi }{8},0,0,0\right) , \end{aligned}$$

(31)

under the controller in (14) with $k_D=0.3270$, $k_P=3.1240$, and $k_V=3.0281$. The results are shown in Figs. 4 and 5.

Fig. 4

Time responses of V, $E-E_\textrm{r}$, and $u_3$ with initial state 1 in (31) under the swing-up controller in (14) and the LQR controller in (28)

Fig. 5

Time responses of $\theta _1$, $\theta _2$, and $\theta _3$ with initial state 1 in (31) under the swing-up controller in (14) and the LQR controller in (28)

Fig. 6

Time responses of V, $E-E_\textrm{r}$, and $u_3$ with initial state 2 in (32) under the swing-up controller in (14) and the LQR controller in (28)

Fig. 7

Time responses of $\theta _1$, $\theta _2$, and $\theta _3$ with initial state 2 in (32) under the swing-up controller in (14) and the LQR controller in (28)

From Fig. 4, we see that Lyapunov function V in (9) decreased to 0, and the total mechanical energy E converged to $E_\textrm{r}$. From Fig. 5, $\theta _3$ converged to 0. This verifies that the closed-loop trajectory converged to $W_\textrm{r}$ in (21), and the objective in (6) is achieved.

Next, by linearizing the closed-loop system at the down–down–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(\pi ,\pi ,0,0,0,0)$ in (22), we obtain the characteristic equation as

$$\begin{aligned} \begin{aligned}&s^6+50.98s^5+416.42s^4+8615.30s^3\\&\quad +46599.37s^2+164756.28s+852119.92=0. \end{aligned} \end{aligned}$$

The roots of the above equation are $-45.53$, $-5.70$, $0.03\pm 4.72j$, and $0.09\pm 12.14j$. This verifies that the down–down–up equilibrium point is strictly unstable. The instability verification for other equilibrium points is omitted.

From Fig. 5, where we plotted $\theta _1$ and $\theta _2$ modulo $2\pi$, the PPA robot entered the vicinity of the UEP in (30) at $t=72.38\ \textrm{s}$, and thus triggered the switch of controller. The local stabilizing controller in (28) then stabilized the robot around the UEP. This demonstrates a successful swing-up and stabilizing control via the combination of controllers in (14) and (28).

The second simulation starts from initial state 2:

$$\begin{aligned} \left( \theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3}\right) =\left( \frac{\pi }{2},\frac{\pi }{2},\frac{\pi }{2},0,0,0\right) , \end{aligned}$$

(32)

under the controller in (14) with $k_D=0.3163$, $k_P=3.1240$, and $k_V=4.5572$. From the results shown in Figs. 6 and 7, we see that the closed-loop trajectory converged to $W_\textrm{r}$ in (21). This indicates that the objective in (6) is achieved for another initial state. Under the energy-based controller in (14), the PPA robot was driven to the UEP at $t=50.57\ \textrm{s}$, the switch of controller was then executed to stabilize the robot.

Finally, the third simulation starts from initial state 3:

$$\begin{aligned} \left( \theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3}\right) =\left( \frac{\pi }{6},\frac{\pi }{7},\frac{\pi }{8},0,0,0\right) , \end{aligned}$$

(33)

under the controller in (14) with $k_D=0.3527$, $k_P=3.1240$, and $k_V=4.9321$. The simulation results are shown in Figs. 8 and 9. The analysis of the closed-loop trajectory is similar to previous simulations and hence is omitted for brevity.

Fig. 8

Time responses of V, $E-E_\textrm{r}$, and $u_3$ with initial state 3 in (33) under the swing-up controller in (14) and the LQR controller in (28)

Fig. 9

Time responses of $\theta _1$, $\theta _2$, and $\theta _3$ with initial state 3 in (33) under the swing-up controller in (14) and the LQR controller in (28)

Fig. 10

Time responses of V, $E-E_\textrm{r}$, and $u_3$ with initial state 1 in (31) in the presence of linear viscous friction under the swing-up controller in (14) and the LQR controller in (28)

Fig. 11

Time responses of $\theta _1$, $\theta _2$, and $\theta _3$ with initial state 1 in (31) in the presence of linear viscous friction under the swing-up controller in (14) and the LQR controller in (28)

5.2 Swing-up and stabilizing with linear viscous friction

Generally, if friction exists, then the energy-based control approach cannot theoretically guarantee that (6) holds. However, it is suggested in [1] that the effect of friction can be well reduced by increasing $E_\textrm{r}$ with an excess of $10\%$-$20\%$ over the theoretical value in (6). This would inject more energy than theoretically needed into the system to compensate the energy loss due to friction.

Below, we demonstrate the swing-up and stabilizing task in the presence of linear viscous friction:

$$\begin{aligned} \varvec{f}({\dot{\varvec{\theta }}})=\left[ \mu _1{\dot{\theta }}_1,\ \mu _2{\dot{\theta }}_2,\ \mu _3{\dot{\theta }}_3\right] ^{\textrm{T}}, \end{aligned}$$

where $\mu _i\ (i=1,2,3)$ are set to 0.001. We take $E_\textrm{r}=1.1(\beta _1+\beta _2+\beta _3)$, where $\beta _1+\beta _2+\beta _3$ is the theoretical value in (6) for the frictionless case. The control gains are tuned as $k_D=0.3346$, $k_P=3.2810$, and $k_V=2.1549$.

Starting from initial state 1 in (31), the simulation results are depicted in Figs. 10 and 11. As can be observed, a successful switch from the swing-up controller in (14) to the local stabilizing controller in (28) was achieved at $t=44.93\ \textrm{s}$, and the PPA robot was stabilized at the UEP in spite of the existence of friction. This indicates the robustness of our proposed control approach.

6 Conclusion

This paper studied a three-link planar robot with active last link (the PPA robot). In this paper, we made the following contributions: First, we presented a property of the PPA robot with a strict proof. This property reveals that if the active last link of the PPA robot remains stationary under a constant control input, then the whole system maintains an equilibrium configuration. Though similar properties have been proved for the double pendulum on a cart and the three-link planar robot with active first link, we showed in this paper that the proof for the PPA robot demonstrates new challenges and distinctions, which demand more complicated manipulations and extra discretion. Second, with the above property, we derived an energy-based controller and studied the behavior of the closed-loop system without any prior assumption on the robot’s mechanical parameters. The results are: $\textrm{i})$ we presented a necessary and sufficient condition to rid the energy-based controller of singular points, and showed that the total mechanical energy and the angle of the active last link converge under this controller; $\textrm{ii})$ we derived a sufficient condition for the controller to ensure that the robot stays at one of three equilibrium points with link 3 being upward, provided that the energy convergence does not equal its value at the upright equilibrium point (UEP); $\textrm{iii})$ we showed that all three equilibrium points are strictly unstable, and thus proved that the energy-based control objective targeting the UEP can be achieved for almost all initial states. In addition, we presented numerical simulations to validate the developed theoretical results, and to demonstrate the effectiveness of applying the derived controller along with an LQR controller to the swing-up and stabilizing task of the PPA robot. This paper gained an insight into the complexity of analyzing the motion of underactuated systems with underactuation degree of two under the energy-based control.

Appendices

Proof of Theorem 1

We extend the method in [15] to prove Theorem 1. Algebraic manipulations are performed using Mathematica 12.1.

To start with, define coordinate transformation:

$$\begin{aligned} \phi _1=\theta _3^{*}-\theta _1,\quad \phi _2=\theta _3^{*}-\theta _2. \end{aligned}$$

(A1)

Using (A1) with $\theta _3=\theta _3^{*}$ and $u_3=u_3^{*}$, we rewrite the dynamics in (1) as

$$\begin{aligned}{} & {} -b\ddot{\phi }_1-\ddot{\phi }_2\cos \left( \phi _1-\phi _2\right) -{\dot{\phi }}_2^2\sin \left( \phi _1-\phi _2\right) \nonumber \\{} & {} \quad =f\sin \left( \theta _3^{*}-\phi _1\right) , \end{aligned}$$

(A2)

$$\begin{aligned}{} & {} -\ddot{\phi }_1\cos \left( \phi _1-\phi _2\right) -e\ddot{\phi }_2+{\dot{\phi }}_1^2\sin \left( \phi _1-\phi _2\right) \nonumber \\{} & {} \quad =d\sin \left( \theta _3^{*}-\phi _2\right) , \end{aligned}$$

(A3)

$$\begin{aligned}{} & {} -a\ddot{\phi }_1\cos \phi _1-\ddot{\phi }_2\cos \phi _2+a{\dot{\phi }}_1^2\sin \phi _1 +{\dot{\phi }}_2^2\sin \phi _2\nonumber \\{} & {} \quad =\displaystyle \frac{u_3^{*}+\beta _3\sin \theta _3^{*}}{\alpha _{23}}, \end{aligned}$$

(A4)

where

$$\begin{aligned} a=\frac{\alpha _{13}}{\alpha _{23}},\ b=\frac{\alpha _{11}}{\alpha _{12}},\ d=\frac{\beta _{2}}{\alpha _{12}},\ e=\frac{\alpha _{22}}{\alpha _{12}},\ f=\frac{\beta _{1}}{\alpha _{12}}. \end{aligned}$$

(A5)

The newly defined parameters in (A5) are determined by (2) and (3) and thus are positive constants. They are used to reduce the complexity of following discussion. Please refer Remark 2 for a detailed explanation about these parameters and the rewritten dynamics in comparison with the counterpart in [15].

Below, we present two lemmas concerning the properties of the parameters in (A5). To prove Theorem 1, we take full advantage of these properties.

Lemma 2

Regarding the parameters in (A5), the inequalities below hold:

$$\begin{aligned}&0<a<b, \end{aligned}$$

(A6)

$$\begin{aligned}&f>ad, \end{aligned}$$

(A7)

$$\begin{aligned}&be>1, \end{aligned}$$

(A8)

$$\begin{aligned}&b+e>2. \end{aligned}$$

(A9)

Proof

Equations (A6), (A7), and (A8) can be shown by using (2) and (3) directly. Using (A8) with (2) yields $b+e\ge 2\sqrt{be}>2$, which shows (A9). $\square$

Lemma 3

If

$$\begin{aligned} e=\frac{1+a^2-ab}{a}, \end{aligned}$$

(A10)

then $a\ne 1$.

Proof

Assume that $a=1$, we then obtain $b+e=2$ from (A10), which contradicts (A9). Thus, we have $a\ne 1$. $\square$

Using $\theta _3=\theta _3^{*}$ with (5) gives $E(\varvec{\theta },{{\dot{\varvec{\theta }}}})=E^{*}$, where $E^{*}$ is a constant. In what follows, two steps are undertaken to prove Theorem 1.

Step 1 By progressively eliminating the nonlinear coupling in (A2)–(A4), we obtain a holonomic constraint of underactuated variable $\phi _1$ (or $\theta _1$, equivalently) alone in the following high-order polynomial form:

$$\begin{aligned} L=\sum _{i=0}^{28}\xi _{i}\sin ^i\phi _1\left( t\right) =0,\quad \textrm{for}\ \forall t, \end{aligned}$$

(A11)

where $\xi _{i}\ (i=0,1,\ldots ,28)$ are constants consisting of the parameters in (A5), sine and cosine of any possible $\theta _3^{*}$, and any possible $E^{*}$. We partition Step 1 into the following substeps and present the details.

Step 1.1 Performing the integration of (A4) with respect to time t gives

$$\begin{aligned} -a{\dot{\phi }}_1\cos \phi _1-{\dot{\phi }}_2\cos \phi _2=\frac{\left( u_3^{*} +\beta _3\sin \theta _3^{*}\right) t}{\alpha _{23}}+\lambda _1, \end{aligned}$$

(A12)

with $\lambda _1$ being constant. The boundedness of ${\dot{\phi }}_1$ and ${\dot{\phi }}_2$ are guaranteed by $E=E^{*}$. This leads to $u_3^{*}+\beta _3\sin \theta _3^{*}=0$. Thus, integrating (A12) yields

$$\begin{aligned} -a\sin \phi _1-\sin \phi _2=\lambda _1t+\lambda , \end{aligned}$$

(A13)

with $\lambda$ being constant. Using the boundedness of sine and cosine in (A13) gives $\lambda _1=0$. Thus, from (A12) and (A13), we have

$$\begin{aligned}&a{\dot{\phi }}_1\cos \phi _1+{\dot{\phi }}_2\cos \phi _2=0, \end{aligned}$$

(A14)

$$\begin{aligned}&a\sin \phi _1+\sin \phi _2=\lambda . \end{aligned}$$

(A15)

In what follows, we replace $\sin \phi _2$ with (A15), and we keep the highest order of $\cos \phi _1$ or $\cos \phi _2$ equals to one by using

$$\begin{aligned}&\cos ^2\phi _1=1-\sin ^2\phi _1,\ \textrm{or}\nonumber \\&\cos ^2\phi _2=1-\sin ^2\phi _2=1-\left( \lambda -a\sin \phi _1\right) ^2. \end{aligned}$$

(A16)

Step 1.2 We eliminate $\ddot{\phi }_1$ and $\ddot{\phi }_2$ in this substep. To this end, using (A2)–(A4) gives

$$\begin{aligned} \begin{bmatrix} -b &{} -\cos \left( \phi _1-\phi _2\right) &{} \sigma _1\\ -\cos \left( \phi _1-\phi _2\right) &{} -e &{} \sigma _2\\ -a\cos \phi _1 &{} -\cos \phi _2 &{} \sigma _3 \end{bmatrix} \begin{bmatrix} \ddot{\phi }_1\\ \ddot{\phi }_2\\ 1 \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned}&\sigma _1=-{\dot{\phi }}_2^2\sin \left( \phi _1-\phi _2\right) -f\sin \left( \theta _3^{*}-\phi _1\right) ,\\&\sigma _2={\dot{\phi }}_1^2\sin \left( \phi _1-\phi _2\right) -d\sin \left( \theta _3^{*}-\phi _2\right) ,\\&\sigma _3=a{\dot{\phi }}_1^2\sin \phi _1+{\dot{\phi }}_2^2\sin \phi _2. \end{aligned}$$

To avoid contradiction, the determinant of the square matrix in the above equation must equal zero. This leads to

$$\begin{aligned} F_1{\dot{\phi }}_1^2+F_2{\dot{\phi }}_2^2+F_3=0, \end{aligned}$$

(A17)

where $F_i\ (i=1,2,3)$ comprise $\sin \phi _1$, $\cos \phi _1$, and $\cos \phi _2$.

Step 1.3 We eliminate ${\dot{\phi }}_1$ and ${\dot{\phi }}_2$ in this substep. First, substituting (A1), (A15), and $E=E^{*}$ into (4) and using (A5), we obtain

$$\begin{aligned}&\frac{b}{2}{\dot{\phi }}_1^2+\frac{e}{2}{\dot{\phi }}_2^2+\cos \theta _3^{*} \left( f\cos \phi _1+d\cos \phi _2\right) \nonumber \\&\quad +\dot{\phi _1}{\dot{\phi }}_2\cos \left( \phi _1-\phi _2\right) \nonumber \\&\quad +\sin \theta _3^{*}\left( f\sin \phi _1+d\sin \phi _2\right) =\gamma , \end{aligned}$$

(A18)

where constant $\gamma$ is defined as

$$\begin{aligned} \gamma =\frac{E^{*}-\beta _3\cos \theta _3^{*}}{\alpha _{12}}. \end{aligned}$$

(A19)

Next, we use (A14) to eliminate terms of ${\dot{\phi }}_2$ via two ways. By computing ((A17)$\times e/2$-(A18)$\times F_2)\times \cos \phi _2$, we obtain

$$\begin{aligned} G_{11}+G_{12}{\dot{\phi }}_1^2=0. \end{aligned}$$

(A20)

By computing $E\times \cos ^2\phi _2$, we obtain

$$\begin{aligned} G_{21}+G_{22}{\dot{\phi }}_1^2=0, \end{aligned}$$

(A21)

where $G_{ij}\ (i,j=1,2)$ comprise $\sin \phi _1$, $\cos \phi _1$, and $\cos \phi _2$.

Finally, eliminating ${\dot{\phi }}_1$ from (A20) and (A21) gives

$$\begin{aligned} G_{11}G_{22}-G_{12}G_{21}=Q_1+Q_2\cos \phi _2=0, \end{aligned}$$

(A22)

where $Q_i\ (i=1,2)$ comprise $\sin \phi _1$ and $\cos \phi _1$. Note that the order of $\cos \theta _3^{*}$ remains to be one during the above derivation. Thus, $Q_i\ (i=1,2)$ can be expressed as

$$\begin{aligned}&Q_1=Q_{11}+Q_{12}\cos \theta _3^{*}, \end{aligned}$$

(A23)

$$\begin{aligned}&Q_2=Q_{21}+Q_{22}\cos \theta _3^{*}, \end{aligned}$$

(A24)

where the explicit expressions of $Q_{ij}\ (i=1,2)$ are omitted.

Step 1.4 Using (A22), we obtain

$$\begin{aligned} Q_1^2-Q_2^2\cos ^2\phi _2=Q_1^2-Q_2^2\left( 1-\sin ^2\phi _2\right) =0. \end{aligned}$$

(A25)

By using (A15), (A25) can be further expressed as

$$\begin{aligned} R_1+R_2\cos \phi _1=0, \end{aligned}$$

(A26)

where $R_1$ and $R_2$ are polynomials in terms of $\sin \phi _1$ with respective orders of 14 and 13. Deleting $\cos \phi _1$ from (A26) yields (A11); that is,

$$\begin{aligned} L=R_1^{2}-R_2^{2}\left( 1-\sin ^{2}\phi _{1}\right) =0. \end{aligned}$$

(A27)

Notably, if $\cos \theta _3^*=0$, then $R_2$ in (A26) equals zero, and $\cos \phi _1$ does not exist in (A25). Indeed, $Q_{11}$ can be written as ${\widehat{Q}}_{11}\times \cos \phi _1$ with ${\widehat{Q}}_{11}$ not containing $\cos \phi _1$, and $Q_{21}$ itself does not contain $\cos \phi _1$. Thus, from (A23) and (A24), if $\cos \theta _3^{*}=0$, then (A25) becomes $(1-\sin ^2\phi _1){\widehat{Q}}_{11}^2-Q_{21}^2(1-\sin ^2\phi _2)=0$, where $\cos \phi _1$ does not exist. In this case, (A27) can be simplified to $L=R_1$.

Step 2 Assume ${\dot{\phi }}_{1}=-{\dot{\theta }}_{1}\not \equiv 0$; that is, the PPA robot is not at an equilibrium configuration under the derived holonomic constraint in (A11). This is equivalent to the polynomial equation having infinite number of solutions, since $\sin \phi _1$ is time-varying. Thus, the coefficients in (A11) must satisfy

$$\begin{aligned} \xi _{i}=0,\quad i=0,1,\ldots ,28. \end{aligned}$$

(A28)

In this step, we reveal the existence of at least one nonzero coefficient for any possible mechanical parameters and any given values of $\theta _3^{*}$ and $E^{*}$. Consequently, this proves that (A28) does not hold. The details are given below.

To start with, consider $\xi _{28}$ in (A11); that is,

$$\begin{aligned}&\xi _{28}=16a^{16}\left( 1+a^2-ab-ae\right) ^2 \nonumber \\&\quad \left( \left( f-ad\right) ^2 +4adf\sin ^2\theta _3^{*}\right) \nonumber \\&\qquad \hspace{5.0pt}\times \left( \left( 1-3a^2+2ab\right) ad +\left( -3+a^2+2ae\right) f\right) ^2. \end{aligned}$$

(A29)

Using $f>ad$ in Lemma 2 yields $\left( f-ad\right) ^2+4adf\sin ^2\theta _3^{*}\ne 0$. Thus, from (A29) and $\xi _{28}=0$, we discuss the following two cases based on whether

$$\begin{aligned} 1+a^2-ab-ae\ne 0, \end{aligned}$$

(A30)

which is equivalent to $e\ne \left( 1+a^2-ab\right) /a$ holds or not:

Case 1: $e=\left( 1+a^2-ab\right) /a$

Case 2: $e\ne \left( 1+a^2-ab\right) /a$

Case 1: In this case, we obtain $\xi _{27}=0$ and

$$\begin{aligned}{} & {} \xi _{26}=1024a^{18}\left( a-b\right) ^4\left( f-ad\right) ^2\left( \left( f-ad\right) ^2\cos ^2\theta _3^{*} \right. \\{} & {} \quad \left. +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) \lambda ^2. \end{aligned}$$

Since $0<a<b$ and $f>ad$ from Lemma 2, we see that $\xi _{26}=0$ shows $\lambda =0$. This further yields $\xi _{25}=0$ and

$$\begin{aligned}{} & {} \xi _{24}=a^{12}\left( -1+a^2\right) ^2\left( f-ad\right) ^2\left( \left( f-ad\right) ^2\cos ^2\theta _3^{*} \right. \\{} & {} \quad \left. +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) \eta ^2, \end{aligned}$$

where

$$\begin{aligned} \eta =\left( 1+3a^2-4ab\right) \left( 1+5a^2-6ab\right) . \end{aligned}$$

(A31)

From Lemma 3, we have $a\ne 1$ for Case 1 and all its subcases. Thus, $\xi _{24}=0$ shows $\eta =0$. Regarding whether $b=\left( 1+3a^2\right) /\left( 4a\right)$, we consider the following two cases:

Case 1.1: $e=\left( 1+a^2-ab\right) /a$ and $b=\left( 1+3a^2\right) /\left( 4a\right)$

Case 1.2: $e=\left( 1+a^2-ab\right) /a$ and $b\ne \left( 1+3a^2\right) /\left( 4a\right)$

Below we present the details of each case.

Case 1.1: We have $\xi _{23}=\xi _{22}=\xi _{21}=0$, but

$$\begin{aligned}&\xi _{20}=\frac{1}{16}a^8\left( -1+a^2\right) ^6\left( 1+a^2\right) ^2\left( f-ad\right) ^2\\&\qquad \hspace{5.0pt}\times \left( \left( f-ad\right) ^2\cos ^2\theta _3^{*} +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) >0, \end{aligned}$$

which contradicts (A28).

Case 1.2: From (A31) and $\eta =0$, we have $b=(1+5a^2)/(6a)$. This yields $\xi _{23}=0$ and

$$\begin{aligned}&\xi _{22}=\frac{4}{81}a^{12}\left( -1+a^2\right) ^6\gamma ^2\left( \left( f-ad\right) ^2 \cos ^2\theta _3^{*} \right. \nonumber \\&\quad \left. +\left( f+ad\right) ^2\sin ^2\theta _3^{*}\right) . \end{aligned}$$

(A32)

From (A32) and $\xi _{22}=0$, we have $\gamma =0$. To avoid analyzing complicated coefficients, we always search for the one with the simplest structure in the remainder of Step 2. For this case, we skip the intermediate coefficients and obtain

$$\begin{aligned} \xi _0=\frac{\left( -1+a^2\right) ^{12}\left( af-d\right) ^4\sin ^4\theta _3^{*}}{1679616a^8}. \end{aligned}$$

(A33)

From (A33) and $\xi _0=0$, if $\sin \theta _3^{*}=0$, we obtain

$$\begin{aligned} \xi _4=\frac{\left( -1+a^2\right) ^{12}\left( d^2-f^2\right) ^2}{20736a^4}. \end{aligned}$$

Note that $\xi _{4}=0$ shows $f=d$, and thus gives

$$\begin{aligned}{} & {} \xi _{20}=\frac{1}{144}a^8\left( -1+a^2\right) ^{10}\left( 1+a\right) ^6 \\{} & {} \quad \left( 5\left( -\frac{1}{5}+a\right) ^2+\frac{24}{5}\right) ^2d^4>0, \end{aligned}$$

which contradicts (A28).

If $\sin \theta _3^{*}\ne 0$, to render $\xi _0=0$, we have $f=d/a$ yielding

$$\begin{aligned} \xi _{20}&=\frac{25}{144}a^4\left( -1+a^2\right) ^8 \left( 1+a^2\right) ^2d^4\\&\quad \Big (\left( -1+a^2\right) ^2\cos ^4\theta _3^{*}\\&\quad +2\left( 1+a^4\right) \cos ^2\theta _3^{*} \sin ^2\theta _3^{*}\\&\quad +\left( 1+a^2\right) ^2\sin ^4\theta _3^{*}\Big )>0, \end{aligned}$$

which contradicts (A28).

Case 2: In this case, we obtain from (A29) and $\xi _{28}=0$ that

$$\begin{aligned} \left( 1-3a^2+2ab\right) ad+\left( -3+a^2+2ae\right) f=0. \end{aligned}$$

(A34)

Note that

$$\begin{aligned} -3+a^2+2ae\ne 0. \end{aligned}$$

(A35)

Otherwise, if $-3+a^2+2ae=0$, then (A34) yields $1-3a^2+2ab=0$; that is, $b=\left( -1+3a^2\right) /\left( 2a\right)$, since $ad>0$. This further yields

$$\begin{aligned} e=\frac{3-a^2}{2a}=\frac{1+a^2+a\displaystyle \frac{1-3a^2}{2a}}{a}=\frac{1+a^2-ab}{a}, \end{aligned}$$

which raises a contradiction. Thus, from (A34), we have

$$\begin{aligned} f=\frac{-\left( 1-3a^2+2ab\right) ad}{-3+a^2+2ae}. \end{aligned}$$

(A36)

By substituting (A36) into (A11), we obtain

$$\begin{aligned} \xi _{26}&=\frac{256a^{18}\left( 1+a^2-ab-ae\right) ^2}{\left( -3+a^2+2ae\right) ^4}\nonumber \\&\quad \Big (\left( 1+a^2-ab-ae\right) ^2\cos ^2\theta _3^{*}\nonumber \\&\quad \hspace{5.0pt}+\left( 2-2a^2+ab-ae\right) ^2\sin ^2 \theta _3^{*}\Big )d^2\epsilon , \end{aligned}$$

(A37)

where

$$\begin{aligned}&\epsilon \ =\epsilon _1^2+\epsilon _2^2,\nonumber \\&\epsilon _1=\left( 1-14a^2+a^4+6ab+6a^3e\right) d\lambda \cos \theta _3^{*}, \end{aligned}$$

(A38)

$$\begin{aligned}&\epsilon _2=\left( -1+a^2\right) \left( -3+a^2+2ae\right) \gamma \nonumber \\&\quad -\left( 1-14a^2+a^4+6ab+6a^3e\right) d\lambda \sin \theta _3^{*}. \end{aligned}$$

(A39)

Note that

$$\begin{aligned} 2-2a^2+ab-ae\ne 0. \end{aligned}$$

(A40)

Otherwise, putting $ae=2-2a^2+ab$ into (A36) yields $f=-ad$, which contradicts the fact that f in (A5) is always positive. Thus, from (A37) and $\xi _{26}=0$, we have $\epsilon =0$. This yields $\epsilon _1=0$ and $\epsilon _2=0$.

Before proceeding to discuss Case 2 further, we first analyze a special circumstance of $a=1$. From (A38) and (A39), if $a=1$, then we have $\epsilon =36d^2(-2+b+e)^2\lambda ^2=0$. This shows $\lambda =0$, since $b+e>2$ from Lemma 2. However, this further renders all the coefficients of polynomial L in (A11) to become zero; that is, (A28) holds. To deal with this, we derive and study another holonomic constraint of $\phi _1$. From (A15) and $\lambda =0$, we have

$$\begin{aligned} \phi _1=-\phi _2,\quad {\dot{\phi }}_1=-{\dot{\phi }}_2,\quad \ddot{\phi }_1=-\ddot{\phi }_2, \end{aligned}$$

(A41)

which implies a specific configuration for the PPA robot that $\theta _1+\theta _2=2\theta _3^{*}$. By adding (A41) into the derivation in Step 1 with $a=1$, $\lambda =0$, and (A36), the derived holonomic constraint becomes

$$\begin{aligned} L_{a}=\sum _{i=0}^{12}\xi _{ia}\sin ^i\phi _1\left( t\right) =0,\quad \textrm{for}\ \forall t. \end{aligned}$$

(A42)

Consider $\xi _{12a}$ in (A42); that is,

$$\begin{aligned} \xi _{12a}=\frac{16d^2\left( \left( -2+b+e\right) ^2\cos ^2\theta _3^{*} +\left( b-e\right) ^2\sin ^2\theta _3^{*}\right) }{\left( -1+e\right) ^2}. \end{aligned}$$

Note that $e\ne 1$. Otherwise, we have $-3+a^2+2ae=0$, which contradicts (A35). We now show $b-e\ne 0$. On the contrary, assume $b-e=0$, then putting $b=e$ and $a=1$ into (A36) yields $f=-d$. This, together with $b+e>2$ from Lemma 2, gives $\xi _{12a}>0$ and thus concludes the discussion for (A42).

Thus, returning to the analysis of (A11), we just need to consider $a\ne 1$ for Case 2 and all its subcases. In such circumstance, from (A38) and (A39), we have

$$\begin{aligned}&\left( 1-14a^2+a^4+6ab+6a^3e\right) \lambda \cos \theta _3^{*}=0, \end{aligned}$$

(A43)

$$\begin{aligned}&\gamma =\frac{\left( 1-14a^2+a^4+6ab+6a^3e\right) d\lambda \sin \theta _3^{*}}{\left( -1+a^2\right) \left( -3+a^2+2ae\right) }. \end{aligned}$$

(A44)

We start by proving

$$\begin{aligned} 1-14a^2+a^4+6ab+6a^3e>0 \end{aligned}$$

(A45)

in (A43) and (A44). By using $be>1$ in (A8), we have $6ab+6a^3e\ge 12a^2\sqrt{be}>12a^2$. This, together with $1+a^4\ge 2a^2$, yields $1-14a^2+a^4+6ab+6a^3e>2a^2+12a^2-14a^2=0$. Based on (A43) and (A44), we consider the following two cases for $\xi _{26}=0$:

Case 2.1: $e\ne \left( 1+a^2-ab\right) /a$ and $\cos \theta _3^{*}\ne 0$

Case 2.2: $e\ne \left( 1+a^2-ab\right) /a$ and $\cos \theta _3^{*}=0$

Below we present the details of each case.

Case 2.1: From (A43) and (A44), we have $\lambda =0$ and thus $\gamma =0$. These lead to

$$\begin{aligned} \xi _0=\frac{\left( -1+a^2\right) ^4\left( -2a+b+a^2e\right) ^4d^4 \omega ^4\sin ^4\theta _3^{*}}{\left( -3+a^2+2ae\right) ^4}, \end{aligned}$$

(A46)

where

$$\begin{aligned} \omega =4a-3b-3a^2e+2abe. \end{aligned}$$

(A47)

Note that $-2a+b+a^2e\ge -2a+2a\sqrt{be}>-2a+2a=0$ due to $be>1$ in (A8). We now show $\omega \ne 0$. On the contrary, assume $\omega =0$, substituting (A47) into (A36) gives $f=\left( 3a-2b\right) d$. It immediately follows that $0<a<b$ and $f>ad$ do not hold simultaneously. This contradicts Lemma 2.

Thus, from (A46) and $\xi _0=0$, we have $\sin \theta _3^{*}=0$ yielding

$$\begin{aligned} \xi _{24}=\frac{144a^{16}\left( -1+a^2\right) ^2\left( 1+a^2-ab-ae\right) ^ 4d^4\varepsilon ^2}{\left( -3+a^2+2ae\right) ^4}, \end{aligned}$$

(A48)

where

$$\begin{aligned} \varepsilon =1-6a^2+a^4+ab-a^3b+a\left( -1+a^2+4ab\right) e. \end{aligned}$$

(A49)

From (A30), we see that $\xi _{24}=0$ gives $\varepsilon =0$. We now show $-1+a^2+4ab\ne 0$ in (A49) by contradiction. Substituting $-1+a^2+4ab=0$ into (A49) gives $\left( -5+a^2\right) \left( -1+5a^2\right) /4=0$. If $-5+a^2=0$ holds, then $-1+a^2+4ab=4+4ab>0$. If $-1+5a^2=0$ holds, then by using (A6) we have $-1+a^2+4ab>-1+5a^2=0$.

Thus, from (A48) and $\xi _{24}=0$, we have

$$\begin{aligned} e=\frac{-1+6a^2-a^4-ab+a^3b}{a\left( -1+a^2+4ab\right) }. \end{aligned}$$

(A50)

This further yields

$$\begin{aligned} \xi _{20}&=\frac{1600a^{18}\left( -1+a^2\right) ^6\left( a-b\right) ^6\left( 1+a^2+6ab\right) ^2d^4}{\left( -1+a^2+4ab\right) ^2\left( -1-8a^2+a^4+14ab-6a^3b\right) ^4}\\&\quad \hspace{5.0pt}\times \left( \left( -7+a^2-2ab\right) ^2\left( -3+a^2+2ab\right) ^2\right) . \end{aligned}$$

Note that the denominator of $\xi _{20}$ does not equal zero. Otherwise, under (A36) and (A50), $-1-8a^2+a^4+14ab-6a^3b=0$ yields $-3+a^2+2ae=0$; $-7+a^2-2ab=0$ yields $a>b$; and $-3+a^2+2ab=0$ yields $f=ad$. These are all impossible due to (A35) and Lemma 2. Thus, we have $\xi _{20}>0$, which contradicts (A28).

Case 2.2: In this case, if $\lambda =0$, then $\gamma =0$ and we can use (A46) with $\sin \theta _3^*=\pm 1$ to show $\xi _0\ne 0$. Thus, we just need to consider $\lambda \ne 0$. Note that from Step 1.1, by substituting (A1) into (A15) with $\cos \theta _3^{*}=0$ and using (A5) with (2), we obtain

$$\begin{aligned} l_1\cos \theta _1+l_2\cos \theta _2=l_2\lambda . \end{aligned}$$

This implies that link 3 of the PPA robot is in the horizontal position and maintains a constant height. Moreover, from Step 1.4, we have $R_2=0$ when $\cos \theta _3^{*}=0$. Thus, in this case, we study $L=R_1=0$ instead of (A11). By using (A36) and (A44) with $\cos \theta _3^{*}=0$, we obtain from $R_1$ a polynomial equation of $\sin \phi _1$ with the highest order being equal to 12; that is,

$$\begin{aligned} L=\sum _{i=0}^{12}\xi _{i}\sin ^i\phi _1\left( t\right) =0,\quad \textrm{for}\ \forall t. \end{aligned}$$

(A51)

Consider $\xi _{12}$ in (A51); that is,

$$\begin{aligned}&\xi _{12}=\frac{4a^8\left( 1+a^2-ab-ae\right) \left( 2-2a^2+ab-ae\right) d^2}{\left( -1+a^2\right) \left( -3+a^2+2ae\right) ^2}\nonumber \\&\qquad \quad \times \left( \left( -1+a^2\right) ^2 \varTheta _{12}+12a\varDelta _{12}\lambda ^2\right) , \end{aligned}$$

(A52)

where

$$\begin{aligned} \varTheta _{12}&=6+20a^2+6a^4-9ab-3a^3b \nonumber \\&\quad -\left( 3a+9a^3+8a^2b\right) e, \end{aligned}$$

(A53)

$$\begin{aligned} \varDelta _{12}&=-6a-6a^3+b+3a^2b\nonumber \\&\quad +\left( 3a^2+a^4+2ab+2a^3b\right) e. \end{aligned}$$

(A54)

By using (A30), (A35), and (A40), from (A52) and $\xi _{12}=0$, we have

$$\begin{aligned} \left( -1+a^2\right) ^2\varTheta _{12}+12a\varDelta _{12}\lambda ^2=0. \end{aligned}$$

(A55)

Below we show $\varDelta _{12}\ne 0$. Suppose that $\varDelta _{12}$ equals zero, then from (A55), $\varTheta _{12}$ must also equal zero since $a\ne 1$. Using (A53) and (A54), we obtain b and the corresponding e from $\varTheta _{12}=0$ and $\varDelta _{12}=0$ as

$$\begin{aligned}&b=\frac{3-a^2}{2a},\quad \hspace{5.0pt}\; e=\frac{-1+3a^2}{2a}, \end{aligned}$$

(A56)

$$\begin{aligned}&\textrm{or}\nonumber \\&b=\frac{2a^3+6a^5}{5+3a^4},\ e=\frac{6+2a^2}{3a+5a^5}. \end{aligned}$$

(A57)

Substituting (A56) into (A36) gives $f=ad$, which contradicts Lemma 2. As for (A57), by using $be>1$ in (A8), we have $(2a^3+6a^5)(6+2a^2)-(5+3a^4)(3a+5a^5)=-3a(-1+a^2)^2(5+6a^2+5a^4)>0$, which raises a contradiction. Thus, $\varDelta _{12}\ne 0$.

From (A55), we have

$$\begin{aligned} \lambda ^2=-\frac{\left( -1+a^2\right) ^2\varTheta _{12}}{12a\varDelta _{12}}. \end{aligned}$$

(A58)

By using (A58), we obtain

$$\begin{aligned} \xi _i=k_i{\widehat{\xi }}_i,\quad i=11,10,9, \end{aligned}$$

(A59)

where $k_i\ (i=11,10,9)$ are guaranteed to be nonzero terms. We omit the explicit expressions of other ${\widehat{\xi }}_i$ in (A59) and present only that of ${\widehat{\xi }}_{11}$ below:

$$\begin{aligned} {\widehat{\xi }}_{11}&=-42+52a^2+124a^4\\&\quad +52a^6-42a^8+9ab-33a^3b-63a^5b+39a^7b\\&\quad \quad \hspace{5.0pt}-9a^2b^2+18a^4b^2-9a^6b^2\\&\quad +\big (39a-63b^3-33a^5+9a^7+24b-86a^2b\\&\quad \quad \hspace{5.0pt}-68a^4b-86a^6b+24a^8b+18ab^2\\&\quad +6a^3b^2+36a^5b^2-12a^7b^2\big )e\\&\quad \quad \hspace{5.0pt}+\big (-9a^2+18a^4-9a^6-12ab\\&\quad +36a^3b+6a^5b+18a^7b+16a^2b^2\\&\quad \quad \hspace{5.0pt}+16a^4b^2+16a^6b^2\big )e^2. \end{aligned}$$

Thus, $\xi _i=0\ (i=11,10,9)$ are equivalent to

$$\begin{aligned} {\widehat{\xi }}_i=0,\quad i=11,10,9. \end{aligned}$$

(A60)

Note that (A60) can be viewed as polynomial equations with a, b, and e as variables, where the highest order of e in ${\widehat{\xi }}_{11}$, ${\widehat{\xi }}_{10}$, and ${\widehat{\xi }}_{9}$ are equal to 2, 4, and 5, respectively. Moreover, we obtain $\xi _8$ from (A51). Below we show that (A60) and $\xi _8=0$ do not hold simultaneously.

Starting with the assumption that (A60) holds, we first eliminate e and derive the following three polynomial equations in terms of a and b from (A60):

$$\begin{aligned} \delta _i=0,\quad i=1,2,3. \end{aligned}$$

(A61)

To this end, we divide ${\widehat{\xi }}_{10}$ by ${\widehat{\xi }}_{11}$ with respect to e to obtain

$$\begin{aligned} {\widehat{\xi }}_{10}=p_{10}{\widehat{\xi }}_{11}+k_{10}r_{10}, \end{aligned}$$

(A62)

where $p_{10}$ is the quotient and $k_{10}r_{10}$ is the remainder with $k_{10}$ being the nonzero term. The same notations (or with bars) apply to the following process of the derivation of (A61). From ${\widehat{\xi }}_{10}=0$ and ${\widehat{\xi }}_{11}=0$ in (A62), we have $r_{10}=0$ in which the highest order of e has been reduced to 1. Moreover, we iterate the division by taking the divisor and nonzero part of the remainder in (A62) as the new dividend and divisor; that is, we divide ${\widehat{\xi }}_{11}$ by $r_{10}$ with respect to e to obtain

$$\begin{aligned} {\widehat{\xi }}_{11}=p_{11}r_{10}+k_{11}\delta _1, \end{aligned}$$

where $\delta _1=0$ is now the first polynomial equation, since ${\widehat{\xi }}_{11}=0$ and $r_{10}=0$. Similarly, we replace ${\widehat{\xi }}_{10}$ with ${\widehat{\xi }}_9$ and obtain

$$\begin{aligned} {\widehat{\xi }}_9=p_9{\widehat{\xi }}_{11}+k_{9}r_{9},\quad {\widehat{\xi }}_{11}={\overline{p}}_{11}r_9+{\overline{k}}_{11}\delta _2, \end{aligned}$$

where the highest order of e in $r_9$ is equal to 1. From ${\overline{k}}_{11}\delta _9$, we obtain the second polynomial equation $\delta _2=0$. Finally, we use $r_9$ and $r_{10}$ to obtain

$$\begin{aligned} r_9={\overline{p}}_{9}r_{10}+{\overline{k}}_{9}\delta _3. \end{aligned}$$

This gives the third polynomial equation $\delta _3=0$ and thus leads to (A61). Note that the highest orders of b in $\delta _1$, $\delta _2$, and $\delta _3$ are equal to 12, 12, and 10, respectively.

Next, by using (A61), we eliminate b and derive two polynomial equations solely in terms of a. To this end, we take $\delta _1$ and $\delta _3$ as the initial dividend and divisor with respect to b and obtain

$$\begin{aligned} \delta _1=m_1\delta _3+{\widetilde{k}}_1n_1, \end{aligned}$$

where $m_1$ is the quotient and ${\widetilde{k}}_1n_1$ is the remainder with ${\widetilde{k}}_1$ being the nonzero part. This gives $n_1=0$ with the highest order of b being equal to 9. We omit the subsequent process since it replicates the derivation of $\delta _1=0$ with more iteration. From the remainder of the final division, we obtain the following polynomial equation with $z=a^2>0$:

$$\begin{aligned} P_1=\sum _{i=0}^{362}\varsigma _{1,i}z^i=\varPhi {\widehat{P}}_1=0, \end{aligned}$$

(A63)

where $\varsigma _{1,i}\ (i=0,1,\ldots ,362)$ are constants and ${\widehat{P}}_1$ and $\varPhi$ are polynomials of z. Same derivation using $\delta _2$ as the initial dividend instead of $\delta _1$ yields the second polynomial equation with $z=a^2>0$:

$$\begin{aligned} P_2=\sum _{i=0}^{382}\varsigma _{2,i}z^i=\varPhi {\widehat{P}}_2=0, \end{aligned}$$

(A64)

where $\varsigma _{2,i}\ (i=0,1,\ldots ,382)$ are constants and ${\widehat{P}}_2$ is a polynomial of z. The explicit expressions of ${\widehat{P}}_1$, ${\widehat{P}}_2$, and $\varPhi$ are omitted.

Then, note that both $P_1=0$ and $P_2=0$ are derived from (A61), while (A61) is derived from (A60). Thus, a necessary condition for (A60) is that (A63) and (A64) hold simultaneously. In this case, it is equivalent to the common positive real solutions of ${\widehat{P}}_1=0$ and ${\widehat{P}}_2=0$ and the positive real solutions of $\varPhi =0$; that is,

$$\begin{aligned}&z=0.125043,\quad z=0.514811,\quad z=1.942459, \end{aligned}$$

(A65)

$$\begin{aligned}&\textrm{and}\nonumber \\&z=0.066778,\quad z=0.125043,\nonumber \\&\quad z=0.140556,\quad z=0.250000,\nonumber \\&z=4.000000,\quad z=7.114591,\nonumber \\&\quad z=7.997246,\quad z=14.97492, \end{aligned}$$

(A66)

respectively. We give a detailed explanation of these solutions in Remark 4.

Finally, we conduct an examination to see whether $\xi _8=0$ holds under these solutions. Specifically, we substitute each positive a obtained from (A65) and (A66) into $\delta _1=0$ in (A61), and solve b from the resulting equation. Combining with its corresponding a, we then substitute the obtained b into ${\widehat{\xi }}_{11}=0$ in (A60) to solve e and obtain the combination of (a, b, e). Now, for each combination, we first check whether the properties in Lemma 2 are satisfied with the aid of (A36). If so, we then substitute this combination into $\xi _8$ and check whether $\xi _8=0$ or not. Following such examination, we find that none of the solutions in (A65) or (A66) renders $\xi _8=0$; that is, (A60) and $\xi _8=0$ do not hold simultaneously. The details are omitted.

Thus, we conclude from (A59) that there exists at least one nonzero coefficient among $\xi _{11}$, $\xi _{10}$, $\xi _{9}$, and $\xi _{8}$, which contradicts (A28). We give some discussion concerning the analysis of Case 2.2 in Remark 3.

Thus far, we have located at least one nonzero coefficient for every case. This proves that (A28) does not hold in any circumstance. As a result, ${\dot{\theta }}_1=-{\dot{\phi }}_1\equiv 0$, which leads to $\sin \phi _2=\lambda _0$ with $\lambda _0$ being a constant. Consequently, ${\dot{\theta }}_2=-{\dot{\phi }}_2\equiv 0$, and hence completes the proof. $\square$

The three remarks given below concern the newly defined parameters in (A5), the analysis of Case 2.2 in comparison with [15], and the numerical solutions in (A65) and (A66), respectively.

Remark 2

The definition of newly defined parameters varies with actuator configuration of the three-link robot. From [15], the rewritten dynamics of the three-link planar robot with active first link are

$$\begin{aligned}&a\ddot{\phi }_2\cos \phi _2+\ddot{\phi }_3\cos \phi _3-a{\dot{\phi }}_2^2\sin \phi _2-{\dot{\phi }}_3^2 \sin \phi _3 \nonumber \\&\quad =\displaystyle \frac{\tau _1^{*}+\beta _1\sin \theta _1^{*}}{\alpha _{13}}, \end{aligned}$$

(A67)

$$\begin{aligned}&b\ddot{\phi }_2+\ddot{\phi }_3\cos \left( \phi _3-\phi _2\right) -{\dot{\phi }}_3^2\sin \left( \phi _3-\phi _2\right) \nonumber \\&\quad =ad\sin \left( \phi _2+\theta _1^{*}\right) , \end{aligned}$$

(A68)

$$\begin{aligned}&\ddot{\phi }_2\cos \left( \phi _3-\phi _2\right) +e\ddot{\phi }_3 +{\dot{\phi }}_2^2\sin \left( \phi _3-\phi _2\right) \nonumber \\&\quad =d\sin \left( \phi _3+\theta _1^{*}\right) , \end{aligned}$$

(A69)

where the angle of the first link and the control input are constants, and

$$\begin{aligned} a=\frac{\alpha _{12}}{\alpha _{13}},\ b=\frac{\alpha _{22}}{\alpha _{23}},\ d=\frac{\beta _3}{\alpha _{23}},\ e=\frac{\alpha _{33}}{\alpha _{23}}. \end{aligned}$$

(A70)

From (A70), we see that the set of newly defined parameters in (A5) inherits the notations but differs in content, since the PPA robot studied in this paper is actuated by the last link instead of the first. Note that although the underactuated parts of the dynamics in (A2) and (A3) coincide with (A68) and (A69) in structure, comparing (A5) with (A70) shows that there is one more newly added parameter f for the PPA robot. This difference takes root in the fundamental structure of mechanical parameters in (2) and (3). Indeed, the counterpart of f in (A68) can be expressed by $a\times d$, since $a=\alpha _{12}/\alpha _{13}=\beta _2/\beta _3$ holds. However, we cannot find similar connection between f and the rest in (A5). Consequently, the existence of f significantly complicates the coefficients of the polynomial in (A11) compared to that in [15]. To deal with this increased complexity, we take full advantage of the properties of the newly defined parameters in Lemma 2 to simplify the discussion and further identify nonzero coefficient(s).

Remark 3

The condition of Case 2.2 is similar to that of Case 2.2.2 in [15]; that is, the actuated link is in the horizontal position. It is very difficult to discuss these two cases, since no useful information can be drawn to directly ease the strong coupling of the newly defined parameters inside $\xi _i$. To unveil a nonzero coefficient, we obtain two polynomial equations solely in terms of a from $\xi _i$. This is achieved by performing a series of iterative polynomial division, which is a method used in [15] of eliminating targeted variable(s) from multi-variable polynomial equations at the expense of increasing the highest order of other variable(s). However, unlike the counterpart in [15] where parameter e is fixed, in Case 2.2 it remains indefinite, and thus should be treated as a targeted variable to eliminate in the same manner as for b. This difference inevitably aggravates the complexity of iteration, as demonstrated in Case 2.2. As a result, we end up with high-order polynomial equations of a, which demand further analysis and inspection not encountered in [15].

Remark 4

The numerical solutions in (A65) and (A66) are calculated using the Mathematica function “NSolve”. The “WorkingPrecision” option of this function is set to 50 to provide solutions with adequate precision of 50-digit, while a lower precision would also suffice to yield the same conclusion in Case 2.2. For brevity, we only present the first six digits of these solutions in (A65) and (A66).

Stability analysis of equilibrium points

By calculating the characteristic polynomial of the robot’s linearization at the down–up–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(\pi ,0,0,0,0,0)$, we obtain

$$\begin{aligned}{} & {} \left| s\varvec{I}-\varvec{J}_{duu} \right| \\{} & {} \quad =s^6+a_1s^5+a_2s^4+a_3s^3+a_4s^2+a_5s+a_6, \end{aligned}$$

where $\varvec{J}_{duu}$ is the corresponding Jacobian matrix, and

$$\begin{aligned}&a_1\cdot \varPi _{duu}=-k_V\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) ,\\&a_2\cdot \varPi _{duu}=-k_P\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) +k_D \left( -\alpha _{22}\beta _1+\alpha _{11}\beta _2\right) \\&\qquad +2\beta _1\Big (-\alpha _{23}^2\beta _1+\left( \alpha _{13}^2-\alpha _{11}\alpha _{33}\right) \beta _2 \\&\qquad +\alpha _{12}^2\beta _3+\alpha _{22}\left( \alpha _{33}\beta _1-\alpha _{11}\beta _3\right) \Big ),\\&a_3\cdot \varPi _{duu}=k_V\left( -\alpha _{22}\beta _{1}+\alpha _{11}\beta _2\right) ,\\&a_4\cdot \varPi _{duu}=k_P\left( -\alpha _{22}\beta _1+\alpha _{11}\beta _2\right) +\beta _1\Big (\left( k_D-2\alpha _{33}\beta _1\right) \beta _2\\&\qquad \qquad \quad \hspace{5.0pt}+2\left( -\alpha _{22}\beta _1+\alpha _{11}\beta _2\right) \beta _3\Big ),\\&a_5\cdot \varPi _{duu}=k_V\beta _1\beta _2,\quad a_6\cdot \varPi _{duu}=\beta _1\beta _2\left( k_P+2\beta _1\beta _3\right) , \end{aligned}$$

with

$$\begin{aligned} \varPi _{duu}&=-\Big (k_D\big (\alpha _{11}\alpha _{22}-\alpha _{12}^2\big ) +2\beta _1\nonumber \\&\quad \big (\alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23}\nonumber \\&\quad \hspace{5.0pt}+\alpha _{11}\alpha _{23}^2-\big (\alpha _{11}\alpha _{22} -\alpha _{12}^2\big )\alpha _{33}\big )\Big ). \end{aligned}$$

(B1)

We recall the requirement on $k_D$ in Lemma 1 for the controller in (14) to be nonsingular. From (15), we have

$$\begin{aligned}&k_D>\left( E_\textrm{r}-P\left( \varvec{\theta }\right) \right) \left( \varvec{B}^\textrm{T}\varvec{M}^{-1} \left( \varvec{\theta }\right) \varvec{B}\right) ^{-1}\Big |_{\varvec{\theta }=[\pi ,0,0]^\textrm{T}}\nonumber \\&\quad \hspace{5.0pt}=\frac{-2\beta _1}{\alpha _{11}\alpha _{22}-\alpha _{12}^2} \left( \alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23} \right. \nonumber \\&\quad \left. +\alpha _{11}\alpha _{23}^2+\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) \alpha _{33}\right) . \end{aligned}$$

(B2)

By using (B1), (B2), and $\alpha _{11}\alpha _{22}-\alpha _{12}^2>0$ due to $\varvec{M}(\varvec{\theta })|_{\varvec{\theta }=\varvec{0}_3}>0$, we have $\varPi _{duu}<0$. This leads to $a_5<0$ and $a_6<0$, regardless of control gains and mechanical parameters. Hence, it can be concluded that the down–up–up equilibrium point is strictly unstable, since $\varvec{J}_{duu}$ possesses no less than one eigenvalue in the open right-half plane. The instability of the up–down–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},{\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(0,\pi ,0,0,0,0)$ can be proved similarly.

Regarding the down–down–up equilibrium point $(\theta _{1},\theta _{2},\theta _{3},$ ${\dot{\theta }}_{1},{\dot{\theta }}_{2},{\dot{\theta }}_{3})=(\pi ,\pi ,0,$ 0, 0, 0), calculating its characteristic polynomial yields

$$\begin{aligned} \left| s\varvec{I}-\varvec{J}_{ddu} \right| =s^6+a_1s^5+a_2s^4+a_3s^3+a_4s^2+a_5s+a_6, \end{aligned}$$

where $\varvec{J}_{ddu}$ is the corresponding Jacobian matrix, and

$$\begin{aligned}&a_1\cdot \varPi _{ddu}=-k_V\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) ,\\&a_2\cdot \varPi _{ddu}=-k_P\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) \\&\quad -k_D \left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) -2\left( \beta _1+\beta _2\right) \\&\quad \hspace{5.0pt}\times \left( \alpha _{23}^2\beta _1+\alpha _{13}^2\beta _2 -\alpha _{12}^2\beta _3 \right. \\&\quad \left. -\alpha _{33}\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) +\alpha _{11}\alpha _{22}\beta _3\right) ,\\&a_3\cdot \varPi _{ddu}=-k_V\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) ,\\&a_4\cdot \varPi _{ddu}=-k_P\left( \alpha _{22}\beta _1+\alpha _{11}\beta _2\right) \\&\quad -\beta _1\beta _2\left( k_D-2\alpha _{33}\left( \beta _1+\beta _2\right) \right) \\&\quad \qquad \quad \hspace{5.0pt}-2\left( \beta _1+\beta _2\right) \left( \alpha _{22}\beta _1 +\alpha _{11}\beta _2\right) \beta _3, \\&a_5\cdot \varPi _{ddu}=-k_V\beta _1\beta _2, a_6\cdot \varPi _{ddu}\\&\quad =-\beta _1\beta _2 \left( k_P+2\left( \beta _1+\beta _2\right) \beta _3\right) , \end{aligned}$$

with

$$\begin{aligned} \varPi _{ddu}&=-\Big (k_D\big (\alpha _{11}\alpha _{22}-\alpha _{12}^2\big )+2\big (\beta _1 +\beta _2\big )\\&\quad \big (\alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23}\\&\quad \hspace{5.0pt}+\alpha _{11}\alpha _{23}^2 -\big (\alpha _{11}\alpha _{22}-\alpha _{12}^2\big )\alpha _{33}\big )\Big ). \end{aligned}$$

Similarly, exploiting the requirement on $k_D$ in Lemma 1 gives

$$\begin{aligned}&k_D>\left( E_\textrm{r}-P\left( \varvec{\theta }\right) \right) \left( \varvec{B}^\textrm{T}\varvec{M}^{-1} \left( \varvec{\theta }\right) \varvec{B}\right) ^{-1}\Big |_{\varvec{\theta }=[\pi ,\pi ,0]^\textrm{T}}\\&\quad \hspace{5.0pt}=\frac{-2\left( \beta _1+\beta _2\right) }{\alpha _{11}\alpha _{22} -\alpha _{12}^2}\\&\quad \left( \alpha _{13}^2\alpha _{22}-2\alpha _{12}\alpha _{13}\alpha _{23} +\alpha _{11}\alpha _{23}^2-\left( \alpha _{11}\alpha _{22}-\alpha _{12}^2\right) \alpha _{33}\right) , \end{aligned}$$

which leads to $\varPi _{ddu}<0$. Thus, we have $a_1$, $a_3$, $a_5$, and $a_6$ being positive, regardless of control gains and mechanical parameters. However, the signs of $a_2$ and $a_4$ are left undetermined. To reveal the instability of this equilibrium point, we further compute the Hurwitz determinant

$$\begin{aligned} D_3= \begin{vmatrix} a_1&\quad a_3&\quad a_5\\ 1&\quad a_2&\quad a_4\\ 0&\quad a_1&\quad a_3 \end{vmatrix} =a_1a_2a_3-a_3^2-a_1^2a_4+a_1a_5, \end{aligned}$$

which yields

$$\begin{aligned} D_3\cdot \varPi _{ddu}^3&=2k_V^2\left( \beta _1+\beta _2\right) \\&\quad \Big (\alpha _{22} \beta _1^2\left( \alpha _{13}\alpha _{22}-\alpha _{12}\alpha _{23}\right) ^2 +\alpha _{11}\beta _2^2\big (\alpha _{12}\alpha _{13}\\&\quad \hspace{5.0pt}-\alpha _{11}\alpha _{23}\big )^2 +2\alpha _{12}\beta _1\beta _2\left( \alpha _{13}\alpha _{22}-\alpha _{12}\alpha _{23}\right) \\&\quad \left( \alpha _{12}\alpha _{13}-\alpha _{11}\alpha _{23}\right) \Big ). \end{aligned}$$

Straightforward calculation with (2) and using $m_il_il_{ci}\ge J_i+m_il_{ci}^2$ from [28] shows $\alpha _{13}\alpha _{22}-\alpha _{12}\alpha _{23}\le 0$ and $\alpha _{12}\alpha _{13}-\alpha _{11}\alpha _{23}<0$. Thus, $D_3<0$ since $\varPi _{ddu}<0$. Hence, $\varvec{J}_{ddu}$ has one eigenvalue in the open right-half plane at a minimum, indicating that the down–down–up equilibrium point is strictly unstable. $\square$