Global motion analysis of energy-based control for 3-link planar robot with a single actuator at the first joint

Abstract

This paper studies nonlinear control of a 3-link planar robot moving in the vertical plane with only the first joint being actuated while the two other revolute joints are passive (called the APP robot below). A nonlinear energy-based controller is proposed, whose objective is to drive the APP robot into an invariant set where the first link is in the upright position and the total mechanical energy converges to its value at the upright equilibrium point (all three links are in the upright position). By presenting and using a new property of the motion of the APP robot, without any condition on its mechanical parameters, this paper proves that if the control gains are larger than specific lower bounds, then only a measure-zero set of initial conditions converges to three strictly unstable equilibrium points instead of converging to the invariant set. This paper presents numerical results for a physical 3-link planar robot to validate the obtained theoretical results and to demonstrate a switch–and–stabilize maneuver in which the energy-based controller is switched to a linear state feedback controller that stabilizes the APP robot at its upright equilibrium point.

1 Introduction

Studies on underactuated mechanical systems, which possess fewer actuators than degrees of freedom (DOF), have received considerable interest in the last two decades. In mobile robotic locomotion (legged, wheeled, swimming, flying, etc.), underactuation is an inherent property of the system since the degrees of freedom that describe net body motion are not directly actuated. Moreover, underactuation may alternatively be a consequence of on-purpose “minimalistic” design without using full actuation or that of the failure of one or more actuators. However, it is difficult to control these systems due to their complex nonlinear dynamics and nonholonomic behavior, see pioneer works in [10, 15, 25, 26], and other interesting results in [2,3,4, 7,8,9, 13, 18, 19, 22, 24, 27,28,29].

Many researchers investigated the notion of energy shaping in controlling underactuated mechanical systems since energy is an important variable related to the motion of the systems. For an underactuated mechanical system with generalized coordinate ${\varvec{\theta }}(t)$, [10] and [15] addressed the simultaneous control of both its total mechanical energy $E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))$ and actuated variable(s) ${\varvec{\theta }}_a(t)$; that is, whether one can design a controller to achieve

$$\begin{aligned}&\lim _{t\rightarrow \infty } E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))=E_r, \end{aligned}$$

(1)

$$\begin{aligned}&\lim _{t\rightarrow \infty } {\varvec{\theta }}_a(t)={\varvec{\theta }}_{ar}, \quad \lim _{t\rightarrow \infty } \dot{{\varvec{\theta }}}_a(t)={\varvec{0}}, \end{aligned}$$

(2)

where $E_r$ is a given constant, ${\varvec{\theta }}_{ar}$ is a given constant vector, and ${\varvec{0}}$ is zero column vector with a compatible size.

For the Pendubot [11, 15], and the Acrobot [32], objectives (1) and (2) have been shown to be achievable for the swing-up and stabilizing control problem, which is to drive the robot to a small neighborhood of its UEP (upright equilibrium point) and then stabilize it around that point, where all links are in the upright position. The above energy-based control is applied to stabilize an unstable equilibrium point of the butterfly robot in [6]. However, [31] showed that objectives (1) and (2) cannot be achieved simultaneously for the swing-up and stabilizing control problem of a 2-link underactuated robot with a particular counterweight connected to the passive first joint. For a set-point control for a folded configuration of 3-link gymnastic planar robot with the first joint being passive (unactuated) and the second and third joints being active (actuated), we proved in [17] that objectives (1) and (2) can be achieved simultaneously if the mechanical parameters of the robot satisfy certain conditions, and we show via a numerical example that objectives (1) and (2) are not achieved simultaneously when the mechanical parameters of the robot do not satisfy these conditions. Thus, for an underactuated system with particular mechanical parameters, although objective (2) can be achieved for example by the partial feedback linearization in [26], it is not clear whether objectives (1) and (2) can be achieved simultaneously.

Although there are many results for mechanical systems with underactuation degree one [1, 10, 12], that is, the number of control inputs is one less than that of degrees of freedom, designing and analyzing controllers for mechanical systems with underactuation degree greater than one are still a challenging problem. For the double pendulum in a cart, [30] showed that objectives (1) and (2) can be achieved with $E_r$ being the highest potential energy of the double pendulum for almost all initial conditions of the system. Building on this previous research, for a 3-link planar robot in a vertical plane with its first joint being active and the rest joints being passive, this paper studies a theoretically challenging problem, that is, whether objectives (1) and (2) corresponding to the UEP (all three links are in the upright position), and objective (3)

$$\begin{aligned} \lim _{t\rightarrow \infty } {\varvec{\theta }}(t)={\varvec{0}}_{3}, \quad \lim _{t\rightarrow \infty } \dot{{\varvec{\theta }}}(t)={\varvec{0}}_{3}, \end{aligned}$$

(3)

are achievable for almost every initial condition, where ${\varvec{\theta }}(t)$ is the vector of three link angles of the robot, and ${\varvec{0}}_{3}$ denotes a zero column vector with size 3. This is the ultimate objective of stabilizing the robot at the UEP. We call this robot APP (Active Passive Passive) robot below.

This paper applies the procedure in [10, 15] to derive an energy-based controller for the APP robot. By presenting and using a new property of the motion of the APP robot, without any condition on its mechanical parameters, this paper proves that if the control gains are larger than specific lower bounds, then objectives (1) and (2) corresponding to the UEP are achievable for all initial conditions with the exception of a set of Lebesgue measure zero.

Indeed, first, the new property is that if link 1 of the APP robot does not move under a constant torque on joint 1, then links 2 and 3 do not move. To the best of our knowledge, this property has not yet been proved. We present a strict proof of this property for any mechanical parameters of the APP robot, any constant angle of joint 1, and corresponding constant torque by using some properties of the mechanical parameters of the APP robot. Second, the measure-zero set of initial conditions converges to three strictly unstable equilibrium points: the up–up–down, up–down–up, and up–down–down equilibrium points, where, for example, up–up–down means that links 1, 2, and 3 are in the upright, upright, and downward positions, respectively.

The presented control law achieves objectives (1) and (2) corresponding to the UEP for almost all initial conditions but does not achieve objective (3), since the UEP becomes strictly unstable. This motivates the use of the additional LQR-based linear state feedback law. It is worth pointing out that the linear controller succeeds in achieving only local stabilization, from initial conditions in a close neighborhood of the UEP. The combination of switching between the two control laws is then shown to practically achieve all objectives (1), (2), and (3), but no formal proof is found yet that shows that this ALWAYS works.

The remainder of the paper is organized as follows: Sect. 2 gives some preliminary knowledge and problem formulation. Section 3 presents the main results of this paper. Section 4 makes some discussions. Section 5 gives numerical simulation results for a physical 3-link planar robot in [20]. Section 6 makes some concluding remarks. Certain proofs whose details are not central to the flow of the paper are gathered in the appendices. For brevity, we omit time argument t in the expression of a variable if it is clear from the context.

2 Preliminary knowledge and problem formulation

2.1 Preliminary knowledge

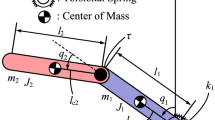
Consider a 3-link planar robot with a single actuator at joint 1 (at the origin) shown in Fig. 1. For link i ($i=1, 2, 3$), $m_i$ is its mass, $l_i$ is its length, $l_{ci}$ is the distance from joint i to its center of mass (COM), and $J_{i}$ is the moment of inertia around its COM, $\tau _1$ is the torque acting at joint 1, and $\theta _i$ is the angle measured counterclockwise from the positive Y-axis. In this paper, $\theta _1$, the angle of active joint 1, is dealt in ${\mathbb {R}}$; $\theta _2$ and $\theta _3$, the angles of the passive links, are dealt with in ${\mathbb {S}}^2$ (a torus) and take value in $(-\pi , \pi ]$.

Fig. 1

APP robot: 3-link planar robot with a single actuator at the first joint

The motion equation of the APP robot is

$$\begin{aligned} {\varvec{M}}({\varvec{\theta }})\ddot{{\varvec{\theta }}}+ {\varvec{C}}({\varvec{\theta }},\dot{{\varvec{\theta }}})\dot{{\varvec{\theta }}}+ {\varvec{g}}({\varvec{\theta }} )={\varvec{b}}\tau _1, \end{aligned}$$

(4)

where ${\varvec{\theta }}= \left[ \begin{array}{ccc} \theta _1,&\theta _2,&\theta _3 \end{array}\right] ^\mathrm{T}$ and

$$\begin{aligned}&{\varvec{M}}({\varvec{\theta }} )\nonumber \\&\quad = \left[ \begin{array}{l@{\quad }l@{\quad }l} \alpha _{11} &{} \alpha _{12}\cos (\theta _2-\theta _1) &{} \alpha _{13}\cos (\theta _3-\theta _1)\\ \alpha _{12}\cos (\theta _2-\theta _1) &{} \alpha _{22} &{} \alpha _{23}\cos (\theta _3-\theta _2)\\ \alpha _{13}\cos (\theta _3-\theta _1) &{} \alpha _{23}\cos (\theta _3-\theta _2)&{} \alpha _{33} \end{array} \right] , \end{aligned}$$

(5)

$$\begin{aligned}&{\varvec{C}}({\varvec{\theta }},\dot{{\varvec{\theta }}})\nonumber \\&\quad = \left[ \begin{array}{l@{\quad }l@{\quad }l} 0 &{} -\alpha _{12}\dot{\theta }_2\sin (\theta _2-\theta _1) &{} -\alpha _{13}\dot{\theta }_3\sin (\theta _3-\theta _1) \\ \alpha _{12}\dot{\theta }_1\sin (\theta _2-\theta _1) &{} 0 &{} -\alpha _{23}\dot{\theta }_3\sin (\theta _3-\theta _2)\\ \alpha _{13}\dot{\theta }_1\sin (\theta _3-\theta _1) &{} \alpha _{23}\dot{\theta }_2 \sin (\theta _3-\theta _2)&{} 0 \end{array} \right] ,\end{aligned}$$

(6)

$$\begin{aligned}&{\varvec{g}}({\varvec{\theta }} )= \left[ \begin{array}{c} -\beta _1 \sin \theta _1 \\ -\beta _2 \sin \theta _2 \\ -\beta _3 \sin \theta _3 \end{array} \right] ,\quad {\varvec{b}}= \left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] \end{aligned}$$

(7)

with

$$\begin{aligned} \left\{ \begin{array}{l} \alpha _{11}=J_1+m_1l_{c1}^2+(m_2+m_3)l_1^2,\\ \alpha _{22}=J_2+m_2l_{c2}^2+m_3l_2^2, \\ \alpha _{33}=J_3+m_3l_{c3}^2,\\ \alpha _{12}= (m_2l_{c2}+m_3l_2)l_1,\\ \alpha _{13}= m_3l_1l_{c3}, \\ \alpha _{23}= m_3l_2l_{c3},\\ \beta _1=(m_1l_{c1}+m_2l_1+m_3l_1)g,\\ \beta _2=(m_2l_{c2}+m_3l_2)g, \\ \beta _3=m_3l_{c3}g, \end{array} \right. \end{aligned}$$

(8)

where g is the acceleration of gravity.

The total mechanical energy of the APP robot is

$$\begin{aligned} E({\varvec{\theta }},\dot{{\varvec{\theta }}})=\frac{1}{2}\dot{{\varvec{\theta }}}^{\mathrm {T}}{\varvec{M}}({\varvec{\theta }}) \dot{{\varvec{\theta }}} + P({\varvec{\theta }}), \end{aligned}$$

(9)

where $P({\varvec{\theta }})$ is its potential energy defined by

$$\begin{aligned} P({\varvec{\theta }})=\beta _1 \cos \theta _1 +\beta _2 \cos \theta _2 +\beta _3 \cos \theta _3. \end{aligned}$$

(10)

From (4), we have

$$\begin{aligned} \dot{E}({\varvec{\theta }},\dot{{\varvec{\theta }}})&=\dot{{\varvec{\theta }}}^{\mathrm {T}}{\varvec{M}}({\varvec{\theta }})\ddot{{\varvec{\theta }}}+\frac{1}{2}\dot{{\varvec{\theta }}}^{\mathrm {T}}\dot{{\varvec{M}}}({\varvec{\theta }})\dot{{\varvec{\theta }}}+\dot{{\varvec{\theta }}}^{\mathrm {T}}{\varvec{g}}({\varvec{\theta }})\nonumber \\&=\dot{{\varvec{\theta }}}^{\mathrm {T}}\left( -{\varvec{C}}({\varvec{\theta }},\dot{{\varvec{\theta }}})\dot{{\varvec{\theta }}}-{\varvec{g}}({\varvec{\theta }})+{\varvec{b}} \tau _1\right) \nonumber \\&\quad +\frac{1}{2}\dot{{\varvec{\theta }}}^{\mathrm {T}}\dot{{\varvec{M}}}({\varvec{\theta }})\dot{{\varvec{\theta }}}+\dot{{\varvec{\theta }}}^{\mathrm {T}}{\varvec{g}}({\varvec{\theta }})\nonumber \\&=\dot{{\varvec{\theta }}}^{\mathrm {T}}{\varvec{b}} \tau _1+\frac{1}{2}\dot{{\varvec{\theta }}}^{\mathrm {T}}(\dot{{\varvec{M}}}({\varvec{\theta }})-2 {\varvec{C}}({\varvec{\theta }},\dot{{\varvec{\theta }}})) \dot{{\varvec{\theta }}} \end{aligned}$$

(11)

$$\begin{aligned}&=\dot{\theta }_1\tau _1, \end{aligned}$$

(12)

where the second term in the right-hand side of (11) is 0 since $\dot{{\varvec{M}}}({\varvec{\theta }})-2 {\varvec{C}}({\varvec{\theta }},\dot{{\varvec{\theta }}})$ is a skew-symmetric matrix which can be verified directly by using (5) and (6).

2.2 Problem formulation

Consider the following UEP:

$$\begin{aligned} {\varvec{{\varvec{\theta }}}}(t)={\varvec{0}}_{3}, \; \; \dot{{\varvec{\theta }}}(t)={\varvec{0}}_{3}. \end{aligned}$$

(13)

For $E({\varvec{\theta }},\dot{{\varvec{\theta }}})$, $\theta _1$, and $\dot{\theta }_1$, we design and analyze a controller to address whether objectives (1) and (2) can be achieved, where $E_r$ is the highest potential energy of the APP robot expressed as:

$$\begin{aligned} E_{r}={\displaystyle E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))\left| ^{}_{{\varvec{\theta }}(t)={\varvec{0}}_{3},\;\; \dot{{\varvec{\theta }}}(t)={\varvec{0}}_{3}}\right. }=\beta _1+\beta _2+\beta _3,\nonumber \\ \end{aligned}$$

(14)

${\varvec{\theta }}_a(t)=\theta _1(t)$, and ${\varvec{\theta }}_{ar}=0$.

3 Main results

Define the following controller:

$$\begin{aligned}&\tau _1(t)\nonumber \\&\quad =\frac{k_DB^{\mathrm {T}}{\varvec{M}}^{-1}({\varvec{\theta }}(t))({\varvec{C}} ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t)) \dot{{\varvec{\theta }}}(t)+{\varvec{g}}({\varvec{\theta }}(t)))-k_V \dot{\theta }_1(t) -k_P {\theta }_1(t)}{\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))}, \end{aligned}$$

(15)

where

$$\begin{aligned} \eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))= & {} E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))-E_r + k_D {\varvec{b}}^{{\mathrm {T}}}{\varvec{M}}^{-1}({\varvec{\theta }}(t)) {\varvec{b}}.\nonumber \\ \end{aligned}$$

(16)

Below we present the following five lemmas and one theorem. Lemma 1 is about a condition on gain $k_D$ to guarantee that controller (15) is well defined, whose proof is given in “Appendix 1.”

Lemma 1

$\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))$ in (16) is positive for any $({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))$ if and only if $k_D$ satisfies

(17)

Lemma 2 is about the invariant set to which every solution of the closed-loop system converges, whose proof is given in “Appendix 2.”

Lemma 2

Consider the closed-loop system consisting of APP robot (4) and controller (15). If $k_D$ satisfies (17), and

$$\begin{aligned}&k_V>0, \end{aligned}$$

(18)

$$\begin{aligned}&k_P>0, \end{aligned}$$

(19)

then the closed-loop solution, $({\varvec{\theta }}(t),~\dot{{\varvec{\theta }}}(t))$, converges to the following invariant set:

$$\begin{aligned} W=&\Bigl \{ ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t) ) \ \Bigl . \Bigr | \ \frac{1}{2}\alpha _{22}\dot{\theta }^{2}_2(t) + \alpha _{23}\dot{\theta }_2(t)\dot{\theta }_3(t)\nonumber \\&\quad \times \cos {(\theta _3(t)-\theta _2(t))}+ \frac{1}{2}\alpha _{33}\dot{\theta }^{2}_3(t)\nonumber \\&\quad + P({\varvec{\theta }}(t) )\equiv E^*, \quad \theta _1(t) \equiv \theta _1^*\Bigr \}, \end{aligned}$$

(20)

where “$\equiv$” denotes the equation holds for all t.

Lemma 3 shows a new property of the motion of the APP robot with its proof in “Appendix 3.”

Lemma 3

Consider APP robot (4). Suppose $\theta _1(t)\equiv \theta _1^*$ and $\tau _1(t)\equiv \tau _1^*$ with $\theta _1^*$ and $\tau _1^*$ being constants; that is, link 1 does not move under a constant torque on joint 1. Then, links 2 and 3 do not move; that is,

$$\begin{aligned} \dot{\theta }_2(t)\equiv 0, \quad \dot{\theta }_3(t)\equiv 0 \end{aligned}$$

(21)

for any mechanical parameters described in (8) for the APP robot, $\theta _1^*$, and $\tau _1^*$.

Lemma 4 characterizes the invariant set the W in (20) further under a condition on gain $k_P$, whose proof is presented in “Appendix 4.”

Lemma 4

Consider the closed-loop system consisting of APP robot (4) and controller (15). Suppose that $k_D$ satisfies (17), $k_V$ satisfies (18), and $k_P$ satisfies

$$\begin{aligned}&k_P> k_{Pm}=\max _{\pi \le w \le 2\pi }\nonumber \\&\quad \times \frac{\displaystyle - \beta _1 \left( \beta _1(1-\cos w)+2\beta _2 + 2\beta _3\right) \sin w}{w}. \end{aligned}$$

(22)

Then, the invariant set W in (20) becomes the union

$$\begin{aligned} W=W_r\cup \Omega _s, \end{aligned}$$

(23)

where

$$\begin{aligned} W_r&=\Bigl \{ ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t) ) \ \Bigl . \Bigr | \ \frac{1}{2}\alpha _{22}\dot{\theta }^{2}_2(t) \nonumber \\&\quad + \alpha _{23}\dot{\theta }_2(t)\dot{\theta }_3(t) \cos {(\theta _3(t)-\theta _2(t))} + \frac{1}{2}\alpha _{33}\dot{\theta }^{2}_3(t) \nonumber \\&\quad + \beta _2 (\cos \theta _2(t)-1) +\beta _3 (\cos \theta _3(t)-1)=0, \; \; \nonumber \\&\qquad \theta _1(t)\equiv 0 \Bigr \} \end{aligned}$$

(24)

and

$$\begin{aligned} \Omega _s= & {} \left\{ ({\varvec{\theta }}^*, {\varvec{0}}_{3}) ~ |~ {\varvec{\theta }}^*\equiv \left[ \begin{array}{ccc} 0, &{} 0, &{} \pi \\ \end{array} \right] ^{\mathrm {T}}, ~ \left[ \begin{array}{ccc} 0, &{} \pi , &{} 0 \\ \end{array} \right] ^{\mathrm {T}},\right. \nonumber \\&\times \left. \left[ \begin{array}{ccc} 0, &{} \pi , &{} \pi \\ \end{array} \right] ^{\mathrm {T}}\right\} . \end{aligned}$$

(25)

Moreover, the UEP is the only equilibrium point in $W_r$.

Lemma 5 is about the stability of all equilibrium points of the closed-loop system, whose proof is presented in “Appendix 5.”

Lemma 5

Consider the closed-loop system consisting of APP robot (4) and controller (15). Given the bounds on the gains in (17), (18), and (22). The UEP and the equilibrium points in $\Omega _s$ are all strictly unstable.

We present the following main result of this paper.

Theorem 1

Consider the closed-loop system consisting of APP robot (4) and controller (15). Given the bounds on the gains in (17), (18), and (22). The closed-loop solution, $({\varvec{\theta }}(t),~\dot{{\varvec{\theta }}}(t))$, converges to the invariant set $W_r$ in (24), except for the measure-zero set of initial conditions that converge to the strictly unstable equilibrium points in the $\Omega _s$ in (25). The UEP is the only equilibrium point in $W_r$ and is strictly unstable. Controller (15) achieves objectives (1) and (2) corresponding to the UEP for almost all initial conditions but does not achieve objective (3).

Proof

From Lemmas 4 and 5, since each equilibrium point of $\Omega _s$ is strictly unstable; that is, the Jacobian matrix evaluated at each equilibrium point of $\Omega _s$ has at least one eigenvalue in the open right-half plane, the set of initial conditions from which the closed-loop solution converges to $\Omega _s$ is of Lebesgue measure zero, see, e.g., [21] (p. 1225). In other words, from all initial conditions with the exception of a set of Lebesgue measure zero, the closed-loop solution $({\varvec{\theta }}(t), \dot{{\varvec{\theta }}}(t))$ converges to the invariant set $W_r$. Thus, controller (15) achieves objectives (1) and (2) corresponding to the UEP for almost all initial conditions. From Lemmas 4 and 5, we know that the UEP is the only equilibrium point in $W_r$ and is strictly unstable. Therefore, controller (15) does not achieve objective (3). $\square$

4 Discussion

4.1 On the invariant set $W_r$

Theorem 1 shows that objectives (1) and (2) corresponding to the UEP are achieved for almost all initial conditions under the proposed energy-based controller (15), provided that the conditions on control gains are satisfied. Even though the UEP is contained in the invariant set $W_r$ in (24) in $t\in (0, ~\infty )$, it is unclear that the solution trajectories will come into a close neighborhood of the UEP. In this sense, this paper does not give a general algorithm to guarantee theoretically for achieving the true practical objective of the APP control: stabilization of the UEP from almost any initial conditions.

From our simulation results for the APP robot with mechanical parameters in [20], under the proposed controller (15) there existed moments in $t\in (0, ~\infty )$ when the robot came into a close neighborhood of the UEP for several initial conditions we simulated. Please refer two examples in Sects. 5.1 and 5.2. The combination of switching between the two control laws is shown by simulation to practically achieve all objectives (1), (2), and (3), but no formal proof is found yet that shows that this ALWAYS works. We would like to investigate it further in the future.

4.2 On Lemma 3 and its proof

There are various applications of symbolic computation in robot manipulator design and analysis, for example, in kinematics, dynamics, trajectory planning, and control [23]. This paper also shows an application of symbolic computation in the proof of Lemma 3, which is important for proving Theorem 1. Below we discuss Lemma 3 and its proof.

First, Lemma 3 means that for APP robot (4), if link 1 is at rest under a constant torque on joint 1, then the entire system is in an equilibrium point. Lemma 3 seems to be intuitive: As long as links 2 and 3 move, the forces acting at the distal joint of link 1 (joint 2) will change which results in a varying moment at the proximal joint of link 1 (joint 1); thus, a varying torque must be applied at joint 1 to keep link 1 balanced. However, by analyzing all the forces acting at three joints, we cannot find more information than motion equation (4). The details are omitted.

Second, it is very difficult to prove Lemma 3 for any mechanical parameters described in (8) for the APP robot, any constant angle of joint 1, and corresponding constant torque because of the strong nonlinear coupling of two passive joints of the APP robot when link 1 of the robot is at rest under a constant torque. Indeed, in its proof we used the properties of the mechanical parameters shown in Lemmas 6 and 7. If $\sin \theta ^{*}_1 =0$ (link 1 at the vertical position), then the proof of Lemma 3 can be simplified considerably (without need to use symbolic computation), please refer the result for the double pendulum in a cart in [30]. However, if $\sin \theta ^{*}_1 \ne 0$ (link 1 not at the vertical position), then the proof is much more involved as shown in “Appendix 3.”

If the mechanical parameters of links 2 and 3 of the robot satisfy $a^2 - a b -a e+1 \ne 0$, where a, b, and e are defined in (34), then we do not need the analysis of Case 2 ($a^2 - a b -a e+1 =0$) in the proof of Lemma 3 which is complicated and involved, please refer “Eq. 37 of Appendix 3.” Note that the physical 3-link robot in [20] which is used in the simulation in Sect. 5 satisfies $a^2 - a b -a e+1 \ne 0$. Moreover, when link 2 of a 3-link robot has a massless rod with a point mass at its end; that is, $l_{c2}=l_{2}$ and $J_2=0$, then from (8) we obtain

$$\begin{aligned} a=\frac{\beta _2}{\beta _3}=\frac{(m_2+m_3)l_2}{m_3l_{c3}}, \quad b=\frac{\alpha _{22}}{\alpha _{23}}=\frac{(m_2+m_3)l_2}{m_3l_{c3}}. \end{aligned}$$

Thus, $a=b$; together with $ae>1$ due to Lemma 6, $a^2 - a b -a e+1 < 0$. Note that the massless rod assumption is often used in pendulum-type systems, see, e.g., [5].

5 Simulation results

We present numerical simulation results for an APP robot with its mechanical parameters being given in Table 1, which are taken from the physical 3-link planar robot in [20]. We took $g=9.8\,\text {m/s}^2$.

Table 1 Mechanical parameters of the physical 3-link planar robot in [20]

From Theorem 1, under controller (15) with conditions (17) and (22); that is, $k_D>11.2100 {\,\mathrm J}^2 {\,\mathrm s}^2$ and $k_P>81.1069 {\,\mathrm J}^2$ for this APP robot, and with condition $k_V>0$, objectives (1) and (2) corresponding to the UEP are achievable from all initial conditions with the exception of a set of Lebesgue measure zero.

Since the UEP is strictly unstable under the proposed energy-based controller according to Lemma 5, when the APP robot is swung up close to the UEP, to stabilize it around the UEP, we need to switch the energy-based controller to a local stabilizing controller designed by LQR method. Define ${\varvec{x}}(t) = \left[ \begin{array}{cccccc} \theta _1(t), &{} \theta _{2}(t), &{} \theta _{3}(t),&{} \dot{\theta }_1(t),&{} \dot{\theta }_2(t), &{} \dot{\theta }_3(t) \\ \end{array} \right] ^{\mathrm {T}}$. The LQR controller is

$$\begin{aligned} \tau _1(t)=-{\varvec{K}} {\varvec{x}}(t), \end{aligned}$$

(26)

where

$$\begin{aligned} {\varvec{K}}= & {} \left[ \begin{array}{cccccc} 24.8073,&-125.5004,&276.3903,&10.9221,&5.2260,&39.4850 \end{array} \right] , \end{aligned}$$

which was obtained by using the MATLAB function “lqr” for which the weight related to the torque was chosen to be 1, and the weight matrix related to state ${\varvec{x}}(t)$ was chosen to be a diagonal matrix of $6\times 6$ with the diagonal elements from (1, 1) to (6, 6) being 1, 1, 1, 0.1, 0.1, and 0.1.

The condition for switching controller (15) to controller (26) was set as

$$\begin{aligned} d(t)= & {} |\theta _1(t)|+|\theta _2(t)|+|\theta _3(t)|\nonumber \\&+\, 0.1|\dot{\theta }_1(t)|+0.1|\dot{\theta }_2(t)|+0.1|\dot{\theta }_3(t)|<\epsilon _0\nonumber \\ \end{aligned}$$

(27)

for given $\epsilon _0>0$. Indeed, small $\epsilon _0$ is good for achieving a successful switch from controller (15) to controller (26). On the other hand, big $\epsilon _0$ is good for achieving a quick switch from controller (15) to controller (26). In this paper, we chosen $\epsilon _0=0.5$ in (27) by trial and error to achieve a successful and quick switch from controller (15) to controller (26).

Since links 2 and 3 may have rotated several times when the LQR controller is switched, $\theta _i(t)$ $(i=2,3)$ may take value out of $(-\pi , \pi ]$. Therefore, $\theta _2(t)$ and $\theta _3(t)$ in (26) and (27) are used under modulo operation with divisor $2\pi$ and take values in $( -\pi , \pi ]$. Note that controller (15) needs more knowledge of the system’s parameters and more computation time than controller (26).

Below, we report our simulation results for two initial conditions.

5.1 Initial condition 1

We took an initial condition

$$\begin{aligned}&\left( \theta _1(0),\theta _2(0),\theta _3(0),\dot{\theta }_1(0),\dot{\theta }_2(0),\dot{\theta }_3(0)\right) \nonumber \\&\quad =\left( \frac{5\pi }{6},\frac{6\pi }{7},\frac{7\pi }{8}, 0,0,0\right) , \end{aligned}$$

(28)

which is close to the downward equilibrium point

$$\begin{aligned}&(\theta _1(t),\theta _2(t),\theta _3(t),\dot{\theta }_1(t),\dot{\theta }_2(t),\dot{\theta }_3(t))\\&\quad =( \pi ,\pi ,\pi ,0,0,0). \end{aligned}$$

To swing the APP robot up quickly close to the UEP, we took $k_D=12.8495 {\,\mathrm J}^2 {\,\mathrm s}^2$, $k_P=101.6513 {\,\mathrm J}^2$, and $k_V= 34.9863 {\,\mathrm J}^2 \mathrm{s}$. Under controller (15), we present the simulation results for $t\in [0, 200]~$s to show whether the switching condition in (27) is satisfied. The simulation results under the energy-based controller (15) are shown in Figs. 2, 3 and 4. From Fig. 2, there were many moments when (27) was satisfied.

Fig. 2

Time responses of d(t) in (27) under controller (15) with initial condition (28)

Figure 3 shows that V(t) and $E(t)-E_r$ converged to 0 and $\tau _1(t)$ was not constant. Figure 4 shows that $\theta _1(t)$ converged to 0, and $\theta _2(t)$ and $\theta _3(t)$ were time varying. Though $\theta _2(t)$ and $\theta _3(t)$ are treated in ${\mathbb {S}}^2$, plots of $\theta _2(t)$ and $\theta _3(t)$ in Fig. 4 were not plotted modulo $2\pi$ to avoid confusing artificial points of apparent discontinuity. From Figs. 3 and 4, we validated that objectives (1) and (2) corresponding to the UEP were achieved.

In Fig. 3, the control torque $\tau _1(t)$ satisfied $-44.4371 \text {Nm} \le \tau _1(t) \le 30.5831~\text {Nm}$. To see whether these values are small or large, we compare those with the torque where link 1 is horizontal while the two other links are upward vertical. In such a position, we have $\tau _1(t)=-\beta _1=-12.3835~\text {Nm}$.

Fig. 3

Time responses of V(t), $E(t)-E_r$, and $\tau _1(t)$ under controller (15) with initial condition (28)

Fig. 4

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controller (15) with initial condition (28)

When switching condition (27) was satisfied, we switched controller (15) to controller (26). From Fig. 5, the switch was taken at $t=4.67\,$s. Note that the final convergence of $\theta _3(t)$ is $-6.2832\text { rad}=-2\pi \text { rad}$ which is $0\text { rad}$ under modulo operation with divisor $2\pi$. From Fig. 6, we found that the swing-up control and stabilizing control of the APP robot in Table 1 were achieved under controllers (15) and (26).

Fig. 5

Time responses of V(t), $E(t)-E_r$, and $\tau _1(t)$ under controllers (15) and (26) with initial condition (28), where the dashed vertical line indicates the switching time

Fig. 6

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controllers (15) and (26) with initial condition (28), where the dashed vertical line indicates the switching time

The simulation result under control (26) for $t\in [0, ~ 0.2]$ s is depicted in Fig. 7, which indicates that controller (26) did not stabilize the APP robot to the UEP from initial condition (28). The maximal value of $\tau _1(t)$ in $t\in [0, ~ 0.2]$ s was $1.0283 \times 10^6$ Nm. This shows that to stabilize the APP robot to the UEP from initial condition (28), the proposed controllers (15) and (26) are better than controller (26) only.

Fig. 7

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controller (26) with initial condition (28)

5.2 Initial condition 2

We took an initial condition

$$\begin{aligned}&\left( \theta _1(0),\theta _2(0),\theta _3(0),\dot{\theta }_1(0),\dot{\theta }_2(0),\dot{\theta }_3(0)\right) \nonumber \\&\quad =\left( \frac{\pi }{2},\frac{\pi }{2},\frac{\pi }{2}, 0,0,0\right) , \end{aligned}$$

(29)

where all links are at a stretched horizontal position.

The simulation results under the energy-based controller (15) are shown in Figs. 8, 9 and 10. From Fig. 8, we can see that there were several moments when (27) was satisfied. Figure 9 shows that V(t) and $E(t)-E_r$ converged to 0 and $\tau _1(t)$ was not constant. In Fig. 9, the control torque $\tau _1(t)$ satisfied $-32.7102~\text {Nm} \le \tau _1(t) \le 30.2021~\text {Nm}$. Figure 10 shows that $\theta _1(t)$ converged to 0, and $\theta _2(t)$ and $\theta _3(t)$ were time varying. From Figs. 9 and 10, we validated that objectives (1) and (2) corresponding to the UEP were achieved.

Fig. 8

Time responses of d(t) in (27) with initial condition (29) under controller (15)

Fig. 9

Time responses of V(t), $E(t)-E_r$, and $\tau _1(t)$ under controller (15) with initial condition (29)

Fig. 10

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controller (15) with initial condition (29)

When switching condition (27) was satisfied, we switched controller (15) to controller (26). From Fig. 11, the switch was taken at $t=107.70\,$s. From Fig. 12, we found that the swing-up control and stabilizing control of the APP robot in Table 1 were achieved under controllers (15) and (26). We also provide Figs. 13 and 14 only for a short period of the time after switching to the LQR law (26), which will enable zooming into the scale for more effectively displaying the final convergence. Note that the final convergence of $\theta _3(t)$ is $408.4070~\text {rad}=2\pi \times 65~\text {rad}$ which is $0~\text {~rad}$ under modulo operation with divisor $2\pi$.

Fig. 11

Time responses of V(t), $E(t)-E_r$, and $\tau _1(t)$ under controllers (15) and (26) with initial condition (29), where the dashed vertical line indicates the switching time

Fig. 12

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controllers (15) and (26) with initial condition (29), where the dashed vertical line indicates the switching time

Fig. 13

Time responses of V(t), $E(t)-E_r$, and $\tau _1(t)$ under controllers (15) and (26) with initial condition (29) after the switching at $t =107.701$ s

Fig. 14

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controllers (15) and (26) with initial condition (29) after the switching at $t = 107.701$ s

The simulation result under controller (26) for $t\in [0, ~ 0.2]$ s is depicted in Fig. 15, which indicates that controller (26) did not stabilize the APP robot to the UEP from initial condition (29). The maximal value of $\tau _1(t)$ in $t\in [0, ~ 0.2]$ s was $9.0179 \times 10^5$ Nm. It can be seen that the linear control law (26) achieves only local stabilization of the UEP from initial conditions in the close neighborhood of the UEP. Only the combination of both control laws (15) and (26) with the switching rule (27) practically achieves almost global stabilization.

Fig. 15

Time responses of $\theta _1(t)$, $\theta _2(t)$, and $\theta _3(t)$ under controller (26) with initial condition (29)

6 Conclusion

For a 3-link planar robot with only the first joint being active (the APP robot), we presented a nonlinear energy-based controller whose objective is to drive the APP robot into an invariant set where the first link is in the upright position and the total mechanical energy converges to its value at the UEP. By presenting and using a new property of the motion of the APP robot, without any condition on the mechanical parameters of the robot, we proved that if the control gains are larger than specific lower bounds, then only a measure-zero set of initial conditions converges to three strictly unstable equilibrium points instead of converging to the invariant set $W_r$ in (24). The new property described in Lemma 3 is that if link 1 of the APP robot does not move under a constant torque on joint 1, then links 2 and 3 do not move. Three strictly unstable equilibrium points are the up–up–down, up–down–up, and up–down–down equilibrium points of the APP robot. The presented energy-based control law achieves objectives (1) and (2) corresponding to the UEP for almost all initial conditions but does not achieve objective (3), since the UEP becomes strictly unstable. We presented numerical results for the physical 3-link planar robot in [20] to validate the obtained theoretical results and to show a successful application to the swing-up and stabilizing control of the APP robot.

Even though the UEP is contained in the invariant set $W_r$ in (24), we are unable to formally prove that the solution is ALWAYS guaranteed to come into a small neighborhood of the UEP at some time. Nevertheless, simulations under physically realistic parameter values show that this is indeed satisfied in practical scenarios.

Appendices

Appendix 1: Proof of Lemma 1

Using $E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t)) \ge P({\varvec{\theta }}(t))$ and $\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))$ in (16), we obtain $\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t)) \ge P({\varvec{\theta }}(t))- E_r + k_D {\varvec{b}}^{{\mathrm {T}}}{\varvec{M}}^{-1}({\varvec{\theta }}(t)) {\varvec{b}}$. Thus, if (17) holds, then $\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t)) >0$.

To show that (17) is also necessary such that $\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t)) >0$, for any given $k_D$ satisfying $0< k_D \le k_{Dm}$, we just need to show that there exists an initial condition $({\varvec{\theta }}(0), \dot{{\varvec{\theta }}}(0))$ at which $\eta ({\varvec{\theta }}(0),\dot{{\varvec{\theta }}(0)})=0$. Indeed, letting ${\varvec{\zeta }} \in {\mathbb {R}}^3$ be a value of ${\varvec{\theta }}(t)$ with $-\pi \le \theta _i(t)\le \pi$ ($i=1,2,3$) that maximizes the function in the right-hand side of (17); that is, $k_{Dm}= (E_r-P({\varvec{\zeta }}))({\varvec{b}}^{\mathrm {T}}{\varvec{M}}^{-1}({\varvec{\zeta }}) {\varvec{b}})^{-1}$.

Choosing ${\varvec{\zeta }}_d \in {\mathbb {R}}^3$ such that

$$\begin{aligned} \frac{1}{2}{\varvec{\zeta }}_d^{{\mathrm {T}}}{\varvec{M}}({\varvec{\zeta }}){\varvec{\zeta }}_d = (k_{Dm}- k_D){\varvec{b}}^{\mathrm {T}}{\varvec{M}}^{-1}({\varvec{\zeta }}) {\varvec{b}} \ge 0, \end{aligned}$$

we obtain

$$\begin{aligned} \eta ({\varvec{\zeta }},{\varvec{\zeta }}_d) = E({\varvec{\zeta }},{\varvec{\zeta }}_d)-E_r + k_D {\varvec{b}}^{{\mathrm {T}}}{\varvec{M}}^{-1}({\varvec{\zeta }}) {\varvec{b}}=0. \end{aligned}$$

Thus, $\eta ({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))>0$ for any $({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))$ if and only if (17) holds. $\square$

Appendix 2: Proof of Lemma 2

First, take the following Lyapunov function candidate:

$$\begin{aligned} V(t)= & {} \frac{1}{2}(E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))-E_r)^2\nonumber \\&+\,\frac{k_D}{2}\dot{\theta }^{2}_1(t)+\frac{k_P}{2}{\theta }^{2}_1(t), \end{aligned}$$

(30)

where scalars $k_D>0$ and $k_P>0$ are control gains. Using (12), we obtain the time derivative of V along the trajectories of (4) as follows:

$$\begin{aligned} \dot{V}(t)= & {} \dot{\theta }_1(t) \left( (E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))-E_r)\tau _1(t)\right. \nonumber \\&\left. +\,k_D\ddot{\theta }_1(t)+k_P \theta _1(t) \right) . \end{aligned}$$

(31)

Under the control law of $\tau _1(t)$ defined in (15) which is well defined for all initial conditions when $k_D$ satisfies (17) (see Lemma 1), by obtaining $\ddot{\theta }_1(t)$ from (4), we can show that the following relation holds

$$\begin{aligned}&(E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t))-E_r)\tau _1(t) +k_D\ddot{\theta }_1(t)+k_P \theta _1(t)\nonumber \\&\quad =-k_V\dot{\theta }_1(t), \end{aligned}$$

(32)

which implies

$$\begin{aligned} \dot{V}(t)=-k_V\dot{\theta }^{2}_1(t) \le 0. \end{aligned}$$

(33)

Second, from $\dot{V}(t)\le 0$ in (33), it follows that V(t) is monotonically nonincreasing and is thus bounded. Using LaSalle’s invariance principle [14] shows that the solution of the closed-loop system consisting of (4) and (15) converges to the largest invariant set W where $\dot{V}(t)\equiv 0$; that is, $\dot{\theta }_1(t)\equiv 0$ holds. Thus, V(t) and $\theta _1(t)$ are constants inside the invariant set W. From V(t) in (30), E(t) is also a constant inside the invariant set W. By denoting the constants corresponding to $\theta _1(t)$ and E(t) as $\theta _1^*$ and $E^*$, respectively, and putting $E(t)\equiv E^*$ and $\theta _1(t)\equiv \theta _1^*$ into (9), we show that W is expressed as in (20).

Appendix 3: Proof of Lemma 3

To start with, we provide two lemmas for proving Lemma 3 in “Eq. 34 of Appendix 3.” Then, we present two steps of the proof of Lemma 3 in “Eq.35 of Appendix 3” and describe the details of two steps in “Eq.36 of Appendix 3” and “Eq. 37 of Appendix 3.” Some algebraic manipulations are carried out with the aid of Mathematica. Please see Sect. 4.2 for the discussion about this proof.

1.1 Two preliminary results

Io order to prove Lemma 3, we provide two preliminary results below. Define

$$\begin{aligned} a =\frac{\beta _2}{\beta _3},~~ b=\frac{\alpha _{22}}{\alpha _{23}},~~ d=\frac{\beta _3}{\alpha _{23}},~~ e=\frac{\alpha _{33}}{\alpha _{23}}, \end{aligned}$$

(34)

which are determined by the mechanical parameters of links 2 and 3 of the APP robot. We recall a property of the mechanical parameters of a 2-link planar robot presented in Lemma 1 of [32] for links 2 and 3 of the APP robot.

Lemma 6

For the parameters in (34), the following statements hold:

$$\begin{aligned}&a \ge b>0, \end{aligned}$$

(35)

$$\begin{aligned}&a e >1. \end{aligned}$$

(36)

Note that $m_il_i l_{ci} \ge J_i+ m_i l_{ci}^2$ is shown for $i=1$ in [32] which is critical for showing (35). Equation (36) can be shown by using (8) directly. Using Lemma 6, we obtain the following lemma.

Lemma 7

If

$$\begin{aligned} e=\frac{1+a^2-ab}{a}, \end{aligned}$$

(37)

then

$$\begin{aligned} a\ne 1, ~~~ a> b. \end{aligned}$$

(38)

Proof

If $a=1$, from (37), we have $b+e=2$. From (34), we have $b+e\ge 2 \sqrt{be} =2 \sqrt{\alpha _{22} \alpha _{33}/\alpha _{23}^2}>2$, where $\alpha _{22} \alpha _{33}>\alpha _{23}^2$ can be shown by using (8). This raises a contradiction. Thus, $a\ne 1$. If $a=b$, then from (37), $ae=1$ which contradicts (36). Thus, from (35), we have $a>b$. $\square$

1.2 Two steps

Using $\theta _1(t)\equiv \theta _1^*$ and (12), we obtain $\dot{E}(t)=0$. Thus, E(t) is a constant, which is denoted as $E^*$. Define the following coordinate transformation:

$$\begin{aligned} \phi _2(t)=\theta _2(t)-\theta _1^*, \quad \phi _3(t)=\theta _3(t)-\theta _1^*, \end{aligned}$$

(39)

we prove (21) by the following two steps.

Step 1 Obtain a holonomic constraint of the angle of link 2 described by the following polynomial equation:

$$\begin{aligned} L=\sum _{i=0}^{N} \xi _i \sin ^i\phi _2 (t)=0, \quad \text {for} ~ \forall t, \end{aligned}$$

(40)

in terms of $\sin \phi _2(t)$, where N is a positive integer to be determined and $\xi _i$ ($i=0,1,\ldots , N$) are functions of the mechanical parameters in (8), any possible $\theta _1^*$ and $E^*$.

Step 2 By contradiction, we assume $\dot{\phi }_2(t) =\dot{\theta }_2(t) \not \equiv 0$. Since differentiable function $\phi _2(t)$ is not constant, the polynomial equation in (40) in terms of $\sin \phi _2(t)$ has infinite number of solutions which shows

$$\begin{aligned} \xi _{i}=0,~~~ i=0, 1, \ldots , N. \end{aligned}$$

(41)

Otherwise, if there exists at least one i ($0\le i\le N$) such that $\xi _i \ne 0$, then (40) has finite number of solutions. We prove that (41) does not hold for any mechanical parameters described in (8), any possible $\theta _1^*$ and $E^*$. Thus, $\dot{\phi }_2(t) = \dot{\theta }_2(t) \equiv 0$. Moreover, we prove $\dot{\phi }_3(t)=\dot{\theta }_3(t)\equiv 0$.

We present the details of two steps in the following two subsections. For brevity, the time argument t of a variable is omitted below.

1.3 Details of Step 1

We carry out Step 1 further by the following substeps.

Step 1.1 Integrate the dynamics of (4) related to joint 1 with $\theta _1\equiv \theta _1^*$ and $\tau _1\equiv \tau _1^*$ to obtain

$$\begin{aligned}&a\dot{\phi }_2 \cos \phi _2 + \dot{\phi }_3 \cos \phi _3 =0 , \end{aligned}$$

(42)

$$\begin{aligned}&a \sin \phi _2 + \sin \phi _3 =\lambda , \end{aligned}$$

(43)

where $\lambda$ is a constant. Moreover, if $\sin \theta _1^*=0$, then $\lambda =0$.

Step 1.2 Eliminate $\ddot{\phi }_2$ and $\ddot{\phi }_3$ from (4) to obtain

$$\begin{aligned} F_2 \dot{\phi }^2_2 + F_3\dot{\phi }_3^2+F_1=0, \end{aligned}$$

(44)

where $F_i$ $(i=1,2,3)$ are functions of $\sin \phi _2$, $\cos \phi _2$, and $\cos \phi _3$. Moreover, obtain the following equation using $E=E^*$ with (39) and (43):

$$\begin{aligned}&\frac{b}{2}\dot{\phi }_2^2 +\dot{\phi }_2\dot{\phi }_3 \cos (\phi _3- \phi _2)\nonumber \\&\quad +\, \frac{e}{2} \dot{\phi }_3^2 +(a \cos \phi _2+ \cos \phi _3 )d \cos \theta _1^*=\gamma , \end{aligned}$$

(45)

where $\gamma$ is a constant defined by

$$\begin{aligned} \gamma = \frac{E^*-\beta _1\cos \theta _1^*}{\alpha _{23}}+ \lambda d \sin \theta _1^*. \end{aligned}$$

(46)

Step 1.3 Eliminate $\dot{\phi }_2$ and $\dot{\phi }_3$ from (42), (44), and (45) to obtain

$$\begin{aligned} Q_1+Q_2 \cos \phi _3=0, \end{aligned}$$

(47)

where $Q_{i}$ $(i=1,2)$ are functions of $\sin \phi _2$ and $\cos \phi _2$.

Step 1.4 Eliminate $\cos \phi _3$ from (47) by using (43) to obtain

$$\begin{aligned} Q_1^2 - Q_2^2(1-\sin ^2\phi _3)=R_1+R_2 \cos \phi _2=0, \end{aligned}$$

(48)

where $R_{1}$ and $R_2$ are polynomials of $\sin \phi _2$ with the highest orders of 14 and 13, respectively. If $\cos \theta _1^*=0$, then $R_2=0$, and we obtain (40) as:

$$\begin{aligned} L= R_1=0, \quad \text {with } N=14. \end{aligned}$$

(49)

If $\cos \theta _1^*\ne 0$, deleting $\cos \phi _2$ from (48) yields that (40), we obtain a polynomial equation of $\sin \phi _2$, as:

$$\begin{aligned} L= R_1^2 - R_2^2(1-\sin ^2\phi _2)=0, \quad \text {with } N=28. \end{aligned}$$

(50)

Regarding Step 1.1, using $a={\beta _2}/{\beta _3}={\alpha _{12}}/{\alpha _{13}}$ due to (8) and using (4) with $\theta _1\equiv \theta _1^*$, $\tau _1\equiv \tau _1^*$, and (39), we obtain

$$\begin{aligned}&a \ddot{\phi }_2 \cos \phi _2 +\ddot{\phi }_3 \cos \phi _3 -a \dot{\phi }_2^2 \sin \phi _2-\dot{\phi }_3^2 \sin \phi _3 \nonumber \\&\quad = \displaystyle \frac{\tau _1^*+\beta _1 \sin \theta _1^*}{\alpha _{13}}, \end{aligned}$$

(51)

$$\begin{aligned}&b \ddot{\phi }_2 +\ddot{\phi }_3 \cos (\phi _3 - \phi _2 ) -\dot{\phi }_3^2 \sin (\phi _3 -\phi _2) \nonumber \\&\quad = ad \sin (\phi _2+\theta _1^*) , \end{aligned}$$

(52)

$$\begin{aligned}&\ddot{\phi }_2 \cos (\phi _3 -\phi _2 ) + e \ddot{\phi }_3 + \dot{\phi }_2^2 \sin (\phi _3 -\phi _2) \nonumber \\&\quad = d \sin (\phi _3+\theta _1^*) . \end{aligned}$$

(53)

Integrating (51) gives

$$\begin{aligned} a \dot{\phi }_2 \cos \phi _2 + \dot{\phi }_3 \cos \phi _3=\frac{(\tau _1^{*}+\beta _1\sin {\theta ^{*}_1})t}{\alpha _{13}} + \lambda _1, \nonumber \\ \end{aligned}$$

(54)

where $\lambda _1$ is a constant. Since $E=E^*$ is bounded, the left-hand side term of (54) is bounded for all t. Thus,

$$\begin{aligned} \tau _1^{*}=-\beta _1\sin {\theta ^{*}_1}; \end{aligned}$$

(55)

otherwise, the right-hand side term of (54) is infinite as $t\rightarrow \infty$. Integrating (54) yields

$$\begin{aligned} a \sin \phi _2 + \sin \phi _3 = \lambda _1 t +\lambda . \end{aligned}$$

(56)

Since the left-hand side term of (56) is bounded for all t, $\lambda _1 =0$ must hold; otherwise, the right-hand side term of (56) is infinite as $t\rightarrow \infty$. Thus, (42) and (43) hold.

If $\sin \theta _1^*=0$, summing (52) and (53) and using (56) with $\lambda _1 =0$ yields

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}(b\dot{\phi }_2 +e \dot{\phi }_3 +(\dot{\phi }_2 + \dot{\phi }_3 )\cos (\phi _2-\phi _3)) =\pm d \lambda ,\nonumber \\ \end{aligned}$$

(57)

where “$+$” and “−” correspond to $\theta _1^*=0$ and $\theta _1^*=\pi$ ($\text {mod}~ 2\pi$), respectively. Integrating (57) with respect to time t gives

$$\begin{aligned} b\dot{\phi }_2 +e \dot{\phi }_3 +(\dot{\phi }_2 + \dot{\phi }_3 )\cos (\phi _2-\phi _3) =\pm d \lambda t+ \lambda _2,\nonumber \\ \end{aligned}$$

(58)

where $\lambda _2$ is a constant. Since the left-hand-side term of (58) is bounded due to the boundedness of $E^*$, we obtain $\lambda = 0$; otherwise, the right-hand side term of (58) is infinite as $t\rightarrow \infty$.

To obtain the polynomial in (40) in terms of $\sin \phi _2$, in the following derivation, we eliminate $\sin \phi _3$ by using $\sin \phi _3= \lambda -a \sin \phi _2$ due to (43), and we eliminate $\cos ^i\phi _2$ or $\cos ^i\phi _3$ with $i\ge 2$ if exists via using

$$\begin{aligned}&\cos ^2\phi _2=1-\sin ^2\phi _2,\; \mathrm{or}~\nonumber \\&\cos ^2\phi _3=1-\sin ^2\phi _3=1-(\lambda -a \sin \phi _2)^2, \end{aligned}$$

(59)

which guarantees the highest order of $\cos \phi _2$ or $\cos \phi _3$ if exists equal to one.

Regarding Step 1.2, using (51)–(53) with (55) gives

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l} a \cos \phi _2 &{}\cos \phi _3 &{} \sigma _{11} \\ b &{} \cos (\phi _3-\phi _2) &{} \sigma _{12} \\ \cos (\phi _3-\phi _2) &{} e &{} \sigma _{13} \end{array} \right] \left[ \begin{array}{c} \ddot{\phi }_2 \\ \ddot{\phi }_3 \\ 1 \end{array} \right] =\left[ \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right] , \end{aligned}$$

(60)

where

$$\begin{aligned} \sigma _{11}&= -a \dot{\phi }_2^2 \sin \phi _2 -\dot{\phi }_3^2 \sin \phi _3, \\ \sigma _{12}&= -\dot{\phi }_3^2 \sin (\phi _3-\phi _2) - a d \sin (\phi _2+\theta _1^*), \\ \sigma _{13}&= \dot{\phi }_2^2 \sin (\phi _3-\phi _2) - d \sin (\phi _3+\theta _1^*). \end{aligned}$$

Thus, the determinant of the $3\times 3$ matrix in (60) is 0; otherwise, $\left[ \begin{array}{ccc} \ddot{\phi }_2,&\ddot{\phi }_3,&1 \end{array} \right] = \left[ \begin{array}{ccc} 0,&0,&0 \end{array} \right]$ which raises a contradiction. By computing the determinant and using (59), we obtain (44), where

$$\begin{aligned} F_1&= d \biggl (\sin \left( \theta _1^*\right) \Bigl (-2 a+b+a^2 e+2 a \lambda ^2-b \lambda ^2\\&\quad -2 a \lambda \left( 2 a-b+\cos \left( \phi _2\right) \cos \left( \phi _3\right) \right) \\&\quad \times \sin \left( \phi _2\right) + a \bigl (2+2 a^2-a (b+e)-2 \lambda ^2\\&\quad +2 a \cos \left( \phi _2\right) \cos \left( \phi _3\right) \bigr ) \sin ^2 (\phi _2)\\&\quad +4 a^2 \lambda \sin ^3 \left( \phi _2\right) -2 a^3 \sin ^4 \left( \phi _2\right) \Bigr )+ \cos \left( \theta _1^*\right) \\&\quad \times \Bigl (a (-1+a e) \cos \left( \phi _2\right) \sin \left( \phi _2\right) \\&\quad +(a-b) \cos \left( \phi _3\right) \left( -\lambda +a \sin \left( \phi _2\right) \right) \Bigr )\biggr ),\\ F_2&=-(a-b) \cos \left( \phi _2\right) \cos \left( \phi _3\right) \left( -\lambda +a \sin \left( \phi _2\right) \right) \\&\quad +\sin \left( \phi _2\right) \Bigl (a \lambda ^2-b \left( -1+a e+\lambda ^2\right) \\&\quad +2 a (-a+b) \lambda \sin \left( \phi _2\right) +a^2 (a-b) \sin ^2\left( \phi _2\right) \Bigr ),\\ F_3&=(a-b) e \lambda +(a (-a+b) e+(1-a e) \cos \\&\quad \times \left( \phi _2\right) \cos \left( \phi _3\right) ) \sin \left( \phi _2\right) \\&\quad +\lambda ( 1-a e) \sin ^2\left( \phi _2\right) +a (-1+a e) \sin ^3\left( \phi _2\right) . \end{aligned}$$

Writing out $E=E^*$ with (9), $\theta _1\equiv \theta _1^*$, (34), (39) and (43), we obtain (45) directly.

Regarding Step 1.3, first, we eliminate $\dot{\phi }_3$. To this end, by computing ((44)$\times e /2-$(45)$\times F_3)\times \cos \phi _3$ and using (42) to eliminate $\dot{\phi }_3 \cos \phi _3$, we obtain

$$\begin{aligned} G_{11}+ G_{12} \dot{\phi }_2^2=0, \end{aligned}$$

(61)

where $G_{1i}$ $(i=1,2)$ are the following functions of $\sin \phi _2$, $\cos \phi _2$, and $\cos \phi _3$:

$$\begin{aligned} G_{11}&= \frac{1}{2} \Biggl (-2 \cos \left( \phi _2\right) \sin \left( \phi _2\right) \left( -1+\lambda ^2\right. \nonumber \\&\quad \left. -2 a \lambda \sin \left( \phi _2\right) +\,a^2 \sin ^2 \left( \phi _2\right) \right) \nonumber \\&\quad \times \left( \gamma -a e \gamma +a d e \sin \left( \theta _1^*\right) \left( -\lambda +a \sin \left( \phi _2\right) \right) \right) \nonumber \\&\quad +d \cos \left( \theta _1^*\right) \biggl (\left( -1+\lambda ^2-2 a \lambda \sin \left( \phi _2\right) +a^2 \sin ^2 \left( \phi _2\right) \right) \nonumber \\&\quad \times \bigl (3 (a-b) e \lambda +a (2-5 a e+3 b e) \sin \left( \phi _2\right) \nonumber \\&\quad -2 (-1+a e) \lambda \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +4 a (-1+a e) \sin ^3 \left( \phi _2\right) \bigr ) +\cos \left( \phi _2\right) \cos \nonumber \\&\quad \quad \left( \phi _3\right) \Bigl (2 a (-a+b) e \lambda \nonumber \\&\quad +\left( 2 a^3 e+a^2 e (-2 b+e)+2 \left( -1+\lambda ^2\right) \right. \nonumber \\&\left. \quad +\,a \left( e-2 e \lambda ^2\right) \right) \sin \left( \phi _2\right) \nonumber \\&\quad +6 a (-1+a e) \lambda \sin ^2 \left( \phi _2\right) -4 a^2 (-1+a e) \sin ^3 \left( \phi _2\right) \Bigr )\biggr ) \nonumber \\&\quad +\cos \left( \phi _3\right) \biggl (-2 \gamma \left( \lambda -a \sin \left( \phi _2\right) \right) \left( (-a+b) e\right. \nonumber \\&\quad \left. +(-1+a e) \sin ^2 \left( \phi _2\right) \right) \nonumber \\&\quad +d e \sin \left( \theta _1^*\right) \Bigl (b+a^2 e-b \lambda ^2+2 a \left( -1+\lambda ^2\right) \nonumber \\&\quad +2 a (-2 a+b) \lambda \sin \left( \phi _2\right) \nonumber \\&\quad +a \left( 2+2 a^2-a (b+e)-2 \lambda ^2\right) \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +4 a^2 \lambda \sin ^3 \left( \phi _2\right) -2 a^3 \sin ^4 \left( \phi _2\right) \Bigr )\biggr )\Biggr ), \end{aligned}$$

(62)

$$\begin{aligned} G_{12}&= \frac{1}{2} \Biggl (\cos \left( \phi _3\right) \biggl (\left( 2 a^2-3 a b+b^2\right) e \lambda \nonumber \\&\quad -e \Bigl (2 a^3-3 a^2 b+a \left( b^2+b e-\lambda ^2\right) \nonumber \\&\quad +b \left( -1+\lambda ^2\right) \Bigr ) \sin \left( \phi _2\right) \nonumber \\&\quad +\left( -b-8 a^2 e+a (4+5 b e)\right) \lambda \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +a \left( b+7 a^2 e-4 a (1+b e)\right) \sin ^3 \left( \phi _2\right) \nonumber \\&\quad +4 a (-1+a e) \lambda \sin ^4 \left( \phi _2\right) \nonumber \\&\quad -4 a^2 (-1+a e) \sin ^5 \left( \phi _2\right) \biggr )\nonumber \\&\quad +\cos \left( \phi _2\right) \biggl (-(a-b) e \lambda \left( -1+\lambda ^2\right) \nonumber \\&\quad +\Bigl (b \left( -1+\lambda ^2\right) +a^2 e \left( -3+7 \lambda ^2\right) \nonumber \\&\quad -2 a \left( -1+\lambda ^2+b e \left( -1+3 \lambda ^2\right) \right) \Bigr )\nonumber \\&\quad \times \sin \left( \phi _2\right) \nonumber \\&\quad +a \left( -2 b-11 a^2 e+a (4+9 b e)\right) \lambda \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +a \left( -2+5 a^3 e-2 a^2 (1+2 b e)+4 \lambda ^2\right. \nonumber \\&\quad \left. +a \left( b+2 e-4 e \lambda ^2\right) \right) \sin ^3 \left( \phi _2\right) \nonumber \\&\quad +8 a^2 (-1+a e) \lambda \sin ^4 \left( \phi _2\right) -4 a^3 (-1+a e) \sin ^5 \left( \phi _2\right) \biggr )\Biggr ). \end{aligned}$$

(63)

Next, multiplying $\cos ^2\phi _3$ to (45) and using (42) to eliminate $\dot{\phi }_3 \cos \phi _3$ to obtain

$$\begin{aligned} G_{21}+ G_{22} \dot{\phi }_2^2=0, \end{aligned}$$

(64)

where $G_{2i}$ $(i=1,2)$ are the following functions of $\sin \phi _2$, $\cos \phi _2$, and $\cos \phi _3$:

$$\begin{aligned} G_{21}&=\left( \gamma -d \cos \left( \theta _1^*\right) \left( a \cos \left( \phi _2\right) +\cos \left( \phi _3\right) \right) \right) \nonumber \\&\quad \times \left( -1+\lambda ^2 -2 a \lambda \sin \left( \phi _2\right) +a^2 \sin ^2 \left( \phi _2\right) \right) , \end{aligned}$$

(65)

$$\begin{aligned} G_{22}&=\frac{1}{2} \biggl (b+a^2 e-b \lambda ^2+2 a \left( -1+\lambda ^2\right) \nonumber \\&\quad -\,2 a \lambda \left( 2 a-b+\cos \left( \phi _2\right) \cos \left( \phi _3\right) \right) \nonumber \\&\quad \times \sin \left( \phi _2\right) +a \left( 2+2 a^2-a (b+e)\right. \nonumber \\&\quad \left. -\,2 \lambda ^2+2 a \cos \left( \phi _2\right) \cos \left( \phi _3\right) \right) \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +\,4 a^2 \lambda \sin ^3 \left( \phi _2\right) -2 a^3 \sin ^4 \left( \phi _2\right) \biggr ).\end{aligned}$$

(66)

Eliminating $\dot{\phi }_2^2$ from (61) and (64) yields

$$\begin{aligned} G_{11}G_{22}-G_{12}G_{21}=0. \end{aligned}$$

(67)

By using (59), we can guarantee that the highest order of $\cos \phi _3$ of the left-hand side term of the above equation is less than or equal to one. Thus, (67) can be expressed by (47), where

$$\begin{aligned} Q_1&=Q_{11}+Q_{12} \cos \theta _1^*, \end{aligned}$$

(68)

$$\begin{aligned} Q_2&=Q_{21}+Q_{22} \cos \theta _1^*, \end{aligned}$$

(69)

where $Q_{ij}$ $(i,j=1,2)$ are the following functions of $\sin \phi _2$ and $\cos \phi _2$:

$$\begin{aligned} Q_{11}&=2 \cos \left( \phi _2\right) \left( -1+\lambda ^2-2 a \lambda \sin \left( \phi _2\right) +a^2 \sin ^2 \left( \phi _2\right) \right) \nonumber \\&\quad \biggl ((a-b) \gamma \lambda \left( -1+\lambda ^2\right) \nonumber \\&\quad +a\Bigl (\gamma \left( a \left( a e-3 \lambda ^2\right) +b \left( -1+3 \lambda ^2\right) \right) \nonumber \\&\quad +2 d \lambda \Bigl (b+a^2 e-b \lambda ^2\nonumber \\&\quad +2 a \big (-1+\lambda ^2\big )\Bigr ) \sin \left( \theta _1^*\right) \Bigr ) \sin \left( \phi _2\right) +a^2 \Bigl (3 (a-b) \gamma \lambda \nonumber \\&\quad -2 d \left( b+a^2 e-3 b \lambda ^2+a \left( -2+6 \lambda ^2\right) \right) \sin \left( \theta _1^*\right) \Bigr ) \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +a^2 \Bigl (\left( 1-a^2+a (b-e)\right) \gamma \nonumber \\&\quad -2 d \lambda \left( -2-6 a^2+3 a b+a e+2 \lambda ^2\right) \sin \left( \theta _1^*\right) \Bigr )\nonumber \\&\quad \times \sin ^3 \left( \phi _2\right) +2 a^3 d \Bigl (-2-2 a^2+a (b+e)+6 \lambda ^2\Bigr ) \sin \left( \theta _1^*\right) \nonumber \\&\quad \quad \sin ^4 \left( \phi _2\right) -12 a^4 d \lambda \sin \left( \theta _1^*\right) \sin ^5 \left( \phi _2\right) \nonumber \\&\quad +4 a^5 d \sin \left( \theta _1^*\right) \sin ^6 \left( \phi _2\right) \biggr ), \end{aligned}$$

(70)

$$\begin{aligned} Q_{12}&=-d \left( -1+\lambda ^2-2 a \lambda \sin \left( \phi _2\right) +a^2 \sin ^2 \left( \phi _2\right) \right) \nonumber \\&\quad \biggl (-(a-b) \lambda \left( b+3 a^2 e-b \lambda ^2\right) \nonumber \\&\quad +\Bigl (5 a^4 e-a^3 (2+3 b e)-2 b \left( -1+\lambda ^2\right) ^2\nonumber \\&\quad +a^2 \left( b-3 b \lambda ^2\right) \nonumber \\&\quad + a \Bigl (-2 b e \left( -1+\lambda ^2\right) +2 \lambda ^2 \left( -1+\lambda ^2\right) \nonumber \\&\quad +b^2 \big (-1+3 \lambda ^2\big )\Bigr )\Bigr ) \sin \left( \phi _2\right) \nonumber \\&\quad +a \lambda \Bigl (3 a^2 (b+e)+a \left( 4-3 b^2+b e-8 \lambda ^2\right) \nonumber \\&\quad +8 b \left( -1+\lambda ^2\right) \Bigr ) \sin ^2 \left( \phi _2\right) \nonumber \\&\quad +a^2 \Bigl (-a^2 (b+7 e)+4 b \left( 1-3 \lambda ^2\right) +a \left( 2+b^2\right. \nonumber \\&\left. \quad +b e+12 \lambda ^2\right) \Bigr ) \sin ^3 \left( \phi _2\right) \nonumber \\&\quad +8 a^3 (-a+b) \lambda \sin ^4 \left( \phi _2\right) +2 a^3 \nonumber \\&\quad \quad \left( -1+a^2+a (-b+e)\right) \sin ^5 \left( \phi _2\right) \biggr ), \end{aligned}$$

(71)

$$\begin{aligned} Q_{21}&=-2 \gamma \Biggl (a^2 (-a+b) e \lambda -\biggl (-a \left( a^3 e-\lambda ^2+\lambda ^4\right) \nonumber \\&\quad +b \Bigl (a^3 e+a e \left( -1+\lambda ^2\right) \nonumber \\&\quad +\left( -1+\lambda ^2\right) ^2\Bigr )\biggr )\sin \left( \phi _2\right) \nonumber \\&\quad +a \lambda \Bigl (2 a^2 e+a \left( 1+b e-4 \lambda ^2\right) +4 b \left( -1+\lambda ^2\right) \Bigr ) \nonumber \\&\quad \times \sin ^2 \left( \phi _2\right) +2 a^2 \left( b-3 b \lambda ^2+a \left( -a e+3 \lambda ^2\right) \right) \sin ^3 \left( \phi _2\right) \nonumber \\&\quad +a^2 \left( 1-4 a^2+4 a b-a e\right) \lambda \sin ^4\left( \phi _2\right) \nonumber \\&\quad + a^3 \left( -1+a^2+a (-b+e)\right) \nonumber \\&\quad \times \sin ^5\left( \phi _2\right) \Biggr )+d \sin \left( \theta _1^*\right) \nonumber \\&\quad \quad \biggl (\left( b+a^2 e-b \lambda ^2+2 a \left( -1+\lambda ^2\right) \right) ^2\nonumber \\&\quad -4 a (2 a-b) \lambda \left( b+a^2 e-b \lambda ^2+2 a \left( -1+\lambda ^2\right) \right) \sin \left( \phi _2\right) \nonumber \\&\quad + 2 a \Bigl (2 a^4 e-a^3 \left( 4+b e+e^2-12 \lambda ^2\right) +2 b \left( -1+\lambda ^2\right) ^2\nonumber \\&\quad -4 a^2 \left( e \left( -1+\lambda ^2\right) +b \left( -1+3 \lambda ^2\right) \right) \nonumber \\&\quad +a \left( -4+10 \lambda ^2-6 \lambda ^4+b e \left( -1+\lambda ^2\right) +b^2 \right. \nonumber \\&\quad \quad \left. \left( -1+3 \lambda ^2\right) \right) \Bigr ) \sin ^2 \left( \phi _2\right) \nonumber \\&\quad -4 a^2 \lambda \left( 4 a^3-4 a^2 (b+e)+a \left( 10+b^2+b e-12 \lambda ^2\right) \right. \nonumber \\&\quad \left. +4 b \left( -1+\lambda ^2\right) \right) \nonumber \\&\quad \times \sin ^3 \left( \phi _2\right) + a^2 \Bigl (4+4 a^4-4 a^3 (b+2 e)-12 \lambda ^2+8 \lambda ^4\nonumber \\&\quad +a^2 \left( 20+b^2+2 b e+e^2-72 \lambda ^2\right) + 4 a \left( e \left( -1+\lambda ^2\right) \right. \nonumber \\&\left. \quad +b \left( -2+6 \lambda ^2\right) \right) \Bigr )\nonumber \\&\quad \times \sin ^4 \left( \phi _2\right) +8 a^3 \lambda \left( 3+6 a^2-a (2 b+e)-4 \lambda ^2\right) \sin ^5 \left( \phi _2\right) \nonumber \\&\quad + 4 a^4 \left( -3-3 a^2+a (b+e)+12 \lambda ^2\right) \sin ^6 \left( \phi _2\right) \nonumber \\&\quad -32 a^5 \lambda \sin ^7 \left( \phi _2\right) +8 a^6 \sin ^8 \left( \phi _2\right) \biggr ), \end{aligned}$$

(72)

$$\begin{aligned} Q_{22}&=d \cos \left( \phi _2\right) \biggl (-2 (a-b) \lambda \left( a^3 e+\left( -1+\lambda ^2\right) ^2\right) \nonumber \\&\quad +a \Bigl (-a^2 e+a^3 e (-2 b+e)\nonumber \\&\quad +2 a^4 e -a \left( 2+3 b e-10 \lambda ^2\right) \left( -1+\lambda ^2\right) \nonumber \\&\quad -5 b \left( 1-3 \lambda ^2 +2 \lambda ^4\right) \Bigr )\sin \left( \phi _2\right) \nonumber \\&\quad +2 a^2 \lambda \left( 2 a^2 e+a \right. \nonumber \\&\quad \left. \left( 5\!+\!2 b e\!-\!10 \lambda ^2\right) +b \left( -9+10 \lambda ^2\right) \right) \sin ^2 \left( \phi _2\right) \nonumber \\&\quad -a^3 \left( -7 b-e+4 a^2 e+20 b \lambda ^2\right. \nonumber \\&\left. \quad +a \left( 2+b e+e^2-20 \lambda ^2\right) \right) \sin ^3 \left( \phi _2\right) \nonumber \\&\quad -2 a^3 \left( -1+5 a^2+a (-5 b+e)\right) \lambda \sin ^4\left( \phi _2\right) \nonumber \\&\quad +2 a^4 \left( -1+a^2+a (-b+e)\right) \sin ^5 \left( \phi _2\right) \biggr ). \end{aligned}$$

(73)

Regarding Step 1.4, from (47), we obtain $Q_1^2 - Q_2^2\cos ^2\phi _3=Q_1^2 - Q_2^2(1-\sin ^2\phi _3)=0$, which can be expressed as (48) by using (59), where the expressions of $R_1$ and $R_2$ are omitted for brevity. If $\cos \theta _1^*=0$, we can show that $R_2$, the coefficient of $\cos \phi _2$ of $Q_1^2 - Q_2^2\cos ^2\phi _3$, is 0. Indeed, from (68) and (70), we obtain $Q_1=Q_{11}=\cos (\phi _2) \widehat{Q}_{11}$ with $\widehat{Q}_{11}$ not containing $\cos \phi _2$; from (69) and (72), we know that $Q_2= Q_{21}$ does not contain $\cos (\phi _2)$. Thus, $Q_1^2 - Q_2^2(1-\sin ^2\phi _3)=Q_{11}^2 - Q_{21}^2(1-\sin ^2\phi _3) = (1-\sin ^2\phi _2)\widehat{Q}^2_{11}- Q_{21}^2(1-\sin ^2\phi _3)$ does not contain $\cos \phi _2$. Hence, this shows that if $\cos \theta _1^*=0$, then $R_2=0$.

1.4 Details of Step 2

Regarding Step 2, we prove that (41) does not hold by showing that there exists $0<i\le N$ such that $\xi _i \ne 0$ for any mechanical parameters a, b, d, and e defined by (34), and parameters $\theta _1^*$, $\lambda$, and $\gamma$. To start, regarding (50), from

$$\begin{aligned} \xi _{28}= 256a^{20} d^4 (a^2 - a b -a e+1)^4 \sin ^2\theta _1^*\end{aligned}$$

(74)

and $\xi _{28}=0$, we need to consider whether

$$\begin{aligned} a^2 - a b -a e+1 \ne 0; \end{aligned}$$

(75)

that is, $e \ne (1+a^2-ab)/a$, and we analyze Cases 1 and 2 below:

Case 1: $e \ne (1+a^2-ab)/a$

From (74) and $\xi _{28}=0$, we have $\sin \theta _1^*=0$. This yields

$$\begin{aligned} \xi _{24}= & {} 16a^{16} d^4 (a^2 - ab+ ae -1)^2\nonumber \\&\quad (a^2 - a b -a e+1)^4>0, \end{aligned}$$

(76)

which contradicts (41). Indeed, $a^2 - ab+ ae -1>0$ due to $a\ge b>0$ and $ae >1$ from Lemma 6.

Case 2: $e=(1+a^2-ab)/a$

From Lemma 7, we have $a\ne 1$ and $a>b$. In this case, we obtain

$$\begin{aligned} \xi _{24}=256a^{18} (a - b)^2 d^2 \lambda ^2 \sin ^2(\theta _1^*) \epsilon , \end{aligned}$$

(77)

where

$$\begin{aligned} \epsilon =&(1-7 a^2 +6 a b)^2 d^2 \lambda ^2 \cos ^2\theta _1^*\nonumber \\&+ ((1 - 3 a^2 + 2 a b) \gamma - 4 a (a - b) d \lambda \sin \theta _1^*)^2. \end{aligned}$$

(78)

From (77) and $\xi _{24}=0$, we consider two cases of $\lambda =0$ and $\lambda \ne 0$, separately.

Case 2.1: $e=(1+a^2-ab)/a$ and $\lambda =0$

We obtain

$$\begin{aligned} \xi _{0}= (-1 + a^2)^8 (a - b)^8 d^4 \sin ^4\theta _1^*. \end{aligned}$$

(79)

Since $a\ne 1$ and $a>b$ from Lemma 7, we see that $\xi _{0}=0$ shows $\sin \theta _1^*=0$. This yields

$$\begin{aligned} \xi _{18}\!= \!16 a^{14} (-1 \!+\! a^2)^2 (a \!-\! b)^4 (1 \!+ \!3 a^2\! -\! 4 a b)^2 d^2 \gamma ^2.\nonumber \\ \end{aligned}$$

(80)

Regarding whether $1 + 3 a^2 - 4 a b \ne 0$ holds or not, we consider Cases 2.1.1 and 2.1.2 below:

Case 2.1.1: $e=(1+a^2-ab)/a$, $\lambda =0$, and $b \ne (1+3 a^2)/(4a)$

From (80) and $\xi _{18}=0$, we obtain $\gamma =0$. This yields

$$\begin{aligned} \xi _{16}\!=\!9 a^{12} (-1 \!+\! a^2)^4 (a \!-\! b)^4 (1 \!+\! 3 a^2 \!-\! 4 a b)^2 d^4>0,\nonumber \\ \end{aligned}$$

(81)

which contradicts (41).

Case 2.1.2: $e=(1+a^2-ab)/a$, $\lambda =0$, and $b = (1+3 a^2)/(4a)$

We have

$$\begin{aligned} \xi _{12}=\frac{a^4 (-1 + a^2)^{10} (1 + a^2)^2 d^4}{1024}>0, \end{aligned}$$

(82)

which contradicts (41).

Case 2.2: $e=(1+a^2-ab)/a$ and $\lambda \ne 0$

We show $\sin \theta _1^*\ne 0$. On the contrary, assume $\sin \theta _1^*= 0$, from Step 1.1, we have $\lambda = 0$ which raises a contradiction. Thus, from (77) and $\xi _{24}=0$, we have $\epsilon =0$ yielding $1 - 3 a^2 +2 a b \ne 0$ due to (78); otherwise, if $1 - 3 a^2 +2 a b = 0$, then $\epsilon \ge (4 a (a - b) d \lambda \sin \theta _1^*)^2>0$. Thus, $\epsilon =0$ shows

$$\begin{aligned}&(1-7 a^2 +6 ab)\cos \theta _1^*=0, \end{aligned}$$

(83)

$$\begin{aligned}&\gamma =\frac{4 a (a - b)d\lambda \sin \theta _1^*}{1 - 3 a^2 +2 a b}. \end{aligned}$$

(84)

We treat $\cos \theta _1^*\ne 0$ and $\cos \theta _1^*= 0$, separately.

Case 2.2.1: $e=(1+a^2-ab)/a$, $\lambda \ne 0$, and $\cos \theta _1^*\ne 0$

From (83), we obtain $b=(7 a^2-1)/(6a)$. This together with (84) gives

$$\begin{aligned} \xi _{22}= \frac{16}{9}a^{14}(-1 + a^2)^2 d^4 \lambda ^2 \sin ^2(\theta _1^*) \rho , \end{aligned}$$

(85)

where

$$\begin{aligned} \rho= & {} 9((-1 + a^2)^2 - 2 (1 + a^2) \lambda ^2)^2 \cos ^2\theta _1^*\\&+ (5 (-1 + a^2)^2 - 6 (1 + a^2) \lambda ^2)^2 \sin ^2\theta _1^*\ge 0. \end{aligned}$$

From (85) and $\xi _{22}= 0$, we have $\rho =0$ which yields $(-1 + a^2)^2 - 2 (1 + a^2) \lambda ^2 =0$ and $5 (-1 + a^2)^2 - 6 (1 + a^2) \lambda ^2=0$. Deleting $\lambda ^2$ from these two equalities yields $-1+a^2=0$ which contradicts $a \ne 1$ in (38).

Case 2.2.2: $e=(1+a^2-ab)/a$, $\lambda \ne 0$, and $\cos \theta _1^*=0$

From Step 1.4, using $\cos \theta _1^*=0$ shows $R_2=0$, below we study $L=R_1=0$ in (49) rather than $L=R_1^2=0$ in (50). Though the highest order of $R_1$ in (49) is 14, when $e=(1+a^2-ab)/a$ and (84) hold, we find that $\xi _{14}=\xi _{13}=\xi _{12}=0$ holds, and

$$\begin{aligned} \xi _{11}\!=\!\frac{16 a^8 (a \!-\! b) d^2 \lambda \bigl (12 a (1 \!+\! a^2) (a \!-\! b) \lambda ^2 -(-1 \!+\! a^2)^2 (1 \!+\! 3 a^2 \!-\! 4 a b)\bigr ) }{-1\!+\! 3 a^2 - 2 a b }. \end{aligned}$$

(86)

Using $\xi _{11}=0$, $a>b$, and $\lambda \ne 0$, we obtain

$$\begin{aligned} \lambda ^2=\frac{(-1 + a^2)^2 (1 + 3 a^2 - 4 a b)}{12 a (1 + a^2) (a - b) }. \end{aligned}$$

(87)

Using (87), we have

$$\begin{aligned} \xi _{i}=k_{i} \widehat{\xi }_{i}, \quad i=10,9,8, \end{aligned}$$

(88)

where $k_{i}$ are nonzero terms due to $a\ne 1$ and $\lambda \ne 0$, and

$$\begin{aligned} \widehat{\xi }_{10}&=6 -14a^2 - 23 a^4 - 14 a^6 + 21 a^8 \nonumber \\&\quad + a (23 + a^2 + 31 a^4 - 7 a^6) b \nonumber \\&\quad - 8 a^2 (1 + a^2 + a^4) b^2, \end{aligned}$$

(89)

$$\begin{aligned} \widehat{\xi }_{9}&=11 - 2 a^2 - 125 a^4 - 97 a^6 + 138 a^8 + 315 a^{10} \nonumber \\&\quad + a(8 + 196 a^2 + 94 a^4 + 80 a^6- 570 a^8) b\nonumber \\&\quad + 2 a^2 (-89 + 17 a^2 - 163 a^4 + 67 a^6) b^2 \nonumber \\&\quad + 96 a^3 (1 + a^2 + a^4) b^3, \end{aligned}$$

(90)

$$\begin{aligned} \widehat{\xi }_{8}&=35 - 209 a^2 - 240 a^4 + 1420 a^6 + 2159 a^8 \nonumber \\&\quad - 933 a^{10} - 3042 a^{12} + 2538 a^{14} \nonumber \\&\quad + (185 a \!-\! a^3 (266 \!+ \!2211 a^2 \!+\! 1808 a^4 \nonumber \\&\quad +\! 3193 a^6 - 7050 a^8 + 4941 a^{10})) b \nonumber \\&\quad +2 a^2 (-11 + 1091 a^2 - 678 a^4 + 2714 a^6 \nonumber \\&\quad - 1439 a^8+ 915 a^{10}) b^2 \nonumber \\&\quad + 96 a^3 (3 - 10 a^2 - 6 a^4 - 9 a^6 + 4 a^8) b^3. \end{aligned}$$

(91)

Thus, $\xi _{i}=0$ ($i=10,9,8$) are equivalent to

$$\begin{aligned} \widehat{\xi }_{i}=0, \quad i=10,9,8. \end{aligned}$$

(92)

Below we show that there do not exist $a\ne 1$ and b satisfying (92). To this end, first, we use $\widehat{\xi }_{10}=0$ and $\widehat{\xi }_{9}=0$ to delete b to obtain the following polynomial equation:

$$\begin{aligned}&\delta _1\!= \!3703 \!-\!7609 z \!+\! 3744 z^2 \!-\! 7609 z^3\! +\! 3703 z^4=0, \;\nonumber \\&\quad \text {with } z=a^2>0. \end{aligned}$$

(93)

Indeed, to derive $\delta _1$ in (93), since the highest order of b in (89) is 2, we divide $\widehat{\xi }_{9}$ by $\widehat{\xi }_{10}$ with respect to b to obtain $\widehat{\xi }_{9}= p_{9} \widehat{\xi }_{10}+r_{9}$, where $p_{9}$ is the quotient and $r_{9}$ is the remainder with the highest order of b being equal to 1. Using $r_{9}=\widehat{k}_9\widehat{r}_9$, where $\widehat{k}_9 \ne 0$ due to $a\ne 1$, and

$$\begin{aligned} \widehat{r}_9&=-338+512 a^2+1437 a^4+2795 a^6+1945 a^8\nonumber \\&\quad +1785 a^{10}-a \big (1447+1010 a^2\nonumber \\&\quad +3222 a^4+1010 a^6+1447 a^8\big ) b. \end{aligned}$$

(94)

From $\widehat{\xi }_{10}=0$ and $\widehat{\xi }_{9}=0$, we have $r_{9}=0$ and $\widehat{r}_9=0$. Moreover, we divide $\widehat{\xi }_{10}$ by $\widehat{r}_{9}$ with respect to b to obtain $\widehat{\xi }_{10}= p_{10}\widehat{r}_9+r_{10}$ with $p_{10}$ being the quotient and $r_{10}$ being the remainder. From $\widehat{\xi }_{10}=0$ and $\widehat{r}_9=0$, we have $r_{10}=0$. Using $r_{10}=\psi _{10} \delta _1$ with $\psi _{10} \ne 0$ due to $a\ne 1$ yields $\delta _1=0$ in (93).

Next, we use $\widehat{\xi }_{10}=0$, $\widehat{\xi }_{8}=0$, and $\widehat{r}_{9}=0$ to delete b to obtain the following polynomial equation:

$$\begin{aligned} \delta _2=&244+355 z-1726 z^2+355 z^3+244 z^4=0, \; \nonumber \\&\text {with } z=a^2>0. \end{aligned}$$

(95)

To derive $\delta _2$ in (95), we divide $\widehat{\xi }_{8}$ by $\widehat{\xi }_{10}$ with respect to b to obtain $\widehat{\xi }_{8}= p_{8} \widehat{\xi }_{10}+r_{8}$, where $p_{8}$ is the quotient and $r_{8}$ is the remainder with the highest order of b being equal to 1. Using $r_{8}=\widehat{k}_8\widehat{r}_8$, where $\widehat{k}_8 \ne 0$ due to $a\ne 1$ and

$$\begin{aligned} \widehat{r}_8&= 2558-5332 a^2-12433 a^4-9329 a^6\nonumber \\&\quad +13432 a^8+29542 a^{10}\nonumber \\&\quad +36075 a^{12}+25839 a^{14}+\Bigl (10873 a\nonumber \\&\quad +1174 a^3+3937 a^5-a^7 \nonumber \\&\quad \times \big (19216+35113 a^2+21046 a^4+20961 a^6\big )\Bigr ) b. \end{aligned}$$

(96)

From $\widehat{\xi }_{10}=0$ and $\widehat{\xi }_{8}=0$, we have $r_{8}=0$ and $\widehat{r}_8=0$. Finally, we divide $\widehat{r}_8$ by $\widehat{r}_9$ with respect to b to obtain $\widehat{r}_8= \widehat{p}_{8}\widehat{r}_9+d_{8}$ with $\widehat{p}_{8}$ being the quotient and $d_8$ being the remainder. Thus, from $\widehat{r}_8=0$ and $\widehat{r}_9=0$, we obtain $d_8=0$. Using $d_{8}=\psi _{8} \delta _2$ with $\psi _{8} \ne 0$ due to $a\ne 1$ yields $\delta _2=0$ in (95).

Since $z=a^2>0$ and the positive real solutions of (93) and (95) are

$$\begin{aligned} z&=0.5148, \quad z =1.9425, \end{aligned}$$

(97)

$$\begin{aligned} z&= 0.5486, \quad z=1.8228, \end{aligned}$$

(98)

respectively, (93) and (95) do not have a common positive solution; thus, they do not hold simultaneously. This contradicts (92), equivalently, (88), and thus contradicts (41).

For Cases 1 and 2, we have shown that (41) does not hold for any mechanical parameters a, b, d, and e defined by (34), and any possible parameters $\theta _1^*$, $\lambda$, and $\gamma$. Thus, $\dot{\theta }_2=\dot{\phi }_2\equiv 0$. From (42), we have $\dot{\phi }_3 \cos \phi _3=0$. Integrating it with respect to time yields $\sin \phi _3=\lambda _0$ with $\lambda _0$ being a constant. Thus, $\phi _3$ is a constant and $\dot{\theta }_3=\dot{\phi }_3\equiv 0$. This completes the proof of Lemma 3. $\square$

Appendix 4: Proof of Lemma 4

We characterize the invariant set W in (20) by studying $E^*=E_r$ and $E^*\ne E_r$, separately. To start, putting $E({\varvec{\theta }}(t),\dot{{\varvec{\theta }}}(t)) \equiv E^{*}$ and $\theta _1(t)\equiv \theta ^{*}_1$ into (32) (from which we derived controller (15)) yields

$$\begin{aligned} (E^{*}-E_r)\tau _1 (t)+ k_P \theta ^{*}_1 \equiv 0. \end{aligned}$$

(99)

If $E^{*}=E_r$, then $\theta ^{*}_1=0$ from (99). Putting $\theta ^{*}_1=0$ into the W in (20), we obtain the $W_r$ in (24). Putting $\dot{\theta }_2(t)=0$ and $\dot{\theta }_3(t)=0$ into the $W_r$ in (24) to obtain equilibrium points in the $W_r$ in (24), we obtain $\cos \theta _2(t)=1$ and $\cos \theta _3(t)=1$. This shows that $\theta _2(t)=0$ and $\theta _3(t)=0$ ($\text {mod}~ 2\pi$). Thus, the UEP is the only equilibrium point in $W_r$.

If $E^{*}\ne E_r$, then $\tau _1(t)$ is a constant from (99), denoted as $\tau _1^*$. From Lemma 3, links 2 and 3 do not move. Thus, the APP robot stays at an equilibrium an equilibrium configuration ${\varvec{\theta }}^*=\left[ \begin{array}{ccc} \theta _1^*, &{}\theta _2^*, &{}\theta _3^*\\ \end{array} \right] ^{\mathrm {T}}$. Below we show that if $k_P$ satisfies (22), then the APP robot stays at an equilibrium point belongs to $\Omega _s$ in (25). Using (4) and (32) (from which we derived controller (15)) with equilibrium torque $\tau _1^*=-\beta _1 \sin \theta _1^*$ and the energy at the point $E^*=P({\varvec{\theta }}^*)$, we have

$$\begin{aligned}&\sin \theta _2^*\equiv 0, ~~\sin \theta _3^*\equiv 0, \end{aligned}$$

(100)

$$\begin{aligned}&\beta _1 (E_r-P({\varvec{\theta }}^*))\sin \theta _1^*+ k_P \theta _1^*= 0. \end{aligned}$$

(101)

Note that (100) gives

$$\begin{aligned} \theta _i^*= 0 ~~ \text {or}~~ \pi ~~~ (\text {mod}~~ 2\pi ), ~~ i=2, 3. \end{aligned}$$

(102)

Clearly, $\theta _1^*=0$ is a solution of (101). When $\theta _1^*\ne 0$, we rewrite (101) as

$$\begin{aligned} k_P= f_0(\theta ^*_1), \end{aligned}$$

(103)

where

$$\begin{aligned} f_0(\theta ^*_1)=\frac{-\beta _1 ( E_r -P({\varvec{\theta }}^*)) \sin \theta ^*_1}{\theta ^*_1}, \;\; \theta ^*_1 \ne 0. \end{aligned}$$

(104)

Since $f_0(\theta ^*_1)$ is an even function of $\theta ^*_1$, we can see that (103) has no solution $\theta ^*_1$ if and only if

$$\begin{aligned} k_P> \max _{\theta ^*_1>0}f_0(\theta ^*_1). \end{aligned}$$

(105)

Since the numerator of $f_0(\theta ^*_1)$ is a periodic function with period $2\pi$ and is nonnegative in $[\pi ,\; 2\pi ]$, we have

$$\begin{aligned} \max _{\theta ^*_1>0}f_0(\theta ^*_1)=\max _{\pi \le \theta ^*_1 \le 2\pi }f_0(\theta ^*_1). \end{aligned}$$

(106)

For all $\theta _2^*$ and $\theta _3^*$ in (102), since $P({\varvec{\theta }}^*) \ge \beta _1 \cos \theta _1^*-\beta _2 - \beta _3$, we can see that (103) has no solution if and only if $k_P$ satisfies (22).

Thus, under controller (15) with the bounds on the gains in (17), (18), and (22), the closed-loop solution $({\varvec{\theta }}(t), \dot{{\varvec{\theta }}}(t))$ converges to either the $W_r$ in (24) when $E^*=E_r$ or the $\Omega _s$ in (25) when $E^*\ne E_r$. $\square$

Appendix 5: Proof of Lemma 5

The proof of the four equilibrium points being strictly unstable is similar to that in [30]. First, let $J_{uuu}$ be the Jacobian matrix evaluated at the UEP $(\theta _1, \theta _2, \theta _3, \dot{\theta }_1, \dot{\theta }_2,\dot{\theta }_3)=(0, 0, 0, 0,0,0)$. Straightforward calculation of the characteristic polynomial of that point yields

$$\begin{aligned} |s I- J_{uuu}|= & {} s^6+a_1s^5+a_2s^4+a_3s^3\\&+a_4s^2+a_5s+a_6, \end{aligned}$$

where

$$\begin{aligned} a_1&=\frac{k_V}{k_D}, \\ a_2&=\frac{k_P}{k_D}- \frac{\alpha _{33} \beta _2+\alpha _{22}\beta _3}{\alpha _{22} \alpha _{33}- \alpha _{23}^2},\\ a_3&=-\frac{k_V( \alpha _{33} \beta _2+ \alpha _{22} \beta _3)}{k_D (\alpha _{22} \alpha _{33}- \alpha _{23}^2)}, \\ a_4&=\frac{-k_P (\alpha _{23} \beta _2+ \alpha _{22} \beta _{3})+k_D\beta _{2} \beta _3}{k_D (\alpha _{22} \alpha _{33}- \alpha _{23}^2)},\\ a_5&=\frac{k_V \beta _2 \beta _3}{k_D (\alpha _{22} \alpha _{33}- \alpha _{23}^2)}, \\ a_6&= \frac{k_P \beta _2 \beta _3}{k_D (\alpha _{22} \alpha _{33}- \alpha _{23}^2)}. \end{aligned}$$

Since $\alpha _{22} \alpha _{33}- \alpha _{23}^2>0$ which can be verified directly by using (8), $a_3<0$ holds for all mechanical parameters of the APP robot in (8) and control gains $k_D>0$, $k_P>0$, and $k_V>0$. Therefore, $J_{uuu}$ has at least one eigenvalue in the open right-half plane. This shows that the UEP is strictly unstable.

Second, let $J_{uud}$ be the Jacobian matrix evaluated at the up–up–down equilibrium point $(\theta _1, \theta _2, \theta _3, \dot{\theta }_1, \dot{\theta }_2,\dot{\theta }_3)=(0, 0, \pi , 0,0,0)$. Straightforward calculation of the characteristic polynomial of that point yields

$$\begin{aligned} |s I- J_{uud}|= & {} s^6+a_1s^5+a_2s^4+a_3s^3\\&+a_4s^2+a_5s+a_6, \end{aligned}$$

where

$$\begin{aligned} a_1 \Delta&=(\alpha _{22}\alpha _{33} -\alpha _{23}^2 ) k_V,\\ a_2 \Delta&=(\alpha _{22}\alpha _{33} -\alpha _{23}^2 ) k_P+ (-\alpha _{33} \beta _2 + \alpha _{22} \beta _3)k_D \nonumber \\&\quad + 2\beta _3 ((\alpha _{22} \alpha _{33}-\alpha _{23}^2) \beta _1 + (\alpha _{11} \alpha _{33} - \alpha _{13}^2) \beta _2\\&\quad -(\alpha _{11} \alpha _{22}-\alpha _{12}^2) \beta _3),\\ a_3 \Delta&=(-\alpha _{33} \beta _2 + \alpha _{22} \beta _3)k_V,\\ a_4 \Delta&=2\beta _3 (\alpha _{11}\beta _1\beta _2+ \alpha _{22} \beta _1 \beta _3-\alpha _{33} \beta _1 \beta _2)\\&\quad +(-\alpha _{33}\beta _2+ \alpha _{22} \beta _3)k_P -\beta _2\beta _3 k_D, \\ a_5 \Delta&=-\beta _2 \beta _3 k_V,\\ a_6 \Delta&=-\beta _2\beta _3(k_P+2 \beta _1 \beta _3), \end{aligned}$$

with $\Delta = (\alpha _{22} \alpha _{33} - \alpha _{23}^2 )k_D+ 2(\alpha _{12} ^2 \alpha _{33} + \alpha _{22} \alpha _{13}^2 -2 \alpha _{12} \alpha _{13} \alpha _{23} - \alpha _{11}(\alpha _{22} \alpha _{33} - \alpha _{23}^2 ))\beta _3.$

Below we show $\Delta >0$. From condition (17), we have $k_D > k_{uud}$, where

$$\begin{aligned} k_{uud}=&\left( E_{r} -P({\varvec{\theta }}) \right) ({\varvec{b}}^{{\mathrm {T}}}{\varvec{M}}^{-1}({\varvec{\theta }}){\varvec{b}})^{-1}|_{\theta _1=0,~\theta _2=0, ~ \theta _3 =\pi }\\ =&\frac{\rho _1}{\alpha _{22} \alpha _{33} -\alpha _{23}^2 }, \end{aligned}$$

with $\rho _1=2\beta _3 (\alpha _{11} \alpha _{22} \alpha _{33} - \alpha _{12}^2 \alpha _{33} - \alpha _{22} \alpha _{13}^2 +2 \alpha _{12} \alpha _{13} \alpha _{23} - \alpha _{11} \alpha _{23}^2)$. Thus, we have $\Delta =(k_D-k_{uud}) (\alpha _{22} \alpha _{33} - \alpha _{23}^2 )> 0$. This shows that $a_5<0$ and $a_6<0$ for all mechanical parameters of the APP robot in (8) and control gains $k_D>0$, $k_P>0$, and $k_V>0$. Therefore, $J_{uud}$ has at least one eigenvalue in the open right-half plane. This shows that the up–up–down equilibrium point is strictly unstable. Similarly, we can show that the up–down–up equilibrium point $(\theta _1, \theta _2, \theta _3, \dot{\theta }_1, \dot{\theta }_2,\dot{\theta }_3)=(0, \pi , 0, 0,0,0)$ is also strictly unstable; the detail is omitted for brevity.

Finally, regarding the up–down–down equilibrium point $(\theta _1, \theta _2, \theta _3, \dot{\theta }_1, \dot{\theta }_2,\dot{\theta }_3)$ $=(0, \pi , \pi , 0,0,0)$, different from the other two equilibrium points in $\Omega _s$, we cannot show its instability from the signs of coefficients of the characteristic polynomial of that point, and we need to compute the Hurwitz determinants (see, e.g., [16]). Let $J_{udd}$ be the Jacobian matrix evaluated at that point. Straightforward calculation of the characteristic polynomial of that point yields

$$\begin{aligned} |s I- J_{udd}|= & {} s^6+a_1s^5+a_2s^4+a_3s^3\\&+\,a_4s^2+a_5s+a_6, \end{aligned}$$

where

$$\begin{aligned} a_1 \Xi&=(\alpha _{22}\alpha _{33} -\alpha _{23}^2 ) k_V,\\ a_2 \Xi&=(\alpha _{22}\alpha _{33} -\alpha _{23}^2 ) k_P+ (\alpha _{33} \beta _2 + \alpha _{22} \beta _3)k_D \\&\quad + 2 (\beta _2 + \beta _3) \\&\quad \times \bigl ((\alpha _{22} \alpha _{33}-\alpha _{23}^2) \beta _1- (\alpha _{11} \alpha _{33} - \alpha _{13}^2) \beta _2\\&\quad -(\alpha _{11} \alpha _{22}-\alpha _{12}^2) \beta _3\bigr ),\\ a_3 \Xi&= (\alpha _{33} \beta _2 + \alpha _{22} \beta _3)k_V,\\ a_4 \Xi&=(\alpha _{33} \beta _2 + \alpha _{22} \beta _3)k_P+\beta _2 \beta _3 k_D \\&\quad - 2(\alpha _{11} \beta _2 \beta _3 -\alpha _{22} \beta _1 \beta _3 -\alpha _{33} \beta _1 \beta _2 ) (\beta _2 + \beta _3), \\ a_5 \Xi&=\beta _2 \beta _3 k_V,\\ a_6 \Xi&=\beta _2\beta _3(k_P+2 \beta _1 (\beta _2+\beta _3)), \end{aligned}$$

with $\Xi = (\alpha _{22} \alpha _{33} - \alpha _{23}^2 )k_D-2(\alpha _{11} \alpha _{22} \alpha _{33} - \alpha _{12}^2 \alpha _{33} - \alpha _{22} \alpha _{13}^2 + 2 \alpha _{12} \alpha _{13} \alpha _{23} - \alpha _{11} \alpha _{23}^2)(\beta _2+\beta _3)$.

Similar to $\Delta >0$, we can show $\Xi >0$. In fact, from condition (17), we have $k_D > k_{udd}$, where

$$\begin{aligned} k_{udd}= & {} \left( E_{r} -P({\varvec{\theta }}) \right) ({\varvec{b}}^{{\mathrm {T}}}{\varvec{M}}^{-1}({\varvec{\theta }}){\varvec{b}})^{-1}|_{\theta _1=0,~\theta _2=\pi , ~ \theta _3 =\pi } \\= & {} \frac{\rho _2}{\alpha _{22} \alpha _{33} -\alpha _{23}^2 }, \end{aligned}$$

where $\rho _2=2(\beta _2 +\beta _3)(\alpha _{11} \alpha _{22} \alpha _{33} - \alpha _{12}^2 \alpha _{33} - \alpha _{22} \alpha _{13}^2 + 2 \alpha _{12} \alpha _{13} \alpha _{23} - \alpha _{11} \alpha _{23}^2)$. Thus, $\Xi =(k_D-k_{udd}) (\alpha _{22} \alpha _{33} - \alpha _{23}^2 )> 0$. Using $\Xi >0$ shows $a_1>0$, $a_3>0$, $a_5>0$, and $a_6>0$ for any mechanical parameters described in (8) for the APP robot, and control gains $k_D>0$, $k_P>0$, and $k_V>0$. However, the sign of $a_2$ or $a_4$ depends on the mechanical and control gains. We obtain the Hurwitz determinant

$$\begin{aligned} D_3= \left| \begin{array}{ccc} a_1 &{}a_3 &{}a_5 \\ 1 &{}a_2 &{}a_4 \\ 0 &{}a_1 &{}a_3 \\ \end{array}\right| = a_1 a_2 a_3 - a_3^2 - a_1^2 a_4 + a_1 a_5, \end{aligned}$$

which satisfies

$$\begin{aligned}&D_3 \Xi ^3\\&\quad = -2 k_V^2(\beta _2 +\beta _3) \Bigl (2\alpha _{23}\beta _2 \beta _3 (\alpha _{12} \alpha _{23}- \alpha _{22} \alpha _{13})\\&\quad (\alpha _{12} \alpha _{33} -\alpha _{13}\alpha _{23}) +\alpha _{33} \beta _2 ^2 (\alpha _{12}\alpha _{33} -\alpha _{13}\alpha _{23})^2 \\&\quad +\alpha _{22}\beta _3^2 (\alpha _{22}\alpha _{13} - \alpha _{12} \alpha _{23})^2 \Bigr ). \end{aligned}$$

Using Lemma 6 shows $\alpha _{12} \alpha _{23}- \alpha _{22} \alpha _{13} \ge 0$ and $\alpha _{12} \alpha _{33}-\alpha _{13} \alpha _{23}>0$. Thus, $D_3<0$. Therefore, $J_{udd}$ has at least one eigenvalue in the open right-half plane. This shows that the up–down–down equilibrium point is strictly unstable. $\square$