Nonlinear adaptive control for an unmanned aerial payload transportation system: theory and experimental validation

Abstract

In this paper, the position control and swing motion control problem are investigated for an aerial payload transportation system which consists of a quadrotor unmanned aerial vehicle (UAV) and a suspended payload. Under the constraints of underactuated properties and unknown system parameters, a nonlinear adaptive control strategy is designed based on the energy methodology, which achieves accurate position control of the UAV as well as the payload’s fast swing suppression during the flight. The stability of the closed-loop system, asymptotic convergence of the UAV’s position error and payload swing suppression are proved via Lyapunov-based stability analysis. Real-time experimental results validate the effectiveness of the developed technique.

1 Introduction

A quadrotor UAV has many advantages in respect of its rapid maneuvering, precise hovering and vertical taking-off and landing (VTOL) features [1,2,3,4,5,6], which plays an important role in many fields such as search and rescue [7], aggressive maneuvering [8], fire fighting [9], environmental monitoring [10], infrastructure reconstruction [11] and so on. The cargo transporting by using a quadrotor UAV is a promising application area.

The control of unmanned aerial vehicle such as satellite or quadrotor UAVs has been a topic of considerable interests. The modeling and control for unmanned aerial vehicle has been intensively studied over the past decades [12, 13], especially the nonlinear robust control under the uncertainties [14,15,16,17,18]. However, the task for the quadrotor aerial transportation system is extremely hazardous because the quadrotor dynamic is affected by the suspended payload through the tension force along the connecting cable. In the past few years, researchers have paid great attentions on the quadrotor aerial transporting system, the applications of the system vary from obstacle avoidance [19, 20], payload lift maneuvering [21, 22], transporting a payload via flexible cable [23, 24], multiple quadrotors cooperative transporting [25,26,27] and so on. The control objective for the system is to deliver slung-payload to its destination in a smooth, safe and efficient way. Two main methods have been adopted to solve the control problem. One is the open loop strategy to generate the desired trajectory via different methodologies such as dynamic programming, differential flatness approach and so on. Palunko et al. present a discrete piecewise linear model of the quadrotor slung-payload system in [28], then a dynamic programming approach is used to generate the swing-free trajectory. In [29], Sreenath et al. propose a nominal trajectory generation method by using differential flatness property of the quadrotor slung-payload system, meanwhile a controller is designed which enables tracking of the quadrotor’s attitude and the payload’s position. The second method is the closed-loop strategy which utilizes the payload swing angles directly for the control development. A reinforcement learning-based control algorithm is proposed in [30] for a quadrotor slung-payload system to achieve trajectory tracking of the quadrotor UAV without exact model knowledge of the system’s dynamics. In [31], a nonlinear hierarchical control scheme is proposed for the system. For the outer-loop subsystem, the position controller is designed based on an energy storage function, and then, a coordinate-free geometric attitude controller is designed for the inner-loop subsystem.

Despite the aforementioned achievements, there are still some important problems about the system that need to be addressed: (1) Some existing control algorithms are developed based a simplified 2D dynamic model (i.e, only the horizontal motion of the quadrotor aerial is considered) and the payload’s swing angles are assumed to be very small thus the coupling between the quadrotor motion and the payload’s swing motion can be neglected. (2) Some existing works utilize a linear dynamic model which is obtained via linearizing the nonlinear model near a specified equilibrium point, normally chosen near the hovering mode. Thus the controller is only valid for a very restricted flight envelope. (3) Few works have considered about the uncertainties associated with the dynamic model of the system, meanwhile the exact model knowledge of the system is not easy to be obtained. (4) For many existing works, only numerical simulation results are presented which prevent their application from the practical aerial transporting operation.

In this paper, the flight control strategy is designed based on a three-dimensional dynamic model, and thus, both the horizontal motion and the vertical motion are included for the control development. Motivated by passivity property of the system’s energy, we construct a nonlinear adaptive controller, which can achieve position control of quadrotor as well as suppression of payload swing motion. Finally, the stability of the closed-loop system is proved via Lyapunov-based analysis, and the effectiveness of the proposed control strategy are validated via real-time experimental results. Therefore, the main contributions of the proposed nonlinear controller include the following: (1) A nonlinear dynamic model is employed to formulate the proposed control strategy without linearization; thus, the operation range of the controller is not limited to a very narrow scope near the system’s equilibrium point. (2) Nonlinear adaptive estimation laws are developed to compensate for the unknown system parameters; thus, explicit model knowledge of the nonlinear model is not required. (3) The proposed anti-swing controller can regulate the quadrotor to its destination asymptotically and suppress swing motion effectively without restriction on the payload’s swing motion while most existing works require the payload’s swing angle should stay in a small range (i.e, assuming that $sin\theta \approx \theta$ [32, 33]). (4) The proposed controller is developed based on a three-dimensional model of the system, so it is more suitable for the real flight of the quadrotor aerial transporting system.

Comparing with the most recent work in [34], the main difference of this paper can be summarized as: (1) In [34], the disturbances are considered to be small enough that can be ignored. In this paper, it is shown that the proposed control strategy is robust against the unknown external air turbulence both theoretically and experimentally. (2) The payload’s mass is considered to be exactly known in [34]. In this paper, not only the influence of the uncertainty of the payload’s mass can be compensated, but also the proposed parameter update law can accurately estimate the payload’s mass online. (3) In addition to the basic regulation control verification and robustness to initial swing disturbance in [34], the robustness to different payload’s mass and the external disturbances during the transportation are considered in this paper.

The rest contents of this paper are organized as follows. The nonlinear dynamic model of the quadrotor aerial transporting system is described in Sect. 2. Section 3 provides a nonlinear adaptive controller inspired by energy analysis of the system. In Sect. 4, we detail the stability analysis of the quadrotor aerial transporting system with the proposed controller by using Lyapunov-based analysis. Section 5 shows experimental results and compares the proposed controller with linear quadratic regulator (LQR) controller with regard to the control performance. Finally, some concluding remarks are presented in Sect. 6.

2 Problem formulation

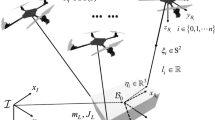
This section describes the three-dimensional dynamic model for the quadrotor with a cable suspended load. As Fig. 1 shows, the payload is attached to a quadrotor via a massless and unstretchable cable. And the payload is hinged by mean of a ball joint at the quadcopter’s center of mass.

Fig. 1

Schematic of the quadrotor UAV slung-payload system

To describe the kinematics of the quadrotor, let ${\mathscr {I}}=\{X_{I},Y_{I},Z_{I}\}$ represent a right hand inertia frame with $Z_{I}$ being the vertical direction to the earth. The body fixed frame is denoted by ${\mathscr {B}}=\{X_\mathrm{B},Y_\mathrm{B},Z_\mathrm{B}\}$. By using the Eulerian–Lagrangian formulation, the three-dimensional quadrotor with a slung-payload is given as follows:

(1)

where $q(t)=[x(t),y(t),z(t),\gamma _{x}(t),\gamma _{y}(t)]^{T}\in {\mathbb {R}}^{5}$ denotes the system state vector, x(t), y(t), z(t) represent the quadrotor position in the $X_{I}$, $Y_{I}$, $Z_{I}$ directions, respectively, $\gamma _{x}(t)$, $\gamma _{y}(t)$ represent the payload swing angle about $X_{I}$ and $Y_{I}$, respectively, as shown in Fig. 1. The terms $M_{c}(q),C(q,{\dot{q}})\in {\mathbb {R}}^{5\times 5}$, G(q), f(t), $f_{d} (t)\in {\mathbb {R}}^{5}$ in (1) denote the inertia matrix, the centripetal-Coriolis matrix, the gravity vector, the control input vector, the aerodynamic drag force vector, respectively, which are defined as

$$\begin{aligned}&\left\{ \begin{array} [c]{l} M_{c}(q)=\left[ \begin{array} [c]{ccccc} m_{c11} &{}\quad 0 &{}\quad 0 &{}\quad m_{c14} &{}\quad m_{c15}\\ 0 &{}\quad m_{c22} &{}\quad 0 &{}\quad 0 &{}\quad m_{c25}\\ 0 &{}\quad 0 &{}\quad m_{c33} &{}\quad m_{c34} &{}\quad m_{c35}\\ m_{c41} &{}\quad 0 &{}\quad m_{c43} &{}\quad m_{c44} &{}\quad 0\\ m_{c51} &{}\quad m_{c52} &{}\quad m_{c53} &{}\quad 0 &{}\quad m_{c55} \end{array} \right] \\ m_{c11}=m_{c22}=m_{c33}=m_{q}+m_{p}\text { }m_{c55}=m_{p}l^{2}\\ m_{c44}=m_{p}l^{2}C_{y}^{2}\text { }m_{c14}=m_{c41}=m_{p}lC_{x}Cy\\ m_{c15}=m_{c51}=-m_{p}lS_{x}S_{y}\text { }m_{c25}=m_{c52}=m_{p}lC_{y}\\ m_{c34}=m_{c43}=m_{p}lS_{x}C_{y}\text { }m_{c35}=m_{c53}=m_{p}lC_{x}S_{y} \end{array} \right. , \nonumber \\\end{aligned}$$

(2)

$$\begin{aligned}&\left\{ \begin{array} [c]{l} C(q,{\dot{q}})=\left[ \begin{array} [c]{ccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad c_{14} &{}\quad c_{15}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad c_{25}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad c_{34} &{}\quad c_{35}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad c_{44} &{}\quad c_{45}\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad c_{54} &{}\quad 0 \end{array} \right] \\ c_{14}=-\,m_{p}l{\dot{\gamma }}_{x}S_{x}C_{y}-m_{p}l{\dot{\gamma }}_{y}C_{x}S_{y}\\ c_{15}=-\,m_{p}l{\dot{\gamma }}_{x}C_{x}S_{y}-m_{p}l{\dot{\gamma }}_{y}S_{x}C_{y}\\ c_{25}=-\,m_{p}l{\dot{\gamma }}_{y}S_{y}\text { }c_{44}=-\,m_{p}l_{y}^{2}\dot{\gamma }_{y}C_{y}S_{y}\\ c_{45}=-\,m_{p}l_{x}^{2}{\dot{\gamma }}_{x}C_{y}S_{y}\text { }c_{54}=m_{p}l_{x} ^{2}{\dot{\gamma }}_{x}C_{y}S_{y}\\ c_{34}=m_{p}l{\dot{\gamma }}_{x}C_{x}C_{y}+m_{p}l{\dot{\gamma }}_{y}S_{x}S_{y}\\ c_{35}=m_{p}l{\dot{\gamma }}_{x}S_{x}S_{y}+m_{p}l{\dot{\gamma }}_{y}C_{x}C_{y} \end{array} \right. , \end{aligned}$$

(3)

$$\begin{aligned}&\left\{ \begin{array} [c]{l} G(q)=\left[ \begin{array} [c]{ccccc} 0 &{}\quad 0 &{}\quad g_{31} &{}\quad g_{41} &{}\quad g_{51} \end{array}x \right] ^{T}\\ g_{31}=(m_{q}+m_{p})g\\ g_{41}=m_{p}glS_{x}C_{y}\text { }g_{51}=m_{p}glC_{x}S_{y} \end{array} \right. , \end{aligned}$$

(4)

$$\begin{aligned}&f=\left[ \begin{array} [c]{ccccc} f_{x}&\quad f_{y}&\quad f_{z}&\quad 0&\quad 0 \end{array} \right] ^{T}, \end{aligned}$$

(5)

$$\begin{aligned}&f_{d}=\left[ \begin{array} [c]{ccccc} -\,c_{x}{\dot{x}}&\quad -c_{y}{\dot{y}}&\quad -c_{z}{\dot{z}}&\quad -c_{\gamma _{x}}\dot{\gamma }_{x}&\quad -c_{\gamma _{y}}{\dot{\gamma }}_{y} \end{array} \right] ^{T}. \nonumber \\ \end{aligned}$$

(6)

In (2)–(6), $m_{q}$, $m_{p}$ are the mass of the quadrotor and the payload, respectively, and $m_{p}$ is unknown, l is the cable length, g is the acceleration of gravity, $f_{x}(t)$, $f_{y}(t)$, $f_{z}(t)$ denote the control inputs in $X_{I}$, $Y_{I}$, $Z_{I}$ directions, respectively, $c_{x}$, $c_{y}$, $c_{z}$, $c_{\gamma _{x}}$, $c_{\gamma _{y}}$ are unknown aerodynamic drag force coefficients, $C_{x}$, $C_{y}$, $S_{x}$, $S_{y}$ are abbreviations of $\cos \gamma _{x}$, $\cos \gamma _{y}$, $\sin \gamma _{x}$ and $\sin \gamma _{y}$, respectively.

Remark 1

The control inputs $f_{x}(t)$, $f_{y}(t)$ and $f_{z}(t)$ in inertia frame ${\mathscr {I}}$ can be converted to actual lift forces and torque generated by four motors in body fixed frame ${\mathscr {B}}$ via the similar procedure in [1].

Remark 2

The quadrotor itself is an underactuated system [1]. The introducing of the payload results in the increase in system’s degree of freedom. That is, the quadrotor’s states x(t), y(t) and z(t) are affected by the input $f_{x}(t)$, $f_{y}(t)$ and $f_{z}(t)$ directly while the payload’s swing angles $\gamma _{x}(t)$ and $\gamma _{y}(t)$ are not controlled directly with $f_{x}(t)$, $f_{y}(t)$ and $f_{z}(t)$. Thus, the dynamic system in (1) is underactuated.

The inertia matrix $M_{c}(q)$ has the following properties [35, 36]:

Property 1

The inertia matrix $M_{c}(q)$ is symmetric and positive definite. Furthermore, for any vector $\chi \in {\mathbb {R}}^{5}$, there always exist two positive constants $\lambda _{m}$ and $\lambda _{M}$ which satisfy the following inequality

$$\begin{aligned} \lambda _{m}\left\| \chi \right\| ^{2}\le \chi ^{T}M_{c}(q)\chi \le \lambda _{M}\left\| \chi \right\| ^{2}. \end{aligned}$$

(7)

Property 2

The inertia matrix $M_{c}(q)$ and the centripetal-Coriolis matrix $C(q,{\dot{q}})$ satisfy the following equation

$$\begin{aligned} {\dot{M}}_{c}(q)=C^{T}(q,{\dot{q}})+C(q,{\dot{q}}). \end{aligned}$$

(8)

Although the controller design is under the condition of the unknown payload’s mass $m_{p}$, we can usually obtain a prior information about the upper and lower bounds for $m_{p}$ as follows:

$$\begin{aligned} {\underline{\text {m}}}_{p}\le m_{p}\le {\bar{m}}_{p}. \end{aligned}$$

(9)

According to the practical flight scenarios, the following assumptions will be invoked in the subsequent control development and stability analysis..

Assumption 1

The payload is always below the quadrotor, and the swing angle $\gamma _{x}(t)$, $\gamma _{y}(t)$ satisfy

$$\begin{aligned} -\,\frac{\pi }{2}\le \gamma _{x}(t)\le \frac{\pi }{2}&\quad -\,\frac{\pi }{2}\le \gamma _{y}(t)\le \frac{\pi }{2} . \end{aligned}$$

(10)

Remark 3

For most quadrotor UAV, the rotational dynamics converge faster than the translational dynamics, thus a lot of existing works do not take the rotational dynamics into consideration [28, 37, 38]. Similarly, the controller design developed in this paper mainly focuses on the translational dynamics of the quadrotor.

In this paper, we will develop an adaptive nonlinear controller of the quadrotor with a slung-payload subject to unknown parameters such as payload mass and air damping coefficients. The control objective is to ensure that the quadrotor moves to the target position precisely, while the payload’s swing angles are suppressed rapidly, which can be described as follows:

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }\left[ x(t)\text { }y(t)\text { }z(t)\text { }\gamma _{x}(t)\text { }\gamma _{y}(t)\right] =\left[ x_{d}\text { }y_{d}\text { }z_{d}\text { }0\text { }0\right] . \nonumber \\ \end{aligned}$$

(11)

where $x_{d}$, $y_{d}$, $z_{d}\in {\mathbb {R}}$ denote the target position of the quadrotor.

To quantify the control performance, regulation error signals are defined as follows:

$$\begin{aligned} \begin{array} [c]{l}\begin{array} [c]{ccc} e_{x}(t)=x(t)-x_{d} &{}\quad e_{y}(t)=y(t)-y_{d} &{}\quad e_{z}(t)=z(t)-z_{d} \end{array} \\ e(t)=\left[ \begin{array} [c]{ccccc} e_{x}(t) &{}\quad e_{y}(t) &{}\quad e_{z}(t) &{}\quad \gamma _{x}(t) &{}\quad \gamma _{y}(t) \end{array} \right] ^{T} \end{array}. \nonumber \\ \end{aligned}$$

(12)

3 Control development

In this section, an adaptive controller will be presented firstly based on energy analysis of the system. Then, a parameter adaptive update law will be proposed in the presence of the unknown plant parameters (including payload’s mass and drag coefficients of aerodynamic drag force).

The energy E(t) of the quadrotor slung-payload system, combining the kinetic and potential energy, can be denoted as follows:

$$\begin{aligned} E(t)=\frac{1}{2}{\dot{q}}^{T}M_{c}{\dot{q}}+m_{p}gl(1-C_{x}C_{y}). \end{aligned}$$

(13)

Taking the time derivative of (13), and substituting (5) and (6) into the resulting equation yields

$$\begin{aligned} {\dot{E}}&={\dot{q}}^{T}\left[ f+f_{d}-G(q)\right] +m_{p}gl{\dot{\gamma }} _{x}S_{x}C_{y}\nonumber \\&\quad -m_{p}gl{\dot{\gamma }}_{y}C_{x}S_{y}\nonumber \\&={\dot{x}}(f_{x}-\delta _{x}\xi _{x})+{\dot{y}}(f_{y}-\delta _{y}\xi _{y})+\dot{z}(f_{z}-\delta _{z}^{T}\xi _{z})\nonumber \\&\quad -\,c_{\gamma _{x}}{\dot{\gamma }}_{x}^{2}-c_{\gamma _{y}}{\dot{\gamma }}_{y}^{2}. \end{aligned}$$

(14)

where $\delta _{x}(t)$, $\delta _{y}(t)$, $\delta _{z}(t)$ and $\xi _{x}$, $\xi _{y}$, $\xi _{z}$ are defined as

$$\begin{aligned} \begin{array} [c]{lll} \delta _{x}={\dot{x}}&\delta _{y}={\dot{y}}&\delta _{z}=\left[ \begin{array} [c]{cc} 1 &{} {\dot{z}} \end{array} \right] ^{T}\\ \xi _{x}=c_{x} &{} \xi _{y}=c_{y} &{} \xi _{z}=\left[ \begin{array} [c]{cc} (m_{q}+m_{p})g &{} c_{z} \end{array} \right] \end{array} . \end{aligned}$$

(15)

Based on the passivity property of the quadrotor slung-payload system energy, the adaptive controller can be designed as [39]:

$$\begin{aligned} \left\{ \begin{array} [c]{l} f_{x}(t)=-\,k_{px}e_{x}-k_{\text {d}x}{\dot{x}}-\varDelta _{x}+k_{\text {d}\gamma _{x}}{\dot{\gamma }} _{x}+\delta _{x}{\hat{\xi }}_{x}\\ f_{y}(t)=-\,k_{py}e_{y}-k_{\text {d}y}{\dot{y}}-\varDelta _{y}+k_{\text {d}\gamma _{y}}{\dot{\gamma }} _{y}+\delta _{y}{\hat{\xi }}_{y}\\ f_{z}(t)=-\,k_{pz}e_{z}-k_{\text {d}z}{\dot{z}}-\varDelta _{z}+\delta _{z}^{T}{\hat{\xi }}_{z} \end{array} \right. \nonumber \\ \end{aligned}$$

(16)

where $\varDelta _{x}(t)=\kappa _{x}\varsigma _{x}e_{x}(t)$, $\varDelta _{y} (t)=\kappa _{y}\varsigma _{y}e_{y}(t)$, $\varDelta _{z}(t)=\kappa _{z}e_{z}(t)$ with $\varsigma _{x}=\left[ \frac{\sqrt{2}(x_{d}+\varepsilon _{x})}{(x_{d} +\varepsilon _{x})^{2}-x^{2}(t)}\right] ^{2}$, $\varsigma _{y}=\left[ \frac{\sqrt{2}(y_{d}+\varepsilon _{y})}{(y_{d}+\varepsilon _{y})^{2}-y^{2} (t)}\right] ^{2}$, $\varsigma _{z}=\left[ \frac{\sqrt{2}(z_{d}+\varepsilon _{z})}{(z_{d}+\varepsilon _{z})^{2}-z^{2}(t)}\right] ^{2}$, and $k_{px}$, $k_{\text {d}x}$, $k_{\text {d}\gamma _{x}}$, $k_{py}$, $k_{\text {d}y}$, $k_{\text {d}\gamma _{y}}$, $k_{pz}$, $k_{\text {d}z}$, $\kappa _{x}$, $\kappa _{y}$, $\kappa _{z}\in {\mathbb {R}}^{+}$ are some positive gains. The gains $\varepsilon _{x}$, $\varepsilon _{y}$, $\varepsilon _{z}\in {\mathbb {R}}^{+}$ in (16) are introduced to restrict the maximum overshoots for $e_{x}(t)$, $e_{y}(t)$, $e_{z}(t)$, respectively, where they satisfy

$$\begin{aligned} \begin{array} [c]{ccc} \varepsilon _{x}>\left| x_{d}-x(0)\right|&\varepsilon _{y}>\left| y_{d}-y(0)\right|&\varepsilon _{z}>\left| z_{d}-z(0)\right| \end{array} . \nonumber \\ \end{aligned}$$

(17)

The dynamic estimates ${\hat{\xi }}_{x}(t)$, ${\hat{\xi }}_{y}(t)$ and $\hat{\xi }_{z}(t)$ are estimations for the unknown parameters $\xi _{x}$, $\xi _{y}$ and $\xi _{z}$, respectively, and denoted as

$$\begin{aligned} \begin{array} [c]{ccc} {\hat{\xi }}_{x}={\hat{c}}_{x}&{\hat{\xi }}_{y}={\hat{c}}_{y}&{\hat{\xi }}_{z}=\left[ \begin{array} [c]{cc} (m_{q}+{\hat{m}}_{p})g&{\hat{c}}_{z} \end{array} \right] \end{array} . \end{aligned}$$

(18)

Remark 4

The controller in (16) is referred to [39], but it is different from the one in [39]. The system’s degree of freedom in this paper is bigger than the one in [39], and consequently, the stability analysis becomes much more complicated. On the other hand, new auxiliary functions $\varDelta _{x}(t)$, $\varDelta _{y}(t)$ and $\varDelta _{z}(t)$ are added in the controller for the consideration of overshoot restriction in this paper while the control design in [39] does not take this issue into account. This will also make the stability analysis in this paper is much different from the one in [39].

By substituting (16) into (14), it can be obtained that

$$\begin{aligned} {\dot{E}}&=-\,k_{\text {d}x}{\dot{x}}^{2}-k_{\text {d}y}{\dot{y}}^{2}-k_{\text {d}z}{\dot{z}}^{2} -c_{\gamma _{x}}{\dot{\gamma }}_{x}^{2}-c_{\gamma _{y}}{\dot{\gamma }}_{y}^{2} -k_{px}{\dot{x}}e_{x}\nonumber \\&\quad -k_{py}{\dot{y}}e_{y}-k_{pz}{\dot{z}}e_{z}+k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x} {\dot{x}}+k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y}{\dot{y}}-\delta _{x}{\tilde{\xi }}_{x} {\dot{x}}\nonumber \\&\quad -\delta _{y}{\tilde{\xi }}_{y}{\dot{y}}-\delta _{z}^{T}{\tilde{\xi }}_{z}\dot{z}-\varDelta _{x}{\dot{x}}-\varDelta _{y}{\dot{y}}-\varDelta _{z}{\dot{z}}, \end{aligned}$$

(19)

where ${\tilde{\xi }}_{x}(t)$, ${\tilde{\xi }}_{y}(t)$, ${\tilde{\xi }}_{z}(t)$ are online errors for $\xi _{x}$, $\xi _{y}$, $\xi _{z}$, respectively, and defined as follows:

$$\begin{aligned} \begin{array} [c]{ccc} {\tilde{\xi }}_{x}=\xi _{x}-{\hat{\xi }}_{x}&{\tilde{\xi }}_{y}=\xi _{y}-{\hat{\xi }}_{y}&{\tilde{\xi }}_{z}=\xi _{z}-{\hat{\xi }}_{z} \end{array} . \end{aligned}$$

(20)

Based on the subsequent stability analysis, the parameter estimates $\hat{\xi }_{x}(t)$, ${\hat{\xi }}_{y}(t)$ and ${\hat{\xi }}_{z}(t)$ are updated via the following adaption algorithm

$$\begin{aligned} \left\{ \begin{array} [c]{l} \overset{\cdot }{{\hat{\xi }}}_{x}=-\,\varGamma _{x}\delta _{x}\left[ \alpha {\dot{x}} +\rho \left( \frac{e_{x}}{2}\right) \right] \\ \overset{\cdot }{{\hat{\xi }}}_{y}=-\,\varGamma _{y}\delta _{y}\left[ \alpha {\dot{y}} +\rho \left( \frac{e_{y}}{2}\right) \right] \\ \overset{\cdot }{{\hat{\xi }}}_{z}=-\,\varGamma _{z}\delta _{z}\left[ \alpha {\dot{z}} +\rho \left( \frac{e_{z}}{2}\right) \right] \end{array} \right. \end{aligned}$$

(21)

where $\varGamma _{x}=\mu _{x}>0$, $\varGamma _{y}=\mu _{y}>0$, $\varGamma _{z} =diag\{\mu _{m_{p}},\mu _{z}\}>0$ and $\alpha \in {\mathbb {R}}^{+}$ are some positive gains. The function $\rho (s)$ in (21) is a differential saturation function, which is defined as

$$\begin{aligned} \rho (s)=\left\{ \begin{array} {ll} 1,&{}\quad s>\frac{\pi }{2}\\ \sin (s),&{}\quad \left| s\right| \le \frac{\pi }{2}\\ -\,1,&{}\quad s<-\frac{\pi }{2} \end{array} \right. . \end{aligned}$$

(22)

It can be proved that the following properties hold for $\rho (s)$ in (22):

• 1. for any value $s\in {\mathbb {R}}$, $\left| \rho (s)\right| \le 1$,

• 2. the partial derivative of $\rho (s)$ with respect to s can be expressed as

  $$\begin{aligned} \rho _{s}(s)=\frac{\partial \rho (s)}{\partial s}=\left\{ \begin{array} [c]{ll} 0,&{}\quad \left| s\right| >\pi /2\\ \cos (s),&{}\quad \left| s\right| \le \pi /2 \end{array} \right. \end{aligned}$$

  (23)

  and for any $s\in {\mathbb {R}}$, $\left| \rho _{s}(s)\right| \le 1$,

• 3. for any $s\in {\mathbb {R}}$, $\rho ^{2}(s)\le s\rho (s)$.

4 Stability analysis

The main stability result of the adaptive controller proposed in (16) and (21) can be stated by the following theorem.

Theorem 1

The proposed adaptive controller in (16) and (21) ensure that all the closed-loop signals are bounded, and quadrotor’s positive errors are asymptotically regulated in the sense that

$$\begin{aligned} \left\{ \begin{array} [c]{c} \underset{t\rightarrow \infty }{\lim }\left[ \begin{array} [c]{ccc} e_{x}(t)&e_{y}(t)&e_{z}(t) \end{array} \right] =\left[ \begin{array} [c]{ccc} 0 &{} 0 &{} 0 \end{array} \right] \\ \underset{t\rightarrow \infty }{\lim }\left[ \begin{array} [c]{ccc} {\dot{e}}_{x}(t) &{} {\dot{e}}_{y}(t) &{} {\dot{e}}_{z}(t) \end{array} \right] =\left[ \begin{array} [c]{ccc} 0&0&0 \end{array} \right] \end{array} \right. , \end{aligned}$$

(24)

the payload’s swing angles are asymptotically regulated in the sense that

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }\left[ \gamma _{x}(t)\text { }\gamma _{y}(t)\text { }{\dot{\gamma }}_{x}(t)\text { }{\dot{\gamma }}_{y}(t)\right] =\left[ 0\text { }0\text { }0\text { }0\right] . \end{aligned}$$

(25)

Meanwhile, the quadrotor’s motion during the flight procedure are ensured to stay in a bounded region in the sense that

$$\begin{aligned} \begin{array} [c]{ccc} x(t)<x_{d}+\varepsilon _{x}&y(t)<y_{d}+\varepsilon _{y}&z(t)<z_{d} +\varepsilon _{z} \end{array} . \end{aligned}$$

(26)

The estimate for the unknown mass of the payload converges to its real value such that

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }{\hat{m}}_{p}(t)=m_{p}. \end{aligned}$$

(27)

Proof

To prove the above theorem, a nonnegative Lyapunov function candidate V(t) is chosen as follows:

$$\begin{aligned} V&=\frac{1}{2}\alpha {\dot{q}}^{T}M_{c}(q){\dot{q}}+\alpha m_{p}gl(1-C_{x} C_{y})+\frac{1}{2}\alpha k_{px}e_{x}^{2}\nonumber \\&\quad +\frac{1}{2}\alpha k_{py}e_{y}^{2}+\frac{1}{2}\alpha k_{pz}e_{z}^{2} +\rho _{e}^{T}\left( \frac{e}{2}\right) M_{c}(q){\dot{q}}\nonumber \\&\quad +\,\frac{1}{2}{\tilde{\xi }}_{x}^{T} \varGamma _{x}^{-1}{\tilde{\xi }}_{x}\nonumber \\&\quad +\,\frac{1}{2}{\tilde{\xi }}_{y}^{T}\varGamma _{y}^{-1}{\tilde{\xi }}_{y}+\frac{1}{2}{\tilde{\xi }}_{z}^{T}\varGamma _{z}^{-1}{\tilde{\xi }}_{z}+\frac{\kappa _{x}\alpha }{(x_{d}+\varepsilon _{x})^{2}-x^{2}}e_{x}^{2}\nonumber \\&\quad +\,\frac{\kappa _{y}\alpha }{(y_{d}+\varepsilon _{y})^{2}-y^{2}}e_{y}^{2} +\,\frac{\kappa _{z}\alpha }{(z_{d}+\varepsilon _{z})^{2}-z^{2}}e_{z}^{2} \end{aligned}$$

(28)

where $\rho _{e}(\frac{e}{2})$ is defined as

$$\begin{aligned} \rho _{e}\left( \frac{e}{2}\right) =\left[ \rho \left( \frac{e_{x}}{2}\right) \text { }\rho \left( \frac{e_{y} }{2}\right) \text { }\rho \left( \frac{e_{z}}{2}\right) \text { }\rho \left( \frac{\gamma _{x}}{2}\right) \text { }\rho \left( \frac{\gamma _{y}}{2}\right) \right] ^{T}. \nonumber \\ \end{aligned}$$

(29)

To show that V(t) is nonnegative, we can rearrange the first four terms in (28), denoted as $V_{f4}(t)$, as follows:

$$\begin{aligned} V_{f4}(t)&=\frac{1}{2}\alpha {\dot{q}}^{T}M_{c}(q){\dot{q}}\nonumber +2\alpha \left[ k_{px}\left( \frac{e_{x}}{2}\right) ^{2}\right. \nonumber \\&\left. +\,k_{py}\left( \frac{e_{y}}{2} \right) ^{2}+k_{pz}\left( \frac{e_{z}}{2}\right) ^{2}\right] \nonumber \\&+\,\alpha m_{p}gl\left( 2\sin ^{2}\frac{\gamma _{x}}{2}+2\sin ^{2}\frac{\gamma _{x}}{2}\right. \nonumber \\&\left. -\,4\sin ^{2}\frac{\gamma _{x}}{2}\sin ^{2}\frac{\gamma _{x}}{2}\right) \nonumber \\ \ge&\frac{1}{2}\alpha {\dot{q}}^{T}M_{c}(q){\dot{q}}+2\alpha \left[ k_{px}\left( \frac{e_{x}}{2}\right) ^{2}+k_{py}\left( \frac{e_{y}}{2} \right) ^{2}\right. \nonumber \\&\left. +\,k_{pz}\left( \frac{e_{z}}{2}\right) ^{2}\right] \nonumber \\&+\,\alpha m_{p}gl(2\sin ^{2}\frac{\gamma _{x}}{2}+2\sin ^{2}\frac{\gamma _{x}}{2})\nonumber \\ \ge&\frac{1}{2}\alpha {\dot{q}}^{T}M_{c}(q){\dot{q}}+2\alpha \rho _{e}^{T} \left( \frac{e}{2}\right) \nonumber \\&\times \mathrm{diag}\{k_{px},k_{py},k_{pz},m_{p}gl,m_{p}gl\}\rho _{e}\left( \frac{e}{2}\right) . \end{aligned}$$

(30)

By using the Young’s inequality, $V_{f4}(t)$ in (30) can be lower bounded as follows:

$$\begin{aligned} V_{f4}(t)&\ge \frac{1}{2}\alpha {\dot{q}}^{T}M_{c}(q){\dot{q}}+2\alpha \cdot \nonumber \\&\quad \min \{k_{px},k_{py},k_{pz},\underline{\text {m}}_{p}gl,\underline{\text {m}}_{p} gl\}\cdot \left\| \rho _{e}\left( \frac{e}{2}\right) \right\| ^{2}\nonumber \\&\ge 2\alpha \sqrt{\lambda _{m}\cdot \min \{k_{px},k_{py},k_{pz},\underline{\text {m} }_{p}gl,\underline{\text {m}}_{p}gl\}}\nonumber \\&\quad \times \left\| {\dot{q}}\right\| \cdot \left\| \rho _{e}\left( \frac{e}{2}\right) \right\| \nonumber \\&\ge 2\alpha \sqrt{\lambda _{m}\cdot \underline{\text {m}}_{p}gl}\left\| \dot{q}\right\| \cdot \left\| \rho _{e}\left( \frac{e}{2}\right) \right\| . \end{aligned}$$

(31)

Here, the control gains $k_{px}$, $k_{py}$, and are $k_{pz}$ chosen to satisfy

$$\begin{aligned} \begin{array} [c]{ccc} k_{px}>\underline{\text {m}}_{p}gl&k_{py}>\underline{\text {m}}_{p}gl&k_{pz}>\underline{\text {m} }_{p}gl \end{array} . \end{aligned}$$

(32)

Besides, the fifth term in (28) can be lower bounded as

$$\begin{aligned} \rho _{e}^{T}\left( \frac{e}{2}\right) M_{c}(q){\dot{q}}\ge -\lambda _{M}\cdot \left\| {\dot{q}}\right\| \cdot \left\| \rho _{e}\left( \frac{e}{2}\right) \right\| . \end{aligned}$$

(33)

The control gain $\alpha$ is selected to satisfy the following inequality

$$\begin{aligned} \alpha >\frac{\lambda _{M}}{2\sqrt{\lambda _{m}\cdot \underline{\text {m}}_{p}gl}} \end{aligned}$$

(34)

Thus, it is not difficult to check that $V_{f4}(t)+\rho _{e}^{T}(\frac{e}{2})M_{c}(q){\dot{q}}\ge 0$ holds, and consequently V(t) in (28) is nonnegative.

The time derivative of (28) can be expressed as follows:

$$\begin{aligned} {\dot{V}}&=-\,\alpha k_{\text {d}x}{\dot{x}}^{2}-\alpha k_{\text {d}y}{\dot{y}}^{2}-\alpha k_{\text {d}z}{\dot{z}}^{2}\nonumber \\&\quad -\alpha c_{\gamma _{x}}{\dot{\gamma }}_{x}^{2}-\alpha c_{\gamma _{y}}{\dot{\gamma }}_{y}^{2}+\alpha k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}{\dot{x}}\nonumber \\&\quad +\alpha k_{\text {d}\gamma _{y}} {\dot{\gamma }}_{y}{\dot{y}}-\alpha \delta _{x}{\tilde{\xi }}_{x}{\dot{x}}-\alpha \delta _{y}{\tilde{\xi }}_{y}{\dot{y}}\nonumber \\&\quad -\,\alpha \delta _{z}^{T}{\tilde{\xi }}_{z}{\dot{z}}+\rho _{e}^{T}\left( \frac{e}{2} \right) M_{c}(q)\ddot{q}+\rho _{e}^{T}\left( \frac{e}{2}\right) {\dot{M}}_{c}(q){\dot{q}}\nonumber \\&\quad +\,{\dot{\rho }}_{e}^{T}\left( \frac{e}{2}\right) M_{c}(q){\dot{q}}+{\tilde{\xi }}_{x}^{T} \varGamma _{x}^{-1}\overset{\cdot }{{\tilde{\xi }}}_{x}\nonumber \\&\quad +\,{\tilde{\xi }}_{y}^{T}\varGamma _{y}^{-1}\overset{\cdot }{{\tilde{\xi }}}_{y} +\,{\tilde{\xi }}_{z}^{T}\varGamma _{z}^{-1}\overset{\cdot }{{\tilde{\xi }}}_{z}. \end{aligned}$$

(35)

For $\rho _{e}^{T}(\frac{e}{2})M_{c}(q)\ddot{q}$ in (35) denoted as $H_{0}(t)$, substituting (1) into it yields

$$\begin{aligned} H_{0}&=-\,k_{px}e_{x}\rho \left( \frac{e_{x}}{2}\right) -k_{\text {d}x}{\dot{x}}\rho \left( \frac{e_{x}}{2}\right) +k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}\rho \left( \frac{e_{x}}{2}\right) \nonumber \\&\quad -\,\delta _{x}{\tilde{\xi }}_{x}\rho \left( \frac{e_{x}}{2}\right) -\varDelta _{x}\rho \left( \frac{e_{x} }{2}\right) -k_{py}e_{y}\rho \left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -\,k_{\text {d}y}{\dot{y}}\rho \left( \frac{e_{y}}{2}\right) +k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y} \rho \left( \frac{e_{y}}{2}\right) -\delta _{y}{\tilde{\xi }}_{y}\rho \left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -\,\varDelta _{y}\rho \left( \frac{e_{y}}{2}\right) -k_{pz}e_{z}\rho \left( \frac{e_{z}}{2} \right) -k_{\text {d}z}{\dot{z}}\rho \left( \frac{e_{z}}{2}\right) \nonumber \\&\quad -\,\delta _{z}^{T}{\hat{\xi }}_{z}\rho \left( \frac{e_{z}}{2}\right) -\varDelta _{z}\rho \left( \frac{e_{z}}{2}\right) -c_{\gamma _{x}}{\dot{\gamma }}_{x}\rho \left( \frac{\gamma _{x}}{2}\right) \nonumber \\&\quad -\,m_{p}glS_{x}C_{y}\rho \left( \frac{\gamma _{x}}{2}\right) -c_{\gamma _{y}}{\dot{\gamma }} _{y}\rho \left( \frac{\gamma _{y}}{2}\right) \nonumber \\&\quad -\,m_{p}glC_{x}S_{y}\rho \left( \frac{\gamma _{y}}{2}\right) -\rho _{e}^{T}\left( \frac{e}{2}\right) C(q,{\dot{q}}){\dot{q}}. \end{aligned}$$

(36)

For $\rho _{e}^{T}(\frac{e}{2}){\dot{M}}_{c}(q){\dot{q}}$ in (35) denoted as $H_{1}(t)$, by utilizing the expression of (8), it can be obtained that

$$\begin{aligned} H_{1}=\rho _{e}^{T}\left( \frac{e}{2}\right) C(q,{\dot{q}}){\dot{q}}+{\dot{q}}^{T}C(q,{\dot{q}} )\rho _{e}\left( \frac{e}{2}\right) . \end{aligned}$$

(37)

For ${\tilde{\xi }}_{x}^{T}(t)\varGamma _{x}^{-1}\overset{\cdot }{{\tilde{\xi }}} _{x}(t)+{\tilde{\xi }}_{y}^{T}(t)\varGamma _{y}^{-1}\overset{\cdot }{{\tilde{\xi }}} _{y}(t)+{\tilde{\xi }}_{z}^{T}(t)\varGamma _{z}^{-1}\overset{\cdot }{{\tilde{\xi }}} _{z}(t)$ in (35) denoted as $H_{2}(t)$, substituting (21) into it yields

$$\begin{aligned} H_{2}&=\alpha {\tilde{\xi }}_{x}^{T}\delta _{x}{\dot{x}}+\alpha {\tilde{\xi }} _{y}^{T}\delta _{y}{\dot{y}}+\alpha {\tilde{\xi }}_{z}^{T}\delta _{z}{\dot{z}} +{\tilde{\xi }}_{x}^{T}\delta _{x}\rho \left( \frac{e_{x}}{2}\right) \nonumber \\&\quad +\,{\tilde{\xi }}_{y}^{T}\delta _{y}\rho \left( \frac{e_{y}}{2}\right) +{\tilde{\xi }}_{z} ^{T}\delta _{z}\rho \left( \frac{e_{z}}{2}\right) . \end{aligned}$$

(38)

After substituting (36)–(38) into the (35), the following expression for ${\dot{V}}(t)$ can be obtained

$$\begin{aligned} {\dot{V}}&=-\,\alpha k_{\text {d}x}{\dot{x}}^{2}-\alpha k_{\text {d}y}{\dot{y}}^{2}-\alpha k_{\text {d}z}{\dot{z}}^{2}-\alpha c_{\gamma _{x}}{\dot{\gamma }}_{x}^{2}\nonumber \\&\quad -\alpha c_{\gamma _{y}}{\dot{\gamma }}_{y}^{2}+\alpha k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}{\dot{x}}+\alpha k_{\text {d}\gamma _{y}} {\dot{\gamma }}_{y}{\dot{y}}\nonumber \\&\quad -\varDelta _{x}\rho \left( \frac{e_{x}}{2}\right) -\varDelta _{y}\rho \left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -\,\varDelta _{z}\rho \left( \frac{e_{z}}{2}\right) -k_{px}e_{x}\rho \left( \frac{e_{x}}{2} \right) -k_{py}e_{y}\rho \left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -\,k_{pz}e_{z}\rho \left( \frac{e_{z}}{2}\right) -k_{\text {d}x}{\dot{x}}\rho \left( \frac{e_{x}}{2} \right) -k_{\text {d}y}{\dot{y}}\rho \left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -\,k_{\text {d}z}{\dot{z}}\rho \left( \frac{e_{z}}{2}\right) +k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x} \rho \left( \frac{e_{x}}{2}\right) +k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y}\rho (\frac{e_{y}}{2})\nonumber \\&\quad -\,c_{\gamma _{x}}{\dot{\gamma }}_{x}\rho \left( \frac{\gamma _{x}}{2}\right) -c_{\gamma _{y} }{\dot{\gamma }}_{y}\rho \left( \frac{\gamma _{y}}{2}\right) \nonumber \\&\quad -\,m_{p}glS_{x}C_{y}\rho \left( \frac{\gamma _{x}}{2}\right) +{\dot{q}}^{T}C(q,{\dot{q}} )\rho _{e}\left( \frac{e}{2}\right) \nonumber \\&\quad -\,m_{p}glC_{x}S_{y}\rho \left( \frac{\gamma _{y}}{2}\right) +{\dot{\rho }}_{e}^{T}\left( \frac{e}{2}\right) M_{c}(q){\dot{q}}. \end{aligned}$$

(39)

From (39), by defining

$$\begin{aligned} H_{3} =&-\,\varDelta _{x}(t)\rho \left( \frac{e_{x}(t)}{2}\right) -\varDelta _{y}(t)\rho \left( \frac{e_{y} (t)}{2}\right) \nonumber \\&-\,\varDelta _{z}(t)\rho \left( \frac{e_{z}(t)}{2}\right) \nonumber \\&-\,k_{px}e_{x}(t)\rho \left( \frac{e_{x}(t)}{2}\right) -k_{py}e_{y}(t)\rho \left( \frac{e_{y}(t)}{2}\right) \nonumber \\&-\,k_{pz}e_{z}(t)\rho \left( \frac{e_{z}(t)}{2}\right) \end{aligned}$$

(40)

the following inequality can be obtained upon the use of the third property of $\rho (s)$

$$\begin{aligned} H_{3}&\le -\,2\kappa _{x}\varsigma _{x}\rho ^{2}\left( \frac{e_{x}}{2}\right) -2\kappa _{y}\varsigma _{y}\rho ^{2}\left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -2\kappa _{z}\varsigma _{z}\rho ^{2}\left( \frac{e_{z}}{2}\right) \nonumber \\&\quad -\,2k_{px}\rho ^{2}\left( \frac{e_{x}}{2}\right) -2k_{py}\rho ^{2}(\frac{e_{y}}{2} )-2k_{pz}\rho ^{2}\left( \frac{e_{z}}{2}\right) . \end{aligned}$$

(41)

For $-\,k_{\text {d}x}{\dot{x}}(t)\rho \left( \frac{e_{x}(t)}{2}\right) -k_{\text {d}y}{\dot{y}}(t)\rho (\frac{e_{y}(t)}{2})-k_{\text {d}z}{\dot{z}}(t)\rho (\frac{e_{z}(t)}{2})$ in (39) denoted as $H_{4}(t)$, the following inequality holds upon the use of the Young’s inequality

$$\begin{aligned} H_{4} \le \,&\frac{k_{\text {d}x}^{2}}{2}{\dot{x}}^{2}+\frac{k_{\text {d}y}^{2}}{2}{\dot{y}} ^{2}+\frac{k_{\text {d}z}^{2}}{2}{\dot{z}}^{2}+\frac{1}{2}\rho ^{2}\left( \frac{e_{x}}{2}\right) \nonumber \\&\quad +\frac{1}{2}\rho ^{2}\left( \frac{e_{y}}{2}\right) +\frac{1}{2}\rho ^{2}\left( \frac{e_{z}}{2}\right) . \end{aligned}$$

(42)

For $-m_{p}glS_{x}(t)C_{y}(t)\rho (\frac{\gamma _{x}(t)}{2})-m_{p} glC_{x}(t)S_{y}(t)\rho (\frac{\gamma _{y}(t)}{2})$ in (39) denoted as $H_{5}(t)$, the following inequality can be obtained

$$\begin{aligned}&H_{5}\le -2m_{p}glC_{y}\left( \sin \frac{\gamma _{x}}{2}\cos \frac{\gamma _{x}}{2} \right) ^{2}\nonumber \\&\quad -\,2m_{p}glC_{x}\left( \sin \frac{\gamma _{y}}{2}\cos \frac{\gamma _{y}}{2}\right) ^{2}. \end{aligned}$$

(43)

For ${\dot{q}}^{T}C(q,{\dot{q}})\rho _{e}(\frac{e}{2})$ in (39) denoted as $H_{6}(t)$, after substituting (3) and (29) into it and some mathematical manipulation, the following inequality can be obtained

$$\begin{aligned}&H_{6}\le 2m_{p}^{2}{\dot{x}}^{2}+\frac{1}{4}m_{p}^{2}{\dot{y}}^{2}+2m_{p}^{2} {\dot{z}}^{2}+2l^{2}{\dot{\gamma }}_{x}^{2}\nonumber \\&\quad +\,3l^{2}{\dot{\gamma }}_{y}^{2}+m_{p} l^{2}{\dot{\gamma }}_{x}^{2}. \end{aligned}$$

(44)

For $k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}(t)\rho (\frac{e_{x}(t)}{2})+k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y}(t)\rho (\frac{e_{y}(t)}{2})$in (39) denoted as $H_{7}(t)$, similarly, the following inequality holds

$$\begin{aligned} H_{7}\le \frac{1}{2}k_{\text {d}\gamma _{x}}^{2}{\dot{\gamma }}_{x}^{2}+\frac{1}{2} \rho ^{2}\left( \frac{e_{x}}{2}\right) +\frac{1}{2}k_{\text {d}\gamma _{y}}^{2}{\dot{\gamma }}_{y} ^{2}+\frac{1}{2}\rho ^{2}\left( \frac{e_{y}}{2}\right) . \nonumber \\ \end{aligned}$$

(45)

For ${\dot{\rho }}_{e}^{T}(\frac{e}{2})M_{c}(q){\dot{q}}$ in (39), based on the second property of $\rho (s)$ and (7), it is implied that

$$\begin{aligned}&{\dot{\rho }}_{e}^{T}\left( \frac{e}{2}\right) M_{c}(q){\dot{q}}\nonumber \\&\quad \le \frac{\max \left\{ \rho _{\frac{e_{_{x}}}{2}}\left( \frac{e_{x}}{2} \right) ,\rho _{\frac{e_{y}}{2}}\left( \frac{e_{y}}{2}\right) ,\rho _{\frac{e_{z}}{2}}(\frac{e_{z} }{2}),\rho _{\frac{\gamma _{x}}{2}}\left( \frac{\gamma _{x}}{2}\right) ,\rho _{\frac{\gamma _{y}}{2}}\left( \frac{\gamma _{y}}{2}\right) \right\} }{2}\nonumber \\&\lambda _{M}\left\| {\dot{q}}\right\| ^{2}\nonumber \\&\quad \le \frac{1}{2}\lambda _{M}({\dot{x}}^{2}+{\dot{y}}^{2}+{\dot{z}}^{2}+\dot{\gamma }_{x}^{2}+{\dot{\gamma }}_{y}^{2}). \end{aligned}$$

(46)

Substituting (41)–(45) and (46) into (39) yields

$$\begin{aligned} {\dot{V}}(t)\le -\varLambda (t)-c_{\gamma _{x}}{\dot{\gamma }}_{x}\rho \left( \frac{\gamma _{x} }{2}\right) -c_{\gamma _{y}}{\dot{\gamma }}_{y}\rho \left( \frac{\gamma _{y}}{2}\right) . \end{aligned}$$

(47)

where $\varLambda (t)$ is defined as

$$\begin{aligned} \varLambda (t)\overset{\varDelta }{=}&-\,\left( \alpha k_{\text {d}x}-\frac{1}{2}k_{\text {d}x}^{2}-\frac{1}{2}\lambda _{M}-2m_{p}^{2}\right) {\dot{x}}^{2}\nonumber \\&-\left( \alpha k_{\text {d}y}-\frac{1}{2}k_{\text {d}y}^{2}-\frac{1}{2}\lambda _{M}-\frac{1}{4}m_{p}^{2}\right) {\dot{y}}^{2}\nonumber \\&-\left( \alpha k_{\text {d}z}-\frac{k_{\text {d}z}^{2}}{2}-\frac{1}{2}\lambda _{M}-2m_{p}^{2} \right) {\dot{z}}^{2}\nonumber \\&-\left( \alpha c_{\gamma _{x}}-\frac{1}{2}\lambda _{M}-2l^{2}-m_{p}l^{2}-\frac{1}{2}k_{\text {d}\gamma _{x}}^{2}\right) {\dot{\gamma }}_{x}^{2}\nonumber \\&-\left( \alpha c_{\gamma _{y}}-\frac{1}{2}\lambda _{M}-3l^{2}-\frac{1}{2} k_{\text {d}\gamma _{y}}^{2}\right) {\dot{\gamma }}_{y}^{2}\nonumber \\&-(2k_{px}+2\kappa _{x}\varsigma _{x}-1)\rho ^{2}\left( \frac{e_{x}}{2}\right) \nonumber \\&-(2k_{py}+2\kappa _{y}\varsigma _{y}-1)\rho ^{2}\left( \frac{e_{y}}{2}\right) \nonumber \\&-\left( 2k_{pz}+2\kappa _{z}\varsigma _{z}-\frac{1}{2}\right) \rho ^{2}\left( \frac{e_{z}}{2}\right) \nonumber \\&-2m_{p}glC_{y}\left( \sin \frac{\gamma _{x}}{2}\cos \frac{\gamma _{x}}{2}\right) ^{2}+\alpha k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}{\dot{x}}\nonumber \\&-2m_{p}glC_{x}\left( \sin \frac{\gamma _{y}}{2}\cos \frac{\gamma _{y}}{2}\right) ^{2}+\alpha k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y}{\dot{y}}. \end{aligned}$$

(48)

If the positive gains $\alpha$, $k_{\text {d}x}$, $k_{\text {d}y}$, $k_{\text {d}z}$, $k_{px}$, $k_{py}$, $k_{pz}$, $k_{\text {d}\gamma _{x}}$, $k_{\text {d}\gamma _{y}}$, $\kappa _{x}$, $\kappa _{y}$, $\kappa _{z}$ are chosen to satisfy the following conditions

$$\begin{aligned} \left\{ \begin{array} [c]{l} k_{\text {d}x}=k_{\text {d}y}=k_{\text {d}z}=\frac{1}{r}\alpha \\ \max \left\{ \frac{\lambda _{M}}{2\sqrt{\lambda _{m}\cdot \underline{\text {m}}_{p}gl}} ,r\sqrt{\frac{\lambda _{M}+4m_{p}^{2}}{2r-1}},\beta _{1},\beta _{3}\right\} \\ \quad<\alpha <\min \{\beta _{2},\beta _{4}\}\\ k_{px}>\max \{\frac{1}{2},\underline{\text {m}}_{p}gl\}\text {\ \ }k_{py}>\max \{\frac{1}{2},\underline{\text {m}}_{p}gl\}\\ k_{pz}>\max \{\frac{1}{4},\underline{\text {m}}_{p}gl\}\text { }\kappa _{x}>0\text { }\kappa _{y}>0\text { }\kappa _{z}>0 \end{array} \right. \end{aligned}$$

(49)

it can be guaranteed that $-\varLambda (t)$ is negative definite, where the gains $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, $\beta _{4}$ and r are chosen to satisfy

$$\begin{aligned} \left\{ \begin{array} [c]{l} \beta _{1}=r^{2}c_{\gamma _{x}}-r\sqrt{r^{2}c_{\gamma _{x}}^{2}-(4l^{2}+2\bar{m}_{p}l^{2}+\lambda _{M})}\\ \beta _{2}=r^{2}c_{\gamma _{x}}+r\sqrt{r^{2}c_{\gamma _{x}}^{2}-(4l^{2}+2\bar{m}_{p}l^{2}+\lambda _{M})}\\ \beta _{3}=r^{2}c_{\gamma _{y}}-r\sqrt{r^{2}c_{\gamma _{y}}^{2}-(6l^{2} +\lambda _{M})}\\ \beta _{4}=r^{2}c_{\gamma _{y}}+r\sqrt{r^{2}c_{\gamma _{y}}^{2}-(6l^{2} +\lambda _{M})}\\ r>\max \left\{ \frac{1}{2},\frac{\sqrt{4l^{2}+2{\bar{m}}_{p}l^{2}+\lambda _{M}} }{c_{\gamma _{x}}^{2}},\frac{\sqrt{6l^{2}+\lambda _{M}}}{c_{\gamma _{y}}^{2}}\right\} \end{array} \right. . \end{aligned}$$

(50)

The details for how to obtain the conditions in (49) and (50) are presented in the “Appendix”.

By integrating both sides of (47) with respect to time, it can be obtained that

$$\begin{aligned} V(t)-V(0) \le&-\,\int _{0}^{t}\varLambda (\tau )\text {d}\tau \nonumber \\&+2c_{\gamma _{x}}\left[ \cos \frac{\gamma _{x}(t)}{2}-\cos \frac{\gamma _{x}(0)}{2}\right] \nonumber \\&+2c_{\gamma _{y}}\left[ \cos \frac{\gamma _{y}(t)}{2}-\cos \frac{\gamma _{y}(0)}{2}\right] \nonumber \\ \le&4c_{\gamma _{x}}+4c_{\gamma _{y}}. \end{aligned}$$

(51)

Thus, it indicates that

$$\begin{aligned} V(t)\le V(0)+4c_{\gamma _{x}}+4c_{\gamma _{y}}\ll +\infty . \end{aligned}$$

(52)

Now, it is not difficult to obtain that $\left| e_{x}(0)\right| <x_{d}+\varepsilon _{x}$, $\left| e_{y}(0)\right| <y_{d}+\varepsilon _{y}$, $\left| e_{z}(0)\right| <z_{d}+\varepsilon _{z}$ from (17). Assuming that $e_{x}(t)$ (respectively, $e_{y}(t)$, $e_{z}(t)$) tends to exceed the boundary of $\left| e_{x}(t)\right| <x_{d} +\varepsilon _{x}$ from the interior (respectively, $\left| e_{y} (t)\right| <y_{d}+\varepsilon _{y}$, $\left| e_{z}(t)\right| <z_{d}+\varepsilon _{z}$), then we can conclude from (28) that $V(t)\rightarrow \infty$ which invalidates $V(t)\ll +\infty$ in (52). Thus, we have

$$\begin{aligned}&\left| e_{x}(t)\right|<x_{d}+\varepsilon _{x}\text { }\left| e_{y}(t)\right|<y_{d}+\varepsilon _{y}\text { }\left| e_{z} (t)\right| \nonumber \\&\quad <z_{d}+\varepsilon _{z}. \end{aligned}$$

(53)

It is not difficult to show that ${\dot{x}}(t)$, ${\dot{y}}(t)$, ${\dot{z}}(t)$, ${\dot{\gamma }}_{x}(t)$, ${\dot{\gamma }}_{y}(t)$, $e_{x}(t)$, $e_{y}(t)$, $e_{z}(t)$, ${\tilde{\xi }}_{x}(t)$, ${\tilde{\xi }}_{y}(t)$, ${\tilde{\xi }}_{z}(t)\in L_{\infty }$, and $\frac{e_{x}^{2}(t)}{(x_{d}+\varepsilon _{x})^{2}-x^{2}(t)}$, $\frac{e_{y}^{2}(t)}{(y_{d}+\varepsilon _{y})^{2}-y^{2}(t)}$, $\frac{e_{z} ^{2}(t)}{(z_{d}+\varepsilon _{z})^{2}-z^{2}(t)}\in L_{\infty }$ according to (28) and (52). Moreover if $e_{x}(t)\rightarrow 0$, then $\frac{1}{(x_{d}+\varepsilon _{x})^{2}-x^{2}(t)}\rightarrow \frac{1}{(x_{d}+\varepsilon _{x})^{2}-x_{d}^{2}}\in L_{\infty }$. In addition, if $e_{x}(t)$ does not converge to 0, then it follows from $e_{x}(t)\in L_{\infty }$ and $\frac{e_{x}^{2}(t)}{(x_{d}+\varepsilon _{x})^{2}-x^{2}(t)}\in L_{\infty }$ that $\frac{1}{(x_{d}+\varepsilon _{x})^{2}-x^{2}(t)}\in L_{\infty }$. Similar analysis can be applied on $\frac{1}{(y_{d}+\varepsilon _{y} )^{2}-y^{2}(t)}$ and $\frac{1}{(z_{d}+\varepsilon _{z})^{2}-z^{2}(t)}$, thus we can obtain that $\frac{1}{(y_{d}+\varepsilon _{y})^{2}-y^{2}(t)}\in L_{\infty }$, $\frac{1}{(z_{d}+\varepsilon _{z})^{2}-z^{2}(t)}\in L_{\infty }$. Consequently due to (16), we can obtain that $f_{x}(t)$, $f_{y}(t)$, $f_{z}(t)\in L_{\infty }$. Then, based on the structure of the system dynamics in (1), it is not difficult to conclude that $\ddot{x}(t)$, $\ddot{y} (t)$, $\ddot{z}(t)$, $\ddot{\gamma }_{x}(t)$, $\ddot{\gamma }_{y}(t)\in L_{\infty }$. Moreover, we can obtain $\int _{0}^{t}\varLambda (e_{x}(\tau )$, $e_{y}(\tau )$, $e_{z}(\tau )$, $\gamma _{x}(\tau )$, $\gamma _{y}(\tau )$, $\dot{x}(\tau )$, ${\dot{y}}(\tau )$, ${\dot{z}}(\tau )$, ${\dot{\gamma }}_{x}(\tau )$, ${\dot{\gamma }}_{y}(\tau ))\text {d}\tau \in L_{\infty }$ since $V(t)\in L_{\infty }$. And it implies from (64) that ${\dot{x}}(t)$, ${\dot{y}}(t)$, ${\dot{z}}(t)$, ${\dot{\gamma }}_{x}(t)$, ${\dot{\gamma }}_{y}(t)$, $\rho (\frac{e_{x}(t)}{2})$, $\rho (\frac{e_{y}(t)}{2})$, $\rho (\frac{e_{z}(t)}{2})$, $\sin \gamma _{x}(t)$, $\sin \gamma _{y}(t)\in L_{2}$. By invoking Barbalat’s lemma, we can conclude that

$$\begin{aligned} \left\{ \begin{array} [c]{l} \underset{t\rightarrow \infty }{\lim }e_{x}(t),e_{y}(t),e_{z}(t)=0\text { }\underset{t\rightarrow \infty }{\lim }\gamma _{x}(t),\gamma _{y}(t)=0\\ \underset{t\rightarrow \infty }{\lim }{\dot{x}}(t),{\dot{y}}(t),{\dot{z}}(t)=0\text { }\underset{t\rightarrow \infty }{\lim }{\dot{\gamma }}_{x}(t),{\dot{\gamma }}_{y}(t)=0 \end{array} \right. . \end{aligned}$$

(54)

By applying (54) to the first and second entry of (16), it leads to the fact that $\underset{t\rightarrow \infty }{\lim }f_{x}(t)=0$, $\underset{t\rightarrow \infty }{\lim }f_{y}(t)=0$. Substituting (54) into the dynamics of x(t), y(t) in (1), it can be concluded that

$$\begin{aligned} \left\{ \begin{array} [c]{l} \underset{t\rightarrow \infty }{\lim }\left[ (m_{q}+m_{p})\ddot{x} (t)+m_{p}l\ddot{\gamma }_{x}(t)\right] =0\\ \underset{t\rightarrow \infty }{\lim }\left[ m_{p}l\ddot{x}(t)+m_{p}l^{2} \ddot{\gamma }_{x}(t)\right] =0\\ \underset{t\rightarrow \infty }{\lim }\left[ (m_{q}+m_{p})\ddot{y} (t)+m_{p}l\ddot{\gamma }_{y}(t)\right] =0\\ \underset{t\rightarrow \infty }{\lim }\left[ m_{p}l\ddot{y}(t)+m_{p}l^{2} \ddot{\gamma }_{y}(t)\right] =0 \end{array} \right. . \end{aligned}$$

(55)

Thus, we have

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }\left[ \ddot{x}(t)\text { }\ddot{y}(t)\right] =\left[ 0\text { }0\right] \text { }\underset{t\rightarrow \infty }{\lim }\left[ \ddot{\gamma }_{x}(t)\text { }\ddot{\gamma }_{y}(t)\right] =\left[ 0\text { }0\right] . \end{aligned}$$

(56)

According to the dynamics of z(t) in (1), we can obtain that

$$\begin{aligned}&(m_{q}+m_{p})(\ddot{z}(t)+g)\nonumber \\&\quad =-\,k_{pz}e_{z}-k_{\text {d}z}{\dot{z}}-\varDelta _{z}+(m_{q}+{\hat{m}}_{p})g+{\hat{c}}_{z} {\dot{z}}-c_{z}{\dot{z}}\nonumber \\&\qquad -m_{p}lC_{y}(\ddot{\gamma }_{x}S_{x}+{\dot{\gamma }}_{x}^{2}C_{x})-2m_{p} l{\dot{\gamma }}_{x}{\dot{\gamma }}_{y}S_{x}S_{y}\nonumber \\&\qquad -m_{p}lC_{x}(\ddot{\gamma }_{y}S_{y}+{\dot{\gamma }}_{y}^{2}C_{y}). \end{aligned}$$

(57)

The expression in (57) leads to

$$\begin{aligned} (m_{q}+m_{p})\ddot{z}(t)={\tilde{m}}_{p}(t)g+\varXi (t) \end{aligned}$$

(58)

where $\varXi (t)$ is defined as follows:

$$\begin{aligned} \varXi (t)&=k_{pz}e_{z}-k_{\text {d}z}{\dot{z}}-\varDelta _{z}+{\hat{c}}_{z}{\dot{z}}-c_{z} {\dot{z}}\nonumber \\&\quad -\,2m_{p}l{\dot{\gamma }}_{x}{\dot{\gamma }}_{y}S_{x}S_{y}-m_{p}lC_{y}(\ddot{\gamma }_{x}S_{x}+{\dot{\gamma }}_{x}^{2}C_{x})\nonumber \\&\quad -\,m_{p}lC_{x}(\ddot{\gamma }_{y}S_{y}+{\dot{\gamma }}_{y}^{2}C_{y}). \end{aligned}$$

(59)

Based on (54) and (56), it can be concluded that

$$\begin{aligned} \lim _{t\rightarrow \infty }\varXi (t)=0, \end{aligned}$$

(60)

and from the third entry of (21), we can obtain

$$\begin{aligned} \overset{\cdot }{{\tilde{m}}}_{p}(t)g=-\,\mu _{m_{p}}\left[ \alpha {\dot{z}} +\rho \left( \frac{e_{z}}{2}\right) \right] \in L_{\infty }, \end{aligned}$$

(61)

and $\overset{\cdot }{{\tilde{m}}}_{p}(t)g\in L_{\infty }$. Based on (58), (60) and (61), the extended Barbalat’s lemma [40] can be invoked to show that

$$\begin{aligned} \begin{array} [c]{ccc} \lim \limits _{t\rightarrow \infty }\ddot{z}(t)=0&\,&\lim \limits _{t\rightarrow \infty }{\tilde{m}}_{p}(t)g=0 \end{array} . \end{aligned}$$

(62)

Thus, it can be concluded that

$$\begin{aligned} \lim _{t\rightarrow \infty }{\hat{m}}_{p}(t)=m_{p} \end{aligned}$$

(63)

since g is a nonzero positive constant. $\square$

5 Experimental results

To validate the control performance of the proposed strategy, real-time experiments are performed on a self-build UAV testbed shown in Fig. 2. The testbed consists of a small-size quadrotor, a cable-connected payload, a motion capture system, a ground station, and a XBee based wireless data link. For the quadrotor platform, the STM32 chip is used as a real-time engine, which can provide the accurate attitude information with the gyroscope and accelerometer sensors integrated on the board. In addition, the real-time embedded controller offers the attitude controller and position controller. The motion capture system Optitrack is employed to measure the positions of quadrotor and the payload. Based on these position informations, the swing angles can be calculated and then the data packets are transmitted to the ground stations via the Ethernet. The ground station PC plays two roles. On the one hand, the ground station is used to record the experimental data during the flight. On the other hand, the ground station is responsible for parsing the data packets transferred from the Optitrack. In order to achieve the communication between the Optitrack and the quadrotor, we use two XBee modules which provide cost-effective wireless connectivity to devices in ZigBee networks. One is connected to controller chip of the quadrotor and the other one is connected to the Serial port of the ground station.

Fig. 2

The experiment testbed

The parameters of the quadrotor slung-payload system are listed as $m_{q}=1.0082$ kg, $m_{p}=0.0761$ kg, $l=1.085$ m and $g=9.81\,\mathrm{m}/\mathrm{s}^{2}$. In all cases, the initial and desired positions for the quadrotor are set as $x(0)=-\,0.5$ m, $y(0)=1.5$ m, $z(0)=-\,1.6$ m, $x_{d}=0.5$ m, $y_{d}=-\,1.0$ m and $z_{d}=-\,1.7$ m. And the control parameters of the proposed adaptive controller for the quadrotor slung-payload system are set $\alpha =0.5$, $\varGamma _{x}=\varGamma _{y}=2.0$, $\varGamma _{z}=\mathrm{diag}\{1.2,10\}$, $k_{px}=k_{py}=4.9$, $k_{\text {d}x}=k_{\text {d}y}=8.0$, $k_{pz}=16.0$, $k_{\text {d}z}=9.0$, and $k_{\text {d}\gamma _{x} }=k_{\text {d}\gamma _{y}}=0.7$.

To compare and analyze the effectiveness of the proposed methodology, a LQR controller is also implemented on the testbed. The dynamic mode in (1) is linearized to obtain the LQR controller. The LQR controller is designed as $f(t)=-\,Kx(t)$, where $x(t)=\left[ \right. e_{x}(t)\text { }e_{y}(t)\text { } e_{z}(t)\text { }{\dot{x}}(t)\text { }{\dot{y}}(t)\text {}{\dot{z}}(t)\text { }$$\gamma _{x}(t)\text { }\gamma _{y}(t)\left. {\dot{\gamma }}_{x}(t)\text { } {\dot{\gamma }}_{y}(t) \right] ^{T}\in {\mathbb {R}}^{10\times 1}$, K is control gain matrix which is the optimal solution in theory calculated via MATLAB toolbox.

For the convenience of quantitative analysis of the experimental results, some definitions in this paper are given as follows:

• 1. The steady-state value is the region when the deviation between the actual value and desired state value stay in the given range $\varTheta$, in this paper, $\varTheta _{x}=0.08$ m, $\varTheta _{y}=0.1$ m, $\varTheta _{z}=0.03$ m, $\varTheta _{\gamma _{x}}=3^{\circ }$, $\varTheta _{\gamma _{y}}=3.5^{\circ }$.

• 2. The adjusting time $T_{a}$ is defined as the required time to reach the steady-state process.

Fig. 3

The quadrotor’s position (x, y, z) and the payload’s swing angle $(\gamma _{x},\gamma _{y})$ in case 1 [blue line: the proposed controller; red line: LQR controller]

Fig. 4

The control output $(f_{x},f_{y},f_{z})$ in case 1 [blue line: the proposed controller; red line: LQR controller]

Fig. 5

The estimation of payload’s mass in case 1 [blue line: the proposed controller]

Table 1 Quantitative analysis of data in case 1

In this section, four cases of experiments are implemented on the testbed.

Case 1–Comparison with LQR controller The experimental results are shown in Figs. 3, 4, 5, which, respectively, represent the quadrotor’s positions, the payload’s swing angles, the control outputs of the proposed controller and LQR controller and the estimation of payload’s mass of the proposed controller. We analyze the data in a quantitative form as listed in Table 1, which includes adjusting time $T_{a}=\left[ t_{ax}\text { }t_{ay}\text { }t_{az}\text { }t_{a\gamma _{x}}\text { } t_{a\gamma _{y}}\right]$, standard deviation of steady-state process $\varSigma _{d}=\left[ \sigma _{\text {d}x}\text { }\sigma _{dy\text { }}\sigma _{\text {d}z}\text { }\sigma _{\text {d}\gamma _{x}}\text { }\sigma _{\text {d}\gamma _{y}}\right]$ and maximum residual of steady-state process $M_{r}=\left[ m_{rx}\text { }m_{ry}\text { }m_{rz}~m_{r\gamma _{x}}\text {}m_{r\gamma _{y}}\right]$. From Figs. 3, 4 and Table 1, one can see that the proposed controller can achieve higher positioning accuracy and faster convergence for horizontal motion of the quadrotor, meanwhile suppress the payload swing angle faster. Particularly, maximum payload residual swing angles in steady-state process for the proposed controller are far less than that LQR controller. In particular, when the system reaches the steady-state process, the proposed controller has better performance than LQR controller according to both standard deviation and maximum residual. From Fig. 5, we can see that the estimation of the unknown payload mass is about 0.0743 kg, and the estimation error is about 0.0018 kg, which indicates the online estimation for payload’s mass converges nearly to its real value. And the result is consistent with theoretical analysis.

Fig. 6

The quadrotor’s position (x, y, z) and the payload’s swing angle $(\gamma _{x},\gamma _{y})$ in case 2

Fig. 7

The control output $(f_{x},f_{y},f_{z})$ in case 2

Fig. 8

The estimation of payload’s mass in case 2

Case 2–Robustness to different payload’s mass We change the payload from 0.0761 to 0.1789 kg, the experimental results of the proposed controller are shown in Figs. 6, 7, 8, which, respectively, represent the quadrotor’s positions, the payload swing angles, the control outputs, and the estimation of payload’s mass of the proposed controller. Similarly, the quantitative results are listed in Table 2. Compared with the experimental results in case 1, it can be seen obviously that overall control performance of the proposed controller does not vary much although the payload’s mass has changed. We can obtain that the steady-state mean in vertical direction of the proposed controller is about $-\,1.7037$ m, which indicates the final position of the proposed controller is almost to its desired position. According to Fig. 8, the online estimation for the payload’s weight is approximately 0.1825 kg that means the estimation error is about 0.0036 kg. So we can conclude that the proposed online estimator for payload’s weight can converge to its true value precisely.

Table 2 Quantitative analysis of data in case 2

Fig. 9

The quadrotor’s position (x, y, z) and the payload’s swing angle $(\gamma _{x},\gamma _{y})$ in case 3

Case 3–Robustness to initial disturbances We consider the system is perturbed by initial swing angles. The initial payload’s swing angles $\gamma _{x}(t)$, $\gamma _{y}(t)$ are set as $22.1^{\circ }$, $13.5^{\circ }$, respectively, as shown in Fig. 9. The corresponding experimental results are shown in Figs. 9, 10, which represent the quadrotor’s positions, the payload’s swing angles and the control outputs of the proposed controller, respectively. And the relevant quantitative results are shown in Table 3. We can see that adjusting time $T_{a}$ is a bit long because of the large initial swing angles. However, the payload’s swing angles $\gamma _{x}(t)$, $\gamma _{y}(t)$ drop down to half of maximum swing angles ($\gamma _{x\max }=23.9^{\circ }$, $\gamma _{y\max }=21.2^{\circ }$) in a short time (about 2.6 s, 5.2 s, respectively), which indicates the proposed controller has good effect in reducing the large swing angles. From Figs. 9, 10 and Table 3, we can see that the overall control performance keeps good in terms of steady-state mean error, standard deviation and maximum residual in steady state. These experimental results demonstrate that the proposed control law has good robustness to the initial swing disturbances.

Fig. 10

The control output $(f_{x},f_{y},f_{z})$ in case 3

Table 3 Quantitative analysis of data in case 3

Case 4–Robustness to external disturbances In this case, we introduce some disturbance at about 19.5 s when the quadrotor has reached the definition for a while. The disturbance induced swing angles $\gamma _{x}(t)$, $\gamma _{y}(t)$ are approximately $32.5^{\circ }$ and $36.0^{\circ }$, respectively. The experimental results are shown in Figs. 11, 12, which represent the quadrotor’s positions, the payload’s swing angles and the control outputs of the proposed controller, respectively. And the quantitative results are shown in Table 4. We can see that the control force changes due to disturbance, as a result, the quadrotor’s positions are regulated by the controller in order to suppress the payload’s swing motion. From the adjusting time $T_{a}$ in Table 4, we can conclude that the regulation process is quick with small adjusting time for the quadrotor’s position x(t), y(y) in $X_\mathrm{B}$, $Y_\mathrm{B}$ directions and payload’s swing angles $\gamma _{x}(t)$, $\gamma _{y}(t)$. The payload’s swing angles $\gamma _{x}(t)$, $\gamma _{y}(t)$ reach the steady-state process in 4.490 s, 6.299 s, respectively, under the large interferences, which shows the satisfying robustness of the proposed controller with respect to the external disturbances. From the third entry of Table 4, one can conclude that behaviors in the steady state stay very well with small standard deviation of steady-state process $\varSigma _{d}$ and small maximum residual of steady-state process $M_{r}$.

Fig. 11

The quadrotor’s position (x, y, z) and the payload’s swing angle $(\gamma _{x},\gamma _{y})$ in case 4

Fig. 12

The control output $(f_{x},f_{y},f_{z})$ in case 4

Table 4 Quantitative analysis of data in case 4

6 Conclusion

A nonlinear adaptive controller for the quadrotor slung-payload system has been presented under the unknown aerodynamic drag force and unknown system parameters, which can achieve accurate quadrotor positioning and rapid payload swing suppression simultaneously. Besides, a parameter online estimation can precisely identify the unknown payload’s mass. The Lyapunov-based analysis is used to prove the stability of the proposed control laws. Experiment results performed on the self-build testbed confirm its superior performance and robustness.

About the future work, we will extend the current design to multiple quadrotor cooperative aerial transportation system. In addition, since the actual flight is susceptible to external gust disturbance, the corresponding adaptive robust controller will be designed considering the coexistence of unknown parameters and external wind disturbance.

Appendix

1.1 Parameter condition derivation

The function $\varLambda (t)$ in (48) can be expressed as follows:

$$\begin{aligned} -\varLambda (t)&=-\,\eta _{1}{\dot{x}}^{2}-\eta _{2}{\dot{y}}^{2}-\eta _{3}{\dot{z}} ^{2}-\eta _{4}{\dot{\gamma }}_{x}^{2}-\eta _{5}{\dot{\gamma }}_{y}^{2}\nonumber \\&\quad -\,\eta _{6} \rho ^{2}\left( \frac{e_{x}}{2}\right) \nonumber \\&\quad -\,\eta _{7}\rho ^{2}\left( \frac{e_{y}}{2}\right) -\eta _{8}\rho ^{2}\left( \frac{e_{z}}{2}\right) +\alpha k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}{\dot{x}}\nonumber \\&\quad +\,\alpha k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y}{\dot{y}}-2m_{p}glC_{x}\left( \sin \frac{\gamma _{y}}{2}\cos \frac{\gamma _{y}}{2}\right) ^{2}\nonumber \\&\quad -\,2m_{p}glC_{y}\left( \sin \frac{\gamma _{x}}{2}\cos \frac{\gamma _{x}}{2}\right) ^{2} \end{aligned}$$

(64)

where $\eta _{1}$, $\eta _{2}$, $\eta _{3}$, $\eta _{4}$, $\eta _{5}$, $\eta _{6}$, $\eta _{7}$, $\eta _{8}$ are defined as

$$\begin{aligned} \left\{ \begin{array} [c]{l} \eta _{1}\overset{\varDelta }{=}\alpha k_{\text {d}x}-\frac{1}{2}k_{\text {d}x}^{2}-\frac{1}{2}\lambda _{M}-2m_{p}^{2}\\ \eta _{2}\overset{\varDelta }{=}\alpha k_{\text {d}y}-\frac{1}{2}k_{\text {d}y}^{2}-\frac{1}{2}\lambda _{M}-\frac{1}{4}m_{p}^{2}\\ \eta _{3}\overset{\varDelta }{=}\alpha k_{\text {d}z}-\frac{k_{\text {d}z}^{2}}{2}-\frac{1}{2}\lambda _{M}-2m_{p}^{2}\\ \eta _{4}\overset{\varDelta }{=}\alpha c_{\gamma _{x}}-\frac{1}{2}\lambda _{M} -2l^{2}-m_{p}l^{2}-\frac{1}{2}k_{\text {d}\gamma _{x}}^{2}\\ \eta _{5}\overset{\varDelta }{=}\alpha c_{\gamma _{y}}-\frac{1}{2}\lambda _{M} -3l^{2}-\frac{1}{2}k_{\text {d}\gamma _{y}}^{2}\\ \eta _{6}\overset{\varDelta }{=}2k_{px}+2\kappa _{x}\varsigma _{x}-1\\ \eta _{7}\overset{\varDelta }{=}2k_{py}+2\kappa _{y}\varsigma _{y}-1\\ \eta _{8}\overset{\varDelta }{=}2k_{pz}+2\kappa _{z}\varsigma _{z}-\frac{1}{2} \end{array} \right. . \end{aligned}$$

(65)

Now, we define S(t) as follows:

$$\begin{aligned} S&=-\,\eta _{1}{\dot{x}}^{2}-\eta _{2}{\dot{y}}^{2}-\eta _{3}{\dot{z}}^{2}-\eta _{4}{\dot{\gamma }}_{x}^{2}\nonumber \\&\quad -\eta _{5}{\dot{\gamma }}_{y}^{2}+\alpha k_{\text {d}\gamma _{x}}{\dot{\gamma }}_{x}\dot{x}+\alpha k_{\text {d}\gamma _{y}}{\dot{\gamma }}_{y}{\dot{y}}\nonumber \\&=sPs^{T} \end{aligned}$$

(66)

where P is a $5\times 5$ matrix, $s=$$\left[ \begin{array} [c]{ccccc} {\dot{x}}&{\dot{y}}&{\dot{z}}&{\dot{\gamma }}_{x}&{\dot{\gamma }}_{y} \end{array} \right] \in {\mathbb {R}}^{1\times 5}$ and denoted via the following equations

$$\begin{aligned} \left\{ \begin{array} [c]{l} P=\left[ \begin{array} [c]{ccccc} \eta _{1} &{} 0 &{} 0 &{} p_{14} &{} 0\\ 0 &{} \eta _{2} &{} 0 &{} 0 &{} p_{25}\\ 0 &{} 0 &{} \eta _{3} &{} 0 &{} 0\\ p_{41} &{} 0 &{} 0 &{} \eta _{4} &{} 0\\ 0 &{} p_{52} &{} 0 &{} 0 &{} \eta _{5} \end{array} \right] \\ p_{14}=p_{41}=-\,\frac{1}{2}\alpha k_{\text {d}\gamma _{x}}\text { }p_{25}=p_{52} =-\,\frac{1}{2}\alpha k_{\text {d}\gamma _{y}} \end{array} \right. , \end{aligned}$$

(67)

Consequently, S(t) in (66) can be described as

$$\begin{aligned} S=-\,{\dot{e}}^{T}(t)P{\dot{e}}(t). \end{aligned}$$

(68)

By substituting (68) into (64), we can obtain

$$\begin{aligned} -\varLambda (t)&=-\,{\dot{e}}^{T}(t)P{\dot{e}}(t)-\eta _{6}\rho ^{2}(\frac{e_{x}}{2})-\eta _{7}\rho ^{2}\left( \frac{e_{y}}{2}\right) \nonumber \\&\quad -\,\eta _{8}\rho ^{2}\left( \frac{e_{z}}{2}\right) -2m_{p}glC_{x}\left( \sin \frac{\gamma _{y}}{2}\cos \frac{\gamma _{y}}{2}\right) ^{2}\nonumber \\&\quad -\,2m_{p}glC_{y}\left( \sin \frac{\gamma _{x}}{2}\cos \frac{\gamma _{x}}{2}\right) ^{2}. \end{aligned}$$

(69)

In order to ensure $-\varLambda (t)$ to be negative definite, it is implied that P need to be positive definite, then the conditions can denote as follows:

$$\begin{aligned} \left\{ \begin{array} [c]{l} \begin{array} [c]{ccc} \eta _{1}>0 &{} \eta _{1}\eta _{2}>0 &{} \eta _{1}\eta _{2}\eta _{3}>0 \end{array} \\ \begin{array} [c]{cc} \eta _{1}\eta _{2}\eta _{3}\eta _{4}+(\frac{1}{2}\alpha k_{\text {d}\gamma _{x}})^{2} \eta _{2}\eta _{3}>0 &{} \eta _{1}\eta _{2}\eta _{3}\eta _{4}\eta _{5}>0 \end{array} \end{array},\right. \nonumber \\ \end{aligned}$$

(70)

and it yields from (70) that

$$\begin{aligned} \begin{array} [c]{ccccc} \eta _{1}>0&\eta _{2}>0&\eta _{3}>0&\eta _{4}>0&\eta _{5}>0 \end{array} . \end{aligned}$$

(71)

Suppose that $k_{\text {d}x}=k_{\text {d}y}=k_{\text {d}z}=\frac{1}{r}\alpha$ where $r\in {\mathbb {R}}^{+}$ is positive constant. Hence, (71) can be denoted as

$$\begin{aligned} \left\{ \begin{array} [c]{l} \eta _{1}=\left( \frac{1}{r}-\frac{1}{2r^{2}}\right) \alpha ^{2}-\frac{1}{2}\lambda _{M}-2m_{p}^{2}>0\\ \eta _{2}=\left( \frac{1}{r}-\frac{1}{2r^{2}}\right) \alpha ^{2}-\frac{1}{2}\lambda _{M} -\frac{1}{4}m_{p}^{2}>0\\ \eta _{3}=\left( \frac{1}{r}-\frac{1}{2r^{2}}\right) \alpha ^{2}-\frac{1}{2}\lambda _{M}-2m_{p}^{2}>0\\ \eta _{4}=-\,\frac{1}{2r^{2}}\alpha ^{2}+c_{\gamma _{x}}\alpha -\frac{1}{2} \lambda _{M}-2l^{2}-m_{p}l^{2}>0\\ \eta _{5}=-\,\frac{1}{2r^{2}}\alpha ^{2}+c_{\gamma _{y}}\alpha -\frac{1}{2} \lambda _{M}-3l^{2}>0 \end{array} \right. . \end{aligned}$$

(72)

By making some mathematical manipulation, it is reduced as

$$\begin{aligned} \left\{ \begin{array} [c]{l} (2r-1)\alpha ^{2}>(\lambda _{M}+4m_{p}^{2})r^{2}\\ \alpha ^{2}-2r^{2}c_{\gamma _{x}}\alpha +r^{2}(4l^{2}+2m_{p}l^{2}+\lambda _{M})>0\\ \alpha ^{2}-2r^{2}c_{\gamma _{y}}\alpha +r^{2}(6l^{2}+\lambda _{M})>0 \end{array} \right. . \nonumber \\ \end{aligned}$$

(73)

Thus, $\alpha$ should be selected to satisfy

$$\begin{aligned} \max \left\{ \beta _{1}\text { }\beta _{3}\text { }r\sqrt{\frac{\lambda _{M} +4m_{p}^{2}}{2r-1}}\right\}<\alpha <\min \left\{ \beta _{2}\text { }\beta _{4}\right\} \nonumber \\ \end{aligned}$$

(74)

with

$$\begin{aligned} \left\{ \begin{array} [c]{l} \beta _{1}=r^{2}c_{\gamma _{x}}-r\sqrt{r^{2}c_{\gamma _{x}}^{2}-(4l^{2}+2\bar{m}_{p}l^{2}+\lambda _{M})}\\ \beta _{2}=r^{2}c_{\gamma _{x}}+r\sqrt{r^{2}c_{\gamma _{x}}^{2}-(4l^{2}+2\bar{m}_{p}l^{2}+\lambda _{M})}\\ \beta _{3}=r^{2}c_{\gamma _{y}}-r\sqrt{r^{2}c_{\gamma _{y}}^{2}-(6l^{2} +\lambda _{M})}\\ \beta _{4}=r^{2}c_{\gamma _{y}}+r\sqrt{r^{2}c_{\gamma _{y}}^{2}-(6l^{2} +\lambda _{M})} \end{array} \right. , \nonumber \\ \end{aligned}$$

(75)

and r should be chosen to satisfy

$$\begin{aligned} r\ge \max \left\{ \frac{1}{2},\frac{\sqrt{4l^{2}+2{\bar{m}}_{p}l^{2}+\lambda _{M}} }{c_{\gamma _{x}}^{2}},\frac{\sqrt{6l^{2}+\lambda _{M}}}{c_{\gamma _{y}}^{2}}\right\} . \nonumber \\ \end{aligned}$$

(76)

On the other hand, considering the negative property of $-\varLambda (t)$, the following inequalities hold

$$\begin{aligned} \left\{ \begin{array} [c]{l} \eta _{6}=2k_{py}+2\kappa _{x}\varsigma _{x}-1>0\\ \eta _{7}=2k_{py}+2\kappa _{y}\varsigma _{y}-1>0\\ \eta _{8}=2k_{pz}+2\kappa _{z}\varsigma _{z}-\frac{1}{2}>0 \end{array} \right. , \end{aligned}$$

(77)

that means

$$\begin{aligned} k_{px}>\frac{1}{2}\text { }k_{py}>\frac{1}{2}\text { }k_{pz}>\frac{1}{4}\text { }\kappa _{x}>0\text { }\kappa _{y}>0\text { }\kappa _{z}>0. \nonumber \\ \end{aligned}$$

(78)

Thus, combined with (32) and (34), we can obtain the conditions for $\alpha$, $k_{\text {d}x}$, $k_{\text {d}y}$, $k_{\text {d}z}$, $k_{px}$, $k_{py}$, $k_{pz}$, $k_{\text {d}\gamma _{x}}$, $k_{\text {d}\gamma _{y}}$, $\kappa _{x}$, $\kappa _{y}$, $\kappa _{z}$ in (49) and (50) based on (71)-(78).