1 Introduction

The last two decades have witnessed considerable progress in the study of underactuated multibody systems, which possess fewer actuators than degrees of freedom (the number of configuration variables), from the perspectives of lightening weight, increasing reliability and saving energy [4, 8, 12, 15, 19, 21, 26, 27]. They appear in a broad range of applications including robotics, aerospace systems, marine systems, flexible systems, mobile systems, and locomotive systems. Examples of such systems include gymnastic robots [19, 20] and manipulators with passive joints [11], underwater vehicles [14], and aircraft [1, 3], rotational/translational actuator [7]. Due to nonholonomic constraints relations arising in the models of underactuated multibody systems, the control of these systems is still challenging [16].

One of the important control problems for underactuated robots with passive joint(s) is the set-point control (regulation or stabilization) of a desired equilibrium point of the robots, that is, finding a feedback controller that makes the desired equilibrium point asymptotically stable [2]. Many researchers studied a particular problem of the set-point control called the swing-up control for a planar robot with passive joint(s) moving in the vertical plane, see, e.g., [5, 6, 10, 19]. Indeed, the swing-up control is to swing the robot to a small neighborhood of the upright equilibrium point and then balance it about that point, where all links are in the upright position.

In spite of some research progress on the swing-up control for planar robots with passive joint(s), the set-point control for these robots is still open. This paper concerns a 3-link gymnastic planar robot moving in the vertical plane with its first joint being passive (unactuated) and the second and third joints being active (actuated), which is called PAA robot below. The first, second, and third joints of this robot correspond to the hands, shoulders, and hips of a human gymnast, respectively. Different from the fully stretched out equilibrium configuration related to the swing-up control shown in plot (a) of Fig. 1, this paper studies the set-point control for a folded configuration of the PAA robot shown in plot (b) of Fig. 1. The control objective is to drive the PAA robot from any initial state to any small neighborhood of the UDD (up–down–down) equilibrium point, where link 1 is in the upright position and links 2 and 3 are in the downward position. This corresponds to the goal configuration of the kip motion of a human gymnast on the high bar (plot (b) of Fig. 1), where the upper limb and the trunk of the gymnast are folded. Note that the kip motion is a basic element performed on the high bar, in which the gymnast jumps on the bar, swings his legs forward, brings his legs up to the bar and lifts his body up to the bar.

Fig. 1
figure 1

Goal configurations of the swing-up motion (plot (a)) and the kip motion (plot (b)) of a human gymnast

Full size image

To the best of authors’ knowledge, nonlinear control toward such an equilibrium configuration has not been reported in the literature. We investigate whether we can extend the energy-based control approach developed in the seminal works of [5, 10, 20] and the notion of VCL (virtual composite link) in [25] for the swing-up control problem to such a folded configuration control problem. First, by treating links 2 and 3 of the PAA robot as a VCL, we design a controller, and present a necessary and sufficient condition for avoiding singular points in the presented controller. Second, to obtain a global motion analysis of the PAA robot, we clarify the structure of the closed-loop equilibrium configuration by iteratively studying two robots of the Acrobot type (two links with a passive first joint) rather than directly studying the original 3-link robot. We find that the tackled problem is more difficult than the usual swing-up maneuver. Specifically, different from the swing-up control problem in [25], a new result of this paper is that in addition to some conditions on control parameters, a constraint on the mechanical parameters of the PAA robot is needed for achieving the set-point control of the folded configuration. The proposed constraint guarantees the linear controllability of the Acrobot (degenerated from the PAA robot) whose actuated second link is the merge of links 2 and 3 of the PAA robot with all possible relative angles.

This paper is organized as follows: Sect. 2 presents some preliminary knowledge and problem formulation. Section 3 describes an energy- and VCL-based controller for the folded configuration of the PAA robot. Section 4 analyzes the global motion of the PAA robot under that controller. Section 5 shows simulation results for two 3-link robots to validate the theoretical results. Section 6 makes some concluding remarks.

2 Preliminary knowledges and problem formulation

2.1 Model of the PAA robot

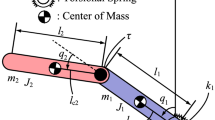
Consider the PAA robot shown in Fig. 2, where for the ith (i=1,2,3) link, l i is its length, l ci is the distance from the joint i to its COM (center of mass), and J i is the moment of inertia around its COM.

Fig. 2
figure 2

A three-link underactuated planar robot (PAA robot)

Full size image

Partition the generalized coordinate vector \(q \in {\mathbb {R}}^{3}\) as \(q=[ q_{1}, q_{a}^{{\mathrm {T}}}]^{{\mathrm {T}}}\), with q a =[q 2,q 3]T, where the subscript a denotes “actuated” in this paper. The motion equation of the PAA robot is:

$$\begin{aligned} M(q)\ddot{q} + H(q, \dot{q}) + G(q) = B\tau, \end{aligned}$$
(1)

where

$$ M(q)=\left [ \begin{array}{c@{\quad}c@{\quad}c} M_{11}& M_{12} &M_{13}\\ M_{21}&M_{22}&M_{23}\\ M_{31}&M_{32}&M_{33} \end{array} \right ] $$
(2)

is a symmetric positive definite inertia matrix, \(H(q, \dot{q}) \in {\mathbb {R}}^{3}\) contains Coriolis and centrifugal terms, \(G(q) \in {\mathbb {R}}^{3}\) contains gravitational terms, and \(\tau= [ \tau_{2}, \tau_{3} ]^{{\mathrm {T}}}\in {\mathbb {R}}^{2}\) is the input torque vector produced by two actuators at the active joints 2 and 3. We express the detail of the matrices in (1) as follows:

$$\begin{aligned} M_{11} =&\alpha_{11}+\alpha_{22}+ \alpha_{33}+2\alpha _{12}\cos q_2+2 \alpha_{13}\cos(q_2+q_3) +2\alpha_{23} \cos q_3, \\ M_{12} =& M_{21}=\alpha_{22}+\alpha_{33}+ \alpha_{12}\cos q_2+\alpha_{13} \cos(q_2+q_3)+2\alpha_{23}\cos q_3, \\ M_{13} =&M_{31}=\alpha_{33}+\alpha_{13} \cos(q_2+q_3)+\alpha _{23}\cos q_3, \\ M_{22} =&\alpha_{22}+\alpha_{33}+2 \alpha_{23} \cos q_3, \\ M_{23} =&M_{32}=\alpha_{33}+\alpha_{23} \cos q_3, \\ M_{33} =&\alpha_{33}, \\ H_1 =&-\alpha_{12}(2\dot{q}_1+\dot{q}_2) \dot{q}_2\sin q_2 -\alpha_{13}(2 \dot{q}_1+\dot{q}_2+\dot{q}_3) ( \dot{q}_2+\dot{q}_3) \sin (q_2+q_3) \\ &{} - \alpha_{23}(2\dot{q}_1+2\dot{q}_2+ \dot{q}_3)\dot {q}_3 \sin q_3, \\ H_2 =&\alpha_{12}\dot{q}_1^2\sin q_2 + \alpha_{13}\dot {q}_1^2 \sin(q_2+q_3) -\alpha_{23}(2 \dot{q}_1+2\dot{q}_2+\dot{q}_3)\dot {q}_3\sin q_3, \\ H_3 =&\alpha_{13}\dot{q}_1^2 \sin(q_2+q_3) + \alpha _{23}( \dot{q}_1+\dot{q}_2)^2\sin q_3, \\ G_1 =&-\beta_1\sin q_1 - \beta_2 \sin(q_1+q_2)-\beta_3 \sin (q_1+q_2+q_3), \\ G_2 =&-\beta_2\sin(q_1+q_2)- \beta_3\sin(q_1+q_2+q_3), \\ G_3 =& -\beta_3\sin(q_1+q_2+q_3), \end{aligned}$$

where

$$\begin{aligned} &\left \{ \begin{array}{l} \alpha_{11}=J_1+m_1l_{c1}^2+(m_2+m_3)l_1^2, \\ \alpha_{22}=J_2+m_2l_{c2}^2+m_3l_2^2, \\ \alpha_{33}=J_3+m_3l_{c3}^2, \\ \alpha_{12}= (m_2l_{c2}+m_3l_2)l_1,\\ \alpha_{13}= m_3l_1l_{c3}, \\ \alpha_{23}= m_3l_2l_{c3}, \end{array} \right . \end{aligned}$$
(3)
$$\begin{aligned} & \left \{ \begin{array}{l} \beta_1=(m_1l_{c1}+m_2l_1+m_3l_1)g,\\ \beta_2=(m_2l_{c2}+m_3l_2)g, \\ \beta_3=m_3l_{c3}g, \end{array} \right . \end{aligned}$$
(4)

where g is the acceleration of gravity, and

$$ B = \left [ \begin{array}{c@{\quad}c} 0&0\\ 1&0\\ 0&1 \end{array} \right ]. $$
(5)

The total mechanical energy of the PAA robot is expressed as

$$ E(q, \dot{q})=\frac{1}{2}\dot{q}^{\mathrm {T}}M(q) \dot{q}+P(q), $$
(6)

where the potential energy P(q) is set as

$$ P(q)=\beta_1 \cos q_1 + \beta_2 \cos(q_1+q_2) +\beta_3 \cos(q_1+q_2+q_3). $$
(7)

2.2 Problem formulation: set-point control for folded configuration

Consider the following UDD equilibrium point:

$$ q_1=0\ (\mbox{mod}\, 2 \pi), \qquad q_2=-\pi,\qquad q_3=0, \qquad \dot{q}_1=\dot {q}_2=\dot{q}_3=0. $$
(8)

Letting E r be the total mechanical energy of the PAA robot at the UDD equilibrium point yields

$$ E_{r}=\beta_1-\beta_2- \beta_3. $$
(9)

In this paper, to apply the energy-based control approach, we need to assume that E r >0 which indicates the COM of the PAA robot at the UDD equilibrium point is above the horizontal axis.

To realize the set-point control for the UDD equilibrium point, for \(E(q,\dot{q})\), \(\dot{q}_{a}\), and q a , if one can design a controller such that

$$ \lim_{t\to\infty} E(q,\dot{q})=E_r, \qquad\lim_{t\to\infty} \dot {q}_a=0, \qquad\lim _{t\to\infty} q_a=q_{ar}, $$
(10)

where

$$ q_{ar}=\left [ \begin{array}{c@{\quad }c} -\pi, & 0 \\ \end{array} \right ]^{\mathrm {T}}, $$
(11)

we will show in Sect. 4 that there exists a sequence of times that the PAA robot can be driven to any small neighborhood of the UDD equilibrium point so that we can use a local stabilizing controller to balance the PAA robot at that point.

A conventional Lyapunov function candidate for designing such τ is

$$\begin{aligned} V_C =&\frac{1}{2} (E-E_r)^2+ \frac{1}{2}k_D \dot{{q}}_a ^{\mathrm {T}}\dot{{q}}_a+ \frac{1}{2}k_P (q_a-q_{ar})^{{\mathrm {T}}}(q_a-q_{ar}), \end{aligned}$$
(12)

where scalars k D >0 and k P >0 are control parameters. However, we find that it is difficult to obtain the relationship between the control parameter k P and the closed-loop equilibrium configurations for determining whether the control objective can be achieved. To overcome this difficulty, our idea is to use the notion of VCL which considering links 2 and 3 as a virtual link [25] and to use the new Lyapunov function candidate shown in (34).

For preparation, in Sect. 2.3 we recall the notion of VCL developed in [25], and in Sect. 2.4 we discuss the linear controllability for an Acrobot-type robot whose actuated second link is the merge of links 2 and 3 of the 3-link robot with a constant relative angle.

2.3 Virtual composite link

For the PAA robot, we consider its links 2 and 3 as a VCL shown in Fig. 3, where the VCL starts from joint 2, and the COM of the VCL is the same as the joint COM of links 2 and 3.

Fig. 3
figure 3

Merge of links 2 and 3 into a VCL (virtual composite link)

Full size image

Let \(\overline {q}_{2}\) be the angle of the VCL with respect to link 1, and let θ(q 3) be the angle of the VCL with respect to link 2, shown in Fig. 3. We obtain

$$ \overline {q}_2=q_2+ \theta(q_3). $$
(13)

Moreover, when link 2 and the VCL are stretched out in a straight line, it is reasonable to define

$$\begin{aligned} \theta(q_3) \big|_{q_3=0}=0. \end{aligned}$$
(14)

To determine θ(q 3), we use a coordinate system (x,y) with its origin at joint 2 and its x-axis lying on link 2, see Fig. 3. In this coordinate system, the coordinates of the COMs of links 2 and 3 are (l c2,0) and (l 2+l c3cosq 3,l c3sinq 3), respectively. Let (x c ,y c ) be the coordinates of joint COM of links 2 and 3. We obtain

$$(x_{c}, y_{c})= \frac{(\beta_2+\beta_3 \cos q_3, \beta_{3} \sin q_3 ) }{ (m_2+m_3)g }. $$

Letting \(\overline {l}_{c2}\) be the distance between joint 2 and the COM of the VCL, we have

$$ \overline {l}_{c2}(q_3)=\sqrt {x_{c}^2+ y_{c}^2} = \frac{\overline {\beta }_2(q_3)}{(m_2+m_3) g}, $$
(15)

where

$$ \overline {\beta}_2(q_3):= \sqrt{ \beta_2^2 +\beta_3^2 + 2 \beta_2\beta_3 \cos q_3}. $$
(16)

Thus, θ(q 3) satisfies

$$ \left \{ \begin{array}{l} \sin\theta(q_3) =\displaystyle\frac{y_{c}}{\overline {l}_{c2}}= \displaystyle\frac{\beta_3 \sin q_3}{\overline {\beta}_2(q_3) }, \\ \cos\theta(q_3) = \displaystyle\frac{x_{c}}{\overline {l}_{c2}}=\displaystyle\frac{\beta_2+\beta_3 \cos q_3}{\overline {\beta }_2(q_3) }. \end{array} \right . $$
(17)

Consider the following coordinate transformation on q a :

$$ \overline {q}_a = \left [ \begin{array}{c} \overline {q}_2 \\ {q}_3 \\ \end{array} \right ]. $$
(18)

From (13) and (14), the transformation from q a to \(\overline {q}_{a}\) is

$$ \overline {q}_a =0 \quad \Longleftrightarrow\quad {q}_a =0. $$
(19)

Using the time-derivative of tanθ(q 3) yields

$$\begin{aligned} \dot{\theta}(q_3)=\psi(q_3) \dot{q}_3, \quad\psi(q_3)=\frac{\beta_3(\beta_3+\beta_2\cos q_3)}{\overline {\beta }_2^2(q_3)}. \end{aligned}$$
(20)

This shows

$$ \dot{\overline {q}}_a = \varPsi\dot{q}_a, \quad\varPsi= \left [ \begin{array}{c@{\quad }c} 1 & \psi(q_3) \\ 0 &1 \\ \end{array} \right ]. $$
(21)

2.4 Linear controllability at folded configuration

Let us consider the Acrobot (2-link case) in this section, which can be treated as a special case of the 3-link case by assuming the relative angle between links 2 and 3 being constant denoted as \(q_{3}^{\ast}\), that is, \(q_{3}(t)\equiv q_{3}^{\ast}\). Different from \(\overline {q}_{2}\) in (13), we define

$$\begin{aligned} \widetilde{q}_2=q_2+ \theta \bigl(q_3^\ast\bigr). \end{aligned}$$

We obtain the motion equation of the Acrobot derived from (1) as follows:

$$\begin{aligned} \widetilde{M}(\widetilde{q})\ddot{\widetilde{q}}+ \widetilde {H}(\widetilde{q}, \dot{\widetilde{q}})+ \widetilde{G}(\widetilde {q})=B_A \tau_2, \end{aligned}$$
(22)

where \(\widetilde{q}= [ q_{1}, \widetilde{q}_{2} ]^{{\mathrm {T}}}\), B A =[0,1]T, and

$$\begin{aligned} & \widetilde{M}(\widetilde{q}) =\left [ \begin{array}{c@{\quad}c} \overline {\alpha}_1+\overline {\alpha}_2+ 2 \overline {\alpha}_3 \cos \widetilde{q}_2& \; \overline {\alpha}_2+\overline {\alpha}_3 \cos \widetilde{q}_2 \\ \overline {\alpha}_2+\overline {\alpha}_3 \cos\widetilde{q}_2 & \overline {\alpha}_2 \end{array} \right ], \end{aligned}$$
(23)
$$\begin{aligned} & \widetilde{H}(\widetilde{q},\dot{\widetilde{q}})= \overline { \alpha}_3 \left [ \begin{array}{c} -2 \dot{q}_1 \dot{\widetilde{q}}_2-\dot{\widetilde{q}}_2^2 \\ \dot{q}_1^2 \\ \end{array} \right ]\sin \widetilde{q}_2, \end{aligned}$$
(24)
$$\begin{aligned} & \widetilde{G}(\widetilde{q})= \left [ \begin{array}{c} -\overline {\beta}_1 \sin q_1 - \overline {\beta}_2 \sin(q_1+\widetilde {q}_2) \\ -\overline {\beta}_2 \sin(q_1+\widetilde{q}_2) \end{array} \right ], \end{aligned}$$
(25)

where

$$ \left \{ \begin{array}{l} \overline {\alpha}_1=\alpha_{11},\\ \overline {\alpha}_2(q_3^{\ast})= \alpha_{22}+ \alpha_{33}+ 2 \alpha _{23} \cos q_3^\ast, \\ \overline {\alpha}_3(q_3^{\ast})=l_1\overline {\beta}_2(q_3^{\ast})/g, \\ \overline {\beta}_1=\beta_1,\\ \overline {\beta}_2(q_3^{\ast}) =\sqrt{\beta_2^2 +\beta_3^2 + 2\beta _2\beta_3 \cos q_3^\ast}. \end{array} \right . $$
(26)

Let \(w= [ q_{1}, \widetilde{q}_{2}, \dot{q}_{1},\dot{\widetilde{q}}_{2} ]^{{\mathrm {T}}}\) and \(w^{e}= [ q_{1}^{e}, \widetilde{q}_{2}^{e}, 0,0 ]^{{\mathrm {T}}}\) be the state and an equilibrium point of the Acrobot. Let \(\tau_{2}^{e}= -\beta_{2} \sin(q_{1}^{e}+\widetilde{q}_{2}^{e})\) be the equilibrium torque. Then the linearized model of the Acrobot around the above equilibrium point can be expressed as:

$$ \dot{\xi}=A\xi+N u, $$
(27)

where ξ=w−w e, \(u=\tau_{2}- \tau_{2}^{e}\), A and N are matrices determined by the mechanical parameters of the Acrobot and the equilibrium point and are omitted for brevity. The Acrobot is linearly controllable at the equilibrium point if (A,N) is controllable. Note that (A,N) is controllable if and only if the controllability matrix U=[N,AN,A 2 N,A 3 N] has full row rank, that is, |U|≠0.

Let U uu and U ud be the controllability matrices of linearized models of the Acrobot around the upright equilibrium point (links 1 and 2 are in the upright position) and up–down equilibrium point (links 1 and 2 are in the upright and downward positions, respectively), respectively. Then

$$\begin{aligned} |U_\mathit{uu}|=-\frac{\overline {\rho}^2}{(\overline {\alpha}_1\overline {\alpha }_2-\overline {\alpha}_3^2)^4},\qquad |U_\mathit{ud}|=- \frac{\overline {\delta }^2}{(\overline {\alpha}_1\overline {\alpha}_2-\overline {\alpha}_3^2)^4}, \end{aligned}$$
(28)

where

$$\begin{aligned} &\overline {\rho}= (\overline {\alpha}_{2}+ \overline { \alpha}_{3}){\overline {\beta}}_{1} -( {\overline { \alpha}}_{1}+\overline {\alpha}_{3})\overline { \beta}_{2}, \end{aligned}$$
(29)
$$\begin{aligned} &\overline {\delta}= (\overline {\alpha}_2-\overline { \alpha}_3){\overline {\beta }}_1+({\overline { \alpha}}_1-\overline {\alpha}_3) \overline { \beta}_2. \end{aligned}$$
(30)

Lemma 1 in [24] for this Acrobot directly gives the following two inequalities:

$$\begin{aligned} & \overline {\alpha}_2 \overline {\beta}_1 -\overline {\alpha}_3 \overline {\beta}_2 >0, \end{aligned}$$
(31)
$$\begin{aligned} & \overline {\alpha}_3 \overline {\beta}_1 - \overline {\alpha}_1 \overline {\beta}_2\geq0. \end{aligned}$$
(32)

Thus, \(\overline {\rho}>0\) since \(\overline {\rho}\) is the sum of left-hand side terms of (31) and (32); \(\overline {\delta}\) may be zero since \(\overline {\delta}\) is the difference of left-hand side terms of (31) and (32). We give the following lemma.

Lemma 1

The linearized model of the Acrobot around the upright equilibrium point is controllable; while the linearized model of the Acrobot around the up–down equilibrium point is controllable if and only if \(\overline {\delta}\neq0\).

We recall a property of the motion of the Acrobot in [24].

Lemma 2

Assume that the up–down equilibrium point of the Acrobot is linearly controllable, that is, \(\overline {\delta} \neq0\) for δ in (30). If \(q_{2}(t)\equiv{q}_{2}^{\ast}\) and \(\tau_{2}(t) \equiv \tau_{2}^{\ast}\) with \({q}_{2}^{\ast}\) and \(\tau_{2}^{\ast}\) being constant, then

$$ \dot{q}_1(t) \equiv0, \qquad \tau_2^\ast=0, \qquad q_2^\ast=-\pi\ (\mathrm{mod}\,2 \pi), $$
(33)

where “≡” means that the equation holds for all time t.

Note that there exist 2-link planar robots satisfying \(\overline {\delta }=0\), see [24, p. 1521]. In this paper, to drive the PAA robot close to the UDD equilibrium point, we need a constraint on the mechanical parameters of the PAA robot similar to the constraint \(\overline {\delta}\neq0\) for the Acrobot.

3 Controller design and avoidance of singular points

We present the following Lyapunov function candidate:

$$ V=\frac{1}{2} (E-E_r)^2+ \frac{1}{2}k_D \dot{{q}}_a ^{\mathrm {T}}\dot{{q}}_a + \frac{1}{2}k_P e^{\mathrm {T}}e, $$
(34)

where \(e=\bar{q}_{a}-q_{ar}\) is used instead of q a −q ar in (12).

Taking the time-derivative of V along the trajectories of (1), and using \(\dot{E}= \dot{q}_{a}^{{\mathrm {T}}}\tau\) and using \(\dot {\overline {q}}_{a}^{{\mathrm {T}}}= \dot{q}_{a}^{{\mathrm {T}}}\varPsi^{{\mathrm {T}}}\) owing to (21), we obtain

$$\dot{V}=\dot{q}_a^{\mathrm {T}}\bigl((E-E_r) \tau+ k_D \ddot{q}_a+k_P \varPsi^{{\mathrm {T}}} e \bigr). $$

Thus, if we can choose τ such that

$$ (E-E_r) \tau+ k_D \ddot{q}_a+k_P \varPsi^{{\mathrm {T}}}e= -k_V \dot{q}_a $$
(35)

holds for some constant k V >0, then we have

$$ \dot{V}=-k_V\dot{q}_a^{\mathrm {T}}\dot{q}_a \leq0. $$
(36)

From (1) and q a =B T q, we obtain

$$ \varLambda(q,\dot{q}) \tau= k_DB^{\mathrm {T}}M^{-1}(H+G)-k_V \dot{q}_a-k_P \varPsi^{{\mathrm {T}}}e, $$
(37)

where

$$\begin{aligned} \varLambda(q,\dot{q}) = \bigl(E(q,\dot{q})-E_r\bigr) I_{2}+ k_D B^{{\mathrm {T}}}M^{-1}(q)B, \end{aligned}$$
(38)

with I 2 being the 2×2 identity matrix. Therefore, when

$$ \bigl| \varLambda(q,\dot{q})\bigr| \neq0, \quad\mbox{for}\ \forall q, \forall \dot{q} $$
(39)

holds, the following controller obtained from (37) has no singular points for any (q, \(\dot{q}\)):

$$ \tau=\varLambda^{-1} \bigl(k_DB^{\mathrm {T}}M^{-1}(H+{G})-k_V \dot{q}_a -k_P \varPsi ^{{\mathrm {T}}} e \bigr). $$
(40)

We use the fact that M(q) is a matrix function of q 2 and q 3 to derive a necessary and sufficient condition such that (39) holds. Then, we apply LaSalle’s invariance principle [9] to the closed-loop system consisting of (1) and (40) to determine the largest invariant set that the closed-loop solution approaches as t goes infinity. We present the following lemma with its proof given in Appendix A.

Lemma 3

Consider the closed-loop system consisting of (1) and (40). Suppose that k D >0, k P >0, and k V >0. Then controller (40) has no singular points for any (q, \(\dot{q}\)) if and only if

$$ k_D> k_{Dm}=\max_{q_2,q_3} \bigl\{ (E_r+\mu)\lambda_{\mathrm{max}} \bigl(\bigl( B^{{\mathrm {T}}}M^{-1}B\bigr)^{-1} \bigr) \bigr\} , $$
(41)

where λ max(A) denotes the maximal eigenvalue of A>0 and

$$\begin{aligned} \mu= \Biggl(\sum_{i=1}^{3} \beta_i^2 + 2 \sum_{i=1}^{2} \sum_{j>i}^{3}\beta_i \beta_j \cos\sum_{k=i+1}^{j} q_k \Biggr)^{1/2}. \end{aligned}$$
(42)

In this case,

$$\begin{aligned} &\lim_{t\to\infty} V=V^\ast, \qquad\lim _{t\to\infty} E=E^\ast, \end{aligned}$$
(43)
$$\begin{aligned} & \lim_{t\to\infty}q_a=q_a^\ast, \qquad\lim_{t\to\infty} \overline {q}_a= \overline {q}_a^{\;\ast}, \end{aligned}$$
(44)

where V ∗, E ∗, \(q_{a}^{\ast}\), and \(\overline {q}_{a}^{\;\ast }\) are constants. Moreover, as t→∞, every closed-loop solution, \((q(t), \dot{q}(t))\), approaches the invariant set:

$$ W= \biggl\{ (q, \dot{q}) \Bigm| \dot{q}_1^2 = \displaystyle{\frac{2(E^\ast-P(q))}{ M_{11}(q)}} \bigg|_{q_a=q_a^{\ast}}, q_a \equiv q_a^{\ast} \biggr\} . $$
(45)

4 Motion analysis: new results related to folded configuration

We characterize the invariant set W in (45) by analyzing the limit value V ∗ of the Lyapunov function V in (34). Since lim t→∞ V=0 is equivalent to (10), we analyze the two cases, V ∗≠0 and V ∗=0, separately. Note that

$$\begin{aligned} q_a^\ast= \left [ \begin{array}{c} q_2^\ast \\ q_3^\ast \\ \end{array} \right ], \qquad \overline {q}_{a}^{\;\ast }= \left [ \begin{array}{c} q_2^\ast+ \theta(q_3^\ast) \\ q_3^\ast \\ \end{array} \right ]. \end{aligned}$$
(46)

4.1 Constraint on mechanical parameters

Regarding the case of V ∗=0, from (34) and (19), we have E ∗=E r , \(\overline {q}_{a}^{\;\ast}= q_{ar}\) with q ar in (11). Using \(q_{3}^{\ast}=0\) yields \(\overline {q}_{2}^{\;\ast}= q_{2}=-\pi\) and \({q}_{a}^{\ast}=q_{ar}\). From (6), we obtain

$$\begin{aligned} \dot{q}_1^2 = \displaystyle{ \frac{2E_r}{M_{11}(q_{ar})}} (1-\cos q_1). \end{aligned}$$
(47)

Therefore, the closed-loop solution \((q(t), \dot{q}(t))\) approaches the following invariant set as t→∞:

$$ W_r=\bigl\{ (q, \dot{q})\;|\; (q_1, \dot{q}_1)\ \mbox{satisfies (47)}; q_a\equiv q_{ar}\bigr\} . $$
(48)

Since (47) is a homoclinic orbit converging to the equilibrium point \((q_{1}, \dot{q}_{1})=(0, 0)\) as t→∞, \((q_{1}(t), \dot {q}_{1}(t))\) will have \((q_{1}, \dot{q}_{1})=(0, 0)\) as an ω-limit point [17, p. 44], that is, there exists a sequence of times t m (m=1,…,∞) such that t m →∞ as m→∞ for which \(\lim_{m \to\infty}(q_{1}(t_{m}), \dot{q}_{1}(t_{m}))=(0, 0)\), and this implies that the PAA robot can enter any small neighborhood of the UDD equilibrium point.

Regarding the case of V ∗≠0, substituting E≡E ∗ and \(\overline {q}_{a}\equiv \overline {q}_{a}^{\;\ast}\) into (35) yields

$$ k_P\varPsi^{{\mathrm {T}}} \bigl(q_3^\ast \bigr) \bigl(\overline {q}_{a}^{\;\ast }-q_{ar}\bigr)+ \bigl(E^\ast-E_r\bigr) \tau=0. $$
(49)

This shows that E ∗≠E r . On the contrary, assume that E ∗=E r holds, then from (49), we have \(\overline {q}_{a}^{{\;\ast }}=q_{ar}\). This yields V ∗=0 which contradicts V ∗≠0. Using E ∗≠E r shows that τ is a constant vector τ ∗ satisfying the following equation:

$$ k_P \varPsi^{{\mathrm {T}}}\bigl(q_3^\ast \bigr) \bigl(\overline {q}_{a}^{\;\ast }-q_{ar}\bigr)+ \bigl(E^{\ast }-E_r\bigr)\tau^\ast=0. $$
(50)

Since \(q_{3}(t)\equiv q_{3}^{\ast}\) holds in the invariant set W defined in (45), there exists no relative motion between links 2 and 3; as shown in Fig. 4, we consider the PAA robot as an Acrobot whose first link is link 1 of the PAA robot and the second link is the merge of links 2 and 3 of the PAA robot with relative angle \(q_{3}(t)\equiv q_{3}^{\ast}\). Thus, as described in Sect. 2.4, such an Acrobot has the following five parameters described in (26).

Fig. 4
figure 4

PAA robot with \(q_{3}\equiv q_{3}^{\ast}\) and an Acrobot

Full size image

According to Lemma 2 and (30), since \(\overline {q}_{2}^{{\;\ast }}\) is a constant, q 1(t) is a constant in the invariant set W provided that the Acrobot in Fig. 4 is linearly controllable at the folded configuration, that is, from Lemma 1,

$$\begin{aligned} (\overline {\alpha}_2-\overline {\alpha}_3) \beta_1+(\overline {\alpha}_1-\overline {\alpha}_3) \overline {\beta}_2 \bigl(q_3^\ast\bigr) \neq0,\quad \mbox{for}\ \forall q_3^\ast. \end{aligned}$$
(51)

This is equivalent to

$$\begin{aligned} \varGamma \overline {\beta}_{2}\bigl(q_{3}^{*} \bigr)\neq\varXi\cos q_{3}^{*}+\varLambda, \quad \mbox{for}\ 0 \leq q_3^\ast\leq2\pi, \end{aligned}$$
(52)

where Γ, Ξ, and Λ are the following constants determined by the mechanical parameters of the 3-link robot:

$$\begin{aligned} & \varGamma =l_1\beta_1-\alpha_{11}g, \\ &\varXi= 2(g\alpha_{23}\beta_{1} - l_1 \beta_{2}\beta_{3}), \\ &\varLambda= g(\alpha_{22} + \alpha_{33}) \beta_{1}-l_1\bigl(\beta_{2}^{2} + \beta_{3}^{2}\bigr). \end{aligned}$$

As shown in Appendix B, we obtain

$$ \varGamma\geq0,\quad \varLambda> \varXi>0. $$
(53)

Thus, (52) is equivalent to

$$\begin{aligned} f(z):=\frac{\varGamma \overline {\beta}_{2}(z)}{\varXi\cos z+\varLambda} \neq1, \quad \mbox{for}\ 0\leq z \leq2\pi. \end{aligned}$$
(54)

Assume that constraint (54) holds. Then, from Lemma 2, we know that q 1(t) is a constant in the invariant set W. Therefore, substituting \(\dot {q}=0\), \(\ddot{q}=0\), \(q= q^{\ast}=[ q_{1}^{\ast}, q_{2}^{\ast}, q_{3}^{\ast}]^{{\mathrm {T}}}\), and τ=τ ∗ into (1) and from (50), we obtain

$$\begin{aligned} & \beta_1\sin q_1^\ast+ \beta_2 \sin\bigl(q_1^\ast+ q_2^\ast\bigr)+ \beta_3 \sin \bigl(q_1^\ast+ q_2^\ast+ q_3^\ast\bigr) =0, \end{aligned}$$
(55)
$$\begin{aligned} & k_P\varPsi^{{\mathrm {T}}}\bigl(q_3^\ast \bigr) \bigl(\overline {q}_a^{\;\ast}-q_{ar}\bigr) + \bigl(P\bigl(q^\ast \bigr)-E_r\bigr)\tau^\ast=0, \; P\bigl(q^\ast\bigr) \neq E_r, \end{aligned}$$
(56)

and τ ∗=B T G(q ∗). Therefore, as t→∞ the closed-loop solution \((q(t), \dot {q}(t))\) approaches the following equilibrium set

$$ \varOmega= \bigl\{ \bigl(q^\ast, 0\bigr)\;|\; q^\ast\mbox{ satisfies (55) and (56)}\bigr\} . $$
(57)

To summarize the above results, we give the following lemma.

Lemma 4

Consider the PAA robot given in (1). Assume the mechanical parameters of the PAA robot satisfy constraint (54). Suppose that k D satisfies (41), k P >0 and k V >0 hold. Then under controller (40), as t→∞, the closed-loop solution \((q(t), \dot{q}(t))\) approaches

$$ W=W_r\cup\varOmega, \quad\mathit{with}\ W_r \cap\varOmega= \emptyset, $$
(58)

where W r is defined in (48), Ω is the set of equilibrium points defined in (57), and ∅ denotes the empty set.

We give a remark on constraint (54).

Remark 1

Equation (54) is a constraint on the mechanical parameters of the PAA robot, which corresponds to the linear controllability at the folded equilibrium configuration of the Acrobot (degenerated from the PAA robot) whose passive first link is link 1 of the PAA robot and actuated second link is the merge of links 2 and 3 of the PAA robot with all possible relative angles. Under such a constraint, we can use Lemma 2 to analyze the motion of the PAA robot for the case of V ∗≠0.

4.2 Conditions on control gains

If Ω in (57) contains a stable equilibrium point in the sense of Lyapunov, then the PAA robot cannot be driven arbitrarily close to the UDD equilibrium point from some neighborhoods close to the stable equilibrium point. Thus, we aim at providing some conditions on the control parameter k P such that the set Ω contains no stable equilibrium points. It is easy to check that the set Ω contains at least one element of the DUU (down–up–up) equilibrium point for any given k P , where link 1 is at the downward position and links 2 and 3 are in the upright position, that is, \((q_{1}, q_{2}, q_{3}, \dot{q}_{1}, \dot{q}_{2}, \dot{q}_{3})=(-\pi, -\pi,0,0,0,0)\). We will show that if k P is sufficiently large, then Ω contains only the DUU equilibrium point, we will provide a lower bound for k P .

Define

$$\begin{aligned} &\eta_1:=\beta_1 \max_{{\scriptsize\begin{matrix} y \in[0,\pi]\cr z \in[0, 2\pi]\end{matrix}}} {\displaystyle\frac{\overline {\beta}_{2}(z)(\varPhi(y, z) + E_{r}) \sin y }{\varPhi(y, z) (y+\pi) }}, \end{aligned}$$
(59)
$$\begin{aligned} &\eta_2:=\beta_{2} \beta_{3} \max_{z \in[\pi, 2\pi]} {\displaystyle\frac{-(\beta_{1}-\overline {\beta}_{2}(z)+E_{r}) \sin z }{\overline {\beta_{2}}(z) z}}, \end{aligned}$$
(60)

where

$$\begin{aligned} \varPhi(y,z):=\sqrt{\beta_1^2 +\overline { \beta}_2^2(z)+ 2 \beta_1\overline { \beta}_2(z) \cos y} \end{aligned}$$
(61)

and \(\overline {\beta}_{2}(z)\) is defined in (16). Using the assumption E r =β 1−β 2−β 3>0, we have \(\varPhi(y,z)\geq \beta_{1}-\overline {\beta}_{2}(z)\geq E_{r}>0\) for all y and z. We present the main result of this paper with its proof in Appendix C.

Theorem 1

Consider the PAA robot given in (1). Assume the mechanical parameters of the PAA robot satisfy constraint (54) and E r >0. Suppose that k D satisfies (41), k P >0 and k V >0 hold. If k P satisfies

$$ k_{P} > \eta_1 $$
(62)

and

$$ k_P > \eta_2, $$
(63)

then under the controller (40), as t→∞, the closed-loop solution \((q(t), \dot{q}(t))\) approaches

$$ W=W_r\cup\bigl\{ (-\pi, -\pi,0,0,0,0)\bigr\} , $$
(64)

where W r is defined in (48). Moreover, the DUU equilibrium point in (64) is unstable in the closed-loop system.

We give a remark on the difference of the control for up–down–down position in this paper and the swing-up control for the up–up–up position in [25].

Remark 2

The control law for the up–down–down position is similar to that for the up–up–up position in [25] since they are obtained by using the energy-based control approach and the virtual composite link. The goal configurations of the two control laws are different, and the conditions on the mechanical parameters and control parameters for achieving the control goals are different. Indeed, to drive the PAA robot toward the UDD equilibrium point, we need to assume that E r >0 and the mechanical parameters of the PAA robot satisfy constraint (54); however, there are no such conditions on the mechanical parameters for swinging the PAA robot up to the upright equilibrium point. From a numerical example in Sect. 5.2, we can see that for a PAA robot which does not satisfy constraint (54), we fail to drive the PAA robot toward the UDD equilibrium point.

Next remark is about the stabilizing controller for balancing the PAA robot about the UDD equilibrium point.

Remark 3

The PAA robot cannot be kept at the UDD equilibrium point by the controller (40) since that point is not stable, either. When the PAA robot enters a prescribed neighborhood of that point, we need to switch the controller (40) to a local stabilizing controller to balance the PAA robot about that point. Since such a stabilizing controller can be designed, for example, by using the LQR method for the linearized model of the PAA robot around that point. This is standard and is omitted.

5 Numerical simulation results

We validated the theoretical results in this paper via two numerical examples. Here we took \(g=9.81~\mbox{m/s$^{2}$}\). From (4), the physical unit of β 1, β 2, and β 3 is J (the unit of energy). From (34), the physical value of V is J2, the physical units of k P and k D are J2 and J2 s2, respectively. From (35), the physical unit of k V is J2 s. In this paper, to show whether E−E r approaches 0 or not, we present the time response of E−E r rather than E.

5.1 Example 1: satisfaction of constraint (54) on mechanical parameters

In [22], the kip motion of a human gymnast was experimentally analyzed by using (1) for modeling the gymnast. See Table 1 for the parameters of the model in [22].

Table 1 Parameters in the model of the gymnast [22]
Full size table

For this PAA robot, we obtain β 1=289.5323 J, β 2=148.6215 J, and β 3=59.8901 J. Thus, E r =β 1−β 2−β 3>0 holds. As to constraint (54), we depict f(z) for 0≤z≤2π in Fig. 5. From Fig. 5, we know that 0<f(z)<1 holds and thus f(z)≠1 in constraint (54) holds. Moreover, we verified numerically that the UDD equilibrium point of this PAA robot is linearly controllable.

Fig. 5
figure 5

Satisfaction of constraint (54)

Full size image

For this PAA robot, the necessary and sufficient condition for avoiding the singular points given in (41) is k D >4503 J2 s2. Next, the conditions (62) and (63) on k P are k P >15863 J2 and k P >3591 J2, respectively.

We took an initial condition of

$$\begin{aligned} q_1(0)=-\pi, \qquad q_2(0)=q_3(0)=0, \qquad \dot{q}_1(0)=\dot{q}_2(0)=\dot {q}_3(0)=0, \end{aligned}$$
(65)

which is the downward equilibrium point. The simulation results under the controller (40) with

$$\begin{aligned} k_D=4550~\mbox{J}^2\,\mbox{s}^2, \qquad k_P=16000~\mbox{J}^2, \qquad k_V=5000~\mbox{J}^2\,\mbox{s} \end{aligned}$$
(66)

are depicted in Figs. 6–8.

Fig. 6
figure 6

Time responses of V and E−E r of the controller (40) for the PAA satisfying constraint (54)

Full size image

From Fig. 6, we observe that V and E−E r converge to zero. From Fig. 7, we see that link 1 is swung up close to the upright position in a large motion (vibrates by over 2π around), and q 2 and q 3 converge to −π and 0, respectively. There exists a sequence of times such that the robot is driven close to the UDD equilibrium point, which motivates the switching to the stabilizing control. These figures show that the case of V ∗=0, rather than the case of V ∗≠0, occurs, and show that the closed-loop solution \((q, \dot{q})\) approaches W r defined in (48) and there exists a sequence of times for which the PAA robot is swung up close to the UDD equilibrium point. These simulation results validated our results in Theorem 1. From Fig. 8, we observe that as a whole the magnitude of |τ 2(t)| is greater than that of |τ 3(t)| in this simulation. This supports the statement in [24] mentioned by expert gymnasts saying that “shoulders take a more important role than hips to achieve an effective swing”.

Fig. 7
figure 7

Time responses of q 1, q 2+π, and q 3 of the controller (40) for the PAA satisfying constraint (54)

Full size image
Fig. 8
figure 8

Time responses of τ 2 and τ 3 of the controller (40) for the PAA satisfying constraint (54)

Full size image

As mentioned in Remark 3, when the PAA robot enters into a prescribed neighborhood of that point, we can switch the controller (40) to a locally stabilizing controller designed by the LQR method to stabilize the PAA robot to that point,

$$ \tau=-K x, $$
(67)

where \(x =[ x_{1}, x_{2}, x_{3}, x_{4}, x_{5}, x_{6} ]^{{\mathrm {T}}}= [ q_{1}, q_{2}+\pi, q_{3}, \dot{q}_{1}, \dot{q}_{2}, \dot{q}_{3} ]^{{\mathrm {T}}}\), and the element of x i (i=1,2,3) of x is treated by modular 2π for the stabilization, and

$$K =\left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} -954.1353 & 975.5020 & 222.8941 & -236.6196 & 119.2518 & -19.0996\\ -353.4632 & 325.2489 & 147.5021 & -93.9428 & 7.4978 & 93.4635 \end{array} \right ], $$

which was computed by using the Matlab function “lqr” with the weight matrix related to state x being 10000I 6 and the weight related to the torque being I 2. The condition for switching the controller (40) to the controller (67) was taken as

$$ |x_i| < \frac{\pi}{6}, \quad |x_{i+3}|< 0.5, \quad i=1, 2, 3. $$
(68)

The time responses of q and τ of the controller (40) and the LQR controller (67) are depicted in Figs. 9 and 10. From Figs. 9 and 10, we find that the switch was taken at about t=13.38 s, and we can see that the control objective of this paper has been achieved.

Fig. 9
figure 9

Time responses of q 1, q 2+π, and q 3 of the controller (40) and the LQR controller (67) for the PAA satisfying constraint (54)

Full size image
Fig. 10
figure 10

Time responses of τ 2 and τ 3 of the controller (40) and the LQR controller (67) for the PAA satisfying constraint (54)

Full size image

We have made extensive numerical simulations for many other initial conditions for this robot, we only observed V ∗=0. From Theorem 1 in this paper, since the constraint on the robot is satisfied, if V ∗≠0, then the robot is at the DUU (down–up–up) equilibrium point which is unstable in the closed-loop system. If the initial condition of the robot is the DUU equilibrium point, theoretically, the robot will remain at that point, and the corresponding V ∗ is not zero.

Finally, for the closed-loop system of this robot and the controller (40) with the control parameters in (66), we checked the stability of the DUU equilibrium point. Direct computation yields the characteristic equation of the Jacobian matrix evaluated at DUU equilibrium point as follows:

$$\begin{aligned} s^6 - 0.2265s^5 +16.10 s^4-12.74 s^3-1000.88 s^2-1366.68 s-8640.19=0, \end{aligned}$$

which has the roots: 0.3060±6.1184j, 5.7411, −4.9394, −0.5935±2.7869j. Thus, the Jacobian matrix has three eigenvalues in the open left-half plane, and three eigenvalues in the open right-half plane. The set of initial conditions from which the robot starts will converge to the DUU equilibrium point is determined by the eigenspace of the stable eigenvalues; and the set has Lebesgue measure zero due to the existence of the unstable eigenvalues [13]. Therefore, for all initial conditions with the exception of a set of Lebesgue measure zero of this robot, under the controller (40) with the control parameters in (66), as t→∞, the closed-loop solution approaches W r defined in (48). This guarantees that there exists a sequence of times such that the robot is driven close to the UDD equilibrium point for a successful switch to the stabilizing control.

5.2 Example 2: dissatisfaction of constraint (54) on mechanical parameters

Consider the following PAA robot with its mechanical parameters shown in Table 2. For this robot, we obtain β 1=44.1450 J, β 2=3.6788 J, and β 3=1.2263 J. Thus, E r =β 1−β 2−β 3>0 holds. We verified numerically that the UDD equilibrium point of this PAA robot is linearly controllable, and E r >0 holds. However, as to (54), we depict f(z) for 0≤z≤2π in Fig. 11. From Fig. 11, we know that (54) does not hold since f(z)=1 at z=0 and z=2π. This means that the Acrobot, which is degenerated from this PAA with the angle between links 2 and 3 being 0 constantly, is not linearly controllable at its up–down equilibrium point.

Fig. 11
figure 11

Dissatisfaction of constraint (54)

Full size image
Table 2 Parameters of PAA robot
Full size table

For this PAA robot, the necessary and sufficient condition for avoiding the singular points given in (41) is k D >30.31 J2 s2. Next, the conditions (62) and (63) on k P are k P >87.73 and k P >23.06 J2, respectively. We took the same initial condition (65), and we chose k D =31 J2 s2, k P =90 J2, and k V =90 J2 s.

The simulation results under the controller (40) with the above control parameters are depicted in Figs. 12–14. From Fig. 12, we observe that neither V nor E−E r converges to zero. From Fig. 13, although q 2 and q 3 converge to −π and 0, respectively, we see that link 1 does not swing up close to the upright position (q 1=0). These show that V ∗≠0 occurs with q 1(t) being not a constant and the controller (40) failed to drive the PAA robot close to the UDD equilibrium point. From Fig. 14, we see that τ 2 and τ 3 are not equal to zero at the beginning of the control and approach 0 as t increases.

Fig. 12
figure 12

Time responses of V and E−E r of controller (40) for the PAA not satisfying constraint (54)

Full size image
Fig. 13
figure 13

Time responses of q 1, q 2+π, and q 3 of controller (40) for the PAA not satisfying constraint (54)

Full size image
Fig. 14
figure 14

Time responses of τ 2 and τ 3 of the controller (40) for the PAA not satisfying constraint (54)

Full size image

6 Conclusion

This paper studied a set-point control for a folded configuration of a PAA robot moving in the vertical plane with the first joint being passive and the other two joints being active. The control objective is to drive the PAA robot from any initial state to any small neighborhood of the UDD equilibrium point and then balance the robot about that point, which corresponds to the goal configuration of the kip motion of a gymnast on the high bar. Such a control problem has not been studied in the literature.

We used the energy-based control approach and the notion of VCL to combine links 2 and 3 into a virtual link for designing a controller and provided a global motion analysis of the PAA robot. We presented a necessary and sufficient condition for avoiding singular points in the presented controller. In this paper, we showed that the control toward such a folded configuration is more difficult than the well-known swing-up control problem. In addition to some conditions on control parameters, this paper showed that the proposed constraint on the mechanical parameters of the PAA robot guarantees the success of the proposed set-point controller. The proposed constraint guarantees the linear controllability for the folded configuration of the Acrobot (degenerated from the PAA robot), whose actuated second link is the merge of links 2 and 3 of the PAA robot with all possible relative angles. The simulation results for two PAA robots were provided to validate the effectiveness of the proposed controller and the necessity of the constraint. Specifically, for a PAA robot whose mechanical parameters do not satisfy the constraint, our numerical investigation shows that the proposed controller cannot drive the robot close to the UDD equilibrium point from some initial conditions. This paper provides some insights into the difficulty and complexity of controlling different equilibrium configurations of multi-degree-of-freedom underactuated mechanical systems beyond a fully stretched configuration related to the swing-up control.

The robust control of underactuated robotic systems with uncertainties and/or measurement noise is an interesting and challenging subject for future study. To compare with the feedback law presented in this paper, it is an interesting future subject to see how it behaves in comparison to feedforward control based on optimal control for underactuated robotic systems [18, 23].