Prediction of soliton evolution and equation parameters for NLS–MB equation based on the phPINN algorithm

Abstract

To enhance the precision and efficiency of result prediction, we proposed a parallel hard-constraint physics-informed neural networks (phPINN) by combining the parallel fully-connected neural network structure and the residual-based adaptive refinement method. We discussed the forward and inverse problems of the nonlinear Schrödinger–Maxwell–Bloch equation via the phPINN. In the forward problem, we predict five forms of soliton solutions and rogue wave dynamics under corresponding initial and boundary conditions; In the inverse problem, we predict the equation parameter using the training data with different noise intensities, initial values, and solution forms. The predicted parameters achieve a relative error of less than 1%. These results validate the effectiveness of the phPINN algorithm in solving forward and inverse problems of three-component coupled equations.

1 Introduction

Deep learning has made significant advancements in various fields, including computer vision, natural language processing, speech recognition, and recommendation systems. It has achieved or even surpassed human-level performance in tasks such as image classification, object detection, machine translation, and speech recognition, garnering extensive attention and research interest. In the domains of science and engineering, solving partial differential equations (PDEs) becomes the core of many important problems. The physics-informed neural networks (PINN) approach was introduced by Raissi et al. [1], leveraging the universal approximation theorem of neural network architecture and the widespread use of automatic differentiation technology. The PINN offers an innovative method for solving PDEs by embedding physical constraints into the training process of neural networks to approximate unknown solution functions and extract system behavior information from data. This approach not only circumvents the expensive discretization process but also handles complex boundary conditions and geometric shapes, which makes the PINN highly promising for solving PDEs [2,3,4].

In recent years, researchers have employed the PINN to solve problems in nonlinear optics by modifying network architecture, loss function expressions, and configuration point sampling methods [5,6,7,8]. Jiang et al. demonstrated the strong characterization ability of PINN in simulating pulse evolution under various physical effects [9]. Chen et al. applied PINN to solve different inverse scattering electromagnetic problems in nano-optics and metamaterial technology [10]. Lin et al. proposed a two-stage PINN method based on conserved quantities to improve prediction accuracy and generalization ability [11]. Fang et al. successfully predicted the dynamic behavior of solitons from detuned steady-state to stable locked mode [12,13,14,15].

In erbium-doped fibers, the propagation properties of optical pulses can be described by the coupled nonlinear Schrödinger–Maxwell–Bloch (NLS–MB) equation [16]

$$\begin{gathered} E_{z} = i\alpha _{1} E_{{tt}} - i\alpha _{2} \left| E \right|^{2} E + 2p \hfill \\ p_{t} = 2i\omega _{0} p + 2E\eta \hfill \\ \eta _{t} = - \left( {Ep^{*} + E^{*} p} \right) \hfill \\ \end{gathered}$$

(1)

where z and t respectively represent the normalized propagation distance and time, while complex envelope E is the slowly changing electric field, p is a measure of polarization of resonant medium, $\eta$ represents the degree of particle number inversion, and symbol * represents the complex conjugation. ${\alpha }_{1}$ and ${\alpha }_{2}$ are the group velocity dispersion parameter and Kerr nonlinearity parameters respectively, ${\omega }_{0}$ denotes the offset of the measured resonance frequency. The NLS–MB system was first proposed by Maimistov and Manykin [16] to describe the propagation of extremely short pulses in Kerr nonlinear media. This system also plays a crucial role in addressing the limited transmission distance caused by the fiber loss. This Eq. (1) possesses the mixed and coexisting state of self-induced-transparency (SIT) solitons and NLS solitons, known as SIT-NLS solitons, which has been extensively studied in fiber optic communication [17, 18].

The objective of this work is to predict soliton and rogue wave solutions under different initial and boundary conditions of the NLS–MB equation and unknown equation parameters. However, the traditional PINN encounters challenges when dealing with the coupled NLS–MB equation due to multiple coupling and nonlinear terms. The inaccurate prediction may arise from difficulties in simultaneously handling these terms and accurately modeling the interaction relationships between them. It is essential to ensure that the network accurately satisfies the initial and boundary conditions while designing suitable network structures to address coupling and nonlinear terms.

To address these challenges, we incorporate the initial condition as the hard constraint into the network structure in the forward problem. We also propose effective improvement strategies for the phPINN, including resampling training points during the training process and utilizing the residual-based adaptive refinement(RAR) method to enhance the distribution of residual training points. Specifically, for the rogue wave problem, we adjust the weights of the boundary conditions due to the sensitivity of rogue wave initial values [19]. By applying the phPINN to inverse problems, we can identify unknown equation parameters using data that is difficult or impossible to obtain. Our work demonstrates the application of phPINN in predicting unknown parameters based on various types of soliton solutions and initial parameter values for the NLS–MB equation, which proves the good applicability of the inverse problem framework of phPINN in different noise instances. The estimated parameters exhibit a relative error within 1% when compared with the true values in all test cases. The excellent prediction accuracy in our work provides more accurate numerical solutions for understanding and applying coupled NLS–MB equations, offering a promising framework for nonlinear system identification. This study helps the exploration of soliton generation, propagation, and interaction characteristics to optimize the stability and reliability of soliton transmission in the frame of the NLS–MB equation in fiber optic communication.

This article is structured as follows. Section 2 provides a concise discussion on the phPINN algorithm with a parallel fully-connected neural network(PFNN) structure and RAR residual point sampling strategy for the NLS–MB equation, including considerations on training data, loss function, optimization method, and training environment. Additionally, the algorithm flowchart and stepwise procedure of the enhanced phPINN model are presented in detail. Section 3 employs the phPINN to demonstrate the forward problem by predicting soliton solutions and rogue wave dynamics of the NLS–MB equation. Section 4 presents the inverse problem, where the phPINN is applied to predict unknown equation parameters in a set of test instances. Finally, the last section concludes all results and provides further discussion.

2 phPINN algorithm with PFNN structure and RAR residual point sampling strategy

The classical PINN algorithm has been widely utilized as a versatile and efficient deep learning framework for addressing both forward and inverse problems associated with nonlinear PDEs. However, when applying this algorithm to complicated nonlinear systems that involve intricate solitons and rogue wave solutions, several challenges may arise, including slow training speed, non-convergence of the loss function, and unsatisfactory prediction performance. To overcome these limitations, we propose the phPINN method to solve the forward and inverse problems of the NLS–MB system, and provide detailed information about the neural network structure, loss function and the specific technical considerations of the RAR residual point sampling strategy.

2.1 phPINN with PFNN structure

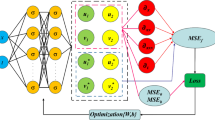
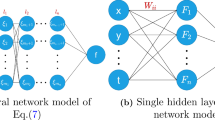
In the case of PDEs with multiple physical components, the neural network needs to output multiple variables simultaneously. The conventional approach involves constructing a large fully-connected neural network (FNN) that outputs all variables jointly. Alternatively, multiple smaller networks can be constructed with each network responsible for outputting a single component. This network structure is referred to the PFNN. Particularly, studying the complicated, multi-component coupled equation in this paper, the traditional approach with employing a large network can become excessively intricate and challenging to train. Given the significant differences among different components, using multiple small networks to output each component individually can lead to improved prediction results. Hence, we adopt the PFNN framework to address this concern.

Incorporating the hard constraint enables the embedding of known initial conditions into the neural network, ensuring that the network output automatically satisfies precise initial conditions, which greatly enhances prediction accuracy [20]. Instead of minimizing the mean squared error between the predicted and the real values at the initial time, we utilize hard constraint initial conditions, and thus there is no need to include the loss of initial conditions. Figure 1 illustrates the training process of the phPINN. Initially, we initialize the network parameters to obtain initial estimates of the real and imaginary parts of variables E, p, and η in Eq. (1). Following the initial estimation, we formulate a loss function to minimize the residuals of the PDEs, as well as the errors between the ground truth and the approximations at the boundaries. The network parameters are iteratively updated until the total loss converges.

Fig. 1

The phPINN framework structure for the NLS–MB equation, wherein we utilize five independent FNNs and enforce hard constraint initial conditions for all examples

2.2 NLS–MB system constraint

We adopt the (1 + 1) dimensional coupled NLS–MB equation as the physical constraint to construct the phPINN above. The E and p in NLS–MB Eq. (1) are the complex solutions of z and t, which will be determined subsequently, necessitating the separation of the real and imaginary components. Furthermore, η denotes the real-valued solution of z and t, determined at a later stage. We obtain the model corresponding to Eq. (1) for the phPINN as

$$ \left\{ \begin{gathered} f_{1} : = \;\alpha _{1} {\text{Re}}\left\{ {E_{{tt}} } \right\} - \alpha _{2} {\text{Re}}\left\{ E \right\}\left( {{\text{Re}}\left\{ E \right\}^{2} + {\text{Im}}\left\{ E \right\}^{2} } \right) + 2{\text{Im}}\left\{ p \right\} - {\text{Im}}\left\{ {E_{z} } \right\}, \hfill \\ f_{2} : = \;\alpha _{1} {\text{Im}}\left\{ {E_{{tt}} } \right\} - \alpha _{2} {\text{Im}}\left\{ E \right\}\left( {{\text{Re}}\left\{ E \right\}^{2} + {\text{Im}}\left\{ E \right\}^{2} } \right) - 2{\text{Re}}\left\{ p \right\} + {\text{Re}}\left\{ {E_{z} } \right\}, \hfill \\ f_{3} : = \;2{\text{Im}}\left\{ E \right\}\eta - {\text{Im}}\left\{ {p_{t} } \right\} + 2\omega _{0} {\text{Re}}\left\{ p \right\}, \hfill \\ f_{4} : = \; - 2{\text{Re}}\left\{ E \right\}\eta + {\text{Re}}\left\{ {p_{t} } \right\} + 2\omega _{0} {\text{Im}}\left\{ p \right\}, \hfill \\ f_{5} : = \;2{\text{Im}}\left\{ p \right\}{\text{Im}}\left\{ E \right\} + 2{\text{Re}}\left\{ p \right\}{\text{Re}}\left\{ E \right\} + \eta _{t} , \hfill \\ \end{gathered} \right.$$

(2)

where Re{·} and Im{·} represent the real and imaginary parts of the respective quantities.

2.3 Loss functions and optimization algorithm

Given the utilization of a hard constraint in the initial condition, the loss function employed in the optimization process does not encompass the initial condition. The specific form of the loss function is defined as

$$ Loss = w_{b} Loss_{b} + w_{f} Loss_{f} $$

(3)

where

$$ Loss_{b} = \frac{1}{{N_{b} }}\left[ {\sum\limits_{i = 1}^{{N_{b} }} {\left| {E^{i} - \hat{E}\left( {z^{i} ,t^{i} } \right)} \right|^{2} } + \sum\limits_{i = 1}^{{N_{b} }} {\left| {p^{i} - \hat{p}\left( {z^{i} ,t^{i} } \right)} \right|^{2} } + \sum\limits_{i = 1}^{{N_{b} }} {\left| {\eta^{i} - \hat{\eta }\left( {z^{i} ,t^{i} } \right)} \right|^{2} } } \right] $$

(4)

$$ Loss_{f} = \frac{1}{{N_{f} }}\left[ {\sum\limits_{j = 1}^{{N_{f} }} {\left| {f_{1} \left( {z_{f}^{j} ,t_{f}^{j} } \right)} \right|^{2} } + \sum\limits_{j = 1}^{{N_{f} }} {\left| {f_{2} \left( {z_{f}^{j} ,t_{f}^{j} } \right)} \right|^{2} } + \sum\limits_{j = 1}^{{N_{f} }} {\left| {f_{3} \left( {z_{f}^{j} ,t_{f}^{j} } \right)} \right|^{2} } + \sum\limits_{j = 1}^{{N_{f} }} {\left| {f_{4} \left( {z_{f}^{j} ,t_{f}^{j} } \right)} \right|^{2} } + \sum\limits_{j = 1}^{{N_{f} }} {\left| {f_{5} \left( {z_{f}^{j} ,t_{f}^{j} } \right)} \right|^{2} } } \right] $$

(5)

and $w_{b} ,w_{f}$ are the weights, and $\left\{ {z^{i} ,t^{i} ,E^{i} ,p^{i} ,\eta^{i} } \right\}_{i = 1}^{{N_{b} }}$ represents the input boundary value data in Eq. (2). Moreover, $\hat{E}\left( {z^{i} ,t^{i} } \right)$, $\hat{p}\left( {z^{i} ,t^{i} } \right)$ and $\hat{\eta }\left( {z^{i} ,t^{i} } \right)$ denotes the optimal output data obtained by training the neural network. The collocation points on networks $Loss_{f}$ are denoted via $\left\{ {z_{f}^{j} ,t_{f}^{j} } \right\}_{j = 1}^{{N_{f} }}$.

The phPINN algorithm employed in this study aims to identify optimized parameters, including weights, deviations, and additional coefficients in activation, to minimize the loss function. To evaluate the training errors, the relative L2-error is defined as

$$ Error = \frac{{\sqrt {\sum\limits_{k = 1}^{N} {\left| {q^{exact} \left( {X_{k} } \right) - q^{predict} \left( {X_{k} ;\overline{\Theta } } \right)} \right|^{2} } } }}{{\sqrt {\sum\limits_{k = 1}^{N} {\left| {q^{exact} \left( {X_{k} } \right)} \right|^{2} } } }} $$

(6)

where $q^{predict} \left( {X_{k} ;\overline{\Theta } } \right)$ represents the predicted solution obtained during the model training, and $q^{exact} \left( {X_{k} } \right)$ represents the exact analytical expression at point $X_{k} = \left( {t_{k} ,z_{k} } \right)$. Additionally, the joint Adam and L-BFGS algorithms are employed to optimize all loss functions in this method. The Adam optimization algorithm is a variant of the conventional stochastic gradient descent algorithm, while the L-BFGS optimization algorithm is a second-order algorithm based on quasi-Newton’s method, which performs full batch gradient descent optimization. Adam is a first-order algorithm that may not effectively optimize the error to a very small value, but its initial convergence is rapid. Therefore, we initially utilize Adam for tens of thousands of optimization steps (depending on the specific problem), and subsequently replace the optimization algorithm with L-BFGS to further reduce the error to a smaller magnitude.

2.4 Training points resample and RAR method

The phPINN primarily focuses on optimizing loss functions of PDEs to ensure the consistency of the trained network with the PDE being solved. The evaluation of losses of PDEs is performed at a set of randomly distributed residual points. From an intuitive standpoint, the influence of residual points on phPINN is similar to the impact of grid points on the Finite Element Method (FEM). Consequently, the position and distribution of these residual points are crucial for the performance of phPINN. However, previous literatures [21,22,23] about the PINN commonly employed sampling methods that neglect the significance of residual points, leading to inadequate predictive performance in unsampled regions. In this study, we propose a resampling approach for the residual training points in the network after a specific number of training iterations, allowing for the inclusion of additional points without increasing the total number of residual points to prevent the overfitting.

Although the uniform sampling proves effective for certain simple PDEs, it may not be suitable for solutions exhibiting steep gradients. To illustrate this point, let us consider rogue wave as an example. Intuitively, it is necessary to allocate more points near sharp edges to accurately capture the discontinuities. The manual selection of residual points in a non-uniform manner can enhance the accuracy, while this approach heavily depends on the specific problem and often becomes burdensome and time-consuming. Thus, in this article we focus on automatic and adaptive non-uniform sampling. Inspired by the adaptive mesh refinement technique in the FEM, Lu et al. [24] introduced the first adaptive non-uniform sampling method for PINN, known as the RAR method, which introduces new residual points in regions with large PDE residuals, iteratively adding them during training until the average residual falls below a specified threshold. By adaptively adjusting the distribution of training points throughout the training process, the RAR method further enhances the performance of phPINN.

In our approach, we perform resampling of the residual training points every 5000 training iterations, exclusively utilizing the RAR method during the training phase of the Adam optimizer. Specifically, we incorporate the 50 points with the highest residuals every 2000 iterations, resulting in a total of 5 sessions.

2.5 Training data and network environment

In the context of supervised learning, the training data plays a crucial role in effectively training neural networks. In this particular problem, we can acquire the training data from various sources, which include accurate solutions (if available), high-resolution numerical solutions (utilizing methods such as spectral methods, finite element methods, Chebfun numerical methods, discontinuous Galerkin methods, among others), as well as high fidelity datasets generated through meticulously executed physical experiments. For nonlinear systems like the NLS–MB equation, fortunately, there exist effective methods to obtain exact localized wave solutions, thereby offering a rich sample space from which training data can be extracted.

Furthermore, in our approach, we employ Xavier initialization and hyperbolic tangent (tanh) function as the activation function. In this study, a pseudorandom number generator with the PCG-64 algorithm is employed to generate residual training points [25]. All codes in this article are developed using the DeepXDE library [24], implemented in Python 3.10 and Tensorflow 2.10. The numerical experiments presented herein are executed on a computer system equipped with a 12th Gen Intel (R) Core (TM) i7-12,700 processor, 16 GB of memory, and a 6GB Nvidia GeForce RTX 2060 graphics card.

3 Prediction of soliton evolution for NLS–MB Equation

In this section, we focus on solving the forward problems associated with NLS–MB equation, namely the prediction of soliton evolution, considering a hard constraint initial condition and Dirichlet boundary conditions through the utilization of the aforementioned phPINN algorithm. The NLS–MB equation, subject to the specified initial and boundary conditions, can be expressed as

$$ \left\{ \begin{aligned} \quad \quad E_{z} = & i\alpha_{1} E_{tt} - i\alpha_{2} \left| E \right|^{2} E + 2p,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; \\ \,\quad \quad p_{t} = & 2i\omega_{0} p + 2E\eta ,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \,\quad \quad \eta_{t} = & - \left( {Ep^{*} + E^{*} p} \right),\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; \\ E\left( {L_{0} ,z} \right) = & E^{lb} (z),p\left( {L_{0} ,z} \right) = p^{lb} (z),\eta \left( {L_{0} ,z} \right) = \eta^{lb} (z),\quad \quad \quad \quad \quad \quad \; \\ E\left( {L_{1} ,z} \right) = & E^{ub} (z),p\left( {L_{1} ,z} \right) = p^{ub} (z),\eta \left( {L_{1} ,z} \right) = \eta^{ub} (z),\quad \quad \quad \quad \quad \quad \\ E\left( {t,T_{0} } \right) = & E^{0} (t),p(t,T_{0} ) = p^{0} (t),\eta \left( {t,T_{0} } \right) = \eta^{0} (t),z \in \left[ {L_{0} ,L_{1} } \right],t \in \left[ {T_{0} ,T_{1} } \right] \\ \end{aligned} \right. $$

(7)

where "i" is an imaginary number, the subscript represents the partial derivative of each quantities with respect to space z and time t, $L_{0}$ and $L_{1}$ represent the upper and lower boundaries of time t, and $T_{0}$ and $T_{1}$ represent the initial time and final time of the spatial variable z, respectively. Furthermore, $\cdot^{0} (t)$ represents the initial value at $\cdot = T_{0}$, while $\cdot^{lb} (z)$ and $\cdot^{ub} (z)$ correspond to the lower and upper boundaries of $t = L_{0}$ and $t = L_{1}$, respectively.

3.1 Bright-M-W shaped one soliton

Set the parameters $\alpha_{1} = \frac{1}{2}$, $\alpha_{2} = - 1$ and $\omega_{0} = - 1$, the bright-M-W shaped one soliton solution of the NLS–MB Eq. (1) is given by [26]

$$ \begin{gathered} E(z,t) = \frac{2\exp ( - 2it)}{{\cosh (2t + 6z)}}, \hfill \\ p(z,t) = \frac{{\exp ( - 2it)\left\{ {\exp ( - 2t - 6z) - \exp (2t + 6z)} \right\}}}{{\cosh (2t + 6z)^{2} }}, \hfill \\ \eta (z,t) = \frac{{\cosh (2t + 6z)^{2} - 2}}{{\cosh (2t + 6z)^{2} }}. \hfill \\ \end{gathered} $$

(8)

To obtain the original training dataset for the specified initial and boundary conditions, the spatial region [− 2, 2] and the temporal region [− 3, 3] are discretized into 512 points, and the exact bright-M-W shaped one soliton solution is discretized accordingly. These data will be used to calculate the relative L2-error. Furthermore, by randomly selecting the boundary data points ${N}_{b}$ = 100 from the original dataset, a smaller training set containing boundary data is generated. The initial value of the number of PDE residual training points is ${N}_{f}$ = 20,000. With 30,000 iterations using the Adam optimizer and an additional 11,563 iterations using the L-BFGS optimizer, the phPINN framework successfully learns the bright-M-W shaped one soliton utilizing five subnetworks. The network achieves a relative L2 error of E as 9.158e−03, p as 9.960e−03, η as 2.603e−03, with a total of 41,563 iterations and a training time of 2839 s.

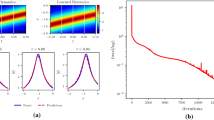
Figure 2 illustrates the deep learning results of bright-M-W shaped solitons based on the NLS–MB equation using the phPINN. Figures 2A and B demonstrate the propagation of a soliton from left to right along the t-axis, indicating that the soliton’s amplitude remains constant over time. Figures 2C and D present cross-sectional views of the predicted and exact solutions generated by phPINN at different time. It can be observed that the predicted solution closely matches the exact solution. Figure 2F shows that the error in the prediction solution gradually adds with the evolution, with a maximum value of only 0.087 at t = 3. Figure 2E displays the oscillatory behavior of the loss function curve during optimization using Adam, while L-BFGS exhibits linear convergence. The final loss value drops to 3.339e−07. Additionally, we compare and present the prediction results of the standard PINN from reference [1] in Fig. 3. From Fig. 3, it can be observed that the prediction results of the standard PINN are not satisfactory, indicating the superiority of our phPINN framework for the given example.

Fig. 2

Prediction results of bright-M-W shaped one soliton. A Exact solution, B predicted solution. The comparison between the exact (solid curve) and predicted (dash curve) solutions at C t = − 2 and D t = 2. E The Loss function curve obtained through the combined usage of the Adam and L-BFGS optimization algorithms. F The point-by-point absolute error between the predicted and exact solutions

Fig. 3

A Predicted solution of standard PINN for the bright-M-W shaped one soliton. B The comparison between the exact (solid curve) and predicted (dash curve) solutions at time t = − 2

3.2 Bright-bright-dark one soliton

Considering the NLS–MB Eq. (1) with the parameter values $\alpha_{1} = \frac{1}{2}$, $\alpha_{2} = - 1$ and $\omega_{0} = 1$, the bright-bright-dark one-soliton solution can be derived as [26]

$$ \begin{aligned} E(z,t) = & \frac{{2\exp \left( { - \frac{2}{5}i(5t - 2z)} \right)}}{{\cosh \left( {2t + \frac{22}{5}z} \right)}}, \\ p(z,t) = & \frac{{ - \frac{1}{5}i\exp \left( { - \frac{2}{5}i(5t - 2z)} \right)\left\{ {( - 2 + i)\exp \left( { - 2t - \frac{22}{5}z} \right) - (2 + i)\exp \left( {2t + \frac{22}{5}z} \right)} \right\}}}{{\cosh \left( {2t + \frac{22}{5}z} \right)^{2} }}, \\ \eta (z,t) = & \frac{{5\cosh \left( {2t + \frac{22}{5}z} \right)^{2} - 2}}{{5\cosh \left( {2t + \frac{22}{5}z} \right)^{2} }}. \\ \end{aligned} $$

(9)

In a similar manner, the spatiotemporal region is defined as [− 2, 2] × [− 3, 3]. The soliton is discretized into a grid of 512 × 512 data points, which includes the initial boundary value conditions. The selection method and quantity of dataset are consistent with those in Sect. 3.1. Furthermore, the initial number of residual training points for the equation is set to 20,000. By conducting 30,000 Adam iterations and 8832 L-BFGS iterations, bright-bright-dark solitons are effectively learned. The network achieves a relative L2 error of E as 1.871e−03, p as 2.626e−3, and η as 6.669e−04. The total number of iterations is 38,832, with a training time of 2057 s.

Figure 4 presents the deep learning results of bright-bright-dark one soliton based on the NLS–MB equation using the phPINN. The three-dimensional prediction dynamics diagrams 4A–C demonstrate the propagation of solitons along the t-axis, indicating that the soliton’s amplitude remains constant over time t. Cross-sectional views of the predicted and exact solutions generated by phPINN at different time are depicted in Figs. 4D and E. It can be observed that the predicted solutions align well with the exact solutions. The density plot and the corresponding peak scale plot in Fig. 4F illustrate the point-by-point absolute error dynamics, where it is evident that the maximum error value does not exceed 0.02.

Fig. 4

Prediction results of the bright-bright-dark one soliton. A–C The three-dimensional evolution diagram of the predicted solution. The comparison between the predicted results (dash curve) and the exact solution (solid curve) at D t = − 2 and E t = 2. (F) Point-by-point absolute error between the predicted and exact solutions

3.3 Two solitons

Assuming parameters $\alpha_{1} = 1$, $\alpha_{2} = - 2$, and $\omega_{0} = 1$, the explicit double soliton solution can be found in Eq. (16) of reference [27]. Specifically, we select parameters ${w}_{1}$ = 1 + 0.5i, ${w}_{2}$ = 1 − 0.5i, ${\theta }_{10}$ = 1 and ${\theta }_{20}$ = 1. To obtain the original training dataset of double solitons, we divide the spatial region [− 5, 5] and the temporal region [− 5, 5] into 512 points each, which will be used to calculate the relative L2-error. Furthermore, considering the complexity of the solution, we increase the number of data points on the boundary by randomly selecting ${N}_{b}$ = 200 from the original dataset, and generate a training dataset that includes boundary data. The initial number of residual training points for the equation is also increased to ${N}_{f}$ = 25,000. With 30,000 Adam iterations and a weight ${w}_{b}$ = 100 for the boundary condition in the loss function, followed by 14,810 L-BFGS iterations, the double soliton interaction solution is successfully learned. The network achieves a relative L2-error of E as 2.651e−03, p as 2.739e−03, and η as 7.598e−04. The total number of iterations is 44,810.

Figure 5 illustrates the deep learning results of the interaction between two solitons in the NLS–MB equation using the phPINN approach. Specifically, Figs. 5A, B and D depict density plots and corresponding peak scales for different dynamics, including precise dynamics, predictive dynamics, and absolute error dynamics, respectively. These plots demonstrate the head-on interaction between two bidirectional solitons. Bright solitons for E and p can be observed, while, dark soliton for η can be observed. After the interaction, the solitons maintain their shapes unchanged except for a phase shift, with a maximum error of 0.008. Figure 5C displays the change of the loss function, which eventually decreases to 2.137e−07.

Fig. 5

Prediction results of two solitons. A Exact solution, B predicted solution, C loss function curve using the combined Adam and L-BFGS optimization algorithm, D point-by-point absolute error between the predicted and exact solutions

3.4 Bound-state solitons

Assuming parameters $\alpha_{1} = 1$, $\alpha_{2} = - 2$ and $\omega_{0} = 1$, the exact bound-state solution is obtained as described in Eq. (16) of reference [23]. Here the parameters ${w}_{1}$ = 1, ${w}_{2}$ = 0.4, ${\theta }_{10}$ = 0 and ${\theta }_{20}$ = 0 are selected. The dataset selection method and quantity for bound-state solitons are the same as those in Sect. 3.3, and the initial number of residual training points for the equation is also set to 25,000. By conducting 30,000 Adam iterations and 22,948 L-BFGS iterations, the phPINN successfully learn the bound-state solitons. The network achieves a relative L2 error of E: 3.649e−03, p: 3.707e−03, and η: 1.115e−03. The total number of iterations performed was 52,948.

Figure 6 illustrates the deep learning results of the bound-state solitons for the NLS–MB Eq. (1) using the phPINN approach. Both the precise dynamics in Fig. 6A and the predicted dynamics in Fig. 6B indicate the existence of bound-state solitons when two solitons have the same velocity. Figure 6C presents a cross-sectional view of the corresponding predicted and exact solutions generated by phPINN at time t = − 1. It can be observed that the predicted solutions align well with the exact solutions. Figure 6D depicts the point-by-point absolute error between the predicted and exact solutions, where the maximum error value does not exceed 0.01.

Fig. 6

Prediction results of bound-state solitons. A Exact solution, B predicted solution, C comparison of predicted results (dash curve) with exact solutions (solid curve) at t = − 1, and D point-by-point absolute error between the predicted and exact solutions

3.5 Rogue waves

Rogue waves are a significant research area within the field of ocean dynamics and nonlinear optics. Machine learning methods have also been extensively studied for their application to rogue waves [19, 28, 29]. In fact, the phPINN demonstrates enhanced convergence speed of the loss function, improved stability, and superior approximation capabilities, and thus enables accurate prediction of these rare and unusual wave phenomena.

Assuming parameters $\alpha_{1} = \frac{1}{2}$, $\alpha_{2} = - 1$ and $\omega_{0} = \frac{1}{2}$, the exact solution of rogue wave can be found in Eqs. (6)–(8) of reference [30] with here considering the specific choices d = 1 and b = 1.5. By randomly selecting boundary data points ${N}_{b}$ = 200 from the original dataset, a reduced training dataset that includes boundary information is generated. Notably, for rogue waves, the weight ${w}_{b}$ of boundary conditions is increased to 1000 in the loss function, and the initial number of residual training points ${N}_{f}$ is set to 25,000. Employing 30,000 Adam iterations and 20,589 L-BFGS iterations, the phPINN successfully predicts rogue wave solutions. The network achieves relative L2 errors of E as 7.698e−04, p as 7.830e−04, and η as 2.580e−03. The total number of iterations is 50,589, which indicates the additional computation required to capture the complicated localized wave behaviors.

Figure 7 presents the deep learning results for rogue wave solutions of the NLS–MB Eq. (1) using the phPINN. E represents a typical rogue wave, while p and η corresponds to the dark rogue wave. Comparing Fig. 7A with Fig. 7B, we hardly observe their difference between the predicted and exact solutions. Figure 7C displays the convergence behavior of the loss function, which eventually reaches a value of 1.475e-05. The maximum point-by-point absolute error shown in Fig. 7D is 0.023.

Fig. 7

Prediction results of rogue waves. A Exact solution, B predicted solution, C loss function curve using the combined Adam and L-BFGS optimization algorithm, D point-by-point absolute error between the predicted and exact solutions

By extensive numerical training, we have demonstrated that this phPINN algorithm performs exceptionally well in describing relatively smooth solutions and effectively learns complicated dynamic behaviors of rogue wave solution. Table 1 summarizes the results obtained from solving various forward problems of the NLS–MB equation using the phPINN.

Table 1 Results of solving different forward problems of NLS–MB equation using the phPINN

4 Prediction of equation parameters for NLS–MB Equation

In this section, we focus on the inverse problem of the NLS–MB equation, specifically the parameter estimation of the NLS–MB equation using small training datasets. To learn the unknown parameters ${\alpha }_{1},{\alpha }_{2}$ and ${\omega }_{0}$ in Eq. (1), we employ the same phPINN framework as described in Sect. 3. Firstly we utilize the bright-bright-dark one soliton as our dataset. One advantage of the phPINN algorithm for the inverse problem is its ability to work with very small training datasets. Therefore, we consider data within the range t ∈ [0, 1] and z ∈ [− 1, 1], and then randomly extract ${N}_{q}$ = 2000 data points from the original dataset to form a small training dataset. The equation residual is computed by using the ${N}_{f}$ = 10,000 points generated by the pseudorandom method. After preparing the training dataset, the unknown parameters $\alpha_{1} ,\alpha_{2}$ and ${\omega }_{0}$ are all initialized to 2.0. Following 20,000 Adam iterations and additional L-BFGS iterations, all learnable parameters of the phPINN are optimized, and the loss function is adjusted to predict the unknown parameters $\alpha_{1} ,\alpha_{2}$ and ${\omega }_{0}$. The relative error of unknown parameters is defined as

$${\text{RE}} = \left| {\frac{{\delta - \delta }}{\delta }} \right| \times 100\%$$

(10)

where $\widehat{\delta }$ and $\delta$ represent the predicted and true values, respectively. In this section, we introduce the noise interference to the selected small dataset as follows.

$$ Data\, = \,Data\, + \,noise*np.std(Data)*np.random.randn(Data.shape\left[ 0 \right],Data.shape[1]) $$

Where, Data refers to the selected dataset, and noise represents the intensity of the noise. The function np.std(·) calculates the standard deviation of array elements, and np.random.randn(·,·) generates a set of samples with a standard normal distribution.

Figure 8 illustrates our prediction results. Figure 8A shows the randomly selected 2000 points (marked with “x” symbols) in each component to constitute the dataset. Figure 8B presents the convergence of the loss curve under different noise conditions by utilizing both Adam and L-BFGS optimizers. The minimum value of the loss function increases with the amount of noise. Figures 8C–E depict the numerical variations of the unknown parameters α₁, α₂, and ω₀, respectively. The shadow represents the error range of ± 10%, the dotted line and solid curve represent the true value and learned parameters, respectively. It can be observed that the phPINN framework accurately predicts the unknown parameters under different noise conditions, which demonstrates its robustness to noise. Figure 8F displays the relative error of the learned parameter. In general, the error increases with increasing noise but remains below 1% in all cases.

Fig. 8

Parameter estimation results of NLS–MB equation by using the bright-bright-dark one soliton as dataset. A selected points (marked with “x” symbols) of solitons in t ∈ [0,1] to form the dataset, B the loss function under different noise conditions. The evolution of the unknown parameters of the NLS–MB equation during the training process under noise levels of C 0%, D 5%, and E 10%, respectively. F Error results of parameter under different noise conditions

Next, we explore the parameter estimation capability under different datasets. We select the rogue waves solution as the dataset and employ the same sampling method as used for the one soliton solution mentioned above. Notably, we set different initial values for the parameters under various noise conditions to test the parameter inversion ability of the phPINN framework. Figure 9 presents our prediction results. Figure 9A shows the randomly selected 2000 points (marked with “x” symbols) in each component to form the training dataset. Figure 9B shows the convergence of the loss curve under different noise conditions by utilizing both the Adam optimizer and the L-BFGS optimizer. The minimum value of the loss function adds with the increasing noise. Figure 9C–E illustrate the numerical variations of the unknown parameters α₁, α₂, and ω₀, respectively. The shadow, dotted line, and solid line have the same interpretations as those in Fig. 8. It is evident that the phPINN framework accurately predicts the unknown parameters under different noise conditions, which also demonstrates its robustness in this scenario. Figure 9F illustrates the relative error of the final learned parameter. Generally, the error increases with the level of noise but remains below 1% in all cases. These results demonstrate the satisfactory performance of the phPINN, incorporating both the PFNN structure and the RAR method, in addressing the inverse problem of the NLS–MB system.

Fig. 9

Parameter estimation results of NLS–MB equation by using the rogue wave solution as the dataset. A selected points (marked with “x” symbols) of rogue wave to form the dataset, B the loss function under different noise conditions. The evolution of the unknown parameters of the NLS–MB equation during the training process under noise levels of C 0%, D 5%, and E 10%, respectively. F Error results of parameter under different noise conditions

In summary, this section presents the results and corresponding analysis of the phPINN to study the inverse problem of the NLS–MB equation under different conditions. The utilization of a pre-trained network can reduce the training time for similar variant problems. However, its effectiveness may vary depending on the specific scenario. In this work, we implement the inverse problem of two examples from scratch without relying on a pre-trained network, which highlights the inherent generalizability of this phPINN framework.

5 Conclusion

Utilizing the phPINN algorithm with PFNN structure and RAR residual point sampling strategy, this study presents the forward and inverse problems of coupled NLS–MB equations. Based on the numerical evidence presented in this article, the phPINN framework is an effective approach for predicting solutions of the NLS–MB equation, encompassing single solitons, multiple solitons, and rogue waves, even with a small sample dataset. The analysis of the absolute error graph revealed that the errors associated with solitons primarily concentrated in the farthest region from the initial moment, while errors related to rogue waves were concentrated in the sharp regions. Moreover, the phPINN algorithm successfully addresses the parameter estimation problem associated with the NLS–MB equation, showcasing its capability in accurately retrieving parameters under diverse conditions, including variations in data types, noise levels, and initial values. These findings provide essential theoretical foundations and numerical experiences for conducting more specialized research on the NLS–MB equation [31, 32]. The future work is mainly to optimize our algorithm and apply it to more complex nonlinear systems. It is foreseeable that our work will continue to play an important role in the field of nonlinear dynamics, potentially leading to novel breakthroughs and advancements in this domain.