1 Introduction

The nonlinear Schrödinger equation (NLSE) is

$$\begin{aligned} i Q_{t}+Q_{x x}+2|Q |^{2} Q=0, \quad (x, t) \in {\mathbb {R}}^{2}, \end{aligned}$$
(1)

where Q(x, t) are complex-valued solutions. Equation (1) describes the optical pulse propagation when the pulse width is greater than 100 femtosecond, such as in nonlinear optics [1], plasmas [2], fluid mechanics [3], and ocean [4]. The NLSE was first introduced by Hull et al. [5] as a model for superfluid helium behavior, but its importance was not fully realized until the development of optical fiber communication technology in the 1970 s. With some further research undergoing, the NLSE can only describe the nonlinear behavior in continuous media and cannot handle the discrete nonlinear phenomena in discrete systems. Therefore, Mio et al. [6] introduced the discrete time derivative term in NLSE and then put forward the derivative nonlinear Schrödinger equation (DNLS). Kaup and Newell [7] solved the appropriate inverse scattering problem and obtained the single soliton solution of DNLS. Xiang et al. and Jia et al. [8, 9] obtained the breather, soliton, and rogue wave solutions of coupled DNLS using the Darboux transformation. However, with the deep study of physical phenomena, researchers began to realize that the low-order nonlinear Schrödinger equation could not completely describe all phenomena. For ultrashort pulse systems (e.g., electron dynamics of graphene nanoring [10], ranging systems [11]), high-order dispersion and nonlinear effects are the key influential factors in the propagation of sub-picosecond or femtosecond pulses [12, 13]. The dynamics of such systems are described by the high-order nonlinear Schrödinger equation (HNLSE). The third-order NLS equation (alias the Hirota equation [14]) is a basic HNLSE physical model, and it is completely integrable. In recent decades, many scholars have spent a great deal of time and done a lot of work studying the Hirota equation. Zhang and Yuan [15] studied the defocusing Hirota equation, constructed the Nth-iterated binary Darboux transformation by the limit technique, derived multi-dark soliton solutions from the nonzero background, and discussed the properties of dark solitons. By using the Hirota bilinear method, Zuo et al. [16] obtained the higher-order solutions of the generalized Hirota equation and the exact solutions of the S-symmetric, T-symmetric, and ST-symmetric nonlocal Hirota equations. Hao and Zhang [17] studied the interaction of different types of solitons and gave the corresponding approximate eigenvalue and interaction period formula. Recently, richer solutions and new physical phenomena of the Hirota equation and its variants have been revealed by various methods [18,19,20,21,22].

In recent years, with the explosion of data volume and the rapid development of computer hardware, deep learning algorithms represented by neural networks have achieved brilliant results in computer vision [23], natural language processing [24], reinforcement learning [25], and so on. Thus, some scholars use neural networks to solve partial differential equations (PDEs) [26,27,28]. Compared with traditional numerical methods, neural networks do not need to grid generation the solution region, and more importantly, they can handle high-dimensional PDEs [29, 30]. However, pure data-driven algorithms often have poor robustness, cannot guarantee the convergence of the algorithm, and lack physical interpretability. For this reason, some researchers utilize the Gaussian process regression method to solve PDE [31]. But the Gaussian process itself has some limitations [32]. Therefore, Raissi et al. [33,34,35] proposed a physics-informed neural network method (PINN), which embeds known physical prior knowledge into the network for learning. Specifically, the control equation is used as part of the loss function, and then, the network is trained using the general approximation ability of the neural network [36] and automatic differentiation (AD) techniques [37]. PINN has been successfully applied to complex problems in computational science and engineering, such as cardiovascular systems [38], finance [39], and turbulence [40]. Particularly, for integrable equations, Fang et al. [41] designed a conservation law constrained PINN method. They used the law of conservation of energy and the law of conservation of momentum to constrain the loss function of PINN and studied the soliton solutions and rogue wave solutions of the NLSE, Korteweg–de Vries, and modified Korteweg–de Vries equations. However, for HNLSE with higher-order dispersion and nonlinear effects, there are not given the corresponding conservation laws combined with neural networks for solving. Zhou and Yan [42] used the original PINN to solve the forward and inverse problems of the Hirota equation, but it requires a large number of collocation points. Bai [43] utilized the PINN with a local adaptive activation function to obtain the bright soliton solution and rogue wave solution of the Hirota equation, yet it needs more iterations. Inspired by these works, to predict data-driven of the Hirota equation with less data, we propose an improved PINN (IPINN) method embedded with energy conservation laws, which is constructed by utilizing the Lax pair formulation. We will mainly focus on the bright soliton solution and the rogue wave solution, and parameter inversion of the Hirota equation simulated by using the IPINN method. In short, the main contributions of this paper are as follows:

  1. (1)

    The energy conservation law of the Hirota equation is derived using Lax pairs and embedding into the traditional neural network to impose stricter constraints on the loss function of the network, which improves the performance of the traditional PINN with less training data;

  2. (2)

    Compared with the traditional PINN method, the new IPINN method can more accurately predict the bright soliton solution, the rogue wave solution, the second-order term, the third-order term coefficients, and the parameters contained in the third-order term;

  3. (3)

    For the rogue wave solution, the influences of noise and network structure on the IPINN method are also investigated, and the results show that IPINN can also predict the behavioral changes of the rogue wave solution under noisy data well.

This paper is organized as follows. In Sect. 2, the energy conservation law for the Hirota equation is constructed through Lax pair and embed into the IPINN method. In Sect. 3, the bright soliton solution and the rogue wave solution of the Hirota equation are obtained by the IPINN method and compared with the traditional PINN method’s, and the robustness of the IPINN method is discussed under different number of network layers, each hidden layer neurons, sampling points, and noises. In Sect. 4, the unknown parameters in Hirota equation are identified by the proposed method. Finally, the conclusion is given in Sect. 5.

2 Methodology

In this section, we consider the Hirota equation along with Dirichlet boundary conditions given by

$$\begin{aligned} \left\{ \begin{array}{l} i Q_{t}+\alpha (Q_{x x}+2|Q |^{2} Q)+i \beta (Q_{x x x}+6|Q |^{2} Q_{x})=0, \\ x \in (-L, L), t \in (t_{0}, t_{1}), \\ Q(x, t_{0})=Q_{0}(x), x \in [-L, L], \\ Q(-L, t)=Q(L, t), t \in [t_{0}, t_{1}], \end{array}\right. \end{aligned}$$
(2)

where \(i=\sqrt{-1}\). \(-L\) and L represent the upper and lower boundaries of the spatial domain x, respectively. \(t_{0}\) and \(t_{1}\) denote the start time and end time of the time domain t, respectively. Q(x, t) is a complex envelope field. Assume \(Q(x, t)=u(x, t)+i v(x, t)\), where u(x, t) and v(x, t) are the real and imaginary parts of Q(x, t), respectively. \(\alpha \) represents the group velocity dispersion coefficient, and \(\beta \) denotes the third-order dispersion coefficient. We solve Eq. (2) in terms of the real and imaginary parts and define

$$\begin{aligned}{} & {} -v_{t}+\alpha (u_{x x}+2(u^{2}+v^{2}) u)\nonumber \\{} & {} \quad -\beta (v_{x x x}+6(u^{2}+v^{2}) v_{x})=0, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} u_{t}+\alpha (v_{x x}+2(u^{2}+v^{2}) v)\nonumber \\{} & {} \quad +\beta (u_{x x x}+6(u^{2}+v^{2}) u_{x})=0. \end{aligned}$$
(4)

Next, the deep neural network is used to approximate the solutions of Eqs. (3) and (4), and then, the governing equation is embedded into the network. The derivative of the solution to time and space is obtained by using AD technique. Specifically, we define the residual networks \(f_{u}(x, t)\) and \(f_{v}(x, t)\), which are given by the left-hand side of Eqs. (3) and (4), respectively

$$\begin{aligned} f_{\hat{u}}:= & {} -\hat{v}_{t}+\alpha (\hat{u}_{x x}+2(\hat{u}^{2}+\hat{v}^{2}) \hat{u})\nonumber \\{} & {} \quad -\beta (\hat{v}_{x x x}+6(\hat{u}^{2}+\hat{v}^{2}) \hat{v}_{x}), \end{aligned}$$
(5)
$$\begin{aligned} f_{\hat{v}}:= & {} \hat{u}_{t}+\alpha (\hat{v}_{x x}+2(\hat{u}^{2}+\hat{v}^{2}) \hat{v})\nonumber \\{} & {} \quad +\beta (\hat{u}_{x x x}+6(\hat{u}^{2}+\hat{v}^{2}) \hat{u}_{x}). \end{aligned}$$
(6)

where \(N_{u}\) and \(N_{v}\) are nonlinear operators consisting of functions of real-valued solutions and functions of spatial derivatives, respectively.

Next, we will adopt the Lax pair [44] to construct the infinitely many conservation laws for Eq. (2) as the following forms:

$$\begin{aligned} \Phi _{x}=U \Phi , \Phi _{t}=V \Phi , \end{aligned}$$
(7)

where \(\Phi =(\Phi _{1}, \Phi _{2})^{T}\) is the eigenfunction (the symbol “T” represents the transpose of the vector), \(\Phi _{1}\) and \(\Phi _{2}\) are the functions of x and t, and U and V are specifically in the form of

$$\begin{aligned} U= & {} \left( \begin{array}{cc} \lambda &{} Q^{*} \\ Q &{} -\lambda \end{array}\right) , \end{aligned}$$
(8)
$$\begin{aligned} V= & {} \left( \begin{array}{cc} A &{} B^{*} \\ B &{} -A \end{array}\right) , \end{aligned}$$
(9)

with

$$\begin{aligned} \left\{ \begin{array}{l} A=-i|Q |^{2}+\beta Q^{*} Q_{x}-\beta Q Q_{x}^{*}-2 i \lambda \beta |Q |^{2}+2 i \lambda ^{2}+4 i \lambda ^{3} \beta , \\ B=-Q_{x}-i \beta Q_{x x}-2 i \beta |Q |^{2} Q+\lambda [-2 \beta Q_{x}+2 i Q]+4 i \lambda ^{2} \beta Q, \end{array}\right. \end{aligned}$$
(10)

where \(\lambda \) is a complex eigenvalue parameter, and the symbol “*” denotes to the complex conjugation. Further, based on Eq. (7), introduce the fractional function \(\Gamma =\Phi _{2} / \Phi _{1}\). We can obtain the following Riccati equation:

$$\begin{aligned} \Gamma _{x}=i Q-2 i \lambda \Gamma -i Q^{*} \Gamma ^{2}. \end{aligned}$$
(11)

Then, setting [45]

$$\begin{aligned} \Gamma =\sum _{m=1}^{\infty } \gamma _{m} \lambda ^{-m}, \end{aligned}$$
(12)

substituting Eq. (12) into Eq. (11), and letting the coefficients of the same power of \(\lambda \) equal zero, we can get

$$\begin{aligned} \left\{ \begin{array}{l} \gamma _{1}=\frac{1}{2} Q \\ \gamma _{2}=\frac{1}{4} i Q_{t}, \\ \gamma _{3}=\frac{1}{8}(-|Q |^{2} Q-Q_{x x}) \\ \vdots \\ \gamma _{n+1}=\frac{i}{2}(\gamma _{n, t}+i Q \sum _{k=0}^{n-1} \gamma _{k} \gamma _{n-k}),(n=2,3, \ldots ), \end{array}\right. \end{aligned}$$
(13)

where \(\gamma _{m}{ }^{\prime } s(m=1,2,3, \ldots )\) are the functions of x and t to be determined. Using, compatibility conditions \((\ln \Phi _{1})_{x t}=(\ln \Phi _{1})_{t x}\), we can obtain

$$\begin{aligned} (i \lambda +i Q^{*} \Gamma )_{t}=(A+B \Gamma )_{x}. \end{aligned}$$
(14)

Similarly, substituting Eqs. (10), (12), and (13) into Eq. (14) and collecting the coefficients of the same power of \(\lambda \), we can yield the infinitely many conservation laws for Eq. (2) as follows:

$$\begin{aligned} \frac{\partial }{\partial t} \Gamma _{m}+\frac{\partial }{\partial x} \Theta _{m}=0, \end{aligned}$$
(15)

with

$$\begin{aligned} \left\{ \begin{array}{l} \Gamma _{1}=\frac{1}{2} i|Q |^{2}, \\ \Theta _{1}=\frac{1}{2}[\alpha (Q Q_{x}-Q Q_{x}^{*})-i \beta (Q_{x} Q_{x}^{*}-Q^{*} Q_{x x}-Q Q_{x x}^{*}-3|Q |^{4})], \\ \Gamma _{2}=-\frac{1}{4} Q^{*} Q_{x}, \\ \Theta _{2}=\frac{1}{4}[i \alpha (|Q |^{4}-Q_{x} Q_{x}^{*}+Q^{*} Q_{x x})-\beta (6 Q^{*} Q_{x}|Q |^{2} \\ -Q_{x}^{*} Q_{x x}+Q_{x} Q_{x x}^{*}+Q^{*} Q_{x x x})] \\ \vdots \\ \Gamma _{l}=i Q^{*} \gamma _{x}, l=3,4, \ldots , \\ \Theta _{l}=[i \beta Q_{x x}^{*}-\alpha Q_{x}^{*}+2 i \beta Q^{*}|Q |^{2}] \gamma _{l}-2[i \alpha Q^{*}+\beta Q_{x}^{*}] \gamma _{l+1} \\ -4 i \beta Q^{*} \gamma _{l+2}, \end{array}\right. \end{aligned}$$
(16)

where \(\Gamma _{m}{ }^{\prime } s\) and \(\Theta _{m}{ }^{\prime } s\) are the conserved densities and conserved fluxes, respectively. Substituting \(\Gamma _{1}\) and \(\Theta _{1}\) into Eq. (15), we can obtain the energy conservation law of Eq. (2), which can be described as

$$\begin{aligned}{} & {} i[u u_{t}+v v_{t}+\alpha (u v_{x x}-v u_{x x})+\beta (u u_{x x x}+v v_{x x x}\nonumber \\{} & {} \quad +6(u^{2}+v^{2})(u u_{x}+v v_{x}))]=0. \end{aligned}$$
(17)

In the following, the real and imaginary parts of Eq. (17) are separated and defined as

$$\begin{aligned} f_{E C_{-} \hat{u}}:= & {} 0, \end{aligned}$$
(18)
$$\begin{aligned} f_{E C_{-} \hat{v}}:= & {} \hat{u} \hat{u}_{t}+\hat{v} \hat{v}_{t}+\alpha (\hat{u} \hat{v}_{x x}-\hat{v} \hat{u}_{x x})+\beta (\hat{u} \hat{u}_{x x x}+\hat{v} \hat{v}_{x x x}\nonumber \\{} & {} \quad +6(\hat{u}^{2}+\hat{v}^{2})(\hat{u} \hat{u}_{x}+\hat{v} \hat{v}_{x})). \end{aligned}$$
(19)

Now, we can give the loss function for solving Eq. (2) using IPINN specifically as follows:

$$\begin{aligned} Loss=Loss_{\hat{i}}+Loss_{\hat{b}}+Loss_{\hat{f}}+Loss_{\hat{c}}, \end{aligned}$$
(20)

where

$$\begin{aligned} \left\{ \begin{array}{l} Loss_{\hat{i}}=\frac{1}{N_{0}} \sum _{i=1}^{N_{0}}(\mid \hat{u}(x_{u}^{i}, t_{u}^{i})-u^{i}\mid ^{2}+\mid \hat{v}(x_{v}^{i}, t_{v}^{i})-v^{i}\mid ^{2}), \\ Loss_{\hat{b}}=\frac{1}{N_{b}} \sum _{j=1}^{N_{b}}(\mid \hat{u}(-L, t_{u}^{j})-\hat{u}(L, t_{u}^{j})\mid ^{2}+\mid \hat{v}(-L, t_{v}^{j})-\hat{v}(L, t_{v}^{j})\mid ^{2}), \\ Loss_{\hat{f}}=\frac{1}{N_{f}} \sum _{k=1}^{N_{f}}(\mid f_{\hat{u}}(x_{f_{u}}^{k}, t_{f_{u}}^{k})\mid ^{2}+\mid f_{\hat{v}}(x_{f_{v}}^{k}, t_{f_{v}}^{k})\mid ^{2}), \\ Loss_{\hat{c}}=\frac{1}{N_{f}} \sum _{k=1}^{N_{f}}[(\mid f_{E C_{-} \hat{u}}(x_{f_{u}}^{k}, t_{f_{u}}^{k})\mid ^{2}+\mid f_{E C_{-} \hat{v}}(x_{f_{v}}^{k}, t_{f_{v}}^{k})\mid ^{2}), \end{array}\right. \end{aligned}$$
(21)

Here, \(\{x_{u}^{i}, t_{u}^{i}, u^{i}\}_{i=1}^{N_{0}}\) and \(\{x_{v}^{i}, t_{v}^{i}, v^{i}\}_{i=1}^{N_{0}}\) represent the training points sampled from the initial conditions of Eq. (2). \(\{-L, t_{u}^{j}, u^{j}\}_{j=1}^{N_{b}}\), \(\{L, t_{u}^{j}, u^{j}\}_{j=1}^{N_{b}}\), \(\{-L, t_{v}^{j}, v^{j}\}_{j=1}^{N_{b}}\) and \(\{L, t_{v}^{j}, v^{j}\}_{j=1}^{N_{b}}\) are boundary data points of Eq. (2). \(\{x_{f_{u}}^{k}, t_{f_{u}}^{k}\}_{k=1}^{N_{f}}\) and \(\{x_{f_{v}}^{k}, t_{f_{v}}^{k}\}_{k=1}^{N_{f}}\) denote configuration points specified by \(f_{\hat{u}}\), \(f_{\hat{v}}\), \(f_{E C_{-} \hat{u}}\), and \(f_{E C_{-} \hat{v}}\). The loss function (20) consists of three parts. Specifically, \(Loss_{\hat{i}}\) and \(Loss_{\hat{b}}\) are the error generated by the initial and boundary data, respectively. \(Loss_{\hat{f}}\) and \(Loss_{\hat{c}}\) are the errors caused by imposing Eq. (2) and its conservation law at a finite set of configuration points, respectively.

Fig. 1
figure 1

Schematic of IPINN for the Hirota equation

Full size image

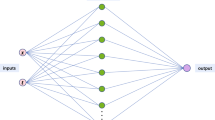
Finally, we give the network structure figure for solving the Hirota equation using the IPINN method, as shown in Fig. 1. Specifically, the solution process can be divided into three parts: (I) Input x and t, and use the deep neural network to solve \(\hat{u}\) and \(\hat{v}\); (II) take the training data points, Eqs. (5) and (6), and conservation laws (18) and (19) as the loss functions of the network; and (III) optimize the network parameters by employing Adam [46] and L-BFGS [47] techniques.

3 Data-driven solution for Hirota equation

In this section, we will use two different types of methods, including PINN and IPINN, to calculate the bright soliton solution and rogue wave solution of Eq. (2), and compare them with the known Hirota equation exact solution.

In addition, in all numerical simulations, we choose a neural network with four hidden layers, and each layer has 50 neurons. Network weights are initialized using the Xavier algorithm. The activation function is hyperbolic tangent. Loss function is simply optimized by using Adam and L-BFGS algorithms. All the code in this paper is based on Python 3.7 and Tensorflow 1.15, and all numerical experiments are run on a computer with Intel(R) Core(TM) i7-4790 @ 3.60GHz processor and 16 GB memory.

3.1 Bright soliton solution

Firstly, we use the PINN method and the IPINN method to simulate the bright soliton solution of Eq. (2). Now, we give the bright soliton solution [14] of Eq. (2) as follows:

$$\begin{aligned} Q(x, t)=sech(x-\beta t) e^{i t}, \end{aligned}$$
(22)

where \(\beta \) is the wave velocity. When \(\beta >0\), the wave propagates to the right; conversely, it propagates to the left. We can set \(\alpha =1\), \(\beta =0.01\) and take x and t in Eq. (2) as \([-10,10]\) and [0, 5], respectively. Therefore, we can get the initial value of Eq. (2), which is as follows:

$$\begin{aligned} Q(x, 0)=sech(x). \end{aligned}$$
(23)

We obtain the training data from Eq. (2) by MATLAB. Specifically, dividing space \([-10,10]\) into 501 points and time [0, 5] into 256 points, bright soliton solution Q(x, t) is discretized into 256 snapshots accordingly. We try to use a small amount of data for simulation experiments. First, we randomly sample 50 points from the initial and boundary conditions, that is, \(N_{0}=50\) and \(N_{b}=50\), respectively. Then, the Latin hypercube sampling (LHS) [48] strategy is used to select \(N_{f}=1000\) points from the spatio-temporal region. We minimize the loss function (20) by using 5000 steps Adam and 10,000 steps L-BFGS. After giving the training dataset, the bright soliton solution Q(x, t) is successfully learned by optimizing the parameters of the neural network. The PINN method achieves a final mean squared error loss \({\mathbb {L}}_{2}\) of 2.7122055\(\textrm{e}-\)06 at 8637 iterations. However, the IPINN model reaches a final mean squared error loss \({\mathbb {L}}_{2}\) of 1.8600642\(\textrm{e}-\)06 at 8786 iterations.

In Fig. 2, the three-dimensional motion and density diagrams of the bright soliton solution Q(x, t) with the exact, PINN, and IPINN methods are plotted, respectively, as well as the iteration number curves of the two data-driven methods. We find that the IPINN method can accurately predict the bright soliton solution. It is not difficult to see that the training loss curve in Fig. 2d shows the relationship between the number of iterations and the loss function. Obviously, the optimization effect of IPINN method is better than that of PINN method. In Fig. 3, we give the error results between the predicted solution and exact solution of PINN and IPINN methods. Moreover, the relative \({\mathbb {L}}_{2}\) errors of Q(x, t), u(x, t), and v(x, t), respectively, are 1.273869\(\textrm{e}-\)02, 7.944935\(\textrm{e}-\)02, 6.070850\(\textrm{e}-\)02 in PINN method, and 6.496740\(\textrm{e}-\)03, 3.690088\(\textrm{e}-\)02, 2.759208\(\textrm{e}-\)02 in IPINN method. In Fig. 4, we show the comparison between the exact solution and the predicted solution obtained by using PINN and IPINN methods at different times \(t=3.50,3.92,4.50,4.90\). The results show that the predictions of IPINN method match well with the evolution described by the exact solution.

Fig. 2
figure 2

Prediction of bright soliton solution (22) using PINN and IPINN. a Exact solution; b prediction solution of PINN method; c prediction solution of IPINN method; d loss curve function curves for the optimization iterations of PINN and IPINN methods

Full size image
Fig. 3
figure 3

The error comparison of bright soliton solution (22) is solved by PINN and IPINN methods. a Error of solution using PINN method; b error of solution using IPINN method

Full size image
Fig. 4
figure 4

Comparison of exact, PINN, and IPINN methods of the bright soliton solution (22) at different times

Full size image

3.2 Rogue wave solution

In this section, we consider using two types of methods (PINN and IPINN methods) to solve the rogue wave solution of Eq. (2). The rogue wave solution [49] of Eq. (2) can be expressed as follows:

$$\begin{aligned} Q(x, t)=\left[ 1-\frac{4(1+4 i t)}{4(x-6 \beta t)^{2}+16 t^{2}+1}\right] e^{2 i t}. \end{aligned}$$
(24)

Here, we still assume \(\alpha =1\), \(\beta =0.01\) and choose the spatio-temporal region of Eq. (2) as \((x, t) \in [-2.5,2.5] \times [-0.5,0.5]\). Thus, the initial solution of Eq. (2) can be obtained as

$$\begin{aligned} Q(x,-0.5)=\left[ 1-\frac{4(1-2 i)}{4(x+0.03)^{2}+5}\right] e^{-i}. \end{aligned}$$
(25)

Next, we divide time \([-0.5,0.5]\) into 201 points and space \([-2.5,2.5]\) into 256 points. The rogue wave solution Q(x, t) is discretized into 201 snapshots accordingly by MATLAB. It is worth noting that we do not select boundary data. The sampling number of initial condition and solution region, and the training number, is the same as in Sect. 3.1. Based on the above selection, we use PINN and IPINN methods to numerically simulate the rogue wave solution of Eq. (2). This is the case for the PINN method, which achieves a final mean squared error loss \({\mathbb {L}}_{2}\) of 1.0907666\(\textrm{e}-\)04 and a number of iterations of 10358. Nevertheless, by using the IPINN method, it reaches a final mean squared error loss \({\mathbb {L}}_{2}\) of 1.7176968\(\textrm{e}-\)05 and a number of iterations of 10390.

Figure 5a–c shows the comparison between the predicted solution and the exact solution of the rogue wave with the help of PINN and IPINN methods, and we find that IPINN method can simulate the evolution of the rogue wave, while PINN method cannot. In Fig. 5d, we can clearly see that the loss function curve of IPINN method decreases faster and smoother at 5001 iterations compared to PINN method. Figure 6 shows the comparison of the error between the two methods when simulating the rogue wave solution and the exact solution, and it can be obviously found that the error of IPINN method is significantly lower than PINN method, and meanwhile, the relative \({\mathbb {L}}_{2}\) errors of Q(x, t), u(x, t), and v(x, t), respectively, are 4.192447\(\textrm{e}-\)02, 1.414866\(\textrm{e}\)+00, 1.676037\(\textrm{e}\)+00 in PINN method, and 8.522858\(\textrm{e}-\)03, 1.436250\(\textrm{e}\)+00,1.666065\(\textrm{e}\)+00 in IPINN method. In Fig. 7, we show the comparison between the exact and predicted solutions of the rogue wave solution at different times \(t=-0.355,-0.105,0.045,0.095\). Obviously, the predicted solution of the IPINN method is very close to the exact solution, while the PINN method is very poor.

In practical engineering applications, the data obtained by sampling are inevitably noisy, so we add various degree of noises (1%, 2% Gaussian noise, as shown in Fig. 8) to the training data to verify the robustness of the IPINN method. Based on the different noisy data, we simulate the rogue wave solution (24) using the PINN and IPINN methods. The results show that for the noise as 1%, 2%, the relative \({\mathbb {L}}_{2}\) errors of Q(x, t) are 4.311988\(\textrm{e}-\)02, 4.891149\(\textrm{e}-\)02 in the PINN method and 1.344709\(\textrm{e}-\)02, 1.040529\(\textrm{e}-\)02 in the IPINN method, respectively.

In Figs. 8, 9, and 10, we show a series of experimental results for solving the rogue wave solution (24) using the PINN method and the IPINN method under various noises. We find that the IPINN method can predict the rogue wave solution accurately, whereas the PINN method cannot. Therefore, the IPINN method has better robustness for noisy data.

Fig. 5
figure 5

Prediction of rogue wave solution (24) using PINN and IPINN. a Exact solution; b prediction solution of PINN method; c prediction solution of IPINN method; d loss curve function curves for the optimization iterations of PINN and IPINN

Full size image
Fig. 6
figure 6

The error comparison of rogue wave solution (24) is solved by PINN and IPINN. a Error of solution using PINN method; b error of solution using IPINN method

Full size image
Fig. 7
figure 7

Comparison of exact, PINN, and IPINN of the rogue wave solution (24) at different times

Full size image
Fig. 8
figure 8

Training data with different noises. a The noise is 1%; b the noise is 2%

Full size image
Fig. 9
figure 9

Density and error diagrams of the PINN and IPINN methods for predicting rogue wave solution (24) when the noise is 1%. a Exact solution; b prediction solution of PINN method; c prediction solution of IPINN method; d error of PINN method; e error of IPINN method

Full size image

Furthermore, in the case of a four-layer neural network and 50 neurons, we discuss the effect of the number of initial condition sampling points \(N_{0}\) and space-time domain sampling points \(N_{f}\) on solving the rogue wave of the Hirota equation by the IPINN algorithm, as shown in Table 1. The results show that, overall, when \(N_{f}\) is fixed, the larger the number of \(N_{0}\), the smaller the relative \({\mathbb {L}}_{2}\) error. When \(N_{0}\) is fixed, the error does not decrease with the increase of \(N_{f}\). To sum up, we can conclude that the relative \({\mathbb {L}}_{2}\) error is mainly determined by the initial condition sampling points \(N_{0}\). Similarly, assume that \(N_{0}=50\) and \(N_{f}=1000\) remain constant. Table 2 shows the effect of the number of network layers and neurons on the performance of the IPINN method. The results show that when the number of network layers is fixed, the relative \({\mathbb {L}}_{2}\) error generally decreases with the increase of the number of neurons. When the number of neurons is fixed, the influence of the number of network layers on the relative\({\mathbb {L}}_{2}\) error is not obvious.

Fig. 10
figure 10

Density and error diagrams of the PINN and IPINN methods for predicting rogue wave solution (24) when the noise is 2%. a Exact solution; b prediction solution of PINN method; c prediction solution of IPINN method; d error of PINN method; e error of IPINN method

Full size image
Table 1 The rogue wave solution (24) of the Hirota equation by using the IPINN: Relative \({\mathbb {L}}_{2}\) error of Q(x, t) for different number of \(N_{0}\) and \(N_{f}\)
Full size table
Table 2 The rogue wave solution (24) of the Hirota equation by using the IPINN: Relative \({\mathbb {L}}_{2}\) error of Q(x, t) for different number of hidden layers and neurons in each layer
Full size table

4 Data-driven parameter discovery for Hirota equation

Next, we will consider the using of the IPINN method to simulate the parameter discovery of Eq. (2). The IPINN method is first used to identify the parameters \(\alpha \) and \(\beta \) in Eq. (2). In addition, we use this method to predict the parameters of the higher-order terms of Eq. (2).

4.1 Parameter discovery for \(\alpha \) and \(\beta \)

In this section, we use two different methods to identify the coefficients \(\alpha \) and \(\beta \) of the second-order and third-order terms in the Hirota equation as follows:

$$\begin{aligned} i Q_{t}+\alpha (Q_{x x}+2|Q |^{2} Q)+i \beta (Q_{x x x}+6|Q |^{2} Q_{x})=0, \end{aligned}$$
(26)

where \(\alpha \), \(\beta \) are unknown real constants. We consider the bright soliton solution of Eq. (26) and set \(\alpha =1\), \(\beta =0.1\), \(L=10\), \(t_{0}=0\), \(t_{1}=5\). We will divide the space \([-10,10]\) into 501 points, time [0, 5] into 256 points, and discrete the bright soliton solution Q(x, t) into 256 snapshots. The LHS strategy is used to select \((x, t) \in [-10,10] \times [0,5]\) data points from the spatio-temporal domain for parameter discovery. The rest of the settings are the same as in Sect. 3.1.

Table 3 The parameter discovery and error comparison of \(\alpha \) and \(\beta \) by PINN and IPINN methods
Full size table

The results show that the final mean squared error loss \({\mathbb {L}}_{2}\) of IPINN is 1.485\(\textrm{e}-\)04, and the relative \({\mathbb {L}}_{2}\) errors of Q(x, t), u(x, t), and v(x, t) are 1.928966\(\textrm{e}-\)04, 2.932726\(\textrm{e}-\)04, and 2.912337\(\textrm{e}-\)04, respectively. However, the final mean squared error loss \({\mathbb {L}}_{2}\) of PINN is 1.763\(\textrm{e}-\)04, and the relative \({\mathbb {L}}_{2}\) errors of Q(x, t), u(x, t), and v(x, t) are 2.137185\(\textrm{e}-\)04, 3.144962\(\textrm{e}-\)04, and 3.041743\(\textrm{e}-\)04, respectively. Table 3 exhibits the learning parameters \(\alpha \), \(\beta \) in Eq. (26) under the cases of PINN and IPINN, and their errors of \(\alpha \), \(\beta \) are 3.600\(\textrm{e}-\)05, 2.932\(\textrm{e}-\)04 and 9.800\(\textrm{e}-\)06, 1.756\(\textrm{e}-\)04, respectively.

4.2 Parameter discovery for \(\mu \) and \(\nu \)

In this section, we will use the PINN and IPINN methods to predict the parameters of the higher-order terms in the Hirota equation, and we consider the Hirota equation of the form with two parameters, as following

$$\begin{aligned} i Q_{t}+Q_{x x}+2|Q |^{2} Q+\frac{i}{2}(\mu Q_{x x x}+\nu |Q |^{2} Q_{x})=0, \end{aligned}$$
(27)

where \(\mu \) is the third-order dispersion coefficient. \(\nu \) is related to the time-delay correction for the cubic nonlinearity term \(|Q |^{2} Q\). We assume \(\mu =1\), \(\nu =6\). At the same time, we still consider the bright soliton solution of Eq. (27), and all the experimental settings are the same as Sect. 4.1.

Table 4 The parameter discovery and error comparison of \(\mu \) and \(\nu \) by PINN and IPINN methods
Full size table

This is the case for the PINN method, which achieves a final mean squared error loss \({\mathbb {L}}_{2}\) of 2.563\(\textrm{e}-\)04. Nevertheless, by using the IPINN method, it reaches a final mean squared error loss \({\mathbb {L}}_{2}\) of 2.177\(\textrm{e}-\)04. The relative \({\mathbb {L}}_{2}\) errors of Q(x, t), u(x, t) and v(x, t), respectively, are 2.846415\(\textrm{e}-\)04, 3.969635\(\textrm{e}-\)04, 3.787746\(\textrm{e}-\)04 in PINN method, and 2.594493\(\textrm{e}-\)04, 3.892033\(\textrm{e}-\)04, 3.499485\(\textrm{e}-\)04 in IPINN method. Table 4 illustrates the learning parameters \(\mu \), \(\nu \) in Eq. (27) under the cases of PINN and IPINN, and their errors of \(\mu \), \(\nu \) are 6.248\(\textrm{e}-\)04, 5.342\(\textrm{e}-\)04 and 3.704\(\textrm{e}-\)04, 3.297\(\textrm{e}-\)04, respectively.

5 Conclusion

In this paper, we proposed a new PINN method embedded with the conservation law, called IPINN, to solve the classical integrable Hirota equation. This algorithm improves the performance of the traditional PINN with less training data by adding the conservation laws of the equations to the neural network and imposing stricter constraints on the loss function of the network.

In our numerical experiments, the bright soliton solution and the rogue wave solution of the Hirota equation are simulated by using IPINN method, and we compared the present algorithm with traditional PINN. We found that, noticeably, for the rogue wave solution, the effects of different noisy data and network structures on the IPINN method are studied, and the results show that IPINN can also predict the evolution process of the rogue wave solution well under noisy data. Furthermore, in the inverse problem, the second-order term, the third-order term coefficient, and the parameters contained in the third-order term of the Hirota equation are identified through IPINN.

In general, numerical results show that our presented IPINN method is more effective than the PINN method in accurately recovering the different evolutionary processes and parameter discovery of the Hirota equation. The IPINN method is a promising method to improve the solution of integrable equations. Since IPINN can use less data to simulate the evolution process of integrable equations, in future research, we consider combining deep learning with integrable system theory to solve more complex integrable equations.