1 Introduction

The formation of solitons is a complex dynamic balance process, typically arising from a delicate balance between nonlinear effects, dispersion effects and possible diffraction effects. When the balance is reached, stable localized wave packets, known as optical solitons, are formed in optical media. According to the nature of the formation mechanism, optical solitons can be divided into spatial solitons, temporal solitons and spatiotemporal solitons [1]. The study of solitons is crucial for a deeper understanding of nonlinear wave phenomena, particularly in applications of optics [2], Bose–Einstein condensates [3], water waves [4], and other related fields [5, 6]. To find soliton solutions to nonlinear equations, more and more methods have been proposed, such as Inverse scattering transform method, Hirota bilinear method, Darboux transformation method, etc.

It is well known that in the fields of science and engineering, numerical simulation is an important method for solving complex physical problems. Traditional numerical methods, such as the finite element method and the finite difference method, usually require discretization of the space and time domains of the problem and may be limited by high-dimensional problems, complex boundary conditions and multi-scale phenomena. These methods are difficult to simulate the propagation of solitons. Some important results have been achieved in terms of and interactions, but there are still challenges in dealing with nonlinear terms, boundary conditions, and multi-soliton interactions. In recent years, the widespread application of neural networks has given rise to some innovative research ideas. In 2019, Maziar Raissi [7, 8] embedded neural networks to solve nonlinear evolution equation, as well as inverse problems. This study explores the use of deep learning in modeling nonlinear dynamics and underscores the advantages of Physics-Informed Neural Networks (PINN) in data-driven modeling. It does not require explicit solutions, instead, it can generate continuous solutions across the entire input space by learning the system's behavior from data [9]. At present, the PINN method has been applied to fractional [10, 11] and stochastic partial differential equations [12].

In order to improve the accuracy and robustness of PINN, many extensions have been proposed, such as multi-subnetwork structure [13], the space–time multiple sub-domains [14], and adaptive weights and flexible learning rates [15]. George Em Karniadakisa et al. added an adaptive activation function to the neural network to speed up the convergence speed of the physical information neural network [16]. Li et al. proposed two neural network models and gradient-optimized PINN [17, 18]. We used PINN to drive data-driven soliton solutions, rogue wave solutions, and breathing wave solutions for high order nonlinear Schrödinger equation (NLSE) and coupled NLSE [13, 15, 19, 20]. Chen et al. [21, 22] predicted the rogue periodic wave of the Chen–Lee–Liu equation and solved bright and dark solitons for the nonlocal integrable Hirota equation. They also proposed PTS-PINN to solve PT symmetric non local equations [23, 24].

The nonlocal NLSE [25] describes that the behavior of a point in the system is not only affected by its neighboring points, but also by other points, which results in a more complex equation form. How to use neural networks to predict the soliton dynamic behavior of coupled nonlocal equations has so far been rarely studied. Solving nonlocal nonlinear problems is challenging for the development of new algorithms. Such research helps to discover the formation of novel solitons, which has deeper significance for revealing new phenomena and understanding the natural world. We propose an improved PINN structure to predict the degenerate and non degenerate soliton solutions of CNNLSE, using prior information as a supplementary term to the loss function, and optimizing the prediction by the stepwise training using adaptive weights and adaptive activation functions. Finally, compared with the PINN, we improve the prediction accuracy of soliton solutions by optimizing on two orders of magnitude, and effectively solve the problem of the accuracy decline over time and multi-objective competition in neural networks.

In the prediction of data-driven solutions, as the evolution distance of time becomes longer, the prediction accuracy of PINN becomes worse and worse. The existing PINN method cannot reasonably use the known physical quantities at a certain point and cannot simulate long-time partial differential equations. PINN requires specialized design and modification of hyperparameters, and its simple extension cannot fully solve different problems [26]. To overcome the shortcomings of existing PINN, we propose to add prior information to the loss function to improve prediction accuracy. When faced with many equation terms, the prediction results of the model are often unsatisfactory, so we propose step-by-step training of the loss function to solve the multi-objective competition problem of the loss function and use the back propagation of the network to optimize network prediction.

The outline of this paper is as follows. In Sect. 2, we first review the PINN model, and then introduce our proposed hybrid training network model that adds prior information. In Sect. 3, we use PINN, boundary prior PINN and adaptive prior PINN models to predict the nondegenerate one-soliton and degenerate double-soliton of the coupled nonlocal nonlinear Schrödinger equation(CNNLSE) with parity-time(PT) symmetric potential. In Sect. 4, we also perform the data-driven coefficient discovery inverse problem for nondegenerate one soliton. Then, the stability of PINN for inverse problems is verified through numerical results. Finally, the last section provides analysis and discussion.

2 Physical information neural network with improved strategy

The Manakov system is an integrable coupled NLSE [27]. Its integrability allows to find multiple soliton solution by appropriate algorithms and methods. Understanding the Manakov system helps to understand and optimize the transmission properties of pulses in optical fiber communication systems, which has practical application value for improving the efficiency and performance of communication systems [28]. So, in this section, we will introduce how to use the improved strategy PINN algorithm to learn the soliton solution of the CNNLSE with PT symmetric potential under Dirichlet boundary conditions [29]

$$ \begin{gathered} iq_{j,t} (x,t) + q_{j,xx} (x,t) + 2\sigma \sum\limits_{p = 1}^{2} {V(x,t)q_{p} (x,t)} = 0,j = 1,2, \hfill \\ V(x,t) = q_{p}^{*} ( - x,t)q_{p} (x,t). \hfill \\ \end{gathered} $$
(1)
$$ \left\{ {\begin{array}{*{20}l} {x \in \left[ {x_{1} ,x_{2} } \right],t \in \left[ {t_{1} ,t_{2} } \right],} \\ {q_{j} (x,t_{1} ) = q_{0} (x),q_{j} (x_{1} ,t) = q_{{lb}} (t),} \\ {q_{j} (x_{2} ,t) = q_{{ub}} (t),f = q_{t} + N[q].} \\ \end{array} } \right. $$
(2)

In Eq. (1), \(q_{j} (x,t),j = 1,2\) are complex-valued functions with respect to distance x and time t, “*” represents complex conjugation. The coefficient \(\sigma\) represents focusing and defocusing nonlinearity, taking 1 and − 1 respectively. This equation contains the self-induced electric potential that satisfies the PT symmetry condition \(V^{*} ( - x,t) = V(x,t)\) [30]. Equation (1) has important physical significance for revealing the principles and possible applications of nonlinear optical and quantum mechanical phenomena. It can provide useful information for the design of new optical communication systems and quantum information processing devices.

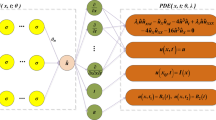
In Eq. (2), we define the initial and boundary conditions, where x1 and x2 respectively represent the left and right boundaries corresponding to x, and t1 and t2 respectively represent the initial and final values corresponding to t. We let \(f = q_{t} + N[q]\) be the residual of Eq. (2). To introduce intuitively how the PINN algorithm numerically approximates the soliton solution of the CNNLSE with PT symmetric potential, the improved PINN model is shown in Fig. 1.

Fig. 1
figure 1

Improved PINN for solving CNNLSE

Full size image

We have tried a dual subnet structure [13] to represent the imaginary and real parts of the two components and the corresponding nonlocal terms to improve prediction speed and accuracy, but the results were unsatisfactory. It is likely that the predictions were distorted due to the characteristics of the CNNLSE, and a single network model is ultimately adopted in this paper. In Fig. 1, x, t are used as neural network inputs. When the loss function does not produce gradient disappearance, we use a 7 hidden layer with 40 neurons in each hidden layer. Because the predicted CNNLSE contains PT symmetry terms, which is different from the local equation, and Python cannot handle the mixture of real and imaginary parts, we set the last layer of the neural network to have 8 outputs, including the imaginary and real parts of two components of soliton solution and their corresponding nonlocal terms with \(q_{j} = u_{j} + i \cdot v_{j}\), \(q_{j}^{*} = u_{j}^{*} + i \cdot v_{j}^{*}\), \(j = 1,2\).

In order to help better capture different patterns and features in the input data, we define the product of the adaptive activation function coefficients multiplied by the hyperbolic tangent function (tanh) as the nonlinear activation of the model function, the weights w and bias b in all models are initialized using the Xavier method. The neural network will continuously minimize the loss function composed of initial conditions and nonlinear evolution equation through the gradient descent method to learn shared parameters (such as weights and biases), so that the neural network can learn nonlinear evolution equations, and finally obtain predicting solution.

The loss function Loss consists of three parts: initial condition error MSE0, boundary condition error MSEb, and equation residual MSEf. The form is:

$$ L{\text{oss}} = \alpha \cdot MSE_{0} + \beta \cdot MSE_{b} + \gamma \cdot MSE_{f} $$
(3)

with

$$ MSE_{0} = \frac{1}{{N_{0} }}\sum\limits_{i = 1}^{{N_{0} }} {\left( {\left| {u_{1} (x^{i} ,t^{i} ) - u_{1}^{i} } \right|^{2} + \left| {v_{1} (x^{i} ,t^{i} ) - v_{1}^{i} } \right|^{2} + \left| {u_{2} (x^{i} ,t^{i} ) - u_{2}^{j} } \right|^{2} + \left| {v_{2} (x^{i} ,t^{i} ) - v_{2}^{j} } \right|^{2} } \right)} $$
(4)
$$ \begin{aligned} MSE_{b} & = \frac{1}{{N_{b} }}\sum\limits_{{j = 1}}^{{N_{b} }} {\left( {\left| {u_{1} (x^{j} ,t^{j} ) - u_{1}^{j} } \right|^{2} + \left| {v_{1} (x^{j} ,t^{j} ) - v_{1}^{j} } \right|^{2} } \right.} \\ & \quad + \left. {\left| {u_{2} (x^{j} ,t^{j} ) - u_{2}^{j} } \right|^{2} + \left| {v_{2} (x^{j} ,t^{j} ) - v_{2}^{j} } \right|^{2} } \right) \\ \end{aligned} $$
(5)
$$ \begin{aligned} MSE_{f} & = \frac{1}{{N_{f} }}\sum\limits_{{k = 1}}^{{N_{f} }} {\left( {\left| {f_{{r1}} (x^{k} ,t^{k} )} \right|^{2} + \left| {f_{{r2}} (x^{k} ,t^{k} )} \right|^{2} } \right.} \\ & \quad + \left. {\left| {f_{{m1}} (x^{k} ,t^{m} )} \right|^{2} + \left| {f_{{m2}} (x^{m} ,t^{m} )} \right|^{2} } \right) \\ \end{aligned} $$
(6)

We have added adaptive weight coefficients α, β, γ to the loss function to make the model better adapt to different samples or features, help the model learn more effectively, and improve the performance of the model on specific tasks. In Eq. (6), fr, fm represent the real and imaginary parts of the residuals respectively. In the neural network, we use random sampling for Dirichlet boundary conditions. The initial point is N0 = 100, the left and right boundary points are Nb = 100, the Latin hypercube [31] is used as the sampling method, and the configuration point is Nf = 10,000. We use two optimizers, L-BFG-S and Adam. By using optimization algorithms such as gradient descent, the network propagates errors backward from the output layer and updates the weights to reduce the loss function. On the existing PINN model, we have added adaptive weight coefficients and adaptive activation functions to allow the network to adapt to different input distributions, so that the neural network can better handle input data of different scales and ranges, improve the robustness of the model, and prevent the model overfitted, and thus the generalization ability of the model is improved.

However, these improved strategies often lead to the occurrence of numerous errors in predicting results for more complicated nonlinear evolution equations. For certain equations, we may have knowledge of some physical quantities or specific values within the equations, but there is a lack of a reasonable method to incorporate them into PINN. Therefore, we consider the usage of this prior information as constraints to augment the training points. The specific approach is to introduce an additional term of prior information into the loss function as a constraint on the neural network, and allow these additional terms to reflect the physical laws that the system should satisfy or the specific values of certain physical quantities at moments. This enhances the learning efficiency and numerical approximation capabilities of the neural network. Although prior information can bring these advantages, overly strong or inaccurate prior information may also lead to a decline in model performance. Therefore, using prior information requires caution and is customized for specific tasks.

When we introduce additional terms to the loss function, it involves optimizing a multi-objective optimization problem. Different objective functions may have varying priorities or competitive relationships, which makes the optimization path of the model more complicated and results in unpredictable outcomes. Additionally, using multiple loss functions may increase the risk of overfitting, and thus it needs to assure the generalization capabilities of this model. We propose a step-wise training of the loss function to make the model reasonably use newly added loss term without causing multi-objective competition problems in the case of ensuring the advantages of PINN. By adjusting the construction of the loss function, we divide the training process into two steps (See detailed procedure in Sect. 3).

All codes are programmed using Python3.10, Tensorflow2.10.1 and Tensorflow1.15. The data reported in this article are all from running on a computer with 2060 graphics card, 2.10 GHz, 12th Gen Intel(R) Core (TM) i7-12700 processor, and 16GB of memory.

3 Prediction of data-driven solutions to the CNNLSE

3.1 Data-driven prediction of nondegenerate one-soliton evolution

Recently, Geng used the non-standard Hirota method [32] to obtain non-degenerate one-soliton and double-soliton solutions [33] for CNNLSE. We first consider the predictions of coupled nondegenerate one-soliton solutions with one and double humps. In the exact nondegenerate one-soliton solution expressed as Eq. (9) in Ref. [34], the parameters are taken as \(k_{1} \, = \, 0.4 + 0.1i, k_{2} \, = \, 0.4 - 0.1i,\alpha_{1} \, = \, 0.45 + 0.5i,\alpha_{2} \, = \, 0.5 + 0.55i\). The initial conditions are selected to be \(q_{0} (x) = q_{j} (x,0)\), and the Dirichlet boundary conditions are \(q_{lb} (t) = q_{j} ( - 40,t),q_{ub} (t = )q_{j} (40,t),t \in [0,10]\). The Pseudo-spectral method is used to discretize the exact nondegenerate one-soliton solution into [256, 201] data points to obtain the data set.

From Fig. 2a, b, the fitting effect of predicted solution by the traditional PINN and exact solution performs well in the early stage, but as the evolution time t becomes longer, the fitting effect becomes worse and worse. Inspired by the ideas of pseudo boundary points and prior training points proposed by Chen [35] and Li [18] we add end boundary points Np = 100 as the prior items of the loss function. From Fig. 2a, b, at t = [0, 2], the prediction accuracy is significantly improved via the PINN with the boundary prior, compared with the traditional PINN. However, when the evolution time t increases, the accuracy gradually decreases. This still cannot achieve the results we expected.

Fig. 2
figure 2

Waterfall comparison plots between the predicted and exact solutions for components a q1 and b q2. Top views of exact solutions for components c q1 and d q2. Legends a, b, c, and d respectively denote exact solution, predicted solutions via traditional PINN, PINN with boundary priors, and PINN with adaptive priors

Full size image

Therefore, we proposed a PINN with adaptive priors. Like PINN with boundary priors, we use some points as prior information to calculate the mean square error between predicted and exact solutions. The neural network will adaptively select some points with larger error values based on the prediction situation to calculate the average, and add these points into the loss function for gradient descent of the optimizer. In order to solve the problem that different objective functions with different priorities or competing relationships often lead to deformed prediction results, we adopt a step-by-step training model as follows. In the first step, let \(Loss = \alpha \cdot MSE_{0} + \beta \cdot MSE_{b} + \gamma \cdot MSE_{f}\). After training for 30,000 times via the traditional PINN, the predicted and exact solutions are close each other; then in the second step, let \(Loss = \frac{1}{{N_{p} }}\sum\limits_{j = 1}^{{N_{p} }} {\left( {\left| {u_{1} (x^{y} ,t^{y} ) - u_{1}^{y} } \right|^{2} + \left| {v_{1} (x^{y} ,t^{y} ) - v_{1}^{y} } \right|^{2} + \left| {u_{2} (x^{y} ,t^{y} ) - u_{2}^{y} } \right|^{2} + \left| {v_{2} (x^{y} ,t^{y} ) - v_{2}^{y} } \right|^{2} } \right)}\). At this time, after training 30,000 times, the neural network fit the prior information we added, and can obtain a higher precision solution than that via the traditional PINN.

In Fig. 3c, d, the neural network with adaptive prior uses a sampling points NP = 5000. Comparison between PINN with boundary priors and adaptive priors shows that the latter exhibits the superior fitting capabilityy, and the predictions is closer to exact solution at all cases. After integrating the prior information, the prediction time is close to that of the traditional PINN. However, the PINN with adaptive prior can produce predicted solutions with higher accuracy.

Fig. 3
figure 3

a, b 3D diagram of two-component exact solution and c, d cross-sectional comparison diagrams of two-component predicted and exact solutions at different time. Legends a, b, and c respectively represent exact solution and the predicted solutions via PINN with boundary prior and adaptive prior

Full size image

Next, we consider the predictions of coupled nondegenerate one-soliton solution with both double-hump structures. In the exact nondegenerate one-soliton solution expressed as Eq. (9) in Ref. [34], the parameter is chosen as \(k_{1} \, = \, 0.4 + 0.1 \cdot i, k_{2} \, = \, 0.4 - 0.1 \cdot i,\alpha_{1} \, = \, 0.45 + 0.5 \cdot i,\)\(\alpha_{{2}} { = 0}{\text{.5 + 0}}{.55} \cdot i\). Under the range of the space–time region is \(\left[ {x_{1} ,x_{2} } \right] = [ - 40,40]\) and \(\left[ {t_{1} ,t_{2} } \right] = [0,10]\), we obtain the initial and boundary conditions of CNNLS. Using the PINN with adaptive prior, taking points Np = 5000 as prior information, the predicted solution at evolution time t = 20 is shown in Fig. 4a, b, and the corresponding L2 norm relative error is

$$ error = \frac{{\sqrt {\sum\nolimits_{j} {[{\text{q}}_{j} - {\text{q}}_{j} (x_{j} ,t)]^{2} } } }}{{\sqrt {\sum\nolimits_{j} {[{\text{q}}_{j} (x_{j} ,t)]^{2} } } }} $$
(7)

with the predicted solution qj. The relative errors of the two-components are respectively 1.3898e−2 and 1.4943e−2, which shows that this method can effectively use the specific values of physical laws we know or the behavior of a certain physical quantity at a certain position as part of the loss function to improve the accuracy. Compared with predicted solutions via the PINN with boundary prior, predicted solutions via the PINN with adaptive prior in Fig. 3c, d have higher accuracy.

Fig. 4
figure 4

a, b Two-component predicted solution via PINN with adaptive prior and c, d Waterfall comparison diagrams of two-component predicted and exact solutions. Legends a, b, and c respectively represent exact solution and the predicted solutions via PINN with boundary prior and adaptive prior

Full size image

In Table 1, “epoch” means the number of training iterations, “step” indicates the training steps after incorporating step-wise training. Compared the predicted results via different optimization methods in Table 1, the impact of learning rate optimization on predicted results is not particularly pronounced. The inclusion of boundary priors improves the prediction accuracy to a certain extent, while the addition of adaptive priors significantly enhances the prediction accuracy about 2–3 orders of magnitude. Taking more prior information points means the reduction of unknown points and improvement of the prediction accuracy of the neural network, which involves a trade-off issue. We try to add different numbers of prior points from 100 to 30,000. The more prior information points we add, the greater the accuracy improvement. But when we add 5000 points, the improvement in accuracy begins to slow down, and the order of magnitude is not significantly improved. Therefore, we use 5000 adaptive prior points as the optimization plan in the following discussion.

Table 1 L2 norm error of predicted solutions for two-components q1 and q2 via various optimization methods
Full size table

3.2 Data-driven prediction of degenerate double-soliton collision

We will predict three collision scenarios of the degenerate double-soliton solutions expressed as Eq. (4) in Ref. [36]. Firstly, we set parameters as \(\begin{gathered} k_{1} = 0.5 + 0.8 \cdot i,\mathop k\limits^{ - }_{1} = - 0.5 + 0.8 \cdot i,k_{2} = - 2 + i,\mathop k\limits^{ - }_{2} = 2 + i,\alpha_{1}^{1} = 1 + i,\alpha_{2}^{1} = 1.5 + i, \hfill \\ \alpha_{1}^{2} = 0.5 + i,\alpha_{2}^{2} = 2 + i, \hfill \\ \end{gathered}\)\(\beta_{1}^{1} = 1 - i,\beta_{1}^{2} = - 0.5 - i,\beta_{2}^{1} = - 1.5 - i,\beta_{2}^{2} = 2 - i\). After making the discrete data points into a data set, we can obtain the Type-I collision behavior in Fig. 5. From the comparison in Fig. 5c, d, the PINN method with adaptive prior is also suitable for predicting the collision behavior of double-solitons. The relative errors of the L2 norm of two components are 8.9195 × 10−3 and 7.9951 × 10−3 respectively. As the transmission time increases, the non-fitting phenomenon will not occur, and this method has high accuracy for the prediction of complicated solitons.

Fig. 5
figure 5

a, b Predicted Type-I collision of degenerate double-soliton via PINN with adaptive prior and c, d cross-sectional comparison diagram of two-component predicted and exact solutions at different time. Legends a and b respectively represent exact solution and predicted solution via PINN with adaptive prior

Full size image

To obtain the Type-II collision expressed as Eq. (4) in Ref. [36], we take the parameters \(k_{1} = - 1.5 + 0.8 \cdot i,\mathop k\limits^{ - }_{1} = 1 + 0.8 \cdot i,k_{2} = 2 + i,\mathop k\limits^{ - }_{2} = - 2 + i,\alpha_{1}^{1} = 1 + i,\alpha_{2}^{1} = 1.5 + i,\alpha_{1}^{2} = 0.5 + i,\) \(\alpha_{2}^{2} = 2 + i,\beta_{1}^{1} = 1 - i,\beta_{1}^{2} = - 0.5 - i,\beta_{2}^{1} = - 1.5 - i,\beta_{2}^{2} = 2 - i\). From Fig. 6, as time increases, the error of the predicted solution does not increase. The PINN with adaptive prior has good performance in various spatiotemporal domains, and the relative errors of the L2 norm of two components are 2.5960 × 10−2 and 2.5839 × 10−2 respectively, which further shows its good stability and high accuracy.

Fig. 6
figure 6

a, b Predicted Type-II collision of degenerate double-soliton via PINN with adaptive prior and c, d cross-sectional comparison diagram of two-component predicted and exact solutions at different time. Legends a and b respectively represent exact solution and predicted solution via PINN with adaptive prior

Full size image

We take parameters \(k_{1} = 0.5 + 0.8 \cdot i,\mathop k\limits^{ - }_{1} = - 0.5 + 0.8 \cdot i,k_{2} = 0.5 + 0.81 \cdot i,\mathop k\limits^{ - }_{2} = - 0.5 + 0.81 \cdot i,\) \(\alpha_{1}^{1} = 1 + i,\alpha_{2}^{1} = 1 + i,\alpha_{1}^{2} = 0.1 + i,\alpha_{2}^{2} = 3 + i,\beta_{1}^{1} = 1 - i,\beta_{1}^{2} = - 0.1 - i,\beta_{2}^{1} = - 1 - i,\beta_{2}^{2} = 3 - i\), propagation behavior of soliton molecule in the form of bound states can be obtained. The results show that the relative errors of the L2 norm between the predicted and exact solutions of two components are 7.9275 × 10−3 and 6.9086 × 10−3 respectively. From the dynamic behavior of these data-driven solitons in the cross-section Figs. 7c, d, the learning effect of PINN with adaptive prior is very good and the prediction error is very small.

Fig. 7
figure 7

a, b Predicted degenerate soliton molecule via PINN with adaptive prior and c, d waterfall comparison diagram of two-component predicted and exact solutions at different time. Legends a and b respectively represent exact solution and predicted solution via PINN with adaptive prior

Full size image

4 Inverse problem

In this section we will use PINN to perform data-driven parameter discovery of CNNLSE

$$ iq_{j,t} (x,t) + q_{j,xx} (x,t) + 2\sigma \sum\limits_{p = 1}^{2} {q_{p}^{*} ( - x,t)q_{p} (x,t)q_{p} (x,t)} = 0,j = 1,2 $$
(8)

Soliton solution \(q_{j} = {\text{u}}_{j} + i \cdot v_{j}\), the coefficient \(\sigma\) is the unknown quantity that we need to find by using PINN. The loss function is

$$ \begin{aligned} Loss & = \frac{1}{{N_{f} }}\sum\limits_{{i = 1}}^{{N_{f} }} {\left( {\left| {u_{1} (x^{i} ,t^{i} ) - u_{1}^{i} } \right|^{2} + \left| {v_{1} (x^{i} ,t^{i} ) - v_{1}^{i} } \right|^{2} } \right.} \\ & \quad + \left. {\left| {u_{2} (x^{i} ,t^{i} ) - u_{2}^{j} } \right|^{2} + \left| {v_{2} (x^{i} ,t^{i} ) - v_{2}^{j} } \right|^{2} } \right) \\ & \quad + \left| {f_{{r1}} (x^{k} ,t^{k} )} \right|^{2} + \left| {f_{{r2}} (x^{k} ,t^{k} )} \right|^{2} + \left| {f_{{m1}} (x^{k} ,t^{m} )} \right|^{2} \\ & \quad + \left| {f_{{m2}} (x^{m} ,t^{m} )} \right|^{2} \\ \end{aligned} $$
(9)
$$ f_{j} = iq_{j,t} (x,t) + q_{j,xx} (x,t) + 2\sigma \sum\limits_{p = 1}^{2} {q_{p}^{*} ( - x,t)q_{p} (x,t)q_{p} (x,t)} ,j = 1,2 $$
(10)
$$ f_{j} = f_{r,j} + i \cdot f_{m,j} $$
(11)

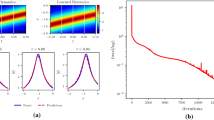
We discretize the nondegenerate one-soliton solution into [256, 201] and perform Pseudo-spectral method to obtain the data set of parameter \(\sigma = 1\). Randomly sample 5000 points as samples from the space–time region \(\left[ {x_{1} ,x_{2} } \right] = [ - 40,40]\), \(\left[ {t_{1} ,t_{2} } \right] = [ - 1,1]\) of the non-degenerate single soliton solution. Data-driven parameter discovery is performed using the loss function (9) and a deep neural network with 6 hidden layers of 50 neurons each. Figure 8 shows the sampling points in the top view of exact solution and the training convergence of the loss function. We get \(\sigma = 1.0461\), and the L2 relative error is 4.61%.

Fig. 8
figure 8

Top view of the sampling points of components a q1 and b q2 in inverse problem, and c loss function iterates with epoch after adding different noises

Full size image

In order to study the impact of noise on the inverse problem, we added 0–15% Gaussian noise as interference to the sampling points. We find that PINN can still predict unknown parameters stably under different noises, but the loss function will change. After training 15,000 times, the loss functions are listed in Table 2. From Table 2, we find that PINN can correctly predict unknown parameters even if a certain proportion of Gaussian noise is added to the data set. In Fig. 8c, the loss function has the best convergence effect when the noise is 0. As the noise increases, the error gradually adds, and the convergence effect of the loss function becomes worse and worse. In summary, data-driven parameter prediction via PINN can also predict correct results within a certain noise range, which also proves the stability and high adaptability of PINN.

Table 2 Prediction of parameter \(\sigma\) and L2 relative error under different noises
Full size table

5 Conclusion

In summary, we propose an improved PINN structure for predicting degenerate and nondegenerate soliton solutions of the CNNLSE. After comparing various optimization methods, we choose to add adaptive prior information, adaptive activation functions and adaptive weights to PINN to improve the generalization ability of the model and accelerate the training process. We also change the composition of the loss function and perform step-by-step training in order to handle the multi-objective competition problem. The addition of boundary prior information and adaptive prior information to the loss function effectively solves the problem of accuracy degradation of neural networks over time, improving the prediction accuracy of two orders of magnitude for isolated solutions of neural networks. In addition, we also discuss the impact of Gaussian noise on data-driven parameter discovery of the CNNLSE. We have verified that the high stability and adaptability of PINN can be applied to solve coupled nonlocal integrable systems, but there are still many open problems, such as how to optimize neural networks? How to effectively combine various methods to improve accuracy and stability? This is still a direction we need to study and move forward, and these issues will be further studied in our future work.