1 Introduction

The responses of the nonlinear systems subjected to either harmonic stimulation or modulated random stimulation have been studied by many investigators due to the multiple applicability in various science and engineering areas [1, 2]. By utilizing analytical methods and approximation techniques, numerous dynamical phenomena have been identified. Actually, the circumstance that multiple stimulations exist simultaneously often occurs, and many studies have been focused on the situation where the oscillators are concurrently subjected to multiple stimulations [3].

In general, acquiring the analytical stationary solutions of the nonlinear oscillators under random stimulations requires some restrictive conditions [4,5,6]. It can be more difficult or impossible at the moment to acquire the analytical transient solutions of the oscillators subjected to harmonic and modulated random stimulations. The nonlinearly damped oscillators subjected to combined broadband random stimulation and multiplicative harmonic stimulation were ever studied by some researchers [7], where a set of stochastic differential equations can be acquired by employing stochastic averaging technique for the averaged system [8, 9]. The analytical solutions of the averaged systems were obtained according to the stationary potential theory. The behaviors of the Duffing oscillator subjected to harmonic and random stimulations were investigated by utilizing the traditional harmonic balance technique and stochastic averaging technique [10]. The transient behaviors of a Duffing oscillator excited by sinusoidal and random stimulations were studied by adopting the path integration technique based on the principle of Gauss-Legendre integration [11, 12], which was initially proposed to solve the quantities-functional problems [13]. The transient behaviors can be then captured from the initial state to the evolutionary state. A modified path integral technique with non-Gaussian transition was proposed to acquire the probabilistic solutions of the oscillators due to harmonic and random stimulations [14]. The periodic solutions of the nonlinear oscillators due to harmonic and random stimulations were acquired by utilizing the Gaussian closure approach and implicit harmonic balance technique [15], which was initially established to solve the harmonic problems [16, 17]. Beside the methods mentioned above, certain approaches which were also utilized such as the equivalent linearization (EL) method [18,19,20], which is equivalent to the Gaussian closure approach in the case that the nonlinear system is subjected to purely external random stimulation. It was extended to improve the PDF solutions of a cubic nonlinear oscillator with Gaussian mixture technique [21]. An improved moment equation technique is utilized to obtain the responses of stochastic oscillators under random stimulations with quasi-moment neglect closure [22, 23]. The transition responses of the strongly nonlinear systems due to random stimulation were analyzed with the smoothed particle hydrodynamics approach [24]. The cell mapping technique was proposed with the short-time Gaussian approximation to acquire the numerous transient solutions and stationary solution for the stochastic oscillators under parametric random stimulations [25]. It is still a significant challenge for the finite element method to maintain the probability density being positive, especially in the probabilistic tails [26,27,28]. The meshless technique was proposed to obtain the transient solutions of nonlinear oscillators under multiplicative random stimulations with the unity finite element method [29]. The responses of weakly nonlinear oscillators were analyzed by utilizing the perturbation technique [30]. Utilizing MCS is a straightforward way to acquire the transition solutions of stochastic differential equations, but large effort of computation is necessary, especially when strong nonlinearity of the systems is encountered and the tails of the probability density are required for reliability analysis [31, 32]. The cumulant-neglect closure technique was utilized to acquire the responses of the nonlinear oscillator under parametric and external random stimulations [33, 34]. The maximum entropy approach was proposed to investigate the responses for the nonlinear systems under random stimulations [35]. To overcome the occurrence of negative values in the PDF tails acquired from the A-type Gram-Charlier expansion [36, 37], an expansion of C-type form was adopted for the single-degree-of freedom oscillator or 2-dimensional FPK equation [38]. Meanwhile, a more generally utilized method named exponential-polynomial-closure (EPC) method was proposed [39], which worked for the oscillators with 2\(\sim \)4-dimensional FPK equations [40, 41]. It has been verified to be an efficient technique to acquire the PDF solutions of nonlinear oscillators effectively. Later, the EPC method was extended to acquire the transient PDF solutions of the Duffing oscillator under Guassian white noise [42]. However, no verification on the effectiveness of the presented solution was given by comparison with MCS. The neural network technique was also utilized to solve the FPK equation recently, which is an interesting topic [43, 44].

Till now, capturing the transient solutions of the nonlinear systems subjected to combined harmonic and modulated random stimulations is still a challenging problem though many real problems can be characterized by this class of oscillators. In this paper, an advanced procedure is presented to complement the conventional EPC method by adopting an evolutionary exponential-polynomial function with time-dependent undefined parameters as the transient PDF solution. Four oscillators are investigated to show the accuracy and efficiency of the advanced procedure. In addition, solving the problems by utilizing the advanced procedure is one of the crucial steps in the process of extending the state-space-split EPC technique to acquire the transient solutions of the high-dimensional nonlinear systems in the future work [45, 46].

2 Problem formulation

Consider a stochastic oscillator with various nonlinear terms and excited by combined harmonic and modulated random stimulations as follows.

$$\begin{aligned} \ddot{Y}(t) + h_0\left( {Y(t),\dot{Y}(t)} \right) =Q\mathrm{{sin}}(\omega t)+g(t)\eta (t) \end{aligned}$$
(1)

where Y(t) and \({\dot{Y}}(t)\) are the time-dependent system responses, namely, the displacement and velocity, respectively; \(h_0\left( {Y(t),\dot{Y}(t)} \right) \) is a nonlinear function constituted by the combination of response components in \({\textbf{Y}}(t) = \left\{ Y(t),\dot{Y}(t) \right\} ^{T}\); Q is the amplitude of harmonic stimulation and \(\omega \) is the frequency of harmonic stimulation; g(t) is a time-varying function; \( \eta (t) \) is the random stimulation being Gaussian white noise characterized by

$$\begin{aligned} \begin{array}{lr} E\left[\eta (t)\right]=0, \\ E\left[{\eta (t)\eta \left( {t + \tau } \right) } \right]=D_0\delta (\tau ) \\ \end{array} \end{aligned}$$
(2)

where \( E[\cdot ]\) represents the probabilistic average of \([\cdot ]\); \(D_0\) is the intensity of the random stimulation \(\eta (t)\); \(\delta (\tau )\) is the Dirac delta function; The time-varying intensity function is defined as

$$\begin{aligned} D(t)=|g(t)|^{2}D_0 \end{aligned}$$
(3)

where g(t) is described as the modulated function of the random stimulation, which is given as [47]

$$\begin{aligned} g(t)=\left\{ \begin{array}{lr} \lambda _1te^{-\lambda _2t}&{}, (t\ge 0) \\ 0&{}, (t < 0) \\ \end{array} \right. \end{aligned}$$
(4)

where \(\lambda _1\) and \(\lambda _2\) \((\lambda _1,\lambda _2 >0)\) are the shape factors of the modulated function g(t). The maximum amplitude of g(t) is defined as

$$\begin{aligned} \mathop {\mathrm{{max}}}\limits _{t}|g(t)|=1 \end{aligned}$$
(5)

where \(\mathrm{{max}}\) donates the maximum value of the modulated function. It is observed that g(t) can be made to produce various non-stationary random noise by introducing certain combinations of \(\lambda _1\) and \(\lambda _2\). The modulated random process \(g(t)\eta (t)\) with the shape factors \(\lambda _1=0.5456\) and \(\lambda _2=0.2006\) is demonstrated in Fig. 1.

Fig. 1
figure 1

Modulated random process

Full size image

Subjected to random stimulation, Eq. (1) can be characterized in Stratonovich’s form as

$$\begin{aligned} \begin{aligned} {\dot{Y}}_{1}(t)&=Y_{2}(t)\\ {\dot{Y}}_{2}(t)&=- h_0\left( {Y_1(t),Y_2(t)} \right) +Q\mathrm{{sin}}(\omega t)+g(t)\eta (t) \end{aligned} \end{aligned}$$
(6)

in which \(Y_1(t)=Y(t), Y_2(t)={\dot{Y}}(t)\).

Under the random stimulation, the transient joint PDF of the nonlinear oscillator is governed by the following FPK equation

$$\begin{aligned}{} & {} \dfrac{\partial p}{\partial t} + y_{2}\dfrac{\partial p}{\partial y_{1}}-\dfrac{\partial h_0}{\partial y_{2}}p-h_0\dfrac{\partial p}{\partial y_{2}}+Q\mathrm{{sin}}(\omega t)\dfrac{\partial p}{\partial y_{2}}\nonumber \\{} & {} \quad -\dfrac{1}{2} D(t)\dfrac{\partial ^2 p}{\partial y_{2}^2}=0 \end{aligned}$$
(7)

where \(p=p(y,{\dot{y}},t|y_0,\dot{y}_0,t_0)\). The responses \(Y_0\) and \({\dot{Y}}_0\) are assumed to be Gaussian with zero means and variance being \(\sigma _{y_0}\) and \(\sigma _{{\dot{y}}_0}\), respectively. p should comply with the following criteria.

$$\begin{aligned} \left\{ \begin{array}{lr} \lim \limits _{y,\dot{y}\rightarrow \pm \infty } p(y,{\dot{y}},t|y_0,\dot{y}_0,t_0)=0, &{}\\ \int _{-\infty }^{+\infty } \int _{-\infty }^{+\infty } {p(y,{\dot{y}},t|y_0,\dot{y}_0,t_0)}d{\dot{y}}dy =1 &{} \\ p(y,{\dot{y}},t|y_0,\dot{y}_0,t_0)\ge 0, ~~~~~y,\dot{y}\in {\mathbb {R}}^2 \end{array} \right. \end{aligned}$$
(8)

3 The advanced EPC methodology

There is no available analytical solution to Eq. (7) at the moment. Therefore, it is necessary to utilize approximate method to acquire the transient solution. By the advanced procedure, the approximate transient PDF is specified as

$$\begin{aligned} \begin{aligned} {\hat{p}}\left( {\textbf{y}},t; {\textbf{b}}\right)&=e^{\Gamma _n \left( {\textbf{y}},t;{\textbf{b}}\right) }\\&=\exp \left( {\sum _{r_1^\prime =0}^{n}\sum _{r_2^\prime = 0}^{r_1^\prime }b_r\left( t \right) y_1^{r_1^\prime -r_2^\prime }y_2^{r_2^\prime }}\right) \end{aligned} \end{aligned}$$
(9)

where \(\Gamma _n\left( {\textbf{y}},t;{\textbf{b}}\right) \) is an evolutionary nth-degree polynomial function of \({\textbf{y}} = \left\{ y_1,y_2\right\} ^{T}\); \({\textbf{b}}=\{b_0(t), b_1(t),...,\) \(b_{m-1}(t)\}\), which includes m time-related unknown variables and \(m=\dfrac{1}{2}n^2+\dfrac{3}{2}n+1\).

The residual error can be yielded as follows after the approximation \({\hat{p}}\left( {\textbf{y}},t; {\textbf{b}}\right) \) is adopted to replace p in Eq. (7).

$$\begin{aligned} \begin{aligned} {\mathbb {R}}\left( {\textbf{y}},t;{\textbf{b}}\right)&= \dfrac{\partial {\hat{p}}}{\partial t} + y_{2}\dfrac{\partial {\hat{p}}}{\partial y_{1}}-\dfrac{\partial h_0}{\partial y_{2}}{\hat{p}}-h_0\dfrac{\partial {\hat{p}}}{\partial y_{2}}\\&\quad +Q\mathrm{{sin}}(\omega t)\dfrac{\partial {\hat{p}}}{\partial y_{2}} -\dfrac{1}{2}D(t)\dfrac{\partial ^2 {\hat{p}}}{\partial y_{2}^2} \\&=\left\{ \dfrac{\partial \Gamma _n}{\partial t}+y_{2}\dfrac{\partial \Gamma _n}{\partial y_{1}} - \dfrac{\partial h_0}{\partial y_{2}} - h_0\dfrac{\partial \Gamma _n}{\partial y_2}\right. \\&\quad +Q\mathrm{{sin}}(\omega t)\dfrac{\partial \Gamma _n}{\partial y_{2}}\\&~ ~ ~-\left. \dfrac{1}{2} D(t) \left[ \dfrac{\partial ^2 \Gamma _n}{\partial y_{2}^2} + \left( \dfrac{\partial \Gamma _n}{\partial y_{2}} \right) ^2 \right] \right\} {\hat{p}}\\&=\Delta \left( {\textbf{y}},t;{\textbf{b}} \right) {\hat{p}} \end{aligned} \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{aligned} \Delta \left( {\textbf{y}},t;{\textbf{b}} \right)&=\dfrac{\partial \Gamma _n}{\partial t}+y_{2}\dfrac{\partial \Gamma _n}{\partial y_{1}} - \dfrac{\partial h_0}{\partial y_{2}} - h_0\dfrac{\partial \Gamma _n}{\partial y_2}\\&\quad +Q\mathrm{{sin}}(\omega t)\dfrac{\partial \Gamma _n}{\partial y_{2}}\\&~~~-\dfrac{1}{2} D(t) \left[ \dfrac{\partial ^2 \Gamma _n}{\partial y_{2}^2} +\left( \dfrac{\partial \Gamma _n}{\partial y_{2}}\right) ^2 \right] \end{aligned} \end{aligned}$$
(11)

Generally \({\hat{p}}\left( {\textbf{y}},t;{\textbf{b}}\right) \ne 0\), \(\Delta \left( {\textbf{y}},t;{\textbf{b}} \right) = 0\) is the only possible choice for \({\hat{p}}\left( {\textbf{y}},t;{\textbf{b}}\right) \) to comply with Eq. (7). However, \(\Delta \left( {\textbf{y}},t;{\textbf{b}} \right) \ne 0\) in general since \({\hat{p}}\left( {\textbf{y}},t;{\textbf{b}}\right) \) is just an approximation of the analytical solution. Thus, a number of independent evolutionary base functions \({\mathbb {U}}_k({\textbf{y}},t) \) spanning the \({\mathbb {R}}^2\) space are introduced here. The integration of \(\Delta \left( {\textbf{y}},t;{\textbf{b}} \right) \) on the evolutionary \({\mathbb {R}}^2\) space is made zero so that Eq. (7) is established in the weak sense as follows.

$$\begin{aligned} \int _{{\mathbb {R}}^2}{\Delta \left( {\textbf{y}},t;{\textbf{b}} \right) {\mathbb {U}}_k({\textbf{y}},t)}d{\textbf{y}}=0, \quad k=0, 1,2,...,m-1\nonumber \\ \end{aligned}$$
(12)

where \({\mathbb {U}}_k({\textbf{y}},t)\) are determined as follows.

$$\begin{aligned} \mathbb U_k({\textbf{y}},t)=y_1^{k_1-k_2}y_2^{k_2}\psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma }) \end{aligned}$$
(13)

in which \(k_1=0,1,...,n\) and \(k_2=0,1,...,k_1\), \((k_1\ge k_2)\). \(\psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma })\) is a specific choice of bivariate Gaussian PDF; \(\varvec{\mu },\varvec{\sigma }\) represent the mean value and variance vectors of the response \({\textbf{y}}=\left\{ y_1,y_2 \right\} ^{T}\), respectively, acquired by utilizing EL at time instant t.

$$\begin{aligned} \begin{aligned} \psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma })~ =&~\dfrac{1}{2\pi \sigma _1(t)\sigma _2(t)\sqrt{1-\rho ^2(t)}}\\&\quad \times \exp \left\{ -\dfrac{1}{2\left( 1-\rho ^2(t)\right) } \right. \\&\left. \left[ \dfrac{({y_1}-\mu _1(t))^2}{\sigma _1^2(t)}+ \dfrac{({y_2}-\mu _2(t))^2}{\sigma _2^2(t)}\right. \right. \\&-\left. \left. \dfrac{2\rho (t) \left( {y_1}-\mu _1(t)\right) \left( {y_2}-\mu _2(t)\right) }{\sigma _1(t)\sigma _2(t)} \right] \right\} \end{aligned} \end{aligned}$$
(14)

in which \(\rho (t)\) is the correlation coefficient of the response \({\textbf{y}}=\left\{ y_1,y_2 \right\} ^{T}\) at time instant t, which can be acquired by

$$\begin{aligned} \rho (t)=\dfrac{cov(y_1,y_2)}{\sigma _1\sigma _2}=\dfrac{E[(y_1-\mu _1)(y_2-\mu _2)]}{\sigma _1\sigma _2} \end{aligned}$$
(15)

Resulted by the coupling action between the harmonic and modulated random stimulations in this oscillator, the mean values of the response components in \({\textbf{y}}=\left\{ y_1,y_2 \right\} ^{T}\) are nonzero. The integration terms in Eq. (12) can be stated as

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^2}y_1^{h_1}y_2^{h_2}\psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma })\mathrm{{d}}{\textbf{y}}\\&= ~\int _{{\mathbb {R}}^2}\left( x_1+\mu _1 \right) ^{h_1}\left( x_2+\mu _2\right) ^{h_2}\psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma })\mathrm{{d}}{\textbf{y}}\\&=~\sum _{i^\prime =0}^{h_1}\sum _{j^\prime =0}^{h_2} \begin{pmatrix} h_{1} \\ i^\prime \\ \end{pmatrix} \begin{pmatrix} h_{2} \\ j^\prime \\ \end{pmatrix} \mu _1^{h_1-i^\prime }\mu _2^{h_2-j^\prime }\\&\quad \int _{\mathbb R^2}x_1^{i^\prime }x_2^{j^\prime }\psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma })\mathrm{{d}}{\textbf{y}} \end{aligned} \end{aligned}$$
(16)

where \(x_i=y_i-\mu _i\) and

$$\begin{aligned} \begin{pmatrix} h_{1} \\ i^\prime \\ \end{pmatrix}= \dfrac{h_1!}{i^\prime !(h_1-i^\prime )!} \end{aligned}$$
(17)

Thus, Eq. (12) can be formulated by adopting the Isserlis’s theorem as

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^2}x_1^{h_1}x_2^{h_2}\psi ({\textbf{y}},t;\varvec{\mu },\varvec{\sigma })\mathrm{{d}}{\textbf{y}}\\&=\left\{ \begin{array}{lr} ~\sum \prod E\left[ (y_i-\mu _i)(y_j-\mu _j);t\right] , ~ ~\text {if} ~h_1\\ +h_2~ \text {is even}\\ 0,~ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text {otherwise}\\ \end{array} \right. \end{aligned} \end{aligned}$$
(18)

Integrating the weighted residual error, m nonlinear ordinary differential equations related to the evolutionary variables \({\textbf{b}}(t)\) can be constructed from Eq. (12). Those evolutionary variables can be computed by utilizing Runge–Kutta method numerically. In view that the nonlinear oscillator is under combined harmonic and modulated random stimulations, the evolutionary PDF solution of the oscillator responses with nonzero mean can be resulted. Meanwhile, as the given modulated function approaches zero, hence the random stimulation disappears as time elapses, which could make the oscillator completely under harmonic stimulation in the last.

4 Numerical cases

To acquire the transient PDFs of the nonlinear oscillator responses under combined harmonic and modulated random stimulations, the numerical analysis is conducted to ascertain the suitability of the advanced procedure by considering four cases in the following. The MCS is utilized to acquire the numerical PDF solutions in those cases with a sample size being \(10^8\). The polynomial order \(n=6\) of the exponential approximate function is utilized in the advanced procedure to acquire the transient PDFs of the nonlinear oscillator responses. Comparing the numerical results from the advanced procedure with EL and MCS reflects the superiority of the advanced procedure for the evolutionary PDFs of the oscillator responses. In all the figures in the following to show the PDF solutions, the PDF of a response is plotted when the response value is within \([m-4\sigma , m+4\sigma ]\) where m is the mean of a response and \(\sigma \) is the standard deviation of a response given by EL.

4.1 Case 1: Duffing oscillator

First, a Duffing oscillator under both harmonic and modulated random stimulations is considered.

$$\begin{aligned} \ddot{Y} + 2\xi \omega _n{\dot{Y}} + \omega _n^2Y + \varepsilon Y^3= Q\mathrm{{sin}}(\omega t)+g(t)\eta (t) \nonumber \\ \end{aligned}$$
(19)

where \(\xi =0.25\); \(\omega _n=1\); \(\varepsilon =1\); \(Q=0.3\) and \(\omega =1\). The modulated function is considered as \(g(t)=0.5456t\exp (-0.2006t)\); the random stimulation is represented with the correlation function \(E\left[ \eta (t)\eta (t+\tau ) \right] =\delta (\tau )\); A Gaussian distribution is characterized as the initial PDF of Y and \(\dot{Y}\) at \(t=0s\) with \(\mu _{Y}=\mu _{\dot{Y}}=0\) and \(\sigma _{Y}^2=\sigma _{\dot{Y}}^2=0.02\). In order to guarantee solution convergence, the time evolutionary process is performed with the step being \(\Delta t=0.1s\) for the EL and the presented advanced EPC solution procedures and \(\Delta t=0.02s\) for MCS. In all the solution procedures, the 4th Runge-Kutta method is adopted.

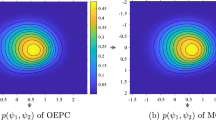
The maximum variance of displacement is around \(t=7s\) as shown in Fig. 4. The transient PDF of the response Y at \(t=7s\) and \(t=10s\), respectively, are shown in Figs. 2 and 3. It is noticed that the transient results of the response Y acquired by the advanced procedure coincide well with MCS, especially in the PDF tails as demonstrated in the logarithmic PDFs, which are essential for reliability analysis. However, the results from EL are far from MCS due to the hypothesis that the system responses are Gaussian, which merely fits the real circumstances where the nonlinear system responses are generally non-Gaussian. It reveals the effectiveness of the advanced procedure which can solve the transient solution of the Duffing oscillator due to combined harmonic and modulated random stimulations. In addition, the oscillator responses are resulted in nonzero means and zero variances if the system is under only harmonic stimulation. Similarly, the responses of this oscillator are resulted in zero means and nonzero variances if the system is under only external modulated random stimulation. From the transient PDFs of the response Y, it is also observed that the PDFs are asymmetric about its means at different time instants due to the coupled impact of the combined harmonic and modulated random stimulations. In the time evolutionary process, the transient PDFs of the response \(\dot{Y}\) obtained by the advanced procedure, EL and MCS overlap, which means the transient PDF of velocity is always Gaussian distributed. Therefore, the transient PDF of the response \(\dot{Y}\) is not displayed here.

Fig. 2
figure 2

Transient PDF of the response Y at time \(t=7s\) in the Case 1

Full size image
Fig. 3
figure 3

Transient PDF of the response Y at time \(t=10s\) in the Case 1

Full size image

The mean and variance of Y evolved with time are displayed in Fig. 4. It is noticed that the mean of the response Y acquired by the advanced procedure is nonzero due to the harmonic stimulation. On the other hand, the variance is also nonzero due to the external modulated random stimulation. The PDF solutions acquired by the advanced procedure coincide with MCS as time elapses, which reveals that the advanced procedure works well for acquiring the transient PDFs of the oscillator responses. However, the results acquired by EL cannot match well with those acquired by MCS and the advanced procedure. It is noteworthy that the responses fluctuate as time elapses due to the coupled impact of the combined harmonic and modulated random stimulations. The modulated function can make the random stimulation disappear as time elapses, which could finally make the oscillator under harmonic stimulation only.

Fig. 4
figure 4

Evolutionary mean and variance of Y, acquired by various techniques in the Case 1

Full size image

Besides, it is noted that the advanced procedure takes only 34s to acquire the accurate transient solution at \(t=20s\), but 18.34 hours is required for MCS to acquire the transient solution at \(t=20s\) on the laptop with Intel i7-7700HQ processor (RAM 16GB, CPU @2.80GHz). The advanced procedure increases the computational efficiency dramatically by about 1,940 times.

4.2 Case 2: oscillator with complex nonlinearity

The following oscillator with complex nonlinearity under combined harmonic and modulated random stimulations is considered.

$$\begin{aligned}{} & {} \ddot{Y} + 2\xi \omega _n{\dot{Y}} +\varepsilon _1{\dot{Y}}^3 + \omega _n^2 Y + \varepsilon _2 Y^3 +\varepsilon _3{\dot{Y}}^2 Y + \varepsilon _4{\dot{Y}}Y^2\nonumber \\{} & {} \quad = Q\mathrm{{sin}}(\omega t)+g(t)\eta (t) \end{aligned}$$
(20)

where \(\xi =0.25\); \(\omega _n=1\); \(\varepsilon _1=0.5\); \(\varepsilon _2=1\); \(\varepsilon _3=\varepsilon _4=0.2\); \(Q=0.5\) and \(\omega =1\) are given as the harmonic parameters. The modulated function is considered as the same as that in the Case 1. The random stimulation is represented with the correlation function \(E\left[ \eta (t)\eta (t+\tau ) \right] =\delta (\tau )\); the initial Y and \(\dot{Y}\) at \(t=0s\) are characterized to be Gaussian with \(\mu _{Y}=\mu _{\dot{Y}}=0\) and \(\sigma _{Y}^2=\sigma _{\dot{Y}}^2=0.02\). The evolutionary PDF solution of the oscillator is analyzed with step being \(\Delta t=0.1s\) for both the EL and advanced EPC solution procedures, and \(\Delta t=0.02s\) for MCS.

The maximum variance of displacement is around \(t=5s\) as shown in Fig. 7. The transient PDFs of the oscillator responses at \(t=5s\) and \(t=8s\), respectively, are shown in Figs. 5\(\sim \)6. It is noticed that the transient results of the responses Y and \(\dot{Y}\) acquired by the advanced procedure still match well with MCS after adding various nonlinear terms to the oscillator, especially in the PDF tails as demonstrated in the logarithmic figures which play a key role in reliability analysis. However, the results of Y and \(\dot{Y}\) from EL deviate from MCS due to the hypothesis that the system responses are Gaussian, which cannot fit the real response because the oscillator responses are non-Gaussian in this case. It further reveals the workability of the advanced procedure, which can give the PDF solutions of the oscillators with various strong nonlinearity and subjected to combined harmonic and modulated random stimulations. In addition, the transient responses Y and \(\dot{Y}\) are both of nonzero means due to the impact of harmonic stimulation. It is also observed that the PDFs are asymmetric about the response means at different time instants resulted by the coupling action of the combined harmonic and modulated random stimulations.

Fig. 5
figure 5

Transient PDFs of the responses Y and \(\dot{Y}\) at time \(t=5s\) in the Case 2

Full size image
Fig. 6
figure 6

Transient PDFs of the responses Y and \(\dot{Y}\) at time \(t=8s\) in the Case 2

Full size image

The means and variances of Y and \(\dot{Y}\) vary with time are displayed in Fig. 7. It is noticed that the means of the responses Y and \(\dot{Y}\) acquired by the advanced procedure are nonzero due to the harmonic stimulation. On the other hand, the variances are also nonzero due to the external modulated random white noise. The evolutionary PDF solutions acquired by the advanced procedure coincide with MCS, which reveals that the advanced procedure also works well for acquiring the transient PDFs of the oscillator with the strong and more complicated nonlinear terms in this case. However, the results acquired by EL cannot match well with those acquired by MCS. The means and variances fluctuate as time elapses owing to the coupling impact of the combined harmonic and modulated random stimulations. The modulated function can make the random stimulation approach zero as time elapses, which could finally make the oscillator under harmonic stimulation only.

Fig. 7
figure 7

Evolutionary means and variances of Y and \(\dot{Y}\), respectively, acquired by various techniques in the Case 2

Full size image

Regarding the computational efficiency, it is observed that the advanced procedure takes only 36s to acquire the transient solution at \(t=20s\), but the time needed by MCS is about 18.6 hours for acquiring the transient solution at \(t=20s\) on the laptop with Intel i7-7700HQ processor (RAM 16GB, CPU @2.80GHz). The computational time spent by the advanced procedure is dramatically decreased by about 1,860 times in comparison with that spent by MCS.

4.3 Case 3: oscillator under resonance frequency

Consider the following oscillator under resonance frequency, subjected to combined harmonic and modulated random stimulations.

$$\begin{aligned}{} & {} \ddot{Y} + 2\xi \omega _n{\dot{Y}} +\varepsilon _1{\dot{Y}}^2Y +\varepsilon _2{\dot{Y}}Y^2 + \omega _n^2 Y + \varepsilon _3 Y^3\nonumber \\{} & {} \quad =Q\mathrm{{sin}}(\omega t)+g(t)\eta (t) \end{aligned}$$
(21)

where \(\xi =0.1\); \(\omega _n=1\); \(\varepsilon _1=\varepsilon _2=0.5\); \(\varepsilon _3=1\); \(Q=0.2\). The resonant frequency of this oscillator is found to be \(\omega =1.19\) in the sense of determinate vibration. The frequency of the external harmonic excitation is taken to be the resonance frequency, i.e., \(\omega =1.19\). The modulated function is considered as the same as that of Case 1. The random stimulation is represented with the correlation function \(E\left[ \eta (t)\eta (t+\tau ) \right] =0.2\delta (\tau )\); The initial Y and \(\dot{Y}\) at \(t=0s\) are characterized to be Gaussian with \(\mu _{Y}=\mu _{\dot{Y}}=0\) and \(\sigma _{Y}^2=\sigma _{\dot{Y}}^2=0.02\). The evolutionary PDF solution of the oscillator is analyzed with step \(\Delta t=0.1s\) for both the EL and advanced EPC solution procedures, and \(\Delta t=0.02s\) for MCS.

The maximum variance of displacement is around \(t=9s\) as shown in Fig. 10. The transient PDFs of the oscillator responses at \(t=9s\) and \(t=15s\), respectively, are shown in Figs. 8\(\sim \)9. It is observed that the transient results of the responses Y and \(\dot{Y}\) obtained by the advanced procedure still well fit with MCS even in the resonant situation. However, the results of Y and \(\dot{Y}\) from EL deviate from MCS due to the hypothesis that the system responses are Gaussian. In addition, the transient responses Y and \(\dot{Y}\) are both of nonzero means and asymmetric due to the impact of harmonic stimulation.

Fig. 8
figure 8

Transient PDFs of the responses Y and \(\dot{Y}\) at time \(t=9s\) in the Case 3

Full size image
Fig. 9
figure 9

Transient PDFs of the responses Y and \(\dot{Y}\) at time \(t=15s\) in the Case 3

Full size image

Actually, the resonance cannot happen due to the influence of white noise even if the harmonic frequency equals the resonance frequency of the oscillator in the sense of determinate vibration. However, numerical experiments show that the resonance can become more and more obvious as the modulated white noise becomes weaker and weaker after \(t=20s\) as shown in Fig. 1, which means that the determinate stimulation dominates the oscillator responses in this situation. On the other hand, when the influence of noise on the oscillator responses becomes so weak that it can be neglected after \(t=20s\), the oscillator needs to be analyzed by the methods for determinate oscillation in this situation [1].

The means and variances of Y and \(\dot{Y}\) vary with time are displayed in Fig. 10. It is noticed that the means of the responses Y and \(\dot{Y}\) obtained by the advanced procedure are nonzero due to the harmonic stimulation. On the other hand, the variances are also nonzero due to the external modulated random white noise. The evolutionary PDF solutions acquired by the advanced procedure coincide with MCS, which reveals that the advanced procedure also works well for acquiring the transient PDFs of the oscillator under resonant situation in this case. However, the results acquired by EL cannot match well with those acquired by MCS. The means and variances fluctuate as time elapses owing to the coupling impact of the combined harmonic stimulation and modulated random stimulation.

Fig. 10
figure 10

Evolutionary means and variances of Y and \(\dot{Y}\), respectively, acquired by various techniques in the Case 3

Full size image

Regarding the computational efficiency, it is observed that the advanced procedure takes only 35s to acquire the transient solution at \(t=20s\), but the time needed by MCS is 19 hours for acquiring the transient solution at \(t=20s\) on the laptop with Intel i7-7700HQ processor (RAM 16GB, CPU @2.80GHz). The computational time spent by the advanced procedure is dramatically decreased by about 1,954 times in comparison with that spent by MCS.

4.4 Case 4: oscillator with non-smooth nonlinear function

The following oscillator with non-smooth function of both damping and stiffness terms under both harmonic and modulated random stimulations is considered.

$$\begin{aligned}{} & {} \ddot{Y} + 2\xi \omega _n{\dot{Y}} + \varepsilon _1{\dot{Y}}|{\dot{Y}}|+ \varepsilon _2{\dot{Y}}^3+\varepsilon _3 Y^2{\dot{Y}}-\omega _n^2 Y \nonumber \\{} & {} +\quad \varepsilon _4Y|Y|+\varepsilon _5 Y^3= Q\mathrm{{sin}}(\omega t)+g(t)\eta (t) \end{aligned}$$
(22)

where \(\omega _n^2=0.1\); \(2\xi \omega _n=0.4\); \(\varepsilon _1=0.2\); \(\varepsilon _2=0.4\); \(\varepsilon _3=0.2\); \(\varepsilon _4=0.1\) and \(\varepsilon _5=0.05\). \(Q=0.1\) and \(\omega =1\). The modulation function is considered the same as that of Case 1. The random stimulation is represented with the correlation function \(E\left[ \eta (t)\eta (t+\tau ) \right] =0.3\delta (\tau )\); The initial PDFs of Y and \(\dot{Y}\) at \(t=0s\) are characterized as Gaussian variables with \(\mu _{Y}=\mu _{\dot{Y}}=0\) and \(\sigma _{Y}^2=\sigma _{\dot{Y}}^2=0.05\). The time evolutionary process is performed with step being \(\Delta t=0.1s\) for the EL and advanced EPC solution procedures, and \(\Delta t=0.02s\) for MCS.

The maximum variance of displacement is around \(t=8s\) as shown in Fig. 13. The transient PDFs of the oscillator responses at \(t=8s\) and \(t=17s\), respectively, are shown in Figs. 11 and 12. The PDF of displacement shows bimodal behavior in this case due to the negative coefficient of Y. It is observed that the transient PDF solutions of the responses Y and \(\dot{Y}\) acquired by the advanced procedure also coincide well with MCS, especially in the PDF tails as demonstrated in the logarithmic figures, which are essential for reliability analysis. However, the results of Y and \(\dot{Y}\) from EL are far from MCS due to the hypothesis that the system responses are Gaussian. It further reveals that the presented advanced procedure also works effectively when the response of the oscillator has transient bimodal PDF solution and when there are nonlinear terms which are non-smooth function of both displacement and velocity. In addition, both the PDFs of Y and \(\dot{Y}\) are asymmetric about their nonzero means due to the impact of harmonic stimulation.

Fig. 11
figure 11

Transient PDFs of the responses Y and \(\dot{Y}\) at time \(t=8s\) in the Case 4

Full size image
Fig. 12
figure 12

Transient PDFs of the responses Y and \(\dot{Y}\) at time \(t=17s\) in the Case 4

Full size image

The means and variances of displacement Y and velocity \(\dot{Y}\) varying with time are displayed in Fig. 13. It is noticed that the means of Y and \(\dot{Y}\) acquired by the advanced procedure are nonzero due to the harmonic stimulation. On the other hand, the variances are also nonzero due to the external modulated random stimulation. The responses acquired by the advanced procedure coincide with MCS as time elapses, which reveals that the advanced procedure also works well for acquiring the transient PDFs of the oscillator responses in this case. However, the variances acquired by EL cannot match well with those acquired by MCS. It is noteworthy that the responses fluctuate as time elapses owing to the coupling impact of the combined harmonic and modulated random stimulations. The modulated function can make the random stimulation disappear as time elapses, which could finally make the oscillator under pure harmonic stimulation.

Fig. 13
figure 13

Evolutionary means and variances of Y and \(\dot{Y}\), respectively, acquired by various techniques in the Case 4

Full size image

Notably, it is observed that the advanced procedure takes 135s to acquire the transient solution at \(t=20s\), but the MCS needs 19.10 hours to acquire the transient solution at \(t=20s\) on the laptop with Intel i7-7700HQ processor (RAM 16GB, CPU @2.80GHz). The computational time needed by the advanced procedure is decreased by about 509 times in comparison to MCS.

5 Conclusions

In this study, the advanced EPC procedure is formulated and presented for solving the challenging problems about the transient solutions of different oscillators under combined harmonic and modulated random stimulations. The results obtained by the advanced procedure, MCS and EL, respectively, are compared in various cases. The impact of determinate resonance frequency on the transient solutions of the oscillator responses is also studied. The outcomes reveal that (1) the advanced procedure works well for the transient PDF solutions of the oscillators under both the harmonic and modulated random stimulations despite of the various nonlinear terms in the systems; (2) even if there are both harmonic and modulated random stimulations in the system, the PDF and moment solutions of the oscillator responses can still well fit the MCS results in the extendable ranges of MCS solutions; (3) the advanced procedure is also suitable for the oscillators with bimodal PDF solutions; (4) the advanced procedure works well for the oscillators with non-smooth nonlinear terms in both displacement and velocity. Notably, the probabilistic tails obtained by the advanced procedure match well with MCS as demonstrated in the logarithmic figures, which play a key role in reliability analysis. More accurately predicting the probabilistic tails of the strongly nonlinear oscillators subjected to both harmonic and modulated random stimulations by utilizing MCS requires a larger sample size, which in turn demands tremendous computational effort. In this case, utilizing the advanced EPC solution procedure can lead to significant decrease in computational effort without sacrificing the accuracy of PDF solutions in contrast to MCS when the sample size is adopted to be \(10^8\). More computational burden can be increased if the MCS solution is to extend to the probabilistic tails as demonstrated in the numerical cases. It is also noted that the PDFs of the oscillator responses are of nonzero means and asymmetrical due to the influence of harmonic stimulation.