1 Introduction

In the field of stochastic engineering dynamics, classical continuum (or discretized) mechanics theories have been traditionally used for modeling the governing equations of motion of the dynamic system under consideration. Nevertheless, the need for more accurate media behavior modeling has led recently to advanced mathematical tools such as fractional calculus (e.g., [1,2,3]). Besides the fact that fractional calculus can be construed as a generalization of classical calculus (and thus, provides with enhanced modeling flexibility), it has been successfully employed in theoretical and applied mechanics for developing non-local continuum mechanics theories (e.g., [4, 5]), as well as for viscoelastic material modeling. Indeed, experimental viscoelastic response data obtained via creep and relaxation tests agree extremely well with such kind of modeling (e.g., [6]). Further, indicative applications in structural engineering where theoretical developments are in agreement with experimental data include modeling of viscoelastic dampers used for vibration control, or for seismic isolation purposes [7,8,9,10,11].

From a mathematics perspective, the equation of motion typically takes the form of a fractional differential equation to be solved for the oscillator response. Note that due to the convolution integral associated with the definition of the fractional operator, a brute force naive numerical solution can be a highly demanding task computationally. In fact, in many cases the above modeling is also coupled with complex nonlinearities and hysteresis; thus, rendering even the deterministic solution of such equations an open issue and an active research topic. Clearly, solving the stochastic counterparts of these equations becomes significantly more challenging. Therefore, there is a need for developing efficient solution schemes for determining the stochastic response and assessing the reliability of dynamic systems endowed with fractional derivative terms. Indicative solution techniques for linear and nonlinear (continuous or discretized) oscillators with fractional derivative terms can be found in Refs [12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Nevertheless, to the best of the authors’ knowledge, very limited results exist referring to the response determination of nonlinear oscillators with fractional derivative elements subject to non-stationary stochastic excitation described by evolutionary (potentially non-separable) power spectra; see for instance [26, 27] for some relevant recent developments on stochastic joint time-frequency response analysis of such systems based on the harmonic wavelet transform.

In this regard, a novel approximate technique for determining the non-stationary response amplitude probability density function (PDF) of nonlinear/hysteretic oscillators endowed with fractional derivative elements and subjected to evolutionary stochastic excitation is developed herein. Specifically, resorting to a stochastic linearization/averaging treatment of the problem yields a first-order stochastic differential equation governing the oscillator response amplitude. Next, assuming a time-dependent PDF of the Rayleigh kind for the response amplitude, the associated Fokker–Planck partial differential equation is solved for determining the oscillator non-stationary response amplitude PDF in closed-form and at a minimal computational cost. An additional advantage of the technique is that it can handle arbitrary forms of the excitation evolutionary power spectrum, even of the non-separable kind. The numerical examples include a hardening Duffing and a bilinear hysteretic nonlinear oscillators with fractional derivative terms, while the accuracy of the analytical results is assessed by comparisons with pertinent Monte Carlo simulation (MCS) data. Overall, the technique developed in this paper can be construed as a generalization of the concepts and results obtained in [28] to account for fractional derivative terms in the oscillator’s equation of motion.

2 Mathematical formulation

2.1 Equivalent linear oscillator determination

In this section, based on statistical linearization of the original nonlinear equation of motion, an equivalent linear time-variant oscillator is introduced. This treatment facilitates in the ensuing analysis the determination of a novel closed-form approximate expression for the oscillator non- stationary response amplitude PDF.

2.1.1 Equivalent linear amplitude-dependent stiffness and damping elements

A nonlinear oscillator with fractional derivative terms is considered in the ensuing analysis, whose governing equation of motion is given by

$$\begin{aligned} \ddot{x}(t) + \beta \mathscr {D}^{\alpha }_{0,t}x(t) + z(t,x,\dot{x}) = w(t) \end{aligned}$$
(1)

where \(z(t,x,\dot{x})\) represents an arbitrary nonlinear function that can also account for hysteretic behaviors; and w(t) denotes a Gaussian, zero-mean, non-stationary stochastic process with an evolutionary broad-band power spectrum \(S(\omega ,t)\). Further, \(\beta \) is a coefficient and \(\mathscr {D}^{\alpha }_{0,t}x(t)\) denotes a Caputo fractional derivative defined as

$$\begin{aligned} \mathscr {D}^{\alpha }_{0,t}x(t) = \frac{1}{\varGamma (1-\alpha )} \int _{0}^{t} \frac{\dot{x}(\tau )}{(t-\tau )^\alpha } \mathrm{d}\tau \end{aligned}$$
(2)

for \(0<\alpha <1\). Next, resorting to the assumption of light damping for the oscillator of Eq. (1), it can be argued that it exhibits a pseudo-harmonic behavior described by the equations [28, 29]

$$\begin{aligned} x(t) = A(t)\cos (\omega (A)t+\psi (t)) \end{aligned}$$
(3)

and

$$\begin{aligned} \dot{x}(t) = -\omega (A)A(t)\sin (\omega (A)t+\psi (t)) \end{aligned}$$
(4)

where the equivalent natural frequency \(\omega (A)\), to be determined in the following, is approximated as a function of the response amplitude \(A=A(t)\). Taking into account Eqs. (3) and (4), the oscillator response amplitude A(t) and phase \(\psi (t)\) are given by

$$\begin{aligned} A^2(t) = x^2(t) + \left( \frac{\dot{x}(t)}{\omega (A)} \right) ^2 \end{aligned}$$
(5)

and

$$\begin{aligned} \psi (t) = -\omega (A)t - \mathrm{arctan}\left( \frac{\dot{x}(t)}{x(t)\omega (A)} \right) \end{aligned}$$
(6)

respectively. They are considered to be slowly varying functions with respect to time, and approximately constant over one cycle of oscillation; see also [29, 30].

Next, Eq. (1) is recast, equivalently, in the form [31, 32]

$$\begin{aligned} \ddot{x}(t) + \beta _0 \dot{x}(t) + h(t,x,\mathscr {D}^{\alpha }_{0,t}x,\dot{x}) = w(t) \end{aligned}$$
(7)

where

$$\begin{aligned} h(t,x,\mathscr {D}^{\alpha }_{0,t}x,\dot{x}) = \beta \mathscr {D}^{\alpha }_{0,t}x(t) + z(t,x,\dot{x}) - \beta _0 \dot{x} \end{aligned}$$
(8)

and \(\beta _0=2\zeta _0\omega _0\) is a damping coefficient, with \(\omega _0\) denoting the natural frequency of the corresponding linear oscillator and \(\zeta _0\) representing the ratio of critical damping. Following Ref. [31] (see also [29]), an equivalent linear oscillator is defined as

$$\begin{aligned} \ddot{x}(t) + [\beta _0 + \beta (A)]\dot{x}(t) + \omega ^2(A)x(t) = w(t) \end{aligned}$$
(9)

Applying an error minimization procedure in the mean square sense between Eqs. (7) and (9) yields the equivalent linear amplitude-dependent damping and stiffness coefficients in the form [30, 31]

$$\begin{aligned} \beta (A)= & {} -\frac{1}{\pi A\omega (A)} \left\{ \int _{0}^{2\pi } z(A\cos \phi ,\right. \nonumber \\&-\, A\omega \sin \phi )\sin \phi \mathrm{d}\phi \nonumber \\&\left. +\, \beta \int _{0}^{2\pi } \mathscr {D}^{\alpha }_{0,t}(A\cos \phi )\sin \phi \mathrm{d}\phi +\pi \beta _0 A\omega (A) \right\} \nonumber \\ \end{aligned}$$
(10)

and

$$\begin{aligned} \omega ^2(A)= & {} \frac{1}{\pi A} \left\{ \int _{0}^{2\pi } z(A\cos \phi ,-A\omega \sin \phi )\cos \phi \mathrm{d}\phi \right. \nonumber \\&+ \left. \beta \int _{0}^{2\pi } \mathscr {D}^{\alpha }_{0,t}(A\cos \phi )\cos \phi \mathrm{d}\phi \right\} \end{aligned}$$
(11)

where \(\phi (t) = \omega (A)t+\psi (t)\).

Note that the expressions in Eqs. (10) and (11) can be further simplified by appropriately approximating the involved fractional derivatives according to Refs [32, 33]. In this regard, Eq. (10) becomes

$$\begin{aligned} \beta (A) = \frac{1}{A\omega (A)}S(A) + \frac{\beta }{\omega ^{1-\alpha }(A)} \sin \left( \frac{\alpha \pi }{2}\right) - \beta _0\nonumber \\ \end{aligned}$$
(12)

and Eq. (11) takes the form

$$\begin{aligned} \omega ^2(A)= & {} \frac{1}{A}F(A) + \beta \omega ^{\alpha }(A) \cos \left( \frac{\alpha \pi }{2}\right) \end{aligned}$$
(13)

where

$$\begin{aligned} S(A) = -\frac{1}{\pi } \int _{0}^{2\pi } z\left( A\cos \phi ,-A\omega (A) \sin \phi \right) \sin \phi \mathrm{d}\phi \nonumber \\ \end{aligned}$$
(14)

and

$$\begin{aligned} F(A)= & {} \frac{1}{\pi } \int _{0}^{2\pi } z\left( A\cos \phi ,-A\omega (A) \sin \phi \right) \cos \phi \mathrm{d}\phi \nonumber \\ \end{aligned}$$
(15)

For completeness, additional details on the derivation of Eqs. (12) and (13) are provided in the Appendix of Sect. 5. For the ensuing analysis, it is important to note that a stochastic averaging technique [29] can be applied to the linearized Eq. (9) with the aim of reducing its order, and potentially its complexity from a solution perspective. This yields a first-order stochastic differential equation for the response amplitude A(t), while the corresponding Fokker–Planck partial differential equation governing the evolution in time of the response amplitude PDF is given in the form [24, 31]

$$\begin{aligned}&\frac{\partial p(A,t)}{\partial t}\nonumber \\&\quad = -\left\{ \left[ \frac{1}{2}\beta _0+\beta (A) \right] A - \frac{\beta _0\omega _0^2}{2A\omega ^2(A)} \right\} \frac{\partial p(A,t)}{\partial A} \nonumber \\&\qquad +\, \left[ \frac{\beta _0\omega _0^2}{2\omega ^2(A)} \right] \frac{\partial ^2 p(A,t)}{\partial A^2} \end{aligned}$$
(16)

Note that although an analytical solution of Eq. (16) for the general case is, perhaps, impossible, a solution for the special case of a linear oscillator (i.e., \(z(t,x,\dot{x})=\omega _0^2x\)) with \(\frac{\partial p(A,t)}{\partial t}=0\) and \(S(\omega ,t)=S_0\) is readily attainable. Indeed, as shown in Ref. [24], the stationary response amplitude PDF of a linear oscillator with fractional derivative elements subjected to Gaussian white noise excitation is given by

$$\begin{aligned} p(A) = \frac{\sin \left( \frac{\alpha \pi }{2}\right) A}{\omega _0^{1-\alpha }\sigma ^2}\exp \left( - \frac{\sin (\frac{\alpha \pi }{2})}{\omega _0^{1-\alpha }\sigma ^2}\frac{A^2}{2} \right) \end{aligned}$$
(17)

where \(\sigma ^2 = \frac{\pi S_0}{\beta \omega _0^2}\) represents the stationary response variance of a linear oscillator under white noise excitation. Motivated by the form of Eq. (17), a novel approximate analytical solution is developed in the following section for the non-stationary response amplitude PDF p(A, t) of the general nonlinear oscillator of Eq. (1) (or, equivalently Eq. (7)).

2.1.2 Non-stationary response amplitude PDF and equivalent linear time-dependent stiffness and damping elements

It can be readily seen that one of the main difficulties in solving the general Fokker–Planck Eq. (16) and determining the non-stationary response amplitude PDF p(A, t) relates to the fact that the equivalent linear elements \(\omega ^2(A)\) and \(\beta (A)\) are amplitude-dependent. This increases the complexity of the Fokker–Planck Eq. (16), and renders its analytical solution a rather daunting task. In fact, it is no wonder that once the corresponding linear oscillator is considered in Eq. (1), i.e., \(z(t, x, \dot{x})=\omega _0^2x\), the solution of the time- independent (\(\frac{\partial p(A,t)}{\partial t}=0\)) Fokker–Planck Eq. (16) is possible, yielding the stationary response PDF of Eq. (17).

In this regard, to facilitate the solution of the general Fokker–Planck equation and determine, in an analytical form, the non-stationary response amplitude PDF p(A, t) corresponding to the nonlinear oscillator of Eq. (1), time-dependent equivalent linear elements \(\omega _\mathrm{{eq}}(t)\) and \(\beta _\mathrm{{eq}}(t)\) are introduced in the following. These correspond to an alternative to Eq. (9) equivalent linear oscillator of the form

$$\begin{aligned} \ddot{x}(t) + (\beta _0+\beta _\mathrm{{eq}}(t))\dot{x}(t) + \omega ^2_\mathrm{{eq}}(t) x(t) = w(t) \end{aligned}$$
(18)

where, by employing Eqs. (12) and (13), \(\beta _\mathrm{{eq}}(t)\) and \(\omega _\mathrm{{eq}}^2(t)\) are defined as

$$\begin{aligned} \beta _\mathrm{{eq}}(t)= & {} - \beta _0 + \int _0^{\infty } \frac{S(A)}{A\omega (A)} p(A,t)\mathrm{d}A \nonumber \\&+\, \beta \sin \left( \frac{\alpha \pi }{2}\right) \int _0^{\infty } \frac{1}{\omega ^{1-\alpha }(A)} p(A,t)\mathrm{d}A\nonumber \\ \end{aligned}$$
(19)

and

$$\begin{aligned} \omega ^2_\mathrm{{eq}}(t)= & {} ~ \int _0^{\infty } \frac{F(A)}{A} p(A,t)\mathrm{d}A \nonumber \\&+\, \beta \cos \left( \frac{\alpha \pi }{2}\right) \int _0^{\infty } \omega ^{\alpha }(A) p(A,t)\mathrm{d}A \end{aligned}$$
(20)

respectively. Clearly, the equivalent linear time-dependent elements of Eqs. (19) and (20) are the non-stationary mean values of the amplitude-dependent elements of Eqs. (12) and (13). To evaluate them, however, knowledge of the non-stationary response amplitude PDF p(A, t) is required. To this aim, motivated by the form of the stationary PDF of Eq. (17), a generalized closed-form solution for the non-stationary response amplitude PDF of nonlinear oscillators with fractional derivative terms is developed herein. This takes the form

$$\begin{aligned} p(A,t) = \frac{\sin \left( \frac{\alpha \pi }{2}\right) A}{\omega _0^{1-\alpha }c(t)} \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \end{aligned}$$
(21)

where c(t) is a time-dependent coefficient to be determined. Equation (21) constitutes a generalization of the developments and the PDF proposed in Ref. [28] to account for fractional derivative terms in the oscillator’s governing equation. Note that due to the form of p(A, t) in Eq. (21), the equivalent elements of Eqs. (19) and (20) become essentially functions of the time-dependent coefficient c(t). Further, for the equivalent linear oscillator of Eq. (18), Eq. (3) becomes

$$\begin{aligned} x(t) = A(t)\cos (\mathbf{\omega }_\mathrm{{eq}}(c(t))t+\mathbf{\psi }(t)) \end{aligned}$$
(22)

Next, for an oscillator with zero initial conditions it can be assumed that the amplitude A(t) and phase \(\psi (t)\) are statistically independent (see Ref. [34] for more details). Considering also that the PDF of \(\psi (t)\) is uniform in the interval \([-\pi ,\pi )\) and the amplitude PDF is given by Eq. (21), their joint PDF takes the form \( p(A(t),\phi (t),t) = p(\phi (t))p(A(t),t) = \frac{1}{2\pi } \frac{\sin \left( \frac{\alpha \pi }{2}\right) A}{\omega _0^{1-\alpha }c(t)} \exp \left( - \frac{\sin (\frac{\alpha \pi }{2})}{\omega _0^{1-\alpha }} \frac{A^2}{2c(t)}\right) \). Taking this into account and evaluating the second moment (coinciding herein with the variance) of x(t) of Eq. (22) yields

$$\begin{aligned} E(x^2)= \frac{\omega _0^{1-\alpha }}{\sin \left( \frac{\alpha \pi }{2} \right) } c(t) \end{aligned}$$
(23)

Based on Eq. (23), the scaled by \(\frac{\omega _0^{1-\alpha }}{\sin \left( \frac{\alpha \pi }{2} \right) }\) time-dependent coefficient c(t), involved in the p(A, t) definition of Eq. (21), can be construed as the oscillator non-stationary response variance.

As shown in the following section, the introduction of the alternative time-variant equivalent linear oscillator of Eq. (18) is instrumental in determining the non-stationary response amplitude PDF in the analytical form of Eq. (21) via the evaluation of c(t). As an additional advantage of the technique, the determination of the equivalent linear time-dependent elements \(\omega ^2_\mathrm{{eq}}(t)\) and \(\beta _\mathrm{{eq}}(t)\), as a by-product of the methodology, is of considerable importance to applications in dynamics related to evaluating the effects of temporal nonstationarity in the frequency content of the excitation on the system response (e.g., [35,36,37,38]). The time-dependent stiffness and damping elements can also be employed for tracking and quantifying “moving resonance phenomena”, which may result in significant response amplifications in nonlinear systems (e.g., [39, 40]).

2.2 Stochastic averaging solution treatment

In this section, based on a stochastic averaging treatment of the equivalent linear time-variant oscillator of Eq. (18), the non-stationary response amplitude PDF of Eq. (21) is determined via evaluating the time-dependent coefficient c(t) in a computationally efficient manner. Specifically, considering the time-dependent equivalent linear damping and stiffness elements in Eqs. (19) and (20), respectively, to be slowly varying with respect to time and approximately constant over one period of oscillation, and taking into account Eq. (22) and its time-derivative, yields

$$\begin{aligned} A^2(t) = x^2(t) + \frac{\dot{x}^2(t)}{\omega _\mathrm{{eq}}^2(c(t))} \end{aligned}$$
(24)

Next, differentiating Eq. (24) with respect to time, employing Eq. (18), and manipulating, leads to (see also [28])

$$\begin{aligned} \dot{A}(t)= & {} - \beta _0 A(t) \sin ^2\phi - \beta _\mathrm{{eq}}(c(t))A(t) \sin ^2\phi \nonumber \\&- \frac{w(t)\sin \phi }{\omega _\mathrm{{eq}}(c(t))} \end{aligned}$$
(25)

Following a standard averaging approach (e.g., [29]), the term \(\sin ^2\phi \) in Eq. (25) is approximated by its average over one cycle of oscillation, i.e., \(\sin ^2\phi =\frac{1}{2}\); thus, Eq. (25) becomes

$$\begin{aligned} \dot{A}(t) = - \frac{1}{2} (\beta _0 + \beta _\mathrm{{eq}}(t))A(t) - \frac{w(t)\sin \phi }{\omega _\mathrm{{eq}}(t)} \end{aligned}$$
(26)

Next, exploiting the wide-band nature of the excitation process w(t) in the frequency domain, and taking ensemble average over w(t) and the phase \(\psi (t)\) for \(t\pm dt\), the last term on the right hand side of Eq. (26) is approximated by

$$\begin{aligned} \frac{w(t)\sin \phi }{\omega _\mathrm{{eq}}(t)} \approx - \frac{\pi S(\omega _\mathrm{{eq}}(t),t)}{2A\omega _\mathrm{{eq}}^2(t)} - \frac{(\pi S(\omega _\mathrm{{eq}}(t),t))^{\frac{1}{2}}}{\omega _\mathrm{{eq}}(t)}\eta (t) \end{aligned}$$
(27)

where \(\eta (t)\) denotes a zero-mean, delta correlated process of intensity one. A detailed presentation on the derivation of Eqs. (26) and (27) can be found in Refs [28, 29, 41].

Combining Eq. (26) with Eq. (27) yields

$$\begin{aligned} \dot{A}(t) = K_1(A,t) + K_2(A,t)\eta (t) \end{aligned}$$
(28)

where the terms \(K_1(A,t)\) and \(K_2(A,t)\) are given by

$$\begin{aligned} K_1(A,t) = - \frac{1}{2} \left( \beta _0 + \beta _\mathrm{{eq}}(t)\right) A + \frac{\pi S(\omega _\mathrm{{eq}}(t),t)}{2A\omega _\mathrm{{eq}}^2(t)} \end{aligned}$$
(29)

and

$$\begin{aligned} K_2(A,t) = \frac{\left( \pi S(\mathbf{\omega }_\mathrm{{eq}}(t),t)\right) ^{1/2}}{\mathbf{\omega }_\mathrm{{eq}}(t)} \end{aligned}$$
(30)

respectively. The corresponding to Eq. (28) Fokker–Planck equation is given by (e.g., [28, 42, 43])

$$\begin{aligned}&\frac{\partial p(A,t)}{\partial t}\nonumber \\&\quad = - \frac{\partial }{\partial A} \left\{ \left( - \frac{1}{2} (\beta _0 + \beta _\mathrm{{eq}}(t))A + \frac{\pi S(\omega _\mathrm{{eq}}(t),t)}{2\omega _\mathrm{{eq}}^2(t) A} \right) \right. \nonumber \\&\qquad \times \, \left. p(A,t) \right\} + \frac{1}{4}\frac{\partial }{\partial A} \left\{ \frac{\pi S(\omega _\mathrm{{eq}}(t),t)}{\omega _\mathrm{{eq}}^2(t)} \frac{\partial p(A,t)}{\partial A}\right. \nonumber \\&\qquad +\, \left. \frac{\partial }{\partial A} \left[ \frac{\pi S(\omega _\mathrm{{eq}},t)}{\omega _\mathrm{{eq}}^2(t)} p(A,t) \right] \right\} \end{aligned}$$
(31)

Next, a solution to the Fokker–Planck Eq. (31) is sought in the analytical form of Eq. (21). Differentiating Eq. (21) yields

$$\begin{aligned}&\frac{\partial p}{\partial t} = \frac{\dot{c}(t)}{c(t)} \left( \frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)} - 1 \right) p \end{aligned}$$
(32)
$$\begin{aligned}&\frac{\partial (Ap)}{\partial A} = -2 \left( \frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }} \frac{A^2}{2c(t)} - 1 \right) p \end{aligned}$$
(33)

and

$$\begin{aligned} \frac{\partial ^2 p}{\partial A^2} = \frac{\partial \left( \frac{p}{A} \right) }{\partial A} - \frac{1}{c(t)} \frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{\partial (Ap)}{\partial A} \end{aligned}$$
(34)

Substituting Eqs. (32)–(34) into Eq. (31), and manipulating, results to the equation

$$\begin{aligned} \frac{\partial p(A,t)}{\partial t}= & {} ~ \left[ \frac{1}{2}(\beta _0 + \beta _\mathrm{{eq}}(c(t))) \right. \nonumber \\&-\, \left. \frac{\pi S(\omega _\mathrm{{eq}}(c(t)),t)}{2\omega _\mathrm{{eq}}^2(c(t))}\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }c(t)} \right] \frac{\partial (Ap)}{\partial A}\nonumber \\ \end{aligned}$$
(35)

Further, utilizing Eq. (32) and manipulating, Eq. (35) leads to

$$\begin{aligned}&\left[ \frac{\dot{c}(t)}{c(t)} + \beta _0 + \beta _\mathrm{{eq}}(c(t)) - \frac{\pi S(\omega _\mathrm{{eq}}(c(t)),t) \sin \left( \frac{\alpha \pi }{2}\right) }{c(t)\omega _\mathrm{{eq}}^2(c(t))\omega _0^{1-\alpha }} \right] \nonumber \\&\qquad \times \left( \frac{A^2\sin \left( \frac{\alpha \pi }{2}\right) }{2\omega _0^{1-\alpha }c(t)} - 1 \right) p=0 \end{aligned}$$
(36)

Thus, Eq. (36) dictates that the time-dependent coefficient c(t) is given as the solution of a deterministic first-order nonlinear ordinary differential equation, which takes the form

$$\begin{aligned} \dot{c}(t)= & {} - \left( \beta _0 + \beta _\mathrm{{eq}}(c(t)) \right) c(t) \nonumber \\&+\, \left( \frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }} \right) \frac{\pi S(\omega _\mathrm{{eq}}(c(t)),t)}{\omega _\mathrm{{eq}}^2(c(t))} \end{aligned}$$
(37)

Equation (37) can be readily solved at a low computational cost by employing any standard numerical integration scheme, such as the Runge–Kutta. As a result, the non-stationary response amplitude PDF is determined by simply substituting c(t) into Eq. (21). Note that setting the fractional derivative order equal to \(\alpha =1\), the equations and formulae developed in this section degenerate to the ones derived in Ref. [28]. In this regard, the herein developed technique can be construed as a generalization and extension of the results in Ref. [28] to account for oscillators endowed with fractional derivative terms. In the following section, the accuracy of the herein developed approximate analytical expressions \(\frac{\omega _0^{1-\alpha }}{\sin \left( \frac{\alpha \pi }{2} \right) }c(t)\) and \(p(A,t) = \frac{\sin \left( \frac{\alpha \pi }{2}\right) A}{\omega _0^{1-\alpha }c(t)} \exp \left( -\frac{\sin (\frac{\alpha \pi }{2})}{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \) in capturing the non-stationary response variance and PDF, respectively, is assessed by considering various numerical examples and comparisons with pertinent MCS data.

3 Numerical examples

In this section, the hardening Duffing and the bilinear hysteretic nonlinear oscillators with fractional derivative elements are considered for assessing the reliability of the developed technique. The oscillators, which are initially at rest, are subjected to non-stationary stochastic excitation described by the non-separable evolutionary power spectrum

$$\begin{aligned} S_w(\omega ,t) = S_0\left( \frac{\omega }{5\pi }\right) ^2\exp (-c_0t)t^2\exp \left( -\left( \frac{\omega }{5\pi }\right) ^2t\right) \end{aligned}$$
(38)

It can be argued that the power spectrum of Eq. (38), originally proposed in Ref. [44], comprises some of the main characteristics of seismic shaking, such as decreasing of the dominant frequency with time (e.g., [36, 39]). Further, for comparisons of the analytical results with MCS data, realizations compatible with Eq. (38) are produced according to the spectral representation methodology (e.g., [45]), while the numerical integration of the governing Eq. (1) is done by resorting to an L1-algorithm [1, 7].

3.1 Duffing oscillator with fractional derivative terms

For the case of a Duffing oscillator with fractional derivative elements, the nonlinear function \(z(t, x, \dot{x})\) in Eq. (1) takes the form

$$\begin{aligned} z(t, x, \dot{x}) = \omega _0^2 x (1 + \varepsilon x^2) \end{aligned}$$
(39)

where the parameter \(\varepsilon > 0\) accounts for the nonlinearity magnitude. Substituting Eq. (39) into Eqs. (19) and (20), and considering the amplitude PDF of Eq. (21), yields

$$\begin{aligned} \beta _\mathrm{{eq}}(c(t))= & {} -\beta _0 + \frac{\beta \sin ^2\left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }c(t)} \nonumber \\&\times \, \int _0^\infty \frac{A}{\omega ^{1-\alpha }(A)} \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A\nonumber \\ \end{aligned}$$
(40)

and

$$\begin{aligned} \omega _\mathrm{{eq}}^2(c(t))= & {} \omega _0^2 + \frac{\beta \sin \left( \frac{\alpha \pi }{2}\right) \cos \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }c(t)} \nonumber \\&\times \, \int _0^\infty A \omega ^\alpha (A) \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A \nonumber \\&+ \frac{3\varepsilon \omega _0^{1+\alpha } \sin \left( \frac{\alpha \pi }{2}\right) }{4c(t)} \nonumber \\&\times \, \int _0^\infty A^3 \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A \end{aligned}$$
(41)

Next, the time-dependent coefficient c(t) is determined by solving numerically the deterministic differential Eq. (37), where \(\beta _\mathrm{{eq}}(c(t))\) and \(\omega _\mathrm{{eq}}^2(c(t))\) are given by Eqs. (40) and (41).

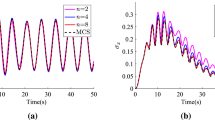
For the numerical implementation, the following values are used for the excitation and the system parameters: \(S_0 = 0.16\), \(c_0 = 0.15\), \(\omega _0=3.62\). In Fig. 1a and b, the non-stationary response variances of a nonlinear Duffing oscillator with \(\varepsilon =2\) determined via Eq. (23) are plotted for fractional derivative orders \(\alpha =1\) and \(\alpha =0.5\), respectively. Thus, the influence of the fractional order derivative on the system response variance can be assessed. The corresponding linear oscillator (\(\varepsilon =0\)) response variances are plotted as well to show the considerable nonlinearity effect on the system response. In all cases, comparisons with MCS-based response variances show a satisfactory degree of accuracy.

Fig. 1
figure 1

a Non-stationary response variance of a Duffing nonlinear oscillator (\(\varepsilon =2\)) with fractional derivative order \(\alpha =1\); b Non-stationary response variance of a Duffing nonlinear oscillator (\(\varepsilon =2\)) with fractional derivative order \(\alpha =0.5\). MCS data are included for comparison

Full size image

Based on the reasonable agreement observed in Fig. 1 between the analytical and the MCS results, the performance of the closed-form expression of Eq. (21) in capturing the oscillator non-stationary response amplitude PDF is assessed next. In this regard, in Fig. 2a, b, the analytical response amplitude PDF of a Duffing oscillator (\(\varepsilon =2\)) with a fractional derivative order \(\alpha =0.5\), and the corresponding MCS-based PDF estimate are plotted, respectively. In Fig. 3, the analytical PDF is plotted for various time instants and compared with corresponding MCS data. It can be readily seen that although the accuracy exhibited is not excellent, the herein developed closed-form expression of Eq. (21) appears capable of capturing both the time-evolution in an average sense and the salient features of the non-stationary response amplitude PDF.

Fig. 2
figure 2

Non-stationary response amplitude PDF of a Duffing oscillator (\(\varepsilon =2\)) with fractional derivative order \(\alpha =0.5\): a analytical PDF; b MCS-based estimate (10,000 realizations)

Full size image
Fig. 3
figure 3

Analytical (Eq. (21)) vis-a-vis MCS-based (10,000 realizations) response amplitude PDFs of a Duffing oscillator (\(\varepsilon =2\)) with fractional derivative order \(\alpha =0.5\), plotted for various time instants

Full size image

3.2 Bilinear hysteretic oscillator with fractional derivative terms

In this example, a bilinear hysteretic oscillator (e.g., [46]) with fractional derivative terms is considered. Denoting by \(x^\star \) the critical value of the displacement at which the yield occurs, the non-dimensional displacement \(y = x/x^\star \) is introduced. Further, denoting by \(\omega _0\) the oscillator natural frequency corresponding to the primary elastic slope, the non-dimensional time quantity \(\tau = \omega _0 t\) is also employed. In this regard, the restoring force of the oscillator defined in Eq. (1) is given by [30, 36]

$$\begin{aligned} z(t, y, \dot{y}) = \gamma y + (1-\gamma )z_0 \end{aligned}$$
(42)

where \(\gamma \) denotes the post- to pre-yield stiffness ratio, and \(z_0\) is the hysteretic force corresponding to the elasto-plastic characteristic, described by the first-order differential equation [30, 36]

$$\begin{aligned} \dot{z}_0 = \dot{y} \left[ 1 - H(\dot{y})H(z_0-1) - H(-\dot{y})H(-z_0-1) \right] \end{aligned}$$
(43)

Taking into account Eq. (42), Eq. (14) becomes

$$\begin{aligned} S(A) = (1-\gamma )S_0(A) \end{aligned}$$
(44)

where

$$\begin{aligned} S_0(A) = - \frac{1}{\pi } \int _0^{2\pi } z_0(A,t) \sin \phi \mathrm{d}\phi \end{aligned}$$
(45)

Further, Eq. (15) takes the form

$$\begin{aligned} F(A) = \gamma A + (1-\gamma )F_0(A) \end{aligned}$$
(46)

where

$$\begin{aligned} F_0(A) = \frac{1}{\pi } \int _0^{2\pi } z_0(A,t) \cos \phi \mathrm{d}\phi \end{aligned}$$
(47)

Following Refs [30, 46] for calculating the integrals of Eqs. (45) and (47), \(S_0(A)\) and \(F_0(A)\) are given by the expressions

$$\begin{aligned} S_0(A) = \left\{ \begin{array}{ll} \frac{4}{\pi }\left( 1-\frac{1}{A}\right) , &{}\quad A > 1 \\ 0, &{}\quad A \le 1 \\ \end{array} \right. \end{aligned}$$
(48)

and

$$\begin{aligned} F_0(A) = \left\{ \begin{array}{ll} \frac{A}{\pi }\left( \Lambda - \frac{1}{2}\sin (2\Lambda )\right) , &{}\quad A > 1 \\ A, &{}\quad A \le 1 \\ \end{array} \right. \end{aligned}$$
(49)

respectively, where \(\Lambda = \arccos (1 - \frac{2}{A})\).

Taking into account Eqs. (44)–(49), the time-dependent equivalent linear elements of Eqs. (19) and (20) become

$$\begin{aligned} \beta _\mathrm{{eq}}(c(t))= & {} - \beta _0 + \frac{\beta \sin ^2\left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }c(t)} \nonumber \\&\times \, \int _0^\infty \frac{A}{\omega ^{1-\alpha }(A)} \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A \nonumber \\&+\, \frac{4(1-\gamma )\sin \left( \frac{\alpha \pi }{2}\right) }{\pi \omega _0^{1-\alpha } c(t)} \nonumber \\&\times \, \int _1^\infty \frac{1-\frac{1}{A}}{\omega (A)} \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A\nonumber \\ \end{aligned}$$
(50)

and

$$\begin{aligned} \omega ^2_\mathrm{{eq}}(c(t))= & {} 1 - (1-\gamma ) \left\{ \exp \left( - \frac{\sin \left( \frac{\alpha \pi }{2}\right) }{2c(t)\omega _0^{1-\alpha }} \right) \right. \nonumber \\&-\, \frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\pi \omega _0^{1-\alpha } c(t)} \nonumber \\&\times \, \int _1^\infty \left( \Lambda - \frac{1}{2}\sin (2\Lambda )\right) A \nonumber \\&\times \, \left. \exp \left( -\frac{\sin (\frac{\alpha \pi }{2})}{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A \right\} \nonumber \\&+\, \frac{\beta \sin \left( \frac{\alpha \pi }{2}\right) \cos \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }c(t)} \nonumber \\&\times \, \int _0^\infty \omega ^{\alpha }(A) A \exp \left( -\frac{\sin \left( \frac{\alpha \pi }{2}\right) }{\omega _0^{1-\alpha }}\frac{A^2}{2c(t)}\right) \mathrm{d}A\nonumber \\ \end{aligned}$$
(51)

respectively. As in the example of Sect. 3.1, the time-dependent coefficient c(t) is determined by solving numerically Eq. (37), in conjunction with \(\beta _\mathrm{{eq}}(c(t))\) and \(\omega _\mathrm{{eq}}^2(c(t))\) given by Eqs. (50) and (51).

The excitation and system parameter values used in this numerical example are: \(S_0 = 0.08\), \(c_0 = 0.12\), \(\omega _0=2.34\), \(\beta =0.1\), \(\gamma = 0.06\). Next, the bilinear hysteretic oscillator non-stationary response variances for fractional derivative orders equal to \(\alpha =1\) and \(\alpha =0.5\) are depicted in Fig. 4a and b, respectively, while results referring to the corresponding linear oscillator (\(\gamma =1\)) are included as well for assessing the nonlinearity degree. It is seen that the analytical solution for the non-stationary system response variances is in satisfactory agreement with the MCS-based estimates.

Fig. 4
figure 4

a Non-stationary response variance of a bilinear hysteretic oscillator (\(\gamma =0.06\)) with fractional derivative order \(\alpha =1\); b Non-stationary response variance of a bilinear hysteretic oscillator (\(\gamma =0.06\)) with fractional derivative order \(\alpha =0.5\). MCS data are included for comparison

Full size image

Next, the closed-form expression given by Eq. (21) is used for determining the non-stationary response amplitude PDF. In this regard, the analytical solution for the response amplitude PDF of the bilinear hysteretic oscillator (\(\gamma =0.06\)) with a fractional derivative order \(\alpha =0.5\) is depicted in Fig. 5a, whereas Fig. 5b shows the corresponding MCS-based estimate. In Fig. 6, the analytical PDF is plotted for various time instants and compared with MCS-based estimates. Similarly as in example 3.1, the accuracy of the technique appears satisfactory in capturing approximately the main features of the response amplitude PDF, as well as its evolution in time in an average sense.

Fig. 5
figure 5

Non-stationary response amplitude PDF of a bilinear hysteretic oscillator (\(\gamma =0.06\)) with fractional derivative order \(\alpha =0.5\): a analytical PDF; b MCS-based estimate (10,000 realizations)

Full size image
Fig. 6
figure 6

Analytical (Eq. (21)) vis-a-vis MCS-based (10,000 realizations) response amplitude PDFs of a bilinear hysteretic oscillator (\(\gamma =0.06\)) with fractional derivative order \(\alpha =0.5\), plotted for various time instants

Full size image

4 Concluding remarks

In this paper, an approximate analytical technique has been developed for determining the non-stationary response amplitude PDF of nonlinear/hysteretic oscillators endowed with fractional derivative elements and subjected to evolutionary stochastic excitation. Specifically, a stochastic averaging/linearization treatment has led to a dimension reduction of the governing equation of motion and to a first-order stochastic differential equation for the oscillator response amplitude. Next, assuming an appropriately chosen time-dependent PDF form of the Rayleigh kind for the response amplitude, and substituting into the associated Fokker–Planck partial differential equation, has yielded a deterministic first-order ordinary differential equation for the time-dependent PDF coefficient. This can be readily solved numerically via standard deterministic integration schemes, such as Runge–Kutta. Thus, the non-stationary response amplitude PDF has been approximately determined in closed-form in a computationally efficient manner. The technique can account for arbitrary excitation evolutionary power spectrum forms, even of the non-separable kind. An additional advantage of the technique relates to the determination, as a by-product, of equivalent linear time-dependent stiffness and damping elements. This can be of considerable importance, potentially, to tracking and quantifying “moving resonance phenomena”, which may result to significant response amplifications in nonlinear systems. A hardening Duffing and a bilinear hysteretic nonlinear oscillators with fractional derivative elements have been considered in the numerical examples section for assessing the accuracy of the technique. Based on comparisons with pertinent MCS data, although the accuracy is not excellent as anticipated given the approximations of the technique, it has been shown that the herein developed closed-form PDF expression of Eq. (21) appears capable of capturing both the time-evolution in an average sense and the salient features of the non-stationary response amplitude PDF.

Regarding the limitations of the technique, it is noted that the formulation relies on a response representation (see Eq. (3) or Eq. (22)) that involves an effective natural frequency, or in other words, the oscillator response is assumed to exhibit a pseudo-harmonic behavior. Although this may be a reasonable approximation for certain kinds of nonlinearities (as also shown in the herein considered numerical examples), it may be inadequate, for instance, for oscillators with multiple static equilibrium positions. Indicatively, for a Duffing oscillator with two static equilibrium positions (see section 5.3.8 in Ref. [30]), the response behavior depends on the magnitude of the excitation. In particular, for low excitation levels the response is “trapped” for a relatively long time duration in one of the two wells of the potential function. Thus, an indicative realization would oscillate about a mean value centered around the lowest point of the well. As the excitation magnitude increases, the interchange between the two wells becomes more frequent, while the response distribution converges to the one of the standard hardening Duffing oscillator with a single equilibrium position. Therefore, it is readily seen that a modification of the herein developed technique is required to account for the rather complex and strongly non-Gaussian response behavior of such systems with multiple static equilibrium positions. A potential future research route relates to considering various different excitation magnitude-dependent effective natural frequency representations corresponding to the distinct response patterns; see for instance Ref. [47] for some relevant work.

Further, the generalization of the technique to MDOF systems entails several challenges to be addressed, and is identified as a topic of future research. An indicative research route relates to applying directly the amplitude-phase response representation on the modal component of the i-th nonlinear mode of vibration of the MDOF system (e.g., [48]). An alternative potential research route relates to employing standard dimension reduction methodologies, such as complex modal analysis (e.g., [30]), in conjunction with statistical linearization and stochastic averaging. Note, however, that applying complex modal analysis to MDOF systems with fractional derivative elements is not straightforward. In fact, this has been possible only relatively recently, and under the limitation/assumption that the fractional derivatives are of rational order [49].