1 Introduction

Use of cables is quite common in the structures, mooring systems, and the power transmission system. Nonlinear vibration of cables has been studied by many researchers. However, there are few studies on nonlinear random vibration of cables modeled by multi-degree-of-freedom (MDOF) system [1]. Moment closure method and Monte Carlo simulation were adopted to investigate the responses of the cables excited by random noise [2–4]. In general, cable systems and many other nonlinear systems in science and engineering can be modeled as nonlinear stochastic dynamical (NSD) systems with multiple degrees of freedom excited by random noise [5–7]. In case of white noise or filtered white noise, the probabilistic solution of the system is governed by the Fokker–Planck–Kolmogorov (FPK) equation [5–9]. It is known that the analysis on the probabilistic solutions of MDOF–NSD systems or high-dimensional FPK equation has been a challenge for almost a century because of the so-called curse of dimensionality [10, 11], especially for the systems with strongly coupled state variables, strong nonlinearity, or many nonlinear terms.

Instead of solving the high-dimensional FPK equations for the probability density function (PDF) of the responses, responses or response moments are determined numerically. There are three methods widely employed to study the MDOF–NSD systems in the past decades. One is the equivalent linearization (EQL) method which was first proposed by Booton [12] in the research on nonlinear random vibration of circuit and further investigated by many other researchers thereafter [13–16]. The second is the Monte Carlo simulation (MCS) method which was first proposed by Metropolis and Ulam [17] in their researches on the problems in nuclear physics and further investigated by many other researchers in science, engineering, and mathematics [18–22]. It is well known that the EQL method is only suitable for the weakly nonlinear systems for obtaining the first and second moments of system responses. There are some challenges with MCS method in analyzing the strongly nonlinear stochastic dynamical systems being of multiple degree of freedoms, such as the problems of round-off error, numerical stability, convergence, and requirement for huge sample size. The third is the cumulant-neglect closure method. With this method, the moment equations derived from Ito’s derivative rule were solved to obtain statistical moments by introducing the cumulant-neglect closure to moment equations to make the hierarchy of moment equations closed to a desired level [23–26]. The moments obtained with this method are exact for linear systems excited by additive and multiplicative Gaussian white noises and appear to be accurate for weakly nonlinear systems excited by additive Gaussian white noises.

On the other hand, some methods were developed or extended for obtaining the approximate probabilistic solutions of NSD systems, such as the path integral method [27, 28], stochastic average method [29], perturbation method [30], A-type Gram–Charlier series or Hermite-polynomial closure method [31], C-type Gram–Charlier series method [32], finite difference method [33], finite element method [34], and exponential polynomial closure (EPC) method [35]. It is known that most of these methods only work for analyzing the single-degree-of-freedom (SDOF) systems or solving the two-dimensional FPK equations in steady state under some conditions. Some of the methods may also suffer from the loss of accuracy of the PDF in the tail regions which play an important role in system reliability analysis.

In order to solve the high-dimensional FPK equations corresponding to MDOF–NSD systems, some methods were proposed in the last decades. One of the methods is EPC method [35, 36], which works for the systems with few degrees of freedom or low-dimensional FPK equations. Various two-dimensional and four-dimensional FPK equations corresponding to SDOF and 2-DOF systems with polynomial type of nonlinearity were analyzed accurately with the EPC method. The precision of tails of the PDFs obtained with EPC method was examined with MCS. High-order finite difference scheme was used to solve FPK equation corresponding to the 2-DOF spring system when the Gaussian white noise in one equation of motion is independent of the Gaussian white noise in another equation of motion [37]. The weighted orthogonal Hermite-polynomial functions were used to formulate the approximate PDF in solving the high-dimensional FPK equations [38, 39]. A 2-DOF nonlinear system and a 3-DOF nonlinear system were analyzed with this method. The method of tensor decomposition was extended to solve the high-dimensional FPK equations [11]. With this method, the FPK equations corresponding to 1-DOD to 5-DOF nonlinear systems were solved when the Gaussian white noise in one equation of motion is independent of the Gaussian white noises in other equations of motion. It seems that the computational time needed by the tensor decomposition method for analyzing the 4-DOF or 5-DOF systems is larger than that needed by MCS. Since the tails of the PDFs of system responses have major contribution to system reliability analysis, the precision of tails of the PDFs of system responses obtained with various methods is much concerned. Therefore, it can be desirable to compare the values of logarithmic PDFs obtained with a given method to that obtained with MCS so that the tail behavior of the PDFs of system responses obtained with a given method can be revealed. It is well known that improving the precision of tails of the PDFs of system responses has been a challenge in the area of nonlinear random vibration for decades. Recently, a new method named state-space-split (SSS) method was proposed for the probabilistic solutions of some large MDOF–NSD systems which are solvable with EQL method or for solving the relevant FPK equations in high dimensionality [40, 41]. It was extended thereafter for analyzing the systems excited by Poissonian white noise [42] and colored noise being filtered Gaussian white noise [43]. With the SSS method, the high-dimensional FPK equation can be reduced to the low-dimensional FPK equation which is solvable with the EPC method.

In this paper, the SSS–EPC method is further adopted to analyze the probabilistic solutions of the in-plane transverse vibration of the cable with small sag-to-span ratio and excited by Gaussian white noise uniformly distributed on the cable. The excitation applied on the cable is assumed to be Gaussian white noise in this paper. It is only an idealization of the real-life colored noise. The equation of motion of the cable is a nonlinear partial differential equation in time and space [44, 45]. The nonlinear partial differential equation governing the motion of the cable is reduced to MDOF–NSD system by Galerkin’s method. The results obtained with the SSS–EPC method are compared with those obtained with EQL method and MCS to show the effectiveness of the SSS–EPC method in this case and the advantage of the SSS–EPC method over the EQL method and MCS in analyzing the probabilistic solutions of the formulated MDOF–NSD systems with large number of nonlinear terms including both even and odd terms being of strong nonlinearity.

Fig. 1
figure 1

Inclined cable

Full size image

2 Nonlinear stochastic dynamical system of in-plane cable with small sag

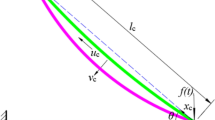
Consider a uniform inclined cable hanging between two supports as shown in Fig. 1. The analysis of the nonlinear random vibration of the cable is based on the following assumptions. (1) The flexural rigidity, torsional rigidity, and shear stiffness of the cable are neglected. (2) The sag-to-span ratio is small. (3) The component of the cable weight and dynamical force parallel to the chord line of the cable are so small that they can be neglected compared to the pretension in the cable. The static curve of the cable with initial sag is approximately expressed as parabolic curve. (4) The constitutive relation of the cable satisfies the Hooke’ s law, and the stress on the cross section of the cable is uniform. The initial static sag of the inclined cable is caused by the self-weight of cable, but the sag-to-span ratio is small due to the high pretension applied in the cable ends such as the cables in some catenary structures. If the distributed stochastic dynamical force \(f_y(x,t)\) is perpendicular to the chord line of the cable and in view that the stiffness in the chord-line direction is much larger than that in the transverse direction, the displacement component in chord-line direction is small compared to that in transverse direction. Then the displacement in the chord-line direction is neglected and only the in-plane transverse displacement of the cable is considered. Under the action of uniformly distributed load, the equation of transverse motion of the cable with small sag-to-span ratio can be written as follows [44].

$$\begin{aligned}&\rho w_{tt}-Hw_{xx}-\frac{EA}{L_{e}}\bigg (w_{xx}-\frac{8d}{l^2}\bigg )\int _{0}^{l}\nonumber \\&\quad \times \bigg [\frac{4d}{l}\bigg (1-\frac{2x}{l}\bigg )w_{x} +\frac{1}{2}w_{x}^{2}\bigg ]\mathrm{d}x=f_{y}(x,t) \end{aligned}$$
(1)

where w is the in-plane dynamical transverse displacement of the cable, E is Young’s modulus, \(\rho \) is the mass of the cable per unit length, A is the area of the cable cross section, l is the total length of the cable and it approximately equals the distance between two supports when the sag-to-span ratio is small, d is the static sag in the middle span of the cable and it is given by \(d=\frac{\rho g l^{2}\cos \theta }{8H}\), H is the x-axis component of the static tensile force in the cable, g is gravitational acceleration, \(\theta \) is the inclined angle of the cable chord with respect to the horizontal plane, \(L_{e}=[1+8(\frac{d}{l})^{2}]\), \(f_y(x,t)=q_0W(t)\), \(q_0\) is constant, and W(t) is assumed to be Gaussian white noise which power spectral density is denoted as S.

3 Multi-degree-of-freedom nonlinear stochastic dynamical system of the cable

The symmetric mode functions of the linear cable with small sag-to-span ratio and boundary conditions \(w(0)=w(l)=0\) are given to be \(\varPhi _{i}(x)=k_i(1-\tan \frac{\omega _{i}}{2}\sin \frac{\omega _{i}x}{l}-\cos \frac{\omega _{i}x}{l})\), \((i=1,2,\ldots )\), in which \(\omega _i\) is the ith natural frequency of the linear cable and \(k_i\) is normalization constant [44, 45]. For small sag-to-span ratio, these mode functions can be approximately expressed by

$$\begin{aligned} \phi _{i}(x)=\sin \frac{(2i-1)\pi x}{l}\quad i=1,2,\ldots \end{aligned}$$
(2)

which are used as shape functions in formulating the MDOF systems of the cable with Galerkin method in the following. Under the action of transverse uniformly distributed excitation, the deflection of the cable with small sag-to-span ratio is expressed by

$$\begin{aligned} w(x,t)=\sum _{i=1}^{N}q_{i}(t)\phi _{i}(x) \end{aligned}$$
(3)

With Galerkin’s method and \(\phi _{i}(x)\) being used as shape functions and weight functions, the following nonlinear stochastic dynamical system is formulated from Eq. (1) if the damping ratio \(\xi \) for each mode is the same.

$$\begin{aligned}&\ddot{q}_{m}(t)+2\xi \omega _m\dot{q}_{m}(t)+\omega _m^2q_{m}(t)\nonumber \\&\quad +\sum _{i=1}^N\sum _{j=1}^Nb_{ijm}q_{i}(t)q_{j}(t)\nonumber \\&\quad +\sum _{i=1}^N\sum _{j=1}^N\sum _{k=1}^Nc_{ijkm}q_{i}(t)q_{j}(t)q_{k}(t)=g_mW(t)\nonumber \\&\qquad (m=1,2,\ldots ,N) \end{aligned}$$
(4)

where \(\omega _m\) is the mth natural frequency of the linear cable, and

$$\begin{aligned} g_m= & {} \frac{q_0}{a_m}\int _{0}^{l}\phi _m(x)\mathrm{d}x\end{aligned}$$
(5)
$$\begin{aligned} a_m= & {} \rho \int _0^l\phi ^2_m(x)\mathrm{d}x\end{aligned}$$
(6)
$$\begin{aligned} b_{ijm}= & {} \frac{1}{a_m}\int _0^lB_{ij}(x)\phi _m(x)\mathrm{d}x\end{aligned}$$
(7)
$$\begin{aligned} B_{ij}(x)= & {} \frac{4EAd}{L_el^2}\bigg [-2\phi _i^{{\prime }{\prime }}(x)\int _0^l\phi _j(x)\mathrm{d}x\nonumber \\&+\int _0^l\phi _i^{\prime }(x)\phi _j^{\prime }(x)\mathrm{d}x\bigg ]\end{aligned}$$
(8)
$$\begin{aligned} c_{ijkm}= & {} \frac{1}{a_m}\int _0^lC_{ijk}(x)\phi _m(x)\mathrm{d}x\end{aligned}$$
(9)
$$\begin{aligned} C_{ijk}(x)= & {} -\frac{EA}{2L_e}\phi _i^{{\prime }{\prime }}(x)\int _0^l\phi _j^{\prime }(x)\phi _k^{\prime }(x)\mathrm{d}x \end{aligned}$$
(10)

If the joint PDF of the deflection \(w_0(t)=w(x_0,t)\) and velocity \(\dot{w}_0(t)=\dot{w}(x_0,t)\) is interested, the following system can be formulated with Eqs. (3) and (4).

$$\begin{aligned}&\ddot{w}_0(t)+2\xi \sum _{m=1}^N\phi _m(x_0)\omega _m\dot{q}_{m}(t)\nonumber \\&\quad +\sum _{m=1}^N\phi _m(x_0)\omega _m^2q_{m}(t)\nonumber \\&\quad +\sum _{m=1}^N\sum _{i=1}^{N}\sum _{j=1}^{N}\phi _m(x_0)b_{ijm}q_{i}(t)q_{j}(t)\nonumber \\&\quad +\sum _{m=1}^N\sum _{i=1}^{N}\sum _{j=1}^N\sum _{k=1}^{N}\phi _m(x_0)c_{ijkm}q_{i}(t)q_{j}(t)q_{k}(t)\nonumber \\&\quad =W(t)\sum _{m=1}^N\phi _m(x_0)g_m \end{aligned}$$
(11)
$$\begin{aligned}&\ddot{q}_{m}(t)+2\xi \omega _m\dot{q}_{m}(t)+\omega _m^2q_{m}(t)\nonumber \\&\quad +\sum _{i=1}^N\sum _{j=1}^Nb_{ijm}q_{i}(t)q_{j}(t)\nonumber \\&\quad +\sum _{i=1}^{N}\sum _{j=1}^{N}\sum _{k=1}^{N}c_{ijkm}q_{i}(t)q_{j}(t)q_{k}(t)=g_mW(t)\nonumber \\&\qquad (m=2,3,\ldots ,N) \end{aligned}$$
(12)

Equation (11) is given in order to analyze the joint PDF of \(w_0\) and \(\dot{w}_0\) with SSS–EPC method in the following. With Eq. (3), the amplitude \(q_1(t)\) of the first mode is expressed in terms of \(w_0, q_2, q_3,\ldots , q_N\), so Eqs. (11)–(12) in which \(q_1(t)=\phi ^{-1}_1(x_0)[w_0(t)-\sum _{i=2}^Nq_{i}(t)\phi _i(x_0)]\) and \(\dot{q}_1(t)=\phi ^{-1}_1(x_0)[\dot{w}_0(t)-\sum _{i=2}^N\dot{q}_{i}(t)\phi _i(x_0)]\) formulate a complete NSD system with N degrees of freedom about \(w_0, q_2, q_3,\) \(\ldots , q_N\), or 2N-dimensional system about state variables \(w_0, q_2, q_3, \ldots , q_N\) and \(\dot{w}_0, \dot{q}_2,\) \(\dot{q}_3, \ldots , \dot{q}_N\).

4 Dimensionality reduction with state-space-split method

In the following discussion, the summation convention applies unless stated otherwise. The random state variable or vector is denoted with capital letter, and the corresponding deterministic state variable or vector is denoted with the same letter in lowercase.

The system governed by Eqs. (11) and (12) can be generally expressed by the following MDOF–NSD system or generalized Langevin equations.

$$\begin{aligned}&\ddot{Y}_i+c_{ij}\dot{Y}_j+h_{io}(\mathbf{Y})=h_iW(t)\nonumber \\&\quad i,j=1,2,\dots , n_\mathbf{y} \end{aligned}$$
(13)

where \(Y_i\in \mathbb {R}, (i=1,2,\dots ,n_\mathbf{y})\), are the components of the vector process \(\mathbf{Y}\in \mathbb {R}^{n_\mathbf{y}}\); \(h_{i0}(\mathbf{Y})\) are the polynomial type of nonlinear functions of \(\mathbf Y\) and \(h_{i0}(\mathbf{Y}): \mathbb {R}^{n_\mathbf{y}}\rightarrow \mathbb {R}\); \(h_i\) and \(c_{ij}\) are constants; W(t) is the excitation which is assumed to be the Gaussian white noise with zero mean and correlation

$$\begin{aligned} E[W(t)W(t+\tau )]=S\delta (\tau ) \end{aligned}$$
(14)

where \(\delta (\tau )\) is Dirac delta function and S is the constant representing the power spectral density of W(t).

Setting \(Y_i=X_{2i-1}\), \(\dot{Y}_i=X_{2i}\), \(f_{2i-1}=X_{2i}\), \(f_{2i}=-c_{ij}X_{2j}-h_{io}(\mathbf{X})\), \(g_{2i-1}=0\), \(g_{2i}=h_i\) \((i=1,2,\dots ,n_\mathbf{y})\), and \(n_\mathbf{x}=2n_\mathbf{y}\), then Eq. (13) can be written as follows.

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}X_i=f_i(\mathbf{X})+g_iW(t)\quad i=1,2,\dots ,n_\mathbf{x} \end{aligned}$$
(15)

where \(\mathbf{X}\in \mathbb {R}^{n_\mathbf{x}}\); \(X_i\) \((i=1, 2, \ldots , n_\mathbf{x})\), are the components of the state vector process \(\mathbf X\); \(f_i(\mathbf{X}): \mathbb {R}^{n_\mathbf{x}}\rightarrow \mathbb {R}\).

The state vector process \(\mathbf X\) is Markovian, and the PDF \(p(\mathbf{x},t)\) of the Markovian vector is governed by the FPK equation. In the case that the white noise W(t) is Gaussian, the stationary PDF \(p(\mathbf{x})\) of the Markovian vector is governed by the following reduced FPK equation [5]:

$$\begin{aligned} \frac{\partial }{\partial x_j}\left[ f_j(\mathbf{x})p(\mathbf{x})\right] -\frac{1}{2}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ G_{ij}p(\mathbf{x})\right] =0 \end{aligned}$$
(16)

where \(\mathbf{x}\) is the deterministic state vector, \(\mathbf{x}\in \mathbb {R}^{n_\mathbf{x}}\), and \(G_{ij}=g_ig_jS\).

It is assumed that the solution to Eq. (16) fulfills the following conditions:

$$\begin{aligned}&\lim _{x_i\rightarrow \pm \infty }f_i(\mathbf{x})p(\mathbf{x})=0\quad \hbox {and }\lim _{x_i\rightarrow \pm \infty }\frac{\partial p(\mathbf{x})}{\partial x_i}=0\nonumber \\&\quad i=1,2,\ldots ,n_\mathbf{x} \end{aligned}$$
(17)

which can be fulfilled by the deflection and the velocity of the cable presented above.

Separate the state vector \(\mathbf X\) into two parts as \(\mathbf{X}_1\in \mathbb {R}^{n_{\mathbf{x}_1}}\) and \(\mathbf{X}_2\in \mathbb {R}^{n_{\mathbf{x}_2}}\), i.e., \(\mathbf{X}=\{\mathbf{X}_1, \mathbf{X}_2\}\in \mathbb {R}^{n_{\mathbf{x}}}=\mathbb {R}^{n_{\mathbf{x}_1}}\times \mathbb {R}^{n_{\mathbf{x}_2}}\). In analyzing the above cable system, define the vector \(\mathbf{X}_1\) such that it contains the deflection \(w(x_0,t)\) and the corresponding velocity \(\dot{w}(x_0,t)\) of the cable. The joint PDF of \(\mathbf{X}_1\) or \(w(x_0,t)\) and \(\dot{w}(x_0,t)\) is analyzed in the following with the SSS–EPC method [40, 41].

Denote the PDF of \(\mathbf{X}_1\) as \(p_1(\mathbf{x}_1)\). In order to obtain \(p_1(\mathbf{x}_1)\), integrating both sides of Eq. (16) over \(\mathbb {R}^{n_{\mathbf{x}_2}}\) gives

$$\begin{aligned}&\int _{\mathbb {R}^{n_{\mathbf{x}_2}}}\frac{\partial }{\partial x_j}\left[ f_j(\mathbf{x})p(\mathbf{x})\right] \mathrm{d}\mathbf{x}_2\nonumber \\&\quad -\,\frac{1}{2}\int _{\mathbb {R}^{n_{\mathbf{x}_2}}}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ G_{ij}p(\mathbf{x})\right] \mathrm{d}{} \mathbf{x}_2=0 \end{aligned}$$
(18)

Because of the conditions in Eq. (17), we have

$$\begin{aligned} \int _{\mathbb {R}^{n_{\mathbf{x}_2}}}\frac{\partial }{\partial x_j}\left[ f_j(\mathbf{x})p(\mathbf{x})\right] \mathrm{d}\mathbf{x}_2=0\quad x_j\in \mathbb {R}^{n_{\mathbf{x}_2}} \end{aligned}$$
(19)

and

$$\begin{aligned} \int _{\mathbb {R}^{n_{\mathbf{x}_2}}}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ G_{ij}p(\mathbf{x})\right] \mathrm{d}\mathbf{x}_2=0\quad x_i \text{ or } x_j\in \mathbb {R}^{n_{\mathbf{x}_2}} \end{aligned}$$
(20)

Equation (18) can then be written after integration by part as

$$\begin{aligned}&\int _{\mathbb {R}^{n_{\mathbf{x}_2}}}\frac{\partial }{\partial x_j}\left[ f_j(\mathbf{x})p(\mathbf{x})\right] \mathrm{d}\mathbf{x}_2\nonumber \\&\quad -\,\frac{1}{2}\int _{\mathbb {R}^{n_{\mathbf{x}_2}}}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ G_{ij}p(\mathbf{x})\right] \mathrm{d}\mathbf{x}_2=0\nonumber \\&\quad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}} \end{aligned}$$
(21)

which can be equivalently written as

$$\begin{aligned}&\frac{\partial }{\partial x_j}\left[ \int _{\mathbb {R}^{n_{\mathbf{x}_2}}}f_j(\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x}_2\right] \nonumber \\&\quad -\,\frac{1}{2}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ \int _{\mathbb {R}^{n_{\mathbf{x}_2}}}G_{ij}p(\mathbf{x})\mathrm{d}\mathbf{x}_2\right] =0\nonumber \\&\qquad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}} \end{aligned}$$
(22)

Cluster the terms purely in \(\mathbf{x}_1\) in one part and the other terms in the other part. Then \(f_j(\mathbf{x})\) is expressed in terms of two parts as

$$\begin{aligned} f_j(\mathbf{x})=f_j^\mathrm{I}(\mathbf{x}_1)+f_j^\mathrm{II}(\mathbf{x}) \end{aligned}$$
(23)

Substituting Eq. (23) in Eq. (22) gives

$$\begin{aligned}&\frac{\partial }{\partial x_j}\left[ f_j^\mathrm{I}(\mathbf{x}_1)p_1(\mathbf{x}_1)+\int _{\mathbb {R}^{n_{\mathbf{x}_2}}}f_j^\mathrm{II}(\mathbf{x})p(\mathbf{x})\mathrm{d}\mathbf{x}_2\right] \nonumber \\&\quad -\,\frac{1}{2}\frac{\partial ^2[G_{ij}p_1(\mathbf{x}_1)]}{\partial x_i\partial x_j}=0\quad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}} \end{aligned}$$
(24)

Express \(f_j^\mathrm{{II}}(\mathbf{x})\) as \(\sum _kf_j^\mathrm{{II}}(\mathbf{x}_1,\mathbf{z}_k)\) in which \(\mathbf{z}_k\in \mathbb {R}^{n_{\mathbf{z}_k}}\subset \mathbb {R}^{n_{\mathbf{x}_2}}\) and \(n_{\mathbf{z}_k}\) denotes the number of the state variables in \(\mathbf{z}_k\). Then Eq. (24) can be written as

$$\begin{aligned}&\frac{\partial }{\partial x_j}\bigg [f_j^\mathrm{I}(\mathbf{x}_1)p_1(\mathbf{x}_1)+\sum _k\int _{\mathbb {R}^{n_{\mathbf{z}_k}}}f_j^\mathrm{II}(\mathbf{x}_1,\mathbf{z}_k)\nonumber \\&\quad p_k(\mathbf{x}_1,\mathbf{z}_k)\mathrm{d}\mathbf{z}_k\bigg ]-\frac{1}{2}\frac{\partial ^2 [G_{ij}p_1(\mathbf{x}_1)]}{\partial x_i\partial x_j}=0\nonumber \\&\qquad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}} \end{aligned}$$
(25)

in which \(p_k(\mathbf{x}_1,\mathbf{z}_k)\) denotes the joint PDF of \(\{\mathbf{X}_1,\mathbf{Z}_k\}\). The summation convention not applies for the indexes k in Eq. (25) and in the following discussions.

From Eq. (25), it is seen that the coupling of \(\mathbf{X}_1\) and \(\mathbf{X}_2\) comes from \(f_j^\mathrm{II}(\mathbf{x}_1,\mathbf{z}_k)p_k(\mathbf{x}_1,\mathbf{z}_k)\). Because

$$\begin{aligned} p_k(\mathbf{x}_1,\mathbf{z}_k)=p_1(\mathbf{x}_1)q_k(\mathbf{z}_k;\mathbf{x}_1) \end{aligned}$$
(26)

where \(q_k(\mathbf{z}_k;\mathbf{x}_1)\) is the conditional PDF of \(\mathbf{Z}_k\) for given \(\mathbf{X}_1=\mathbf{x}_1\), substituting Eq. (26) in Eq. (25) gives

$$\begin{aligned}&\frac{\partial }{\partial x_j}\bigg \{\bigg [f_j^\mathrm{I}(\mathbf{x}_1)+\sum _k\int _{\mathbb {R}^{n_{\mathbf{z}_k}}}f_j^\mathrm{II}(\mathbf{x}_1,\mathbf{z}_k)q_k(\mathbf{z}_k;\mathbf{x}_1)\mathrm{d}\mathbf{z}_k\bigg ]\nonumber \\&\quad p_1(\mathbf{x}_1)\bigg \}-\frac{1}{2}\frac{\partial ^2 [G_{ij}p_1(\mathbf{x}_1)]}{\partial x_i\partial x_j}=0\quad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}}\nonumber \\ \end{aligned}$$
(27)

Approximately replacing the conditional PDF \(q_k(\mathbf{z}_k;\mathbf{x}_1)\) by that obtained with EQL, then Eq. (27) is written as

$$\begin{aligned}&\frac{\partial }{\partial x_j}\bigg \{\bigg [f_j^\mathrm{I}(\mathbf{x}_1)+\sum _k\int _{\mathbb {R}^{n_{\mathbf{z}_k}}}f_j^\mathrm{II}(\mathbf{x}_1,\mathbf{z}_k)\overline{q}_k(\mathbf{z}_k;\mathbf{x}_1)\mathrm{d}\mathbf{z}_k\bigg ]\nonumber \\&\quad \tilde{p}_1(\mathbf{x}_1)\bigg \}-\frac{1}{2}\frac{\partial ^2 [G_{ij}\tilde{p}_1(\mathbf{x}_1)]}{\partial x_i\partial x_j}=0\quad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}}\nonumber \\ \end{aligned}$$
(28)

where \(\overline{q}_k({\mathbf{z}_k;\mathbf x}_1)\) is the approximate conditional PDF of \(\mathbf{Z}_k\) obtained with EQL for given \(\mathbf{X}_1=\mathbf{x}_1\) and \(\tilde{p}_1(\mathbf{x}_1)\) is then the approximate PDF of \(\mathbf{X}_1\). It is noted that the approximate conditional PDF \(\overline{q}_k({\mathbf{z}_k;\mathbf x}_1)\) leads to the difference between the approximate solution \(\tilde{p}_1(\mathbf{x}_1)\) and exact solution \(p_1(\mathbf{x}_1)\). Denote

$$\begin{aligned} \tilde{f}_j(\mathbf{x}_1)=f_j^\mathrm{I}(\mathbf{x}_1)+\sum _k\int _{\mathbb {R}^{n_{\mathbf{z}_k}}}f_j^\mathrm{{II}}(\mathbf{x}_1,\mathbf{z}_k)\overline{q}(\mathbf{z}_k;\mathbf{x}_1)\mathrm{d}{} \mathbf{z}_k, \end{aligned}$$
(29)

Then Eq. (28) can be finally written as

$$\begin{aligned}&\frac{\partial }{\partial x_j}\left[ \tilde{f}_j(\mathbf{x}_1)\tilde{p}_1(\mathbf{x}_1)\right] -\frac{1}{2}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ G_{ij}\tilde{p}_1(\mathbf{x}_1)\right] =0\nonumber \\&\quad x_i, x_j\in \mathbb {R}^{n_{\mathbf{x}_1}} \end{aligned}$$
(30)

which is the approximate FPK equation for the joint PDF of the state variables in the subspace \(\mathbb {R}^{n_{\mathbf{x}_1}}\) or the deflection \(w_0\) and velocity \(\dot{w}_0\) of the cable at \(x=x_0\).

It is seen that \(\mathbf{X}_1\) only contains two state variables, i.e., \(\mathbf{X}_1=\{w_0,\dot{w}_0\}\). Hence, the resulting approximate FPK equation is two-dimensional. The EPC method is employed to solve Eq. (30) in the following numerical analysis [35].

5 Solution procedure of exponential polynomial closure method

Consider the following reduced low-dimensional FPK equation.

$$\begin{aligned} \frac{\partial }{\partial x_j}\left[ f_j(\mathbf{x})p(\mathbf{x})\right] -\frac{1}{2}\frac{\partial ^2}{\partial x_i\partial x_j}\left[ G_{ij}(\mathbf{x})p(\mathbf{x})\right] =0 \end{aligned}$$
(31)

where \(\mathbf{X}\in \mathbb {R}^{n_\mathbf{x}}\) with the assumption that \(n_\mathbf{x}\) is small or \(n_\mathbf{x}=1\sim 4\).

The approximate solution \(\mathop {p}\limits ^{\sim }(\mathbf{x;a})\) of Eq. (31) is assumed to be

$$\begin{aligned} \mathop {p}\limits ^{\sim }(\mathbf{x;a})=c\exp ^{Q_n(\mathbf{x};\mathbf{a})} \end{aligned}$$
(32)

where \(\mathbf a\) is unknown parameter vector, \(\mathbf{a}=\{a_1, a_2, \ldots ,\) \(a_{N_p}\}\), \(N_p\) is the total number of unknown parameters, and \(Q_n(\mathbf{x}; \mathbf{a})\) is a n-degree polynomial in \(\mathbf{x}\in \mathbb {R}^{n_\mathbf{x}}\). This replacement may cause some error in the approximate solution and hence some residual error in the FPK equation.

Equation (31) can also be written in the following form:

$$\begin{aligned}&\frac{\partial f_j}{\partial x_j}p+f_j\frac{\partial p}{\partial x_j}-\frac{1}{2}\bigg (\frac{\partial ^2G_{ij}}{\partial x_i\partial x_j}p+\frac{\partial G_{ij}}{\partial x_j}\frac{\partial p}{\partial x_i}\nonumber \\&\quad +\,\frac{\partial G_{ij}}{\partial x_i}\frac{\partial p}{\partial x_j}+\,G_{ij}\frac{\partial ^2p}{\partial x_i\partial x_j}\bigg )=0 \end{aligned}$$
(33)

Generally, Eq. (33) can not be satisfied exactly with \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\) because \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\) is only an approximation of \(p(\mathbf x)\) and the number \(N_p\) of the unknown parameters is limited in practice. Substituting \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\) for \(p(\mathbf{x})\) in Eq. (33) leads to the following residual error.

$$\begin{aligned}&\varDelta (\mathbf{x};\mathbf{a})=\frac{\partial f_j}{\partial x_j}\mathop {p}\limits ^{\sim }+f_j\frac{\partial \mathop {p}\limits ^{\sim }}{\partial x_j}-\frac{1}{2}\bigg (\frac{\partial ^2G_{ij}}{\partial x_i\partial x_j}\mathop {p}\limits ^{\sim }\nonumber \\&\quad +\,\frac{\partial G_{ij}}{\partial x_j}\frac{\partial \mathop {p}\limits ^{\sim }}{\partial x_i}+\frac{\partial G_{ij}}{\partial x_i}\frac{\partial \mathop {p}\limits ^{\sim }}{\partial x_j}+G_{ij}\frac{\partial ^2\mathop {p}\limits ^{\sim }}{\partial x_i\partial x_j}\bigg ) \end{aligned}$$
(34)

Substituting \(\mathop {p}\limits ^{\sim }(\mathbf{x;a})=c\exp ^{Q_n(\mathbf{x};\mathbf{a})}\) in Eq. (34) gives

$$\begin{aligned} \varDelta (\mathbf{x};\mathbf{a})=\delta (\mathbf{x};\mathbf{a})\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a}) \end{aligned}$$
(35)

where

$$\begin{aligned} \delta (\mathbf{x};\mathbf{a})= & {} f_j\frac{\partial Q_n}{\partial x_j}-\frac{1}{2}\bigg (\frac{\partial G_{ij}}{\partial x_j}\frac{\partial Q_n}{\partial x_i}+\frac{\partial G_{ij}}{\partial x_i}\frac{\partial Q_n}{\partial x_j}\nonumber \\&+\,G_{ij}\frac{\partial ^2Q_n}{\partial x_i\partial x_j}+G_{ij}\frac{\partial Q_n}{\partial x_i}\frac{\partial Q_n}{\partial x_j}\bigg )+\frac{\partial f_j}{\partial x_j}\nonumber \\&-\,\frac{1}{2}\frac{\partial ^2G_{ij}}{\partial x_i\partial x_j} \end{aligned}$$
(36)

Because \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\not =0\), therefore, the only possibility for \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\) to satisfy Eq. (33) is \(\delta (\mathbf{x};\mathbf{a})=0\). However, usually \(\delta (\mathbf{x};\mathbf{a})\not =0\) because \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\) is only an approximation of \(p(\mathbf{x})\). In this case, a set of mutually independent functions \(h_k(\mathbf x)\) which span space \(\mathbb {R}^{N_p}\) are introduced to make the projection of \(\delta (\mathbf{x};\mathbf{a})\) on \(\mathbb {R}^{N_p}\) vanish, which leads to

$$\begin{aligned} \int _{\mathbb {R}^{n_x}}\delta (\mathbf{x}; \mathbf{a})\, h_k(\mathbf{x})\mathrm{d}\mathbf{x}=0,\quad k=1,2,\ldots ,N_p \end{aligned}$$
(37)

or

$$\begin{aligned}&\int _{\mathbb {R}^{n_x}}\bigg \{f_j\frac{\partial Q_n}{\partial x_j}-\frac{1}{2}\bigg (\frac{\partial G_{ij}}{\partial x_j}\frac{\partial Q_n}{\partial x_i} +\frac{\partial G_{ij}}{\partial x_i}\frac{\partial Q_n}{\partial x_j}\nonumber \\&\quad +\,G_{ij}\frac{\partial ^2Q_n}{\partial x_i\partial x_j}+G_{ij}\frac{\partial Q_n}{\partial x_i}\frac{\partial Q_n}{\partial x_j}\bigg )+\frac{\partial f_j}{\partial x_j}\nonumber \\&\quad -\,\frac{1}{2}\frac{\partial ^2G_{ij}}{\partial x_i\partial x_j}\bigg \} h_k(\mathbf{x})\mathrm{d}\mathbf{x}=0\nonumber \\&\qquad k=1,2,\ldots ,N_p \end{aligned}$$
(38)

The above equation (38) means that the reduced FPK equation is satisfied with \(\mathop {p}\limits ^{\sim }(\mathbf{x};\mathbf{a})\) in the weak sense of integration if \(\delta (\mathbf{x}; \mathbf{a})\, h_k(\mathbf{x})\) is integrable in \(\mathbb {R}^{n_x}\).

By selecting \(h_k(\mathbf{x})\) as \(x_1^{k_1}x_2^{k_2}\ldots x_n^{k_n}f_N(\mathbf{x})\), being \(k_1,\) \(k_2, \ldots , k_n=\) \(0,1,2,\ldots ,N_p\) and \(k=k_1+k_2+\cdots +k_n\) such that \(\delta (\mathbf{x}; \mathbf{a})\, h_k(\mathbf{x})\) is integrable in \(\mathbb {R}^{n_x}\), \(N_p\) nonlinear algebraic equations in terms of \(N_p\) undetermined parameters can be obtained from Eq. (38). The algebraic equations can be solved to determine the parameters. Numerical experience shows that a convenient and effective choice for the function \(f_N(\mathbf{x})\) is the PDF obtained from EQL or Gaussian closure procedure. Hence, it is a normal PDF.

6 Probabilistic solutions of the cable system excited by uniformly distributed Gaussian white noise

6.1 Example 1

Consider the steel cable with Young’s modulus \(E=2.1\times 10^{11}\,\hbox {N/m}^2\), damping ratio for each mode \(\xi =0.01\), cable length \(l=120\,\hbox {m}\), diameter of the cable cross section 0.1m, material density \(\rho /A=7850\,\hbox {kg/m}^3\), sag-to-span ratio 1 / 250, and the inclined angle \(\theta =30^\circ \). The cable is excited by uniformly distributed force with density \(100W(t)\,\hbox {N/m}\) in which W(t) is Gaussian white noise with power spectral density being 1. The PDF of the deflection and the velocity at the center of the cable with \(x=0.5l\) is analyzed. In this case, the \(\mathbf{X}_1\) is given by \(\mathbf{X}_1=\{w(0.5l,t),\dot{w}(0.5l,t)\}\) in the SSS dimension-reduction procedure.

Fig. 2
figure 2

The PDFs of the deflection in the middle of the cable modeled as SDOF system in Example 1

Full size image
Fig. 3
figure 3

Logarithm of PDFs of the deflection in the middle of the cable modeled as SDOF system in Example 1

Full size image
Fig. 4
figure 4

The PDFs of the deflection in the middle of the cable modeled as 5-DOF system in Example 1

Full size image
Fig. 5
figure 5

Logarithm of PDFs of the deflection in the middle of the cable modeled as 5-DOF system in Example 1

Full size image

Modeling the cable by one shape function, the resulting equation of motion is a SDOF oscillator. The PDFs of the deflection at the center of the cable are obtained with the EPC method, EQL method, and MCS, respectively. It is known that the exact PDF of the response of this SDOF oscillator is obtainable. Actually, the PDF of the response obtained with EPC method is the same as the exact solution for this SDOF oscillator. They are shown and compared in Fig. 2. The symbol n appearing in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15 denotes the polynomial degree of the polynomial function adopted in the EPC procedure. It is known that the tails of the PDF of deflection play an important role in system reliability analysis. The tails of the PDFs of the deflection obtained with various methods are also shown and compared in Fig. 3. In these figures, \(\sigma _w\) denotes the standard deviation of the deflection obtained with EQL at the center of the cable. It is observed in Figs. 2 and 3 that the result obtained with EPC is the same as exact solution or MCS while the result obtained with EQL deviates a lot from exact solution. When the number of the shape functions increases to 5, the 5-DOF system is formulated. The exact probabilistic solution of this 5-DOF system is not obtainable. The PDFs of the deflection at the center of the cable are obtained with the SSS–EPC method, MCS, and EQL, respectively. They are shown and compared in Fig. 4. The tails of the PDFs obtained with various methods are also compared in Fig. 5. The sample size in MCS is \(10^8\). The simulation about this 5-DOF system was conducted on the original 5-DOF system rather than on the SDOF system resulted from the SSS dimension-reduction procedure.

Fig. 6
figure 6

The MCRs of the deflection in the middle of the cable modeled as SDOF system in Example 1

Full size image
Fig. 7
figure 7

Logarithm of MCRs of the deflection in the middle of the cable modeled as SDOF system in Example 1

Full size image
Fig. 8
figure 8

Logarithm of MCRs of the deflection in the middle of the cable modeled as 5-DOF system in Example 1

Full size image

It is observed in Figs. 4 and 5 that the result obtained with SSS–EPC is close to MCS while the result corresponding to EQL deviates a lot from MCS. Numerical experience showed that further increasing the number of mode functions to be greater than five can not make the solution further changed obviously. Hence, the solution of this 5-DOF system can be considered as the converged solution in the sense of analysis with Galerkin method. The polynomial degree used in the EPC solution procedure is four.

Fig. 9
figure 9

The PDFs of the deflection in the middle of the cable modeled as SDOF system in Example 2

Full size image
Fig. 10
figure 10

Logarithm of PDFs of the deflection in the middle of the cable modeled as SDOF system in Example 2

Full size image
Fig. 11
figure 11

The PDFs of the deflection in the middle of the cable modeled as 5-DOF system in Example 2

Full size image
Fig. 12
figure 12

Logarithm of PDFs of the deflection in the middle of the cable modeled as 5-DOF system in Example 2

Full size image

Further increasing the number of response samples to be greater than \(10^8\) in analyzing the 5-DOF system with MCS can make the computational effort huge due to the huge number of nonlinear terms in the system. There are about 250 nonlinear terms in the formulated 5-DOF system. It is one of the challenges inherent in MCS. The computational time spent with SSS–EPC solution procedure is about 5 s which are mainly spent on the linearization procedure because all the nonlinear terms need to be linearized in the linearization procedure and the result from equivalent linearization is needed in the SSS–EPC solution procedure. The computational time spent by MCS with \(10^8\) samples is about 2.5 h for this 5-DOF system in the same computer with Inter(R) CPU B950@2.10 GHz, and 3.16 GB RAM, and the same running environment. From Figs. 3 and 5 it is observed that there is some difference between the PDF of the deflection obtained by modeling the system as a SDOF system and that obtained by modeling the system as a 5-DOF system. The PDF of the deflection obtained from the 5-DOF system is about 1.03–1.44 times of that obtained from the SDOF system when the deflection changes from \(-3.136\sigma _w\) to \(-4.136\sigma _w\) and about 1.19–2.19 times of that obtained from the SDOF system when the deflection changes from \(2.864\sigma _w\) to \(3.864\sigma _w\), where \(\sigma _w=0.865\,\hbox {m}\) obtained with EQL is the standard deviation of the deflection in the middle of the cable. The difference of the values of \(\sigma _w\) of the SDOF system and the 5-DOF system is less than 1 %. For either the SDOF system or the 5-DOF system, the result obtained with EQL is far from being acceptable. Numerical results show that the PDF of velocity at midspan is close to Gaussian or close to that obtained from EQL. Hence, they are not given here. The similar behavior was observed on the PDF of velocity in the following Example 2.

Fig. 13
figure 13

The MCRs of the deflection in the middle of the cable modeled as SDOF system in Example 2

Full size image
Fig. 14
figure 14

Logarithm of MCRs of the deflection in the middle of the cable modeled as SDOF system in Example 2

Full size image
Fig. 15
figure 15

Logarithm of MCRs of the deflection in the middle of the cable modeled as 5-DOF system in Example 2

Full size image

The mean up-crossing rate (MCR) at threshold \(w=a\), denoted as \(\nu ^+(a)\), is a quantity that is frequently used in system reliability analysis. It is calculated by

$$\begin{aligned} \nu ^+(a)=\int _0^{+\infty }\dot{w}p(a,\dot{w})\mathrm{d}\dot{w} \end{aligned}$$
(39)

In order to show the difference of the MCRs obtained with various methods, the MCRs obtained with various methods are shown and compared in Fig. 6 when the cable is modeled as SDOF system. Since the figure about the MCRs obtained with various methods when the cable is modeled as 5-DOF system looks very close to Fig. 6, it is not presented here. In order to show the difference of the tail behavior of the MCRs obtained with various methods, the MCRs in logarithmic scale are shown and compared in Figs. 7 and 8 when the cable is modeled as SDOF and 5-DOF system, respectively. From these figures it is seen that the MCRs obtained with SSS–EPC are close to those obtained with MCS even in the tails of the MCRs and the error in the MCRs obtained with EQL is too large to be acceptable. The MCR of the deflection obtained from the 5-DOF system is about 1.07–1.55 times of that obtained from the SDOF system when the deflection changes from \(-3.136\sigma _w\) to \(-4.136\sigma _w\) and about 1.24–2.37 times of that obtained from the SDOF system when the deflection changes from \(2.864\sigma _w\) to \(3.864\sigma _w\).

6.2 Example 2

All the parameter values are the same as those in Example 1 except the cable length l equals \(240\,\hbox {m}\) and the sag-to-span ratio is 1 / 125. The PDF of the deflection and the velocity at the center of the cable with \(x=0.5l\) is analyzed. In this case, the \(\mathbf{X}_1\) is still given by \(\mathbf{X}_1=\{w(0.5l,t),\dot{w}(0.5l,t)\}\) in the SSS dimension-reduction procedure.

The observations and discussions about the results in Example 2 are the same as those in Example 1 except that the nonlinearity of the cable in Example 2 is stronger than that in Example 1, which can be reflected by the results shown in Figs. 9, 10, 11, 12, 13, 14, and 15. In this case, about \(10^{10}\) response samples are needed if the PDF of the deflection of the 5-DOF system is to be simulated to the tail end at \(w=4\sigma _w\), which means that the computer needs to run about 250 h or 10 days with the Monte Carlo simulation. The results obtained from the 5-DOF system is about 0.91–1.18 times of the solution of the SDOF system when the deflection changes from \(-3.278\sigma _w\) to \(-4.278\sigma _w\) and about 1.19–2.54 times of the solution of the SDOF system when the deflection changes from \(2.722\sigma _w\) to \(3.722\sigma _w\), where \(\sigma _w=2.16\,\hbox {m}\) obtained with EQL is the standard deviation of the deflection in the middle of the cable. The difference of the values of \(\sigma _w\) of the SDOF system and the 5-DOF system is less than 1 %. For either the SDOF system or the 5-DOF system, the result obtained with EQL is far from being acceptable.

The MCRs obtained with various methods are shown and compared in Fig. 13 when the cable is modeled as SDOF system. Since the figure about the MCRs obtained with various methods when the cable is modeled as 5-DOF system looks very close to Fig. 13, it is not shown here. In order to show the difference of the tail behavior of the MCRs obtained with various methods, the MCRs in logarithmic scale are shown and compared in Figs. 14 and 15 when the cable is modeled as SDOF and 5-DOF system, respectively. From these figures it is observed that the MCRs obtained with SSS–EPC are also close to those obtained with MCS and the error in the MCRs obtained with EQL is also too large to be acceptable. The MCR of the deflection obtained from the 5-DOF system is about 0.94–1.28 times of that obtained from the SDOF system when the deflection changes from \(-3.278\sigma _w\) to \(-4.278\sigma _w\) and about 1.66–2.78 times of that obtained from the SDOF system when the deflection changes from \(2.822\sigma _w\) to \(3.722\sigma _w\).

7 Conclusions

The MDOF–NSD system is formulated for the cables with small sag and excited by uniformly distributed Gaussian white noise. The dimension-reduction procedure of the state-space-split method is adopted to reduce the problem from solving high-dimensional FPK equation to two-dimensional FPK equation. Then the exponential polynomial closure method is adopted to solve the two-dimensional FPK equation. The numerical results and comparison with Monte Carlo simulation and equivalent linearization method show that the SSS–EPC method gives accurate results for the PDF of the cable deflection. Cables modeled as a SDOF system and 5-DOF system are studied. The values in the tails of the PDF of middle deflection of the cable described by the 5-DOF system are bigger than those from the SDOF system. It is observed that the computational time with Monte Carlo simulation and sample size being \(10^8\) for the 5-DOF system is a thousand times more than that with the SSS–EPC method for the studied cables and that equivalent linearization method does not give acceptable results in the tail regions of the PDFs and MCRs of cable deflection.