1 Introduction

Since solitary wave was observed by Scott [1, 2], the studies of solitons have developed into an important theory of nonlinear science. Because of its irreplaceable application in the propagation of nonlinear waves, many remarkable methods were proposed to investigate the soliton solutions for different fundamental physics models. Apart from the inverse scattering transform method [3,4,5] and Darboux transformation [6, 7], the KP hierarchy reduction method [8, 9] and Hirota direct method [10, 11] are considered to be efficient methods in constructing the structure of soliton-type solutions. Among these models, the NLS equation was studied significantly for its essential role in physics and mathematics. Physically, the integrable NLS equation along with its higher order ones has numerous applications, spanning from nonlinear optical fiber-propagation to planar waveguides, water waves, and Bose–Einstein condensates [12,13,14,15]. From a mathematical perspective, solitons [16,17,18,19], rogue waves [20,21,22,23] and breathers [24] have been obtained in the NLS equation and NLS-type equations. Besides, the dynamics of these equations has been well introduced [25,26,27,28,29,30,31,32].

Recently, the study of nonlocal equations has attracted substantial attention in the field of integrable systems. It is a growing tendency that investigating novel nonlocal equations and utilizing various methods to derive their soliton, rogue wave and breather solutions. As the starting point for this trend, Ablowitz and Musslimani reported an integrable nonlocal NLS equation [33]

$$\begin{aligned} \begin{aligned} i q_{t}(x,t)&= q_{xx}(x,t) + 2 \sigma q^2(x,t) q^{*}(-x,t), \end{aligned} \end{aligned}$$
(1)

by an innovative and remarkable integrable symmetry reduction to the Ablowitz–Kaup–Newell–Segur (AKNS) system [34], where q(x, t) is a complex-valued function and \(\sigma = \mp 1\) denotes the defocusing and focusing NLS equation. The \({\mathcal {P}}{\mathcal {T}}\) symmetry property of equation (1) takes crucial advantage of mathematical and physical research. The \({\mathcal {P}}{\mathcal {T}}\) symmetric equations are invariant under the \({\mathcal {P}}{\mathcal {T}}\) operator, which is a very concern issue in solving partial differential equations. On the other hand, \({\mathcal {P}}{\mathcal {T}}\) symmetry is widely employed in classical optics, quantum mechanics, and topological photonics [35,36,37,38,39,40,41,42]. In subsequent years, there is a surge of interest in studying \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal nonlinear equations, especially the \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation. Gerdjikov first investigated the complete integrability of a subset of the nonlocal NLS equation and revealed that there are two types of soliton solutions with the aid of Lax operator [43]. Thereafter, Ablowitz introduced the inverse scattering transform of the nonlocal NLS equation in detail and demonstrated many important properties of this equation, ranging from the time-reversal symmetry to Gauge invariance, Complex translation invariance, \({\mathcal {P}}{\mathcal {T}}\) symmetry and Galilean invariance [44]. Being motivated by the study of Ablowitz, Li and Xu derived a chain of nonsingular localized-wave solutions for a nonlocal nonlinear Schrodinger equation with the self-induced \({\mathcal {P}}{\mathcal {T}}\) symmetric potential via the Nth Darboux transformation [45]. Based on these research results, Rao derived some soliton and soliton-type solutions for various nonlocal integrable equations [46,47,48].

In 2021, a series of integrable space/time shifted nonlocal nonlinear equations were introduced by Ablowitz and Musslimani [49], including the space shifted \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation, time shifted \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation, and space-time shifted \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation. In this paper, we focus on the space shifted \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation

$$\begin{aligned} i q_{t}(x,t)= & {} q_{xx}(x,t) - 2 \sigma q^{2}(x,t) q^{*}(x_{0}-x, t) , \end{aligned}$$
(2)

where \(x_{0}\) is an arbitrary real parameter. Equation (2) can be obtained by substituting

$$\begin{aligned} r(x,t)= & {} \sigma q^{*}(x_{0} - x, t), \end{aligned}$$
(3)

to (q, r) system

$$\begin{aligned} \begin{aligned} i q_{t}(x,t)&= q_{xx}(x,t) - 2 q^2(x,t) r(x,t) ,\\ - i r_{t}(x,t)&= r_{xx}(x,t) - 2 r^2(x,t) q(x,t), \end{aligned} \end{aligned}$$
(4)

which are well known in integrability theory and derived by AKNS. In Ref. [49], Ablowitz and Musslimani provided the Lax pair and constructed the exact one-soliton solution for equation (2) via the inverse scattering transform. Recently, Gürses have discussed all cases of integrable shifted nonlocal NLS and MKdV equations and derived one- and two-soliton solutions by Hirota direct method [50]. The soliton and RW solutions of the space shifted \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation were derived by Darboux transformation [51,52,53]. Since the KP hierarchy reduction method was widely used to derive multiple soliton solutions and the lack of asymptotic analysis, we consider the defocusing nonlocal space shifted NLS equation.

This article is organized as follows. In Sect. 2, we investigate the multiple soliton solutions by the KP hierarchy reduction method and present them as \(2 N \times 2N \) Gram-type determinants. In Sect. 3, we analyze the interactions of two-solitons and four-solitons. The amplitude values and collision coordinates of two-soliton solutions are calculated, and some dynamical behaviors of them are shown in Figs. 1 and 2. It can be seen from Fig. 3 that a four-soliton solution is superposition of two-soliton solutions. Similarly, the higher order multiple dark and antidark soliton solutions may consist of some two-soliton solutions.

2 Derivation of multiple soliton solutions to the space shifted \({\mathcal {P}}{\mathcal {T}}\) symmetric nonlocal NLS equation

In this section, we construct multiple soliton solutions to the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2) by employing the KP hierarchy reduction method and Hirota’s bilinear technique. First, we transform the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2) into the system of bilinear equations

$$\begin{aligned}&\left( D_{x}^{2} - i D_{t} \right) g \cdot f = 0 , \end{aligned}$$
(5)
$$\begin{aligned}&D_{x}^{2} f \cdot f = 2 \rho ^2\left( f^2 - g g^{*}(x_{0}-x,t)\right) , \end{aligned}$$
(6)

by the variable transformation

$$\begin{aligned} q = \rho e^{2 i \rho ^2 t} \frac{g}{f}, \end{aligned}$$
(7)

where \(\rho \) is a real constant, f, g are complex-valued functions of variables x, t, and the function f is subject to the symmetry and complex conjugate condition

$$\begin{aligned} f(x,t) = f^{*}(x_{0}-x,t). \end{aligned}$$
(8)

Here, D is the Hirota bilinear differential operator,

$$\begin{aligned} D_x^m D_t^n f\cdot g= & {} \left( \frac{\partial }{\partial x} - \frac{\partial }{\partial x'} \right) ^{m} \left( \frac{\partial }{\partial t} - \frac{\partial }{\partial t'} \right) ^{n} \nonumber \\&\left[ f(x,t) g(x',t') \right] \big |_{x'=x,t'=t}. \end{aligned}$$
(9)

Then, we start with the following tau functions for single-component KP hierarchy expressed in Gram-type determinants:

$$\begin{aligned} \tau _{n} = \det \left( m_{sj}^{\left( n\right) } \right) _{1\le s,j \le M}, \end{aligned}$$
(10)

with the matrix elements being defined as

$$\begin{aligned} m_{sj}^{\left( n\right) }= & {} C_{s,j} + \frac{1}{p_{s} + q_{j}}\left( - \frac{p_{s}}{q_{j}}\right) ^{n} e^{\xi _{s} + \eta _{j}},\\ \xi _{s}= & {} \frac{1}{p_{s}} x_{-1} + p_{s} x_{1} + p_{s}^{2} x_{2} + \bar{\xi _{s}},\\ \eta _{j}= & {} \frac{1}{q_{j}} x_{-1} + q_{j} x_{1} - q_{j}^{2} x_{2} + \bar{\eta _{j}}, \end{aligned}$$

where \(C_{s,j},p_{s},q_{j},\bar{\xi _{s}},\bar{\eta _{j}}\) are constants, M is a positive integer. According to the Sato theory [54] and the Jacobi identity of determinants [55], the above tau functions can satisfy the following bilinear equations

$$\begin{aligned} \left( D_{x_{1}}^{2} - D_{x_{2}} \right) \tau _{n+1} \cdot \tau _{n}= & {} 0, \end{aligned}$$
(11)
$$\begin{aligned} \left( D_{x_{1}} D_{x_{-1}} -2 \right) \tau _{n} \cdot \tau _{n}= & {} -2 \tau _{n+1} \tau _{n-1}. \end{aligned}$$
(12)

Finally, the KP hierarchy (11), (12) can be reduced to the bilinear equations (5) and (6), so we could obtain the solutions of the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2). To this end, we take the following parametric conditions:

$$\begin{aligned} C_{sj} = c_{s} \delta (s,j),\quad p_{s} q_{s} = \rho ^2, \end{aligned}$$
(13)

for \(s,j = 1, \cdots ,M\) and \(\delta _{i,j}\) is the Kronecker delta, which further constrain the tau functions (10) meeting the following dimension reduction:

$$\begin{aligned} \partial _{x_{-1}} \tau _{n} = \frac{1}{\rho ^2} \partial _{x_{1}} \tau _{n}. \end{aligned}$$
(14)

Then, the bilinear equation (12) would become:

$$\begin{aligned} \left( D_{x_{1}}^2-2{\rho ^2} \right) \tau _{n} \cdot \tau _{n}=-2{\rho ^2}\tau _{n+1} \tau _{n-1}. \end{aligned}$$
(15)

Since the bilinear equations (5) and (6) do not involve derivatives with respect to \(x_{-1}\), we take \(x_{-1}=0\) for simplicity. Under this dimension reduction, after taking the following variable transformations in the above tau functions (10):

$$\begin{aligned} x_{1} = x, \quad x_{2} = - i t . \end{aligned}$$
(16)

further assuming the following symmetry and complex conjugate condition:

$$\begin{aligned} \tau _n(x_0-x,t)=\tau ^*_{-n}(x,t), \end{aligned}$$
(17)

the bilinear equations (11), (12) of KP hierarchy would become the bilinear equations (5), (6) of the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2) for \(\tau _0=f,\tau _1=g,\tau _{-1}=g^*(x_0-x,t)\). To constrain the tau function satisfy the symmetry and complex conjugate condition (17), we take the following parametric conditions:

$$\begin{aligned} \begin{aligned}&M = 2N, \quad q_{j}^{*} = p_{j}, \quad {\bar{\xi }}_{j} = p_{j} k_{j}, \quad {\bar{\eta }}_{j} = q_{j} k_{j},\\&c_{N+s} = - c_{s}^{*}, \quad p_{N+s} = - p_{s}, \quad k_{N+s} = -(x_0+ k_{s}), \end{aligned}\nonumber \\ \end{aligned}$$
(18)

then we have

$$\begin{aligned}&m_{s,j}^{(n)}(x,t) = c_{s} \delta (s,j) + \frac{1}{p_{s} + p^{*}_{j}} \left( - \frac{p_{s}}{p^{*}_{j}} \right) ^{n} e^{\xi _{s}+\xi ^{*}_{j}},\\&\left( \xi _{s} + \xi _{j}^{*} \right) (x,t) \\&\quad = (p_{s} + p_{j}^{*} ) x - i (p_{s}^{2} - p_{j}^{* 2} )t + p_{s} k_{s} + p_{j}^{*} k_{j},\\&(\xi _{N+s} + \xi _{N+j}^{*})(x_0-x,t)\\&\quad = - (p_{s}+ p_{j}^{*})(x_0- x) - i (p_{s}^{2}-p_{j}^{* 2}) t\\&\qquad + p_{s}( x_0 + k_{s} ) + p_{j}^{*} (x_0 + k_{j})\\&\quad = \left( \xi _{j} + \xi _{s}^{*} \right) ^{*}(x,t),\\&m_{N+s, N+j}^{(n)}(x_0-x,t)\\&\quad = -c_{s}^{*} \delta (s,j) - \frac{1}{p_{s} + p^{*}_{j}} \left( - \frac{p_{s}}{p^{*}_{j}} \right) ^{n} e^{\xi _{N+s}+\xi ^{*}_{N+j}}\\&\quad = -\left( c_{s} \delta (s,j) + \frac{1}{p_{j} + p^{*}_{s}} \left( - \frac{p_{j}}{p^{*}_{s}} \right) ^{(-n)} e^{\left( \xi _{j} + \xi _{s}^{*} \right) (x,t)} \right) ^{*}\\&\quad = - \left( m_{j, s}^{(-n)}(x,t) \right) ^{*}. \end{aligned}$$

Similarly, we can obtain

$$\begin{aligned} m_{N+s, j}^{(n)}(x_0-x,t)= & {} - \left( m_{N+j, s}^{(-n)}(x,t) \right) ^{*},\\ m_{s, N+j}^{(n)}(x_0-x,t)= & {} - \left( m_{j, N+s}^{(-n)}(x,t) \right) ^{*}, \end{aligned}$$

hence

$$\begin{aligned} \begin{aligned}&\tau _{n}(x_0 - x,t)\\&\quad = \left|\begin{array}{cc} m_{s, j}^{(n)}(x_0 - x,t) &{} m_{N+s, j}^{(n)}(x_0 - x,t) \\ m_{s ,N+j}^{(n)}(x_0 - x,t) &{} m_{N+s, N+j}^{(n)}(x_0 - x,t) \end{array}\right|\\&\quad = \left|\begin{array}{cc} m_{N+j, N+s}^{(-n)}(x,t) &{} m_{N+j,s}^{(-n)}(x,t) \\ m_{j ,N+s}^{(-n)}(x,t) &{} m_{j, s}^{(-n)}(x,t) \end{array}\right|^{*} \\&\quad = \tau _{-n}^{*}(x,t) . \end{aligned} \end{aligned}$$

In summary, we can present the multiple soliton solutions to the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2) by the following Theorem.

Theorem 1

The S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2) admits the following multiple dark and antidark soliton solutions

$$\begin{aligned} \begin{aligned} u=\rho {e^{2i\rho ^2t}\frac{g}{f}}, \end{aligned} \end{aligned}$$
(19)

where

$$\begin{aligned} \begin{aligned} g=&\left|c_{s} \delta (s,j) + \frac{1}{p_{s} + p^{*}_{j}} \left( - \frac{p_{s}}{p^{*}_{j}} \right) e^{\xi _{s}+\xi ^{*}_{j}}\right|_{1\le s,j\le 2N}, \\ f=&\left|c_{s} \delta (s,j) + \frac{1}{p_{s} + p^{*}_{j}} e^{\xi _{s}+\xi ^{*}_{j}}\right|_{1\le s,j\le 2N}, \\ \end{aligned}\nonumber \\ \end{aligned}$$
(20)

and

$$\begin{aligned} \begin{aligned} \xi _{s} = p_{s} x - i p^{2}_{s} t +p_{s} k_{s}. \end{aligned} \end{aligned}$$
(21)

Here, N is a positive integer, the complex parameters \(c_s, p_s\) and real parameters \(k_s,x_0,\rho \) satisfy the following constraints

$$\begin{aligned} \begin{aligned} |p_{s}|^2=&\rho ^{2}, c_{N + s}= - c_{s}^{*},\\ p_{N+s}=&- p_{s}, k_{N+s}= -(x_{0} + k_{s}), \end{aligned} \end{aligned}$$
(22)

for \(s=1,2, \cdots , N\).

3 Dynamics of multiple dark and antidark soliton interactions

In this section, we focus on the dynamics of collisions between the multiple dark and antidark solitons in the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2).

3.1 Collisions of two dark/antidark solitons

By taking \(N=1\), Theorem 1 yields the two dark/antidark solitons solution to the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation (2). The explicit form of the two dark/antidark solitons solution is expressed as :

$$\begin{aligned} \begin{aligned} u=\rho {e^{2i\rho ^2t}}\frac{g}{f}, \end{aligned} \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{aligned} f&= \left|\begin{array}{cc} c + \frac{1}{p + p^{*} } e^{\xi _{1} + \xi _{1}^{*}} &{} \frac{1}{p - p^{*}} e^{\xi _{1} + \xi _{2}^{*}} \\ \frac{1}{-p + p^{*}} e^{\xi _{2} + \xi _{1}^{*}} &{} -c^{*} - \frac{1}{p+p^{*}} e^{\xi _{2} + \xi _{2}^{*}} \end{array}\right|,\\ g&= \left|\begin{array}{cc} c - \frac{p}{p^{*}}\frac{1}{p + p^{*} } e^{\xi _{1} + \xi _{1}^{*}} &{} -\frac{p}{p^{*}}\frac{1}{p - p^{*}} e^{\xi _{1} + \xi _{2}^{*}} \\ -\frac{p}{p^{*}}\frac{1}{-p + p^{*}} e^{\xi _{2} + \xi _{1}^{*}} &{} -c^{*} + \frac{p}{p^{*}}\frac{1}{p+p^{*}} e^{\xi _{2} + \xi _{2}^{*}} \end{array}\right|,\\ \end{aligned}\nonumber \\ \end{aligned}$$
(24)

with

$$\begin{aligned} \xi _{1} {=} p x - i p^{2} t {+} p k ,\quad \xi _{2} = -p x - i p^{2} t + p (x_0 - k). \end{aligned}$$

For simplicity, we take \(p=\rho e^{i \theta }\), then the functions f, g of solution (23) can be rewritten as

$$\begin{aligned} f= & {} - \left|c\right|^{2} \left[ 1 + \frac{1}{2 \rho c \cos \theta } e^{\zeta _{1}} + \frac{1}{2 \rho c^{*} \cos \theta } e^{\zeta _{2}} \right. \\&\left. + \left( \frac{1}{\rho \left|c\right|\sin 2 \theta }\right) ^{2} e^{\zeta _{1} + \zeta _{2}}\right] ,\\ g= & {} - \left|c\right|^{2} \left[ 1 - \frac{e^{2 i \theta }}{2 \rho c \cos \theta } e^{\zeta _{1}} - \frac{e^{2 i \theta }}{2 \rho c^{*} \cos \theta } e^{\zeta _{2}}\right. \\&\left. + \left( \frac{e^{2 i \theta }}{\rho \left|c\right|\sin 2 \theta }\right) ^{2} e^{\zeta _{1} + \zeta _{2}}\right] , \end{aligned}$$

where

$$\begin{aligned} \zeta _{1}= & {} 2 \rho \cos \theta (x + 2 \rho t \sin \theta + k),\\ \zeta _{2}= & {} 2 \rho \cos \theta (x_0 - x + 2 t \rho \sin \theta + k). \end{aligned}$$

To reveal the collision properties of the two dark/antidark solitons solution, we consider the asymptotic behaviors of the two solitons. Without losing generality, we assume \(\theta \in \left( 0,\frac{\pi }{2}\right) \) and \(\rho > 0\) and define the soliton moving along the line \(\zeta _1\approx 0\) as soliton 1, and the soliton along the line \(\zeta _2\approx 0\) as soliton 2. The asymptotic forms for the two dark/antidark solitons solution are expressed as:

  1. (i)

    Before collision \((t \rightarrow -\infty )\):

          Soliton 1 \((\zeta _{1} \approx 0, \zeta _{2} \approx - \infty )\)

    $$\begin{aligned} \begin{aligned} A_{1}^{-} \simeq \rho e^{2 i \rho ^{2} t} \frac{c - e^{2 i \theta } \nu _1}{c + \nu _1}, \end{aligned} \end{aligned}$$
    (25)

          Soliton 2 \((\zeta _{1} \approx - \infty , \zeta _{2} \approx 0)\)

    $$\begin{aligned} \begin{aligned} A_{2}^{-} \simeq \rho e^{2 i \rho ^{2} t} \frac{c^{*} - e^{2 i \theta } \nu _2}{c^{*} + \nu _2}, \end{aligned} \end{aligned}$$
    (26)

    where \( \nu _{1} = \frac{e^{\zeta _{1}}}{2 \rho \cos \theta }, \quad \nu _{2} = \frac{e^{\zeta _{2}}}{2 \rho \cos \theta }. \)

  2. (ii)

    After collision \((t \rightarrow +\infty )\):

          Soliton 1 \((\zeta _{1} \approx 0, \zeta _{2} \approx + \infty )\)

    $$\begin{aligned} \begin{aligned} A_{1}^{+} \simeq -\rho e^{2 i \rho ^{2} t + 2 i \theta } \frac{c - e^{2 i \theta } \nu _3}{c + \nu _3}, \end{aligned} \end{aligned}$$
    (27)

          Soliton 2 \((\zeta _{1} \approx + \infty , \zeta _{2} \approx 0)\)

    $$\begin{aligned} \begin{aligned} A_{2}^{+} \simeq -\rho e^{2 i \rho ^{2} t + 2 i \theta } \frac{c^{*} - e^{2 i \theta } \nu _4}{c^{*} + \nu _4}, \end{aligned} \end{aligned}$$
    (28)

where \( \nu _{3} = \frac{e^{\zeta _{1}}}{2 \rho \sin ^{2} \theta \cos \theta }, \quad \nu _{4} = \frac{e^{\zeta _{2}}}{2 \rho \sin ^{2} \theta \cos \theta }. \)

Since \(A_j^{(-)}(\zeta _j)=A_j^{(+)}(\zeta _j - 2 \log (\sin \theta ))\) for \(j=1,2\) and here \(\log \) is natural logarithms, the two solitons occur elastic collisions. Further more, the properties of two solitons including shapes, velocity, amplitudes remain same after collision except for an finite phase shift. Along the centers of the two solitons

$$\begin{aligned} \zeta _j - \log (2 \rho \left|c\right|\cos \theta ) - 2\log \sin \theta \displaystyle \prod _{i = 1}^{2}(j-i) = 0, \end{aligned}$$

we can obtain the intensities of the two solitons are:

$$\begin{aligned} \left|A_{j}\right|_{Inten}&= \Gamma _j+\rho , \end{aligned}$$
(29)

where

$$\begin{aligned} \Gamma _j=\left|\sin \theta + (-1)^{j}\cos \theta \tan \frac{\theta _{0}}{2}\right|-\rho , \end{aligned}$$
(30)

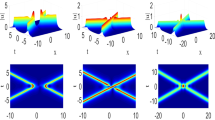
for \(j=1,2\), and \(e^{i\theta _0}=\frac{c}{\left|c\right|}\). According to the values of \(\Gamma _j\), the soliton j is classified into three patterns: an antidark soliton for \(\Gamma _j>0\), a dark soliton for \(\Gamma _j<0\) and vanishing one for \(\Gamma _j=0\). Since the system of equations, \(\Gamma _1=0\) and \(\Gamma _2=0\), has no real roots, the two dark/antidark solitons cannot vanish in the same time. Hence, the combination of the two dark/antidark solitons possesses \(2^3\) patterns: antidark–dark soliton when \(\Gamma _1>0,\Gamma _2<0\), antidark-vanishing soliton when \(\Gamma _1>0,\Gamma _2=0\), antidark–antidark soliton when \(\Gamma _1>0,\Gamma _2>0\), vanishing-dark soliton when \(\Gamma _1=0,\Gamma _2<0\), vanishing-antidark soliton when \(\Gamma _1=0,\Gamma _2>0\), dark–dark soliton when \(\Gamma _1<0,\Gamma _2<0\), dark-vanishing soliton when \(\Gamma _1<0,\Gamma _2=0\) and dark–antidark soliton when \(\Gamma _1<0,\Gamma _2>0\), namely, four types of non-degenerate soliton and four types of degenerate soliton (See Table 1). Fig. 1 shows five patterns of two dark/antidark solitons solutions. The three patterns of the non-degenerate soliton are displayed in the first line of Fig. 1, namely, the dark–dark soliton (see Fig. 1(a)), the antidark–antidark soliton (see Fig. 1(b)) and dark–antidark soliton (see Fig. 1(c)). The two patterns of degenerate soliton are exhibited in the second line of Fig. 1, namely, the vanishing-antidark-soliton solution (see Fig. 1(d)) and the dark-vanishing-soliton solution (see Fig. 1(e)). We also calculate the amplitude values of two-soliton solutions in Fig. 1 and express it as \((\left|A_{1}\right|_{Inten},\left|A_{2}\right|_{Inten})\). We default \(\rho = 1, \theta = \frac{\pi }{6},\theta _{0} = \frac{\pi }{2},k = 0, x_0 = 0,|c|= 1\).

By setting \(x_0=0, k=0\) and comparing the coordinates of two solitons before and after the collision

  1. (i)

    Before collision

    $$\begin{aligned} x = \frac{x_{0}}{2}, \quad t = \frac{\log (2 \rho |c|\cos \theta ) - \rho (x_0 + 2 k) \cos \theta }{2 \rho ^{2} \sin 2 \theta }, \end{aligned}$$
  2. (ii)

    After collision

    $$\begin{aligned} x {=} \frac{x_{0}}{2}, \quad t {=} \frac{\log (\rho |c|\sin 2 \theta \cos \theta ) - \rho (x_0 + 2 k) \cos \theta }{2 \rho ^{2} \sin 2 \theta }, \end{aligned}$$

we find the exact interaction should occur from point \(\left( 0,\frac{\log (\frac{\sqrt{3}}{4})}{2 \sqrt{3}}\right) \) to point \(\left( 0,\frac{\log (3)}{2 \sqrt{3}}\right) \). This interaction process is shown in Fig. 2(a). Notice that, the angle between Soliton 1 and Soliton 2 is \(\theta _{-}^{-} {=} 2 \arctan (2 \rho \sin \theta )\), which will increase while \(\theta \) changes from 0 to \(\frac{\pi }{2}\) (See Fig. 2(b)). Besides, we can change the collision point by choosing different parameter values (See Fig. 2(c)).

Table 1 The classification of two dark/antidark solitons solution
Full size table
Fig. 1
figure 1

(Color online) The first line is non-degenerate types: a \(\theta _{0} = 0\). b \(\theta _{0} = \frac{5\pi }{6}\). c \(\theta _{0} = \frac{\pi }{2}\). The second line is degenerated types: d (Soliton 1 vanished) \(\theta _{0} = \frac{2\pi }{3}\). e (Soliton 2 vanished) \(\theta _{0} = \frac{\pi }{3}\). In the above five two-soliton cases, the amplitude values are \((\frac{1}{2},\frac{1}{2})\), \((1 + \sqrt{3},2 + \sqrt{3})\),\((\frac{\sqrt{3} - 1}{2}, \frac{\sqrt{3} + 1}{2}),(1,2)\) and (0, 1), respectively

Full size image
Fig. 2
figure 2

(Color online) a The time evolution of dark–antidark-soliton, the collision point is \((0,-0.08)\). b \(\theta _{-}^{-}\) are \(54.7^{\circ }, 90^{\circ }\) and \( 125.3^{\circ }\), respectively. c \((x_0,k)\) are \((0,0),(10 \sqrt{3},0),(-10\sqrt{3},10\sqrt{3})\) and \((0,10\sqrt{3})\)

Full size image

3.2 Collisions of four dark/antidark solitons

In Theorem 1, for \(N = 2\), we have four dark/antidark Solitons solutions

$$\begin{aligned} \begin{aligned} f&= \left|\begin{array}{cccc} c_{1} + \frac{1}{p_{1} + p_{1}^{*} } e^{\xi _{1} + \xi _{1}^{*}} &{} \frac{1}{p_{1} + p_{2}^{*} } e^{\xi _{1} + \xi _{2}^{*}} &{} \frac{1}{p_{1} - p_{1}^{*} } e^{\xi _{1} + \xi _{3}^{*}} &{} \frac{1}{p_{1} - p_{2}^{*} } e^{\xi _{1} + \xi _{4}^{*}} \\ \frac{1}{p_{2} + p_{1}^{*} } e^{\xi _{2} + \xi _{1}^{*}} &{} c_{2} + \frac{1}{p_{2} + p_{2}^{*} } e^{\xi _{2} + \xi _{2}^{*}} &{} \frac{1}{p_{2} - p_{1}^{*} } e^{\xi _{2} + \xi _{3}^{*}} &{} \frac{1}{p_{2} - p_{2}^{*} } e^{\xi _{2} + \xi _{4}^{*}} \\ \frac{1}{-p_{1} + p_{1}^{*} } e^{\xi _{3} + \xi _{1}^{*}} &{} \frac{1}{p_{2} + p_{2}^{*} } e^{\xi _{3} + \xi _{2}^{*}} &{} -c_{1}^{*} - \frac{1}{p_{1} + p_{1}^{*} } e^{\xi _{3} + \xi _{3}^{*}} &{} - \frac{1}{p_{1} + p_{2}^{*} } e^{\xi _{3} + \xi _{4}^{*}} \\ \frac{1}{-p_{2} + p_{1}^{*} } e^{\xi _{4} + \xi _{1}^{*}} &{} \frac{1}{-p_{2} + p_{2}^{*} } e^{\xi _{4} + \xi _{2}^{*}} &{} - \frac{1}{p_{2} + p_{1}^{*} } e^{\xi _{4} + \xi _{3}^{*}} &{} -c_{2}^{*} - \frac{1}{p_{2} + p_{2}^{*} } e^{\xi _{4} + \xi _{4}^{*}} \\ \end{array}\right|,\\ \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} g&= \left|\begin{array}{cccc} c_{1} - \frac{1}{p_{1} + p_{1}^{*} } \frac{p_{1}}{p_{1}^{*}}e^{\xi _{1} + \xi _{1}^{*}} &{} -\frac{1}{p_{1} + p_{2}^{*} } \frac{p_{1}}{p_{2}^{*}} e^{\xi _{1} + \xi _{2}^{*}} &{} \frac{1}{p_{1} - p_{1}^{*} } \frac{p_{1}}{p_{1}^{*}} e^{\xi _{1} + \xi _{3}^{*}} &{} \frac{1}{p_{1} - p_{2}^{*} } \frac{p_{1}}{p_{2}^{*}} e^{\xi _{1} + \xi _{4}^{*}} \\ -\frac{1}{p_{2} + p_{1}^{*} } \frac{p_{2}}{p_{1}^{*}} e^{\xi _{2} + \xi _{1}^{*}} &{} c_{2} - \frac{1}{p_{2} + p_{2}^{*} } \frac{p_{2}}{p_{2}^{*}} e^{\xi _{2} + \xi _{2}^{*}} &{} \frac{1}{p_{2} - p_{1}^{*} } \frac{p_{2}}{p_{1}^{*}} e^{\xi _{2} + \xi _{3}^{*}} &{} \frac{1}{p_{2} - p_{2}^{*} } \frac{p_{2}}{p_{2}^{*}} e^{\xi _{2} + \xi _{4}^{*}} \\ \frac{1}{-p_{1} + p_{1}^{*} } \frac{p_{1}}{p_{1}^{*}} e^{\xi _{3} + \xi _{1}^{*}} &{} \frac{1}{-p_{1} + p_{2}^{*} } \frac{p_{1}}{p_{2}^{*}} e^{\xi _{3} + \xi _{2}^{*}} &{} -c_{1}^{*} + \frac{1}{p_{1} + p_{1}^{*} } \frac{p_{1}}{p_{1}^{*}} e^{\xi _{3} + \xi _{3}^{*}} &{} \frac{1}{p_{1} + p_{2}^{*} } \frac{p_{1}}{p_{2}^{*}} e^{\xi _{3} + \xi _{4}^{*}} \\ \frac{1}{-p_{2} + p_{1}^{*} } \frac{p_{2}}{p_{1}^{*}} e^{\xi _{4} + \xi _{1}^{*}} &{} \frac{1}{-p_{2} + p_{2}^{*} } \frac{p_{2}}{p_{2}^{*}} e^{\xi _{4} + \xi _{2}^{*}} &{} \frac{1}{p_{2} + p_{1}^{*} } \frac{p_{2}}{p_{1}^{*}} e^{\xi _{4} + \xi _{3}^{*}} &{} -c_{2}^{*} - \frac{1}{p_{2} + p_{2}^{*} } \frac{p_{2}}{p_{2}^{*}} e^{\xi _{4} + \xi _{4}^{*}} \\ \end{array}\right|,\\ \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \xi _{1}= & {} p_{1} x - i p_{1}^{2} t + p_{1} k_{1} ,\\ \xi _{3}= & {} -p_{1} x - i p_{1}^{2} t + p_{1} (x_0 - k_{1}),\\ \xi _{2}= & {} p_{2} x - i p_{2}^{2} t + p_{2} k_{2} ,\\ \xi _{4}= & {} -p_{2} x - i p_{2}^{2} t + p_{2} (x_0 - k_{2}). \end{aligned}$$

After performing a row-column elementary transformation on f and g, we get

$$\begin{aligned} \begin{aligned} f&= \left|\begin{array}{cc} f_1 &{} ~\sim \\ \sim &{} ~f_2 \\ \end{array}\right|,\\ \end{aligned} \quad \begin{aligned} g&= \left|\begin{array}{cc} g_1 &{} ~\sim \\ \sim &{} ~g_2 \\ \end{array}\right|,\\ \end{aligned} \end{aligned}$$

where \(u_1 =\rho {e^{2i\rho ^2t}} \frac{g_1}{f_1}\) and \(u_2 = \rho {e^{2i\rho ^2t}} \frac{g_2}{f_2}\). Since \(u_1\) and \(u_2\) are both in the form of a first-order \((N=1)\) solution, a four dark/antidark solitons solution consists of two two-dark/antidark solitons solutions. Higher order soliton solutions also share the similar superposition of two-soliton solutions. We call \(u_1\) and \(u_2\) as A-two-soliton and B-two-soliton, respectively. Letting

$$\begin{aligned} p_{1}= & {} \rho e^{i \theta _{1}},\quad p_{1}^{*} = \rho e^{-i \theta _{1}},\\ p_{2}= & {} \rho e^{i \theta _{2}},\quad p_{2}^{*} = \rho e^{-i \theta _{2}},\\ c_{1}= & {} |c_{1}|e^{i \theta _{3}},\quad c_{2} = |c_{2}|e^{i \theta _{4}}, \end{aligned}$$

we get the amplitude values of A-two-soliton and B-two-soliton under the condition \(\theta _{1} \ne \theta _{2},\theta _{j} \in \left( 0,\frac{\pi }{2}\right) ,j=1,2\)

  1. (i)

    A-two-soliton

    $$\begin{aligned} \begin{array}{cc} \begin{aligned} \left|A_{j}\right|_{Inten} &{}{=} \sqrt{\frac{1 -\sin (2 \theta _{1} + (-1)^{j+1}\theta _{3})}{1 + (-1)^{j+1} \sin \theta _{3}}} \\ &{} = \Gamma _{j}^{A} + \rho , \end{aligned} \end{array} \end{aligned}$$
    (31)
    $$\begin{aligned} \Gamma _{j}^{A} {=} \left|\sin \theta _{1} {+} ({-}1)^{j}\cos \theta _{1} \tan \frac{\theta _{3}}{2}\right|{-} \rho ,\quad j {=} 1,2, \end{aligned}$$
  2. (ii)

    B-two-soliton

    $$\begin{aligned} \begin{array}{cc} \begin{aligned} \left|B_{j}\right|_{Inten} &{}{=} \sqrt{\frac{1 {-}\sin (2 \theta _{2} {+} (-1)^{j+1}\theta _{4})}{1 {+} ({-}1)^{j+1} \sin \theta _{4}}} \\ &{} {=} \Gamma _{j}^{B} + \rho , \end{aligned} \end{array} \end{aligned}$$
    (32)
    $$\begin{aligned} \Gamma _{j}^{B} = \left|\sin \theta _{2} + (-1)^{j}\cos \theta _{2} \tan \frac{\theta _{4}}{2}\right|- \rho , \quad j = 1,2. \end{aligned}$$

According to \(\left|A_{j}\right|_{Inten}\) and \(\left|B_{j}\right|_{Inten}\), there are 64 patterns of A-two-soliton and B-two-soliton, theoretically. Some of them are displayed in Fig. 3.

Fig. 3
figure 3

(Color online) The four dark/antidark solitons solutions with parameter values \(\rho = 1, \theta _{1} = \frac{\pi }{6}, \theta _{2} = \frac{\pi }{3}, k_{1}=k_{2}= 0, x_0 = 0, |c_{1}|=|c_{2}|= 1\): a \(\theta _{3} = \frac{11\pi }{12},\theta _{4} = \frac{11\pi }{12}\). b \(\theta _{3} = 0,\theta _{4} = \frac{1\pi }{2}\). c \(\theta _{3} = 0,\theta _{4} = 0\). d \(\theta _{3} = \frac{\pi }{2},\theta _{4} = \frac{\pi }{2}\). e \(\theta _{3} = \frac{\pi }{2},\theta _{4} = \frac{5\pi }{6}\). f \(\theta _{3} = -\frac{2\pi }{3},\theta _{4} = -\frac{5\pi }{6}\). g \(\theta _{3} = \frac{\pi }{3},\theta _{4} = \frac{\pi }{6}\). h \(\theta _{3} = \frac{\pi }{3},\theta _{4} = \frac{5\pi }{6}\). In the above 8 four-soliton cases, the amplitude values are (6.1, 7.1, 2.9, 4.7), (0.5, 0.5, 0.37, 1.37), (0.5, 0.5, 0.87, 0.87), (0.37, 1.37, 0.37, 1.37), (0.37, 1.37, 1, 2.7), (2, 1, 2.7, 1), (0, 1, 0.73, 1) and (0, 1, 1, 2.7), respectively

Full size image

4 Conclusion

This paper has constructed the general high-order soliton solutions to the S\({\mathcal {P}}{\mathcal {T}}\)NNLS equation with a plane background. The derivation of the general high-order solitons solution employs the bilinear KP hierarchy reduction method and Hirota’s bilinear technique. These soliton solutions are expressed in the form of \(2N\times 2N\) determinants. Therefore, the general soliton solutions we have obtained are all in pairs. The two dark/antidark-soliton solutions are classified into non-degenerate soliton solutions and degenerate soliton solutions. We have investigated the dynamics of the two kinds of solutions. Under different parametric conditions, we obtained eight different types of soliton solutions in Table 1. Besides, it has been revealed that the four dark/antidark solitons exhibit the superpositions of two dark/antidark-soliton solutions with 64 patterns. Some particular types of these patterns are shown in Fig. 3.

A natural extension of the present paper might be constructing rational solutions and semi-rational solutions via the bilinear KP-reduction method and Hirota’s bilinear technique.