1 Introduction

The coupled nonlinear Schrödinger (CNLS) or CNLS-type equations have attracted considerable attentions because of their wide applications in a wide scope of physical fields, spanning from nonlinear optics to, water waves, atomic condensates, plasma physics, and others [1,2,3,4,5]. In general, these CNLS/CNLS-type equations are non-integrable. However, some variant forms of them with particular parametric choices can become integrable systems [6]. Since their mathematical and physical interests, the exact solutions of these integrable forms of CNLS/CNLS-type equations were well investigated, including solitons, breathers, rogue wave, and coherent structures of them.

Nowadays, investigating nonlocal equations is a hot topic in the field of integrable systems. The first example is the nonlocal NLS equation, which was introduced by Ablowitz and Musslimani from the particular reductions of the Ablowitz–Kaup–Newell–Segur (AKNS) hierarchy [7]. The exact solutions of this nonlocal NLS have been investigated by different methods [7,8,9,10]. Motivated by the seminal works of Ablowitz and Musslimani [7], hierarchies of nonlocal integrable equations and their exact solutions were proposed and studied, including the integrable multidimensional versions of the nonlocal NLS equation [11,12,13,14], and the multi-component forms of the nonlocal NLS equation [11, 15], and the transformations between nonlocal equations and their associated local integrable equations [16], and different nonlocal versions of the NLS/NLS-type Eqs. [17,18,19,20,21]. Very recently, Ablowitz and Mussliman considered a new nonlocal reduction of the AKNS hierarchy called space-shifted nonlocal reduction [22], and proposed the following space-shifted nonlocal NLS equation:

$$\begin{aligned} \begin{aligned}&iu_{t}+u_{xx}\pm u^2u^*(x_0-x,t)=0, \end{aligned} \end{aligned}$$
(1)

where the space-shifted factor \(x_0\) is an arbitrary real parameter. When \(x=x_0\), the shifted nonlocal NLS Eq. (1) reduce back to the usual nonlocal NLS equation [7]. The space shifted nonlocal NLS Eq. (1) is solvable by the inverse scattering transform and admits an infinitely many conservation laws. The bright two-soliton solutions of the focusing case were studied in the framework of Riemann–Hilbert formulations [22]. The higher-order soliton solutions of Eq. (1) were investigated by using the bilinear method [23, 24].

In this paper, we study the space-shifted nonlocal CNLS equation

$$\begin{aligned} \begin{aligned}&iu_{t}+u_{xx}+2\left[ \delta uu^*(x_0-x,t)+\gamma vv^*(x_0-x,t)\right] u=0, \\&iv_{t}+v_{xx}+2\left[ \delta uu^*(x_0-x,t)+\gamma vv^*(x_0-x,t)\right] v=0,\\ \end{aligned}\nonumber \\ \end{aligned}$$
(2)

where \(\delta \) and \(\gamma \) are real coefficients. By scalings of u and v, the nonlinear coefficients \(\delta \) and \(\gamma \) are normalized to be \(\pm 1\) without loss of generality. When the space-shifted factor \(x_0=0\), Eq. (2) would reduce to the usual nonlocal CNLS equation [11]. The single-pole bright solitons and their collisions in the usual nonlocal CNLS equation have been in discussed in [25, 26]. By taking a long wave limit of these obtained single-pole bright solitons, the double-pole solitons can be derived for the usual nonlocal CNLS equation with focusing ( i.e., \(\delta =-1,\gamma =-1\) in Eq. (2)) and the mixed focusing-defocusing (i.e. \(\delta \gamma =-1\) in Eq. (2)) nonlinearities [26]. Here we have to emphasize that although the smooth bright single-pole soliton solutions exist in usual nonlocal CNLS equation with all types of nonlinearities, but the regular double-pole soliton solutions were not found in the usual nonlocal defocusing CNLS equation (i.e.,\(\delta =\gamma =-1,x_0=0\) in Eq. (2)).

The single-pole soliton solutions and higher-order pole soliton solutions have essential differences. The former one are expressed by superpositions of exponential functions, while the later one are given by combinations of exponential functions with rational functions. The higher-order pole soliton solutions can be derived from single pole-soliton solutions through limit procedures [27]. There are lots of researches were reported for the higher-order pole solitons in various local integrable systems. For the NLS equation, the higher-order pole solitons and their interactions were studied in [28,29,30,31,32,33]. The regularities of these higher-order pole soliton solutions were considered in [34]. Particularly, the long time asymptotic behaviours of these large-order pole solitons were systematically analyzed [35]. For the Hirota equation, the double-pole solitons were first constructed in [36], and their asymptotic analysis were studied recently [37, 38]. The modified Korteweg-de Vries equation and sine-Gordon equation have also been proved to admit the higher-order pole soliton solutions [27, 39,40,41,42,43]. In these scalar integrable systems, the amplitudes of these higher-order pole solitons are equal before and after the collision, namely they only occur elastic collisions. However, the higher-order pole soliton in multi-component integrable systems can happen inelastic collisions, namely, their amplitudes alter after collisions [44,45,46]. Even though so much investigations of higher-order pole solitons have been done for the local systems, but related results on higher-order pole solitons are scarce for the nonlocal integrable systems.

In this work, we will investigate the space-shifted nonlocal CNLS Eq. (2) in two aspects:

  • The multiple bright–dark soliton solutions in terms of determinants for the space-shifted nonlocal CNLS Eq. (2) via the bilinear KP hierarchy reduction.

  • The multiple double-pole bright–dark soliton solutions generated from the bright–dark solitons through the long wave limit procedure.

This paper is organized as follows. In Sect. 2, first we construct multiple bright–dark soliton solutions in terms of determinants for the space-shifted nonlocal CNLS Eq. (2) by using the bilinear Kadomtsev–Petviashvili (KP) hierarchy reduction, then we study the collision dynamics of these multiple bright–dark solitons. In Sect. 3, we derive the multiple double-pole bright–dark soliton solutions for the space-shifted nonlocal CNLS Eq. (2) by taking the long wave limit procedure form the obtained single-pole bright–dark solitons. The conclusions are given in Sect. 4.

2 Multiple bright–dark solitons in the space-shifted nonlocal CNLS equation

In this section, we investigate the multiple bright–dark soliton solutions for the space-shifted nonlocal CNLS Eq. (2) by using the bilinear KP hierarchy reduction method [47,48,49,50,51], in which the u and v components correspond to the bright and dark solitons, respectively.

2.1 Multiple bright–dark soliton solutions in forms of determinants

Through the dependent variable transformations \(u=e^{2i\gamma {t}}\frac{g}{f},v=e^{2i\gamma {t}}\frac{h}{f}\), the space-shifted nonlocal CNLS Eq. (2) is transformed into the bilinear form:

$$\begin{aligned} \begin{aligned}&(D_{x}^{2}+iD_{t})g \cdot f =0, \\&(D_{x}^{2}+iD_{t})h \cdot f =0, \\&(D_{x}^2+2\gamma )f \cdot f =2(\gamma {hh^{*}(x_0-x,t)} +\delta gg^{*}(x_0-x,t)), \end{aligned} \end{aligned}$$
(3)

where the function f has to be subject to the following phase-shifted symmetry and complex conjugate condition

$$\begin{aligned} \begin{aligned} f^*(x,t)=f(x_0-x,t), \end{aligned} \end{aligned}$$
(4)

and D is the Hirota’s bilinear differential operator [49]. Based on this bilinear form, we present multiple bright–dark soliton solutions to the space-shifted nonlocal CNLS Eq. (2) in the following theorem.

Theorem 1

The bright–dark soliton solutions for the space-shifted nonlocal CNLS Eq. (2) are

$$\begin{aligned} \begin{aligned} u=e^{2i\gamma {t}}\frac{g}{f},v=e^{2i\gamma {t}}\frac{h}{f}, \end{aligned} \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned} f=&\begin{vmatrix} m_{s,j}^{(0)}&m_{s,N+j}^{(0)}\\ m_{N+s,j}^{(0)}&m_{N+s,N+j}^{(0)} \end{vmatrix},\\ g=&\begin{vmatrix} m_{s,j}^{(0)}&m_{s,N+j}^{(0)}&e^{p_sx+ip_s^2t+\xi _s^{0}}\\ m_{N+s,j}^{(0)}&m_{N+s,N+j}^{(0)}&e^{-p_s(x-x_0)+ip_s^2t+\xi _s^{0*}}\\ -\alpha _j&-\alpha _j^{*}&0 \end{vmatrix}, \\ h=&\begin{vmatrix} m_{s,j}^{(1)}&m_{s,N+j}^{(1)}\\ m_{N+s,j}^{(1)}&m_{N+s,N+j}^{(1)} \end{vmatrix}, \end{aligned} \end{aligned}$$
(6)

and the matrix elements are given by

$$\begin{aligned} \begin{aligned} m_{s,j}^{(n)}&=\left( -\frac{p_s}{p_j^*}\right) ^{n}\frac{e^{(p_s+p_j^*)x+i(p_s^2-p_j^{*2})t +\xi _s^{0}+\xi _j^{0*}}}{p_s+p_j^*}\\&\quad +\frac{\alpha _s\alpha _j}{q_s+q_j^*}, \end{aligned} \end{aligned}$$
(7)

for \(1\le {s,j}\le N\). Here the parameters have to satisfy the following restrictions:

$$\begin{aligned} \begin{aligned} q_s&=-\frac{p_s^2+\gamma }{\delta {p_s}}, p_{M+s}=-p_{s}, \xi _{N+s}^0\\ {}&=\xi _s^{0*}+p_sx_0,\alpha _{N+j}=\alpha _{j}^*, \end{aligned} \end{aligned}$$
(8)

where \(p_s, \xi _s^0,\alpha _j\) are freely complex parameters.

Proof

These bright–dark soliton solutions can be reduced from the following tau functions of multi-component KP hierarchy:

$$\begin{aligned} \begin{aligned} \tau _0^{(n)}=&\begin{vmatrix} M \end{vmatrix}, \tau _1^{(n)}=&\begin{vmatrix} M&\Phi ^{T}\\ -\overline{\Psi }&0 \end{vmatrix}, \tau _{-1}^{(n)}=\begin{vmatrix} M&\Psi ^{T}\\ -\overline{\Phi }&0 \end{vmatrix}, \end{aligned}\nonumber \\ \end{aligned}$$
(9)

where the elements of matrix M are

$$\begin{aligned} \begin{aligned} m_{s,j}^{(n)}=(-\frac{p_s}{\overline{p}_j})^n\frac{e^{\xi _s+\overline{\xi }_j}}{p_s+\overline{p}_j}+\frac{e^{\eta _s+\overline{\eta }_j}}{q_s+\overline{q}_j}, \end{aligned} \end{aligned}$$
(10)

with

$$\begin{aligned} \begin{aligned}&\xi _s=\frac{1}{p_s}x_{-1}+p_sx_1+p_s^2x_2+\xi _{s}^{0},\eta _s={q_s}y+\eta _s^{0}, \\&\overline{\xi }_j=\frac{1}{\overline{p}_j}x_{-1}+\overline{p}_jx_1-\overline{p}_j^2x_2+\overline{\xi }_{j}^{0}, \overline{\eta }_j={\overline{q}_j}y+\overline{\eta }_{j}^{0}, \end{aligned} \end{aligned}$$
(11)

for \(1\le s,j\le K\), and the superscript T represent the transpose, \(\Phi ,\overline{\Phi },\Psi ,\overline{\Psi }\) are row vectors defined by

$$\begin{aligned} \begin{aligned}&\Phi =(e^{\xi _1},e^{\xi _2},\cdots ,e^{\xi _M}),\Psi =(e^{\eta _1},e^{\eta _2},\cdots ,e^{\eta _M}),\\&\overline{\Phi }=(e^{\overline{\xi }_1},e^{\overline{\xi }_2},\cdots ,e^{\overline{\xi }_M}), \overline{\Psi }=(e^{\overline{\eta }_1},e^{\overline{\eta }_2},\cdots ,e^{\overline{\eta }_M}), \end{aligned} \end{aligned}$$
(12)

which satisfy the following bilinear equations in KP hierarchy

$$\begin{aligned} \begin{aligned}&(D^2_{x_1}-D_{x_2})\tau _{0}^{(n+1)} \cdot \tau _{0}^{(n)}=0,\\&(D^2_{x_1}-D_{x_2})\tau _{1}^{(0)} \cdot \tau _{-1}^{(0)} =0, \\&D_{x_1}D_{y}\tau _{0}^{(0)}\cdot \tau _0^{(0)}=-2\tau _{1}^{(0)}\tau _{-1}^{(0)},\\&(D_{x_1}D_{x_{-1}}-2)\tau _{0}^{(0)}\cdot \tau _{0}^{(0)}=-2\tau _{0}^{(n+1)}\tau _{0}^{(n-1)}. \end{aligned} \end{aligned}$$
(13)

The bilinear Eqs. (13) are (3+1) dimensional, while the bilinear Eqs. (3) of the phase-shifted nonlocal CNLS equation are (1+1) dimensional, thus we have to construct a dimensional reduction for the tau function \(\tau _0^{(0)}\) in Eq. (9). To this end, we take the following parameter constraint,

$$\begin{aligned} q_s=-\frac{p_s^2+\gamma }{\delta {p_s}},\overline{q}_s=-\frac{\overline{p}_s^2+\gamma }{\delta {\overline{p}_s}}, \end{aligned}$$

which can further yield the following relation:

$$\begin{aligned} \begin{aligned}&(\partial _{x_1}+\delta \partial _{y}-\gamma \partial _{x_{-1}})m_{s,j}^{(0)}=0, \end{aligned} \end{aligned}$$

namely,

$$\begin{aligned} \begin{aligned}&(\partial _{x_1}+\delta \partial _{y}-\gamma \partial _{x_{-1}}){\tau _0^{(0)}}=0, \end{aligned} \end{aligned}$$

Then, y and \(x_{-1}\) become two dummy variables, which can be treated as zero. Under this dimension reduction, the last two bilinear equations in Eq. (13) generate the following bilinear equation:

$$\begin{aligned} \begin{aligned}&(D_{x_1}^2+2\gamma )\tau _0^{(0)} \cdot \tau _0^{(0)} \\&\quad =-2({\delta \tau _1^{(0)}\tau _{-1}^{(0)}-\gamma \tau _0^{(n+1)}\tau _0^{(n-1)}}). \end{aligned} \end{aligned}$$
(14)

Then this bilinear equation and the first two bilinear equations in Eq. (13) become to the bilinear Eqs. (3) of the space-shifted nonlocal CNLS equation for \(f=\tau _0^{(0)},g=\tau _1^{(0)},g^*(x_0-x,t)=-\tau _{-1}^{(0)},h=\tau _0^{(1)},h^*(x_0-x,t)=\tau _{0}^{(-1)}\) under the variable transformations

$$\begin{aligned} \begin{aligned} x_1=x,x_2=it. \end{aligned} \end{aligned}$$
(15)

We further consider \(2N\times 2N\)(i.e.,\(K=2N\)) matrices for tau functions \(\tau _0^{(n)},\tau _1^{(0)}\) and \(\tau _{-1}^{(0)}\) with the following parameter constraints:

$$\begin{aligned} \begin{aligned} \overline{\xi }_{j}^{0}&=\xi _{j}^{0*}, \overline{\eta }_{j}^{0}=\eta _{j}^{0}, p_{N+s}=-p_s,\\ \overline{p}_{N+s}&=-\overline{p}_s, \overline{p}_s=p_s^*, \eta _{N+s}^{0}=\eta _{j}^{0*},\\ \xi _{N+s}^{0}&=\xi _{s}^{0*}+p_sx_0, \end{aligned} \end{aligned}$$
(16)

for \(j=1,2,\ldots ,2N\), and \(s=1,2,\ldots , N\), then we can get the following relations:

$$\begin{aligned} \begin{aligned}&(\xi _s+\overline{\xi }_{j})^*(x_0-x,t)=(\xi _{N+s}+\overline{\xi }_{N+j})(x,t),\\&\overline{\xi }_s^*(x_0-x,t)=\xi _{N+s}(x,t),\\&( \xi _{s}+\overline{\xi }_{N+j})^*(x_0-x,t)=( \xi _{j}+ \overline{\xi }_{N+s})(x,t),\\&( \xi _{K+s}+ \overline{\xi }_{j})^*(x_0-x,t)=( \xi _{N+j}+ \overline{\xi }_{s})(x,t),\\&( \xi _{N+j}+ \overline{\xi }_{K+s})^*(x_0-x,t)=( \xi _{s}+ \overline{\xi }_{j})(x,t),\\&\overline{\xi }_{N+s}(x,t)=\xi _{s}^*(-x,t), \end{aligned} \end{aligned}$$
(17)

which implies

$$\begin{aligned} \begin{aligned} m_{N+s,N+j}^{(n)*}(x_0-x,t)&=-m^{(-n)}_{j,s}(x,t),\\ m_{N+s,j}^{(n)*}(x_0-x,t)&=-m^{(-n)}_{N+j,s}(x,t),\\ m_{s,N+j}^{(n)*}(x_0-x,t)&=-m_{j,N+s}^{(-n)}(x,t),\\ m_{s,j}^{(n)*}(x_0-x,t)&=-m_{N+j,N+s}^{(-n)}(x,t). \end{aligned} \end{aligned}$$
(18)

Thus, one can derive

$$\begin{aligned} \begin{aligned}&\tau _0^{(n)*}(x_0-x,t)=\tau _0^{(-n)}(x,t),\\ {}&\tau _{1}^{(0)*}(x_0-x,t)=-\tau _{-1}^{(0)}(x,t), \end{aligned} \end{aligned}$$
(19)

namely, the phase-shifted symmetry and complex conjugate condition (4) is realized for \(f=\tau _0^{(0)}\). By further taking \(g=\tau _1^{(0)},g^*(x_0-x,t)=\tau _{-1}^{(0)},h=\tau _0^{(1)},h^*(x_0-x,t)=\tau _{0}^{(-1)}\), Theorem 1 is then proved.

2.2 Dynamics of the bright–dark soliton interactions

By taking \(N=1\) in Theorem 1, the bright–dark two-soliton solutions can be derived, and the functions f, g and h are expressed as:

$$\begin{aligned} \begin{aligned} f=&\begin{vmatrix} m_{1,1}^{(0)}&m_{1,2}^{(0)}\\ m_{2,1}^{(0)}&m_{2,2}^{(0)} \end{vmatrix},\\ g=&\begin{vmatrix} m_{1,1}^{(0)}&m_{1,2}^{(0)}&e^{p_1x+ip_1^2t+ \xi _{1}^{0}}\\ m_{2,1}^{(0)}&m_{2,2}^{(0)}&e^{-p_1(x-x_0)+ip_1^2t+\xi _{1}^{0*}}\\ -\alpha _1&-\alpha _1^{*}&0 \end{vmatrix},\\ h=&\begin{vmatrix} m_{1,1}^{(1)}&m_{1,2}^{(1)}\\ m_{2,1}^{(1)}&m_{2,2}^{(1)} \end{vmatrix}, \end{aligned} \end{aligned}$$
(20)

where \(m_{1,1}^{(n)}=(-\frac{p_1}{p_1^*})^n\frac{e^{\xi _1+\xi _1^*}}{p_1+p_1^*}+\frac{\alpha _1^2}{q_1+q_1^*},m_{1,2}^{(n)}=(\frac{p_1}{p_1^*})^n\frac{e^{\xi _1+\xi _2^*}}{p_1-p_1^*} +\frac{\alpha _1\alpha _1^*}{q_1-q_1^*},m_{2,1}^{(n)}=-m_{1,2}^{(n)*},m_{2,2}^{(n)}=-(-\frac{p_1}{p_1^*})^n\frac{e^{\xi _2+\xi _2^*}}{p_1+p_1^*}-\frac{\alpha _1^{*2}}{q_1+q_1^*}\) and \(\xi _1=p_1x+ip_1^2t+\xi _1^{0},\xi _2=-p_1(x-x_0)+ip_1^2t+\xi _1^{0*}\), and \(q_1=-\frac{p_1^2+\gamma }{\delta {p_1}}\).

These two solitons move along the lines \(\zeta _1=\xi _1+\xi _1^*=x-2p_{1I}t\approx 0\) and \(\zeta _2=\xi _2+\xi _2^*=x+2p_{1I}t\approx 0\), and for convenience they are denoted as soliton 1 and soliton 2, respectively. To study their behaviours, one has to obtain the asymptotic forms of these two solitons. For this purpose, we assume \(p_{1R}>0, p_{1I}>0\) without loss of generality. After some algebraic calculations, the asymptotic expressions of the two solitons are given as follows:

  1. (i)

    \(\underline{Before collision (t \rightarrow -\infty )}\):       Soliton 1 \((\eta _{1} \approx 0, \eta _{2} \approx +\infty )\)

    $$\begin{aligned} \begin{aligned} u_1^{(-)}\approx&\frac{e^{i(2\gamma {t}+\xi _{1I})-\lambda _1}}{4}{X}_1{{\,\mathrm{sech}\,}}(\xi _{1R}+\lambda _1), \\ v_1^{(-)}\approx&\frac{e^{2i\gamma {t}}}{2}(1+y_1+(y_1-1)\tanh \frac{\xi _1+\xi _1+\Phi _1}{2}, \\ \end{aligned} \end{aligned}$$
    (21)

    Soliton 2 \((\eta _{2} \approx 0, \eta _{1} \approx +\infty )\)

    $$\begin{aligned} \begin{aligned} u_2^{(-)}\approx&\frac{e^{i(2\gamma {t}+\xi _{2I})-\lambda _2}}{4}{X}_2{{\,\mathrm{sech}\,}}(\xi _{2R}+\lambda _2), \\ v_2^{(-)}\approx&\frac{e^{2i\gamma {t}}}{2}(1+y_1+(y_1-1)\tanh \frac{\xi _2+\xi _2+\Phi _2}{2}, \\ \end{aligned} \end{aligned}$$
    (22)
  2. (ii)

    \(\underline{After~collision (t \rightarrow +\infty )}\):       Soliton 1 \((\eta _{1} \approx 0, \eta _{2} \approx - \infty )\)

    $$\begin{aligned} \begin{aligned} u_1^{(+)}\approx&\frac{e^{i(2\gamma {t}+{\xi }_{1I})-{\widehat{\lambda }}_1}}{4}{{\widehat{X}}}_1{{\,\mathrm{sech}\,}}(\xi _{1R}+{\widehat{\lambda }}_1), \\ v_1^{(+)}\approx&\frac{e^{2i\gamma {t}}}{2}(1+y_1+(y_1-1)\tanh \frac{\xi _1+\xi _1+{\widehat{\Phi }}_1}{2}, \\ \end{aligned} \end{aligned}$$
    (23)

          Soliton 2 \((\eta _{2} \approx 0,\eta _{1} \approx - \infty )\)

    $$\begin{aligned} \begin{aligned} u_2^{(+)}\approx&\frac{e^{i(2\gamma {t}+{\xi }_{2I})-{\widehat{\lambda }}_2}}{4}{{\widehat{X}}}_2{{\,\mathrm{sech}\,}}(\xi _{2R}+{\widehat{\lambda }}_2), \\ v_2^{(+)}\approx&\frac{e^{2i\gamma {t}}}{2}(1+y_1+(y_1-1)\tanh \frac{\xi _2+\xi _2+{\widehat{\Phi }}_2}{2}, \\ \end{aligned} \end{aligned}$$
    (24)

where

$$\begin{aligned} \begin{aligned} {X}_1&=\frac{2p_1(q_1+q_1^*)}{\alpha _1(p_1-p_1^*)},\\ e^{2\lambda _1}&=-\frac{4p_1p_1^*(q_1+q_1^*)}{\alpha _1^2(p_1+p_1^*)(p_1-p_1^*)^2},\\ {\widehat{X}}_1&=\frac{(q_1+q_1^*)(q_1-q_1^*)}{2\alpha {q_1}},\\ e^{2{\widehat{\lambda }}_1}&=-\frac{(q_1+q_1^*)(q_1-q_1^*)^2}{4\alpha _1^2q_1q_1^*(p_1+p_1^*)},\\ {X}_2&=-\frac{2p_1(q_1+q_1^*)}{\alpha _1^*(p_1-p_1^*)},\\ e^{2\lambda _2}&=-\frac{4p_1p_1^*(q_1+q_1^*)}{\alpha _1^{*2}(p_1+p_1^*)(p_1-p_1^*)^2},\\ {\widehat{X}}_2&=-\frac{(q_1+q_1^*)(q_1-q_1^*)}{\alpha ^*(q_1-q_1)},\\ e^{2{\widehat{\lambda }}_2}&=-\frac{(q_1+q_1^*)(q_1-q_1^*)^2}{4\alpha _1^{*2}q_1q_1^*(p_1+p_1^*)},\\ e^{\Phi _1}&=-\frac{4p_1p_1^*(q_1+q_1^*)}{\alpha _1^2(p_1+p_1^*)(p_1-p_1^*)^2},\\ e^{{\widehat{\Phi }}_1}&=-\frac{(q_1+q_1^*)(q_1-q_1^*)^2}{4\alpha _1^2q_1q_1^*(p_1+p_1^*)}, \\ e^{\Phi _2}&=-\frac{4p_1p_1^*(q_1+q_1^*)}{\alpha _1^{*2}(p_1+p_1^*)(p_1-p_1^*)^2},\\ e^{{\widehat{\Phi }}_2}&=-\frac{(q_1+q_1^*)(q_1-q_1^*)^2}{4\alpha _1^{*2}q_1q_1^*(p_1+p_1^*)},\\ y_1&=-\frac{p_1^*}{p_1}. \end{aligned} \end{aligned}$$
(25)

The above asymptotic analyses indicate that \(|u_j^{(+)}(\xi _{jR})|=|u_j^{(-)}\left( \xi _{jR}+\lambda _j-{\widehat{\lambda }}_j)\right) |\) and \(|v_j^{(+)}(\xi _{jR})|=|v_j^{(-)}\left( \xi _{jR}+\frac{1}{2}(\Phi _j-{\widehat{\Phi }}_j)\right) |\), hence the collisions of these two solitons are elastic in both u and v components, namely the natures of the bright–dark two solitons remain unaltered after collision except for finite shifts, including the amplitudes, speeds and shapes.

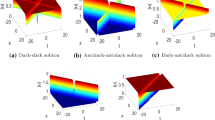
In u component, \(|u_1^{(\pm )}|=|u_2^{(\pm )}|\) means that the amplitudes of the two bright solitons are equal, and the value is \(|u_B|=\sqrt{|\frac{|q_1|^2(p_1+p_1^*)(q_1+q_1^*)}{(\alpha _1-\alpha _1^*)^2}|}\). Figure 1 displays the bright two-soliton solution in u component with same soliton parameters and different signs of nonlinearities \(\delta \) and \(\gamma \) of Eq. (2). It is seen that the space-shifted nonlocal CNLS equation with three different types of nonlinearities admit smooth bright soliton solutions in u component. The different nonlinearities would generate diverse waveforms in the interaction region. In Figs. 1, 2, 3, 4, 5, 6, 7 the top row and bottom row are three-dimensional plots and density plots of corresponding soliton solutions, respectively.

In v component, the amplitudes of the two dark solitons are \(|v_{j}|=\left| \frac{(p_1Y_j-p_1^*|Y_j|)}{p_1(Y_j+|Y_j|)}\right| \) for \(j=1,2\), where \(Y_1=-\frac{4p_1p_1^*(q_1+q_1^*)}{\alpha _1^2(p_1+p_1^*)(p_1-p_1^*)^2},Y_2=-\frac{4p_1p_1^*(q_1+q_1^*)}{\alpha _1^{*2}(p_1+p_1^*)(p_1-p_1^*)^2}\). Thus, the solitons in v can be classified into four different types: two dark solitons for \(|v_j|<1\) (\(j=1,2\)), a mixture of a dark soliton and an antidark soliton for \(|v_j|<1,|v_{3-j}|>1\), two antidark solitons for \(|v_j|>1\), and a degenerated dark two-soliton for \(|v_j|=1,|v_{3-j}|<1\), and a degenerated antidark two-soliton for \(|v_j|=1,|v_{3-j}|>1\). These three types of non-degenerated dark two-soliton and the two types of degenerated dark two-soliton are displayed in Figs. 2 and 3, respectively. It should be noted that expressions of the soliton amplitudes are independent of the phase shift factor \(x_0\), thus the phase shift factor \(x_0\) does not affect the amplitudes of the solitons.

Fig. 1
figure 1

The bright two-soliton solutions (20) in u component of Eq. (2) with parameters \(p_1=\frac{1}{2}+i,\xi _1^{0}=0, x_0=0, \alpha _1=1+(2+\sqrt{5})i\) and different types of nonlinearities in the space-shifted nonlocal CNLS Eq. (2): a \(\delta =1,\gamma =1\); b \(\delta =1,\gamma =-1\); c \(\delta =-1,\gamma =-2\)

Full size image
Fig. 2
figure 2

The two different types of non-degenerated dark two-soliton solutions (20) in v component of Eq. (2) with parameters \(\delta =1,\gamma =1,p_1=\frac{1}{2}+i,\xi _1^{0}=0,x_0=2\) and different values of parameter \(\alpha _1\): a Two antidark solitons with \(\alpha _1=\frac{1}{10}+10i\); b A mixture of a dark soliton and a antidark soliton with \(\alpha _1=2+i\); c Two dark solitons with \(\alpha _1=3-\frac{1}{2}\);

Full size image
Fig. 3
figure 3

The two different types of degenerated dark two-soliton solutions (20) in v component of Eq. (2) with parameters \(\delta =-1,\gamma =-1,p_1=\frac{1}{2}+i,\xi _1^{0}=0,x_0=2\) and different values of parameter \(\alpha _1\): a The degenerated dark two-soliton with \(\alpha _1=1+(2-\sqrt{5})i\); b The degenerated antidark two-soltion with \(\alpha _1=1+(2+\sqrt{5})i\)

Full size image

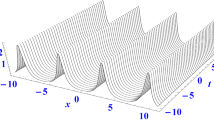
By taking \(N=2\) in Theorem 1, the bright–dark four-soliton solutions of the space-shifted nonlocal CNLS Eq. (2) can be obtained. Since these four solitons move along the line \(x\pm 2p_{jI}t\approx 0\) for \(j=1,2\), thus they can form two pairs of bound-state two-soliton when \(p_{1I}=\pm p_{2I}\). Here the subscripts R and I represent real and imaginary parts of a given parameter or a function, respectively. Figure 4 displays the bright four-soliton in u component and the dark four-soliton in v component for \(p_{1I}\ne \pm p_{p_2I}\). Figure 5 demonstrates two pairs of bound-state two-soliton of bright type in u and dark type in v with \(p_{1I}=p_{2I}\).

3 Multiple double-pole bright–dark solitons in the space-shifted nonlocal CNLS equation

This section mainly focuses the multiple double-pole bright–dark solitons for the space-shifted nonlocal CNLS Eq. (2).

3.1 Multiple double-pole bright–dark soliton solutions

Following the works in [26, 44], the multiple double-pole bright–dark soliton solutions can be derived from the multiple single-pole soliton solutions in Theorem 1 through the long wave limiting procedure. This is done by choosing the parameters in Eq. (6) as

$$\begin{aligned} \begin{aligned} e^{\xi _{s}^0}&={\widetilde{\xi }}_{s}p_{sI}, \alpha _s=\overline{\alpha }_sp_{sI}e^{i\theta _s}, |{\widetilde{\xi }}_{s}|^2(p_{sR}^2-\delta _2)e^{p_{1R}x_0}\\ {}&\quad -\delta _1|\overline{\alpha }_s|^2p_{sR}^2=0, \end{aligned} \end{aligned}$$
(26)

and then taking the limit \(p_{sI}\rightarrow 0\) for \(s=1,2,\cdots N\). After implementing this limit procedure, we can present the multiple double-pole bright–dark soliton solutions for the space-shifted nonlocal CNLS Eq. (2) by the following theorem.

Theorem 2

The multiple double-pole bright–darksoliton solutions for the space-shifted nonlocal CNLS Eq. (2) are

$$\begin{aligned} \begin{aligned} u=e^{2i\gamma {t}}\frac{g}{f},v=e^{2i\gamma {t}}\frac{h}{f}, \end{aligned} \end{aligned}$$
(27)

where

$$\begin{aligned} \begin{aligned} f=&\begin{vmatrix} {\widehat{m}}_{s,j}^{(0)}&{\widehat{m}}_{s,N+j}^{(0)}\\ {\widehat{m}}_{N+s,j}^{(0)}&{\widehat{m}}_{N+s,N+j}^{(0)} \end{vmatrix},\\ g=&\begin{vmatrix} {\widehat{m}}_{s,j}^{(0)}&{\widehat{m}}_{s,N+j}^{(0)}&{\widetilde{\xi }}_{s}e^{p_{sR}x+ip_{sR}^2t}\\ {\widehat{m}}_{N+s,j}^{(0)}&{\widehat{m}}_{N+s,N+j}^{(0)}&{\widetilde{\xi }}_{s}e^{-p_{sR}(x-x_0)+ip_{sR}^2t}\\ -\overline{\alpha }_je^{i\theta _j}&-\overline{\alpha }_je^{-i\theta _j}&0 \end{vmatrix},\\ h=&\begin{vmatrix} {\widehat{m}}_{s,j}^{(1)}&{\widehat{m}}_{s,N+j}^{(1)}\\ {\widehat{m}}_{N+s,j}^{(1)}&{\widehat{m}}_{N+s,N+j}^{(1)} \end{vmatrix}. \end{aligned} \end{aligned}$$
(28)

Here the matrix elements are defined as follows:

$$\begin{aligned}&m_{s,j}^{(n)}=\frac{{\widetilde{\xi }}_{s}{\widetilde{\xi }}_{j}(-\frac{p_{sR}}{p_{jR}})^ne^{(p_{sR}+p_{jR})(x+i(p_{sR}-p_{jR})t)}}{p_{sR}+p_{jR}}\nonumber \\&\quad -\frac{\overline{\alpha }_1\overline{\alpha }_2\delta _1p_{sR}p_{jR}e^{i(\theta _s+\theta _j)}}{(p_{sR}+p_{jR})(p_{sR}p_{jR}+\delta _2)},\nonumber \\ m_{s,N+j}^{(n)}= & {} -\frac{{\widetilde{\xi }}_{s}{\widetilde{\xi }}_{j}(\frac{p_{sR}}{p_{jR}})^ne^{p_{sR}(x+2ip_{sR}t)-p_{jR}(x-x_0+ip_{jR}t)}}{p_{sR}-p_{jR}}\nonumber \\&\quad -\frac{\alpha _s\alpha _j\delta _1p_{sR}p_{jR}e^{i(\theta _s-\theta _j)}}{(p_{sR} -p_{jR})(p_{sR}p_{jR}-\delta _2)}, \end{aligned}$$
(29)
Fig. 4
figure 4

The bright–dark four-soliton solutions (5) of the space-shifted nonlocal CNLS Eq. (2) with parameters \(N=2,\delta =1,\gamma =1,p_1=1+i,p_2=1+2i,\xi _1^{0}=0,\xi _2^0=0,x_0=0,\alpha _1=i,\alpha _2=i\)

Full size image
Fig. 5
figure 5

The bright–dark four-soliton solutions (5) of the space-shifted nonlocal CNLS equation with parameters (5) \(N=2,\delta =1,\gamma =1,p_1=1+i,p_2=2+i,\xi _1^{0}=0, \xi _2^0=0,x_0=0,\alpha _1=5i,\alpha _2=5i\), which feature two pairs of bound-state two-soliton

Full size image

for \(1\le s\ne j\le N\), and

$$\begin{aligned}&m_{s,s}^{(n)}=\frac{c_s(-1)^ne^{2p_{sR}x}}{2p_{sR}}-\frac{\delta _1p_{sR}\overline{\alpha }_s^2e^{2i\theta _s}}{2(p_{sR}^2+\delta _2)},\nonumber \\&m_{s,N+s}^{(n)}=\frac{{\widetilde{\xi }}_{s}e^{p_{sR}x_0}}{2p_{sR}}(x-\frac{x_0}{2}+2ip_{sR}t+\frac{n}{p_{sR}}), \end{aligned}$$
(30)

for \(s=1,2\cdots N\), and

$$\begin{aligned} m_{N+s,j}^{(n)}= & {} -m^{(-n)*}_{j,N+s}({x_0}-x,t),m_{N+s,N+j}^{(n)}\\ {}= & {} -m^{(-n)*}_{N+s,N+j}({x_0}-x,t), \end{aligned}$$

for \(1{\le }s,j\le {N}\). Here the real parameters \({\widetilde{\xi }}_{s},\overline{\alpha }_s\) have to observe the restrictions

$$\begin{aligned}&|{\widetilde{\xi }}_{s}|^2(p_{sR}^2-\delta _2)e^{p_{1R}x_0}\nonumber \\&\quad -\delta _1|\overline{\alpha }_s|^2p_{sR}^2=0,\,s=1,2,\cdots ,N. \end{aligned}$$
(31)

3.2 Dynamics of multiple double-pole bright–dark solitons

By taking \(N=1\) in Theorem 2, the double-pole bright–dark two-soliton solutions can be derived, and the functions f, g and h are expressed as

$$\begin{aligned} \begin{aligned} f=&\left( \frac{{\widetilde{\xi }}_{1}^2e^{2p_{1R}x}}{2p_{1R}}-\frac{\delta _1p_{1R}\overline{\alpha }_1^2e^{2i\theta _1}}{2(p_{1R}^2+\delta _2)}\right) \\&\quad \left( \frac{{\widetilde{\xi }}_{1}^2e^{-2p_{1R}(x-x_0)}}{2p_{1R}}-\frac{\delta _1p_{1R}\overline{\alpha }_1^2e^{-2i\theta _1}}{2(p_{1R}^2+\delta _2)}\right) \\&-{\widetilde{\xi }}_1^4\left[ (x-\frac{x_0}{2})^2+4p_{1R}^2t^2\right] e^{2p_{1R}x_0},\\ g=&-\overline{\alpha }_1e^{i\theta _1}\left[ {\widetilde{\xi }}_{1}^3(x-\frac{x_0}{2}+2ip_{1R}t)e^{-p_{1R}(x-2x_0)+ip_{1R}^2t}\right. \\&+\left( \frac{{\widetilde{\xi }}_{1}^2e^{-2p_{1R}(x-x_0)}}{2p_{1R}}\right. \\&\left. \left. -\frac{\delta _1p_{1R}\overline{\alpha }_1^2e^{-2i\theta _1}}{2(p_{1R}^2+\delta _2)}\right) {\widetilde{\xi }}_{1}e^{p_{1R}x+ip_{1R}^2t}\right] \\&-\overline{\alpha }_1e^{-i\theta _1}\left[ \left( \frac{{\widetilde{\xi }}_{1}^2e^{2p_{1R}x}}{2p_{1R}}-\frac{\delta _1p_{1R}\overline{\alpha }_1^2e^{2i\theta _1}}{2(p_{1R}^2+\delta _2)}\right) \right. \\&\quad {\widetilde{\xi }}_{1}e^{-p_{1R}(x-x_0)+ip_{1R}^2t}\\&\left. +{\widetilde{\xi }}_{1}^3(x-\frac{x_0}{2}-2ip_{1R}t)e^{p_{1R}(x+x_0)+ip_{1R}^2t} \right] \\ h=&\left( \frac{{\widetilde{\xi }}_{1}^2e^{2p_{1R}x}}{2p_{1R}}+\frac{\delta _1p_{1R}\overline{\alpha }_1^2e^{2i\theta _1}}{2(p_{1R}^2+\delta _2)}\right) \\&\times \left( \frac{{\widetilde{\xi }}_{1}^2e^{-2p_{1R}(x-x_0)}}{2p_{1R}}+\frac{\delta _1p_{1R}\overline{\alpha }_1^2e^{-2i\theta _1}}{2(p_{1R}^2+\delta _2)}\right) \\&-{\widetilde{\xi }}_1^4\left[ (x-\frac{x_0}{2})^2+(2ip_{1R}t-i)^2\right] e^{2p_{1R}x_0}. \end{aligned} \end{aligned}$$
(32)

Figure 6 shows this double-pole two-soliton of bright-type in u component and dark-type in v component. As discussed in Sect. 2.2, the single-pole dark two solitons can possess unequal amplitudes (see panel (b) of Fig. 2). However, the amplitudes of the two solitons in the double-pole two-soliton solutions in both u and v components are always equal for all input parameters.

The double-pole bright–dark four-soliton solutions can be derived by taking \(N=2\) in Theorem 2, and their collision dynamics are shown in Fig. 7. Similar to the two pairs of the single-pole bound-state two-soliton displayed in Fig. 5, the double-pole bright–dark four-soliton can also generate temporal periodic waves in their interaction regions.

Fig. 6
figure 6

The bright–dark double pole two-solitons solutions (5) of the space-shifted nonlocal CNLS equation with parameters \(N=2,\delta =1,\gamma =-1,p_{1R}=\frac{1}{2},\overline{\alpha }_1=1,x_0=2,\theta _1=0\)

Full size image
Fig. 7
figure 7

The double-pole bright–dark four-soliton solutions (5) of the space-shifted nonlocal CNLS equation with parameters \(N=2,\delta =1,\gamma =-1,p_{1R}=\frac{1}{2},p_{2R}=\frac{2}{3},x_0=2,\alpha _1=1,\alpha _2=2,\theta _1=0,\theta _2=0\), which feature two pairs of bound-state double-pole two-soliton

Full size image

4 Conclusion

In this paper, the multiple single-pole and double-pole bright–dark solitons and their collisions have been studied for the space-shifted nonlocal CNLS Eq. (2), which provides a multi-component analogue of the scalar space-shifted nonlocal NLS Eq. (1) proposed by Ablowitz and Musslimani very recently [21]. The main results of this paper are summarized as follows:

  1. (1)

    The multiple single-pole soliton solutions were constructed via bilinear KP hierarchy reduction method. To systematically investigated the dynamics of the multiple single pole solitons, we first analyzed asymptotic analysis of the collisions between two single-pole solitons. Based on these analysis, we fund that bright–dark two single-pole solitons only occur elastic collision, namely the identities of bright–dark two single-pole solitons remain unaltered except for a finite phase shift. The bright two solitons in component u possess equal amplitudes (see Fig. 1). The dark two-solitons in component v admits three different non-degenerated patterns (i.e., the dark-dark two-soliton, the dark-antidark two-soliton, the anti-dark-two soliton) (see Fig. 2) and the two different degenerated patterns (i,e.,degenerated dark/antidark two-soliton) (see Fig. 3). The collisions of the bright–dark four-soliton were also exhibited, which illustrate the superpositions of the paired solitons. Particularly, the interaction of these four solitons can lead to two pairs of bound-state two-soliton. These bound-state two-soliton pairs can generate temporal periodic waves in the interaction region (see Fig. 5).

  2. (2)

    The multiple double-pole bright–dark solitons for the space-shifted nonlocal CNLS Eq. (2) were investigated, which were generated from the multiple single-pole bright–dark solitons through the long wave limit procedure. To reveal the dynamics of the multiple double-pole solitons, the double-pole bright–dark two-soliton and four-soliton solutions were discussed in details (see Figs. 6,7).