Performance analysis of a nonlinear inerter-based vibration isolator with inerter embedded in a linkage mechanism

Abstract

This study presents an inerter-based nonlinear vibration isolator with geometrical nonlinearity created by configuring an inerter in a diamond-shaped linkage mechanism. The isolation performance of the proposed nonlinear isolator subjected to force or base-motion excitations is investigated. Both analytical and alternating frequency-time harmonic balance methods as well as numerical integration method are used to obtain the dynamic response. Beneficial performance of the nonlinear isolator is demonstrated by various performance indices including the force and displacement transmissibility as well as power flow variables. It is found that the use of the nonlinear inerter in the isolator can shift and bend the peaks of the transmissibility and time-averaged power flow to the low-frequency range, creating a larger frequency band of effective vibration isolation. It is also shown that the inertance-to-mass ratio and the initial distance of the nonlinear inerter can be effectively tailored to achieve reduced transmissibility and power transmission at interested frequencies. Anti-resonant peaks appear at specific frequency, creating near-zero energy transmission and significantly reducing vibration transmission to a base structure on which the proposed isolator is mounted.

1 Introduction

The inerter is a passive two-node mechanical element and has the property that the applied force across the two terminals is proportional to the relative acceleration between the terminals [1]. The ratio of the output force of the inerter to the relative acceleration is called inertance and is measured in kilograms. There have been a variety of practical designs and physical realisations of mechanical inerters, using flywheel-based [1,2,3,4] and fluid-based [5,6,7] mechanisms. Flywheel-based inerters can be constructed through a ball-screw mechanism consisting of a screw, nut, and flywheel [2,3,4]. The relative linear motion of the terminals is transformed into the rotational motion of flywheels storing kinetic energy. The structure of flywheel-based inerters can also be achieved using a rotating flywheel through a rack, a pinion, and gears, which is also known as rack–pinion inerter [1]. The corresponding inertance is related to the mass and the radius of gyration of the flywheel as well as the radii of the rack pinion, gear wheel, and flywheel pinion. Fluid-based inerters can be realised incorporating fluid flowing through an orifice [5, 6] or helical channel [7]. With a proper design, the inertance (i.e. apparent mass) of an inerter can be much larger than its physical weight. The use of the inerter in an integrated structure can provide inertial coupling between subsystems. In this way, the dynamic property (e.g. the mass matrix) of vibration systems can be tailored such that the amount and the dominant of path vibration transmission in a system can be optimised for desirable performance.

There have been a number of studies investigating the dynamics of inerter-based suppression systems and demonstrating performance benefits. Wang et al. [8] studied the vibration mitigation behaviour of a full-train model incorporating inerter-based mechatronic suspensions. It was found that the parallel inerter configuration improves the dynamic performance of the train and passage comfort. Lazar et al. [9] used the tuned inerter damper for cable vibration suppression. Li et al. [10] studied the potential benefits of the shimmy-suppression devices using inerter for aircraft landing gear. It was shown that the optimised inerter-based configurations have better suppression performance than the conventional spring-damper device. Zhang et al. [11] examined the dynamic behaviour of a multi-storey building structure with the use of inerter-spring-damper. Inerter-based linear vibration isolators with different configurations have also been studied and have shown better dynamic performance in vibration attenuation compared to the traditional isolators [12]. In recent studies, inerters have also been applied to the laminated composite plates [13] and metamaterial beams [14, 15] for vibration suppression. Tuning methods of tuned inerter dampers for nonlinear primary systems have been proposed to achieve equal peaks in the displacement and kinetic energy responses [16].

Potential applications of the nonlinear inerter have also been studied for possible performance benefits. De Haro Moras et al. [17] used a pair of horizontal inerters to replace the springs used in conventional quasi-zero-stiffness (QZS) isolators, which shows the dynamical benefits compared with the traditional spring-damper and spring-damper-inerter isolators in vertical arrangement. Yang et al. [18] investigated the performance of an inerter-based vibration isolator and inerter-QZS hybrid isolator in vibration suppression. Wang et al. [19] studied the dynamic behaviour of a vibration isolator with inerter-based geometrical nonlinearity, and the corresponding isolation performance is compared to the parallel and series-connected configurations. Dong et al. [20] examined the suppression of vibration transmission in coupled systems by using an inerter-based joint exploiting geometric nonlinearity. Apart from the nonlinear isolators, the mechanical inerter can be used in nonlinear energy sink (NES) devices. Zhang et al. [21] employed a combined vibration control technique using a QZS system with an inerter-based NES to achieve better nonlinear isolation and absorption effects. In a recent study, Wagg [22] conducted a comprehensive review for different types of mechanical and fluid-based inerters in linear and nonlinear applications.

There have been a lot of recent research interest in developing high-performance nonlinear vibration isolators [23]. Kovacic et al. [24] studied the dynamic performance of a nonlinear vibration isolator using a QZS mechanism to achieve low-dynamic stiffness for low natural frequency while retaining high-static supporting stiffness for low static deflection. It was found that the periodic doubling bifurcation and chaotic motion may occur under asymmetric excitation of the nonlinear isolator. Carrella et al. [25] investigated the displacement and force transmissibility characteristics of a nonlinear isolator incorporating high-static-low-dynamic stiffness. The previous research has also clearly demonstrated the potential benefits of exploiting inerters in nonlinear vibration isolators for enhanced performance [22]. Therefore, new designs of inerter-based nonlinear vibration isolators are sought. It is noted that for performance evaluation of nonlinear vibration isolators, including inerter-based ones, the force and/or displacement transmissibility is often used as the performance indicator. The vibration energy power flow is widely accepted as an index to assess the effectiveness of vibration isolation. Vibration power flow analysis (PFA) combines force and velocity amplitudes as well as the phase difference into one quantity and provides a better indication of dynamic performance from the energy viewpoint [26]. For instance, Royston and Singh [27] studied the vibratory power transmission from a vibrating engine source to a flexible receiver through a nonlinear path. Xiong et al. [28] investigated the interactional dynamic behaviour with respect to the power flow between a vibrating equipment, a nonlinear isolator, and a flexible ship excited by waves. The nonlinearities were characterised by a general p-th power damping and q-th power stiffness. In recent years, PFA has been applied to study different nonlinear vibration systems. Yang et al. revealed the power flow behaviour of the Duffing oscillator [29] and a nonlinear isolator mounted on a nonlinear base [30]. Shi et al. [31] studied the vibration energy transmission and power flow performance in coupled systems with a bilinear stiffness interface. Dai et al. [32] proposed the use of linear and nonlinear constraints to reveal the energy transmission mechanisms in impact oscillators.

This study presents a nonlinear inerter-based vibration isolator and investigates the dynamics for performance evaluation. The nonlinear inerter, named as the D-inerter, is created by a linear inerter embedded in a four-bar linkage mechanism. With the inclusion of the proposed nonlinear inerter, it is shown that the natural frequency of the system can be reduced, thereby expanding the effective isolation frequency bandwidth. The frequency–response curves bend to the low-frequency range, benefiting vibration isolation. It is also demonstrated the use of the nonlinear inerter leads to enhanced vibration attenuation in terms of both force/displacement transmissibility and energy transmission. The application of the nonlinear isolator in a single-DOF (SDOF) system subjected to force or base-motion excitations and in a two-DOF (2DOF) forced system with a flexible foundation is considered. Different performance indices, including the force and displacement transmissibility, and vibration power flow and energy-based variables are used to evaluate the vibration isolation performance. The first-order harmonic balance (HB) method and the HB with alternating frequency time (AFT) are used to obtain the steady-state responses and the performance indices. The analytical results are validated and compared with the numerical time-marching Runge–Kutta method. The rest of the paper is organised as follows. In Sect. 2, the physical and mathematical model of the nonlinear inerter and its use in single-DOF isolator and 2DOF systems with the isolator mounted on a flexible base are presented. In Sect. 3, the dynamic analysis of the isolation systems and performance indices for the evaluation of the proposed isolators are introduced. In Sect. 4, the performance of the proposed nonlinear D-inerter vibration isolator used in SDOF and 2DOF systems is examined. Conclusions are provided at the end of the paper.

2 Nonlinear inerter based on four-bar linkage mechanism

2.1 The nonlinear inerter

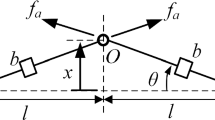
Figure 1a shows the proposed nonlinear inerter configuration based on a four-bar diamond-shaped linkage mechanism. The nonlinear inerter (hereafter referred to as the D-inerter) is created by embedding a linear horizontal inerter in a linkage created by four rigid massless bars AC, AD, BC and BD with equal length $l_{0}$ and pin-joined at points A, B, C and D. An ideal linear inerter with inertance $b$ is configured to the mechanism with its two terminals joined to points C and D. Angle $\theta$, measured from the horizontal direction CD and positive in the anti-clockwise direction, is used to denote the orientation of bar AC. The distances of AB and CD are denoted by $y$ and $z_{{{\text{CD}}}}$, respectively. Point A is subjected to a vertical force $f_{{\text{a}}}$, while point B is pinned to the ground. As the system is symmetric, point A only moves along the vertical direction. Figure 1(b) shows an ideal massless inerter for which the applied force $f_{{\text{b}}}$ is proportional to the relative acceleration of the two terminals [1], i.e. $f_{{\text{b}}} = b\left( {\ddot{z}_{{\text{D}}} - \ddot{z}_{{\text{C}}} } \right) = b\ddot{z}_{{{\text{CD}}}}$, where $\ddot{z}_{{\text{D}}}$ and $\ddot{z}_{{\text{C}}}$ are the acceleration, while $\ddot{z}_{{{\text{CD}}}}$ denotes the relative accelerations.

Fig. 1

a Nonlinear inerter model and b a linear inerter

Based on the geometry of the D-inerter, we have

$$ \begin{gathered} y = 2l_{0} \sin \theta , \hfill \\ z_{{{\text{CD}}}} = 2l_{0} \cos \theta = \sqrt {4l_{0}^{2} - y^{2} } \hfill \\ \end{gathered} $$

(1)

where $y$ and $z_{{{\text{CD}}}}$ represent the distances of AB and CD, respectively, and for practical applications we have $0 < \theta < \pi /2$. From Eq. (1), the expressions of the velocity and acceleration are obtained by taking the first and second derivatives:

$$ \begin{gathered} \dot{y} = 2l_{0} \dot{\theta }\cos \theta , \hfill \\ \ddot{y} = 2l_{0} \left( {\ddot{\theta }\cos \theta - \dot{\theta }^{2} \sin \theta } \right) \hfill \\ \end{gathered} $$

(2)

respectively. The relative velocity and acceleration of terminals C and D are denoted by $\dot{z}_{{{\text{CD}}}}$ and $\ddot{z}_{{{\text{CD}}}}$, respectively, and are expressed as

$$ \begin{gathered} \dot{z}_{{{\text{CD}}}} = - 2l_{0} \dot{\theta }\sin \theta, \;\;\;\; \hfill \\ \ddot{z}_{{{\text{CD}}}} = - 2l_{0} \left( {\ddot{\theta }\sin \theta + \dot{\theta }^{2} \cos \theta } \right). \hfill \\ \end{gathered} $$

(3)

According to the property of the inerter, the inertance force $f_{{\text{b}}}$ applied by the linkage to the inerter is along the direction of CD and expressed by

$$ f_{{\text{b}}} = b\ddot{z}_{{{\text{CD}}}} = - 2bl_{0} \left( {\ddot{\theta }\sin \theta + \dot{\theta }^{2} \cos \theta } \right). $$

(4)

Based on the force equilibrium condition of the linkage structure, the relationship between applied force at point A and the inertance force applied to the horizontal inerter is

$$ f_{{\text{a}}} \left( \theta \right) = - f_{{\text{b}}} \frac{\sin \theta }{{\cos \theta }} = 2bl_{0} \left( {\ddot{\theta }\sin \theta + \dot{\theta }^{2} \cos \theta } \right)\frac{\sin \theta }{{\cos \theta }}. $$

(5)

Using Eqs. (1) and (2) to replace the terms $\dot{\theta }$, $\ddot{\theta }$, $\cos \theta$ and $\sin \theta$ in Eq. (5) with $y, \dot{y}, \ddot{y}$ and $l_{0}$, we have a relationship between the applied force to terminal A of the nonlinear inerter to the corresponding response at the terminal

$$ \begin{aligned} f_{{\text{a}}} \left( {y,\dot{y},\ddot{y} } \right) &; = b\left( {\frac{{\ddot{y}y^{2} }}{{4l_{0}^{2} - y^{2} }} + \frac{{4l_{0}^{2} y\dot{y}^{2} }}{{\left( {4l_{0}^{2} - y^{2} } \right)^{2} }}} \right) \\ & = 2bl_{0} \left( {\frac{{{\ddot{Y}}Y^{2} }}{{1 - Y^{2} }} + \frac{{Y\dot{Y}^{2} }}{{\left( {1 - Y^{2} } \right)^{2} }}} \right) \\ & = f_{{{\text{a}}1}} \left( {Y,\ddot{Y}} \right) + f_{{{\text{a}}2}} \left( {Y,\dot{Y}} \right) \\ \end{aligned} $$

(6)

where $Y = y/\left( {2l_{0} } \right)$ denotes the nondimensional distance between the two terminals of the nonlinear inerter, $f_{{{\text{a}}1}} \left( {Y,\ddot{Y}} \right) = {{2bl_{0} \ddot{Y}Y^{2} } \mathord{\left/ {\vphantom {{2bl_{0} \ddot{Y}Y^{2} } {\left( {1 - Y^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - Y^{2} } \right)}}$ and $f_{{{\text{a}}2}} \left( {Y,\dot{Y} } \right) = 2bl_{0} Y\dot{Y}^{2} /\left( {1 - Y^{2} } \right)^{2}$. Equation (6) shows that the nonlinear inertance force depends on the distance $Y$, the relative velocity $\dot{Y}$ and relative acceleration $\ddot{Y}$ characteristics between the terminals. Note that for the distance $y$ between the two terminals, we have $y > 0$ all the time. Figure 2a shows the variations of $f_{{{\text{a}}1}} \left( {Y,\ddot{Y} } \right)$ against $Y$ and $\ddot{Y}$. It shows that when Y is large, $f_{{{\text{a}}1}} \left( {Y,\ddot{Y}} \right)$ has an approximately linear relationship with $\ddot{Y}$. Figure 2b shows the changes of $f_{{{\text{a}}2}} \left( {Y,\dot{Y} } \right)$ with respect to the distance $Y$ and velocity $\dot{Y}$ of the terminals. It shows that the component of the inertance force $f_{{{\text{a}}2}} \left( {Y,\dot{Y} } \right)$ of the nonlinear inerter is sensitive to the relative velocity of the two terminals when the initial distance $Y$ is large.

Fig. 2

Nonlinear inertance force of the nonlinear D-inerter ($b = 1\, {\text{kg}},\, l_{0} = 0.1 \,{\text{m}}$)

2.2 Nonlinear D-inerter vibration isolator models

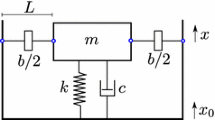
Figure 3a and b shows a single-DOF isolator system with the proposed D-inerter for force excitation and base-motion excitation, respectively. The system model comprises a mass subjected to a harmonic force excitation with amplitude $f_{0}$ or a base-motion excitation with amplitude $q_{0}$ and frequency $\omega$. To suppress the vibration transmission to the base, a nonlinear vibration isolator is inserted between the mass and the base. The isolator consists of a nonlinear D-inerter device, configured in parallel with a linear spring with stiffness coefficient $k_{1}$ and a viscous damper with damping coefficient $c_{1}$. Figure 3c presents the application of the D-inerter to vibration isolation of a force excited machine with mass $m_{1}$ mounting on a flexible single-DOF base via the proposed nonlinear isolator. The single-DOF base structure has mass $m_{2}$, a spring with stiffness coefficient $k_{2}$ and a damper with damping coefficient $c_{2}$. For the systems shown in Fig. 3, the vertical displacement of each mass away from the static equilibrium position is denoted as $x_{1} ,{ }x_{2} ,{ }x_{3}\,{\text{and}}\,x_{4}$. For the three systems, the static equilibrium positions of the masses, where the spring $k_{1}$ is at a length of $y_{0}$ and the displacements $x_{1} ,{ }x_{2} ,{ }x_{3}\,{\text{and}}\,x_{4}$ are zero, are used as the references. Correspondingly, the initial angle parameter of the linkage is denoted by $\theta_{0}$ at the static equilibrium position.

Fig. 3

Application scenarios of nonlinear inerter-based vibration isolators. a SDOF system for force excitation (configuration C1), b SDOF system for base-motion excitation (configuration C2) and c nonlinear isolator mounted on a flexible base (configuration C3)

2.2.1 Force excited SDOF system

The governing equation of motion of the mass shown in Fig. 3a is

$$ m_{1} \ddot{x}_{1} + c_{1} \dot{x}_{1} + k_{1} x_{1} + f_{{{\text{nl}}}} \left( {x_{1} ,\dot{x}_{1} ,\ddot{x}_{1} } \right) = f_{0} {\text{e}}^{{{\text{i}}\omega t}} , $$

(7)

where the nonlinear inertial force is expressed as

$$ \begin{aligned} f_{{{\text{nl}}}} \left( {x_{1} ,\dot{x}_{1} ,\ddot{x}_{1} } \right) = & f_{{\text{a}}} \left( {y_{1} ,\dot{y}_{1} ,\ddot{y}_{1} } \right) = \frac{{b\left( {y_{0} + x_{1} } \right)^{2} \ddot{x}_{1} }}{{4l_{0}^{2} - \left( {y_{0} + x_{1} } \right)^{2} }} \\ & + \frac{{4bl_{0}^{2} \left( {y_{0} + x_{1} } \right)\dot{x}_{1}^{2} }}{{\left( {4l_{0}^{2} - \left( {y_{0} + x_{1} } \right)^{2} } \right)^{2} }}, \\ \end{aligned} $$

(8)

with $y_{1} = y_{0} + x_{1}$. For clearer presentation, the following parameters are introduced

$$ \begin{gathered} \omega_{1} = \sqrt {\frac{{k_{1} }}{{m_{1} }}} ,\,\zeta_{1} = \frac{{c_{1} }}{{2m_{1} \omega_{1} }},\,\lambda = \frac{b }{{m_{1} }},\,X_{1} = \frac{{x_{1} }}{{2l_{0} }},\, \hfill \\ D_{0} = \frac{{y_{0} }}{{2l_{0} }} = \sin \theta_{0} ,\,F_{0} = \frac{{f_{0} }}{{2k_{1} l_{0} }},\,\Omega = \frac{\omega }{{\omega_{1} }},\,\tau = \omega_{1} t, \hfill \\ \end{gathered} $$

(9)

where $\omega_{1}$ is the undamped natural frequency of system without the nonlinear inerter, $\zeta_{1}$ is the damping ratio, $\lambda$ is the inertance-to-mass ratio, $X_{1}$ is the dimensionless displacement of the mass in C1, $D_{0}$ and $\theta_{0}$ represent the original distance of the terminals for the D-inerter and original orientation of the bars for the nonlinear inerter when the mass is at the static equilibrium position, respectively, $F_{0}$ and $\Omega$ are the dimensionless amplitude and excitation frequency, respectively, and $\tau$ is the dimensionless time.

Using these variables and parameters, Eq. (7) is transformed into a dimensionless form as

$$ X_{1}^{\prime \prime } + 2\zeta_{1} X_{1}^{\prime } + X_{1} + \lambda \left( {\frac{{X_{1}^{\prime \prime } \left( {X_{1} + D_{0} } \right)^{2} }}{{1 - \left( {X_{1} + D_{0} } \right)^{2} }} + \frac{{X_{1}^{\prime 2} \left( {X_{1} + D_{0} } \right)}}{{\left( {1 - \left( {X_{1} + D_{0} } \right)^{2} } \right)^{2} }}} \right) = F_{0} {\text{e}}^{{{\text{i}}\Omega \tau }} . $$

(10)

2.2.2 Base-motion excited SDOF system

For the base-excitation case shown in Fig. 3b, the equation of motion of the mass is written as

$$ m_{1} \ddot{x}_{2} + c_{1} \left( {\dot{x}_{2} - \dot{q}} \right) + k_{1} \left( {x_{2} - q} \right) + b\left( {\frac{{\ddot{y}_{2} y_{2}^{2} }}{{4l_{0}^{2} - y_{2}^{2} }} + \frac{{4l_{0}^{2} y_{2} \dot{y}_{2}^{2} }}{{\left( {4l_{0}^{2} - y_{2}^{2} } \right)^{2} }}} \right) = 0, $$

(11)

where $q\left( t \right) = q_{0} {\text{e}}^{{{\text{i}}\omega t}}$ and $y_{2} = y_{0} + x_{2} - q$, Eq. (6) is used for the force from the nonlinear D-inerter. By introducing $z_{2} = x_{2} - q$, Eq. (11) becomes

$$ m_{1} \ddot{z}_{2} + c_{1} \dot{z}_{2} + k_{1} z_{2} + b\left( {\frac{{\ddot{y}_{2} y_{2}^{2} }}{{4l_{0}^{2} - y_{2}^{2} }} + \frac{{4l_{0}^{2} y_{2} \dot{y}_{2}^{2} }}{{\left( {4l_{0}^{2} - y_{2}^{2} } \right)^{2} }}} \right) = - m_{1} \ddot{q} = m_{1} q_{0} \omega^{2} {\text{e}}^{{{\text{i}}\omega t}} . $$

(12)

Following the similar nondimensionalisation procedure shown in Eq. (9), we obtain

$$ X_{2} = \frac{{x_{2} }}{{2l_{0} }},\,Z_{2} = \frac{{z_{2} }}{{2l_{0} }},\,Q_{0} = \frac{{q_{0} }}{{2l_{0} }}, $$

(13)

where $X_{2}$ is the dimensionless displacement of the mass in C2, $Z_{2}$ and $Q_{0}$ are the nondimensional amplitudes of the relative displacement between the two terminals of the D-inerter and that of the base-motion excitation, respectively. Using defined parameters in Eqs. (9) and (13), the nondimensional governing equation of the mass for the base-excitation case (C2) can be written as

$$ Z_{2}^{\prime \prime } + 2\zeta_{1} Z_{2}^{^{\prime}} + Z_{2} + \lambda \left( {\frac{{Z_{2}^{\prime \prime } \left( {Z_{2} + D_{0} } \right)^{2} }}{{1 - \left( {Z_{2} + D_{0} } \right)^{2} }} + \frac{{Z_{2}^{\prime 2} \left( {Z_{2} + D_{0} } \right)}}{{\left( {1 - \left( {Z_{2} + D_{0} } \right)^{2} } \right)^{2} }}} \right) = Q_{0} \Omega^{2} {\text{e}}^{{{\text{i}}\Omega \tau }} . $$

(14)

2.2.3 2DOF system with flexible foundation

The governing equations of the 2DOF system in Fig. 3c can be expressed as

$$ m_{1} \ddot{x}_{3} + c_{1} \left( {\dot{x}_{3} - \dot{x}_{4} } \right) + k_{1} \left( {x_{3} - x_{4} } \right) + f_{{{\text{nl}}}} \left( {y_{3} ,\dot{y}_{3} ,\ddot{y}_{3} } \right) = f_{0} {\text{e}}^{{{\text{i}}\omega t}} , $$

(15a)

$$ m_{2} \ddot{x}_{4} - c_{1} \left( {\dot{x}_{3} - \dot{x}_{4} } \right) - k_{1} \left( {x_{3} - x_{4} } \right) + k_{2} x_{4} + c_{2} \dot{x}_{4} - f_{n1} \left({y_3}, \dot{y}_3, \ddot{y}_3 \right) = 0, $$

(15b)

where $f_{{{\text{nl}}}} \left( {y_{3} ,\dot{y}_{3} ,\ddot{y}_{3} } \right)$ is the expression of the nonlinear force according to Eq. (6), $y_{3} = y_{0} + z_{3}$ and $z_{3} = x_{3} - x_{4}$. In order to facilitate later derivations, the following nondimensional parameters are introduced

$$ \begin{gathered} \omega_{2} = \sqrt {\frac{{k_{2} }}{{m_{2} }}} ,\,\mu = \frac{{m_{2} }}{{m_{1} }},\,\gamma = \frac{{\omega_{2} }}{{\omega_{1} }},\,\zeta_{2} = \frac{{c_{2} }}{{2m_{2} \omega_{2} }}, \hfill \\ \eta = \frac{{k_{2} }}{{k_{1} }},\,X_{3} = \frac{{x_{3} }}{{2l_{0} }},\, X_{4} = \frac{{x_{4} }}{{2l_{0} }},Z_{3} = X_{3} - X_{4} , \hfill \\ \end{gathered} $$

(16)

where $\omega_{2}$ represents the undamped natural frequency of the base structure, $\mu$ is the mass ratio, $\gamma$ is the frequency ratio between the natural frequencies, $\zeta_{2}$ is the damping ratio, $\eta$ is the stiffness ratio,$X_{3}$, $X_{4}$ and $Z_{3}$ are the dimensionless displacements of two masses and their nondimensional relative displacement, respectively. By using parameters and variables in Eqs. (9) and (16), Eq. (15) can be transformed into its dimensionless form as

$$ \begin{gathered} X_{3}^{\prime \prime } + 2\zeta_{1} \left( {X_{3}^{\prime } - X_{4}^{\prime } } \right) + X_{3} - X_{4} + \lambda \left( {\frac{{Z_{3}^{\prime \prime } \left( {Z_{3} + D_{0} } \right)^{2} }}{{1 - \left( {Z_{3} + D_{0} } \right)^{2} }} + \frac{{Z_{3}^{\prime 2} \left( {Z_{3} + D_{0} } \right)}}{{\left( {1 - \left( {Z_{3} + D_{0} } \right)^{2} } \right)^{2} }}} \right) = F_{0} {\text{e}}^{{{\text{i}}\Omega \tau }} , \hfill \\ \mu X_{4}^{\prime \prime } - 2\zeta_{1} X_{3}^{\prime } + \left( {2\mu \gamma \zeta_{2} + 2\zeta_{1} } \right)X_{4}^{\prime } - X_{3} + \left( {\eta + 1} \right)X_{4} - \lambda \left( {\frac{{Z_{3}^{\prime \prime } \left( {Z_{3} + D_{0} } \right)^{2} }}{{1 - \left( {Z_{3} + D_{0} } \right)^{2} }} + \frac{{Z_{3}^{\prime 2} \left( {Z_{3} + D_{0} } \right)}}{{\left( {1 - \left( {Z_{3} + D_{0} } \right)^{2} } \right)^{2} }}} \right) = 0, \hfill \\ \end{gathered} $$

(17)

Note that the dimensionless governing equations of the SDOF isolation system with forced excitation, base-motion excitation and the 2DOF system are presented by Eqs. (10), (14) and (17), respectively. These equations can be further written into a set of first-order ordinary differential equations and can be solved by using a numerical time-marching method such as the fourth-order Runge–Kutta (RK) scheme with variable time steps to obtain the steady-state response of masses.

3 Dynamic analysis and performance evaluation

In this section, the dynamic analysis of the D-inerter isolators is presented. A general analysis procedure using the alternating frequency–time with harmonic balance (HB-AFT) method is introduced to obtain the steady-state response. Analytical derivations of the frequency–response relationship of the SDOF vibration isolator models using the first-order HB approximations are also presented. Various performance indices such as force transmissibility, displacement transmissibility, time-averaged power flow and energy transmission variables of vibration isolators are defined and formulated.

3.1 Harmonic balance with alternating frequency–time

For a general Q-DOF dynamical system, the governing equation can be written in a matrix form as

$$ {\mathbf{MX^{\prime\prime}}} + {\mathbf{CX^{\prime}}} + {\mathbf{KX}} + {\mathbf{F}}_{{{\mathbf{nl}}}} \left( {{\mathbf{X}},{\mathbf{X^{\prime}}},{\mathbf{X^{\prime\prime}}},\tau } \right) = {\mathbf{F}}_{{\mathbf{e}}} \left( \tau \right), $$

(18)

where ${\mathbf{X}}$, ${\mathbf{X^{\prime}}}$ and ${\mathbf{X^{\prime\prime}}}$ are the displacement, velocity and acceleration response vectors, respectively; ${\mathbf{F}}_{{{\mathbf{nl}}}} \left( {{\mathbf{X}},{\mathbf{X^{\prime}}},{\mathbf{X^{\prime\prime}}},\tau } \right)$ is the nonlinear force vector due to the D-inerter, with its expression depending on the specific configurations as shown by Eqs. (10), (14) and (17); ${\mathbf{F}}_{{\mathbf{e}}} \left( \tau \right)$ is the external force vector, ${\mathbf{F}}_{{\mathbf{e}}} \left( \tau \right) = \left\{ { \ldots ,F_{0} {\text{e}}^{{{\text{i}}\Omega \tau }} , \ldots } \right\}^{{\text{T}}}$ for the force excitation applied to j-th DOF ($1 \le j \le Q$) of the system and ${\mathbf{F}}_{{\mathbf{e}}} \left( \tau \right) = \left\{ { \ldots ,Q_{0} \Omega^{2} {\text{e}}^{{{\text{i}}\Omega \tau }} , \ldots } \right\}^{{\text{T}}}$ for the base-motion excitation; ${\mathbf{M}}$, ${\mathbf{C}}$ and ${\mathbf{K}}$ are the mass, stiffness and damping matrices, respectively. For the single-DOF vibration isolator models shown in Fig. 3a and b, we have ${\mathbf{M}} = 1$, ${\mathbf{C}} = 2{\upzeta }_{1}$ and ${\mathbf{K}} = 1$. As for the case of the nonlinear isolator mounted on a flexible base shown in Fig. 3c, relevant matrices become

$$ \begin{gathered} {\mathbf{M}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & \mu \\ \end{array} } \right], \hfill \\ {\mathbf{C}} = \left[ {\begin{array}{*{20}l} {2\zeta_{1} } \hfill & { - 2\zeta_{1} } \hfill \\ { - 2\zeta_{1} } \hfill & {2\mu \gamma \zeta_{2} + 2\zeta_{1} } \hfill \\ \end{array} } \right], \hfill \\ \user2{ }{\mathbf{K}} = \left[ {\begin{array}{*{20}l} 1 \hfill & { - 1} \hfill \\ { - 1} \hfill & {\eta + 1} \hfill \\ \end{array} } \right], \hfill \\ \end{gathered} $$

(19)

The steady-state displacement solutions of Eq. (18) can be calculated by the harmonic balance method with alternating frequency–time (HB-AFT) scheme [33]. This technique is mainly based on numerical determination of the Fourier coefficients for the nonlinear force terms in the governing equation, and it has been used to study both smooth and nonsmooth nonlinear dynamical systems. When using the HB-AFT scheme, the steady-state dimensionless displacement responses ${\mathbf{X}}$ and the nonlinear force ${\mathbf{F}}_{{{\mathbf{nl}}}} \left( {{\mathbf{X}},{\mathbf{X^{\prime}}},{\mathbf{X^{\prime\prime}}},\tau } \right)$ can be approximated by an N-th-order truncated Fourier series

$$ {\mathbf{X}} = \left\{ {\sum\nolimits_{n = 0}^{N} {\tilde{R}_{1,n} {\text{e}}^{{{\text{i}}n\Omega \tau }} ,\sum\nolimits_{n = 0}^{N} {\tilde{R}_{2,n} {\text{e}}^{{{\text{i}}n\Omega \tau }} } } , \ldots , \sum\nolimits_{n = 0}^{N} {\tilde{R}_{Q,n} {\text{e}}^{{{\text{i}}n\Omega \tau }} } } \right\}^{{\text{T}}} , $$

(20)

$$ {\mathbf{F}}_{{{\mathbf{nl}}}} \left( {{\mathbf{X}},{\mathbf{X^{\prime}}},{\mathbf{X^{\prime\prime}}},\tau } \right) = \left\{ {\sum\nolimits_{n = 0}^{N} {\tilde{H}_{1,n} {\text{e}}^{{{\text{i}}n\Omega \tau }} ,\sum\nolimits_{n = 0}^{N} {\tilde{H}_{2,n} {\text{e}}^{{{\text{i}}n\Omega \tau }} } } , \ldots ,\sum\nolimits_{n = 0}^{N} {\tilde{H}_{Q,n} {\text{e}}^{{{\text{i}}n\Omega \tau }} } } \right\}^{{\text{T}}} , $$

(21)

where $\tilde{R}_{1,n}$, $\tilde{R}_{2,n}$ and $\tilde{R}_{Q,n}$ are the complex Fourier coefficients of the n-th order approximations of the first, second and Q-th subsystems, respectively, $\tilde{H}_{Q,n}$ is the complex Fourier coefficient of Q-th subsystem for the nonlinear force at the n-th order. The velocity and acceleration expressions can be further obtained using the first and the second derivatives of Eq. (20). By inserting all these related terms into Eq. (18) and balancing the corresponding harmonic terms of n-th ($0 \le n \le N$) order, we obtain

$$ \left( { - \left( {n\Omega } \right)^{2} {\mathbf{M}} + {\text{i}}n\Omega {\mathbf{C}} + {\mathbf{K}}} \right)\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{R}_{1,n} } \\ {\tilde{R}_{2,n} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\tilde{R}_{Q,n} } \\ \end{array} } \\ \end{array} } \right\} = {\mathbf{S}}_{{\varvec{n}}} - \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{H}_{1,n} } \\ {\tilde{H}_{2,n} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\tilde{H}_{Q,n} } \\ \end{array} } \\ \end{array} } \right\}, $$

(22)

where ${\mathbf{S}}_{{\varvec{n}}} = \left\{ { \ldots ,F_{0} , \ldots } \right\}^{{\text{T}}}$ for the force excitation and ${\mathbf{S}}_{{\varvec{n}}} = \left\{ { \ldots ,Q_{0} \Omega^{2} , \ldots } \right\}^{{\text{T}}}$ for the base-motion excitation. For a Q-DOF system with N-th order HB approximations, there are in total number of $Q\left( {2N + 1} \right)$ real nonlinear algebraic equations, which can be solved by the Newton–Raphson numerical continuation technique [34].

3.2 Analytical investigation of the responses

3.2.1 Free vibration behaviour of SDOF systems

Here the free vibration behaviour of the SDOF system is firstly considered by setting the excitation amplitude zero, i.e. $F_{0} = 0$ in Eq. (10) and $Q_{0} = 0$ in Eq. (14), which leads to

$$ X_{1}^{\prime \prime } + 2\zeta_{1} X_{1}^{\prime } + X_{1} + \lambda \left( {\frac{{X_{1}^{\prime \prime } \left( {X_{1} + D_{0} } \right)^{2} }}{{1 - \left( {X_{1} + D_{0} } \right)^{2} }} + \frac{{X_{1}^{\prime 2} \left( {X_{1} + D_{0} } \right)}}{{\left( {1 - \left( {X_{1} + D_{0} } \right)^{2} } \right)^{2} }}} \right) = 0, $$

(23)

$$ Z_{2}^{\prime \prime } + 2\zeta_{1} Z_{2}^{\prime } + Z_{2} + \lambda \left( {\frac{{Z_{2}^{\prime \prime } \left( {Z_{2} + D_{0} } \right)^{2} }}{{1 - \left( {Z_{2} + D_{0} } \right)^{2} }} + \frac{{Z_{2}^{\prime 2} \left( {Z_{2} + D_{0} } \right)}}{{\left( {1 - \left( {Z_{2} + D_{0} } \right)^{2} } \right)^{2} }}} \right) = 0. $$

(24)

Note that these two equations are mathematically equivalent by replacing $X_{1}$ with $Z_{2}$ in Eq. (23). Therefore, only free vibration behaviour of the mass for the system governed by Eq. (23) is analysed here, which can then be easily extended to the system described by Eq. (24). It is also noted that for practical designs, we need $0 < X_{1} + D_{0} < 1$. Therefore, the range of the nondimensional displacement $X_{1}$ of the mass is

$$ - D_{0} < X_{1} < 1 - D_{0} , $$

(25)

which provides

$$ \begin{gathered} X_{{{\text{low}}}} = - D_{0} = - \sin \theta_{0} , \hfill \\ X_{{{\text{up}}}} = 1 - D_{0} = 1 - \sin \theta_{0} , \hfill \\ \end{gathered} $$

(26)

denoting the lower and the upper limits for the dimensionless displacement $X_{1}$. For a periodic response around the static equilibrium point, the maximum value of the allowed amplitude:

$$ \left| {X_{1} } \right|_{{{\text{max}}}} = {\text{min}}\left( {D_{0} , 1 - D_{0} } \right). $$

(27)

Equations (26) and (27) provide the constraints on the maximum displacement of the proposed structure. By using a second-order Taylor’s expansion for the nonlinear term in Eq. (23), we have

$$ \begin{aligned} G\left( X \right) & = \frac{{\left( {X_{1} + D_{0} } \right)^{2} }}{{1 - \left( {X_{1} + D_{0} } \right)^{2} }} \approx \frac{{D_{0}^{2} }}{{1 - D_{0}^{2} }} + \frac{{2D_{0} }}{{\left( {1 - D_{0}^{2} } \right)^{2} }}X_{1} + \frac{{1 + 3D_{0}^{2} }}{{\left( {1 - D_{0}^{2} } \right)^{3} }}X_{1}^{2} \\ & = \beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{1}^{2} , \\ \end{aligned} $$

(28)

$$ \begin{aligned} H\left( X \right) = & \frac{{\left( {X_{1} + D_{0} } \right)}}{{\left( {1 - \left( {X_{1} + D_{0} } \right)^{2} } \right)^{2} }} \\ & \approx \frac{{D_{0} }}{{\left( {1 - D_{0}^{2} } \right)^{2} }} + \frac{{1 + 3D_{0}^{2} }}{{\left( {1 - D_{0}^{2} } \right)^{3} }}X_{1} + \frac{{6D_{0} \left( {1 + D_{0}^{2} } \right)}}{{\left( {1 - D_{0}^{2} } \right)^{4} }}X_{1}^{2} \\ & = \gamma_{0} + \gamma_{1} X_{1} + \gamma_{2} X_{1}^{2} , \\ \end{aligned} $$

(29)

where the coefficients are expressed by

$$ \beta_{0} = \frac{{D_{0}^{2} }}{{1 - D_{0}^{2} }},\,\beta_{1} = \frac{{2D_{0} }}{{\left( {1 - D_{0}^{2} } \right)^{2} }},\,\beta_{2} = \frac{{1 + 3D_{0}^{2} }}{{\left( {1 - D_{0}^{2} } \right)^{3} }}, $$

(30)

$$ \gamma_{0} = \frac{{D_{0} }}{{\left( {1 - D_{0}^{2} } \right)^{2} }},\,\gamma_{1} = \frac{{1 + 3D_{0}^{2} }}{{\left( {1 - D_{0}^{2} } \right)^{3} }},\,\gamma_{2} = \frac{{6D_{0} \left( {1 + D_{0}^{2} } \right)}}{{\left( {1 - D_{0}^{2} } \right)^{4} }} $$

(31)

depending on the original distance $D_{0}$ between the two terminals of the nonlinear D-inerter.

The total dimensionless nonlinear force by the nonlinear inerter is then approximated by

$$ \begin{aligned} F_{{{\text{nl}}}} \left( {X_{1} ,X_{1}^{\prime } , X_{1}^{\prime \prime } } \right) & = \lambda \left( {\frac{{X_{1}^{\prime \prime } \left( {X_{1} + D_{0} } \right)^{2} }}{{1 - \left( {X_{1} + D_{0} } \right)^{2} }} + \frac{{X_{1}^{^{\prime}2} \left( {X_{1} + D_{0} } \right)}}{{\left( {1 - \left( {X_{1} + D_{0} } \right)^{2} } \right)^{2} }}} \right) \\ & \approx \lambda \left( {X_{1}^{\prime \prime } \left( {\beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{1}^{2} } \right) + X_{1}^{\prime 2} \left( {\gamma_{0} + \gamma_{1} X_{1} + \gamma_{2} X_{1}^{2} } \right)} \right). \\ \end{aligned} $$

(32)

By inserting the approximate expression in Eq. (32) into Eq. (23), we have

$$ X_{1}^{\prime \prime } + 2\zeta_{1} X_{1}^{\prime } + X_{1} + \lambda \left( {X_{1}^{\prime \prime } \left( {\beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{1}^{2} } \right) + X_{1}^{\prime 2} \left( {\gamma_{0} + \gamma_{1} X_{1} + \gamma_{2} X_{1}^{2} } \right)} \right) = 0. $$

(33)

From Eq. (33), the linearized natural frequency of the system is

$$ \Omega_{{{\text{nN}}}} = \sqrt {\frac{1}{{1 + \lambda \beta_{0} }}} . $$

(34)

This equation shows that the linearized natural frequency of the system reduces with the increase of the inertance-to-mass ratio $\lambda$. Note that for the corresponding linear inerter-based vibration isolator, the natural frequency is expressed as

$$ \Omega_{{{\text{nL}}}} = \sqrt {\frac{1}{1 + \lambda }} . $$

(35)

A comparison of Eqs. (34) and (35) shows that the use of the nonlinear linkage mechanism can lead to a lower linearized natural frequency of the isolator when $\beta_{0} > 1$. The requirement is equivalent to:

$$ D_{0} > \frac{\sqrt 2 }{2},\,{\text{i}}.{\text{e}}.,\, \theta_{0} > \frac{\pi }{4}. $$

(36)

3.2.2 Analytical frequency response relationship

Here, the analytical results based on the first-order HB method are given. The HB-AFT method and numerical RK scheme can yield accurate results but with relatively high computational cost. Compared with these two methods, the analytical approximation can provide steady-state solutions with relatively low cost. In addition, the analytical solutions show better insights into nonlinear dynamics and vibration transmission mechanisms affected by system parameters.

For the SDOF oscillator with force excitation (configuration C1), the steady-state response, the displacement, velocity, and acceleration of the mass can be approximated as

$$ \begin{gathered} X_{1} = R_{1} \cos \left( {\Omega \tau - \phi } \right), \hfill \\ X_{1}^{\prime } = - \Omega R_{1} \sin \left( {\Omega \tau - \phi } \right), \hfill \\ X_{1}^{\prime \prime } = - \Omega^{2} R_{1} \cos \left( {\Omega \tau - \phi } \right), \hfill \\ \end{gathered} $$

(37)

respectively. By inserting Eqs. (28), (29) and (37) into Eq. (10) and retaining only the terms at the fundamental oscillation frequency $\Omega$, we have

$$ \begin{gathered} \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}R_{1} \cos \left( {\Omega \tau - \phi } \right) \hfill \\ \quad - 2\zeta_{1} \Omega R_{1} \sin \left( {\Omega \tau - \phi } \right) = F_{0} \cos \Omega \tau . \hfill \\ \end{gathered} $$

(38)

By balancing the coefficients of the harmonic terms with $\cos \left( {\Omega \tau - \phi } \right)$ and $\sin \left( {\Omega \tau - \phi } \right)$ for Eq. (38), we have

$$ \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}R_{1} = F_{0} \cos \phi , $$

(39)

$$ 2\zeta_{1} \Omega R_{1} = F_{0} \sin \phi . $$

(40)

By cancelling out the trigonometric terms in Eqs. (39) and (40), it follows that

$$ \left( {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right)^{2} R_{1}^{2} + 4\zeta_{1}^{2} \Omega^{2} R_{1}^{2} = F_{0}^{2} . $$

(41)

Equation (41) provides a nonlinear algebraic equation for the frequency–response relationship of the mass. It can be solved by a bisection method to obtain $R_{1}$. Subsequently, the phase angle $\phi$ can be determined allowing the steady-state response of the mass to be obtained.

The backbone curves are widely used to characterise the inherent dynamic properties of the nonlinear systems [35]. It corresponds to the frequency–response characteristic of unforced and undamped system, i.e. when $F_{0} = \zeta_{1} = 0$, Eq. (41) becomes

$$ 1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} = 0. $$

(42)

For the configuration C2, the analytical first-order HB expressions of the steady-state relative displacement, velocity, and acceleration are

$$ \begin{gathered} Z_{2} \approx R_{2} \cos \left( {\Omega \tau - \theta } \right), \hfill \\ Z_{2}^{\prime } \approx - \Omega R_{2} \sin \left( {\Omega \tau - \theta } \right), \hfill \\ Z_{2}^{\prime \prime } \approx - \Omega^{2} R_{2} \cos \left( {\Omega \tau - \theta } \right), \hfill \\ \end{gathered} $$

(43)

respectively, where $Z_{2} = X_{2} - Q_{0} \cos \Omega \tau$ is the relative displacement between the mass and the base motion as defined in Eq. (14), $R_{2}$ is the amplitude, and $\theta$ denotes the phase difference between the response and the excitation. Note that the nonlinear force term in Eq. (14) that arises from the nonlinear D-inerter can be approximated by replacing $X_{1}$ with $Z_{2}$ in Eqs. (28) and (29). Following the similar procedure as shown by Eqs. (37)–(41), the frequency–response relations of the system subjected to base-motion excitation can be found. It is found that the resultant mathematical expressions of the frequency response relations for the force and base-motion excitation cases are similar. For clarity, the detailed derivation process is provided in the Appendix.

3.3 Performance indices

To assess the isolation performance of the proposed D-inerter in SDOF and 2DOF systems, different evaluation indices are used, including force transmissibility, displacement transmissibility, time-averaged power flow variables and kinetic energy of the mass.

3.3.1 Force transmissibility

The force transmissibility is widely used to evaluate the performance of nonlinear vibration isolators. Based on Eqs. (10) and (17), the nondimensional transmitted force from the machine mass through the nonlinear isolator to the ground (i.e. configuration C1) or to the flexible base structure (i.e. configuration C3) is expressed by

$$ F_{{\text{T}}} = F_{0} {\text{e}}^{{{\text{i}}\Omega \tau }} - X_{i}^{\prime } , $$

(44)

where $i = 1$ for system C1 and $i = 3$ for system C3. Therefore, the force transmissibility from the machine to the base or the ground can be expressed as

$$ TR = \frac{{\left| {F_{{\text{T}}} } \right|_{{{\text{max}}}} { }}}{{F_{0} }}$$

(45)

where $\left| {F_{{\text{T}}} } \right|_{{{\text{max}}}}$ is the maximum value of the transmitted force in the steady state.

For the configuration C1, the analytical expressions of the transmitted force and the force transmissibility using the first-order approximations can be written as

$$ F_{{\text{T}}} \approx F_{0} \cos \Omega \tau + \Omega^{2} R_{1} \cos \left( {\Omega \tau - \phi } \right), $$

(46)

$$ TR \approx \frac{{\sqrt {\left( {F_{0} + \Omega^{2} R_{1} \cos \phi } \right)^{2} + \left( {\Omega^{2} R_{1} \sin \phi } \right)^{2} } }}{{F_{0} }}, $$

(47)

where Eq. (37) is used for acceleration approximation. Note that to achieve effective isolation of force transmission, we need $TR < 1$, i.e.

$$ \Omega^{4} R_{1}^{2} + 2\Omega^{2} R_{1}^{2} \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\} < 0, $$

(48)

where Eq. (39) is used for derivation. Therefore, the effective isolation of force transmission requires

$$ \Omega_{{{\text{iso}}}} = \sqrt {\frac{2}{{1 + 2\lambda \left( {\beta_{0} + \frac{1}{4}R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)}}} < \sqrt 2 . $$

(49)

It is noted that the expression $2 \lambda \left( {\beta_{0} + \frac{1}{4}R_{1}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)$ is positive according to Eqs. (30) and (31). For a conventional linear spring-damper isolator, the isolation of force transmission is only effective when $\Omega$ is larger than $\sqrt 2$. Equation (49) shows that the use of the D-inerter in the isolator can successfully enlarge the frequency of effective isolation. The response amplitude $R_{1}$ in Eq. (49) takes the critical value with the corresponding force transmissibility TR of one.

Note that at high excitation frequencies, using Eqs. (39), (41) and (47), we have

$$ \begin{aligned} TR_{\infty } & = \mathop {\lim }\limits_{\Omega \to \infty } TR = \frac{{\lambda \beta_{0} }}{{1 + \lambda \beta_{0} }} \\ & = \frac{1}{{\frac{{1/D_{0}^{2} - 1}}{\lambda } + 1}} < 1. \\ \end{aligned} $$

(50)

Equation (50) shows that in the high-frequency range, the force transmissibility $TR$ has an asymptotic value, i.e. $\lambda \beta_{0} /\left( {1 + \lambda \beta_{0} } \right)$. This asymptotic value is smaller than one, indicating that the use of the nonlinear isolator leads to a lower amplitude of the transmitted force, compared to that of the external excitation. It also shows that the asymptotic value in the high-frequency range of the force transmissibility is proportional to the initial distance $D_{0}$ and the inertance-to-mass ratio $\lambda$.

3.3.2 Displacement transmissibility

The displacement transmissibility is used here to evaluate the performance of the configuration C2. It is defined as the ratio between the displacement amplitude of the mass and that of the base:

$$ TR_{{\text{d}}} = \frac{{\left| {X_{2} } \right| }}{{Q_{0} }} \approx \frac{{M_{2} }}{{Q_{0} }}, $$

(51)

where $M_{2}$ is the response amplitude of the mass in C2 and the related expression is given by Eq. (69) in the Appendix. For the effective isolation, we need $TR_{{\text{d}}} < 1$, that is

$$ \sqrt {\left( {R_{2} \cos \theta + Q_{0} } \right)^{2} + R_{2}^{2} \sin^{2} \theta } < Q_{0} , $$

(52)

where Eqs. (62) and (69) in the Appendix are used. Therefore, the isolation of base motion is achieved when the excitation frequency satisfies

$$ \Omega_{{{\text{iso}}}} = \sqrt {\frac{2}{{1 + 2\lambda \beta_{0} + \frac{1}{2}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)}}} < \sqrt 2 , $$

(53)

where $\Omega_{{{\text{iso}}}}$ is used to denote the lower limit of the excitation frequency for effective isolation of base motions. It shows that the use of the D-inerter in the isolator can lead to a wider effective isolation frequency band compared to the conventional linear spring-damper isolator.

It is shown that the relative displacement amplitude has a limiting value $R_{2,\infty }$ at high frequencies, shown in the Appendix by Eq. (67). Therefore, there exists an asymptotic value of the displacement transmissibility as $\Omega$ tends to infinity

$$ \begin{aligned} TR_{{{\text{d}},\infty }} & = \mathop {\lim }\limits_{{{\Omega } \to \infty }} \left( {\frac{{M_{2} }}{{Q_{0} }}} \right) \\ & = \mathop {{\text{lim}}}\limits_{{{\Omega } \to \infty }} \sqrt {\frac{{R_{2}^{2} }}{{Q_{0}^{2} }} + 1 + \frac{{2R_{2}^{2} }}{{Q_{0}^{2} \Omega^{2} }}\left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}} \\ & = \frac{{\left| {Q_{0} - R_{2,\infty } } \right|}}{{Q_{0} }}. \\ \end{aligned} $$

(54)

3.3.3 Vibration power flow and energy

Vibration power flow and energy transmission variables are important performance indices to assess the isolation performance. According to the universal law of energy conservation, over one cycle of a periodic response in the steady state, the mechanical energy of the system remains unchanged and all the input energy by the excitation must be dissipated by the viscous damping within the system. Thus, the time-averaged input power $\overline{P}_{{{\text{in}}}}$ from the excitation equals the time-averaged dissipated power $\overline{P}_{{\text{d}}}$ by the viscous damper:

$$ \overline{P}_{{{\text{in}}}} = \overline{P}_{{\text{d}}} = \frac{1}{{\tau_{s} }}\int_{{\tau_{0} }}^{{\tau_{0} + \tau_{s} }} ({P_{{{\text{d}}1}} + P_{{{\text{d}}2}}) {\text{d}}\tau ,} $$

(55)

where $\tau_{0}$ is the starting time for averaging and $\tau_{s}$ is averaging time span, which is set as one excitation cycle, i.e. $\tau_{s} = 2\pi /\Omega$; $P_{{{\text{d}}1}}$ and $P_{{{\text{d}}2}}$ are the instantaneous dissipated power by the viscous damper $c_{1}$ and $c_{2}$, respectively. It is noted that for system C1, $P_{{{\text{d}}1}} = 2\zeta_{1} X_{1}^{\prime 2}$ and $P_{{{\text{d}}2}} = 0$. For system C2, we have $P_{{{\text{d}}1}} = 2\zeta_{1} \left( {X_{2}^{\prime } - Q^{\prime } } \right)^{2}$ and $P_{{{\text{d}}2}} = 0$. For system C3, $P_{{{\text{d}}1}} = 2\zeta_{1} \left( {X_{3}^{\prime } - X_{4}^{\prime } } \right)^{2}$ and $P_{{{\text{d}}2}} = 2\mu \gamma \zeta_{2} X_{4}^{\prime 2}$.

The analytical expression of the time-averaged input power for configuration C1 is

$$ \overline{P}_{{{\text{in}}}} \approx \zeta_{1} \Omega^{2} R_{1 }^{2} , $$

(56)

where Eq. (37) is used for the approximation. As for the configuration C2, based on Eq. (55), the analytical results of $\overline{P}_{{{\text{in}}}}$ can be easily obtained by replacing $R_{1}$ with $R_{2}$ in Eq. (56), and the value of $R_{2}$ is calculated by Eq. (64) in Appendix.

The nondimensional maximum kinetic energy of the mass excited at a specific excitation frequency is expressed by

$$ K_{{{\text{max}}}} = \frac{1}{2}\left( {\left| {X_{i}^{\prime } } \right|_{{{\text{max}}}} } \right)^{2}, $$

(57)

where $\left| {X_{i}^{\prime } } \right|_{{{\text{max}}}}$ is the maximum magnitude of the velocity of the mass $m_{1}$ in the steady state, $i$ = 1, 2 or 3 for each configuration. The analytical expressions of the maximum kinetic energy of configurations C1 and C2 are

$$ K_{{{\text{max}},{\text{c}}1}} \approx \frac{1}{2}\Omega^{2} R_{1}^{2} ,\,K_{{{\text{max}},{\text{c}}2}} \approx \frac{1}{2}\Omega^{2} M_{2}^{2} , $$

(58)

respectively, the first-order approximation of the velocity shown by Eq. (37) is used. Equations (56) and (58) show that at a fixed value of the damping ratio $\zeta_{1}$, the time-averaged input power is proportional to the maximum kinetic energy of the mass for configuration C1.

For configuration C3, the power transmitted from mass $m_{1}$ to the flexible base is also an important index to evaluate the vibration transmission behaviour. According to the law of energy conservation, the time-averaged transmitted power to the base is entirely dissipated by the viscous damping $c_{2}$ at the bottom. Therefore, we have

$$ \overline{P}_{{\text{t}}} = \overline{P}_{{{\text{d}}2}} = \frac{1}{{\tau_{s} }}\int_{{\tau_{0} }}^{{\tau_{0} + \tau_{s} }} {2\mu \gamma \zeta_{2} X_{4}^{\prime 2} {\text{d}}\tau } . $$

(59)

In addition, the power transmission ratio $R_{{\text{T}}}$ is defined as the ratio between the time-averaged transmitted power $\overline{P}_{{\text{t}}}$ and the time-averaged input power $\overline{P}_{{{\text{in}}}}$:

$$ R_{{\text{T}}} = \frac{{\overline{P}_{{\text{t}}} }}{{\overline{P}_{{{\text{in}}}} }}. $$

(60)

A smaller value of $R_{{\text{T}}}$ is beneficial to achieve effective vibration isolation.

4 Results and Discussion

4.1 Free vibration and result validations

Validations of results obtained by the HB-AFT method, the analytical HB and numerical RK method are firstly considered and presented herein. Figure 4 shows the influence of the inertance-to-mass ratio $\lambda$ and the initial orientation of the bar $\theta_{0}$ on the linearized natural frequency $\Omega_{{{\text{nN}}}}$ of the nonlinear vibration isolator. The lines represent the analytical linearized natural frequency obtained by Eq. (34). The symbols are numerical results of Eq. (23) using RK method for free vibration, where the initial displacement is set as 0.001 and the initial velocity is zero. In Fig. 4a, when $\theta_{0} = 45^\circ$, we have $\beta_{0} = 1$ and $\Omega_{{{\text{nN}}}} = 1/\sqrt {1 + \lambda } = \Omega_{{{\text{nL}}}}$, i.e. the corresponding curve of the linearized natural frequency will coincide with the curve for a linear inerter-based vibration isolator. The figure shows that for a given value of $\theta_{0}$, the increase in the inertance of D-inerter isolator leads to reductions in the linearized natural frequency, which can assist vibration isolation. Figure 4b shows that at a given value of $\lambda$, a larger value of the initial angle $\theta_{0}$ can yield a smaller value of $\Omega_{{{\text{nL}}}}$, which can also benefit vibration isolation.

Fig. 4

Linearized natural frequency of the D-inerter isolator with different a initial orientation and b inertance-to-mass ratios. In a, the dotted, dashed and dash-dotted lines denote analytical linearized natural frequency for $\theta_{0} = 30^\circ ,45^\circ \,{\text{and}}\, 60^\circ$, respectively. In b, the dashed, dotted and dash-dotted lines are analytical results for $\lambda = 5, 10\, {\text{and}} \,15$, respectively. The symbols represent the corresponding numerical results

Figure 5 shows the steady-state response amplitude of the SDOF isolators using the different methods. The solid lines represent the fifth-order HB-AFT results, and dashed lines are the first-order HB approximations. The symbols are the numerical integration results using the time marching method. It is found that the results obtained by each method are almost the same. The resonant peak is slightly bent to the low-frequency range due to the geometric nonlinearity in the D-inerter isolator. It illustrates that for both force excitation and base-motion excitation, the first-order analytical HB approximations can predict the dynamic responses well. To have a balance between the computational efficiency and accuracy, the first-order HB approximations are used for the SDOF nonlinear isolators (i.e. configuration C1 and C2). However, due to the complexity of analytical derivation, the fifth-order HB-AFT scheme is applied to obtain the dynamic response of the 2-DOF isolator system (i.e. configuration C3).

Fig. 5

Validation and comparison of the response amplitude of the SDOF system with a force excitation (configuration C1) and b base-motion excitation (configuration C2) using different methods. Solid lines: HB-AFT 5-th-order approximation; Dashed lines: first-order HB analytical method; symbols: numerical Runge–Kutta method. Parameter values: $\zeta_{1} = 0.01, \lambda = 10,D_{0} = 0.5,F_{0} = 0.002,Q_{0} = 0.01$

4.2 Performance evaluations of the isolator in force-excited SDOF system

In Figs. 6, 7 and 8, the effects of design parameters of the nonlinear D-inerter isolator on the dynamic response of the mass, the force transmissibility and the kinetic energy of the mass are investigated, respectively. Figures 6a, 7a and 8a show the influence of the inertance-to-mass ratio $\lambda$ by setting four possible values of 0, 5, 10 and 20, while the initial distance of terminals $D_{0}$ is fixed as $D_{0} = 0.5$. The dashed, dotted and dash-dotted lines represent the case of $\lambda = 5$, 10 and 20, respectively, and the linear case $\lambda = 0$ corresponding to the system without the D-inerter is denoted by the solid line. Note that a larger value of inertance can also be set to provide better vibration isolation performance in certain frequency ranges. The currently used values of inertance in the case study are selected to avoid the large displacement exceeding the limit for the linkage mechanism. Based on this point, the inertance-to-mass ratio is set to ensure its functionality in a wide frequency range. Figures 6b, 7b and 8b present the effects of the initial distance $D_{0}$ between the terminals of the D-inerter by changing its value from 0.4, to 0.5 and then 0.6, denoted by the dashed, dotted and dash-dotted lines, respectively, while fixing $\lambda$ at 10. The other parameters are set as $F_{0} = 0.002\, {\text{and}}\, \zeta_{1} = 0.01$. The analytical approximation results obtained by the solutions of Eq. (41) are denoted by different types of lines. For cross-verification and comparison, numerical results are also obtained from the fourth-order Runge–Kutta method and are represented by different types of symbols.

Fig. 6

Effects of a the inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b the initial distance $D_{0}$ between the terminals of the D-inerter (with $\lambda = 10$) on the response amplitude $R_{1}$ of the mass

Fig. 7

Effects of a the inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b the initial distance $D_{0}$ between the terminals of the D-inerter (with $\lambda = 10$) on the force transmissibility $TR$

Fig. 8

Effects of a the inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b the initial distance $D_{0}$ between the terminals of the D-inerter (with $\lambda = 10$) on the maximum kinetic energy $K_{{{\text{max}}}}$ of the mass

Figure 6a shows that as the inertance-to-mass ratio $\lambda$ increases from 0 to 5, to 10, and to 20, the resonant peak of the response curve $R_{1}$ shifts to lower frequencies, in accordance with the results shown previously on the linearized natural frequencies. The backbone curves are obtained using Eq. (42) and are denoted using dash-dot-dot lines. At a prescribed value of $\Omega$ in the high-frequency range, the dynamic response level decreases as the $\lambda$ increases. Compared with the corresponding linear isolator case (i.e. $\lambda = 0$), a larger value of $\lambda$ for the nonlinear D-inerter isolator can broaden the bandwidth of the isolation range and is beneficial for vibration suppression. Figure 6a also shows that the peak in each response curve of the D-inerter isolator case bends to the low-frequency range, similar to that of the softening stiffness Duffing oscillator. The reason for the bending is that the mass is having a relatively large displacement near resonance such that the D-inerter can generate a large inertial force. The effects of having the inertial force to increase with the displacement are similar to those of having the stiffness to reduce with the displacement, leading to a left-bending response curve. It is also noted that the resonant peak value increases with the inertance-to-mass ratio. By combining Eqs. (41) and (42), the peak value can be determined analytically as $R_{1P} = F_{0} /\left( {2\zeta_{1} {\Omega }_{r} } \right)$, where ${\Omega }_{r}$ is the corresponding frequency. Therefore, as the inertance-to-mass ratio increases, the resonant frequency ${\Omega }_{r}$ decreases, resulting a larger value of the resonant peak. Figure 6b shows that as the initial distance $D_{0}$ of the D-inerter increases from 0.4 to 0.5 and then to 0.6, the resonant peak of $R_{1}$ shifts to the low-frequency range with larger peak values. This behaviour is associated with the fact that the linearized natural frequency decreases when $D_{0}$ increases. Figure 6b shows when the excitation frequency is large, the response amplitude $R_{1}$ can be reduced by having a larger value of $D_{0}$. In contrast, Fig. 6 shows that the influence of the inertance-to-mass ratio $\lambda$ and initial distance $D_{0}$ on the response amplitude becomes small when the excitation frequency tends to zero.

In Fig. 7, the effects of the design parameters of the D-inerter on the force transmissibility $TR$ of the nonlinear isolator are investigated. It shows that compared with the conventional linear spring-damper isolator (i.e. $\lambda = 0$), the use of the D-inerter introduces an anti-peak in the curve of $TR$. As the value of $\lambda$ increases, the inertial force due to the D-inerter also increases, leading to the shift of both the peak and the anti-peak in each curve of $TR$ to the low-frequency range. This is due to the stronger inertial force by the D-inerter with the increasing $\lambda$. Figure 7b shows the influence of the initial distance $D_{0}$ between the terminals of the D-inerter on the force transmission behaviour. As the value of $D_{0}$ increases from 0.4 to 0.5 and then to 0.6, both the resonant and anti-resonant peaks move to lower frequencies when $D_{0}$ increases. When the excitation frequency is greater than $\Omega_{{{\text{iso}}}}$, the force transmissibility first decreases to the local minimum and then increases with the excitation frequency approaching an asymptotic value in the high-frequency range. In Fig. 7a, when $\lambda$ is 5, 10 and 20, the left bound of the effective isolation frequency ranges starts from nearly 0.37, 0.51 and 0.68 using Eq. (49) and the asymptotic values are approximately 0.63, 0.77 and 0.87 (obtained by $TR_{\infty }$ in Eq. 50), respectively. In Fig. 7b, the starting frequency $\Omega_{{{\text{iso}}}}$ of effective isolation is about 0.40, 0.51 and 0.64 and the asymptotic values of $TR$ are approximately 0.66, 0.77 and 0.85 corresponding to an initial distance $D_{0}$ of 0.4, 0.5 and 0.6, respectively. The figure confirms that the asymptotic value of TR increases with $\lambda$ and $D_{0}$ values but less than 1. Figure 7 shows that with larger values of inertance $\lambda$ or the initial distance $D_{0}$ between the terminals of the D-inerter, the resonant peak of TR twists further to the left due to a larger induced nonlinear inertial force. Figure 7 demonstrates that the inclusion of the nonlinear D-inerter to the isolator can improve the isolation performance by creating a wider frequency band where force transmissibility is less than 1 at high frequencies.

Figure 8a and b shows the effects of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ between the terminals of the D-inerter on the maximum kinetic energy $K_{{{\text{max}}}}$, respectively. As shown in Eqs. (56) and (58), at a prescribed damping coefficient, the time-averaged input power $\overline{P}_{{{\text{in}}}}$ has a linear relationship with the maximum kinetic energy $K_{{{\text{max}}}}$. Therefore, the curves of $\overline{P}_{{{\text{in}}}}$ would have the same patterns as those of $K_{{{\text{max}}}}$. Compared with the curves of TR, Fig. 8 shows that only one peak can be found in each curve of $K_{{{\text{max}}}}$. As the value of $\lambda$ increases from 0 to 20 or the value of $D_{0}$ increases from 0.4 to 0.6, the peak shifts to the left and bends further to lower frequencies, but the peak value changes little. As the excitation frequency $\Omega$ reduces in the low-frequency range, the curves tend to merge and the variations in the values of $\lambda$ and $D_{0}$ can only result in small changes in the curves of $K_{{{\text{max}}}}$. At a prescribed frequency in the high-frequency range, larger values of $\lambda$ or $D_{0}$ will lead to a lower level of the maximum kinetic energy of the primary mass. Figure 8 shows that compared with the linear spring-damper isolator (i.e. $\lambda = 0$), the use of D-inerter can benefit vibration suppression by resulting in a lower level of the power input as well as the maximum kinetic energy of the mass in a wide frequency band.

4.3 Performance evaluations of the isolator in motion-excited SDOF system

In Figs. 9, 10 and 11, the effects of design parameters of the D-inerter isolator on the displacement transmissibility $TR_{{\text{d}}}$, the time-averaged input power $\overline{P}_{{{\text{in}}}}$ and the maximum kinetic energy $K_{{{\text{max}}}}$ of the mass for the system subjected to base-motion excitation are investigated, respectively. Figures 9a, 10a and 11a present the influence of the inertance-to-mass ratio $\lambda$ by changing its value from 0, to 5, 10 and finally to 20, while fixing $D_{0}$ at 0.5. Figures 9b, 10b and 11b show the effects of the initial distance $D_{0}$ between the terminals of the D-inerter by selecting three possible values of 0.5, 0.6 and 0.7 while setting the inertance-to-mass ratio $\lambda = 10$. The other parameters are set as $Q_{0} = 0.01 \,{\text{and}}\, \zeta_{1} = 0.01$. These different lines are obtained by the first-order analytical HB approximation, as shown in the Appendix. Numerical results based on the use of the Runge–Kutta method are also presented by different types of symbols.

Fig. 9

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b initial distance $D_{0}$ between the terminals of the D-inerter (with $\lambda = 10$) on the displacement transmissibility $TR_{{\text{d}}}$

Fig. 10

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b initial distance $D_{0}$ between the terminals of the D-inerter (with $\lambda = 10$) on the time-averaged input power $\overline{P}_{{{\text{in}}}}$

Fig. 11

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b initial distance $D_{0}$ between the terminals of the D-inerter (with $\lambda = 10$) on the maximum kinetic energy $K_{{{\text{max}}}}$ of the mass

Figure 9a and b shows the influence of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ on the displacement transmissibility $TR_{{\text{d}}}$, respectively. The solid line represents the linear conventional isolator case with $\lambda = 0$. It shows that with the use of the D-inerter, the peak of each curve of $TR_{{\text{d}}}$ bends towards to low frequencies. There is also an anti-resonant peak in each curve of $TR_{{\text{d}}}$ for the nonlinear isolator cases. As the value of $D_{0}$ or $\lambda$ increases, both the peak and the anti-peak of $TR_{{\text{d}}}$ curve move further to the low-frequency range. Figure 9a shows that nonlinear isolators with D-inerter have lower peak frequencies of $TR_{{\text{d}}}$, compared with that of the linear case. As the inertance-to-mass ratio $\lambda$ increases from 5 to 10 and then to 20, the starting frequency of the effective isolation frequency band reduces from approximately 0.68 to 0.51 and then to 0.37, in accordance with Eq. (53). The corresponding asymptotic values $TR_{{{\text{d}},\infty }}$ based on Eq. (54) are approximately $6.3 \times 10^{ - 3}$, $7.7 \times 10^{ - 3}$ and $8.7 \times 10^{ - 3}$, respectively. At high excitation frequencies, a larger value of $\lambda$ of the D-inerter leads to a higher level of displacement transmissibility. In the effective isolation frequency band where $TR_{{\text{d}}} < 1$, the displacement transmissibility firstly decreases to a local minimum at the anti-peak frequency and then increases to approach the asymptotic value in the high-frequency range. In the low-frequency range, each curve of $TR_{{\text{d}}}$ tends to merge. Figure 9b shows that when the initial distance $D_{0}$ increases from 0.5 to 0.6 and then to 0.7, the starting frequency $\Omega_{{{\text{iso}}}}$ of the effective isolation frequency band decreases from approximately 0.51 to 0.40 and then to 0.31. Figure 9b also shows that when the excitation frequency $\Omega$ increases, there exist asymptotic values of $TR_{{\text{d}}}$ being approximately $7.7 \times 10^{ - 3}$, $8.5 \times 10^{ - 3}$, and $9.1 \times 10^{ - 3}$ when $D_{0}$ = 0.5, 0.6, and 0.7, respectively. It shows that the asymptotic value of $TR_{{\text{d}}}$ increases with the initial distance $D_{0}$. At a prescribed frequency in the high-frequency range, a smaller value of $D_{0}$ results in a lower value of the displacement transmissibility. Figure 9 shows that larger values of $D_{0}$ or $\lambda$ of the D-inerter in the nonlinear isolator can benefit the vibration isolation performance by creating a wider frequency band of effective isolation.

Figure 10a and b shows the influence of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ on the time-averaged input power $\overline{P}_{{{\text{in}}}}$, respectively. The figure shows that there is only one left-bending resonant peak in each curve of $\overline{P}_{{{\text{in}}}}$. As the initial distance $D_{0}$ between the terminals or inertance of the nonlinear isolator $\lambda$ increases, the resonant peak of $\overline{P}_{{{\text{in}}}}$ shifts to the low-frequency range and the peak value decreases. At a prescribed excitation frequency in the high-frequency range, the time-averaged input power decreases as $D_{0}$ or $\lambda$ increases. In contrast, the values of displacement amplitude and displacement transmissibility $TR_{{\text{d}}}$ increase with parameters $D_{0}$ and $\lambda$ when $\Omega$ is high, as shown in Fig. 9. The figure demonstrates that the design parameters affect $TR_{{\text{d}}}$ and $\overline{P}_{{{\text{in}}}}$ differently. Compared to the variations of $TR_{{\text{d}}}$ with respect to the excitation frequency, there is no asymptotic line or anti-peak found in each power flow curve. In the high-frequency range, the time-averaged input power $\overline{P}_{{{\text{in}}}}$ increases with the excitation frequency. In comparison, for the force excitation case shown in Fig. 8, $\overline{P}_{{{\text{in}}}}$ decreases with the increase of $\Omega$ at high frequencies. It shows that force excitation and base-motion excitation affect the time-averaged input power in different ways. In the low-frequency range, the time-averaged input power increases with the excitation frequency. As $\Omega$ approaches low frequencies towards 0.1, the curves for different cases tend to merge and the effects of the changes in $D_{0}$ and $\lambda$ on $\overline{P}_{{{\text{in}}}}$ become insignificant. Larger values of $D_{0}$ and $\lambda$ can enhance vibration isolation by resulting in a smaller amount of input power at high excitation frequencies.

Figure 11a and b examines the influence of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ between the D-inerter terminals on the maximum kinetic energy $K_{{{\text{max}}}}$ of the mass, respectively. One left-bending peak and one anti-resonant peak are presented in each curve of $K_{{{\text{max}}}}$ for the nonlinear isolator with the D-inerter. When the inertance-to-mass ratio $\lambda$ or the initial distance $D_{0}$ increases, both the peak and the anti-resonant peak move to lower frequencies. When the excitation frequency is in the high- or low-frequency ranges away from the resonances, the value of $K_{{{\text{max}}}}$ increases with the excitation frequency following approximately straight lines. As the excitation frequency $\Omega$ reduces in the low-frequency range, the design parameters $D_{0}$ and $\lambda$ of the D-inerter have little effect on $K_{{{\text{max}}}}$ as the curves for different cases tend to merge. At a prescribed excitation frequency in the high-frequency range, smaller values of $D_{0}$ or $\lambda$ can lead to a lower level of the kinetic energy. This behaviour is of direct contrast to the effect of $D_{0}$ or $\lambda$ on $\overline{P}_{{{\text{in}}}}$. Figures 10 and 11 show that for the nonlinear isolator subjected to base-motion excitation, the parameters $D_{0}$ and $\lambda$ of the embedded D-inerter affect the time-averaged power flow and kinetic energy in a different way.

4.4 Performance evaluations of the isolator in 2DOF system with a flexible base

Here the response amplitude, force transmissibility, power flow and energy transmission characteristics of the 2DOF system with a flexible base are investigated to assess the performance of the isolator. The fifth-order HB-AFT and numerical Runge–Kutta methods are used to obtain the dynamic response. System parameters are set as $F_{0} = 0.005, \gamma = \eta = \mu = 1, \zeta_{1} = \zeta_{2} = 0.01$.

Figure 12a and b shows the effects of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ between the terminals of the D-inerter on the maximum displacement $\left| {X_{3} } \right|$ of the machine mass $m_{1}$. The solid line in Fig. 12a represents the case of a conventional linear isolator without the D-inerter. In this curve of linear isolator case, there are two resonant peaks and one anti-resonant peak. With the addition of the D-inerter, the first peak of $\left| {X_{3} } \right|$ twists to the low-frequency range. In contrast, the second resonant peak remains nearly unbent. As the inertance-to-mass ratio $\lambda$ increases, the peaks and also the anti-resonant shift to lower frequencies. It is also noted that a larger value of the inertance-to-mass ratio (e.g. $\lambda = 20$) can bend the frequency–response curve further to the low-frequency range, and a super-harmonic resonant peak is found at ${\Omega } \approx 0.38$. The reason is that a large inertance value of the D-inerter will generate large nonlinear force, resulting in stronger nonlinearity. Figure 12b shows that as the initial distance $D_{0}$ increases, the values of $\left| {X_{3} } \right|$ at the first peak and at the anti-resonant peak decrease. However, the second resonant peak increases with $D_{0}$ and $\lambda$. In the high-frequency range, the curves of different cases almost coincide, and it demonstrates that the values of $D_{0}$ and $\lambda$ only have weak influence on the response amplitude at high excitation frequencies. It is also noted that comparing with a linear conventional isolator case with $\lambda = 0$, the use of a nonlinear isolator incorporating the D-inerter can lead to a smaller peak response amplitude of the mass, suggesting the suppression effect of the nonlinear isolator on the response. As the excitation frequency reduces in the low-frequency range, the curves tend to merge and the initial distance $D_{0}$ and inertance $\lambda$ have weaker effect on the displacement amplitude of mass $m_{1}$.

Fig. 12

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b initial distance $D_{0}$ (with $\lambda = 8$) in the 2-DOF isolation system on the response amplitude

In Fig. 13, the performance of the nonlinear isolator is examined in terms of the force transmissibility $TR$. Figure 13 shows that there are two peaks and two anti-peaks in each curve of force transmissibility TR. The first resonant peak twists to the left because the nonlinear inertial force by the D-inerter increases with the response amplitude, leading to a stronger transmitted force to the base. As the inertance $\lambda$ increases from 5 to 20 or the initial distance $D_{0}$ increases from 0.4 to 0.6, the two peaks and the first anti-peak move to lower frequencies. This behaviour is beneficial for vibration isolation. The figure shows that regardless of the variations of $D_{0}$ and $\lambda$, the frequency corresponding to the second anti-peak remains to be approximately one. When the excitation frequency is larger than one, the force transmissibility associated with each D-inerter isolator case increases with the excitation frequency $\Omega$ and approaches an asymptotic value in the high-frequency range. This asymptotic value increases with the initial distance $D_{0}$ and the inertance-to-mass $\lambda$, but remains smaller than 1. Based on Eq. (44), the value of $\left| {F_{0} {\text{e}}^{{{\text{i}}\Omega \tau }} - X_{3}^{\prime \prime } } \right|$ is close to a constant when the excitation frequency tends to infinity. Similar phenomenon is also observed in Fig. 7 for the SDOF system, for which the value of $TR$ is predicted analytically by Eq. (50). In the low-frequency range, curves for different cases merge. Compared with the conventional linear isolator case (i.e. $\lambda = 0$), the nonlinear isolator has an extra anti-peak between the two resonant peaks and can lead to a lower level of force transmissibility in the regions. It can also provide a large frequency band in which the force transmissibility is smaller than unity, which is desirable for vibration isolation.

Fig. 13

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b initial distance $D_{0}$ (with $\lambda = 8$) in the 2DOF isolation system on the force transmissibility TR

Figure 14 shows the effects of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ on the time-averaged input power $\overline{P}_{{{\text{in}}}}$ and the maximum kinetic energy $K_{{{\text{max}}}}$ of mass $m_{1}$. Figure 14a and b shows two peaks exist in each curve of $\overline{P}_{{{\text{in}}}}$, but no anti-peak is observed. The first resonant peak of $\overline{P}_{{{\text{in}}}}$ curve bends to lower frequencies due to the nonlinear effect introduced by the nonlinear D-inerter in the vibration isolator. It also shows that as the inertance-to-mass ratio $\lambda$ or initial distance $D_{0}$ increases, the two peaks move to lower frequencies. When the excitation frequency is in the low- or high-frequency ranges, the influence of the changes in $D_{0}$ and $\lambda$ on the power input becomes negligible since different curves almost coincide. As the excitation frequency increases, the time-averaged input power $\overline{P}_{{{\text{in}}}}$ increases at low frequencies and decreases at high frequencies. Compared with the linear isolator case with $\lambda = 0$, the use of the nonlinear isolator can yield a significant reduction of the total input power into the system at a prescribed frequency in the high-frequency range, which benefits vibration isolation. Figure 14c and d shows that one anti-peak appears between the two peaks in each curve of $K_{{{\text{max}}}}$. The peaks and the anti-peak move to lower frequencies as the inertance-to-mass ratio $\lambda$ or the initial distance $D_{0}$ increases. It shows that the inertance-to-mass ratio $\lambda$ and initial distance $D_{0}$ have large effects on the dynamic performance and power transmission where the excitation frequency locates between the two peak frequencies. Figure 14c shows that at a prescribed excitation frequency in the high-frequency range, the values of $K_{{{\text{max}}}}$ of the D-inerter isolator cases are much smaller than that of the linear isolator case. This behaviour demonstrates the benefits of introducing the D-inerter in vibration isolation. Figure 14 demonstrates that with an appropriate design of the parameters of the D-inerter in the nonlinear isolator, a tailored isolation performance can be achieved with low energy input or low level of kinetic energy of the mass.

Fig. 14

Effects of the inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and the initial distance $D_{0}$ (with $\lambda = 8$) in the 2-DOF isolation system on the time-averaged input power $\overline{P}_{{{\text{in}}}}$ in a and b; and the maximum kinetic energy $K_{{{\text{max}}}}$ of mass $m_{1}$ in c and d

The effects of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ on the time-averaged transmitted power $\overline{P}_{{\text{t}}}$ are investigated and shown in Fig. 15a and b, respectively. Figure 15a shows that with the addition of the D-inerter, one anti-peak can be created in the curve of the time-averaged transmitted power, leading to significantly reduction in vibration energy transmission to the base structure. At a prescribed frequency in the high-frequency range, compared with that of the linear isolator case, the use of the D-inerter isolator can lead to larger amount of energy transmission to the base structure. As the inertance-to-mass ratio $\lambda$ increases from 5 to 10 and then to 20, two peaks and the anti-peak in each curve of $\overline{P}_{{\text{t}}}$ shift to lower frequencies. Figure 15b shows that as the initial distance $D_{0}$ increases from 0.4 to 0.5 and then to 0.6, the frequencies associated with the peaks and the anti-peak reduce. In the high-frequency range, a smaller value of the initial distance $D_{0}$ causes a lower level of the transmitted power to the base structure. When the excitation frequency locates in the low-frequency range, the curves for different cases tend to merge and the initial distance $D_{0}$ and the inertance-to-mass ratio $\lambda$ have negligible influence on the time-averaged transmitted power $\overline{P}_{{\text{t}}}$.

Fig. 15

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and the initial distance $D_{0}$ (with $\lambda = 8$) on the time-averaged transmitted power $\overline{P}_{{\text{t}}}$

Figure 16a and b shows the effects of the inertance-to-mass ratio $\lambda$ and the initial distance $D_{0}$ on the power transmission ratio $R_{{\text{T}}}$, respectively. The power transmission ratio $R_{{\text{T}}}$ is the ratio between the time-averaged transmitted power and the time-averaged input power, representing the proportion of total energy transferred to the base structure through the D-inerter. Therefore, it provides a relative measure of vibration transmission. The solid line in Fig. 16a is associated with the linear isolator case with $\lambda = 0$; it has the maximum $R_{{\text{T}}}$ value at approximately $\Omega = 1$ and has nearly zero values in the high-frequency range. With the inclusion of the D-inerter, the power transmission ratio $R_{{\text{T}}}$ is reduced in the low-frequency range, and its value decreases as the increase of $\lambda$ or $D_{0}$. Figure 16 also presents the super-harmonic behaviour with the frequency component $\Omega_{{\text{r}}} = 2\Omega$ due to the use of the nonlinear inerter. As the inertance-to-mass ratio $\lambda$ increases from 5 to 10 and then to 20, the corresponding super-harmonics are found at excitation frequencies equal to 0.44, 0.39 and 0.38, respectively. When the initial distance $D_{0}$ changes from 0.4 to 0.5 and then to 0.6, the super-harmonic responses appear at approximately 0.45, 0.40 and 0.38, respectively. The super-harmonic resonant peak becomes higher when there is a stronger nonlinearity, and correspondingly large power transmission is found. This is one potential shortcomings of the system, apart from the aforementioned constraint on the displacement response. There is also an anti-resonance in each curve of $R_{{\text{T}}}$, where the transmitted power from mass one through the nonlinear D-inerter is almost equal to zero compared with the total input power. The power transmission ratio curves merge at the unity excitation frequency with peak value of one. When the excitation frequency is larger than 1, the power transmission ratio decreases with the increase of the excitation frequency. At a prescribed value of $\Omega$ in the high-frequency range, the increase in the value of $\lambda$ or $D_{0}$ leads to larger values of the power transmission ratio $R_{{\text{T}}}$. At a particular excitation frequency, the value of $R_{{\text{T}}}$ becomes approximately zero, indicating that only a negligible proportion of the input energy is transmitted to the base. This characteristic is desirable in terms of vibration isolation. As the value of $\lambda$ or $D_{0}$ increases, this frequency associated with quasi-zero value of $R_{{\text{T}}}$ reduces.

Fig. 16

Effects of the a inertance-to-mass ratio $\lambda$ (with $D_{0} = 0.5$) and b initial distance $D_{0}$ (with $\lambda = 8$) on the power transmission ratio $R_{{\text{T}}}$

5 Conclusions

This study proposed nonlinear vibration isolators with a nonlinear inerter created by embedding a linear inerter in a diamond-shaped linkage. The performance of the proposed isolators in an SDOF system subjected to force and base-motion excitations and in a two-DOF system with a flexible foundation was considered. The analytical HB approximation and high-order HB-AFT as well as the numerical RK method are used to obtain the steady-state response. Force and displacement transmissibility as well as time-averaged power flow variables were used as performance indices. It was shown that both the single-DOF and 2-DOF isolators with the D-inerter have a wider range of effective isolation frequency compared with the linear conventional isolators and therefore are beneficial for the attenuation of force and power transmission.

For the SDOF nonlinear inerter-based vibration isolator under force excitation or base-motion excitation, the benefits of using the D-inerter in the vibration isolator are demonstrated by (1) bending of the response curve to the low frequencies and significant reduction in the response over a wide frequency range alone with the introduced anti-resonance; (2) a larger band of effective isolation as the transmissibility peak shifts to lower frequencies; (3) much reduced amount of time-averaged input power and lower kinetic energy of the mass in a large frequency band.

For the D-inerter isolator mounted on a flexible base, the results obtained in this investigation indicate that (1) by adding the nonlinear inerter, one anti-resonant peak may appear between the two peaks, leading to a significantly lower level of the dynamic response, force transmissibility or power transmission; (2) the D-inerter will cause near-zero power transmission ratio at a particular excitation to the base structure, demonstrating superior vibration isolation performance using the proposed isolator design.

Appendix

Using Eqs. (28), (29) and (43), governing Eq. (14) of the single-DOF oscillator with base-motion excitation (C2 configuration) becomes

$$ \begin{gathered} \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}R_{2} \cos \left( {\Omega \tau - \theta } \right) \hfill \\ \quad - 2\zeta_{1} \Omega R_{2} \sin \left( {\Omega \tau - \theta } \right) = Q_{0} \Omega^{2} \cos \Omega \tau . \hfill \\ \end{gathered} $$

(61)

The coefficients of the corresponding harmonic terms in Eq. (61) can be balanced, leading to

$$ \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}R_{2} = Q_{0} \Omega^{2} \cos \theta , $$

(62)

$$ - 2\zeta_{1} \Omega R_{2} = - Q_{0} \Omega^{2} \sin \theta . $$

(63)

By using the identity of $\cos^{2} \phi + \sin^{2} \phi = 1$, Eqs. (62) and (63) can be transformed into

$$ \left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}^{2} R_{2}^{2} + \left( {2\zeta_{1} \Omega R_{2} } \right)^{2} = Q_{0}^{2} \Omega^{4} , $$

(64)

$$ \frac{{R_{2} }}{{Q_{0} }} = \frac{{\Omega^{2} }}{{\sqrt {\left\{ {1 - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)\Omega^{2} } \right\}^{2} + \left( {2\zeta_{1} \Omega } \right)^{2} } }}. $$

(65)

Note that Eq. (65) is obtained by rewriting Eq. (64), which can be solved by using a bisection method to obtain the amplitude $R_{2}$ of the relative displacement. The phase angle $\theta$ can then be determined by using Eqs. (62) and (63). When the excitation frequency $\Omega$ approaching infinity, Eq. (65) becomes

$$ \mathop {\lim }\limits_{\Omega \to \infty } \left( {\frac{{R_{2} }}{{Q_{0} }}} \right) = \frac{1}{{1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)}} , $$

(66)

in which, by denoting the corresponding value of $R_{2}$ as $R_{2,\infty }$, we have

$$ \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2,\infty }^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)R_{2,\infty } = Q_{0} , $$

(67)

which is a nonlinear algebraic equation which can be solved by a standard bisection method. It shows that the relative displacement amplitude $R_{2,\infty }$ is only related to the design parameters of $\lambda , D_{0}$ and $Q_{0}$ of the isolator.

It is noted that the nondimensional displacement response $X_{2} \left( \tau \right)$ of the mass in C2 is expressed by

$$ X_{2} \left( \tau \right) = Z_{2} \left( \tau \right) + Q_{0} \cos \Omega \tau \approx R_{2} \cos \left( {\Omega \tau - \theta } \right) + Q_{0} \cos \Omega \tau . $$

(68)

Therefore, the displacement amplitude $M_{2}$ of the mass in C2 can be obtained as

$$ \begin{gathered} M_{2} = \sqrt {\left( {R_{2} \cos \theta + Q_{0} } \right)^{2} + R_{2}^{2} \sin^{2} \theta } \hfill \\ \quad = \sqrt {R_{2}^{2} + Q_{0}^{2} + 2R_{2}^{2} \left\{ {\frac{1}{{\Omega^{2} }} - \left( {1 + \lambda \beta_{0} + \frac{1}{4}\lambda R_{2}^{2} \left( {3\beta_{2} - \gamma_{1} } \right)} \right)} \right\}} , \hfill \\ \end{gathered} $$

(69)

where Eq. (62) is used for the simplification.